Abstract
This study presents a mathematical investigation into the phenomena of radiative heat with an unsteady MHD electrically conducting boundary layer of chemically reactive Casson nanofluid flow due to a pored stretchable sheet immersed in a porous medium in the presence of heat generation, thermophoretic force, and Brownian motion. The surface is assumed to be not flat, and has variable thickness. The magnetic field is time-dependent, and the chemical reaction coefficient is inversely varied with the distance. The nanofluid’s velocity, heat, and concentration at the surface are nonlinearly varied. A similarity transformation is introduced, and the controlling equations are converted into nondimensional forms involving many significant physical factors. The transformed forms are analyzed numerically using a computational method based on the finite difference scheme and Newton’s linearization procedure. The impact of the involved physical parameters is performed in graphical and tabular forms. Some special cases of the current work are compared with published studies, and an excellent agreement is obtained. The main results of the present work indicate that the higher values of the Casson parameter cause an increase in both the shear stress and heat flux, but a decrease in the mass flux. Also, it is noted that the chemical reaction, the nanoparticles’ volume, and the permeability factor enhance the effect the of Casson parameter on both the shear stress and heat flux, while the variable thickness and thermal radiation field reduce it; on the other hand, the variable thickness and nanoparticles’ volume enforce the influence of the Casson parameter on mass flux, but thermal radiation, the permeability factor, and chemical reaction decrease it. The present study has important applications in mechanical engineering and natural sciences. In addition, it has significant applications in devices used for blood transfusion, dialysis and cancer therapy.
1. Introduction
Convective heat through nanofluid flow enhances the surface characteristics of materials by improving the mechanical strength, thermal conductivity, and electromagnetic efficiency, and is a noticed phenomenon. Its importance has been reported in various industrial applications and new biotechnologies. Therefore, many authors are interested in analyzing the characteristics of heat convection in nanofluid flow problems [1,2]. Elbashbeshy [3] investigated the features of unsteady convective heat in the nanofluid flow over a stretchable sheet. Ishak [4] analyzed the influence of a magnetic field on an unsteady convective heat in the fluid flowing over a stretchable sheet with variable velocity and temperature. Ibrahim [5] investigated the characteristics of MHD convective heat in an unsteady fluid flow over a stretchable surface considering the heat generation effect. Makinde et al. [6] studied the thermal radiative and magnetic field effects on convective heat in variable viscosity fluid flowing over a nonlinear heated surface and taking into consideration the thermophoretic force. Sheikholeslami [7] reported the feature of thermal radiation in an unsteady natural convective through nanofluid flow considering the magnetic field. Elbashbeshy et al. [8] studied the impact of thermal radiation on convective heat in viscous fluid flow around a thermal sphere immersed in a porous medium considering Newtonian heat. Eldabe et al. [9] considered the chemically reactive flow of non-Newtonian nanofluid with convective heat over a stretchable sheet in the existing magnetic field. Trivedi et al. [10] studied the magneto-mixed convective heat in nanofluid flow with heat generation. Mahabaleshwar et al. [11] investigated the magnetohydrodynamic-induced fluid flow and mass transfer over a nonlinearly extendable sheet. Khan et al. [12] examined the influence of Dufour and Soret on an electrically conducting non-Newtonian fluid in the existence of a variable magnetic field. Maleki et al. [13] analyzed the properties of convective heat in nanofluid flow over a permeable sheet considering radiative heat and slip boundary conditions. Prodanjani et al. [14] investigated the impacts of thermal radiative heat on magnetoconvective heat transfer in nanofluid flow in a cavity. Chaudhary et al. [15] performed an investigation on heat generation and radiative heat effects on the MHD nanofluid flow of a stagnation point for a heated extendable sheet. Reddy et al. [16] investigated the behavior of heat convective in a reactive flow of nanofluid over an inclined plate immersed in a porous media. Eldabe et al. [17] examined the impact of the magnetic field on a peristaltic flow of non-Newtonian nanofluid embedded in an inclined channel that was immersed in a non-Darcy porous medium. Sedki et al. [18] presented a study on thermal radiative and heat generation effects on an unsteady mixed convective heat in nanofluid flow due to a stretchable surface embedded in porous. The thermophoretic forces, Brownian motion, and surface flow flux are considered. Sedki [19] reported the impacts of thermal radiation on a magneto-mixed convective heat in a reactive flow of steady nanofluid due to a nonlinearly stretchable surface in a porous medium considering a chemical reaction.
Non-Newtonian fluid has various applications in industrial engineering and modern technology. Casson fluid is a characteristic of non-Newtonian fluid and it is sometimes called viscoelastic fluid. Human blood, honey, tomato sauce, and jelly are examples of the Casson fluid. Due to its significant applications, several researchers are focused on the analysis of the Casson fluid behavior. The behavior of Casson fluid flow in an unsteady boundary layer over a stretching surface was investigated by Mukhopadhyay [20]. The shooting numerical scheme is used in solving the involved equations. Makanda et al. [21] performed an investigation on chemical reactive species through unsteady Casson fluid due to stretching surface in a porous medium in the existence of magnetic field effects. The study was analyzed by the Runge–Kutta–Felhberg numerical method. Raju et al. [22] reported the behavior of convective heat in MHD Casson fluid flowing in a porous exponentially stretchable surface considering thermal radiation and chemical reactive flow. Oyelakin et al. [23] reported the characteristics of unsteady Casson fluid flow over a stretchable surface in the existence of radiative heat and heat source/sink. The effect of thermophoresis and Brownian motion are discussed. Krishnamurthy et al. [24] presented a theoretical investigation to discuss the thermal radiation effect on the MHD nanofluid flow through a nonlinearly stretchable sheet. Numerical investigation of thermal radiation on magneto Casson fluid flow, due to an unsteady stretchable sheet immersed in a porous medium considering the heat generation impacts, was introduced by Ullah et al. [25]. Prasad et al. [26] considered the steady Casson nanofluid flow over a stretchable plane with variable thickness considering the magnetic field effect. Tamoor et al. [27] analyzed the magnetic field effect on Casson fluid flowing over a linear stretched cylinder. Naqvi et al. [28] investigated the properties of Casson fluid flow containing nanoparticles over a moving cylinder with thermal radiation and a magnetic field. Shit and Mandal [29] analyzed the behavior of unsteady Casson nanofluid flow due to a moving vertical surface considering thermal radiation and magnetic field. Krishna et al. [30] reported the characteristic of radiative heat in the MHD Casson hybrid nanofluid due to an accelerated vertical permeable surface. Bejawada et al. [31] numerically studied the influence of thermal radiation on a magneto Casson fluid over an inclined surface through a porous medium. Sedki [32] considered the thermal radiative heat and chemically reactive flow of MHD cross nanofluid containing gyrotactic microorganisms due to a permeable horizontal cylinder through a porous medium. Khan et al. [33] examined a magneto-Williamson hybrid nanofluid flow through a thin vertical needle. Joule heating and viscous dissipation were discussed. Further, the impact of thermal radiation and homogeneous reaction were also taken into consideration.
In this study, according to the above literature review, we are interested in analyzing the impact of thermal radiation on the chemically reactive flow of an unsteady electrically conducting MHD Casson nanofluid over a permeable stretchable surface with variable thickness immersed in a porous medium. Furthermore, the heat generation, thermophoretic force, and Brownian motion effects are also taken into account. The surface is assumed to be not flat, and its thickness is time-dependent. The convective boundary conditions of the nanofluid at the porous surface are nonlinearly varying with time and distance.
2. Analysis and Formulation of the Problem
We consider the unsteady MHD-mixed convective through a two-dimensional chemical reactive as an incompressible, viscous Casson nanofluid immersed in a porous medium along a permeable surface. The surface stretches nonlinearly with velocity Uw(x,t), . The coordinates are chosen in which the axis is taken along the sheet. However, the axis is normal to it. The fluid is electrically conducting due to the existing variable magnetic field, which is perpendicular to the sheet, [Tesla], where B0 is a constant. In the absence of an electric field, the electromagnetic Lorentz force is determined as , , where is the electric current, and denotes the vector of the velocity. The magnetic Reynolds number is assumed to be low, so the induced magnetic field is negligible.
The surface is assumed to be not flat and has variable thickness, which is defined as , ; δ is small and so the surface is sufficiently thin. The selected geometry has very strong applications in industrial engineering, such as in the extrusion of a polymer, the process of liquid film condensation, coating emulsion on photographic films, melt-spinning, and hot rolling. Also, it is used in mechanical marine and aerospace industries. The physical flow and the system’s coordinates are drawn in Figure 1.
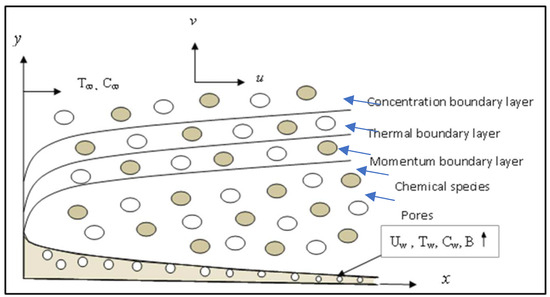
Figure 1.
Schematic of the problem.
The rheological state equation for the Casson fluid flow is given as [20,21]
where .
In the existence of thermal radiation, thermophoretic force, Brownian motion, heat generation, and variable magnetic field, the governing equations of this model are given by [20,21,22,23,24,25].
where .
Here, T and C are the nanofluid’s temperature and concentration. u and v represent the x-component and y-component of the nanofluid’s velocity, the time is assigned by t, and the gravity field is by g [m s−2]. Also, R, qr, and Q are the chemical reaction coefficient, the radiative heat flux, and the heat source, respectively. The coefficient of permeability of a porous medium is denoted by , , where k0 is the initial permeability. are the dynamic viscosity, the density, the effective thermal conductivity, and the electrical conductivity, respectively. The indices f, s, and nf are pointed to the base liquid, the nanoparticles, and the nanofluid, respectively. The specific heat at a fixed pressure is assigned by Cp, the coefficient of thermal expansion by βT, the Brownian motion diffusion by Db, and the thermophoretic diffusion by. The nanoparticles are considered to be spherical and their volume fraction is represented by , the parameter of the Casson fluid by β, and is the ratio of the effective heat capacity of the nanoparticle to that of the fluid. The copper nanoparticles and the base liquid (water) properties are considered as in Sedki [18]. The characteristics of the nanofluid, base liquid, and solid nanoparticles are determined by
Here, are the nanofluid ambient density, temperature, and pressure, respectively. The appropriate boundary conditions are
where
Here, Vw is the velocity of the suction (injection) (Vw > 0 for the suction and Vw < 0 for the injection), the fluid kinematic viscosity is denoted by νf and the ambient temperature by T∞·a and are constants with dimension time−1, where . E1 and E2 are constants with dimension temperature·length−1. The positive values of E1 and E2 are considered for assisting flows, but negative values are for opposing flows where natural convection is considered when E1 = 0 and E2 = 0. The fluid is postulated to be grey and the radiation approximation presented by Rosseland has been applied, and then the radiative heat flux is determined by
Here, is the Stefan–Boltzman constant and k1 denotes the coefficient of mean absorption. Taylor series is applied to expand about , and when the higher order terms are neglected, we obtain . By substituting into Equation (7), we obtain
For a similarity solution, we put
Here, η represents the variable of similarity, ψ denotes the stream function, Θ is the nanofluid dimensionless temperature, and Φ denotes the nanofluid dimensionless concentration. By substitution in the governing Equations (2)–(5), we have
and boundary conditions become
The ratio Gr/Re2 is important in the heat convective and mass transfer correlation. Forced convection is taken into consideration when Gr/Re2 >> 1, while natural convection is considered for Gr/Re2 << 1. The mixed convection is taken into account when Gr/Re2 is of order one (for more details see, Sedki [18]).
The surface is considered not flat, and its thickness varies nonlinearly with the time t. We put
Consider
Now Equations (13)–(15) and the appropriate conditions (16) become
where is the unsteadiness factor, M is the magnetic factor and Pr denotes the Prandtl number. assigns Eckert number, and is the surface flow flux parameter (it represents a suction when and injection when ), The thermal diffusion is assigned by , the mass diffusion by , K denotes porosity parameter, is the thermophoretic parameter, and Nb is the Brownian motion parameter, is the Prandtl number, denotes the Schmidt number, assigns the heat generation factor (it represents heat source when and heat sink when), and Rc assigns the parameter of the chemical reaction. These are given by
The important quantities of interest for this problem are the skin friction Cf [N·m−2] and Nusselt number Nu, and the Sherwood number . They indicate, physically, the surface shear stress τw, surface heat flux qw, and mass flux qc, respectively, and are given by
where τw, qw, and qc are given by
Now we get
3. Numerical Results
The basic equations controlling the study (2)–(7) are converted into similarity forms (18)–(21) that involve many significant physical parameters. The study is computationally analyzed by developing a Matlab algorithm composed of the finite difference scheme with Newton’s linearization procedure. For validation of the computational results, a comparison is presented in Table 1 for special cases of current work with the published results introduced by Elbashbeshy [3], Ishak [4], and Ibrahim [5], and good agreement is obtained. The fixed values of the physical parameters in the current analysis are considered as Pr = 10, β = 0.5, ϕ = 0.05, At = 0.1, Nt = 0.5, fw = 1, Sc = 10.0, Rd = 0.5, λ = 0.2, α = 0.5, Rc = 0.2, K = 0.2, Ec = 0.5, Nb = 0.5, γ = 0.1, m = 1, n = 1.

Table 1.
A comparison of the present results of –θ\(0) for Pr values with M = 0, n = 1, m = 1, ϕ = 0, and λ = 0.0 with that reported by Elbasbeshy [3], Ishak [4], and Ibrahim [5].
The numerical results showing the impacts of the physical factors involved in the nondimensional equations for the nanofluid’s velocity, temperature, and mass concentration profiles are performed in graphical forms (2)–(12), while the impacts of the involved parameters on shear stress, heat flux, and mass flux are presented in tabular forms (2)–(5). The impact of the Casson parameter is performed in Figure 2a–c. It is shown that the increase in the Casson parameter causes acceleration in the concentration, but the inverse results in velocity and temperature occurring near the wall. Physically it is due to the increasing values of the Casson parameter enhancing the viscous forces, which delays the flow and therefore reduces the nanofluid velocity. The effect of surface thickness γ is performed in Figure 3a–c. It is noted that the increase in variable thickness factor causes an increase in both the nondimensional velocity f\ and temperature profiles, but the inverse effect happens on temperature near the wall. Also, the increase in the variable thickness parameter causes a decrease in the concentration C. The impacts of thermal radiation are shown graphically in Figure 4a–c. It is noted that the higher values in thermal radiation cause an increase in both the nondimensional velocity f\ and temperature. Also, it is noted from Figure 4c that the accelerated values of thermal radiation cause an increase in the concentration, but the opposite effect occurs far from the wall. The impact of the permeability parameter fw is presented graphically in Figure 5a–c. It is noted that the increase in the permeability of the surface fw causes a decrease in both the nondimensional velocity and temperature. Also, the rising fw results in a decrease in the concentration, but the effect is changed far from the wall.
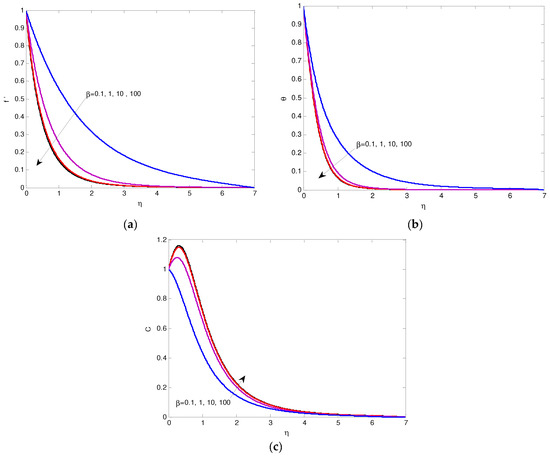
Figure 2.
(a) The velocity f’ for β values. (b) The temperature θ for β values. (c) The mass concentration C for β values.
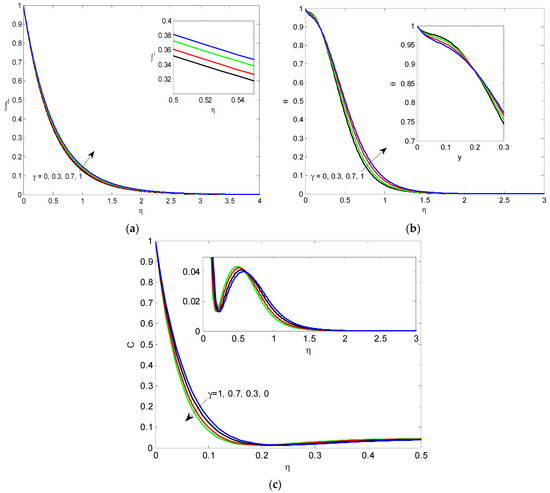
Figure 3.
(a) The velocity f’ for γ values. (b) The temperature θ for γ values. (c) The mass transfer C for γ values.
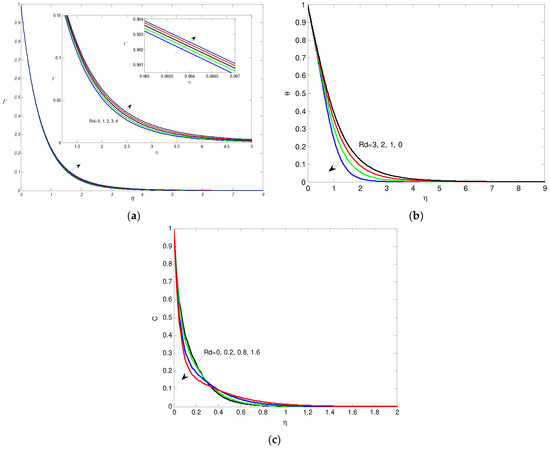
Figure 4.
(a) The velocity f’ for Rd values. (b) The temperature θ for Rd values. (c) The mass transfer C for Rd values.
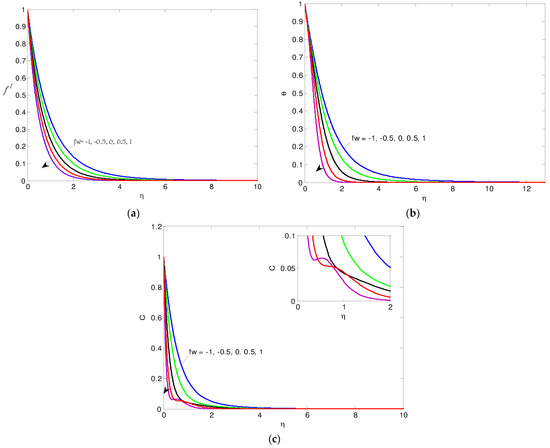
Figure 5.
(a) The velocity for fw values. (b) The temperature θ for fw values. (c) The mass transfer C for fw values.
The influence of the Schmidt parameter is given graphically in Figure 6a–c. It is found that the increase in the Schmidt parameter causes a deceleration in both the nondimensional velocity f\ and mass transfer. Also, the rising Sc values cause a decrease in the temperature, but the opposite effect happens rapidly far from the wall. The impact of the porous medium parameter is introduced in Figure 7a–c. It is shown that the increase in porous medium factor K results in raising the temperature and concentration of the nanofluid; on another hand, opposite effects are given with the nondimensional velocity f\ and the concentration far from the wall. The effect of the Eckert number is presented in Figure 8a–c. It is noticed that the increment in Eckert number increases both the nondimensional velocity f\ and the temperature. Also, the rising Ec causes a deceleration in the concentration, but the inverse effect is placed quickly far from the wall.
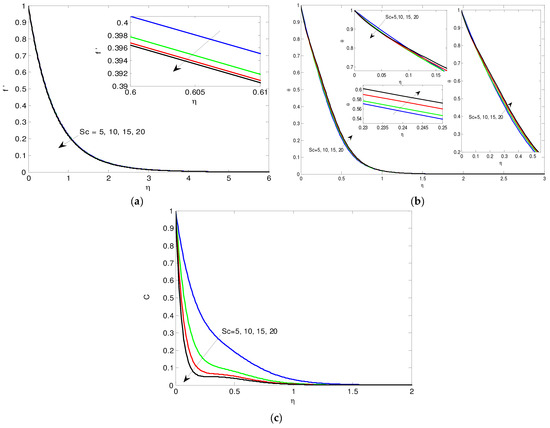
Figure 6.
(a) The velocity via Sc. (b) The temperature θ for Sc values. (c) The mass transfer C for Sc values.
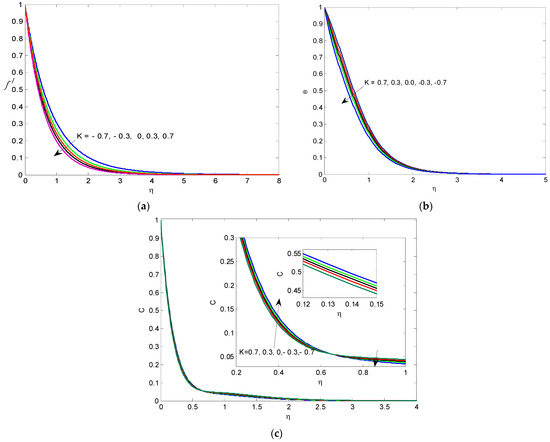
Figure 7.
(a) The velocity via K. (b) The temperature θ for K values. (c) The mass transfer C for K values.
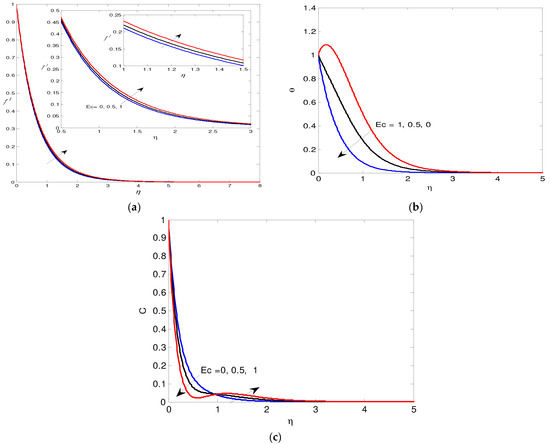
Figure 8.
(a) The velocity via Ec. (b) The temperature for Ec values. (c) The mass transfer C for Ec values.
The impact of the m and n power parameters is presented in Figure 9 and Figure 10. It is shown that the increase in the power m or the power n causes a deceleration in the nondimensional velocity f\, the temperature profiles, and the concentration distributions. The effect of heat generation is presented in Figure 11a–c. It is found that the increase in heat generation λ causes increases in both the nondimensional velocity f\ and the temperature. The growth of the heat generation results in a decrease in the concentration, but the opposite effect is placed far from the wall. The impact of the chemical reaction is shown in Figure 12. It is noted that the increase in the chemical reaction factor leads to deceleration in the mass concentration.
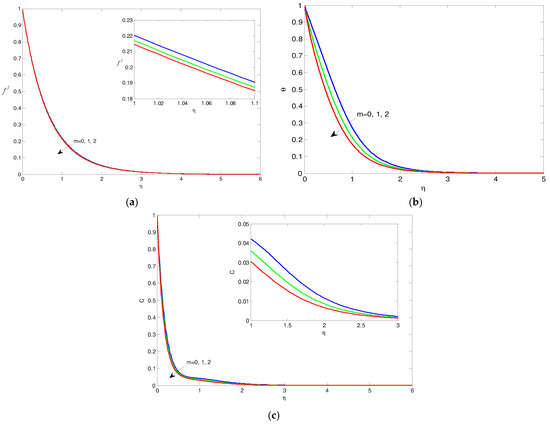
Figure 9.
(a) The velocity via m. (b) The temperature for m values. (c) The mass transfer C for m values.
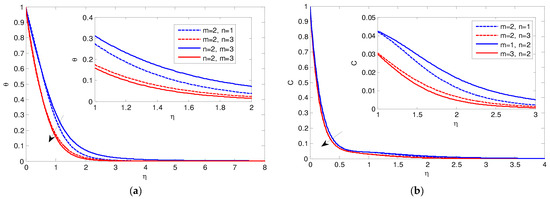
Figure 10.
(a) The temperature θ for m and n values. (b) The mass transfer C for m and n values.
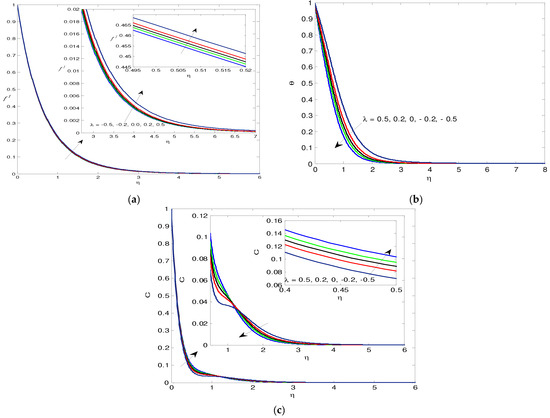
Figure 11.
(a) The velocity via λ values. (b) The temperature for λ values. (c) The mass transfer C for λ values.
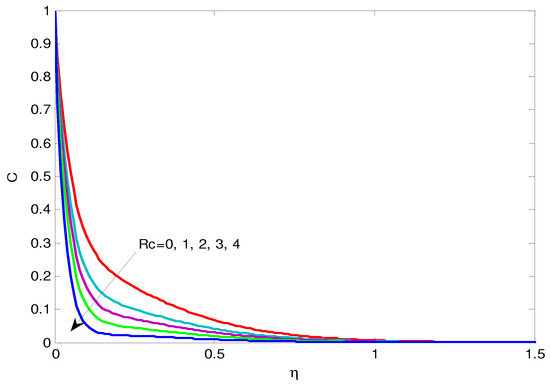
Figure 12.
The mass transfer C for Rc values.
Table 2 illustrates the impacts of the surface’s thickness, Casson parameter, Schmidt number, Magnetic field on shear stress, and the heat flux and mass flux with the values of the involved parameters Pr = 10, β = 0.5, At = 0.1, Nt = 0.5, fw = 1, Sc = 10.0, Rd = 0.5, λ = 0.2, α = 0.5, Rc = 0.2, K = 0.2, Ec = 0.5, Nb = 0.5, γ = 0.1, m = 1, n = 1. It is shown that the growth in the surface’s thickness parameter causes an increase in the Nusselt number, but a decrease in both the shear stress and mass flux is placed. Also, it is noted that the rising values in the Casson parameter cause an increase in values for the skin friction and Nusselt number, but the opposite effect on the Sherwood Number occurred.

Table 2.
The effect of surface variable thickness, Casson parameter, Schmidt number, Magnetic field.
Also, it is noted in Table 2 that the rising Schmidt factor causes an increase in shear stress, heat flux, and mass flux. This is due to the nanofluid with increasing values of Schmidt number has a relatively low diffusion coefficient, which reduces mass diffusion and, as a result, increases the mass transfer rate at the surface. It is found that the increment in the magnetic field parameter causes a decrease in both shear stress and mass flux, but an increase in the heat flux happened. This behavior is acceptable with the physical observation that the application of transverse magnetic field results in Lorentz force, which tends to resist the fluid flow and thus reduces the fluid motion significantly.
The impact of thermal radiative heat, chemically reactive flow, and nanoparticles volume on skin friction, heat flux, and mass flux are presented in Table 3. It is noted that the increment in the parameter of thermal radiation results in an increase in the Sherwood number, but a decrease in values of the skin friction and Nusselt number happened. Also, it is found from Table 4 that the increment in the nanoparticles volume causes growth in the skin friction and Sherwood number, but the inverse effect occurs in the Nusselt number, and it is noted that the acceleration in the chemical reaction results in an increase in the skin friction, heat flux, and mass flux. The influence of the parameters permeability fw is shown in Table 4, it is found that the increment in permeability factor causes an increase in shear stress, heat flux, and mass flux. Also, it is found that the increment in porosity factor K causes an increase in both the shear stress and mass flux, but a decrease in the heat flux is reported. It is noted that the increase in Eckert Ec leads to a fall in values of the shear stress and heat flux, but the increment in mass flux occurred. Also, it is noted from Table 4 that the rise in the power m or the power n causes increasing in shear stress, heat flux, and mass flux.

Table 3.
The effect of thermal radiation Rd, nanoparticles volume, chemical reaction parameters.

Table 4.
The impacts of fw, K, Ec, the powers m, and n parameters.
4. Conclusions
In the current study, the impacts of thermal radiative heat and chemically reactive flow of unsteady MHD electrically conducting Casson nanofluid over the porous stretchable surface with variable thickness immersed in a porous medium is investigated in considering heat generation, thermophoretic forces, and Brownian motion. The controlling equations are converted into nondimensional forms containing many significant physical parameters. The influence of the involved parameters is discussed and it can be summarized as follows:
The shear stress is directly proportional to the Casson parameter β, permeability factor fw, Schmidt number Sc, nanoparticles volume, chemical reaction Rc, the powers m, and n but the opposite effect occurs with, the surface’s thickness variable γ, thermal radiative heat, the magnetic field, and Eckert number.
The heat flux is directly proportional to the Casson parameter β, the magnetic field M, permeability factor fw, Schmidt number Sc, nanoparticles volume, chemical reaction, the powers m, and n, but the opposite results occur with the surface’s thickness variable γ, thermal radiation Rd, porosity factor K, and Eckert number Ec.
The concentration rate increases with the accelerated values of thermal radiation Rd, permeability factor fw, porosity factor K, Schmidt number Sc, chemical reaction, the distance power m, and the time power n, but the inverse effect occurs with Casson parameter β, surface’s thickness variable γ, Eckert number Ec, the magnetic field M, and nanoparticles volume.
The nanofluid velocity accelerates with the growth of the thermal radiation Rd, surface’s thickness variable γ, Eckert number Ec, and the heat generation factor λ, but the opposite results happen with the permeability parameter fw, Schmidt number, porosity factor K, distance power m, and time power n factors.
The nanofluid temperature is directly proportional to the thermal radiation Rd, porosity factor K, Eckert number Ec, and heat generation factor λ, but inversely with Casson parameter β, permeability parameter fw, the distance power m, and the time power n.
The fluid concentration is directly proportional to the surface’s thickness variable γ, and the Casson parameter, but inversely with the permeability fw, Schmidt number, the porosity K, the Eckert number Ec, chemical reaction, the distance power m, and time power n.
Author Contributions
Conceptualization, A.M.S.; Software, A.M.S.; Validation, A.M.S.; Formal analysis, R.Q.; Investigation, A.M.S.; Resources, R.Q.; Writing—original draft, R.Q.; Writing—review & editing, A.M.S. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deanship of Scientific Research, Jazan University for supporting this research work through the Research Units Support Program, Support Number: RUP2-02.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare that there is no conflict of interest.
Nomenclature
| Cf | local skin-friction coefficient (N·m−2) |
| Cp | specific heat at constant pressure (J/kg·K) |
| Gr | Grashof number (-) |
| g | acceleration due to gravity (m s−2) |
| B | strength of the magnetic field (Tesla) |
| kf | thermal conductivity of the fluid (W/m K) |
| ks | thermal conductivity of the solid (W/m K) |
| Ec | Eckert number (-) |
| K | porosity parameter (-) |
| Nt | thermophoretic parameter |
| Nb | Brownian motion parameter |
| Sc | Schmidt number (-) |
| fw | surface flow flux parameter (-) |
| Rc | Chemical reaction parameter |
| M | magnetic parameter (-) |
| NT | temperature ratio parameter (-) |
| Nu | local Nusselt number (-) |
| Pr | Prandtl number (-) |
| qr | radiative heat flux (W/m2) |
| Rd | radiative parameter (-) |
| Re | Reynolds number (-) |
| Shx | Sherwood number (-) |
| Q | heat generation coefficient (J/m2·K·s) |
| Tf | temperature of the fluid (K) |
| qw | surface heat flux (w/m2) |
| qc | mass flux (kg/m2·s) |
| T∞ | temperature of the ambient fluid (K) |
| Tw | temperature at the surface (K) |
| (u, v) | fluid velocities in the x, y-directions (ms−1) |
| (x, y) | axis direction (m) |
| Greek symbols | |
| ψ | stream function (kg/m·s) |
| Θ | nanofluid dimensionless temperature (-) |
| Φ | nanofluid dimensionless concentration (-) |
| τw | shearing stress (N/m2) |
| ρ | density of the fluid (kg m−3) |
| µ | dynamic viscosity of the fluid (N s/m2) |
| υ | kinematic viscosity (N s/m2) |
| γ | thermal variation parameter (W/m3·K) |
| α | conjugate conduction heat parameter |
| θ | dimensionless temperature (-) |
| heat generation factor (-) | |
| volume fraction (-) | |
| β | coefficient of thermal expansion (1/K) |
| η | space variable (-) |
| Subscripts | |
| w | wall conditions |
| ∞ | ambient temperature |
| Superscript | |
| \ | differentiation with respect to y |
References
- Keller, H.B. Numerical Methods in Boundary Layer Theory. Annu. Rev. Fluid Mech. 1978, 10, 417–433. [Google Scholar] [CrossRef]
- Cebeci, T.; Bradshaw, P. Physical and Computational Aspects of Convective Heat Transfer; Springer: New York, NY, USA, 1984. [Google Scholar]
- Elbashbeshy, E.M.A.; Bazid, M.A. Heat transfer over an unsteady stretching surface. Heat Mass Transf. 2004, 41, 1–4. [Google Scholar] [CrossRef]
- Ishak, A. Unsteady MHD flow and heat transfer over a stretching sheet. J. Appl. Sci. 2010, 10, 2127–2131. [Google Scholar] [CrossRef]
- Ibrahim, W.; Shanker, B. Unsteady MHD boundary layer flow and heat transfer due to stretching sheet in the presence of heat source or sink. Comput. Fluids J. 2012, 70, 21–28. [Google Scholar] [CrossRef]
- Makinde, O.D.; Khan, W.A.; Gulham, J.R. MHD variable viscosity reacting flow over a convectively heated plate in a porous medium with thermophoresis and radiative heat transfer. Int. J. Heat Mass Transf. 2016, 93, 595–604. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Numerical simulation of magnetic nanofluid natural convection in porous media. Phy. Lett. A. 2017, 381, 494–503. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.A.; Eldabe, N.T.M.; Sedki, A.M. Effects of pressure stress work and thermal radiation on free convection flow around a sphere embedded in a porous medium with Newtonian heating. Therm. Sci. 2018, 22, 401–412. [Google Scholar] [CrossRef]
- Eldabe, N.T.M.; Ghaly, A.Y.; Mohamoud, M.S.H. MHD boundary layer chemical reacting flow with heat transfer of Eyring-Powell nanofluid past a stretching sheet. Microsyst. Technol. 2018, 24, 4945–4953. [Google Scholar] [CrossRef]
- Trivedi, M.; Ansari, M.S.; Motsa, S.S. Flow and heat transfer of a nanofluid by mixed convection with non-uniform heat source/sink and magnetic field effect: A numerical approach. Comput. Therm. Sci. 2019, 11, 189–203. [Google Scholar]
- Mahabaleshwar, U.S.; Nagaraju, K.R.; Lorenzini, G. Effect of mass transfer and MHD induced Navier’s slip flow due to non-linear stretching sheet. J. Eng. Thermophyscis 2019, 28, 578–600. [Google Scholar] [CrossRef]
- Khan, A.; Naem, S.; Vafai, K. Dufour, and Soret effects on Darcy-Forchheimer flow of second-grade fluid with the variable magnetic field and thermal conductivity. In International Journal of Numerical Methods for Heat and Fluid Flow; Emerald Publishing Limited: Bingley, UK, 2019; ISSN 0961-5539. [Google Scholar] [CrossRef]
- Maleki, H.; Alsarraf, J.; Safaei, M.R. Heat transfer and nanofluid flow over a porous plate with radiation and slip boundary conditions. J. Cent. South Univ. 2019, 26, 1099–1115. [Google Scholar] [CrossRef]
- Pordanjani, A.H.; Aghakhani, S.; Afrand, M. Investigation of free convection heat transfer entropy generation of nanofluid flow inside a cavity affected by a magnetic field and thermal radiation. J. Therm. Anal. Calorim. 2019, 137, 997–1019. [Google Scholar] [CrossRef]
- Chaudhary, S.; Kanika, K.M. Heat generation/absorption and radiation effects on hydromagnetic stagnation point flow of nanofluids toward a heated porous stretching/shrinking sheet with suction/injection. J. Porous Medium 2020, 23, 27–49. [Google Scholar] [CrossRef]
- Reddy, P.S.; Sreedevi, P. MHD boundary layer heat and mass transfer flow of nanofluid through porous media over an inclined plate with chemical reaction. Multidiscip. Model Mater Struct 2021, 17, 317–336. [Google Scholar] [CrossRef]
- Eldabe, N.T.M.; Abou-Zeid, M.Y.; Mohamed, M.A.A. MHD peristaltic non-Newtonianewtonian power-law nanofluid through a non-Darcy porous medium inside a non-uniform inclined channel. Arch. Appl. Mech. 2021, 91, 1067–1077. [Google Scholar] [CrossRef]
- Sedki, A.M.; Abo-Dahab, S.M.; Bouslimi, J.; Mahmoud, K.H. Thermal radiation effect on unsteady mixed convection boundary layer flow and heat transfer of nanofluid over permeable stretching surface through a porous medium in the presence of heat generation. Sci. Prog. 2021, 104, 1–19. [Google Scholar] [CrossRef]
- Sedki, A.M. Effect of thermal radiation and chemical radiation on MHD mixed convective heat and mass transfer in nanofluid flow due to a nonlinear stretching surface through a porous medium. Results Mater. 2022, 16, 100334. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Effects of thermal radiation on Casson fluid flow and heat transfer over an unsteady stretching surface subjected to suction/blowing. Chin. Phys. B 2013, 22, 114702. [Google Scholar] [CrossRef]
- Makanda, G.; Shaw, S.; Sibanda, P. Diffusion of chemically reactive species in Casson fluid flow over an nsteady stretching surface in porous medium in the presence of a magnetic field. Math. Probl. Eng. 2015, 2015, 724596. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Sandeep, N.; Reddy, J.V.R. Heat and mass transfer in magnetohydrodynamic Casson fluid over an exponentially permeable stretching surface. Eng. Sci. Technol. 2016, 19, 45–52. [Google Scholar] [CrossRef]
- Oyelakin, I.S.; Mondal, S.; Sibanda, P. Unsteady Casson nanofluid flow over a stretching sheet with thermal radiation, convective and slip boundary conditions. Alex. Eng. J. 2016, 55, 1025–1035. [Google Scholar] [CrossRef]
- Krishnamurthy, M.R.; Gireesha, B.J.; Gorla, R.S.R. Thermal radiation and chemical reaction effects on boundary layer slip flow and melting heat transfer of nanofluid induced by nonlinearly stretching sheet. Nonlinear Eng. 2016, 5, 147–159. [Google Scholar] [CrossRef]
- Ullah, I.; Bhattacharyya, K.; Shafie, S.; Ilyas Khan, I. Unsteady MHD mixed convection slip flow of Casson fluid over nonlinearly stretching sheet embedded in a porous medium with chemical reaction, thermal radiation, heat generation/absorption, and convective boundary conditions. PLoS ONE 2016, 11, 0165348. [Google Scholar] [CrossRef] [PubMed]
- Prasad, K.V.; Vajravelu, K.; Vaidya, H. MHD Casson nanofluid flow and heat transfer at a stretching sheet with variable thickness. J. Nanofluids 2016, 5, 423–435. [Google Scholar] [CrossRef]
- Tamoor, M.; Waqas, M.; Khan, M.I.; Alsaedi, A.; Hayat, T. Magnetohydrodynamic flow of Casson fluid over a stretching cylinder. Results Phys. 2017, 7, 498–502. [Google Scholar] [CrossRef]
- Naqvi, S.M.R.S.; Muhammad, T.; Asma, M. Hydromagnetic flow of Casson nanofluid over a porous stretching cylinder with Newtonian heat and mass conditions. Phys. A 2020, 550, 123988. [Google Scholar] [CrossRef]
- Shit, G.C.; Mandal, S. Entropy analysis on unsteady MHD flow of Casson nanofluid over a stretching vertical plate with thermal radiation effect. Int. J. Appl. Comput. Math. 2020, 6, 2. [Google Scholar] [CrossRef]
- Krishna, M.V.; Ahammad, N.A.; Chamkha, A.J. Radiative MHD flow of Casson hybrid nanofluid over an infinite exponentially accelerated vertical porous surface. Cas Stud. Therm. Eng. 2021, 27, 101229. [Google Scholar] [CrossRef]
- Bejawada, S.G.; Reddy, Y.D.; Jamshed, W.; Nisar, K.S.; Alharbi, A.N.; Chouikh, R. Radiation effect on MHD Casson fluid flow over an inclined non-linear surface with chemical reaction in a Forchheimer porous medium. Alex. Eng. J. 2022, 61, 8207–8220. [Google Scholar] [CrossRef]
- Sedki, A.M. Computational analysis of MHD Cross nanofluid containing gyrotactic microorganisms over permeable horizontal cylinder through a porous medthe ium in presence of thermal radiation and chemical reaction. Partial Differ. Equ. Appl. Math. 2023, 7, 100508. [Google Scholar] [CrossRef]
- Khan, M.N.; Ahmad, S.; Wang, Z.; Fadhl, B.M.; Irshad, K. Enhancement in the efficiency of heat recovery in a Williamson hybrid nanofluid over a vertically thin needle with entropy generation. Heliyon 2023, 9, 17665. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).