Modified Genetic Algorithm for the Profit-Based Unit Commitment Problem in Competitive Electricity Market
Abstract
:1. Introduction
2. Proposed PBUC Formulation
2.1. Thermal Unit Model
2.2. Compressed Air Energy Storage Model
2.3. Market Model
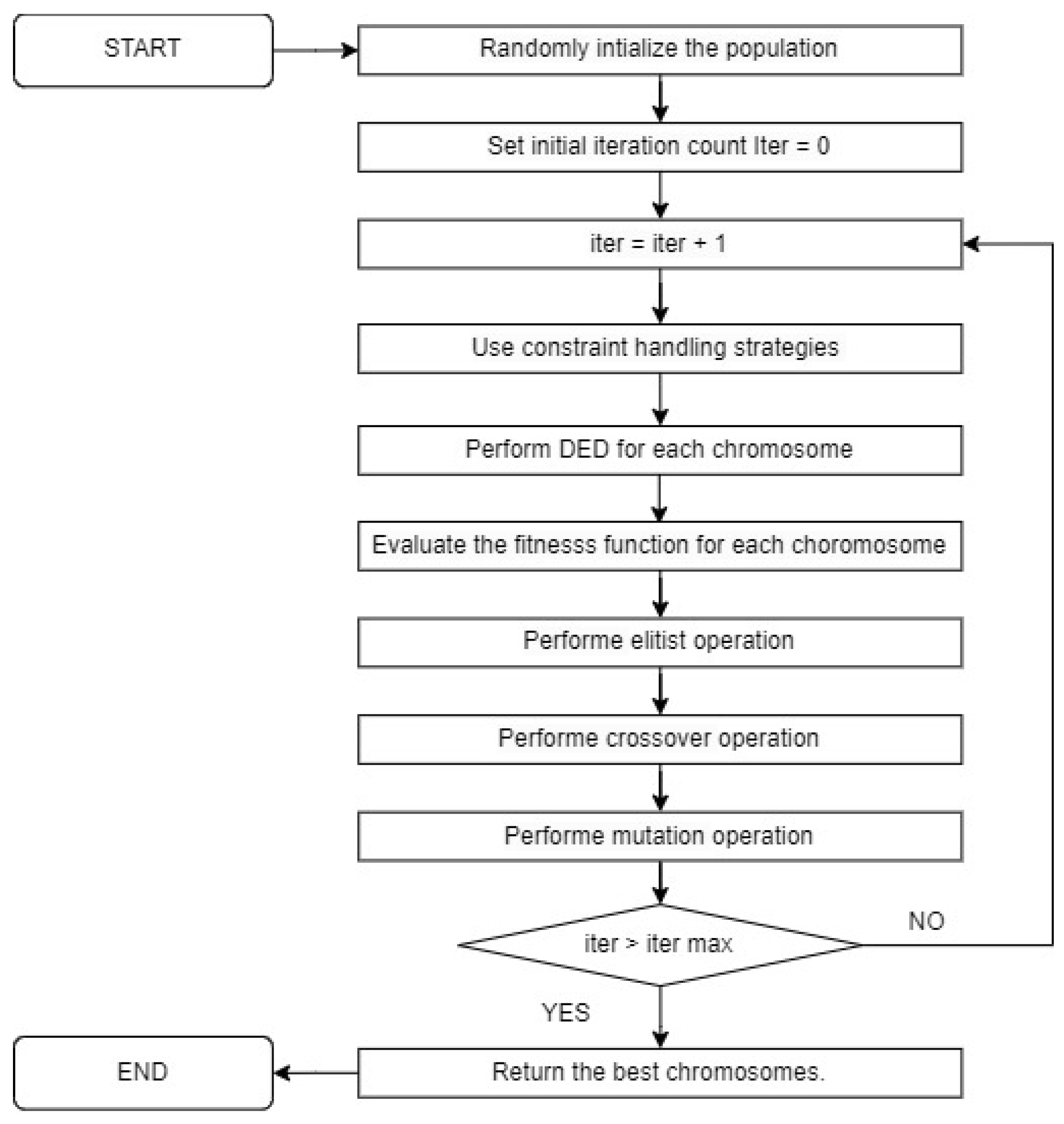
3. Modified GA for Solving PBUC
3.1. Population Initialization
3.1.1. Heuristic Constraints Handling Technique
3.1.2. Minimum up/down Time Constraint Handling
| Algorithm 1 Minimum up/down time constraint handling (Thermo units) |
| Require: Ensure:
|
3.1.3. Exclusive Operation Constraint Handling
3.1.4. Storage Capacity Constraint Handling
3.1.5. Market Constraint Handling
3.2. Dynimic Economic Dispatch Method
- Step 1: In this phase, we determine the amount of power to be consumed from the electrical grid for air injection into the reservoir, as well as the amount of power to be generated by the reservoir for sale.
- Step 2: In the second part of the algorithm, we conduct the dispatch of thermal units, taking into account the generation and consumption of storage systems. This heuristic addresses all the operational constraints previously presented for both storage systems and thermal units.
3.2.1. Stage 1: CAES Dispatch
3.2.2. Heuristic 1: Priority Lists Creation Based on Energy Price Forecasts Sorting
3.2.3. Heuristic 2: Buy and Sell as Minimal as Possible
3.2.4. Heuristic 3: Maximize Profit
- Process 1: Purchase the required amount only if it can be acquired during the selling hours listed in , thus maximizing profit, i.e., if the revenue from sales is greater than the cost of purchase.
- Process 2: Consume the maximum possible amount of power during the selling hours listed in , reducing the amount of power generated in hour h to eliminate violations of Constraint (23) while maximizing profit.
- Process 3: Reduce the amount of power generated in hour h to eliminate violations of Constraint (23).
3.2.5. Stage 2: Thermo Units Dispatch
- If possible, the necessary amount of thermal unit generation is reduced. To achieve this, based on the priority list , the active thermal unit at hour h with the lowest priority in the list will have its generation decreased, respecting , to comply with the market Constraint (25). If it is not possible to satisfy this constraint, the next thermal unit with lower priority in the list will have its power reduced, respecting its respective generation limit .
- If the market constraint is still violated after the previous step, the possibility of reducing the generation of thermal units that are active in the previous hour and the hour before that is examined (i.e., and ). By reducing generation in the previous hour, the generation limits and are altered due to ramping constraints. Therefore, the reduction in generation can be applied at hour h following the same process as before.
3.3. Fitness Evaluation
3.4. Selection, Elitist, Crossover and Mutationand Elitist Operators
3.5. Stopping Criterion
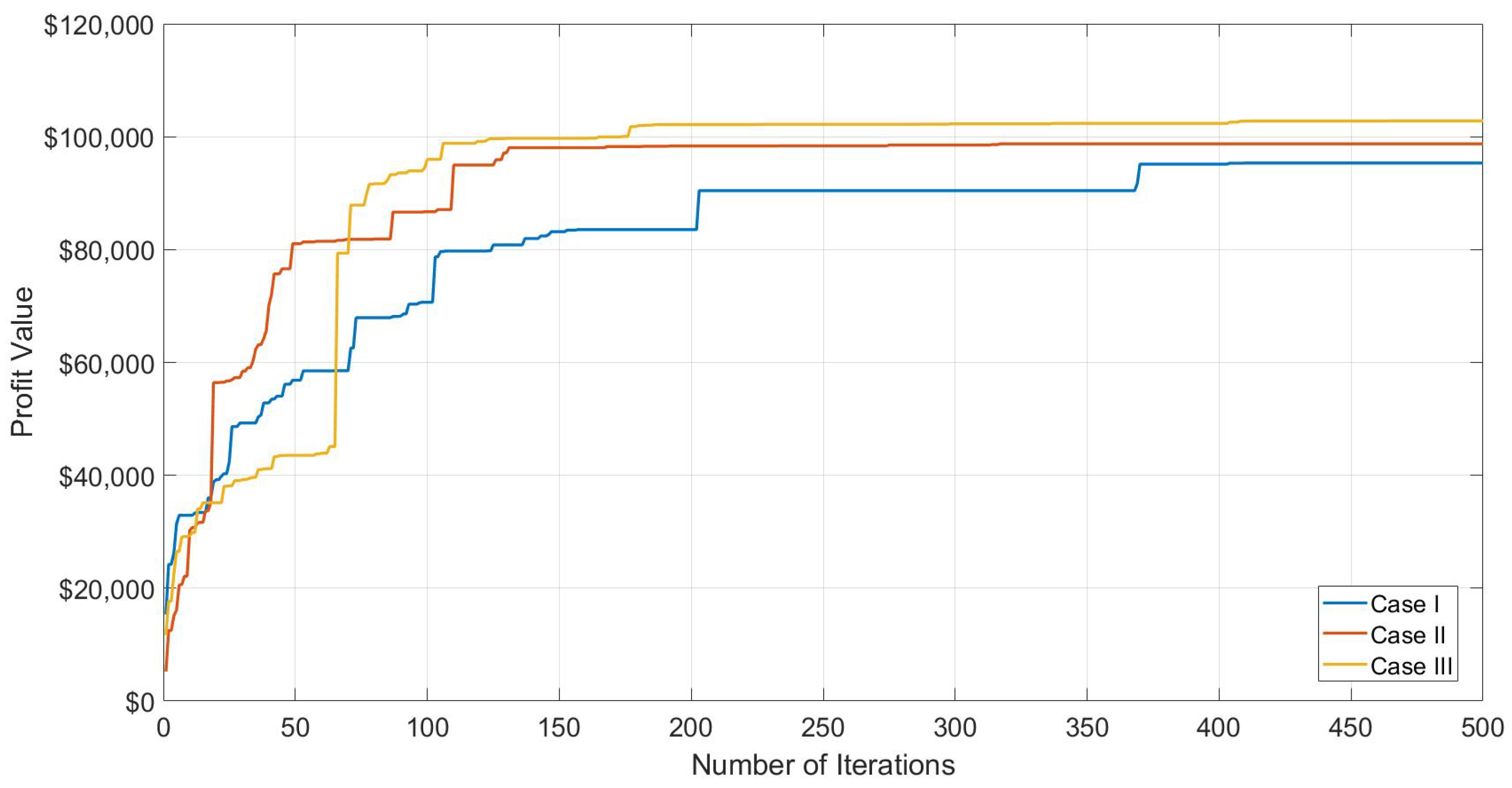
4. Discussion—Simulations and Results
- Case I: An electricity generation company with thermal units only.
- Case II: An electricity generation company with thermal units and one compressed air energy storage system.
- Case III: An electricity generation company with thermal units and three compressed air energy storage systems.
4.1. Case I
4.2. Case II
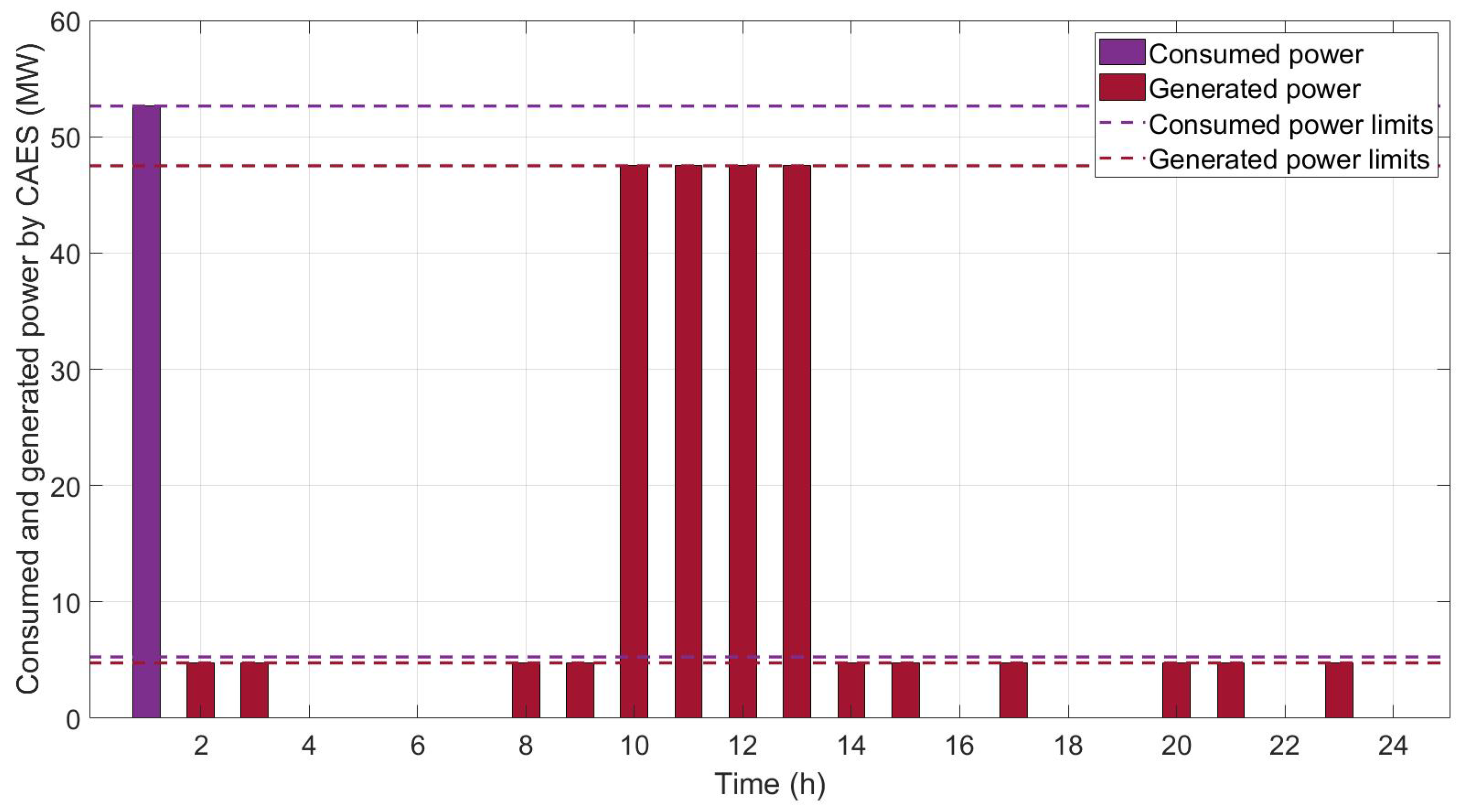
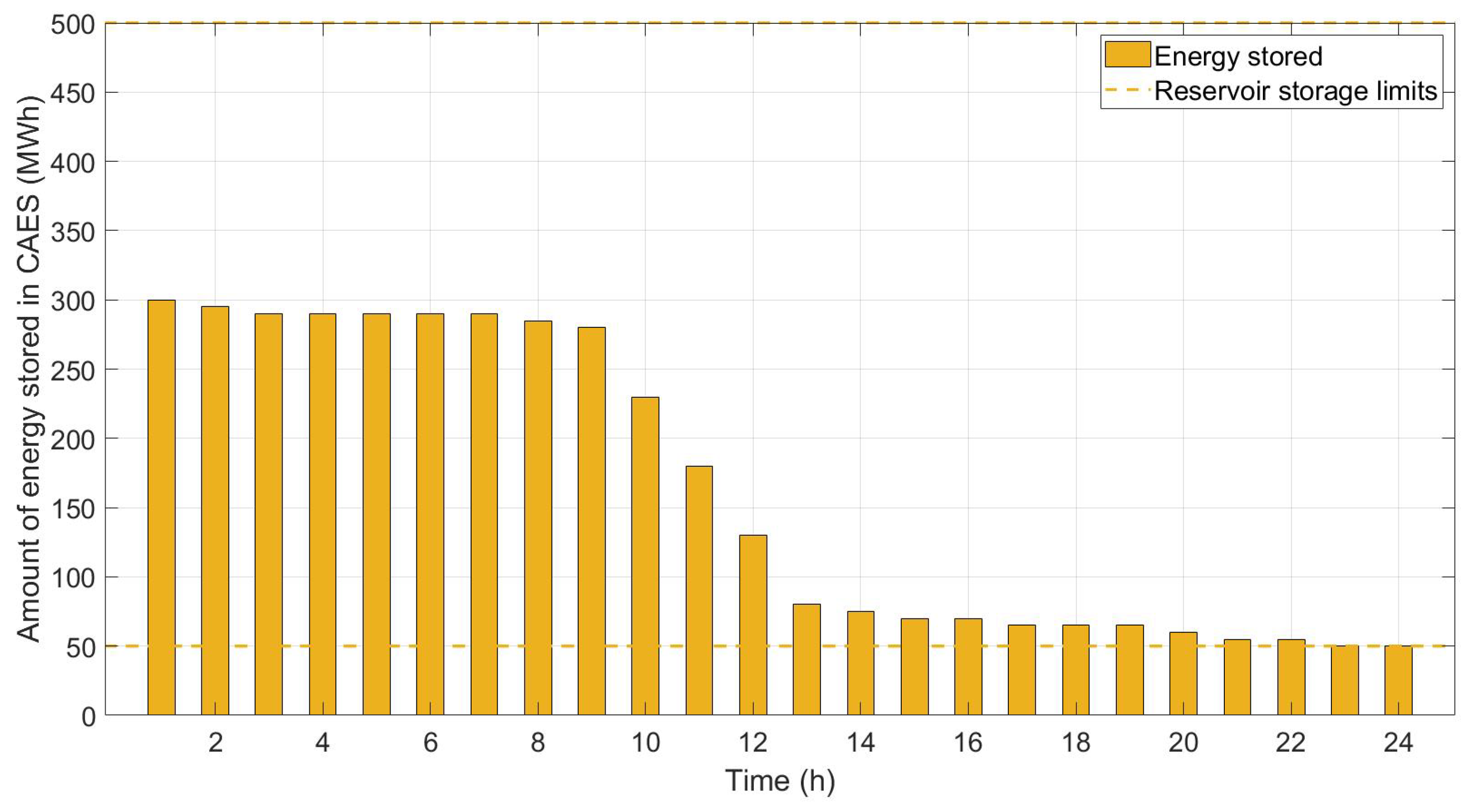
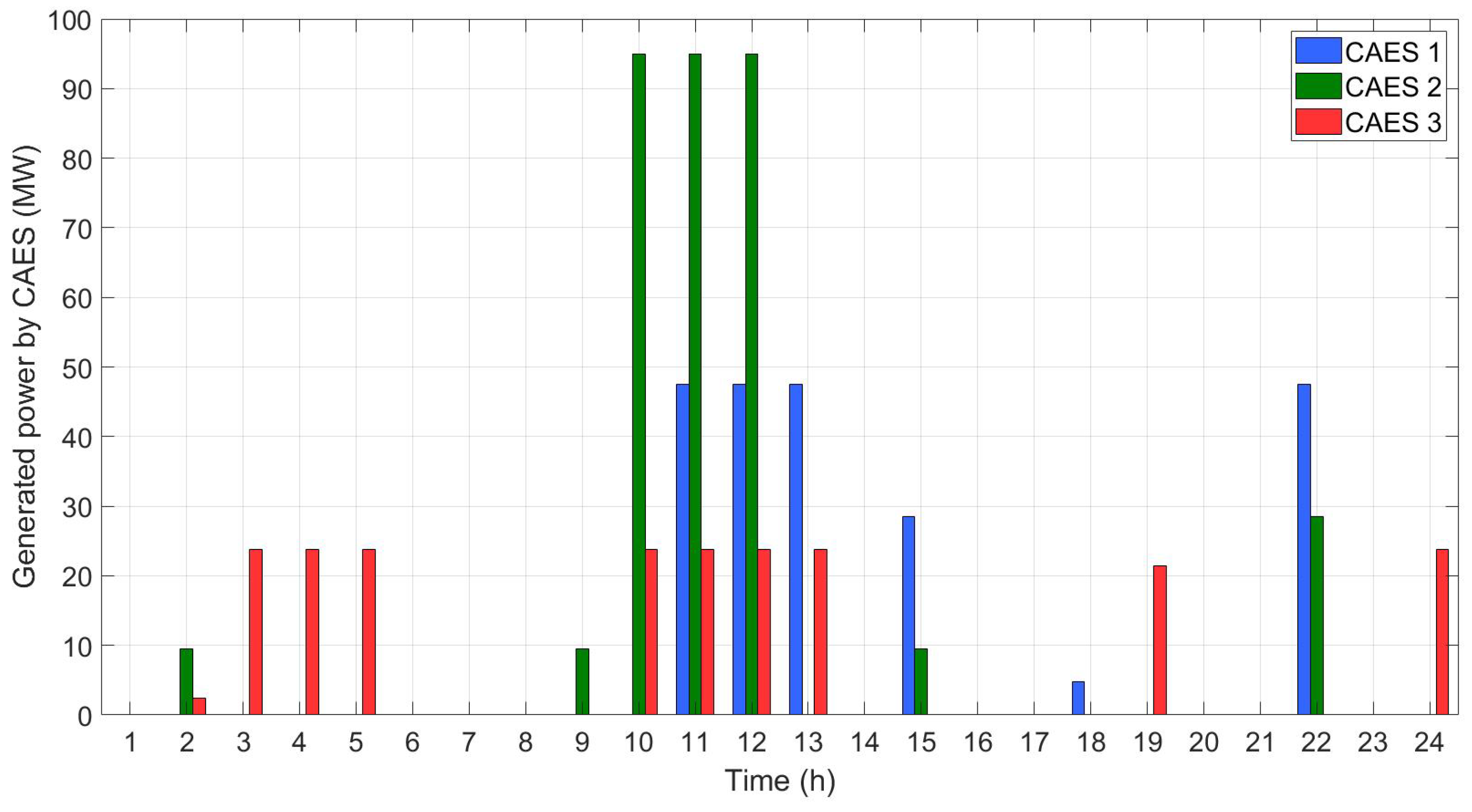
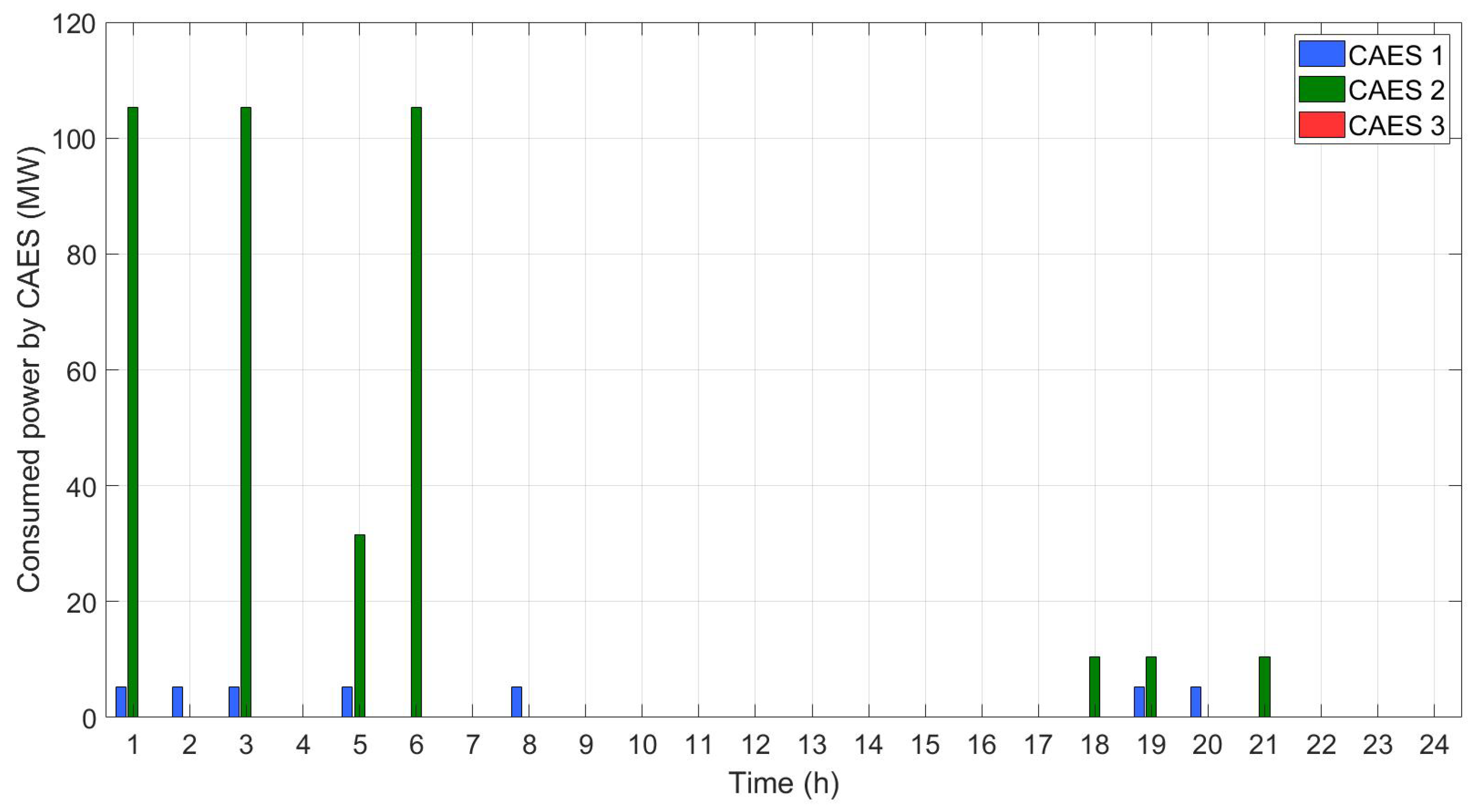
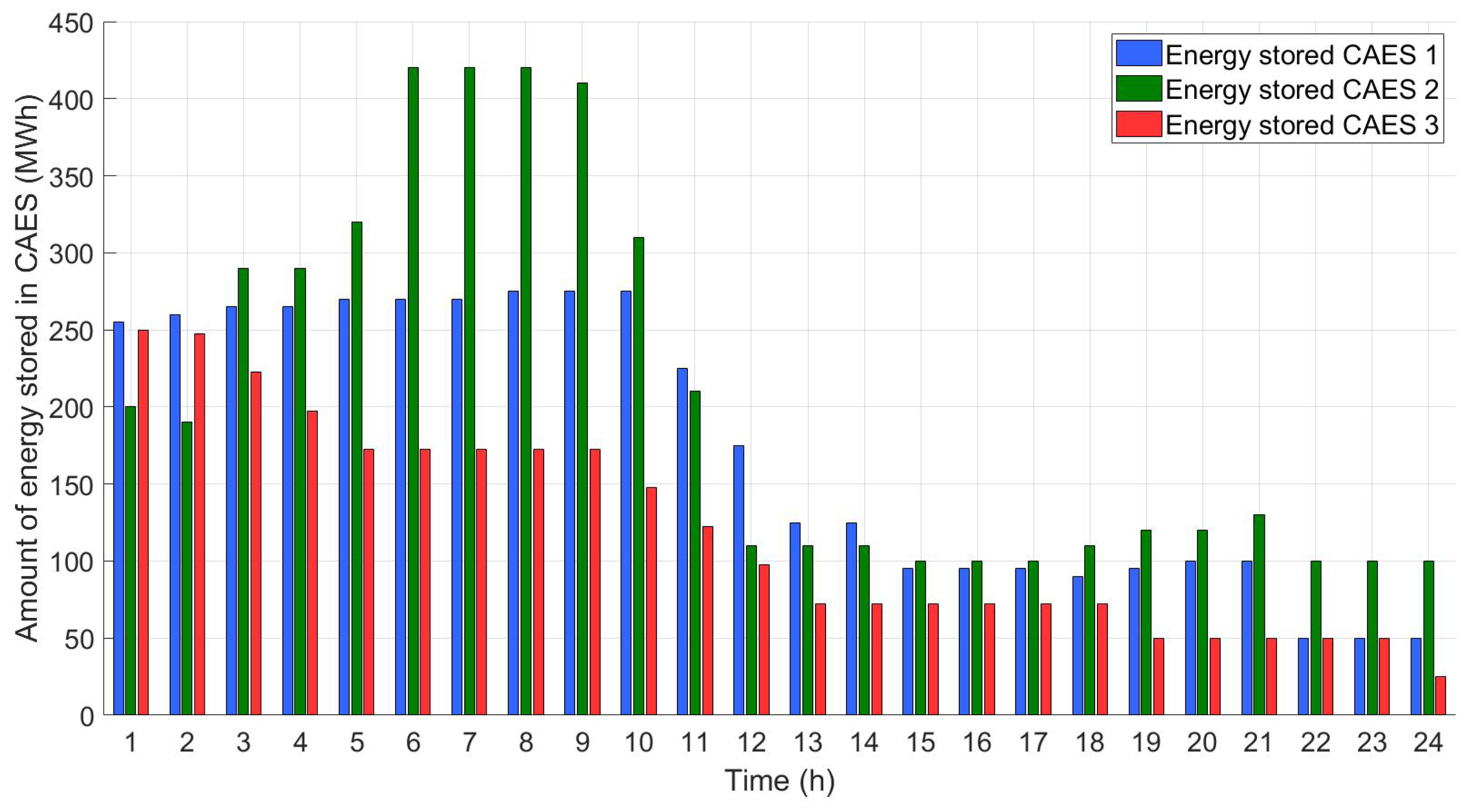
4.3. Case III
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Willis, H.; Philipson, L. Understanding Electric Utilities and De-Regulation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Corinaldesi, C.; Schwabeneder, D.; Lettner, G.; Auer, H. A rolling horizon approach for real-time trading and portfolio optimization of end-user flexibilities. Sustain. Energy Grids Netw. 2020, 24, 100392. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, M.; Lu, W.; Lin, S. Shared-constraint approach for multi-leader multi-follower game of generation companies participating in electricity markets with carbon emission trading mechanism. J. Clean. Prod. 2022, 350, 131424. [Google Scholar] [CrossRef]
- Corinaldesi, C.; Fleischhacker, A.; Lang, L.; Radl, J.; Schwabeneder, D.; Lettner, G. European case studies for impact of market-driven flexibility management in distribution systems. In Proceedings of the 2019 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Beijing, China, 21–23 October 2019; pp. 1–6. [Google Scholar]
- Nandi, A.; Kamboj, V.K. Comparative overview of profit-based unit commitment in competitive electricity market. In International Conference on Intelligent Computing and Smart Communication 2019: Proceedings of ICSC 2019; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1171–1195. [Google Scholar]
- Abdi, H. Profit-based unit commitment problem: A review of models, methods, challenges, and future directions. Renew. Sustain. Energy Rev. 2021, 138, 110504. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, J.; Barquin, J. Self-unit commitment of thermal units in a competitive electricity market. In Proceedings of the 2000 Power Engineering Society Summer Meeting (Cat. No. 00CH37134), Seattle, WA, USA, 16–20 July 2000; Volume 4, pp. 2278–2283. [Google Scholar]
- Shiina, T.; Watanabe, I. Lagrangian relaxation method for price-based unit commitment problem. Eng. Optim. 2004, 36, 705–719. [Google Scholar] [CrossRef]
- Chandram, K.; Subrahmanyam, N.; Sydulu, M. New approach with muller method for profit based unit commitment. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–8. [Google Scholar]
- Krishna, P.; Sao, S. Price based unit commitment problem under deregulation. Int. J. Sci. Eng. Technol. 2012, 1, 177–184. [Google Scholar]
- Kumar, V.; Naresh, R.; Sharma, V. Stochastic profit-based unit commitment problem considering renewable energy sources with battery storage systems and plug-in hybrid electric vehicles. Int. J. Energy Res. 2022, 46, 16445–16460. [Google Scholar] [CrossRef]
- Richter, C.; Sheble, G. A profit-based unit commitment GA for the competitive environment. IEEE Trans. Power Syst. 2000, 15, 715–721. [Google Scholar] [CrossRef]
- Georgilakis, P. Genetic algorithm model for profit maximization of generating companies in deregulated electricity markets. Appl. Artif. Intell. 2009, 23, 538–552. [Google Scholar] [CrossRef]
- Singhal, P.; Naresh, R.; Sharma, V.; Nadakuditi, G. Generator scheduling under competitive environment using Genetic Algorithm. Int. J. Eng. Sci. Technol. 2015, 7, 24–32. [Google Scholar] [CrossRef]
- Yuan, X.; Yuan, Y.; Wang, C.; Zhang, X. An improved PSO approach for profit-based unit commitment in electricity market. In Proceedings of the 2005 IEEE/PES Transmission & Distribution Conference & Exposition: Asia and Pacific, Dalian, China, 18 August 2005; pp. 1–4. [Google Scholar]
- Raglend, I.; Raghuveer, C.; Avinash, G.; Padhy, N.; Kothari, D. Solution to profit based unit commitment problem using particle swarm optimization. Appl. Soft Comput. 2010, 10, 1247–1256. [Google Scholar] [CrossRef]
- Venkatesan, T.; Sanavullah, M. SFLA approach to solve PBUC problem with emission limitation. Int. J. Electr. Power Energy Syst. 2013, 46, 1–9. [Google Scholar] [CrossRef]
- Ghadi, M.; Baghramian, A. A new heuristic method for solving unit commitment problem in competitive environment. Int. J. Soft Comput. Eng. 2013, 2, 2231–2307. [Google Scholar]
- Singhal, P.; Naresh, R.; Sharma, V. Binary fish swarm algorithm for profit-based unit commitment problem in competitive electricity market with ramp rate constraints. IET Gener. Transm. Distrib. 2015, 9, 1697–1707. [Google Scholar] [CrossRef]
- Reddy, S.; Panwar, L.; Panigrahi, B.; Kumar, R.; Alsumaiti, A. Binary grey wolf optimizer models for profit based unit commitment of price-taking GENCO in electricity market. Swarm Evol. Comput. 2019, 44, 957–971. [Google Scholar] [CrossRef]
- Reddy K, S.; Panwar, L.; Panigrahi, B.; Kumar, R. Binary whale optimization algorithm: A new metaheuristic approach for profit-based unit commitment problems in competitive electricity markets. Eng. Optim. 2019, 51, 369–389. [Google Scholar] [CrossRef]
- Kumar, V.; Naresh, R.; Sharma, V. Profit based unit commitment problem solution using metaheuristic optimisation approach. Int. J. Syst. Sci. Oper. Logist. 2023, 10, 2037026. [Google Scholar] [CrossRef]
- Lakshmi, K.; Vasantharathna, S. A profit based unit commitment problem in deregulated power markets. In Proceedings of the 2009 International Conference on Power Systems, Kharagpur, India, 27–29 December 2009; pp. 1–6. [Google Scholar]
- Attaviriyanupap, P.; Kita, H.; Tanaka, E.; Hasegawa, J. A hybrid LR-EP for solving new profit-based UC problem under competitive environment. IEEE Trans. Power Syst. 2003, 18, 229–237. [Google Scholar] [CrossRef]
- Bavafa, M.; Navidi, N.; Monsef, H. A new approach for Profit-Based Unit Commitment using Lagrangian relaxation combined with ant colony search algorithm. In Proceedings of the 2008 43rd International Universities Power Engineering Conference, Padua, Italy, 1–4 September 2008; pp. 1–6. [Google Scholar]
- Rampriya, B.; Mahadevan, K.; Kannan, S. Unit commitment in deregulated power system using Lagrangian firefly algorithm. In Proceedings of the 2010 International Conference On Communication Control And Computing Technologies, Nagercoil, India, 7–9 October 2010; pp. 389–393. [Google Scholar]
- Kumar, R.; Asokan, K.; Kumar, S. Optimal scheduling of generators to maximize GENCOs profit using LR combined with ABC algorithm in deregulated power system. In Proceedings of the 2013 International Conference on Computation of Power, Energy, Information and Communication (ICCPEIC), Chennai, India, 17–18 April 2013; pp. 75–83. [Google Scholar]
- Sudhakar, A.; Karri, C.; Laxmi, A. A hybrid LR-secant method-invasive weed optimisation for profit-based unit commitment. Int. J. Power Energy Convers. 2018, 9, 1–24. [Google Scholar] [CrossRef]
- Shukla, A.; Lal, V.; Singh, S. Profit-based unit commitment problem using PSO with modified dynamic programming. In Proceedings of the 2015 18th International Conference On Intelligent System Application To Power Systems (ISAP), Porto, Portugal, 11–16 September 2015; pp. 1–6. [Google Scholar]
- Chandram, K.; Subrahmanyam, N.; Sydulu, M. Improved pre-prepared power demand table and Muller’s method to solve the profit based unit commitment problem. J. Electr. Eng. Technol. 2009, 4, 159–167. [Google Scholar] [CrossRef]
- Asokan, K.; Ashokkumar, R. Emission controlled Profit based Unit commitment for GENCOs using MPPD Table with ABC algorithm under Competitive Environment. Strategies 2014, 16, 20. [Google Scholar]
- Anand, H.; Narang, N.; Dhillon, J. Profit based unit commitment using hybrid optimization technique. Energy 2018, 148, 701–715. [Google Scholar] [CrossRef]
- Lakshmi, K.; Vasantharathna, S. Hybrid artificial immune system approach for profit based unit commitment problem. J. Electr. Eng. Technol. 2013, 8, 959–968. [Google Scholar] [CrossRef]
- Sundaram, C.; Sudhakaran, M.; Raj, P. Tabu search-enhanced artificial bee colony algorithm to solve profit-based unit commitment problem with emission limitations in deregulated electricity market. Int. J. Metaheurist. 2017, 6, 107–132. [Google Scholar] [CrossRef]
- BP, p.l.c. BP Statistical Review of World Energy 2017; BP p.l.c.: London, UK, 2019. [Google Scholar]
- Olabi, A.; Wilberforce, T.; Ramadan, M.; Abdelkareem, M.; Alami, A. Compressed air energy storage systems: Components and operating parameters—A review. J. Energy Storage 2021, 34, 102000. [Google Scholar] [CrossRef]
- Sharma, A.; Chiu, H.H.; Ahrens, F.O.W.; Ahluwalia, R.K.; Ragsdell, K.O.M. Design of optimum compressed air energy-storage systems. Energy 1979, 4, 201–216. [Google Scholar] [CrossRef]
- Budt, M.; Wolf, D.; Span, R.; Yan, J. A review on compressed air energy storage: Basic principles, past milestones and recent developments. Appl. Energy 2016, 170, 250–268. [Google Scholar] [CrossRef]
- Yucekaya, A. The operational economics of compressed air energy storage systems under uncertainty. Renew. Sustain. Energy Rev. 2013, 22, 298–305. [Google Scholar] [CrossRef]
- Nasouri Gilvaei, M.; Hosseini Imani, M.; Jabbari Ghadi, M.; Li, L.; Golrang, A. Profit-based unit commitment for a GENCO equipped with compressed air energy storage and concentrating solar power units. Energies 2021, 14, 576. [Google Scholar] [CrossRef]
- Lund, H.; Salgi, G.; Elmegaard, B.; Andersen, A. Optimal operation strategies of compressed air energy storage (CAES) on electricity spot markets with fluctuating prices. Appl. Therm. Eng. 2009, 29, 799–806. [Google Scholar] [CrossRef]
- Drury, E.; Denholm, P.; Sioshansi, R. The value of compressed air energy storage in energy and reserve markets. Energy 2011, 36, 4959–4973. [Google Scholar] [CrossRef]
- Soroudi, A. Smart self-scheduling of Gencos with thermal and energy storage units under price uncertainty. Int. Trans. Electr. Energy Syst. 2014, 24, 1401–1418. [Google Scholar] [CrossRef]
- Abbaspour, M.; Satkin, M.; Mohammadi-Ivatloo, B.; Hoseinzadeh Lotfi, F.; Noorollahi, Y. Optimal operation scheduling of wind power integrated with compressed air energy storage (CAES). Renew. Energy 2013, 51, 53–59. [Google Scholar] [CrossRef]
- Shafiee, S.; Zareipour, H.; Knight, A.M.; Amjady, N.; Mohammadi-Ivatloo, B. Risk-constrained bidding and offering strategy for a merchant compressed air energy storage plant. IEEE Trans. Power Syst. 2016, 32, 946–957. [Google Scholar] [CrossRef]
- Akbari, E.; Hooshmand, R.A.; Gholipour, M.; Parastegari, M. Stochastic programming-based optimal bidding of compressed air energy storage with wind and thermal generation units in energy and reserve markets. Energy 2019, 171, 535–546. [Google Scholar] [CrossRef]
- Kumar, V.; Naresh, R.; Singh, A. Investigation of solution techniques of unit commitment problems: A review. Wind Eng. 2021, 45, 1689–1713. [Google Scholar] [CrossRef]
| Hour | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| A | 12.5 | 12.5 | 10.0 | 8.5 | - - - | - - - |
| Unit | (MW) | (MW) | ($/MWh) | ($/MWh) | ($/MWh) | (h) | (h) | ($) | ($) | (h) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 455 | 150 | 1000 | 16.19 | 0.00048 | 8 | 8 | 4500 | 9000 | 5 | 8 |
| 2 | 455 | 150 | 970 | 17.26 | 0.00031 | 8 | 8 | 5000 | 10,000 | 5 | 8 |
| 3 | 130 | 20 | 700 | 16.60 | 0.00200 | 5 | 5 | 550 | 1100 | 4 | −5 |
| 4 | 130 | 20 | 680 | 16.50 | 0.00211 | 5 | 5 | 560 | 1120 | 4 | −5 |
| 5 | 162 | 25 | 450 | 19.70 | 0.00398 | 6 | 6 | 900 | 1800 | 4 | −6 |
| 6 | 80 | 20 | 370 | 22.26 | 0.00712 | 3 | 3 | 170 | 340 | 2 | −3 |
| 7 | 85 | 25 | 480 | 27.74 | 0.00079 | 3 | 3 | 260 | 520 | 0 | −3 |
| 8 | 55 | 10 | 660 | 25.92 | 0.00413 | 1 | 1 | 30 | 60 | 0 | −1 |
| 9 | 55 | 10 | 665 | 27.27 | 0.00222 | 1 | 1 | 30 | 60 | 0 | −1 |
| 10 | 55 | 10 | 670 | 27.79 | 0.00173 | 1 | 1 | 30 | 60 | 0 | −1 |
| CAES | (MWh) | (MWh) | (MWh) | (MWh) | (MWh) | (MWh) | (MWh) | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 500 | 500 | 5 | 5 | 5 | 5 | 0.95 | 0.95 | 250 |
| 2 | 1000 | 1000 | 10 | 10 | 10 | 10 | 0.95 | 0.95 | 100 |
| 3 | 250 | 250 | 2.5 | 2.5 | 2.5 | 2.5 | 0.95 | 0.95 | 250 |
| Hour | Load (MW) | Energy Price ($/MWh) | Hour | Load (MW) | Energy Price ($/MWh) | Hour | Load (MW) | Energy Price ($/MWh) | Hour | Load (MW) | Energy Price ($/MWh) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 700 | 22.15 | 7 | 1150 | 22.50 | 13 | (MW) | 24.60 | 19 | 1200 | 22.20 |
| 2 | 750 | 22.00 | 8 | 1200 | 22.15 | 14 | 1300 | 24.50 | 20 | 1400 | 22.65 |
| 3 | 850 | 23.10 | 9 | 1300 | 22.80 | 15 | 1200 | 22.50 | 21 | 1300 | 23.10 |
| 4 | 950 | 22.65 | 10 | 1400 | 29.35 | 16 | 1100 | 22.30 | 22 | 1100 | 22.95 |
| 5 | 1000 | 23.25 | 11 | 1450 | 30.15 | 17 | 1050 | 22.25 | 23 | 900 | 22.75 |
| 6 | 1100 | 22.95 | 12 | 1500 | 31.65 | 18 | 1000 | 22.05 | 24 | 800 | 22.55 |
| Number of Chromosomes | Number of Iterations | Crossover Rate | Mutate Rate | Number of Tournament Participants | Size of the Elite |
|---|---|---|---|---|---|
| 100 | 500 | 0.8 | 0.2 | 5 | 10 |
| Hour | (MW) | (MW) | (MW) | (MW) | – (MW) | Fuel Cost ($) | Start Up Cost ($) | Revenue from Thermal Units ($) |
|---|---|---|---|---|---|---|---|---|
| 1 | 455.00 | 245.00 | 0 | 0 | 0 | 13,683.13 | 0 | 15,505.00 |
| 2 | 408.75 | 150.00 | 0 | 0 | 0 | 11,263.83 | 0 | 12,292.50 |
| 3 | 455.00 | 250.00 | 0 | 0 | 0 | 13,770.20 | 0 | 16,285.50 |
| 4 | 455.00 | 303.75 | 0 | 0 | 0 | 14,707.15 | 0 | 17,185.69 |
| 5 | 455.00 | 313.75 | 0 | 0 | 0 | 14,881.66 | 0 | 17,873.44 |
| 6 | 455.00 | 403.75 | 0 | 0 | 0 | 16,455.08 | 0 | 19,708.31 |
| 7 | 455.00 | 363.75 | 0 | 0 | 0 | 15,755.16 | 0 | 18,421.88 |
| 8 | 455.00 | 453.75 | 0 | 0 | 0 | 17,331.37 | 0 | 20,128.81 |
| 9 | 455.00 | 455.00 | 0 | 0 | 0 | 17,353.30 | 0 | 20,748.00 |
| 10 | 455.00 | 455.00 | 0 | 107.50 | 0 | 19,831.43 | 1120 | 29,863.63 |
| 11 | 455.00 | 455.00 | 0 | 102.50 | 0 | 19,746.72 | 0 | 30,526.88 |
| 12 | 455.00 | 455.00 | 0 | 130.00 | 0 | 20,213.96 | 0 | 32,916.00 |
| 13 | 455.00 | 455.00 | 0 | 97.50 | 0 | 19,662.11 | 0 | 24,784.50 |
| 14 | 455.00 | 397.50 | 0 | 65.00 | 0 | 18,107.07 | 0 | 22,478.75 |
| 15 | 455.00 | 420.00 | 0 | 0 | 0 | 16,739.71 | 0 | 19,687.50 |
| 16 | 455.00 | 306.25 | 0 | 0 | 0 | 14,750.77 | 0 | 16,975.88 |
| 17 | 455.00 | 361.25 | 0 | 0 | 0 | 15,711.45 | 0 | 18,161.56 |
| 18 | 455.00 | 256.25 | 0 | 0 | 0 | 13,879.05 | 0 | 15,683.06 |
| 19 | 455.00 | 370.00 | 0 | 0 | 0 | 15,864.46 | 0 | 18,315.00 |
| 20 | 455.00 | 455.00 | 0 | 0 | 0 | 17,353.30 | 0 | 20,611.50 |
| 21 | 455.00 | 455.00 | 0 | 0 | 0 | 17,353.30 | 0 | 21,021.00 |
| 22 | 455.00 | 341.25 | 0 | 0 | 0 | 15,361.90 | 0 | 18,273.94 |
| 23 | 455.00 | 227.50 | 0 | 0 | 0 | 13,378.52 | 0 | 15,526.88 |
| 24 | 455.00 | 0 | 0 | 0 | 0 | 8,465.82 | 0 | 10,260.25 |
| Hour | (MW) | (MW) | – (MW) | Fuel Cost ($) | Start Up Cost ($) | Revenue from Thermal Units ($) |
|---|---|---|---|---|---|---|
| 1 | 455.00 | 297.63 | 0 | 14,600.40 | 0 | 16670.79 |
| 2 | 370.12 | 183.88 | 0 | 11,212.25 | 0 | 12,188.00 |
| 3 | 455.00 | 283.88 | 0 | 14,360.60 | 0 | 17,068.16 |
| 4 | 455.00 | 278.87 | 0 | 14,273.20 | 0 | 16,622.12 |
| 5 | 455.00 | 333.88 | 0 | 15,233.18 | 0 | 18,341.50 |
| 6 | 455.00 | 388.88 | 0 | 16,194.80 | 0 | 19,367.08 |
| 7 | 455.00 | 373.87 | 0 | 15,932.12 | 0 | 18,649.54 |
| 8 | 455.00 | 438.88 | 0 | 17,070.63 | 0 | 19,799.48 |
| 9 | 455.00 | 455.00 | 0 | 17,353.30 | 0 | 20,748.00 |
| 10 | 455.00 | 455.00 | 0 | 17,353.30 | 0 | 26,708.50 |
| 11 | 455.00 | 455.00 | 0 | 17,353.30 | 0 | 27,436.50 |
| 12 | 455.00 | 455.00 | 0 | 17,353.30 | 0 | 28,801.50 |
| 13 | 455.00 | 455.00 | 0 | 17,353.30 | 0 | 22,386.00 |
| 14 | 455.00 | 455.00 | 0 | 17,353.30 | 0 | 22,295.00 |
| 15 | 455.00 | 357.75 | 0 | 15,650.26 | 0 | 18,286.88 |
| 16 | 455.00 | 359.75 | 0 | 15,685.23 | 0 | 18,168.93 |
| 17 | 455.00 | 303.00 | 0 | 14,694.06 | 0 | 16,865.50 |
| 18 | 455.00 | 314.50 | 0 | 14,894.75 | 0 | 16,967.48 |
| 19 | 455.00 | 428.25 | 0 | 16,884.27 | 0 | 19,608.15 |
| 20 | 455.00 | 455.00 | 0 | 17,353.30 | 0 | 20,611.50 |
| 21 | 455.00 | 455.00 | 0 | 17,353.30 | 0 | 21,021.00 |
| 22 | 455.00 | 341.25 | 0 | 15,361.90 | 0 | 18,273.94 |
| 23 | 455.00 | 227.50 | 0 | 13,378.52 | 0 | 15,526.88 |
| 24 | 455.00 | 0 | 0 | 8465.82 | 0 | 10,260.25 |
| Hour | (MW) | (MW) | – (MW) | Fuel Cost ($) | Start Up Cost ($) | Revenue from Thermal Units ($) |
|---|---|---|---|---|---|---|
| 1 | 455.00 | 355.53 | 0 | 15,611.39 | 0 | 17,953.16 |
| 2 | 341.25 | 241.78 | 0 | 11,741.91 | 0 | 12,826.58 |
| 3 | 455.00 | 355.53 | 0 | 15,611.39 | 0 | 18,723.16 |
| 4 | 455.00 | 241.78 | 0 | 13,627.00 | 0 | 15,781.98 |
| 5 | 455.00 | 355.53 | 0 | 15,611.39 | 0 | 18,844.74 |
| 6 | 455.00 | 455.00 | 0 | 17,353.30 | 0 | 20,884.50 |
| 7 | 455.00 | 341.25 | 0 | 15,361.90 | 0 | 17,915.63 |
| 8 | 455.00 | 455.00 | 0 | 17,353.30 | 0 | 20,156.50 |
| 9 | 455.00 | 453.00 | 0 | 17,318.22 | 0 | 20,702.40 |
| 10 | 455.00 | 445.75 | 0 | 17,191.06 | 0 | 26,437.01 |
| 11 | 455.00 | 455.00 | 0 | 17,353.30 | 0 | 27,436.50 |
| 12 | 455.00 | 455.00 | 0 | 17,353.30 | 0 | 28,801.50 |
| 13 | 455.00 | 455.00 | 0 | 17,353.30 | 0 | 22,386.00 |
| 14 | 455.00 | 455.00 | 0 | 17,353.30 | 0 | 22,295.00 |
| 15 | 455.00 | 341.25 | 0 | 15,361.90 | 0 | 17,915.63 |
| 16 | 455.00 | 376.25 | 0 | 15,973.78 | 0 | 18,536.88 |
| 17 | 455.00 | 291.25 | 0 | 14,489.09 | 0 | 16,604.06 |
| 18 | 455.00 | 332.03 | 0 | 15,200.77 | 0 | 17,353.93 |
| 19 | 455.00 | 445.78 | 0 | 17,191.52 | 0 | 19,997.23 |
| 20 | 455.00 | 455.00 | 0 | 17,353.30 | 0 | 20,611.50 |
| 21 | 455.00 | 455.00 | 0 | 17,353.30 | 0 | 21,021.00 |
| 22 | 455.00 | 341.25 | 0 | 15,361.90 | 0 | 18,273.94 |
| 23 | 455.00 | 227.50 | 0 | 13,378.52 | 0 | 15,526.88 |
| 24 | 455.00 | 0 | 0 | 8465.82 | 0 | 10,260.25 |
| Case | Best Profit ($) | Total Generated (MW) | Total Cost ($) | Comput. Time (s) |
|---|---|---|---|---|
| I | 90,494.98 | 19,725.00 | 382,740.46 | 8.20 |
| II | 95,343.58 | 19,854.53 | 384,358.18 | 14.50 |
| III | 102,813.86 | 20,370.68 | 397,666.90 | 22.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nepomuceno, L.S.; de Oliveira, L.M.; da Silva Junior, I.C.; de Oliveira, E.J.; de Paula, A.N. Modified Genetic Algorithm for the Profit-Based Unit Commitment Problem in Competitive Electricity Market. Energies 2023, 16, 7751. https://doi.org/10.3390/en16237751
Nepomuceno LS, de Oliveira LM, da Silva Junior IC, de Oliveira EJ, de Paula AN. Modified Genetic Algorithm for the Profit-Based Unit Commitment Problem in Competitive Electricity Market. Energies. 2023; 16(23):7751. https://doi.org/10.3390/en16237751
Chicago/Turabian StyleNepomuceno, Lucas Santiago, Layon Mescolin de Oliveira, Ivo Chaves da Silva Junior, Edimar José de Oliveira, and Arthur Neves de Paula. 2023. "Modified Genetic Algorithm for the Profit-Based Unit Commitment Problem in Competitive Electricity Market" Energies 16, no. 23: 7751. https://doi.org/10.3390/en16237751
APA StyleNepomuceno, L. S., de Oliveira, L. M., da Silva Junior, I. C., de Oliveira, E. J., & de Paula, A. N. (2023). Modified Genetic Algorithm for the Profit-Based Unit Commitment Problem in Competitive Electricity Market. Energies, 16(23), 7751. https://doi.org/10.3390/en16237751






