Effects of Different Channel Geometries of Metallic Bipolar Plates on Proton Exchange Membrane Fuel Cell Performance
Abstract
:1. Introduction
2. Methodology
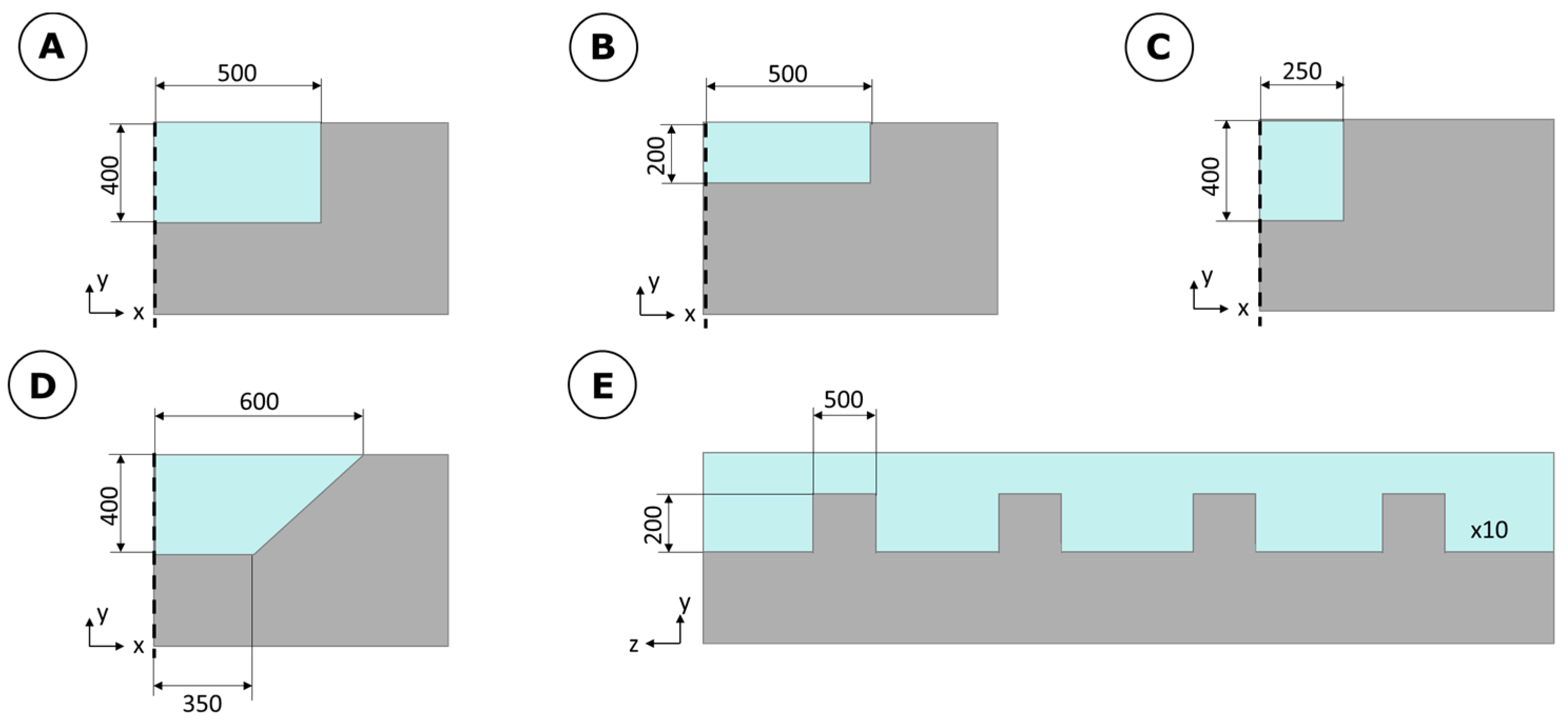
2.1. Analyzed Cases
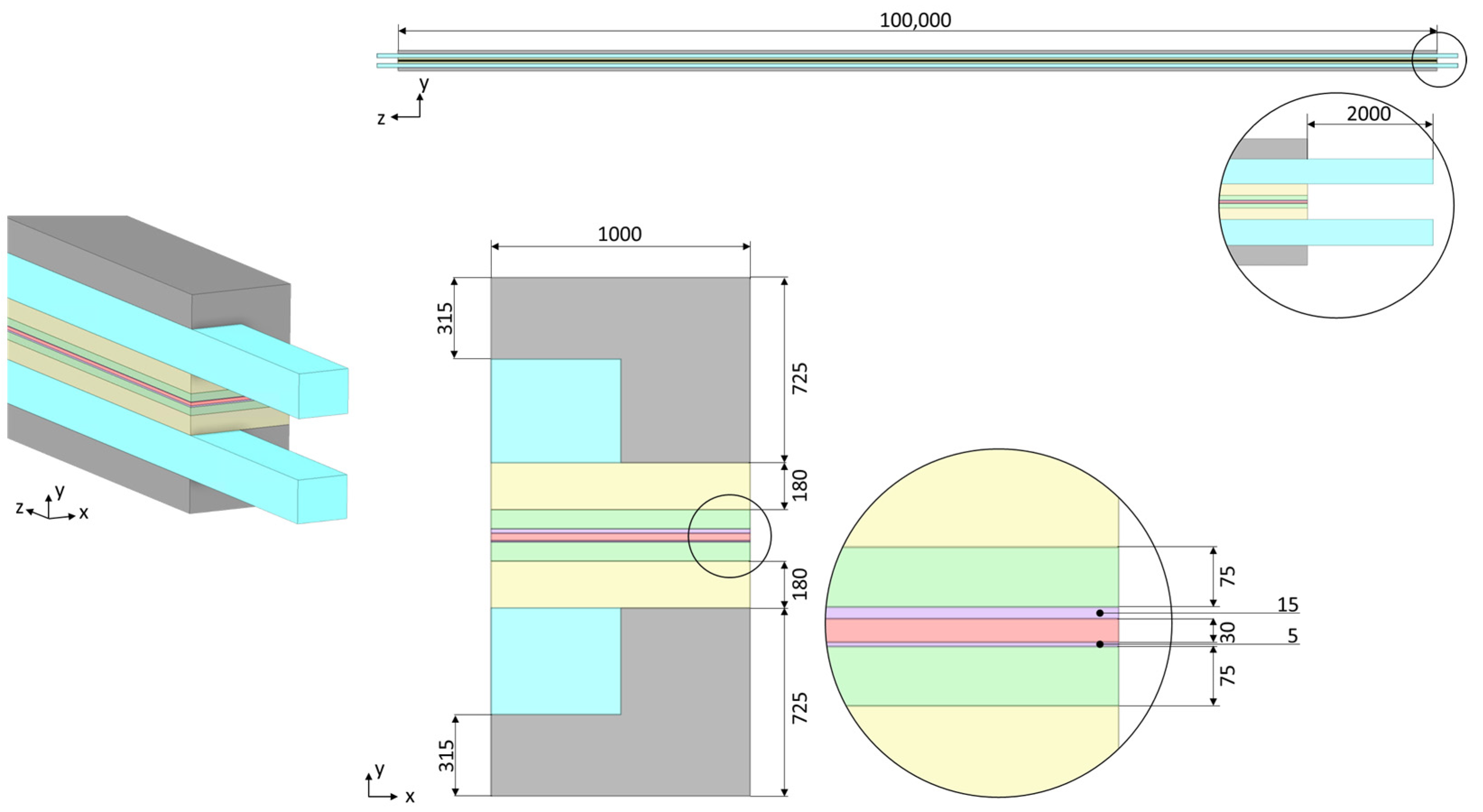
2.2. Geometry
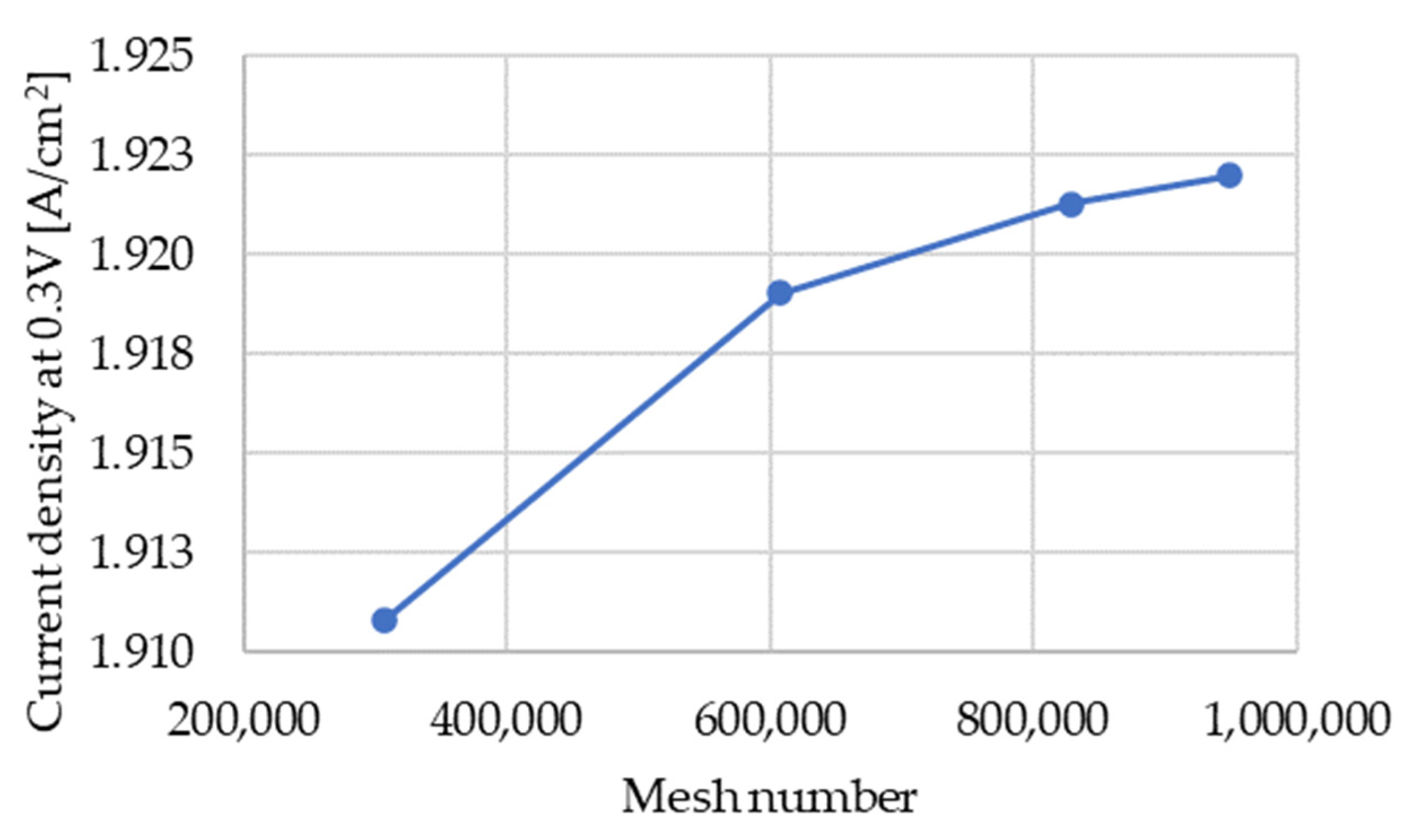
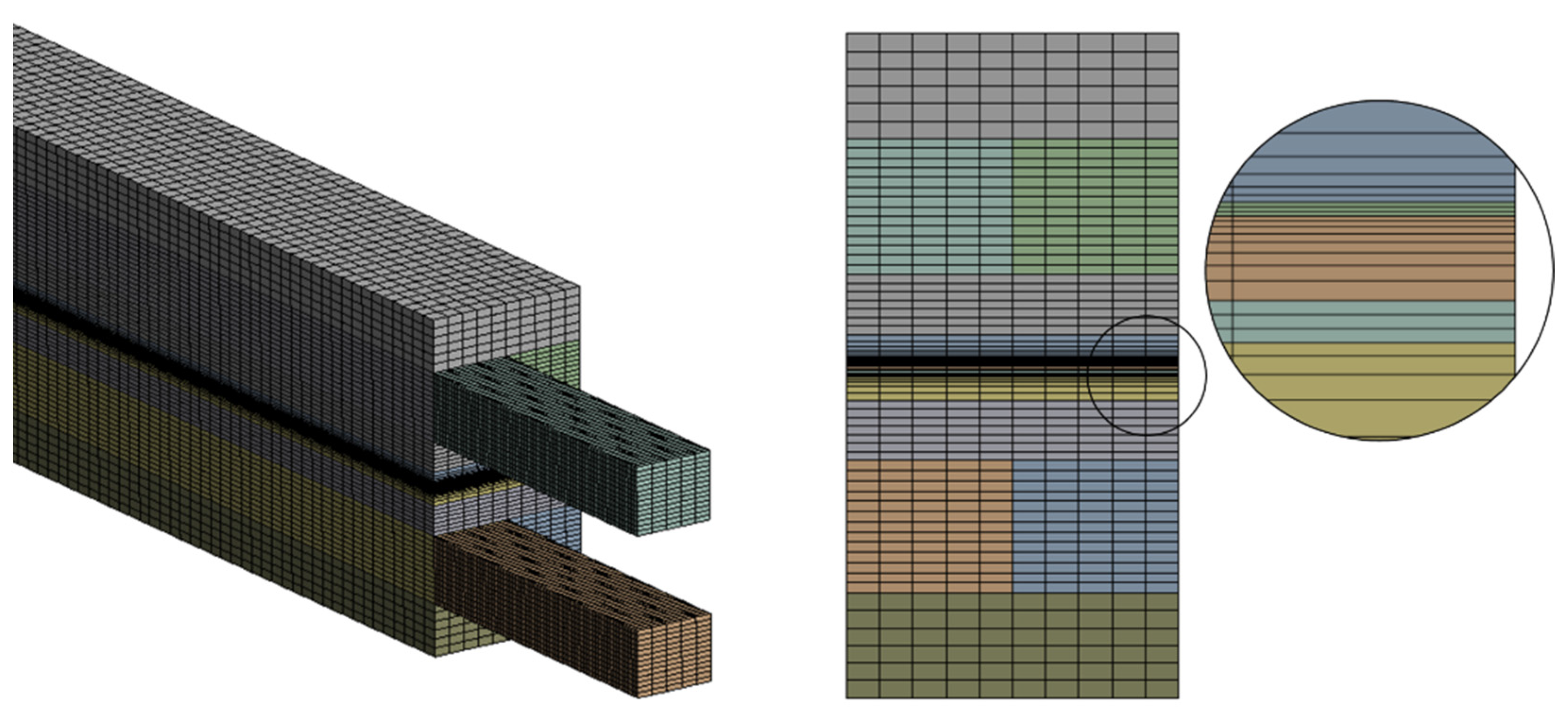
2.3. Mesh
2.4. Model Assumptions and Governing Equations
- Fluid flows are considered to be laminar, as Reynolds number for anode channels is below 35 and for cathode channels is below 255.
- The operation of the PEM fuel cell is under non-isothermal and steady-state conditions.
- Ideal gas laws are followed by all gas species.
- MEA materials are assumed to be isotropic.
- Transport and formation of liquid water are included.
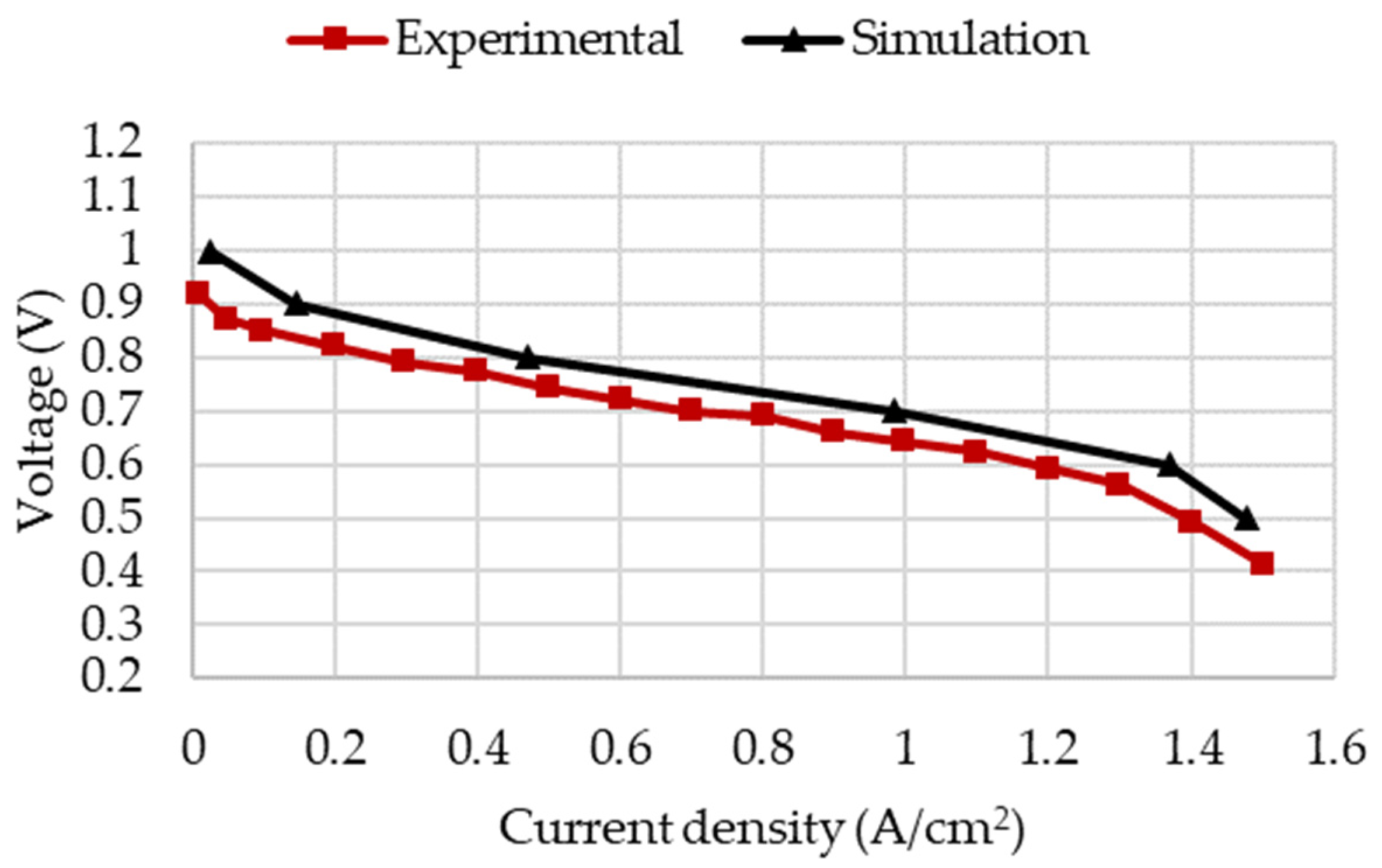
2.5. Model Validation
2.6. Input Parameters, Boundary Conditions, and Material Properties
2.7. Solver Setup
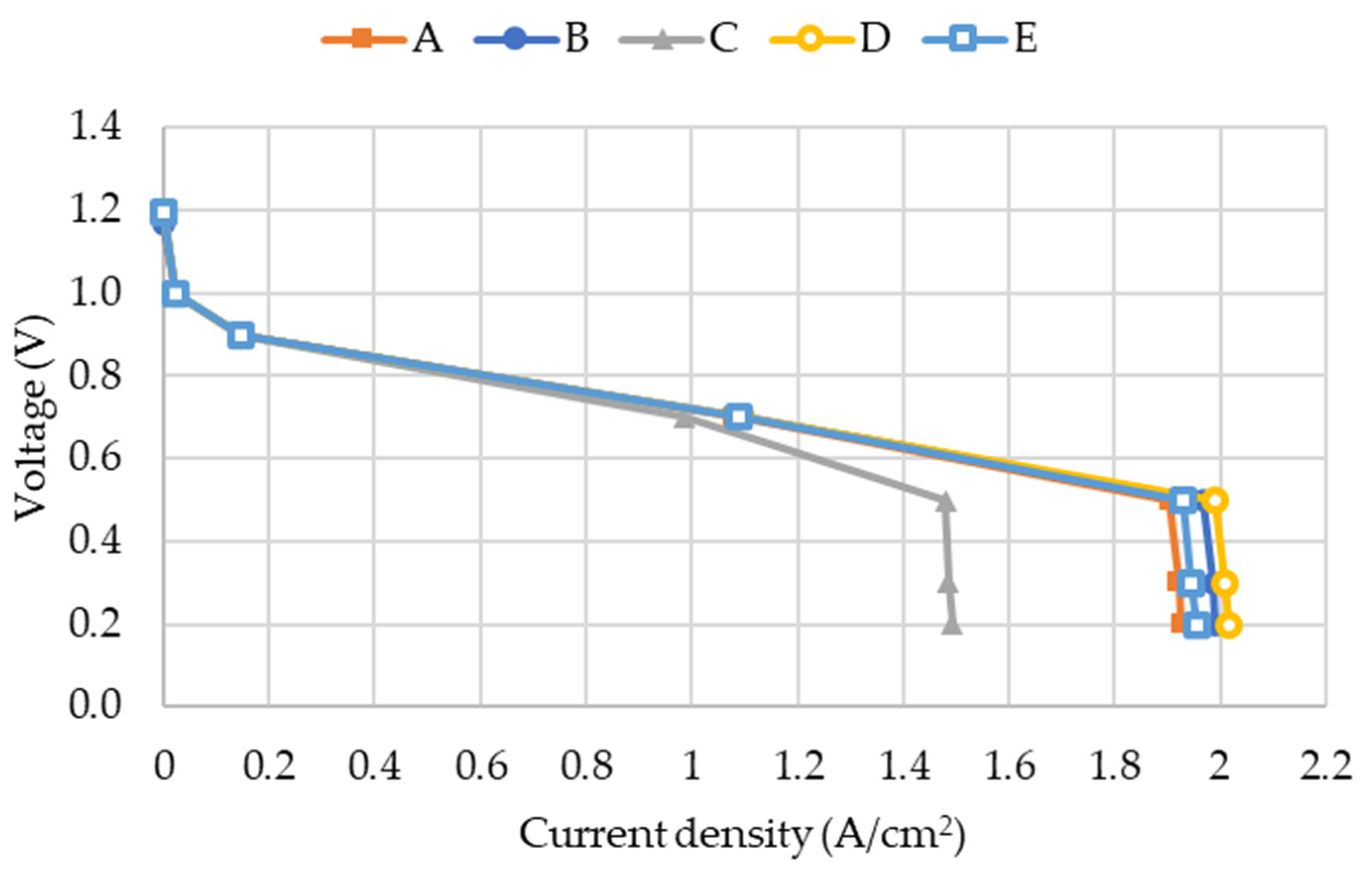
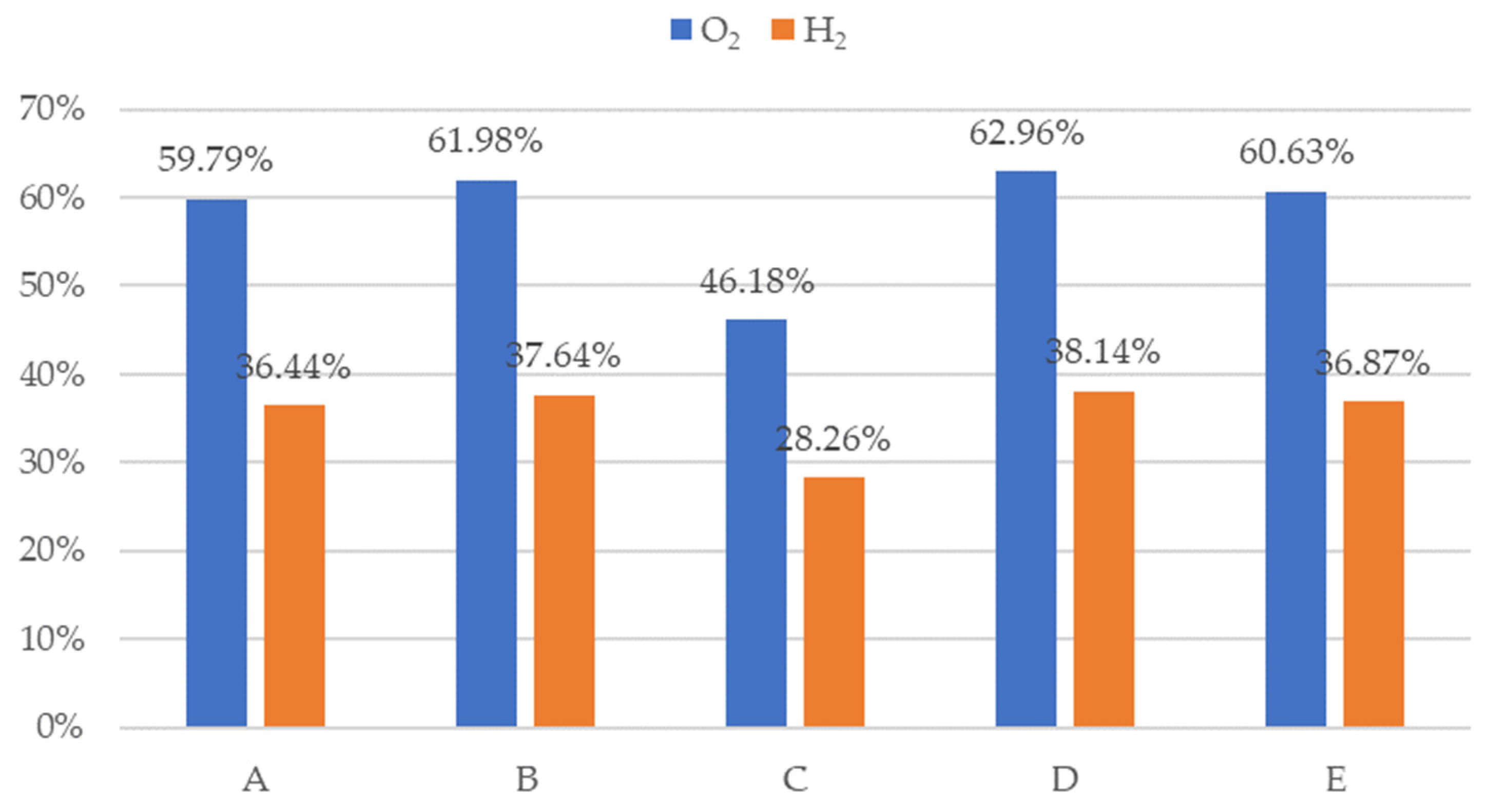
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abdi, H.; Ait Messaoudene, N.; Kolsi, L.; Naceur, M.W. Modeling and Optimization of a Proton Exchange Membrane Fuel Cell Using Particle Swarm Algorithm with Constriction Coefficient. J. Therm. Anal. Calorim. 2021, 144, 1749–1759. [Google Scholar] [CrossRef]
- Choi, Y.; Win, M.Z.; Oo, W.; Min, J.; Ko, K.; Kim, Y.; Choi, H.; Chougule, S.S.; Khikmatulla, D.; Yi, K.B.; et al. Experimental Simulation Study on the Poisoning Effect of Hydrocarbon-Based Ionomers on Pt Catalysts for Fuel Cells. Electrochem. Commun. 2023, 157, 107602. [Google Scholar] [CrossRef]
- Khan, M.I.; Asfand, F.; Al-Ghamdi, S.G. Progress in Research and Technological Advancements of Thermal Energy Storage Systems for Concentrated Solar Power. J. Energy Storage 2022, 55, 105860. [Google Scholar] [CrossRef]
- Guédez, R.; Spelling, J.; Laumert, B.; Fransson, T. Optimization of Thermal Energy Storage Integration Strategies for Peak Power Production by Concentrating Solar Power Plants. Energy Procedia 2014, 49, 1642–1651. [Google Scholar] [CrossRef]
- Deepak Selvakumar, R.; Wu, J.; Ding, Y.; Alkaabi, A.K. Melting Behavior of an Organic Phase Change Material in a Square Thermal Energy Storage Capsule with an Array of Wire Electrodes. Appl. Therm. Eng. 2023, 228, 120492. [Google Scholar] [CrossRef]
- Hu, K.; Zhao, P.; Wang, S.; Wang, Y. Three-Dimensional Multiphase Simulation of a Partially Narrowed Flow Field Configuration for a High-Performance Polymer Electrolyte Membrane Fuel Cell. Appl. Therm. Eng. 2023, 223, 119986. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Ding, H.; Pan, Z.; Huang, X.; Pan, X. Heat and Mass Transfer Characteristics of a Novel Three-Dimensional Flow Field Metal Bipolar Plate for PEMFC by Laser 3D Printing. Int. J. Hydrog. Energy 2023. [Google Scholar] [CrossRef]
- Li, S.; Jin, R.; Li, S.; Wang, L.; Xie, Z.; Li, X.; Wang, Z. High Corrosion Resistance and Conductivity of Al2O3/CrN Coating for Metal Bipolar Plates in PEMFCs: Al2O3 Hinders CrN Columnar Crystals Growth. Int. J. Hydrog. Energy 2023, in press. [Google Scholar] [CrossRef]
- Hazar, H.; Yilmaz, M.; Sevinc, H. The Effects of Different Flow Field Patterns on Polymer Electrolyte Membrane Fuel Cell Performance. Energy Convers. Manag. 2021, 248, 114818. [Google Scholar] [CrossRef]
- Wilberforce, T.; El-Hassan, Z.; Khatib, F.N.; Al Makky, A.; Mooney, J.; Barouaji, A.; Carton, J.G.; Olabi, A.-G. Development of Bi-Polar Plate Design of PEM Fuel Cell Using CFD Techniques. Int. J. Hydrog. Energy 2017, 42, 25663–25685. [Google Scholar] [CrossRef]
- Hu, C.; Zhao, Y.; Zhang, Z.; Zhang, H.; Chen, D. Optimization of Flow Field Structure for Proton Exchange Membrane Fuel Cell Stack by Multi-Physics Coupling Simulation. Int. J. Electrochem. Sci. 2023, 18, 100195. [Google Scholar] [CrossRef]
- Arif, M.; Cheung, S.C.P.; Andrews, J. Numerical Investigation of Effects of Different Flow Channel Configurations on the 100 cm2 PEM Fuel Cell Performance under Different Operating Conditions. Catal. Today 2022, 397–399, 449–462. [Google Scholar] [CrossRef]
- Carcadea, E.; Ismail, M.S.; Ingham, D.B.; Patularu, L.; Schitea, D.; Marinoiu, A.; Ion-Ebrasu, D.; Mocanu, D.; Varlam, M. Effects of Geometrical Dimensions of Flow Channels of a Large-Active-Area PEM Fuel Cell: A CFD Study. Int. J. Hydrog. Energy 2021, 46, 13572–13582. [Google Scholar] [CrossRef]
- Limjeerajarus, N.; Charoen-amornkitt, P. Effect of Different Flow Field Designs and Number of Channels on Performance of a Small PEFC. Int. J. Hydrog. Energy 2015, 40, 7144–7158. [Google Scholar] [CrossRef]
- Al-Okbi, Y.; Al-murshedi, A.S.N.; Nemah, M.N.; Saad, H.A.K. Influence of Design Anode and Cathode Channel on (PEMFC) Fuel Cell Performance. Mater. Today Proc. 2021, 42, 2177–2184. [Google Scholar] [CrossRef]
- Xu, C.; Wang, H.; Cheng, T. Wave-Shaped Flow Channel Design and Optimization of PEMFCs with a Groove in the Gas Diffusion Layer. Int. J. Hydrog. Energy 2023, 48, 4418–4429. [Google Scholar] [CrossRef]
- Xu, C.; Wang, H.; Li, Z.; Cheng, T. Effects of the Design and Optimization of Trapezoidal Channels and Baffles (Number and Position) on the Net Power Density of Proton-Exchange Membrane Fuel Cells. ACS Omega 2022, 7, 4214–4223. [Google Scholar] [CrossRef]
- Xuan, L.; Wang, Y.; Mei, D.; Lan, J. Design and Modelling of 3D Bionic Cathode Flow Field for Proton Exchange Membrane Fuel Cell. Energies 2021, 14, 6044. [Google Scholar] [CrossRef]
- Neto, D.M.; Oliveira, M.C.; Alves, J.L.; Menezes, L.F. Numerical Study on the Formability of Metallic Bipolar Plates for Proton Exchange Membrane (PEM) Fuel Cells. Metals 2019, 9, 810. [Google Scholar] [CrossRef]
- Wilberforce, T.; Ijaodola, O.; Emmanuel, O.; Thompson, J.; Olabi, A.; Abdelkareem, M. Optimization of Fuel Cell Performance Using Computational Fluid Dynamics. Membranes 2021, 11, 146. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wang, Q.; Bai, F.; Chen, L.; Tao, W. Performance Simulation and Key Parameters In-Plane Distribution Analysis of a Commercial-Size PEMFC. Energy 2023, 263, 125897. [Google Scholar] [CrossRef]
- Tzelepis, S.; Kavadias, K.A.; Marnellos, G.E. A Three-Dimensional Simulation Model for Proton Exchange Membrane Fuel Cells with Conventional and Bimetallic Catalyst Layers. Energies 2023, 16, 4086. [Google Scholar] [CrossRef]
- Iranzo, A.; Gregorio, J.M.; Boillat, P.; Rosa, F. Bipolar Plate Research Using Computational Fluid Dynamics and Neutron Radiography for Proton Exchange Membrane Fuel Cells. Int. J. Hydrog. Energy 2020, 45, 12432–12442. [Google Scholar] [CrossRef]
- ANSYS, Inc. Chapter 21: Modeling fuel cells. In Fluent Theory Guide 2023 R2; ANSYS: Ann Arbor, MI, USA, 2023. [Google Scholar]
- Arif, M.; Cheung, S.C.P.; Andrews, J. Diagnostic Analysis of a Single-Cell Proton Exchange Membrane Unitised Regenerative Fuel Cell Using Numerical Simulation. Int. J. Hydrog. Energy 2021, 46, 29488–29500. [Google Scholar] [CrossRef]
- Arif, M.; Cheung, S.C.P.; Andrews, J. A Systematic Approach for Matching Simulated and Experimental Polarization Curves for a PEM Fuel Cell. Int. J. Hydrog. Energy 2020, 45, 2206–2223. [Google Scholar] [CrossRef]
- Al-Baghdadi, M.A.R.S. A CFD Model for Analysis of Performance, Water and Thermal Distribution, and Mechanical Related Failure in PEM Fuel Cells. J. Mechatron. Electr. Power Veh. Technol. 2016, 7, 7–20. [Google Scholar] [CrossRef]
- Hashemi, F.; Rowshanzamir, S.; Rezakazemi, M. CFD Simulation of PEM Fuel Cell Performance: Effect of Straight and Serpentine Flow Fields. Math. Comput. Model. 2012, 55, 1540–1557. [Google Scholar] [CrossRef]
- Woo, C.H.; Benziger, J.B. PEM Fuel Cell Current Regulation by Fuel Feed Control. Chem. Eng. Sci. 2007, 62, 957–968. [Google Scholar] [CrossRef]
- Baghban Yousefkhani, M.; Ghadamian, H.; Daneshvar, K.; Alizadeh, N.; Rincon Troconis, B.C. Investigation of the Fuel Utilization Factor in PEM Fuel Cell Considering the Effect of Relative Humidity at the Cathode. Energies 2020, 13, 6117. [Google Scholar] [CrossRef]



| Contact Area (cm2) | Anode Velocity (m/s) | Cathode Velocity (m/s) | |
|---|---|---|---|
| A | 0.50 | 2.22 | 3.56 |
| B | 0.50 | 4.53 | 7.02 |
| C | 0.25 | 4.44 | 7.08 |
| D | 0.60 | 2.22 | 3.56 |
| E | 0.50 | 2.22 * | 3.56 * |
| Input Parameters | Value |
|---|---|
| ) | 10,000 (A/m2) |
| ) | 10 (A/m2) |
| ) | 1 |
| ) | 1 |
| ) | 9.65 × 104 (C/mol) |
| ) | 8.314 (J/(mol K)) |
| Anode electrode specific active surface area () | 20,000 (m−1) |
| Cathode electrode specific active surface area () | 20,000 (m−1) |
| Region | Boundary Condition |
|---|---|
| Anode channel inlet | ; |
| Cathode channel inlet | |
| Anode channel outlet | |
| Cathode channel outlet | |
| Anode terminal | |
| Cathode terminal | |
| Exterior boundaries | ; ; |
| Operating Parameters | Value |
|---|---|
| Cell temperature | 70 (°C) |
| Operating pressure | 2 (bar) |
| Anode mass flow rate | 1 × 10−7 (kg/s) |
| Anode H2 mass fraction at inlet | 0.60 |
| Anode H2O mass fraction at inlet | 0.40 |
| Cathode mass flow rate | 1.4 × 10−6 (kg/s) |
| Cathode O2 mass fraction at inlet | 0.21 |
| Cathode H2O mass fraction at inlet | 0.05 |
| Property | Catalyst | Current Collector | GDL | Membrane | Micro-Porous Layer |
|---|---|---|---|---|---|
| Density (kg/m3) | 2719 | 2719 | 2719 | 1980 | 2719 |
| Specific heat density (J/(kg K)) | 871 | 871 | 871 | 2000 | 871 |
| Thermal conductivity (W/(m K)) | 10 | 100 | 10 | 2 | 10 |
| Electrical conductivity (S/m) | 5 × 103 | 1 × 106 | 5 × 103 | 1 × 10−16 | 5 × 103 |
| Porosity | 0.2 | - | 0.6 | 0.5 | 0.3 |
| Permeability (m2) | 2 × 10−13 | - | 3 × 10−12 | 1 × 10−18 | 1 × 10−12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Busqué, R.; Bossio, M.; Brigido, A.; Lara, A. Effects of Different Channel Geometries of Metallic Bipolar Plates on Proton Exchange Membrane Fuel Cell Performance. Energies 2023, 16, 7702. https://doi.org/10.3390/en16237702
Busqué R, Bossio M, Brigido A, Lara A. Effects of Different Channel Geometries of Metallic Bipolar Plates on Proton Exchange Membrane Fuel Cell Performance. Energies. 2023; 16(23):7702. https://doi.org/10.3390/en16237702
Chicago/Turabian StyleBusqué, Raquel, Matias Bossio, Albert Brigido, and Antoni Lara. 2023. "Effects of Different Channel Geometries of Metallic Bipolar Plates on Proton Exchange Membrane Fuel Cell Performance" Energies 16, no. 23: 7702. https://doi.org/10.3390/en16237702
APA StyleBusqué, R., Bossio, M., Brigido, A., & Lara, A. (2023). Effects of Different Channel Geometries of Metallic Bipolar Plates on Proton Exchange Membrane Fuel Cell Performance. Energies, 16(23), 7702. https://doi.org/10.3390/en16237702







