1. Introduction
Energy is a fundamental factor for sustainable economic development, as well as a key element required to achieve and maintain the stability of the economy and society [
1]. Over the last 60 years, energy consumption has increased almost fourfold, from 155.88 EJ in 1960 to 595.15 EJ in 2021 [
2]. The global scale of energy needs is well demonstrated by forecasts according to which global energy consumption is expected to increase by 50% by 2050 compared to 2018 [
3]. Currently, most energy comes from fossil fuels—the main energy sources are coal, oil and natural gas [
4]. According to data from 2022, the share of coal in the global energy mix is approximately 26%, oil—31%, and gas—23% [
5]. Unfortunately, fossil fuels, according to research, are responsible for 80% of global CO
2 emissions and are considered the main cause of global warming [
6]. Therefore, out of concern for the environment and the threat of climate change, many regions of the world are trying to gradually reduce the use of fossil fuels and replace them with renewable energy [
7]. The scale of this phenomenon is shown by a comparison of investments in renewable energy sources (RES) in 2004 and 2018. While in 2004 global investments in RES amounted to USD 50 billion, in 2018 it was already six times more, i.e., USD 300 billion [
8]. According to other data, over the years 2010–2019, global investments in RES (excluding hydropower plants) totalled USD 2.7 trillion. The largest financial outlays during this time were made in China (USD 818 billion), United States (USD 392 billion), Japan (USD 211 billion), Germany (USD 183 billion), and United Kingdom (USD 127 billion) [
9]. Together with investments in RES, their production capacity increases. The International Energy Agency (IEA) predicts that by 2026, the increase in RES generation capacity will account for approximately 95% of the total increase in energy capacity in the world [
10]. Therefore, fossil fuels will only contribute to 5% of the increase in production capacity.
Growing investments in renewable energy are justified by a number of benefits that the use of RES brings. First of all, it is recognized that RES do not emit (or emit only minimally) pollutants and greenhouse gases, reducing air and water pollution and limiting climate change [
8,
11]. In addition to the environmental aspect, an important advantage is the diversity of RES, which means that almost every country has some renewable resources [
12]. This translates into reduced dependence on energy exporters, because part of the needed energy can be produced locally and does not have to be imported from other countries that have access to fossil fuels [
8,
11,
13]. Another advantage that reduces dependence on energy exporters is the abundance of RES, so there is no risk of running out of energy in a relatively short time [
8,
11]. Moreover, investments in RES allow for the creation of new jobs and contribute to driving economic growth [
8,
11,
14]. In particular, it was observed that the increase in renewable energy consumption is determined by a higher level of human capital and the stage of country development [
15]. A positive relationship was also noted between increasing renewable energy generation capacity and employment, showing an increase in employment of 0.48% for every 1% increase in renewable energy generation capacity [
16]. The role of RES in a circular economy is important, as recycling and RES have been shown to be important factors in ensuring sustainable economic development with less climate deterioration [
17]. RES also have some disadvantages and limitations, such as the lack of continuity of energy production from RES, the dependence of production on weather conditions and the lack of synchronization of energy generation peaks in RES with energy consumption peaks [
18]. However, currently the greatest disadvantage of RES is the high costs of energy transformation consisting in switching from the use of conventional energy sources (fossil fuels) to renewable sources [
12]. This means that, despite increasingly larger investments and development of RES, the coexistence of renewable energy and energy from fossil fuels is assumed in the next few decades [
13,
18].
The advantages and potential benefits of using RES cause individual countries and groups of countries to engage in the development of renewable energy. Particularly ambitious actions in this area are undertaken by the European Union (EU), which is a world leader in introducing pro-environmental legislation [
12]. The energy transformation of EU countries includes, among others: reducing investments in the extraction of fossil fuels, eliminating coal-fired power plants, and increasing investments in technological innovations related to energy [
18]. Of particular importance in the EU in the context of energy transformation and the transition to the use of RES is the “Green Deal” program adopted in 2019. It assumes that the EU economy will become “zero-emission” by 2050 and gain energy independence [
19]. Moreover, in 2021, the EU adopted the “Fit for 55” package requiring member countries to reduce greenhouse gas emissions by 55% by 2030 and assuming further increases in the use of RES [
12]. It should be noted that between 2000 and 2019, the consumption of energy from RES in all economic sectors and households in the EU-27 increased by over 200%. The largest increase in the use of renewable energy in the EU-27 occurred in the transport sector (by 2200%), the smallest in industry (by 150%), and in the case of households the increase was 165% [
12]. By 2020, nine EU countries have phased out coal-based energy, thirteen countries have set a deadline for phasing out coal, and four more countries are considering possible timetables [
20]. In 2000, 60% of RES consumption in EU households belonged to Germany, Spain, France, Poland, and Romania, while in 2019 the share of these countries increased to 67%. In the industrial sector, in 2000, Sweden, Finland, Spain, France and Portugal together accounted for 67% of RES consumption in the EU, while in 2019, 72% of RES consumption in this sector was accounted for (in order of biggest consumers) by Sweden, Finland, Germany, France, Spain and Poland. As for the transport sector, in 2000, 100% of RES consumption belonged to Germany, France, Spain, Austria, the Czech Republic and Romania. In 2019, the largest consumers of RES in the transport sector were Germany, Spain, France, Italy, Sweden, and Poland, which consumed a total of 71% of the energy produced in the EU from RES [
12].
The data presented above show that the structure of the energy mix of individual countries changes dynamically over time. The order of leading countries in the EU in terms of energy transformation and the transition from fossil fuels to RES in various sectors of the economy is also changing. Taking into account the potential benefits of switching to RES and the EU requirements for member states in this respect, the assessment of the progress of the energy transformation of individual EU countries is an important research problem. This progress needs to be continuously monitored and reviewed to ensure that all EU countries are moving in the same direction. Constant monitoring of the energy transformation will allow us to support and motivate countries that are coping worse with the transformation, as well as to appreciate countries that are leaders in this field. Moreover, it is important to analyze the transformation over a longer period of time in order to reliably assess the entire energy transformation process of EU countries over the last dozen or so years. Therefore, the aim of the article is a temporal analysis of the energy transformation process towards switching to RES and reducing the use of fossil fuels in energy production. The achievement of the indicated goal is the practical contribution of the article. Unfortunately, there is a shortage of methods in scientific methodology that would broadly take into account data from many periods and the dynamics of changes in subsequent periods in the analysis. In order to fill this methodological gap, the dynamic multi-criteria decision-making (DMCDM) framework allowing for the temporal assessment of the progress of energy transformation of individual countries was developed [
21]. The framework uses the Preference Ranking Organization Method for Enrichment Evaluation for Sustainability Assessment (PROSA) [
22] to take into account changes in the structure of the energy mix of a given country compared to other countries examined. The developed approach allows to take into account partial data from many periods, the dynamics of changes in these data and the evolution of individual countries in the context of energy transformation, as well as generate a clear quantitative assessment of the transformation process. This approach is based on the application of the DMCDM framework in combination with the PROSA method is a new methodological issue, previously unheard of in the literature, and is the scientific contribution of the article. The developed approach was formalized in the form of the DMCDM method called Temporal PROSA.
Section 2 presents the state of the art of dynamic and temporal approaches to MCDM. The imperfections of the approaches used and their methodological gaps were pointed out.
Section 3 discusses the proposed form of time representation in the MCDM paradigm. In addition, a newly developed Temporal PROSA method is presented, which fills the previously indicated gaps.
Section 4 discusses the criteria and results of assessing the progress of the energy transformation of EU countries. Both temporal results from subsequent periods, as well as overall results are presented, aggregating individual periods into one assessment value.
Section 5 contains conclusions as well as a discussion of research limitations and further research directions.
4. Results
4.1. Criteria for Assessing the Progress of Energy Transformation
The energy transformation study used 11 criteria related to energy productivity, energy consumption, the share of RES in the energy mix and energy prices. It should be explained here that the analysis of the energy transformation process of individual EU countries cannot be based on absolute values, because each country has different energy needs, depending on population, industrialization, etc. A country that has a larger population and a more developed industry will consume more energy than a country that is less economically developed and has a smaller population. Therefore, a direct comparison of, for example, Germany and Cyprus would be a methodological error. Therefore, the study was based on relative criteria, taking into account, among others, population or energy consumption in previous years. In assessing the progress of the energy transformation of EU countries, the criteria presented in
Table 2 were taken into account.
The C1 criterion (Energy productivity) assesses the quantity of economic output generated per unit of gross available energy. Gross available energy signifies the amount of energy products required to fulfill the demands of entities within the specified geographical area. The economic output is presented in Euros, adjusted for inflation, referencing the year 2010 and utilizing exchange rates from that same year. This allows you to observe the evolution of a given country over time.
The C2 (Primary energy consumption) and C3 (Final energy consumption) criteria measure energy efficiency taking into account energy consumption expressed in Million Tonnes of Oil Equivalent (MTOE). Energy consumption in each country was related to 2005 (base year) for that country. In this way, indexes were established describing the progress of each country in reducing energy consumption over the years.
The C4 criterion (Final energy consumption in households per capita) gauges the amount of electricity and heat an individual utilizes at home, excluding energy devoted to transportation. This metric specifically focuses on the energy consumed by end-users, disregarding the internal energy consumption of the energy sector.
The C5 criterion (GHG emissions intensity of energy consumption) is determined by the ratio of energy-related GHG emissions to the gross inland consumption of energy. This criterion quantifies the number of tonnes of CO2 equivalents emitted from energy-related GHGs in a specific economy per unit of energy consumed. This value was expressed in the form of an index, for which the reference year was 2000. This allowed the assessment to take into account the progress of a given country in reducing greenhouse gas emissions related to energy consumption.
The C6 (Share of energy from RES), C7 (Share of energy from RES in transport), C8 (Share of energy from RES in electricity), and C9 (Share of energy from RES in heating and cooling) criteria measure the share of renewable energy in total energy consumption. The C6 criterion refers to total energy consumption in all sectors of the economy and in households, while C7–C9 criteria refer to specific areas in which energy is used.
The C10 (Electricity prices for medium size households) and C11 (Electricity prices for medium size industrial consumers) criteria present electricity prices charged to final consumers. For household consumers, electricity prices are determined as the average national price in Euros per kWh, encompassing taxes and levies, applicable for the first half of each year. This calculation pertains to medium-sized household consumers falling within a consumption band with an annual consumption ranging from 2500 to 5000 kWh. On the other hand, for non-household consumers, electricity prices are defined as the average national price in Euros per kWh, excluding taxes, applicable for the first half of each year. This calculation applies to medium-sized industrial consumers within a consumption band with an annual consumption ranging from 500 to 2000 MWh. The C1–C9 criteria were previously used in a study of energy systems in European countries presented by Bączkiewicz and Wątróbski [
41]. The C1 and C4–C9 criteria in our study were used in the same form as in the work by Bączkiewicz and Wątróbski, but the data in both works come from different periods. However, the C2 and C3 criteria differ significantly from those used by Bączkiewicz and Wątróbski. In the work by Bączkiewicz and Wątróbski [
41], C2 and C3 were expressed in relations to the number of inhabitants, while in our study we used indexes referring to 2005. The difference is that in the work by Bączkiewicz and Wątróbski, the C2 and C3 criteria present raw numerical data, while in our study these criteria provide direct information about a given country’s progress in reducing energy consumption over subsequent years in relation to previous years. Together with the C5 criterion expressed as an index in relation to the year 2000, the C2 and C3 criteria allow to capture the dynamics of changes in energy consumption and the related dynamics of changes in the intensity of GHG emissions. The C2 and C3 criteria are complemented by the C4 criterion, which measures energy consumption in households; however not as an index, but in absolute values. The other important criteria are C1, C6–C9, C10 and C11. The C1 criterion allows us to determine how efficient the energy sector of a given country is, i.e., what is the economic production per unit of energy. The C6–C9 criteria allow you to measure progress in the transition to renewable energy sources in various sectors of the economy. In turn, the C10 and C11 criteria show to some extent the impact of the energy transition on energy prices. Of course, this is an indirect impact, excluding factors such as inflation.
4.2. Temporal Study of Individual Periods
The data included in the study were expressed in annual periods from 2004 to 2021. The values of the criteria for the examined EU countries are included in
Supplementary File S1. It should be noted that in the case of C10 and C11 criteria, the data referred to the years 2011–2021, while there was no data for the years 2004–2010. The preference model used in the temporal study for each period is presented in
Table 3. The criteria weights were normalized to 100%. The energy productivity criterion (C1) was given a weight of 10%, the energy consumption criteria (C2–C4) were given a total weight of 20%, the single environmental criterion (C5) was given a weight of 20%, the criteria regarding the share of energy from RES (C6–C9) were given a total weight of 40%, and the criteria related to energy prices (C10 and C11) were assigned a weight of 10% in total. For the C1, C6–C9 criteria, the highest possible values are desired, while the remaining criteria are of a cost nature, so their values are expected to be as low as possible. A linear preference function (V-shaped criterion) was used for each criterion. The preference threshold for this function was each time twice the population standard deviation calculated on the basis of the values of all alternatives for a given criterion in the examined period.
The PROMETHEE II method was used o aggregate preferences in each period, the steps of which are identical to the initial steps of the PROSA method, up to the moment of calculating global net flows
[
51,
54]. For each analyzed period, separate values of the
assessment and country rankings were obtained, showing the degree of advancement of the energy transformation in a given year compared to other EU countries. The evaluation results in individual periods are presented in
Table 4, while the country rankings are presented in
Table 5. Additionally,
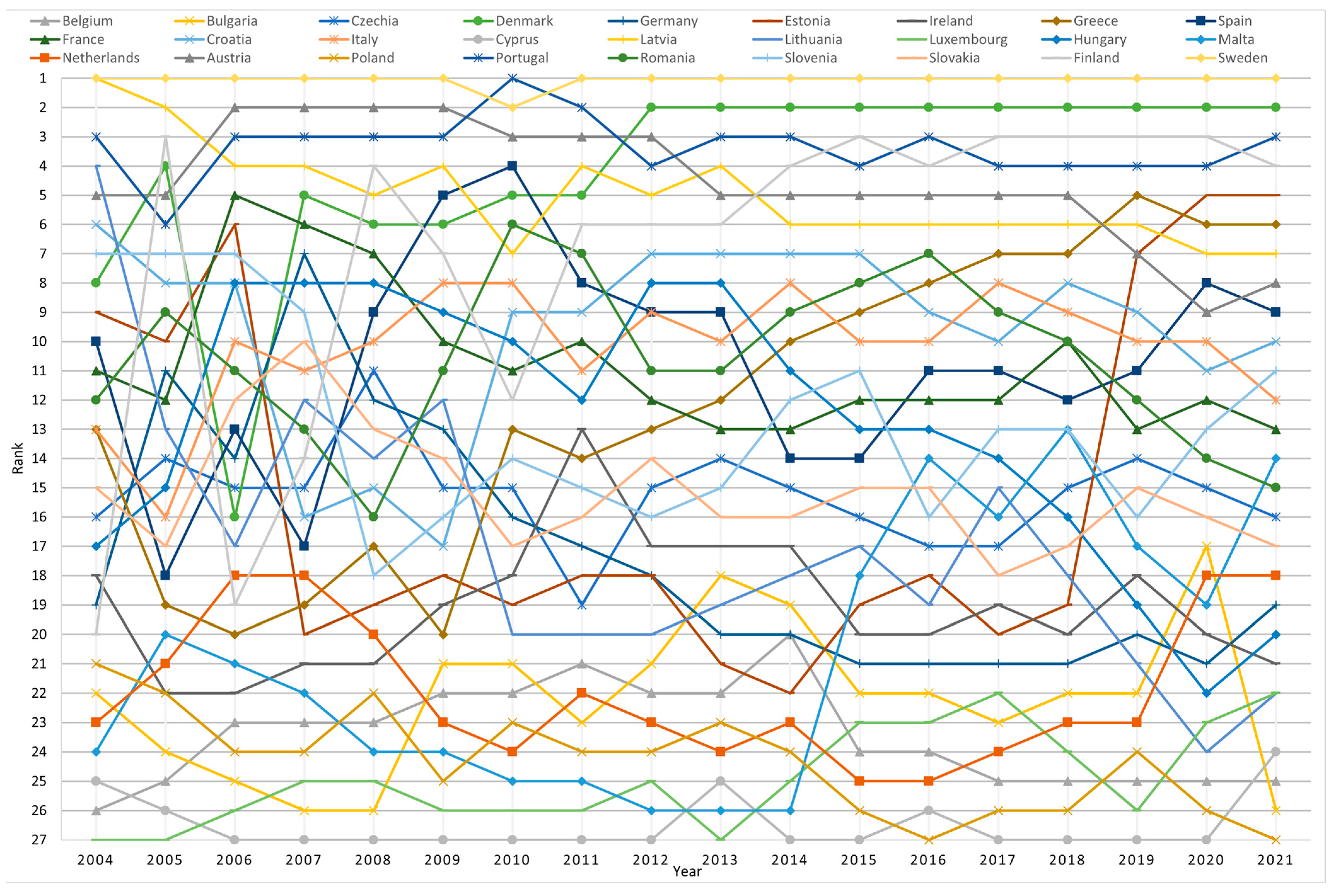
Figure 1 presents the country rankings in subsequent years in a graphical form.
The analysis of temporal results allows us to see the EU countries that have dominated over the last 20 years in terms of energy transformation. The first position in almost all periods was taken by Sweden, only in 2010 it was overtaken by Portugal. Portugal has also been consistently high compared to other countries over the last 20 years. In the case of several countries that have been dynamically modernizing their energy sector in recent years and switching to RES, we can see the progress that has been made since 2004. In particular, we are talking about Finland and Denmark. In the ranking for 2004, Denmark ranked 8th, in 2006–2016, but since 2012 only Sweden has overtaken it. Similarly, Finland was ranked 20th in 2004, while since 2014 it has consistently occupied the 3rd or 4th place in the ranking. The C5 criterion is largely responsible for the distant positions in the rankings of Finland in 2004 and 2006, as well as in Denmark in 2006. In these years, the value of the GHG emissions intensity of energy consumption (C5) index read from Eurostat data increased significantly for the indicated countries. For some countries, e.g., Spain, a “jump” in the ranking can be observed in 2005 compared to other years. These anomalies result from the fact that the values of the C2 and C3 criteria in 2005 for all countries were exactly the same (100%), because it was the base year for the indices represented by C2 and C3. Therefore, these criteria did not in any way influence the ratings of individual countries in 2005, while in the neighbouring years 2004 and 2006 such an influence existed.
In addition to countries such as Denmark, Finland, Greece, and Estonia, which have made significant progress in energy transformation and switching to RES in recent years, there are also countries that have significantly slowed down the transformation. These countries certainly include Latvia, Hungary, Austria, and Germany, which in the following years occupy lower and lower positions in the rankings. The countries making the least progress each year include Belgium, Bulgaria, Cyprus, Luxembourg, and Poland. These countries occupy the last positions in each period in terms of the degree of advancement of the energy transformation.
4.3. Study of the Progress of the Energy Transformations of EU Countries over the Years 2004–2021
In order to generally assess the progress of the energy transformation, the temporal results included in
Table 4 have been aggregated into an overall assessment.
Table 6 shows the preference model used to aggregate the individual periods into a single rating. For all periods, the compensation (balance) coefficient
and the linear preference function
z progiem preferencji
were used. For all periods, the highest possible
values obtained by individual countries were preferred. When weighing individual periods, a “forgetting” strategy was used, so older periods were assigned a correspondingly lower weight.
The results of the overall assessment of the progress of individual EU countries are presented in
Table 7.
Table 7 contains the assessment results and ranking based on the PROSA method (
), as well as WMAD values describing the variability of individual countries’ results over time. Additionally,
Table 7 contains the ratings and ranking obtained using the PROMETHEE II method for comparative purposes.
The ranking determined using the Temporal PROSA method confirms observations from temporal rankings regarding countries that have made the greatest and least progress in energy transformation over the years 2004–2021. Sweden tops the overall ranking, ahead of Portugal and Denmark, followed by Austria, Latvia, and Finland. The ranking is closed by Cyprus, Luxembourg, Poland, Belgium, The Netherlands, and Bulgaria. The Czech Republic and Italy are characterized by the lowest variability over time, and the highest variability over time had Estonia, Denmark, and Finland. By comparing the ranking based on (Temporal PROSA) and (PROMETHEE II), it is possible to observe how the variability of the alternatives influenced their final results. In the case of Estonia, the variability over time resulted in a two-position decline in the ranking based on (Temporal PROSA) compared to the ranking based on (PROMETHEE II). In the case of Denmark, Finland, as well as Germany, Croatia, Hungary, Malta and Finland, the relatively high variability resulted in these countries deteriorating by one position in the PROSA ranking compared to PROMETHEE II ranking. An exception in this study is Greece, where relatively high variability caused a drop in the PROSA ranking by as much as three positions in relation to the PROMETHEE II ranking. In turn, low variability is responsible for the advancement of some countries in the Temporal PROSA ranking compared to the PROMETHEE II ranking. Relatively low variability contributed to Bulgaria, Ireland, Spain, France, Italy, Latvia, Portugal, Romania, Slovenia, and Slovakia moving up one place in the ranking.
5. Discussion
The ranking obtained using the Temporal PROSA method was compared with the DARIA-TOPSIS ranking obtained in the assessment of energy systems in European countries in the article by Bączkiewicz and Wątróbski [
41]. Comparing these rankings is justified due to the similar subject matter of both studies, the similarity of the methodological approach (temporal analysis), as well as the use of a similar set of criteria (see:
Section 4.1) and decision-making alternatives. A comparison of the rankings is presented in
Table 8, but it should be explained that in [
41] 30 countries were taken into account, but
Table 8 omitted three non-EU countries (Iceland, Norway, and United Kingdom).
Analyzing
Table 8, it can be seen that the results obtained only partially overlap. The same or similar position in individual rankings is occupied by: Sweden (Temporal PROSA: 1, DARIA-TOPSIS: 1), Denmark (3, 3), Austria (4, 5), Latvia (5, 7), Croatia (8, 11), Hungary (14, 14), Slovakia (16, 18), Germany (20, 19), Cyprus (27, 25). In turn, the largest differences in terms of positions in the rankings occur in the following countries: Estonia (17, 4), Ireland (19, 6), Spain (9, 23), Italy (7, 21), Luxembourg (26, 10), The Netherlands (23, 13), Poland (25, 12), Portugal (2, 24), Romania (10, 22). It can be concluded that for some countries the differences in rankings are significant. One of the reasons for such large differences in the rankings are the methodological differences between the PROSA and TOPSIS methods. Another reason is the use of completely different approaches to capture variability during temporal aggregation (see:
Section 2.3). In particular, the DARIA-TOPSIS method examines variability over time using the Gini coefficient, and Temporal PROSA uses WMAD for this purpose. Moreover, DARIA-TOPSIS simply corrects the latest temporal ranking using the measured variability, while Temporal PROSA verifies the variability between each subsequent period and based on this variability, adjusts the weighted average of all rankings. Both studies also referred to different periods because the study using the DARIA-TOPSIS method covered the years 2016–2020, while the study using the Temporal PROSA method covered the 2004–2021 period. The final reason for the differences between the DARIA-TOPSIS and Temporal PROSA rankings are differences in the criteria used. Both studies used the same seven criteria, two criteria differed in that one study used numerical criteria and the other used index criteria (see:
Section 4.1). Additionally, in the case of energy consumption criteria (C2 and C3) in the DARIA-TOPSIS study, minimum was indicated as the direction of preference. This is quite strange because energy sustainability is about reducing energy consumption, not increasing it.
6. Conclusions
The aims of the article were a temporal analysis and assessment of the progress made by individual EU countries towards the transition to RES. The study showed that the leaders in this respect among EU countries are Sweden and Portugal. They are followed by Denmark and Finland, which have significantly accelerated their energy transformation in recent years, and Austria and Latvia, which in turn have slowed down the transformation process in recent years. At the opposite extreme are countries such as Bulgaria, The Netherlands, Belgium, Poland, Luxembourg, and Cyprus. Considering the positions of the countries informally managing EU policy, the distant ranking of Germany and the Benelux countries may seem surprising. It is largely Germany and The Netherlands that are lobbying for the EU to pursue an increasingly restrictive energy policy. This time, it turns out that they themselves have a lot to improve in this area.
The analytical study carried out was a practical contribution to the article. In turn, the methodological contribution was the development of the PROSA family of MCDM methods and the development of a new dynamic MCDM method called Temporal PROSA. This method is based on the DMCDM framework and PROSA-C/PROMETHEE II methods. Like other recent temporal approaches, PROSA also uses the dispersion measure to provide information about the variability of a temporal data set. Moreover, PROSA, thanks to the appropriate mathematical formulation, unlike many other temporal methods, allows, among others, for the aggregation of data from many periods into a single final assessment and direct transfer of information from the examined periods to the overall result.
The research conducted and the results obtained obviously have their limitations. The main research limitation is related to the construction of the decision-making model. The study used 11 criteria regarding productivity, consumption, and energy prices, as well as the share of RES in the energy mix. Of course, using different criteria could yield different results. However, the indicated criteria, thanks to their relative nature, made the assessment results largely independent of the economic and population characteristics of the countries. The criteria used are objective measures and indices of energy transformation. The second research limitation concerns the methodology used. The Temporal PROSA method allows the use of any MCDM method giving a total order of alternatives in the first stage. Therefore, the use of a method other than PROMETHEE II in the first stage could also produce slightly different results. However, the use of PROMETHEE II resulted from the fact that it belongs to the same family of methods as the PROSA methods (in practice, the PROSA methods are an extension of the PROMETHEE methods). The above-mentioned research limitations indicate potential directions for further research. This research will include modifying and expanding the set of criteria to include other indicators to measure the progress of the energy transformation. Future research must also take into account the diversity of MCDM methods and the possibility of using a different method than PROMETHEE II in the first stage of Temporal PROSA, which was used in this study.