Analysis of the Wireless Power Transfer System Using a Finite Grid of Planar Circular Coils
Abstract
:1. Introduction
2. Methodology
2.1. System Description
2.2. Equivalent Circuit
2.3. Experimental Study
3. Discussion of the Results
3.1. Results
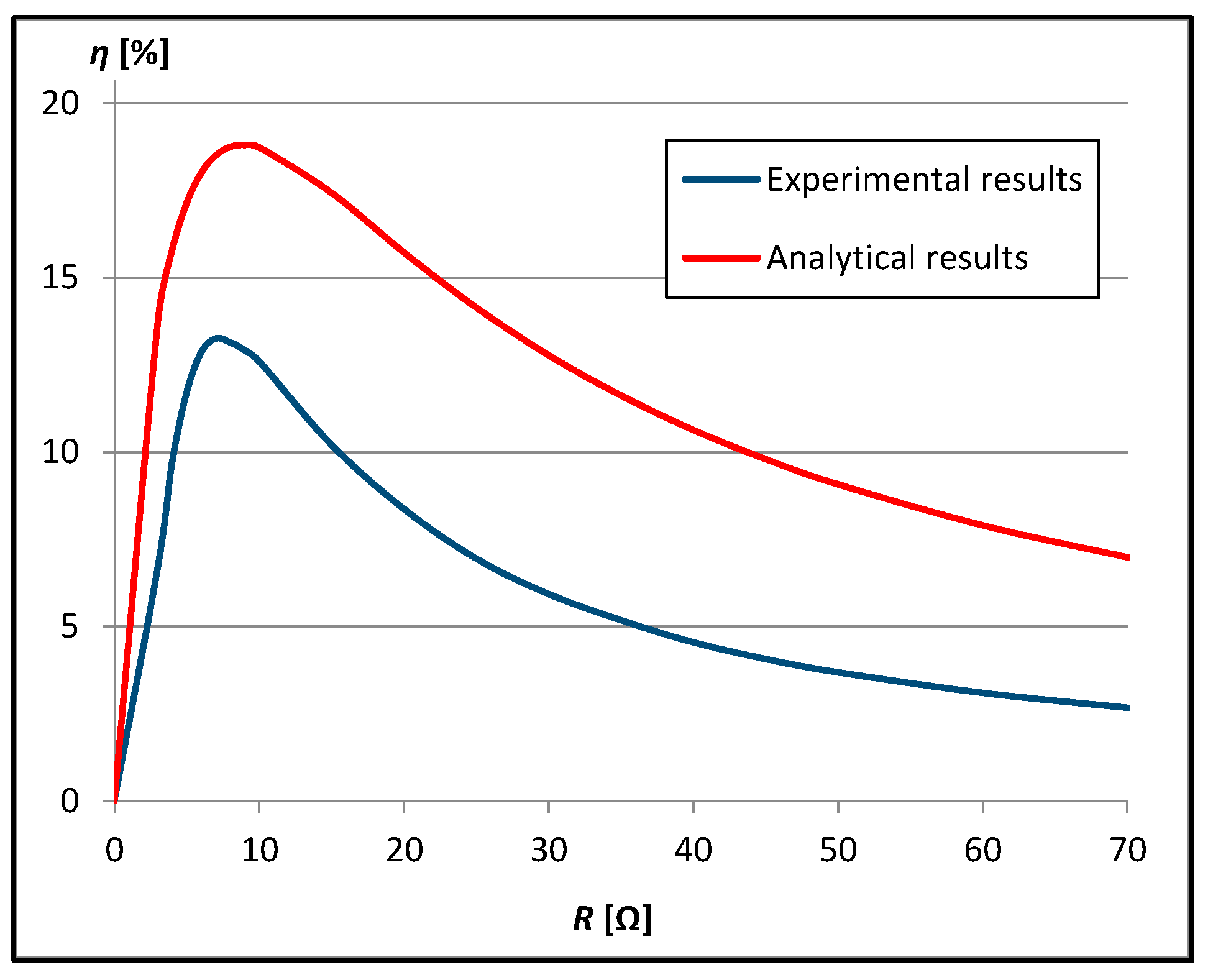
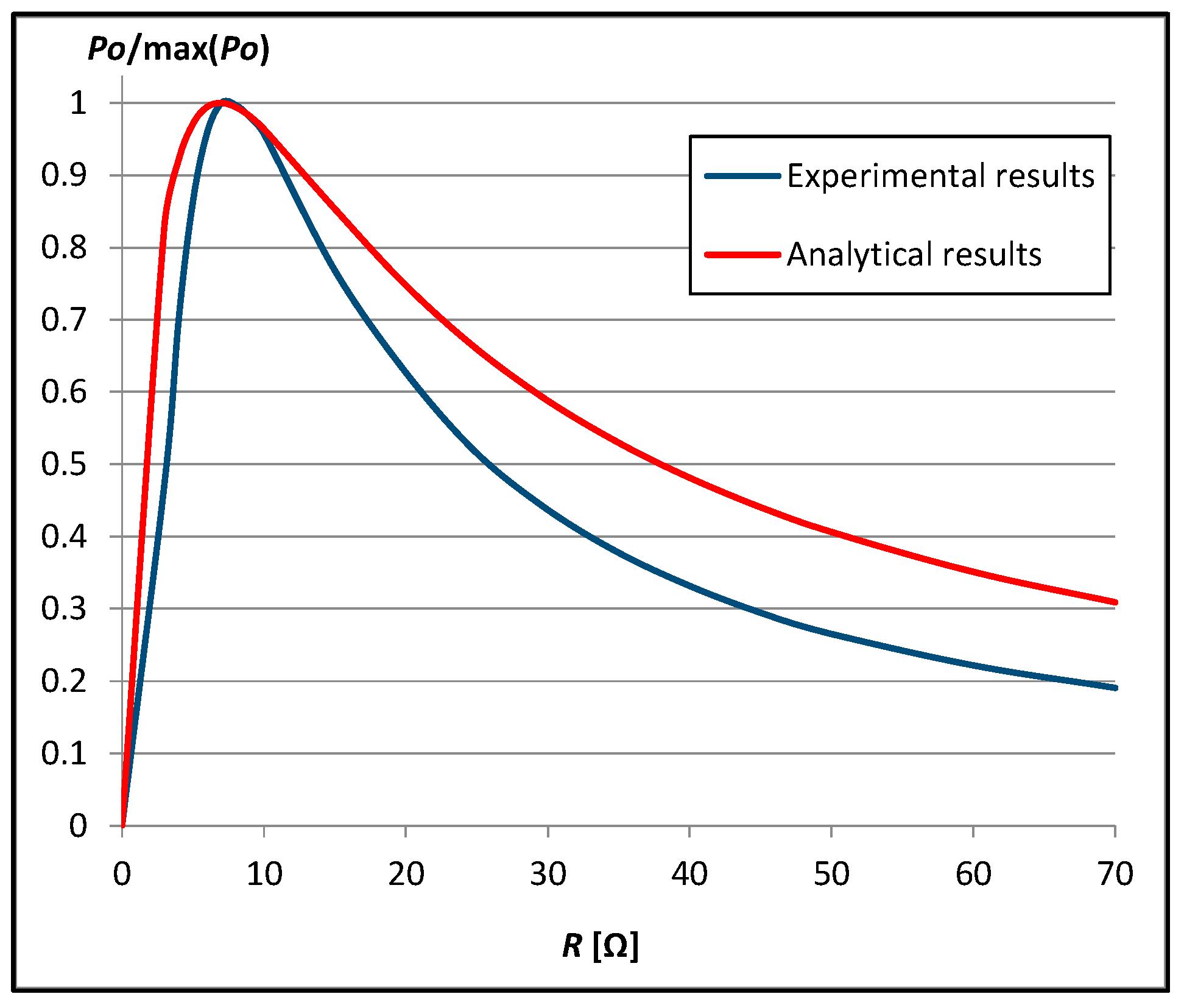
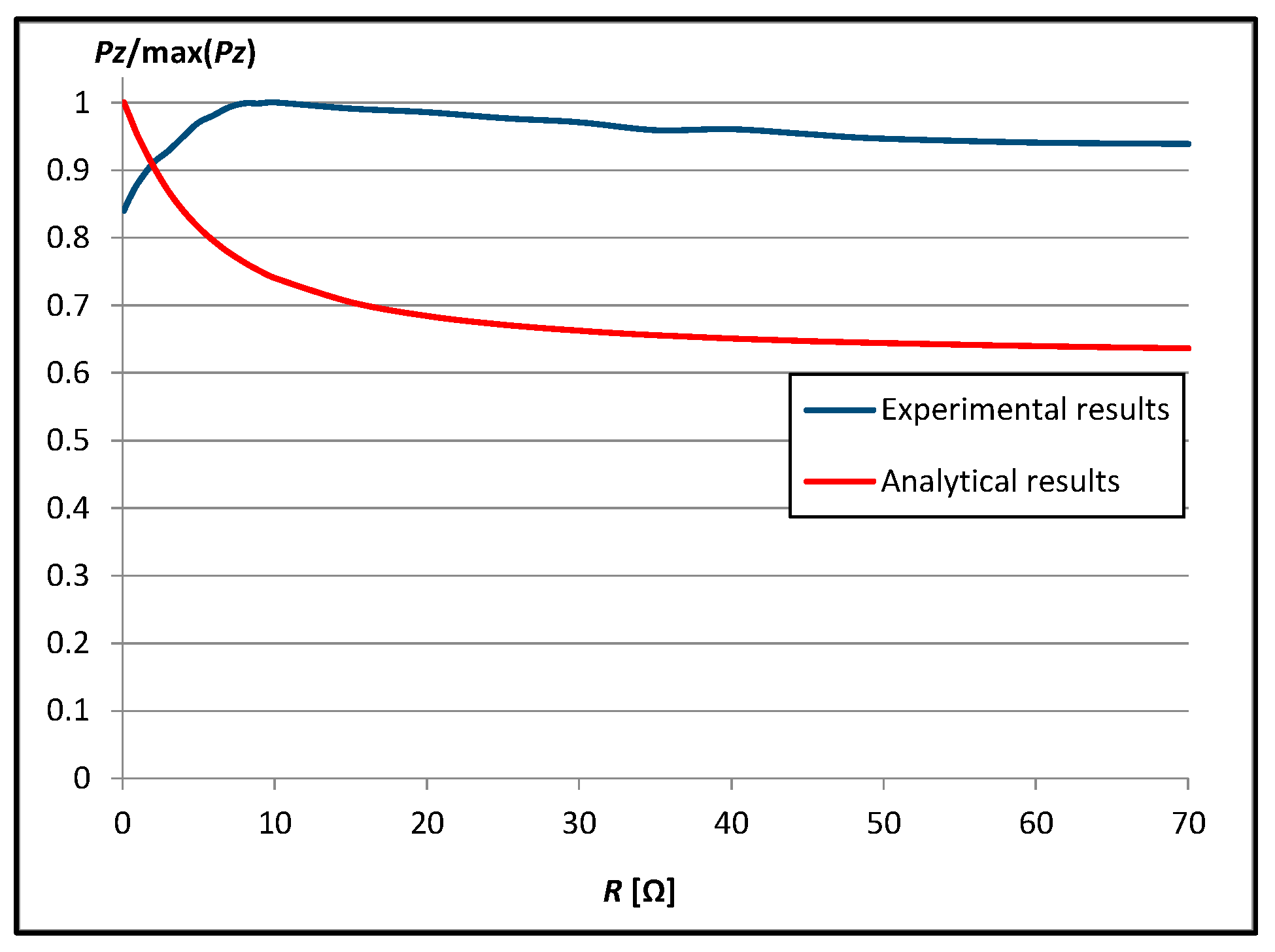
3.1.1. Results at the Distance dz = r/2 = 5 mm
3.1.2. Results at the Distance dz = r = 10 mm
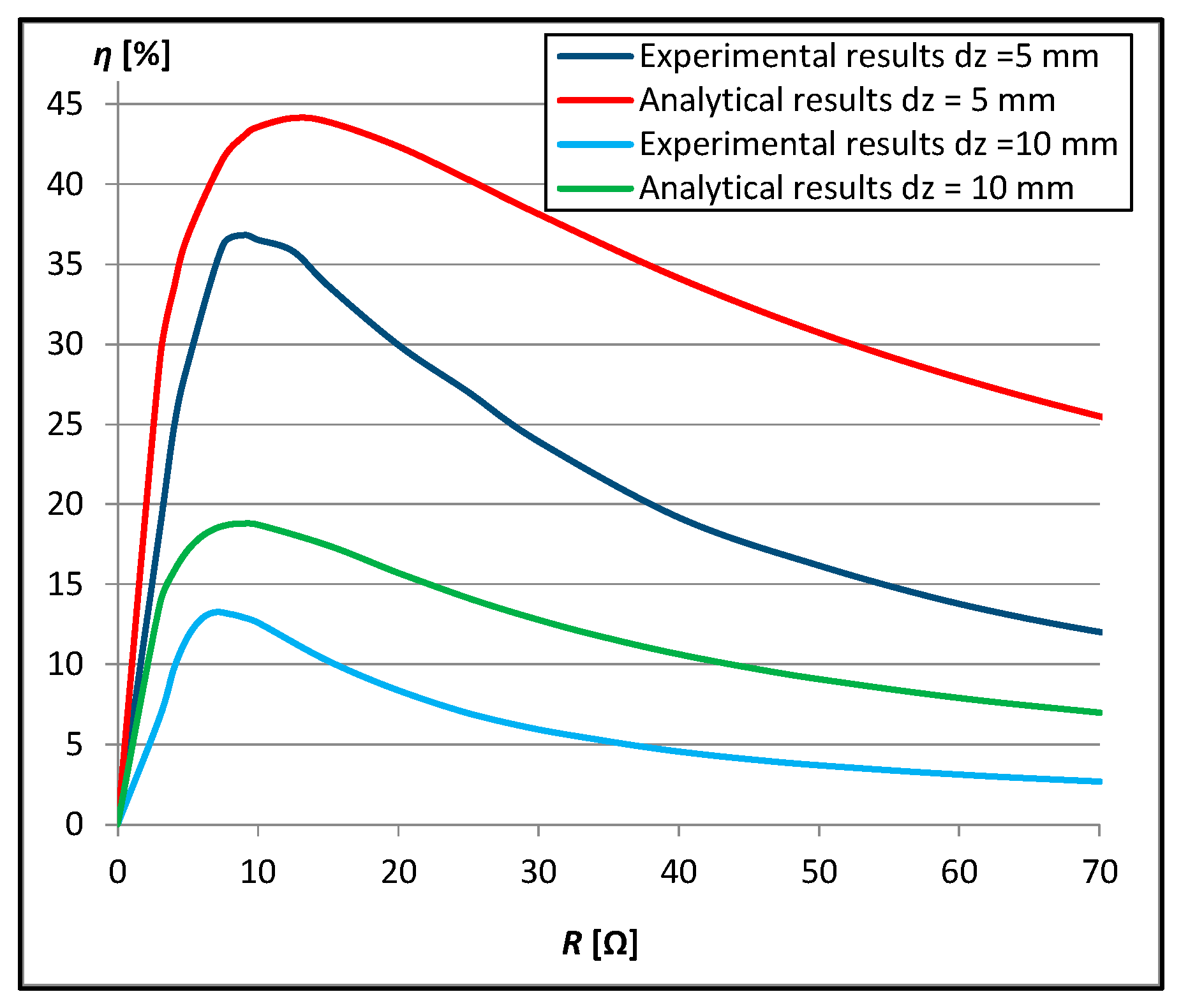
3.2. Comparison of Results at Both Distances between Planes
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sołjan, Z.; Hołdyński, G.; Zajkowski, M. The mathematical concept of the currents’ asymmetrical components in three-phase four-wire systems with sinusoidal and asymmetric voltage supply. Bull. Pol. Acad. Sci. Tech. Sci. 2019, 67, 271–278. [Google Scholar] [CrossRef]
- Sun, L.; Ma, D.; Tang, H. A review of recent trends in wireless power transfer technology and its applications in electric vehicle wireless charging. Renew. Sustain. Energy Rev. 2018, 91, 490–503. [Google Scholar] [CrossRef]
- Okasili, I.; Elkhateb, A.; Littler, T. A Review of Wireless Power Transfer Systems for Electric Vehicle Battery Charging with a Focus on Inductive Coupling. Electronics 2022, 11, 1355. [Google Scholar] [CrossRef]
- Batra, T.; Schaltz, E.; Ahn, S. Effect of ferrite addition above the base ferrite on the coupling factor of wireless power transfer for vehicle applications. J. Appl. Phys. 2015, 117, 17D517. [Google Scholar] [CrossRef]
- Inoue, K.; Kusaka, K.; Itoh, J.I. Reduction in radiation noise level for inductive power transfer systems using spread spectrum techniques. IEEE Trans. Power Electron. 2018, 33, 3076–3085. [Google Scholar] [CrossRef]
- Li, X.; Tang, C.; Dai, X.; Deng, P.; Su, Y. An inductive and capacitive combined parallel transmission of power and data forwireless power transfer systems. IEEE Trans. Power Electron. 2018, 33, 4980–4991. [Google Scholar] [CrossRef]
- Kang, S.H.; Choi, J.H.; Jung, C.W. Magnetic resonance wireless power transfer using three-coil system with single planar receiver for laptop applications. IEEE Trans. Consum. Electron. 2015, 61, 160–166. [Google Scholar]
- Barman, S.D.; Reza, A.W.; Kumar, N.N.; Karim, M.E.; Munir, A.B. Wireless powering by magnetic resonant coupling: Recent trends in wireless power transfer system and its applications. Renew. Sust. Energy Rev. 2015, 51, 1525–1552. [Google Scholar] [CrossRef]
- Nithiyanandam, V.; Sampath, V. Approach-Based Analysis on Wireless Power Transmission for Bio-Implantable Devices. Appl. Sci. 2023, 13, 415. [Google Scholar] [CrossRef]
- Fitzpatrick, D.C. Implantable Electronic Medical Devices; Academic Press: San Diego, CA, USA, 2014; pp. 7–35. [Google Scholar]
- Sugino, M.; Kondo, H.; Takeda, S. Linear motion type transfer robot using the wireless power transfer system. In Proceedings of the 2016 International Symposium on Antennas and Propagation (ISAP), Okinawa, Japan, 24–28 October 2016; pp. 508–509. [Google Scholar]
- Matetić, I.; Štajduhar, I.; Wolf, I.; Ljubic, S. Improving the Efficiency of Fan Coil Units in Hotel Buildings through Deep-Learning-Based Fault Detection. Sensors 2023, 23, 6717. [Google Scholar] [CrossRef]
- Stankiewicz, J.M. Comparison of the efficiency of the WPT system using circular or square planar coils. Przegląd Elektrotechniczny 2021, 97, 38–43. [Google Scholar] [CrossRef]
- Stankiewicz, J.M. Evaluation of the Influence of the Load Resistance on Power and Efficiency in the Square and Circular Periodic WPT Systems. Energies 2023, 16, 2950. [Google Scholar] [CrossRef]
- Micus, S.; Padani, L.; Haupt, M.; Gresser, G.T. Textile-Based Coils for Inductive Wireless Power Transmission. Appl. Sci. 2021, 11, 4309. [Google Scholar] [CrossRef]
- Sun, D.; Chen, M.; Podilchak, S.; Georgiadis, A.; Abdullahi, Q.S.; Joshi, R.; Yasin, S.; Rooney, J.; Rooney, J. Investigating flexible textile-based coils for wireless charging wearable electronics. J. Ind. Text. 2020, 50, 333–345. [Google Scholar] [CrossRef]
- Stankiewicz, J.M. Analysis of the Influence of the Skin Effect on the Efficiency and Power of the Receiver in the Periodic WPT System. Energies 2023, 16, 2009. [Google Scholar] [CrossRef]
- Lee, S.-H.; Lorenz, R.D. Development and validation of model for 95%-efficiency 220-W wireless power transfer over a 30-cm air gap. IEEE Trans. Ind. Appl. 2011, 47, 2495–2504. [Google Scholar] [CrossRef]
- Choroszucho, A.; Pieńkowski, C.; Jordan, A. Electromagnetic wave propagation into building constructions. Przegląd Elektrotech. 2008, 84, 44–49. [Google Scholar]
- Solouma, N.H.; Kassahun, H.B.; Alsharafi, A.S.; Syed, A.; Gardner, M.R.; Alsharafi, S.S. An Efficient Design of Inductive Transmitter and Receiver Coils for Wireless Power Transmission. Electronics 2023, 12, 564. [Google Scholar] [CrossRef]
- Sampath, J.P.K.; Alphones, A.; Shimasaki, H. Coil design guidelines for high efficiency of wireless power transfer (WPT). In Proceedings of the 2016 IEEE Region 10 Conference (TENCON), Singapore, 22–25 November 2016; pp. 726–729. [Google Scholar]
- Prengel, S.; Helwig, M.; Modler, N. Lightweight coil for efficient wireless power transfer: Optimization of weight and efficiency for WPT coils. In Proceedings of the 2014 IEEE Wireless Power Transfer Conference, Jeju, Republic of Korea, 8–9 May 2014; pp. 96–99. [Google Scholar]
- Zhang, Y.; Lu, T.; Zhao, Z. Reducing the impact of source internal resistance by source coil in resonant wireless power transfer. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 845–850. [Google Scholar]
- Stankiewicz, J.M. Estimation of the Influence of the Coil Resistance on the Power and Efficiency of the WPT System. Energies 2023, 16, 6210. [Google Scholar] [CrossRef]
- Choroszucho, A. Analysis of the influence of electrical parameters of concrete and reinforcement inside concrete walls on the values of the electric field intensity. Przegląd Elektrotechniczny 2022, 98, 111–117. [Google Scholar] [CrossRef]
- Stankiewicz, J.M.; Choroszucho, A. Comparison of the Efficiency and Load Power in Periodic Wireless Power Transfer Systems with Circular and Square Planar Coils. Energies 2021, 14, 4975. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Tan, L.; Wang, R. Resistance optimization of a coil with substrate and design of a high-power-density coupler for wireless power transfer. ISA Trans. 2022, 137, 692–705. [Google Scholar] [CrossRef] [PubMed]
- Stankiewicz, J.M. The analysis of the influence of the plane coils geometry configuration on the efficiency of WPT system. Przegląd Elektrotechniczny 2020, 96, 174–178. [Google Scholar] [CrossRef]
- Yuan, Z.; Yang, Q.; Zhang, X.; Ma, X.; Wang, R.; Xue, M.; Zhang, P. A Misalignment Tolerate Integrated S-S-S-Compensated WPT System with Constant Current Output. Energies 2023, 16, 2798. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Z.; Dai, X. Constant Output-Voltage Design for Bi-Directional Wireless Power Transfer System with Multiple Stages. Energies 2020, 13, 3739. [Google Scholar] [CrossRef]
- Rong, C.; Yan, L.; Li, L.; Li, Y.; Liu, M. A Review of Metamaterials in Wireless Power Transfer. Materials 2023, 16, 6008. [Google Scholar] [CrossRef]
- Steckiewicz, A. Efficient Transfer of the Medium Frequency Magnetic Field Using Anisotropic Metamaterials. Energies 2023, 16, 334. [Google Scholar] [CrossRef]
- Liu, S.; Su, J.; Lai, J. Accurate Expressions of Mutual Inductance and Their Calculation of Archimedean Spiral Coils. Energies 2019, 12, 2017. [Google Scholar] [CrossRef]
- Torki, J.; Joubert, C.; Sari, A. Electrolytic capacitor: Properties and operation. J. Energy Storage 2023, 58, 106330. [Google Scholar] [CrossRef]
- Knight, D.W. Practical Continuous Functions for the Internal Impedance of Solid Cylindrical Conductors; G3YNH: Southport, UK, 2016. [Google Scholar] [CrossRef]

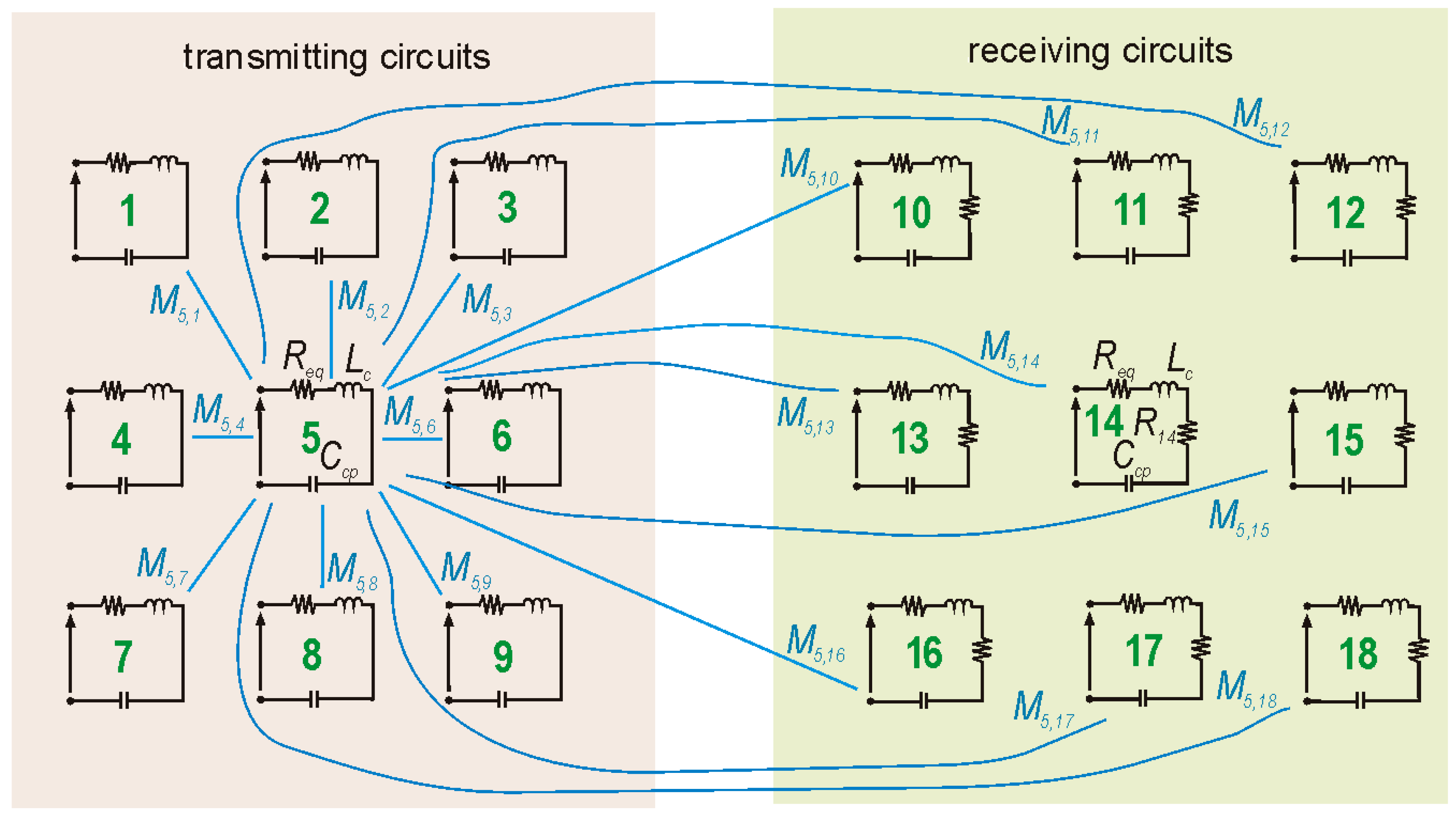

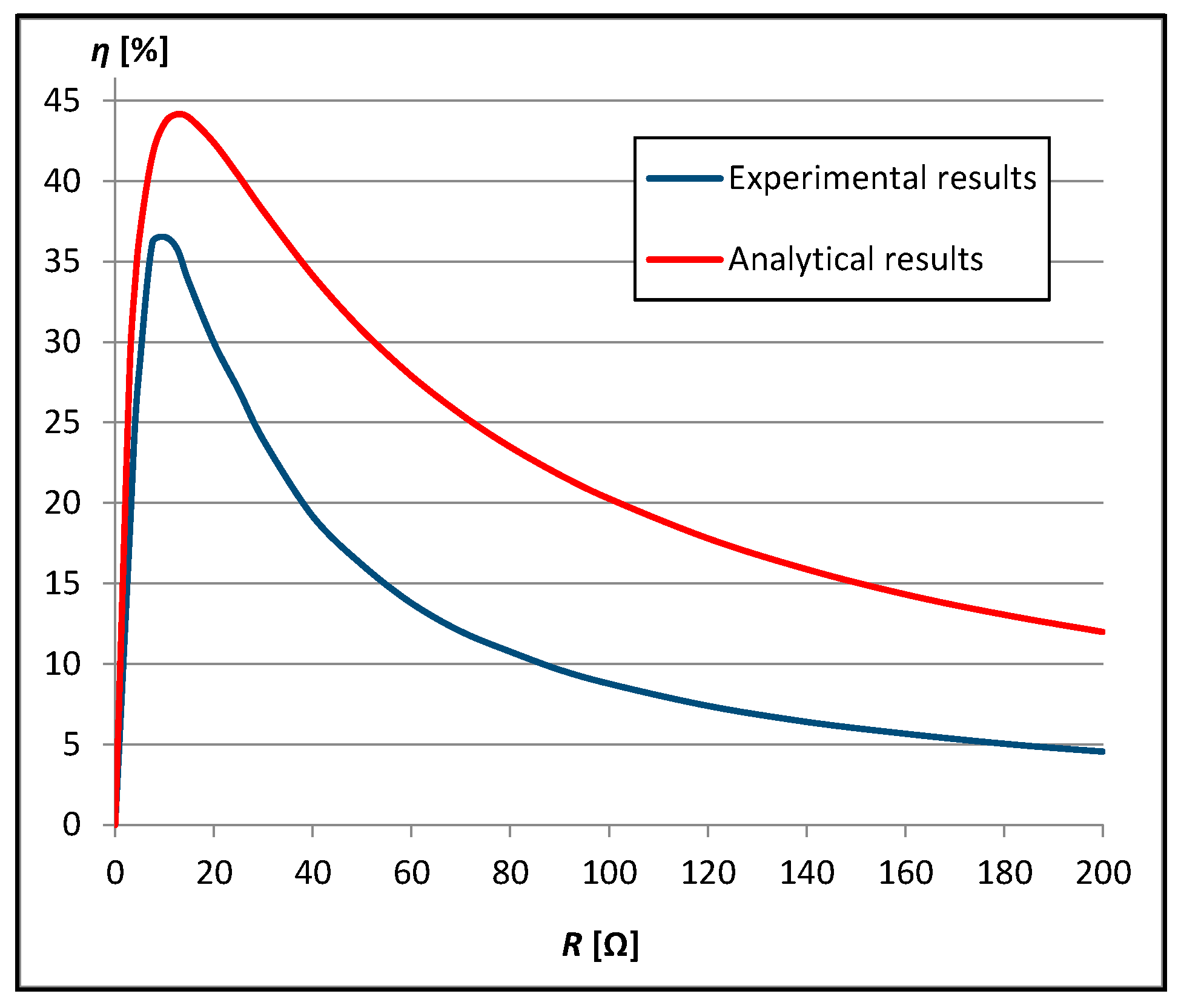
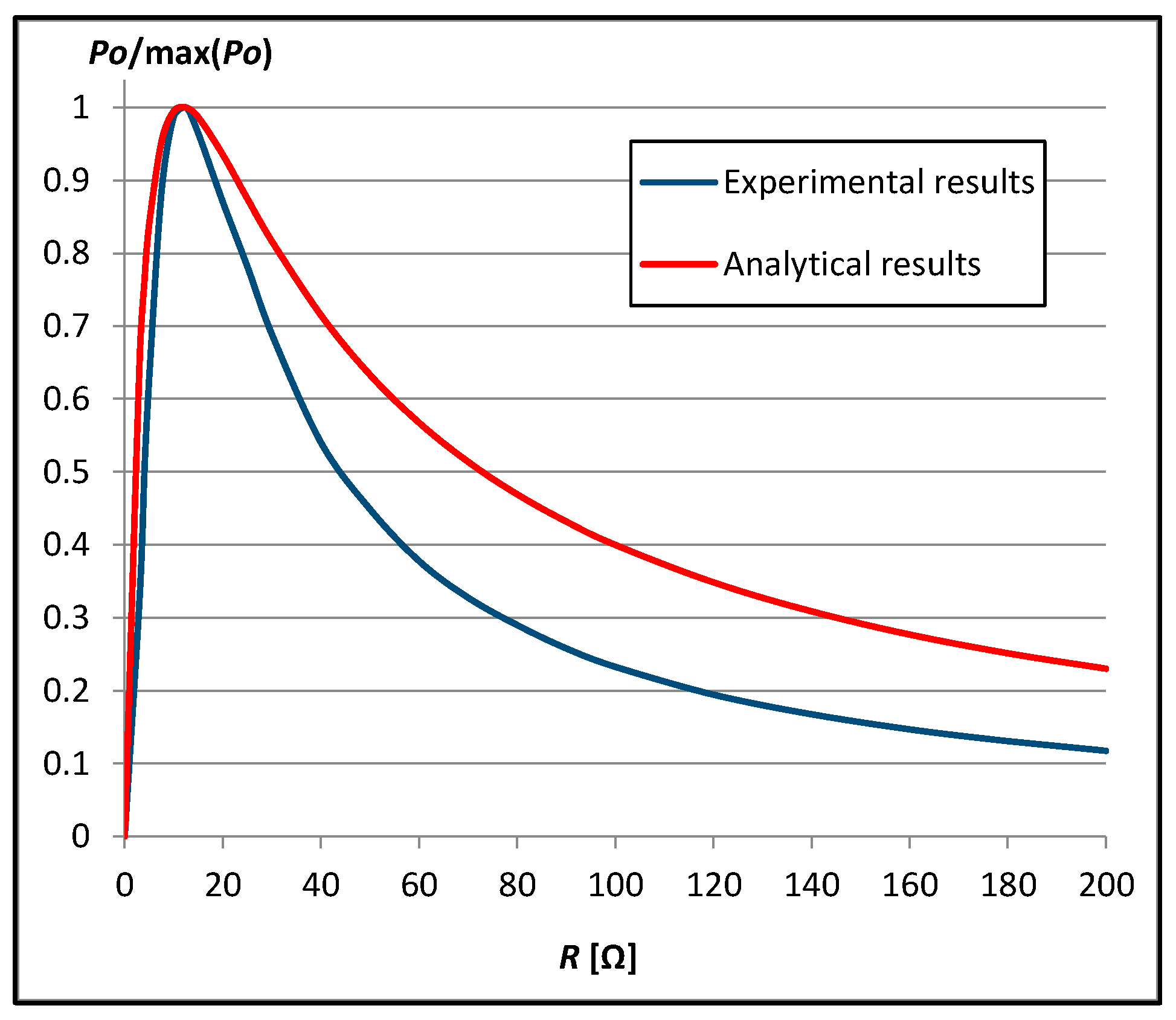
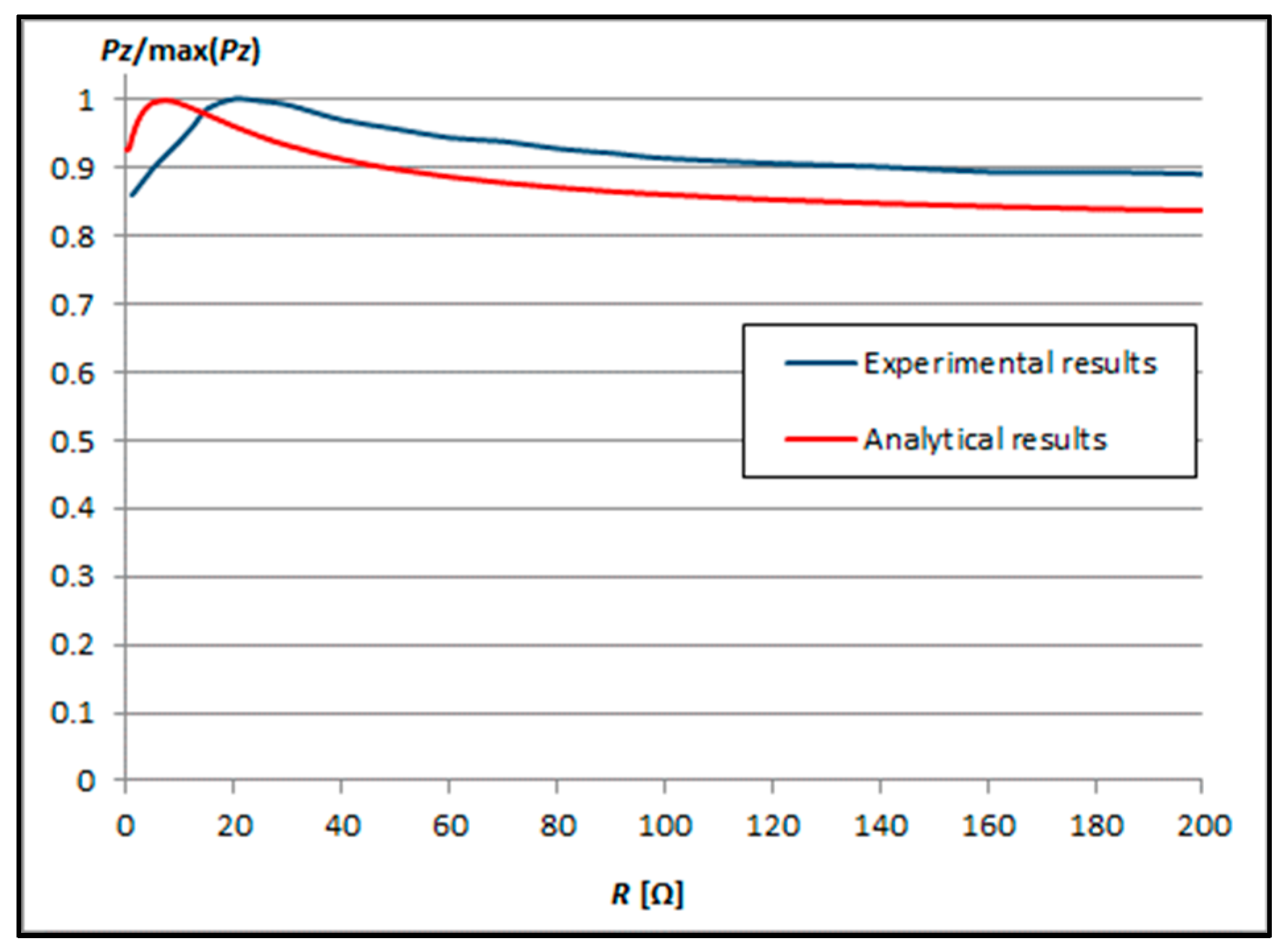

| r (mm) | nt | dz (mm) | |
|---|---|---|---|
| 10 | 30 | 5 | 10 |
| Parameter | Symbol | Value |
|---|---|---|
| wire diameter | wc | 200 µm |
| wire insulation thickness | wi | 5 µm |
| wire conductivity | σw | 5.6 107 S/m |
| resistance increase coefficient | kR | 1.25 |
| dissipation factor | DF | 0.05 |
| separation between coils | ds | 0.025 m |
| design frequency | fc | 500 kHz |
| Load Resistance | η (%) | |||
|---|---|---|---|---|
| Calculations | Measurements | |||
| dz = 5 mm | dz = 10 mm | dz = 5 mm | dz = 10 mm | |
| 3 | 28.89 | 13.73 | 18.40 | 6.70 |
| 4 | 33.47 | 15.79 | 24.73 | 9.71 |
| 5 | 36.78 | 17.14 | 28.74 | 11.72 |
| 7 | 40.91 | 18.50 | 35.26 | 13.25 |
| 7.5 | 41.58 | 18.68 | 36.18 | 13.19 |
| 8 | 42.18 | 18.74 | 36.68 | 13.14 |
| 9 | 43.02 | 18.80 | 36.83 | 12.92 |
| 10 | 43.57 | 18.73 | 36.53 | 12.60 |
| 12.5 | 44.13 | 18.14 | 35.80 | 11.39 |
| 15 | 43.90 | 17.42 | 33.66 | 10.20 |
| 20 | 42.36 | 15.72 | 29.96 | 8.37 |
| 25 | 40.29 | 14.14 | 27.01 | 6.94 |
| 30 | 38.13 | 12.77 | 23.93 | 5.92 |
| 40 | 34.12 | 10.63 | 19.18 | 4.54 |
| 50 | 30.72 | 9.07 | 16.16 | 3.69 |
| 60 | 27.88 | 7.89 | 13.78 | 3.10 |
| 70 | 25.50 | 6.98 | 12.02 | 2.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stankiewicz, J.M. Analysis of the Wireless Power Transfer System Using a Finite Grid of Planar Circular Coils. Energies 2023, 16, 7651. https://doi.org/10.3390/en16227651
Stankiewicz JM. Analysis of the Wireless Power Transfer System Using a Finite Grid of Planar Circular Coils. Energies. 2023; 16(22):7651. https://doi.org/10.3390/en16227651
Chicago/Turabian StyleStankiewicz, Jacek Maciej. 2023. "Analysis of the Wireless Power Transfer System Using a Finite Grid of Planar Circular Coils" Energies 16, no. 22: 7651. https://doi.org/10.3390/en16227651
APA StyleStankiewicz, J. M. (2023). Analysis of the Wireless Power Transfer System Using a Finite Grid of Planar Circular Coils. Energies, 16(22), 7651. https://doi.org/10.3390/en16227651







