Formulation of an Efficiency Model Valid for High Vacuum Flat Plate Collectors
Abstract
1. Introduction
2. Materials and Methods
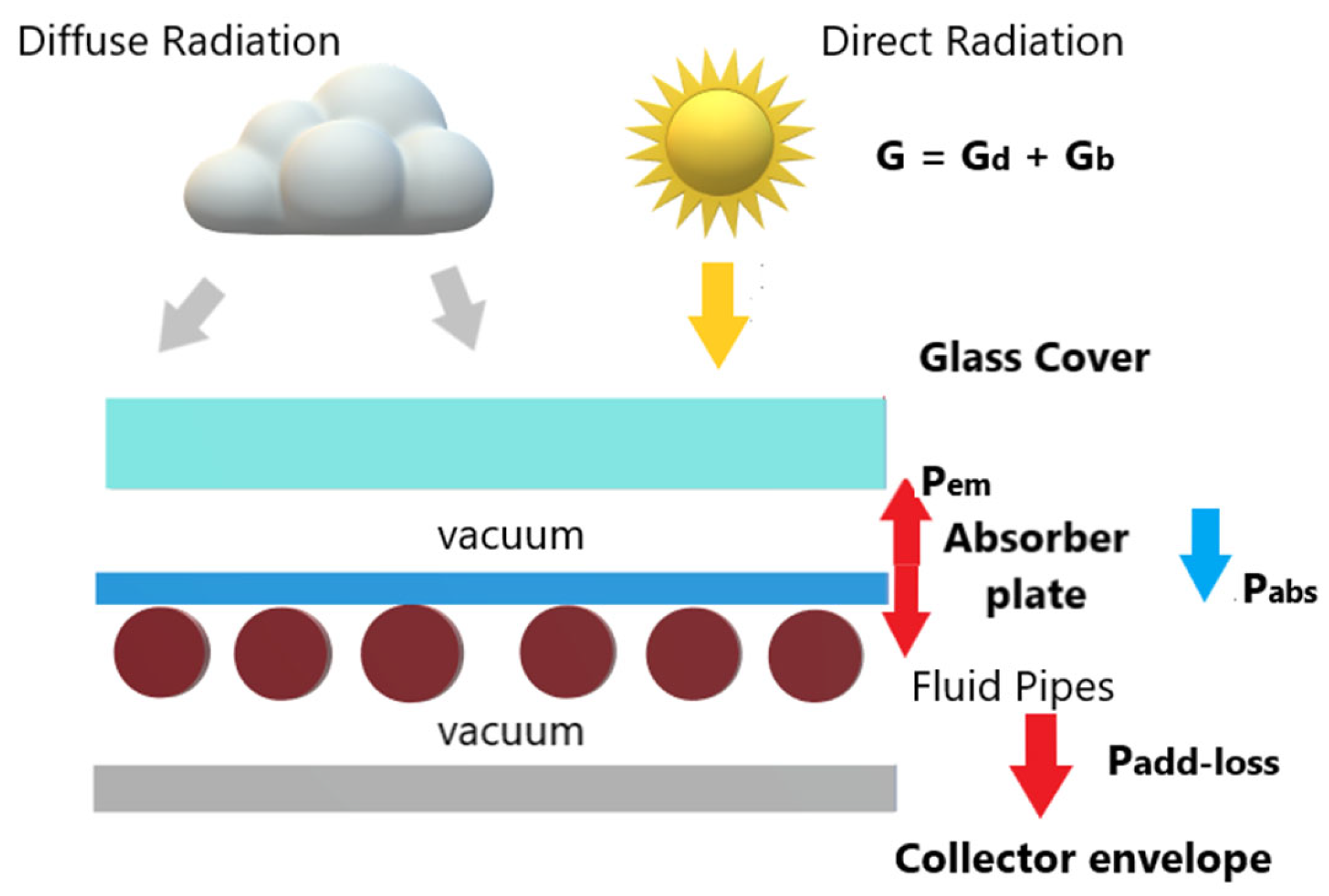
2.1. Efficiency Model for HVFPCs
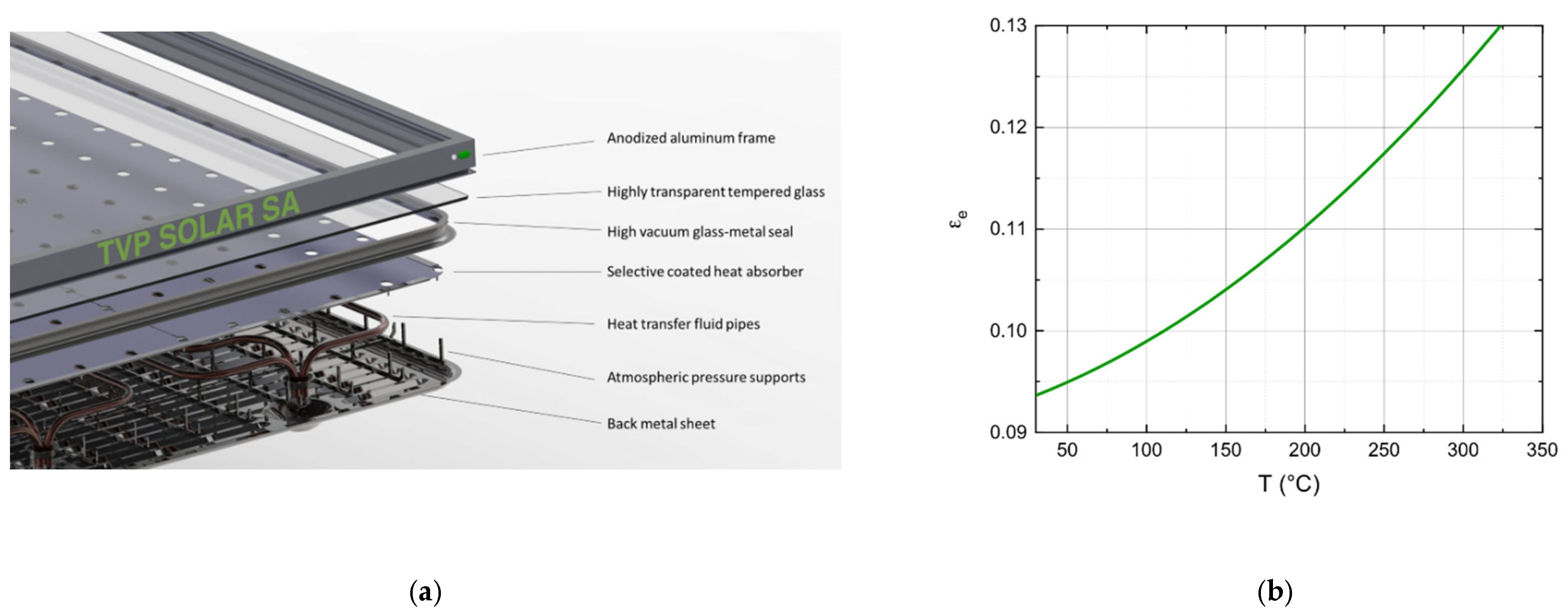
2.2. Application of Proposed HVFPCs Efficiency Model to MT-Power TVP-Solar Collector
3. Results and Discussion
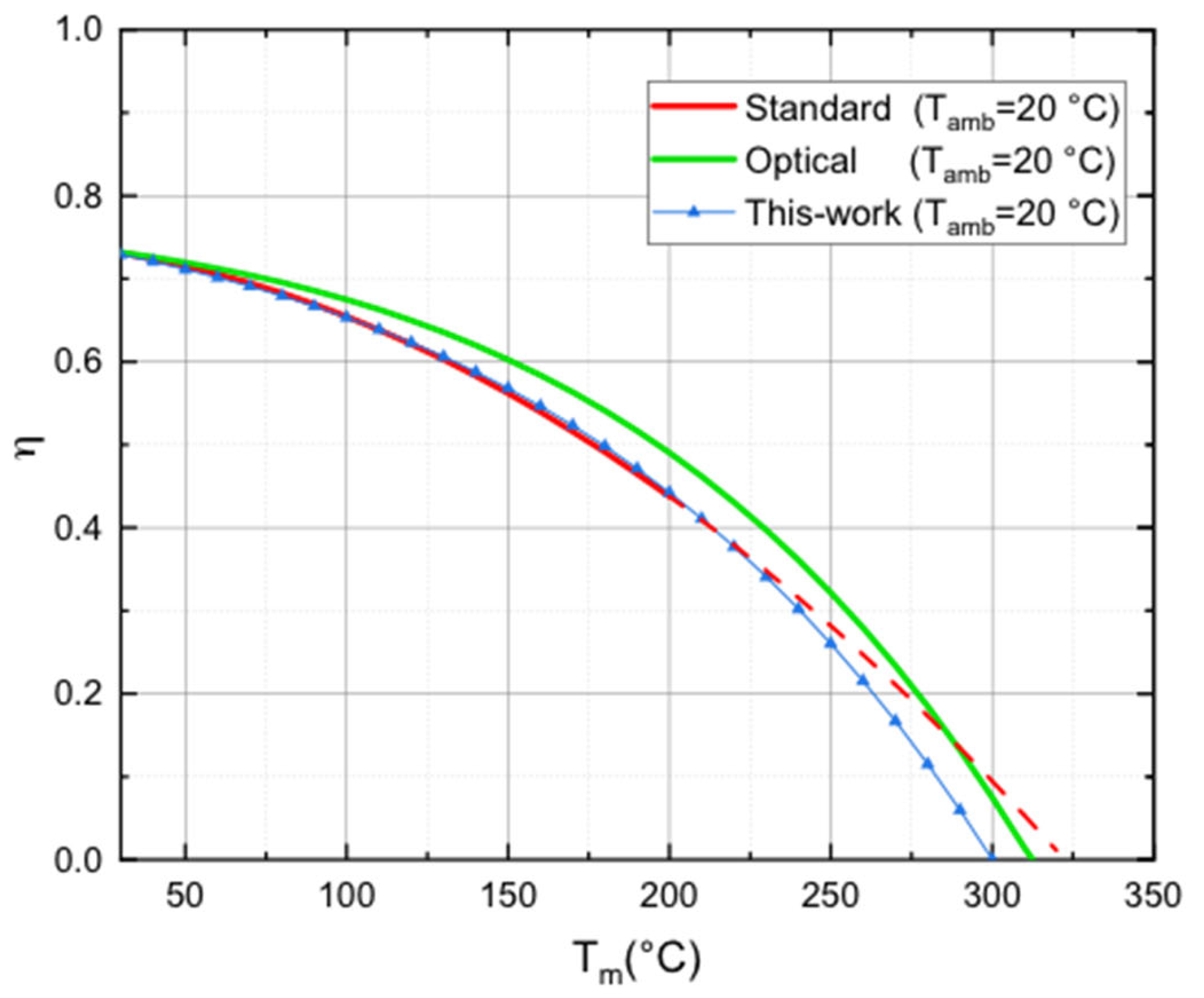
3.1. MT-Power HVFPC Efficiency
3.2. Application of Proposed HVFPCs Efficiency Model to HVFPC Equipped with New Optimized Solar Absorbers
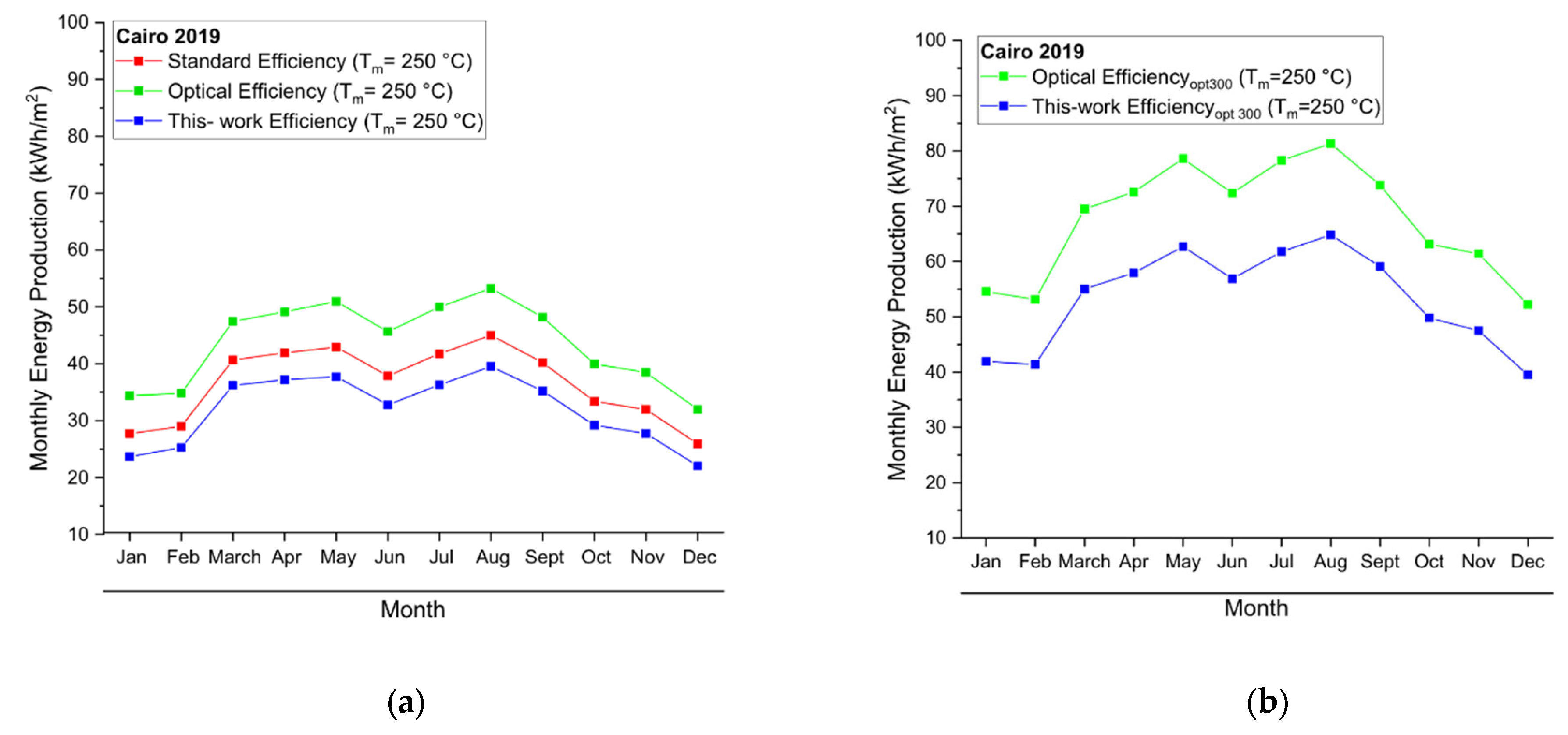
3.3. HVFPCs Annual Energy Producibility Calculation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Aabs | Absorber Surface (m2) |
| Ac | Collector Aperture Surface (m2) |
| c1 | First-Order Heat Loss Coefficient (W/m2 K) |
| c2 | Second-Order Heat Loss Coefficient (W/m2 K2) |
| cp | Specific Heat at Constant Pressure (kJ/kg K) |
| G | Solar Irradiation (W/m2) |
| m | Mass Flow Rate (kg/s) |
| Pabs | Absorbed Power (W) |
| Padd-loss | Lost Power Due to Conductive Losses (W) |
| Pem | Emitted Power (W) |
| PU | Useful Power (W) |
| Tm | Average Temperature (°C) |
| Tamb | Ambient Temperature (°C) |
| Tg | Glass Temperature (°C) |
| Tv | Vessel Temperature (°C) |
| Abbreviations | |
| abs | Absorber |
| comm | Commercial |
| DHW | Domestic Hot Water |
| HTF | Heat Transfer Fluid |
| HVFPC | High Vacuum Flat Plate Collector |
| IAM | Incidence Angle Modifier |
| SSA | Selective Solar Absorber |
| sub | Substrate |
| th | Thermal |
| IR | InfraRed |
| Symbols | |
| α | Spectrally Averaged Absorptivity |
| ε | Spectrally Averaged Emissivity |
| η | Efficiency |
| Zero-Loss Efficiency | |
| σ | Stefan–Boltzmann Constant (W/m2K4) |
| λ | Wavelength |
| k | Conductive Heat Losses Coefficient (W/m2K) |
References
- Climate Change Impacts | US EPA. Available online: https://www.epa.gov/climateimpacts (accessed on 10 June 2023).
- Our World in Data Website. Available online: https://ourworldindata.org/co2-emissions (accessed on 10 June 2023).
- Thiel, G.P.; Stark, A.K. To decarbonize industry, we must decarbonize heat. Joule 2021, 5, 531–550. [Google Scholar] [CrossRef]
- Kumar, L.; Hasanuzzaman, M.; Rahim, N. Global advancement of solar thermal energy technologies for industrial process heat and its future prospects: A review. Energy Convers. Manag. 2019, 195, 885–908. [Google Scholar] [CrossRef]
- IEA. World Energy Statistics and Balances 2020 (Database); International Energy Agency: Paris, France, 2020. [Google Scholar]
- Verma, S.K.; Gupta, N.K.; Rakshit, D. A comprehensive analysis on advances in application of solar collectors considering design, process and working fluid parameters for solar to thermal conversion. Sol. Energy 2020, 208, 1114–1150. [Google Scholar] [CrossRef]
- Bhatia, S.C. (Ed.) Advanced Renewable Energy Systems, (Parts 1 and 2); WPI Publishing: New Delhi, India, 2014. [Google Scholar] [CrossRef]
- Eismann, R. Accurate analytical modeling of flat plate solar collectors: Extended correlation for convective heat loss across the air gap between absorber and cover plate. Sol. Energy 2015, 122, 1214–1224. [Google Scholar] [CrossRef]
- Herwig, H. What Exactly is the Nusselt Number in Convective Heat Transfer Problems and are There Alternatives? Entropy 2016, 18, 198. [Google Scholar] [CrossRef]
- Gao, D.; Li, J.; Ren, X.; Hu, T.; Pei, G. A novel direct steam generation system based on the high-vacuum insulated flat plate solar collector. Renew. Energy 2022, 197, 966–977. [Google Scholar] [CrossRef]
- Benvenuti, C. The SRB solar thermal panel. Eur. News 2013, 44, 16–18. [Google Scholar] [CrossRef]
- TVP Solar. MT-30 Datasheet. Available online: http://www.tvpsolar.com/files/pagine/1464011780_MTPower%20Datasheet%20(v4.2x)(ver5).pdf (accessed on 4 September 2023).
- Moss, R.; Henshall, P.; Arya, F.; Shire, G.; Hyde, T.; Eames, P. Performance and operational effectiveness of evacuated flat plate solar collectors compared with conventional thermal, PVT and PV panels. Appl. Energy 2018, 216, 588–601. [Google Scholar] [CrossRef]
- Mellor, A.; Alvarez, D.A.; Guarracino, I.; Ramos, A.; Lacasta, A.R.; Llin, L.F.; Murrell, A.; Paul, D.; Chemisana, D.; Markides, C.; et al. Roadmap for the next-generation of hybrid photovoltaic-thermal solar energy collectors. Sol. Energy 2018, 174, 386–398. [Google Scholar] [CrossRef]
- Eaton, C.; Blum, H. The use of moderate vacuum environments as a means of increasing the collection efficiencies and operating temperatures of flat-plate solar collectors. Sol. Energy 1975, 17, 151–158. [Google Scholar] [CrossRef]
- Zheng, H.; Xiong, J.; Su, Y.; Zhang, H. Influence of the receiver’s back surface radiative characteristics on the performance of a heat-pipe evacuated-tube solar collector. Appl. Energy 2014, 116, 159–166. [Google Scholar] [CrossRef]
- Gao, D.; Gao, G.; Cao, J.; Zhong, S.; Ren, X.; Dabwan, Y.N.; Hu, M.; Jiao, D.; Kwan, T.H.; Pei, G. Experimental and numerical analysis of an efficiently optimized evacuated flat plate solar collector under medium temperature. Appl. Energy 2020, 269, 115129. [Google Scholar] [CrossRef]
- De Maio, D.; D’Alessandro, C.; Caldarelli, A.; De Luca, D.; Di Gennaro, E.; Russo, R.; Musto, M. A Selective Solar Absorber for Unconcentrated Solar Thermal Panels. Energies 2021, 14, 900. [Google Scholar] [CrossRef]
- Rosen, M.A. Energy efficiency and sustainable development. IEEE Technol. Soc. Mag. 2002, 15, 21–26. [Google Scholar] [CrossRef]
- Prapas, D.; Norton, B.; Probert, S. Optics of parabolic-trough, solar-energy collectors, possessing small concentration ratios. Sol. Energy 1987, 39, 541–550. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Solar thermal collectors and applications. Prog. Energy Combust. Sci. 2004, 30, 231–295. [Google Scholar] [CrossRef]
- Platzer, W.J.; Mills, D.; Gardner, E.W. Linear Fresnel Collector (LFC) solar thermal technology. In Concentrating Solar Power Technology; Elsevier: Amsterdam, The Netherlands, 2021; pp. 165–217. [Google Scholar] [CrossRef]
- Fischer, S.; Drück, H. Standards and Certification Schemes for Solar Thermal Collectors, Stores and Systems—An Overview about the Latest Developments. Energy Procedia 2014, 57, 2867–2871. [Google Scholar] [CrossRef][Green Version]
- Database. Available online: https://solarkeymark.eu/database/ (accessed on 20 October 2023).
- Cao, F.; McEnaney, K.; Chen, G.; Ren, Z. A review of cermet-based spectrally selective solar absorbers. Energy Environ. Sci. 2014, 7, 1615–1627. [Google Scholar] [CrossRef]
- De Maio, D.; D’Alessandro, C.; Caldarelli, A.; De Luca, D.; Di Gennaro, E.; Casalino, M.; Iodice, M.; Gioffre, M.; Russo, R.; Musto, M. Multilayers for efficient thermal energy conversion in high vacuum flat solar thermal panels. Thin Solid Films 2021, 735, 138869. [Google Scholar] [CrossRef]
- D’Alessandro, C.; De Maio, D.; Musto, M.; De Luca, D.; Di Gennaro, E.; Bermel, P.; Russo, R. Performance analysis of evacuated solar thermal panels with an infrared mirror. Appl. Energy 2021, 288, 116603. [Google Scholar] [CrossRef]
- De Luca, D.; Kortge, D.; Di Gennaro, E.; Russo, R.; Bermel, P. Ultra-thin sputter-deposited infrared rugate mirror for enhancing solar-to-thermal energy conversion. Opt. Lett. 2022, 47, 230–233. [Google Scholar] [CrossRef]
- De Maio, D.; D’Alessandro, C.; Caldarelli, A.; Musto, M.; Russo, R. Solar selective coatings for evacuated flat plate collectors: Optimisation and efficiency robustness analysis. Sol. Energy Mater. Sol. Cells 2022, 242, 111749. [Google Scholar] [CrossRef]
- Howell, J.R.; Mengüç, M.P.; Daun, K.; Siegel, R. Thermal Radiation Heat Transfer, 7th ed.; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar] [CrossRef]
- D’Alessandro, C.; De Maio, D.; Caldarelli, A.; Musto, M.; Di Giamberardino, F.; Monti, M.; Mundo, T.; Di Gennaro, E.; Russo, R.; Palmieri, V.G. Calorimetric testing of solar thermal absorbers for high vacuum flat panels. Sol. Energy 2022, 243, 81–90. [Google Scholar] [CrossRef]
- D’Alessandro, C.; De Maio, D.; Mundo, T.; Musto, M.; Di Giamberardino, F.; Monti, M.; Dalena, D.; Palmieri, V.G.; De Luca, D.; Di Gennaro, E.; et al. Low-Cost High Intensity LED Illumination Device for High Uniformity Laboratory Purposes. Sol. Energy 2021, 221, 140–147. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaudino, E.; Caldarelli, A.; Russo, R.; Musto, M. Formulation of an Efficiency Model Valid for High Vacuum Flat Plate Collectors. Energies 2023, 16, 7650. https://doi.org/10.3390/en16227650
Gaudino E, Caldarelli A, Russo R, Musto M. Formulation of an Efficiency Model Valid for High Vacuum Flat Plate Collectors. Energies. 2023; 16(22):7650. https://doi.org/10.3390/en16227650
Chicago/Turabian StyleGaudino, Eliana, Antonio Caldarelli, Roberto Russo, and Marilena Musto. 2023. "Formulation of an Efficiency Model Valid for High Vacuum Flat Plate Collectors" Energies 16, no. 22: 7650. https://doi.org/10.3390/en16227650
APA StyleGaudino, E., Caldarelli, A., Russo, R., & Musto, M. (2023). Formulation of an Efficiency Model Valid for High Vacuum Flat Plate Collectors. Energies, 16(22), 7650. https://doi.org/10.3390/en16227650







