Abstract
Battery energy storage (BES) can provide many grid services, such as power flow management to reduce distribution grid overloading. It is desirable to minimise BES storage capacities to reduce investment costs. However, it is not always clear how battery sizing is affected by battery siting and power flow simultaneity (PFS). This paper describes a method to compare the battery capacity required to provide grid services for different battery siting configurations and variable PFSs. The method was implemented by modelling a standard test grid with artificial power flow patterns and different battery siting configurations. The storage capacity of each configuration was minimised to determine how these variables affect the minimum storage capacity required to maintain power flows below a given threshold. In this case, a battery located at the transformer required 10–20% more capacity than a battery located centrally on the grid, or several batteries distributed throughout the grid, depending on PFS. The differences in capacity requirements were largely attributed to the ability of a BES configuration to mitigate network losses. The method presented in this paper can be used to compare BES capacity requirements for different battery siting configurations, power flow patterns, grid services, and grid characteristics.
1. Introduction
As part of the energy transition, countries around the world are promoting electrification to reduce carbon emissions and combat climate change [1]. In residential areas, electrification primarily consists of increasing distributed generation from rooftop photovoltaic panels (PV), increasing electric vehicle adoption, and switching to electricity-based heating, e.g., heat pumps [2,3]. These developments are expected to increase the magnitude and simultaneity (or coincidence factor) of electricity flows on the distribution grid (DG), resulting in higher and longer sustained peak power flows [4,5]. Residential power flows in particular are expected to become the largest contributor to peak power flows in the electricity grid [6], and residential power flow simultaneity (PFS) is expected to increase from 20–30% to 40–90% in the coming years [5,7]. This development is expected to result in grid components becoming overloaded more frequently, leading to faster grid component degradation and the potential for more local power outages [8,9]. For example, an estimate from the Netherlands indicates that between 5% and 8% of existing distribution transformers and between 6% and 9% of existing substation transformers will be consistently overloaded by 2030 [9]. These numbers are expected to increase to 35% and 45%, respectively, by 2050 [9]. Similar problems are expected for electricity DGs throughout the world [10,11].
When grid component overloading (or threat of overloading) becomes more frequent, distribution system operators (DSOs) will generally need to limit new grid connections to prevent and/or limit overloading. As a result, electrification (and hence energy transition) will slow down, making it more difficult for countries to reach their climate targets [10,12].
Currently, the dominant solution to prevent grid overloading is to reinforce the grid to increase its capacity [13,14]. However, grid reinforcement can be costly and time consuming, and may contribute to overloading problems at higher levels of the grid [4,14,15,16,17,18]. Direct or indirect control of consumer loads (i.e., demand-side management) has the potential to help manage power flows, but faces many regulatory and technical challenges, such as lack of ICT infrastructure, lack of financial incentives, privacy and security concerns, and difficulty in coordinating highly variable power flows [6,19,20]. Another alternative to grid reinforcement is to use battery energy storage (BES) to resolve overloading problems locally [15,16,21,22,23].
1.1. Battery Energy Storage
BES is a relatively well-established and easily implemented form of electricity storage that can provide a variety of services to the grid, including power flow management (PFM), system upgrade deferral, energy arbitrage, peak power supply, transportation loss reduction, emissions reduction, reactive power support, voltage support, PV curtailment reduction, increasing self-consumption of PV energy, and improved grid reliability and resilience [15,24,25,26,27,28].
PFM in particular can help address the problem of grid overloading described above. To prevent grid overloading, BES can be charged to absorb (decentralised) generation peaks or discharged to reduce peak loads locally. By reducing peak power flows on the grid, BES can potentially defer the need for grid reinforcement and enable more/larger grid connections, thus enabling further electrification and advancing the energy transition [4,15,24,27,29,30,31]. However, if uncontrolled or unregulated, BES may be ineffective at resolving grid overloading [32,33,34], or may even exacerbate the problem due to its relatively large power flows [35]. Therefore, there is an argument to allow DSOs to regulate and/or control BES operations to maintain power flows/grid loading at desired levels [32,34,36]. In European countries, DSOs are currently not allowed to own or operate BES systems themselves [37,38]. However, DSOs can contract BES services from a third party (such as an aggregator) [37], or regulations could allow DSOs to throttle battery (dis)charge power during periods with relatively high power flows, as is being considered in Germany [39]. This paper does not discuss this legal hurdle further, but it must be acknowledged that this is a potential challenge for any use of BES systems by a DSO.
This paper considers a situation where batteries are used to provide PFM for a DSO, similarly to the pilot projects performed by Reijnders et al. [40] and van Westering et al. [23]. However, there remains a question as to how such BES systems should be sized and sited to provide grid services in an efficient and effective way (in terms of installed battery capacity and energy use). The costs of implementing BES are often compared with the costs of grid reinforcement [4,14,15,21,30,41]. To reduce investment costs, it is important to minimise the storage capacity of batteries used to provide grid services [29,30]. Battery sizing is primarily dependent on the battery storage capacity and power needed to provide a given service, and the battery’s siting (i.e., location) in the DG [23,42,43]. Battery power and capacity may limit which grid services a battery can provide [42,43]. In this paper, battery power was not considered further, and battery capacity was left as an open variable. Battery siting determines how effectively and efficiently a given service can be provided, in terms of storage capacity requirements. Some of the literature suggests that a more distributed battery configuration (i.e., with batteries located closer to loads/distributed generators) requires less storage capacity to provide a given service, since distributed systems incur fewer network losses due to the closer proximity of the batteries to the loads/generators [15,22,44,45,46,47]. Conversely, some of the literature suggests that a more centralised battery configuration can potentially “share” battery capacity between several loads/generators in different parts of a DG (assuming a relatively low PFS), thus requiring less redundant battery capacity to achieve the same results as a distributed system [14,23,27,48,49,50,51].
This apparent contradiction results from the methods and case-specific details used in various papers. In BES sizing studies, BES (dis)charge losses tend to be simplified as a fixed value or neglected entirely [52,53]. Similarly, network losses and grid constraints tend to be simplified (e.g., so they can be included in a linear optimization algorithm) or omitted [42,54,55]. When network losses/constraints are included, they tend to be implemented in a two-step process: by first selecting a site which minimises network losses for given power flows, and then minimising the battery capacity needed to provide a given service [15,30,37,42,44,49,52,56,57,58,59]. However, optimal battery siting is not always feasible or practical due to access and/or space constraints, and it is not always clear what the trade-off is between different siting configurations in terms of battery capacity requirements. This paper presents a method of comparing the relative battery capacity requirements for different battery siting configurations in a given network.
1.2. Power Flow Simultaneity
A further complicating factor is that battery sizing is also dependent on PFS (or coincidence factors) [7]. Equation (1) defines PFS (g) for a given set of consumers, where Pmax is the maximum coincident net load (or generation) from consumers, and is the sum of the maximum non-coincident loads (or generations) from each individual consumer (i) [60]. PFS gives an indication of the likeliness of individual consumer peak loads/generations to occur concurrently and is often used to establish minimum grid capacity requirements [60]. Note that network losses are not taken into account in this definition.
Increasing PFS generally leads to increasing power flow magnitudes. As power flow magnitudes increase, network losses also increase by a quadratic factor, due to Joule’s Law () [61]. These network losses must be accounted for when sizing BES systems used for PFM. As a result, for a given grid layout and battery siting, the sizing of BES used for PFM is expected to increase quadratically with increasing PFS [7]. The impact of variable PFSs on battery sizing is taken into account in the method presented in this paper.
In summary, this paper describes a newly developed methodology to determine the minimum battery capacity required to manage power flows in a DG. The method is used to compare BES capacity requirements for different battery siting configurations and variable PFSs. The results demonstrate the relative impact of PFS and battery siting on the sizing of BES systems used for PFM. The paper then discusses the implications of these results and how this method can be used to estimate BES sizing requirements for other grid services, such as voltage regulation. The paper concludes with an overview of the paper’s contributions and suggestions for future research. A list of abbreviations used in this paper is included in Abbreviations at the end of the paper.
2. Methodology
A methodology was developed to gain insight into the impacts of PFS and battery siting on the sizing of batteries used to provide grid services. This method consists of the steps listed below. In the following subsections, these steps are detailed further and the method is exemplified by implementing it into a case study. The case study presents a fictional scenario that is representative of current developments in residential DGs, and of where batteries are used to provide PFM to prevent grid component overloading.
- Create a model of a given electricity grid in a power flow simulation software.
- Develop a power flow pattern for each consumer connection.
- Define objectives for the BES system (e.g., maintain power flows below a given threshold).
- Define battery siting configurations.
- Develop a battery control algorithm to calculate the minimum amount of battery capacity needed to meet a given objective for a given battery siting configuration and power flow pattern. Implement this algorithm for a BES system in the grid model. The following generic algorithm was proposed to achieve this:
- a.
- Define batteries in the grid model for a given battery siting configuration.
- b.
- Simulate a given power flow pattern on the grid to determine the state of the grid without BES.
- c.
- Estimate a battery (dis)charge pattern needed to fulfil the BES objectives.
- d.
- Simulate grid power flows including the BES (dis)charge pattern.
- e.
- Evaluate if the BES objectives have been achieved.
- f.
- Adjust the battery (dis)charge pattern as needed to achieve the BES objectives.
- g.
- Calculate the (minimum) battery capacity needed to deliver the required battery (dis)charge.
- Analyse and compare the battery capacity requirements for different power flow patterns and BES siting configurations.
2.1. Electricity Grid Model
When modelling an electricity grid, it is important that grid characteristics (such as cable lengths and resistances) are represented accurately, so that network losses and the impact of grid constraints can be correctly modelled. In the example case, the IEEE 2015 European Low Voltage Test Feeder was chosen to be modelled. This standard test feeder was chosen because it is designed to be representative of radially operated DGs typical in Europe [62], and because it has been used in similar studies, such as Stecca et al. [46] and Mehmood et al. [57]. The test feeder is depicted in Figure 1 and consists of an 800 kW transformer and 55 consumer connections spread over five branching cables.
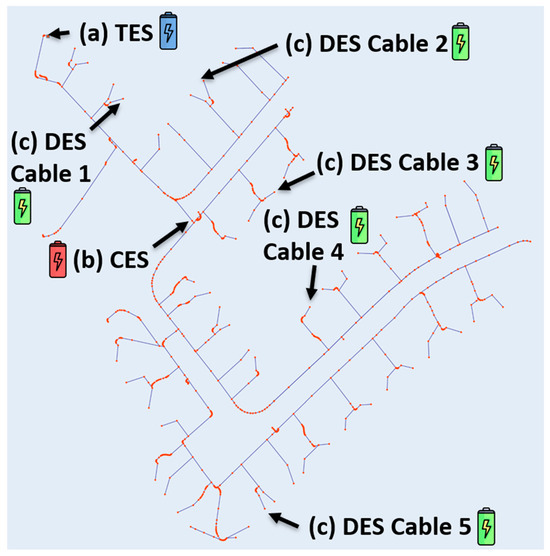
Figure 1.
European test feeder with the following battery configurations: (a) Transformer Energy Storage (TES) (blue); (b) Central Energy Storage (CES) (red); and (c) Distributed Energy Storage (DES), with five batteries spread among the grid cables (green). Blue lines indicate grid cables and red dots indicate inflexion points, junctures, and consumer connection points. The transformer is located at the end of the cable in the upper left of the figure, next to the TES battery.
The grid model was implemented in PandaPower (version 2.7.0) by defining all cable and transformer characteristics as per Schneider et al. [62], and defining a load at each consumer connection point. PandaPower is an open-source, Python-based tool used to model electricity grids, which has been used in several studies and has been validated with industry-standard software tools [63]. The program uses the Newton-Raphson method to solve power flow equations to determine voltage levels and current flows at any point in the grid. Newton-Raphson is a well-established and relatively fast method of calculating power flows, which is described in detail by Grainger et al. [64] and Thurner et al. [63].
PandaPower can also calculate network losses (including time-dependent thermal effects), model grids as a single or three-phase system, and model both active and reactive power flows [63]. In this paper, the DG was modelled as a single-phase system and reactive power flows and thermal effects were omitted. As noted by Thurner et al., these simplifications reduce the time needed to solve power flow equations and reduce the chance of encountering a non-convergence problem [63]. These simplifications also make it easier to identify the causation of results. The potential impacts of these simplifications are expanded upon in the discussion.
PandaPower does have some practical limitations. It is unable to solve power flow equations with very low resistance in the circuit or if component loading exceeds a certain threshold. These limitations result from voltage levels in the grid dropping to zero, leading to unsolvable power flow equations. These limitations are relevant for the experimental design discussed below.
2.2. Power Flow Patterns
Power flow patterns should be designed that are representative of the (future) power flows expected on the grid being modelled so that simultaneity effects can be correctly simulated. In this case, a series of artificial power flow patterns were constructed to reflect future peak power flows in residential DGs and their relative impact on battery sizing requirements. Specifically, it has been identified that residential PFS could increase to 40–90% and a residential DG component loading could increase to 150–680% of their rated capacities, depending on how new technologies are implemented and controlled [5,7].
To model these effects, each of the 55 consumer power flow patterns were modelled individually over a 24 h period in 15-min time steps. Each consumer had no load the majority of the time, with an 18 kW peak load for half an hour of the day. By overlapping more or fewer of these peak loads, grid (over)loading could be achieved with variable PFSs. This principle is illustrated in Figure 2, where four consumer loads are increasingly overlapped to produce an increasing PFS, thus increasing the total (peak) load on the DG. Table 1 shows the number of coincident loads needed to achieve a given PFS, and the resulting peak load on the grid. PFS values were chosen with increments of roughly 10%. This was done to emphasise any non-linear relations between PFS and battery capacity requirements. The PFS values in Table 1 were calculated with Equation (1), where PFS is defined as the peak load value (in kW) divided by 990 kW (55 consumers × 18 kW).
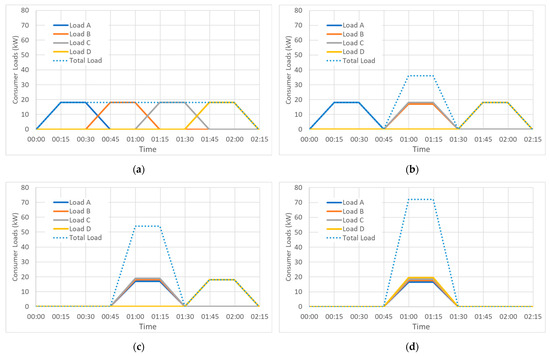
Figure 2.
Individual consumer loads and the sum of consumer loads for (a) 25% PFS, (b) 50% PFS, (c) 75% PFS, and (d) 100% PFS. Note that an artificial difference in load magnitudes was added to clearly illustrate where loads are overlapping.

Table 1.
Number of coincident consumer loads needed to achieve a given PFS and the resulting peak load.
An 18 kW peak load is not typical for an individual residential connection, but it is used here because the test feeder grid components have a relatively high capacity for the number of consumer connections: approximately 14.5 kW of grid capacity per connection. In comparison, in the Netherlands, it is common to have 0.8–2.9 kW of grid capacity per connection in residential DGs [5]. This lower capacity is typical for many European countries, especially in areas where the DG has not been reinforced and gas or heat networks are used for heating [65]. To enable transparency and reproducibility, the European test feeder properties were left unaltered, while the consumer loads were scaled up to achieve a grid loading effect proportionally similar to expected future power flows on lower-capacity DGs [7,9].
Similarly, it is unlikely for a consumer to have no load for most of the day. This simplification was made to demonstrate the impact of battery siting relative to loads on battery capacity requirements. In other words, if all consumer loads contribute to the peak load, it becomes difficult to determine the extent to which each individual consumer load contributes to battery capacity requirements. By omitting some consumer loads, it is obvious that only the active consumer loads affect battery capacity requirements.
Figure 3 illustrates the sum of the consumer loads for power flow patterns with variable simultaneity. As shown, at higher simultaneity, the degree of DG loading increases. For ease of reproducibility, the coincident peak loads were distributed over the test feeder following a simple, recursive logic. The first load was positioned at the connection closest to the transformer, and the second at the connection furthest from the transformer (in terms of total cable length). The third load was positioned at the connection second-closest to the transformer, and the fourth at the connection second-furthest from the transformer. This process was repeated until the desired level of PFS was achieved (i.e., for the number of coincident consumer loads defined in Table 1). The remaining (non-coincident) loads were distributed randomly over the remaining consumer connections. Due to the grid topology, coincident loads tended to be positioned at the ends of cables 4 and 5 before cables 2 and 3, especially at lower PFSs. This consistency was important for establishing the dependence of battery sizing on the siting of batteries relative to consumer loads.
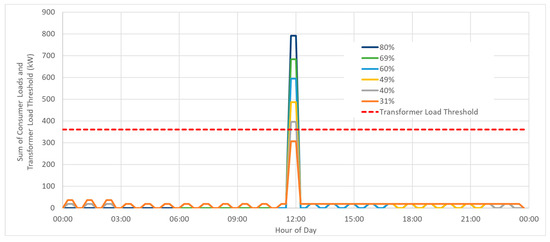
Figure 3.
Sum of consumer loads at different PFS and transformer load thresholds.
2.3. Battery Energy Storage Objectives
The objective of the BES system should be defined on the basis of the problem the system is attempting to solve. In this case, the BES system was programmed to maintain the peak transformer loading at 45% of the transformer’s capacity (i.e., 360 kW). This 45% transformer loading threshold is visualised by the dashed red line in Figure 3. The 45% transformer loading threshold was chosen because it allowed testing of battery PFM over PFS, ranging from 31% to 80%. Although the sum of consumer loads for 31% PFS does not exceed the transformer load threshold, the addition of network losses causes transformer loading to exceed the 45% threshold in this case. At simultaneities above 80%, it was not always possible for power flow equations to be solved due to voltages dropping to zero on parts of the grid. Therefore, power flows with simultaneities above 80% were omitted.
2.4. Battery Energy Storage Siting Configurations
Battery siting configurations should be designed that are reflective of real-world possibilities, so that the relative capacity requirements for implementable BES systems can be compared. In this case, three battery configurations were designed to illustrate the impact of battery siting on battery sizing requirements. The first configuration sites a battery on the low-voltage side of the transformer station, and is referred to as Transformer Energy Storage (TES). The second configuration sites a battery at a central juncture of the DG, and is referred to as Central Energy Storage (CES). The third configuration consists of five batteries spread among the grid’s consumer connections, one battery per cable, each located near the mid-point of their given cable. The third configuration is referred to as Distributed Energy Storage (DES). Figure 1 depicts these battery configurations.
Some variations of the DES configuration were also implemented to test the sensitivity of the results to battery siting. These variations included using fewer than five DES batteries to manage power flows and relocating DES batteries to consumer connections at the ends of their respective cables. The aim of the first sensitivity test was to evaluate the relative effect of a variable number of batteries on the minimum battery capacity requirements needed to provide PFM. Specifically, this test gives insight into the relative capacity advantages (or disadvantages) of deploying an increasing number of distributed batteries. The second sensitivity test gives insight into the impact of battery siting relative to large loads on battery capacity requirements. These tests illustrate the sensitivity of battery capacity requirements when installing (or deploying) a battery at one site versus another. These tests are also indicative of the degree of optimisation that is possible within a battery configuration.
As noted by Nourai et al. [45] and van Someren et al. [7], network losses are a primary distinguishing factor between different battery configurations. To quantify the effect of network losses on battery sizing, a scenario was also made using a CES battery configuration with all cable resistances reduced to nearly zero: 0.01% of their normal value. (Cable resistances could not be fully reduced to zero because this resulted in unsolvable power flow equations). As a result, network losses were nearly zero in this scenario. This is referred to as the Near-Zero (NZ) configuration.
2.5. Battery Energy Storage Control Algorithm and Capacity Minimisation
A BES control algorithm should be designed in such a way that it can provide the desired grid service using a minimum amount of battery capacity. In this case, BES was controlled to manage power flows, such that transformer peak loading was maintained at 45% of the transformer’s rated capacity (dashed red line in Figure 3). To achieve this, a battery control algorithm was designed that used iteration to determine the minimum battery capacity required to maintain the peak transformer load percentage at the 45% threshold. This algorithm was implemented for several different battery siting configurations and variable PFSs, as described above.
The battery control algorithm developed for the case study is visualised in Figure 4. This algorithm is a more detailed, case-specific version of the algorithm described at the beginning of the methodology, but follows the same general steps. In this algorithm, several steps were performed that must be elaborated on. In step 1, a BES system consisting of one or more batteries was implemented in the grid model. In this case, a given BES configuration was modelled by defining energy storage systems at the indicated nodes (see Figure 1) in the grid model. For example, for the TES configuration, an energy storage system was created on the low-voltage side of the transformer.
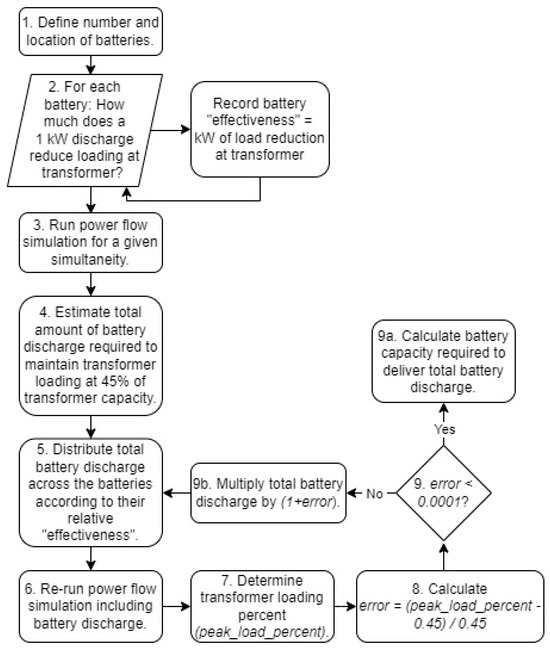
Figure 4.
Battery control and minimum capacity sizing algorithm.
In step 2, the relative “effectiveness” of each battery being modelled was calculated. In this case, battery effectiveness was defined as the relative load reduction at the trans- former when a given battery discharged 1 kW of power during the peak loading of the transformer. This step was skipped for single-battery systems.
In step 3, a power flow simulation was run using a given power flow pattern. The results of this simulation were analysed to determine the degree of transformer (over)loading during the peak power flow. This analysis was used in step 4 to estimate the amount of battery discharge power required to maintain transformer peak loading at 45% of the transformer’s capacity. This estimate was made using Equation (2), where peak_loadtransformer is the maximum simulated transformer load in kW and 360 kW is 45% of the transformer’s capacity. For example, if it was found that transformer loading reached 400 kW, then the expected battery discharge would be 40 kW.
In steps 5 and 6, the power flow simulation was run again, but this time including a battery discharge power (determined in the previous step) during the peak transformer loading. For a multi-battery system, the total discharge power was divided among the batteries according to their relative effectiveness. For example, if the total battery discharge power was 10 kW and there were two batteries, one with an effectiveness of 2 and the other with an effectiveness of 1, the first battery would discharge 6.66 kW and the second battery would discharge 3.33 kW.
In step 7, the results of the power flow simulation were analysed to determine the maximum loading percent of the transformer. In step 8, Equation (3) was used to determine the error in battery discharge power by comparing the maximum transformer loading percent (peak_load_percent) with the desired loading percent (45%). Equation (3) (and step 9b) is based on the method of iterative refinement, first proposed by Wilkinson [66].
In step 9, the calculated error was compared with a given allowable error value (in this case, 0.01% was chosen). If the error did not exceed the allowable error value, the total battery discharge power was converted to kWh and recorded as the minimum battery capacity needed to maintain transformer loading at 45% of transformer capacity. Otherwise, the total battery discharge power was multiplied by (1 + error) and the algorithm was repeated from step 5. For example, if the error value was 2%, the total battery discharge value would be multiplied by 1.02 and the algorithm would be run again from step 5.
Note that this battery control algorithm is not intended to give a mathematically optimal result, but to provide an indication of the relative battery capacity requirements for different battery siting configurations. The battery control algorithm assumes perfect knowledge of grid properties and power flow patterns, and that DES batteries can be perfectly coordinated. Battery efficiency losses and other battery properties were not included because they were assumed to be comparable between scenarios (e.g., all batteries must be oversized by ~10% to account for losses). While this algorithm was specifically designed to minimise the battery capacity needed for PFM, it could be adapted to evaluate battery sizing requirements for other gird services, more complex power flow patterns, and different battery properties/constraints.
2.6. Results Analysis
The results from the various scenarios described above were compared based on the minimum storage capacity required to provide PFM. This metric could be changed to compare BES configurations based on, e.g., system cost or carbon footprint. However, in this case, battery capacity was chosen because it is a relatively straightforward metric to calculate, and because battery capacity is highly correlated with other metrics, such as battery costs and the ability of batteries to provide a given service [23,42,43]. In general, the results of this study give insight into how efficient (in terms of battery capacity and energy requirements) different battery siting configurations are at providing PFM for a given PFS. These results and their implications are discussed in the following sections.
3. Results
The results from the case study are generally indicative of the impacts of battery siting and PFS on the sizing of batteries used for PFM in a DG. The results are also indicative of the sensitivity of the methodology to variable inputs.
Table 2 shows the minimum battery capacities (in kWh) required to maintain peak transformer loading at 45% of transformer capacity for different battery siting configurations and variable PFSs. Notably, there is no result for the TES configuration at a PFS of 80%. This was due to high cable loading driving cable voltage down to zero, resulting in an unsolvable power flow equation.

Table 2.
Minimum battery capacity requirements (in kWh) for managing power flows at different PFSs using different battery siting configurations.
In general, increasing PFS resulted in relatively large increases in battery capacity requirements. This relation is emphasised in Figure 5, which illustrates the way in which minimum battery capacity increases with PFS. As shown, it was observed that the trend line for the NZ configuration had a linear fit, while the trend lines for the TES, CES, and DES configurations all had a quadratic fit and diverged from the NZ trend line at higher PFSs (note the high R2 value in each case). The NZ configuration is an important reference because it allows us to quantify the impact of network losses on battery sizing. The NZ and CES cases are identical, except for network losses, so the difference in battery capacity requirements between these two cases is attributed to network losses. Because network losses are quadratically proportional to power flows (Joule’s Law), the quadratic increase in battery sizing with increasing PFS can also be attributed to network losses.
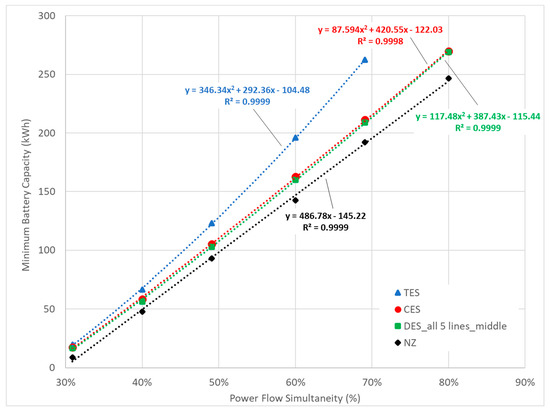
Figure 5.
Minimum battery capacity requirements for PFM for different battery configurations and variable PFSs.
Table 2 and Figure 5 also illustrate how battery siting affects battery sizing. Notably, the minimum required battery capacities for the CES and DES configurations were found to be 10–20% lower than the TES configuration, with the difference in capacity requirements increasing with PFS. This is expected because the CES and DES configurations are better able to reduce power flows over cables due to their closer proximity to consumer connections. This has the effect of reducing network losses and, thereby, reducing battery capacity requirements.
Similarly, the battery capacity requirements for a DES configuration were found to be 0.3–4.7% lower than for a CES configuration. However, in this case, the difference in capacity requirements decreased with PFS. This discrepancy may result from the imperfect coordination of DES batteries, resulting in them being oversized. Regardless, it was found that a DES configuration was technically able to reduce network losses (and, therefore, battery capacity requirements) more than a CES configuration in this case.
Sensitivity Analysis
Table 3 presents the results of the sensitivity test, where the battery capacity requirements for a DES system with a variable number of batteries and different battery siting locations were tested. It was observed that, at lower simultaneities, using only the batteries on cables 4 and 5 had the lowest capacity requirements, while at higher simultaneities, using all five batteries had the lowest capacity requirements. This likely resulted from how the coincident peak loads were distributed throughout the test feeder. At lower simultaneities, the coincident consumer loads were more clustered on cables 4 and 5 (the cables furthest from the transformer), while at higher simultaneities, the coincident loads were more evenly distributed throughout the grid. The reason for this clustering of loads was the systematic method chosen for distributing coincident loads in the grid, described in Section 2.2. As a result, using only the batteries on cables 4 and 5 at lower simultaneities placed the batteries relatively closer to the active consumer connections and, thus, reduced network losses to a larger degree. At higher simultaneities, the more distributed batteries were, on average, closer to the active consumer connections and were better able to reduce network losses. In both cases, the greater the reduction in network losses, the lower the total required battery capacity.

Table 3.
DES capacity requirements (in kWh) for different battery siting locations, number of batteries, and variable PFSs.
Similarly, locating the DES batteries at the ends of their cables reduced capacity requirements only at lower simultaneities. At lower PFSs, the active consumer connections happened to be clustered at the ends of cables, due to the method used to distribute coincident loads on the grid (Section 2.2). If a different method of distributing loads was used instead, it is expected that these results would be different.
Figure 6 illustrates how the battery capacity requirements for two different battery siting locations on the same cable begin to diverge at higher PFSs. At lower simultaneities, network losses are less pronounced and have less impact on battery sizing (i.e., both batteries have similar minimum capacities). But as PFS increases, it can be seen that the minimum battery capacity requirements for the battery furthest from (most of) the active consumer connections (red line) increases at a faster rate than does the more centrally located battery (black line). In both cases, the battery capacity requirements also closely match a quadratic trend line (i.e., there is a high R2 value), for reasons described previously.
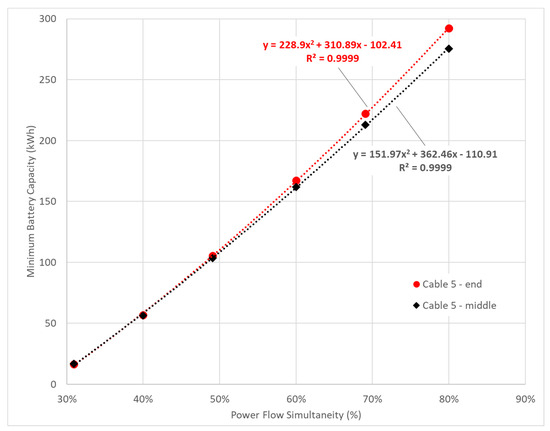
Figure 6.
Battery capacity requirements at variable PFSs for a battery sited at the end of a cable vs. a battery sited in the middle of the same cable.
Regardless, the difference in battery sizing requirements for different DES configurations was found to be relatively minor in this case, especially at lower PFSs. As shown in Table 3, increasing the number of mid-cable batteries from one to five reduced battery capacity requirements by 0.7% at 31% PFS, to 2.4% at 80% PFS. For end-of-cable batteries, increasing the number of batteries reduced battery capacity requirements by less than 0.8% at 31% PFS, to 4.9% at 80% PFS. These results imply that the number of DES batteries had a relatively small impact on battery capacity requirements in this case.
Similarly, as shown in Table 3, locating batteries in the middle of cables versus at the ends of cables can result in an increase in capacity requirements of 0.8%, or a decrease in capacity requirements of up to 5.7%. Again, the capacity differences in this case are relatively minor compared to the effects of PFS and the more general battery siting configurations discussed previously.
In summary, these results illustrate how the methodology presented in this paper can be used to compare battery sizing requirements considering different battery siting configurations and variable PFSs. In this case, it was observed that battery sizing requirements increased quadratically with PFS, primarily due to quadratically increasing network losses. It was also shown that certain battery siting configurations were able to mitigate these losses (and, hence, reduce battery capacity requirements) by reducing power flows in the grid. The sensitivity of battery capacity requirements on the number and location of DES batteries was shown to be relatively small in contrast with the above findings.
4. Discussion
The method presented in this paper provides some important implications for sizing and siting BES systems used to provide grid services in a DG. Foremost among these, it is clear that PFS is a key driver of battery sizing. At higher PFSs, increasing network losses can drive up battery capacity requirements non-linearly. These effects were particularly pronounced for the TES configuration, where increasing network losses led to increasingly high battery capacity requirements as PFS increased. Importantly, these results could be explained using established physical principles, such as Joule’s Law.
It was also demonstrated that network losses (and the quadratic increase in battery capacity requirements) can be limited through proper battery siting, as with the CES and DES configurations. In this case, it was shown that battery capacity requirements for a TES configuration can be 10–20% higher than for a CES or DES configuration. However, a TES configuration may not always be undesirable. The test feeder used in this study had only one main cable leading from the transformer; however, in practice, transformers often serve several main cables. In such a case, a TES configuration could have the advantage of being able to share its capacity across several main cables and require less battery capacity than a CES or DES configuration providing the same service. Of course, these potential advantages could be off-set by installing several batteries across all the main cables, but this might not always be feasible due to access and/or space constraints. In any case, any potential capacity advantage achieved by a TES configuration is liable to be undone by increasing network losses at higher PFSs.
It was also notable that the CES and DES configurations had relatively comparable storage capacity requirements in the case study, within 4.7% of each other. Further, the sensitivity of these results to different numbers and locations of DES batteries was also shown to be relatively small, with less than 5.7% variation in capacity requirements being observed. As a result, there would be little potential for optimising battery siting in these cases. However, different grid characteristics may lead to different results. For example, network losses are expected to be higher in a “weaker” DG, which has smaller, higher-resistance cables, such as those typical in the Netherlands. This could lead to a larger difference in capacity requirements between different CES and DES configurations.
Using batteries to manage power flows from distributed generators (such as PV) was not directly addressed in this paper, but it is expected that similar principles will apply. That is, PV panels in residential areas are prone to relatively high-generation simultaneities due to rooftops (and, therefore, PV panels) having congruent orientations [5]. In this case, siting batteries closer to the generators can better reduce network losses. However, when considering distributed generation, network losses are expected to have less impact on battery sizing (and may even have a negative correlation), since batteries do not necessarily need to be sized to compensate for network losses from distributed generation.
Similarly, the principles established in this paper apply not only to battery siting, but also to battery dispatch. In a situation where a DSO is able to select from several different batteries to manage power flows, it can be beneficial to give preference to batteries which are closer to larger loads. This will allow the DSO to achieve the same power flow reduction with less discharged battery power, thus saving energy and costs.
Battery sizing is also dependent upon battery application. The impacts of PFS and battery siting on battery sizing may be different if the BES system is used for, e.g., voltage control instead of PFM [4,43]. While the general trends presented in this paper are expected to remain consistent for different use cases, the specific characteristics of a BES system used to provide a different grid service should be re-evaluated on a case-by-case basis. For example, if a battery system is designed to manage DG voltage, it may be preferential to site batteries closer to the ends of cables, where voltage problems tend to be most acute [46]. However, network losses and PFS are still expected to impact battery sizing requirements for other battery applications.
Finally, some of the assumptions made in this paper must be addressed. Thermal modelling of the grid was not included in this study. It is expected that thermal effects would enhance the relative storage capacity savings of a DES configuration, because sustained high power flows will overheat cables, thus increasing cable resistance and leading to more network losses. A DES configuration is better able to mitigate such effects by reducing power flows through grid cables. Reactive power flows were also omitted in this paper. Further study is needed to research how their inclusion would impact batter sizing.
The model presented here also simplified the grid to a single-phase system. In reality, the grid is a three-phase system and phase imbalance is an increasingly common occurrence, especially in residential DGs [55,67,68]. In practice, higher PFSs can be more readily achieved on single phases, leading to a greater risk of overloading problems in the grid. In principle, a battery can manage power flows on any of the three phases, but further study is needed to determine how incorporating these factors would affect battery sizing.
The model assumed perfect knowledge of power flows and grid characteristics to minimise storage capacities. In reality, this would not be the case and the batteries in a DES system must be properly coordinated to manage power flows effectively and efficiently. With imperfect knowledge, this coordination can be a challenge, which may lead to oversizing of individual DES batteries. In contrast, a single TES/CES battery is more straightforward to control and size efficiently [14,22].
Specific battery properties, such as (dis)charge efficiency and self-discharge rate, were not considered in this paper. Such properties must be taken into account to accurately estimate the battery capacity requirements for the type(s) of battery being studied [69]. For example, a battery with a relatively low discharge efficiency will need a larger capacity than a battery with a higher discharge efficiency. A battery’s maximum rate of (dis)charge could also limit the services that the battery can provide. These details should be taken into account when developing a battery control algorithm and battery model for a given case study.
Finally, in this study, the coincident loads were distributed systematically in the grid (starting at the furthest ends of the grid and working inwards). This had the effect of giving a preference to battery configurations, which had batteries sited arbitrarily closest to these consumer loads. Varying the distribution of loads in the grid is expected to give different results. However, a DES configuration provides more flexibility in this regard because there will nearly always be a battery located closer to the active consumer connections compared with a CES or TES configuration. Coordination problems aside, this inherent flexibility may allow a DES configuration to adapt to and manage changing power flows in the grid more efficiently.
5. Conclusions
This paper presents a method to evaluate the sizing requirements of batteries used to provide grid services, considering different battery siting configurations and variable PFSs. A case study was implemented using this method to illustrate the degree to which these variables impact the sizing of batteries used for PFM.
A key finding was that at higher PFSs, network losses increased quadratically due to Joule’s Law, leading to a (quadratic) increase in battery capacity requirements. Importantly, proper battery siting was shown to mitigate these effects. In this case, using a CES or DES configuration required 10 to 20% less battery capacity to achieve the same transformer load reduction as a TES configuration (with results varying depending on the PFS). In contrast, the DES configuration was found to require 0.3 to 4.7% less storage capacity than a CES configuration. Similarly, the sensitivity of battery capacity requirements to the number and location of DES batteries was relatively small, with capacity requirements varying by 0% to 5.7%. In all instances, a reduction in storage capacity requirements was largely attributed to a reduction in network losses; a battery siting configuration with batteries located closer to large loads could better reduce network losses and, thereby, reduce battery capacity requirements.
The impact of PFS and battery siting on battery sizing is expected to vary depending on network characteristics, battery application, and battery control strategies, among others. However, the magnitude of results presented in this paper indicate the relative importance of analysing variable PFSs, network losses, and battery siting configurations in BES studies. While the specific details will vary on a case-by-case basis, it is expected that the general relations established in this paper will remain consistent for other use cases. To gain further insight, it would be useful to repeat the experiments presented here using different battery siting configurations, power flow patterns, battery properties/constraints, battery applications, and grid characteristics.
Finally, the principles established in this paper do not only apply to battery siting, but also to battery dispatch. By preferentially dispatching batteries that are closer to loads, network losses can be reduced, thereby reducing the power that must be discharged from the battery, saving energy and costs. This concept will be explored further in a future paper.
Author Contributions
Conceptualization, methodology, software, analysis and writing, C.v.S.; supervision and text review/editing, M.V. and H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded internally by the Hanze University of Applied Sciences.
Data Availability Statement
The data presented in this study are openly available in the 4TU.ResearchData international data repository for science, engineering, and design, https://doi.org/10.4121/4a9dac6d-dd4e-4dc2-a5ba-72e35d86ac93.
Acknowledgments
The authors thank Sandra Bellekom for providing feedback on the paper.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
| BES | Battery Energy Storage |
| CES | Central Energy Storage |
| DES | Distributed Energy Storage |
| DG | Distribution Grid |
| DSO | Distribution System Operator |
| PFM | Power Flow Management |
| PFS | Power Flow Simultaneity |
| PV | Photovoltaic |
| TES | Transformer Energy Storage |
| NZ | Near Zero cable resistance |
References
- International Energy Agency. European Union 2020 Energy Policy Review; IEA Publications: Paris, France, 2020.
- Grond, M.O.W.; Schepers, B.A.; Veldman, E.; Slootweg, J.G.; Gibescu, M. Impact of Future Residential Loads on Medium Voltage Networks. In Proceedings of the IEEE 46th International Universities’ Power Engineering Conference, Soest, Germany, 5–8 September 2011. [Google Scholar]
- Veldman, E.; Gibescu, M.; Slootweg, H.J.G.; Kling, W.L. Scenario-Based Modelling of Future Residential Electricity Demands and Assessing Their Impact on Distribution Grids. Energy Policy 2013, 56, 233–247. [Google Scholar] [CrossRef]
- Gupta, R.; Pena-Bello, A.; Streicher, K.N.; Roduner, C.; Farhat, Y.; Thöni, D.; Patel, M.K.; Parra, D. Spatial Analysis of Distribution Grid Capacity and Costs to Enable Massive Deployment of PV, Electric Mobility and Electric Heating. Appl. Energy 2021, 287, 116504. [Google Scholar] [CrossRef]
- van Someren, C.; Visser, M.; Slootweg, H. Impacts of Electric Heat Pumps and Rooftop Solar Panels on Residential Electricity Distribution Grids. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Espoo, Finland, 18 October 2021. [Google Scholar] [CrossRef]
- Williams, B.; Bishop, D.; Gallardo, P.; Chase, J.G. Demand Side Management in Industrial, Commercial, and Residential Sectors: A Review of Constraints and Considerations. Energies 2023, 16, 5155. [Google Scholar] [CrossRef]
- van Someren, C.; Vissser, M.; Slootweg, H. Impact of Load Simultaneity and Battery Layout on Sizing of Batteries for Preventing Grid Overloading. In Proceedings of the IEEE 17th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Tallinn, Estonia, 14 June 2023. [Google Scholar] [CrossRef]
- Bernards, R. Smart Planning: Integration of Statistical and Stochastic Methods in Distribution Network Planning. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 15 October 2018. [Google Scholar]
- FLEXNET Consortium. Demand and Supply of Flexibility in the Power System of the Netherlands, 2015–2050: Summary Report of the FLEXNET Project; Report ID: ECN-E-17-053; Energy Research Centre of the Netherlands (ECN): Petten, The Netherlands, 2017. [Google Scholar]
- International Energy Agency. Electricity Grids and Secure Energy Transitions: Enhancing the Foundation of Resilient, Sustainable and Affordable Power Systems; IEA Publications: Paris, France, 2023.
- Eurelectric. Europe’s Grid Bottlenecks are Delaying its Energy Transition. 2023. Available online: https://energypost.eu/europes-grid-bottlenecks-are-delaying-its-energy-transition-what-must-we-do/ (accessed on 5 October 2023).
- Eurelectric. Power System of the Future: Keys to Delivering Capacity to the Distribution Grid; Report ID: D/2023/12.105/33; Union of the Electricity Industry—Eurelectric aisbl: Brussels, Belgium, 2023. [Google Scholar]
- Bernards, R.; Morren, J.; Slootweg, H. Incorporating the Smart Grid Concept in Network Planning Practices. In Proceedings of the IEEE 50th International Universities Power Engineering Conference (UPEC), Stoke On Trent, UK, 1–4 September 2015. [Google Scholar] [CrossRef]
- Resch, M.; Bühler, J.; Klausen, M.; Sumper, A. Impact of Operation Strategies of Large Scale Battery Systems on Distribution Grid Planning in Germany. Renew. Sustain. Energy Rev. 2017, 74, 1042–1063. [Google Scholar] [CrossRef]
- de Groot, R.J.W. Optimal Placement and Operation of Novel Grid Technologies in Distribution Grids. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 16 April 2017. [Google Scholar]
- Brinkel, N.B.G.; Schram, W.L.; AlSkaif, T.A.; Lampropoulos, I.; van Sark, W.G.J.H.M. Should We Reinforce the Grid? Cost and Emission Optimization of Electric Vehicle Charging under Different Transformer Limits. Appl. Energy 2020, 276, 115285. [Google Scholar] [CrossRef]
- Netbeheer Nederland. Basisdocument over Energie-Infrastructuur; Netbeheer Nederland: The Hague, The Netherlands, 2019. [Google Scholar]
- Thormann, B.; Kienberger, T. Estimation of Grid Reinforcement Costs Triggered by Future Grid Customers: Influence of the Quantification Method (Scaling vs. Large-Scale Simulation) and Coincidence Factors (Single vs. Multiple Application). Energies 2022, 15, 1383. [Google Scholar] [CrossRef]
- Baharlouei, Z.; Hashemi, M. Demand Side Management Challenges in Smart Grid: A Review. In Proceedings of the IEEE Smart Grid Conference (SGC), Tehran, Iran, 17–18 December 2013. [Google Scholar]
- Strbac, G. Demand Side Management: Benefits and Challenges. Energy Policy 2008, 36, 4419–4426. [Google Scholar] [CrossRef]
- Pierie, F.; van Someren, C.E.J.; Kruse, S.N.M.; Laugs, G.A.H.; Benders, R.M.J.; Moll, H.C. Local Balancing of the Electricity Grid in a Renewable Municipality; Analyzing the Effectiveness and Cost of Decentralized Load Balancing Looking at Multiple Combinations of Technologies. Energies 2021, 14, 4926. [Google Scholar] [CrossRef]
- Saboori, H.; Hemmati, R.; Ghiasi, S.M.S.; Dehghan, S. Energy Storage Planning in Electric Power Distribution Networks—A State-of-the-Art Review. Renew. Sustain. Energy Rev. 2017, 79, 1108–1121. [Google Scholar] [CrossRef]
- van Westering, W.; Hellendoorn, H. Low Voltage Power Grid Congestion Reduction Using a Community Battery: Design Principles, Control and Experimental Validation. Int. J. Electr. Power Energy Syst. 2020, 114, 105349. [Google Scholar] [CrossRef]
- Das, C.K.; Bass, O.; Kothapalli, G.; Mahmoud, T.S.; Habibi, D. Overview of Energy Storage Systems in Distribution Networks: Placement, Sizing, Operation, and Power Quality. Renew. Sustain. Energy Rev. 2018, 91, 1205–1230. [Google Scholar] [CrossRef]
- Sabihuddin, S.; Kiprakis, A.; Mueller, M. A Numerical and Graphical Review of Energy Storage Technologies. Energies 2014, 8, 172–216. [Google Scholar] [CrossRef]
- Sardi, J.; Mithulananthan, N.; Gallagher, M.; Hung, D.Q. Multiple Community Energy Storage Planning in Distribution Networks Using a Cost-Benefit Analysis. Appl. Energy 2017, 190, 453–463. [Google Scholar] [CrossRef]
- Segundo Sevilla, F.R.; Parra, D.; Wyrsch, N.; Patel, M.K.; Kienzle, F.; Korba, P. Techno-Economic Analysis of Battery Storage and Curtailment in a Distribution Grid with High PV Penetration. J. Energy Storage 2018, 17, 73–83. [Google Scholar] [CrossRef]
- Wade, N.S.; Taylor, P.C.; Lang, P.D.; Jones, P.R. Evaluating the Benefits of an Electrical Energy Storage System in a Future Smart Grid. Energy Policy 2010, 38, 7180–7188. [Google Scholar] [CrossRef]
- Parra, D.; Swierczynski, M.; Stroe, D.I.; Norman, S.A.; Abdon, A.; Worlitschek, J.; O’Doherty, T.; Rodrigues, L.; Gillott, M.; Zhang, X.; et al. An Interdisciplinary Review of Energy Storage for Communities: Challenges and Perspectives. Renew. Sustain. Energy Rev. 2017, 20, 730–749. [Google Scholar] [CrossRef]
- Roos, M.H.; Geldtmeijer, D.A.M.; Nguyen, H.P.; Morren, J.; Slootweg, J.G. Optimizing the Technical and Economic Value of Energy Storage Systems in LV Networks for DNO Applications. Sustain. Energy Grids Netw. 2018, 16, 207–216. [Google Scholar] [CrossRef]
- Saboori, H.; Abdi, H. Application of a Grid Scale Energy Storage System to Reduce Distribution Network Losses. In Proceedings of the IEEE 18th Electric Power Distribution Conference, Kermanshah, Iran, 30 April 2013. [Google Scholar] [CrossRef]
- Marra, F.; Yang, G.; Traeholt, C.; Ostergaard, J.; Larsen, E. A Decentralized Storage Strategy for Residential Feeders with Photovoltaics. IEEE Trans. Smart Grid 2014, 5, 974–981. [Google Scholar] [CrossRef]
- Verkaik, P. The Effect of Residential Batteries on Medium Voltage Substations—A Socio-Technical Analysis of the Emergence of Residential Batteries in the Netherlands. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 28 October 2022. [Google Scholar]
- Zhou, H.S.; Passey, R.; Bruce, A.; Sproul, A.B. Impact of Residential Battery Energy Storage Systems on the Peak Reverse Power Flows from Distributed Photovoltaic Systems. J. Energy Storage 2022, 52, 104817. [Google Scholar] [CrossRef]
- Roos, M.; Holthuizen, B. Congestion of LV Distribution Networks by Household Battery Energy Storage Systems Utilized for FCR, aFRR and Market Trading. In Proceedings of the IEEE 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018. [Google Scholar] [CrossRef]
- Fett, D.; Fraunholz, C.; Keles, D. Diffusion and System Impact of Residential Battery Storage under Different Regulatory Settings. Energy Policy 2021, 158, 112543. [Google Scholar] [CrossRef]
- Berg, K.; Rana, R.; Farahmand, H. Quantifying the Benefits of Shared Battery in a DSO-Energy Community Cooperation. Appl. Energy 2023, 343, 121105. [Google Scholar] [CrossRef]
- The European Commission. Directive (EU) 2018/2001 of the European Parliament and of The Council of 11 December 2018 on the Promotion of the Use of Energy from Renewable Sources. 2018. Available online: https://eur-lex.europa.eu/eli/dir/2018/2001/2018-12-21 (accessed on 5 October 2023).
- Bundesnetzagentur. Bundesnetzagentur Startet Zweite Konsultation zur Integration von Steuerbaren Verbrauchseinrichtungen in das Stromnetz. 2023. Available online: https://www.bundesnetzagentur.de/SharedDocs/Pressemitteilungen/DE/2023/20230616_14a.html (accessed on 5 October 2023).
- Reijnders, V.M.J.J.; van der Laan, M.D.; Dijkstra, R. Energy Communities: A Dutch Case Study. In Behind and Beyond the Meter: Digitalization, Aggregation, Optimization, Monetization; Sioshansi, F., Ed.; Academic Press: London, UK, 2020; pp. 137–155. ISBN 978-0-12-819951-0. [Google Scholar] [CrossRef]
- Idlbi, B.; von Appen, J.; Kneiske, T.; Braun, M. Cost-Benefit Analysis of Battery Storage System for Voltage Compliance in Distribution Grids with High Distributed Generation. Energy Procedia 2016, 99, 215–228. [Google Scholar] [CrossRef]
- Gu, T.; Wang, P.; Liang, F.; Xie, G.; Guo, L.; Zhang, X.-P.; Shi, F. Placement and Capacity Selection of Battery Energy Storage System in the Distributed Generation Integrated Distribution Network Based on Improved NSGA-II Optimization. J. Energy Storage 2022, 52, 104716. [Google Scholar] [CrossRef]
- Yang, Y.; Bremner, S.; Menictas, C.; Kay, M. Battery Energy Storage System Size Determination in Renewable Energy Systems: A Review. Renew. Sustain. Energy Rev. 2018, 91, 109–125. [Google Scholar] [CrossRef]
- Motalleb, M.; Reihani, E.; Ghorbani, R. Optimal Placement and Sizing of the Storage Supporting Transmission and Distribution Networks. Renew. Energy 2016, 94, 651–659. [Google Scholar] [CrossRef]
- Nourai, A.; Sastry, R.; Walker, T. A Vision & Strategy for Deployment of Energy Storage in Electric Utilities. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010. [Google Scholar] [CrossRef]
- Stecca, M.; Elizondo, L.R.; Soeiro, T.B.; Bauer, P. Energy Storage Sizing and Location in Distribution Networks Considering Overall Grid Performance. In Proceedings of the IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020. [Google Scholar] [CrossRef]
- Van der Stelt, S.; AlSkaif, T.; van Sark, W. Techno-Economic Analysis of Household and Community Energy Storage for Residential Prosumers with Smart Appliances. Appl. Energy 2018, 209, 266–276. [Google Scholar] [CrossRef]
- Barbour, E.; Parra, D.; Awwad, Z.; González, M.C. Community Energy Storage: A Smart Choice for the Smart Grid? Appl. Energy 2018, 212, 489–497. [Google Scholar] [CrossRef]
- Nick, M.; Cherkaoui, R.; Paolone, M. Optimal Siting and Sizing of Distributed Energy Storage Systems via Alternating Direction Method of Multipliers. Int. J. Electr. Power Energy Syst. 2015, 72, 33–39. [Google Scholar] [CrossRef]
- Parra, D.; Norman, S.A.; Walker, G.S.; Gillott, M. Optimum Community Energy Storage for Renewable Energy and Demand Load Management. Appl. Energy 2017, 200, 358–369. [Google Scholar] [CrossRef]
- Zeh, A.; Rau, M.; Witzmann, R. Comparison of Decentralised and Centralised Grid-Compatible Battery Storage Systems in Distribution Grids with High PV Penetration: Comparison of Decentralised and Centralised Battery Storages. Prog. Photovolt. Res. Appl. 2016, 24, 496–506. [Google Scholar] [CrossRef]
- Stecca, M.; Ramirez Elizondo, L.; Batista Soeiro, T.; Bauer, P.; Palensky, P. A Comprehensive Review of the Integration of Battery Energy Storage Systems into Distribution Networks. IEEE Open J. Ind. Electron. Soc. 2020, 1, 46–65. [Google Scholar] [CrossRef]
- Bobanac, V.; Basic, H.; Pandzic, H. Determining Lithium-Ion Battery One-Way Energy Efficiencies: Influence of C-Rate and Coulombic Losses. In Proceedings of the IEEE EUROCON 19th International Conference on Smart Technologies, Lviv, Ukraine, 6–8 July 2021. [Google Scholar] [CrossRef]
- Khezri, R.; Mahmoudi, A.; Aki, H. Optimal Planning of Solar Photovoltaic and Battery Storage Systems for Grid-Connected Residential Sector: Review, Challenges and New Perspectives. Renew. Sustain. Energy Rev. 2022, 153, 111763. [Google Scholar] [CrossRef]
- Protopapadaki, C.; Saelens, D. Heat Pump and PV Impact on Residential Low-Voltage Distribution Grids as a Function of Building and District Properties. Appl. Energy 2017, 192, 268–281. [Google Scholar] [CrossRef]
- Giannitrapani, A.; Paoletti, S.; Vicino, A.; Zarrilli, D. Optimal Allocation of Energy Storage Systems for Voltage Control in LV Distribution Networks. IEEE Trans. Smart Grid 2017, 8, 2859–2870. [Google Scholar] [CrossRef]
- Khalid Mehmood, K.; Khan, S.U.; Lee, S.; Haider, Z.M.; Rafique, M.K.; Kim, C. Optimal Sizing and Allocation of Battery Energy Storage Systems with Wind and Solar Power DGs in a Distribution Network for Voltage Regulation Considering the Lifespan of Batteries. IET Renew. Power Gener. 2017, 11, 1305–1315. [Google Scholar] [CrossRef]
- Sardi, J.; Mithulananthan, N.; Hung, D.Q. Strategic Allocation of Community Energy Storage in a Residential System with Rooftop PV Units. Appl. Energy 2017, 206, 159–171. [Google Scholar] [CrossRef]
- Wong, L.A.; Shareef, H.; Mohamed, A.; Ibrahim, A.A. Optimal Placement and Sizing of Energy Storage System in Distribution Network with Photovoltaic Based Distributed Generation Using Improved Firefly Algorithms. World Acad. Sci. Eng. Technol. Int. J. Electr. Comput. Energetic Electron. Commun. Eng. 2017, 11, 811–819. [Google Scholar]
- Rusck, S. The Simultaneous Demand in Distribution Network Supplying Domestic Consumers. ASEA J. 1956, 10, 59–61. [Google Scholar]
- Nourai, A.; Kogan, V.I.; Schafer, C.M. Load Leveling Reduces T&D Line Losses. IEEE Trans. Power Deliv. 2008, 23, 2168–2173. [Google Scholar] [CrossRef]
- Schneider, K.P.; Mather, B.A.; Pal, B.C.; Ten, C.-W.; Shirek, G.J.; Zhu, H.; Fuller, J.C.; Pereira, J.L.R.; Ochoa, L.F.; de Araujo, L.R.; et al. Analytic Considerations and Design Basis for the IEEE Distribution Test Feeders. IEEE Trans. Power Syst. 2018, 33, 3181–3188. [Google Scholar] [CrossRef]
- Thurner, L.; Scheidler, A.; Schäfer, F.; Menke, J.-H.; Dollichon, J.; Meier, F.; Meinecke, S.; Braun, M. Pandapower—An Open Source Python Tool for Convenient Modeling, Analysis and Optimization of Electric Power Systems. IEEE Trans. Power Syst. 2018, 33, 18164866. [Google Scholar] [CrossRef]
- Grainger, J.J.; Stevenson, W.D. Power System Analysis; McGraw-Hill, Inc.: New York, NY, USA, 1994; ISBN 0-07-061293-5. [Google Scholar]
- sEEnergies Consortium. Cost and Capacity Analysis for Representative EU Energy Grids Depending on Decarbonisation Scenarios. In sEEnergies: Quantification of Synergies Between Energy Efficiency First Principle and Renewable Energy Systems; Mathiesen, B.V., Ed.; European Union Horizon 2020 Research and Innovation Programme; Europa-Universität Flensburg: Flensburg, Germany, 2021. [Google Scholar] [CrossRef]
- Wilkinson, J.H. Rounding Errors in Algebraic Processes; Prentice-Hall: Englewood Cliffs, NJ, USA, 1963; ISBN 0-486-67999-3. [Google Scholar]
- Akmal, M.; Fox, B.; Morrow, J.D.; Littler, T. Impact of Heat Pump Load on Distribution Networks. IET Gener. Transm. Distrib. 2014, 8, 2065–2073. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, N.; Wang, W.; Guan, X.; Xu, Z.; Dong, B.; Liu, T. Coordinating the Operations of Smart Buildings in Smart Grids. Appl. Energy 2018, 228, 2510–2525. [Google Scholar] [CrossRef]
- Surve, S.P.; Rocca, R.; Hengeveld, E.J.; Martínez, D.; Comech, M.P.; Rivas, D.M. Impact Assessment of Different Battery Energy Storage Technologies in Distribution Grids with High Penetration of Renewable Energies. In Proceedings of the 20th International Conference on Renewable Energies and Power Quality (ICREPQ’22), Vigo, Spain, 27 July 2022. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).