A Novel False Measurement Data Detection Mechanism for Smart Grids
Abstract
:1. Introduction
Contributions
- A nonlinear function-based the variable dummy value model (NF-VDVM) is proposed for the task of false data injection attack detection, and the proposed model has the ability to handle the limitations of the VDVM technique.
- It has been validated through the results of the simulations that the NF-VDVM technique is able to successfully detect FDI attacks that were not detected by the bad data filter as well as the VDVM method, and the smart grid is protected against the FDI attacks.
2. Related Work
3. Proposed Model
4. Evaluation
4.1. Data Generation
4.2. Method to Launch an Attack
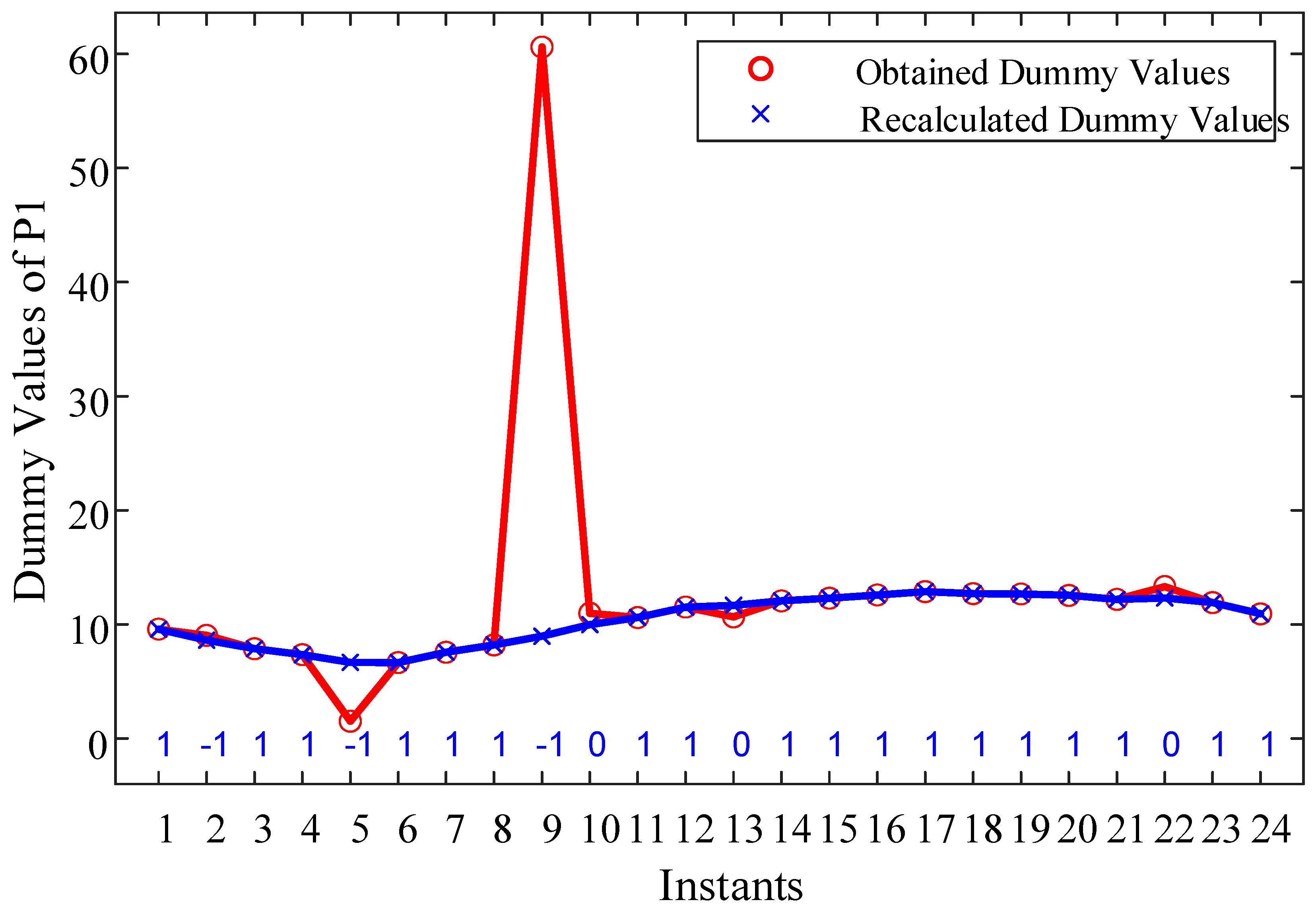
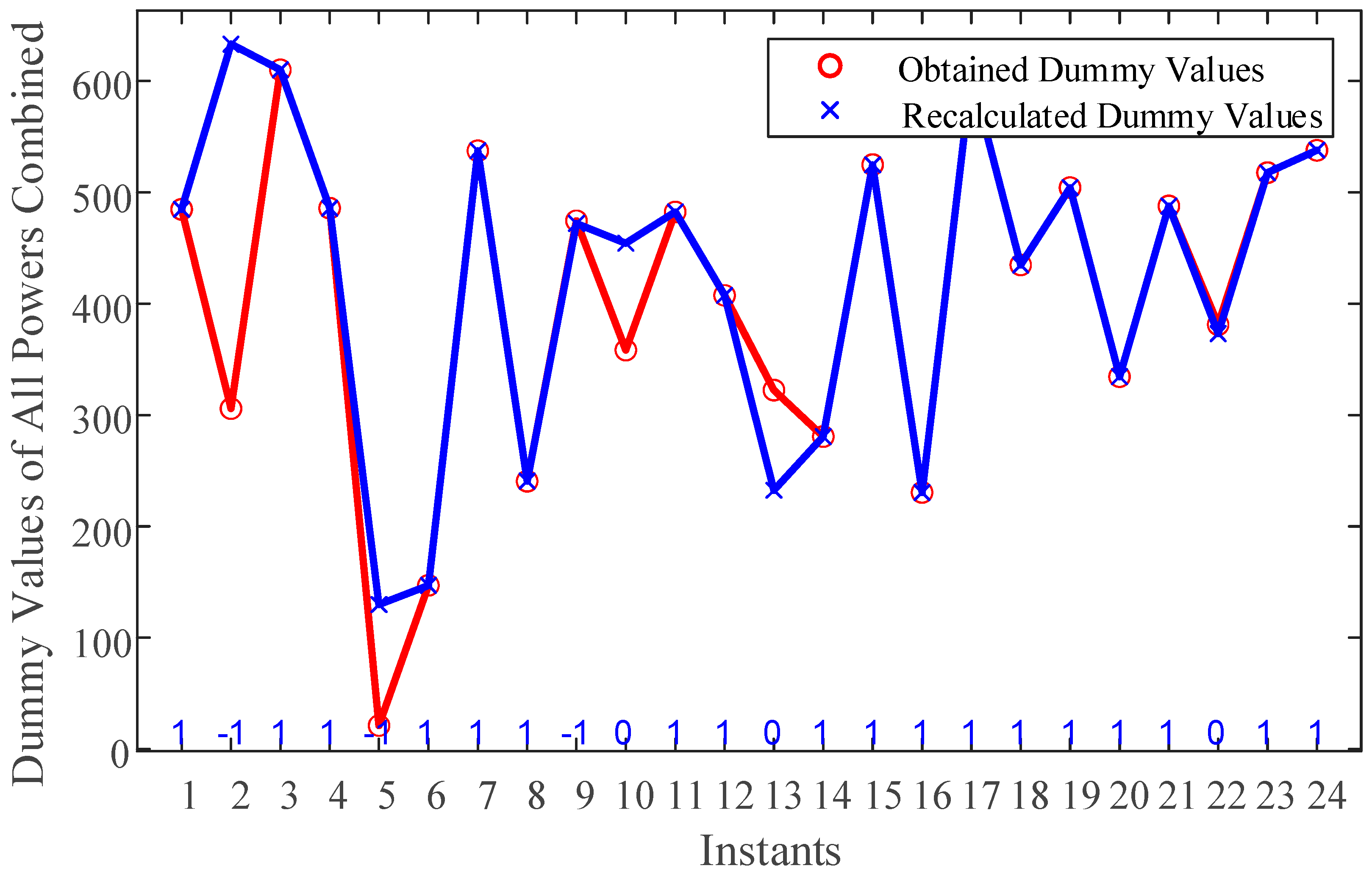
4.3. Limitations of Variable Dummy Value Model
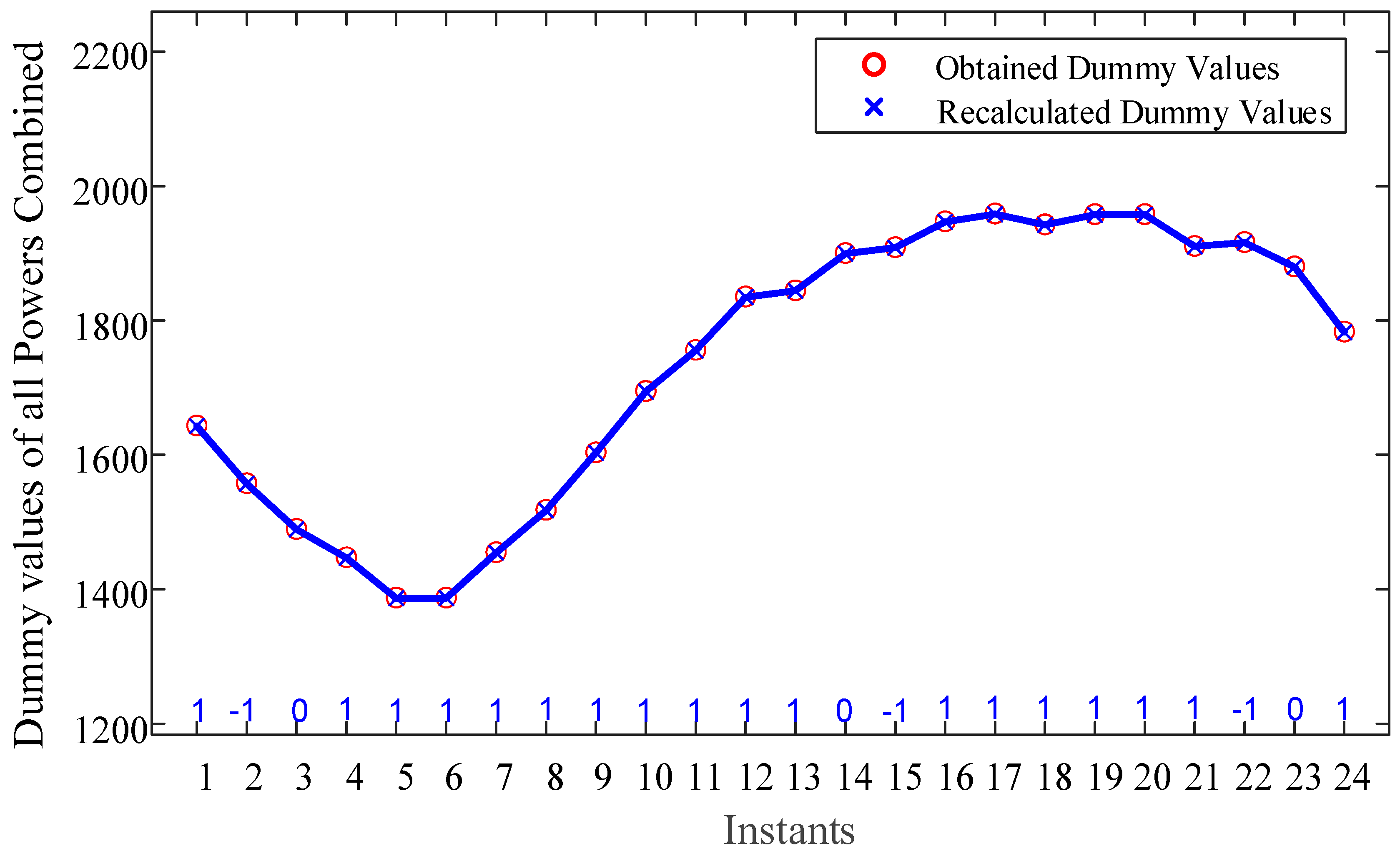
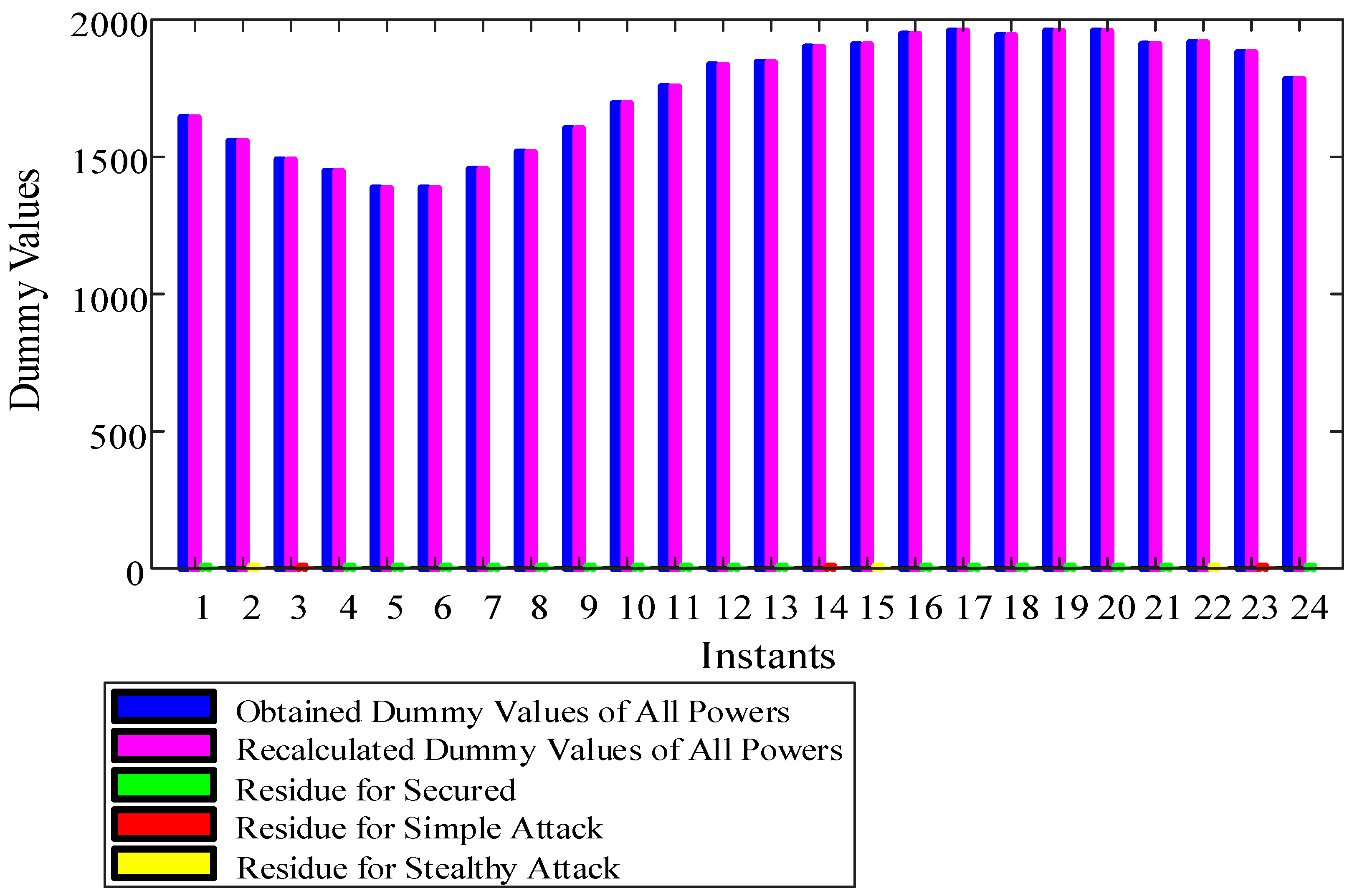
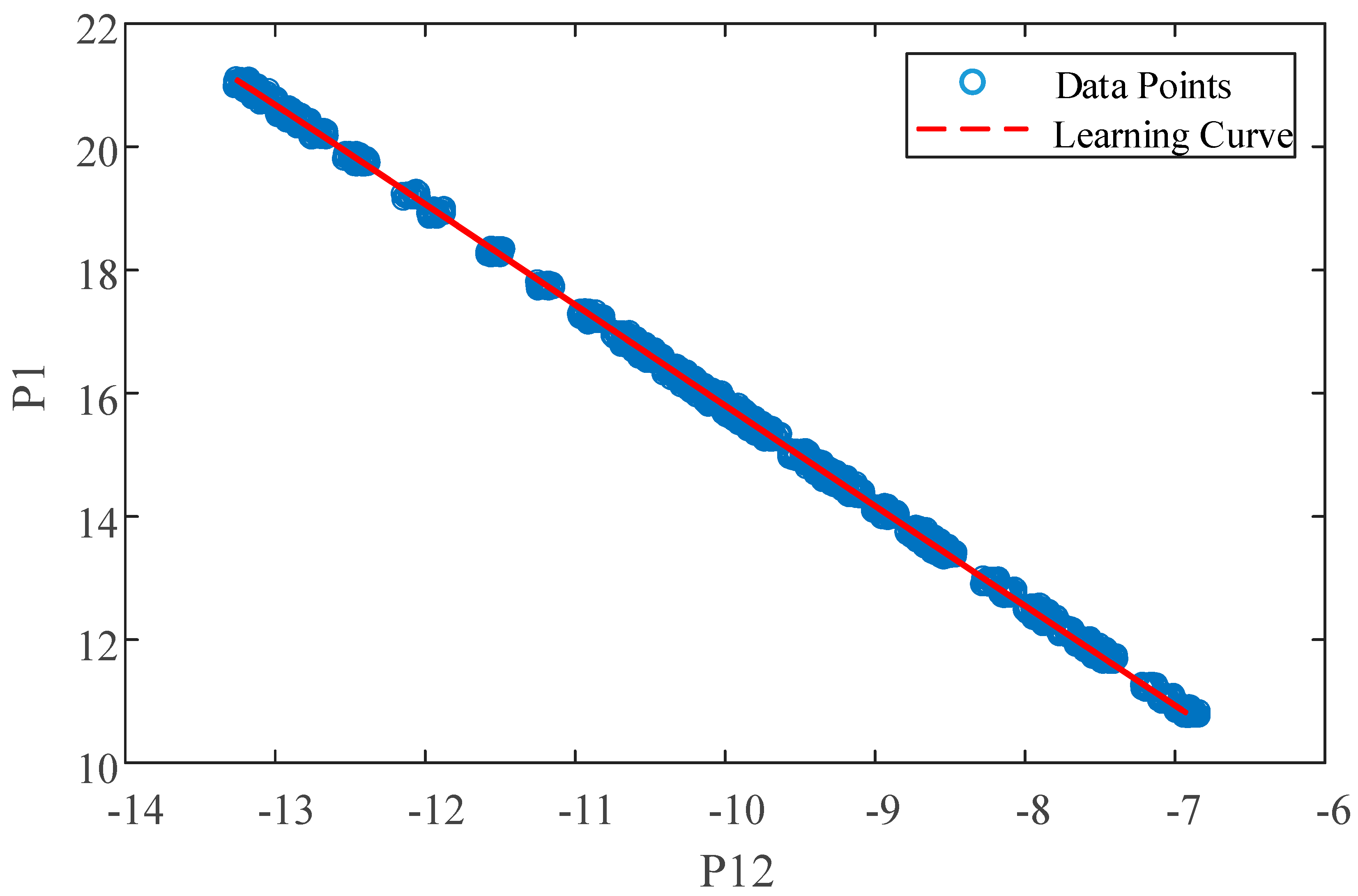
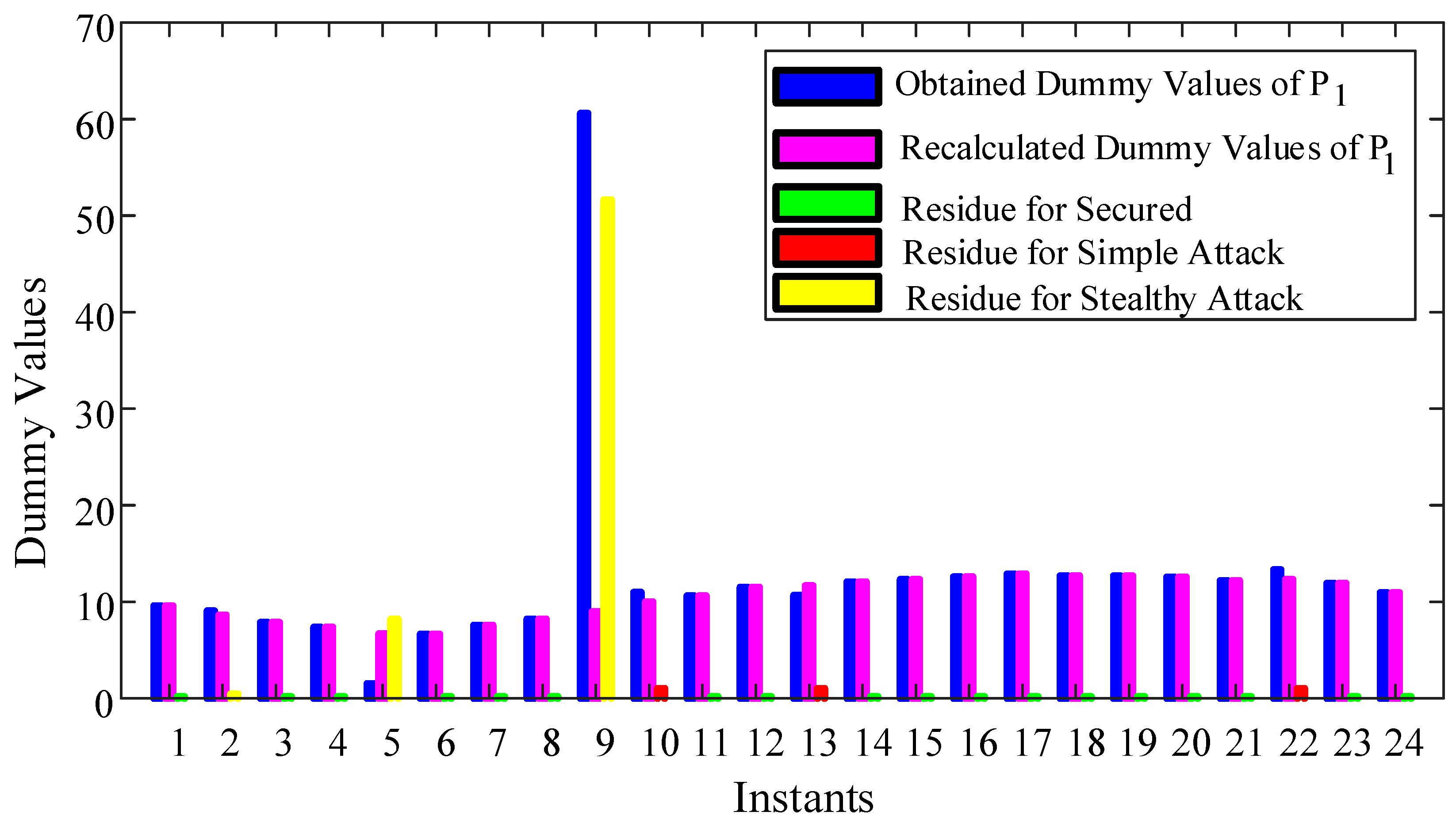
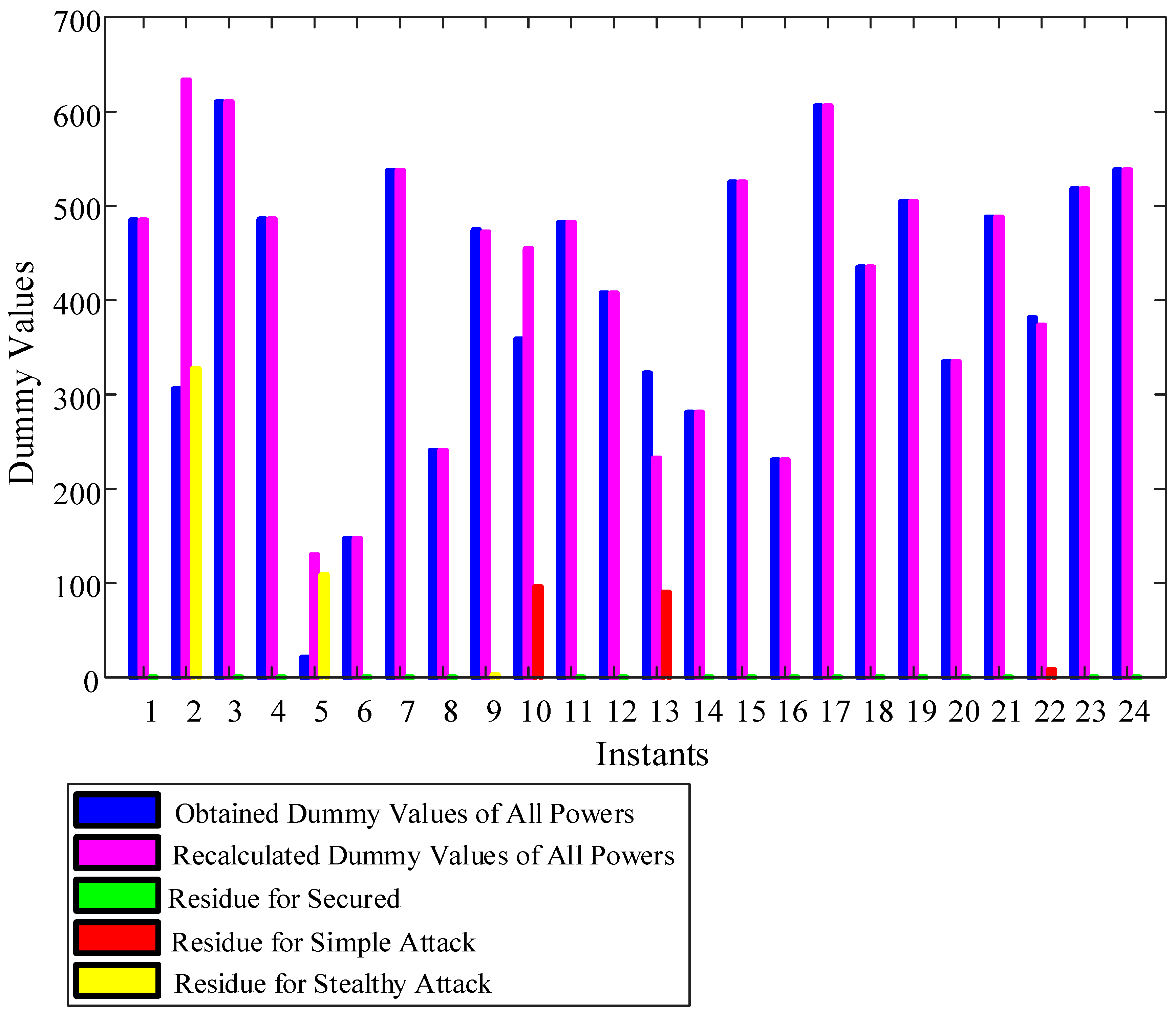
4.4. Results of Nonlinear Function Based Variable Dummy Value Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qays, M.O.; Ahmad, I.; Abu-Siada, A.; Hossain, M.L.; Yasmin, F. Key communication technologies, applications, protocols and future guides for IoT-assisted smart grid systems: A review. Energy Rep. 2023, 9, 2440–2452. [Google Scholar] [CrossRef]
- Ghiasi, M.; Wang, Z.; Mehrandezh, M.; Jalilian, S.; Ghadimi, N. Evolution of smart grids towards the Internet of energy: Concept and essential components for deep decarbonisation. IET Smart Grid 2023, 6, 86–102. [Google Scholar] [CrossRef]
- Fang, X.; Misra, S.; Xue, G.; Yang, D. Smart grid—The new and improved power grid: A survey. IEEE Commun. Surv. Tutor. 2011, 14, 944–980. [Google Scholar] [CrossRef]
- Nawaz, R.; Akhtar, R.; Shahid, M.A.; Qureshi, I.M.; Mahmood, M.H. Machine learning based false data injection in smart grid. Int. J. Electr. Power Energy Syst. 2021, 130, 106819. [Google Scholar] [CrossRef]
- Farhangi, H. The path of the smart grid. IEEE Power Energy Mag. 2009, 8, 18–28. [Google Scholar] [CrossRef]
- Zheng, J.; Gao, D.W.; Lin, L. Smart meters in smart grid: An overview. In Proceedings of the IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 4–5 April 2013. [Google Scholar]
- Mollah, M.B.; Zhao, J.; Niyato, D.; Lam, K.Y.; Zhang, X.; Ghias, A.M.; Koh, L.H.; Yang, L. Blockchain for future smart grid: A comprehensive survey. IEEE Internet Things J. 2020, 8, 18–43. [Google Scholar] [CrossRef]
- Dewangan, F.; Abdelaziz, A.Y.; Biswal, M. Load Forecasting Models in Smart Grid Using Smart Meter Information: A Review. Energies 2023, 16, 1404. [Google Scholar] [CrossRef]
- Ghiasi, M.; Niknam, T.; Wang, Z.; Mehrandezh, M.; Dehghani, M.; Ghadimi, N. A comprehensive review of cyber-attacks and defense mechanisms for improving security in smart grid energy systems: Past, present and future. Electr. Power Syst. Res. 2023, 215, 108975. [Google Scholar] [CrossRef]
- Khurana, H.; Hadley, M.; Lu, N.; Frincke, D.A. Smart-grid security issues. IEEE Secur. Priv. 2010, 8, 81–85. [Google Scholar] [CrossRef]
- Nawaz, R.; Shahid, M.A.; Mahmood, M.H. False Data Injection in smart grid in the presence of Missing Data. In Proceedings of the 1st International Conference on Smart Innovation, Ergonomics and Applied Human Factors (SEAHF), Madrid, Spain, 22–24 January 2019. [Google Scholar]
- Jayachandran, M.; Reddy, C.R.; Padmanaban, S.; Milyani, A.H. Operational planning steps in smart electric power delivery system. Sci. Rep. 2021, 11, 17250. [Google Scholar] [CrossRef]
- Hassan, M.A.; Ali, S.; Imad, M.; Bibi, S. New advancements in cybersecurity: A comprehensive survey. In Big Data Analytics and Computational Intelligence for Cybersecurity; Ouaissa, M., Boulouard, Z., Ouaissa, M., Khan, I.U., Kaosar, M., Eds.; Springer: Cham, Switzerland, 2022; pp. 3–17. [Google Scholar]
- Shahid, M.A.; Nawaz, R.; Qureshi, I.M.; Mahmood, M.H. Proposed defense topology against cyber attacks in smart grid. In Proceedings of the International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), Islamabad, Pakistan, 10–12 September 2018. [Google Scholar]
- Gunduz, M.Z.; Das, R. Analysis of cyber-attacks on smart grid applications. In Proceedings of the International Conference on Artificial Intelligence and Data Processing (IDAP), Malatya, Turkey, 28–30 September 2018. [Google Scholar]
- Esmalifalak, M.; Han, Z.; Song, L. Effect of stealthy bad data injection on network congestion in market based power system. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Paris, France, 1–4 April 2012. [Google Scholar]
- Zhao, Z.; Chen, G. An overview of cyber security for smart grid. In Proceedings of the IEEE 27th International Symposium on Industrial Electronics (ISIE), Cairns, QLD, Australia, 13–15 June 2018. [Google Scholar]
- Esmalifalak, M.; Nguyen, H.; Zheng, R.; Han, Z. Stealth false data injection using independent component analysis in smart grid. In Proceedings of the IEEE international conference on smart grid communications (SmartGridComm), Brussels, Belgium, 17–20 October 2011. [Google Scholar]
- Liu, L.; Esmalifalak, M.; Han, Z. Detection of false data injection in power grid exploiting low rank and sparsity. In Proceedings of the IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013. [Google Scholar]
- Liang, G.; Zhao, J.; Luo, F.; Weller, S.R.; Dong, Z.Y. A review of false data injection attacks against modern power systems. IEEE Trans. Smart Grid 2016, 8, 1630–1638. [Google Scholar] [CrossRef]
- Kosut, O.; Jia, L.; Thomas, R.J.; Tong, L. Limiting false data attacks on power system state estimation. In Proceedings of the 44th Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 17–19 March 2010. [Google Scholar]
- Yang, Q.; Yang, J.; Yu, W.; An, D.; Zhang, N.; Zhao, W. On false data-injection attacks against power system state estimation: Modeling and countermeasures. IEEE Trans. Parallel Distrib. Syst. 2013, 25, 717–729. [Google Scholar] [CrossRef]
- Ashok, A.; Govindarasu, M.; Ajjarapu, V. Online detection of stealthy false data injection attacks in power system state estimation. IEEE Trans. Smart Grid 2016, 9, 1636–1646. [Google Scholar] [CrossRef]
- Huang, Y.; Esmalifalak, M.; Nguyen, H.; Zheng, R.; Han, Z.; Li, H.; Song, L. Bad data injection in smart grid: Attack and defense mechanisms. IEEE Commun. Mag. 2013, 51, 27–33. [Google Scholar] [CrossRef]
- Kosut, O.; Jia, L.; Thomas, R.J.; Tong, L. Malicious data attacks on smart grid state estimation: Attack strategies and countermeasures. In Proceedings of the First IEEE International Conference on Smart Grid Communications, Gaithersburg, MD, USA, 4–6 October 2010. [Google Scholar]
- Shahid, M.A.; Ahmad, F.; Albogamy, F.R.; Hafeez, G.; Ullah, Z. Detection and prevention of false data injection attacks in the measurement infrastructure of smart grids. Sustainability 2022, 14, 6407. [Google Scholar] [CrossRef]
- Bobba, R.B.; Rogers, K.M.; Wang, Q.; Khurana, H.; Nahrstedt, K.; Overbye, T.J. Detecting false data injection attacks on dc state estimation. In Proceedings of the First Workshop on Secure Control Systems, CPSWeek, Stockholm, Sweden, 12 April 2010. [Google Scholar]
- Liu, Y.; Ning, P.; Reiter, M.K. False data injection attacks against state estimation in electric power grids. ACM Trans. Inf. Syst. Secur. 2011, 14, 1–33. [Google Scholar] [CrossRef]
- Liu, L.; Esmalifalak, M.; Ding, Q.; Emesih, V.A.; Han, Z. Detecting false data injection attacks on power grid by sparse optimization. IEEE Trans. Smart Grid 2014, 5, 612–621. [Google Scholar] [CrossRef]
- Ali, S.; Haider, A.; Rahman, M.; Sohail, M.; Zikria, Y.B. Deep learning (DL) based joint resource allocation and RRH association in 5G-multi-tier networks. IEEE Access 2021, 9, 118357–118366. [Google Scholar] [CrossRef]
- Radhoush, S.; Vannoy, T.; Liyanage, K.; Whitaker, B.M.; Nehrir, H. Distribution System State Estimation and False Data Injection Attack Detection with a Multi-Output Deep Neural Network. Energies 2023, 16, 2288. [Google Scholar] [CrossRef]
- Bitirgen, K.; Filik, Ü.B. A hybrid deep learning model for discrimination of physical disturbance and cyber-attack detection in smart grid. Int. J. Crit. Infrastruct. Prot. 2023, 40, 100582. [Google Scholar] [CrossRef]
- Vincent, E.; Korki, M.; Seyedmahmoudian, M.; Stojcevski, A.; Mekhilef, S. Detection of false data injection attacks in cyber–physical systems using graph convolutional network. Electr. Power Syst. Res. 2023, 217, 109118. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; Sun, J.S.; Tomsovic, K.; Qi, H. Towards adversarial-resilient deep neural networks for false data injection attack detection in power grids. arXiv 2021, arXiv:2102.09057. [Google Scholar]
- Niu, X.; Li, J.; Sun, J.; Tomsovic, K. Dynamic detection of false data injection attack in smart grid using deep learning. In Proceedings of the IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 18–21 February 2019. [Google Scholar]
- Zhou, L.; Ouyang, X.; Ying, H.; Han, L.; Cheng, Y.; Zhang, T. Cyber-attack classification in smart grid via deep neural network. In Proceedings of the 2nd International Conference on Computer Science and Application Engineering, Hohhot, China, 22–24 October 2018. [Google Scholar]
- Takiddin, A.; Atat, R.; Ismail, M.; Boyaci, O.; Davis, K.R.; Serpedin, E. Generalized graph neural network-based detection of false data injection attacks in smart grids. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 7, 618–630. [Google Scholar] [CrossRef]
- Han, Y.; Feng, H.; Li, K.; Zhao, Q. False data injection attacks detection with modified temporal multi-graph convolutional network in smart grids. Comput. Secur. 2023, 124, 103016. [Google Scholar] [CrossRef]
- Yin, X.; Zhu, Y.; Xie, Y.; Hu, J. PowerFDNet: Deep learning-based stealthy false data injection attack detection for AC-model transmission systems. IEEE Open J. Comput. Soc. 2022, 3, 149–161. [Google Scholar] [CrossRef]
- Ashrafuzzaman, M.; Chakhchoukh, Y.; Jillepalli, A.A.; Tosic, P.T.; de Leon, D.C.; Sheldon, F.T.; Johnson, B.K. Detecting stealthy false data injection attacks in power grids using deep learning. In Proceedings of the 14th International Wireless Communications & Mobile Computing Conference (IWCMC), Limassol, Cyprus, 25–29 June 2018. [Google Scholar]
- Musleh, A.S.; Chen, G.; Dong, Z.Y.; Wang, C.; Chen, S. Spatio-temporal data-driven detection of false data injection attacks in power distribution systems. Int. J. Electr. Power Energy Syst. 2023, 145, 108612. [Google Scholar] [CrossRef]
- Ruan, J.; Fan, G.; Zhu, Y.; Liang, G.; Zhao, J.; Wen, F.; Dong, Z.Y. Super-Resolution Perception Assisted Spatiotemporal Graph Deep Learning against False Data Injection Attacks in Smart Grid. IEEE Trans. Smart Grid 2023, 14, 4035–4046. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Lu, Z. Graph-based detection for false data injection attacks in power grid. Energy 2023, 263, 125865. [Google Scholar] [CrossRef]
- Shukla, S.; Thakur, S.; Hussain, S.; Breslin, J.G.; Jameel, S.M. Identification of False Stealthy Data Injection Attacks in Smart Meters Using Machine Learning and Blockchain. In Proceedings of the International Congress on Blockchain and Applications, L’Aquila, Italy, 13–15 July 2022; pp. 398–409. [Google Scholar]
- Ayad, A.; Farag, H.E.; Youssef, A.; El-Saadany, E.F. Detection of false data injection attacks in smart grids using recurrent neural networks. In Proceedings of the IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 19–22 February 2018. [Google Scholar]
- Foroutan, S.A.; Salmasi, F.R. Detection of false data injection attacks against state estimation in smart grids based on a mixture Gaussian distribution learning method. IET Cyber-Phys. Syst. Theory Appl. 2017, 2, 161–171. [Google Scholar] [CrossRef]
- Kumar, A.; Saxena, N.; Jung, S.; Choi, B.J. Improving detection of false data injection attacks using machine learning with feature selection and oversampling. Energies 2021, 15, 212. [Google Scholar] [CrossRef]
- Yang, C.; Wang, Y.; Zhou, Y.; Ruan, J.; Liu, W. False data injection attacks detection in power system using machine learning method. J. Comput. Commun. 2018, 6, 276. [Google Scholar] [CrossRef]
- Tahar, B.M.; Amine, S.M.; Hachana, O. Machine Learning-Based Techniques for False Data Injection Attacks Detection in Smart Grid: A Review. In Proceedings of the International Conference on Artificial Intelligence in Renewable Energetic Systems, Tamanghasset, Algeria, 20–22 November 2022. [Google Scholar]
- Ozay, M.; Esnaola, I.; Vural, F.T.Y.; Kulkarni, S.R.; Poor, H.V. Machine learning methods for attack detection in the smart grid. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 1773–1786. [Google Scholar] [CrossRef] [PubMed]
- Qu, Z.; Zhang, X.; Gao, Y.; Peng, C.; Wang, Y.; Georgievitch, P.M. Detection of False Data Injection Attack in AGC System Based on Random Forest. Machines 2023, 11, 83. [Google Scholar] [CrossRef]
- Trevizan, R.D.; Reno, M. Detection of False Data Injection Attacks in Power System State Estimation Using Sensor Encoding. In Proceedings of the IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 25–26 April 2022. [Google Scholar]
- Wu, M.; Xie, L. Online detection of false data injection attacks to synchrophasor measurements: A data-driven approach. In Proceedings of the 50th Hawaii International Conference on System Sciences, Hilton Waikoloa Village, HI, USA, 4–7 January 2017. [Google Scholar]
- Kurt, M.N.; Yılmaz, Y.; Wang, X. Distributed quickest detection of cyber-attacks in smart grid. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2015–2030. [Google Scholar] [CrossRef]
- Kodsi, S.K.M.; Canizares, C.A. Modeling and Simulation of IEEE 14—Bus System with FACTS Controllers; University of Waterloo: Waterloo, ON, Canada, 2003. [Google Scholar]
- PJM Interconnection. Available online: https://www.pjm.com/ (accessed on 4 September 2023).
- Zimmerman, R.D.; Murillo-Sánchez, C.E. Matpower (version 7.0). PSERC Cornell 2019, 9, 19–97. [Google Scholar]

| Trial No. | VDVM (Seconds) | NF-VDVM (Seconds) |
|---|---|---|
| 1 | 0.568 | 0.756 |
| 2 | 0.449 | 0.535 |
| 3 | 0.484 | 0.636 |
| 4 | 0.394 | 0.862 |
| 5 | 0.528 | 0.752 |
| Average Time | 0.485 | 0.708 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahid, M.A.; Ahmad, F.; Nawaz, R.; Khan, S.U.; Wadood, A.; Albalawi, H. A Novel False Measurement Data Detection Mechanism for Smart Grids. Energies 2023, 16, 6614. https://doi.org/10.3390/en16186614
Shahid MA, Ahmad F, Nawaz R, Khan SU, Wadood A, Albalawi H. A Novel False Measurement Data Detection Mechanism for Smart Grids. Energies. 2023; 16(18):6614. https://doi.org/10.3390/en16186614
Chicago/Turabian StyleShahid, Muhammad Awais, Fiaz Ahmad, Rehan Nawaz, Saad Ullah Khan, Abdul Wadood, and Hani Albalawi. 2023. "A Novel False Measurement Data Detection Mechanism for Smart Grids" Energies 16, no. 18: 6614. https://doi.org/10.3390/en16186614
APA StyleShahid, M. A., Ahmad, F., Nawaz, R., Khan, S. U., Wadood, A., & Albalawi, H. (2023). A Novel False Measurement Data Detection Mechanism for Smart Grids. Energies, 16(18), 6614. https://doi.org/10.3390/en16186614









