Energy-Saving Control Method for Factory Mushroom Room Air Conditioning Based on MPC
Abstract
:1. Introduction
- (1)
- Using the Boruta method to filter relevant input data, compared to the Pearson correlation coefficient method, the Boruta method can reduce computational complexity and improve prediction accuracy.
- (2)
- An energy-saving control method for mushroom room air conditioning based on the CNN-GRU-Attention predictive model was proposed from the data, and the influence of predictive time domain and optimization algorithms on the control effect was elucidated. The superiority of the control effect compared to the switch method and PID method was verified.
- (3)
- An energy-saving control method for factory mushroom houses was proposed by combining MPC and PID. MPC was used to calculate the total duration of air conditioning activation in the future period, which was used as a constraint condition. PID was then used to control the air conditioning for a shorter period of time.
2. Case Study: Mushroom House
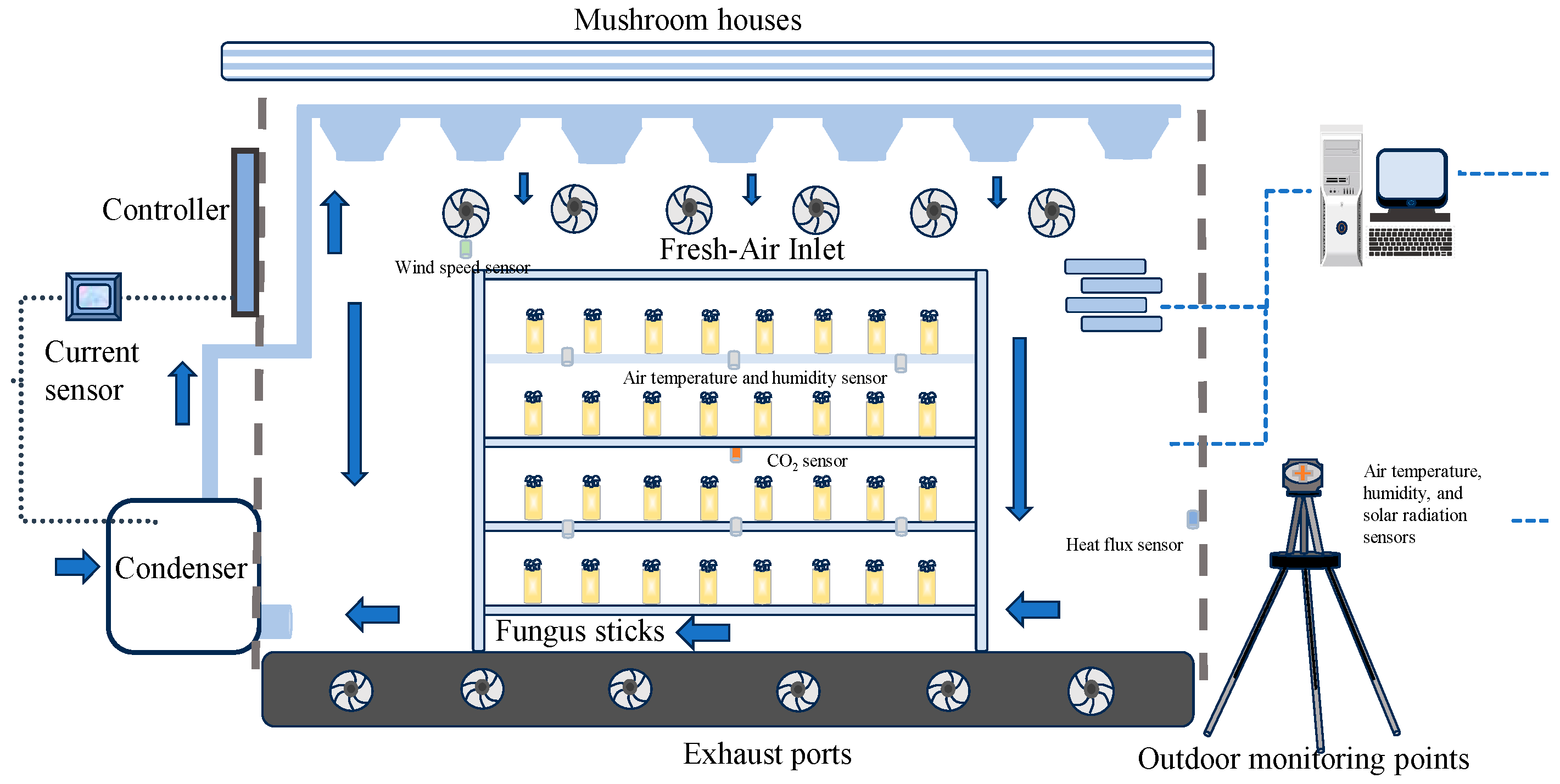
2.1. System Description
2.2. Data Collection
3. Methodology
3.1. Data Pre-Analysis
3.2. Model Performance
3.3. Hardware Environment
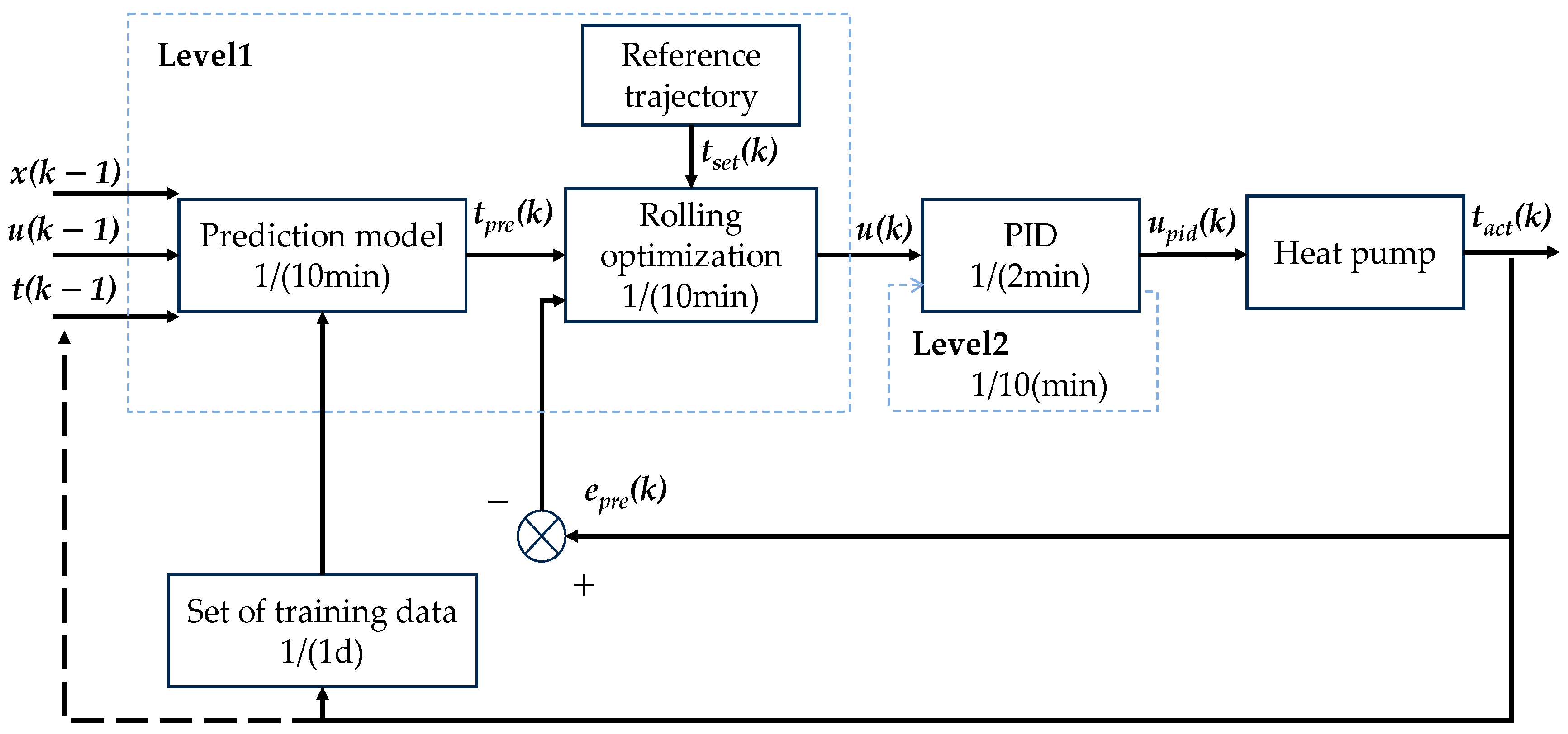
3.4. Controller Design
3.5. Data-Driven MPC
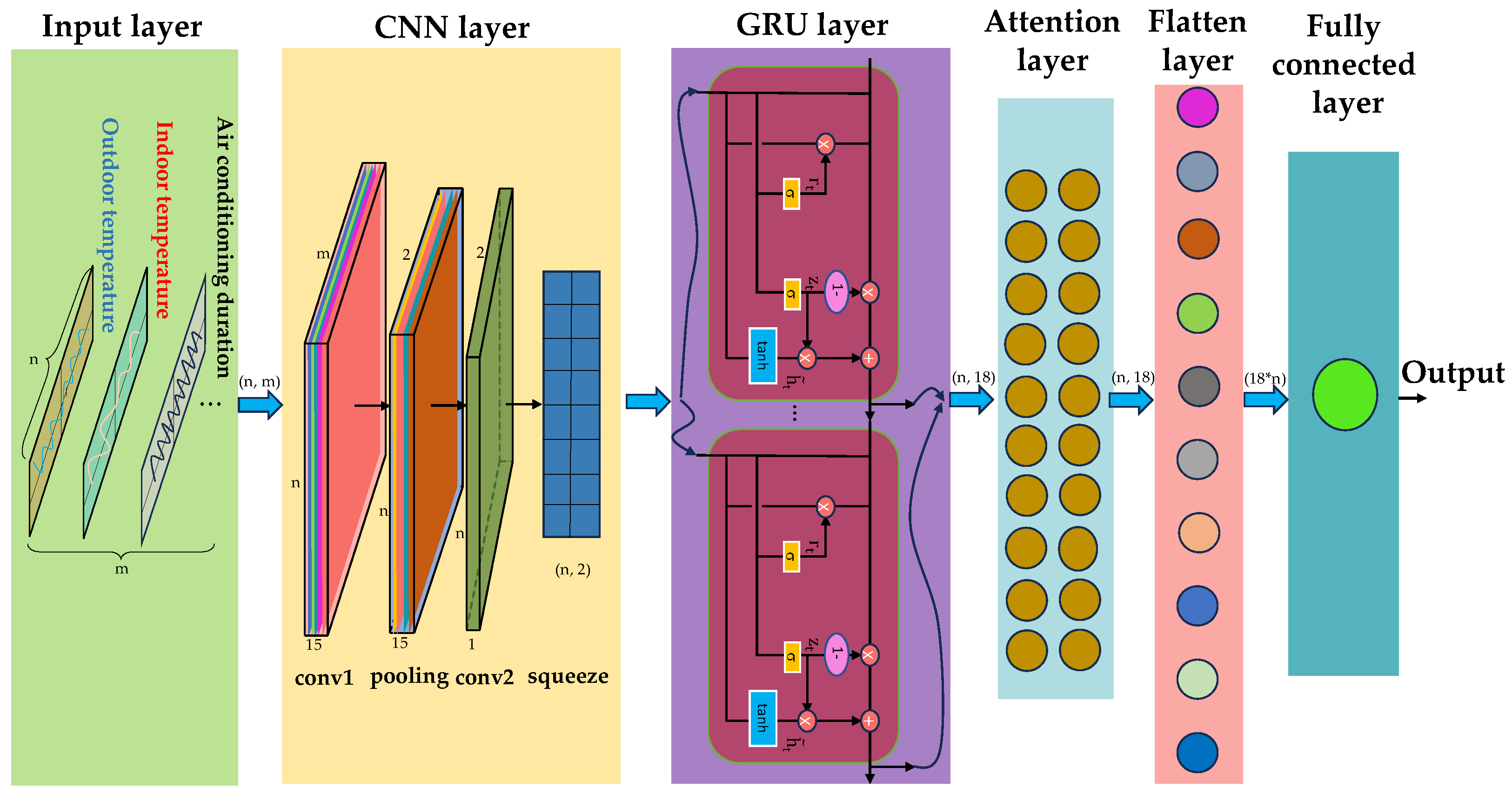
3.5.1. Prediction Model
- Input layer: Preprocessing indoor and outdoor temperatures, air conditioning on time, etc., and then representing them as a two-dimensional matrix of time steps and eigenvectors, with a data dimension of [n,m] where n is the time step in the prediction model, and m is the number of input feature categories. Input 2D data into the prediction model.
- CNN layer: After the input data is processed by the first convolutional layer and the spatiotemporal dimension features in the data are captured, the data dimension becomes [n,m,15]. After pooling, the data dimension becomes [n,2,15] and is sent to the second convolutional layer for processing. The data dimension becomes [n,2,1], and then a squeeze layer is added to compress the output dimension to [n,2] and output to the GRU layer. Both CNN layers use ReLU as the activation function.
- GRU layer: Use L2 normal form regularization to prevent model overfitting. After processing, the data dimension becomes [n,18].
- Attention layer: The attention layer enhances attention to important information through weighting.
- Output layer: The flatten layer converts the output of the attention layer into global features, changes the data dimension to [18 × n], and then connects one fully connected layer to output the prediction results.
3.5.2. Objective Function and Control Optimization
3.5.3. Error Correction
4. Results and Discussion
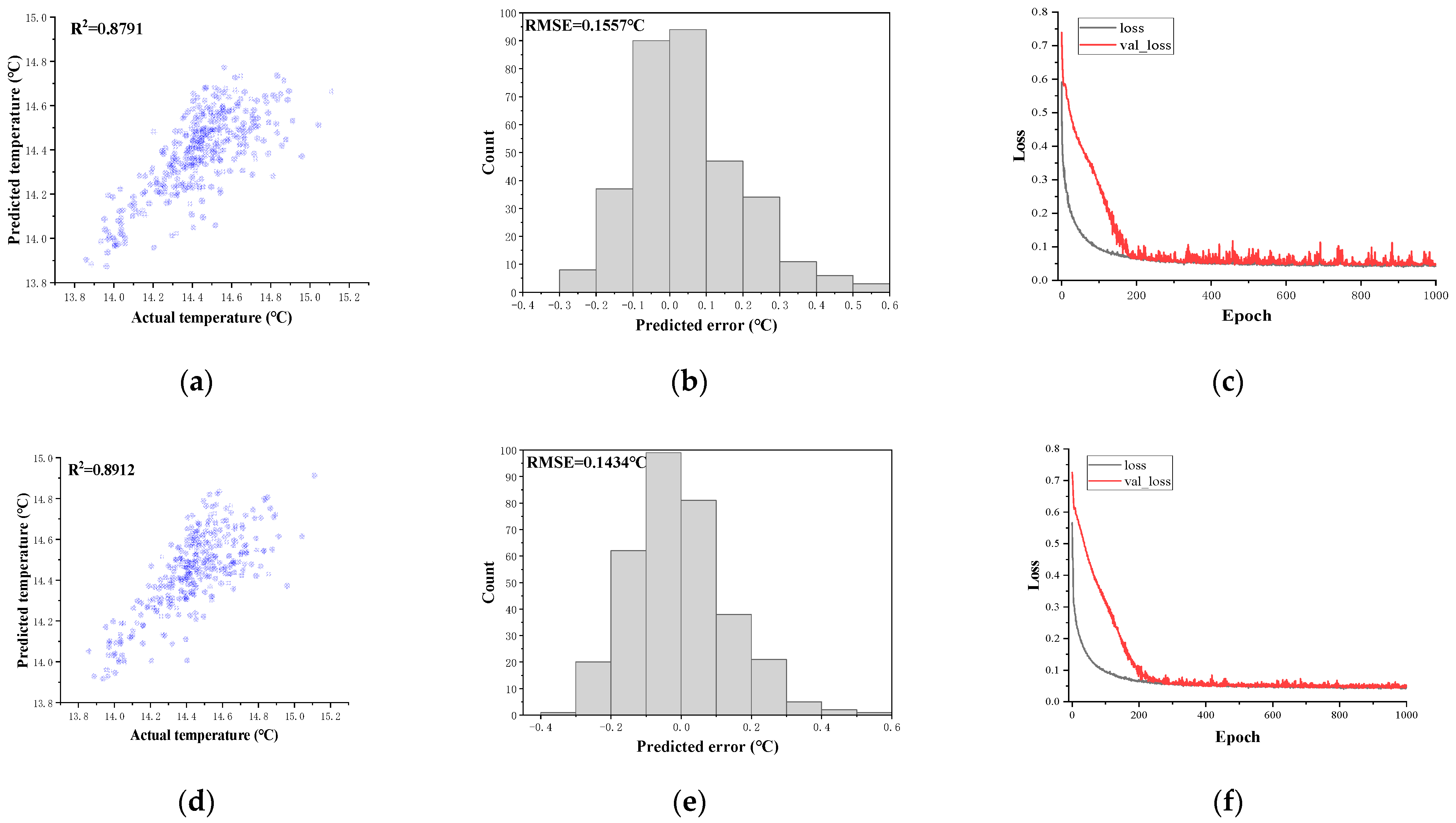
4.1. Analysis of Prediction Model Accuracy
4.1.1. Feature Selection
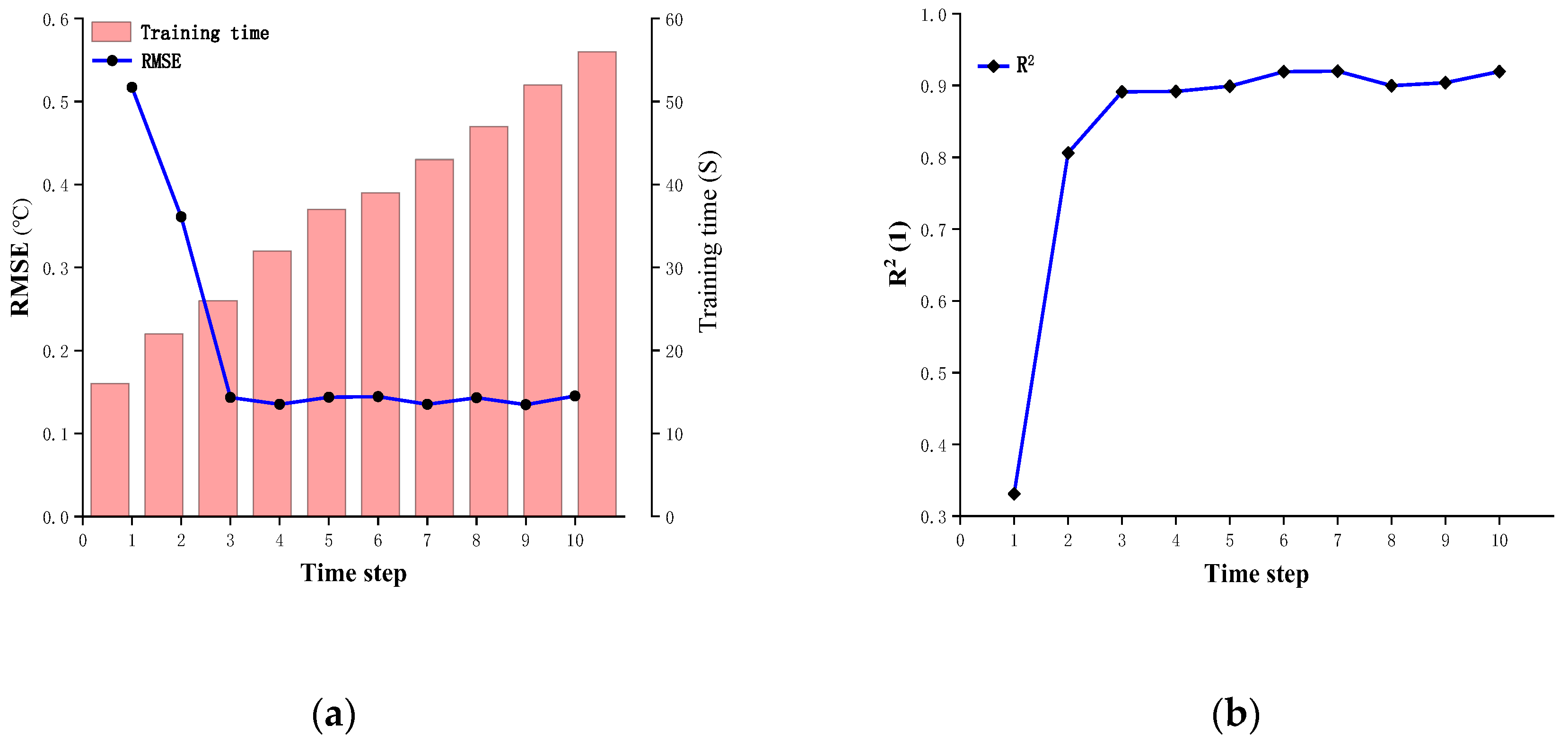
4.1.2. Varying Time Step
4.2. Effect of the Prediction Horizon
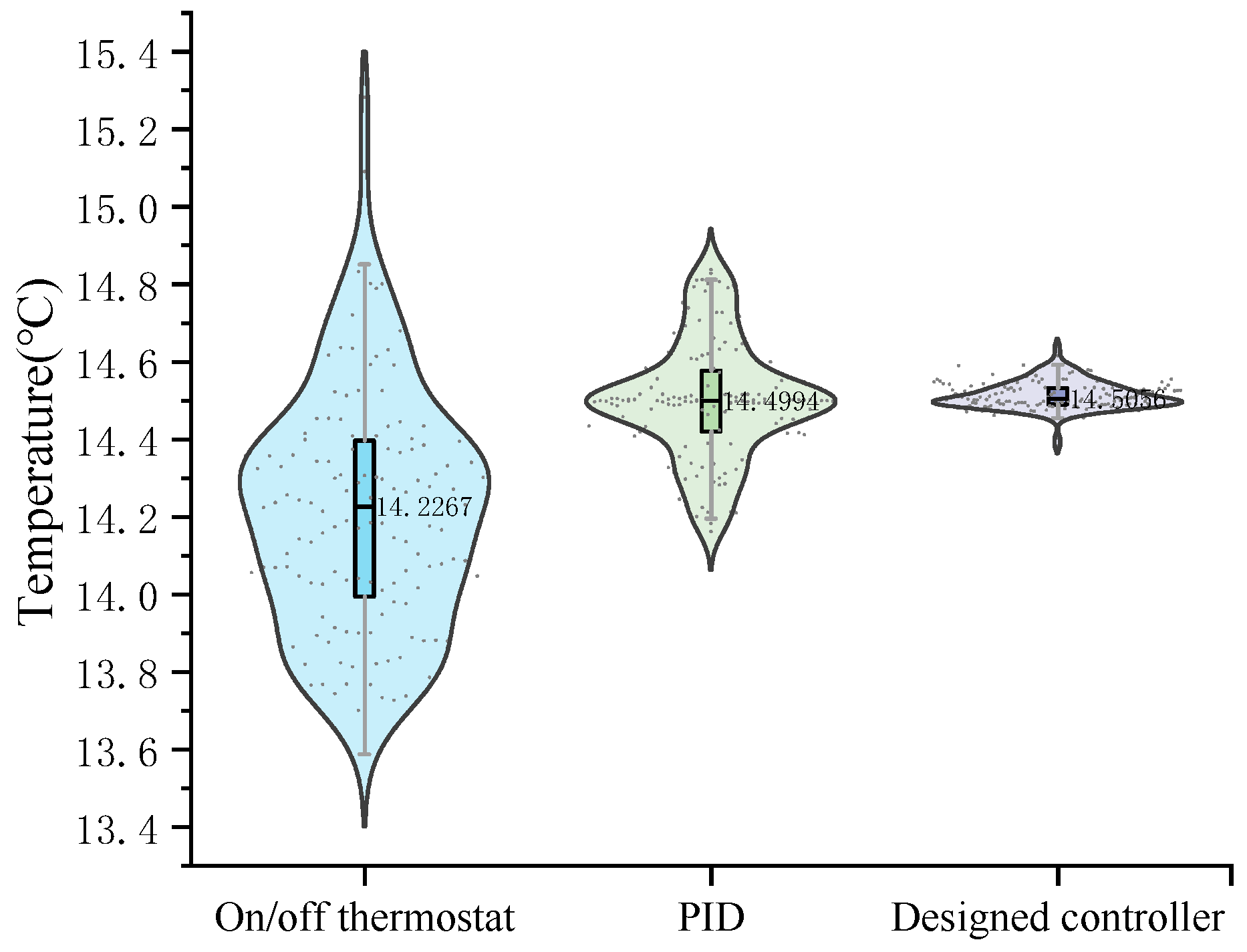
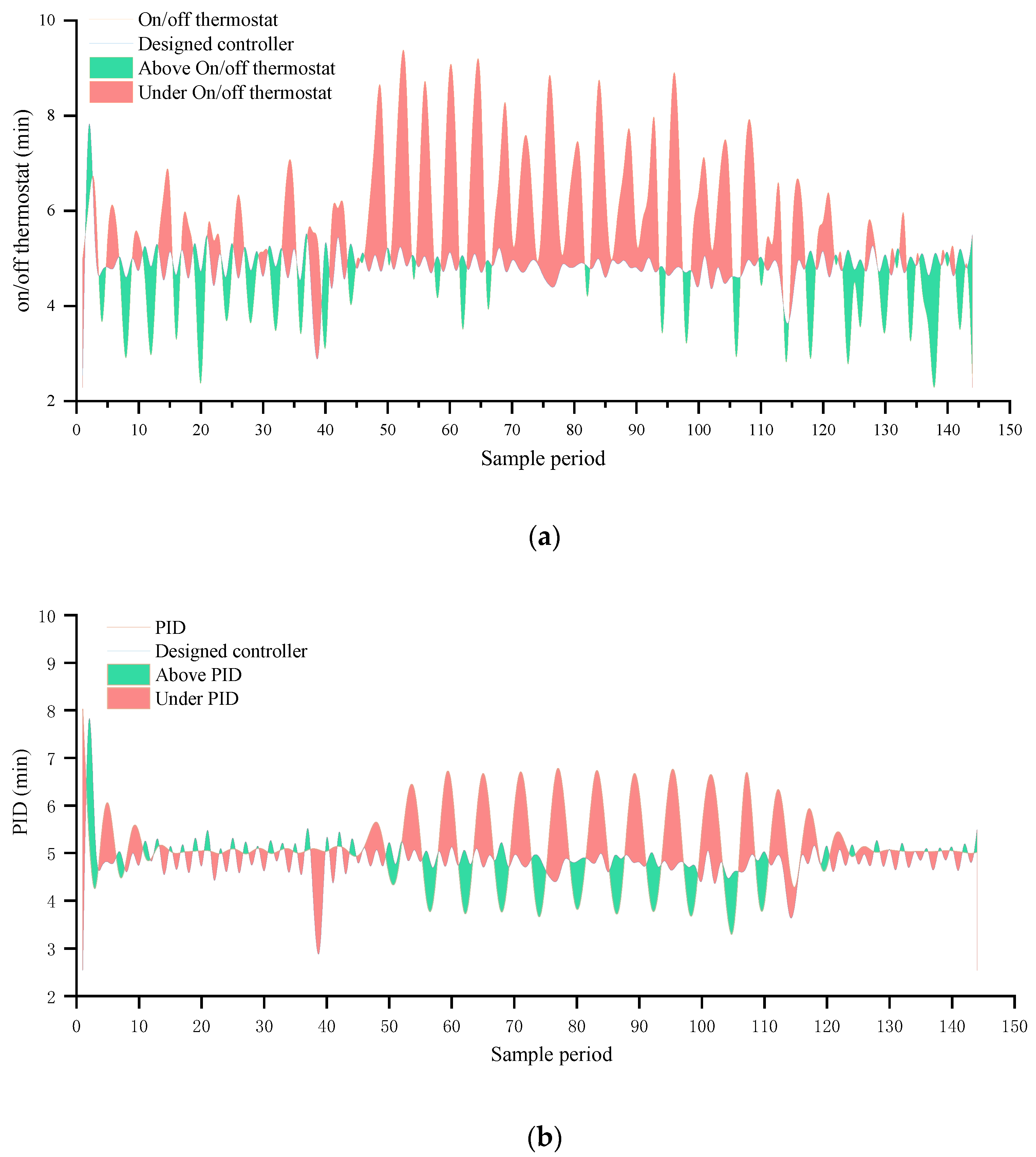
4.3. Performance Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guan, D.P.; Hu, Q.G. Energy saving analysis of industrial production of edible mushrooms. Edible Fungi 2010, 32, 1–3. [Google Scholar]
- Esmaeilzadeh, A.; Deal, B.; Yousefi-Koma, A.; Zakerzadeh, M.R. How Multi-Criterion Optimized Control Methods Improve Effectiveness of Multi-Zone Building Heating System Upgrading. Energies 2022, 15, 8675. [Google Scholar] [CrossRef]
- Jeon, B.K.; Kim, E.J. LSTM-Based Model Predictive Control for Optimal Temperature Set-Point Planning. Sustainability 2021, 13, 894. [Google Scholar] [CrossRef]
- Kim, D.; Lee, J.; Do, S.; Mago, P.J.; Lee, K.H.; Cho, H. Energy Modeling and Model Predictive Control for HVAC in Buildings: A Review of Current Research Trends. Energies 2022, 15, 7231. [Google Scholar] [CrossRef]
- Wang, D.; Chen, Y.Z.; Wang, W.G. Field test of Model Predictive Control in residential buildings for utility cost savings. Energy Build. 2023, 288. [Google Scholar] [CrossRef]
- Drgoňa, J.; Arroyo, J.; Cupeiro Figueroa, I.; Blum, D.; Arendt, K.; Kim, D.; Ollé, E.P.; Oravec, J.; Wetter, M.; Vrabie, D.L.; et al. All you need to know about model predictive control for buildings. Annu. Rev. Control 2020, 50, 190–232. [Google Scholar] [CrossRef]
- Yao, Y.; Shekhar, D.K. State of the art review on model predictive control (MPC) in heating ventilation and air-conditioning (HVAC) field. Build Env. 2021, 200, 107952. [Google Scholar] [CrossRef]
- Henze, G.P. Model predictive control for buildings: A quantum leap? J. Build. Perform. Simul. 2013, 6, 157–158. [Google Scholar] [CrossRef]
- Sangi, R.; Müller, D. A novel hybrid agent-based model predictive control for advanced building energy systems. Energy Convers. Manag. 2018, 178, 415–427. [Google Scholar] [CrossRef]
- Lee, H.; Heo, Y. Simplified data-driven models for model predictive control of residential buildings. Energy Build. 2022, 265, 1122067. [Google Scholar] [CrossRef]
- Killian, M.; Kozek, M. Ten Questions Concerning Model Predictive Control for Energy Efficient Buildings. Build. Environ. 2016, 105, 403–412. [Google Scholar] [CrossRef]
- Aruta, G.; Ascione, F.; Bianco, N.; Mauro, G.M.; Vanoli, G.P. Optimizing heating operation via GA-and ANN-based model predictive control: Concept for a real nearly-zero energy building. Energy Build. 2023, 292, 113139. [Google Scholar] [CrossRef]
- Kathirgamanathan, A.; De Rosa, M.; Mangina, E.; Finn, D.P. Data-driven predictive control for unlocking building energy flexibility: A review Renew. Sustain. Energy Rev. 2021, 135, 110120. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F.; Fung, S.A.; Raahemifar, K. Artificial neural network (ANN) based model predictive control (MPC) and optimization of HVAC systems: A state of the art review and case study of a residential HVAC system. Energy Build. 2017, 141, 96–113. [Google Scholar] [CrossRef]
- Serale, G.; Fiorentini, M.; Capozzoli, A.; Bernardini, D.; Bemporad, A. Model predictive control (MPC) for enhancing building and HVAC system energy efficiency: Problem formulation, applications and opportunities. Energies 2018, 11, 631. [Google Scholar] [CrossRef]
- Kumar, P.; Rawlings, J.B.; Wenzel, M.J.; Risbeck, M.J. Grey-box model and neural network disturbance predictor identification for economic MPC in building energy systems. Energy Build. 2023, 286, 112936. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Review of modeling methods for HVAC systems Appl. Therm. Eng. 2014, 2, 507–519. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Black-box modeling of residential HVAC system and comparison of grey-box and black-box modeling methods. Energy Build. 2015, 94, 121–149. [Google Scholar] [CrossRef]
- Stoffel, P.; Maier, L.; Kümpel, A.; Schreiber, T.; Müller, D. Evaluation of advanced control strategies for building energy systems. Energy Build. 2023, 280, 112709. [Google Scholar] [CrossRef]
- Qiang, G.; Zhe, T.; Yan, D.; Neng, Z. An improved office building cooling load prediction model based on multivariable linear regression. Energy Build. 2015, 107, 445–455. [Google Scholar] [CrossRef]
- Yun, K.; Luck, R.; Mago, J.P.; Cho, H. Building hourly thermal load prediction using an indexed ARX model. Energy Build. 2012, 54, 225–233. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, J.; Yang, J.; Berardi, U.; Cui, G. An hour-ahead predictive control strategy for maximizing natural ventilation in passive buildings based on weather forecasting. Appl. Energy 2023, 333, 120613. [Google Scholar] [CrossRef]
- Lee, D.; Ooka, R.; Ikeda, S.; Choi, W.; Kwak, Y. Model predictive control of building energy systems with thermal energy storage in response to occupancy variations and time-variant electricity prices. Energy Build. 2020, 225, 110291. [Google Scholar] [CrossRef]
- Cox, S.J.; Kim, D.; Cho, H.; Mago, P. Real time optimal control of district cooling system with thermal energy storage using neural networks. Appl. Energy 2019, 238, 466–480. [Google Scholar] [CrossRef]
- Kato, K.; Sakawa, M.; Ishimaru, K.; Ushiro, S.; Shibano, T. Heat load prediction through recurrent neural network in district heating and cooling systems. In Proceedings of the 2008 IEEE International Conference on Systems, Man and Cybernetics, Singapore, 12–15 October 2008. [Google Scholar]
- Suryanarayana, G.; Lago, J.; Geysen, D.; Aleksiejuk, P.; Johansson, C. Thermal load forecasting in district heating networks using deep learning and advanced feature selection methods. Energy 2018, 157, 141–149. [Google Scholar] [CrossRef]
- Wang, D.; Han, C.; Wang, L.; Li, X.; Cai, E.; Zhang, P. Surface roughness prediction of large shaft grinding via attentional CNN-LSTM fusing multiple process signals. Int. J. Adv. Manuf. Technol. 2023, 126, 4925–4936. [Google Scholar] [CrossRef]
- Jung, H.D.; Kim, J.H.; Kim, Y.J.; Lee, S.T.; Park, H.S. Time-serial analysis of deep neural network models for prediction of climatic conditions inside a greenhouse. Comput. Electron. Agric. 2020, 173, 105402. [Google Scholar] [CrossRef]
- Ding, Z.; Chen, W.; Hu, T.; Xu, X. Evolutionary double attention-based long short-term memory model for building energy prediction: Case study of a green building. Appl. Energy 2021, 288, 116660. [Google Scholar] [CrossRef]
- Picard, D.; Drgoňa, J.; Kvasnica, M.; Helsen, L. Impact of the controller model complexity on model predictive control performance for buildings. Energy Build. 2017, 152, 739–751. [Google Scholar] [CrossRef]
- Nelson, J.R.; Johnson, N.G. Model predictive control of microgrids for real-time ancillary service market participation. Appl. Energy 2020, 269, 114963. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Reiter, S.; Rigo, P. A review on simulation-based optimization methods applied to building performance analysis Appl. Energy 2014, 113, 1043–1058. [Google Scholar] [CrossRef]
- Wang, L.; Han, J.; Ma, F.; Li, X.; Wang, D. Accuracy design optimization of a CNC grinding machine towards low-carbon manufacturing. J. Clean. Prod. 2023, 406, 137100. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; De Stasio, C.; Mauro, G.M.; Vanoli, G.P. Multi-stage and multi-objective optimization for energy retrofitting a developed hospital reference building: A new approach to assess cost-optimality. Appl. Energy 2016, 174, 37–68. [Google Scholar] [CrossRef]
- Bünning, F.; Warrington, J.; Heer, P.; Smith, R.S.; Lygeros, J. Robust MPC with data-driven demand forecasting for frequency regulation with heat pumps. Control Eng. Pract. 2022, 122, 105101. [Google Scholar] [CrossRef]
| Hyperparameter | Value |
|---|---|
| Number of convolutional kernels in layer 1 | 15 |
| Convolutional kernel size of layer 1 | 3 × 3 |
| Pooled core size | 1 × 2 |
| Number of convolutional kernels in layer 2 | 1 |
| Convolutional kernel size of layer 2 | 3 × 3 |
| Number of neurons in the GRU layer | 18 |
| Learning rate | 0.001 |
| Epoch | 1000 |
| Batch size | 500 |
| Parameter | Value |
|---|---|
| Parent populations | 70 |
| Offspring populations | 60 |
| Crossover probability | 0.6 |
| Mutation probability | 0.1 |
| Iterations | 40 |
| Control Horizon (min) | Duration of Air Conditioning (min) | Optimization Duration (s) |
|---|---|---|
| 0–10 | 717 | 43 |
| 0–20 | 696 | 60 |
| 0–30 | 686 | 85 |
| 0–40 | 681 | 131 |
| 0–50 | 683 | 156 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Zheng, W.; Zhao, C.; Chen, Y.; Chen, C.; Zhang, X. Energy-Saving Control Method for Factory Mushroom Room Air Conditioning Based on MPC. Energies 2023, 16, 7623. https://doi.org/10.3390/en16227623
Wang M, Zheng W, Zhao C, Chen Y, Chen C, Zhang X. Energy-Saving Control Method for Factory Mushroom Room Air Conditioning Based on MPC. Energies. 2023; 16(22):7623. https://doi.org/10.3390/en16227623
Chicago/Turabian StyleWang, Mingfei, Wengang Zheng, Chunjiang Zhao, Yang Chen, Chunling Chen, and Xin Zhang. 2023. "Energy-Saving Control Method for Factory Mushroom Room Air Conditioning Based on MPC" Energies 16, no. 22: 7623. https://doi.org/10.3390/en16227623
APA StyleWang, M., Zheng, W., Zhao, C., Chen, Y., Chen, C., & Zhang, X. (2023). Energy-Saving Control Method for Factory Mushroom Room Air Conditioning Based on MPC. Energies, 16(22), 7623. https://doi.org/10.3390/en16227623





