A Review of Fuzzy Logic Method Development in Hydraulic and Pneumatic Systems
Abstract
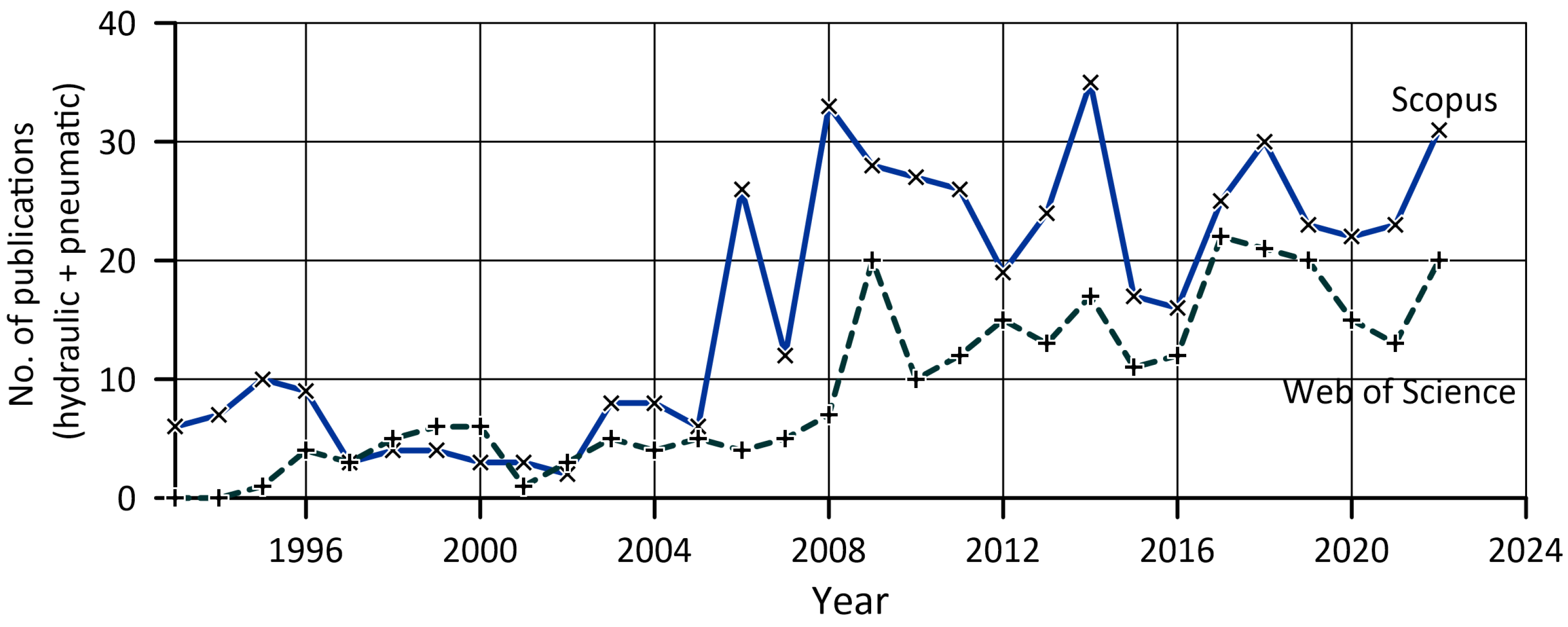
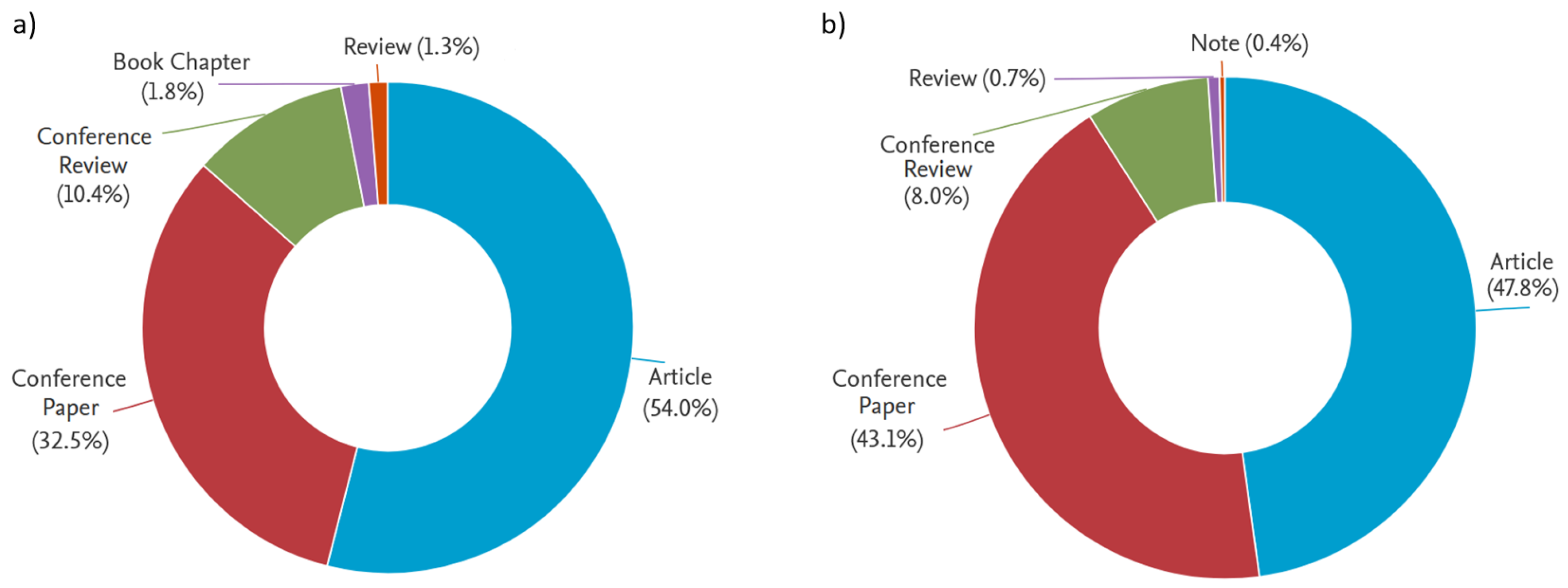
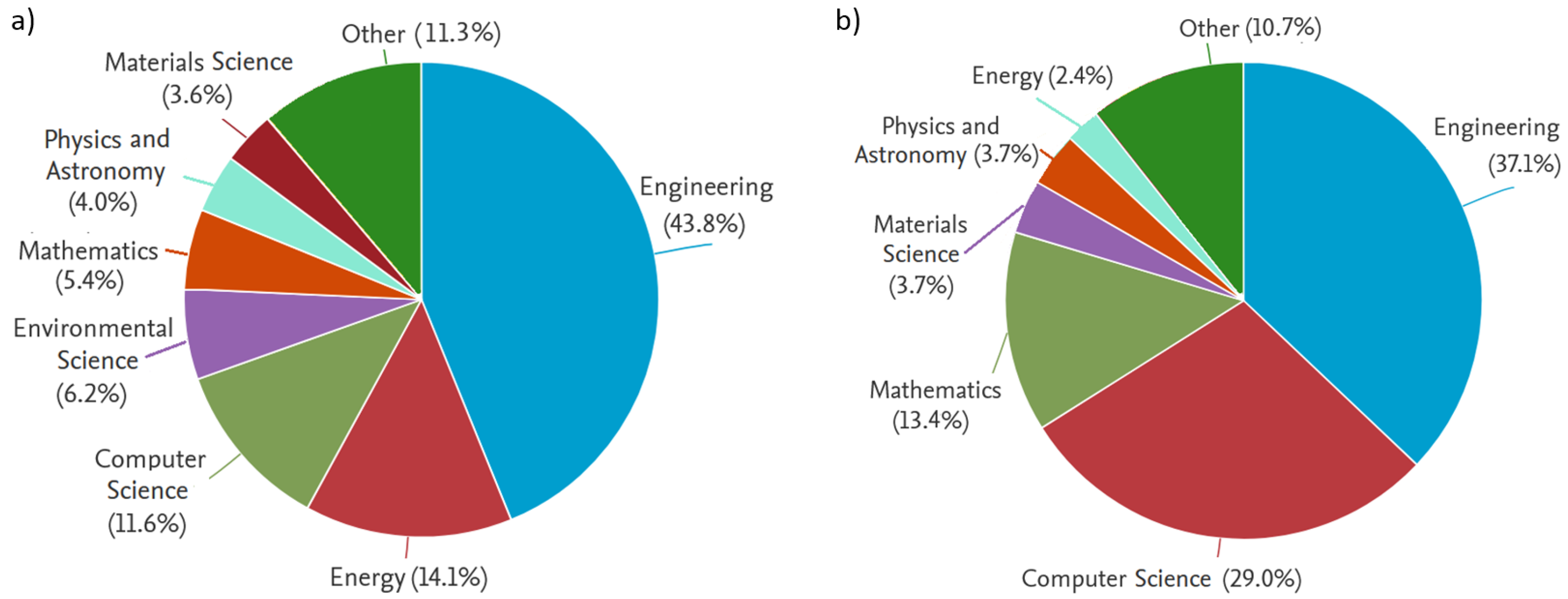
:1. Introduction
2. State-of-the-Art on Fuzzy Logic in Hydraulics and Pneumatics
2.1. Fuzzy Logic in Hydraulic Systems
2.1.1. Hydraulic Pump and Turbine Control Systems
2.1.2. Hydraulic Flow Control Valves and Servo Valves
2.1.3. Fuzzy Risk Assessment and Fault Detection of Hydraulic Systems
2.1.4. Fuzzy Logic with Other AI Techniques in Hydraulics
2.2. Fuzzy Logic in Pneumatic Systems
2.2.1. Pneumatic Control Systems with on/off Valves
2.2.2. Pneumatic Proportional Valves and Servo Valves
2.2.3. Fuzzy Diagnosis and Fault Detection of Pneumatic Systems
2.2.4. Neuro-Fuzzy Pneumatic Systems
3. Discussion
- Input signals: two inputs are used in 65% of cases, while one input is applied in 17% of cases. The second group mainly includes sliding mode controllers. Moreover, 32% units (which is about half of two-signal ones) divide the signals into fuzzy sets. Control error e and its change or derivative account for 57% of cases.
- Output signals: the most popular are single-output (57%) and three-output (25%) units. The second group mainly includes fuzzy-PID systems. Output signals are often divided into seven (30%) or five (24%) fuzzy sets.
- Membership functions: input signals are usually divided into triangular (65%) and Gaussian (27%) fuzzy sets. Regarding the output signals, triangular functions account for 59% and 17%, respectively.
- Rule database: the size of the rule base is an especially variable parameter. The number of rules ranges from 3 to over 200. The most common number of rules is 49 (18% cases), which is related to the popularity of two-input, single-output systems that divide each input signal into seven fuzzy sets.
- Inference system: the Mamdani method is used in approx. 82% cases. The rest are Takagi–Sugeno-type methods (14%) and a few proposals for alternative solutions.
- Fuzzy operators: authors declare the use of the most straightforward MIN-MAX operators (29% of studies). However, these are parameters that usually are not specified (65%).
- Defuzzification method: this is specified in approximately two-thirds of the studies. Various algorithms may be used, including Center of Gravity (CoG), Center of Area (CoA), Centroid, Weighted Average, etc.
4. Conclusions
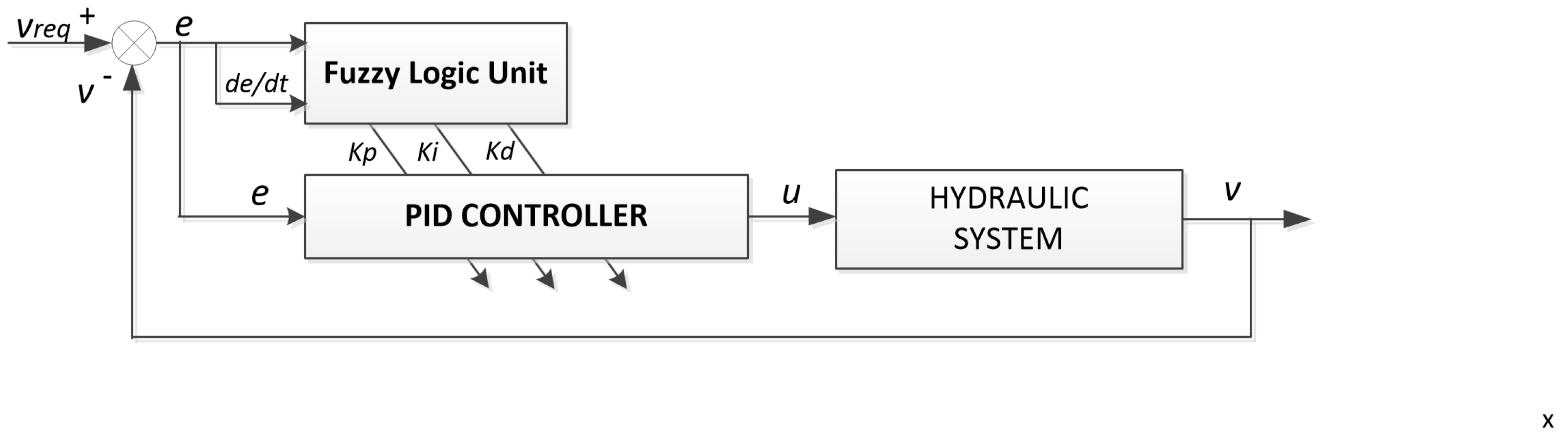
- Fuzzy logic in hydraulic and pneumatic systems is primarily used for control. The most commonly studied practical application is a fuzzy-PID control system, which includes a traditional PID controller whose parameters are adjusted in real-time by a parallel-connected fuzzy logic unit. A considerably less frequently used solution is a stand-alone fuzzy logic system generating a signal directly for a hydraulic or pneumatic control element.
- The most frequently used environment in research on fuzzy logic is Matlab with Simulink and specialized add-ons such as Fuzzy Logic Toolbox or SimMechanics (approx. 80% of studies). Some research was also conducted in AMESim, MSC ADAMS and LabView systems.
- Fuzzy logic models and controllers are built in the form of standard four-module systems, including fuzzification, inference, rule database and defuzzification.
- Risk assessment and fault detection of hydraulic and pneumatic systems are subject areas in which fuzzy logic algorithms are relatively rarely used. However, there is great potential for development here, resulting from the possibility of uniform recording of various types of parameters in the form of fuzzy sets, as well as simple and logical formulation of rules constituting the basis of the decision-making process.
- A Takagi–Sugeno inference method is utilised in less than 15% of publications. This method could be used more often, since it has significantly larger possibilities to model non-linearities, which compensation is crucial in hydraulic and pneumatic systems.
- A relatively new feature in the form of a type-2 membership function is used only in two publications. This function type could be used more often.
- The advantageous solution for future research can be the construction and training of neuro-fuzzy systems. Combining the advantages of neural networks and fuzzy logic could provide greater possibilities for tuning fuzzy logic unit parameters in the ANN-like training process.
- Automatic or autonomic parameter adjustment methods of the fuzzy logic units are not often used. Up to now, expert knowledge-based or trial-and-error methods have usually been utilised. However, there are some promising solutions based on GA or PSO that could be further developed.
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| Centre Average defuzzification method | |
| Centre of Area defuzzification method | |
| Centre of Gravity defuzzification method | |
| Failure Mode & Effects Analysis | |
| Genetic Algorithm | |
| Load Frequency Control technique | |
| Proportional–Derivative | |
| Proportional–Integral–Derivative | |
| Particle Swarm Optimization method | |
| Pulse-Width-Modulation control technique | |
| State-of-Charge (battery) | |
| , , | Smallest-, Medium-, Largest- of Maxima defuzzification method |
| Takagi–Sugeno inference method | |
| Weighted Average defuzzification method | |
| Parameters | |
| acceleration | |
| , , | control error derivative |
| e, | control error |
| , | control error change |
| , , | fuzzy product operator |
| , | fuzzy sum operator |
| p, | pressure |
| Q, | flow rate |
| sliding-mode function | |
| T, | torque |
| v, | velocity |
| x, , , | position |
References
- Web of Science Database. Available online: https://www.webofscience.com/wos/woscc/basic-search (accessed on 6 September 2023).
- Scopus Database. Available online: https://www.scopus.com/home.uri (accessed on 6 September 2023).
- Xu, Y.; Zheng, Y.; Du, Y.; Yang, W.; Peng, X.; Li, C. Adaptive condition predictive-fuzzy PID optimal control of start-up process for pumped storage unit at low head area. Energy Convers. Manag. 2018, 177, 592–604. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, J.; Xue, X.; Fu, W.; Zhu, W.; Li, C. An adaptively fast fuzzy fractional order PID control for pumped storage hydro unit using improved gravitational search algorithm. Energy Convers. Manag. 2016, 111, 67–78. [Google Scholar] [CrossRef]
- El-Koliel, S.M.; Eleissawi, H.; Nada, A.S. Speed control of electrical submersible pumps using fuzzy logic control. Int. J. Power Electron. Drive Syst. 2022, 13, 2515–2528. [Google Scholar] [CrossRef]
- Popescu, D.; Dinu, R.C.; Bratu, C. Fuzzy control of cooling water pumps related to a power plant. In Proceedings of the 11th International Conference on Electromechanical and Power Systems, SIELMEN 2017, Iasi, Romania, 11–13 October 2017; pp. 541–546. [Google Scholar] [CrossRef]
- Li, C.; Mao, Y.; Zhou, J.; Zhang, N.; An, X. Design of a fuzzy-PID controller for a nonlinear hydraulic turbine governing system by using a novel gravitational search algorithm based on Cauchy mutation and mass weighting. Appl. Soft Comput. 2017, 52, 290–305. [Google Scholar] [CrossRef]
- Chen, Z.; Yuan, X.; Yuan, Y.; Lei, X.; Zhang, B. Parameter estimation of fuzzy sliding mode controller for hydraulic turbine regulating system based on HICA algorithm. Renew. Energy 2019, 133, 551–565. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, Z.; Yuan, Y.; Huang, Y. Design of fuzzy sliding mode controller for hydraulic turbine regulating system via input state feedback linearization method. Energy 2015, 93, 173–187. [Google Scholar] [CrossRef]
- Osinski, C.; Villar Leandro, G.; da Costa Oliveira, G.H. Fuzzy PID Controller Design for LFC in Electric Power Systems. IEEE Lat. Am. Trans. 2019, 17, 147–154. [Google Scholar] [CrossRef]
- Hao, Y.; Wang, C.; Song, L. Study on fuzzy-logic PID control system of synchronous jack-up system of turbine runner static equilibrium experiment. In Proceedings of the International Conference on Advanced Mechatronic Systems, Beijing, China, 22–24 August 2015; pp. 273–276. [Google Scholar]
- Liang, J.; Yuan, X.; Yuan, Y.; Chen, Z.; Li, Y. Nonlinear dynamic analysis and robust controller design for Francis hydraulic turbine regulating system with a straight-tube surge tank. Mech. Syst. Signal Process. 2017, 85, 927–946. [Google Scholar] [CrossRef]
- Mushiri, T.; Mbohwa, C. Simulation and Modeling: Design of a Fuzzy Logic based Hydraulic Turbine Governing System; IGI Global: Beijing, China, 2018; pp. 1600–1632. [Google Scholar] [CrossRef]
- Ma, T.; Wang, B. Disturbance observer-based Takagi-Sugeno fuzzy control of a delay fractional-order hydraulic turbine governing system with elastic water hammer via frequency distributed model. Inf. Sci. 2021, 569, 766–785. [Google Scholar] [CrossRef]
- Ma, T.; Wang, B.; Zhang, Z.; Ai, B. A Takagi-Sugeno fuzzy-model-based finite-time H-infinity control for a hydraulic turbine governing system with time delay. Int. J. Electr. Power Energy Syst. 2021, 132, 107152. [Google Scholar] [CrossRef]
- Li, M.; Zhang, Q. Adaptive Robust Fuzzy Impedance Control of an Electro-Hydraulic Actuator. Appl. Sci. 2022, 12. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Q.; Tian, Q.; Feng, X. Extended State Observer-Based Fuzzy Adaptive Backstepping Force Control of a Deep-Sea Hydraulic Manipulator with Long Transmission Pipelines. J. Mar. Sci. Eng. 2022, 10, 1467. [Google Scholar] [CrossRef]
- Do, T.C.; Tran, D.T.; Dinh, T.Q.; Ahn, K.K. Tracking Control for an Electro-Hydraulic Rotary Actuator Using Fractional Order Fuzzy PID Controller. Electronics 2020, 9, 926. [Google Scholar] [CrossRef]
- Ur Rehman, W.; Wang, X.; Hameed, Z.; Gul, M.Y. Motion Synchronization Control for a Large Civil Aircraft’s Hybrid Actuation System Using Fuzzy Logic-Based Control Techniques. Mathematics 2023, 11, 1576. [Google Scholar] [CrossRef]
- Lu, Y.; Cao, P.; Xiong, L.; Xu, B. A Novel Fuzzy Logic Control on the FVVT Lift of Internal Combustion Engine. In Proceedings of the 10th International Conference on Intelligent Control and Information Processing (ICICIP), Marrakesh, Morocco, 14–19 December 2019; pp. 126–132. [Google Scholar]
- Guo, H.; Hu, M.; Li, T.; Li, G. Design and Simulation of Variable Pitch Control System Based on Fuzzy Model Reference Adaptive. In Practical Applications of Intelligent Systems; Wen, Z., Li, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 745–754. [Google Scholar]
- Jin, X.; Chen, K.; Zhao, Y.; Ji, J.; Jing, P. Simulation of hydraulic transplanting robot control system based on fuzzy PID controller. Measurement 2020, 164, 108023. [Google Scholar] [CrossRef]
- Tho, N.H.; Phuong, V.N.Y.; Danh, L.T. Development of an Adaptive Fuzzy Sliding Mode Controller of an Electrohydraulic Actuator Based on a Virtual Prototyping. Actuators 2023, 12, 258. [Google Scholar] [CrossRef]
- Nguyen, M.N.; Tran, D.T.; Ahn, K.K. Robust position and vibration control of an electrohydraulic series elastic manipulator against disturbance generated by a variable stiffness actuator. Mechatronics 2018, 52, 22–35. [Google Scholar] [CrossRef]
- Li, J.; Ji, R.; Liang, X.; Ge, S.S.; Yan, H. Command Filter-Based Adaptive Fuzzy Finite-Time Output Feedback Control of Nonlinear Electrohydraulic Servo System. IEEE Trans. Instrum. Meas. 2022, 71, 3529410. [Google Scholar] [CrossRef]
- Truong, H.V.A.; Tran, D.T.; To, X.D.; Ahn, K.K.; Jin, M. Adaptive Fuzzy Backstepping Sliding Mode Control for a 3-DOF Hydraulic Manipulator with Nonlinear Disturbance Observer for Large Payload Variation. Appl. Sci. 2019, 9, 3290. [Google Scholar] [CrossRef]
- Wrat, G.; Bhola, M.; Ranjan, P.; Mishra, S.K.; Das, J. Energy saving and Fuzzy-PID position control of electro-hydraulic system by leakage compensation through proportional flow control valve. ISA Trans. 2020, 101, 269–280. [Google Scholar] [CrossRef]
- Bao, H.; He, D.; Zhang, B.; Zhong, Q.; Hong, H.; Yang, H. Research on Dynamic Performance of Independent Metering Valves Controlling Concrete-Placing Booms Based on Fuzzy-LADRC Controller. Actuators 2023, 12, 139. [Google Scholar] [CrossRef]
- Tatoglu, A.; Campana, C.; Nolan, J.; Toloczko, G. Fuzzy logic controller design of a single stage fluid valve based robotic arm. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Proceedings (IMECE), Online, 16–19 November 2020; Volume 7B-2020. [Google Scholar] [CrossRef]
- Tony Thomas, A.; Thangarasu, S.; Sowmithra, T. Modeling and Simulation of an Electro-Hydraulic System Using Fuzzy Logic Approach. In Lecture Notes in Mechanical Engineering; Springer: Berlin/Heidelberg, Germany, 2021; pp. 807–822. [Google Scholar] [CrossRef]
- Li, L.; Zhang, T.; Hong, J.; Zhang, H.; Yang, J.; Zhang, Z.; Wu, K. Energy management strategy of a novel mechanical-electro-hydraulic power coupling electric vehicle under smooth switching conditions. Energy Rep. 2022, 8, 8002–8016. [Google Scholar] [CrossRef]
- Hanafi Sheikhha, F.; Afzalaghaeinaeini, A.; Seo, J. Collaborative Tracking Control Strategy for Autonomous Excavation of a Hydraulic Excavator. Eng. Proc. 2021, 10, 43. [Google Scholar] [CrossRef]
- Truong, H.V.A.; Dao, H.V.; Do, T.C.; Ho, C.M.; To, X.D.; Dang, T.D.; Ahn, K.K. Mapping Fuzzy Energy Management Strategy for PEM Fuel Cell-Battery-Supercapacitor Hybrid Excavator. Energies 2020, 13, 3387. [Google Scholar] [CrossRef]
- Delavarpour, N.; Eshkabilov, S.; Bon, T.; Nowatzki, J.; Bajwa, S. The Tractor-Cart System Controller with Fuzzy Logic Rules. Appl. Sci. 2020, 10, 5223. [Google Scholar] [CrossRef]
- Han, J.; Wang, F.; Wang, Y. A Control Method for the Differential Steering of Tracked Vehicles Driven Independently by a Dual Hydraulic Motor. Appl. Sci. 2022, 12, 6355. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, K.; Fu, C. Energy-Management Strategy for Four-Wheel Drive Electrohydraulic Hybrid System with Optimal Comprehensive Efficiency. SAE Int. J. Passeng. Cars Electron. Electrical Syst. 2019, 12, 35–53. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, T.; Hong, J.; Zhang, H.; Zhao, Q.; Meng, Z. Research on driving control strategy and Fuzzy logic optimization of a novel mechatronics-electro-hydraulic power coupling electric vehicle. Energy 2021, 233, 121221. [Google Scholar] [CrossRef]
- Eckert, J.J.; Barbosa, T.P.; da Silva, S.F.; Silva, F.L.; Silva, L.C.; Dedini, F.G. Electric hydraulic hybrid vehicle powertrain design and optimization-based power distribution control to extend driving range and battery life cycle. Energy Convers. Manag. 2022, 252, 115094. [Google Scholar] [CrossRef]
- Eckert, J.J.; Barbosa, T.P.; Silva, F.L.; Roso, V.R.; Silva, L.C.; da Silva, L.A.R. Optimum fuzzy logic controller applied to a hybrid hydraulic vehicle to minimize fuel consumption and emissions. Expert Syst. Appl. 2022, 207, 117903. [Google Scholar] [CrossRef]
- Kargar, V.; Jahangiri, M.; Alimohammadlu, M.; Kamalinia, M.; Mirazahossieninejad, M. Risk assessment of mobile crane overturning in Asymmetric Tandem Lifting (ATL) operation based on fuzzy fault tree analysis (FFTA). Results Eng. 2022, 16, 100755. [Google Scholar] [CrossRef]
- Ghini, Y.; Vacca, A. A method to perform prognostics in electro-hydraulic machines: The case of an independent metering controlled hydraulic crane. Int. J. Hydromechatron. 2018, 1, 197–221. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, Y.; Yao, K. Fault diagnosis of hydraulic power system for coal mine tunnel drilling rig based on T-S fuzzy fault tree. Meitiandizhi Yu Kantan/Coal Geol. Explor. 2022, 50, 194–202. [Google Scholar] [CrossRef]
- Yu, J.; Zeng, Q.; Yu, Y.; Wu, S.; Ding, H.; Gao, H.; Yang, J. An intuitionistic fuzzy probabilistic Petri net method for risk assessment on submarine pipeline leakage failure. Ocean Eng. 2022, 266, 112788. [Google Scholar] [CrossRef]
- Filo, G.; Fabiś-Domagala, J.; Domagala, M.; Lisowski, E.; Momeni, H. The idea of fuzzy logic usage in a sheet-based FMEA analysis of mechanical systems. MATEC Web Conf. 2018, 183, 03009. [Google Scholar] [CrossRef]
- Jiang, C.; Sui, S.; Tong, S. Finite-time fuzzy adaptive output feedback control of electro-hydraulic system with actuator faults. Inf. Sci. 2023, 623, 577–591. [Google Scholar] [CrossRef]
- Li, Z.; Jamshidian, M.; Mousavi, S.; Karimipour, A.; Tlili, I. Develop a numerical approach of fuzzy logic type-2 to improve the reliability of a hydraulic automated guided vehicles. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 1396–1409. [Google Scholar] [CrossRef]
- Kamal, E.; Adouane, L. Intelligent Energy Management Strategy Based on Artificial Neural Fuzzy for Hybrid Vehicle. IEEE Trans. Intell. Veh. 2018, 3, 112–125. [Google Scholar] [CrossRef]
- Gaspar, J.F.; Kamarlouei, M.; Sinha, A.; Xu, H.; Calvário, M.; Faÿ, F.X.; Robles, E.; Soares, C.G. Speed control of oil-hydraulic power take-off system for oscillating body type wave energy converters. Renew. Energy 2016, 97, 769–783. [Google Scholar] [CrossRef]
- Zhang, F.; Lu, J.; Yang, S.; Liu, W.; Tao, R.; Zhu, D.; Xiao, R. Performance improvement of a pump as turbine in storage mode by optimization design based on genetic algorithm and fuzzy logic. J. Energy Storage 2023, 62, 106875. [Google Scholar] [CrossRef]
- Elsayed, M.E.; Attia, A.A.; Abdelrahman, M.; Attia, E.A. Dimensioning of the hydraulic gravity energy storage system using Fuzzy logic based simulation. J. Energy Storage 2021, 42, 103151. [Google Scholar] [CrossRef]
- Doan, D.V.; Nguyen, K.; Thai, Q.V. Load-Frequency Control of Three-Area Interconnected Power Systems with Renewable Energy Sources Using Novel PSO PID-Like Fuzzy Logic Controllers. Eng. Technol. Appl. Sci. Res. 2022, 12, 8597–8604. [Google Scholar] [CrossRef]
- Takosoglu, J.; Dindorf, R.; Wos, P. Design Rules for Fuzzy Logic Controllers for Pneumatic Systems. In Proceedings of the Advances in Hydraulic and Pneumatic Drives and Control 2020, Trzebieszowice, Poland, 21–23 October 2020; Stryczek, J., Warzyńska, U., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 192–204. [Google Scholar]
- Lin, Z.; Wei, Q.; Ji, R.; Huang, X.; Yuan, Y.; Zhao, Z. An Electro-Pneumatic Force Tracking System using Fuzzy Logic Based Volume Flow Control. Energies 2019, 12, 4011. [Google Scholar] [CrossRef]
- Du, H.; Yuan, T.; Xiong, W. Cylinder position control driven by pneumatic digital bridge circuit using a fuzzy algorithm under large stroke and varying load conditions. J. Frankl. Inst. 2023, 360, 5892–5909. [Google Scholar] [CrossRef]
- Essmat Abdul-Lateef, W.; Glebov, N.A.; Hamed Farhood, N.; Khdir, A.H.; Shaker, D.H. Modelling and Controlling of position for electro-pneumatic system using Pulse-Width-Modulation (PWM) techniques and Fuzzy Logic controller. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Coimbatore, India, 22–23 January 2020; Volume 765. [Google Scholar] [CrossRef]
- Lisowski, E.; Filo, G. Automated heavy load lifting and moving system using pneumatic cushions. Autom. Constr. 2015, 50, 91–101. [Google Scholar] [CrossRef]
- Mushiri, T.; Mahachi, A.; Mbohwa, C. A Model Reference Adaptive Control (MRAC) System for the Pneumatic Valve of the Bottle Washer in Beverages Using Simulink. Procedia Manuf. 2017, 7, 364–373. [Google Scholar] [CrossRef]
- Gilián, M.; Szakács, T. Pneumatic Piston Expansion Timing Using Fuzzy Logic Logic. In Proceedings of the 2021 IEEE 19th International Symposium on Intelligent Systems and Informatics (SISY), Subotica, Serbia, 16–18 September 2021; pp. 77–82. [Google Scholar] [CrossRef]
- Mishra, P.; Kumar, V.; Rana, K. A novel intelligent controller for combating stiction in pneumatic control valves. Control Eng. Pract. 2014, 33, 94–104. [Google Scholar] [CrossRef]
- Mishra, P.; Kumar, V.; Rana, K.P.S. Intelligent Ratio Control in Presence of Pneumatic Control Valve Stiction. Arab. J. Sci. Eng. 2016, 41, 677–689. [Google Scholar] [CrossRef]
- Chen, C.; Huang, J.; Wu, D.; Tu, X. Interval Type-2 Fuzzy Disturbance Observer-Based T-S Fuzzy Control for a Pneumatic Flexible Joint. IEEE Trans. Ind. Electron. 2022, 69, 5962–5972. [Google Scholar] [CrossRef]
- Chen, C.; Huang, J.; Liu, L.; Wu, D.R. Data-driven Takagi-Sugeno fuzzy system modeling and predictive control of a pneumatic flexible joint. Kongzhi Lilun Yu Yingyong/Control Theory Appl. 2022, 39, 633–642. [Google Scholar] [CrossRef]
- Woś, P.; Dindorf, R.; Takosoglu, J. Fuzzy Controller to Control the Active Air Suspension. Arch. Automot. Eng. 2020, 89, 75–86. [Google Scholar] [CrossRef]
- Ho, C.M.; Ahn, K.K. Adaptive Fuzzy Output Feedback Control Design for Pneumatic Active Suspension with Unknown Dead Zone. IEEE ACCESS 2023, 11, 66858–66871. [Google Scholar] [CrossRef]
- Ho, C.M.; Ahn, K.K. Design of an Adaptive Fuzzy Observer-Based Fault Tolerant Controller for Pneumatic Active Suspension with Displacement Constraint. IEEE ACCESS 2021, 9, 136346–136359. [Google Scholar] [CrossRef]
- Ho, C.M.; Nguyen, C.H.; Ahn, K.K. Observer-Based Adaptive Fuzzy Controller for Pneumatic Active Suspension with Displacement Constraint and Actuator Failures. In Proceedings of the 2022 13th Asian Control Conference (ASCC), Jeju Island, Republic of Korea, 4–7 May 2022; pp. 1161–1166. [Google Scholar] [CrossRef]
- Van Kien, C.; Son, N.N.; Anh, H.P.H. Adaptive Fuzzy Sliding Mode Control for Nonlinear Uncertain SISO System Optimized by Differential Evolution Algorithm. Int. J. Fuzzy Syst. 2019, 21, 755–768. [Google Scholar] [CrossRef]
- Chiang, C.J.; Chen, Y.C. Incremental fuzzy sliding mode control of pneumatic muscle actuators. Int. J. Innov. Comput. Inf. And Control 2018, 14, 1917–1928. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Trinh, V.C.; Le, T.D. An Adaptive Fast Terminal Sliding Mode Controller of Exercise-Assisted Robotic Arm for Elbow Joint Rehabilitation Featuring Pneumatic Artificial Muscle Actuator. Actuators 2020, 9, 118. [Google Scholar] [CrossRef]
- Anh, H.P.H.; Kien, C.V. Hybrid Fuzzy Sliding Mode Control for Uncertain PAM Robot Arm Plant Enhanced with Evolutionary Technique. Int. J. Comput. Intell. Syst. 2021, 14, 594–604. [Google Scholar] [CrossRef]
- Duong, M.D.; Pham, Q.T.; Vu, T.C.; Bui, N.T.; Dao, Q.T. Adaptive fuzzy sliding mode control of an actuator powered by two opposing pneumatic artificial muscles. Sci. Rep. 2023, 13, 8242. [Google Scholar] [CrossRef]
- Kien, C.V.; Son, N.N.; Anh, H.P.H. Identification of 2-DOF Pneumatic Artificial Muscle System with Multilayer Fuzzy Logic and Differential Evolution Algorithm. In Proceedings of the IEEE Conference on Industrial Electronics and Applications, Siem Reap, Cambodia, 18–20 June 2017; pp. 1264–1269. [Google Scholar]
- Robinson, R.M.; Kothera, C.S.; Wereley, N.M. Control of a Heavy-Lift Robotic Manipulator with Pneumatic Artificial Muscles. Actuators 2014, 3, 41–65. [Google Scholar] [CrossRef]
- Al-Mosawi, H.A.; Al-Ibadi, A.; Abdalla, T.Y. An Adaptive Parallel Fuzzy and Proportional Integral Controller (APFPIC) for the Contractor Pneumatic Muscle Actuator Position Control. In Proceedings of the ICECCME 2022, Maldives, 16–18 November 2022. [Google Scholar] [CrossRef]
- Dan, S.; Cheng, H.; Zhang, Y.; Liu, H. A Fuzzy Indrect Adaptive Robust Control for Upper Extremity Exoskeleton Driven by Pneumatic Artificial Muscle. In Proceedings of the 2022 IEEE International Conference on Mechatronics and Automation (ICMA), Guilin, China, 7–10 August 2022; pp. 839–846. [Google Scholar] [CrossRef]
- Chen, C.; Huang, J.; Wu, D. Nonlinear Disturbance Observer Based T-S Fuzzy Logic Control of Pneumatic Artificial Muscles. In Proceedings of the 2019 IEEE 4th International Conference on Advanced Robotics and Mechatronics (ICARM), Toyonaka, Japan, 3–5 July 2019; pp. 12–17. [Google Scholar] [CrossRef]
- Nazari, V.; Surgenor, B. Improved Position Tracking Performance of a Pneumatic Actuator using a Fuzzy Logic Controller with Velocity, System Lag and Friction Compensation. Int. J. Control Autom. Syst. 2016, 14, 1376–1388. [Google Scholar] [CrossRef]
- Khaziev, E. Control of Linear Servo Pneumatic Drive Based on Fuzzy Controller and Knowledge Base. Lect. Notes Electr. Eng. 2020, 641, 17–25. [Google Scholar] [CrossRef]
- Šitum, Z.; Ćorić, D. Position Control of a Pneumatic Drive Using a Fuzzy Controller with an Analytic Activation Function. Sensors 2022, 22, 1004. [Google Scholar] [CrossRef] [PubMed]
- Azahar, M.I.P.; Irawan, A.; Ismail, R.R. Self-tuning hybrid fuzzy sliding surface control for pneumatic servo system positioning. Control Eng. Pract. 2021, 113, 104838. [Google Scholar] [CrossRef]
- Azahar, M.I.P.; Irawan, A.; Taufika, R.M. Fuzzy Self-Adaptive PID for Pneumatic Piston Rod Motion Control. In Proceedings of the 2019 IEEE 10th Control and System Graduate Research Colloquium (ICSGRC), Shah Alam, Malaysia, 2–3 August 2019; pp. 82–87. [Google Scholar] [CrossRef]
- Azahar, M.I.P.; Irawan, A.; Taufika, R.M.; Suid, M.H. Position Control of Pneumatic Actuator Using Cascade Fuzzy Self-adaptive PID. In Proceedings of the 5th International Conference on Electrical, Control and Computer Engineering (InECCE2019), Pahang, Malaysia, 29–30 July 2019; Springer: Singapore, 2020; pp. 3–14. [Google Scholar]
- Takosoglu, J.; Janus-Galkiewicz, U.; Galkiewicz, J. A Design of a 2-DoF Planar Parallel Manipulator with an Electro-Pneumatic Servo-Drive. Energies 2022, 15, 8482. [Google Scholar] [CrossRef]
- Takosoglu, J.; Janus-Galkiewicz, U.; Galkiewicz, J. A Design of a 2 DoF Planar Parallel Manipulator with an Electro-Pneumatic Servo-Drive—Part 2. Energies 2023, 16, 2970. [Google Scholar] [CrossRef]
- Gao, L.; Wu, C.; Zhang, D.; Fu, X.; Li, B. Research on a high-accuracy and high-pressure pneumatic servo valve with aerostatic bearing for precision control systems. Precis. Eng. 2019, 60, 355–367. [Google Scholar] [CrossRef]
- Irawan, A.; Azahar, M.I.P. Cascade Control Strategy on Servo Pneumatic System with Fuzzy Self-Adaptive System. J. Control Autom. Electr. Syst. 2020, 31, 1412–1425. [Google Scholar] [CrossRef]
- Hasan, A.F.; Abdulridha, A.J. Optimal Interval Type-2 Fuzzy Logic Controller for Pneumatic Servo Actuator System. J. Eng. Sci. Technol. 2022, 17, 1644–1660. [Google Scholar]
- Navada, B.R.; Venkata, S.K. Fusion-Based Online Identification Technique for Pneumatic Actuator Faults. Eng. Sci. 2022, 17, 56–69. [Google Scholar] [CrossRef]
- Ali, D.; Frimpong, S. Artificial intelligence models for predicting the performance of hydro-pneumatic suspension struts in large capacity dump trucks. Int. J. Ind. Ergon. 2018, 67, 283–295. [Google Scholar] [CrossRef]
- Nicolau, V. Fuzzy Diagnostic System for Oleo-Pneumatic Drive Mechanism of High-Voltage Circuit Breakers. Sci. World J. 2013, 2013, 248487. [Google Scholar] [CrossRef] [PubMed]
- Živčák, J.; Kelemen, M.; Virgala, I.; Marcinko, P.; Tuleja, P.; Sukop, M.; Liguš, J.; Ligušová, J. An Adaptive Neuro-Fuzzy Control of Pneumatic Mechanical Ventilator. Actuators 2021, 10, 51. [Google Scholar] [CrossRef]
- Chen, C.; Cao, Y.; Chen, X.; Wu, D.; Xiong, C.; Huang, J. A Fused Deep Fuzzy Neural Network Controller and Its Application to Pneumatic Flexible Joint. IEEE-ASME Trans. Mechatron. 2023. [Google Scholar] [CrossRef]
- Mawlani, P.; Arbabtafti, M. Observer-based self-organizing adaptive fuzzy neural network control for non-linear, non-affine systems with unknown sign of control gain and dead zone: A case study of pneumatic actuators. Trans. Inst. Meas. Control 2022, 44, 2214–2234. [Google Scholar] [CrossRef]

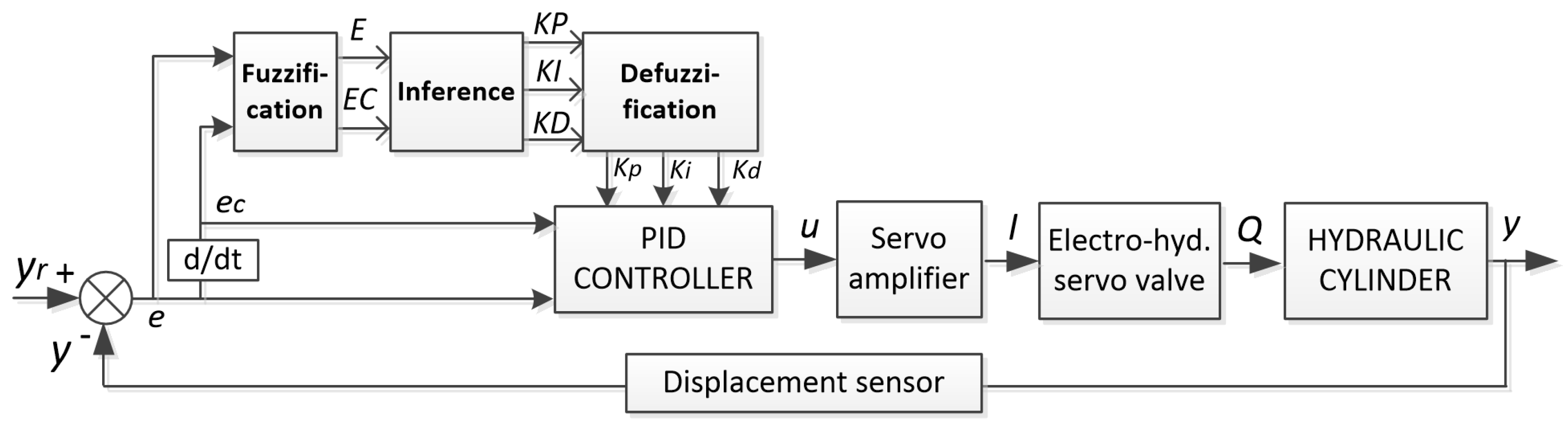
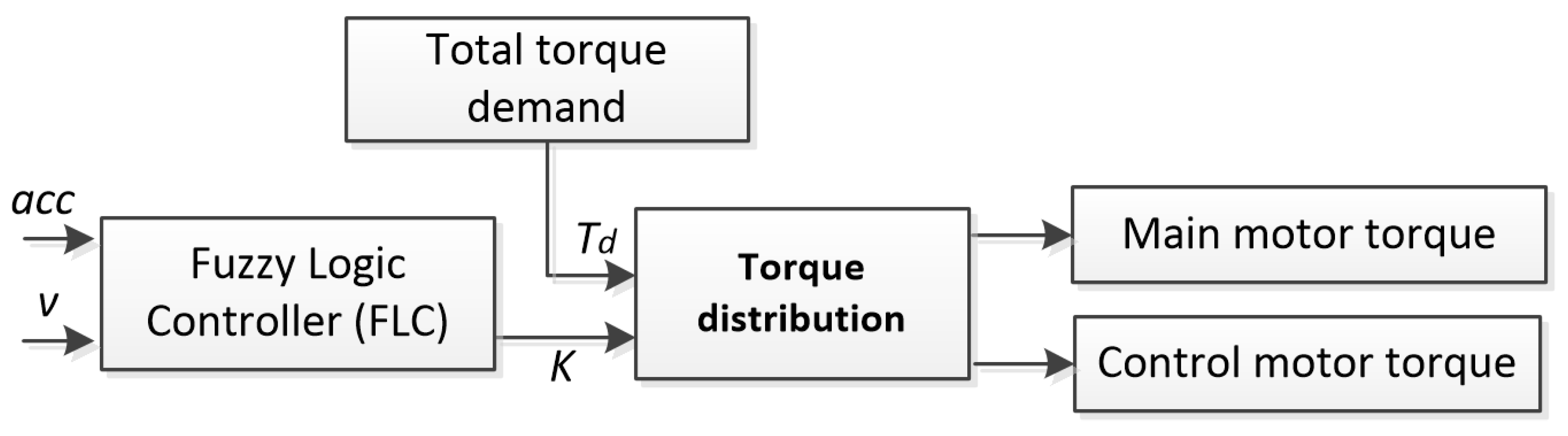

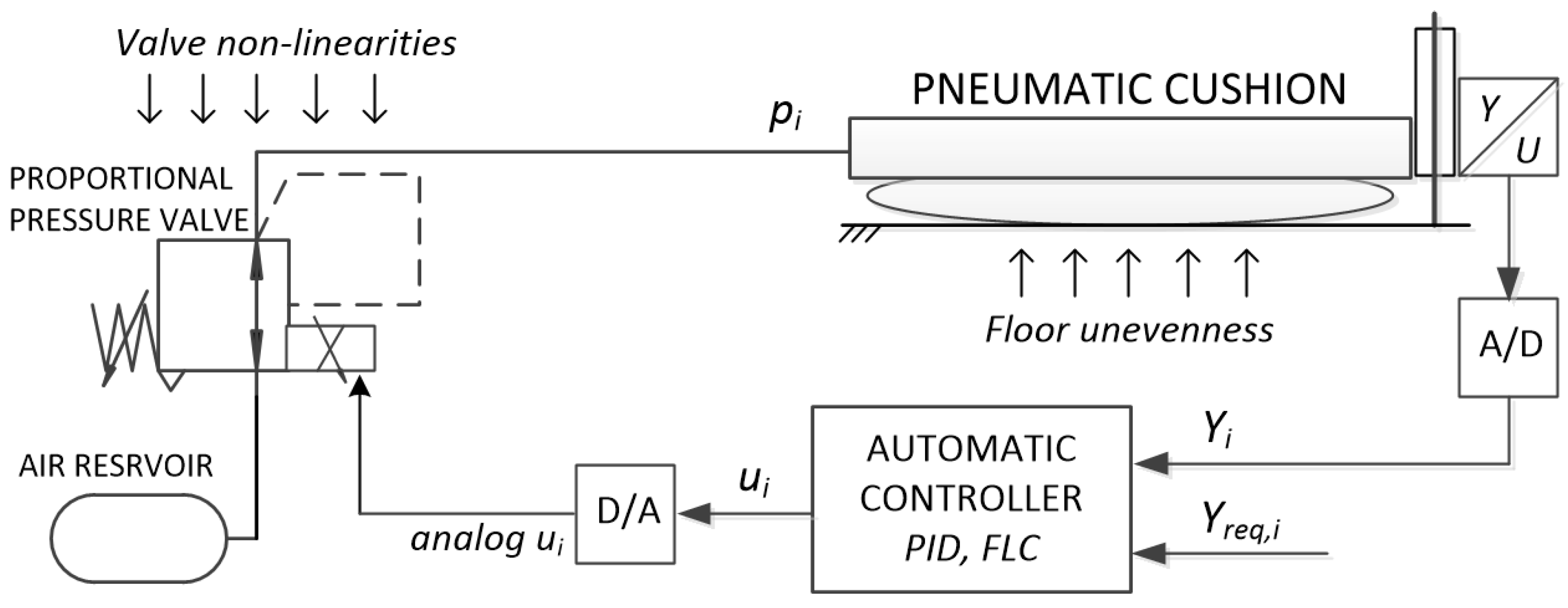
| Ref. | Controlled System | Input Params | No. of Inputs | Input fuz.sets | Input Function | No. of Outputs | Output fuz.sets | Output Function | No. of Rules | Fuzzy Operators | Defuz. Method |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [3] | Pump-turb. unit | e | 2 | triang | 1 | 7 | triang | 49 (7 × 7) | min-max | WAv | |
| [4] | Pumped storage unit | e | 2 | triang | 1 | 7 | triang | 49 (7 × 7) | min-max | CoG | |
| [5] | Submersible pump | e | 2 | Gauss | 1 | 7 | triang | 49 (7 × 7) | no data | no data | |
| [6] | Cooling water sys. | (head) | 1 | 4 | triang | 1 | 5 | triang | 4 | no data | no data |
| [7] | Hydraulic turbine | e | 2 | triang + Gauss | 3 | 7 | Gauss | 147 (3 × 49) | no data | no data | |
| [8] | Hydropower station | 1 | 5 | triang + Gauss | 1 | 5 | triang + Gauss | 5 | min-max | no data | |
| [9] | Hydraulic turbine | 1 | 3 | triang | 1 | 3 | triang | 3 | no data | no data | |
| [10] | Hydraulic power system | e | 2 | triang | 3 | 5 | triang | 75 (3 × 25) | no data | Centroid | |
| [11] | Turbine runner | e | 2 | no data | 3 | 7 | no data | 49 (7 × 7) | no data | unknown | |
| [12] | Hydraulic turbine | 1 | 3 | triang | 1 | 3 | triang | 3 | no data | CAv |
| Ref. | Controlled System | Input Params | No. of Inputs | Input fuz.sets | Input Function | No. of Outputs | Output fuz.sets | Output Function | No. of Rules | Fuzzy Operators | Defuz. Method |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [16] | Electro-hyd. actuator | 2 | triang | 2 | 7 | triang | 50 (2 × 25) | no data | CoG | ||
| [17] | Deep-Sea hyd. manip. | e | 2 | Gauss | 2 | 7 | triang | 98 (2 × 49) | max-min | CoA | |
| [18] | Electro-hyd. rotary actuat. | e | 2 | triang | 3 | 4 | triang | 48 (3 × 16) | max-min | Centroid | |
| [19] | Hybrid actuation sys. | 2 | triang | 1 | 5 | triang | 25 (5 × 5) | no data | no data | ||
| 2 | triang | 2 | 5 | triang | 50 (2 × 25) | ||||||
| [21] | Wind turb. pitch control | 2 | no data | 1 | 15 | no data | no data | min-max | CoA MoM | ||
| [22] | Hyd. transpl. robot | e | 2 | triang | 3 | 7 | triang | 147 (3 × 49) | no data | no data | |
| [23] | Electro-hyd. actuator | ) | 1 | 7 | triang | 1 | 7 | singl. set | 7 | not appl. | CAv |
| [24] | Electro-hyd. elastic manip. | 2 | triang trapez | 3 | 2, 2, 12 | triang | 12 (3-out) | no data | CAv | ||
| [26] | 3DOF hyd. manipulator | e | 2 | triang | 3 | 7 | triang | 147 (3 × 49) | no data | no data | |
| 2 | triang | 3 | 7 | triang | 147 (3 × 49) | ||||||
| [27] | Electro-hyd. system | e | 2 | no data | 3 | 5 | no data | 75 (3 × 25) | no data | no data | |
| [28] | Concrete pump boom | e | 2 | triang | 2 | 6 | triang | 98 (2 × 49) | no data | Centroid | |
| e | 2 | triang | 2 | 5 | triang | 98 (2 × 49) | |||||
| [32] | Hydraulic excavator | 2 | triang | 1 | 5 | triang | 25 (5 × 5) | min-max | Centroid | ||
| [33] | Hybrid excavator | 3 | triang trapez | 3 | 4, 4, 9 | triang trapez | 225 total | no data | no data | ||
| [34] | Tractor cart | 4 | triang | 1 | 3 | triang | 81 () | no data | no data | ||
| [31] | Electric vehicle | v | 2 | Gauss comb. | 1 | 5 | Gauss comb. | 25 (5 × 5) | no data | no data | |
| [37] | El.-hyd. vehicle | v | 2 | Gauss comb. | 1 | 5 | Gauss comb. | 25 (5 × 5) | no data | no data | |
| [38] | Elect.-hyd. vehicle | 2 | trapez | 2 | 3, 3 | trapez | 18 (2 × 9) | no data | SoM | ||
| [39] | Hybrid hyd. vehicle | 3 | triang | 3 | 3, 3, 3 | triang | 54 2-output | no data | MoM, LoM, Centroid | ||
| [35] | Tracked vehicle | 4 | no data | no data | 2 | no data | no data | no data | no data | no data |
| Ref. | Controlled System | Input Params | No. of Inputs | Input fuz.sets | Input Function | No. of Outputs | Output fuz.sets | Output Function | No. of Rules | Fuzzy Operators | Defuz. Method |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [53] | El.-pneum. actuator | e | 2 | triang trapez | 1 | 6 | triang | 49 (7 × 7) | min-max | CoG | |
| [54] | 4 × solen. on/off valve | e | 2 | triang | 3 | 5, 5, 5 | triang | 25 (5 × 5) 3 out | no data | CoG (PWM) | |
| [55] | 4 × solen. on/off valve | e | 2 | triang | 1 | 7 | triang | 49 (7 × 7) | no data | no data (PWM) |
| Ref. | Controlled System | Input Params | No. of Inputs | Input fuz.sets | Input Function | No. of Outputs | Output fuz.sets | Output Function | No. of Rules | Fuzzy Operators | Defuz. Method |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [56] | Pneum.cush. platform | 2 each | 3, 3
each | Gauss | 1 each | 3 each | Gauss | 9 each | min-max prod-por | CoG | |
| [58] | Pneumatic vehicle | 2 | triang trapez | 1 | 5 | trapez | 15 () | no data | no data | ||
| [59] [60] | Pneum.flow system | e r | 2 | Gauss | 1 | no data | Gauss | 4 (T-S) | no data | T-norm | |
| [61] [62] | Pneumatic joint | e | 2 | Gauss Type-2 | 1 | no data | Gauss Type-2 | 3 (T-S) | no data | no data |
| Ref. | Pneumatic Control el. | Input Params | No. of Inputs | Input fuz.sets | Input Function | No. of Outputs | Output fuz.sets | Output Function | No. of Rules | Inference System | Defuz. Method |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [67] | El.-pneum. regulator | 1 | 3 | triang | 1 | 3 | no data | 3 | T-S | funct. | |
| [68] | Proport. valve | 1 | 9 | triang | 1 | 9 | singlet. set | 9 | Mamdani | CAv | |
| [69] | Proport. valve | 1 | 7 | triang | 1 | no data | no data | no data | Mamdani | CAv | |
| [70] | Proport. valve | 1 | 5 | Gauss | 1 | 5 | no data | 5 | T-S | WAv | |
| [73] | Proport. valve | e | 2 | triang | 1 | 7 | triang | 49 (7 × 7) | Mamdani | CoG | |
| [74] | Prop.press. valve | e | 2 | Gauss | 1 | 3 | triang | 9 (3 × 3) | Mamdani | CoG | |
| [75] | Proport. valve | 2 | Gauss | 1 | 5 | triang | 15 (3 × 5) | Mamdani | Centroid | ||
| [76] | Electromag. valve | 1 | 3 | Gauss | 1 | 3 | no data | 3 | T-S | funct. |
| Ref. | Pneumatic Control el. | Input Params | No. of Inputs | Input fuz.sets | Input Function | No. of Outputs | Output fuz.sets | Output Function | No. of Rules | Fuzzy Operators | Defuz. Method |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [77] | press.flow cont.valve | e v | 2 | triang | 1 | 13 | singlet. set | 49 (7 × 7) | prod-max | CAv | |
| [79] | proport. valve | 2 | Gauss | 1 | 20 | singlet. set | n.a | defined function | analytic function | ||
| [80] | 5/3 prop. valve | 1 | 7 | triang | 1 | 7 | triang | 7 | min-max | CoG | |
| [81] | prop.spool valve | e | 2 | triang | 3 | 7, 7, 7 | triang | 49 (7 × 7) 3 out | no data | no data | |
| [83] [84] | proport. valve | e | 2 | triang | 3 | 7, 7, 7 | triang | 147 (3 × 49) | MAX | CoG | |
| [85] | 3/3 prop. valve | e | 2 | triang | 3 | 7, 7, 7 | triang | 49 (7 × 7) 3 out | max-min | Centroid | |
| [86] | proport. valve | e | 2 | triang | 3 | 7, 7, 7 | triang | 49 (7 × 7) 3 out | min-max | CoG |
| Ref. | Pneumatic System | Analysed Params | No. of Inputs | Input fuz.sets | Input Function | No. of Outputs | Output fuz.sets | Output Function | No. of Rules | Fuzzy Operators | Defuz. Method |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [88] | Actuator fault | 2 | triang trapez | 2 | triang trapez | 32 (2 × 16) | min-max | CoA | |||
| [89] | Struts state | 5 var. params | 5 | 32 each | Gauss | 2 | 32,32 | Gauss | 49 each in. | min-max | CoA CoG |
| [90] | Function. state | 4 | triang trapez | 1 | 5 | triang trapez | 81 | no data | no data |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filo, G. A Review of Fuzzy Logic Method Development in Hydraulic and Pneumatic Systems. Energies 2023, 16, 7584. https://doi.org/10.3390/en16227584
Filo G. A Review of Fuzzy Logic Method Development in Hydraulic and Pneumatic Systems. Energies. 2023; 16(22):7584. https://doi.org/10.3390/en16227584
Chicago/Turabian StyleFilo, Grzegorz. 2023. "A Review of Fuzzy Logic Method Development in Hydraulic and Pneumatic Systems" Energies 16, no. 22: 7584. https://doi.org/10.3390/en16227584
APA StyleFilo, G. (2023). A Review of Fuzzy Logic Method Development in Hydraulic and Pneumatic Systems. Energies, 16(22), 7584. https://doi.org/10.3390/en16227584






