A Pragmatic Approach to the Economic Assessment of Green Synthetic Methane Power in the Baltics
Abstract
:1. Introduction
1.1. The Innovative Contribution
- To analyse whether RES being supported by the production and storage of hydrogen and synthetic methane can ensure system adequacy and energy supply to the consumers in the Baltic States; i.e., whether it is possible to fulfil the commitments on the reduction in greenhouse gas emissions into the atmosphere with that strategy.
- To propose a methodology and a modelling framework to define the required installed capacity of the renewable power plants, electrolysers, gas power plants using synthetic methane as well as the capacity of the gas reservoir in a system. The methodology contains a complex optimisation problem, for the solution of which acceptable simplifications were introduced, which made it possible to greatly reduce the amount of input data and use linear programming, and ensured the synthesis of an efficient algorithm.
- To calculate revenues and profitability during a year of operation. To evaluate the rate of return on the investments and the electricity market prices in 2050.
1.2. The Organisation of the Paper
2. Literature Review
2.1. Technologies
2.2. Economic Performance
3. Problem Definition and the Modelling Framework
3.1. The Nord Pool Market
3.2. The Baltic Power System
3.3. The Modelling Framework
- Creating a scenario and a forecast, namely, electricity prices, energy demand, water inflow, solar irradiation, wind and the generating interconnection. We will use multiple deterministic scenarios and time series data collected or forecasted at regular hourly intervals over the course of one year.
- Preparation of generator and consumer bids, i.e., the energy and the prices for each hour [42,43,44]. This is an optimisation problem to be solved by the individual generators and consumers and is described in many publications, for example, Refs. [6,7,45,46,47,48]. During this step, we should simulate the behaviour of each market participant.
- Market clearing and the accepted generator and load energy. In this step, we simulate the actions of a market operator whose task is to choose the cheapest generators, considering energy balancing and interconnection constraints. The result of this step contains hourly schedules for every energy generator, consumer and interconnection, and the MCP for every price zone.
- Calculation of the economic indicators and performance. The previous step provides basic information for calculating economic performance indicators, such as annual energy import and export costs, consumer spending, installed and used capacity and volume of investments, which will show us the revenue for each power plant.
3.4. Assumptions, Heuristic Approximations and Definitions
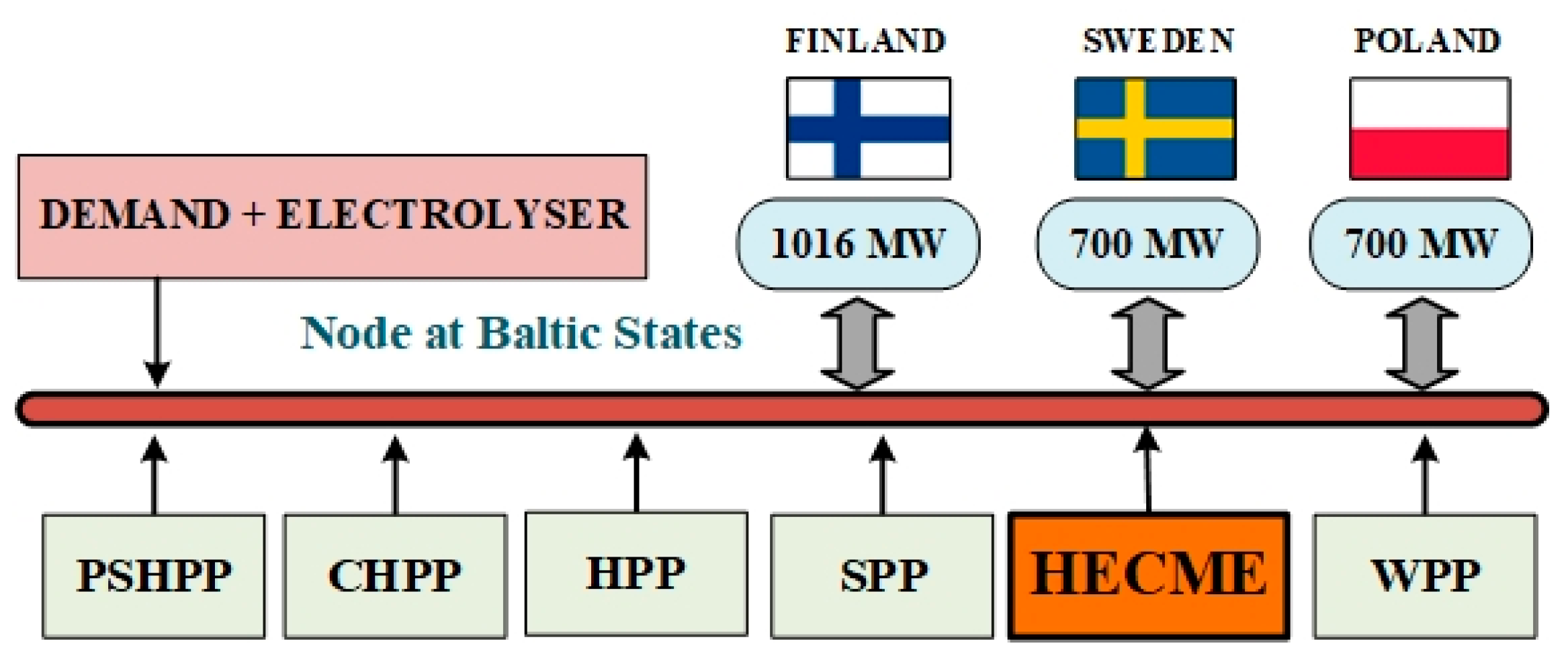
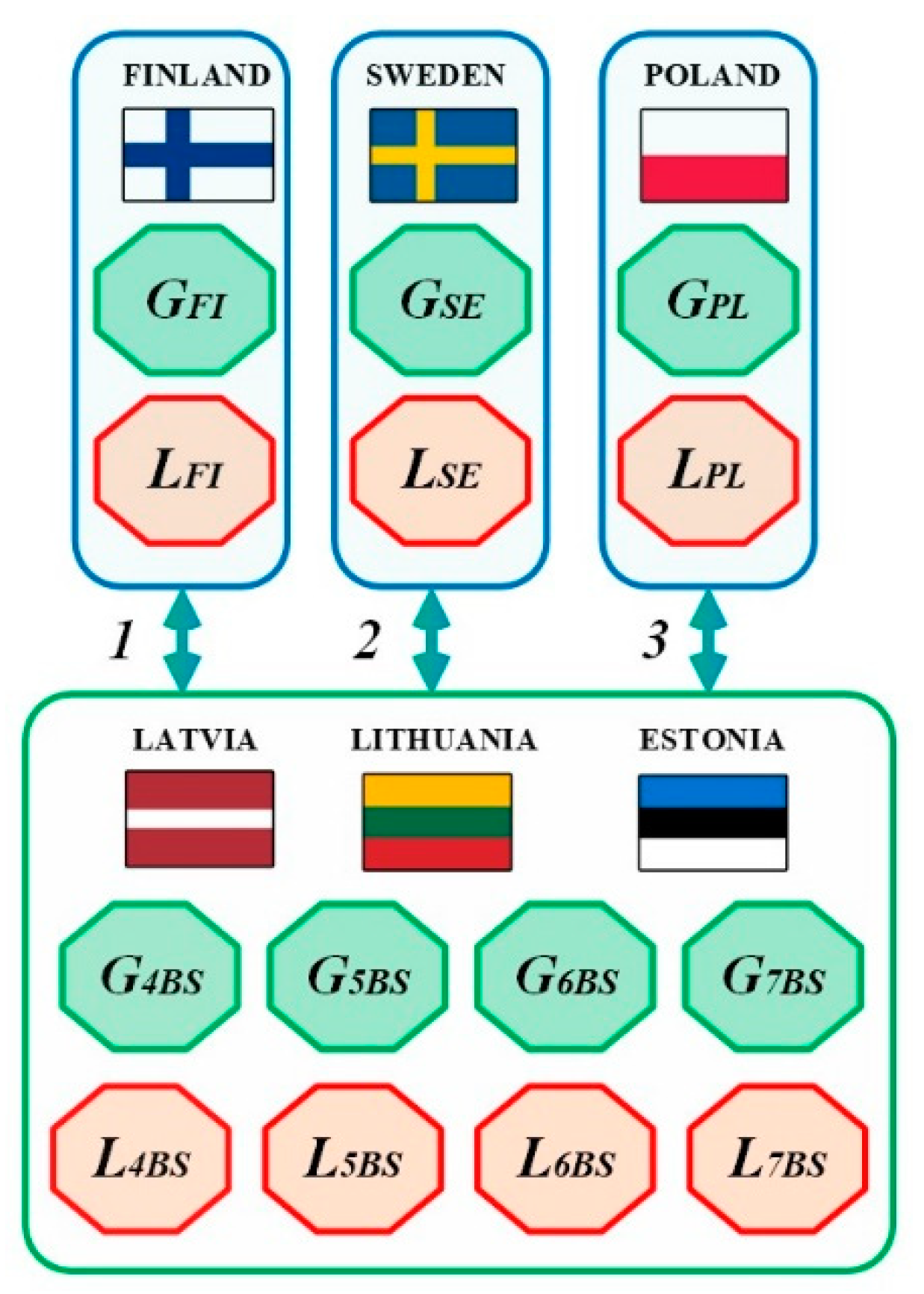
- We assume a “copper plate system” within the Baltic States. The Baltic network can be reduced to one node, see Figure 2.
- We acknowledge that the capacities of the interconnections of the Baltics to Sweden, Poland and Finland are limited, while these countries have significantly larger consumption/production amounts [49], and are strongly linked to the larger energy systems of other European countries. Therefore, we assume the following: (a) the Baltics function as a “price taker” in those markets; (b) the neighbouring systems can always provide import/export power at full interconnection capacity.
- The HECME PP should guarantee system adequacy and provide peak/reserve power and should absorb the residual renewable energy in surplus of the consumption and the exports. We require the total installed capacity of the HECMEs to cover the residual system demand. Additionally, we require that the electrolysers can ensure energy balance at any hour when the consumption is too low otherwise; i.e., all the available renewable generation can be used.
- The capacities of the hydrogen PP and the electrolysers are not limited.
- We consider that electrolysis is the source of green carbon-free hydrogen fed by renewable energy resources. Hydrogen will only be produced when abundant renewable energy is available, when it exceeds domestic demand and a limited export. The electrolyser will only be activated when the market prices are very low.
- The price of HECME energy is higher than that of any other plant. Thus, the generation from the HECME is economically justified at hours when the active power balance can only be provided with the help of gas from a storage reservoir.
- The methane storage is large enough to store any available energy, regardless of the reservoir’s usage schedule in the past or in the future, i.e., an infinite storage; it is assumed that the HECME plant will be located in proximity to the large underground gas reservoirs and will support the operation of the already existing and well-developed gas transmission and distribution system. Thus, there are no extra costs for gas transmission.
- We assume that the consumers’ LBSs are inflexible and are forced to buy energy, at worst, even at the maximum Nord Pool market price, or in its absence, to buy energy at the even higher price of the HECME plant.
- We assume that in compliance with the decisions of the regulator and the government, there is a price cap on the market.
4. The Mathematical Formulation of the Tasks
4.1. Creating a Scenario and a Forecast
4.2. Preparation of Generator and Consumer Bids
4.3. Market Clearing and the Accepted Generator and Load Energy
- The equality constraint for power balance in each hour:
- The inequality constraints for the interconnections’ capacity:
4.4. Calculation of the Economic Indices and Performance
5. The Case Studies
5.1. Scenario Description
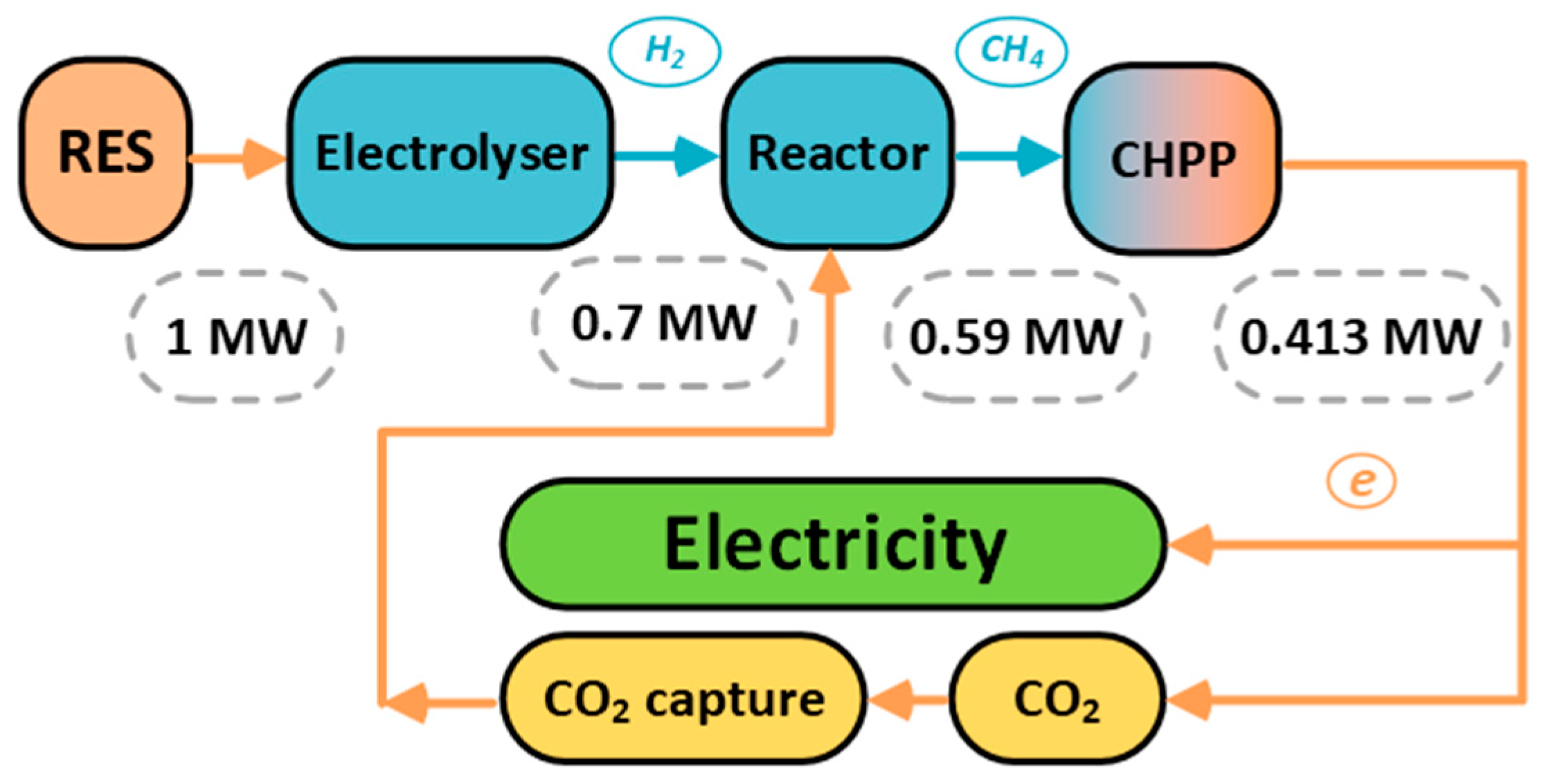
- The efficiency of the electrolyser equals 0.7.
- The efficiency of the H2PP is 0.59.
- The initial state of synthetic methane storage equals the current storage capacity of the underground reservoir—2.32 × 109 m3.
- The density of synthetic methane at 25 °C equals 0.657 kg/m3 [16].
- The thermal capacity of synthetic methane at 25 °C is 39 MJ/m3 = 10.833 kWh/m3 [16].
5.2. Creating Forecasts
5.3. Results
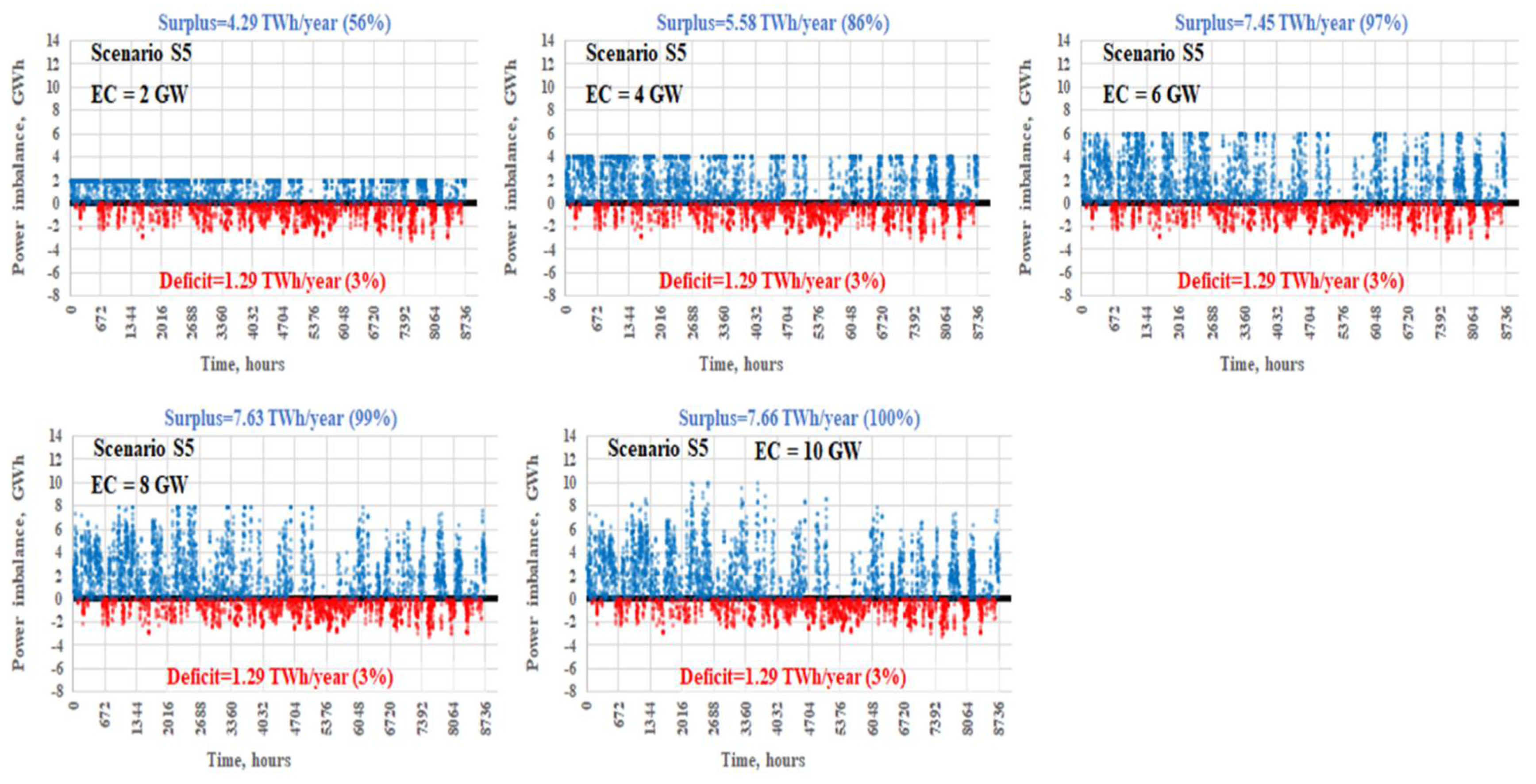
5.3.1. BPS in an Islanded Mode
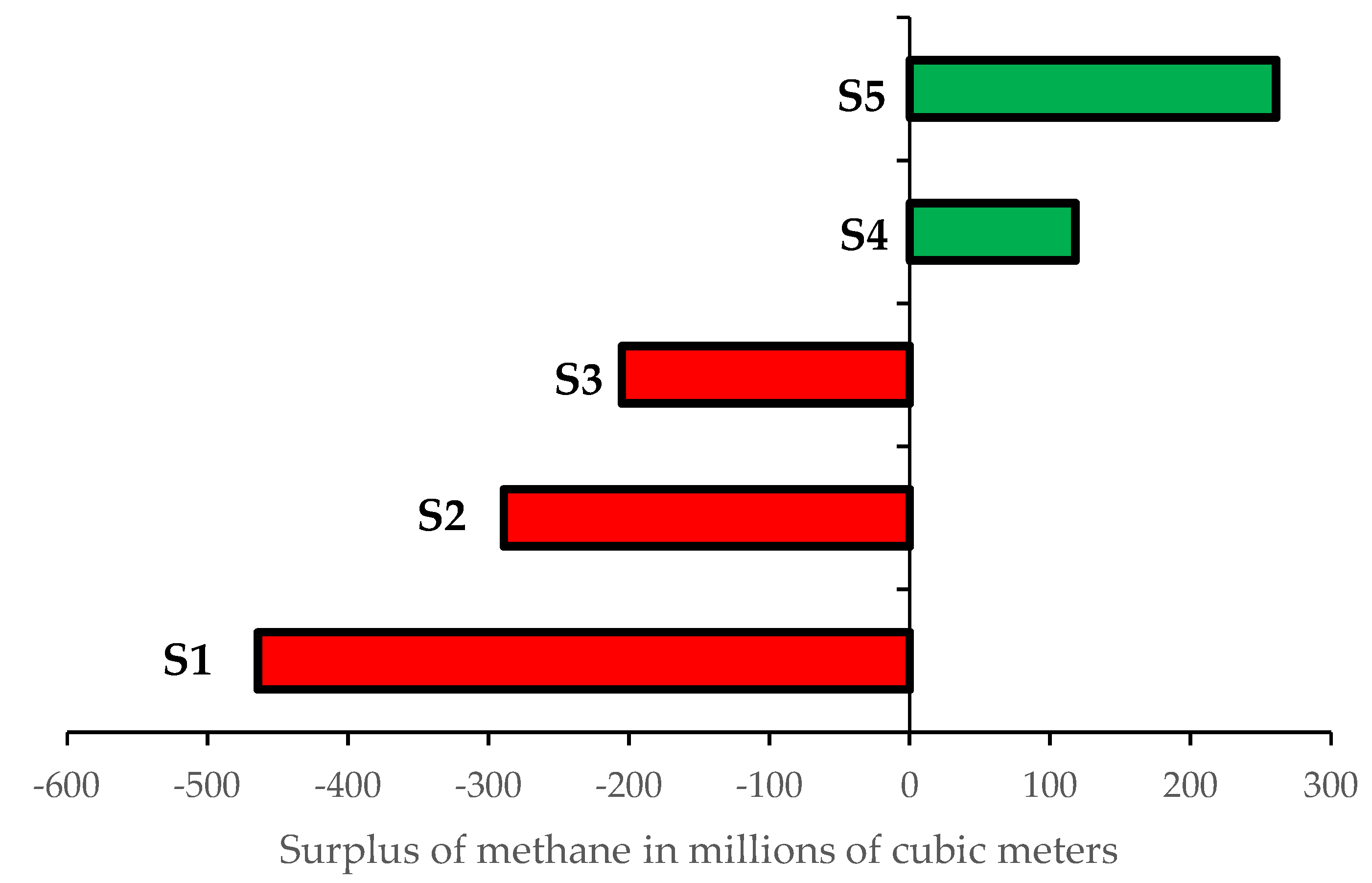
- The “Surplus” shows the amount of energy that must be used by the electrolyser to achieve the balance or wasted otherwise;
- The “Deficit” shows the energy that needs to be produced by using synthetic methane.
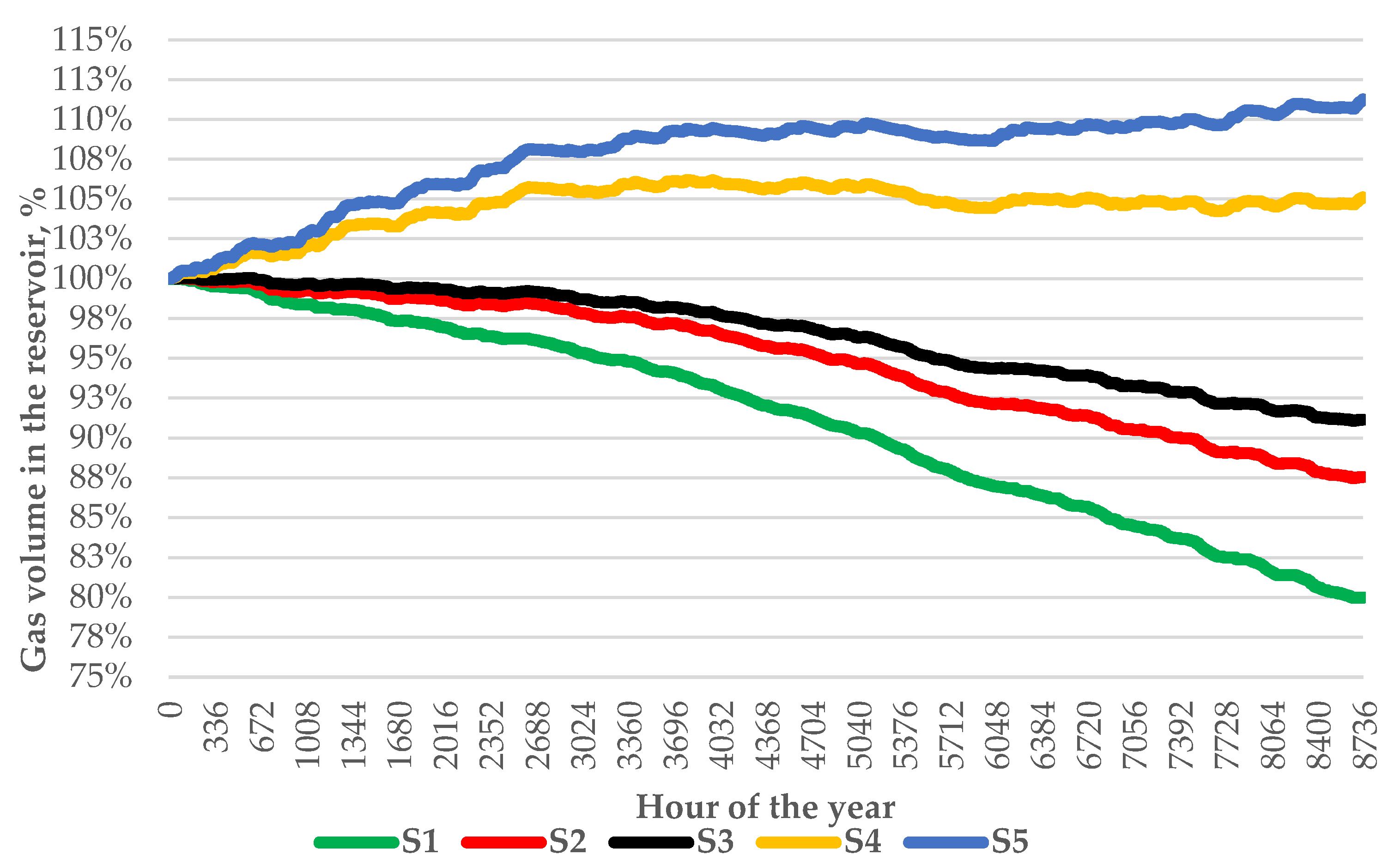
5.3.2. The Energy Balance of BPS after HECME Construction
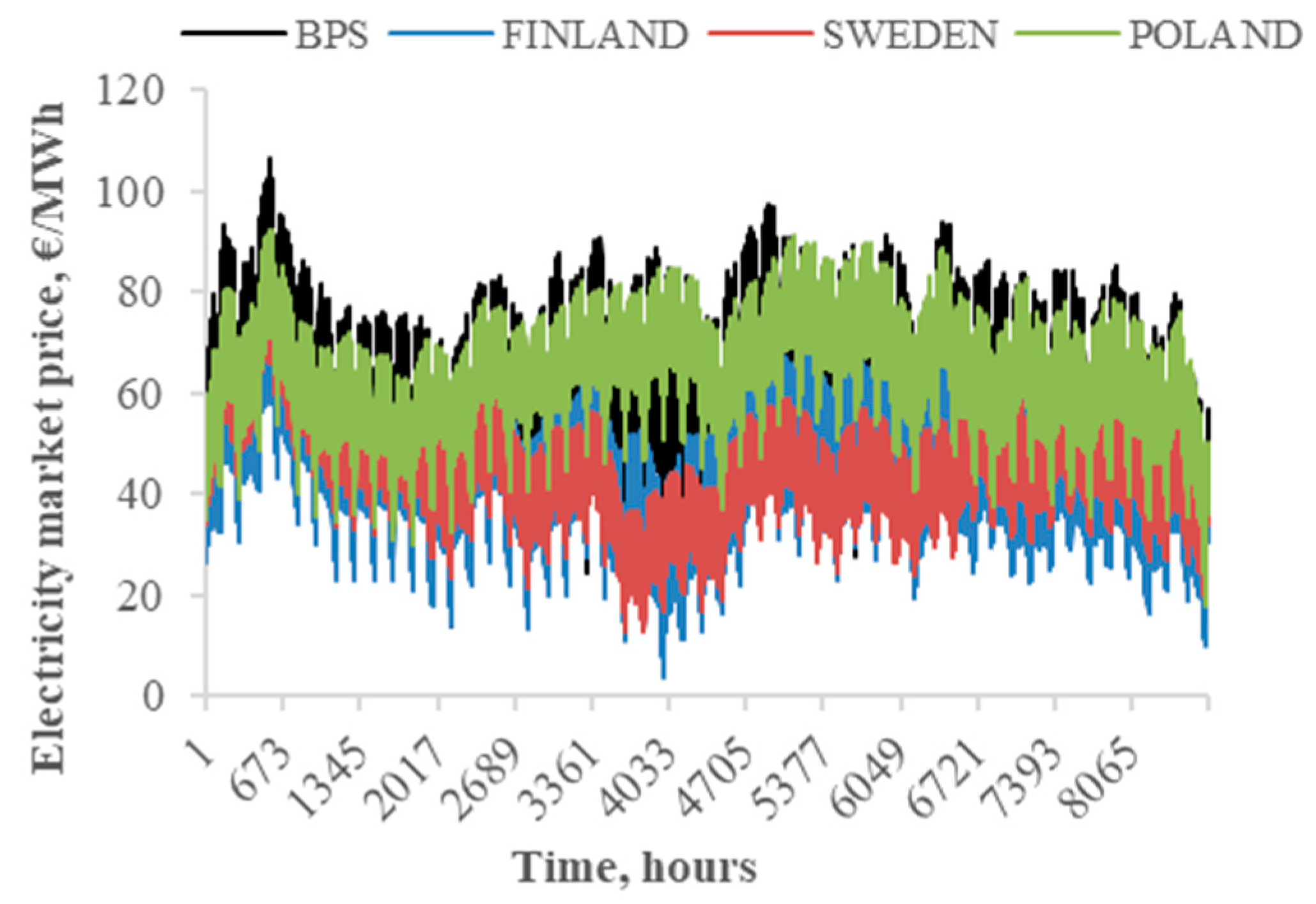
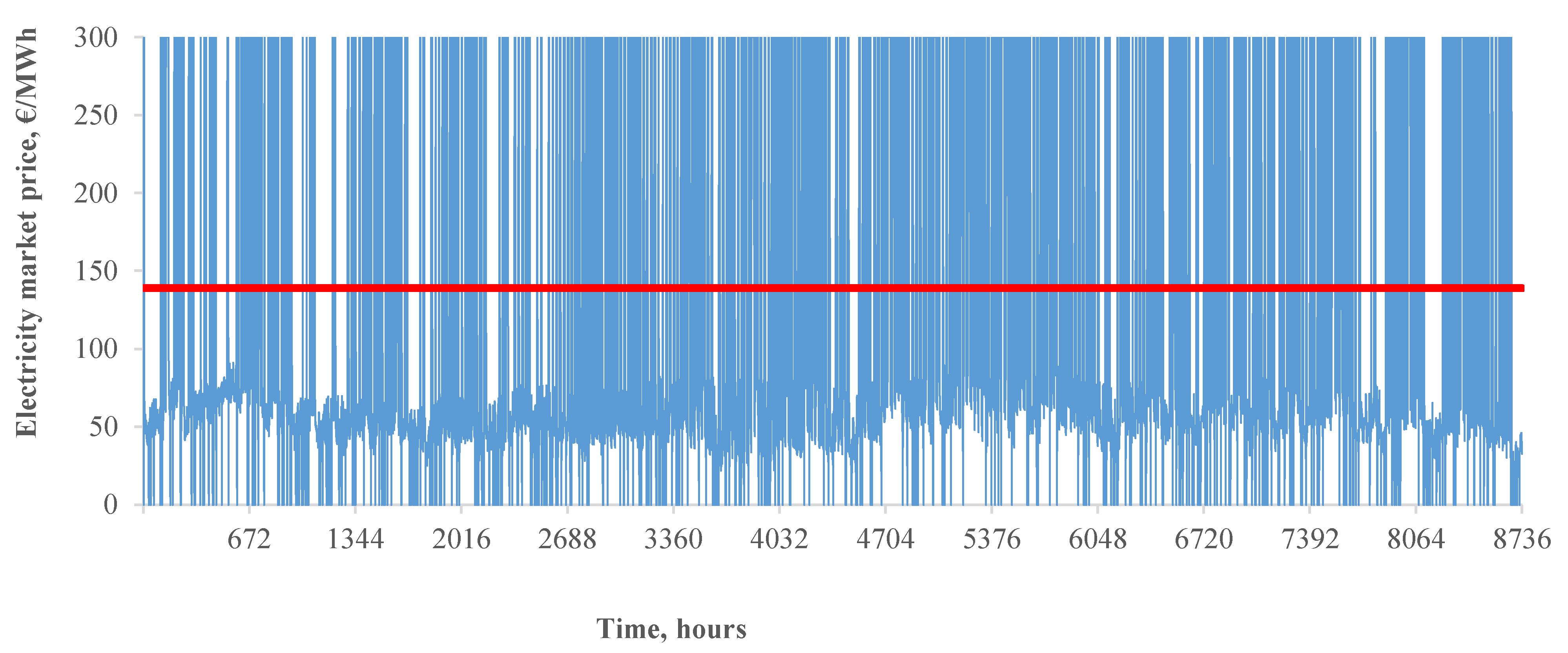
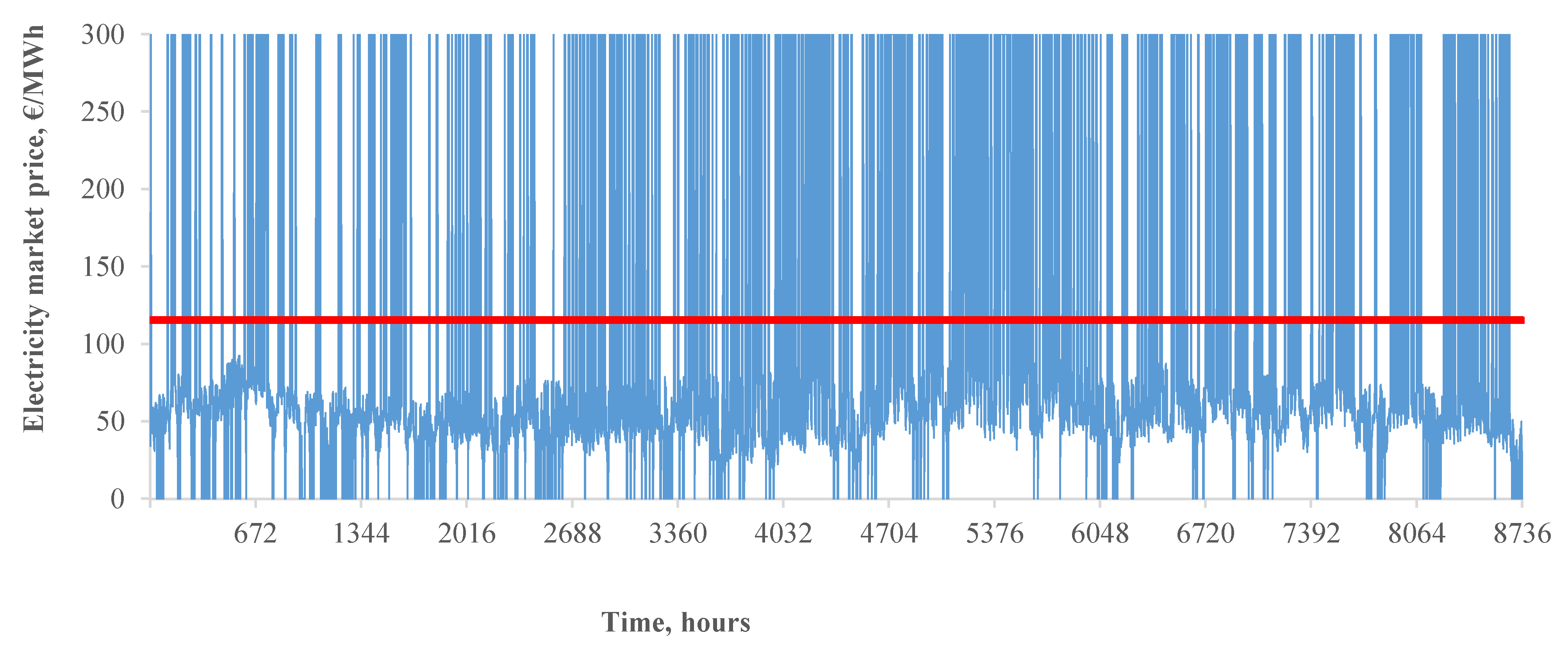
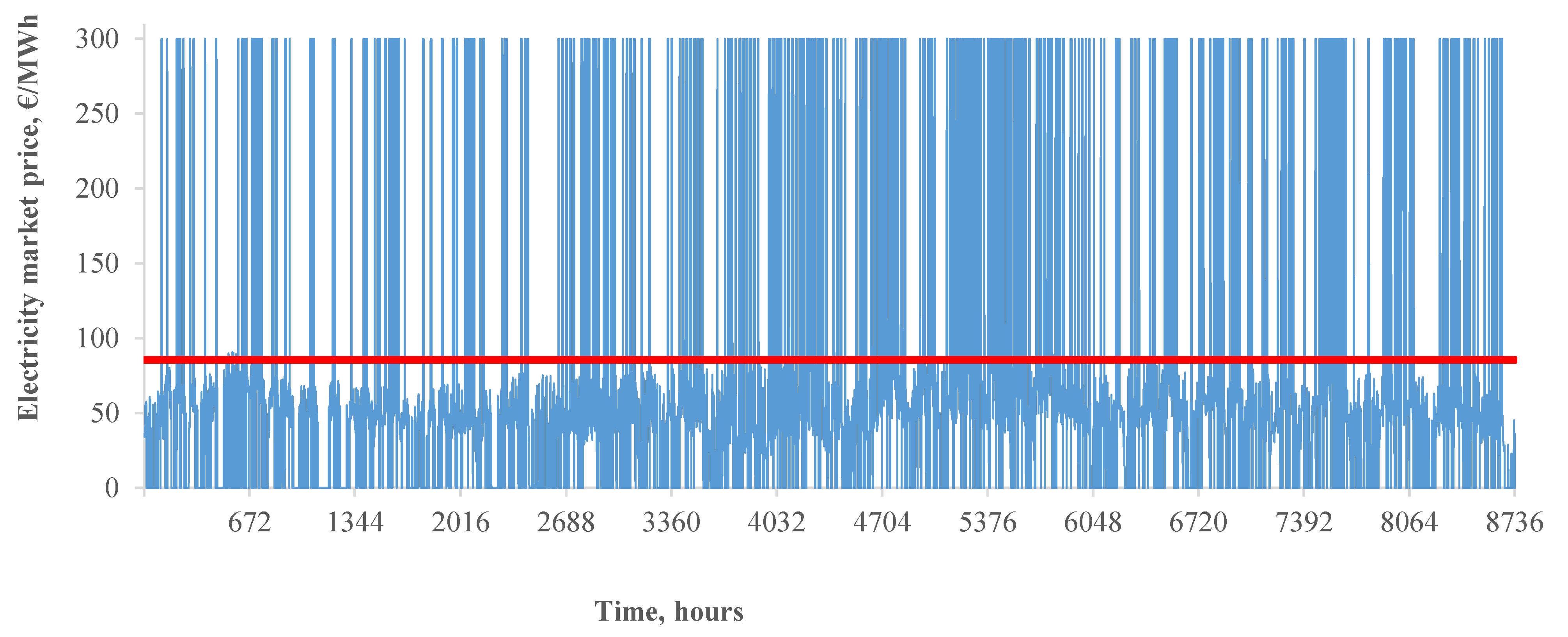
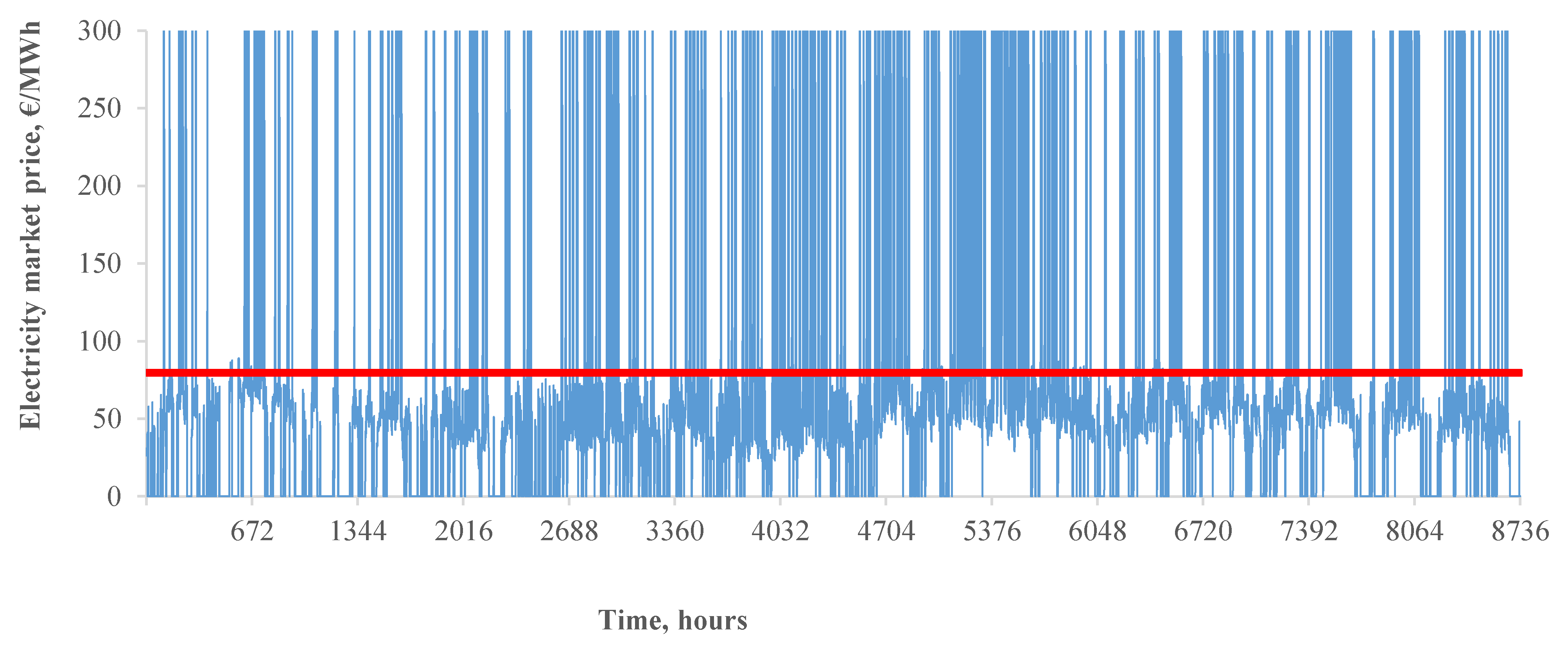
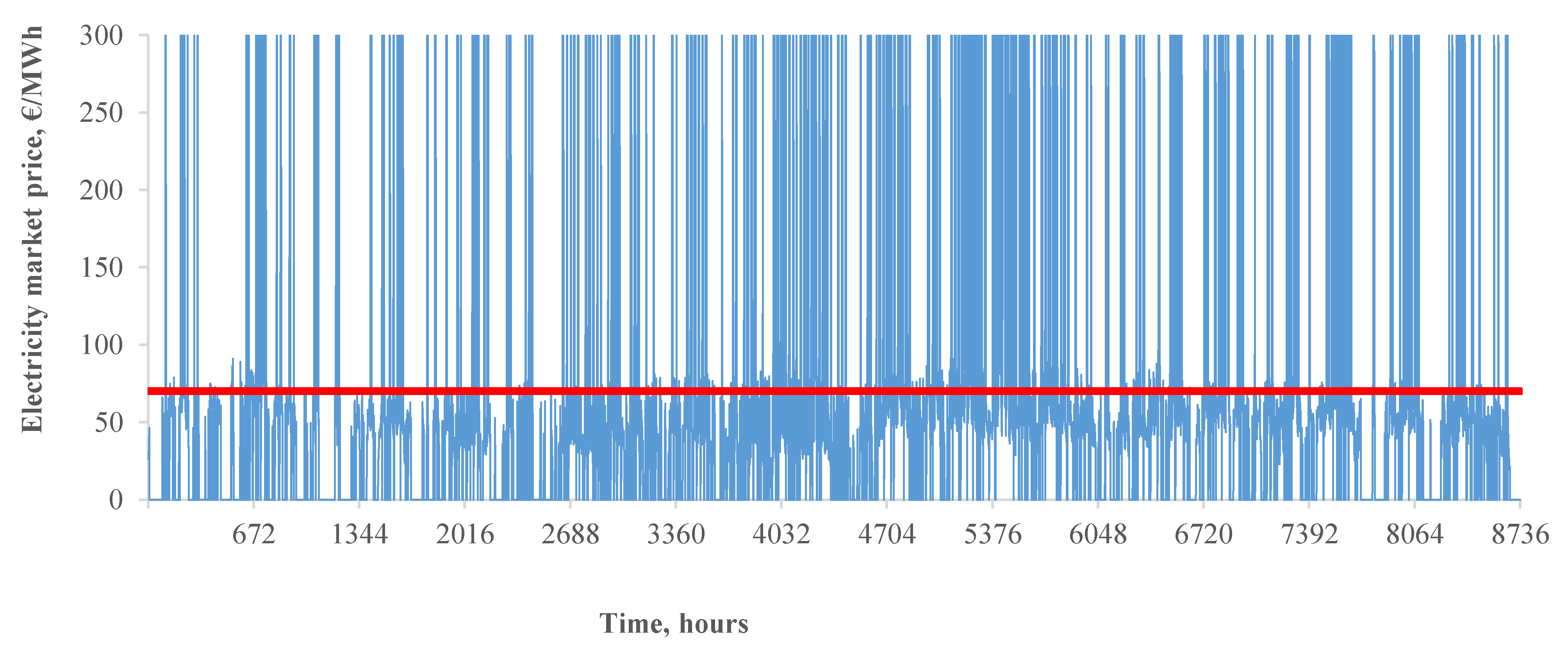
5.3.3. The Impact on the Market Prices
5.3.4. Profitability of Green Power Generation
- Methane production facility.
- Gas power plant with carbon dioxide capture. The construction costs for various power plants are adopted from [56].
6. Conclusions and Directions for Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- European Council. 2030 Climate and Energy Policy Framework EUCO 169/14. 2014. Available online: https://www.eea.europa.eu/policy-documents/euco-169-14 (accessed on 23 October 2023).
- Gul, E.; Baldinelli, G.; Bartocci, P.; Shamim, T.; Domenighini, P.; Cotana, F.; Wang, J.; Fantozzi, F.; Bianchi, F. Transition toward net zero emissions—Integration and optimization of renewable energy sources: Solar, hydro, and biomass with the local grid station in central Italy. Renew Energy 2023, 207, 672–686. [Google Scholar] [CrossRef]
- Siemens Energy. Prospects for Using Hydrogen in Gas Power Plants are Becoming Tangible|Press|Siemens Energy. Available online: https://press.siemens-energy.com/global/en/pressrelease/prospects-using-hydrogen-gas-power-plants-are-becoming-tangible (accessed on 29 July 2023).
- Zhang, H. Regulations for carbon capture, utilization and storage: Comparative analysis of development in Europe, China and the Middle East. Resour. Conserv. Recycl. 2021, 173, 105722. [Google Scholar] [CrossRef]
- Petrichenko, L.; Petrichenko, R.; Sauhats, A.; Baltputnis, K.; Broka, Z. Modelling the Future of the Baltic Energy Systems: A Green Scenario. Latv. J. Phys. Tech. Sci. 2021, 58, 47–65. [Google Scholar] [CrossRef]
- Baltputnis, K.; Broka, Z.; Sauhats, A. Assessing the Value of Subsidizing Large CHP Plants. In Proceedings of the International Conference on the European Energy Market, EEM, Lodz, Poland, 27–29 June 2018. [Google Scholar] [CrossRef]
- Parra, D.; Valverde, L.; Pino, F.J.; Patel, M.K. A review on the role, cost and value of hydrogen energy systems for deep decarbonization. Renew. Sustain. Energy Rev. 2019, 101, 279–294. [Google Scholar] [CrossRef]
- Savelli, I.; Giannitrapani, A.; Paoletti, S.; Vicino, A. An Optimization Model for the Electricity Market Clearing Problem With Uniform Purchase Price and Zonal Selling Prices. IEEE Trans. Power Syst. 2018, 33, 2864–2873. [Google Scholar] [CrossRef]
- Prina, M.G.; Moser, D.; Vaccaro, R.; Sparber, W. EPLANopt optimization model based on EnergyPLAN applied at regional level: The future competition on excess electricity production from renewables. Int. J. Sustain. Energy Plan. Manag. 2020, 27, 35–50. [Google Scholar] [CrossRef]
- Lange, H.; Klose, A.; Lippmann, W.; Urbas, L. Technical evaluation of the flexibility of water electrolysis systems to increase energy flexibility: A review. Int. J. Hydrogen Energy 2023, 48, 15771–15783. [Google Scholar] [CrossRef]
- Brent, A.; Lin, Y.; Lin, W.; Wu, W.; Zhu, Z. Optimal Scheduling of Power Systems with High Proportions of Renewable Energy Accounting for Operational Flexibility. Energies 2023, 16, 5537. [Google Scholar] [CrossRef]
- Epelle, E.I.; Desongu, K.S.; Obande, W.; Adeleke, A.A.; Ikubanni, P.P.; Okolie, J.A.; Gunes, B. A comprehensive review of hydrogen production and storage: A focus on the role of nanomaterials. Int. J. Hydrogen Energy 2022, 47, 20398–20431. [Google Scholar] [CrossRef]
- Zivar, D.; Kumar, S.; Foroozesh, J. Underground hydrogen storage: A comprehensive review. Int. J. Hydrogen Energy 2021, 46, 23436–23462. [Google Scholar] [CrossRef]
- Thorbjörnsson, A.; Wachtmeister, H.; Wang, J.; Höök, M. Carbon capture and coal consumption: Implications of energy penalties and large scale deployment. Energy Strategy Rev. 2015, 7, 18–28. [Google Scholar] [CrossRef]
- Götz, M.; Lefebvre, J.; Mörs, F.; McDaniel Koch, A.; Graf, F.; Bajohr, S.; Reimert, R.; Kolb, T. Renewable Power-to-Gas: A technological and economic review. Renew Energy 2016, 85, 1371–1390. [Google Scholar] [CrossRef]
- Stangeland, K.; Kalai, D.; Li, H.; Yu, Z. CO2 Methanation: The Effect of Catalysts and Reaction Conditions. Energy Procedia 2017, 105, 2022–2027. [Google Scholar] [CrossRef]
- Müller, K.; Fleige, M.; Rachow, F.; Schmeißer, D. Sabatier based CO2-methanation of Flue Gas Emitted by Conventional Power Plants. Energy Procedia 2013, 40, 240–248. [Google Scholar] [CrossRef]
- Brooks, K.P.; Hu, J.; Zhu, H.; Kee, R.J. Methanation of carbon dioxide by hydrogen reduction using the Sabatier process in microchannel reactors. Chem. Eng. Sci. 2007, 62, 1161–1170. [Google Scholar] [CrossRef]
- Reuters. Tokyo Gas Begins Synthetic Methane Trial Using Green Hydrogen|Reuters. Available online: https://www.reuters.com/business/sustainable-business/tokyo-gas-begins-synthetic-methane-trial-using-green-hydrogen-2022-06-24/ (accessed on 29 July 2023).
- Kuckshinrichs, W.; Ball, C.S.; Aniello, G. Levelized profits for residential PV-battery systems and the role of regulatory and fiscal aspects in Germany. Energy Sustain. Soc. 2023, 13, 1–13. [Google Scholar] [CrossRef]
- Guerra, O.J.; Zhang, J.; Eichman, J.; Denholm, P.; Kurtz, J.; Hodge, B.M. The value of seasonal energy storage technologies for the integration of wind and solar power. Energy Environ. Sci. 2020, 13, 1909–1922. [Google Scholar] [CrossRef]
- Morgenthaler, S.; Ball, C.; Koj, J.C.; Kuckshinrichs, W.; Witthaut, D. Site-dependent levelized cost assessment for fully renewable Power-to-Methane systems. Energy Convers. Manag. 2020, 223, 113150. [Google Scholar] [CrossRef]
- Al-Qahtani, A.; Parkinson, B.; Hellgardt, K.; Shah, N.; Guillen-Gosalbez, G. Uncovering the true cost of hydrogen production routes using life cycle monetization. Appl. Energy 2021, 281, 115958. [Google Scholar] [CrossRef]
- Baylin-Stern, A.; Berghout, N. Is Carbon Capture too Expensive?—Analysis—IEA. Available online: https://www.iea.org/commentaries/is-carbon-capture-too-expensive (accessed on 29 July 2023).
- Lazard. Lazard’s Levelized Cost of Hydrogen Analysis-Executive Summary Overview of Analysis. 2021. Available online: https://www.lazard.com/media/erzb5rkv/lazards-levelized-cost-of-hydrogen-analysis-version-20-vf.pdf (accessed on 23 October 2023).
- Dodds, P.E.; Demoullin, S. Conversion of the UK gas system to transport hydrogen. Int. J. Hydrogen Energy 2013, 38, 7189–7200. [Google Scholar] [CrossRef]
- Zhang, J.; Guerra, O.J.; Eichman, J.; Pellow, M.A. Benefit Analysis of Long-Duration Energy Storage in Power Systems with High Renewable Energy Shares. Front. Energy Res. 2020, 8, 527910. [Google Scholar] [CrossRef]
- CSIRO’s Stunning Predictions for Low Cost Battery Storage and Hydrogen Electrolysers|RenewEconomy. Available online: https://reneweconomy.com.au/csiros-stunning-predictions-for-low-cost-battery-storage-and-hydrogen-electrolysers/ (accessed on 5 September 2023).
- Kharel, S.; Shabani, B. Hydrogen as a Long-Term Large-Scale Energy Storage Solution to Support Renewables. Energies 2018, 11, 2825. [Google Scholar] [CrossRef]
- About Us|Nord Pool. Available online: https://www.nordpoolgroup.com/en/About-us/ (accessed on 5 September 2023).
- Membership List|Nord Pool. Available online: https://www.nordpoolgroup.com/en/trading/join-our-markets/membership/ (accessed on 7 September 2023).
- Nord Pool. Rules and Regulations. Available online: https://www.nordpoolgroup.com/en/trading/Rules-and-regulations/ (accessed on 26 June 2023).
- David, A.K.; Wen, F. Strategic bidding in competitive electricity markets: A literature survey. In Proceedings of the IEEE Power Engineering Society Transmission and Distribution Conference, New Orleans, LA, USA, 25–28 April 2022; Volume 4, pp. 2168–2173. [Google Scholar] [CrossRef]
- Cai, T.; Dong, M.; Chen, K.; Gong, T. Methods of participating power spot market bidding and settlement for renewable energy systems. Energy Rep. 2022, 8, 7764–7772. [Google Scholar] [CrossRef]
- Ishimori, H.; Sato, T.; Shiina, T. Solution methods in generator operation optimization considering market transactions. In Proceedings of the 2021 10th International Congress on Advanced Applied Informatics, IIAI-AAI 2021, Niigata, Japan, 11–16 July 2021; pp. 843–848. [Google Scholar] [CrossRef]
- Sauhats, A.; Petrichenko, R.; Baltputnis, K.; Broka, Z.; Varfolomejeva, R. A multi-objective stochastic approach to hydroelectric power generation scheduling. In Proceedings of the 19th Power Systems Computation Conference, PSCC 2016, Genoa, Italy, 20–24 June 2016. [Google Scholar] [CrossRef]
- De, E.-M. How the European Day-Ahead Electricity Market Works Starting Question. March 2017, p. 21. Available online: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwigkJSV7Ir9AhWO9rsIHfXnAtwQFnoECAsQAQ&url=https%3A%2F%2Fbcornelusse.github.io%2Fmaterial%2FCoursEM20170331.pdf&usg=AOvVaw3x8jZV1eh_XxDcvZOEqSW8 (accessed on 23 October 2023).
- NEMO Cometee. EUPHEMIA Public Description. Single price Coupling Algorithm. Report 12. 2020. Available online: https://www.nordpoolgroup.com/globalassets/download-center/single-day-ahead-coupling/euphemia-public-description.pdf (accessed on 23 October 2023).
- EPEX SPOT. PCR (Price Coupling of Regions) EUPHEMIA: Description and functioning. Presentation. 2018. Available online: https://www.epexspot.com/sites/default/files/2020-02/Euphemia_Description%20and%20functioning_1812.pdf (accessed on 23 October 2023).
- CONEXUS. Information about the Storage|Conexus. Available online: https://www.conexus.lv/information-about-storage (accessed on 8 June 2023).
- PCI Examples and Their Benefits. Available online: https://energy.ec.europa.eu/topics/infrastructure/projects-common-interest/pci-examples-and-their-benefits_en (accessed on 5 September 2023).
- Petrichenko, L.; Kozadajevs, J.; Petrichenko, R.; Ozgonenel, O.; Boreiko, D.; Dolgicers, A. Assessment of PV Integration in the Industrial and Residential Sector under Energy Market Conditions. Latv. J. Phys. Tech. Sci. 2021, 58, 82–97. [Google Scholar] [CrossRef]
- Zima-Bockarjova, M.; Sauhats, A.; Petrichenko, L.; Pertichenko, R. Shapley-Value-Based Charging and Discharging Scheduling for Electric Vehicles in a Parking Station. In Proceedings of the 2019 IEEE 60th Annual International Scientific Conference on Power and Electrical Engineering of Riga Technical University, RTUCON 2019–Proceedings, Riga, Latvia, 7–9 October 2019; pp. 1–21. [Google Scholar] [CrossRef]
- Baltputnis, K.; Broka, Z.; Silis, A.; Cingels, G.; Junghans, G. Efficient market-based storage management strategy for FCR provider with limited energy reservoir. In Proceedings of the International Conference on the European Energy Market, EEM, Lappeenranta, Finland, 6–8 June 2023. [Google Scholar] [CrossRef]
- Hering, P.; Mošna, J.; Janecek, E.; Hrycej, D. Optimal scheduling of a pumped-storage hydro power plant operation. In Proceedings of the 2013 13th International Conference on Environment and Electrical Engineering, EEEIC 2013—Conference Proceedings, Wroclaw, Poland, 1–3 November 2013; pp. 166–171. [Google Scholar] [CrossRef]
- Jesudasan, R.N.; Andrew, L.L.H. Scheduling long term energy storage. In Proceedings of the IEEE INFOCOM, Toronto, ON, USA, 27 April–2 May 2014; pp. 634–639. [Google Scholar] [CrossRef]
- Yamin, H.Y. Review on methods of generation scheduling in electric power systems. Electr. Power Syst. Res. 2004, 69, 227–248. [Google Scholar] [CrossRef]
- Lizarraga-Garcia, E.; Ghobeity, A.; Totten, M.; Mitsos, A. Optimal operation of a solar-thermal power plant with energy storage and electricity buy-back from grid. Energy 2013, 51, 61–70. [Google Scholar] [CrossRef]
- Europe—Countries & Regions—IEA. Available online: https://www.iea.org/regions/europe (accessed on 7 September 2023).
- Lütkepohl, H. Vector Autoregressive Models; Springer: Berlin, Germany, 2011. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 2nd ed.; Monash University: Melbourne, Australia, 2018; p. 382. [Google Scholar]
- Petrichenko, L.; Sauhats, A.; Petrichenko, R.; Bezrukovs, D. Long-Term Price Forecasting for the Cost-Benefit Analysis of Power Equipment. In Proceedings of the 2018 IEEE 9th International Scientific Conference on Power and Electrical Engineering of Riga Technical University, RTUCON2018, Riga, Latvia, 15–17 November 2021; pp. 6–10. [Google Scholar]
- Petrichenko, R.; Petrichenko, L.; Baltputnis, K.; Sauhats, A.; Gudzius, S.; Slivikas, A. Selection of the initial state and duration of the planning period in the tasks of managing energy storage systems. In Proceedings of the 2020 IEEE 61st Annual International Scientific Conference on Power and Electrical Engineering of Riga Technical University, RTUCON 2020—Proceedings, Riga, Latvia, 5–7 November 2020; pp. 18–23. [Google Scholar] [CrossRef]
- Return on Assets (ROA): Formula and ‘Good’ ROA Defined. Available online: https://www.investopedia.com/terms/r/returnonassets.asp (accessed on 5 September 2023).
- Projected Costs of Generating Electricity 2020—Analysis—IEA. Available online: https://www.iea.org/reports/projected-costs-of-generating-electricity-2020 (accessed on 5 September 2023).
- Gorre, J.; Ortloff, F.; van Leeuwen, C. Production costs for synthetic methane in 2030 and 2050 of an optimized Power-to-Gas plant with intermediate hydrogen storage. Appl. Energy 2019, 253, 113594. [Google Scholar] [CrossRef]
- IRENA. Making the Breakthrough: Green Hydrogen Policies and Technology Costs|Enhanced Reader. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2020/Nov/IRENA_Green_Hydrogen_breakthrough_2021.pdf?la=en&hash=40FA5B8AD7AB1666EECBDE30EF458C45EE5A0AA6 (accessed on 5 September 2023).
- IRENA. Innovation Outlook Renewable Methanol in Partnership with. 2021, pp. 1–122. Available online: www.irena.org (accessed on 5 September 2023).
- Broka, Z.; Baltputnis, K. Open-source electricity market modelling for the Baltic states: Review and requirements. In Proceedings of the International Conference on the European Energy Market, EEM, Lappeenranta, Finland, 6–8 June 2023. [Google Scholar] [CrossRef]
- Baltputnis, K.; Broka, Z. Future scenarios of the Baltic power system with large penetration of renewables. In Proceedings of the International Conference on the European Energy Market, EEM, Lappeenranta, Finland, 6–8 June 2023. [Google Scholar] [CrossRef]
- The Cost of Capital in Clean Energy Transitions—Analysis—IEA. Available online: https://www.iea.org/articles/the-cost-of-capital-in-clean-energy-transitions (accessed on 5 September 2023).
- Greenhouse Gas Emissions by Country and Sector (Infographic)|News|European Parliament. Available online: https://www.europarl.europa.eu/news/en/headlines/society/20180301STO98928/greenhouse-gas-emissions-by-country-and-sector-infographic (accessed on 18 October 2023).
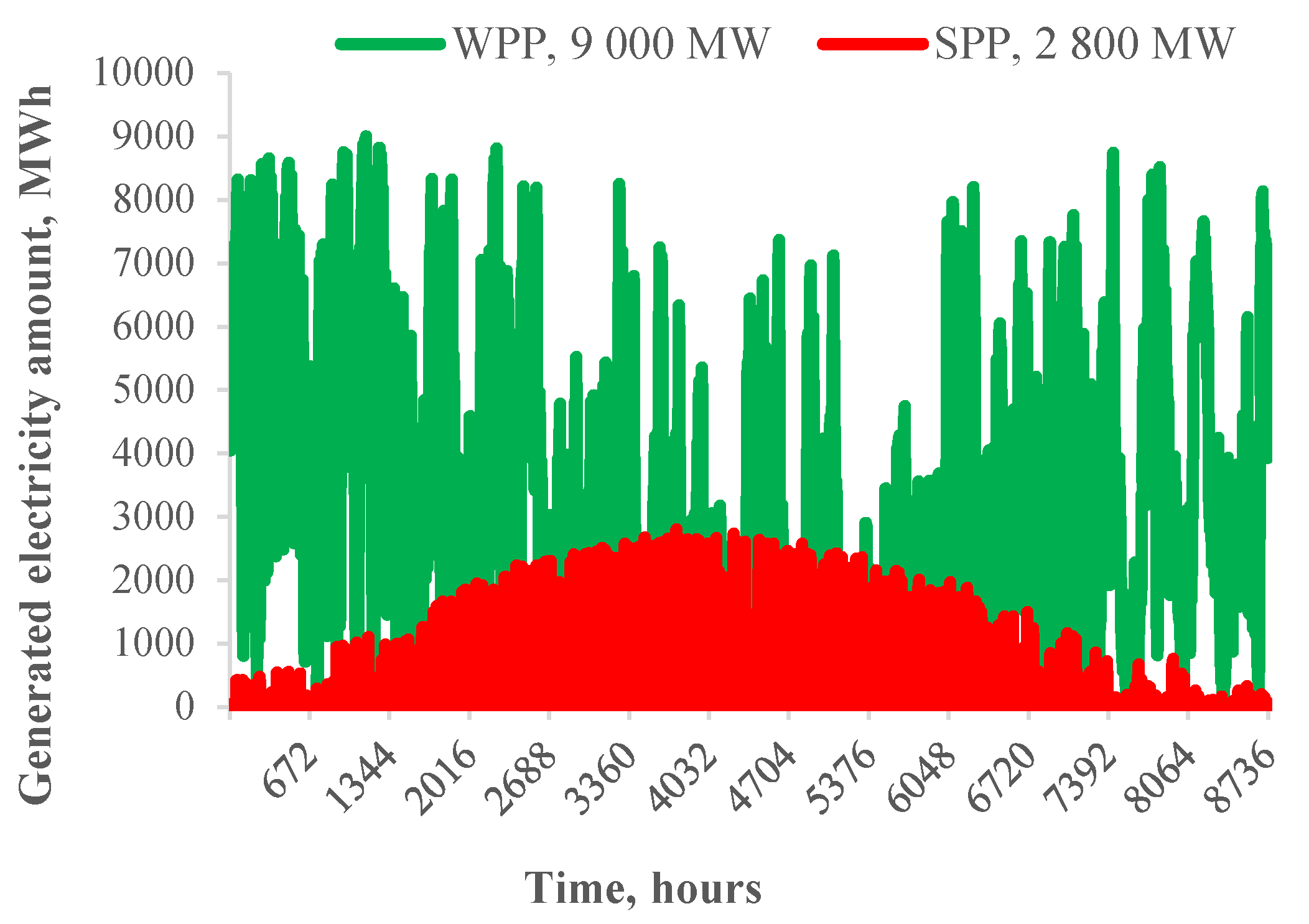
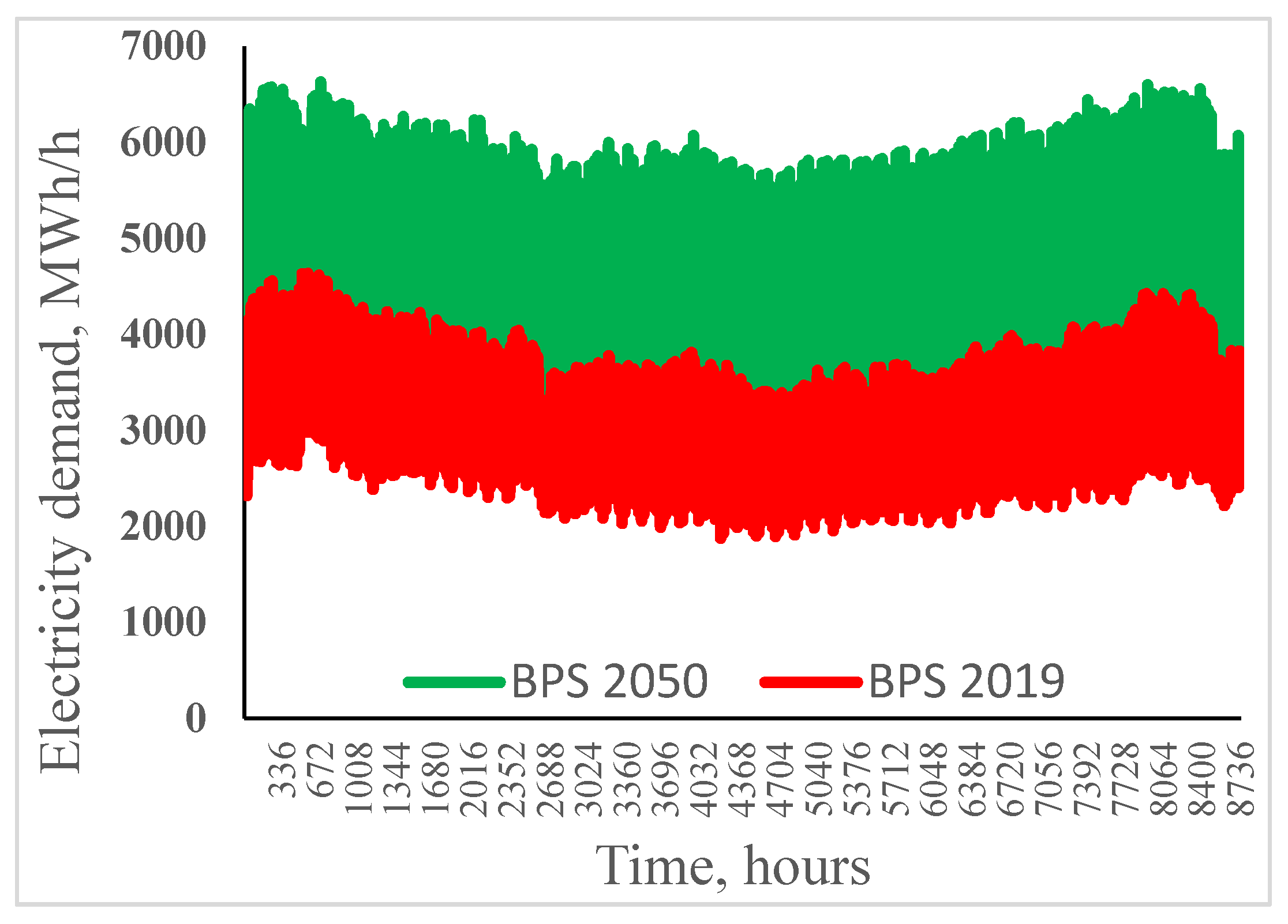
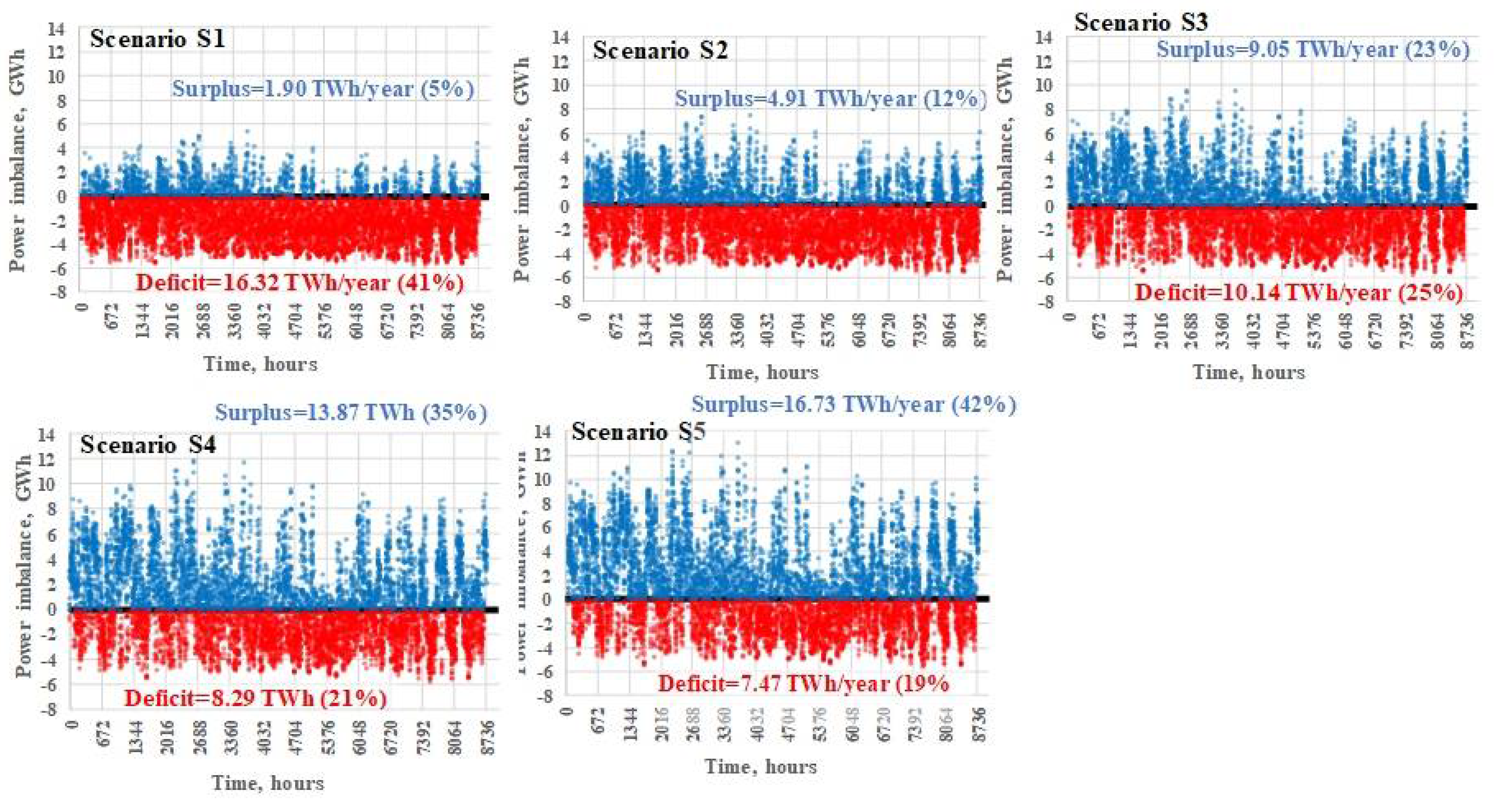
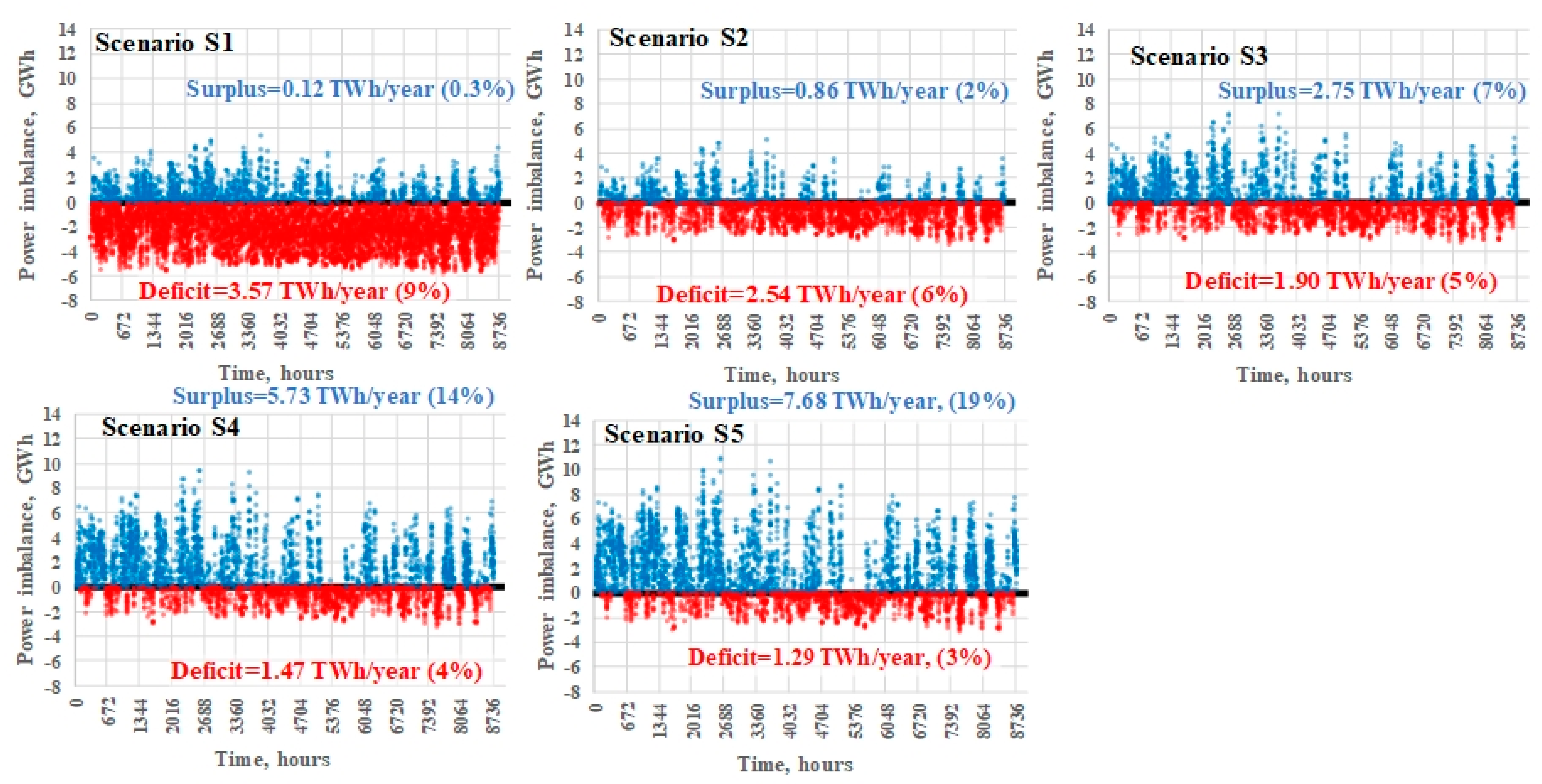
| Scenario | Demand | SPP | WPP | HPP | PSHPP | BPP |
|---|---|---|---|---|---|---|
| S1 | 6629 a 39.83 b | 1600 a 1.87 b | 5000 a 14.92 b | 1727 a 2.24 b | 1625 a 2.85 b | 522 a 3.52 b |
| S2 | 2200 a 2.57 b | 7000 a 20.88 b | ||||
| S3 | 2800 a 3.27 b | 9000 a 26.85 b | ||||
| S4 | 3400 a 3.97 b | 11,000 a 32.82 b | ||||
| S5 | 4000 a 4.67 b | 12,000 a 35.80 b |
| Scenario | ED-HECME | ES-HECME | ED+HECME | ES+HECME | E2CH4 | GCH |
|---|---|---|---|---|---|---|
| TWh/Year, % of Total Demand in BPS | TWh/Year | Mm3/Year | ||||
| S1 | 3.57 (9%) | 0.12 (0.3%) | 0.00 (0%) | −8.53 (−21%) | 8.65 | 798.43 |
| S2 | 2.54 (6%) | 0.86 (2%) | 0.00 (0%) | −5.30 (−13%) | 6.16 | 568.61 |
| S3 | 1.90 (5%) | 2.75 (7%) | 0.00 (0%) | −1.86 (−5%) | 4.61 | 425.51 |
| S4 | 1.47 (4%) | 5.73 (14%) | 0.00 (0%) | 2.17 (5%) | 3.55 | 328.22 |
| S5 | 1.29 (3%) | 7.68 (19%) | 0.00 (0%) | 4.55 (11%) | 3.12 | 288.14 |
| Scenario | S1 | S2 | S3 | S4 | S5 |
|---|---|---|---|---|---|
| Capacity of generator, GW | 3.313 | 3.265 | 3.218 | 3.170 | 3.146 |
| Capacity of electrolyser, GW | 3.041 | 5.148 | 7.254 | 9.518 | 10.901 |
| Scenario | The Initial State (TWh, Mm3, Percentage) | The Final State (TWh, Mm3, Percentage) | Maximal Level (TWh, Mm3, Percentage) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| S_1 | 25.13 | 2320 | 100% | 20.10 | 1856 | 80% | 25.13 | 2320 | 100% |
| S_2 | 25.13 | 2320 | 100% | 22.00 | 2031 | 87% | 25.14 | 2321 | 100% |
| S_3 | 25.13 | 2320 | 100% | 22.91 | 2115 | 91% | 25.14 | 2321 | 100% |
| S_4 | 25.13 | 2320 | 100% | 26.42 | 2439 | 105% | 26.69 | 2464 | 106% |
| S_5 | 25.13 | 2320 | 100% | 27.96 | 2581 | 111% | 27.96 | 2581 | 111% |
| Scenario | SPP (MEUR/Year) | WPP (MEUR/Year) | HPP (MEUR/Year) | PSPP (MEUR/Year) | BPP (MEUR/Year) | HECMEe (MEUR/Year) | HECMEg (MEUR/Year) | AvPr (EUR/MWh) |
|---|---|---|---|---|---|---|---|---|
| S_1 | 119 | 1002 | 142.40 | 173.77 | 482.94 | 1071.66 | −610 | 139 |
| S_2 | 160 | 1308 | 114.54 | 143.27 | 400.25 | 763.19 | −370 | 115 |
| S_3 | 202 | 1656 | 93.86 | 116.74 | 329.70 | 571.13 | −129 | 95 |
| S_4 | 249 | 2013 | 78.51 | 101.45 | 275.22 | 440.54 | +188 | 79 |
| S_5 | 323 | 2504 | 67.74 | 91.43 | 242.03 | 387.76 | +360 | 70 |
| Power Plant Type | Investment (EUR /kW) | Overnight Construction Costs, S5 (MEUR) | Overnight Construction Costs, S5*, (MEUR) | Annual Income, S5 (MEUR) | Annual Income, S5* (MEUR) | ROA, S5 (%) | ROA, S5* (%) |
|---|---|---|---|---|---|---|---|
| SPP | 800 | 3200 | 3200 | 323 | 323 | 10.1 | 10.1 |
| WPP (onshore) | 1500 | 18,000 | 18,000 | 2504 | 2504 | 13.9 | 13.9 |
| HECME (Electrolyzer + methanation) | 1200 | 13,080 | 2400 | - | - | - | - |
| HECME (Gas PP with CC) | 1400 | 4410 | 4410 | 747 | 387 | 4.3 | 5.7 |
| A set of all power plants | - | 38,690 | 28,010 | 3574 | 3214 | 9.24 | 11.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sauhats, A.; Petrichenko, R.; Zima-Bockarjova, M. A Pragmatic Approach to the Economic Assessment of Green Synthetic Methane Power in the Baltics. Energies 2023, 16, 7479. https://doi.org/10.3390/en16227479
Sauhats A, Petrichenko R, Zima-Bockarjova M. A Pragmatic Approach to the Economic Assessment of Green Synthetic Methane Power in the Baltics. Energies. 2023; 16(22):7479. https://doi.org/10.3390/en16227479
Chicago/Turabian StyleSauhats, Antans, Roman Petrichenko, and Marija Zima-Bockarjova. 2023. "A Pragmatic Approach to the Economic Assessment of Green Synthetic Methane Power in the Baltics" Energies 16, no. 22: 7479. https://doi.org/10.3390/en16227479
APA StyleSauhats, A., Petrichenko, R., & Zima-Bockarjova, M. (2023). A Pragmatic Approach to the Economic Assessment of Green Synthetic Methane Power in the Baltics. Energies, 16(22), 7479. https://doi.org/10.3390/en16227479









