Flat-Plate PHP with Gravity-Independent Performance and High Maximum Thermal Load

Abstract

In many energy-related applications, components with high heat loads, such as power electronics, play an important role. Pulsating heat pipes (PHPs) are an effective solution to deal with the increasing heat load of these components. In many real-life applications, the PHP must work against gravity and still be able to operate efficiently. However, the majority of present flat-plate PHP designs do not perform well under this condition. Therefore, this paper presents a flat-plate PHP with a conventional channel design optimized for gravity-independent operation. The PHP was capable of transmitting a heat output of 754 watts in all orientations, while the testing heater in use never exceeded a temperature of 100 °C. No indications of dryout were observed, implying that the maximum thermal load the PHP can handle is even higher. Additionally, three different condenser zone sizes were tested with the PHP. Previously published results indicated that there is a specific range of suitable condenser zone sizes, and performance problems will occur if the condenser zone size falls outside of this range. The findings from this work point in the same direction.

1. Introduction

Power levels and power densities in energy-related applications and electronic devices are increasing continuously and can reach several 100 W/cm². Consequently, moving, spreading, and rejecting waste heat to prevent the overheating of these devices is becoming increasingly challenging. As an emerging technology, pulsating heat pipes (PHPs), also called oscillating heat pipes (OHPs) [1,2], can be a very efficient thermal solution to remove the heat from critical hot spots. PHPs consist of meandering channels filled with a working fluid that moves in an oscillating or pulsating manner to transfer heat. The thermal gradient $dT$ results in vapor pressure difference $dP$ between the hot side and cold side, which is the driver of the fluid motion. In contrast to conventional heat pipes (HPs), PHPs do not require a wick to move the liquid phase back to the hot side, and the majority of heat is carried by sensible heat rather than latent heat [2]. PHPs can either be made as bent capillary tubes or as flat plates with integrated channels and thicknesses of a few millimeters, facilitating integration with electronic components. With advanced methods such as additive manufacturing, even more advanced PHP designs with multilayer channel structures are feasible (see, e.g., [3,4,5,6]). PHPs mostly reach effective thermal conductivities that are much larger than those of the container materials (typically copper or aluminum) and can handle heat fluxes of up to 300 W/cm² [7]. The limiting factor regarding the maximum thermal load is the so-called “dryout”, which can be caused by insufficient amounts of liquid returning to the evaporator at large heat loads. In this case, all liquid slugs and/or liquid films in the heating zone (evaporator area) are completely evaporated, the evaporator area is completely dry, and no heat can be transferred to the condenser area [8]. Extensive theoretical and experimental investigations were conducted to better understand fluid flow and heat transfer mechanisms in PHPs, resulting in many publications. An overview of the current state of the art is given, e.g., in [1,2,9]. Six major parameters were identified that primarily determine the system dynamics and performance [10]: (i) internal channel diameter, (ii) filling ratio of the working liquid, (iii) input heat flux, (iv) total number of turns, (v) device orientation (taking gravity into account), and (vi) the thermophysical properties of the working fluid, particularly the vapor pressure change with temperature, $dP/dT$.

The influence of these factors is analyzed in a significant number of publications, and PHPs with very good thermal transport properties are often achieved. However, there are two important aspects that are often not examined in detail:

Firstly, we observed the operation of a flat-plate PHP under the influence of gravity. In its extreme form, the PHP is arranged vertically, and the PHP’s hot side (evaporator zone) is above the cold side (condenser zone). This operation mode is often called top heat mode (THM), in contrast to the bottom heat mode (BHM), where the PHP is also arranged vertically but the evaporator zone is below the condenser zone, and the horizontal heat mode (HHM), where the PHP is arranged horizontally and both zones are at the same height. The THM is clearly the most challenging operation mode for any heat pipe since gravity impedes the necessary return of the liquid phase to the evaporator. Conventional wick-based heat pipes with sintered wick structures suffer in THM but still work, whereas heat pipes with a grooved structure are difficult to operate in THM, and for PHPs, THM is considered critical, meaning that (i.e.) it results in poor performance [9]. In the majority of publications on PHPs, the THM was either not examined or led to a performance substantially inferior to the other orientations. However, in many real-life applications, due to internal system restrictions, the only viable way to operate a heat pipe is against gravity, and in extreme cases, in THM. Thus, it is important to design a PHP specifically for operation in this orientation.

Secondly, the size of the condenser zone is highly relevant. Even though it is critical to consider the interplay of the PHP´s properties and the condenser size in the target application, the majority of experiments with PHPs published up to now were only carried out for a single fixed condenser zone size. There are only a few experimental publications that deal with this aspect, as will be outlined below in the discussion section. However, most of these publications do not deal specifically with very large condenser area sizes, as, for example, up to the full length of the PHP.

The objective of this work is to analyze these aspects in more depth: (i) A PHP with a design optimized for very good performance in all orientations is presented, (ii) this PHP is characterized for a number of different conditions, (iii) the obtained thermal behavior and performance are discussed with regard to previous results from the literature. The design paradigms that were applied for optimization are given in Section 2.1 below. The main design criterion is the maximization of the number of turns on a given PHP area while maintaining a large enough channel cross-section. Results for various orientations and condenser zone sizes are shown. With dimensions of 125 × 100 × 6 mm³, the PHP is relatively compact and can still carry a thermal power of up to approximately 750 W at a cold end temperature of 20 °C, with the evaporator zone (in this case, the heater) never exceeding a temperature of 100 °C. With these characteristics, the PHP is well suited for heat dissipation in all kinds of energy systems, and one exemplary promising application is the conversion of electrical energy to microwave energy in power amplifiers (see also Appendix A).

2. Materials and Methods

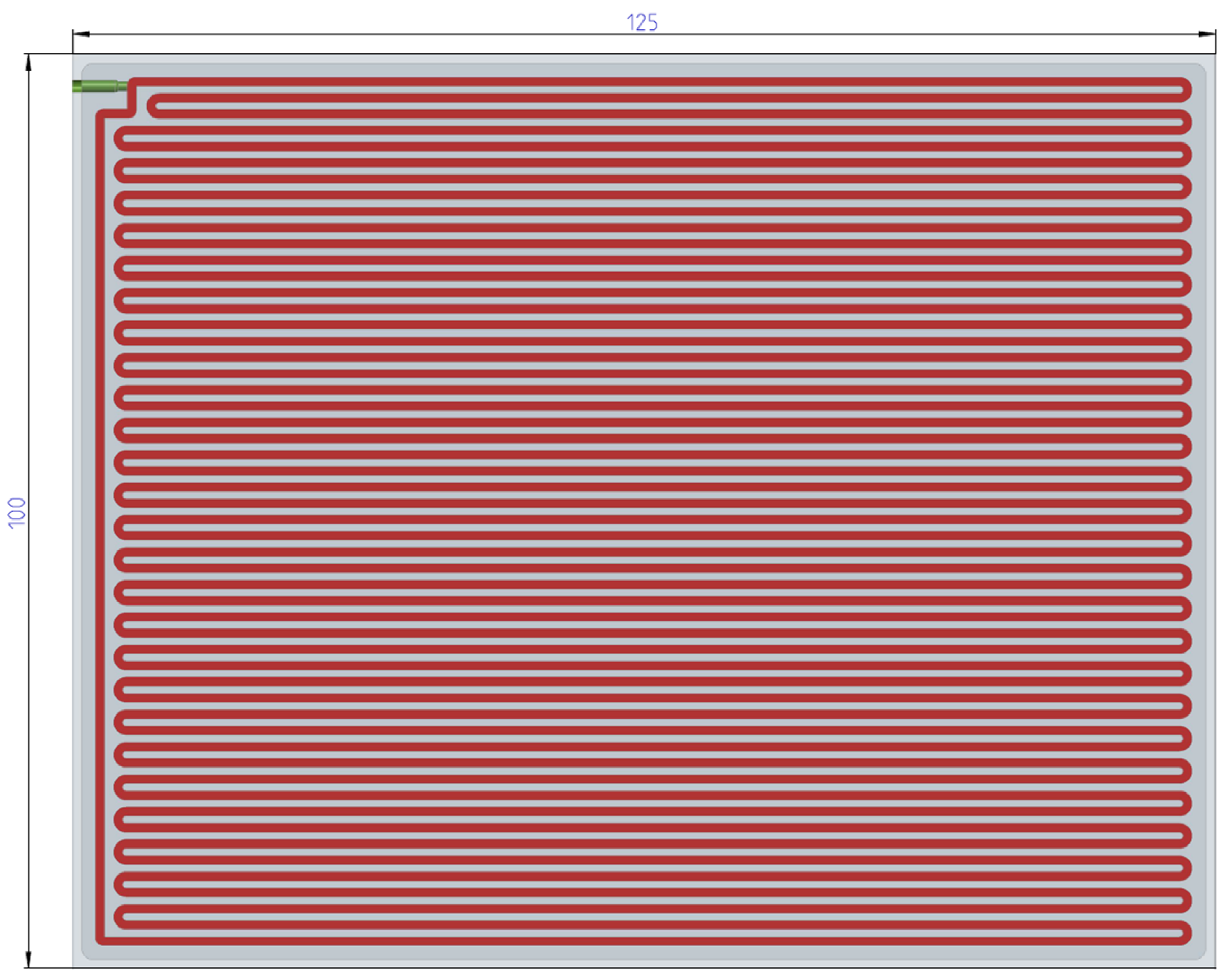
2.1. Design of PHPs

From the literature, certain design paradigms that enhance the ability of the PHP to work against gravity are known. Regarding PHP geometry, the most important paradigm is to increase the number of turns, see, for example, [1] (p. 212) and [11]. It is noted that a high number of channels is beneficial for PHP performance in general. As the number of channels increases, so does the internal perturbation in terms of bubble growth and collapse [10], which is one of the basic processes governing PHP activity and performance. Additionally, the higher level of local perturbations helps to avoid vapor phase recoiling in the evaporator and liquid merging in the condenser [12]. From this, it can be concluded that PHPs with a large number of channels are likely to work more ”stable“ as the pulsating motion can be sustained for a larger range of input powers. A high channel density is also supposed to facilitate the startup process of the heat pipe, i.e., achieving the desired pulsating motion of the fluid and vapor segments already at a relatively low thermal load. However, the channel cross-sections should not become too small since this results in a high hydraulic flow resistance, which can stall the fluid motion and reduce the overall heat throughput capacity [10].

Taking these considerations into account, a channel cross-section of 1 × 1 mm² was finally chosen. In our previous work and together with acetone as a working fluid, this channel cross-section proved to be large enough to not cause a noticeable loss in heat transfer performance due to increased hydraulic resistance [13]. We also note that this cross-section is well below the maximum diameter $D_{max}$ as defined by the bond criterion ($D_{max}$ = 3.17 mm under normal gravity at 300 K [7]). The channels were closely spaced and covered a significant amount of the available space on the PHP without significant channel-free margins, allowing 54 channels (27 turns) to be accommodated in a relatively small total PHP area of 125 × 100 mm². The channels were fabricated by milling half-channels of 1.0 × 0.5 mm² into two separate copper plates (high-purity copper, type CW008A) that were later joined by brazing. The resulting channel structure of the fabricated PHP is shown in Figure 1. The total thickness of this PHP is 6 mm (we note that this relatively high thickness was chosen to prevent warping during the brazing process). For filling, a copper tube was attached to the PHP. Acetone was used as a working fluid. The choice of the working fluid is based on previous literature, particularly the summary given in ref. [14]. Compared to other candidates, acetone has a high gradient of vapor pressure vs. temperature, a low dynamic viscosity, and a low latent heat. All of these characteristics are helpful for starting and sustaining the pulsating fluid motion in the PHP [15]. The filling was conducted at a base pressure in the range of 10⁻⁴ mbar measured at the inlet of the mentioned filling tube (not in the PHP itself). The fluid was thoroughly degassed prior to filling. The resulting filling ratio was 54%.

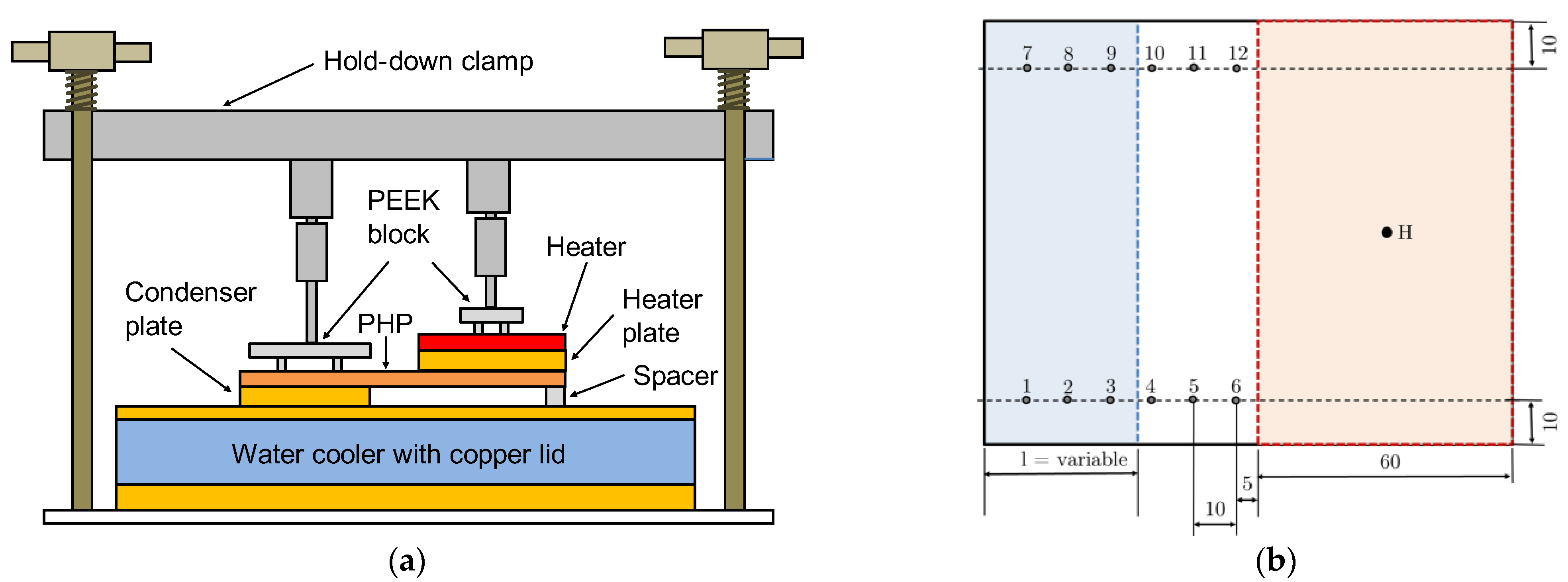
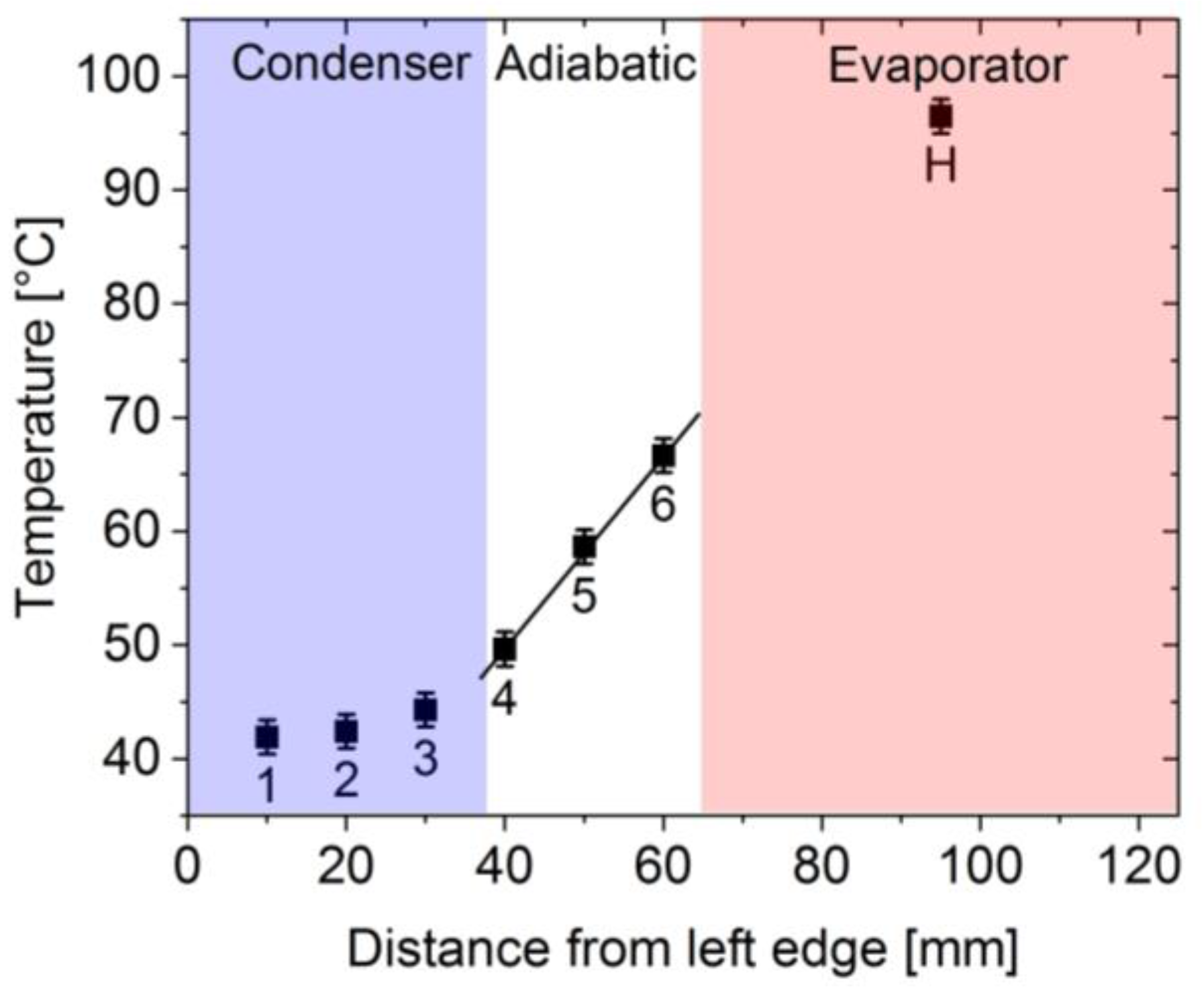
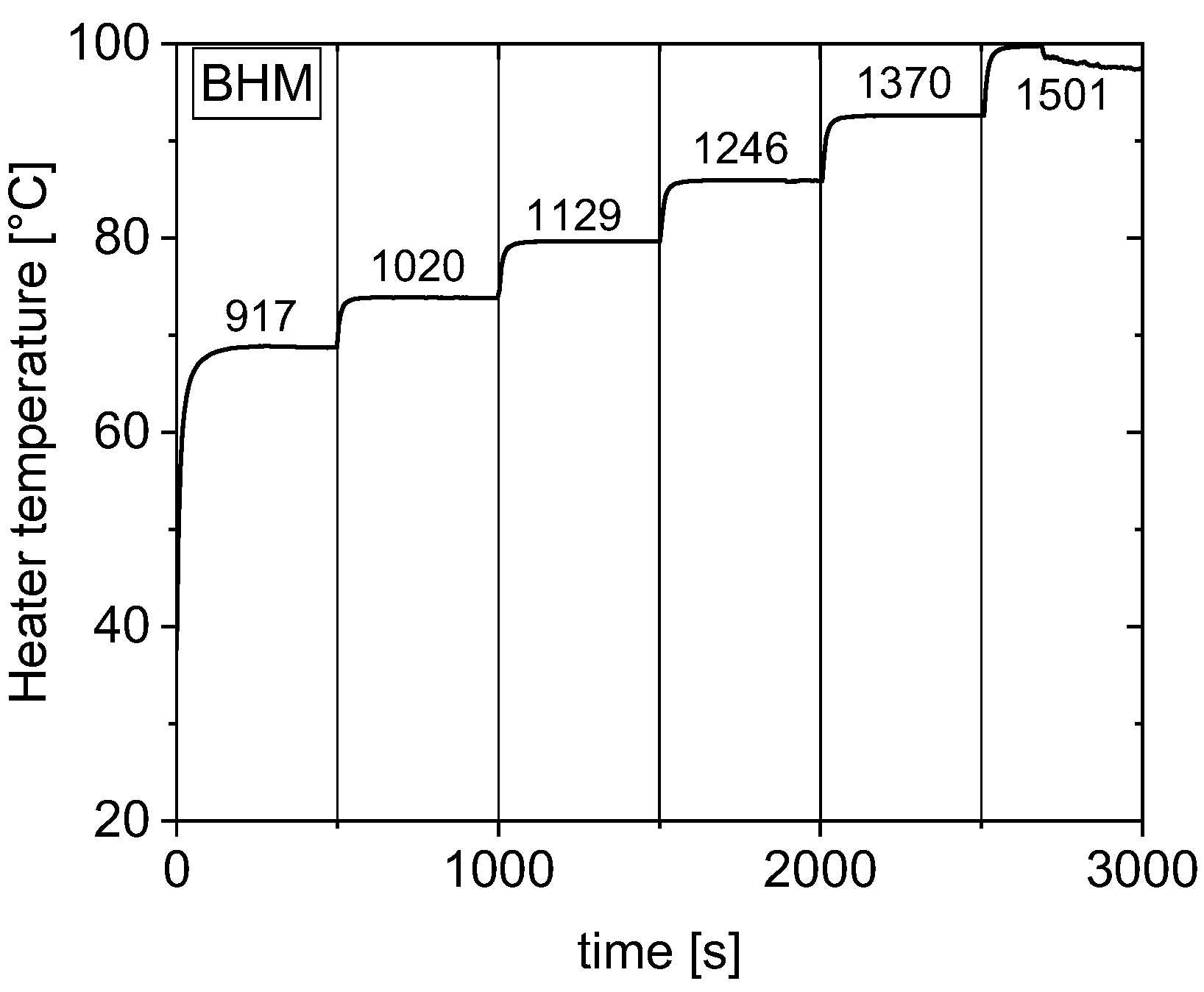
2.2. Setup for Characterization of PHPs

Two basic characteristics define the heat transfer capabilities of a PHP: Firstly, the temperatures of the hot end $T_H$ that result at different heating powers $\dot{Q}$ and secondly, the thermal resistance.

$$R_{th}=\frac{\mathsf{\Delta }T}{\dot{Q}},$$

(1)

where $\mathsf{\Delta }T$ is the temperature difference measured along the heat flow at defined positions on the PHP with thermocouples.

The characterization of the PHPs with regard to these properties was performed with the setup shown in Figure 2a. The shown test bench can be aligned in different orientations with regard to gravity. In this work, the orientation BHM corresponds to the vertical orientation where the heater is at the bottom (in angular notation, +90°), HHM is the horizontal orientation (0°), and THM is the vertical orientation where the heater is at the top (−90°). As a heat source, a ceramic heater with a length of 59 mm, i.e., dimensions of 59 × 74 x 6 mm³ (Si₃N₄, Bach Resistor Ceramics GmbH, Werneuchen, Germany), was used. Below the heater, a copper plate with dimensions of 60 × 100 × 6 mm³ was placed to spread the heat of the ceramic heater evenly (due to its internal heating structure, the temperature distribution along the heater is not perfectly homogeneous). The stack of heaters and copper plates was pressed onto the PHP by a clamp that consists of a screw head, spring, metal rod, metal bar, and a block composed of polyetheretherketone (PEEK). The clamp had a second PEEK block at the condenser zone to evenly apply pressure along the PHP. The contact with the water cooler at the condenser zone of the PHP was established using a copper plate with a width of 100 mm (same as the PHP), a variable length of l, and a height of 6 mm. The variable length of this plate allowed for easily characterizing the PHP with different condenser area sizes. A PEEK spacer of the same height as the condenser copper plate was inserted under the heater to support the PHP. All PEEK blocks and the spacer were designed to minimize the contact area with the PHP to minimize parasitic heat flows. Cooling water with a constant temperature of 20 °C was provided by a circulating chiller (Unichiller 055Tw-H6-spez, Peter Huber Kältemaschinenbau SE, Offenburg, Germany). The heat transfer coefficient achieved by the water cooler was determined to be approximately 5000 W/(m²K). Thermal paste (ARCTIC MX4, ARCTIC GmbH, Braunschweig, Germany) was applied to the interfaces of the heat-carrying parts between the heater, copper plates, the PHP, and the water cooler. The whole setup was insulated by elastomeric foam (AF/Armaflex, Armacell GmbH, Münster, Germany).

A power supply (Elektro-Automatik EA-PS 9360-40, EA Elektro-Automatik, Viersen, Germany) was used to generate defined electrical powers $P_{el}$ for the heater. The applied heating current was provided by the power supply directly, while the voltage was measured by a digital multimeter (Keithley 2700, Keithley Instruments, Solon, OH, USA). According to the data sheets of the mentioned devices, the resulting uncertainty of $P_{el}$ is approximately 0.2%. For the current setup, parasitic heat flows due to thermal radiation, convection, and conduction through the Teflon spacers were estimated to be significantly lower than 10% of the total heat flow. Consequently, it was assumed that the electrical power applied to the heater corresponds to the heat flow through the PHP, i.e., $\dot{Q}\simeq P_{el}$, and the reported values for $\dot{Q}$ (e.g., in data plots) represent the electrical heating power. For the measurement of temperatures, different types of thermocouples were used, and for the determination of the thermal resistance, the actual temperature was acquired by averaging the measured thermocouple temperatures over approximately one minute after temperature equilibration. A sheathed thermocouple was inserted into the heater (insertion depth of 5 mm) to measure the heater temperature $T_H$. The uncertainty $\sigma \left(T_H\right)$ on $T_H$ corresponds to the specified uncertainty for tolerance class 1 type K thermocouples of approximately 1.5 K. The working fluid acetone exhibits a substantial vapor pressure of 3.7 bar at 100 °C and 10 bar at 143 °C [16]. The maximum pressure that the bonding of the copper half-plates can withstand was not clear, and thus, due to safety reasons, a maximum heater temperature of 100 °C was set for the experiments, and the experiment was automatically stopped when the temperature of the heater exceeded this temperature. Furthermore, the temperatures on the PHP surface were measured by fine wire thermocouples type K (TC Mess- and Regeltechnik GmbH, Mönchengladbach, Germany, wire diameter of 80 µm and PFA insulation). A total of 12 thermocouples (Figure 2b, $T_i$ numbered with i = 1–12) were used. The thermocouples were arranged in two lines parallel to the longitudinal axis of the PHP. We note that close attention was paid to the exact placement of the thermocouples in well-defined locations (i.e., the same location for each PHP/copper plate and each comparable test run) to obtain reproducible results. For this, an identical “placement grid” was drawn on each sample using a laser engraver before the thermocouples were attached. The uncertainty of the thermocouple placement was approximately 0.5 mm. For the characterization of the PHP, the most significant temperature distribution is in the adiabatic zone between the heater and condenser. For a condenser plate length of 38 mm, the six thermocouples 4, 5, 6 and 10, 11, 12 were in the adiabatic zone, yielding four temperature differences between neighboring thermocouples $\mathsf{\Delta }{T}_{i-j}$: $\mathsf{\Delta }{T}_{5-4}$, $\mathsf{\Delta }{T}_{6-5}$, $\mathsf{\Delta }{T}_{11-10}$ and $\mathsf{\Delta }{T}_{12-11}$. These temperature differences were averaged to yield the average $\overline{\mathsf{\Delta }{T}_{ad}}$ in the adiabatic zone: $\overline{\mathsf{\Delta }{T}_{ad}}=\frac{1}{4}(\mathsf{\Delta }{T}_{5-4}+\mathsf{\Delta }{T}_{6-5}+\mathsf{\Delta }{T}_{11-10}+\mathsf{\Delta }{T}_{12-11}$). Using this, the thermal resistance in the adiabatic zone is given by:

$$R_{th-ad}=\frac{\overline{\mathsf{\Delta }{T}_{ad}}}{\dot{Q}}.$$

(2)

The uncertainty on $R_{th-ad}$ is assumed to be dominated by the uncertainty $\sigma \left(\overline{\mathsf{\Delta }{T}_{ad}}\right)$ on the measured and averaged temperature difference $\overline{\mathsf{\Delta }{T}_{ad}}$. This means that the relative uncertainty on $R_{th-ad}$ corresponds to the relative uncertainty $\frac{\sigma \left(\overline{\mathsf{\Delta }{T}_{ad}}\right)}{\overline{\mathsf{\Delta }{T}_{ad}}}$ on $\overline{\mathsf{\Delta }{T}_{ad}}$. Here, $\sigma \left(\overline{\mathsf{\Delta }{T}_{ad}}\right)$ is the sample standard deviation divided by the square root of the number of measurements, i.e., $\sigma \left(\overline{\mathsf{\Delta }{T}_{ad}}\right)=\frac{1}{\sqrt{N}}\sqrt{\frac{\sum {\left({∆T}_{i-j}-\overline{\mathsf{\Delta }{T}_{ad}}\right)}^2}{N-1}}$. Here, $N=4$ and the summation is carried out over the above-mentioned $\mathsf{\Delta }{T}_{i-j}$ in the adiabatic zone.

The thermal resistance $R_{th-HC}=\mathsf{\Delta }{T}_{HC}/\dot{Q}$ was also considered, which is defined by the heating power $\dot{Q}$ and the temperature difference $\mathsf{\Delta }{T}_{HC}=T_H$ − $\overline{\mathsf{\Delta }{T}_c}$ between the heater and the average temperature of the condenser zone $\overline{\mathsf{\Delta }{T}_c}=\frac{1}{6}(T_1+T_2+T_3+T_7+T_8+T_9)$. The uncertainty on $\overline{\mathsf{\Delta }{T}_c}$ is again defined as the uncertainty in the mean, this time for the measured temperatures: $\sigma \left(\overline{\mathsf{\Delta }{T}_c}\right)=\frac{1}{\sqrt{N}}\sqrt{\frac{\sum {\left(T_i-\overline{\mathsf{\Delta }{T}_c}\right)}^2}{N-1}}$ with N = 6 and summation over the six thermocouples on the condenser zone. Then, the uncertainty $\sigma \left(\mathsf{\Delta }{T}_{HC}\right)$ on $\mathsf{\Delta }{T}_{HC}$ is given by $\sigma \left(\mathsf{\Delta }{T}_{HC}\right)=\sqrt{\sigma {\left(T_H\right)}^2+\sigma {\left(\overline{\mathsf{\Delta }{T}_c}\right)}^2}$. The uncertainty on $R_{th-HC}$ is assumed to be dominated by the uncertainty on $\mathsf{\Delta }{T}_{HC}$, meaning that the relative uncertainty on $R_{th-HC}$ corresponds to the relative uncertainty $\frac{\sigma \left(\mathsf{\Delta }{T}_{HC}\right)}{\mathsf{\Delta }{T}_{HC}}$ on $\mathsf{\Delta }{T}_{HC}$.

In addition to the properties obtained for the PHP, the respective plots also contain measured values of $R_{th-ad}$ and $T_H$ for a solid full copper plate of the same dimension as the examined PHP, i.e., 125 × 100 × 6 mm³. The same setup was used for PHP and copper plate.

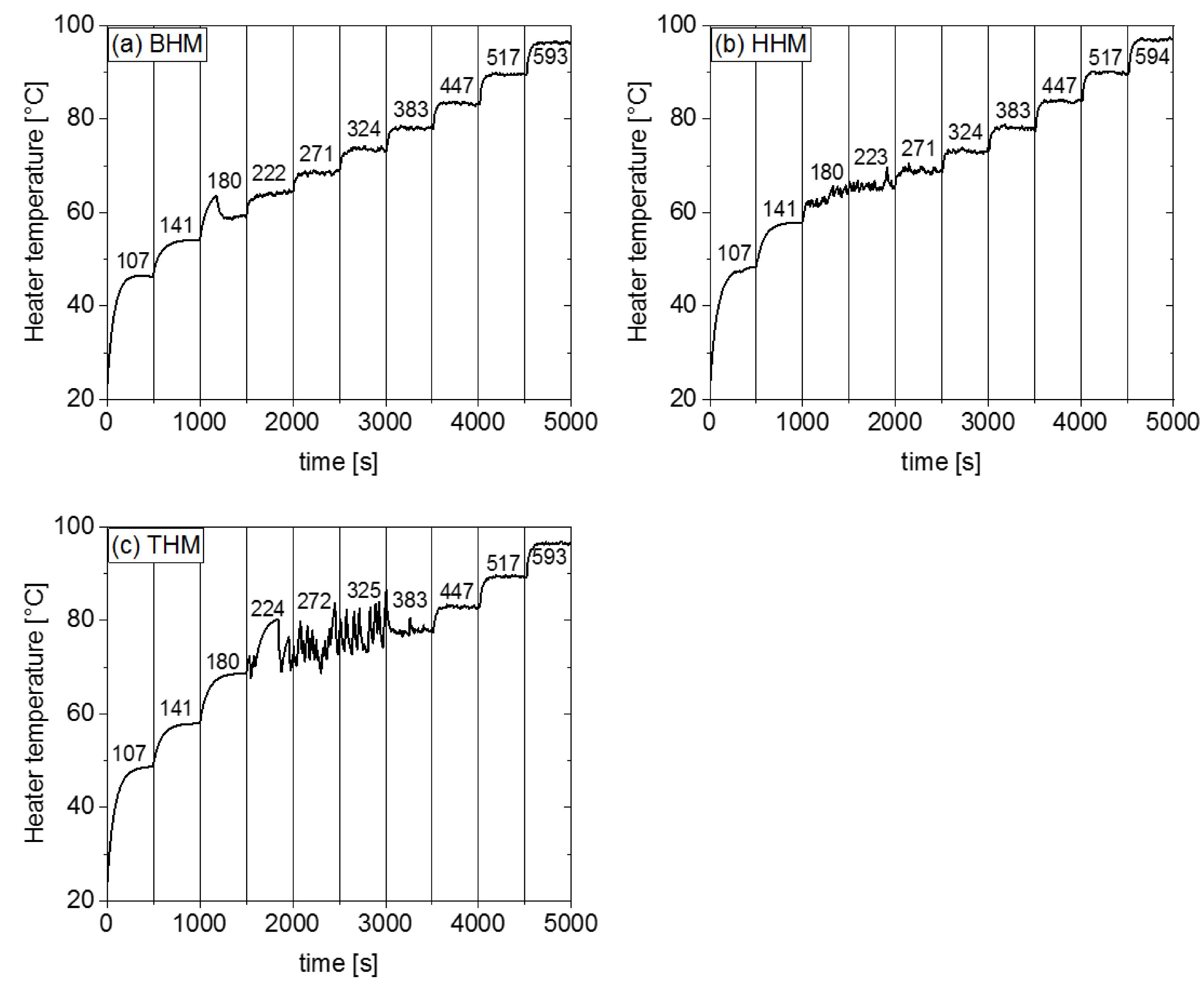
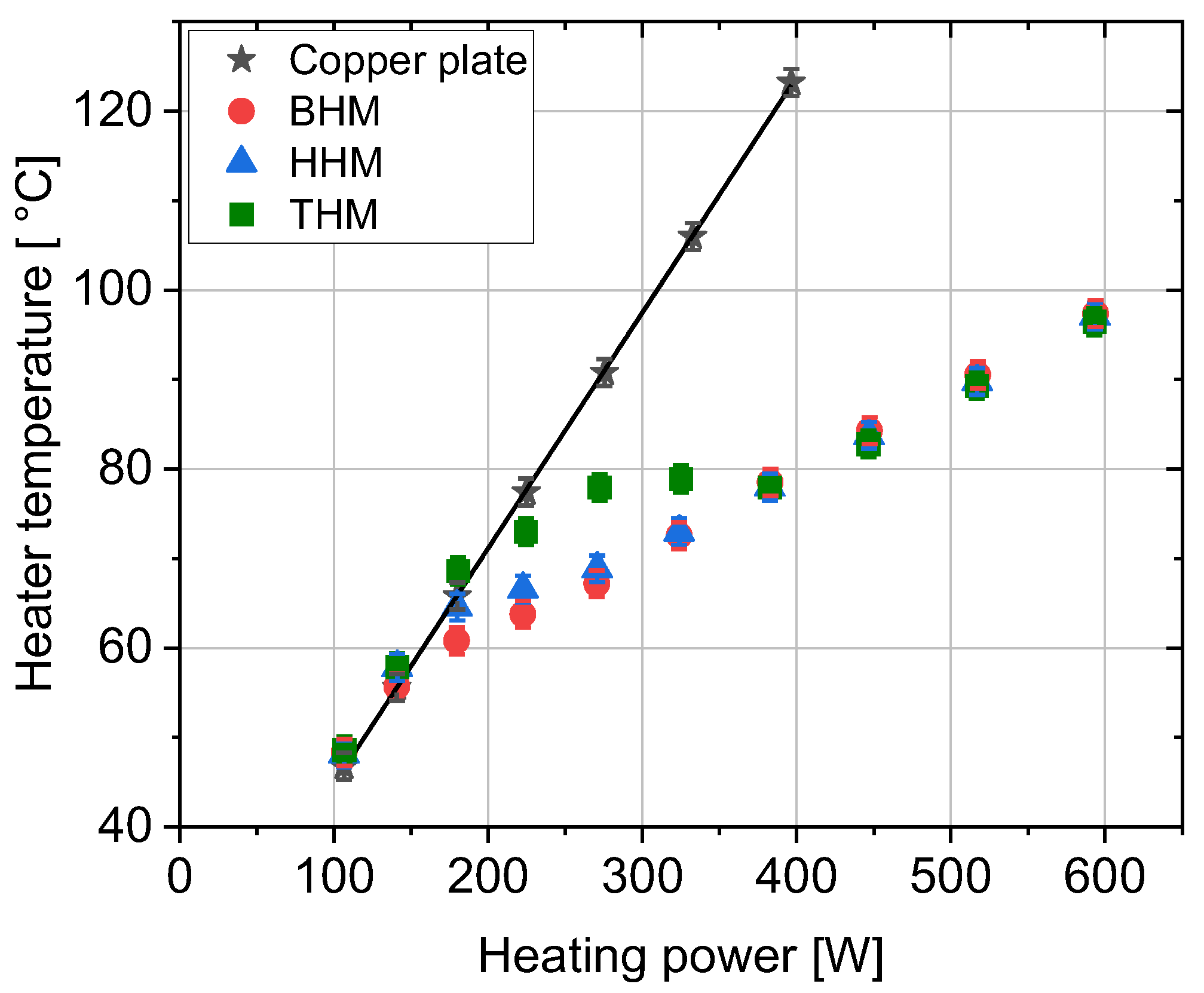
3. Results

The experimental results are structured as follows: Three different lengths of the condenser area (38 mm, 60 mm, and full PHP area) were examined, and the results for each length are shown in a separate section. For each length, three different orientations (BHM, HHM, and THM, as defined above) were tested, and the resulting heater temperatures are plotted as a function of time and heating power. For a condenser length of 38 mm, an adiabatic zone was present, and the thermal resistance $R_{th-ad}$ in the adiabatic zone vs. heating power was also determined.

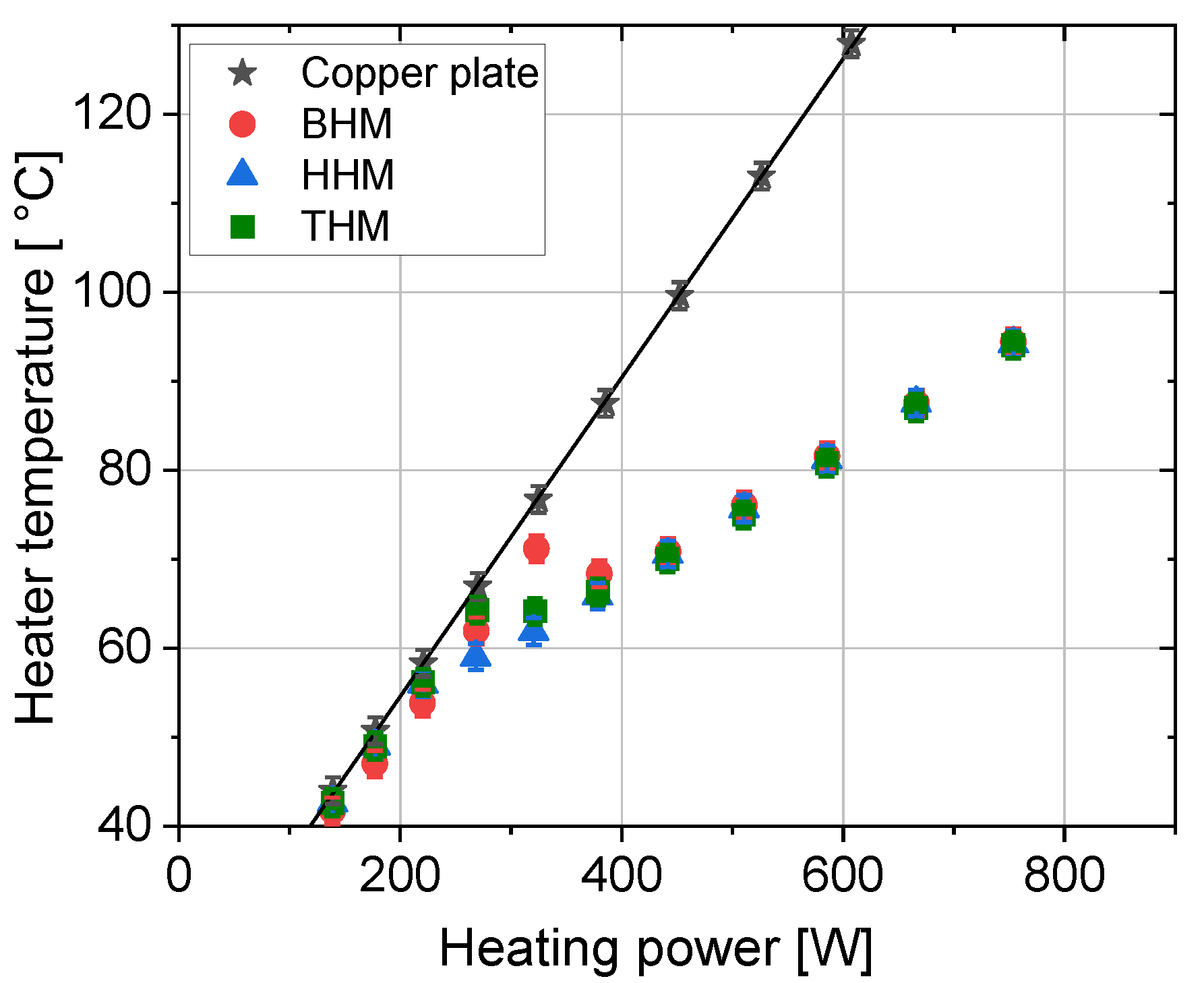
3.1. Condenser Area Length of 38 mm

The resulting heater temperature for different heating powers and a condenser length of 38 mm as a function of time is shown in Figure 3. In BHM orientation, the PHP activated when a power of 180 W was applied and at a heater temperature of 63 °C. The PHP started with full activity immediately, as indicated by the small amplitude of temperature oscillations and the even temperature profile. In HHM orientation, the PHP also activated at a power of 180 W and a heater temperature of 62 °C, with PHP activity not fully evident immediately, i.e., minor temperature spikes occurred at the first power levels after activation. At 324 W, the PHP was fully active, and the temperature profile was smooth. In THM, the first indications of PHP activity were evident when the power was raised to 224 W and at a heater temperature of approximately 70 °C. Then, fluid circulation in the PHP ceased for some time and recommenced at a heater temperature of 80 °C. As can be seen, the PHP was not yet fully active at this and the next two power levels. This was indicated by high-amplitude, low-frequency oscillations caused by the “stop and go” behavior of the liquid plugs and the associated heat transport. This behavior is typically observed during the startup phase of PHPs if the operating conditions are not yet ideal (see, e.g., [14,17,18]). At low heating powers, the governing fluidic processes inside the PHP (bubble growth and collapse, pressure gradient, etc.) that are the driving forces of fluid motion are not yet fully expressed and cannot permanently overcome flow resistance. This has the consequence that fluid motion starts, but soon ceases again due to flow resistance, which manifests itself in the mentioned low-frequency and high-intensity oscillations. Full activity without significant temperature spikes, i.e., sustained, smooth, and constant fluid motion, was observed at a power level of 383 W. For all orientations, including THM, no indications of dryout were evident, even at high heating powers.

The heater temperature and the thermal resistance $R_{th-ad}$ in the adiabatic zone for all orientations and in dependence on heating power are shown in Figure 4 and Figure 5. For comparison, heater temperatures and $R_{th-ad}$ for a copper plate with the same dimensions as the PHP are shown as well. As soon as the PHP activated, the heater temperatures and thermal resistances were clearly lower compared to the copper plate. Note that at 383 W and above, the PHP yielded nearly the same performance in all orientations, even in THM. It is expected that even at the maximum heat load of approximately 600 W in this experiment, the PHP will still be well below the upper limit before dryout occurs: The overall trend in thermal resistance of any heat pipe is characterized by a first phase where the thermal resistance decreases with increasing heating power due to higher fluidic activity until a plateau is reached. When the limits of a heat pipe defined by a dryout condition (based on the used working fluid and the filling ratio) are reached, the thermal resistance rises again, and the heater temperature starts to “run away.” Particularly PHPs with insufficient filling ratios are prone to this phenomenon, see, e.g., [9,19].

Similar to the heater temperature, the total thermal resistances $R_{th-HC}$ from the heater to the condenser zone at the maximum heat power of 593–594 W are nearly identical at all orientations. They are 0.092 ± 0.003 K/W for BHM, 0.091 ± 0.003 K/W for HHM, and 0.091 ± 0.003 K/W for THM, respectively.

The temperatures measured by the thermocouples 1–6 arranged in a line parallel to the longitudinal axis of the PHP, together with the heater temperature, are illustrated in Figure 6. The temperature differences $\mathsf{\Delta }{T}_{6-5}$ and $\mathsf{\Delta }{T}_{5-4}$ are nearly equal, indicating one-dimensional heat flow in the adiabatic zone. Therefore, the thermal resistance $R_{th-ad}$ in the adiabatic zone has a simple relation to the effective thermal conductivity ${\lambda }_{eff}$, the distance $d$ of 10 mm between the thermocouples, and the PHP cross-section $A$ of 600 mm²:

$$R_{th-ad}=\frac{d}{{\lambda }_{eff}\cdot A}\to {\lambda }_{eff}=\frac{d}{R_{th-ad}\cdot A}$$

(3)

For a heating power of 593 W, a $R_{th-ad}$ of 0.0138 ± 0.0005 K/W results (Figure 5), yielding a ${\lambda }_{eff}$ of approximately 1200 W/mK, which is three times the thermal conductivity of pure copper (CW008A, 394 W/mK [20]). It is noted that this value is not at the upper end of effective thermal conductivities reported up to now. For example, a value of up to 2300 W/mK [13] was reported for a conventional copper/acetone flat-plate PHP with a dimension of 100 × 50 × 2.5 mm³, another reference [9] mentions values of up to 10,000 W/mK and with special three-dimensional channel designs in a copper PHP, up to 33,170 W/mK were reported [21]. Other factors influence the obtained effective thermal conductivity as well, besides the actual fluidic activity. Heat transport takes place not only by fluid activity but also by heat conduction through the solid material surrounding the fluid volume. Typically, this corresponds to an arrangement of the thermal resistances of fluidic heat transport and heat conduction through the solid material in series (“cross-plane” heat transport into and out of the fluid channels at the evaporator and condenser) as well as in parallel (“in-plane” heat flow parallel to the fluid channels). The smaller the fluid volume compared to the surrounding volume of the solid, the more the effective thermal resistance of the whole heat pipe approaches that of the solid material. In the design used in this work, the fluid channels have a small height of 1 mm compared to the total thickness of the PHP of 6 mm, and therefore the effective thermal conductivity of the entire PHP is not much higher than that of pure copper.

3.2. Condenser Area Length of 60 mm

The resulting heater temperature in relation to time for different applied heating powers and a condenser length of 60 mm is shown in Figure 7. The behavior is qualitatively similar to the experiments with a condenser length of 38 mm. In BHM, the PHP activated when a power of 378 W was applied and at a heater temperature of 79 °C. The PHP immediately worked with full activity, as indicated by the small amplitude of temperature oscillations and the even temperature profile. In HHM, the PHP also activated at a power of 221 W and a heater temperature of 57 °C, with PHP activity not immediately fully evident, i.e., minor temperature spikes at the first power levels after activation. At 378 W, the PHP was fully active, and the temperature profile was smooth. In THM, the first indications of PHP activity were evident when the power was raised to 322 W and at a heater temperature of ca. 66 °C. The PHP activity was incomplete at this power level, as indicated by oscillations with a large amplitude and low frequency. Full activation was observed at a power level of 441 W. For all orientations, including THM, no indications of dryout were evident, even at high heating powers.

The recorded heater temperatures in relation to heating power for all orientations are shown in Figure 8. For comparison, heater temperatures are also given for a copper plate with the same dimensions as the PHP. As soon as the PHP was activated, the heater temperatures and thermal resistances were significantly lower compared to the copper plate. Note that at 322 W and higher heat powers, the PHP yielded a performance in THM that is on par with BHM and HHM.

The thermal resistance $R_{th-ad}$ in the adiabatic zone is not shown here since there is no adiabatic zone with this condenser length. Instead, $R_{th-HC}$ is given below in Figure 9. Even at the maximum heat load of approximately 750 W in this experiment, the PHP was still well below the upper limit before dryout occurred. Similar to the heater temperature, the total thermal resistances $R_{th-HC}$ from the heater to the condenser zone at the maximum heat power of 754 W are nearly identical for all orientations. They are 0.074 ± 0.002 K/W for BHM, 0.074 ± 0.002 K/W for HHM, and 0.074 ± 0.002 K/W for THM, respectively.

3.3. Condenser Length Corresponding to Full PHP Length

For another experiment, the PHP was placed directly on the water cooler without the copper plate (see Figure 2), and thus the whole backside was in contact with the cooler. The condenser length was therefore equal to the total length of the heat pipe. In this configuration, the PHP was unable to start within the experimental range of investigated power and heater temperatures. Only at the highest power level, a very slight temperature drop and weak oscillations were evident (Figure 10). This behavior was not reproducible, i.e., the mentioned temperature drop was not evident in subsequent measurements, and the PHP exhibited no sign of operation. It is assumed that with a condenser area size as large as the full PHP, the suitable range of condenser areas was exceeded. This aspect is discussed in detail in Section 4.2, below.

4. Discussion

4.1. PHP Operation in Different Orientations: BHM, HHM, and THM

Based on many experiments with PHPs in different orientations, Marengo et al. conclude that “a standard capillary or flat-plate PHP has very poor performance in top heat mode”. However, optimizing certain parameters can actually improve performance in anti-gravity orientation [9]. A major parameter that defines gravity dependence is the number of turns. To provide an overview of the correlation between performance in different orientations and the number of turns, selected results from the literature are summarized in

Table 1. Comparison of obtained thermal resistance in different orientations for PHPs with different working fluids and channel diameters. BHM, HHM, and THM as defined in Section 2.2. Only flat-plate PHPs with conventional two-dimensional channel layouts are considered. The thermal resistance is given at or near the highest tested common heating power ${\dot{Q}}_{max}$ for all orientations. Since the determination of the thermal resistance is based on different methods, temperature measurements, locations etc., it is not directly comparable across different publications.

Author	PHP Size [mm]	Nr. of Turns	${\mathit{d}}_{\mathit{i}}$[mm] a	${\dot{\mathit{Q}}}_{\mathit{m}\mathit{a}\mathit{x}}$ [W]	Fluid	Mode	Thermal Resistance [K/W] b	Ref.
Winkler	125 × 100 × 6	27	1	754	Acetone	BHM	0.074 c	this work
						HHM	0.074 c
						THM	0.074 c
Yang d	180 × 120 × 3	33	1	100	Ethanol	BHM	0.63	[10]
						HHM	0.70
						THM	0.90
Yang d	180 × 120 × 3	20	2	400	Ethanol	BHM	0.15	[10]
						HHM	0.17
						THM	0.19
Laun	300 × 300 × 6	20	1.3	550	Acetone	BHM	0.083	[22]
						HHM	0.091
						THM	0.101
Winkler	100 × 50 × 2.0	13	1	175	Acetone	BHM	0.077 e	[13]
						HHM	0.081 e
						THM	Not tested
Winkler	100 × 50 × 2.5	10	1.5	115	Acetone	BHM	0.057 e	[13]
						HHM	0.084 e
						THM	Not tested
Ayel	200 × 120 × 2	12	1.7	150	FC72	BHM	0.126	[23]
						HHM	0.237
						THM	Not tested
Groeneveld	200 × 50 × 3.5	6	2	100	Methanol	BHM	0.48	[24]
						HHM	No oper. f
						THM	Not tested
Wits g	200 × 50 × 3.5	6	2	100	Water	BHM	0.29	[25]
						HHM	No oper. f
						THM	Not tested
Wits g	200 × 50 × 3.5	6	2	100	Ammonia	BHM	0.15	[25]
						HHM	0.30
						THM	Not tested
Youn	50 × 15.5 × 1.5	5	0.57	100	Ethanol	BHM	524 b	[26]
						HHM	293 b
						THM	Not tested

Abbreviations and remarks: (a) hydraulic diameter, (b) all values given in K/W except for ref. [26]. In ref. [26], the thermal resistance is not reported. Instead, the effective thermal conductivity is given in units of W/mK. (c) Thermal resistance $R_{th-HC}$ from the heater to the condenser for a condenser length of 60 mm. (d) All data taken from Figure 10 in ref. [10]. Data for PHP with 20 turns are not given at the same maximum heat power. (e) Thermal resistance is based on measured temperature differences between neighboring thermocouples on the PHP (mainly in the adiabatic zone). We note that the thermal resistance from this work is not directly comparable to the other works, where the thermal resistance is based on the temperature difference between the heater and condenser. (f) PHP did not operate at all in this orientation. (g) Data for the working fluid methanol corresponds qualitatively to water and is thus not given here. Only the PHP variant with conventional channel design is considered here.

. Here, the discussion shall be focused on analogous conventional flat-plate PHPs. Special forms like capillary PHPs, hybrid PHPs, and PHPs with alternating channel structures, or PHPs with 3D-channel structures, etc., are not listed. The table aims to compare the thermal resistances obtained in the same work for the same PHP in different orientations. Since the determination of the thermal resistance is based on different temperature measurement locations, etc., its absolute value often cannot be compared directly across different publications, and such a comparison is not the aim of Table 1.

Across different working fluids and different channel geometries, there is an evident trend between the number of channels and the performance in HHM and THM. As also evident from a recent review article [27], the PHPs with the highest number of turns (above 20) not only perform similarly well in BHM and HHM but also exhibit similar thermal resistances in THM compared to the other orientations. Among the PHPs with a two-dimensional channel layout that achieved almost equal performance (i.e., resulting heater temperature and thermal resistance) in all orientations, the PHP presented in this work has the smallest cross-section area of 6 cm². Simultaneously, with 750 W, the heating power up to which gravity-independent performance was reported is the highest among all conventional flat-plate PHPs (note that the highest applied heating power given in the mentioned review article is 500 W, see Table A1 in [27].) The obtained thermal resistance is very low compared to other publications, particularly in HHM and THM. The close arrangement of the channels and the absence of significant areas without channels result in a remarkably high thermal power density (relative to the PHP cross-section area) of 126 W/cm². This is higher compared to the PHP designs presented in ref. [10] with 28 and 111 W/cm² and ref. [22] with 31 W/cm² (see also Table 1).

On the other end of the spectrum, the PHPs with the lowest numbers of turns (below 10) exhibit significantly higher thermal resistance in HHM compared to BHM or do not even operate at all in HHM. A successful operation of these PHPs in THM was not shown and is very unlikely. Altogether, the critical number of turns above which an effective operation in HHM is possible seems to be in the range of 10–15 for flat-plate PHPs. This corresponds to the observation by Charoensawan et al. on capillary PHPs that, for an operation in horizontal orientation, the minimum required number of turns is between 11 and 16 [28].

It is noted that gravity-independent performance has also been achieved with other types of PHPs. For example, Lips et al. presented capillary tube PHPs with a large number of turns of 40 and 20 with an inner tube diameter of 1.2 mm and 2.5 mm and water and acetone as working fluid, respectively, and a filling ratio of 50% for both PHPs [29]. Moreover, Thompson et al. examined a flat-plate PHP with a three-dimensional channel layout, a hydraulic diameter of 0.76 mm, acetone as a working fluid, and a filling ratio of 72% [5]. Gravity up to 10 g was added unfavorably (i.e., as a “worst-case scenario” as to challenge the return of liquid to the evaporator during hypergravity loading). The PHP thermal resistance remained nearly independent of gravity and even slightly decreased at 10 g. A novel “hybrid” type of PHP was presented in ref. [30]. In this PHP, the meandering channel (hydraulic diameter of 0.79 mm, acetone and water as a working fluid with filling ratios between 28 and 82%) was formed entirely by a wicking structure instead of the usual solid walls. Even with a low number of turns, only seven in this case, the PHP was operating in THM orientation.

4.2. Effect of Condenser Length

It is known that, among other geometrical parameters, the condenser section length has a rather intricate and not well-understood effect on the PHP behavior [9]. The experimental results shown in this work will be discussed in this section regarding previously published results.

As a rule of thumb, “the condenser area should be larger than the evaporator area to ensure normal operating conditions”, especially for high thermal loads at the evaporator [9]. Typically, in an application, the heat transfer coefficient of a cooling system (water or air cooling) is approximately known. When the application allows that the size of the condenser area can be chosen freely to some extent, the first idea is often to maximize it as far as possible to minimize thermal resistance for the heat transfer from the PHP to the cooling system. Moreover, a very small condenser zone increases the probability of dryout. In our previous work, a PHP in HHM orientation with a surface area of 100 × 50 mm², a channel cross-section of 1.5 × 1.5 mm² and a heater length of 25 mm exhibited dryout already at a heat power of approximately 70 W when the condenser length was 10 mm [13]. Scaling up the condenser zone significantly increased the maximum possible heat load. When the condenser length was scaled up to 50 mm (meaning a length ratio of the evaporator to the condenser of 1:2), no dryout occurred for the entire range of applied thermal power up to circa 300 W. It was concluded that a larger condenser area enhances condensation processes in this area, increasing the probability of liquid formation (enough liquid in the evaporator zone is required to sustain PHP operation).

However, as shown in refs. [31,32], choosing a too-large condenser zone can have a negative impact on PHP operation. The authors of ref. [31] used computational fluid dynamics (CFD) to examine the influence of the length ratio of the evaporator to the condenser on the startup and thermal performance of a single-loop PHP. Length ratios of the evaporator to the condenser of up to 1:1.4 were evaluated. It was concluded that a shorter condenser zone leads to the “hot working fluid´s greater probability of flowing from the evaporator to the condenser. The shorter condenser is helpful to accelerate the start-up of […] PHPs” [31]. Conversely, this means that a large condenser zone significantly increases a PHPs starting time for the same heat load. Extrapolating this behavior, it can be concluded that for very large condensers, a PHPs startup is so severely affected that fluid motion in the PHP does not even start at all in the power range studied, as shown by our experiments above.

Ref. [32] presents experiments pointing in the same direction, i.e., tests of a micro PHP with ten turns and very small length ratios of evaporator to condenser of up to 1:2.5 In this work, the focus was more on the thermal properties of the PHP during operation rather than startup behavior. At constant condenser temperature and up to an optimum length, the evaporator temperature and thermal resistance decreased with increasing condenser length. However, a too-large increase in condenser length resulted in a drastic increase in evaporator temperature and PHP thermal resistance. This was related to the fact that liquid slug displacements decreased when the condenser length exceeded the optimum length and, consequently, insufficient liquid supply to the evaporator, resulting in a partial dryout. With reference to our case, it is likely that the reduced displacement of the liquid slugs also impacts the startup, i.e., it has a delaying effect. Furthermore, in ref. [32] publication, contour maps are given, separating the stable operation range from the unfavorable “dryout” range that occurs for low evaporator to condenser length ratios. In our tests, the heater temperature did not increase when increasing the condenser length from 38 mm to 60 mm. We conclude that 60 mm of condenser length still yields a length ratio that is outside of the “dryout” range where PHP performance deteriorates, but a condenser length of 120 leads to a length ratio within the dryout range. We assume that the ideal condenser length in our case is somewhere between 60 and 120 mm. Another factor is also important in this discussion: With the full back side of the PHP in contact with the water cooler, there is a large direct “cross-plane” heat flow from the heater to the cooler across the PHP height of 6 mm. Consequently, the fluid directly below the heater will effectively reach a much lower temperature and vapor pressure at the same heating power than for the other condenser lengths, where there is no direct thermal path between the heater and the cooler. This will lead to a low vapor pressure difference between the evaporator and the condenser, providing insufficient kinetic energy to start the oscillating motion. We note that Laun et al. performed an analogous experiment using a different PHP configuration with a central heater on the top side of the PHP (i.e., a heat spreader configuration) and the bottom side in full contact with a water cooler [33]. Here, the required startup power was much higher compared to a configuration where the direct cross-plane heat flow from the heater to the cooler was prevented by adding a central hole to the spacer plate connecting PHP and the water cooler. Finally, we note that experiments on capillary PHPs indicate that also the number of turns has an influence on the ideal condenser length [34]. For large condenser lengths, the PHP thermal resistance decreased monotonically with an increasing number of turns, while for a small condenser length, the thermal resistance decreased with an increasing turn number of up to nine. With ten turns, the thermal resistance increased again.

5. Conclusions

In this work, a flat-plate PHP with conventional channel layout is presented whose design is optimized for operation in all orientations, i.e., independent of gravity.

The PHP performance was evaluated for the full spectrum of orientations: the top heat mode (THM) and bottom heat mode (BHM), where the PHP is arranged vertically and the heater is at the top and bottom, respectively, and the horizontal heat mode (HHM), where the PHP is arranged horizontally. The results were discussed with regard to previously published work on PHPs of different sizes, working fluids, and numbers of turns. It became clear once again that the key to high performance in all orientations is a high number of channels. Consistent with this design paradigm, the fabricated PHP was able to transmit a heating power of up to circa 750 W in all orientations without the heater exceeding a temperature of 100 °C. No dryout phenomena were observed, indicating that the maximum heating power the PHP can handle is even higher than the maximum power applied in this work. Compared to previously published reports on PHPs, the PHP from this work attained the highest reported heating power (as well as the highest heat power density per PHP cross section) that could be carried out equally for all orientations, including THM.

Furthermore, the PHP was tested with different condenser areas, and the obtained numbers were compared to previously reported results. Consistent with these results, it was found that there is a certain suitable range for the size of the condenser zone and that problems occur if the condenser zone size falls out of this range. If the condenser area is too small, liquid formation at the condenser will be impaired, the evaporator will run out of liquid, and the PHP will no longer be functional. On the other hand, a large condenser area is suspected of leading to a reduction in liquid slug displacement, causing an insufficient liquid supply to the evaporator, and stalling PHP operation. It is assumed that this was also the case in this work in a configuration where the condenser area spanned the entire PHP length and PHP operation was not observed during the tested heating power range.

In our opinion and as an outlook, the next steps to be addressed are:

• In this work, the maximum heater temperature was limited to 100 °C due to safety reasons (avoiding excessive vapor pressure of the working fluid, which might damage the PHP). The next step is to go above this temperature limit and explore the limits of heat that can be dissipated with the presented PHP (indicated by the appearance of dryout phenomena and a stagnation of fluid motion).
• If the PHP fails during these tests, a failure analysis must be carried out, and the stability of the bonding must be improved.
• General tests on the stability of the PHPs against aging and temperature effects.