Abstract
One test rig comprising two blades and dual under-platform dampers (UPDs) was built to enhance the understanding of the dynamic response behavior of blades with dual UPDs. A turnbuckle was applied to enable the smooth and uninterrupted linear adjustment of the normal load on the dual UPDs. Non-contact vibration-response measurements were achieved through eddy-current displacement sensors. Contact excitation was employed using an electromagnetic exciter to determine the magnitude of the excitation load, which was measured using a force sensor mounted on the excitation rod. A feedback system was established to maintain a constant magnitude of the excitation force throughout the excitation process. The chosen experimental variables include the normal load, the amplitude of the excitation force, the effective contact area, and the position of the damper action. The frequency response function of the blade under various experimental parameters was obtained through frequency sweeping under sinusoidal excitation. The influence of each parameter on the dynamic characteristics of blades was studied. The results demonstrate that the double-layer damping system offers distinct advantages over its single-layer counterpart. The upper damping has a wider frequency-adjustment range and a lower resonance amplitude and takes a larger share of the damping efficiency.
1. Introduction
During the operation of a gas turbine, its blades are always excited in a wide frequency range by the airflow. Resonance occurs when the natural frequency coincides with the harmonic excitation induced by the passing airflow as well as the upstream stators and rotors. Consequently, this often leads to high-cycle fatigue of the blades, which is almost impossible to avoid completely. The vibration energy can be dissipated by increasing the damping. The first method is material damping, which involves the natural characteristics of the material; the materials used in modern aero engines have low damping and weak vibration attenuation [1,2]. The second method is dry friction damping, which has several advantages and is widely used to reduce vibration and increase the high-cycle fatigue life of blades. The friction forces will dissipate vibrational energy when relative motion occurs between frictional contact surfaces, and consequently, the system’s dynamic response and vibratory stress will decrease. Dry friction dampers now have widespread usage in mitigating vibrations in the turbine blades and have taken various forms, such as under-platform dampers (UPDs), shrouds, lockplates, and others [3,4,5,6,7]. Among these, UPDs, as a passively controlled system [8], are extensively employed in turbine designs due to their non-interference with airfoils or airflow passages, as well as their relatively minimal additional centrifugal load.
Various UPD friction contact models, including one-dimensional, two-dimensional, and three-dimensional approaches, have been proposed in prior studies to explore the contact kinematics at the interface. The non-linear response of frictionally constrained blade systems was investigated according to this friction contact model [9,10,11,12,13]. In order to enhance the efficiency of calculating non-linear responses, an analytical Jacobian matrix solution method for frictional contact models has been developed [14,15]. Additionally, a model-reduction technique for high-fidelity finite element models has been developed to reduce the degree of freedom of the solutions [16,17]. However, several key parameters, such as contact stiffness and the friction coefficient, undergo time-varying changes throughout the vibration cycles. A comprehensive theoretical framework capable of precisely describing all these parameters was lacking, rendering the accurate prediction of non-linear responses and the evaluation of the damping efficacy in blades equipped with dry friction dampers challenging. Therefore, experimental results have been widely used to verify and correct these paraments. Koh et al. [18] conducted measurements on the response of a damper with a spherical head and extracted hysteresis curves. These curves were subsequently utilized to derive dimensionless stiffness and damping profiles. Sanliturk et al. [19] applied centrifugal force on a simple damper between two blades by pulling a heavy object through a wire. The vibration characteristics of the blade under different centrifugal forces were studied, and theoretical models were developed to predict the response. Pesaresi et al. [20] measured the dynamic response of the test rig with two blades and a wedge damper. Their research shows that there are two modal shapes in the blade system: the so-called “in-phase” modal shape and the “out-of-phase” modal shape. The damper also has two motions that are dependent on the modal shape: translation and rotation. Firrone et al. [21] investigated the impact of the varying centrifugal forces of dampers on damping effectiveness using a test rig comprising two actual turbine blades and an asymmetric UPD. They machined the UPD to have a given curvature radius in order to obtain line contact with the platform, as this could ascertain the location of the application of the contact force at the contact surface. Zhang et al. [22] established a test rig with three flat blades and two UPDs that used preloaded springs to simulate the centrifugal force. They measured the dynamic response of the three-blade system while the dampers worked by employing different forms, weights, and materials. Then, the influence of these parameters was investigated. Ferhatoglu et al. [23] designed an experimental platform with one blade and two dampers. Through comprehensive measurements of the dynamic frictional contact forces in the time domain and the ensuing response characteristics in the frequency domain, they effectively unveiled and quantified the inherent uncertainty associated with frictional forces. Yuan et al. [24] further addressed the issue of non-uniqueness with respect to friction. They conducted experiments using the conventional two-blade test platform to measure the contact stiffness of the damping contact surface, consequently deriving the corresponding hysteresis curve. Employing statistical methods, they were able to establish an uncertainty band for the dynamic response of a turbine blade system equipped with dampers. Mehrdad et al. [25] established a blade test platform with the full set of dampers and measured the effect of a UPD on the dynamic response of the mistuned bladed disk. Based on the experimental results, a linearized hybrid model was proposed to simulate the effect of detuning on the forced response level. Hoffman et al. [26] measured the influence of asymmetric cylindrical dampers on the system based on a rotating experimental platform while also considering the impact of a mistuned bladed disk on the system results. Laxalda et al. [27] designed a rotating test bench to simulate the realistic working conditions of the damper. They simulated the excitation force by using a permanent magnet that was fixed onto the test rig. However, it is worth noting that the measurement of the vibration responses in this setup is more intricate. As a result, the non-rotating test rig with partial blade participation is more convenient and efficient for testing damping when compared to the rotating test rig.
The friction-damping structure mentioned in the references is only a single kind of friction interface, whether it is the UPD, shroud, or blade root contact. However, the comprehensive investigation of damping characteristics and system vibration behavior for the dual friction dampers, which is applied in engineering applications, remains conspicuously absent from the existing literature. Therefore, this paper aims to investigate the damping characteristics of dual UPDs in gas turbine blades under practical operating conditions. The objective is to establish a basic comprehension of the dynamic attributes associated with this particular damper configuration. To accomplish this objective, a test rig equipped with a closed-loop adjustment system for the excitation force was established. The test rig was utilized to analyze the vibration characteristics of a double-blade system with dual UPDs. Considering the difficulty of the experiment and the accuracy of the results, the actual blade was simplified, and the characteristic structure was retained. The effect of normal load, excitation force, effective contact area, and the action position of the UPDs on the vibration characteristics of the system was measured. Subsequently, the test results were analyzed and evaluated. In addition, some suggested guidelines for the design of dual UPDs are provided.
2. Introduction of the Experimental System
In an actual gas turbine, the UPD is generally placed at the platform between two adjacent blades. During the operation of a gas turbine, the damper exerts pressure on two platforms due to the centrifugal force produced during its rotation, resulting in the generation of a normal force between the contact surfaces. The complete layout of the test rig for blades equipped with UPDs is depicted in Figure 1. Tests involving two blades with a UPD pulled by a wire are not particularly new, as several researchers have used similar rigs in the past [13,28]. The novelty in this is that the tests use simulated components with dual UPD characteristics and can measure the damping effect at different blade neck lengths and different centrifugal force distributions. The experimental setup mainly includes the blades, dampers and their loading system, the excitation system, and the measurement system. In the experiment, the right blade is directly excited by an electromagnetic exciter, and the resulting vibration response is measured using eddy-current displacement sensors located on both sides. The primary components of the test rig are illustrated in Figure 2.
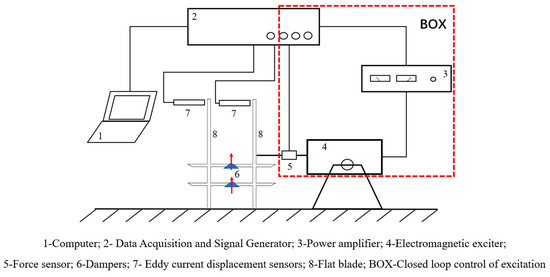
Figure 1.
Overall schematic diagram of test rig.

Figure 2.
Main components of test rig.
2.1. Introduction of Blade
Figure 3 shows the schematic of the dual friction damper structure of a gas turbine blade. It can be seen that this blade has a friction-damping device at the platform groove (position ①). When the blade rotates, the working surface of the damper makes contact with the platform, which results in a frictional damping effect and energy dissipation. Another friction-damping device was applied to position ② at the top of the blade root. The damping structure at this position not only serves as a damping device but also enables gas sealing, utilizing the sealing structure at the rear position.
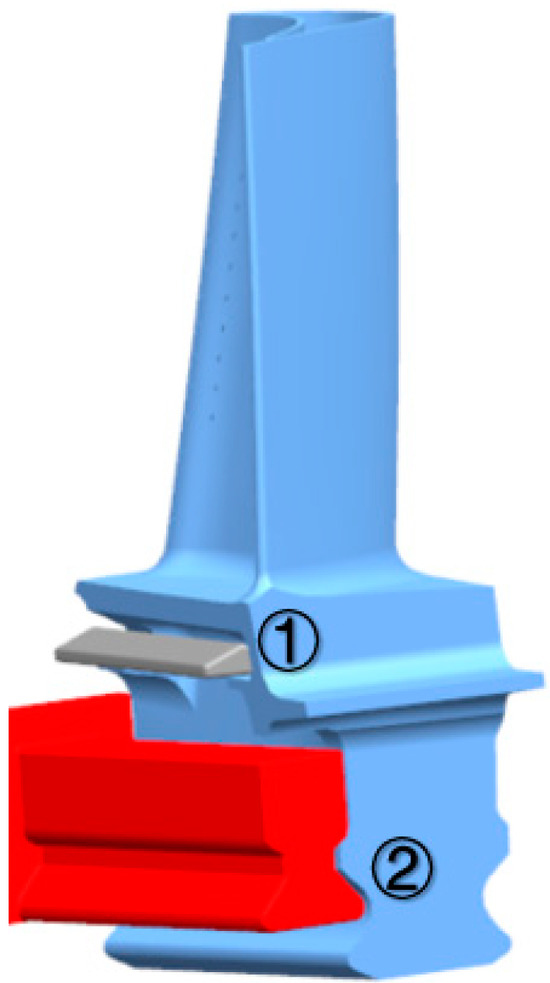
Figure 3.
Real blade structure model.
Using a real turbine blade structure model in the experimental process has some disadvantages, such as: the natural frequency of the first-order bending mode being too high, making it difficult to excite; the frictional damping effect generated when the tenon root position is installed, which is not easily eliminated; and the complex structure of the damping device, which makes it difficult to apply the centrifugal force. In order to avoid the adverse factors mentioned above, the real blade is simplified as an experiment blade, and parts that can easily highlight the structural features are processed, as shown in Figure 4. The experiment blade is made of steel. The upper damping (position ①) and the lower damping (position ②) are provided. In order to highlight the structural features and at the same time facilitate the control of experimental variables, the upper and lower platforms were designed in the same form. To avoid frictional self-locking as well as to observe the damping effect more clearly, the platform angle α was 45° in this experiment, as shown in Figure 4.
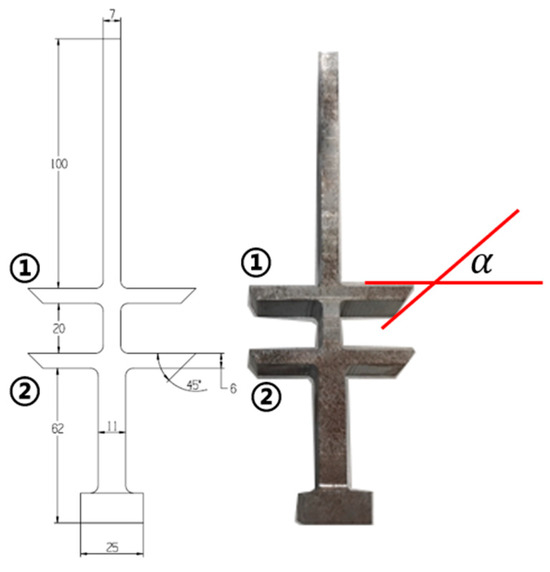
Figure 4.
Simulated blade and platform angle.
2.2. Loading of Centrifugal Load
In the experimental process, the normal load is applied, as shown in Figure 5. This loading method can ensure the stability of the normal load and facilitate its continuous adjustment. One end of the wire rope is wrapped around the bottom of the UPD, and the other end is connected to the tensiometer through the pulley device (the measurement accuracy of the tensiometer is ±0.5 N), and then connected to the other end of the tensiometer and the test rig through a turnbuckle. The normal load applied to the surface of the damper is varied by adjusting the degree of tightening of the turnbuckle, the magnitude of which is measured by a tensiometer. The upper and lower dampers are used in the same way for the application of normal load, as shown in Figure 6. Each UPD is pulled against the blade platforms by two wires. Two wires were chosen instead of one to distribute the load along the damper axis more uniformly. Moreover, the two wires were long enough to ensure flexibility.
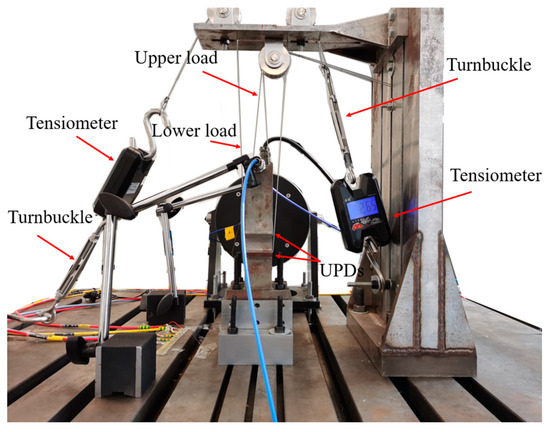
Figure 5.
Dual UPD centrifugal force loading.

Figure 6.
Schematic of wire rope installation.
2.3. Damper Specimens
Typical UPD structures can be categorized into sheet-type, prismatic-type, spring-type, and box-type designs [22,29,30,31]. Among them, prismatic dampers are generally used for the vibration damping of large-sized blades, such as those used in gas turbines. They can be designed with a larger mass to provide greater pressure and a dry friction damping effect, and the outer surface can produce contact with the blade platform at any position. In order to facilitate processing and installation, a semi-cylindrical damper was used in this experiment, as shown in Figure 7, and is made of steel. The dimensions are 40 mm in length, and two different radii, 5 mm (R5) and 7 mm (R7).

Figure 7.
Damper shape.
2.4. Excitation and Vibration-Response Measurement System
The blades can be excited using both contact and non-contact methods. When using non-contact excitation, there is no direct contact with the blade, avoiding the additional influence of the excitation system on the vibration characteristics of the blade. The magnitude of the excitation force is difficult, if not impossible, to directly measure. Therefore, an electromagnetic exciter was used for excitation in the experiment. The electromagnetic exciter is directly connected to the blade, and the magnitude of the excitation force is measured by a force sensor mounted on the top of the exciter. The signal generator sends out a sinusoidal signal, which is amplified by a power amplifier, and then drives the exciter to operate. The force sensor can measure the magnitude of the excitation force in real time and then feed the force signal back to the signal generator. Then, the signal generator adjusts the signal output to ensure that the exciter can output a constant amplitude of excitation force, as shown in the BOX in Figure 1, forming a closed loop. During the experiment, the interaction between the excitation rod and the excited blade will affect the natural characteristics of the blade through exerting additional stiffness and damping effects on the blade [22]. To mitigate this impact, the excitation rod is positioned in close proximity to the nodal line near the blade root.
The blade is made of steel, so the eddy current displacement sensor, as shown in Figure 8, is selected for measurement. The non-contact displacement sensor does not affect the vibration characteristics of the blade system, thus reducing the experimental errors. In this study, the influence of the damping effect can be reflected by the vibration response of the blades.

Figure 8.
Excitation and measurement systems.
2.5. Experimental Errors Analysis
In this research system, the factors that may cause errors are as follows:
Firstly, the form of normal load application causes the error. The wire rope is not equally applied to the surface of the damping device, nor is it completely vertical. In fact, there is a small angle in the vertical direction, but its angle is less than 3°. Therefore, the error of the normal load size caused by this part can be ignored.
Secondly, the reading, as well as the measurement system, causes random errors, which inevitably occur during the adjustment of the excitation force and the reading of the vibration displacement. In order to reduce the effect of this error, several repetitions of the experiment were performed. In addition, in order to avoid accidental errors in the loading of normal loads, the repeated experiments went through two loading paths, i.e., from small to large and from large to small. The results in the following paper are the average values of the two-loading path.
3. Experimental Contents and Experimental Processes
From the theory of harmonic response analysis, it is well known that for a blade with a fully constrained root, the first bending vibration mode has the largest vibration stress and displacement. Therefore, the purpose of the experiment is to excite the first bending mode of the blade and measure the damping effect of the damper during this phase.
3.1. Experimental Contents
Firstly, the natural characteristics of the experiment blade are measured. Secondly, the frequency response function (FRF) curves of the blade are measured when the blade is under different external excitations and the dampers are under different normal loads. Thirdly, the vibration characteristics of the system are measured for two different sizes of semi-cylindrical dampers. Finally, the dynamic response of the system is measured when both upper and lower dampers are used. The effects of different parameters on the vibration response are analyzed from the experimental results.
3.2. Experimental Processes
- Fixing the blade on the test bench. The blade root is fully restrained by the mounting bolts. Then, the first-order natural frequency is measured. In the test process, the blade-mounting bolts need to be repeatedly tightened. The bolt torque used for installing the blade will affect its natural frequency. Therefore, in order to accurately measure the natural frequency of the blade and reduce the impact of bolt connections, it is necessary to adjust the bolt torque and ensure that the difference between the measured values of natural frequency before and after adjustment is less than 1%.
- Applying normal load on the damper. Install the different radii of the dampers between the two platforms and adjust the position of the dampers so that they are parallel to the surface of the platforms and aligned front to back. Install one end of the wire rope on the damper and the other end on the tensiometer and the turnbuckle. Adjust the tightness of the turnbuckle to change the normal load. The value is measured using the tensiometer.
- Measuring response. The FRFs of the blade in frequency range are acquired through frequency sweeps under the sinusoidal excitation. Due to the output characteristics of the exciter, the magnitude of the output force varies with the frequency of the excitation force. Therefore, a feedback loop is set up to feed the force transducer signal back to the signal generation system in real time, and the output signal is changed to control the excitation force to maintain a constant magnitude during the sweeping process. In addition, the sweeping rate will affect the measurement results [22]; thus, the frequency response curve under several sweeping rates was compared. Finally, 0.4 Hz/s was chosen as the sweeping rate for this experiment.
4. Results and Discussion
4.1. Natural Frequency Measurement
In order to investigate the effect of contact excitation on the blade’s inherent characteristics, free vibration (this state is called the non-connected state) and resonance when the exciter is connected (this state is called the connected state) are used in the experiment. The directly excited and indirectly excited blades were measured, and the results are shown in Table 1.

Table 1.
Comparison of natural frequency measurement results.
As can be seen from comparing the results of the two natural frequency test methods used, the relative errors between the natural frequencies obtained in both states are within 3%. Therefore, it can be assumed that the blade in the connected state, although under additional constraints, has a small effect on the vibration characteristics of the linear system [32], thus providing some assurance for the subsequent measurement of the FRF curves.
4.2. Influence of Normal Load
The normal load between two contact surfaces is an important parameter, as it will affect the status of contact and the energy dissipated during vibration. In the following study, an R7 damper was used to act on the upper platform ①, with an excitation force of N and a gradually increasing normal load . The FRF curves (average values) of the directly and indirectly excited blades are plotted in Figure 9, where “” represents the response curves when no damper is used. The horizontal axis represents the frequency ratio, which is the swept frequency divided by the resonant frequency of the first-order bending, and the vertical axis represents the dimensionless amplitude, which is the swept amplitude divided by the resonant amplitude of the first-order bending.
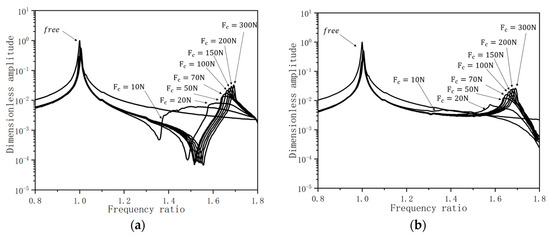
Figure 9.
FRF curves under different normal loads. (a) Directly excited blade. (b) Indirectly excited blade.
As can be seen from Figure 9, two types of bending modes appear in the blade system, namely, in-phase (IP) and out-of-phase (OOP) modes [33,34]. The first peak, with a lower frequency, is the IP resonance peak, while the second peak, with a higher frequency, is the OOP resonance peak.
To illustrate the experimental variations (see Figure 10 and Figure 11), the so-called “performance curves” of the damper in reference to similar curves in the literature [11,35] were plotted. The markers represent the average values of repeated experiments, while the error bars represent the standard deviation arising from measurement repeatability. They illustrate the evolution of dimensionless resonance amplitude and frequency across varying normal loads, encompassing the IP and OOP modes for both directly and indirectly excited blades. From Figure 10, it is evident that the system exhibits non-linear behavior as the normal load increases. The resonance amplitudes of both the directly and indirectly excited blades undergo a reduction of over 80%. Additionally, the amplitudes under the OOP mode are notably lower than those observed in the IP mode. This is due to the dampers taking a major role during the OOP mode of the blade, hence the greater relative displacement of the blade than that of the IP mode [36]. From Figure 11, it is seen that with the increasing normal load, the resonant frequency ratio increases acutely at first, then turns to an invariable value. The reason is that the entire damper tends to be in a complete sticking state when the normal load increases to a certain degree. The additional stiffness that the damper can provide reaches the maximum at this time, so the system tends to be linear. Additionally, the resonance amplitude and frequency have undergone dimensionless processing, with the resonance frequency displaying minimal variation, particularly at the IP mode. As a consequence, the error values consistently remain very small, as shown in Figure 11, with the IP result error value being particularly insignificant; for this reason, it is not highlighted in the figure.

Figure 10.
Dimensionless amplitude curves under different normal loads. (a) Directly excited blade. (b) Indirectly excited blade.
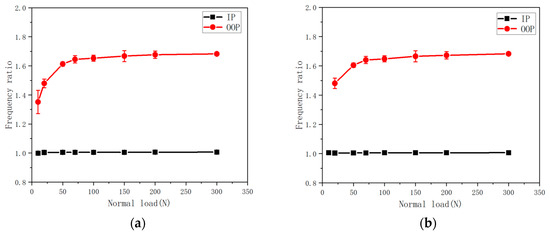
Figure 11.
Resonance frequency ratio curves under different normal loads. (a) Directly excited blade. (b) Indirectly excited blade.
4.3. Influence of Excitation Force
The FRF curves (average values) of the blade system for different excitation forces were obtained using an R7 damper acting at the upper platform ①, and the normal load was kept at , as shown in Figure 12.
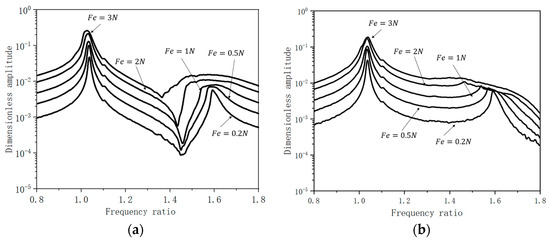
Figure 12.
FRF curves under different magnitudes of excitation force. (a) Directly excited blade. (b) Indirectly excited blade.
It is evident that with the increase in excitation force, the two resonant peaks (IP and OOP modes’ resonant peaks) of the directly and indirectly excited blades show comparable characteristics; that is, the resonance amplitude becomes larger, while the resonance frequency decreases. From Figure 12, one can obtain the variation curve of blade resonance amplitude and resonance frequency along with excitation force, as shown in Figure 13. To simplify the presentation of the results, error bars in the subsequent figures were omitted, and only the average values were displayed. It can be observed that as the excitation force increases, the resonant frequency decreases. According to the input and output relationship of the linear system, the vibration displacement of the blade increases as the excitation force increases. With the same normal load condition, the percentage of slip in the contact process between the platform and the damper will gradually increase, leading to a decrease in contact stiffness. Furthermore, the UPD has a damping effect, but with the increasing excitation force, the energy provided by the excitation force will be much larger than the energy dissipated by the UPD. Although there is a UPD in the system, with the increase in external excitation, the response of the system is still increasing.

Figure 13.
Resonance amplitude/frequency curves under different excitation force. (a) IP mode. (b) OOP mode.
4.4. Influence of Contact Area
When employing an R5 and R7 damper to interact with the upper platform ①, a noteworthy effect emerges. It is established that the contact area between the UPD and the platform diminishes with the augmentation of the damper’s curvature, as elucidated in reference [37].
As shown in Figure 14, the resonant frequencies and amplitudes of the directly and indirectly excited blades were obtained experimentally for two different contact areas in the OOP mode with Fe = 1 N, and only the average values were displayed. (One conclusion that can be made from Section 4.2 is that the damping effect is more obvious in the OOP mode compared to the IP mode. The experimental results are convenient for comparison. Therefore, the discussion in the later sections focuses on the OOP mode).
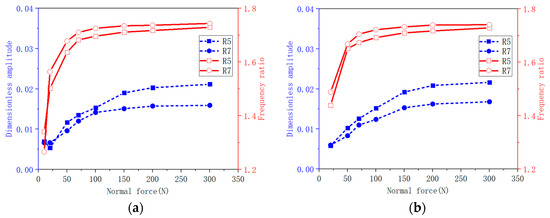
Figure 14.
Resonance amplitude/frequency curve under different normal loads (different dampers in OOP mode). (a) Directly excited blade. (b) Indirectly excited blade.
Observing Figure 14, a noteworthy trend emerges: the R7 damper exhibits a higher resonant frequency compared to the R5 damper. This highlights a direct relationship between the damper’s contact area and the blade’s resonant frequency. Moreover, Figure 14 accentuates that there is a greater contact area for the UPD, and that the platform corresponds to a diminished resonance amplitude. A smaller contact area proves counterproductive for generating efficient energy dissipation. Hence, in practical engineering scenarios, it is imperative to emphasize a larger contact area for the damper in order to enhance its damping efficacy.
4.5. Influence of Damper Position
To explore the vibrational traits of the system when dampers are positioned differently, an R7 damper is placed at positions ① and ②. Based on the FRF curves recorded by the system at N, Figure 15 presents the acquired resonance amplitude and frequency data for both directly and indirectly excited blades in the OOP mode across different normal loads. (Only the average values are displayed.).
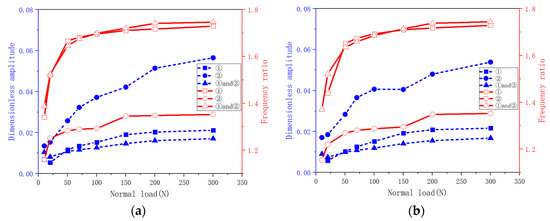
Figure 15.
Resonance amplitude/frequency under different normal loads (different positions on OOP mode). (a) Directly excited blade. (b) Indirectly excited blade.
Analyzing the outcomes presented in Figure 15, it is evident that the placement of the damper at distinct positions yields diverse damping and frequency-adjustment capabilities for the system. When the damper solely operates at the lower position ②, the change in the system’s frequency ratio remains below 20%, coinciding with the highest dimensionless amplitude. Conversely, with damping occurring exclusively at the upper position ① or with the dual damping setup at positions ① and ②, the system’s frequency ratio undergoes fluctuations exceeding 40%. Notably, the most extensive frequency adjustment range and the lowest resonance amplitude are achieved when both dampers at positions ① and ② are concurrently in operation. Moreover, a trend evident in Figure 15 is that with an increase in normal load, both resonance frequency and amplitude exhibit a gradual rise, followed by a tendency toward stabilization. This behavior arises due to the introduction of dampers, which couples the two blades and induces friction forces that shift the system from a linear to a non-linear state. As the normal load steadily increases, the contact surface undergoes a gradual transition from a sliding state to a sticking state. The friction force introduces a stiffening effect, causing the system’s resonance frequency to incrementally rise. Furthermore, the sticking state curtails frictional dissipation, leading to an increase in resonance amplitude. This evolution continues until the contact surface attains complete sticking, at which point the system once again approaches a linear state. The resonance frequency and amplitude subsequently stabilize.
The presence of the UPD plays a large role in changing the stiffness and damping characteristics of the system on the one hand and in imposing additional constraints on the other. Changing the position of the system’s restraint affects the vibration pattern and other factors, thus affecting the frequency regulation. The presence of the double-layer damper provides more equivalent stiffness and damping during vibration, resulting in better damping effects compared to the use of the single-layer damper. Moreover, the normal load on the damper during operation is provided by its centrifugal force. From the formula for centrifugal force, , it can be shown that the centrifugal force of the damper is proportional to its mass at the same speed , when ignoring the small difference of radius . The upper-layer damping provides more equivalent damping and equivalent stiffness during the vibration process. It takes a greater proportion of the damping capacity of the dual UPD system when they have the same conditions, which provides guidance for the design and mass selection of dual UPDs.
5. Conclusions
In this paper, an experimental rig for a two-blade system is established. The dynamic characteristics of the blade–damper system are tested and studied. FRF curves corresponding to the IP and OOP modes of the blade–damper system during the first-order bending mode vibration were obtained. The adopted experimental approach is valid as it allows for the control of variables to obtain the impact of each key design parameter of the UPD. Based on the above analyses, the following results are obtained:
- Normal load on the UPD has a significant influence on damping. The friction damping produced by the UPD leads to a reduction in the amplitude and an increase in the resonance frequency both in the IP and OOP modes. Compared to the IP mode, dampers are more efficient in the OOP mode.
- The variation in excitation force affects the stiffness characteristics of the system. With an increase in external excitation, the relative displacement between platforms increases, the two-blade system shows stiffness softening, and the resonance frequency gradually decreases.
- The contact area affects the damping effect of the damper. Under the same normal load condition, the larger the effective contact area between the damper and the platform, the better the damping effect of the damper.
- The damping effect of the double-layer damping system is better than that of the single-layer damping system. Under the same conditions of damper type and normal load, the upper damping ① has a wider frequency-adjustment range and lower resonance amplitude, which takes a greater share in the damping capacity.
- The experiment conducted in this study was performed using experimental blades, and to facilitate a comparative analysis of the results, certain simplifications were applied to the damper. The static test also did not consider the effect of the centrifugal stiffening effect on the stiffness of the blade system. In the future, based on this experiment, real blades should be used so that dual friction damper vibration-reduction experiments can be carried out under rotating conditions. Additionally, the study of damper wear emerges as a noteworthy avenue for future exploration. Subsequent research could delve into the repercussions of damper wear during operational service on the vibration characteristics of the overall system.
Author Contributions
Conceptualization, J.M. and X.B.; data curation, W.Z.; formal analysis, W.Y.; investigation, J.M. and D.Q.; methodology, X.B.; validation, W.Z. and W.Y.; writing—original draft, J.M.; writing—review and editing, X.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science and Technology Major Project No. 2017-IV-0002-0039.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, Xiang-de Bian, upon reasonable request.
Conflicts of Interest
The authors declare no competing interest.
References
- Chiara, G.; Alfredo, F.; Teresa, B. Forced response prediction of turbine blades with flexible dampers: The impact of engineering modelling choices. Appl. Sci. 2017, 8, 34. [Google Scholar]
- Santhosh, B.; Narayanan, S.; Padmanabhan, C. Nonlinear Dynamics of Shrouded Turbine Blade System with Impact and Friction. Appl. Mech. Mater. 2015, 706, 81–92. [Google Scholar] [CrossRef]
- Zheng, D.; Liu, G.; He, S. Comparative Analysis of Rub-Impact dynamics of shrouded blades based on the bilinear hysteresis model and the Coulomb friction model. Lubricants 2022, 10, 31. [Google Scholar] [CrossRef]
- Ahmed, R.; Firrone, C.M.; Zucca, S. A test rig for the full characterization of the dynamics of shrouded turbine blades. Mech. Syst. Signal Process. 2023, 189, 110080. [Google Scholar] [CrossRef]
- Wu, Y.; Xuan, H.; Wu, C. Study on the Forced Torsional Vibration Response of Multiple Rotating Blades with Underplatform Dampers. Aerospace 2023, 10, 725. [Google Scholar] [CrossRef]
- Mitra, M.; Zucca, S.; Epureanu, B.I. Adaptive Microslip Projection for Reduction of Frictional and Contact Nonlinearities in Shrouded Blisks. J. Comput. Nonlinear Dyn. 2020, 11, 041016. [Google Scholar] [CrossRef]
- Sun, Y.; Denimal, E.; Yuan, J.; Salles, L. Geometric design of friction ring dampers in blisks using nonlinear modal analysis and Kriging surrogate model. Struct. Multidiscip. Optim. 2022, 69, 98. [Google Scholar] [CrossRef]
- Rayegani, A.; Nouri, G. Seismic collapse probability and life cycle cost assessment of isolated structures subjected to pounding with smart hybrid isolation system using a modified fuzzy based controller. Structures 2022, 44, 30–41. [Google Scholar] [CrossRef]
- Csaba, G. Forced response analysis in time and frequency domains of a tuned bladed disk with friction dampers. J. Sound Vib. 1998, 214, 395–412. [Google Scholar] [CrossRef]
- Sanliturk, K.Y.; Ewins, D.J. Modelling two-dimensional friction contact and its application using harmonic balance method. J. Sound Vib. 1996, 193, 511–523. [Google Scholar] [CrossRef]
- Yang, B.D.; Menq, C.H. Characterization of 3d contact kinematics and prediction of resonant response of structures having 3d frictional constraint. J. Sound Vib. 1998, 217, 909–925. [Google Scholar] [CrossRef]
- Yang, B.D.; Chen, J.J.; Menq, C.H. Prediction of Resonant Response of Shrouded Blades with Three-Dimensional Shroud Constraint. In Proceedings of the ASME 1998 International Gas Turbine Aeroengine Congress Exhibition, Stockholm, Sweden, 2–5 June 1998. [Google Scholar]
- Qu, Z.; Hu, D.; Chen, Z. Contact nonlinear analysis for the under-platform dampers of blade based on a frictional energy dissipation model. Structures 2021, 30, 146–155. [Google Scholar] [CrossRef]
- Wang, S.; Yang, G.; Ji, L. Multi-mode vibration attenuation of mistuned bladed disks by frictional tuned mass dampers array. J. Sound Vib. 2022, 536, 117176. [Google Scholar] [CrossRef]
- Quaegebeur, S.; Chouvion, B.; Thouverez, F. Nonlinear dynamic analysis of three-dimensional bladed-disks with frictional contact interfaces based on cyclic reduction strategies. Int. J. Solids Struct. 2022, 236, 111277. [Google Scholar] [CrossRef]
- Pourkiaee, S.M.; Zucca, S.; Parker, R.G. Relative cyclic component mode synthesis: A reduced order modeling approach for mistuned bladed disks with friction interfaces. Mech. Syst. Signal Process. 2022, 163, 108197. [Google Scholar] [CrossRef]
- Gastaldi, C.; Gola, M.M. Nonlinear Damper-Blade Coupling Calculations Reduced to Essentials. J. Eng. Gas Turbines Power 2023, 145, 012016. [Google Scholar] [CrossRef]
- Koh, K.H.; Griffin, J.H. Dynamic Behavior of Spherical Friction Dampers and Its Implication to Damper Contact Stiffness. J. Eng. Gas. Turbines Power 2007, 129, 749–760. [Google Scholar] [CrossRef]
- Sanliturk, K.Y.; Ewins, D.J.; Stanbridge, A.B. Underplatform Dampers for Turbine Blades: Theoretical Modeling, Analysis, and Comparison With Experimental Data. J. Eng. Gas. Turbines Power 2001, 123, 919–929. [Google Scholar] [CrossRef]
- Pesaresi, L.; Salles, L.; Jones, A.; Green, J.; Schwingshackl, C. Modelling the nonlinear behaviour of an underplatform damper test rig for turbine applications. Mech. Syst. Signal Process. 2017, 85, 662–679. [Google Scholar] [CrossRef]
- Firrone, C.M.; Botto, D.; Gola, M.M. Modelling a Friction Damper: Analysis of the Experimental Data and Comparison with Numerical Results. In Proceedings of the 8th Biennial Asme Conference on Eng Syst Des Anal, Torino, Italy, 4–7 July 2006. [Google Scholar]
- Zhang, D.; Gao, B.; Hong, J.; Fu, J.; Ge, X. Experimental investigation on dynamic response of flat blades with underplatform dampers. Chin. J. Aeronaut. 2019, 32, 12. [Google Scholar] [CrossRef]
- Ferhatoglu, E.; Gastaldi, C.; Botto, D. An experimental and computational comparison of the dynamic response variability in a turbine blade with under-platform dampers. Mech. Syst. Signal Process. 2022, 172, 108987. [Google Scholar] [CrossRef]
- Yuan, J.; Fantetti, A.; Denimal, E. Propagation of friction parameter uncertainties in the nonlinear dynamic response of turbine blades with underplatform dampers. Mech. Syst. Signal Process. 2021, 156, 107673. [Google Scholar] [CrossRef]
- Mehrdad Pourkiaee, S.; Berruti, T.; Zucca, S. Experimental and numerical assessment of mistuning effects on vibratory response of a bladed disk with underplatform dampers. J. Eng. Gas. Turbines Power 2021, 143, 031010. [Google Scholar] [CrossRef]
- Hoffmann, T.; Panning-von Scheidt, L.; Wallaschek, J. Measured and simulated forced response of a rotating turbine disk with asymmetric and cylindrical underplatform dampers. J. Eng. Gas. Turbines Power 2020, 142, 051002. [Google Scholar] [CrossRef]
- Laxalde, D.; Gibert, C.; Thouverez, F. Experimental and Numerical Investigations of Friction Rings Damping of Blisks. In Proceedings of the ASME Turbo Expo, Berlin, Germany, 9–13 June 2008. [Google Scholar]
- Bessone, A.; Toso, F.; Berruti, T. Investigation on the Dynamic Response of Blades with Asymmetric Under Platform Dampers. In Proceedings of the ASME Turbo Expo, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Laxalde, D.; Thouverez, F.; Sinou, J.-J.; Lombard, J.-P. Qualitative Analysis of Forced Response of Blisks with Friction Ring Dampers. Eur. J. Mech/A Solids 2007, 26, 676–687. [Google Scholar] [CrossRef]
- Lars, P.; Walter, S.; Karl, P. Spatial Dynamics of Tuned and Mistuned Bladed Disks with Cylindrical and Wedge-Shaped Friction Dampers. Int. J. Rotating Mach. 2007, 9, 219–228. [Google Scholar]
- Zhang, D.; Fu, J.; Zhang, Q.; Hong, J. An effective numerical method for calculating nonlinear dynamics of structures with dry friction: Application to predict the vibration response of blades with underplatform dampers. Nonlinear Dyn. 2016, 88, 223–237. [Google Scholar] [CrossRef]
- Zhao, P.F.; Zhang, Q.; Wu, J.; Zhang, D. Experimental Study of Dynamic Characteristics of Dry Friction Damping of Turbine Blade Steel. Adv. Mater. Res. 2013, 690, 1979–1982. [Google Scholar] [CrossRef]
- Marquina, F.J.; Coro, A.; Gutie’rrez, A.; Alonso, R.; Ewins, D.J.; Girini, G. Friction Damping Modeling in High Stress Contact Areas Using Microslip Friction Model. In Proceedings of the ASME Turbo Expo. 2008: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008. [Google Scholar]
- Zucca, S.; Botto, D.; Gola, M.M. Range of variability in the dynamics of semi-cylindrical friction dampers for turbine blades. In Proceedings of the ASME Turbo Expo: Power for Land, Sea & Air, Berlin, Germany, 9–13 June 2008. [Google Scholar]
- Zucca, S.; Berruti, T.; Cosi, L. Experimental and Numerical Investigations on the Dynamic Response of Turbine Blades with Tip Pin Dampers; Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2016; Volume 744, p. 012131. [Google Scholar]
- Firrone, C.M. Measurement of the kinematics of two underplatform dampers with different geometry and comparison with numerical simulation. J. Sound Vib. 2009, 323, 313–333. [Google Scholar] [CrossRef]
- Allara, M. A model for the characterization of friction contacts in turbine blades. J. Sound Vib. 2009, 320, 527–544. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).