RANS Prediction of Losses and Transition Onset in a High-Speed Low-Pressure Turbine Cascade
Abstract
1. Introduction
2. Test Case
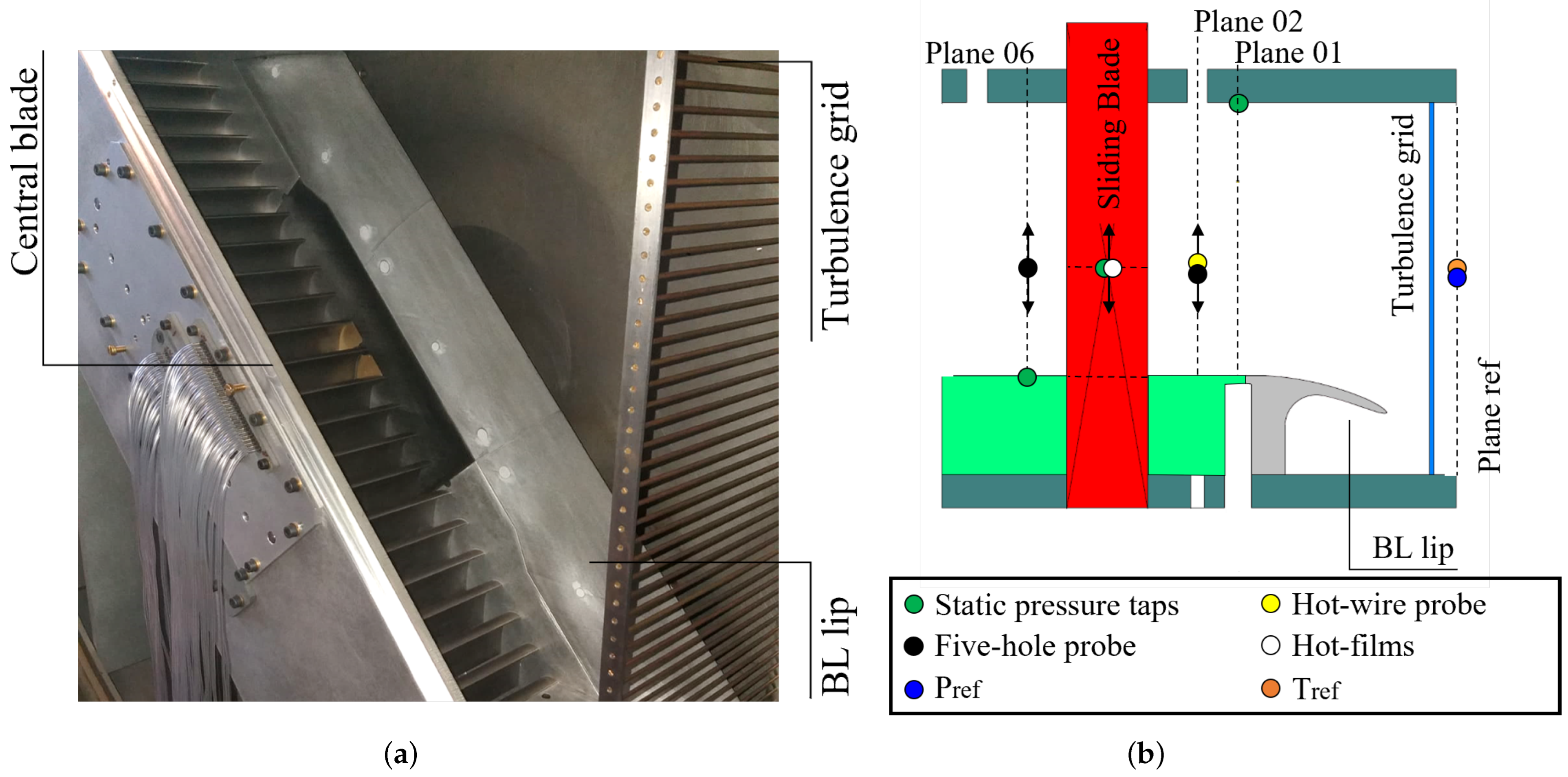
2.1. Experimental Setup
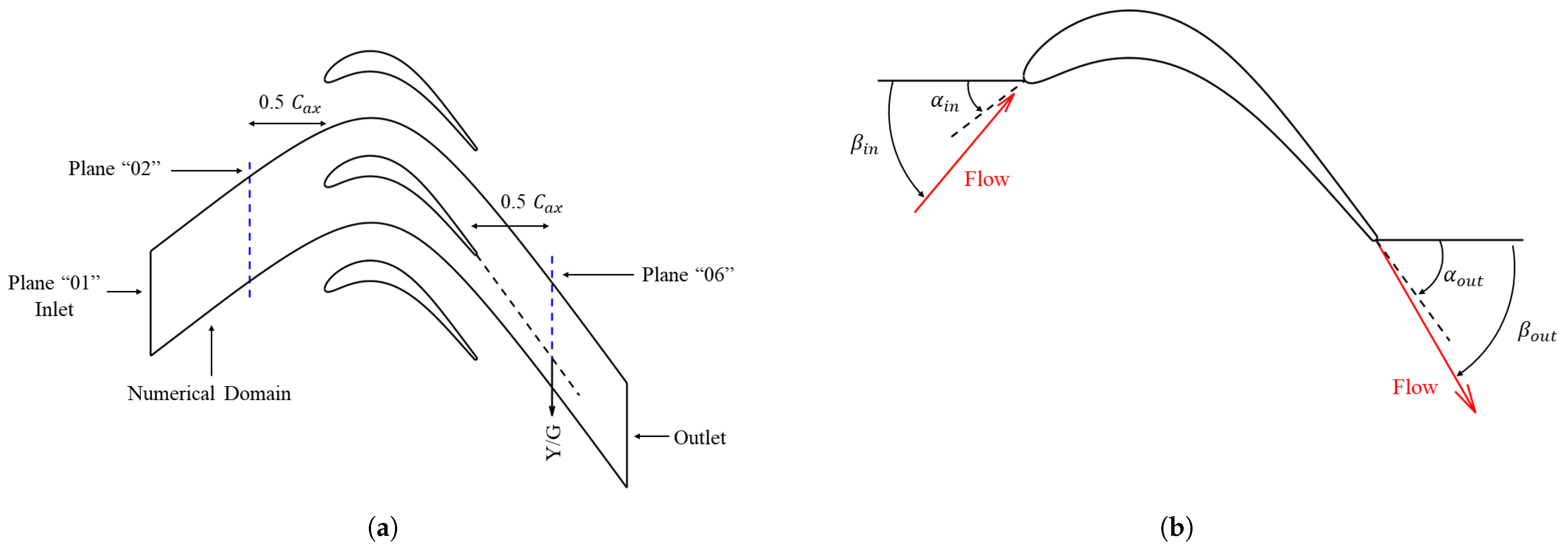
2.2. Numerical Setup
2.3. Turbulence Modeling
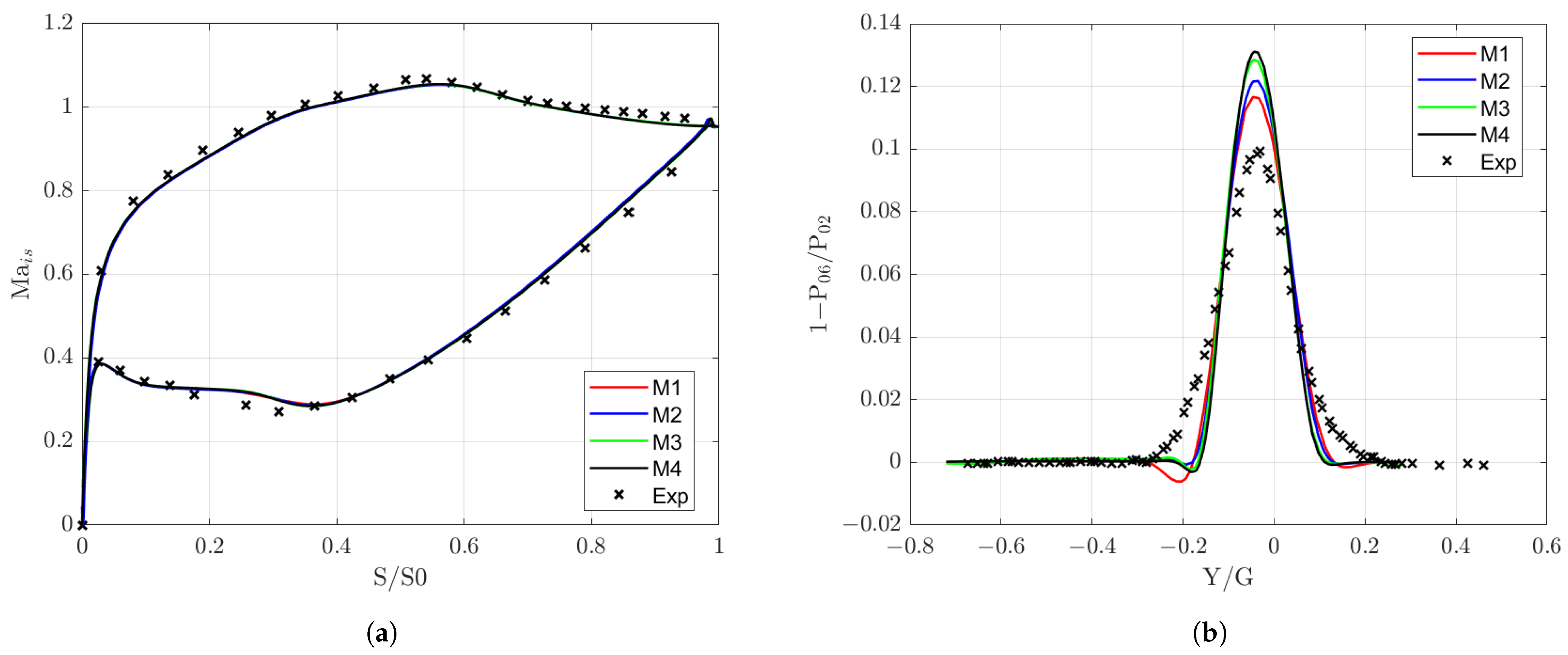
2.4. Mesh Sensitivity
3. Results and Discussion
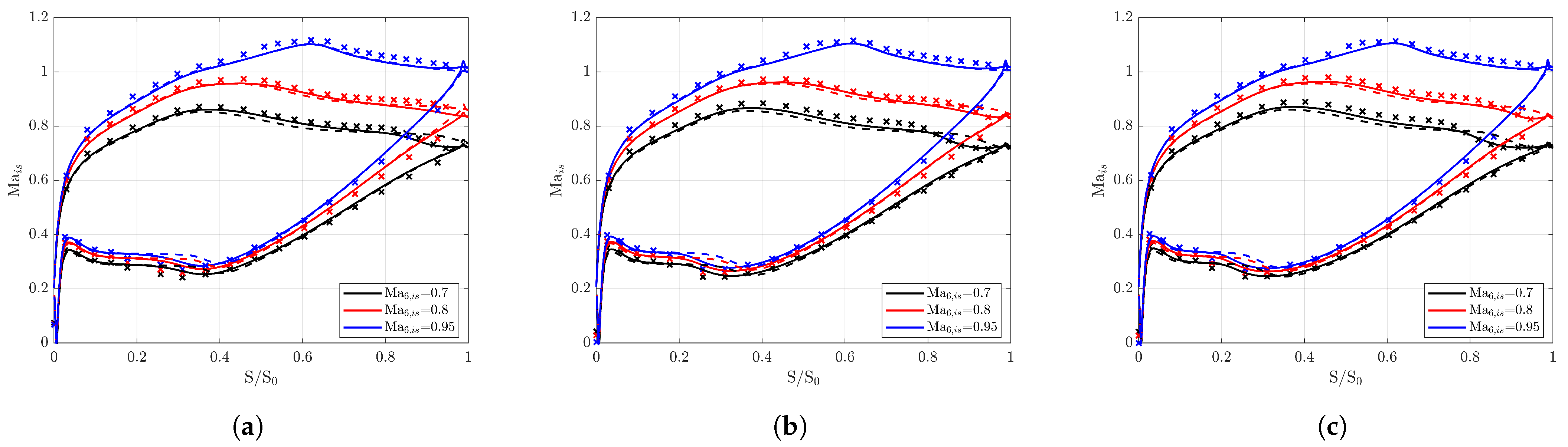
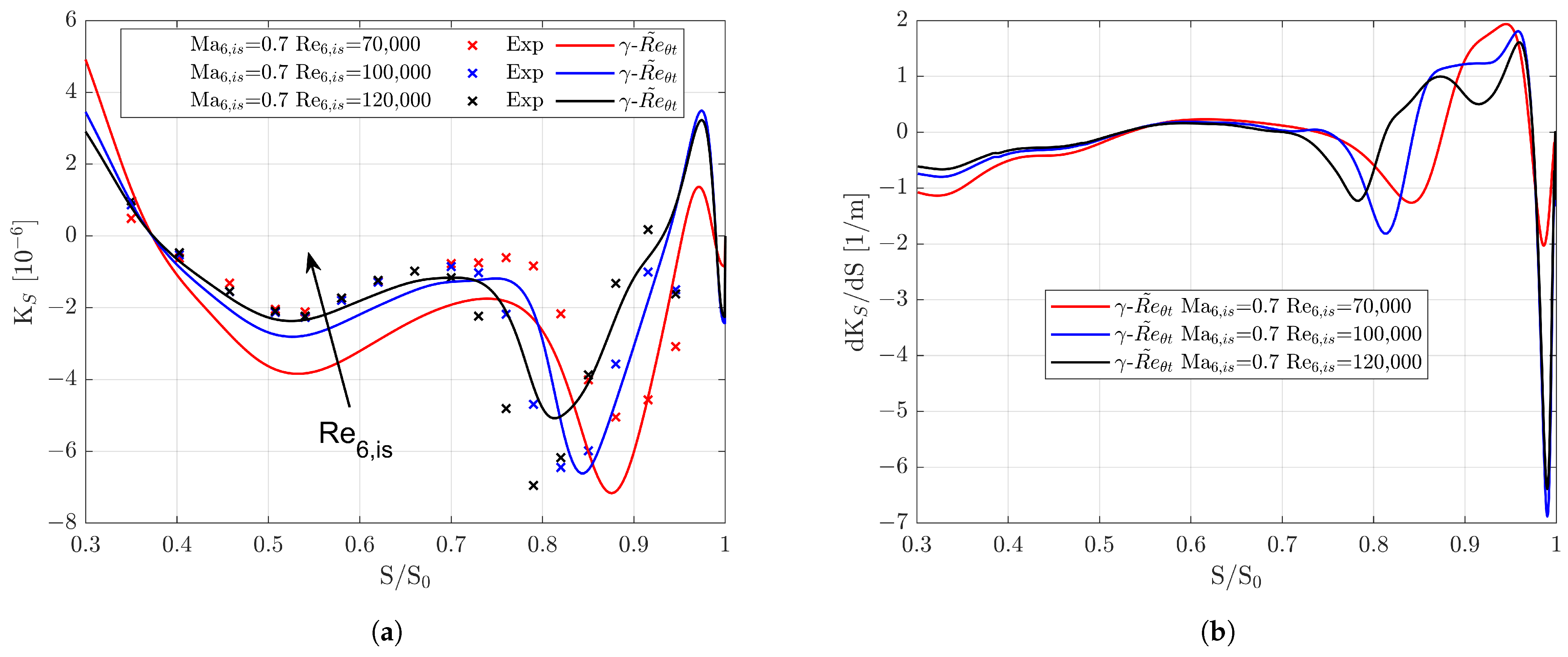
3.1. Blade Loading
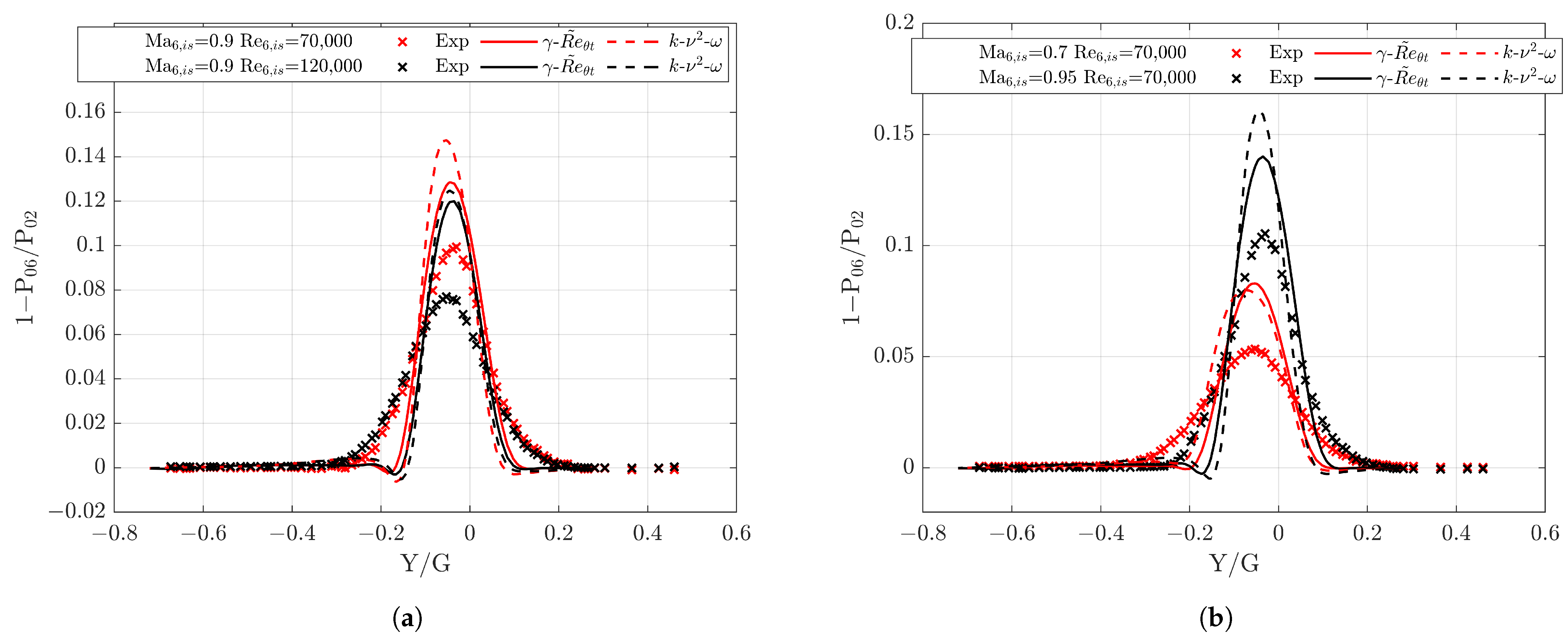
3.2. Wake Prediction
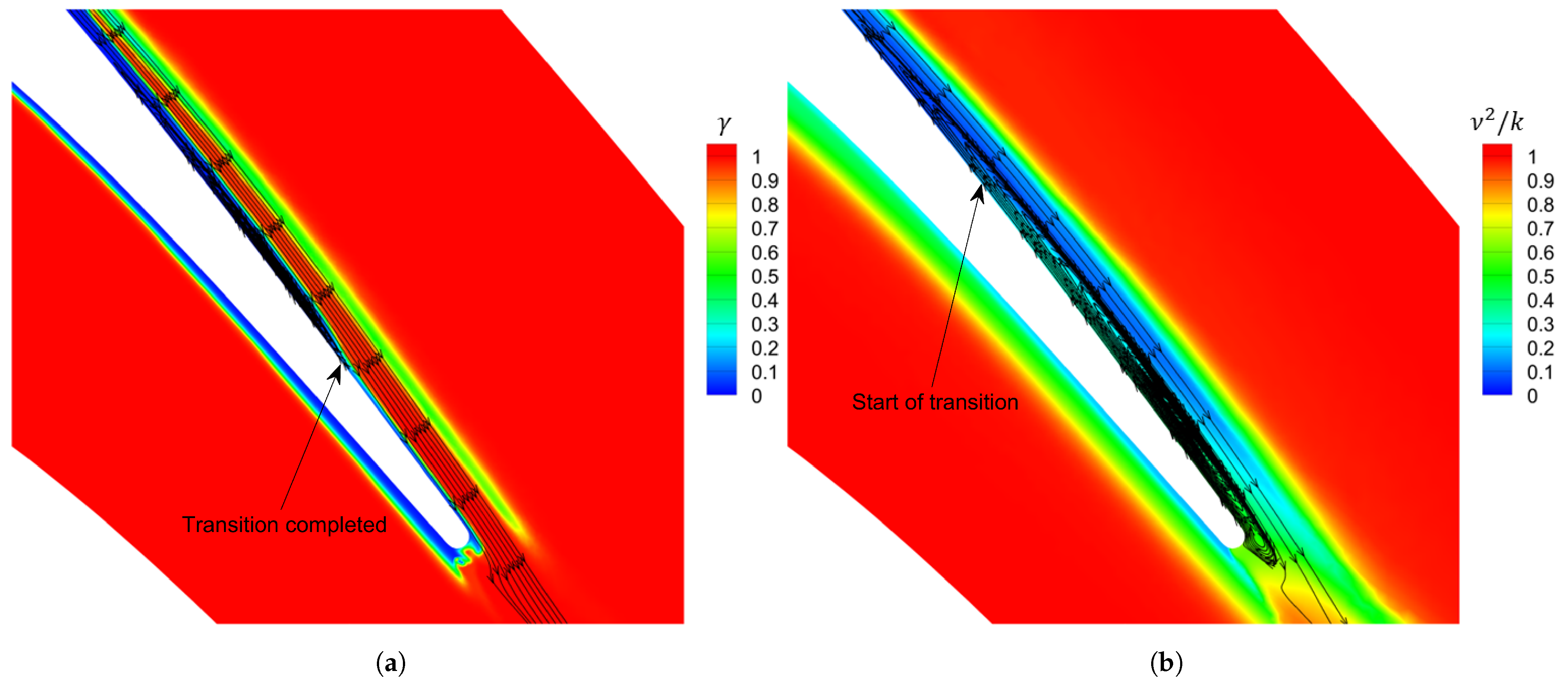
3.3. Boundary Layer Analysis
3.3.1. Separation and Reattachment Prediction
3.3.2. Wall Shear Stress
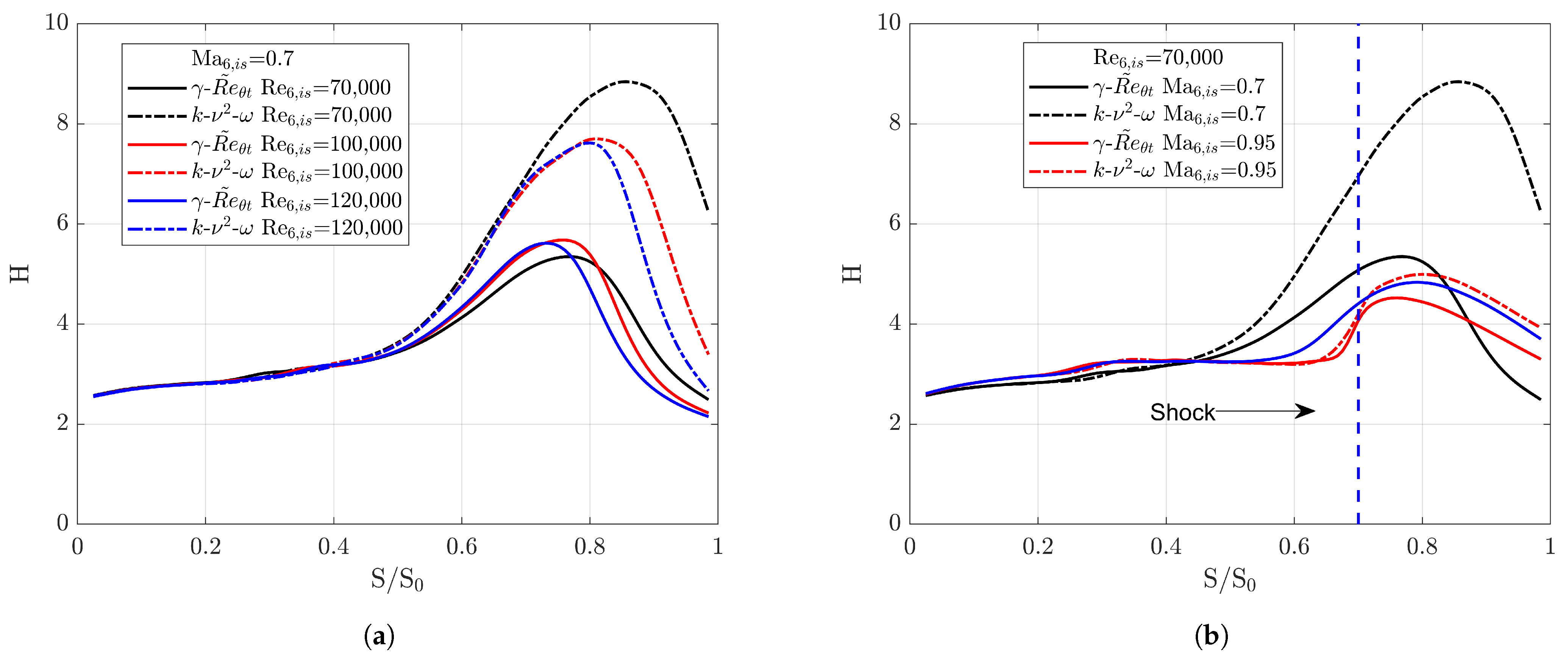
3.3.3. Shape Factor
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviations | |
| C | Blade true chord |
| Blade axial chord | |
| C5HP | Cobra-shaped five-hole probe |
| d | Deviation angle |
| DNS | Direct numerical simulation |
| FSTI | Freestream turbulence intensity |
| G | Pitch |
| GMRES | Generalized Minimal Residual |
| H | Shape factor |
| HF | Surface mounted hot-film sensor |
| i | Incidence angle |
| ILS | Integral length scale |
| k | Heat capacity ratio |
| K | Acceleration parameter |
| LE | Leading edge |
| LES | Large-Eddy simulation |
| LKE | Laminar kinetic energy |
| L5HP | L-shaped five-hole probe |
| Ma | Mach number |
| PS | Pressure side |
| P | Total pressure |
| RANS | Reynolds-Averaged Navier-Stokes |
| Re | Reynolds number |
| Re | Reynolds number at separation point |
| Re | Reynolds number at reattachment point |
| S | Curvilinear coordinate |
| S | Curve length |
| SS | Suction side |
| SST | Shear stress transport |
| TE | Trailing edge |
| TI | Turbulence intensity |
| U | Experimental uncertainty |
| V | Velocity magnitude |
| Y | Pitchwise coordinate |
| Subscripts and Superscripts | |
| Freestream | |
| Relative to the inlet | |
| Isentropic | |
| Metallic | |
| Relative to the outlet | |
| Random | |
| Systematic | |
| 2 | Relative to Plane 02 |
| 6 | Relative to Plane 06 |
| Greek Letters | |
| Blade metal angle | |
| Flow angle | |
| Displacement thickness | |
| Kinematic viscosity | |
| Density | |
| Wall shear stress | |
| Reference wall shear stress | |
| Momentum thickness | |
References
- Curtis, E.M.; Hodson, H.P.; Banieghbal, M.R.; Denton, J.D.; Howell, R.J.; Harvey, N.W. Development of Blade Profiles for Low-Pressure Turbine Applications. J. Turbomach. 1997, 119, 531–538. [Google Scholar] [CrossRef]
- Lou, W.; Hourmouziadis, J. Separation Bubbles Under Steady and Periodic-Unsteady Main Flow Conditions. J. Turbomach. 2000, 122, 634–643. [Google Scholar] [CrossRef]
- Michálek, J.; Monaldi, M.; Arts, T. Aerodynamic Performance of a Very High Lift Low Pressure Turbine Airfoil (T106C) at Low Reynolds and High Mach Number with Effect of Free Stream Turbulence Intensity. J. Turbomach. 2012, 134, 061009. [Google Scholar] [CrossRef]
- Brunner, S.; Fottner, L.; Schiffer, H.P. Comparison of Two Highly Loaded Low Pressure Turbine Cascades Under the Influence of Wake-Induced Transition. In Proceedings of the ASME Turbo Expo 2000: Power for Land, Sea, and Air, Munich, Germany, 8–11 May 2000; Volume 3: Heat Transfer, Electric Power; Industrial and Cogeneration. p. V003T01A073. [Google Scholar] [CrossRef]
- Michelassi, V.; Wissink, J.; Rodi, W. Analysis of DNS and LES of Flow in a Low Pressure Turbine Cascade with Incoming Wakes and Comparison with Experiments. Flow Turbul. Combust. 2002, 69, 295–329. [Google Scholar] [CrossRef]
- de Wiart, C.C.; Hillewaert, K.; Geuzaine, P. DNS of a Low Pressure Turbine Blade Computed with the Discontinuous Galerkin Method. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenaghen, Denmark, 11–15 June 2012; Volume 8: Turbomachinery, Parts A, B, and C, pp. 2101–2111. [Google Scholar] [CrossRef]
- Garai, A.; Diosady, L.; Murman, S.; Madavan, N. DNS of Flow in a Low-Pressure Turbine Cascade Using a Discontinuous-Galerkin Spectral-Element Method. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; Volume 2B: Turbomachinery, p. V02BT39A023. [Google Scholar] [CrossRef]
- Baert, L.; Chérière, E.; Sainvitu, C.; Lepot, I.; Nouvellon, A.; Leonardon, V. Aerodynamic Optimization of the Low-Pressure Turbine Module: Exploiting Surrogate Models in a High-Dimensional Design Space. J. Turbomach. 2020, 142, 031005. [Google Scholar] [CrossRef]
- Giovannini, M.; Rubechini, F.; Marconcini, M.; Arnone, A.; Bertini, F. Reducing Secondary Flow Losses in Low-Pressure Turbines: The “Snaked” Blade. Int. Turbomach. Propuls. Power 2019, 4, 28. [Google Scholar] [CrossRef]
- Menter, F.R.; Langtry, R.B.; Likki, S.R.; Suzen, Y.B.; Huang, P.G.; Völker, S. A Correlation-Based Transition Model Using Local Variables—Part I: Model Formulation. J. Turbomach. 2004, 128, 413–422. [Google Scholar] [CrossRef]
- Langtry, R.B.; Menter, F.R. Correlation-Based Transition Modeling for Unstructured Parallelized Computational Fluid Dynamics Codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Mayle, R.E.; Schulz, A. The Path to Predicting Bypass Transition. In Proceedings of the ASME 1996 International Gas Turbine and Aeroengine Congress and Exhibition, Birmingham, UK, 10–13 June 1996; Volume 1: Turbomachinery, p. V001T01A065. [Google Scholar] [CrossRef]
- Walters, D.K.; Cokljat, D. A Three-Equation Eddy-Viscosity Model for Reynolds-Averaged Navier–Stokes Simulations of Transitional Flow. J. Fluids Eng. 2008, 130, 121401. [Google Scholar] [CrossRef]
- Pacciani, R.; Marconcini, M.; Fadai-Ghotbi, A.; Lardeau, S.; Leschziner, M.A. Calculation of High-Lift Cascades in Low Pressure Turbine Conditions Using a Three-Equation Model. J. Turbomach. 2010, 133, 031016. [Google Scholar] [CrossRef]
- Babajee, J.; Arts, T. Investigation of the Laminar Separation-Induced Transition with the - Transition Model on Low-Pressure Turbine Rotor Blades at Steady Conditions. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; Volume 8: Turbomachinery, Parts A, B, and C, pp. 1167–1178. [Google Scholar] [CrossRef]
- Minot, A.; de Saint Victor, X.; Marty, J.; Perraud, J. Advanced Numerical Setup for Separation-Induced Transition on High-Lift Low-Pressure Turbine Flows Using the - Model. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Cnanda, 15–19 June 2015; Volume 2B: Turbomachinery, p. V02BT39A010. [Google Scholar] [CrossRef]
- Pichler, R.; Zhao, Y.; Sandberg, R.; Michelassi, V.; Pacciani, R.; Marconcini, M.; Arnone, A. Large-Eddy Simulation and RANS Analysis of the End-Wall Flow in a Linear Low-Pressure Turbine Cascade, Part I: Flow and Secondary Vorticity Fields Under Varying Inlet Condition. J. Turbomach. 2019, 141, 121005. [Google Scholar] [CrossRef]
- Führing, A.; Kožulović, D.; Bode, C.; Franke, M. Steady State Modeling of Unsteady Wake Induced Transition Effects in a Multistage Low Pressure Turbine. In Proceedings of the ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition, Virtual, Online, 21–25 September 2020; Volume 2C: Turbomachinery, p. V02CT35A012. [Google Scholar] [CrossRef]
- Wang, X.; Cui, B.; Xiao, Z. Numerical investigation on ultra-high-lift low-pressure turbine cascade aerodynamics at low Reynolds numbers using transition-based turbulence models. J. Turbul. 2021, 22, 114–139. [Google Scholar] [CrossRef]
- Pacciani, R.; Marconcini, M.; Arnone, A.; Bertini, F. URANS Prediction of the Effects of Upstream Wakes on High-lift LP Turbine Cascades Using Transition-sensitive Turbulence Closures. Energy Procedia 2014, 45, 1097–1106. [Google Scholar] [CrossRef]
- Pacciani, R.; Marconcini, M.; Arnone, A.; Bertini, F. Predicting High-Lift Low-Pressure Turbine Cascades Flow Using Transition-Sensitive Turbulence Closures. J. Turbomach. 2013, 136, 051007. [Google Scholar] [CrossRef]
- Kubacki, S.; Jonak, P.; Dick, E. Evaluation of an algebraic model for laminar-to-turbulent transition on secondary flow loss in a low-pressure turbine cascade with an endwall. Int. J. Heat Fluid Flow 2019, 77, 98–112. [Google Scholar] [CrossRef]
- Kubacki, S.; Dick, E. An algebraic intermittency model for bypass, separation-induced and wake-induced transition. Int. J. Heat Fluid Flow 2016, 62, 344–361. [Google Scholar] [CrossRef]
- Lopez, M.; Walters, D.K. Prediction of transitional and fully turbulent flow using an alternative to the laminar kinetic energy approach. J. Turbul. 2016, 17, 253–273. [Google Scholar] [CrossRef]
- Simonassi, L.; Lopes, G.; Gendebien, S.; Torre, A.F.M.; Patinios, M.; Lavagnoli, S.; Zeller, N.; Pintat, L. An Experimental Test Case for Transonic Low-Pressure Turbines—Part I: Rig Design, Instrumentation and Experimental Methodology. In Proceedings of the ASME Turbo Expo 2022: Turbomachinery Technical Conference and Exposition, Rotterdam, The Netherlands, 13–17 June 2022; Volume 10B: Turbomachinery—Axial Flow Turbine Aerodynamics, Deposition, Erosion, Fouling, and Icing; Radial Turbomachinery Aerodynamics. p. V10BT30A012. [Google Scholar] [CrossRef]
- Lopes, G.; Simonassi, L.; Torre, A.F.M.; Patinios, M.; Lavagnoli, S. An Experimental Test Case for Transonic Low-Pressure Turbines—Part 2: Cascade Aerodynamics at On- and Off-Design Reynolds and Mach Numbers. In Proceedings of the ASME Turbo Expo 2022: Turbomachinery Technical Conference and Exposition, Rotterdam, The Netherlands, 13–17 June 2022; Volume 10B: Turbomachinery—Axial Flow Turbine Aerodynamics, Deposition, Erosion, Fouling, and Icing; Radial Turbomachinery Aerodynamics. p. V10BT30A027. [Google Scholar] [CrossRef]
- Lopes, G.; Simonassi, L.; Lavagnoli, S. Impact of Unsteady Wakes on the Secondary Flows of a High-Speed Low-Pressure Turbine Cascade. Int. J. Turbomach. Propuls. Power 2023, 8, 36. [Google Scholar] [CrossRef]
- Simonassi, L.; Lopes, G.; Lavagnoli, S. Effects of Periodic Incoming Wakes on the Aerodynamics of a High-Speed Low-Pressure Turbine Cascade. Int. J. Turbomach. Propuls. Power 2023, 8, 35. [Google Scholar] [CrossRef]
- Lavagnoli, S.; Lopes, G.; Simonassi, L.; Torre, A.F.M. SPLEEN—High Speed Turbine Cascade—Test Case Database. 2023. Available online: https://zenodo.org/records/8075795 (accessed on 1 July 2023).
- Adami, P.; Salvadori, S.; Chana, K.S. Unsteady Heat Transfer Topics in Gas Turbine Stages Simulations. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; Volume 6: Turbomachinery, Parts A and B, pp. 1733–1744. [Google Scholar] [CrossRef]
- Adami, P.; Belardini, E.; Martelli, F.; Michelassi, V. Unsteady Rotor/Stator Interaction: An Improved Unstructured Approach. In Proceedings of the ASME Turbo Expo 2001: Power for Land, Sea, and Air, New Orleans, LA, USA, 4–7 June 2001; Volume 1: Aircraft Engine, Marine; Turbomachinery; Microturbines and Small Turbomachinery. p. V001T03A051. [Google Scholar] [CrossRef]
- Adami, P.; Martelli, F.; Michelassi, V. Three-Dimensional Investigations for Axial Turbines by an Implicit Unstructured Multi-Block Flow Solver. In Proceedings of the ASME Turbo Expo 2000: Power for Land, Sea, and Air, Munich, Germany, 8–11 May 2000; Volume 1: Aircraft Engine, Marine; Turbomachinery; Microturbines and Small Turbomachinery. p. V001T03A108. [Google Scholar] [CrossRef]
- Roe, P. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Ollivier-Gooch, C.; Jalali, A. Accuracy Assessment of Finite Volume Discretizations of Diffusive Fluxes on Unstructured Meshes. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, Tennessee, 9–12 January 2012. [Google Scholar] [CrossRef]
- Ollivier-Gooch, C.; Ollivier-Gooch, C. High-order ENO schemes for unstructured meshes based on least-squares reconstruction. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1997. [Google Scholar] [CrossRef]
- Saad, Y.; Schultz, M.H. GMRES: A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems. SIAM J. Sci. Stat. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef]
- Xu, S.; Mohanamuraly, P.; Wang, D.; Müller, J.D. Newton–Krylov Solver for Robust Turbomachinery Aerodynamic Analysis. AIAA J. 2020, 58, 1320–1336. [Google Scholar] [CrossRef]
- Available online: https://www.centaursoft.com/ (accessed on 1 February 2023).
- Content, C.; Houdeville, R. Application of the - laminar-turbulent transition model in Navier-Stokes computations. In Proceedings of the 40th Fluid Dynamics Conference and Exhibit, Chicago, IL, USA, 28 June–1 July 2010. [Google Scholar] [CrossRef]
- Suluksna, K.; Dechaumphai, P.; Juntasaro, E. Correlations for modeling transitional boundary layers under influences of freestream turbulence and pressure gradient. Int. J. Heat Fluid Flow 2009, 30, 66–75. [Google Scholar] [CrossRef]
- Akolekar, H.D.; Weatheritt, J.; Hutchins, N.; Sandberg, R.D.; Laskowski, G.; Michelassi, V. Development and Use of Machine-Learnt Algebraic Reynolds Stress Models for Enhanced Prediction of Wake Mixing in Low-Pressure Turbines. J. Turbomach. 2019, 141, 041010. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar] [CrossRef]
- Akolekar, H.D.; Waschkowski, F.; Zhao, Y.; Pacciani, R.; Sandberg, R.D. Transition Modeling for Low Pressure Turbines Using Computational Fluid Dynamics Driven Machine Learning. Energies 2021, 14, 4680. [Google Scholar] [CrossRef]
- Akolekar, H.D.; Zhao, Y.; Sandberg, R.D.; Pacciani, R. Integration of Machine Learning and Computational Fluid Dynamics to Develop Turbulence Models for Improved Low-Pressure Turbine Wake Mixing Prediction. J. Turbomach. 2021, 143, 121001. [Google Scholar] [CrossRef]
- Hatman, A.; Wang, T. A Prediction Model for Separated-Flow Transition. J. Turbomach. 1999, 121, 594–602. [Google Scholar] [CrossRef]
- Mayes, C.; Schlichting, H.; Krause, E.; Oertel, H.; Gersten, K. Boundary-Layer Theory; Physic and Astronomy; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]


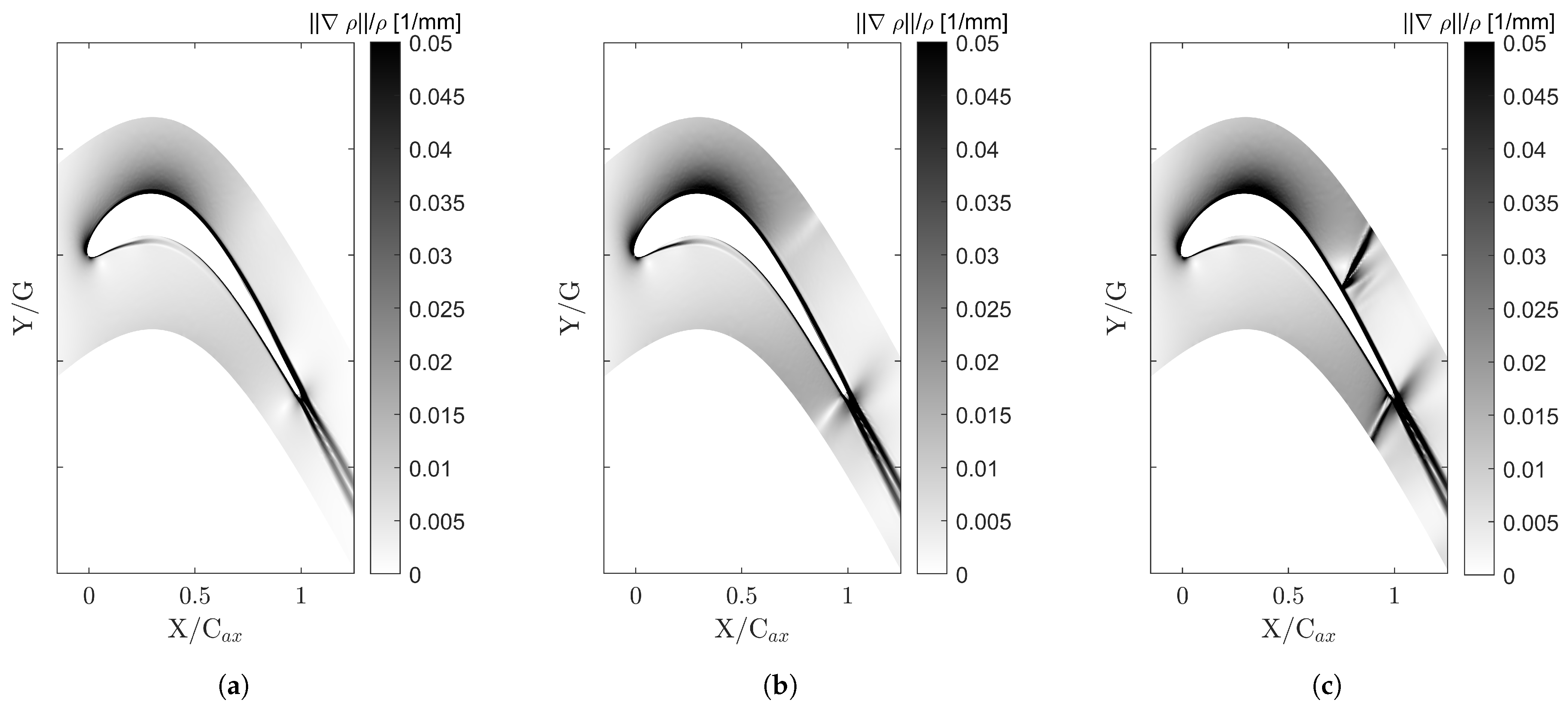



| Axial chord, [mm] | 47.614 |
| Blade chord, C [mm] | 52.285 |
| Pitch-to-chord ratio [-] | 0.63 |
| Height-to-chord ratio [-] | 3.16 |
| Inlet blade metal angle, [deg] | 37.30 |
| Outlet blade metal angle, [deg] | 53.80 |
| Inlet incidence, i [deg] | −1 |
| Outlet Mach number, Ma [-] | 0.70–0.90 |
| Outlet Reynolds number, Re [×] | 70–120 |
| Freestream turbulence intensity, FSTI [%] | ∼ |
| Integral length scale, ILS [mm] | ∼12 |
| Instrumentation | Qt. | Unit | ||
|---|---|---|---|---|
| Fixed instrumentation | K | 0.002 | 0.518 | |
| Pa | / | 25 | ||
| Pa | 7.13 | 29.22 | ||
| , | - | 0.0007 | 0.0053 | |
| Blade | - | 0.0007 | 0.0054 | |
| C5HP | i | deg | 0.24 | 1.11 |
| - | 0.001 | 0.005 | ||
| L5HP | deg | 0.24 | 0.36 | |
| - | 0.0010 | 0.0046 | ||
| - | 0.0019 | 0.0095 | ||
| HW | FSTI | % | / | 0.20 |
| ILS | - | / | 3.92 |
| Name | Total Elements [×10] | Quadrilateral Layers | Profile Elements | Max y |
|---|---|---|---|---|
| M1 | ≈50 | 25 | 305 | 0.12 |
| M2 | ≈70 | 25 | 573 | 0.12 |
| M3 | ≈90 | 25 | 737 | 0.12 |
| M4 | ≈100 | 25 | 763 | 0.12 |
| Ma | Re | 1 − | 1 − | 1− |
|---|---|---|---|---|
| Experimental | - | -- | ||
| 0.7 | 70,000 | 0.011 | 0.012 | 0.013 |
| 0.9 | 70,000 | 0.015 | 0.017 | 0.016 |
| 0.95 | 70,000 | 0.016 | 0.019 | 0.017 |
| 0.8 | 120,000 | 0.011 | 0.012 | 0.013 |
| 0.9 | 120,000 | 0.014 | 0.015 | 0.014 |
| Ma | Re | d [deg] | d [deg] | d [deg] |
|---|---|---|---|---|
| Experimental | - | -- | ||
| 0.7 | 70,000 | −0.7 (±0.4) | −0.4 | −0.3 |
| 0.9 | 70,000 | −0.9 (±0.4) | −0.2 | −0.1 |
| 0.95 | 70,000 | −0.9 (±0.4) | 0.0 | 0.0 |
| 0.8 | 120,000 | −0.9 (±0.4) | −0.4 | −0.3 |
| 0.9 | 120,000 | −0.9 (±0.4) | −0.2 | −0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosafio, N.; Lopes, G.; Salvadori, S.; Lavagnoli, S.; Misul, D.A. RANS Prediction of Losses and Transition Onset in a High-Speed Low-Pressure Turbine Cascade. Energies 2023, 16, 7348. https://doi.org/10.3390/en16217348
Rosafio N, Lopes G, Salvadori S, Lavagnoli S, Misul DA. RANS Prediction of Losses and Transition Onset in a High-Speed Low-Pressure Turbine Cascade. Energies. 2023; 16(21):7348. https://doi.org/10.3390/en16217348
Chicago/Turabian StyleRosafio, Nicola, Gustavo Lopes, Simone Salvadori, Sergio Lavagnoli, and Daniela Anna Misul. 2023. "RANS Prediction of Losses and Transition Onset in a High-Speed Low-Pressure Turbine Cascade" Energies 16, no. 21: 7348. https://doi.org/10.3390/en16217348
APA StyleRosafio, N., Lopes, G., Salvadori, S., Lavagnoli, S., & Misul, D. A. (2023). RANS Prediction of Losses and Transition Onset in a High-Speed Low-Pressure Turbine Cascade. Energies, 16(21), 7348. https://doi.org/10.3390/en16217348










