Abstract
So far it is believed that, for every series-parallel planetary gear system (PGS), as a coupled gear, a very harmful phenomenon of power circulation must occur in at least one of its closed circuits. In this paper (Part I) and in the next two (Part II and Part III), it will be shown that it is possible to construct a three-row series-parallel PGS in which this phenomenon can be avoided. For this purpose, in Part I, a detailed analysis of the kinematics and statics of a planetary gear with power circulation inside a closed loop was carried out. The determination of the angular velocities of gears and carriers is carried out using Willis formulas and the graphical-analytical method (for verification), while the torques are determined using free body diagrams. The magnitudes of angular velocities and torques were used to determine the directions of power flows with improved energy balance equations in the reference frame related to the stationary gear body and, additionally, only to verify the energy balance equation in the mobile reference frame related to the carrier (). The improvement of the methods was based on the use of the original concept of distinguishing active torque from reactive torque, as well as active power from reactive power, which made it very easy to determine the directions of the power flow. The determined paths of the power flow, including the power circulation in the analysed PGS, are presented graphically.
1. Introduction
Cylindrical series-parallel planetary gear systems (PGSs) are a special variety of complex and most-commonly coupled planetary transmissions. They consist of at least two subsystems (units) in the form of elementary 2KH planetary gears connected in parallel and possibly in series. Each of the subsystems connected in parallel has a mobility equal to two [1,2,3,4,5,6]. This means that all of the gears are moving along with the carriers. On the other hand, subsystems connected in series have a mobility equal to 1, which means that they can work as a typical planetary type system with a stationary rim gear. Very rarely, these are solar-type units with stationary sun gear or star-type units, i.e., multi-path units with fixed satellite axes due to the stationary carrier. Depending on the number and types of subsystems connected in series, the entire series-parallel gearbox may have a mobility from 1 to 3. They are characterized by the fact that they have multiple paths of power transmission, which may cause the phenomenon of power closure inside at least one parallel-connected elementary subsystem. Such power coupling in the form of its circulation [7,8,9,10,11] can even be a source of a large overload of gears, shafts, and/or bearings of a closed subsystem. In the case of an unfavourable distribution of power on individual paths, an additional reduction in efficiency may be revealed. Therefore, after determining the directions of the power flow, the power losses caused by friction in the meshing and efficiency should be determined.
This important problem was presented in several versions of analytical methods in the literature [12,13,14,15,16,17]. The analytical method used in this study uses three basic equations of planetary transmissions, i.e., the kinematics equation (usually the Willis dependence), statics equation (moment balance equation), and energy (power) balance equation. Thus, this method allows for the direct analysis of kinematics and statics, and, thus, for the direct identification of the power flow directions in coupled planetary gears with a mobility of one or more [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33], in automatic gearboxes [25,34,35,36,37,38,39,40,41,42], and in power-split hybrid systems consisting of planetary units with mechanical or hydro-mechanical continuously variable transmissions (CVT) [43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64] or in power-split hybrid electric vehicle (PSHEV) planetary transmission in single-motor (1-PG) or two-motor (2-PG) versions, sometimes with an additional internal combustion engine (ICE) [65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116]. In the last two types of transmission, i.e., in the power-split powertrain (with CVT applied, but without an additional motor) and PSHEV planetary transmission, the power flow occurs as power splitting and power circulation. A great facilitation of the analysis of such gear trains, as well as complex and coupled gear transmissions with any possible mobility, is the possibility of their decomposition into elementary subsystems, called blocks, branches, or geared entities [45,46,47,48,64,97]. In the first modified version of the analytical method used in this paper, the kinematics and statics are analysed using the matrix method, which makes the form of the equations which are used more compact and the computer calculations easier to perform [116,117]. In an equally popular variant, angular velocities and torques are determined using the lever analogy method and nomograms [118,119,120,121,122,123,124,125,126,127,128,129,130]. Also very interesting is the combined method of determining the power flow and efficiency epicyclic transmission presented in references [131,132,133,134,135,136,137,138,139,140], where the Lagrange multipliers and kinematic constraints are used to determine the power flow and to verify the normal power flow balance. The accuracy is increased in this method by including virtual power in the analysis, where virtual power was determined in a non-inertial frame of epicyclic planetary gear.
The method based on the graph representation of planetary gears (based on the graph representation) is the best technique for analysing kinematics and statics, and, thus, detecting the directions of power flow. The kinematic analysis of planetary gear trains is largely simplified in this way. This applies in particular to complex and coupled planetary gear transmissions with a mobility being equal to any number, automatic transmissions, power-split hybrid systems, and power-split hybrid electric vehicles. Interactive computer programs for the global analysis of kinematics and statics, and the identification of active and passive gears, i.e., power flow directions, are very helpful and easy to develop. The most commonly used of these are undirected graphs, directed graphs, topological graphs, hypergraphs, matroid, signal flow graphs, and bond graphs [140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195,196]. Graph or hypergraph methods can be combined with the matrix method [83,116,185]. There are also papers in which graphs were used primarily to synthesize the structure of the gear with the required ratio and possibly to determine the angular velocity, while the torques of the wheels and arms were determined by the method of torque balance or matrix, lever analogy, or other techniques.
From the above review of the literature on methods for determining the directions of power flow in complex series-parallel planetary gears, no case of a non-occurrence of power circulation was found. Therefore, in this three-part article, a comparison of the power flows and meshing efficiency of two three-row series-parallel PGSs with very similar geometrical structures will be conducted. In the first planetary gear there will be power circulation, while in the second there will not. To analyse these two planar gears, classical analytical and graphic-analytical methods will be used.
The rest of this paper is as follows. Section 2 (Materials and Methods) discusses in detail the problem of dividing complex serial-parallel PGSs into subsystems and details the analytical method of determining the active and passive shafts of each subsystem, i.e., the paths and directions of power flow. This method was used in Section 3 (Case Study), where angular velocities, active and reaction torques, and active and passive subsystem shafts were determined for the coupled and complex serial-parallel PGS. Verifications of the calculations of angular velocities, torques, and powers, along with power ratios, are presented in Appendix A, Appendix B, Appendix C, and Appendix D. The final result of the analysis is shown in Section 4. However, the main comments regarding the analysis are given in the Section 5.
2. Materials and Methods
2.1. Kinematic and Block Models of Series-Parallel PGSs
2.1.1. Geometric Structure of Series-Parallel PGSs
Complex planetary gear systems can be divided into series and series-parallel gear systems (PGS) [12,13,14,15,16]. Series gears are multi-stage gear systems, consisting of at least two single-stage gear subsystems called stages. Each gear stage, like the entire gear system, has a mobility equal to one, which means that there is only one way to transmit the power stream. Therefore, in a relatively simple way, it is possible to carry out not only an analysis of the kinematics and statics of such gears, but also an assessment of the power losses and efficiency. For example, the total gear ratio and the gear efficiency of a series gear resulting only from the power losses in the meshing are, respectively, the products of the gear ratios and the efficiency of the individual stages.
Cylindrical PGSs are complex closed mechanisms and, therefore, are called coupled planetary gears, and have a mobility of at least one. They consist of at least one elementary planetary gear connected in parallel, hereinafter referred to as a subsystem, not a stage. Such complex and coupled gears are characterized by a constant ratio of relatively high value (Figure 1a). Methods of their synthesis are presented in [12,14,16,17]. Due to the series-parallel structure of such gears, they cannot be divided into kinematic stages, which means that their analysis cannot use the facilities associated with multi-stage gears. Therefore, due to this and their having a more complex structure, they have not found such wide application in industrial practice as series multi-stage planetary gears. On the other hand, modified types of series-parallel gear systems are very popular. It is possible to attach an additional subsystem to such transmissions in the form of mechanical or hydro-mechanical CVT, thanks to which the obtained ratio can change continuously. In the synthesis process, series-parallel transmissions can also be relatively easily converted into step-variable transmissions, i.e., automatic gearboxes or power-split hybrid electric vehicle planetary transmission in single-, two-, and even three-motor versions plus one internal combustion engine (ICS). An example may be a gearbox with several gears (Figure 1b) obtained from the transformation of the series-parallel gearbox shown in Figure 1a. Other examples of such gearboxes are presented, for example, in [37,69,89,90,115,122,125,151].
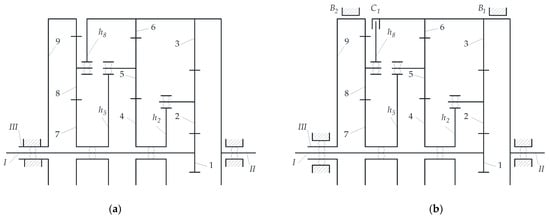
Figure 1.
Kinematic diagrams of (a) PGS and (b) automatic gear train.
Most series-parallel transmissions are structurally and dynamically coupled. However, there are also only structurally coupled gear systems due to the fact that their subsystems connected in parallel have the form of closed loops. Dynamically coupled gears are characterized by the fact that part of the power locked in these loops simultaneously circulates in them [7,8,9,10,11,24,28,56,93]. In Part I of this paper, only series-parallel transmission is analysed, which turns out to be structurally and dynamically coupled.
Figure 1 shows an exemplary kinematic diagram of a complex and coupled PGS. This system consists of three main shafts, I, II, and III. In the case of a reduction gear with a mobility equal to one, shaft I is the input shaft, shaft II is the output shaft, and the hollow shaft III is fixed. When all three shafts are moving together with ring gear 9, the gear has a mobility of two. The gear system consists of three sun gears, 1, 4, and 7, three sets of planet gears, 2, 5, and 8, three rim gears, 3, 6, 9, and three carriers, , , and .
Mobility is an important parameter of each planetary gear, including each of its subsystems. This is the number of constraints that should be imposed on the kinematic chain composed of gear elements in order to lock it. The measure of mobility is, therefore, the number of DoF relative to the stationary base. In practice, however, it is the number of drives (input shafts) that must ensure a strictly defined movement of all of the moving elements (gears and carriers). Thus, the number of independent input motions must equal the number of DoFs, so that the basic condition of its correct structure, i.e., no redundant members, is ensured. The analysed cylindrical planetary gears are planar mechanisms, so their mobility is calculated from the formula [1,184]:
where n is the number of active members, i.e., without frames, is the number of lower pairs, i.e., with one DoF, and is the number of higher pairs, also called half pairs, i.e., with two DoFs.
A characteristic feature of the series-parallel transmission shown in Figure 1 is that it comprises two closed loops. The first loop is bounded by carrier and the gears 2, 3, 6, 5, and 4, while the second loop is bounded by carrier and the gears 5, 6, 7, and 8. In the closed loops of most PGSs, power can circulate in a direction that can be determined by the method presented in this paper. In the exemplary transmission (Figure 1), all directions of power flows are possible with two exceptions. Namely, in the first loop, the power flows on carrier and rim gear 3 cannot be directed towards each other at the same time (they cannot converge), and the same is true for the power flows on rim gear 6 and carrier in the second loop. The power circulating in a closed loop can even exceed the power applied to the subsystem, which can cause a devastating overload of the gears.
2.1.2. Decomposition of Series-Parallel Gear System into Subsystems
The series-parallel gear system can be decomposed into subsystems in the form of separate single planetary gears with a mobility equal to 2 or 1, i.e., subsystems with two or one DoFs respectively. The condition for including the planetary gear in the family of series-parallel gears is the possibility of separating at least one subsystem with the number of two DoFs from it.
Figure 2 shows six basic types of two-DoF subsystems in block form. Each of these subsystems consists of a sun gear, rim gear, and carrier (hidden in the block as in a “black box”), as well as three movable shafts. At least one of these shafts must be the input shaft to the subsystem, i.e., the active shaft marked with an arrow pointing towards the block, and at least one—the output shaft of the subsystem, i.e., the passive shaft marked with an arrow pointing outwards from the block. In addition, individual shafts are marked with the letters , , and h; specifically the letter —sun gear shaft, the letter —rim gear shaft, and the letter h—carrier shaft.
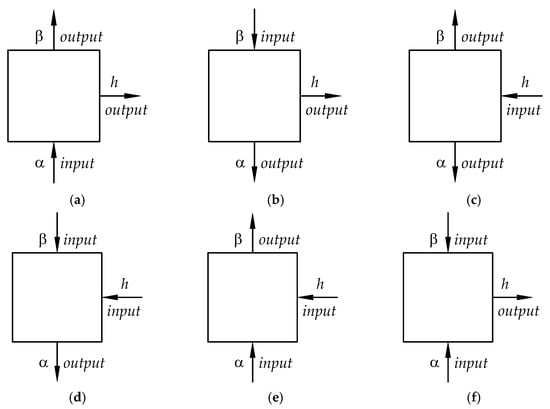
Figure 2.
Block diagrams (a–f) of possible types of subsystems with two DoFs differing in the directions of power flow through shafts , , h of the sun gear, ring gear and carrier, respectively.
In Figure 3, six basic types of subsystems with a single DoF are presented in block form. Also, here, each of the subsystems, just like each stage in a multi-stage planetary gear (series), consists of a sun gear, a rim, several planet gears, a carrier (hidden in the block as in a “black box”), and three coaxial shafts, one of which is locked together with the internal element of the subsystem connected to it. Thus, in a single DoF subsystem, only one shaft is active and one shaft is passive. The designations of these shafts are the same as for the shafts in the two-DoF subsystems. Subsystems with a fixed carrier (Figure 3b,d) are multipath gears with fixed planet gear axes (so-called star gears).
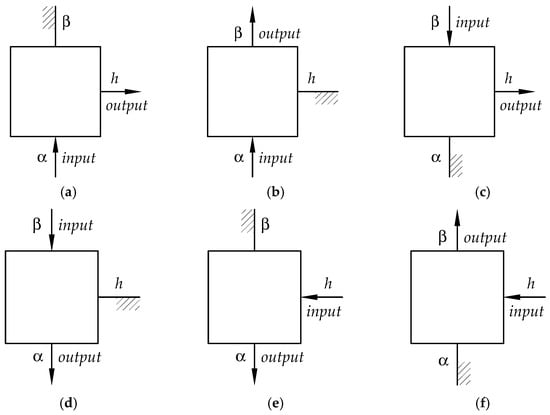
Figure 3.
Block diagrams (a–f) of possible types of single-DOF subsystems differing in the directions of power flow through shafts , , h of the sun gear, ring gear and carrier, respectively.
2.2. Analysis Algorithm of the Power Stream Flow in PGS without Power Loss
2.2.1. Method Algorithm
During operation, the shafts of the subsystems of a series-parallel planetary gear may rotate in directions that are consistent with or opposite to the directions of torque action. In the case of matching turns, the power on the shaft is called active power transferred to the analysed subsystem, and when the turns are opposite—reactive power transferred outside the subsystem. Since the power on the shaft is equal to the product of the angular velocity and torque, active power is assigned a plus sign (“+”), and reactive power—a minus sign (“−”).
The above simple principle is the basis for determining the flow directions of power streams in closed and complex planetary gears. It is enough to distinguish the active power from the reactive power and, accordingly, the active shaft from the passive one. Of course, each subsystem must have at least one active shaft and one passive shaft. In practice, determining the active and passive shafts in each subsystem is quite a laborious task because, beforehand, a detailed analysis of kinematics, i.e., the determination of angular velocities, and statics, i.e., the determination of torques without considering power losses, should be carried out.
An algorithm for determining the direction of power flow is presented below:
- (a)
- Gearbox geometry analysis—determination of gearbox mobility (1), decomposition of the gearbox into kinematic subsystems and their classification depending on the number of DoFs—Figure 2 and Figure 3, Section 2.2.2, Section 3.1, and Section 3.2;
- (b)
- Determination of the magnitudes and directions of angular velocities of gears and carriers in subsequent subsystems—Section 2.2.3 and Section 3.3.1 and Appendix A and Appendix B;
- (c)
- Determination of the magnitudes and directions of action of the torques loading the shafts of each of the subsystems (at this stage of calculation, without considering power losses)—Section 2.2.4 and Section 3.3.3 and Appendix C;
- (d)
- Determining the active and passive shafts of each of the transmission subsystems and the directions of the flow of power streams—Section 2.2.5, Section 3.3.4, and Section 3.3.5.
A detailed algorithm for determining the direction of the power flow is presented below.
Knowing the directions of power flow in each of the subsystems, it is possible to determine the torques and powers, considering friction in the meshing as well as power losses and transmission efficiency. The solution to this problem will be presented in Part III of this paper.
2.2.2. Analysis of the Geometry of Series-Parallel Gear Systems and Classification of Its Components
The presented method of identifying the directions of the power flow of the analysed PGS, and later (in Part III) also power losses, consists in determining these directions and power losses separately for each subsystem from the input to the output of the gear. Therefore, it is necessary to start the analysis by dividing the gear into subsystems and determining their mobility. The classification of subsystems is carried out on the basis of the number of DoFs, in accordance with Formula (1). The method of dividing the example series-parallel transmission (Figure 1) into subsystems and the classification of possible subsystems of such transmissions (Figure 2 and Figure 3) are discussed in Section 2.1.2. A detailed analysis of the geometry of the gear subsystems (Figure 4) is carried out in Section 3.1.
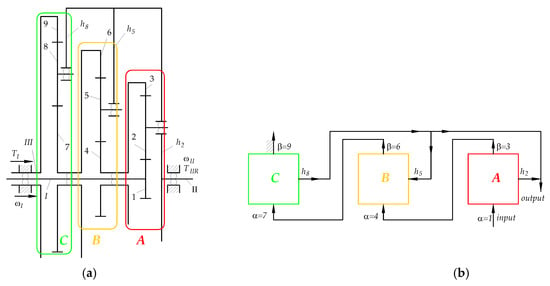
Figure 4.
Diagrams of the analysed PGS; (a) kinematic, (b) block.
2.2.3. Analysis of the Kinematics of Series-Parallel Gears
In order to determine the directions of the flow of power streams and to estimate the power losses in the meshing, it is necessary to determine the magnitudes and directions of the angular velocity vectors of the gears and carriers of each gear subsystem in advance (blocks, units, or branches) [195]. In practice, the Willis formula [12,13,14,15,16,17,163,178] is often used for this purpose, although graph methods (linear, contour, signal flow, bond graphs, matroids, and hypergraphs) are gaining more and more recognition, thanks to their advantages [143,162,164,165,166,167,168,169,171,172,173,174,175,176,177,179,180,181,182,183,184,185,186,189,192,194]. The nomograph method and, especially, the lever analogy are also promising as universal methods for kinematics, statics, and power flow analysis of the most complex PSHEV planetary transmission [88,118,119,120,121,126,128,129,130,160,161,164,188]. The effectiveness of the above-mentioned methods can be additionally increased by the matrix notation of the obtained equations [117,187,196].
Angular velocities of gears and carriers of the analysed PGS subsystems are determined in Section 3.3.1. A detailed analysis of the kinematics of these gears is presented in Appendix A and Appendix B. For this purpose, Willis formulas and other kinematic relations were used, which are briefly presented below. As well, the method of saving individual parameters was also explained.
The gear ratio of each gear transmission, both with fixed axes and a planetary gear with a single DoF, i.e., gears containing one active (a) and one passive (p) shaft, is determined from the formula:
where and are the absolute angular velocities of the active and passive shafts, respectively, i.e., their motion relative to the stationary gear housing.
Two Willis formulas for two drive directions in the analysed subsystems are presented below:
where is the transmission ratio (otherwise fixed carrier gear ratio), which is determined in the reference system associated with the carrier h, binding the angular velocity of the active shaft with the sun gear and the angular velocity of the passive shaft with rim gear , while is the fixed carrier gear ratio, binding the angular velocity of the active shaft with rim gear and the angular velocity of the passive shaft with sun gear .
In this way, two Willis formulas were derived for two possible directions of transmission of the drive, respectively, from the shaft with the sun gear to the shaft with the rim gear and vice versa in the reference system related to the carrier shaft h. The fixed carrier gear ratios and can also be expressed by geometric formulas depending on the type and number of teeth of the sun and rim gears of the subsystem, such as for type 2K-H:
where , , and are the tooth numbers of the sun, planet, and rim gears, respectively. Comparing the left-hand sides of Formulas (3) and (4) gives practical forms of the Willis equations:
The magnitudes and directions of the unknown angular velocity vectors of the gears and carriers are determined from a system of equations of type (5) derived for each of the subsystems of the PGS and supplemented with equations that enable the determination of the position of instant centres of rotation (Appendix B).
2.2.4. Static Analysis without Considering Meshing Friction
To determine the active and passive shafts of each of the subsystems of the PGS, and thus to determine the directions of the power flow, it is necessary to determine the magnitudes and directions of the torque vectors acting on the shafts of the sun gears, ring gears, and carriers of each subsystem. At this stage of calculations, it is possible to determine the magnitudes and directions of the torque without considering power losses, using graphical and analytical methods, including the free body diagram [172,173] and lever or nomograph methods [119,120,121,126,128,129,130,144,145,146,149,155]. The most popular techniques due to the possibility of automating calculations are the methods of classical directed or undirected graphs, signal graph, and contour graphs [12,142,144,145,146,162,169,177]. In Appendix C of this paper, the free body diagram method was used. Especially in order to facilitate the detection of the active and passive shafts of the subsystems, reaction torques have been additionally included. However, on the basis of only the data determined so far (angular velocities and torques), it is difficult to distinguish the active shaft(s) from the passive shaft(s). It is best to additionally use the equation of moment equilibrium and energy balance.
2.2.5. Identification of Active and Passive Shafts and Power Flow Directions
It is known that the dot product of the same-directed vectors of torque and angular velocity is , where , i.e., power is active, meaning that power is supplied to the subsystem through the active shaft. In the case of these vectors being oppositely directed, their product , i.e., the power is reactive, meaning that the power is discharged from the subsystem through the passive shaft. Then, the torque vector is a reaction torque, marked , which represents the resistance moment of the shaft of the adjacent driven subsystem. Thus, when identifying the active and passive shafts of subsystems connected in series or in parallel, two basic conditions for transferring power from or to a subsystem are used:
- (1)
- For the driving shaft, the vectors of the angular velocity and the torque are in the same direction ();
- (2)
- For the driven shaft, the vectors of the angular velocity and the reaction torque are oppositely directed ().
Unfortunately, these are only the conditions that must be met. The sufficient conditions are a system of governing equations derived separately for each of the subsystems with a mobility equal to 1 or 2. Each such system consists of a torque equilibrium equation and, practically, one energy balance equation in the reference system related to the stationary body, because the second equation of the energy balance in the system associated with the carrier can only be used for verification. A certain difficulty in deriving these equations for the subsystem with a mobility equal to 2 is the lack of identified characters of the two shafts (Figure 2). The nature of the third shaft is known because it is either the input or output shaft of the PGS, or it is an extension of the shaft of the adjacent subsystem whose shafts have been identified earlier (Figure 4). If, for instance, the shaft of an adjacent subsystem is passive, then the shaft of the analysed subsystem is active.
In the general case, there are three versions of the governing equations, assuming that the shaft of the sun gear is active.
First version modelling the type 2(a) subsystem:
where conditions for active and passive shafts are as follows: , and .
Second version modelling the type 2(e) subsystem:
where conditions for active and passive shafts are as follows: , and .
Third version modelling the type 2(f) subsystem:
where conditions for active and passive shafts are as follows: , and .
The fourth version, with three active shafts, is impossible to implement, both from a mathematical and technical point of view. The reasons for this are that the positive terms of the sum cannot be zero and that each gear transmission must have at least one input and one output.
Using the “trial and error” method, it is possible to choose the right version of the governing equations, because the magnitude of the active and reactive torques, as well as the products of the torques and angular velocities () and (), are known.
Of course, in the case of subsystems with a mobility equal to 1, there is no problem with identifying the power flow path, because such a subsystem, depending on the type, (Figure 3) has known input and output shafts. Moreover, its third shaft is fixed and, hence, its angular velocity and power are, respectively, and , where , or h. Then, the subsystem equilibrium equations are determined directly without fitting the conditions for active and passive shafts with one of the three versions of the Equations ((6), (7)), ((8), (9)) or ((10), (11)).
The directions of the power flow in a PGS are independent of whether power losses are considered or not when calculating the torques. The reason for this is that the active and reactive torque vectors calculated without taking into account the power losses and , respectively, differ only in magnitude from the corresponding torque vectors calculated taking into account these losses, and , respectively. This will be demonstrated in Part III of this paper.
The active and passive shafts of the transmission subsystems of the PGS determined in the above manner are presented in Section 3.3.4.
3. Case Study
3.1. Case Study Subjects
The purpose of this section is to present in detail the graphical and analytical method of determining the directions of the power stream flow in a PGS. In Part II, a very similar planetary gear in terms of geometric structure will be presented. However, such important parameters as the gear ratios , input angular velocities , and input torques of both systems will be the same. The forms of the PGSs have been specially selected so that their kinematic and dynamic similarities and differences can be demonstrated.
Figure 4 shows the diagrams of the analysed PGSs in the forms of (a) kinematic and (b) block, while Figure 5 shows diagram only in the expanded block form.
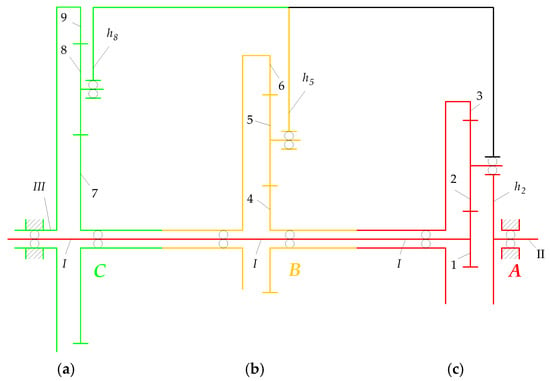
Figure 5.
Expanded block diagrams of analysed PGS subsystems (according to Table 1): (a) C—type 2(a), (b) B—type 2(e), (c) A—type 1(a).
The names of the subsystem types (according to Figure 2 and Figure 3) are shown in Table 1. For example, the subsystem A of type (2a) belonging to the analysed PGS corresponds to the block shown in Figure 2a.

Table 1.
Numbers of DoFs of the PGS subsystems.
3.2. Data
Table 2 presents data on the geometry of the gears of the analysed PGS.

Table 2.
Data on PGS.
Parameter symbols:
, , —number of teeth and pitch diameters, and gear modules ( to 9);
, —carriers radii and number of planet gears (), respectively. There is also input torque and input angular velocity (rotation velocity) ().
3.3. Power Flow Paths in PGS
3.3.1. Calculations of Angular and Tangential Velocities
The values of the fixed carrier transmission ratios of the subsystems A, B, and C and pairs of sun and planet gears are listed in Table 3 based on calculations in Appendix A. These parameters are necessary to determine the angular velocity of the gears and the carriers of the PGS.

Table 3.
Values of fixed carrier transmission ratio of subsystems of analysed PGS.
Designations of fixed carrier transmission ratios from Table 3: , , and —the ratios of the subsystems A, B, and C, respectively; , , and —the ratios of the sun–planet gear pairs , , and , respectively.
Detailed calculations of the angular and tangential velocities of the sun, ring, and planet gears and carriers are provided in Appendix A and Appendix B. In addition, the angular velocity magnitudes are presented in Table 4 and their directions are shown Figure A1, Figure A2 and Figure A3. Also, the directions of the tangential velocity vectors are shown in Figure A1, Figure A2 and Figure A3 and their magnitudes in Table A1 and Table A2.

Table 4.
Magnitudes of angular velocities of the PGS in .
From Equations (A1)–(A4), the formula for the total gear ratio of the PGS can be derived:
where the fixed carrier transmission ratio is:
3.3.2. Transmission Ratios on Power Flow Paths in Subsystems of Analysed PGS
According to Figure 4a, Figure 4b and Figure 5 and Table 1, the PGS consists of subsystems A and B with two DoFs each and subsystem C with a single DoF. Each single-DoF subsystem has only one power flow path, so the transmission ratio on the power flow paths of such a subsystem is equal to its gear ratio. In contrast, each two-DoF subsystem has two power flow paths. For this reason, for subsystems with two DoFs, it is possible to determine only the transmission ratios on individual paths of the power flow, considering the angular velocity of the third element of each subsystem. The values of these ratios have been calculated in Appendix D and presented in Table 5. According to the algorithm (Section 2), they will be used to determine the torque acting on the sun and rim gears and the carriers of each of the A, B, and C subsystems and the power on the individual power flow paths (Appendix D).

Table 5.
The transmission ratios on the power flow paths in subsystems of analysed PGS.
3.3.3. Calculations of the Shaft Torques of Subsystems A, B, C
- Shaft torques of the two DoF subsystem A
According to Figure 4a and Table 3, the torque acting on the input shaft I of the PGS is given as . Therefore, it was used to calculate the active and reactive torques , and , on the shafts of carrier and rim gear 3, respectively, in Appendix C. Equilibrium Equations (A32) and (A41)–(A44) were derived using the free body diagram based on Figure A4. The magnitudes of the calculated torques are presented in Table 6. In Section 3.3.4, they will be used together with the magnitudes of angular velocities and (from Table 4) to select the appropriate system of equations to determine the two power flow paths in subsystem A.

Table 6.
Torque magnitudes , and , .
- Shaft torques of the two DoF subsystem B
According to Equation (A45) and Figure A5, the torque , acting on the input shaft of sun gear 4, is equal to . Therefore, it was used to calculate the active and reactive torques , and , of the carrier and rim gear 6 shafts, respectively. The magnitudes and vector directions of these torques were determined in Appendix C from the equilibrium Equations (A46) and (A55)–(A58) based on Figure A6.
The magnitudes of the calculated torques are presented in Table 7. In Section 3.3.4, they will be used together with the angular velocities and (from Table 6) to select the appropriate system of equations to determine the two power flow paths in subsystem B.

Table 7.
Torque magnitudes , and , .
- Shaft torques of the single DoF subsystem C
According to Equations (A59) and (A60) and Figure A7, the torque acting on the shaft of rim gear 7 is given as . Therefore, it was used to calculate the active and reactive torques , and , of the shafts of carrier and rim gear 9, respectively. The magnitudes and directions of these torques were determined in Appendix C from the equilibrium Equations (A67), (A68), (A71), and (A72) based on Figure A8. The magnitudes of the calculated torques are presented in Table 8. In Section 3.3.4, they will be used together with the angular velocities and (from Table 4) to select the appropriate equation to determine the one power flow path in subsystem C.

Table 8.
Torque magnitudes , and , .
3.3.4. Power Flow Paths in the Subsystems A, B, C of the PGS
- Identification of the power flow paths in type 2(a), 2(e) or 2(f) subsystem A
In Section 2.2.5, it was shown that one of the three versions of the system of Equations ((6), (7)), ((8), (9)) or ((10), (11)) can be a great help in identifying active and passive shafts in series-parallel connected PGS subsystems. Each system of equations in these three versions models the subsystems of type 2(a), 2(e), and 2(f) in order. The chosen version of the system of equations is the one that is satisfied by one of the following pairs of necessary conditions:
It can easily be shown that the system of Equations ((6), (7)) is satisfied by a pair of conditions (14). The adapted version of the selected system of Equations ((6), (7)) for the new indices of subsystem A elements took the form:
where the new indices are adapted as , , and (according to Figure 2a).
The above two Equations are a mathematical model of subsystem A type 2(a), in which the input shaft of sun gear 1 is assumed to be driving (), while the shafts of carrier and ring gear 3 are driven ( and ). The directions of torques , , and are shown in Figure 6.
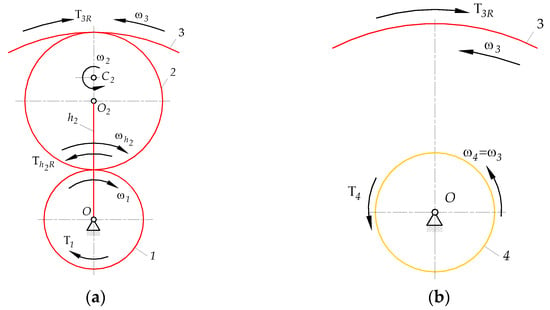
Figure 6.
Angular velocities and torques (a) of elements of subsystem A, (b) of gear pair 3, 4.
Torque must also satisfy the additional equation of energy balance in the carrier mobile frame of reference (19), so there is a second method to check its magnitude in addition to the free body diagram used in Appendix C (Equation (A44)):
Identification of the power flow paths in type 2(a), 2(e) or 2(f) subsystems B
A possible condition to satisfy one of the three versions of Equation pairs ((6), (7)), ((8), (9)), or ((10), (11)) for subsystem B is among the three below:
The system of Equations ((8), (9)) is satisfied by a pair of conditions (21); therefore, the adapted version of these equations takes the following form for subsystem B indices:
where the new indices are adapted as , , and (according to Figure 2e).
Equations (23) and (24) are a mathematical model of subsystem B type 2(e), in which the input shaft of sun gear 4 must be driving (), while the shaft of rim gear 6 is driven () and the shaft of carrier is driving (). The directions of torque vectors , , and are shown in Figure 7.
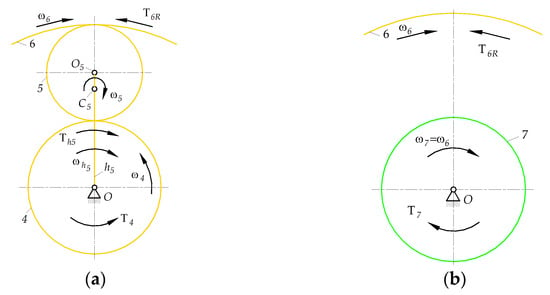
Figure 7.
Angular velocities and torques (a) of elements of subsystem B, (b) of gear pair 6, 7.
Torque must also satisfy the additional equation of the energy balance in the mobile reference frame related to carrier (25), so there is a second method to check its magnitude in addition to the free body diagram used in Appendix C (Equation (A58)):
- Identification of the power flow path in the type 1(a) subsystem C
According to Figure 3a, Figure 4, and Figure 6a and Table 1, subsystem C has one DoF and is type 1(a). Therefore, it has one power flow path from the input shaft of sun gear 7 to the output shaft of carrier because the shaft of ring gear 9 is fixed. In this case, the governing equation can be determined directly without fitting the conditions for active and passive shafts by one of the three versions of Equations ((6), (7)), ((8), (9)) or ((10), (11)):
where the new indices are adapted as , , (according to Figure 3a) and (according to Equations (A57) and (A60)).
The form of these equations is consistent with the assumption that, in this subsystem which has one DoF, the shaft of sun gear 7 is driving, the shaft of carrier is driven, and ring gear 9 is fixed (). These assumptions correspond to the conditions , , and . The directions of the torque vectors and are shown in Figure 8 and Figure A8.
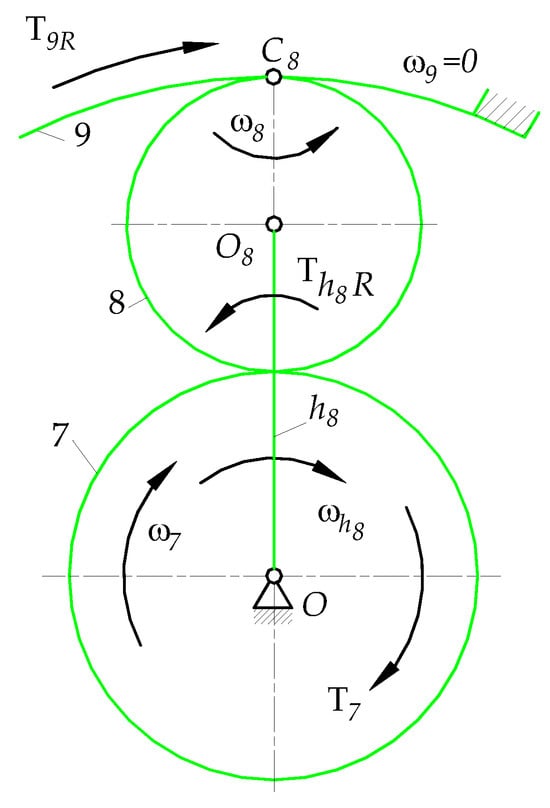
Figure 8.
Angular velocities and torques of elements of subsystem C.
The torque must also satisfy the additional energy balance equation in the reference frame related to the carrier (28), so there is a second method to check its magnitude in addition to the free body diagram used in Appendix C (Equation (A68)):
For the previously determined torques acting on the shafts of carriers , , and , it is possible to calculate the total torque on the output shaft II of the analysed PGS:
and check the total gear ratio (for efficiency ):
- Identification of the power flow path in analysed PGS (summary)
Based on Equations (17), (18), (23), and (24), and (28) and (29), and Table 6, collective Table 9 was prepared, which presents the active and passive gears and carriers of the analysed PGS, and thus the active and passive shafts of these elements.

Table 9.
Active and reactive shafts of analysed PGS.
3.3.5. Powers and Power Ratios on the Shafts of Subsystems A, B, C of Analysed PGS
- Calculations of powers and power ratios on the shafts of subsystem A
The power calculations and power ratios in the subsystem A were made in Appendix D (Equations (A73) to (A79)). The values of the power and power ratios are presented in Table 10 and Table 11, respectively.

Table 10.
Values of active and reactive power on the shafts of subsystem A.

Table 11.
Power ratios on the shafts of subsystem A.
Table 11 shows that only 1% of the power supplied to subsystem A is transferred to the PGS output shaft, while the rest is supplied to subsystem B through the shafts of rim gear 3 and sun gear 4.
- Calculations of powers and power ratios of subsystem B
The power calculations and power ratios in subsystem B were made in Appendix D (Equations (A80) to (A87)). The values of the power and power ratios are presented in Table 12 and Table 13, respectively.

Table 12.
Values of active and reactive power on the shafts of subsystem B.

Table 13.
Power ratios on the shafts of subsystem B.
Table 12 shows that the shafts of sun gear 4 and the carrier of subsystem B are active because the powers and .
- Calculations of powers and power ratios on the shafts of subsystem C
The power calculations and power ratios in subsystem C were made in Appendix D (Equations (A88)–(A96)). The values of the power and power ratios are presented in Table 14 and Table 15, respectively.

Table 14.
Values of active and reactive power on the shafts of subsystem C.

Table 15.
Power ratios on the shafts of subsystem C.
The shaft of rim gear 9 is fixed, so the power (Table 14). Table 15 shows, among others, the value of the power ratio equal to , which means that, according to the assumption, no power loss occurred in the analysed PGS. However, Table 13 and Table 15 show that the bearings and shafts of ring gear 6, sun gear 7, planet gear 8, and the carriers and are overloaded by more than 10%. The reason for this is that the above-mentioned elements of the B and C subsystems form a closed loop inside which the power transmitted by the carrier shaft is closed. Colloquially, it is often said that this power circulates in a closed loop, but unfortunately it is not a vector.
4. Results
Figure 9 shows the paths and directions of the flow of the power streams in the coupled serial-parallel planetary gear system without taking friction losses into account. To determine these paths, a modified classical method was used by explicitly introducing reaction moments (Section 3.3.4 and Table 9). The calculations showed that the analysed PGS is coupled not only structurally through two closed circuits, but also dynamically. Namely, in the second circuit, there is a phenomenon of power circulation because the shaft of carrier is active in contrast to the shafts of carriers and , which are passive. Through the shaft of carrier , the power is transmitted to the inside of the second PGS circuit according to calculation results (A81) and (A85), presented in Table 13, which increased the power ratio to 110.7% according to calculation results (A86), (A91), and (A92). Through the shafts of carriers and , the power is transmitted to the output shaft II PGS, i.e., outside according to calculation results (A75) and (A92). As a result of the power circulation, the meshing of gears 5–6, 7–8, and 8–9 and the adjacent rolling bearings are overloaded. The output power, despite the power circulation in a closed circuit, reached 100% of the input power (according to formula (96) and Table 15).
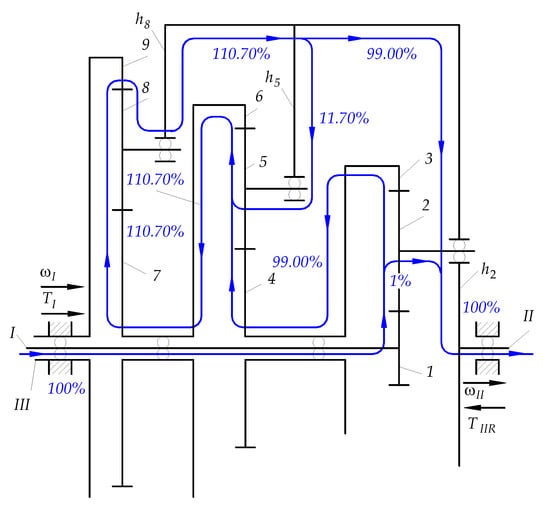
Figure 9.
Directions of power stream flows and power ratios in the coupled PGS.
5. Conclusions
In this paper, which is the first part of a three-part study, a systematic methodology for determining the paths and directions of power flow in coupled serial-parallel PGSs has been presented. These single-degree-of-freedom PGSs consisted of three 2KH type subsystems and two closed circuits. The aim of developing the three parts of this study was:
- (1)
- The comparison of power flow paths and directions without considering power losses in two structurally similar PGSs, the first of which turned out to be structurally coupled (with a closed circuit) and dynamically coupled (with the power circulation phenomenon) during the analysis carried out in Part I, while the second PGS, analysed in part II, turned out to only be structurally coupled without power circulation;
- (2)
- The comparison of power flow paths and directions, considering power losses in gear meshing, and the determination of the power ratios and efficiency of these two PGSs (in Part III).
The algorithm of the method was as follows (assuming that the geometric parameters of the PGS are already given):
- (1)
- Checking the PGS mobility, dividing the PGS structure into blocks (subsystems) and closed circuits, and determining the fixed carrier transmission ratio of individual subsystems;
- (2)
- The determination of the magnitudes of the angular velocities of the gears and carriers, as well as gear ratios of the individual subsystems and PGSs using the Willis relationship;
- (3)
- Determining the magnitudes of the active and reactive torques, as well as the tangential and radial forces, using the free body diagram, which is necessary to calculate the active or reactive powers transmitted by the shafts of individual subsystems;
- (4)
- The determination of the paths with power flow directions by defining the role of individual subsystem shafts (active shafts—supplying power to the subsystem, passive shafts—discharging power from the subsystem)—an original method using the concepts of active and reactive torques, as well as active and reactive powers;
- (5)
- The calculation of power values and power ratios as a check of the algorithm.
Author Contributions
Conceptualization, J.D. and T.K.; methodology, J.D. and T.K.; software, K.S.; formal analysis, T.K.; writing—original draft preparation, J.D. and T.K.; writing—review and editing, J.D.; visualization, J.D., J.R. and K.S.; funding acquisition, J.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Willis Formulas for Subsystems A, B, C and PGS
- Equation for subsystem A (Figure A1):
- Equation for subsystem B (Figure A2):
- Equation for subsystem C (Figure A3):
Appendix A.2. Willis Formulas for Sun Gear and Planet Gear Pairs
- Equation for sun gear 1 and planet gear 2:
- Equation for sun gear 4 and planet gear 5:
- Equation for sun gear 7 and planet gear 8:
Appendix A.3. Calculations of Angular Velocities of Gears and Carriers of PGS
- Angular velocities of the carriers h2, h5 and h8:
- Angular velocities of rim gear 3 and sun gear 4:
- Angular velocities of rim gear 6 and sun gear 7:
- Angular velocity of planet gear 2:
- Angular velocity of planet gear 5:
- Angular velocity of planet gear 8:
Appendix B
Appendix B.1. Calculation of Tangential Velocities of the Gears of PGS
- Assumption that the tangential velocities of the planet gears , , , , , are equal to the respective velocities of the sun and rim gears at their points of contact (according to Figure A1, Figure A2 and Figure A3):, , , , , .The calculated magnitudes of these velocities are given in Table A1.

Table A1.
Calculated magnitudes of tangential velocities in .
Table A1.
Calculated magnitudes of tangential velocities in .
| 1.385 | −1.372 | −0.229 | 0.256 | 0.047 | 0 |
Appendix B.2. Determination of Instantaneous Centre of Zero Velocity and Velocities of the Carrier
- The coordinate of the instantaneous centre of zero velocity of planet gear 2 (Figure A1a):
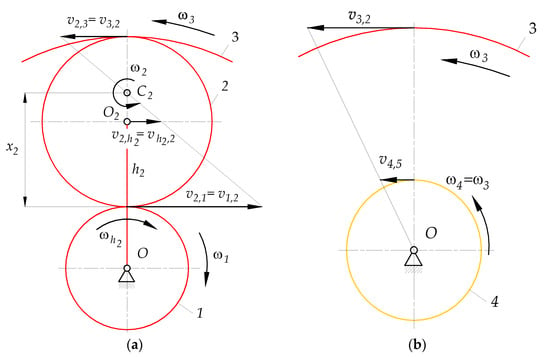
Figure A1.
Angular and tangential velocities (a) of the elements of subsystem A (b) of the pair of gears 3, 4.
- Angular velocity of the planet gear 2 (check (A13)):
- Tangential velocities and of the centre of planet gear 2 and carrier , respectively (Figure A1a):
- Angular velocities of carrier (Figure A1a):
- Tangential velocity of sun gear 4 at the point of contact with planet gear 5 (Figure A1b):
Appendix B.3. Determination of Instantaneous Centre of Zero Velocity and Velocities of the Carrier
- The coordinate of the instantaneous centre of zero velocity of planet gear 5 (Figure A2a):
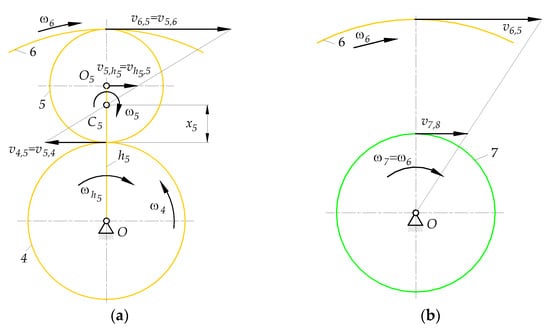
Figure A2.
Angular and tangential velocities (a) of the elements of subsystem B (b) of the pair of gears 6, 7.
- Angular velocity of planet gear 5 (check (A14)):
- Tangential velocities and of the centre of planet gear 5 and carrier , respectively (Figure A2a):
- Angular velocity of carrier (Figure A2a):
- Tangential velocity of sun gear 7 at the point of contact with the planet gears 8 (Figure A2b):
Appendix B.4. Determination of Instantaneous Centre of Zero Velocity and Velocities of the Carrier
- The coordinate of the instantaneous centre of zero velocity of planet gear 8 (Figure A3):
Instantaneous centre of zero velocity of gear 8 is at the point of contact with stationary ring gear 8, because (Figure A3). Thus, tangential velocities and are equal .
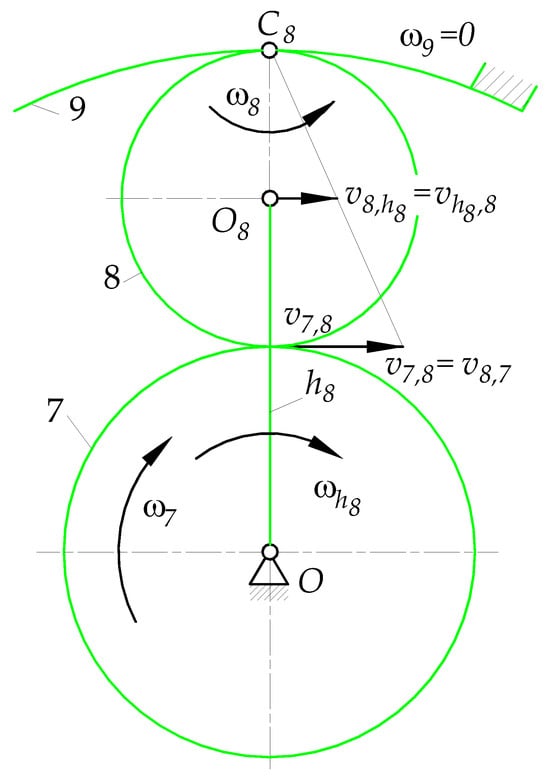
Figure A3.
Angular and tangential velocities of subsystem C.
- Angular velocity of planet gear 8 (check (A15)):
- Magnitude of velocities and , respectively, of the centre of planet gear 8 and carrier (Figure A3):
- Angular velocity of carrier (Figure A3):

Table A2.
Velocity magnitudes of the centres of planet gears 2, 5, and 8 and carriers , , and in .
Table A2.
Velocity magnitudes of the centres of planet gears 2, 5, and 8 and carriers , , and in .
| 0.007 | 0.014 | 0.024 |
Appendix C
Appendix C.1. Calculation of Torques, Tangential and Radial Forces Acting on Gears 1, 2, 3 and Carrier
- The tangential force exerted by planet gear 2 on sun gear 1 (Figure A4a):
- The radial force exerted by planet gear 2 on sun gear 1:
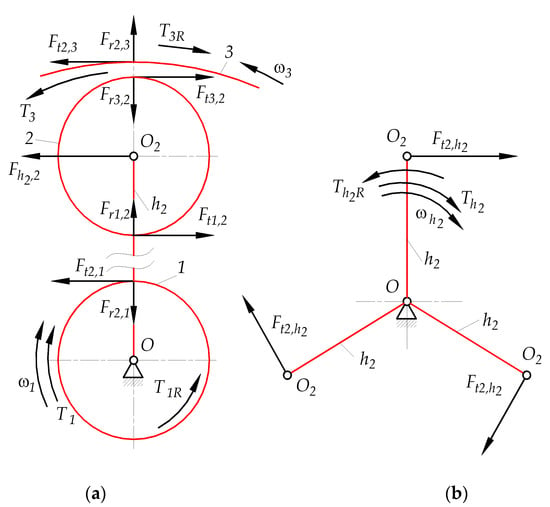
Figure A4.
Free body diagrams of the subsystem A elements: (a) gears 1, 2, 3, (b) carrier .
- The tangential force exerted by sun gear 1 on planet gear 2:
- The radial force exerted by sun gear 1 on planet gear 2:
- The tangential force exerted by ring gear 3 on planet gear 2:
- The tangential force exerted by planet gear 2 on ring gear 3:
- The radial forces and exerted, respectively, by planet gear 2 on ring gear 3 and vice versa by ring gear 3 on planet gear 2:
- The force exerted by carrier on the centre of planet gear 2 (Figure A4b):
- The tangential force exerted by the centre of planet gear 2 on carrier :
- The active torque transmitted to the shaft of the working machine II through the shaft of carrier :
- The reaction torque (generated by the resistance of the working machine) balancing the active torque :
- The active torque transmitted to the shaft of sun gear 4 through the shaft of ring gear 3):
- The reaction torque (generated by the resistance of subsystem B) balancing the active torque :
Appendix C.2. Calculation of Torques, Tangential and Radial Forces Acting on Gears 4, 5, 6 and Carrier
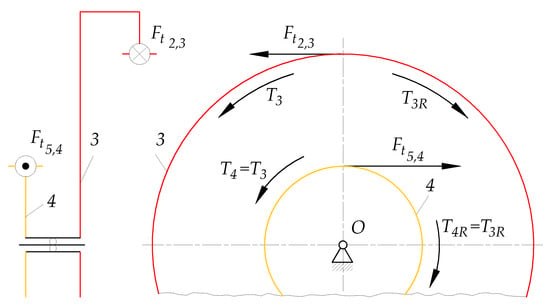
Figure A5.
Balance of active and reaction torques acting on ring gear 3 and sun gear 4.
- The reaction torque balancing the active torque :
- The tangential force exerted by planet gear 5 on sun gear 4 (Figure A6a):
- The tangential force exerted by sun gear 4 on planet gear 5:
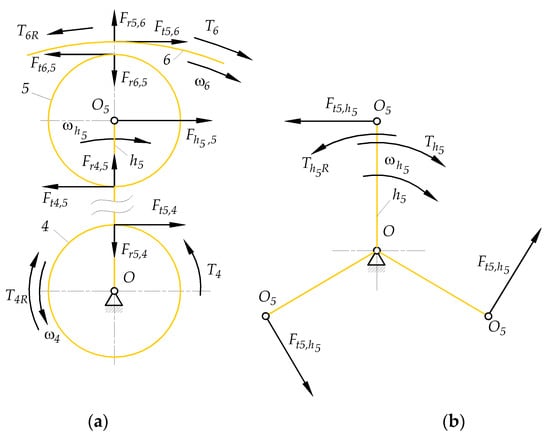
Figure A6.
Free body diagrams of the subsystem B elements: (a) gears 4, 5, 6, (b) carrier .
- The radial forces and exerted respectively by planet gear 5 on sun gear 4 and vice versa by sun gear 4 on planet gear 5 (Figure A6a):
- The tangential force exerted by ring gear 6 on planet gear 5:
- The tangential force exerted by planet gear 5 on ring gear 6:
- The radial forces and exerted, respectively, by planet gear 5 on ring gear 6 and vice versa by ring gear 6 on planet gear 5 (Figure A6a):
- The force exerted by the carrier on the centre of planet gear 5 (Figure A6b):
- The tangential force exerted by the centre of planet gear 5 on carrier :
- The active torque driving the shaft of carrier and carrier according to Figure A6b:
- The reaction torque balancing the active torque :
- The active torque driving the shaft of sun gear 7 through the shaft of ring gear 6 (Figure A7):
- The reaction torque balancing the active torque :
Appendix C.3. Calculation of Torques, Tangential and Radial Loads Acting on Gears 7, 8, 9 and Carrier
- The reaction torque balancing the active torque (Figure A7):
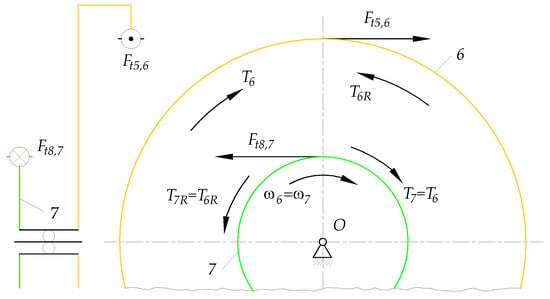
Figure A7.
Balance of active and reaction torques acting on ring gear 6 and sun gear 7.
- The active torque driving the shaft of sun gear 7 (Figure A7):
- The tangential force exerted by planet gear 8 on sun gear 7 according to Figure A8a:
- The tangential force exerted by sun gear 7 on planet gear 8:
- The radial forces and exerted, respectively, by planet gear 8 on sun gear 7 and vice versa by sun gear 7 on planet gear 8 (Figure A8a):
- The tangential force exerted by ring gear 9 on planet gear 8:
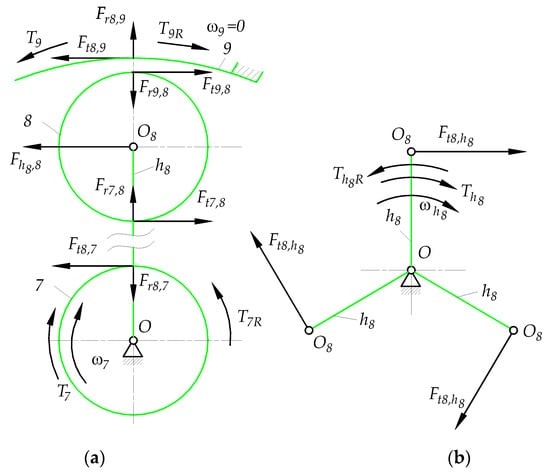
Figure A8.
Free body diagrams of the subsystem C elements: (a) gears 7 8, 9, (b) carriers .
- The tangential force exerted by planet gear 8 on ring gear 9:
- The radial forces and exerted, respectively, by ring gear 9 on planet gear 8 and vice versa by planet gear 8 on ring gear 9 (Figure A8a):
- The active torque loading fixed ring gear 9:
- The reaction torque balancing the active torque :
- The force exerted by the carrier on the centre of planet gear 8 (Figure A8a):
- The tangential force exerted by the centre of planet gear 8 on carrier (Figure A8b):
- The active torque driving the shaft of carrier :
- The reaction torque balancing the active torque :
Appendix D
Appendix D.1. Calculations of Powers and Power Ratios of Subsystem A
- Power transmitted to subsystem A by the shaft I of sun gear 1 ():
- Power transmitted outside subsystem A by the shaft of ring gear 3 ():
- Power transmitted outside subsystem A by the shaft of carrier ():
- Power ratio in the power flow path from the input shaft to the shaft of carrier (Figure 9):
- Power ratio in the power flow path from the input shaft I to the shaft of ring gear 3 (Figure 9):
- Power ratio in the power flow paths from the input shaft I to the shafts of carrier and rim gear 3 (checking the absence of the power losses in subsystem A):
Appendix D.2. Calculations of Powers and Power Ratios of Subsystem B
- Power transferred to subsystem B by the shaft of sun gear 4:
- Power transmitted to subsystem B by the shaft of carrier :
- Power transmitted outside subsystem B by the shaft of ring gear 6:
- Power ratio in the power flow path from the shaft of rim gear 3 to the shaft of sun gear 4 i.e., from subsystem A to subsystem B (Figure 9):
- Power ratio in the power flow path from the shaft of carrier to subsystem B due to the coupling phenomenon (Figure 9):
- Power ratio in the power flow path from the shaft of rim gear 6 to the shaft of sun gear 7 i.e., from subsystem B to subsystem C (Figure 9):
- Power ratio in the power flow paths from the shafts of sun gear 4 and carrier to the shaft of rim gear 6 (checking for no power loss in subsystem B):
Appendix D.3. Calculations of Powers and Power Ratios of Subsystem C
- Power transmitted to subsystem C by the shaft of sun gear 7:
- Power transmitted to the fixed shaft of ring gear 9 ():
- Power transmitted to the outside of the subsystem C by the shaft of carrier :
- Power ratio in the power flow path from the shaft of rim gear 6 to the shaft of sun gear 7 i.e., from subsystem B to subsystem C (Figure 9):
- Power ratio in the power flow path from the shaft of sun gear 7 to the shaft of carrier (Figure 9):
- Power ratio in the power flow path along the shaft of carrier from connection point with the carriers shafts and before connection point with the carrier (Figure 9):
- Power transmitted by the output shaft II of the PGS:
- Power ratio in the power flow paths between input shaft I and output shaft II (confirmation of no power loss):
- The efficiency of the PGS (confirmation of no power loss):
- Torque acting on the output shaft II:
- Total gear ratio (for ):
References
- Davies, T. An extension of Manolescu’s classification of planar kinematic chains and mechanisms of mobility M ≥ 1, using graph theory. J. Mech. 1968, 3, 87–100. [Google Scholar] [CrossRef]
- Gogu, G. Mobility of mechanisms: A critical review. Mech. Mach. Theory 2005, 40, 1068–1097. [Google Scholar] [CrossRef]
- Gogu, G. Chebychev–Grübler–Kutzbach’s criterion for mobility calculation of multi-loop mechanisms revisited via theory of linear transformations. Eur. J. Mech. 2005, 24, 427–441. [Google Scholar] [CrossRef]
- Liberati, A.; Belfiore, N.P. A method for the identification of the connectivity in multi-loop kinematic chains: Analysis of chains with total and partial mobility. Mech. Mach. Theory 2006, 41, 1443–1466. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, J.; Li, Q. A Unified Methodology for Mobility Analysis Based on Screw Theory. In Smart Devices and Machines for Advanced Manufacturing; Wang, L., Xi, J., Eds.; Springer: London, UK, 2008; pp. 49–76. [Google Scholar]
- Zhua, X.; Shena, H.; Wua, C.; Chablat, D.; Yang, T. Computer-aided mobility analysis of parallel mechanisms. Mech. Mach. Theory 2020, 148, 103810. [Google Scholar] [CrossRef]
- Laughlin, H.; Holowenko, A.; Hall, A. How to determine circulating power in controlled epicyclic gear systems. Mach. Des. 1956, 28, 132–136. [Google Scholar]
- Gupta, A.K.; Ramanarayanan, C.P. Analysis of circulating power within hybrid electric vehicle transmissions. Mech. Mach. Theory 2013, 64, 131–143. [Google Scholar] [CrossRef]
- Bottiglione, F.; De Pinto, S.; Mantriota, G. Infinitely Variable Transmissions in neutral gear: Torque ratio and power recirculation. Mech. Mach. Theory 2014, 74, 285–298. [Google Scholar] [CrossRef]
- Hussen, H.A.; Hussain, R.A.; Esmail, E.L. A Simplified Algorithm for Detecting Power Recirculation within 1-Dof Multi-Entity Planetary Gear Trains. In Proceedings of the 3rd International Conference on Sustainable Engineering Techniques, Baghdad, Iraq, 15 April 2020; IOP Publishing: Bristol, UK, 2020. [Google Scholar] [CrossRef]
- Chen, H.; Chen, X.-A. Recirculation of Parallel-Connected Planetary Gear Trains. Chin. J. Mech. Eng. 2022, 35, 27. [Google Scholar] [CrossRef]
- Kudrjavtzev, V.N.; Kirdjashev, J.N. (Eds.) Planetary Gears—Handbook; Mashinostroenie Moskwa: Moscow, Russia, 1977. (In Russian) [Google Scholar]
- Rudenko, B.N. Planetary and Wave Gears; Mashinostroenie Moskwa: Moscow, Russia, 1980. (In Russian) [Google Scholar]
- Looman, J. Zahnradgetriebe; Springer: Berlin/Heidelberg, Germany, 1996. (In German) [Google Scholar]
- Müller, L.; Wilk, A. Planetary Gears; PWN: Warsaw, Poland, 1996. (In Polish) [Google Scholar]
- Arnaudov, K.; Karaivanov, D.P. Planetary Gear Trains; CRC Press: London, UK; Taylor & Francis Group: New York, NY, USA, 2019. [Google Scholar]
- Krukowski, A. Fundamentals of planetary gear theory. In Machine Design Basics; Dietrich, M., Ed.; PWN: Warsaw, Poland, 1991; Volume 4, pp. 330–360. (In Polish) [Google Scholar]
- Radzimovsky, E.I. A Simplified Approach for Determining Power Losses and Efficiency of Planetary Gear Drives. Mach. Des. 1956, 28, 101–110. [Google Scholar]
- Radzimovsky, E.I. How to find efficiency, speed and power losses in planetary gear drives. Mach. Des. 1959, 31, 144–153. [Google Scholar]
- Macmillan, R.H. Power flow and loss in differential mechanisms. J. Mech. Eng. Sci. 1961, 3, 37–41. [Google Scholar] [CrossRef]
- Sanger, D. The determination of power flow in multiple-path transmission systems. Mech. Mach. Theory 1972, 7, 103–109. [Google Scholar] [CrossRef]
- Salgado, D.R.; Del Castillo, J.M. Selection and Design of Planetary Gear Trains Based on Power Flow Maps. J. Mech. Des. 2005, 127, 120–134. [Google Scholar] [CrossRef]
- Bu, Z.; Liu, G.; Wu, L.; Liu, Z. Kinematics and Statics Analysis for Power Flow Planet Gear Trains. In Global Design to Gain a Competitive Edge; Yan, X.-T., Eynard., B., Ion, W.J., Eds.; Springer: London, UK, 2008; pp. 631–640. [Google Scholar]
- Dooner, D.; Yoon, H.-D.; Seireg, A. Kinematic considerations for reducing the circulating power effects in gear-type continuously variable transmissions. Proc. IMechE Part D J. Automob. Eng. 1998, 212, 436–478. [Google Scholar] [CrossRef]
- Hedman, A. Transmission Analysis—Automatic Derivation of Relationships. J. Mech. Des. 1993, 115, 1031–1037. [Google Scholar] [CrossRef]
- Rabindran, D.; Tesar, D. ParametricDesign and Power-Flow Analysis of Parallel Force/Velocity Actuators. J. Mech. Robot. 2009, 1, 011007-1. [Google Scholar] [CrossRef]
- Rabindran, D.; Tesar, D. ParametricDesign of Parallel Force/Velocity Actuators: Force Distribution Analysis. J. Mech. Robot. 2010, 2, 011013-1. [Google Scholar] [CrossRef]
- Wang, C.; Cui, H.-Y. The analysis of power circulation and the simplified expression of the transmission efficiency of 2K-H closed epicyclic gear trains. Meccanica 2013, 48, 1071–1080. [Google Scholar] [CrossRef]
- Arnaudov, K.; Karaivanov, D. Alternative Method for Analysis of Complex Compound Planetary Gear Trains: Essence and Possibilities. In Power Transmissions, Mechanisms and Machine Science 13; Dobre, G., Ed.; Springer Science & Business Media: Dordrecht, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q. Power analysis and efficiency calculation of the complex and closed planetary gears transmission. Energy Procedia 2016, 100, 423–433. [Google Scholar]
- Nutakor, C.; Kłodowski, A.; Sopanen, J.; Mikkola, A.; Pedrero, J.I. Planetary gear sets power loss modeling: Application to wind turbines. Tribol. Int. 2017, 105, 42–54. [Google Scholar] [CrossRef]
- Theochari, G.; Troha, S.; Karaivanov, D. Reducer with a planetary gear train for a hoisting mechanism of dangerous goods cranes. Int. Scient. J. “Trans Motauto World” 2020, 5, 125–128. [Google Scholar]
- Hussen, H.A.; Essam Lauibi Esmail, E.L.; Hussen, R.A. Power Flow Simulation for Two-Degree-of-Freedom Planetary Gear Transmissions with Experimental Validation. Hindawi Model. Simul. Eng. 2020, 2020, 8837605. [Google Scholar] [CrossRef]
- Sun, Z.; Gao, B.; Jin, J.; Sanada, K. Power Loss Evaluation of Automated Manual Transmission with Gearshift Assistant Mechanism. Int. J. Automot. Technol. 2021, 22, 441–454. [Google Scholar] [CrossRef]
- Kahraman, A.; Ligata, H.; Kienzle, K.; Zini, D.M. A Kinematics and Power Flow Analysis Methodology for Automatic Transmission Planetary Gear Trains. J. Mech. Des. 2004, 126, 1071–1081. [Google Scholar] [CrossRef]
- Dong, P.; Liu, Y.; Tenberge, P.; Xu, X. Design and analysis of a novel multi-speed automatic transmission with four degrees-of-freedom. Mech. Mach. Theory 2017, 108, 83–96. [Google Scholar] [CrossRef]
- Liu, J.; Yu, L.; Zeng, Q.; Li, Q. Synthesis of multi-row and multi-speed planetary gear mechanism for automatic transmission. Mech. Mach. Theory 2018, 128, 616–627. [Google Scholar] [CrossRef]
- Hwang, W.-M.; Huang, Y.-L. Connecting clutch elements to planetary gear trains for automotive automatic transmissions via coded sketches. Mech. Mach. Theory 2011, 46, 44–52. [Google Scholar] [CrossRef]
- Ciobotaru, T.; Frunzeti, D.; Rus, I.; Jantschi, L. Method for analyzing multi-path power flow transmissions. Proc. IMechE Part B J. Eng. Manuf. 2009, 224, 1447–1454. [Google Scholar] [CrossRef]
- Chen, H.; Chen, X.A. New Methodology for Multistage Multispeed Planetary Transmission Design Based on Geometry. J. Mech. Des. 2021, 143, 113401. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, X. Optimization of the Quality of the Automatic Transmission Shift and the Power transmission Characteristics. Energies 2022, 15, 4672. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, J.; Zhang, W. Influence of a New Type of Two-Speed Planetary Gear Automatic Transmission on the Performance of Battery Electric Vehicles. Energies 2022, 15, 4162. [Google Scholar] [CrossRef]
- Mangialardi, L.; Mantriota, G. The advantages of using continuously variable transmission in wind power systems. Renew. Energy 1992, 2, 201–209. [Google Scholar] [CrossRef]
- Mangialardi, L.; Mantriota, G. Power flows and efficiency in infinitely variable transmissions. Mech. Mach. Theory 1999, 34, 973–994. [Google Scholar] [CrossRef]
- Mantriota, G. Theoretical and experimental study of power split CVT systems: Part I. Proc. IMechE Part D J. Automob. Eng. 2001, 215, 837–850. [Google Scholar] [CrossRef]
- Mantriota, G. Theoretical and experimental study of power split CVT systems: Part II. Proc. IMechE Part D J. Automob. Eng. 2001, 215, 851–864. [Google Scholar] [CrossRef]
- Mucino, V.H.; Lu, Z.; Smith, J.E.; Kimcikiewicz, M.; Cowan, B. Design of continuously variable power split transmission systems for automotive applications. Proc. IMechE Part D J. Automob. Eng. 2001, 215, 469–478. [Google Scholar] [CrossRef]
- Mantriota, G. Performances of a series infinitely variable transmission with type I power flow. Mech. Mach. Theory 2002, 37, 579–597. [Google Scholar] [CrossRef]
- Mantriota, G. Performances of a parallel infinitely variable transmissions with a type II power flow. Mech. Mach. Theory 2002, 37, 555–578. [Google Scholar] [CrossRef]
- Zhao, X.; Maißer, P. A novel power splitting drive train for variable speed wind power generators. Renew. Energy 2003, 28, 2001–2011. [Google Scholar] [CrossRef]
- Linares, P.; Méndez, V.; Catalán, H. Design parameters for continuously variable power-split transmissions using planetaries with 3 active shafts. J. Terramechanics 2010, 47, 323–335. [Google Scholar] [CrossRef]
- Macor, A.; Rossett, A. Optimization of hydro-mechanical power split transmissions. Mech. Mach. Theory 2011, 46, 1901–1919. [Google Scholar] [CrossRef]
- Bottiglione, F.; Mantriota, G. Power Flows and Efficiency of Output Compound e-CVT. Intern. J. Veh. Des. 2015, 2015, 136437. [Google Scholar] [CrossRef]
- Mantriota, G. Power split transmissions for wind energy systems. Mech. Mach. Theory 2017, 117, 160–174. [Google Scholar] [CrossRef]
- Ismaeil, E.L. Comments on “Power flow and efficiency analysis of epicyclic gear transmission with split power”. Mech. Mach. Theory 2017, 115, 237–243. [Google Scholar]
- Esmail, E.L. Comments on “Analysis of circulating power within hybrid electric vehicle transmissions”, Mechanism and Machine Theory 64 (2013) 131–143, by A.K. Gupta, C.P. Ramanarayanan. Mech. Mach. Theory 2018, 121, 425–429. [Google Scholar] [CrossRef]
- Cammalleri, M.; Rotella, D. Functional design of power-split CVTs: An uncoupled hierarchical optimized model. Mech. Mach. Theory 2017, 116, 294–309. [Google Scholar] [CrossRef]
- Rotella, D.; Cammalleri, M. Direct analysis of power-split CVTs: A unified method. Mech. Mach. Theory 2018, 121, 116–127. [Google Scholar] [CrossRef]
- Rotella, D.; Cammalleri, M. Power losses in power-split CVTs: A fast black-box approximate method. Mech. Mach. Theory 2018, 128, 528–543. [Google Scholar] [CrossRef]
- Xiong, S.; Wilfong, G.; Lumkes, J., Jr. Components Sizing and Performance Analysis of Hydro-Mechanical Power Split Transmission Applied to a Wheel Loader. Energies 2019, 12, 1613. [Google Scholar] [CrossRef]
- Wang, G.; Song, Y.; Wang, J.; Wanqiang Chen, W.; Cao, Y.; Wang, J. Study on the Shifting Quality of the CVT Tractor under Hydraulic System Failure. Appl. Sci. 2020, 10, 681. [Google Scholar] [CrossRef]
- Neagoe, M.; Saulescu, R.; Jaliu, C.; Simionescu, P.A. A Generalized Approach to the Steady-State Efficiency Analysis of Torque-Adding Transmissions Used in Renewable Energy Systems. Energies 2020, 13, 4568. [Google Scholar] [CrossRef]
- Lin, A.-D.; Hung, T.-D.; Kuang, J.-H.; Tsai, H.-A. Power Flow Analysis on the Dual Input Transmission Mechanism of Small Wind Turbine Systems. Appl. Sci. 2020, 10, 7333. [Google Scholar] [CrossRef]
- Mantriota, G.; Reina, G.; Ugenti, A. Performance Evaluation of a Compound Power-Split CVT for Hybrid Powertrains. Appl. Sci. 2021, 11, 8749. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, Z.; Bai, J.; Zhang, T.; Gai, F. Development of compound power-split hybrid power system for commercial vehicles. Int. J. Automot. Technol. 2022, 23, 135–147. [Google Scholar] [CrossRef]
- Li, X.; Kang, X.; Ba, X.; Peng, Z.; Yang, S.; Zhao, Z. A Design Methodology for Dual-Mode Electro-Mechanical Transmission Scheme Based on Jointing Characteristics. Energies 2022, 15, 5482. [Google Scholar] [CrossRef]
- Kukla, M.; Wieczorek, B.; Warguła, Ł.; Rybarczyk, D.; Górecki, J. Manual Wheelchair Equipped with a Planetary Gear-Research Methodology and Preliminary Results. Appl. Sci. 2022, 12, 7737. [Google Scholar] [CrossRef]
- Wang, L.; Cui, Y.; Zhang, F.; Li, G. Architectures of Planetary Hybrid Powertrain System: Review, Classification and Comparison. Energies 2020, 13, 329. [Google Scholar] [CrossRef]
- Ngo, H.-T.; Yan, H.-S. Configuration synthesis of parallel hybrid transmissions. Mech. Mach. Theory 2016, 97, 51–71. [Google Scholar] [CrossRef]
- Yang, F.; Feng, J.; Du, F. Design and Power Flow Analysis for Multi-Speed Automatic Transmission with Hybrid Gear Trains. Int. J. Automot. Technol. 2016, 17, 629–637. [Google Scholar] [CrossRef]
- Ahn, K.; Cho, S.-T.; Lim, W.; Park, Y.-I.; Lee, J.M. Performance analysis and parametric design of the dual-mode planetary gear hybrid powertrain. Proc. IMechE Part D J. Automob. Eng. 2006, 220, 1601–1614. [Google Scholar] [CrossRef]
- Kim, N.; Kim, J.; Kim, H. Control of Dual Mode Power Split Transmission for a Hybrid Electric Vehicle. World Electr. Veh. J. 2008, 2, 353–362. [Google Scholar] [CrossRef]
- Cammalleri, M.; Castellano, A. Analysis of hybrid vehicle transmissions with any number of modes and planetary gearing: Kinematics, power flows, mechanical power losses. Mech. Mach. Theory 2021, 162, 104350. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, Z.; Zhang, T.; Guo, H. Control optimization of a compound power-split hybrid power system for commercial vehicles. Proc. IMechE Part D J. Automob. Eng. 2021, 235, 2509–2524. [Google Scholar] [CrossRef]
- Van Harselaar, W.; Brouwer, M.; Hofman, T. A generic transmission model for hybrid electric drives. Forsch. Ingenieurwes. 2019, 83, 1–9. [Google Scholar] [CrossRef]
- Yang, F.; Feng, J.; Zhang, H. Power flow and efficiency analysis of multi-flow planetary gear trains. Mech. Mach. Theory 2015, 92, 86–99. [Google Scholar] [CrossRef]
- Yin, C.; Tang, D.; Deng, Z. Research on configurations of multi-axis speed-differential mechanisms based on 2K-H gear train. Mech. Mach. Theory 2020, 148, 103783. [Google Scholar] [CrossRef]
- Gu, J.; Zhao, Z.; Chen, Y.; He, L.; Zhan, X. Integrated optimal design of configuration and parameter of multimode hybrid powertrain system with two planetary gears. Mech. Mach. Theory 2020, 143, 103630. [Google Scholar] [CrossRef]
- Kim, H.; Wi, J.; Yoo, J.; Son, H.; Park, C.; Kim, H. A Study on the Fuel Economy Potential of Parallel and Power Split Type Hybrid Electric Vehicles. Energies 2018, 11, 2103. [Google Scholar] [CrossRef]
- De Carlo, M.; Mantriota, G. Electric vehicles with two motors combined via planetary gear train. Mech. Mach. Theory 2020, 148, 103789. [Google Scholar] [CrossRef]
- Mantriota, G.; Reina, G. Dual-Motor Planetary Transmission to Improve Efficiency in Electric Vehicles. Machines 2021, 9, 58. [Google Scholar] [CrossRef]
- Cipek, M.; Pavkovic’, D.; Petric, J. A control-oriented simulation model of a power-split hybrid electric vehicle. Appl. Energy 2013, 101, 121–133. [Google Scholar] [CrossRef]
- Son, H.; Kim, H. Development of Near Optimal Rule-Based Control for Plug-In Hybrid Electric Vehicles Taking into Account Drivetrain Component Losses. Energies 2016, 9, 420. [Google Scholar] [CrossRef]
- Yang, W.; Liang, J.; Yang, J.; Zhang, N. Investigation of a Novel Coaxial Power-Split Hybrid Powertrain for Mining Trucks. Energies 2018, 11, 172. [Google Scholar] [CrossRef]
- Kim, S.J.; Kim, K.-S. Experimental Investigation of the Seamless Gearshift Mechanism Using an Electric Motor and a Planetary Gear-Set. Energies 2020, 13, 6705. [Google Scholar] [CrossRef]
- Kim, J.; Kang, J.; Kim, Y.; Kim, T.; Min, B.; Kim, H. Design of Power Split Transmission: Design of Dual Mode Power Split Transmission. Int. J. Automot. Technol. 2010, 11, 565–571. [Google Scholar] [CrossRef]
- Wang, W.; Song, S.; Guo, M.; Liu, S. Analysis on compound-split configuration of power-split hybrid electric vehicle. Mech. Mach. Theory 2014, 78, 272–288. [Google Scholar] [CrossRef]
- Esmail, E.L. Hybrid Transmission for Mobile Robot. J. Mech. Des. 2012, 134, 021001. [Google Scholar] [CrossRef]
- Ho, T.T.; Hwang, S.J. Configuration synthesis of two-mode hybrid transmission systems with nine-link mechanisms. Mech. Mach. Theory 2019, 142, 103615. [Google Scholar] [CrossRef]
- Li, H.; Hu, X.; Fu, B.; Wang, J.; Zhang, F.; Zhou, Y. Effective optimal control strategy for hybrid electric vehicle with continuously variable transmission. Adv. Mech. Eng. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Yang, H.; Chom, S.; Kim, N.; Lim, W.; Cha, S. Analysis of Planetary Gear Hybrid Powertrain System. Part 1: Input Split System. Intern. J. Automot. Technol. 2007, 8, 771–780. [Google Scholar]
- Yang, H.; Kim, N.; Par, Y.; Lim, W.; Cha, S. Analysis of Planetary Gear Hybrid Powertrain System. Part 2: Output Split System. Intern. J. Automot. Technol. 2009, 10, 381–390. [Google Scholar] [CrossRef]
- Schulz, M. Circulating mechanical power in a power-split hybrid electric vehicle transmission. Proc. IMech Part D J. Automob. Eng. 2004, 218, 1419–1425. [Google Scholar] [CrossRef]
- Kim, I.; Kim, H. Configuration Analysis of Plug-in Hybrid Systems using Global Optimization. World Electr. Veh. J. 2013, 6, 391–404. [Google Scholar] [CrossRef]
- Szumanowski, A.; Liu, Z.; Krawczyk, P. Analyse of Clutch-brake System Control Based on Experimental Tests and Applied in Hybrid Power Train. World Electr. Veh. J. 2013, 6, 353–363. [Google Scholar] [CrossRef]
- Zou, Y.; Huang, R.; Wu, X.; Zhang, B.; Zhang, Q.; Wang, N.; Qin, T. Modeling and energy management strategy research of a power-split hybrid electric vehicle. Adv. Mech. Eng. 2020, 12, 1–14. [Google Scholar] [CrossRef]
- De Pinto, S.; Mantriota, G. Power Flows in Compound Transmissions for Hybrid Vehicles. Machines 2019, 7, 19. [Google Scholar] [CrossRef]
- Mazali, I.I.; Daud, Z.H.C.; Hamid, M.K.A.; Tan, V.; Samin, P.M.; Jubair, A.; Ibrahim, K.A.; Kob, M.S.C.; Xinrui, W.; Talib, M.H.A. Review of the Methods to Optimize Power Flow in Electric Vehicle Powertrains for Efficiency and Driving Performance. Appl. Sci. 2022, 12, 1735. [Google Scholar] [CrossRef]
- Wang, S.; Li, J.; Shi, D.; Sun, X.; Yao, Y. Energy Management Strategy of Dual Planetary Hybrid Electric Vehicle Based on Optimal Transmission Efficiency. J. Theor. Appl. Mech. 2019, 57, 383–396. [Google Scholar] [CrossRef]
- Huang, K.; Xiang, C.; Ma, Y.; Wang, W.; Langari, R. Mode Shift Control for a Hybrid Heavy-Duty Vehicle with Power-Split Transmission. Energies 2017, 10, 177. [Google Scholar] [CrossRef]
- Li, L.; Yana, B.; Songa, J.; Zhanga, Y.; Jiang, G.; Li, L. Two-step optimal energy management strategy for single-shaft series-parallel powertrain. Mechatronics 2016, 36, 147–158. [Google Scholar]
- Zhang, D.; Chen, J.; Hsieh, J.; Rancourt, J.; Schmidt, M.R. Dynamic modelling and simulation of two-mode electric variable transmission. Proc. IMechE Part D J. Automob. Eng. 2001, 215, 1217–1223. [Google Scholar] [CrossRef]
- Yaohua, L.; Wang Ying, W.; Xuan, Z. Modelling and Simulation Study on a Series-parallel Hybrid Electric Vehicle. World Electr. Veh. J. 2015, 7, 133–141. [Google Scholar]
- Chen, H.; Li, L.; Küçükay, F. Study of Series-Parallel and Power-Split DHT for Hybrid Powertrains. Automot. Innov. 2021, 4, 23–33. [Google Scholar] [CrossRef]
- Weichao Zhuang, W.; Zhang, X.; Peng, H.; Wang, L. Simultaneous Optimization of Topology and Component Sizes for Double Planetary Gear Hybrid Powertrains. Energies 2016, 9, 411. [Google Scholar] [CrossRef]
- Wu, J.; Liang, J.; Ruan, J.; Zhang, N.; Walker, P.D. Efficiency comparison of electric vehicles powertrains with dual motor and single motor input. Mech. Mach. Theory 2018, 128, 569–585. [Google Scholar] [CrossRef]
- Liang, J.; Yang, H.; Wu, J.; Zhang, N.; Walker, P.D. Shifting and power sharing control of a novel dual input clutchless transmission for electric vehicles. Mech. Syst. Signal Process. 2018, 104, 725–743. [Google Scholar] [CrossRef]
- Tom Verstraten, T.; Furnémont, R.; López-García, P.; Rodriguez-Cianca, D.; Cao, H.-L.; Vanderborght, B.; Lefeber, D. Modeling and design of an energy-efficient dual-motor actuation unit with a planetary differential and holding brakes. Mechatronics 2018, 49, 134–148. [Google Scholar] [CrossRef]
- Han, J.-O.; Shin, J.-W.; Kim, J.-C.; Oh, S.-H. Design 2-Speed Transmission for Compact Electric Vehicle Using Dual Brake System. Appl. Sci. 2019, 9, 1793. [Google Scholar] [CrossRef]
- Hu, J.; Mei, B.; Peng, H.; Jiang, X. Optimization Design and Analysis for a Single Motor Hybrid Powertrain Configuration with Dual Planetary Gears. Appl. Sci. 2019, 9, 707. [Google Scholar] [CrossRef]
- Zhao, X.; Tang, J. Modeling and Optimal Shift Control of a Planetary Two-Speed Transmission. World Electr. Veh. J. 2019, 10, 53. [Google Scholar] [CrossRef]
- Nazari, S.; Siegel, J.; Middleton, R.; Stefanopoulou, A. Power Split Supercharging: A Mild Hybrid Approach to Boost Fuel Economy. Energies 2020, 13, 6580. [Google Scholar] [CrossRef]
- Tota, A.; Galvagno, E.; Dimauro, L.; Vigliani, A.; Velardocchia, M. Energy Management Strategy for Hybrid Multimode Powertrains: Influence of Inertial Properties and Road Inclination. Appl. Sci. 2021, 11, 11752. [Google Scholar] [CrossRef]
- Castellano, A.; Cammalleri, M. Power Losses Minimization for Optimal Operating Maps in Power-Split HEVs: A Case Study on the Chevrolet Volt. Appl. Sci. 2021, 11, 7779. [Google Scholar] [CrossRef]
- Yang, W.; Li, C. Symmetry Detection and Topological Synthesis of Mechanisms of Powertrains. Energies 2022, 15, 4755. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, J.; Zheng, L.; Tang, H.; Chen, X. Study and Analysis of a Multi-Mode Power Split Hybrid Transmission. World Electr. Veh. J. 2020, 11, 46. [Google Scholar] [CrossRef]
- Dong, P.; Zuo, S.; Liu, T.; Xu, X.; Guo, W.; Liu, Y.; Wu, H.; Wang, S. A matrix-based method for searching configurations of planetary gear trains. Mech. Mach. Theory 2023, 180, 105161. [Google Scholar] [CrossRef]
- Benford, H.L.; Leising, M.B. The Lever Analogy: A New Tool in Transmission Analysis. SAE Trans. 1981, 90, 429–437. [Google Scholar] [CrossRef]
- Esmail, E.L.; Hussen, H. Nomographs for Kinematics, Statics and Power Flow Analysis of Epicyclic Gear Trains. In Proceedings of the 2009 ASME International Mechanical Engineering Congress and Exposition, Lake Buena Vista, FL, USA, 13–19 November 2009. [Google Scholar]
- Esmail, E.L.; Pennestrì, E.; Juber, A.H. Power Losses in Two-Degrees-of-Freedom Planetary Gear Trains: A Critical Analysis of Radzimovsky’s Formulas. Mech. Mach. Theory 2018, 128, 191–204. [Google Scholar] [CrossRef]
- Marciniec, A.; Sobolak, M.; Połowniak, P. Graphical method for the analysis of planetary gear trains. Alex. Eng. J. 2022, 61, 4067–4079. [Google Scholar] [CrossRef]
- Xie, T.; Hu, J.; Peng, Z.; Liu, C. Synthesis of seven-speed planetary gear trains for heavy-duty commercial vehicle. Mech. Mach. Theory 2015, 90, 230–239. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, X.; Yin, C.; Yuan, S. Development and Simulation of a Type of Four-Shaft ECVT for a Hybrid Electric Vehicle. Energies 2016, 9, 141. [Google Scholar] [CrossRef]
- Liao, Y.G.; Chen, M.-Y. Analysis of multi-speed transmission and electrically continuous variable transmission using lever analogy method for speed ratio determination. Adv. Mech. Eng. 2017, 9, 1–12. [Google Scholar] [CrossRef]
- Ho, T.-T.; Hwang, S.-J. Configuration Synthesis of Novel Hybrid Transmission Systems Using a Combination of a Ravigneaux Gear Train and a Simple Planetary Gear Train. Energies 2020, 13, 2333. [Google Scholar] [CrossRef]
- Yang, X.; Yu, W.; Shao, Y.; Xu, Z.; Zeng, Q.; Nie, C.; Peng, D. An Augmented Lever Analogy Method for Kinematic Analysis of Dual-Input Planetary/Epicyclic Gear Sets Involving Planet Gear. IEEE Access 2022, 10, 101137–101148. [Google Scholar] [CrossRef]
- Chen, X.-A.; Chen, H. Analytical geometry method of planetary gear trains. Sci. China Technol. Sci. 2012, 55, 1007–1021. [Google Scholar] [CrossRef]
- Esmail, E.L. Kinematic nomographs of epicyclic-type transmission mechanisms. Emir. J. Eng. Res. 2007, 12, 47–55. [Google Scholar]
- Esmail, E.L. Nomographs for synthesis of epicyclic-type automatic transmissions. Meccanica 2013, 48, 2037–2049. [Google Scholar] [CrossRef]
- Esmail, E.L. Nomographs and Feasibility Graphs for Enumeration of Ravigneaux-Type Automatic Transmissions. Adv. Mech. Eng. 2013, 5, 120324. [Google Scholar] [CrossRef]
- Del Castillo, J.M. The Analytical Expression of the Efficiency of Planetary Gear Trains. Mech. Mach. Theory 2002, 37, 197–214. [Google Scholar] [CrossRef]
- Chen, C.; Angeles, J. Virtual-power flow and mechanical gear-mesh power losses of epicyclic gear trains. J. Mech. Des. 2007, 129, 107–113. [Google Scholar] [CrossRef]
- Chen, C.; Liang, T.T. Theoretic Study of Efficiency of Two-DOFs of Epicyclic Gear Transmission via Virtual Power. J. Mech. Des. 2011, 133, 031007. [Google Scholar] [CrossRef]
- Chen, C. Power Analysis of Epicyclic Transmissions Based on Constraints. J. Mech. Robot. 2012, 4, 041004. [Google Scholar] [CrossRef]
- Chen, C. Power Flow and Efficiency Analysis of epicyclic gear transmission with split power. Mech. Mach. Theory 2013, 59, 96–106. [Google Scholar] [CrossRef]
- Chen, C.; Chen, J. Power analysis of two-dof epicyclic gear transmission and experimental validation. In Proceedings of the International Gear Conference, Lyon, France, 26–28 August 2014; pp. 646–658. [Google Scholar]
- Chen, C.; Chen, J. Efficiency analysis of two degrees of freedom epicyclic gear transmission and experimental validation. Mech. Mach. Theory 2015, 87, 115–130. [Google Scholar] [CrossRef]
- Wang, C. The effect of planetary gear/star gear on the transmission efficiency of closed differential double helical gear train. Proc. IMech Part C J. Mech. Eng. Sci. 2019, 233, 5647–5658. [Google Scholar] [CrossRef]
- Chen, C. Power Flow analysis of Compound Epicyclic Gear Transmission: Simpson Gear Train. J. Mech. Des. 2011, 133, 094502. [Google Scholar] [CrossRef]
- Li, J.; Wu, T.; Chi, W.; Hu, Q.; Meen, T. Integrated Analysis of Influence of Multiple Factors on Transmission Efficiency of Loader Drive Axle. Energies 2019, 12, 4540. [Google Scholar] [CrossRef]
- Esmail, E.L.; Pennestri, E.; Cirelli, M. Power-Flow and Mechanical Efficiency Computation in Two-Degrees-of-Freedom Planetary Gear Units: New Compact Formulas. Appl. Sci. 2021, 11, 5991. [Google Scholar] [CrossRef]
- Wojnarowski, J. Letters to the Editor Comments on “The Determination of Power Flow in Multiple-Path Transmission Systems”. Mech. Mach. Theory 1975, 10, 261–266. [Google Scholar] [CrossRef]
- Wojnarowski, J.; Lidwin, A. The application of signal flow graphs—The kinematic analysis of planetary gear trains. Mech. Mach. Theory 1975, 10, 17–31. [Google Scholar] [CrossRef]
- Wojnarowski, J. The Graph Method of Determining the Loads in Complex Gear Trains. Mech. Mach. Theory 1976, 11, 103–121. [Google Scholar] [CrossRef]
- Pennestri, E.; Freudenstein, F. A systematic approach to power-flow and static-force analysis in epicyclic spur-gear trains. J. Mech. Des. 1993, 115, 639–644. [Google Scholar] [CrossRef]
- Pennestri, E.; Freudenstein, F. The Mechanical Efficiency of Epicyclic Gear Trains. J. Mech. Des. 1993, 115, 645–651. [Google Scholar] [CrossRef]
- Valentini, P.P.; Pennestri, E. A Review of Formulas for the Mechanical Efficiency Analysis of Two Degrees-of-Freedom Epicyclic Gear Trains. J. Mech. Des. 2003, 125, 602–608. [Google Scholar] [CrossRef]
- Pennestri, E.; Mariti, L.; Valentini, P.P.; Mucino, V.H. Efficiency evaluation of gearboxes for parallel hybrid vehicles: Theory and applications. Mech. Mach. Theory 2012, 49, 157–176. [Google Scholar] [CrossRef]
- Del Pio, G.; Pennestri, E.; Valentini, P.P. Kinematic and power-flow analysis of bevel gears planetary gear trains with gyroscopic complexity. Mech. Mach. Theory 2013, 70, 523–537. [Google Scholar] [CrossRef]
- Geitner, G.-H.; Kömürgöz, G. Generic power split modelling for compound epicyclic four speed gears. Mech. Mach. Theory 2017, 116C, 50–68. [Google Scholar] [CrossRef]
- Geitner, G.-H.; Kömürgöz, G. Bond Graph Based Synthesis of Generic Power Split Modelling for Epicyclic Four-Speed Gears. In Graph-Based Modelling in Science, Technology and Art; Zawiślak, S., Rysiński, J., Eds.; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Salgado, D.R.; del Castillo, J.M. Analysis of the transmission ratio and efficiency ranges of the four-, five-, and six-link planetary gear trains. Mech. Mach. Theory 2014, 73, 218–243. [Google Scholar] [CrossRef]
- Pennestrì, E.; Belfiore, N.P. On Crossley’s contribution to the development of graph based algorithms for the analysis of mechanisms and gear trains. Mech. Mach. Theory 2015, 89, 92–106. [Google Scholar] [CrossRef]
- Cui, Y.; Gao, J.; Ji, X.; Zhou, X.; Yan, H. The multi-attribute topological graph method and its application on power flow analysis in closed planetary gear trains. J. Adv. Mech. Eng. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Esmail, E.L.; Hassan, S.S. An approach to power-flow and static force analysis in multi-input multi-output epicyclic-type transmission trains. J. Mech. Des. 2010, 132, 0110091–01100910. [Google Scholar] [CrossRef]
- Ayats, J.R.G.; Calvet, J.V.; Canela, J.M.; Diego-Ayala, U.; Artes, F.F. Power transmitted through a particular branch in mechanisms comprising planetary gear trains and other fixed or variable transmissions. Mech. Mach. Theory 2011, 46, 1744–1754. [Google Scholar] [CrossRef]
- Ayats, J.R.G.; Diego-Ayala, U.; Artes, F.F. The singular point transition concept: A novel continuously variable transmission comprising planetary gear trains and a variator. J. Power Sources 2012, 197, 125–135. [Google Scholar] [CrossRef]
- Mantriota, G. Comments on “Power transmitted through a particular branch in mechanisms comprising planetary gear trains and other fixed or variable transmissions”. Mech. Mach. Theory 2014, 73, 101–102. [Google Scholar] [CrossRef]
- Xue, H.L.; Liu, G.; Yang, X.H. A review of graph theory application research in gears. Proc. IMechE Part C J. Mech. Eng. Sci. 2015, 30, 1697–1714. [Google Scholar] [CrossRef]
- Esmail, E.L. Meshing Efficiency Analysis of Two Degree-of-Freedom Epicyclic Gear Trains. J. Mech. Des. 2016, 138, 083301. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, W.; Tang, X.; Lin, X.; He, Z. Power Flow and Efficiency Analysis of High-Speed Heavy Load Herringbone Planetary Transmission Using a Hypergraph-Based Method. Appl. Sci. 2020, 10, 5849. [Google Scholar] [CrossRef]
- Freudenstein, F.; Yang, A.T. Kinematics and Statics of Coupled Epicyclic Spur Gear Trains. Mech. Mach. Theory 1972, 7, 263–375. [Google Scholar] [CrossRef]
- Willis, R.J., Jr. On the Kinematics of the Closed Epicyclic Differential Gears. J. Mech. Des. 1982, 104, 712–719. [Google Scholar] [CrossRef]
- Gibson, D.; Kramer, S. Symbolic Notation and Kinematic Equations of Motion of the Twenty-Two Basic Spur Planetary Gear Trains. J. Mech. Trans. Autom. 1984, 106, 333–340. [Google Scholar] [CrossRef]
- Hsu, C.-H. A graph notation for the kinematic analysis of differential gear trains. J. Frankl. Inst. 1992, 329, 859–867. [Google Scholar] [CrossRef]
- Hsu, C.-H.; Lam, K.-T. A New Graph Representation for the Automatic Kinematic Analysis of Planetary Spur-Gear Trains. J. Mech. Des. Mar. 1992, 114, 196–200. [Google Scholar] [CrossRef]
- Ma, R.; Gupta, K.C. Signal Flow Graphs for Spatial Gear Trains. J. Mech. Des. 1994, 116, 326–331. [Google Scholar] [CrossRef]
- Hsieh, H.-I.; Tsai, L.-W. Kinematic Analysis of Epicyclic-Type Transmission Mechanisms Using the Concept of Fundamental Geared Entities. J. Mech. Des. 1996, 118, 294–299. [Google Scholar] [CrossRef][Green Version]
- Lang, S.Y.T. Graph-theoretic modelling of epicyclic gear systems. Mech. Mach. Theory 2005, 40, 511–529. [Google Scholar] [CrossRef]
- Mathis, R.; Remond, Y. Kinematic and dynamic simulation of epicyclic gear trains. Mech. Mach. Theory 2009, 44, 412–424. [Google Scholar] [CrossRef]
- Drewniak, J.; Zawiślak, S. Graph methods in kinematical analysis of multi-speed epicyclic gears. Int. J. Appl. Mech. Eng. 2010, 17, 791–798. [Google Scholar]
- Drewniak, J.; Zawiślak, S. Linear graph and contour graph based models of planetary gears. J. Theor. Appl. Mech. 2010, 48, 415–433. [Google Scholar]
- Zawiślak, S. The Graph-Based Methodology as an Artificial Intelligence Aid for Mechanical Engineering Design; Publishing House Bielsko-Biala University: Bielsko-Biala, Poland, 2010. [Google Scholar]
- Amirinezhad, S.V.; Uyguroğlu, M.K. Kinematic analysis of geared robotic mechanism using Matroid and T–T graph methods. Mech. Mach. Theory 2015, 88, 16–30. [Google Scholar] [CrossRef][Green Version]
- Uyguroglu, M.; Tokad, Y. Kinematic Analysis of Robotic Bevel-Gear Trains: An Application of Network Model Approach. Meccanica 1998, 33, 177–194. [Google Scholar] [CrossRef]
- Uyguroglu, M.; Demirel, H. Kinematic analysis of bevel-gear trains using graphs. Acta Mech. 2005, 177, 19–27. [Google Scholar] [CrossRef]
- Drewniak, J.; Kopeć, J.; Zawislak, S. Kinematical and Efficiency Analysis of Planetary Gear Trains by Means of Various Graph-Based Approaches. In Theory and Practice of Gearing and Transmissions; Goldfarb, V., Barmina, N., Eds.; Part of the Book Series: Mechanisms and Machine Science; Springer: Cham, Switzerland, 2016; Volume 34, pp. 263–284. [Google Scholar] [CrossRef]
- Esmail, E.L. A universal kinematic analysis of geared mechanisms. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 2253–2258. [Google Scholar] [CrossRef]
- Wojnarowski, J.; Kopeć, J.; Zawiślak, S. Gears and Graphs. J. Theoret. Appl. Mech. 2006, 44, 139–162. [Google Scholar]
- Liu, C.-P.; Chen, D.-Z.; Tsung Chang, Y.-T. Kinematic analysis of geared mechanisms using the concept of kinematic fractionation. Mech. Mach. Theory 2004, 39, 1207–1221. [Google Scholar] [CrossRef]
- Liu, C.-P.; Chen, D.-Z. On the Embedded Kinematic Fractionation of Epicyclic Gear Trains. J. Mech. Des. 2000, 122, 479–483. [Google Scholar] [CrossRef]
- Gao, M.-F.; Hu, J.-B. Kinematic Analysis of Planetary Gear Trains Based on Topology. J. Mech. Des. 2018, 140, 012302. [Google Scholar] [CrossRef]
- Penaud, J.; Alazard, D.; Amiez, A. Kinematic Analysis of Spatial Geared Mechanisms. J. Mech. Des. 2012, 134, 021009. [Google Scholar] [CrossRef]
- Marghitu, D.B. Kinematic Chains and Machine Components Design; Elsevier: Amsterdam, The Netherlands; Academic Press: London, UK, 2005. [Google Scholar]
- Ayats, J.R.G.; Diego-Ayala, U.; Canela, J.M.; Fenollosa, F.; Vivancos, J. Hypergraphs for the analysis of complex mechanisms comprising planetary gear trains and other variable or fixed transmissions. Mech. Mach. Theory 2012, 51, 217–229. [Google Scholar] [CrossRef]
- Drewniak, J.; Kopeć, J.; Zawiślak, S. Graph Models of Automobile Gears—Kinematics. Int. J. Appl. Mech. Eng. 2010, 19, 563–573. [Google Scholar] [CrossRef]
- Hussen, H.A.; Esmail, E.L. Application of incidence matrix to topological structure and kinematic analysis of multi-planet gear trains. Results Eng. 2021, 12, 100305. [Google Scholar] [CrossRef]
- Esmail, E.L. Teaching Planetary Gear Trains with the Aid of Nomographs. Adv. Mech. Eng. 2013, 5, 978418. [Google Scholar] [CrossRef]
- Talpasanu, I.; Yih, T.C.; Simionescu, P.A. Application of Matroid Method in Kinematic Analysis of Parallel Axes Epicyclic Gear Trains. J. Mech. Des. 2006, 128, 1307–1314. [Google Scholar] [CrossRef]
- Ke, T.; Ding, H.; Gong, C.; Geng, M. Configuration synthesis of nine-speed automatic transmissions based on structural decomposition. Mech. Mach. Theory 2021, 164, 104421. [Google Scholar] [CrossRef]
- Ding, H.; Cai, C.; Chen, Z.; Ke, T.; Mao, B. Confguration Synthesis and Performance Analysis of 9-Speed Automatic Transmissions. Chin. J. Mech. Eng. 2020, 33, 50. [Google Scholar] [CrossRef]
- Wojnarowski, J.; Drewniak, J.; Kądziołka, T.; Kopeć, J.; Stańco, K.; Zawiślak, S. Application of Contour Equations to Kinematic Analysis of Complex and Compound Planetary Gears. In Advances in Mechanism and Machine Science; Uhl, T., Ed.; Mechanisms and Machine Science 73; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, L.; Lu, Z.; Qian, J.; Zhang, H.; Zhao, Y.; Cheng, Z.; Wang, X. Transmission Parameter Design and Characteristic Analysis of Three-Row Parallel Planetary Gear HMCVT. Machines 2022, 10, 740. [Google Scholar] [CrossRef]
- Wu, J.; Yan, H.; Liu, S.; Zhang, Y.; Tan, W. Bond Graph-Based Approach to Modeling Variable-Speed Gearboxes with Multi-Type Clutches. Appl. Sci. 2022, 12, 6181. [Google Scholar] [CrossRef]
- Tsai, M.-C.; Huang, C.-C.; Lin, B.-J. Kinematic analysis of planetary gear systems using block diagrams. J. Mech. Des. 2010, 132, 065001. [Google Scholar] [CrossRef]
- Tian, L.; Li-Qiao, L. Matrix System for the Analysis of Planetary Transmissions. J. Mech. Des. 1997, 119, 333–337. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).