An Experimental Study on the Heat and Mass Transfer Characteristics of an Evaporative Cooler
Abstract
:1. Introduction
2. Experimental Study
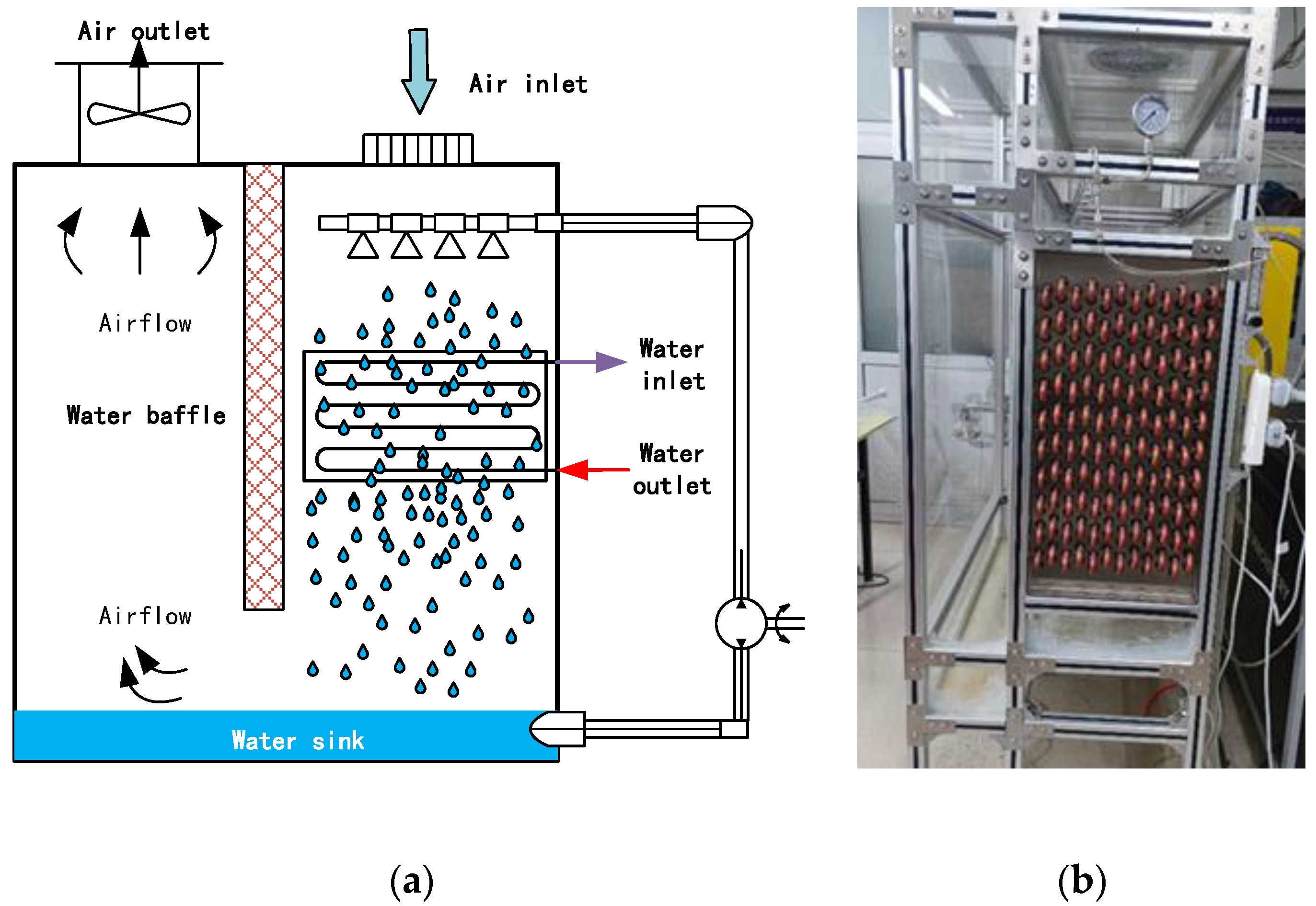
2.1. Experimental Device
2.2. Test System
2.3. Experimental Design
3. Results and Discussion
3.1. Effects of Various Influencing Factors on Heat Dissipation
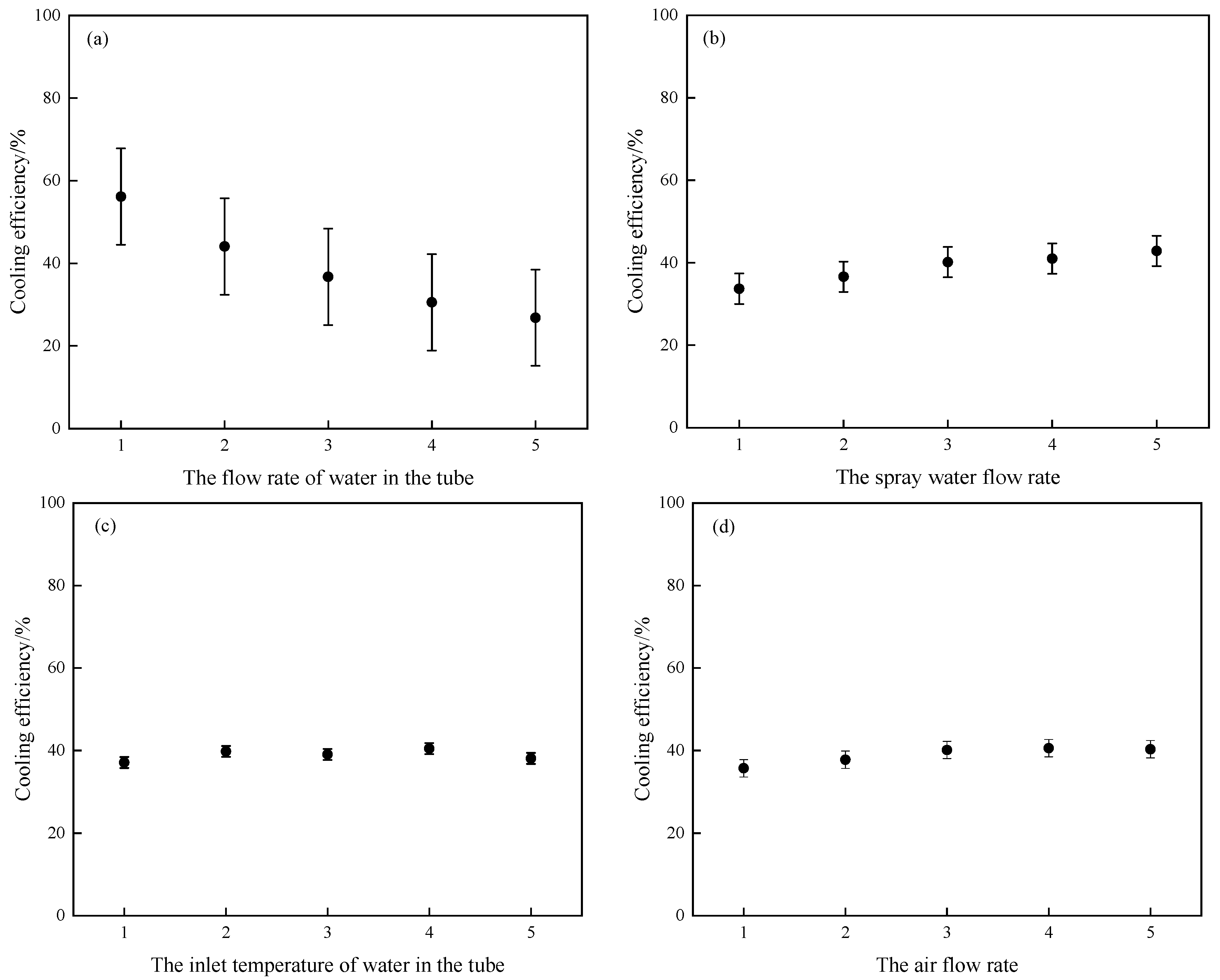
3.2. Effects of Various Influencing Factors on Cooling Efficiency
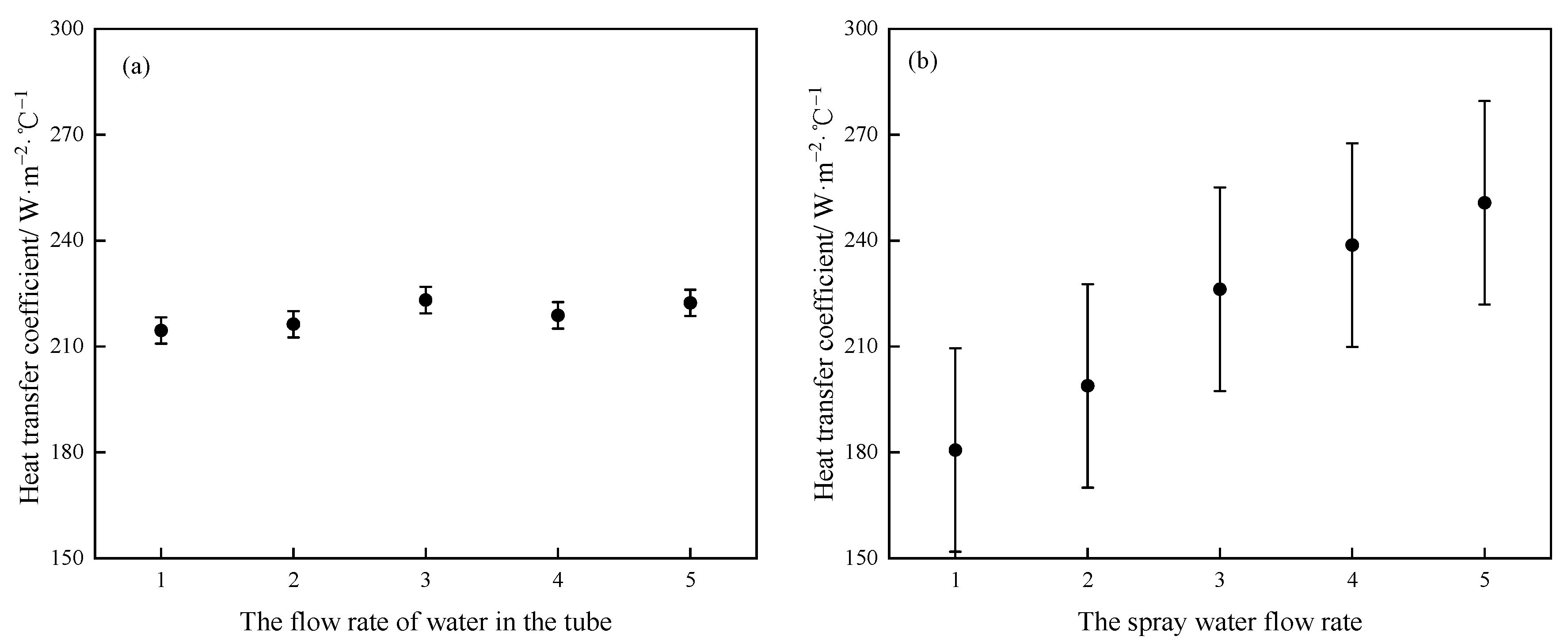
3.3. Effects of Various Influencing Factors on the Heat Transfer Coefficient
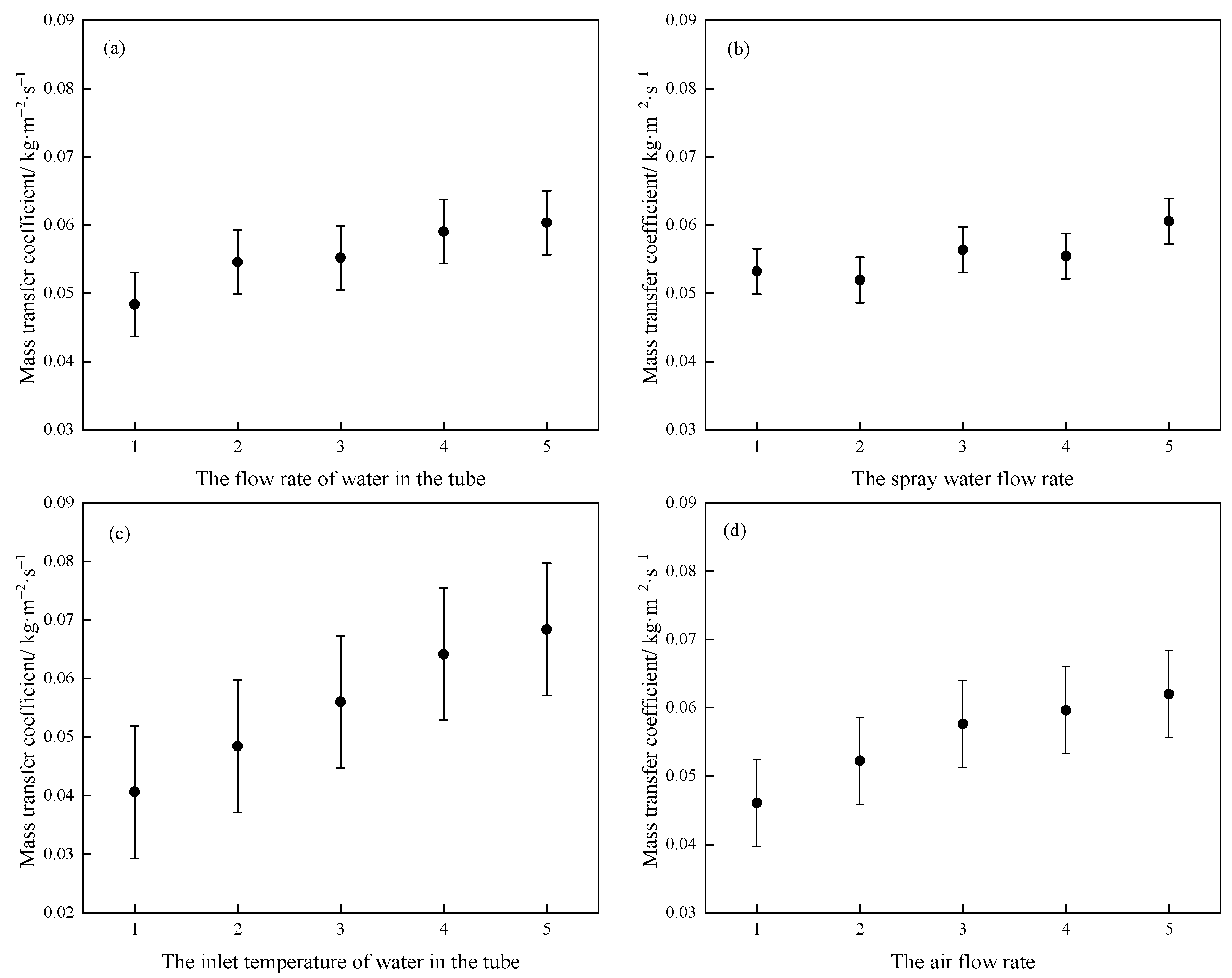
3.4. Effects of Various Influencing Factors on the Mass Transfer Coefficient
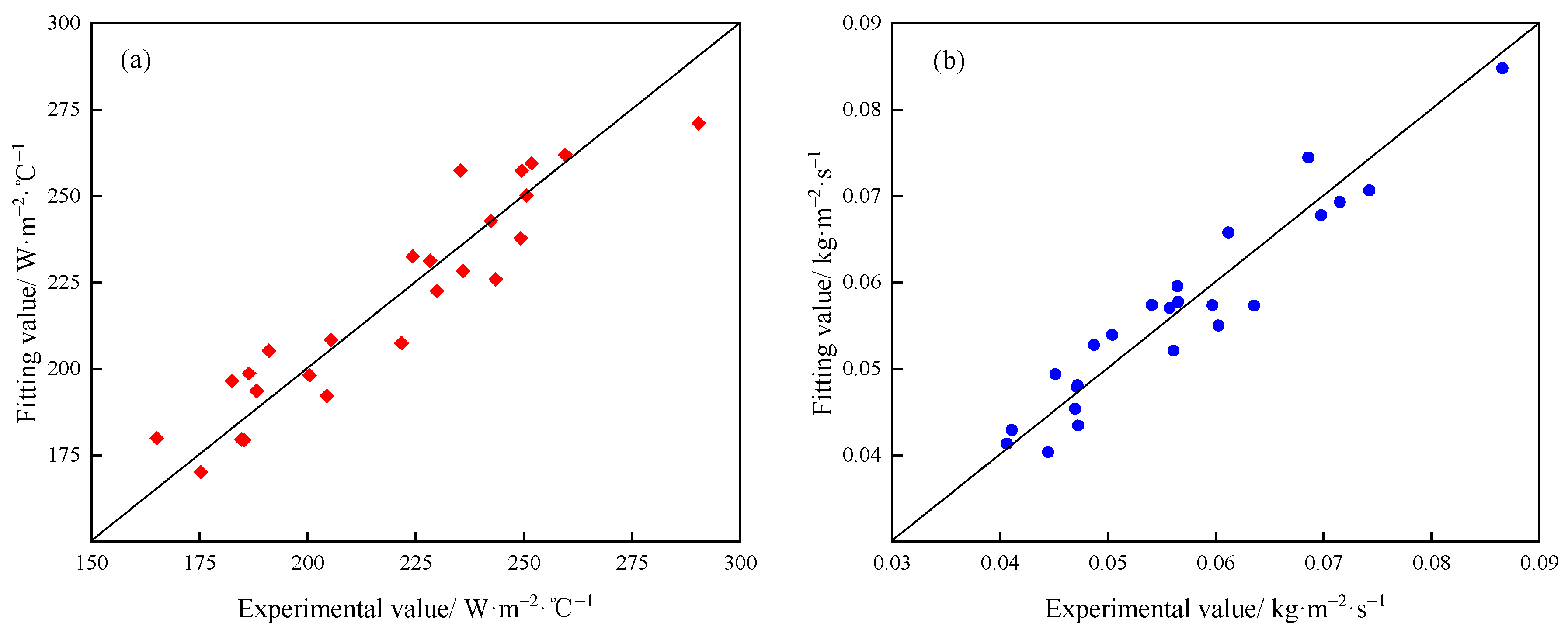
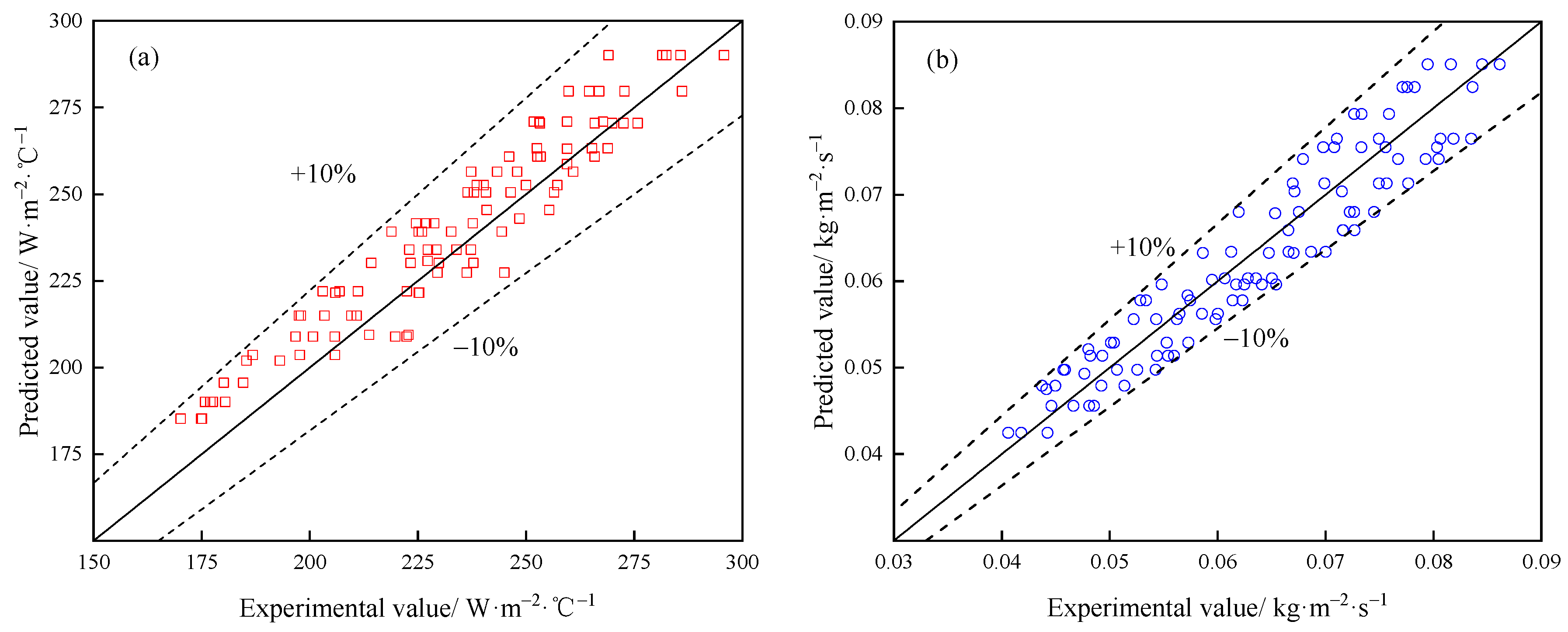
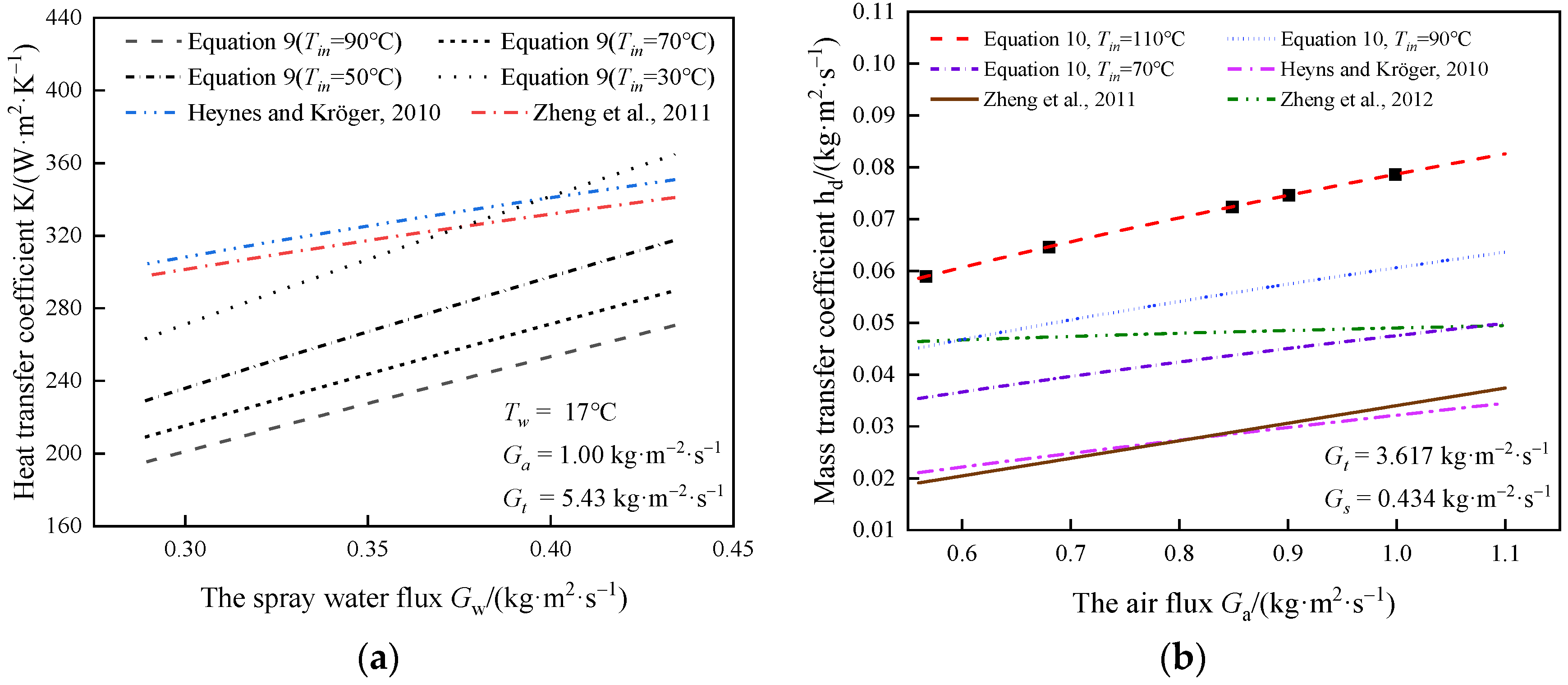
3.5. Correlation Equations of the Heat and Mass Coefficients
4. Conclusions
- (1)
- The flow rate and the inlet temperature of water in the tube have the most significant influence on the heat dissipation of the evaporative cooler, followed by the spray water flow rate, and the air flow rate has a weaker effect. If it is necessary to increase the heat dissipation of the evaporative cooler, the flow rate, the inlet temperature of water in the tube, and the spray water flow rate can be increased.
- (2)
- The spray water flow rate has the most significant effect on the heat transfer coefficient of the evaporative cooler, followed by the inlet temperature of water in the tube and the air flow rate, and the flow rate of water in the tube has no obvious effect on the heat transfer coefficient.
- (3)
- The inlet temperature of water in the tube has the most significant effect on the mass transfer coefficient of the evaporative cooler, followed by the flow rate of water in the tube and the air flow rate, and the spray water flow rate has no obvious effect on the mass transfer coefficient.
- (4)
- Under the working conditions of this study, the correlation equations of the heat and mass transfer coefficients for the evaporative cooler are and , respectively.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Y.; Zhang, P.; Zhao, J.; Yang, H.; Bai, Y. Experimental study on performance of a closed wet cooling tower for air wet-bulb temperature near 0 °C. J. Therm. Sci. 2019, 28, 1015–1023. [Google Scholar] [CrossRef]
- Alhamid, M.I.; Bismo, S.; Nainggolan, F.; Yatim, A. Analysis of the effectiveness of ozonation on corrosion and bacteria on closed system cooling towers. AIP Conf. Proc. 2019, 2062, 020046. [Google Scholar]
- Liu, J.; Zhang, L.; Lin, Z.; Gao, M.; Chen, H. Research of technical and economic performance of plastic capillary mats used as the heat exchanger of a closed-circuit cooling tower. Appl. Therm. Eng. 2019, 153, 800–807. [Google Scholar] [CrossRef]
- Wagner, T.V.; Parsons, J.R.; Rijnaarts, H.H.M.; de Voogt, P.; Langenhoff, A.A.M. A review on the removal of conditioning chemicals from cooling tower water in constructed wetlands. Crit. Rev. Environ. Sci. Technol. 2018, 48, 1094–1125. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhu, X.; Ding, X. Theoretical investigation on thermal performance of new structure closed wet cooling tower. Heat Transf. Eng. 2018, 39, 460–472. [Google Scholar] [CrossRef]
- Bhuva, J.H. Improvement in the performance of cooling tower of thermal power plant: A review. Int. J. Res. Appl. Sci. Eng. Technol. 2018, 6, 3043–3046. [Google Scholar] [CrossRef]
- Nadjahi, C.; Louahlia, H.; Lemasson, S. A review of thermal management and innovative cooling strategies for data center. Sustain. Comput. Inform. Syst. 2018, 19, 14–28. [Google Scholar] [CrossRef]
- Facão, J.; Oliveira, A.C. Thermal behaviour of closed wet cooling towers for use with chilled ceilings. Appl. Therm. Eng. 2000, 20, 1225–1236. [Google Scholar] [CrossRef]
- Hasan, A.; Sirén, K. Performance investigation of plain and finned tube evaporatively cooled heat exchangers. Appl. Therm. Eng. 2003, 23, 325–340. [Google Scholar] [CrossRef]
- Yoo, S.; Kim, J.; Han, K. Thermal performance analysis of heat exchanger for closed wet cooling tower using heat and mass transfer analogy. J. Mech. Sci. Technol. 2010, 24, 893–898. [Google Scholar] [CrossRef]
- Heyns, J.A.; Kröger, D.G. Experimental investigation into the thermal-flow performance characteristics of an evaporative cooler. Appl. Therm. Eng. 2010, 30, 492–498. [Google Scholar] [CrossRef]
- Zheng, W.Y.; Zhu, D.S.; Song, J.; Zeng, L. Experimental investigation of heat and mass transfer of novel closed circuit cooling tower. Chem. Eng. 2011, 39, 34–37. [Google Scholar]
- Zheng, W.Y.; Zhu, D.S.; Song, J.; Zeng, L.-D.; Zhou, H.-J. Experimental and computational analysis of thermal performance of the oval tube closed wet cooling tower. Appl. Therm. Eng. 2012, 35, 233–239. [Google Scholar] [CrossRef]
- Zheng, W.Y. Experimental Investigation and Numerical Simulation of the Heat and Mass Transfer in Evaporative Cooler; East China University of Science and Technology: Shanghai, China, 2013. [Google Scholar]
- Jiang, J.; Liu, X.; Jiang, Y. Experimental and numerical analysis of a cross-flow closed wet cooling tower. Appl. Therm. Eng. 2013, 61, 678–689. [Google Scholar] [CrossRef]
- Tu, A.; Liu, S.; Mo, X.; Chen, E.; Zhan, X.; Zhu, D. Experimental Study of a Novel Non-Packing Closed Evaporative Cooling Tower with Vertical 3D Deformation Tubes. Energies 2022, 15, 9336. [Google Scholar] [CrossRef]
- Yu, Y.; Qi, X.; Hou, X.; Qu, X.; Guo, Q.; Zhu, H. Heat and mass transfer performance and exergy performance evaluation of seawater cooling tower considering different inlet parameters. Thermal Sci. 2022, 26 Pt A, 3715–3728. [Google Scholar] [CrossRef]
- Ruiz, J.; Navarro, P.; Hernández, M.; Lucas, M.; Kaiser, A. Thermal performance and emissions analysis of a new cooling tower prototype. Appl. Therm. Eng. 2022, 206, 118065. [Google Scholar] [CrossRef]
- Stabat, P.; Marchio, D. Simplified model for indirect-contact evaporative cooling-tower behaviour. Appl. Energy 2004, 78, 433–451. [Google Scholar] [CrossRef]
- Papaefthimiou, V.D.; Rogdakis, E.D.; Koronaki, I.P.; Zannis, T. Thermodynamic study of the effects of ambient air conditions on the thermal performance characteristics of a closed wet cooling tower. Appl. Therm. Eng. 2012, 33, 199–207. [Google Scholar] [CrossRef]
- Zheng, W.Y.; Zhu, D.S.; Song, J.; Zeng, L.; Zhou, H. Simulation of closed wet cooling towers. J. Chem. Eng. Chin. Univ. 2012, 26, 216–221. [Google Scholar]
- Nasr, M.R.J.; Behfar, R. A novel design for evaporative fluid coolers. Appl. Therm. Eng. 2010, 30, 2746–2752. [Google Scholar] [CrossRef]
- Nasr, M.R.J.; Jafarifar, S. Extension of the rapid design algorithm for twisted-tube evaporative fluid coolers. Chem. Eng. Technol. 2015, 38, 787–796. [Google Scholar] [CrossRef]
- Qasim, S.M.; Hayder, M.J. Investigation of the effect of packing location on performance of closed wet cooling tower based on exergy analysis. IOP Conf. Ser. Mater. Sci. Eng. 2016, 145, 32009–32014. [Google Scholar] [CrossRef]
- Mahdi, Q.S.; Jaffal, H.M. Energy and exergy analysis on modified closed wet cooling tower in Iraq. Ai-Khawarizmi Eng. J. 2016, 12, 45–49. [Google Scholar]
- Wei, X.; Li, N.; Peng, J.; Cheng, J.; Hu, J.; Wang, M. Performance analyses of counter-flow closed wet cooling towers based on a simplified calculation method. Energies 2017, 10, 282. [Google Scholar] [CrossRef]
- Xie, X.; He, C.; Xu, T.; Zhang, B.; Pan, M.; Chen, Q. Deciphering the thermal and hydraulic performances of closed wet cooling towers with plain, oval, and longitudinal fin tubes. Appl. Therm. Eng. 2017, 120, 203–218. [Google Scholar] [CrossRef]
- Xie, X.; Zhang, Y.; He, C.; Xu, T.; Zhang, B.; Chen, Q. Bench-scale experimental study on the heat transfer intensification of a closed wet cooling tower using aluminum oxide nanofluids. Ind. Eng. Chem. Res. 2017, 56, 6022–6034. [Google Scholar] [CrossRef]
- Xie, X.; Liu, H.; He, C.; Zhang, B.; Chen, Q.; Pan, M. Deciphering the heat and mass transfer behaviors of staggered tube bundles in a closed wet cooling tower using a 3-d vof model. Appl. Therm. Eng. 2019, 161, 114202. [Google Scholar] [CrossRef]
- Lee, Y.; Hong, S.; Dang, C.; Chien, L.-H.; Yang, A.-S. Effect of counter current airflow on film dispersion and heat transfer of evaporative falling film over a horizontal elliptical tube. Int. J. Heat Mass Transf. 2019, 141, 964–973. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, B.; Chen, Q.; He, C.; Foo, D.C.; Ren, J.; Yu, H. Model reductions for multiscale stochastic optimization of cooling water system equipped with closed wet cooling towers. Chem. Eng. Sci. 2020, 224, 115773. [Google Scholar] [CrossRef]
- Zhao, R.; Bu, S.; Zhao, X.; Zhang, L.; Xu, W.; Yu, Z.; Fang, J.; Ji, Y.; Hu, Y.; Bao, B. Study on thermal performance of new finned heat exchange tube bundles in cooling tower. Int. J. Therm. Sci. 2021, 168, 107064. [Google Scholar] [CrossRef]
- Fang, J.; Zhao, X.; Zhang, L.; Bu, S.; Yu, Z.; Xu, W.; Hu, Y.; Shan, Y.; Li, Y. Thermodynamic Investigation on the Performance of Closed Wet Cooling Tower. J. Therm. Sci. Eng. Appl. 2022, 14, 031010. [Google Scholar] [CrossRef]
- Deng, W.; Sun, F.; Chen, K.; Zhang, X. Numerical study on performance of hybrid mechanical draft wet cooling tower. Int. J. Heat Mass Transf. 2023, 201, 123574. [Google Scholar] [CrossRef]
- Xi, Y.; Yu, Z.; Zhang, L.; Yu, A.; Liu, L.; Bao, B.; Zhao, Y.; Zhou, C.; Wu, B.; Dong, K. Research on heat and mass transfer characteristics of a counterflow wet cooling tower using a new type of straight wave packing. Int. J. Therm. Sci. 2023, 193, 108540. [Google Scholar] [CrossRef]
- Deng, W.; Sun, F. Performance analysis and multi-objective optimization of mechanical draft wet cooling towers based on water saving, plume and cooling characteristics. Int. J. Therm. Sci. 2024, 196, 108656. [Google Scholar] [CrossRef]
- Fang, J.; Yin, X.; Wang, A.; Sun, X.; Liu, Y.; Cao, F. Cooling performance enhancement for the automobile transcritical CO2 air conditioning system with various internal heat exchanger effectiveness. Appl. Therm. Eng. 2021, 196, 117274. [Google Scholar] [CrossRef]
- Abud-Archila, M.; Vázquez-Mandujano, D.G.; Ruiz-Cabrera, M.A.; Grajales-Lagunes, A.; Moscosa-Santillán, M.; Ventura-Canseco, L.; Gutiérrez-Miceli, F.; Dendooven, L. Optimization of osmotic dehydration of yam bean (Pachyrhizus erosus) using an orthogonal experimental design. J. Food Eng. 2008, 84, 413–419. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, S.; Shen, S.; Ni, S.; Shi, X.; Qiu, Q. Experimental study on the heat and mass transfer characteristics of air-water two-phase flow in an evaporative condenser with a horizontal elliptical tube bundle. Appl. Therm. Eng. 2020, 168, 114825. [Google Scholar] [CrossRef]


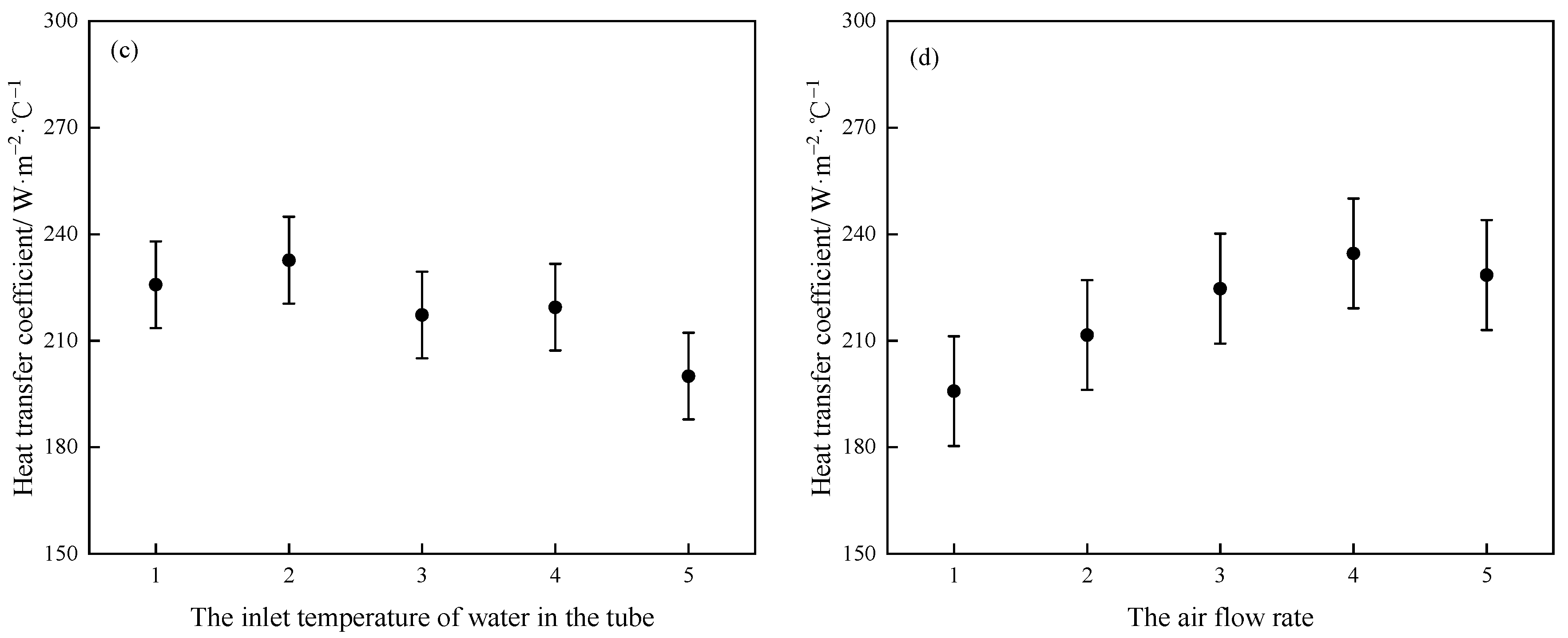
| Authors | Year | Medium | Water Temperature in the Tube/°C | Spray Water Temperature/°C | Dry Bulb Air Temperature/°C | Wet Bulb Air Temperature/°C |
|---|---|---|---|---|---|---|
| Facão and Oliveira [8] | 2000 | Water | 15–28 | - | - | 10–20 |
| Hasan and Sirén [9] | 2002 | Water | 21 | 17–18 | 19–20 | 16 |
| Stabat and Marchio [19] | 2004 | Water | 23–42 | - | - | 16–24 |
| Nasr and Behfar [22] | 2010 | Water | 15.6 | - | 10 | 8.5 |
| Yoo et al. [10] | 2010 | Water | 32–42 | - | - | 27 |
| Heyns and Kröger [11] | 2010 | Water | - | 35–53 | 16–22 | 14–18 |
| Zheng et al. [12] | 2011 | Water | 13.7–36 | 11–28 | 4–15 | 2.1–9.6 |
| Zheng et al. [13] | 2012 | Water | 13.7–36 | 11–28 | 4–15 | 2.1–9.6 |
| Zheng et al. [21] | 2012 | Water | 15–24 | 15.1–25.4 | 13.1–32.5 | 10.5–19.8 |
| Papaefthimiou et al. [20] | 2012 | Water | 35 | 20 | 10–45 | 8.1–30.3 |
| Jiang et al. [15] | 2013 | Water | 30.1–36.6 | 25–26 | 27.2 | 20–25 |
| Zheng et al. [14] | 2013 | Water | 13.7–55 | 11–28 | - | 18–28 |
| Nasr and Jafarifar [23] | 2015 | Water | 45 | 13 | - | - |
| Mahdi and Jaffal [24] | 2016 | Water | 35–55 | - | - | 7–24 |
| Wei et al. [26] | 2017 | Water | 16–37 | 13.6–18.1 | - | 10–23 |
| Xie et al. [27] | 2017 | Water | 37 | 10–35 | 10–34 | - |
| Lee et al. [30] | 2019 | Water | - | 25 | 25 | 19.5 |
| Zhu et al. [31] | 2020 | Water | 40–57 | - | - | - |
| Zhao et al. [32] | 2021 | Water | - | 35–41 | 25–37 | 28 |
| Tu et al. [16] | 2022 | Water | 32–44 | - | 26–34 | 23–28 |
| Yu et al. [17] | 2022 | Water | - | 38–56 | 26–30 | 21–25 |
| Ruiz et al. [18] | 2022 | Water | - | 28–33 | 23–28 | 19.2–23.2 |
| Fang et al. [33] | 2022 | Water | 35–42 | 32–37 | 32–36 | - |
| Deng et al. [34] | 2023 | Water | 27–39 | - | 2–28 | 1.5–27.0 |
| Xi et al. [35] | 2023 | Water | - | 41 | 16 | - |
| Deng and Sun [36] | 2024 | Water | - | 33–39 | 5 | 1.5 |
| Parameter | Unit | Value |
|---|---|---|
| Outer diameter of the tube | mm | 12.0 |
| Thickness of the tube | mm | 1.2 |
| Length of the tube | mm | 1000 |
| Number of rows in a bundle | N/A | 20 |
| Number of columns of bundles | N/A | 12 |
| Row spacing of bundles | mm | 40 |
| Column spacing of bundles | mm | 60 |
| Parameter | Sensor | Accuracy |
|---|---|---|
| The spray water flow rate | Rotameter (DK800-6, Shuanghuan, Changzhou, China) | ±2 L/h |
| The air flow rate | Vane anemometer (GT8907, Benetech, Shenzhen, China) | ±0.01 m/s |
| Ambient temperature and humidity | Thermometer (VICTOR 231, Victor, Sehnzhen, China) | ±0.1 °C/±0.1%RH |
| Outlet air temperature | Thermocouple (K-type, YHT, Beijing, China) | ±0.75% t |
| Outlet air humidity | Humidity sensor (TH10S-B, Rongchi, Shenzhen, China) | ±0.1%RH |
| The inlet temperature of water in the tube | Temperature control unit (MPWT-20T-20, MAIPT, Suzhou, China) | ±0.1 °C |
| The outlet temperature of water in the tube | Temperature control unit (MPWT-20T-20, MAIPT, Suzhou, China) | ±1 °C |
| The flow rate of water in the tube | Rotameter (LZB-25, Shuanghuan, Changzhou, China) | ±10 L/h |
| Level | Factor A: The Flow Rate of Water in the Tube (kg·h−1) | Factor B: The Spray Water Flow Rate (kg·h−1) | Factor C: The Inlet Temperature of Water in the Tube (°C) | Factor D: The Air Flow Rate (m3·h−1) |
|---|---|---|---|---|
| 1 | 200 | 40 | 70.0 | 83.25 |
| 2 | 300 | 45 | 80.0 | 99.90 |
| 3 | 400 | 50 | 90.0 | 124.65 |
| 4 | 500 | 55 | 100.0 | 132.30 |
| 5 | 600 | 60 | 110.0 | 146.70 |
| Factor | Average Deviation Sum of Squares | F0.05(4, 8) | F Value | Significance of Difference |
|---|---|---|---|---|
| Factor A | 14.57 | 3.84 | 17.43 | Significant |
| Factor B | 6.47 | 3.84 | 7.74 | Significant |
| Factor C | 33.17 | 3.84 | 39.68 | Significant |
| Factor D | 1.53 | 3.84 | 1.82 | Not significant |
| Factor | Average Deviation Sum of Squares | F0.05(4, 8) | F Value | Significance of Difference |
|---|---|---|---|---|
| Factor A | 0.0681 | 3.84 | 114.81 | Significant |
| Factor B | 0.0068 | 3.84 | 11.38 | Significant |
| Factor C | 0.0009 | 3.84 | 1.51 | Not significant |
| Factor D | 0.0022 | 3.84 | 3.75 | Not significant |
| Factor | Average Deviation Sum of Squares | F0.05(4, 8) | F Value | Significance of Difference |
|---|---|---|---|---|
| Factor A | 69.45 | 3.84 | 0.51 | Not significant |
| Factor B | 4151.75 | 3.84 | 30.61 | Significant |
| Factor C | 745.17 | 3.84 | 5.49 | Significant |
| Factor D | 1197.63 | 3.84 | 8.83 | Significant |
| Factor | Average Deviation Sum of Squares | F0.05(4, 8) | F Value | Significance of Difference |
|---|---|---|---|---|
| Factor A | 0.00011 | 3.84 | 4.19 | Significant |
| Factor B | 0.00006 | 3.84 | 2.12 | Not significant |
| Factor C | 0.00064 | 3.84 | 24.49 | Significant |
| Factor D | 0.00020 | 3.84 | 7.78 | Significant |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Guo, B.; Wang, L. An Experimental Study on the Heat and Mass Transfer Characteristics of an Evaporative Cooler. Energies 2023, 16, 7330. https://doi.org/10.3390/en16217330
Zhang P, Guo B, Wang L. An Experimental Study on the Heat and Mass Transfer Characteristics of an Evaporative Cooler. Energies. 2023; 16(21):7330. https://doi.org/10.3390/en16217330
Chicago/Turabian StyleZhang, Peikun, Bingfa Guo, and Li Wang. 2023. "An Experimental Study on the Heat and Mass Transfer Characteristics of an Evaporative Cooler" Energies 16, no. 21: 7330. https://doi.org/10.3390/en16217330
APA StyleZhang, P., Guo, B., & Wang, L. (2023). An Experimental Study on the Heat and Mass Transfer Characteristics of an Evaporative Cooler. Energies, 16(21), 7330. https://doi.org/10.3390/en16217330






