Shale Gas Reservoir Pore Pressure Prediction: A Case Study of the Wufeng–Longmaxi Formations in Sichuan Basin, Southwest China
Abstract
:1. Introduction
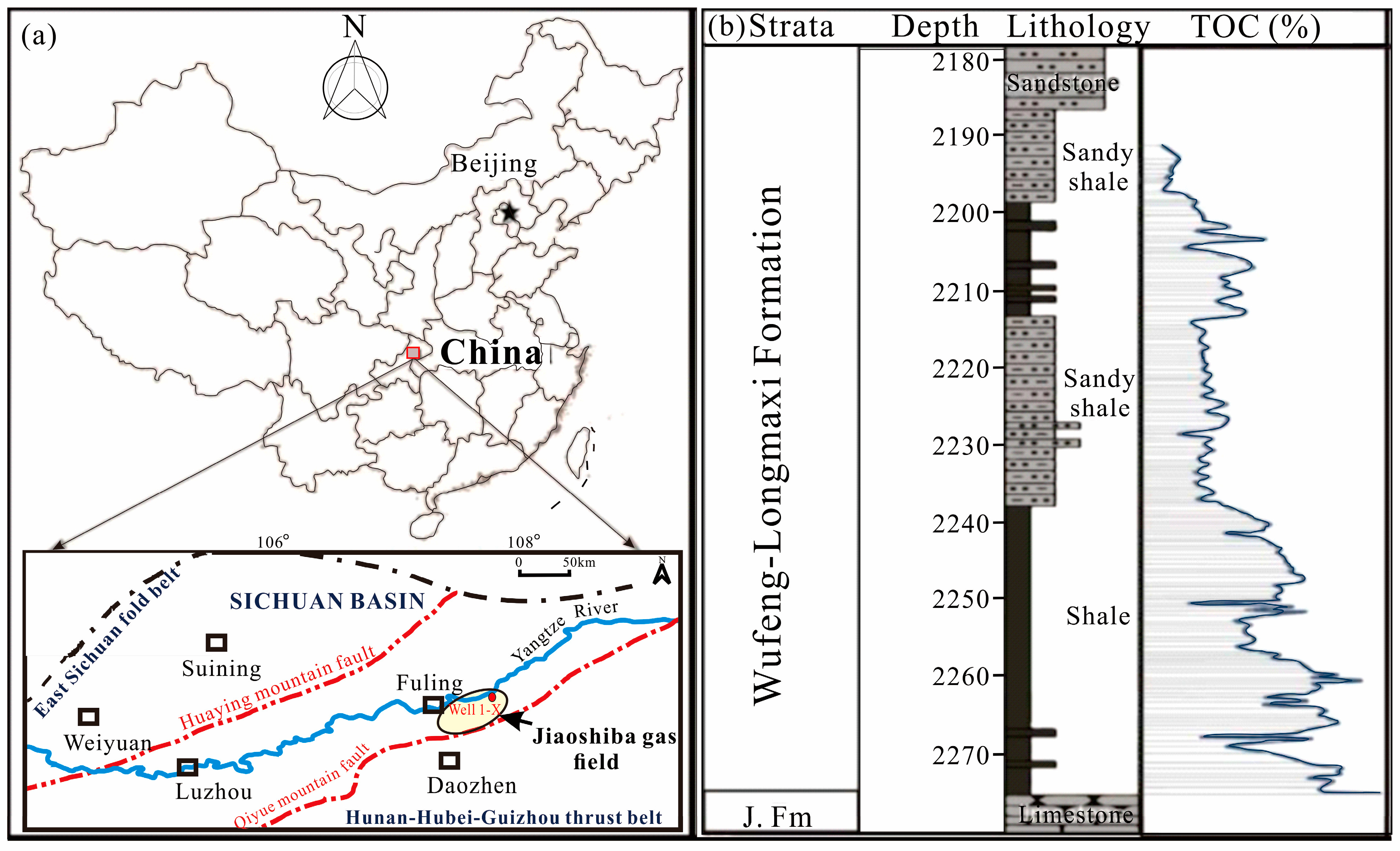
2. Geological Setting
3. Methodology
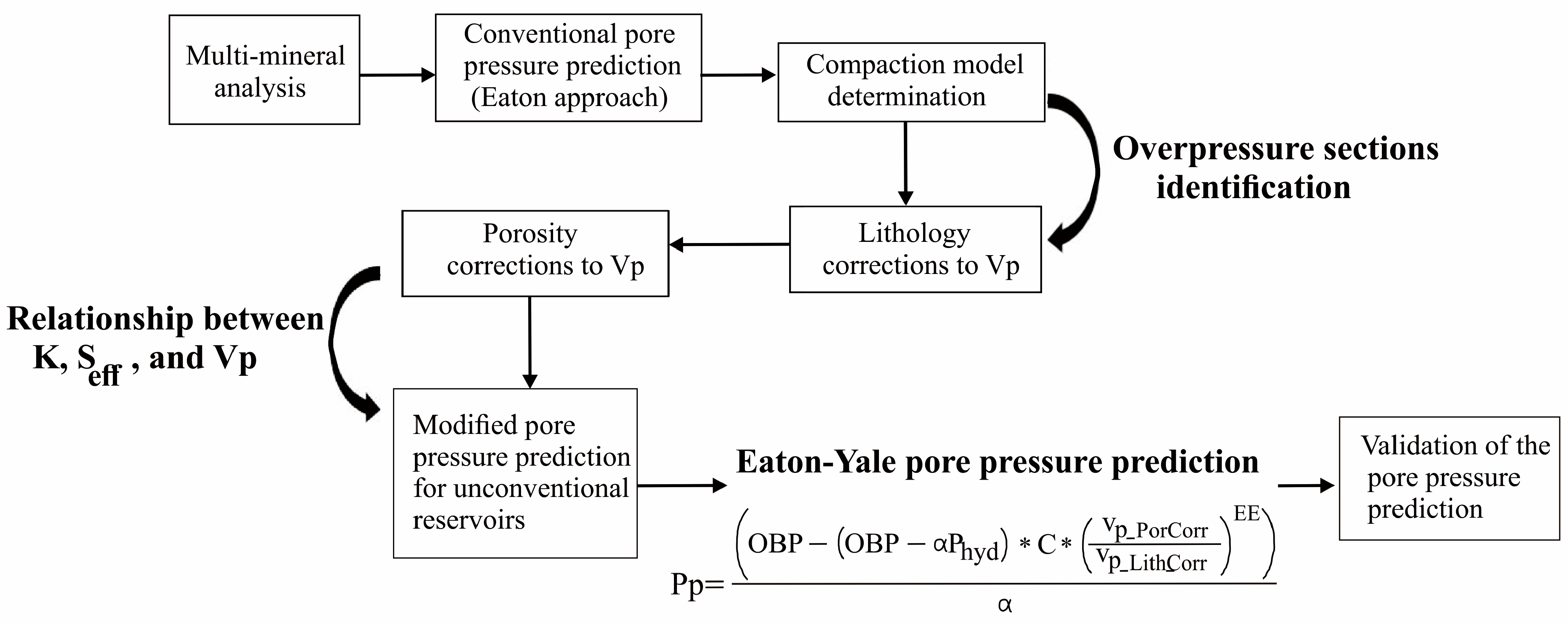
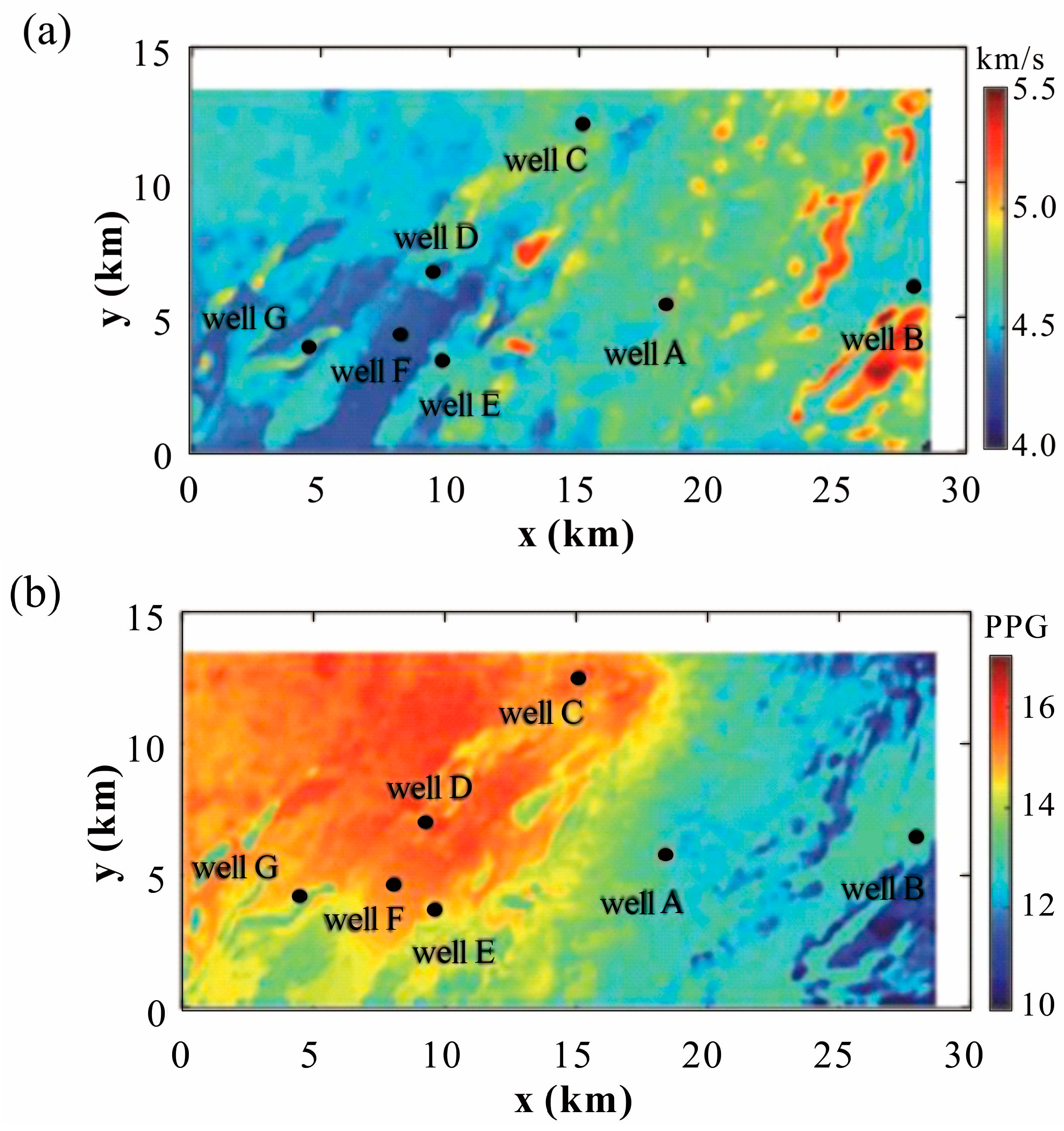
3.1. Data Overview and Workflow
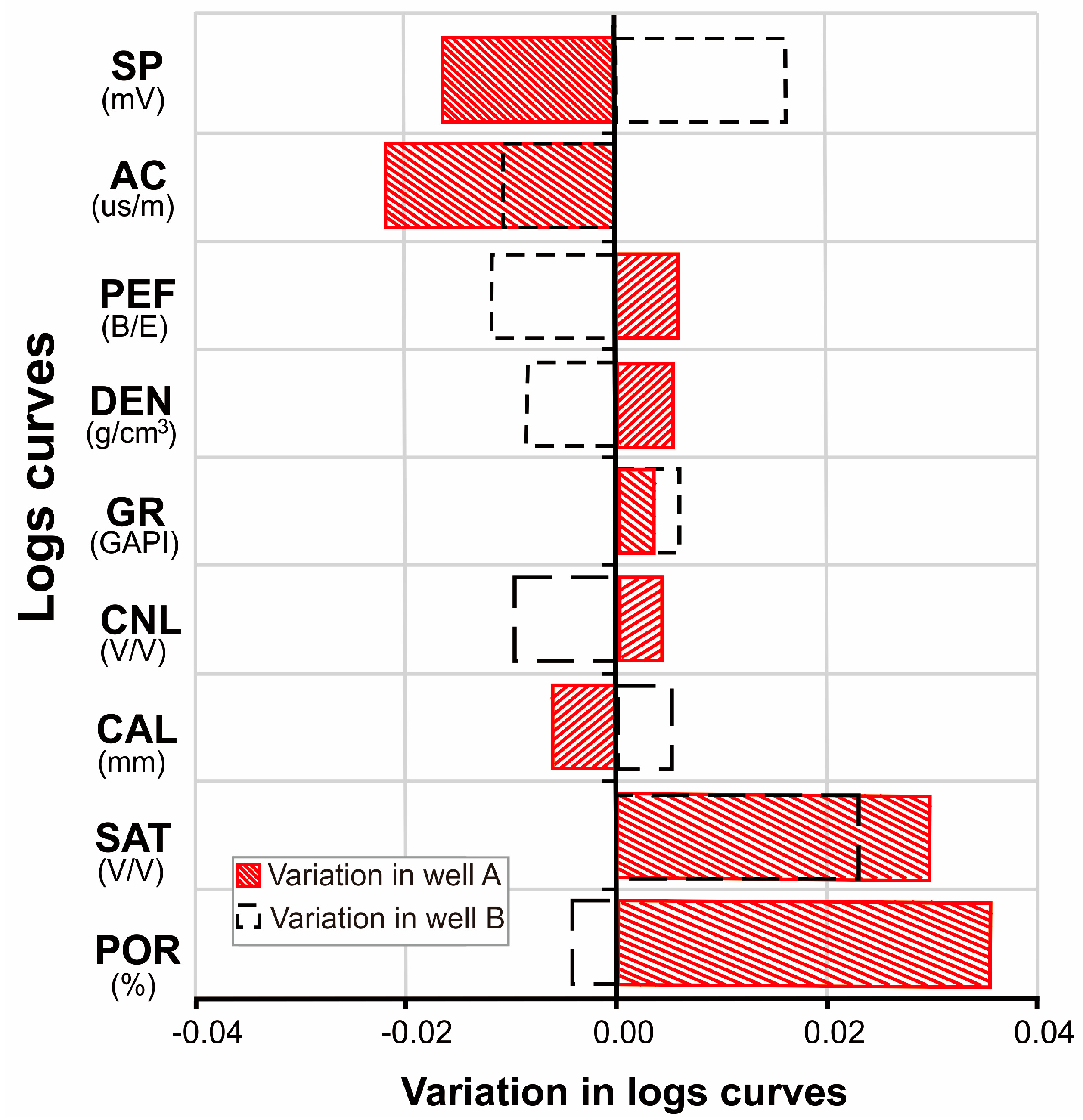
3.2. Multi-Mineral and Multi-Fluids Analysis
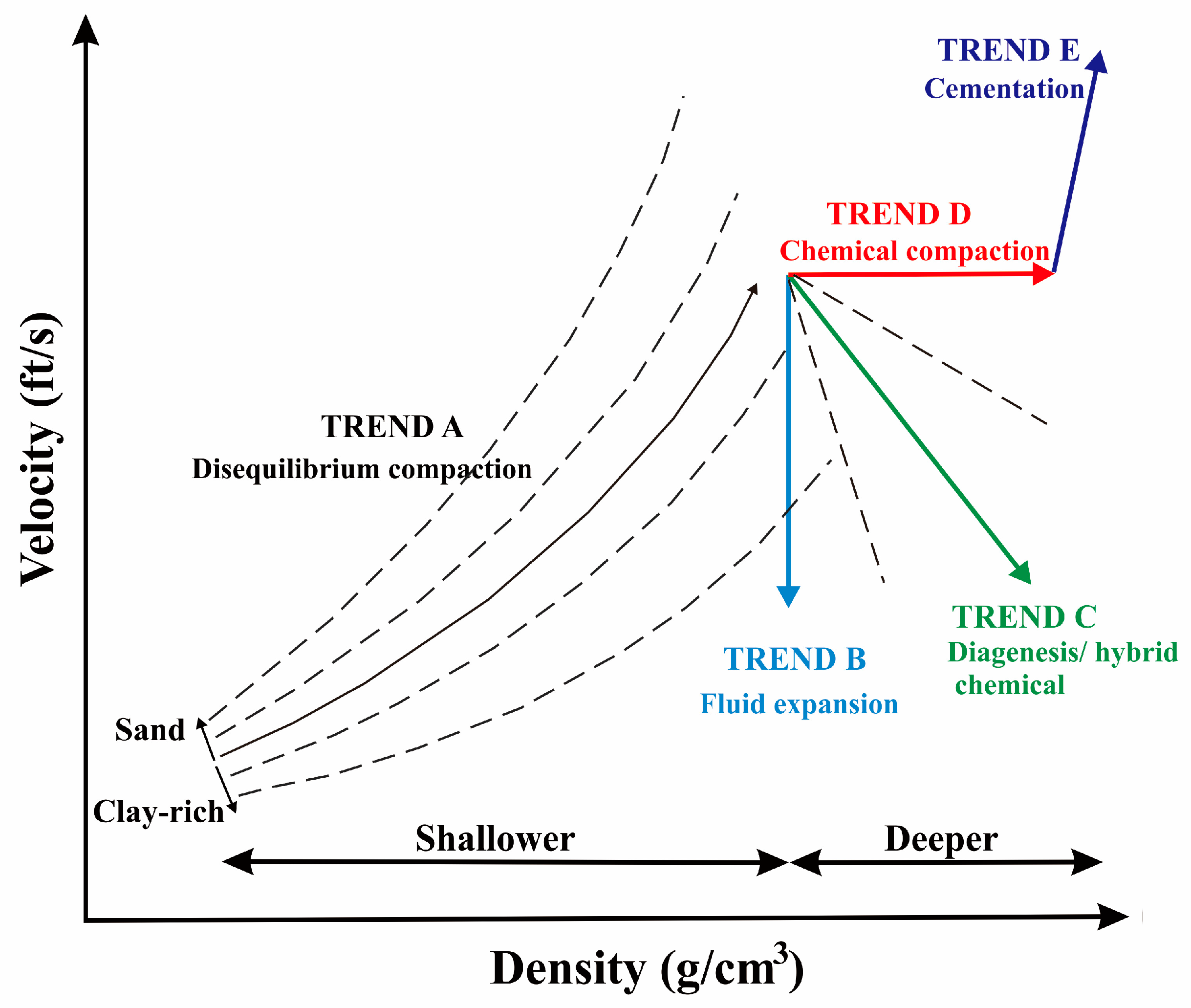
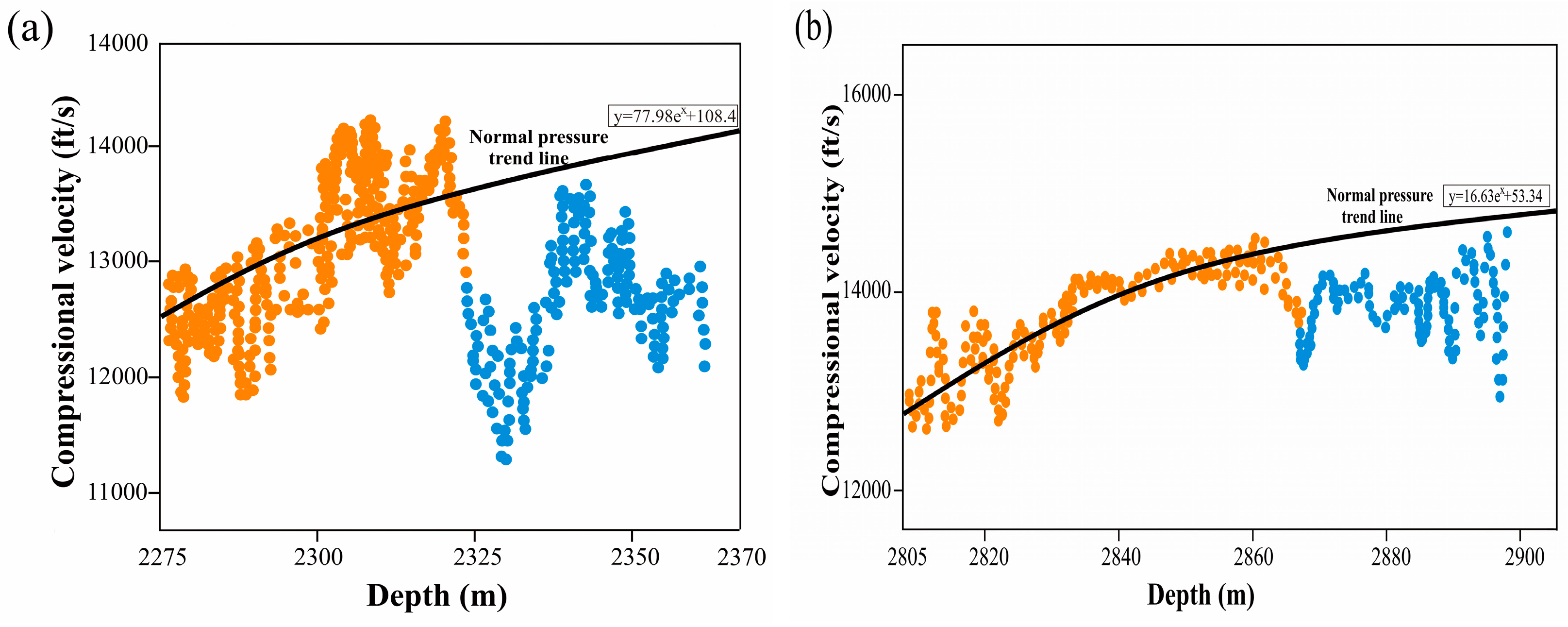
3.3. Compaction Model
- -
- Trend A: normal compaction trend (overpressure due to disequilibrium).
- -
- Trend B: fluid expansion trend (relatively low increase in density and significant decrease in velocity).
- -
- Trend C: hybrid trend (density increase and velocity decrease).
- -
- Trend D: early chemical diagenesis trend (low increase in velocity and relative density increases).
- -
- Trend E: later diagenetic alteration at high density and low porosity when velocity increases rapidly due to very low porosity.
3.4. Standard Eaton Pore Pressure Approach
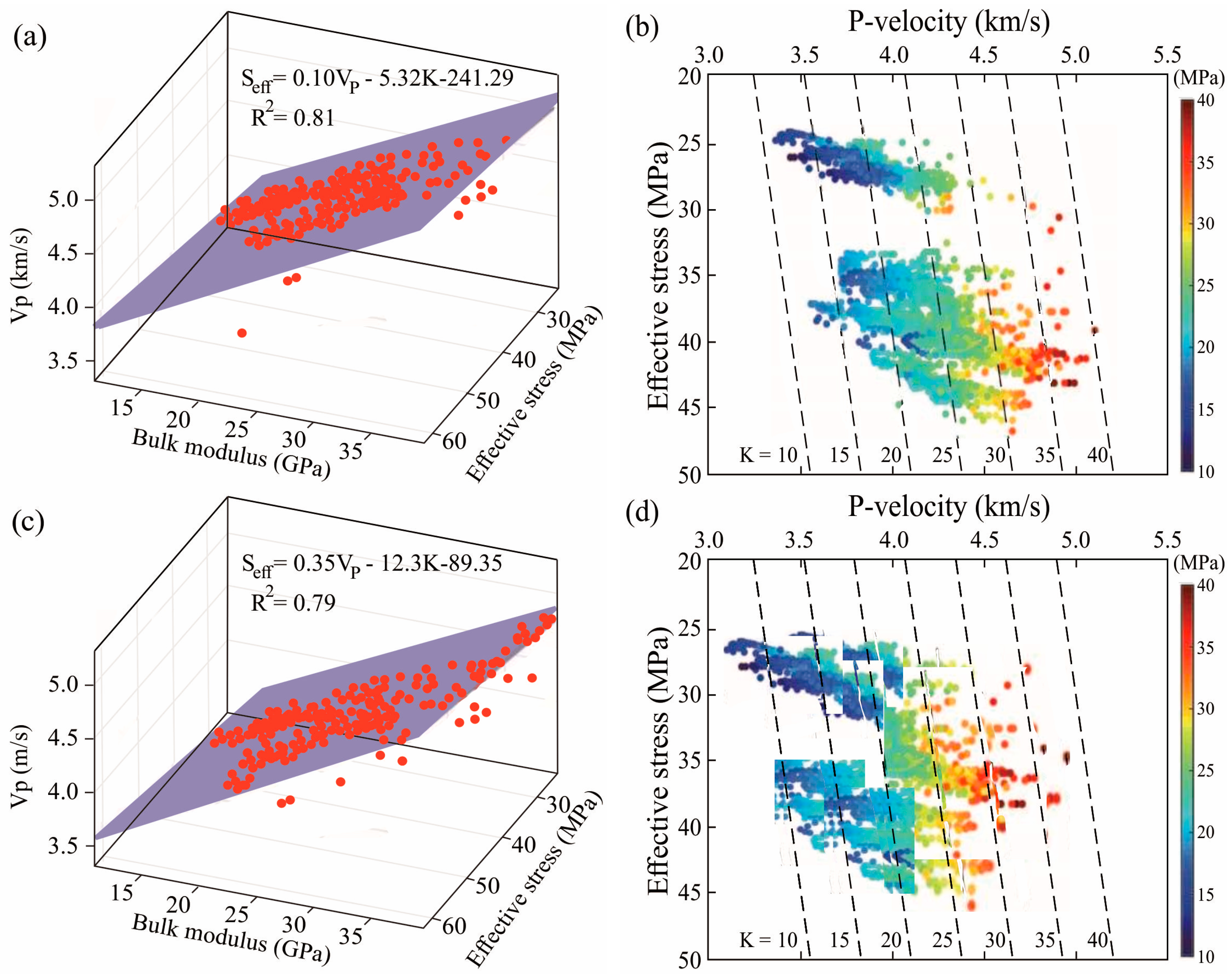
3.5. Compressional Modulus Lithology and Porosity Correction
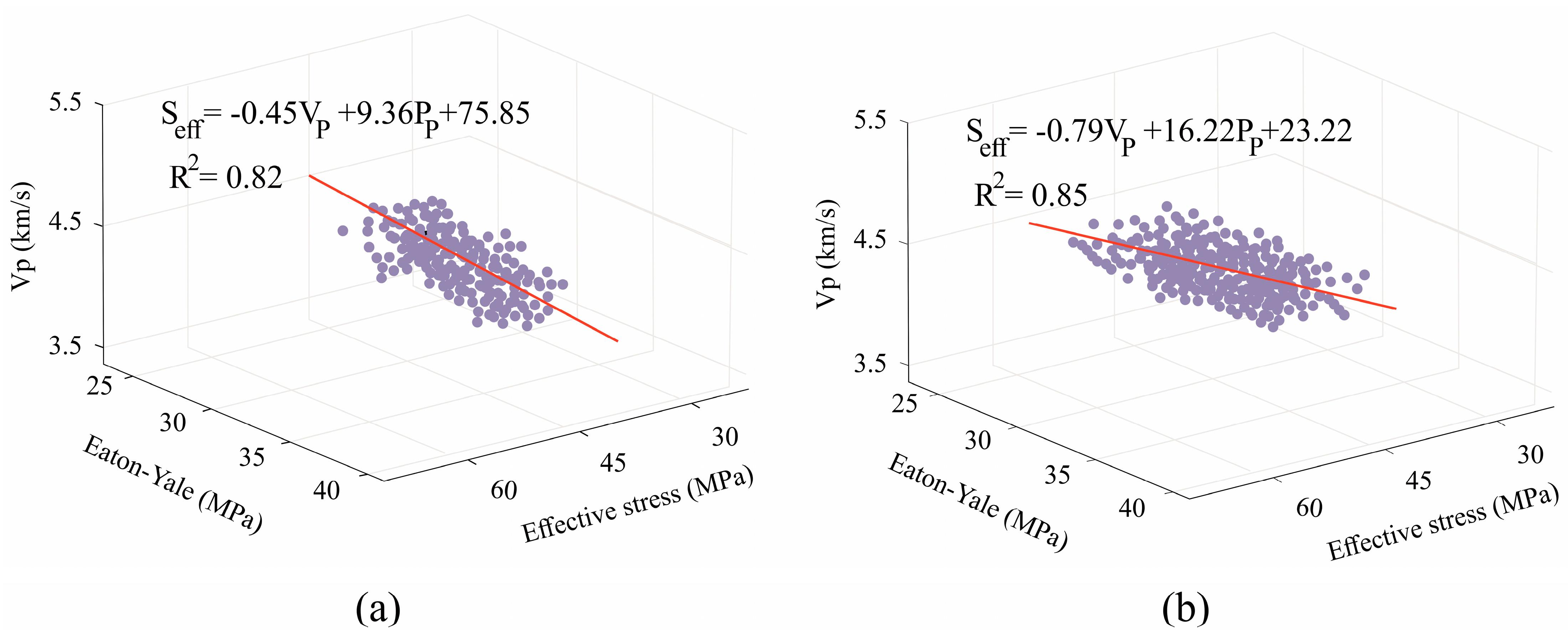
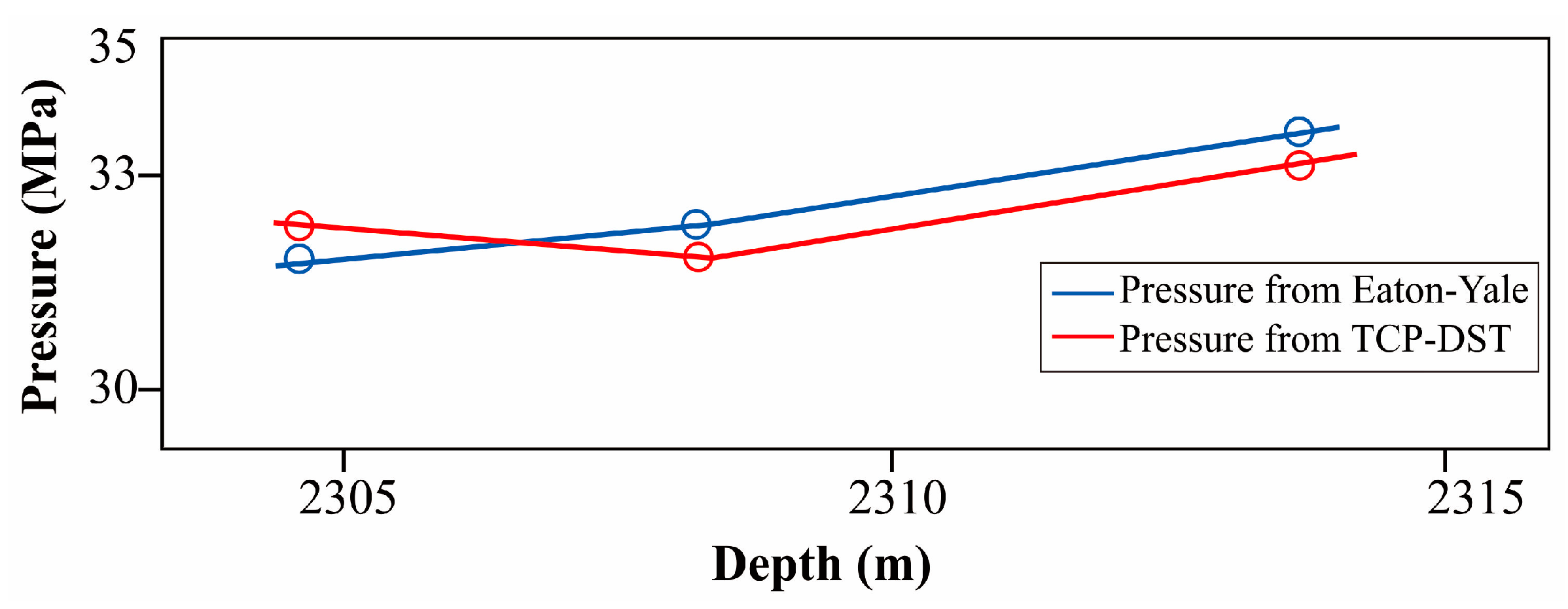
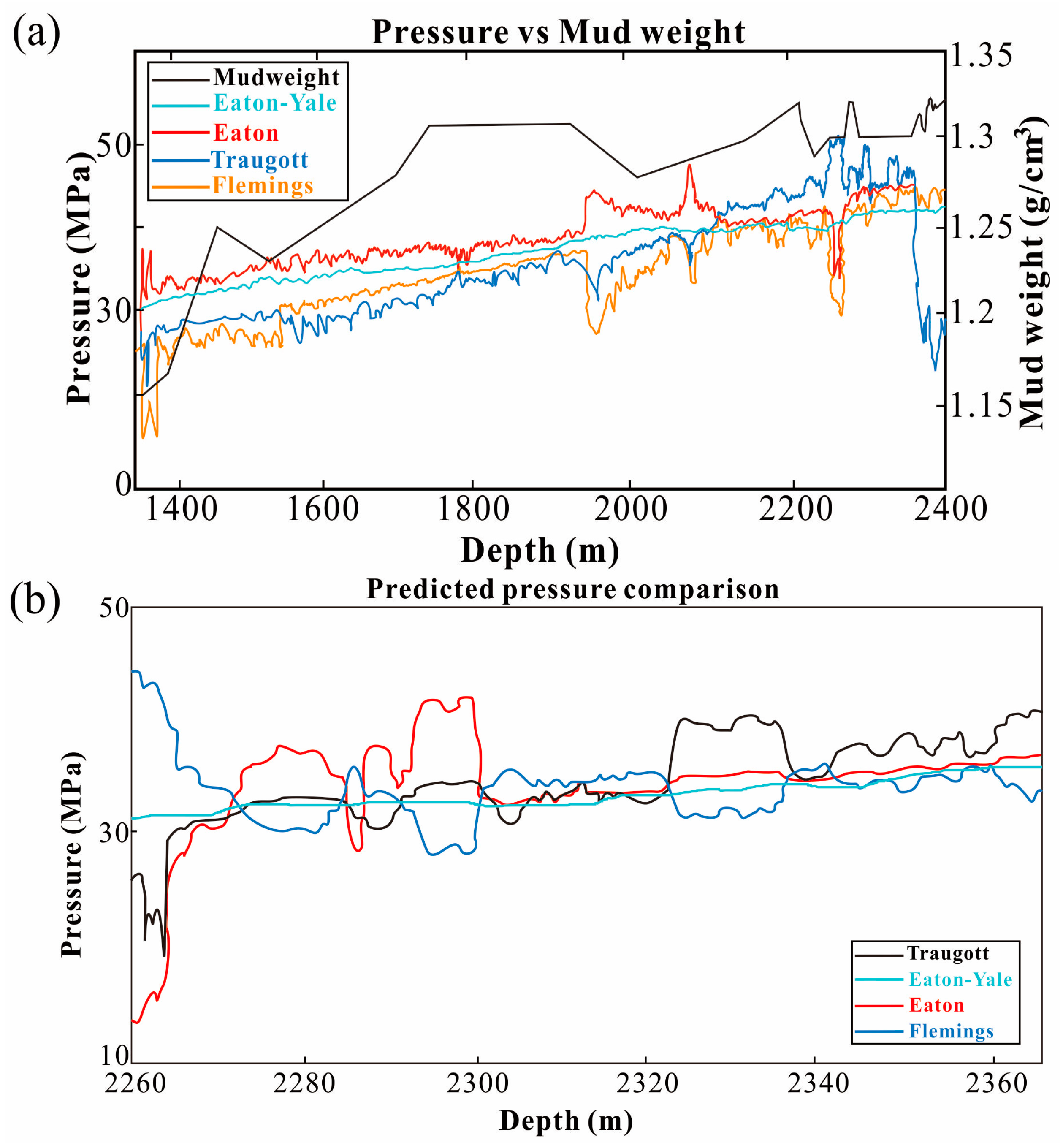
3.6. Eaton–Yale Pore Pressure Prediction and Validation
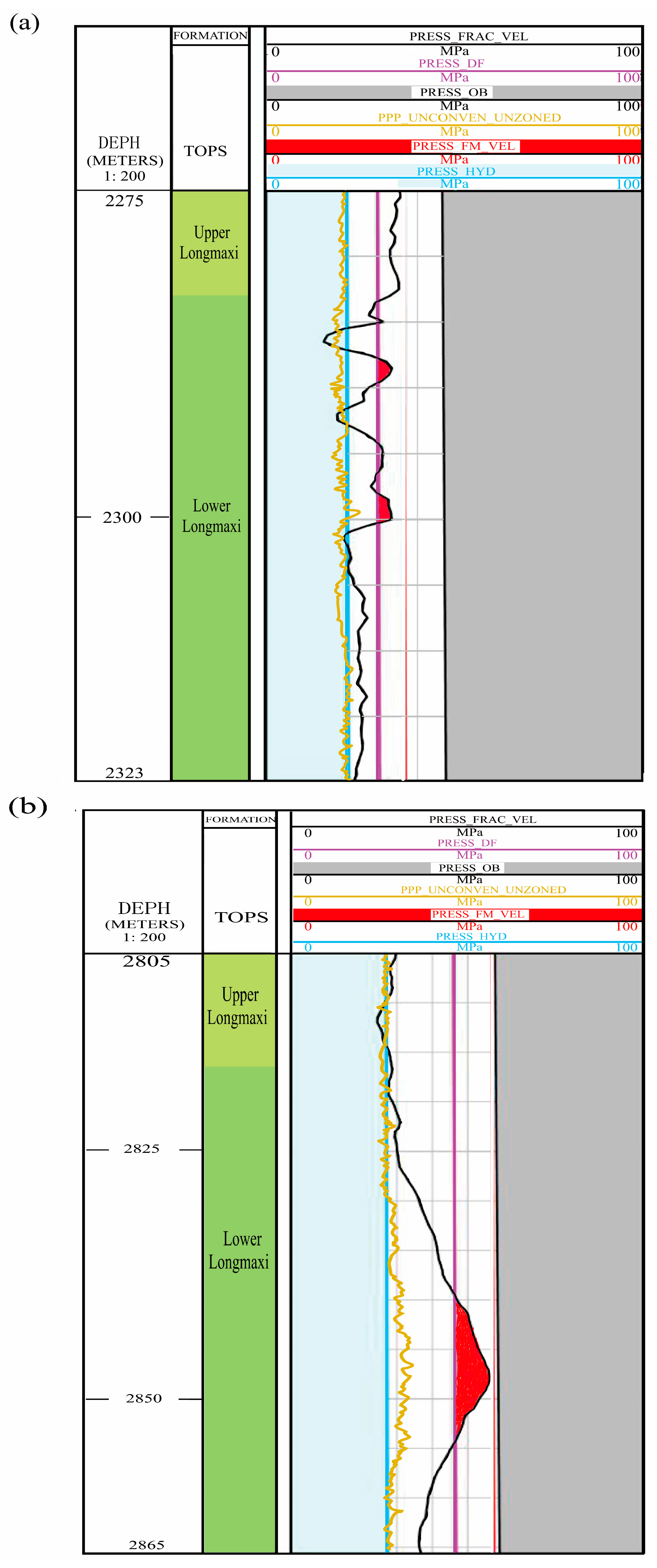
4. Results
5. Discussion
5.1. Comparative Evaluation of the Proposed Workflow
5.2. Limitations and Validation of the Eaton–Yale Approach
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bahmaei, Z.; Hosseini, E. Pore pressure prediction using seismic velocity modeling: Case study, Sefid-Zakhor gas field in Southern Iran. J. Pet. Explor. Prod. Technol. 2020, 10, 1051–1062. [Google Scholar] [CrossRef]
- Yale, D.P.; Perez, A.; Raney, R. Novel pore pressure prediction technique for unconventional reservoirs. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Houston, TX, USA, 23 July 2018. [Google Scholar]
- Lei, T.; Yin, X.; Zong, Z. Pore pressure prediction in orthotropic medium based on rock physics modeling of shale gas. J. Nat. Gas Sci. Eng. 2020, 74, 103091. [Google Scholar] [CrossRef]
- Dong, D.; Liang, F.; Guan, Q.; Jiang, Y.; Zhou, S.; Yu, R.; Gu, Y.; Zhang, S.; Qi, L.; Liu, Y. Development model and identification of evaluation technology for Wufeng Formation–Longmaxi Formation quality shale gas reservoirs in the Sichuan Basin. Nat. Gas. Ind. B 2023, 10, 165–182. [Google Scholar] [CrossRef]
- Chen, T.; Mukerji, T.; Ma, G.; Wei, Y.; Jin, J.; Song, X. Pore Pressure Prediction for a Paleozoic Marine Shale in South China. In Proceedings of the 81st EAGE Conference and Exhibition, London, UK, 3–6 June 2019. [Google Scholar]
- Mgimba, M.M.; Jiang, S.; Mwakipunda, G.C. The identification of normal to underpressured formations in the Southeastern Sichuan basin. J. Pet. Sci. Eng. 2022, 219, 111085. [Google Scholar] [CrossRef]
- Liu, R.; Zheng, J.; Hao, F.; Nie, Z.; Heng, D.; Tan, X.; Jiang, D. Variation in pore systems with tectonic stress in the overthrust Wufeng-Longmaxi shale of the southern Sichuan Basin, China. J. Nat. Gas Sci. Eng. 2020, 83, 103617. [Google Scholar] [CrossRef]
- Sun, C.; Nie, H.; Dang, W.; Chen, Q.; Zhang, G.; Li, W.; Lu, Z. Shale gas exploration and development in China: Current status, geological challenges, and future directions. Energy Fuels 2021, 35, 6359–6379. [Google Scholar] [CrossRef]
- Das, B.; Chatterjee, R. Mapping of pore pressure, in-situ stress and brittleness in unconventional shale reservoir of Krishna-Godavari basin. J. Nat. Gas Sci. Eng. 2018, 50, 74–89. [Google Scholar] [CrossRef]
- Hottmann, C.E.; Johnson, R.K. Estimation of formation pressures from log-derived shale properties. J. Pet. Technol. 1965, 17, 717–722. [Google Scholar] [CrossRef]
- Eaton, B.A. The equation for geopressure prediction from well logs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 28 September 1975. [Google Scholar]
- Terzaghi, K.; Peck, R.B.; Mesri, G. Soil Mechanics in Engineering Practice, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 1996; pp. 44–53. [Google Scholar]
- Bowers, G.L. Pore pressure estimation from velocity data: Accounting for overpressure mechanisms besides undercompaction. SPE Drill. Complet. 1995, 10, 89–95. [Google Scholar] [CrossRef]
- Flemings, P.B.; Stump, B.B.; Finkbeiner, T.; Zoback, M. Flow focusing in overpressured sandstones: Theory, observations, and applications. Am. J. Sci. 2002, 302, 827–855. [Google Scholar] [CrossRef]
- Schneider, J.; Flemings, P.B.; Dugan, B.; Long, H.; Germaine, J.T. Overpressure and consolidation near the seafloor of Brazos-Trinity Basin IV, northwest deepwater Gulf of Mexico. J. Geophys. Res. Solid. 2009, 114. [Google Scholar] [CrossRef]
- Couzens-Schultz, B.A.; Axon, A.; Azbel, K.; Haugland, M.; Sarker, R.; Tichelaar, B.; Wiesneck, J.B.; Wilheml, R.; Zhang, J.; Zhang, Z. Pore pressure prediction in unconventional resources. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26 March 2013. [Google Scholar]
- Xia, X.; Wallace, J.; Du, L. Modeling of abnormal fluid pressure in unconventional plays due to uplift. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Denver, CO, USA, 12–14 August 2013. [Google Scholar]
- Friedrich, M.; Monson, G. Two practical methods to determine pore pressure regimes in the Spraberry and Wolfcamp formations in the Midland basin. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 12–14 August 2013. [Google Scholar]
- Rittenhouse, S.; Currie, J.; Blumstein, R. Using mud weights, DST, and DFIT data to generate a regional pore pressure model for the Delaware Basin, New Mexico and Texas. In Proceedings of the Unconventional Resources Technology Conference, San Antonio, TX, USA, 1–3 August 2013. [Google Scholar]
- Swarbrick, R.; Lahann, R.; O’Connor, S.; Hoskin, E. Limitations of seismic pore pressure prediction-what is the alternative? In Proceedings of the 75th EAGE Conference & Exhibition-Workshops, London, UK, 10 June 2013. [Google Scholar]
- Devine, P.E. Toward Understanding Over-Pressure in a Basin with Burial and Uplift: Preliminary Results of a Study Measuring Under-Compaction with DT Logs. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 25–27 August 2014. [Google Scholar]
- Han, T.; Pervukhina, M.; Ben Clennell, M.; Neil Dewhurst, D. Model-based pore-pressure prediction in shales: An example from the Gulf of Mexico, North America. Geophysics 2017, 82, M37–M42. [Google Scholar] [CrossRef]
- Sayers, C.; Den Boer, L. Seismic pore pressure estimation in unconventional reservoirs. In Proceedings of the Second EAGE/AMGP/AMGE Latin American Seminar in Unconventional Resources, Mexico City, Mexico, 14–15 November 2019. [Google Scholar]
- Liang, Z.; Jiang, Z.; Wu, W.; Guo, J.; Wang, M.; Nie, Z.; Li, Z.; Xu, D.; Xue, Z.; Chen, R.; et al. Study and Classification of Porosity Stress Sensitivity in Shale Gas Reservoirs Based on Experiments and Optimized Support Vector Machine Algorithm for the Silurian Longmaxi Shale in the Southern Sichuan Basin, China. ACS Omega 2022, 7, 33167–33185. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zheng, H.; Wang, G.; Liu, Z.; Qi, Y.; Huang, Z.; Fan, X. In-situ stresses, abnormal pore pressures and their impacts on the Triassic Xujiahe reservoirs in tectonically active western Sichuan basin. Mar. Pet. Geol. 2020, 122, 104708. [Google Scholar] [CrossRef]
- Ou, C.; Li, C.; Rui, Z.; Ma, Q. Lithofacies distribution and gas-controlling characteristics of the Wufeng–Longmaxi black shales in the southeastern region of the Sichuan Basin, China. J. Pet. Sci. Eng. 2018, 165, 269–283. [Google Scholar] [CrossRef]
- Shu, Y.; Lu, Y.; Chen, L.; Wang, C.; Zhang, B. Factors influencing shale gas accumulation in the lower Silurian Longmaxi formation between the north and South Jiaoshiba area, Southeast Sichuan Basin, China. Mar. Pet. Geol. 2020, 11, 905–917. [Google Scholar] [CrossRef]
- Urpi, L.; Rinaldi, A.P.; Rutqvist, J.; Wiemer, S. Fault stability perturbation by thermal pressurization and stress transfer around a deep geological repository in a clay formation. J. Geophys. Res. Solid. Earth 2019, 124, 8506–8518. [Google Scholar] [CrossRef]
- Swarbrick, R. Review of pore-pressure prediction challenges in high-temperature areas. Lead. Edge 2012, 31, 1288–1294. [Google Scholar] [CrossRef]
- Mavko, G.; Mukerji, T.; Dvorkin, J. The Rock Physics Handbook, 3rd ed.; Cambridge University Press: Cambridge, UK, 2020; pp. 345–351. [Google Scholar]
- Vernik, L. Seismic Petrophysics in Quantitative Interpretation; Society of Exploration Geophysicists: Houston, TX, USA, 2016; pp. 145–153. [Google Scholar]
- Traugott, M. Pore/fracture pressure determinations in deep water. World Oil 1997, 218, 68–70. [Google Scholar]




| Well | Depth Interval (m) | Thickness (m) | Formation |
|---|---|---|---|
| Well A | 2264.3–2283.8 | 19.5 | Upper Longmaxi |
| 2283.8–2356.3 | 12.5 | Lower Longmaxi | |
| 2356.3–2363.0 | 6.7 | Wufeng formation | |
| Well B | 2804.0–2817.2 | 13.2 | Upper Longmaxi |
| 2817.2–2890.0 | 72.8 | Lower Longmaxi | |
| 2890.0–2898.0 | 8.0 | Wufeng formation |
| Well A | Well B | ||
|---|---|---|---|
| Depth (m) | PRESS_FM_VEL (MPa) | Depths (m) | PRESS_FM_VEL (MPa) |
| 2275–2280 | 41.834 | 2805–2810 | 31.675 |
| 2280–2285 | 32.955 | 2810–2815 | 30.172 |
| * 2285–2290 | 41.786 | 2815–2820 | 31.910 |
| 2290–2295 | 29.834 | 2820–2825 | 32.172 |
| * 2295–2305 | 40.712 | 2825–2835 | 33.966 |
| 2305–2310 | 30.490 | * 2835–2845 | 42.166 |
| 2310–2315 | 31.982 | * 2845–2855 | 48.356 |
| 2315–2323 | 33.650 | 2855–2865 | 33.909 |
| Well Name | Calcite (%) | Illite (%) | Quartz (%) | Kerogen (%) |
|---|---|---|---|---|
| Well A | 10.4 | 34.2 | 53.4 | 2.0 |
| Well B | 10.0 | 50.0 | 35.0 | 5.0 |
| Rock Composition | P-Velocity (m/s) | S-Velocity (kg/m3) | Density (kg/m3) | Compressional Modulus (MPa) |
|---|---|---|---|---|
| Calcite | 6377.6 | 3534 | 2710 | 110,220 |
| Illite | 3571.4 | 2100 | 2780 | 35,450 |
| Quartz | 6047.8 | 4118 | 2650 | 96,920 |
| Kerogen | 2381.3 | 1200 | 1300 | 7370 |
| Well A | Well B | ||
|---|---|---|---|
| Depths (m) | PRESS_FM_VEL (MPa) | Depths (m) | PRESS_FM_VEL (MPa) |
| 2275–2280 | 33.450 | 2805–2810 | 31.545 |
| 2280–2285 | 33.955 | 2810–2815 | 32.296 |
| * 2285–2290 | 32.631 | 2815–2820 | 32.974 |
| 2290–2295 | 30.354 | 2820–2825 | 32.172 |
| * 2295–2305 | 33.962 | 2825–2835 | 33.958 |
| 2305–2310 | 32.043 | * 2835–2845 | 34.091 |
| 2310–2315 | 33.225 | * 2845–2855 | 34.959 |
| 2315–2323 | 32.056 | 2855–2865 | 33.017 |
| Time | Depth (m) | Operations | Semi-Logarithmique Extrapolation Pressure (MPa) | Fitting Pressure (MPa) | Temperature (°C) |
|---|---|---|---|---|---|
| 17: 05 | - | Circulation started | - | - | - |
| 07: 00 | - | Circulation stopped | - | - | - |
| 13:00 | 2304.62 | Shut 1 | 26.94 | 31.85 | 79.89 |
| 17:00 | 2308.10 | Shut 2 | 28.15 | 32.31 | 82.98 |
| 23:00 | 2313.39 | Shut 3 | 29.65 | 33.62 | 86.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kablan, O.A.B.K.; Chen, T. Shale Gas Reservoir Pore Pressure Prediction: A Case Study of the Wufeng–Longmaxi Formations in Sichuan Basin, Southwest China. Energies 2023, 16, 7280. https://doi.org/10.3390/en16217280
Kablan OABK, Chen T. Shale Gas Reservoir Pore Pressure Prediction: A Case Study of the Wufeng–Longmaxi Formations in Sichuan Basin, Southwest China. Energies. 2023; 16(21):7280. https://doi.org/10.3390/en16217280
Chicago/Turabian StyleKablan, Or Aimon Brou Koffi, and Tongjun Chen. 2023. "Shale Gas Reservoir Pore Pressure Prediction: A Case Study of the Wufeng–Longmaxi Formations in Sichuan Basin, Southwest China" Energies 16, no. 21: 7280. https://doi.org/10.3390/en16217280
APA StyleKablan, O. A. B. K., & Chen, T. (2023). Shale Gas Reservoir Pore Pressure Prediction: A Case Study of the Wufeng–Longmaxi Formations in Sichuan Basin, Southwest China. Energies, 16(21), 7280. https://doi.org/10.3390/en16217280






