Electric Arc Furnace Electrode Movement Control System Based on a Fuzzy Arc Length Identifier

Abstract

From the point of view of the synthesis of control influences, arc steelmaking furnaces are complex nonlinear objects with strongly expressed mutual influences. It has been demonstrated that at a given supply voltage, the distribution of the current values of the phase currents in the quasi-steady-state mode makes it possible to estimate the situation in the arc space of an arc steelmaking furnace and identify the value of arc lengths. This dependence is preserved in transient modes. In order to identify arc lengths from the phase currents, it is proposed to use an approach based on the theory of fuzzy sets. The construction of the fuzzy arc length identifier rule base was carried out in two stages: the first stage used data from quasi-steady-state modes and the Wang–Mendel algorithm; the second stage involved adding a new rule to the database if the activity level of the formed rules was lower than the established level α for the data obtained in the dynamic mode. Further optimization of the parameters of the fuzzy identifier for operation in dynamic modes was carried out using the “back-propagation” algorithm. Based on the identified values of arc lengths, a control system for the movement of electrodes in an arc steelmaking furnace was synthesised. The proposed control system makes it possible to eliminate unproductive electrode movements due to changes in the situation in other phases of the arc steelmaking furnace and simplifies the application of modern methods of synthesising a control system for such complex objects. The results obtained in the mathematical model have confirmed the effectiveness of the proposed control system for the movement of electrodes in an arc steelmaking furnace.

1. Introduction

Electric arc furnaces (EAF) produce steel by melting down scrap metal using a three-phase electrical grid as the main source of energy. Melting takes place with the help of powerful electric arcs, which involves significant electricity consumption. Thanks to technological innovations [1,2] that have significantly reduced energy consumption and increased the productivity of arc furnaces while satisfying customer demands for steel quality, the EAF process is becoming increasingly competitive in terms of cost and quality compared to other technologies. The cost of producing a batch of steel depends on both the cost of raw materials and the costs associated with not achieving management targets.

A modern EAF consumes about 350 kWh/tonne of electricity [1]. Further improvement of the EAF performance is possible through the use of various additives and heat recovery systems, as well as the improvement of existing control systems. One such system is the electrode movement control system. The electrode movement control system, due to the constantly changing situation in the arc gap, has a significant impact on many important aspects of furnace performance, such as energy consumption, average arc current, stability of arc burning, energy and electrode losses. All of these parameters are interrelated in a complex way, and therefore there are many interpretations to understand “optimal” control strategies [3]. An important aspect of all optimal strategies is power consumption and losses [4,5,6]. Analysing the energy consumption of EAFs, factors related to the technological mode, in particular the power transferred to the arc gap, is traditionally considered. A significant number of publications [7,8,9,10] have been devoted to solving this problem, including methods of forecasting electricity consumption [11] and the use of artificial intelligence systems [12,13].

The problem of reducing energy consumption encourages leading electrical engineering companies to create and implement new EAFs control systems. Today, the technological solutions are provided by such leading companies as Siemens (SIMETAL system), Danieli (HI-REG and Q-REG+ systems), and others. A commonly applicable “standard” strategy for controlling the electrical mode of EAFs is the formation of an “impedance control principle” [3,14,15]. Such a control system is based on phase voltage and current signals. The effective values of voltage and current are transmitted to the divider unit, at the output of which a signal with information about the total arc resistance occurs. This signal is compared with the given arc resistance value to generate a mismatch signal. If the voltage and current are at the given level selected by the steelmaker, the controller output signal is zero. If the current exceeds this level, a mismatch occurs and a signal is generated to raise the electrode to reduce the current. The disadvantages of this method include insufficient accuracy of electrode movement control due to the lack of direct dependence of arc lengths on their voltages, as well as the dependence of changes in arc voltage on changes in currents in other phases.

In EAFs, regulators are also used, which generate a control influence based on the deviation of current [16] or voltage [17] from a given value. In the case of a current regulator, random changes in current in one of the phases caused by changes in arc length lead to changes the current in the other two phases, which creates unproductive electrode movements that can occur as a result of accidents. It is also necessary to take into account the nonlinearity of the current dependence on arc length, which complicates the synthesis of the control system. According to a number of authors, control systems based on voltage deviation are more efficient. Traditionally, it is assumed that there is a linear relationship between arc length and voltage [18,19]. However, works [20,21] show a nonlinear relationship between arc voltage and arc length. The model of arc voltage versus arc length with a variable gradient along the arc length is presented in [22].

Existing control systems for EAFs, under conditions of continuous disturbances in the power circuit, allow for a significant dispersion of electrical mode parameters during the steelmaking process, especially during the charge-melting period. The relationship between electrical parameters and arc length plays a major role in the heat transfer processes in EAF. Reducing the arc length after scrap melting will protect the furnace roof and sides from radiation, while increasing the arc length will increase the average temperature of the metal bath [12]. Thus, the importance of arc length control for industrial furnaces to ensure their efficient operation, identify energy reserves, and improve technical and economic characteristics, such as specific energy consumption, operating time, and heating time, is obvious.

The length of the electric arc in industrial EAF is difficult to measure experimentally. Traditionally, arc length is evaluated on the basis of voltage. This leads to the implementation of a control system based on the deviation from the given voltage value. In addition, the arc voltage signal in each phase is taken equal to the voltage between the point of connection of the flexible power cables to the output of the furnace transformer and the arc furnace ground [23]. This signal differs from the actual arc voltage, which adversely affects the quality of control of the arc furnace electrical mode.

Thus, it can be argued that the problem of synthesising a high-speed system for moving the electrodes of an arc steelmaking furnace remains actual. The material of this article is devoted to the development a fuzzy arc length identifier based on the three-dimensional vector of EAF phase currents and the creation on this basis of a control system for the movement of electrodes. The synthesis of the control influence based on the deviation of the arc length from the given value will allow for avoiding mutual influences between the phases of the EAF due to changes in the situation in the arc space, and thus improve the quality of control.

The novelty of the research lies in the application of a three-dimensional vector of effective values of the EAF phase currents to identify arc lengths; the proposed approach is to synthesise a control system for the electrodes’ movement based on the deviation of the arc length from the given value and the creation of a fuzzy arc length identifier based on easily measurable coordinates of the electrical mode of the EAF.

2. Mathematical Model of the Electrical Complex “Power Supply Network—Arc Steelmaking Furnace”

The system model presented in [24] was used for the study. The adequacy of this model is confirmed by the coincidence of the obtained results with the results of experimental studies and the results of theoretical calculations obtained by other authors [15,24]. The model uses the representation of the EAF elements (power grid M, furnace transformer TR, electric line with arc SL) in the form of multipoles. The multipole model is described in terms of the average-voltage-in-integration-step (AVIS) method [25] and has the following form:

$${\overline{\mathrm{i}}}_e+G_e\frac{1}{\Delta t}{\displaystyle \underset{t_0}{\overset{t_0+\Delta t}{\int }}{\overline{\mathrm{v}}}_{e}dt}+C_e=0, e\to N, \mathit{TR}, \mathit{SL}$$

(1)

where ${\overline{\mathrm{i}}}_e$—the vector of currents of external branches at the end of the integration step; ${\overline{\mathrm{v}}}_e$—vector of pole potentials; $G_e,C_e$—the matrix of coefficients and the vector of free terms determined by the element parameters and initial conditions.

The vector Equation (1) is formed on the basis of the AVIS method equation for an electrical branch, which generally contains an electromotive force source e(t), inductance L, capacitance C, and a voltage U [25]:

$$\begin{array}{l}U+E-u_{R0}-u_{C0}+\left(\frac{R}{m+1}+\frac{\Delta t}{C}\cdot \frac{2-\left(m+1\right)\left(m+2\right)}{2\left(m+1\right)\left(m+2\right)}+\frac{L_0}{\Delta t}\right)i_0\\ -{\displaystyle \sum _{k=1}^{m-1}\left(\frac{R\Delta t^k}{\left(k+1\right)!}\cdot \frac{m-k}{m+1}+\frac{\Delta t^{k+1}}{C\left(k+2\right)!}\cdot \frac{\left(m+1\right)\left(m+2\right)-\left(k+1\right)\left(k+2\right)}{\left(m+1\right)\left(m+2\right)}\right)\frac{d^{\left(k\right)}{i}_0}{d{t}^{\left(k\right)}}}\\ -\left(\frac{R}{m+1}+\frac{\Delta t}{C\left(m+1\right)\left(m+2\right)}+\frac{L_1}{\Delta t}\right)i_1=0\end{array}$$

(2)

where $u_{R0},u_{C0}$—voltage values on the active resistance and on the capacitor at the beginning of the integration step; $i_0,i_1$—branch current at the beginning and at the end of the integration step (hereafter, the index zero means the value at the beginning of the step; the index one—the value at the end of the step); Δt—numerical integration step value; m—the order of the method, which is determined by the order of the polynomial, which describes the change in the branch current at the numerical integration step (in this model, the first-order method with linear approximation of the current at the step is used); C—capacity; U, E—the average values of the voltage applied to the circuit and the EMF, which are calculated based on the instantaneous values of voltage u and EMF as

$$U=\frac{1}{\Delta t}{\displaystyle \underset{t_0}{\overset{t_0+\Delta t}{\int }}udt}, E=\frac{1}{\Delta t}{\displaystyle \underset{t_0}{\overset{t_0+\Delta t}{\int }}edt},$$

(3)

On the basis of Equation (2) for the first order AVIS method, the equation for an electric branch with an arc was derived in [24]:

$$U-u_{R0}-u_{arc0}-\left(\frac{R+R_{d0}}{2}+\frac{L}{\Delta t}\right)\left(i_1-i_0\right)=0$$

(4)

where u_R0, u_arc0 are the values of voltages on the active resistance of the branch and on the arc at the beginning of the step; R, L are the active resistance and inductance of the branch; $R_d=\frac{d{u}_{arc}}{di}$ is the dynamic arc resistance, which is determined on the basis of instantaneous values of the arc voltage u_arc and current i using the approximation expressions for the arc volt-ampere characteristics given in [24].

Based on the coefficients in Equation (1) of each element that is part of the system and the incidence matrices of these elements, a vector algebraic equation is formed to determine the average values of the potentials of the independent system nodes at the integration step

$$G_S\frac{1}{\Delta t}{\displaystyle \underset{t_0}{\overset{t_0+\Delta t}{\int }}{\overline{v}}_{S}dt}+C_S=0,$$

(5)

where ${\overline{v}}_S={\left(v_1,v_2,v_3,v_4,v_5,v_6,v_7,v_8,v_9\right)}^T$—the vector of potentials of independent system nodes; ${\overline{V}}_S=\frac{1}{\Delta t}{\displaystyle \underset{t_0}{\overset{t_0+\Delta t}{\int }}{\overline{v}}_{S}dt}$—vector of averages at the integration step values of potential of the independent system nodes; $G_S$, $C_S$—matrices of coefficients, which are determined by the formulas:

$$G_S={\displaystyle \sum _j{\Pi }_j{G}_j{\Pi }_j^T}, C_S={\displaystyle \sum _j{\Pi }_j{\overrightarrow{C}}_j}, \mathrm{j}\to N, \mathit{TR}, \mathit{SL}.$$

(6)

Based on the average values of the potentials of the system independent nodes obtained from Equation (5), we determine the average values of the poles potentials for each element-multipole during the integration step:

$${\overline{V}}_j=\frac{1}{\Delta t}{\displaystyle \underset{t_0}{\overset{t_0+\Delta t}{\int }}{\overline{v}}_{j}dt}={\Pi }_j^T\cdot {\overline{V}}_S={\Pi }_j^T\cdot \left(\frac{1}{\Delta t}{\displaystyle \underset{t_0}{\overset{t_0+\Delta t}{\int }}{\overline{v}}_{S}dt}\right), \mathrm{j}\to N, \mathit{TR}, \mathit{SL}$$

(7)

Next, for each element, we determine the currents of the external branches at the end of the integration step using the known vector of the average values of poles potentials at the integration step from (1).

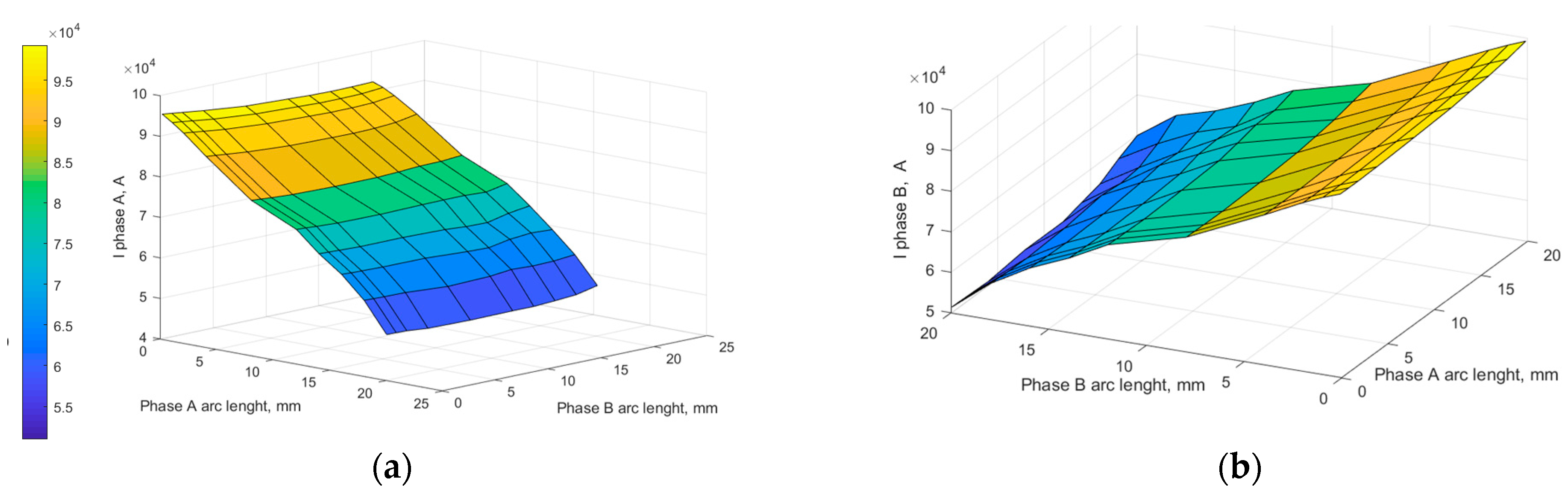
The research with the application of the mathematical model was carried out as follows. At constant arc lengths in phases B and C, the arc length in phase A was changed from the mode close to a short circuit to the mode close arc break. After the transient process was completed, the current values of the phase currents were saved. At the next stage, the value of the arc length in phase B was changed, the value of the arc length in phase C remained unchanged, and the arc length in phase A was again changed from the short-circuit mode to the near-arc breakdown mode. As a result, the dependences of the currents change at a constant arc length in phase C and changes in arc lengths in phases A and B from the short-circuit mode to the arc breakdown mode were obtained. The obtained surfaces of the currents in phases A and B are shown in Figure 1.

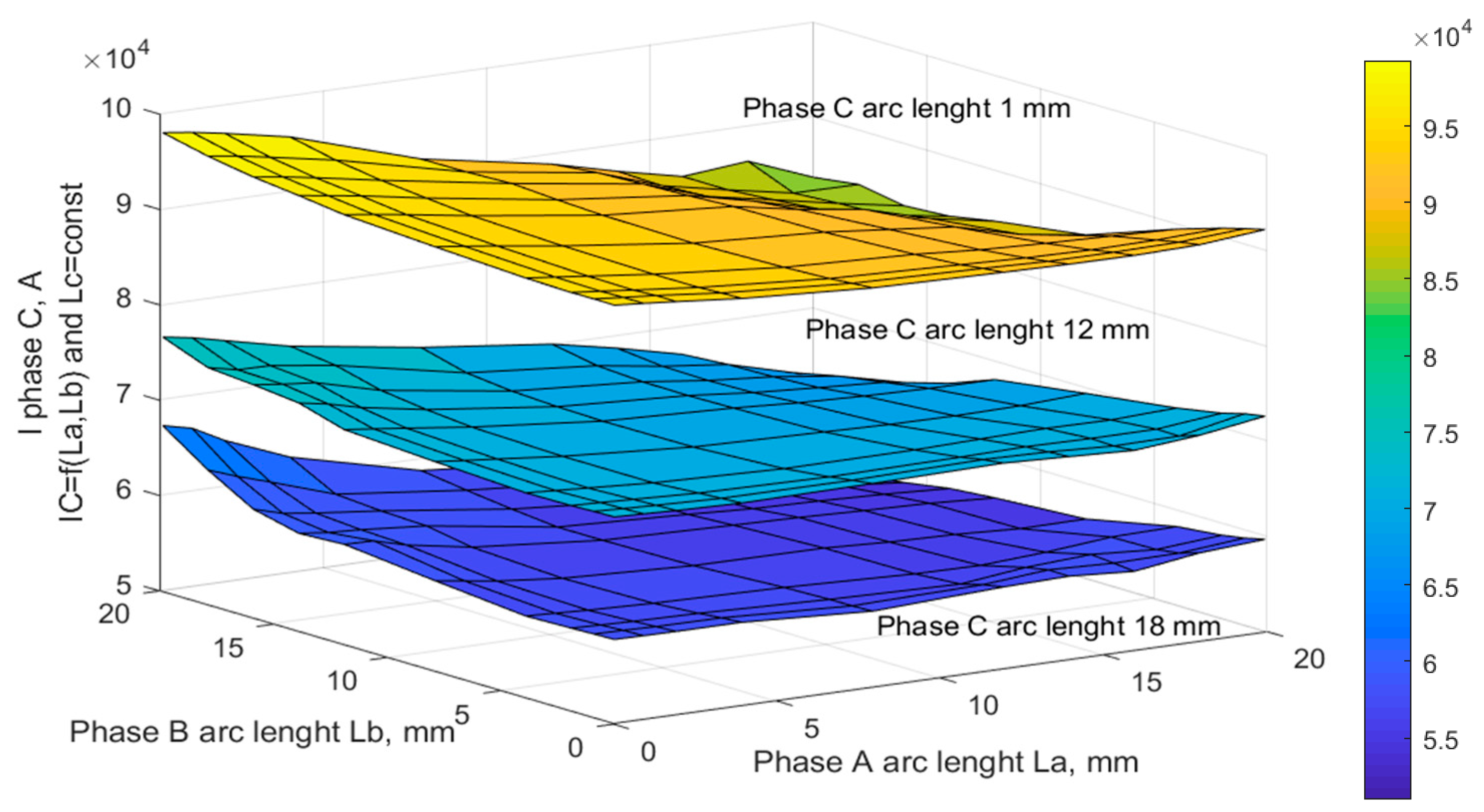
By changing the value of the arc length in phase C and performing calculations when changing the arc lengths in phases A and B, we obtain the surfaces of the phase C current change as a function of the arc lengths in phases A and B at a given arc length in phase C. The obtained surfaces are shown in Figure 2.

These dependences also demonstrate the mutual influence of phases during the operation of an arc steelmaking furnace, depending on the state in which the system is located.

Similar surfaces can be constructed for the currents of other phases. Thus, it can be argued that each state of the arc space of the EAF at a given supply voltage uniquely corresponds to a certain distribution of phase currents. Thus, it is possible to solve the inverse problem: to find the arc lengths from the distribution of phase currents of an arc steelmaking furnace.

3. Fuzzy Arc Length Identifier Synthesis

When applying intelligent control methods, this problem can be solved by combining the use of the theory of artificial neural networks (state classification) and fuzzy logic (calculation of arc lengths based on arc lengths determined in the classified states). To solve the problem of identifying arc lengths based on a certain vector of effective values of phase currents, we will use the apparatus of fuzzy set theory [26]. As is known from the theory of intelligent control, MISO systems are much easier to synthesise and in many cases provide a better result compared to MIMO systems. Therefore, to solve the identification problem, we will form a generalised fuzzy model with three inputs and one output. In a three-dimensional Cartesian coordinate system, each point of the phase current distribution will correspond to a vector whose projections on the axes of the coordinate system will be equal to the phase currents. To build a fuzzy controller, we select the following variables as input parameters:

$$cos{F}_x=\frac{I_x}{\sqrt{I_x^2+I_y^2+I_z^2}};cos{F}_y=\frac{I_y}{\sqrt{(I_x^2+I_y^2+I_z^2}} \mathrm{and} I_z$$

(8)

where $I_x, I_y, I_z$—currents of the EAF phases.

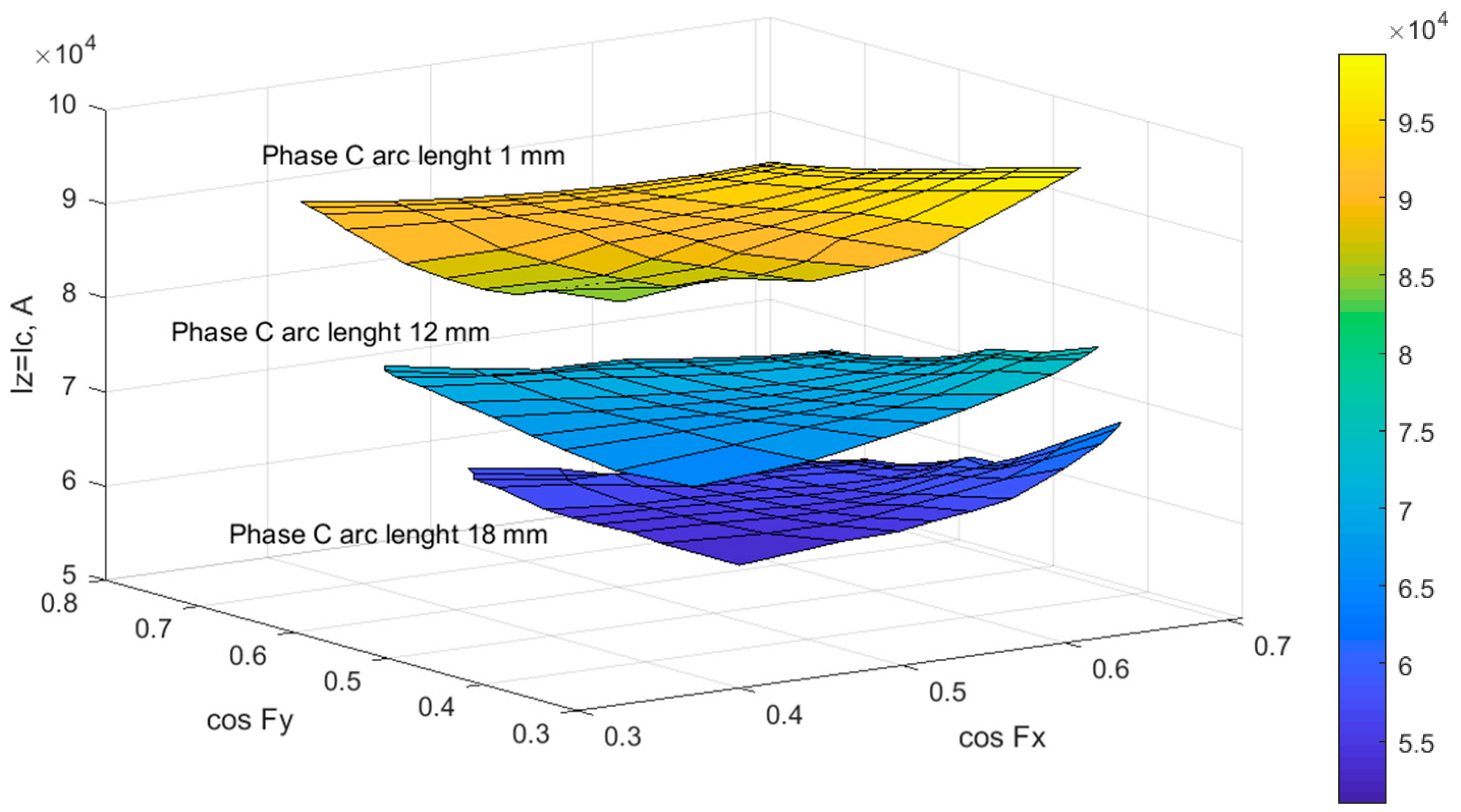
The surface of the phase C current change in the new coordinate basis will have the form shown in Figure 3.

The projection of the surfaces of the phase C current change obtained during the calculations onto the XY plane (Figure 4) demonstrates the lack of overlap of the obtained neighbouring planes at different values of the arc length in phase C. This can cause significant errors in identifying the arc length in this phase. This drawback can be eliminated by adding data obtained at other arc lengths or by applying data addition technology, similar to padding in machine learning systems.

Nowadays, as is well known, there are no general methodological principles for the synthesis of fuzzy identifiers. The classical method for synthesising fuzzy systems based on data is the Wang–Mendel method [27,28]. Other approaches are based either on the use of data clustering or the hierarchical approach to building the rule base [29,30].

The large size of the rule base in the case of a large amount of inputs is one of the main disadvantages of traditional methods of fuzzy identifiers’ synthesis. In our case, the number of inputs equals three. Considering the inputs to the fuzzy identifier (see Figure 4), we can assume that the problem of rule base size is not crucial, since the output value is unchanged for significant ranges of input changes. Therefore, the Wang–Mendel method proposed in [27] is used to synthesize a fuzzy identifier. 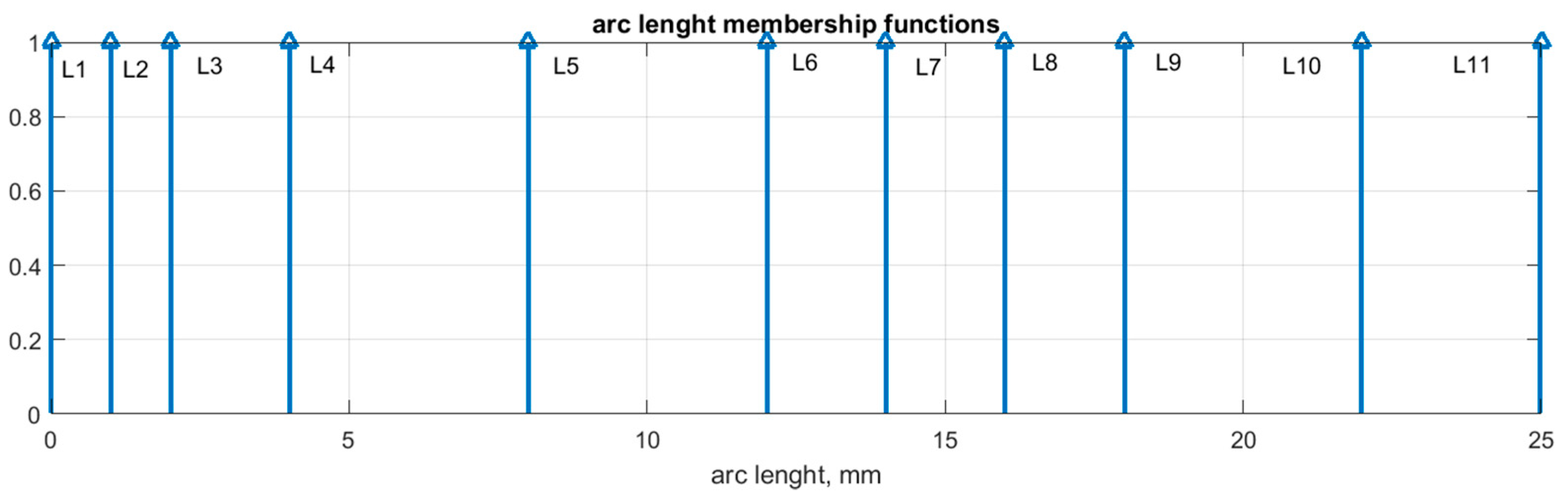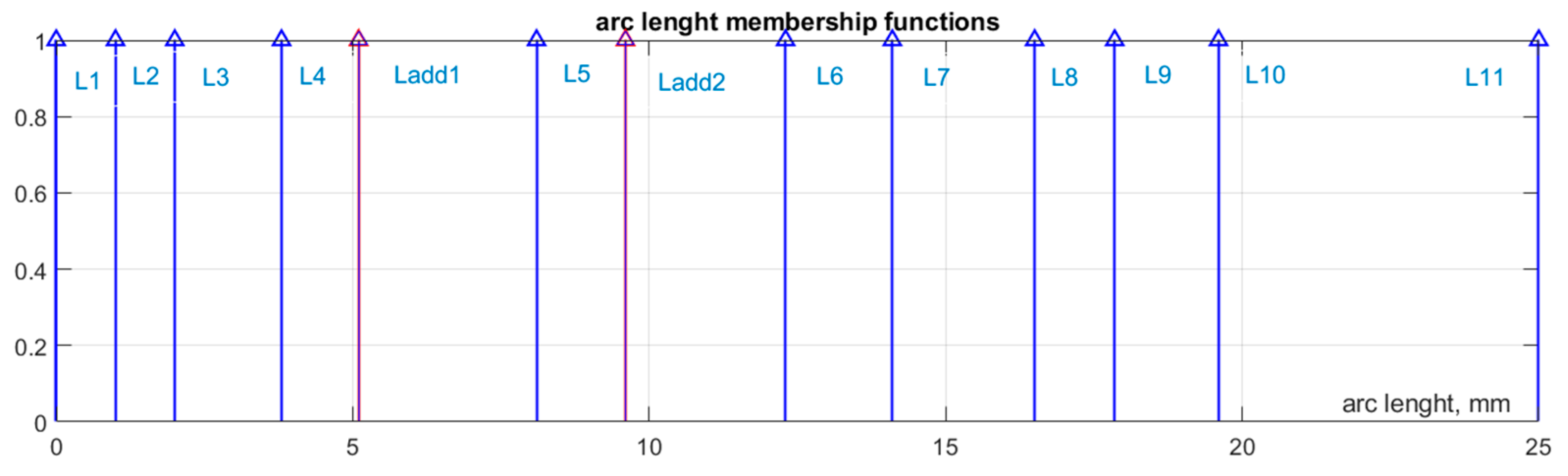Figure 5 shows the fuzzification functions of the input variables. Considering that the data were obtained at the specified values of arc lengths, the singleton function was chosen as the membership function of the output variable (Figure 6):

The experimental results obtained with the help of the mathematical model are divided into two groups. One of them is used to form the rule base, the other for verification. At the stage of forming the rule base, the weight function of an individual rule is implemented. This function is modified based on the “winner-take-all” strategy according to the obtained rule activity levels calculated for each data set. In the case of applying the singleton function to an output value, the rule structure of the Mamdani representation and the Takagi–Sugeno representation are equivalent. The Takagi–Sugeno model will be used. In this case, a separate rule at the stage of forming a rule base will look like this:

$$If cos{F}_x\in A_i and cos{F}_y\in B_j and I_z \in C_m than L=L_n$$

(9)

In the synthesized rule base, rules with low values of the weighting function are additionally verified using data that were unapplied in the rule generation stage. At the next stage, rules with the same output are aggregated:

$$\begin{array}{l}If \left(cos{F}_x\in A_i and cos{F}_y\in B_j and I_z \in C_m\right)\\ ⋮\\ or \left(cos{F}_x\in A_i and cos{F}_y\in B_j and I_z \in C_l\right)\\ ⋮\\ or \left(cos{F}_x\in A_i and cos{F}_y\in B_g and I_z \in C_l\right) than L=L_n\end{array}$$

After that, the rules are further simplified:

$$\begin{array}{l}If \left(cos{F}_x\in A_i and \left(cos{F}_y\in B_j or cos{F}_y\in B_k \right) and \left(I_z \in C_m or I_z \in C_l or\dots \right)\right)\\ ⋮\\ or \left(cos{F}_x\in A_i and cos{F}_y\in B_g and I_z \in C_h\right) than L=L_n\end{array}$$

To obtain the arc length value, defuzzification based on the simplified centroid method was applied:

$$L_{arc}=\frac{{\sum }_{k=1}^{11}{\mu }_k{L}_k}{{\sum }_{k=1}^{11}{\mu }_k}$$

(10)

where ${\mu }_k=f\left({\mu }_{A_i} , {\mu }_{B_j} , {\mu }_{C_m}\right)$ is the degree of activity of the k-th rule, which is determined on the basis of the values of the membership functions of linguistic variables A_i, B_j, C_m; L_k is the value of the arc length for the k-th rule.

The fuzzy arc length identifier, synthesized with a given membership function distribution, showed relatively good results on the verification data. The maximum error did not exceed 7% and occurred for the data obtained in the following situation in arc space: one phase in the short-circuit mode and the other two phases or one of the phases in the arc-fault mode; two phases in the short-circuit mode and the third phase in the arc-fault mode; three phases in the arc-fault mode.

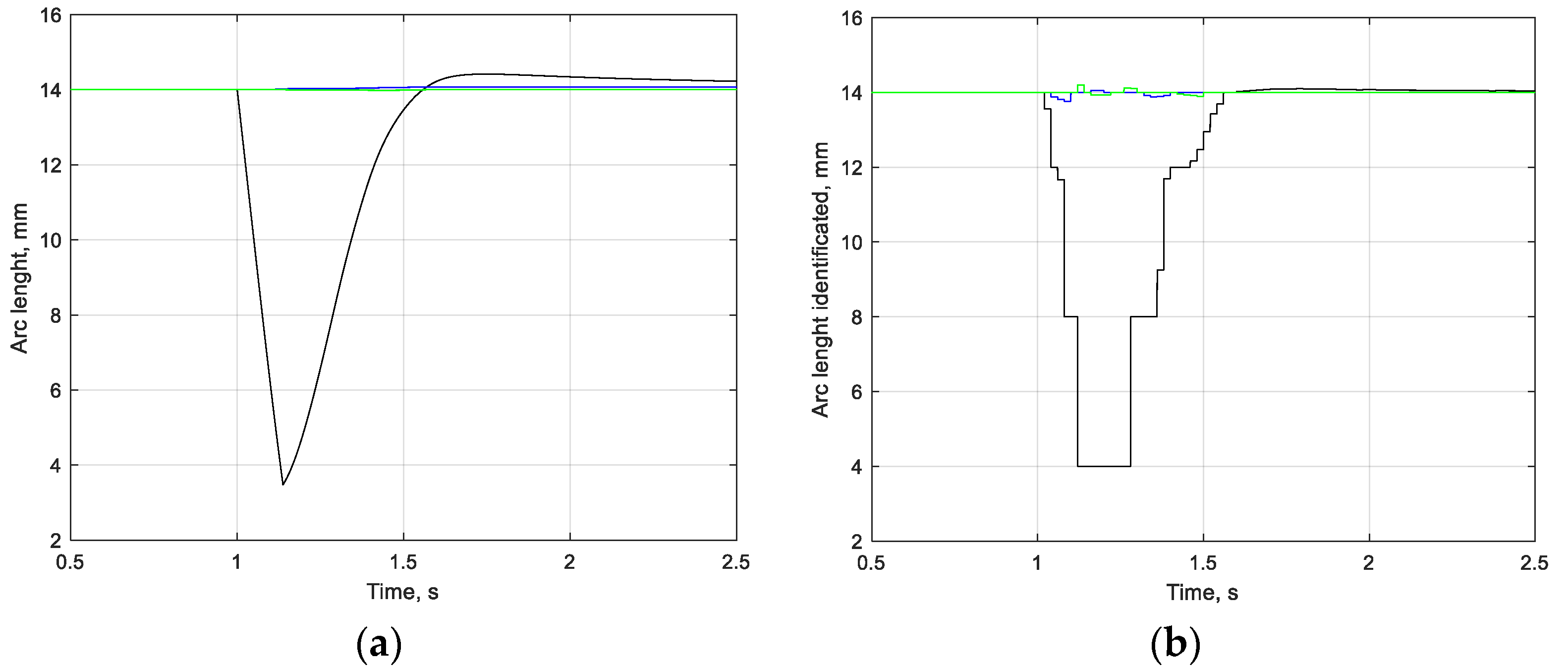
Further testing of the proposed fuzzy identifier was carried out in dynamic modes using data obtained directly from the EAF model during the operation with given disturbances. At the same time, in dynamic processes, due to the action of transient currents, as well as the entry of signals into areas for which there is no overlap (see Figure 4), the quality of identification in the intervals of changing arc lengths from 3 to 12 mm significantly decreased (Figure 7).

To eliminate this drawback, the number of terms of the output variable was increased by 2 and the fuzzy identifier rule base was modified according to the data obtained for arc lengths of 6 mm and 10 mm. The parametric optimization of the fuzzy arc length identifier was also performed using the back-propagation algorithm [28].

Following this algorithm, the output signal of each rule is modified according to the Equation (11):

$$L_k\left(t+1\right)=L_k\left(t\right)-\eta \cdot \left(L_{arc}-L_{arc}^{real}\right)\frac{{\mu }_k}{{\sum }_{k=1}^{11}{\mu }_k}$$

(11)

where η—is the learning constant; $L_{arc},L_{arc}^{real}$—identified and real value of the arc length; µ_k—the degree of activity of the k-th rule.

Taking into account that for the abovementioned structure of the regulator, the degree of activity of the k-th rule is determined as (12):

$${\mu }_k=\sum {\mu }_{A_i} \cdot {\mu }_{B_j} \cdot {\mu }_{C_m}=\sum e^{-\frac{{\left(cosFx-Centr{e}_{A_i}\right)}^2}{{\sigma }_{A_i}^2}}\cdot e^{-\frac{{\left(cosFy-Centr{e}_{B_j}\right)}^2}{{\sigma }_{B_j}^2}}\cdot e^{-\frac{{\left(Iz-Centr{e}_{C_m}\right)}^2}{{\sigma }_{C_m}^2}}$$

(12)

where ${\mu }_{A_i} , {\mu }_{B_j} , {\mu }_{C_m}$—membership functions of linguistic variables; Centre_Ai, Centre_Bj, Centre_Cm—the centres of the membership functions of linguistic variables; ${\sigma }_{A_i}, {\sigma }_{B_j}, {\sigma }_{C_m}$—window widths of the membership functions of linguistic variables; the derivative of the error function:

$$E=\frac{1}{2}{\left(L_{arc}-L_{arc}^{real}\right)}^2$$

(13)

by the parameter of the membership function Centre_Ai will have the form:

$$\frac{\mathit{\partial }E}{\mathit{\partial }Centr{e}_{A_i} }=\left(L_{arc}-L_{arc}^{real}\right)\cdot \frac{\mathit{\partial }{L}_{arc}}{\mathit{\partial }{\mu }_{A_i} }\cdot \frac{\mathit{\partial }{\mu }_{A_i} }{\mathit{\partial }Centr{e}_{A_i}}$$

(14)

and by the parameter of the membership function ${\sigma }_{A_i}$ will have the following form:

$$\frac{\mathit{\partial }E}{\mathit{\partial }{\sigma }_{A_i}}=\left(L_{arc}-L_{arc}^{real}\right)\cdot \frac{\mathit{\partial }{L}_{arc}}{\mathit{\partial }{\mu }_{A_i} }\cdot \frac{\mathit{\partial }{\mu }_{A_i} }{\mathit{\partial }{\sigma }_{A_i}}$$

(15)

The derivative $(\mathit{\partial }L\_arc)/(\mathit{\partial }\mu \_(A\_i )$ for a given defuzzification method and a given fuzzy identifier structure is defined as follows:

$$\begin{array}{cc}\hfill L_{arc}\frac{\mathit{\partial }{L}_{arc}}{\mathit{\partial }{\mu }_{A_i} }& =\frac{{\sum }_{k=1}^{11}{\mu }_k\frac{\mathit{\partial }{\sum }_{k=1}^{11}{\mu }_k{L}_k}{\mathit{\partial }{\mu }_{A_i}}-\left({\sum }_{k=1}^{11}{\mu }_k{L}_k\right)\frac{\mathit{\partial }{\sum }_{k=1}^{11}{\mu }_k}{\mathit{\partial }{\mu }_{A_i}}}{{\left({\sum }_{k=1}^{11}{\mu }_k\right)}^2}=\frac{\frac{\mathit{\partial }{\sum }_{k=1}^{11}{\mu }_k{L}_k}{\mathit{\partial }{\mu }_{A_i}}-\frac{\left({\sum }_{k=1}^{11}{\mu }_k{L}_k\right)}{{\sum }_{k=1}^{11}{\mu }_k}\frac{\mathit{\partial }{\sum }_{k=1}^{11}{\mu }_k}{\mathit{\partial }{\mu }_{A_i}}}{{\sum }_{k=1}^{11}{\mu }_k}=\hfill \\ & =\frac{\frac{\mathit{\partial }{\sum }_{k=1}^{11}{\mu }_k{L}_k}{\mathit{\partial }{\mu }_{A_i}}-L_{arc}\frac{\mathit{\partial }{\sum }_{k=1}^{11}{\mu }_k}{\mathit{\partial }{\mu }_{A_i}}}{{\sum }_{k=1}^{11}{\mu }_k}=\frac{\frac{\mathit{\partial }{\sum }_{k=1}^{11}{\mu }_k\left(L_k-L_{arc}\right)}{\mathit{\partial }{\mu }_{A_i}}}{{\sum }_{k=1}^{11}{\mu }_k}\hfill \end{array}$$

(16)

The derivatives $(\mathit{\partial }{\mu }_{A_i}/\mathit{\partial }{Centre}_{A_i})$ and $(\mathit{\partial }{\mu }_{A_i}/\mathit{\partial }{\sigma }_{A_i})$ are given by the equations:

$$\frac{\mathit{\partial }{\mu }_{A_i} }{\mathit{\partial }Centr{e}_{A_i}}=\frac{\mathit{\partial } e^{-\frac{{\left(cosFx-Centr{e}_{A_i}\right)}^2}{{\sigma }_{A_i}^2}} }{\mathit{\partial }Centr{e}_{A_i}}=\frac{2\left(cosFx-Centr{e}_{A_i}\right)}{{\sigma }_{A_i}^2} \cdot e^{-\frac{{\left(cosFx-Centr{e}_{A_i}\right)}^2}{{\sigma }_{A_i}^2}}$$

(17)

$$\frac{\mathit{\partial }{\mu }_{A_i} }{\mathit{\partial }{\sigma }_{A_i}}=\frac{\mathit{\partial } e^{-\frac{{\left(cosFx-Centr{e}_{A_i}\right)}^2}{{\sigma }_{A_i}^2}} }{\mathit{\partial }{\sigma }_{A_i}}=\frac{2{\left(cosFx-Centr{e}_{A_i}\right)}^2}{{\sigma }_{A_i}^3} \cdot e^{-\frac{{\left(cosFx-Centr{e}_{A_i}\right)}^2}{{\sigma }_{A_i}^2}}$$

The expressions for changing the centres and window widths of the input variable membership functions when applying the back-propagation algorithm will look like this:

$$\begin{array}{l}Centr{e}_{A_i}\left(t+1\right)=Centr{e}_{A_i}\left(t\right)-\eta \left(L_{arc}-L_{arc}^{real}\right)\frac{\frac{\mathit{\partial }{\sum }_{k=1}^{11}{\mu }_k\left(L_k-L_{arc}\right)}{\mathit{\partial }{\mu }_{A_i}}}{{\sum }_{k=1}^{11}{\mu }_k}\cdot \frac{2\left(cosFx-Centr{e}_{A_i}\right)}{{\sigma }_{A_i}^2} e^{-\frac{{\left(cosFx-Centr{e}_{A_i}\right)}^2}{{\sigma }_{A_i}^2}}\\ {\sigma }_{A_i}\left(t+1\right)={\sigma }_{A_i}\left(t\right)-\eta \left(L_{arc}-L_{arc}^{real}\right)\frac{\frac{\mathit{\partial }{\sum }_{k=1}^{11}{\mu }_k\left(L_k-L_{arc}\right)}{\mathit{\partial }{\mu }_{A_i}}}{{\sum }_{k=1}^{11}{\mu }_k}\cdot \frac{2{\left(cosFx-Centr{e}_{A_i}\right)}^2}{{\sigma }_{A_i}^3} \cdot e^{-\frac{{\left(cosFx-Centr{e}_{A_i}\right)}^2}{{\sigma }_{A_i}^2}}\end{array}$$

(18)

Similar expressions can be obtained for other membership functions of the input variables.

As a result of the optimisation, we obtained the distribution of singleton functions of the output variable arc length shown in Figure 8.

Table 1. Parameter values of membership functions that have changed during the optimisation process.

$A\left(i\right)=\exp \left(-\frac{{\left(x-Centr{e}_{A_i}\right)}^2}{2{\sigma }_{A_i}{}^2}\right)$		$B\left(i\right)=\exp \left(-\frac{{\left(x-Centr{e}_{B_i}\right)}^2}{2{\sigma }_{B_i}{}^2}\right)$
${Centre}_{A_9 }$ = 0.5676;	${\sigma }_{A_9}$ = 0.010484;	${Centre}_{B_8}$ = 0.5303;	${\sigma }_{B_8}$ = 0.010760;
${Centre}_{A_{10}}$ = 0.5871;		${Centre}_{B_9}$ = 0.5474;	${\sigma }_{B_9}$ = 0.010754;
			${\sigma }_{B_{10}}$ = 0.010507;
		${Centre}_{B_{11}}$ = 0.5969;	${\sigma }_{B_{11}}$ = 0.010703;

also shows the centres and window widths of the membership functions of the input variables cosFx, cosFy, which have changed in the process of parametric optimisation.

The changes in the parameters of the membership functions of the input variables cosFx, cosFy obtained as a result of optimisation do not exceed 5%. This suggests that the introduction of additional terms of the output variable function and the associated expansion of the rule base had a decisive impact on the identification accuracy.

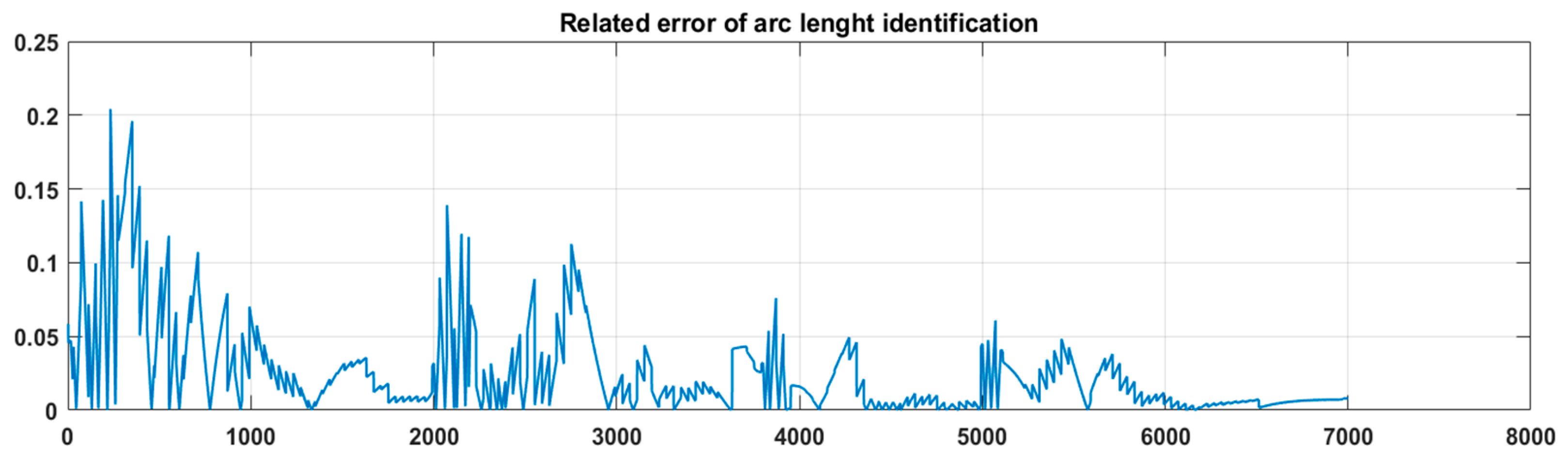
The enhanced and optimized arc length identifier, applied to the dynamic mode data shown in Figure 9, demonstrates quite good results. The relative error of arc length identification is shown in Figure 10. The maximum relative error is obtained when modelling the decrease in arc length.

4. Studying the Efficiency of the Proposed Control System

The synthesised fuzzy arc length identifier makes it possible to implement an electrode movement control system based on the deviation of the identified arc length from the given value. Such a system will avoid the disadvantages of existing electrode movement control systems associated with the necessity to adapt the coefficients to the nonlinearity of the dependence of arc current versus arc length. At the same time, control by deviation from the setpoint is a traditional approach to the design of control systems and makes it possible to apply the modern control theory methods to synthesize control influences in EAF.

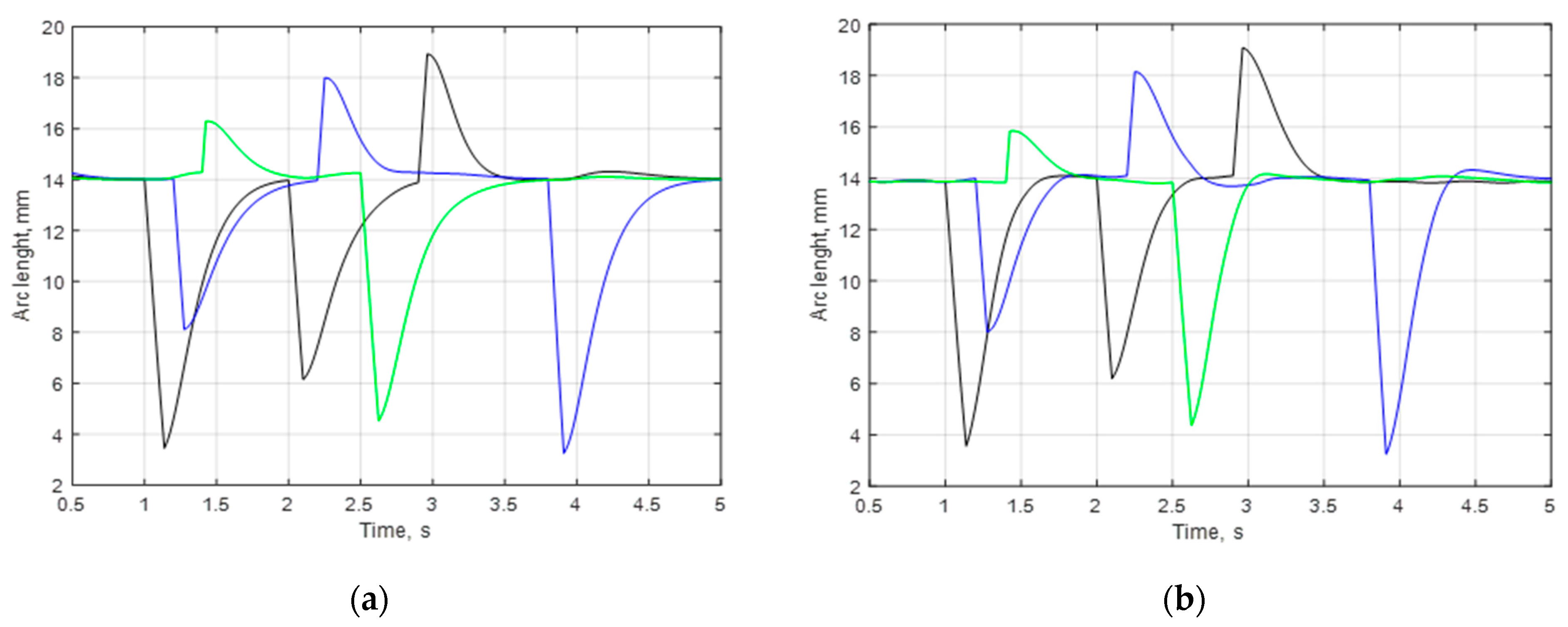
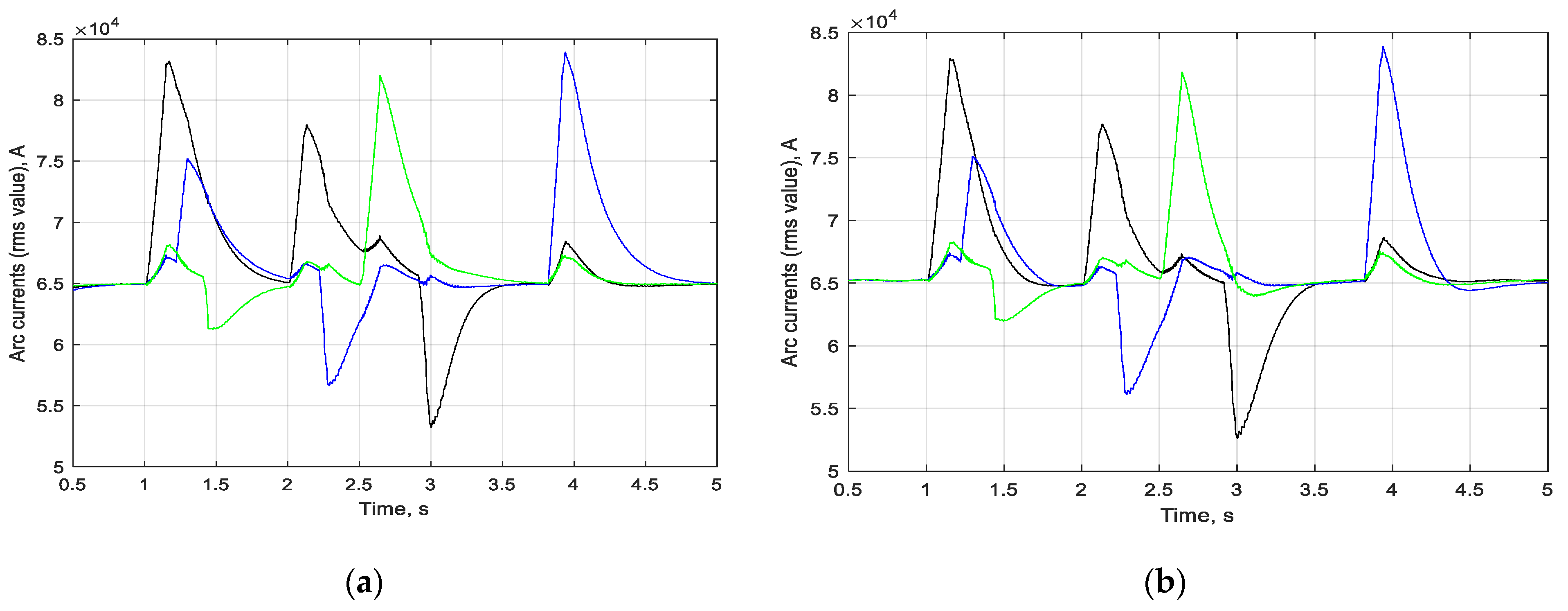
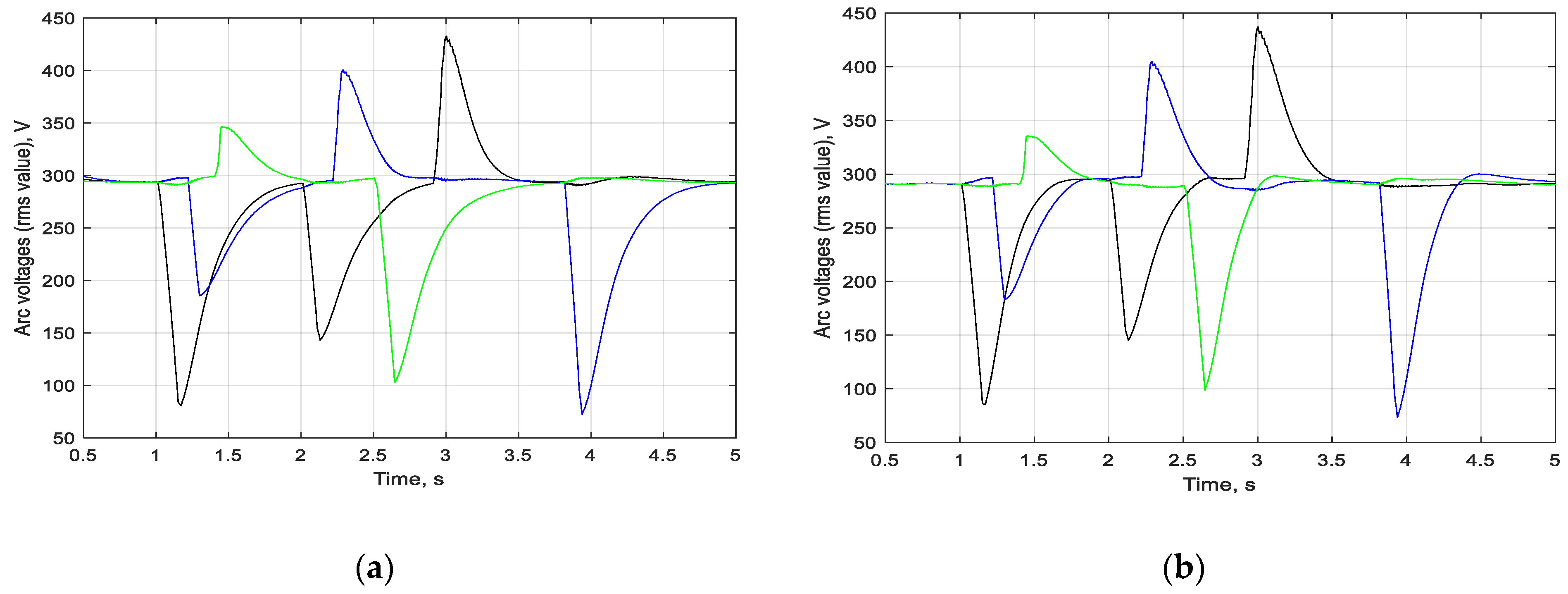
In Figure 11, Figure 12, Figure 13 and Figure 14 are shown the change in arc lengths, effective values of arc currents and voltages, and arc power in phases A, B, and C received by using control systems with an impedance regulator (a) and based on the arc length estimated by the fuzzy identifier (b) under the influence of various disturbances in all phases.

The results shown in the figures demonstrate that the control system based on arc length estimated by fuzzy identifier is stable, provides higher control performance and better arc length stabilisation. The calculated arc power dispersion for phases A, B, and C (see

Table 2. Dispersion of arc power.

Method of Adjustment	Power Dispersion
	Phase A	Phase B	Phase C
Impedance	1.98	1.91	1.35
By arc length mismatch and fuzzy identifier	1.69	1.62	1.05

) demonstrate that the use of the arc-length-based control system reduces the power dispersion by almost 15%, which significantly increases the energy efficiency of the EAF.

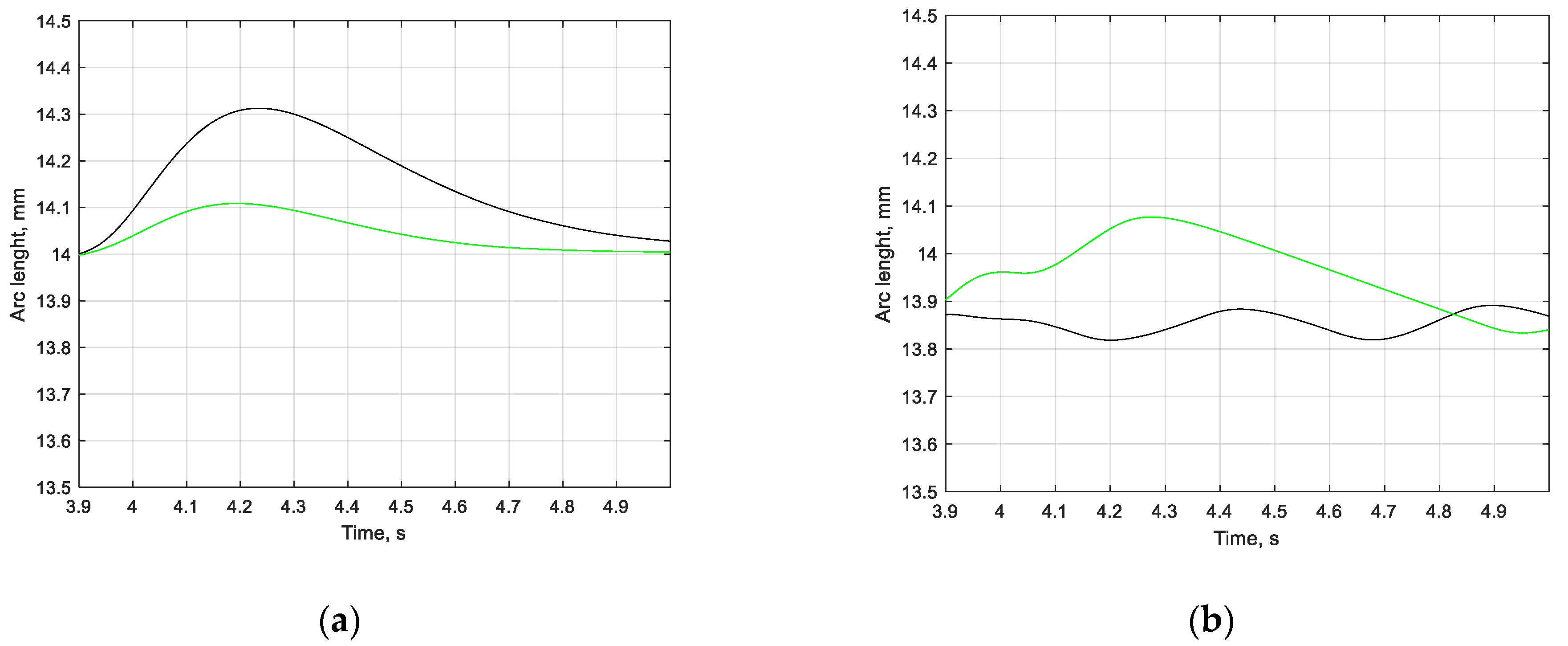
Figure 15 shows a fragment of an enlarged oscillogram of arc length changes in phases A and C under arc length disturbances in phase B (time interval from 4 to 5 s).

The mutual influence of phase currents in the event of a disturbance in one phase leads to changes in currents in other phases and, consequently, to unproductive electrode movements in phases without arc disturbance. At the same time, as shown in Figure 15, in the case of using the control system based on the arc length determined by fuzzy identifier, the unproductive (“false”) movement of electrodes in phase A under a disturbance in phase B is almost three times less. Thus, the proposed control method improves arc stabilization in phases and increases the system’s robustness to disturbances in the neighbouring phases.

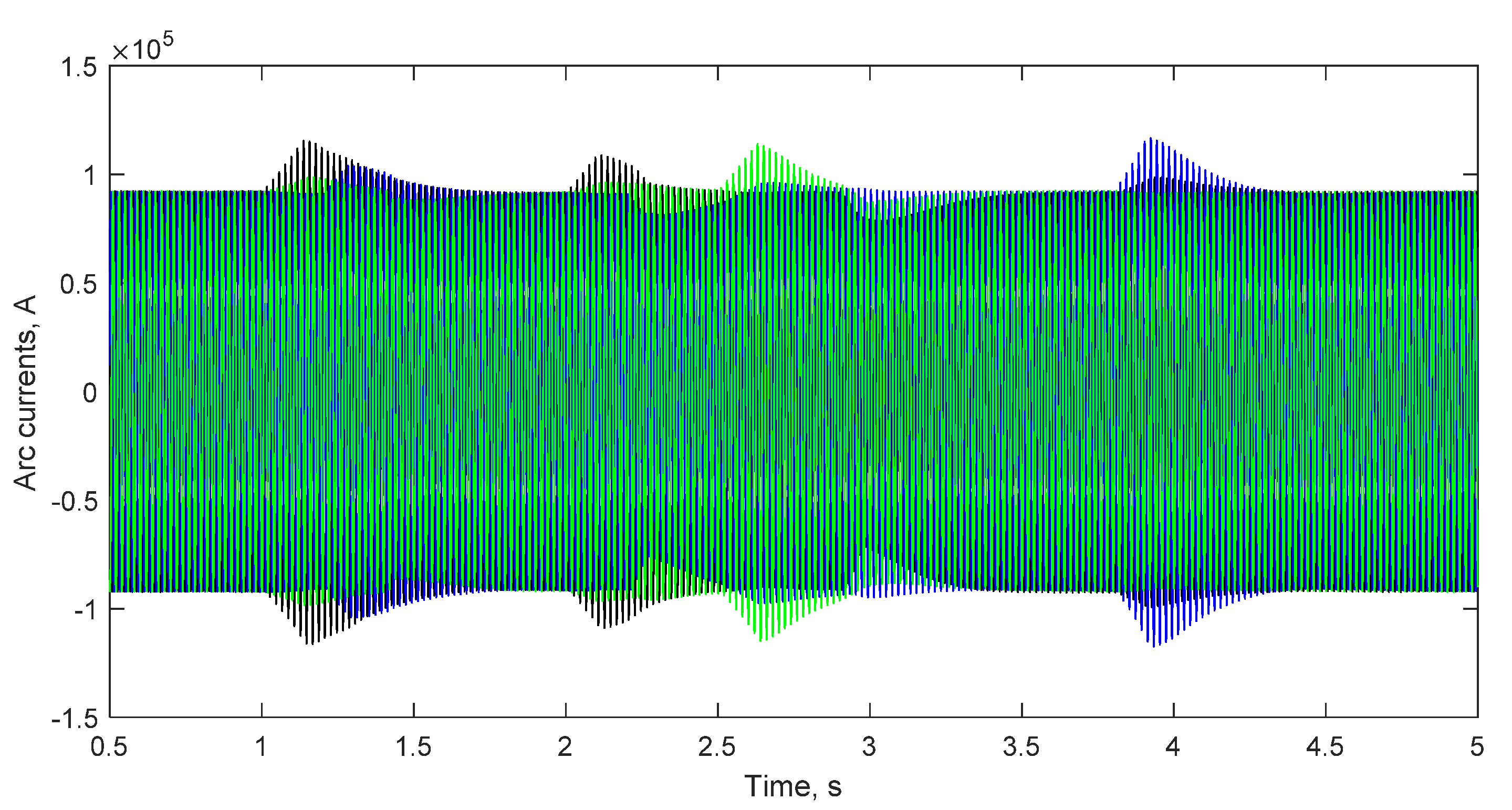
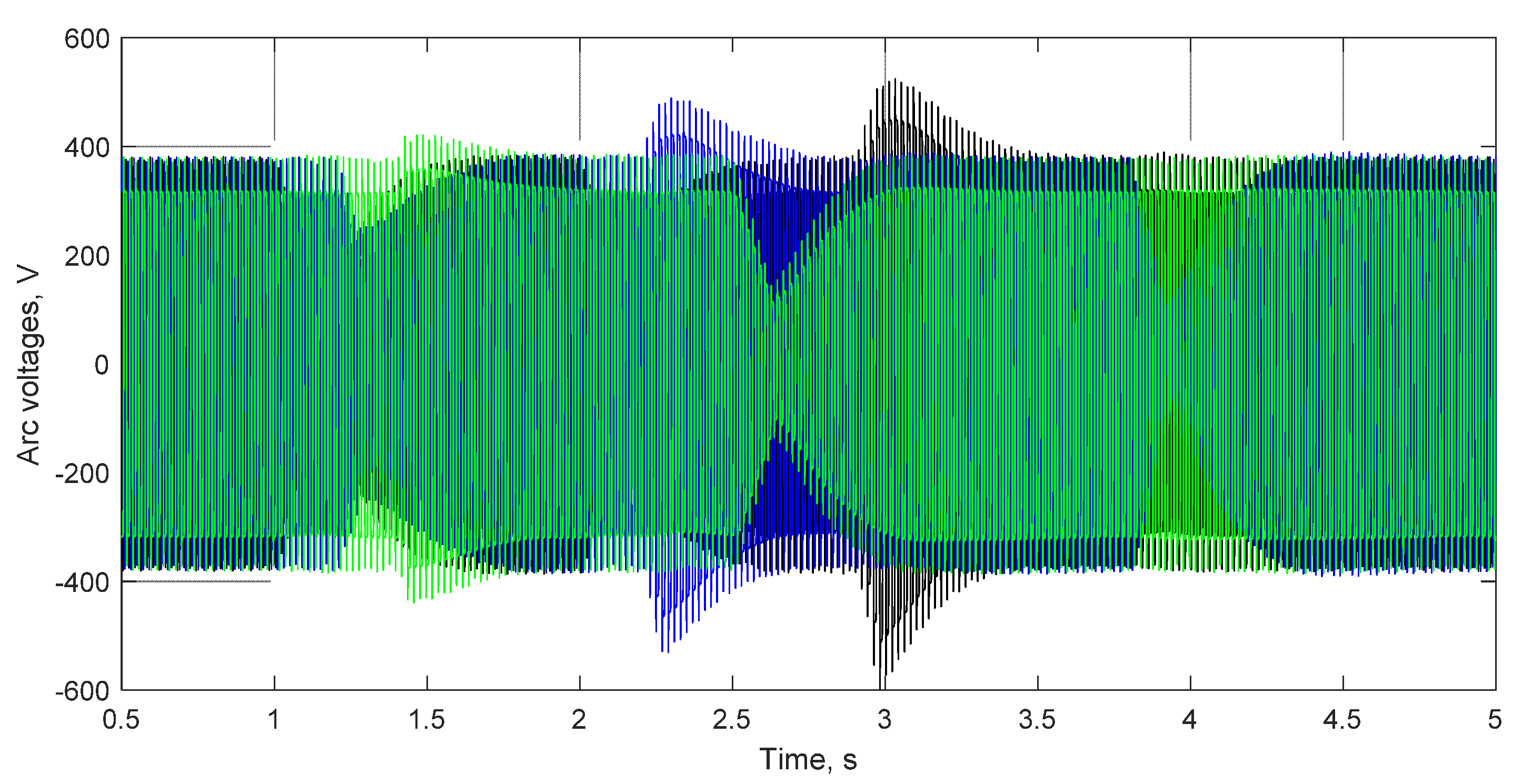
Figure 16 and Figure 17 show the simulated instantaneous values of arc currents and voltages in phases A, B, and C, which were used to determine the effective values. The results are presented for the proposed control system based on arc length determined by a fuzzy identifier.

5. Discussion

The fuzzy arc length identifier allows us to decrease the mutual influences between phases and compensate nonlinearity, which are significant problems in existing control systems of the movement of electrodes in an arc steelmaking furnace. This feature may be the subject of further research, as well as the process of forming a rule base, selecting membership functions, and a defuzzification method.

The implementation of a control system based on the deviation of the arc length from the given value simplifies the use of traditional controllers, including fractional-order PID controllers, in the control system. The effectiveness of such approaches in a system with a fuzzy arc length identifier also requires further research.

6. Conclusions

The three-dimensional vector of the effective values of the phase currents allows us to accurately identify the situation in the arc space of EAF.

The construction of a fuzzy identifier of the arc lengths of the EAF based on the phase current values obtained in quasi-steady-state modes leads to significant errors in dynamic modes (see Figure 7b), which can be eliminated by increasing the number of terms of linguistic variables (see Figure 9 and Figure 10), which will lead to a complication of the rule base (increase of more than 100 rules of type (9)) and by optimization of the parameters of the membership functions.

The creation of an electrode motion control system based on the arc length determined by a fuzzy identifier eliminates mutual influences caused by changes in the situation in other phases of the arc steelmaking furnace and significantly improves the quality of control. An increase in the speed of the disturbance response along the arc length by 25–40% ensures a reduction in the power dispersion by almost 15% in comparison with the conventional impedance control method.