Explainable Approaches for Forecasting Building Electricity Consumption

Abstract

Building electric energy is characterized by a significant increase in its uses (e.g., vehicle charging), a rapidly declining cost of all related data collection, and a proliferation of smart grid concepts, including diverse and flexible electricity pricing schemes. Not surprisingly, an increased number of approaches have been proposed for its modeling and forecasting. In this work, we place our emphasis on three forecasting-related issues. First, we look at the forecasting explainability, that is, the ability to understand and explain to the user what shapes the forecast. To this extent, we rely on concepts and approaches that are inherently explainable, such as the evolutionary approach of genetic programming (GP) and its associated symbolic expressions, as well as the so-called SHAP (SHapley Additive eXplanations) values, which is a well-established model agnostic approach for explainability, especially in terms of feature importance. Second, we investigate the impact of the training timeframe on the forecasting accuracy; this is driven by the realization that fast training would allow for faster deployment of forecasting in real-life solutions. And third, we explore the concept of counterfactual analysis on actionable features, that is, features that the user can really act upon and which therefore present an inherent advantage when it comes to decision support. We have found that SHAP values can provide important insights into the model explainability. In our analysis, GP models demonstrated superior performance compared to neural network-based models (with a 20–30% reduction in Root Mean Square Error (RMSE)) and time series models (with a 20–40% lower RMSE), but a rather questionable potential to produce crisp and insightful symbolic expressions, allowing a better insight into the model performance. We have also found and reported here on an important potential, especially for practical, decision support, of counterfactuals built on actionable features, and short training timeframes.

1. Introduction

1.1. The Forecasting Timeframe and Scope of Our Current Application

The literature on building electricity forecasting approaches differs with regard to the envisaged timeframe. Typically, we have short-term forecasts (timeframe ranging from minutes up to 1 week), midterm forecasts (timeframe ranging from 1 week up to months), and long-term forecasts (timeframe of years), which are useful for planning infrastructure and grid investments [1], and also very long-term, policy-oriented forecasting exercises. TIMES (an acronym for The Integrated Markal Efom System) allows us to model supply and anticipated technology shifts over such a very long-term horizon, often extending as far away in time as 2100 where anticipated changes of technology are accounted for. Forecasts may also differ based on the scope of their application, which can range from a single building (to be reviewed in detail below), to a collection of buildings (e.g., neighborhood, district, etc.) [2], and up to countries [3,4,5]. The forecasting timeframe selection, the forecasting application context, and the envisaged decision support are all tightly linked together. For example, decisions related to building operational aspects are typically linked to more short-term investigations and timeframes as well as the scope of the particular building. Decisions on policy action, such as fuel taxation, may be supported by long-term timeframes and the scope of the particular country.

In our investigation, the overarching decision framework is that of demand response. Demand response is, in its narrow sense, about adapting consumption patterns to make the most of the pricing scheme in place [6,7]. However, the term is also used in a broader sense, whereby demand response may be any user action and response informed by electricity prices. For example, a lowering of the winter thermostat settings in time slots when prices rise is also referred to in the literature [8] as a demand response scheme; it is indeed a response, even if not a time shift response. Thus, demand response is more broadly about the user who takes action in response to changing prices.

Thus, a demand response-related forecasting timeframe must necessarily follow the respective building electricity price change timeframe. As we move to more fast-changing and flexible pricing schemes, it follows that our case is clearly that of a short-term timeframe. Indeed, in most cases, retailer prices have an hourly resolution, which is also the one selected in this work. There are, however, also cases where the price change impact manifests over longer timeframes and might be related to cumulative consumption. For example, in the case of consumption tier pricing, prices are also determined according to the consumption levels within the billing period, which typically spans several months. In such a case, a forecast spanning a timeframe that equals the billing period also becomes pertinent.

We also need to set the timeframe in a way that is unambiguously user-friendly. Along with the above considerations, the timeframe for our investigation is set in two different and alternative ways. First, there is an hourly forecast for the next full calendar day. This means that when a user runs the forecast, she will receive 24 hourly forecasts corresponding to the consumption of the very next calendar day. Second, there is a remaining day forecast. In this alternative formulation, the user would receive forecasts for the remainder of the day. Thus, if the forecast is run at 17:15, the user would receive 6 hourly forecasts, corresponding to the six full hours remaining from 18:00 to 23:00. (Note: the forecast of 18:00 is the consumption between 18:00 and 19:00). A forecast for, literally, the next 24 h was not considered as it is essentially a subset of the two above schemes and rather less intuitive in itself. Additionally, a third timeframe that in principle needs to be considered is that of the billing period. As explained above, this may be pertinent in the case of consumption tier pricing.

In the description below, we have opted to focus on one of these three pertinent timeframes and in particular that of the next day’s 24 h forecast. The benchmarking that will be attempted in the following will be conducted on the data collected and modeled on this timeframe.

1.2. The Key Modeling Approaches and Features Used in Short-Term Forecasting

Forecasting in short timeframes has been consistently addressed in the literature via a number of different approaches, both with regard to the model type as well as the parameters (features) used [9,10,11,12,13]. Approaches in the literature have evolved in two main directions. On the one hand, there are methods that rely on conventional approaches (e.g., regression, stochastic time series, ARIMA, etc.) which, due to their relative simplicity, still receive some interest in the literature. And, on the other hand, there are artificial intelligence (AI)-based methods [14,15,16,17]. Indeed, AI approaches have received increased attention and a lot of sophisticated approaches have been proposed; there is a wide consensus on the nonlinearity of the underlying phenomena in building energy, which renders AI approaches particularly pertinent.

Islam [18] has provided a comparison of these two broad approaches. In the recent decade, among AI approaches, the support vector machine (SVM) has been popular with researchers, due to the fact that it may rely on small quantities of training data. This SVM is a typical supervised learning method applied for categorization and regression, and has a solid legacy, having been introduced by Cortes and Vapnik in the 1990s [19]. It ranks high in the context of accuracy and can solve nonlinear problems using small quantities of training data. The SVM is based on the structure risk minimization (SRM) with the idea of minimizing the upper bounds of error of the object function.

More recently, hybrid methods have also been introduced by researchers [20], in an attempt to combine more than one modeling approach. Swarm intelligence (SI) approaches have been combined with ANNs as well as the SVM in search of a better forecasting accuracy. SI has been inspired by the behavior of insects and other animals, and comes in various forms such as particle swarm optimization (PSO), ant colony optimization (ACO), and artificial bee colony (ABC).

Similarly, Daut [12] has provided for an exhaustive summary of the SVM and ANN as well as hybrid approaches pursued. These authors conclude that the hybrid methods (ANN and SAI and even more SVM and SI) have shown some improvement in the performance of the accuracy of building load forecasting. Indeed, ANN has been widely utilized in different applications, but its hybridization with other methods seems to improve the accuracy of forecasting the electrical load of buildings. The same authors also expanded into reviewing the type of features typically used in the modeling exercise. Indeed, a great diversity of possible combinations have been tried out in the literature. In a categorization of 17 approaches, these authors have found that historical consumption loads are used across all of them. Diverse weather data (temperature, dry bulb temperature, dew point temperature, wet point temperature, air temperature, humidity, wind speed, wind direction, brightness of sun, precipitation, vapor pressure, global/solar radiation, sky condition) have been used in the modeling, although only a few appear consistently across the models (temperature in 11 out of the 17 cases, global/solar radiation in 9 out of the 17 cases, and humidity in 8 out of the 17 cases). Finally, indoor conditions (temperature, occupancy) as well as calendar data are also used in the modeling, albeit less frequently.

Bourdeau [21] has also provided for a review and a classification of methods for building energy consumption modeling and forecasting. He addressed both physical and data-driven approaches. As far as the latter are concerned, they also confirm the two main approaches and orientations, that is, they are mostly time series reliant as well as machine learning based. The authors analyzed 110 papers in the period between 2007 and 2019, and reported that 22 among them were based on ANN approaches, 20 on SVM approaches, 17 on time series and regression approaches, and 16 combining more than one approach. These authors referred to this last category as ensemble approaches, while reserving the term hybrid to describe the combined use of data and physical approaches. Although this represents a notable semantic difference with regard to the previous exclusively data-driven work reviewed, the results between this team and the previous one [12] converge overall. The authors also provide a thorough analysis of the features used in the modeling exercise. First in frequency is the outdoor temperature that is included in 32 of the papers reviewed; humidity and solar radiation also appear often (19 and 18 instances, respectively). Past loads are again found to be intensely used (21 instances). As to calendar data, here, the authors provide some more detailed analysis considering four types of calendar data, and, in particular, type of day (13 instances), day of the week (13 instances), time of the day (12 instances), and month of the year (8 instances). Occupancy data appear in 7 instances while indoor temperature only in 1 instance (although other types of indoor data appear in 2 more instances). Overall, there seems to be a good convergence with the related analysis of feature frequency presented by the previous researchers. This is also confirmed by Nti [22], who examined the various aspects of electricity load forecasting. The findings indicated that weather factors are employed in 50% of the electricity demand predictions, while 38.33% rely on historical energy usage. Additionally, 8.33% of the forecasts considered household lifestyle, with 3.33% taking even stock indices into account.

1.3. Approaches Used for Explainable Demand Forecasts

All approaches reviewed above aim at reducing the forecasting error, by means of the typical error metrics used: the Root Mean Squared Error (RMSE), the Mean Absolute Error (MAE), and the Mean Average Percentage Error (MAPE). Thus, accuracy is typically the sole optimization criterion.

In time, however, it became apparent that there are also other important issues besides accuracy related to the forecasting. In particular, explainability considerations, implying the ability to understand why the forecast works the way it does and get this understanding over to the user, have started receiving increased attention over the last few years. The need to study and analyze the possible tradeoff between accuracy and explainability emerges now in a natural way and is something we will also engage with in the following.

In the energy domain, Mouakher [23] introduced a framework seeking to provide explainable daily, weekly, and monthly predictions for the electricity consumption of building users of a LSTM-based neural network model, based on consumption data as well as external information, and, in particular, weather conditions and dwelling type. To this extent, in addition to their predictive model, the authors also developed an explainable layer that could explain to users the particular, every time, forecast of energy consumption. The proposed explainable layer was based on partial dependence plots (PDPs) which unveiled what happens to energy consumption whenever a feature changes while keeping all other features constant.

Kim [24] attempted to explain the feature dependence of a deep learning model by taking account of the long-term and short-term properties of the time series forecasting. The model consisted of two encoders that represented the power information for prediction and explanation, a decoder to predict the power demand from the concatenated outputs of encoders, and an explainer to identify the most significant attributes for predicting the energy consumption.

Shajalal [25] also embarked on the task of energy demand forecasting and its explainability. The focus was on household energy consumption, for which they trained an LSTM-based model. For the interpretability component, they combined DeepLIFT and SHAP, two techniques that explain the output of a machine learning model. This approach enabled the illustration of time association with the contributions of individual features.

2. Concept and Setup

The pertinence of explainability varies from case to case and should by no means be considered as an ubiquitous modeling requirement. Thus, there may well be cases where the concept is irrelevant and its consideration would add little, if any, value. Undoubtedly, health applications of AI are an area where explainability is greatly important [26]. Indeed, the ability to explain to the patient the suggested approach may be key to her decision and eventually to her medical treatment. Explainable approaches have been increasingly showing up in various technological areas as well as the social sciences [27].

Admittedly, energy applications do not represent such a clear-cut case for explainability. We would, however, argue that there are cases where the concept would indeed add value. Such is, in particular, the case of demand response, the overarching application context of this work. Demand response, at least in the narrow sense of the term, implies responding to energy price signals. The literature clearly identifies user risk as a main factor preventing a wider adoption of such demand response schemes [28,29] and benefiting from the many advantages they may bring to users, energy retailers, and grid operators, in terms of lower costs, as well as to renewable deployment planners who will find more opportunity for viable renewable energy. Thus, in this particular application context, we would argue that explainability indeed comes with a clear potential to mitigate this well-identified risk; this would come with important and unique value, increasing the chances of demand response adoption.

In an attempt to gain more insight into what would be important information for the users as regards to the forecast they receive, we carried out interviews with four building energy experts/facility managers to discuss in more depth what information and functionality would add value to them or their building users when delivering the forecasting results. What came out in these discussions were the following two requirements: First, the concept of feature importance, that is, information on how exactly each feature contributed to the forecast, perhaps with a seasonal variation, and second, the concept of counterfactuals [30], that is, the empowerment of users to consider what-if scenarios. At this point, the issue of actionability was also raised. Counterfactuals built around actionable features were highlighted as having a higher potential. Indeed, users cannot affect the weather; therefore, a weather counterfactual can only be of an indirect use and cannot contribute to any direct action. On the contrary, the indoor conditions (temperature, humidity, etc.) are actionable features as the user can typically act upon them, for example, via thermostat settings. Surprisingly, as shown in the above literature review regarding features used in the forecasting, the indoor conditions are relatively rarely used among the selected feature set. Due to the inherent actionability of indoor conditions, a decision was made at this point to prioritize them in the modeling.

Indeed, as shown above in Section 1.3, there is a gradual and rather recent appreciation of explainability and its importance in forecasting. A number of explainable approaches that have very recently appeared in the energy literature were discussed there; as shown, these were variants of neural networks which incidentally are also the predominant approach used in energy forecasting exercises. However, neural networks inherently perform very poorly as regards to explainability. Their complex and black box structure makes it impossible to gain insight and therefore confidence in their performance.

In this work, we consider two distinct approaches to explainability. First, we will use genetic programming (GP) modeling. In artificial intelligence, GP is an evolutionary approach, that is, a technique of evolving programs, starting from a population of random programs, fit for a particular task. Operations analogous to natural genetic processes are then applied; such are the selection of the fittest programs for reproduction (called crossover) and mutation according to a predefined fitness measure. Crossover swaps random parts of selected pairs (parents) to produce new and different offspring that become part of the new generation of programs, while mutation involves the substitution of some random part of a program with some other random part of a program. GP is a distinct modeling approach that results in symbolic expressions which can potentially offer insights into the model performance. In addition, GP is a classic case of so-called global-level explainability. It provides insights into the overall model performance. Up to this moment and to the best of our knowledge, GP has not been used in the building energy forecasting literature. On the contrary, counterfactuals are referred to as instance or local-level explainability as they do not relate to the model itself but only to a particular instance.

A second approach that we will use for explainability purposes will be that of SHAP —which stands for SHapley Additive exPlanations. This approach was first published in 2017 by Lundberg [31]. In short, SHAP values provide for a quantification of the contribution that each feature brings to the model. Thus, it is an excellent way to track feature importance, which has already been highlighted above as a key mandate for explainability, especially within the demand response application context.

Therefore, although GP is a distinct modeling approach, SHAP values are not anything close; they are an approach that can be used regardless of the underlying model and its purpose is to highlight feature importance. For this reason, they are called model agnostic; they are equally relevant regardless of the model used, which could be a gradient boosting, a neural network, or anything that takes some features as input and produces some forecasts as output.

Interestingly, SHAP values have been recently [32] employed in a counterfactual context, making them also appropriate for our second explainability use case. The proposed method generates counterfactual explanations that show how changing the values of a feature would impact the prediction of a machine learning model.

Furthermore, it may be that explainability comes with an accuracy tradeoff. Thus, we considered it important to benchmark the GP performance in terms of accuracy and for this purpose, we opted for two mainstream modeling approaches in the forecasting literature. First, there are the structural time series (STS) models which are a family of probability models for time series that include and generalize many standard time series modeling ideas including: autoregressive processes, moving averages, local linear trends, seasonality, and regression and variable selection on external covariates (other time series potentially related to the series of interest). And, second, there are the neural networks and, in particular, their LSTM variant which is often used in the energy forecasting literature.

We have opted not to use hybrid models; although it is often reported that they come with some increased accuracy, they would be a very poor selection in terms of explainability as we would also need to understand the relative impact of every model for the various space instances. This would be an impressive task also if SHAP were to be applied. Overall, without denying the accuracy benefits that hybrid approaches may bring, we consider them an inappropriate path when explainability considerations are deemed important, as they are in our use case.

Finally, as the investigation was prompted by the design needs of a demand response controller, additionally to the GP- and SHAP-related explainability investigations, there were two further issues that were deemed important. Indeed, if a demand response controller seeks to provide user support, then seeking to run counterfactuals on actionable features seems to be a value-adding approach. Actionable features are those that the user of the controller can act upon. Such is, for example, the case of indoor temperature that can be acted upon by changing the thermostat settings. Conversely, features such as weather, consumption history, or day of the week and hour of the day, features that dominate the forecasting literature, are inherently non-actionable. Also, the fast deployment of a real-life controller would be directly impacted upon by the duration of the training period. Thus, the investigation of a fast training option of the forecasting algorithm would come at a clear benefit and would be preferable, provided performance is not overtly eroded.

3. The Methodological Approach

Yearly real-time data were collected via a smart meter and a set of indoor environmental sensors in an office building of around 1300 square meters at the Hellenic Mediterranean University in Crete, Greece. The energy meter was a Shelly 3M, 3x 120A (with an accuracy of 2%) reporting energy data every four minutes. The three indoor environmental sensors were Shelly H&T type (with an accuracy of 2% for temperature and 4% for humidity) and were used to collect measurements of temperature and humidity. The resolution of this data collection was not fixed. To secure battery longevity, these sensors report only when there is a 0.5 degrees change in temperature or a 2% change in humidity. This typically occurred between 1/2 an hour and 5 h. Additionally, weather data were sourced from a local weather station, via the OpenWeatherMap provider https://openweathermap.org/ (accessed on 31 December 2022) API. Although temperature, humidity, wind, and cloud coverage data were collected, a preliminary analysis revealed that the predominant weather driver of electricity consumption was that of air temperature, something that converges well with the literature.

Data were split into the four seasons. In the first two seasons (winter and spring months) we tested all three approaches (STS, NN-LSTM, and GP) to investigate and validate the relative performance of the GP approach with regard to the more traditional time series and NN approaches. Different feature subsets were used to train models, including various combinations of weather, past consumption, hour of the day, day of the week, and indoor temperature (monitored and averaged across three points in the building). Indoor temperature was considered important if we were to achieve models that could be actionable. Indeed, from all other parameters tried, indoor temperature was the only actionable one.

As far as the training validation and test sets, the approach was as follows:

After we collected evidence that GP was performing well, in the next two seasons, we restricted the modeling on GP alone and shifted the focus onto investigating SHAP explainability and feature importance, running counterfactuals on actionable features (indoor temperature) and analyzing the impact of the training duration on model performance.

All primary sensor data can be visualized via a public dashboard at the address https://wsn.wirelessthings.biz/v2/stef (accessed on 31 December 2022). Data exported from this dashboard were cleaned and then used to calculate hourly values of all features used.

Data (in Excel sheets) as well as models (as Jupyter notebooks) including a model index are publicly available at the Open Science Framework at https://osf.io/epw4n/ (accessed on 31 December 2022).

In

Table 1. List of models used.

Winter Models
Model Code	Type	Features Used
Model 1	LSTM	Weekly history
Model 2a	LSTM	Weekly history, day of week
Model 2b	LSTM	Weekly history, indoor temperature
Model 2c	LSTM	Weekly history, day of week, indoor temperature
Model 2c′	LSTM	Weekly history, indoor temperature, day of week, hour of day
Model 3a	LSTM	Weekly history, day of week, outdoor temperature, wind
Model 3b	LSTM	Weekly history, day of week, outdoor temperature
Model 3c	LSTM	Weekly history, day of week, wind
Model 4a	LSTM	Weekly history, day of week, outdoor temperature, indoor temperature
Model 4b	LSTM	Weekly history, day of week, wind, indoor temperature
Model 4c	LSTM	Weekly history, day of week, outdoor temperature, wind, indoor temperature
Model 4a′	LSTM	Weekly history, day of week, outdoor temperature, indoor temperature, hour of day
Model 5	LSTM	Same day past week consumption
Model 6a	LSTM	Same day past week consumption, outdoor temperature, wind, indoor temperature
Model 6b	LSTM	Same day past week consumption, outdoor temperature, wind, day of week
Model 7a	LSTM	Same day past week consumption, outdoor temperature, wind, indoor temperature
Model 7b	LSTM	Same day past week consumption, outdoor temperature, wind, indoor temperature, day of week
Model 7c	LSTM	Same day past week consumption, indoor temperature
Model 7d	LSTM	Same day past week consumption, indoor temperature, day of week
Model 2c	GP	Weekly history, day of week, indoor temperature
Model 2c′	GP	Weekly history, day of week, hour of day, indoor temperature
Model 3a	GP	Weekly history, day of week, hour of day, outdoor temperature
Model 3a′	GP	Weekly history, day of week, hour of day, ABS (absolute value of difference between indoor and outdoor temperature)
Model 3a″	GP	Weekly history, day of week, ABS
Model 8	STS	Consumption, day of week, indoor temperature
Model 8′	STS	Consumption, day of week, hour of day, indoor temperature
Spring Models
Model Code	Type	Features Used
Model 2c	LSTM	Weekly history, day of week, indoor temperature
Model 2c′	LSTM	Weekly history, indoor temperature, day of week, hour of day
Model 3a	LSTM	Weekly history, day of week, outdoor temperature
Model 3a′	LSTM	Weekly history, outdoor temperature, day of week, hour of day
Model 4a	LSTM	Weekly history, day of week, outdoor temperature, indoor temperature
Model 4a′	LSTM	Weekly history, indoor temperature, outdoor temperature, day of week, hour of day
Model 6b	LSTM	Same day past week consumption, outdoor temperature, day of week
Model 7b	LSTM	Same day past week consumption, outdoor temperature, indoor temperature, day of week
Model 2c	GP	Weekly history, day of week, indoor temperature
Model 2c′	GP	Weekly history, day of week, hour of day, indoor temperature
Model 3a	GP	Weekly history, day of week, hour of day, outdoor temperature
Model 3a′	GP	Weekly history, day of week, hour of day, ABS
Model 3a″	GP	Weekly history, day of week, ABS
Model 8	STS	Consumption, day of week, indoor temperature
Model 8′	STS	Consumption, day of week, hour of day, indoor temperature
Summer Models
Model Code	Type	Features Used
Model 8	STS	Consumption, holiday, ABS, hour of day
Model 9	GP	Weekly history, ABS, holiday (includes weekends)
Model 10	GP	Weekly history, holiday (includes weekends)
Model 11	GP	3-day history, ABS, hour of day, holiday (includes weekends)
Model 12	GP	3-h history, ABS, Hour of day, Holiday (includes weekends)
Model 13	GP	active electricity(t-23), ABS, holiday (includes weekends)
Model 14	GP	active electricity(t-23), indoor temperature, outdoor temperature, holiday (includes weekends)
Model 15	GP	active electricity(t-23), indoor temperature, outdoor temperature, work hour
Autumn Models
Model Code	Type	Features Used
Model 16a1	GP	active electricity(t-7), indoor temperature, outdoor temperature, (only work hours of work days considered)
Model 16b1	GP	active electricity(t-15) (non-work hours of work days considered)
Model 16b2	GP	active electricity(t-23) (non-work hours of holidays considered)

Note: The ‘hour’ was the resolution of the forecasting and the hourly forecast of the next day was the key objective.

below, we provide a summary of all the models that have been used in this work and can be downloaded from the above URL. Not all of these models will be reviewed below as we selectively browsed through the most important findings.

The Recursive Approach Pursued

Although in the case of the LSTM block, 24-h forecasts are possible, in the case of GP, only next-hour forecasts are possible. To this extent, and in order to abide by the mandate for next-day forecasting, a recursive approach was necessary. Depending on the features used, there are various approaches to this recursion. For example, let us consider that our forecast of consumption, denoted as Con [t], uses the feature of past hour consumption, denoted as Con [t-1], for its training. Let us imagine now that we are at 17:15 and run the daily forecast. We would first forecast the consumption for Con [17:00] (which corresponds to the consumption between 17:00 and 18:00 of the same day) based on the actual value of Con [16:00]. We would then forecast Con [18:00] by using the previously forecasted value of Con [17:00]. We would carry on similarly until Con [24:00] of the next day. In this approach, our recursion would be heavily relying on forecasts rather than actual values.

An alternative and better formulation of recursion would be to use history data in the modeling not as Con [t-1] but, in principle, rather as Con [t-24], which corresponds to the observed consumption at the same hour of the past day. We say here ‘in principle’ because one may also have to account for the difference between work and non-work days. We will come back to this issue in the next section. For now, it suffices to realize that our new formulation of ‘history’ has the advantage that it implicitly takes account of the ‘hour of the day’ and does not require this to be entered as an additional feature, as often occurs in the forecasting literature. This recursion setup also has the additional advantage that the next-hour forecast will now rely far more on actual data rather than forecast data. Indeed, in this recursive approach our next-day forecasting of Con [t], and from t = 0 … 16, would now rely on actual, measured data. Only the Con [t], from t = 17 … 23, would rely on forecasted data.

To conclude with the discussion of the recursive approach pursued, we also need to describe the approach pursued as regards to weather data. Whenever weather [t] was used among the features for the forecasting of Con [t], we used the forecast provided by the weather station itself. We found this approach more intuitive than treating weather [t] in a recursive fashion as in the case of history data.

4. Results and Discussion

4.1. Comparing STS, LSTM, and GP Performance: Winter and Spring Data

As mentioned above, the approach in the first two seasons aimed at benchmarking the GP approach against the more traditional STS and LSTM approaches. Overall, we validated that GP was performing in a comparable way, even with a better performance when compared to its two ‘competitors’. We will present below the best-performing models in all three cases for winter and spring.

4.1.1. Winter Models

Table 2. Relative performance of GP, LSTM, and STS approaches for the winter data.

Winter Period
Modeling Approach	Best-Performing Model	RMSE
GP	model 3a′	4460
LSTM	model 2c′	5441
STS	model 8	5529

below summarizes the relative performance of the three approaches for the winter data.

4.1.2. Spring Models

Table 3. Relative performance of GP, LSTM, and STS approaches for the spring data.

Spring Period
Modeling Approach	Best-Performing Model	RMSE
GP	model 3a′	2798
LSTM	model 2c′	3824
STS	model 8	4566

below illustrates the relative performance of the three approaches for the spring data.

4.2. The Training Duration

In order to test how a faster model training would affect performance, we tested fast training protocols with the spring data: one week and two weeks of training data.

Table 4. Impact of training period duration on GP models. The test set comprises one week of data for all cases.

	MAPE
GP model 3a″; training on 71 days	25.45%
GP model 3a″; one week training (7 days)	25.78%
GP model 3a″; two weeks training (14 days)	30.11%

below illustrates the findings.

The impact on performance was insignificant in the case of the GP models. However, in the case of the STS, model 8, fast training performance rapidly declined. This is shown in

Table 5. Impact of training period duration on STS models.

	MAPE
STS model 8; training on 71 days	26.22%
STS model 8; one week training (7 days)	39.51%
STS model 8; two weeks training (14 days)	46.07%

below.

4.3. Results

GP appears to perform well and outperform other well-established approaches (STS, LSTM) by 20–40%. One may notice here that the best-performing models have been selected and used for comparing the respective performances. Indeed, we could have provided a similar comparison of the three models across all same-feature sets. However, the purpose of the analysis here was not to compare performances across all the many feature sets tested, but to eliminate the hypothesis that ‘GP suffers some inherent performance issue’. Singling out the best-performing models and showing that in this case there is even a notable performance advantage of GP is sufficient evidence for this.

However, the associated symbolic expressions that have resulted appear to be very complex and quite useless in providing explainable insights at the model level. Figure 1 below, illustrates such a daunting symbolic expression.

Thus, although in terms of accuracy it appears that GP approaches are quite promising, in terms of their global explainability potential, the results have been quite disappointing. Of course, this was a very first attempt at touching the surface of the issue. It remains to be seen how potentially a guided pruning of the symbolic expressions into more simple forms would affect performance. This is an exercise we are currently working on in the framework of the EU TRUST AI project, where an environment that can prune and manipulate symbolic expressions in a guided way is implemented. This environment will then allow us to reduce the complexity, assess the accuracy tradeoff, and exploit the explainable potential of the resulting more simple and crisp symbolic expressions.

Additionally, some encouraging first evidence was collected that showed the length of training did not affect the GP model performance in any significant way. This was not the case for the STS approach, where the accuracy rapidly deteriorated as short timeframes were used in place of the typical ones.

4.4. SHAP Analysis and Actionability Considerations: Summer and Autumn Data

In the next two seasons, the investigation shifted towards concepts of local explainability, feature importance, and counterfactual analysis, along with a further assessment of the impact of the reduction of the training time. In both summer and autumn we used only GP models.

4.4.1. The Case of Summer

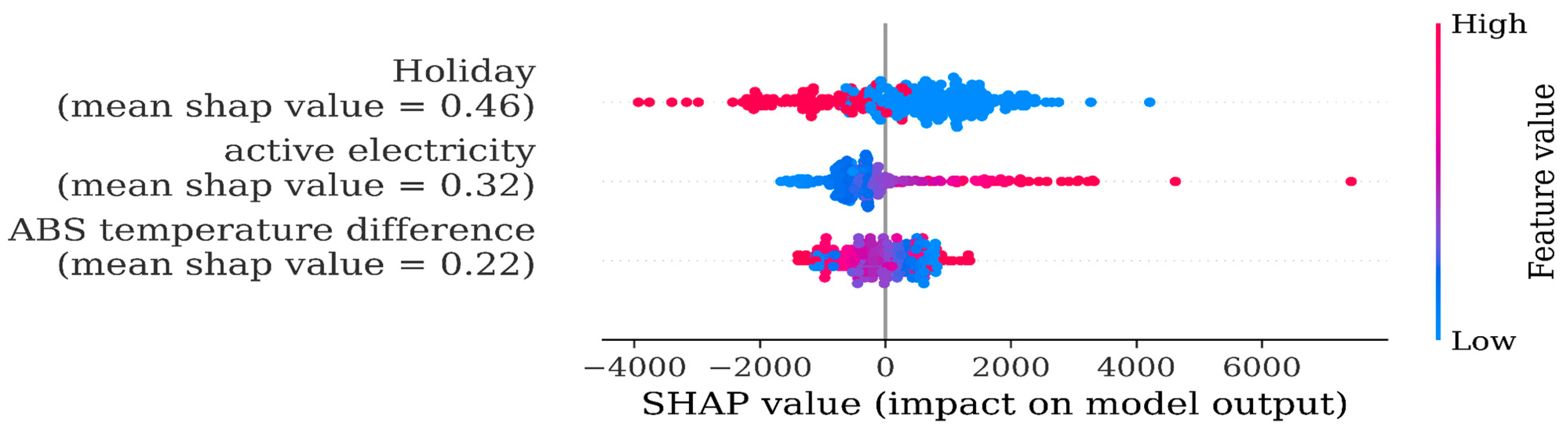
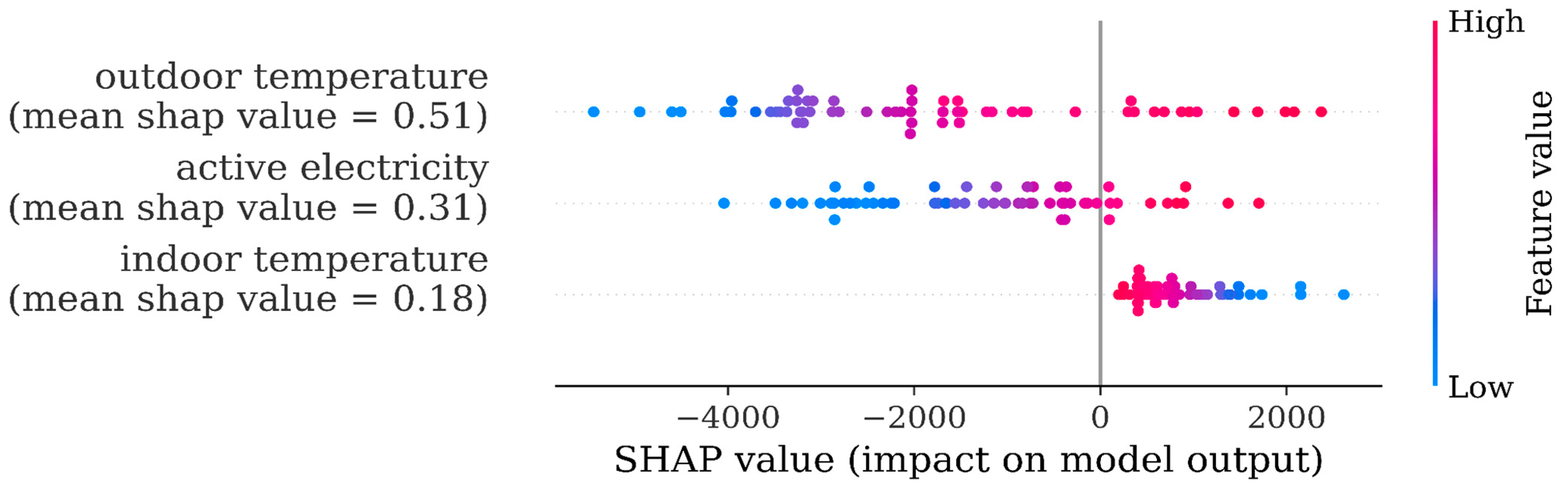
A first GP model that was developed for the summer (model 13) was based on the introduction of a combined parameter called ABS and defined as the absolute value of the difference between indoor and outdoor temperatures. The idea was that this temperature difference is essentially driving cooling requirements and would allow us to end up with a more compact feature set. Second, because of holidays in this season, we also introduced a holiday feature (Boolean; 1-holiday, 0-work day). The third feature was the past 24-h consumption. We carried out our first SHAP analysis on this model wishing to investigate the relative significance of these three features.

The SHAP plots that follow below illustrate on the vertical axis the feature importance. Also, a feature that turns from blue (low values) to red (high values) as the SHAP values increase on the horizontal axis signifies that an increase in the feature value also increases the predicted value.

The SHAP analysis (see Figure 2 below) in this case was particularly counterintuitive. It indicated no clear trend of the SHAP values for our ABS feature. Even worse, in Figure 3, the ABS feature, although of high importance in the model, appeared to turn from red into blue as the SHAP increases, implying a reverse relationship between this feature and electricity consumption, something not acceptable for the summer season.

The reason for this aforementioned behavior was that our compact ABS feature did not account for building thermal inertia. This was most apparent in the early afternoon hours when people left work. In this period, consumption went down; however, due to thermal inertia, the ABS feature was still on the rise.

Following this finding, we concluded that we should abandon any effort to jointly include the indoor and outdoor temperatures in one feature like the ABS. In following modeling, these two features were separately considered as distinct features.

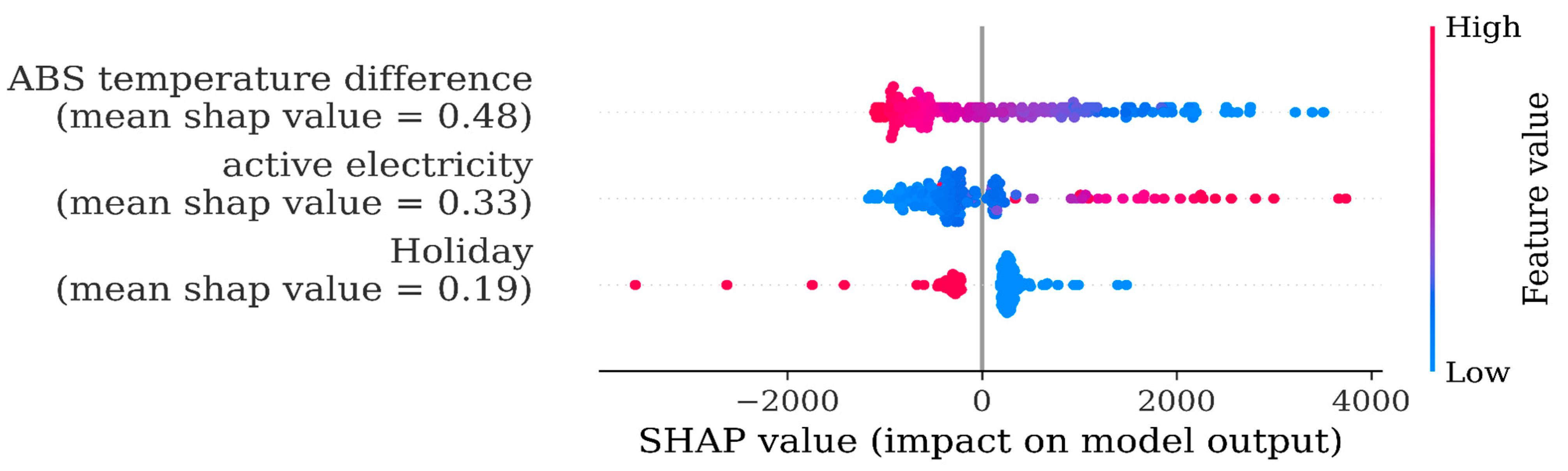
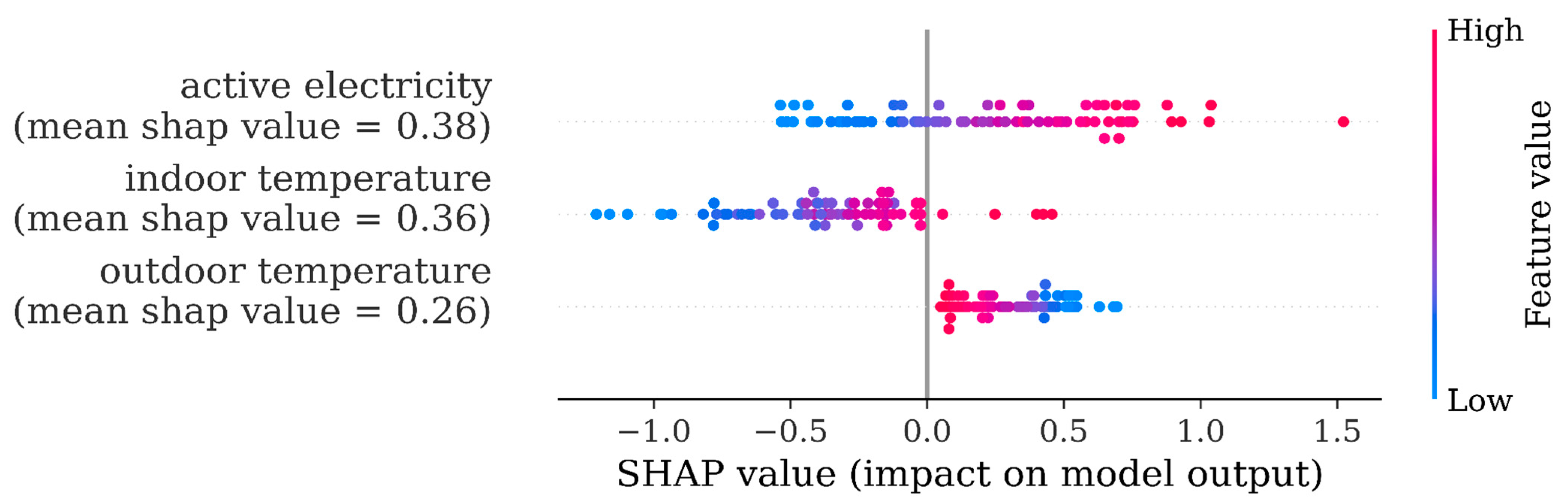
Thus, the amended model 14 was based on four features: indoor temperature, outdoor temperature, holiday, and past consumption. The SHAP analysis is shown in Figure 4. An important result was that the indoor temperature was now the main driver of the forecast and, of course, in the right direction, that is, dots turn from red into blue implying that as the indoor temperature decreases the predicted variable will increase. Indeed, this was the first meaningful and useful result of our SHAP analysis, highlighting the high importance of indoor temperature on the forecast, which indeed now appeared as its key driver.

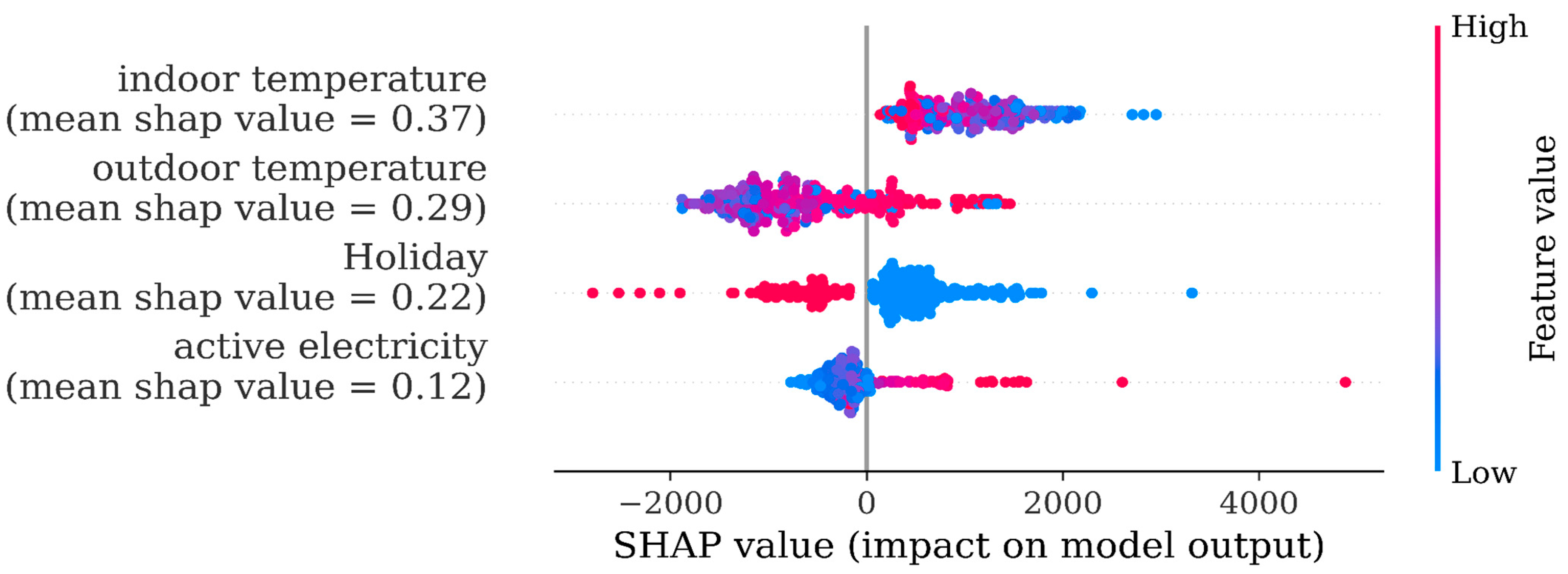
Following this finding, we set up model 15, wherein we introduced the ‘work hour’ feature to signify whether a given hour was a work hour or a non-work hour. This feature eliminated the need for the holiday feature, too, as they were included as non-work hours.

In this case, SHAP analysis showed the newly introduced work hour as the most significantly contributing feature to the model output. The importance of indoor temperature in this model has now been much reduced. Additionally, there is no conclusive evidence that the increase in indoor temperature (dots turning in red color) would have some impact on the predicted variable (SHAP value clearly increasing or decreasing). These remarks prompted us to adapt the model features so that we could potentially raise the importance of indoor temperature in the model forecasts (Figure 5).

As the work hour appeared now to be the key driver, we considered building separate models for work/non-work hours and holidays, denoted as 16a1, 16b1, and 16b2, respectively. Due to the 24-h recursive approach pursued, it was necessary to have separate models for holidays and non-work hours.

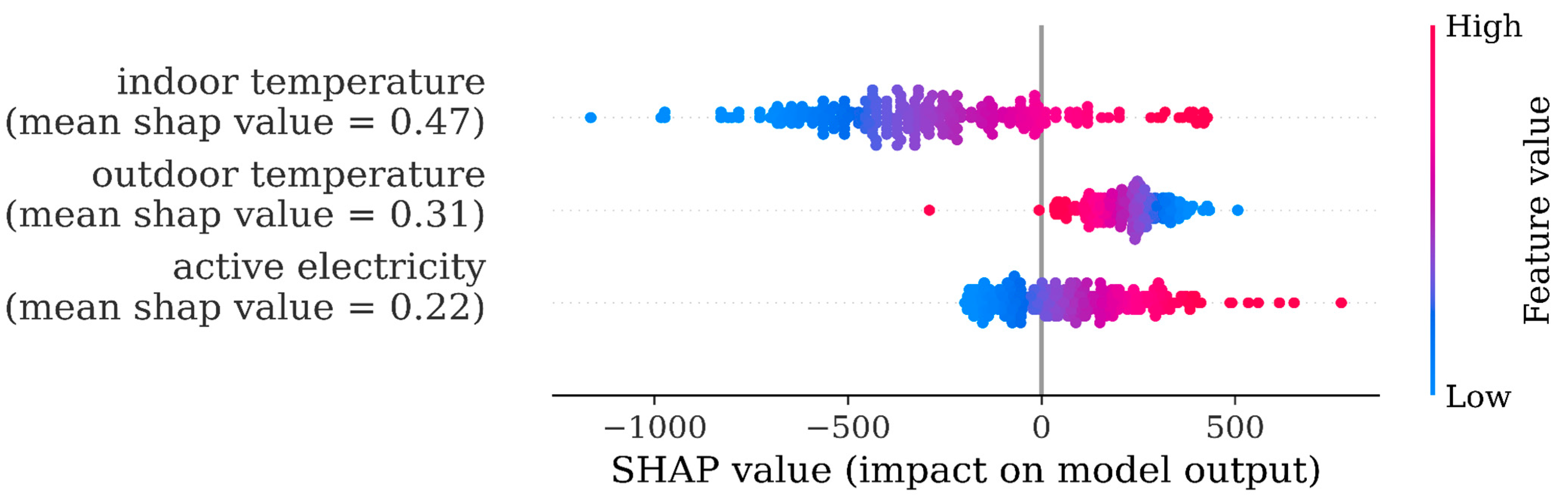
The SHAP analysis in model 16a1 revealed now (Figure 6 below) that outdoor temperature was the most important driver while indoor came third. However, in this plot, indoor temperature dots turn from red into blue as the SHAP values increase, indicating that as the indoor temperature is lowered (increased cooling) consumption will rise. This is now clearly in line with our intuition.

We also tried changing the training duration of these three models. We experimented with three training to test sizes: 85/15 (long training), 50/50 (medium training), and (15/85) short training. Again, we found that there was no notable impact on the MAPE values calculated, which once again suggests that the GP models do not deteriorate when the training timeframe reduces.

Table 6. Impact of training period duration of GP models on MAPE values.

Model	Train/Test = 85/15	Train/Test = 50/50	Train/Test = 15/85
16a1	30%	30%	30%
16b1	18%	18%	18%
16b2	20%	13%	13%

summarizes these results.

4.4.2. The Autumn Data and Models

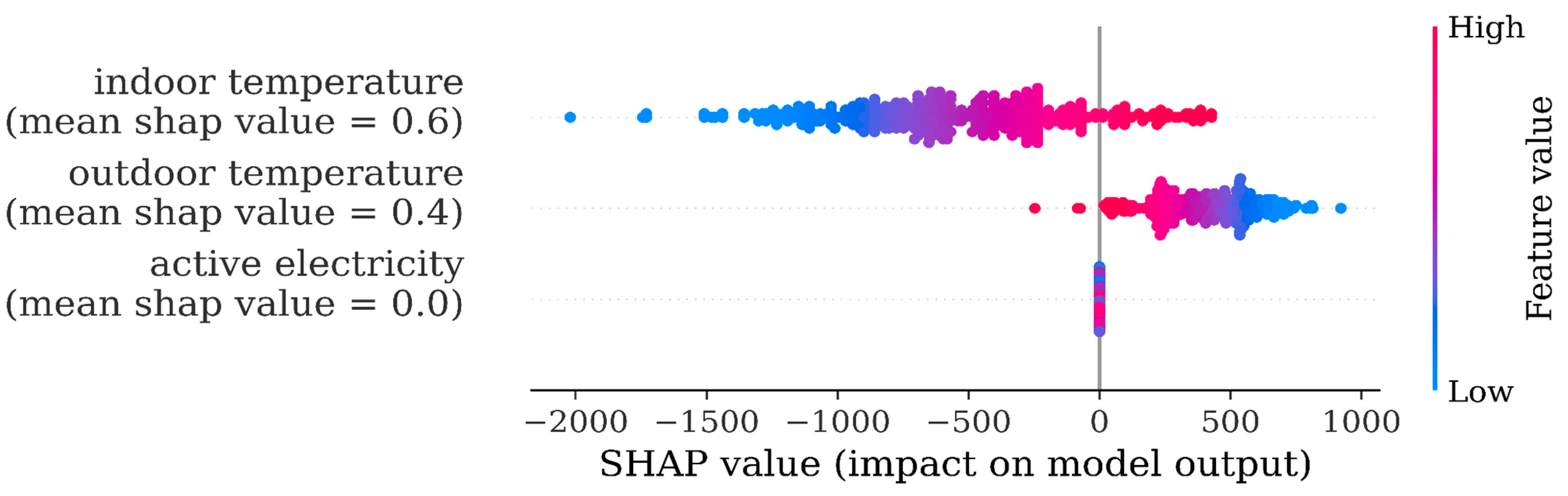
The same models 16a1, 16b1, and 16b2 were used in the autumn period. The SHAP analysis of the 16a1 model (work hours) highlighted the indoor temperature as an important contributor both in the long and short timeframe models (Figure 7, Figure 8 and Figure 9).

Interestingly, SHAP analysis revealed that the indoor impact has now shifted to positive. This means that an increase in indoor temperature (dots turning from blue into red) results in an increase in consumption. This, of course, is no surprise and is due to the autumn period (defined as the October, November, and December calendar months). Indeed, an increase in indoor temperature is now associated with heating and will be reflected in an increased consumption.

As in summer, in the autumn period, once again, no noticeable change occurred when reducing the training timeframe.

4.4.3. Results

SHAP analysis proved helpful in figuring out the important drivers in every model. Thus, they were found to provide important insights into feature importance. Indoor temperature appeared to be an important driver, often the most important one, but at other times was surpassed by outdoor temperature. Also, the SHAP sign in all cases coincided with intuition. SHAP analysis helped us to understand the inherent error in trying to combine the indoor and outdoor temperatures into just one parameter and to avoid any such modeling approach.

Having analytically firmly established that indoor settings are important, and keeping in mind that indoor temperature is actionable, we have confirmed that counterfactual analysis is pertinent. If indoor settings are important and actionable then one may consider ‘what if’ I change the indoor temperature? How would the forecast evolve? These investigations are the focus of the section below.

4.5. Counterfactual Analysis

In this section, we present results from the counterfactuals which were run both for the winter and for the summer period. The model used in both cases was the work hour model 16a1. Indeed, it is when building users are at work that counterfactual findings may result in user action.

For what-if counterfactuals to be meaningful, they must be generated on conditions that really make sense. As we will see, setting such conditions is a key aspect of the counterfactual analysis and can itself reveal important findings.

Let us look at the case of summer. For the summer data, we have opted to generate counterfactuals on meaningful instances that simultaneously satisfy two conditions: indoor temperature less than 25 degrees (Tin < 25), as well as more than two degrees less than the outdoor temperature (Tin < Tout-2).

The condition Tin < 25 aims at defining ‘excessive’ cooling, which are the instances where a what-if analysis leading to user action may make sense. In this case, by selecting 25 degrees, we have defined that if the indoor temperature is above 25 degrees, no claim for ‘excessive’ cooling can possibly be made, so any ‘what if’ would be of no practical purpose. Indeed, we could have set this value lower at 23 degrees, in which case we would have limited the sample space where meaningful counterfactuals could be generated.

The condition Tin < Tout-2 aims at excluding instances where the indoor temperature may be low, not due to ‘excessive’ cooling but due to a relatively cool summer day.

Thus, the counterfactual analysis under this condition revealed that increasing the indoor temperature by an average of 2.15 degrees causes a mean decrease of consumption by 6.44%.

Similarly, for the winter period, meaningful counterfactual instances were selected to fulfill the two following conditions: indoor temperature higher than 21 degrees (Tin > 21), as well as more than two degrees higher than the outdoor temperature (Tin > Tout + 2).

In this case, the result was as follows: decreasing the indoor temperature by an average of 2.3 degrees causes a mean decrease of consumption by 3.4%.

Table 7. Counterfactual analysis.

	Initial Indoor Temperature (°C)	Outdoor Temperature (°C)	Predicted Consumption (Wh)	New Indoor Temperature (°C)	Consumption Prediction for New Indoor Temperature (Wh)	Change in Indoor Temperature by Degrees (°C)	Percent Change in Consumption (%)
Summer Model 16a1
count	12	12	12	12	12	12	12
mean	24.36	27.65	16,740.58	26.51	15,671.90	2.15	−6.44
std	0.25	0.71	1053.16	0.92	1193.52	0.75	2.38
Winter Model 16a1
count	100	100	100	100	100	100	100
mean	22.84	16.91	11,927.82	20.55	11,523.75	−2.3	−3.4
std	0.58	1.89	1412.25	0.74	1383.14	0.68	1.0

below illustrates the results of the counterfactual analysis. The above two key statements can be tracked in the ‘mean’ rows.

In Figure 10 below, the blue circles are the generated counterfactuals, and indicate the percent consumption change vs a respective change of the indoor temperature. As one can see, in the summer season, an increase of the indoor temperature by 1 degree causes a decrease of consumption of approximately 3.36%; an increase by 2 degrees causes a consumption reduction by 5.52% and by 3 degrees causes a reduction by 9.65%. Similarly, for the winter season, decreasing the indoor temperature by 1 degree causes a decrease of consumption of 1.52%; a decrease by 2 degrees causes a reduction of 2.98% and by 3 degrees causes a reduction by 4.50%.

Of course, these counterfactuals above apply only to the valid counterfactual instances, that is, that part of the test set that fulfills the conditions set.

Table 8. Impact of conditions set on the counterfactual space.

Summer	Valid Counterfactual Instances from Test Set	Winter	Valid Counterfactual Instances from Test Set
Tin < 25	11	Tin > 21	67
Tin < 24	2	Tin > 22	64
Tin < 23	0	Tin > 23	28

illustrates the conditions and how they effectively reduce the counterfactual space.

As can be seen, the conditions set affect the scope of counterfactual analysis and help us to understand to what extent the particular building/user interaction context could benefit from the analysis. The more valid instances there are, the greater the potential of counterfactual analysis in the specific context.

Results

Counterfactuals applied on the demand forecasting allow users to be supported in decisions as regards to their energy use. Additionally, they can reveal important information related to the building operation.

The average figures calculated and reported above demonstrate the average impact on consumption when acting upon the indoor temperature. In this way, the figures are important in understanding building performance and especially what the impact of a more energy-conscious behavior would eventually be.

These figures should of course always be assessed together with the enumeration of the valid counterfactual instances (called counterfactual space), which again is a direct result of the conditions set. If this space is too limited, then the scope for action driven by counterfactuals is limited. One should also realize that the conditions set should reflect the thermal comfort as perceived by the users and should only be set by taking strong account of them.

The aforementioned are side benefits of the counterfactual analysis. Of course, the key aspired benefit in our demand response context is not related to the average values; the use of counterfactuals in the demand response context would be instance centered and would work as follows:

• If a valid counterfactual instance is identified, one that fulfills the conditions that have been set up, then

  -

  run the instance counterfactual and calculate the impact on consumption of 1/2/3 degrees change, respectively;

  -

  communicate this information to the building users, especially those able to act upon the thermostat and make effective use of the information communicated.

Last, we have introduced here the counterfactual analysis with regard to the indoor temperature, a feature that we have beforehand established as being important in the forecasting analysis of the specific building in question.

Indoor temperature is by no means the only building parameter users can act upon. Whenever a user can interact with a building feature (e.g., act on drapes to reduce/increase heat gains, switch lights on/off, turn on/off the aeration, etc.), counterfactuals are pertinent. Perhaps these may not be pertinent for the building overall, but in smaller and more targeted forecasting scopes. However, we believe they deserve more attention in the various building modeling aspects as they can link to tangible action that is the heart of effective decision support.

5. Conclusions and Currently Ongoing Work

In this work, we focused on forecasting explainability, and we sought to test a number of approaches of global (model)- or local (instance)-level explainability.

At the model level, we started with a number of modeling approaches including LSTM and STS as well as purely explainable models based on genetic programming (GP). Although the analysis did not aim at providing a detailed analysis of the three modeling approaches’ performance across the many feature sets used, we did find evidence that GP does not suffer from any performance issue when compared to LSTM and STS approaches. Indeed, when comparing the best-performing models, across all the feature sets used, GP even outperformed, in terms of RMSE, LSTM, and STS by 20–40%. However, the symbolic expressions that resulted were very complex and would not allow us to reach any insight into the model performance. We also found that GP quality, contrary to STS, does not deteriorate when shorter training timeframes are selected. This investigation was triggered from an industry requirement, as from a practical point of view, a demand response controller that would be able to train a GP model and become productive in a short period of time, one or two weeks, would have a practical deployment advantage. Of course, new and more accurate models, trained on more extensive data sets, can later be uploaded in such a controller; however, the fact that an industry controller can be put to work in a short period of time with an acceptable accuracy has some practical value.

At the instance explainability level, we introduced SHAP analysis in order to investigate the critical issue of feature importance. Although we applied this in general and across all features, we were particularly interested in the indoor temperature feature as this was an actionable one. The indoor temperature often, in terms of its SHAP value, emerged as an important feature, and in some models even as the most important one. SHAP values of the indoor temperature were also always intuitive: negative in summer when a decrease in indoor temperature results, because of the cooling, in an increase in consumption, and positive in winter, when an increase in the indoor temperature results in an increased consumption due to heating.

After having verifiably, via SHAP, established the importance of the indoor temperature in the forecasting, we introduced counterfactual (or what-if) analysis, seeking to gain a numerical indication of the change of consumption, with a respective change of the indoor temperature. Of course, in order to run meaningful counterfactual analyses, one first has to set some specific conditions that secure the validity and meaningfulness of the counterfactual. These conditions also reflect our perception of thermal comfort. If, for example, we consider an indoor temperature of 24 degrees as an overheating event, we might be interested in restricting the counterfactual space to instances where the indoor temperature is greater than 24 degrees.

The counterfactual analysis is useful from two distinct perspectives:

First, at a building level, it provides insight into the true scope of counterfactuals’ driven action. It allows us to answer questions such as: What economy will I have on average, if in winter time I reduce the set point by 1 (2 or 3, etc.) degrees in all instances where according to the conditions set, an overheating event is identified? One can also change the conditions and see how things develop. Of course, changing the conditions is equivalent to redefining the thermal comfort in the building and it should only be conducted with this kept in mind. In addition to the insight into the building performance, such questions can also allow users to make and implement informed decisions about thermostat settings.

And second, in a (demand) controller environment, counterfactual analysis allows us to answer questions such as: What economy will I have if at the specific moment that I am notified of an overheating event I reduce the set point by 1 (2 or 3, etc.) degrees?

Finally, counterfactuals have, in our case, been set up with regard to the indoor temperature alone, because this was the only essentially actionable feature considered. Could we, for example, have set up counterfactuals for the outdoor temperature, which was also consistently used in the modeling? The answer is, in principle, yes, but there would be some important limitations. At the building level, similarly to the above description of the indoor temperature, we would now be still able to ask questions such as: How will my building consumption evolve if tomorrow I will have an outdoor temperature that is 2 degrees higher? But now, contrary to the indoor temperature case, there is nothing here that I, as a building user, can do about this; I cannot act upon the outdoor temperature or set up any building policy with regard to it. Therefore, my analysis is of limited importance. Similarly, in the second use case discussed above (controller case), a counterfactual based on the outdoor temperature would be meaningless, as the building user has again no possibility of acting upon the outdoor temperature.

Taking a broader perspective on counterfactuals in the building energy forecasting context, we would argue that they can be particularly useful when actionable parameters, such as indoor temperature, humidity, lighting levels, aeration, etc., are included in the model. Therefore, an important result is that the inclusion of such parameters would empower our model with the additional capabilities summarized above. This result calls into question the relatively limited use of such parameters in forecasting models as discussed in the literature review. Currently, we are exploring such additional uses of counterfactuals on actionable features.

Additionally, a key focus is on the GP symbolic expressions. At the moment, we have found them to be complex and of no true insight. In TRUST AI, a framework for working with symbolic expressions, for pruning and, more generally, editing them, is being developed. We are looking forward to exploiting it to see if the symbolic expressions can be edited and shortened so that they may result in some explainable models. In addition, we will examine what the performance expense of such a symbolic expression compacting exercise would eventually be.