Optimal Planning Strategy for Reconfigurable Electric Vehicle Chargers in Car Parks
Abstract
:1. Introduction
- The proposed optimal planning strategy can be applied as a planning tool for car parks deploying REVCs under various scenarios.
- The proposed optimal planning strategy can be applied as an operation controller for REVCs to allocate charging powers and spaces for individual EVs.
- The proposed optimal planning strategy can not only determine the size (number of REVCs) of EV car parks but also determine the optimal power rating for PMs and each REVC.
- A grouping method is proposed to aggregate EV charging demands for scenarios with a large number of EVs.
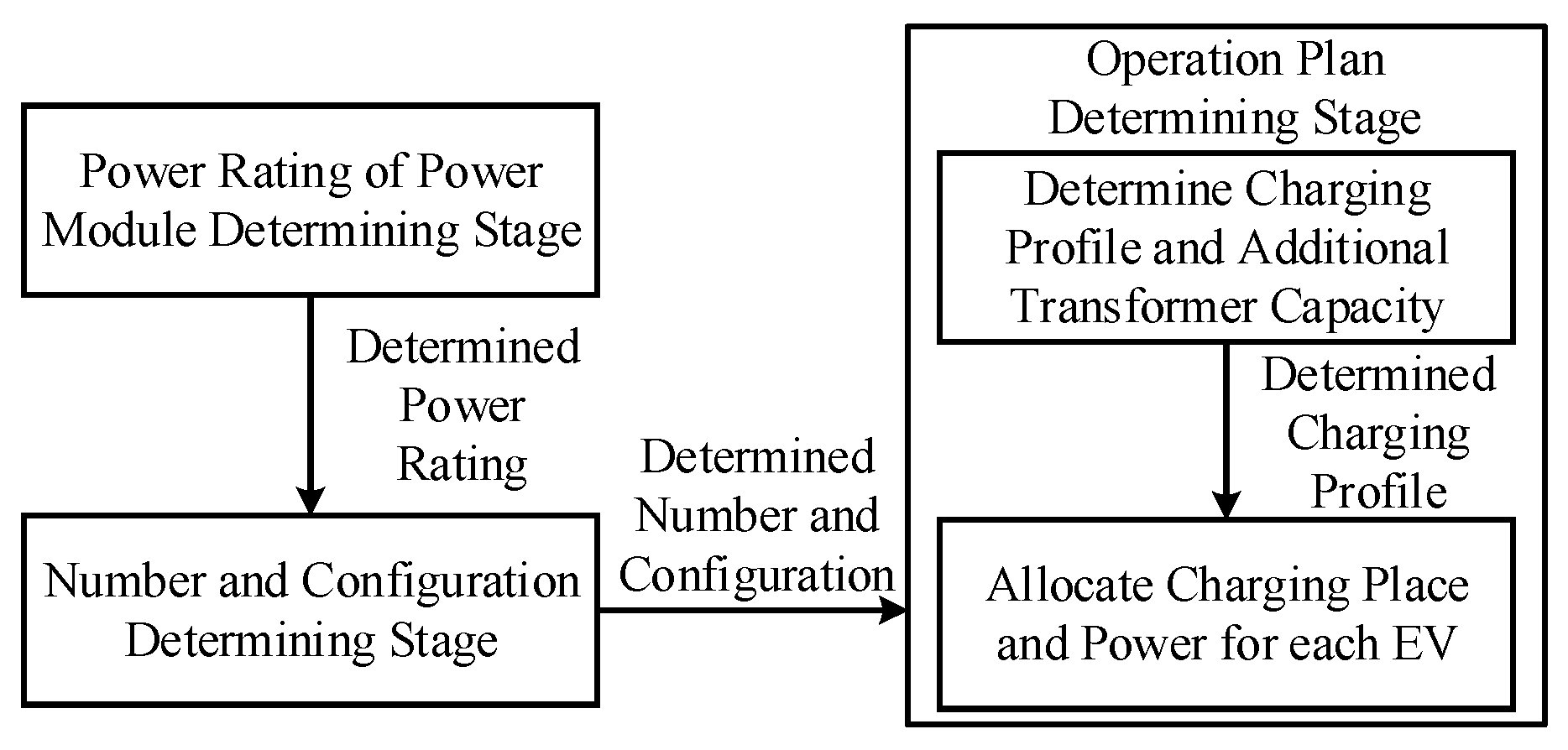
2. Overall Framework for Optimal Planning Strategy
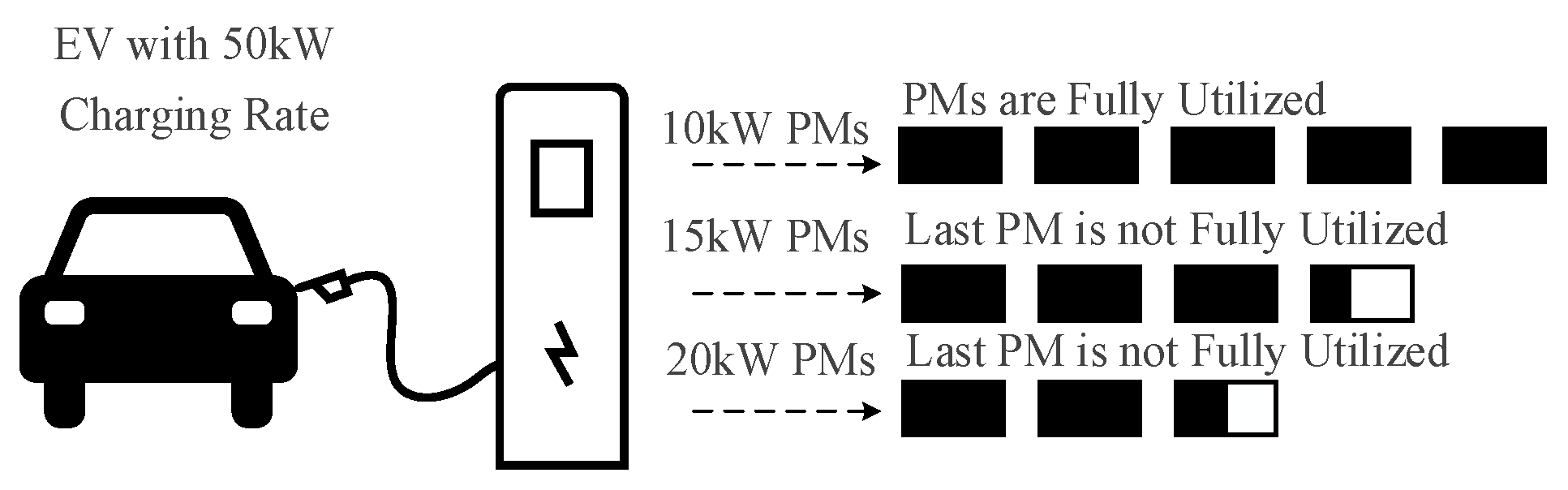
3. Model for Determining the Power Rating of Power Modules
4. Model for Determining the Number and Configuration of REVCs
4.1. Objective Function
4.2. Constraints
5. Model for Determining the Operation Plan
5.1. Determining the Charging Profile and Additional Transformer Capacity to Be Upgraded
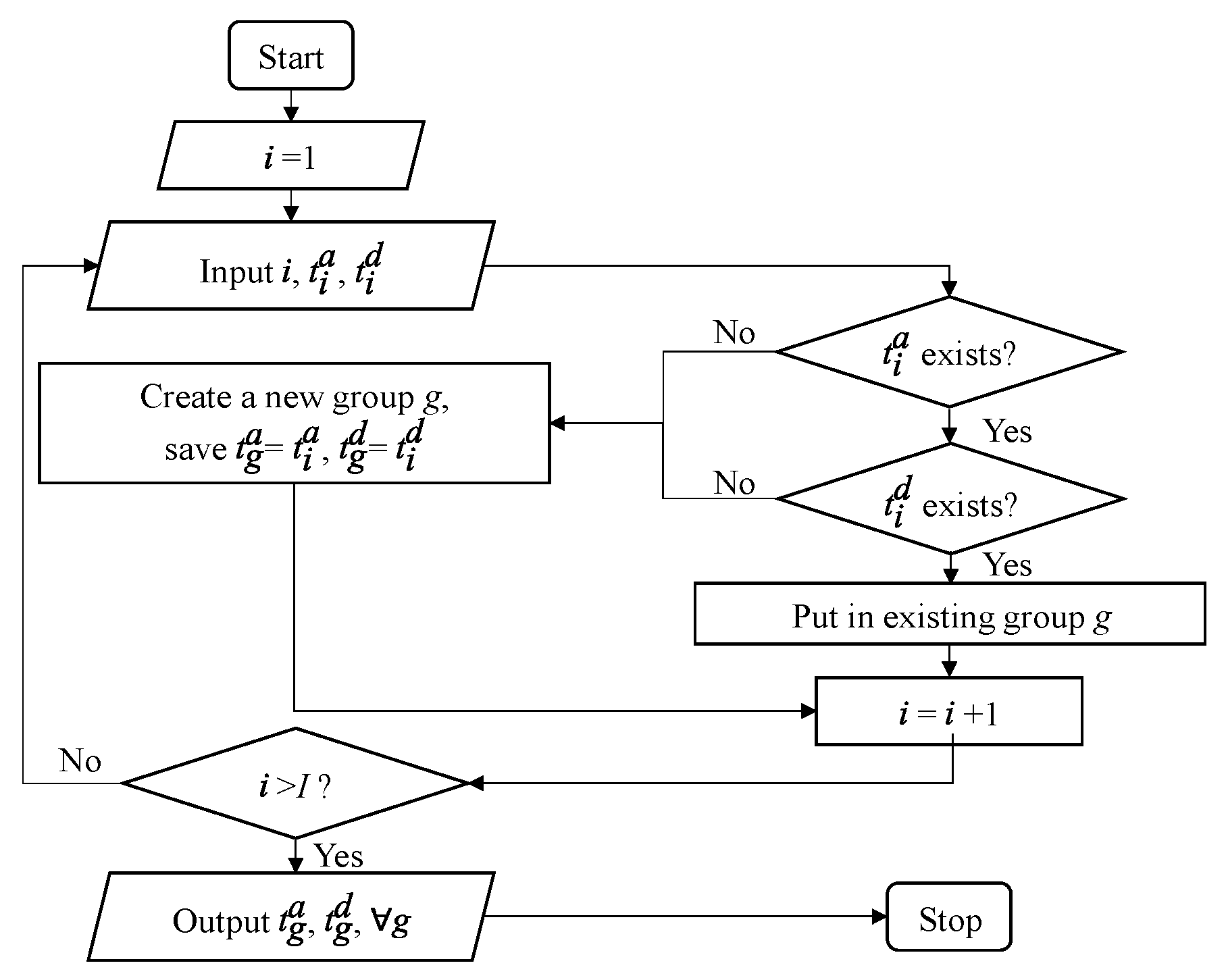
5.2. Allocation of Charging Spaces and Powers for EVs
6. Case Study
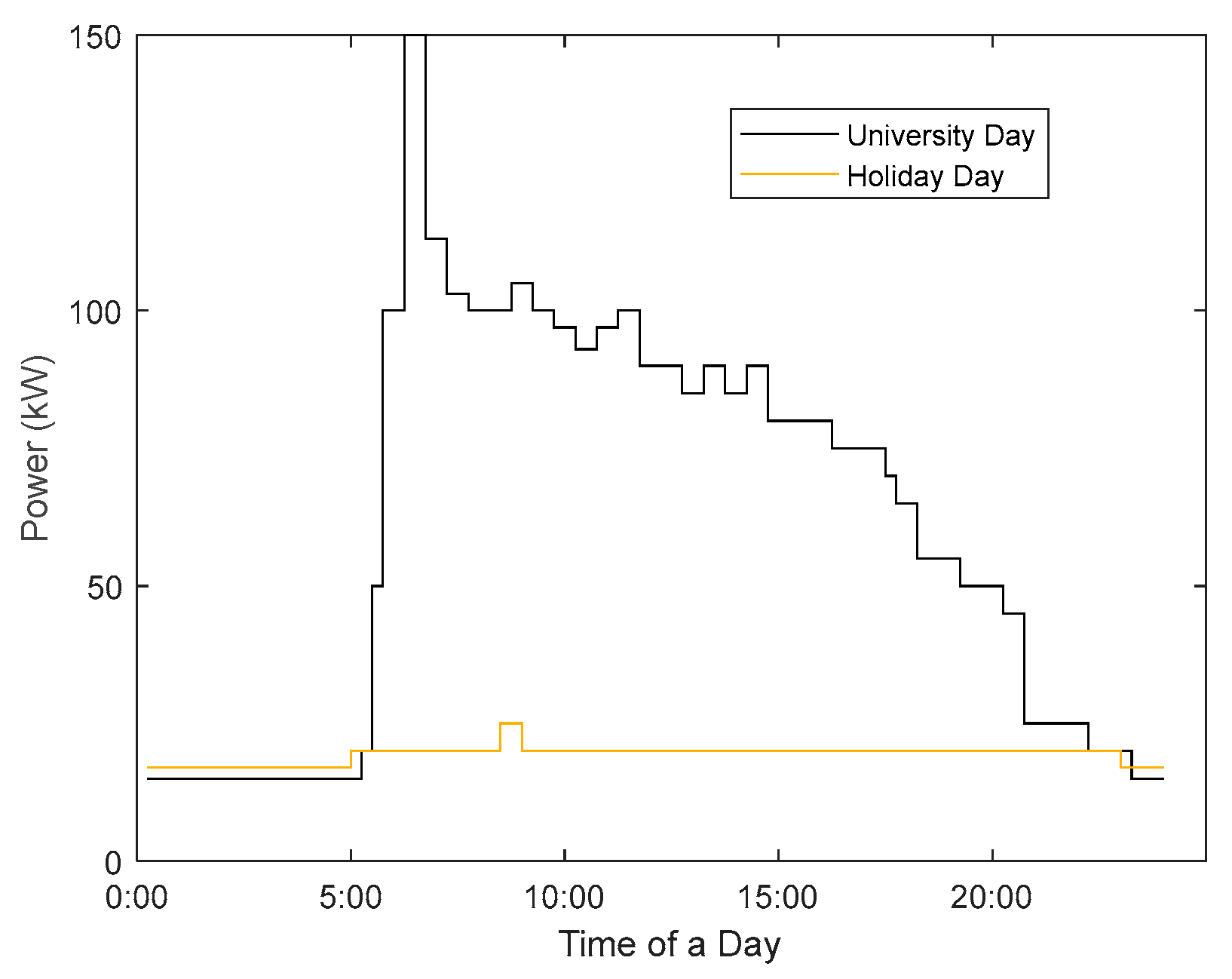
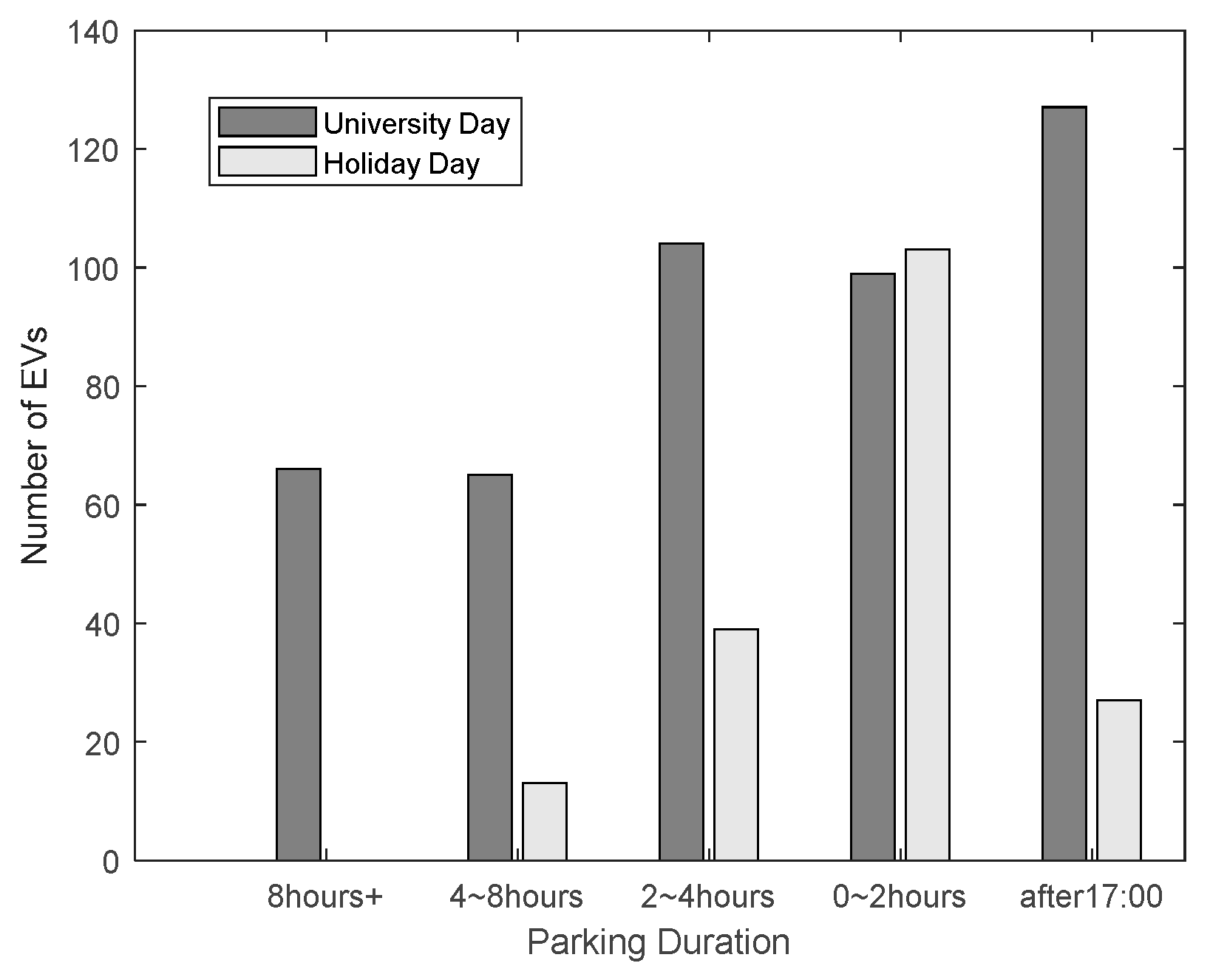
6.1. Case Overview and Parameter Settings
6.2. Optimal Power Rating of PMs
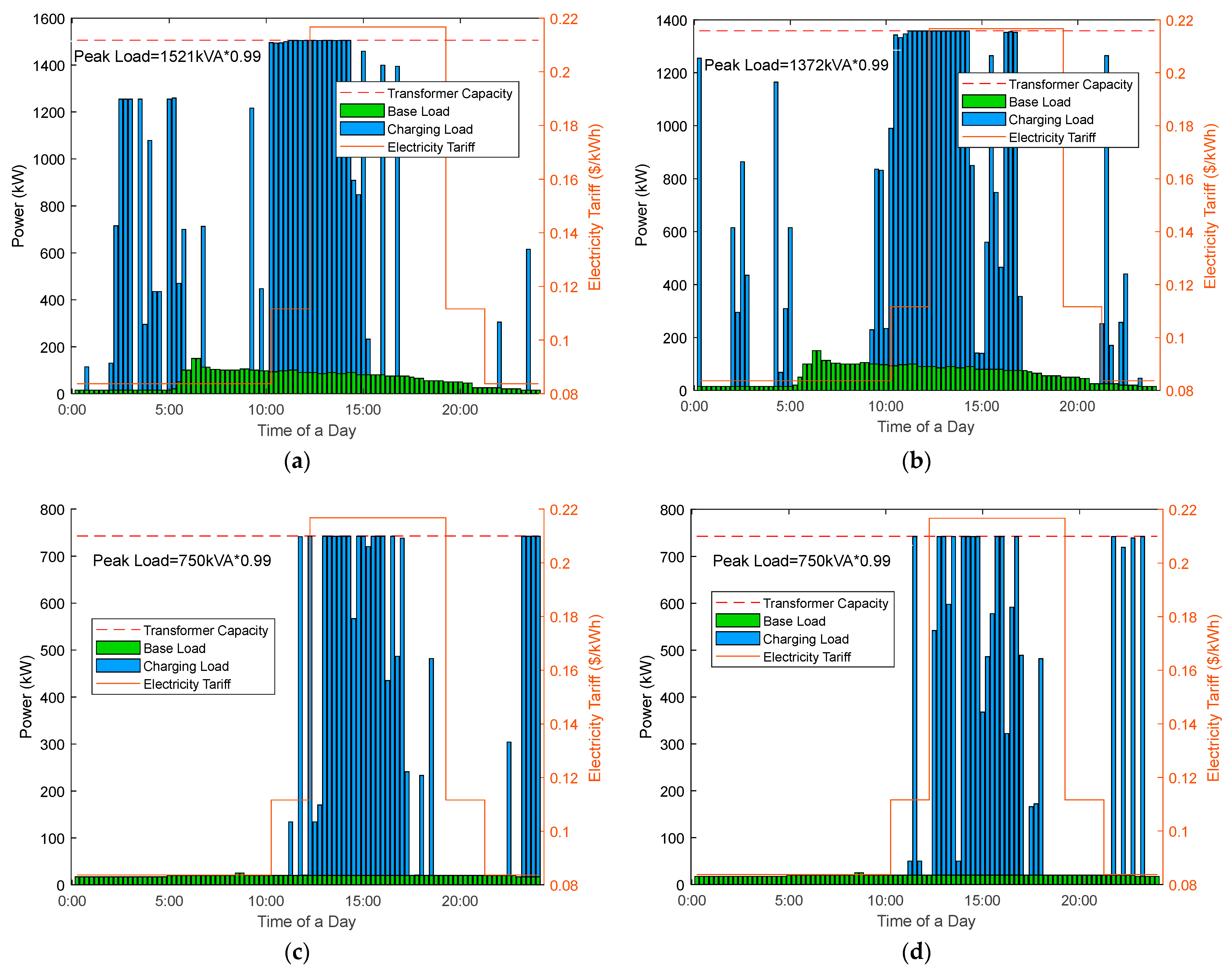
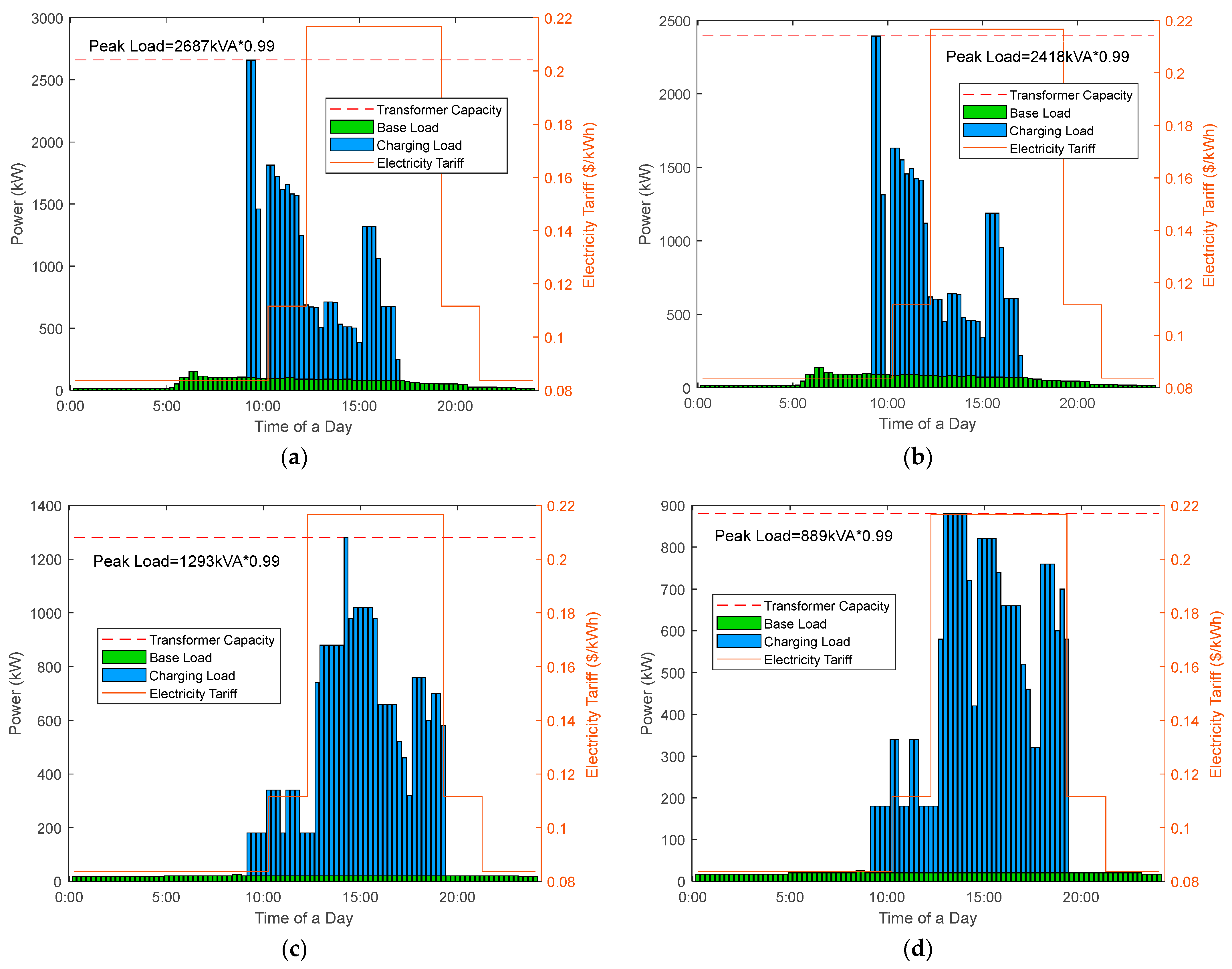
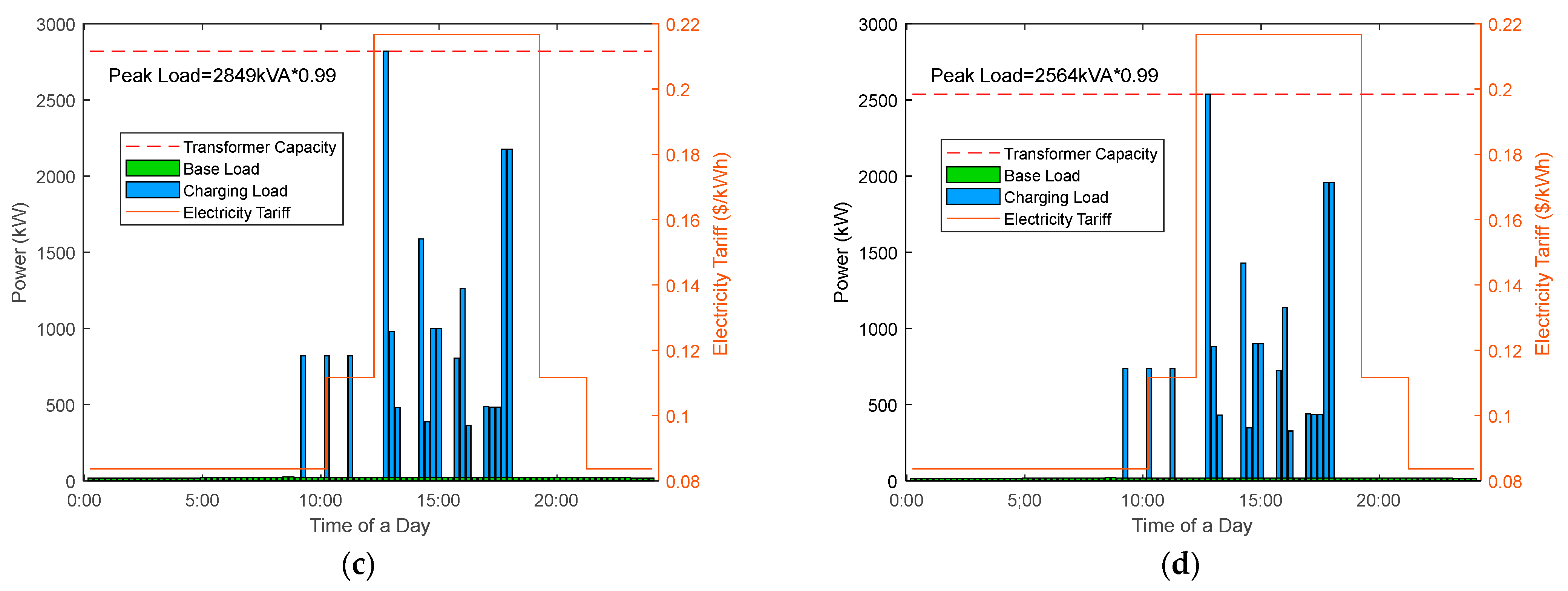
6.3. Planning Results
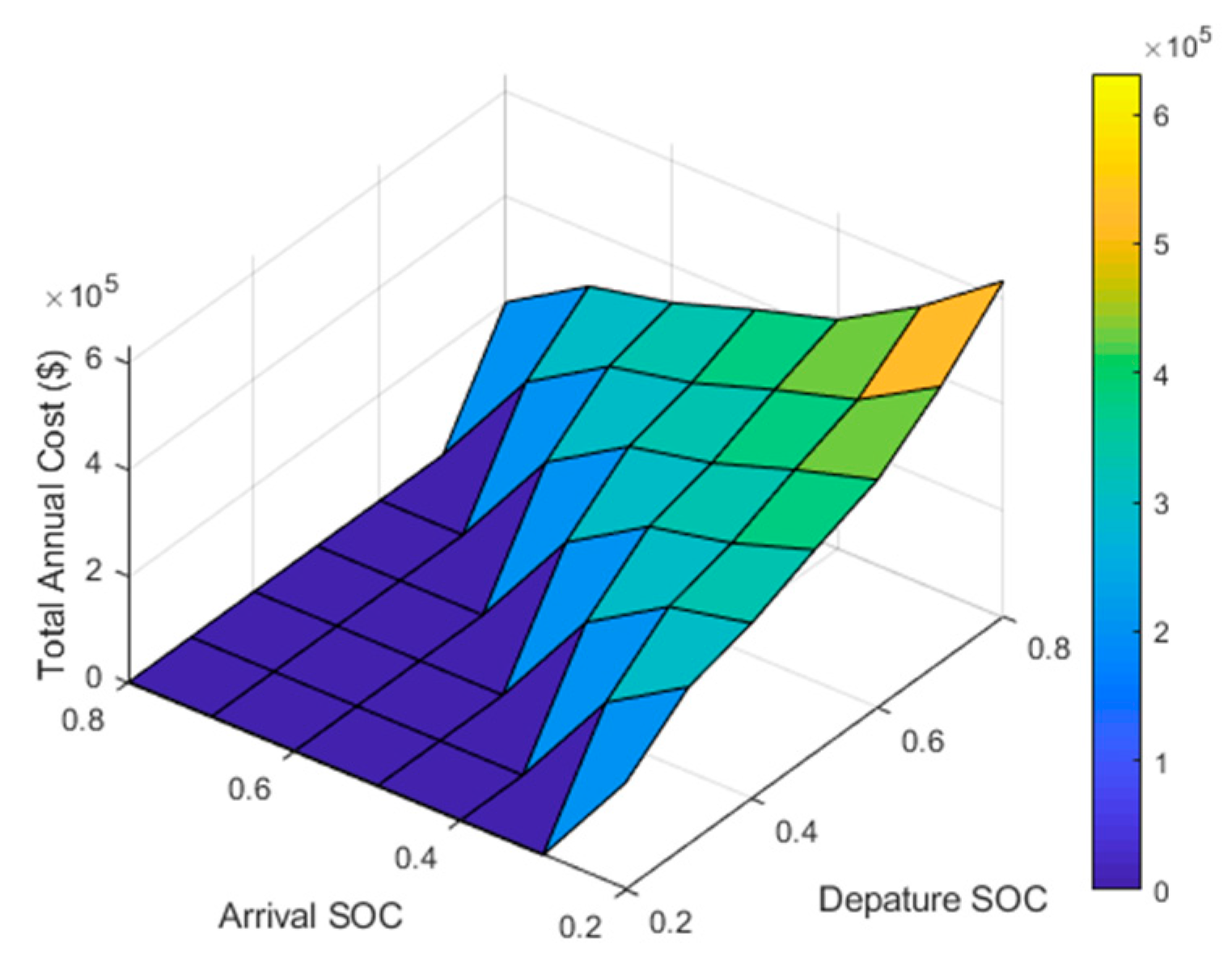
6.4. Influence of State-of-Charge
6.5. Comparison of Split-Type and Integrated-Type REVCs
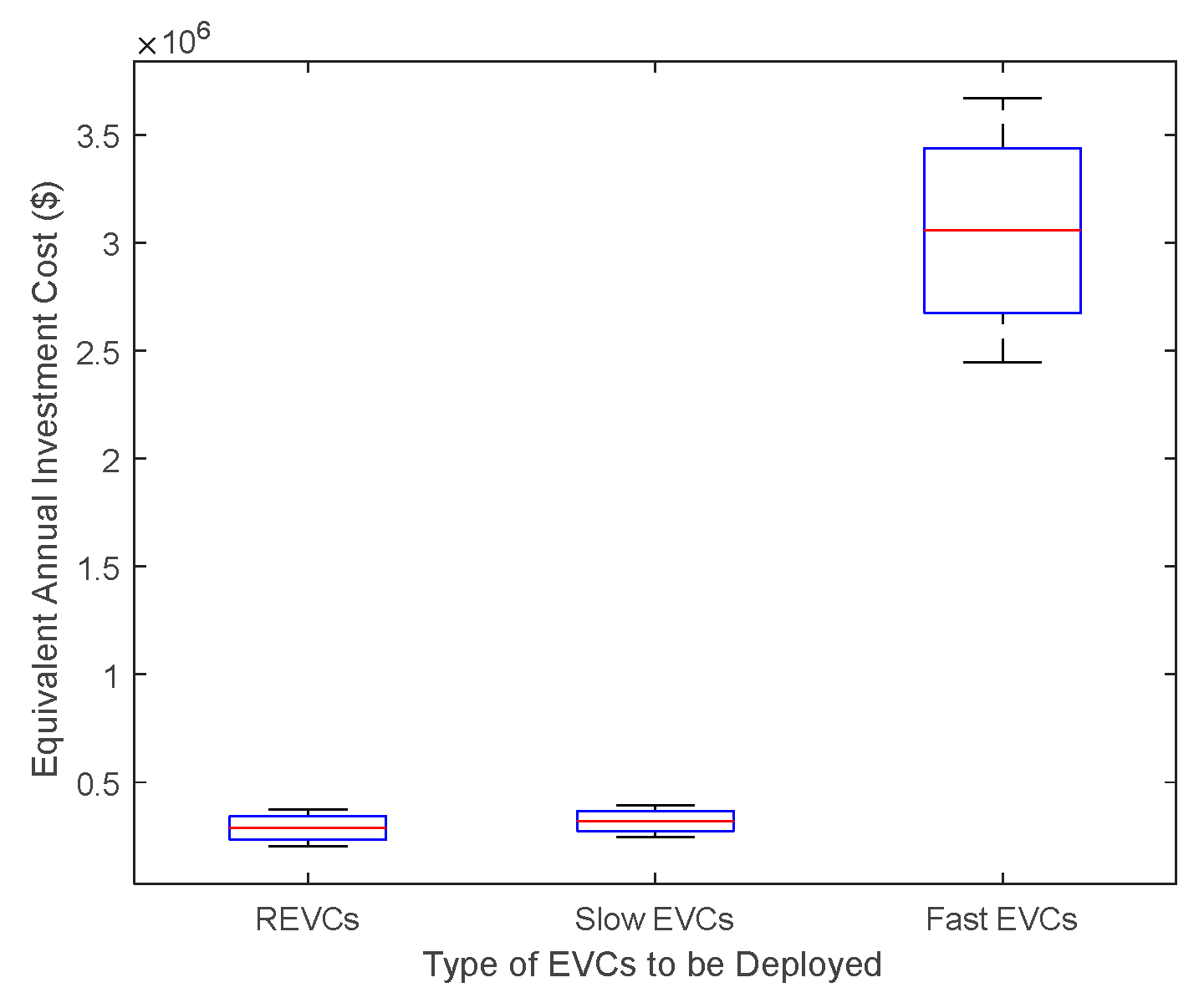
6.6. Sensitivity Analysis for REVC Component Costs
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Singh, P.P.; Wen, F.; Palu, I.; Sachan, S.; Deb, S. Electric Vehicles Charging Infrastructure Demand and Deployment: Challenges and Solutions. Energies 2023, 16, 7. [Google Scholar] [CrossRef]
- Aduama, P.; Al-Sumaiti, A.S.; Al-Hosani, K.H. Electric Vehicle Charging Infrastructure and Energy Resources: A Review. Energies 2023, 16, 1965. [Google Scholar] [CrossRef]
- Town, G.; Taghizadeh, S.; Deilami, S. Review of Fast Charging for Electrified Transport: Demand, Technology, Systems, and Planning. Energies 2022, 15, 1276. [Google Scholar] [CrossRef]
- Mathieu, L. Recharge EU: How Many Charge Points Will Europe and Its Member States Need in the 2020s; Transport & Environment: Brussels, Belgium, 2020. [Google Scholar]
- Palmer, R.; Vipond, S.; Fisher, E.; Roling, S. Progress and Insights Report 2021; Climate Group EV 100: New York, NY, USA, 2021. [Google Scholar]
- Song, B.; Madawala, U.; Baguley, C. A Review of Grid Impacts, Demand Side Issues and Planning Related to Electric Vehicle Charging. In Proceedings of the 2021 IEEE Southern Power Electronics Conference (SPEC), Kigali, Rwanda, 6–9 December 2021. [Google Scholar]
- Schettini, T.; dell’Amico, M.; Fumero, F.; Jabali, O.; Malucelli, F. Locating and Sizing Electric Vehicle Chargers Considering Multiple Technologies. Energies 2023, 16, 4186. [Google Scholar] [CrossRef]
- Campaña, M.; Inga, E.; Cárdenas, J. Optimal Sizing of Electric Vehicle Charging Stations Considering Urban Traffic Flow for Smart Cities. Energies 2021, 14, 4933. [Google Scholar] [CrossRef]
- Liu, Z.; Wen, F.; Ledwich, G. Optimal planning of electric vehicle charging stations in distribution systems. IEEE Trans. Power Del. 2013, 28, 102–110. [Google Scholar] [CrossRef]
- Guo, C.; Yang, J.; Yang, L. Planning of Electric Vehicle Charging Infrastructure for Urban Areas with Tight Land Supply. Energies 2018, 11, 2314. [Google Scholar] [CrossRef]
- Wang, X.; Shahidehpour, M.; Jiang, C.; Li, Z. Coordinated Planning Strategy for Electric Vehicle Charging Stations and Coupled Traffic-Electric Networks. IEEE Trans. Power Syst. 2019, 34, 268–279. [Google Scholar] [CrossRef]
- Micari, S.; Polimeni, A.; Napoli, G.; Andaloro, L.; Antonucci, V. Electric vehicle charging infrastructure planning in a road network. Renew. Sustain. Energy Rev. 2017, 80, 98–108. [Google Scholar] [CrossRef]
- Dong, X.; Mu, Y.; Jia, H.; Wu, J.; Yu, X. Planning of fast EV charging stations on a round freeway. IEEE Trans. Sustain. Energy 2016, 7, 1452–1461. [Google Scholar] [CrossRef]
- Wang, M.; Ismail, M.; Shen, X.; Serpedin, E.; Qaraqe, K. Spatial and temporal online charging/discharging coordination for mobile PEVs. IEEE Wirel. Commun. 2015, 22, 112–121. [Google Scholar] [CrossRef]
- Maigha; Crow, M.L. Cost-constrained dynamic optimal electric vehicle charging. IEEE Trans. Sustain. Energy 2017, 8, 716–724. [Google Scholar] [CrossRef]
- Gan, L.; Topcu, U.; Low, S.H. Optimal decentralized protocol for electric vehicle charging. IEEE Trans. Power Syst. 2013, 28, 940–951. [Google Scholar] [CrossRef]
- Mou, Y.; Xing, H.; Lin, Z.; Fu, M. Decentralized optimal demand side management for PHEV charging in a smart grid. IEEE Trans. Smart Grid 2015, 6, 726–736. [Google Scholar] [CrossRef]
- Kisacikoglu, M.C.; Erden, F.; Erdogan, N. Distributed control of PEV charging based on energy demand forecast. IEEE Trans. Ind. Inform. 2018, 14, 332–341. [Google Scholar] [CrossRef]
- Xu, Z.; Su, W.; Hu, Z.; Song, Y.; Zhang, H. A Hierarchical Framework for Coordinated Charging of Plug-In Electric Vehicles in China. IEEE Trans. Smart Grid 2016, 7, 428–438. [Google Scholar] [CrossRef]
- Jian, L.; Xue, H.; Xu, G.; Zhu, X.; Zhao, D.; Shao, Z.Y. Regulated Charging of Plug-in Hybrid Electric Vehicles for Minimizing Load Variance in Household Smart Microgrid. IEEE Trans. Ind. Electron. 2013, 60, 3218–3226. [Google Scholar] [CrossRef]
- Borlaug, B.; Yang, F.; Pritchard, E.; Wood, E.; Gonder, J. Public Electric Vehicle Charging Station Utilization in the United States. Transp. Res. Part D Transp. Environ. 2023, 114, 103564. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, Z.; Xu, Z.; Song, Y. An Integrated Planning Framework for Different Types of PEV Charging Facilities in Urban Area. IEEE Trans. Smart Grid 2016, 7, 2273–2284. [Google Scholar] [CrossRef]
- Ismail, M.; Bayram, I.S.; Abdallah, M.; Serpedin, E.; Qaraqe, K. Optimal planning of fast PEV charging facilities. In Proceedings of the 2015 First Workshop on Smart Grid and Renewable Energy (SGRE), Doha, Qatar, 22–23 March 2015. [Google Scholar]
- Yang, Q.; Sun, S.; Deng, S.; Zhao, Q.; Zhou, M. Optimal Sizing of PEV Fast Charging Stations with Markovian Demand Characterization. IEEE Trans. Smart Grid 2019, 10, 4457–4466. [Google Scholar] [CrossRef]
- Yang, Z.; Huang, X.; Gao, T.; Liu, Y.; Gao, S. Real-Time Energy Management Strategy for Parking Lot Considering Maximum Penetration of Electric Vehicles. IEEE Access 2022, 10, 5281–5291. [Google Scholar] [CrossRef]
- Mokgonyana, L.; Smith, K.; Galloway, S. Reconfigurable Low Voltage Direct Current Charging Networks for Plug-In Electric Vehicles. IEEE Trans. Smart Grid 2019, 10, 5458–5467. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, Z.; Xu, Z.; Song, Y. Optimal Planning of PEV Charging Station with Single Output Multiple Cables Charging Spots. IEEE Trans. Smart Grid 2019, 8, 2119–2128. [Google Scholar] [CrossRef]
- Chen, H.; Hu, Z.; Luo, H.; Qin, J.; Rajagopal, R.; Zhang, H. Design and Planning of a Multiple-Charger Multiple-Port Charging System for PEV Charging Station. IEEE Trans. Smart Grid 2019, 10, 173–183. [Google Scholar] [CrossRef]
- Vaughan, P.; Baxter, D.; Hagenmaier, C.F.; Tran, J.P.K.; Matsuno, C.T.; Eldridge, G.A.; Romano, P. Dynamic Allocation of Power Modules for Charging Electric Vehicles. U.S. Patent 010150380B2, 11 December 2018. [Google Scholar]
- ChargePoint Express 250 Specifications and Ordering Information. Available online: https://chargepoint.ent.box.com/v/CPE250-DS-EN-US (accessed on 27 September 2023).
- INFY POWER Split Type HP Fast DC Charger. Available online: https://www.infypower.com/split-type-hp-fast-dc-charger.html (accessed on 27 September 2023).
- ABB Electric Vehicle Infrastructure Terra High Power—GEN III. Available online: https://search.abb.com/library/Download.aspx?DocumentID=9AKK107991A9632&LanguageCode=en&DocumentPartId=&Action=Launch (accessed on 27 September 2023).
- SIEMENS CPC150—The 150 kW Compact Power Charge. Available online: https://assets.new.siemens.com/siemens/assets/api/uuid:c9041d4a-79fe-4e80-8b2a-439fbea5946a/broschuere-sicharge-cpc150-print.pdf (accessed on 27 September 2023).
- ChargePoint Express Plus. Available online: https://www.chargepoint.com/businesses/dc-stations/express-plus (accessed on 27 September 2023).
- SENKU 150V-1000VDC 60KW—160KW DC EV Charger. Available online: http://www.senkumachinery.com/product/-ev-car-charging-station.html (accessed on 27 September 2023).
- SCU EV Charging Stack EVMS EV Charging Stack (EV Power Unit + EV Charger Post). Available online: https://www.scupower.com/ev-charger/evse-ev-charging-stack/ (accessed on 27 September 2023).
- EVTEC Sspresso&Charge 6in1. Available online: https://www.evtec.ch/application/files/9716/1329/3826/factsheet_espressocharge_6in1_en.pdf (accessed on 27 September 2023).
- EVBox Troniq Modular. Available online: https://evbox.com/en/ev-chargers/troniq-modular (accessed on 27 September 2023).
- ChargePoint Express 250 Review: New Charger on the Block. Available online: https://www.youtube.com/watch?v=xgKo-zxGw9k (accessed on 9 October 2023).
- Annual Reports. Available online: https://at.govt.nz/about-us/reports-publications/annual-reports (accessed on 10 October 2023).
- Wang, R.; Xing, Q.; Chen, Z.; Zhang, Z.; Liu, B. Modeling and Analysis of Electric Vehicle User Behavior Based on Full Data Chain Driven. Sustainability 2022, 14, 8600. [Google Scholar] [CrossRef]
- Jonas, T.; Daniels, N.; Macht, G. Electric Vehicle User Behavior: An Analysis of Charging Station Utilization in Canada. Energies 2023, 16, 1592. [Google Scholar] [CrossRef]
- Khan, S.; Brandherm, B.; Swamy, A. Electric Vehicle User Behavior Prediction using Learning-based Approaches. In Proceedings of the 2020 IEEE Electric Power and Energy Conference (EPEC), Edmonton, AB, Canada, 9–10 November 2020. [Google Scholar]
- The New ChargePoint Mobile App Is Here. Available online: https://www.chargepoint.com/about/news/new-chargepoint-mobile-app-here/ (accessed on 10 October 2023).
- EVgo Mobile App. Available online: https://www.evgo.com/download-app/ (accessed on 10 October 2023).
- Mobile App. Available online: https://www.tesla.com/ownersmanual/model3/en_us/GUID-F6E2CD5E-F226-4167-AC48-BD021D1FFDAB.html (accessed on 10 October 2023).
- AUT Semester Dates. Available online: https://www.aut.ac.nz/study/semester-dates (accessed on 27 September 2023).
- Winter & Cold Weather EV Range Loss in 7000 Cars. Available online: https://www.recurrentauto.com/research/winter-ev-range-loss (accessed on 27 September 2023).
- Kostopoulos, E.; Spyropoulos, G.; Kaldellis, J. Real-world study for the optimal charging of electric vehicles. Energy Rep. 2020, 6, 418–426. [Google Scholar] [CrossRef]
- Common DC Fast Charging Curves and How to Find Yours. Available online: https://www.chargepoint.com/blog/common-dc-fast-charging-curves-and-how-find-yours (accessed on 9 October 2023).
- How DC Fast Charging Really Works and an Intro to Charging Curves. Available online: https://www.chargepoint.com/blog/how-dc-fast-charging-really-works-and-intro-charging-curves (accessed on 9 October 2023).
- Reducing EV Charging Infrastructure Costs. Available online: https://rmi.org/wp-content/uploads/2020/01/RMI-EV-Charging-Infrastructure-Costs.pdf (accessed on 27 September 2023).
- Rate BEVT Business Electric Vehicle Time-of-Use. Available online: https://www.alabamapower.com/content/dam/alabama-power/pdfs-docs/Rates/BEVT.pdf (accessed on 27 September 2023).
- Schedule GT (SC) General Service Time-of-Use. Available online: https://dms.psc.sc.gov/Attachments/Matter/0c8ffb07-d245-f293-036bd9115ebae6ad (accessed on 27 September 2023).
- Schroeder, A.; Traber, T. The economics of fast charging infrastructure for electric vehicles. Energy Policy 2012, 43, 136–144. [Google Scholar] [CrossRef]
- New Median Wage Will Apply from 27 February 2023. Available online: https://www.immigration.govt.nz/about-us/media-centre/news-notifications/new-median-wage-will-apply-from-27-february-2023 (accessed on 27 September 2023).
- Drivers Spend an Average of 17 Hours a Year Searching for Parking Spots. Available online: https://www.usatoday.com/story/money/2017/07/12/parking-pain-causes-financial-and-personal-strain/467637001/ (accessed on 27 September 2023).
- SCU EV Charger Module. Available online: https://www.scupower.com/ev-charger/ev-charger-module/ (accessed on 27 September 2023).
- INFY POWER Module. Available online: https://www.infypower.com/module/ (accessed on 27 September 2023).
- IBM ILOG CPLEX Optimization Studio. Available online: https://www.ibm.com/products/ilog-cplex-optimization-studio (accessed on 27 September 2023).
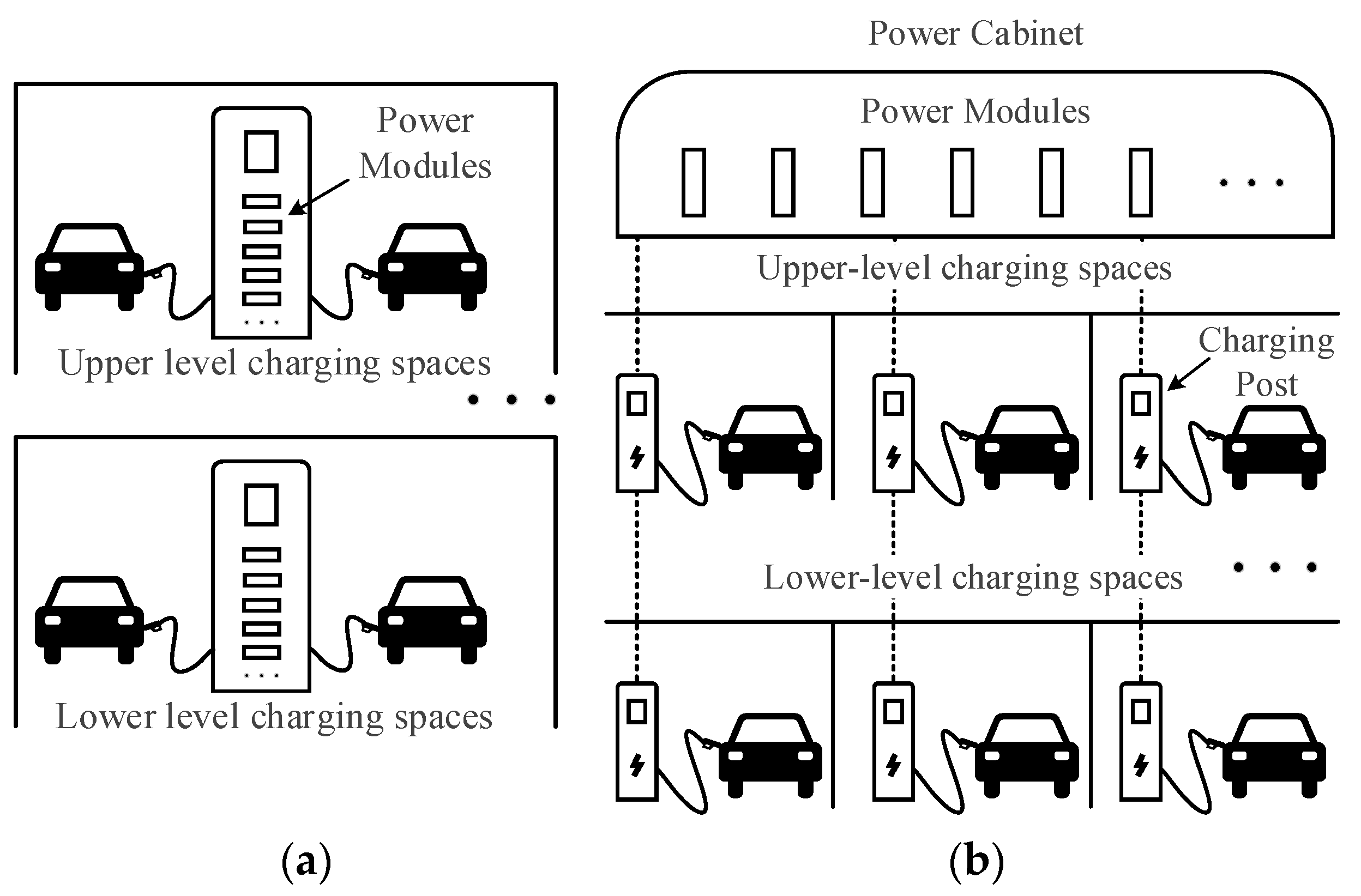





| EVC Type | Slow EVC | Conventional Fast EVC | REVC |
|---|---|---|---|
| AC or DC | AC | DC | DC |
| Number of EVs Charged Concurrently | 1 | 1 | >1 |
| Flexibility | Low | Low | High |
| Degree of Resource Utilization | Low | Low | High |
| EV Type | Nissan Leaf | BMW i3 | Hyundai Kona | Renault Zoe |
|---|---|---|---|---|
| Battery Capacity | 62 kWh | 42.2 kWh | 67.5 kWh | 54.7 kWh |
| Maximum Charging Power | 100 kW | 49 kW | 77 kW | 46 kW |
| Parameter | Value | Parameter | Value | |
|---|---|---|---|---|
| 480 kW (split-type) | 160 kW (integrated-type) | costcable | NZD 1500 | |
| 120 kW (split-type) | 100 kW (integrated-type) | costother | NZD 1500 | |
| 12 (split-type) | 3 (integrated-type) | PF | 0.99 | |
| 2 (either type) | Cex | 750 kVA | ||
| NZD 100/kW | NZD 150/kVA | |||
| costCP | NZD 1500 | η | 95% | |
| Period Type | Tariff (NZD/kWh) | Times (Hour) |
|---|---|---|
| Peak | 0.2167 | (12:00~19:00] |
| Shoulder | 0.1116 | (10:00~12:00] and (19:00~21:00] |
| Off-peak | 0.0837 | (21:00~10:00] |
| Power Rating of PMs (kW) | Degree of Utilization |
|---|---|
| 10 | 87% |
| 15 | 38.14% |
| 16 | 36.875% |
| 20 | 73.5% |
| 30 | 48.74% |
| EVC Type | REVC (Split-Type) | Slow EVC | Fast EVC | Slow EVC | Fast EVC |
|---|---|---|---|---|---|
| Operation Manner | Coordinated | Coordinated | Coordinated | Uncoordinated | Uncoordinated |
| EVC Number | 30 | 362 | 360 | 362 | 360 |
| Charging Post/cable per EVC | 12 | 1 | 1 | 1 | 1 |
| EVC Power Rating (kW) | 120 | 20 | 100 | 20 | 100 |
| Upgraded Transformer Capacity (kVA) | 750 + 771 | 750 + 771 | 750 + 771 | 750 + 1937 | 750 + 5762 |
| Equivalent Annual Investment Cost (k NZD) | 201.764 | 245.921 | 2445.623 | 245.921 | 2445.623 |
| Equivalent Annual Time Cost (Dissatisfaction Degree) (k NZD) | 1.370 | 0 | 1.370 | 0 | 1.370 |
| Annual Operation Cost (k NZD) | 102.674 | 102.674 | 102.674 | 319.620 | 986.262 |
| Annual Cost of Demand Charge (k NZD) | 154.412 | 154.412 | 154.412 | 281.515 | 661.098 |
| Equivalent Annual Transformer Upgrade Cost (k NZD) | 6.914 | 6.914 | 6.914 | 39.476 | 117.431 |
| Total Annual Cost (k NZD) | 428.789 | 471.576 | 2672.648 | 886.532 | 4211.784 |
| Component | Cost Range |
|---|---|
| Power Module | 100~150 (NZD/kW) |
| Charging Post | 1500~2500 (NZD) |
| Cable | 1500~3500 (NZD) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, B.; Madawala, U.K.; Baguley, C.A. Optimal Planning Strategy for Reconfigurable Electric Vehicle Chargers in Car Parks. Energies 2023, 16, 7204. https://doi.org/10.3390/en16207204
Song B, Madawala UK, Baguley CA. Optimal Planning Strategy for Reconfigurable Electric Vehicle Chargers in Car Parks. Energies. 2023; 16(20):7204. https://doi.org/10.3390/en16207204
Chicago/Turabian StyleSong, Bingkun, Udaya K. Madawala, and Craig A. Baguley. 2023. "Optimal Planning Strategy for Reconfigurable Electric Vehicle Chargers in Car Parks" Energies 16, no. 20: 7204. https://doi.org/10.3390/en16207204
APA StyleSong, B., Madawala, U. K., & Baguley, C. A. (2023). Optimal Planning Strategy for Reconfigurable Electric Vehicle Chargers in Car Parks. Energies, 16(20), 7204. https://doi.org/10.3390/en16207204








