3.1. Rules for Generation of Tree Graphs
An (
N + 1)-link (solid vertex) tree graph can be generated by adding a solid vertex with a revolute edge into an
N-link tree graph. Based on the Characteristic 1 introduced in
Section 2, the rules for generating (
N + 1)-link tree graphs from
N-link tree graphs are proposed in this section. According to the level of the newly added revolute edge, the generation of (
N + 1)-link tree graphs can be divided into the following two cases.
Case 1. The level of the added revolute edge is different from the levels of all revolute edges in the given N-link tree graph.
According to Characteristic 1, all the revolute edges incident with the same hollow vertex have the same level. Therefore, the connection method of the added revolute edge satisfies the following rule: The added revolute edge can be connected to any solid vertex, but not to any hollow vertex. Obviously, the number
x1 of (
N + 1)-link tree graphs generated in Case 1 is equal to the number
N of solid vertices in the given
N-link tree graph, namely,
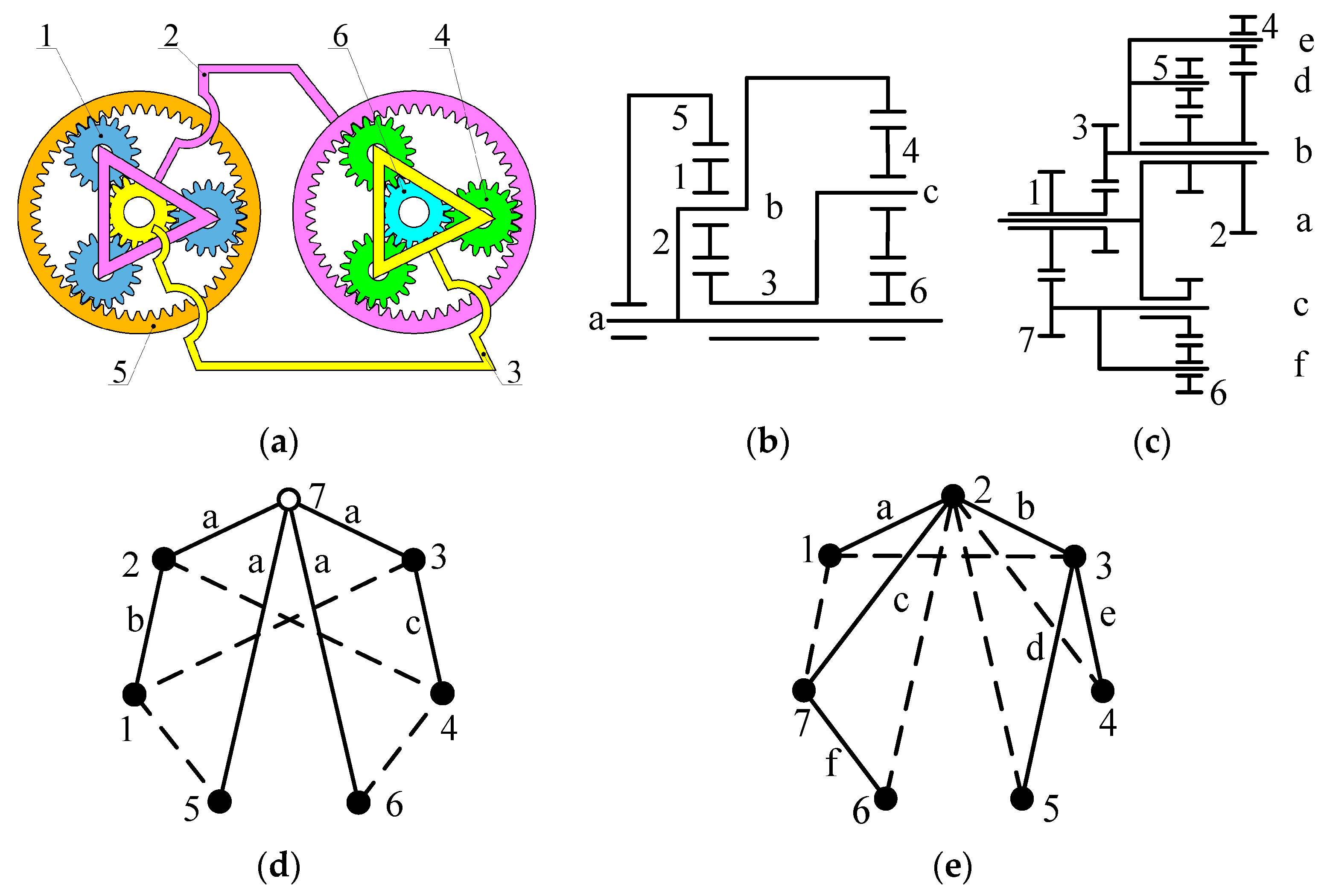
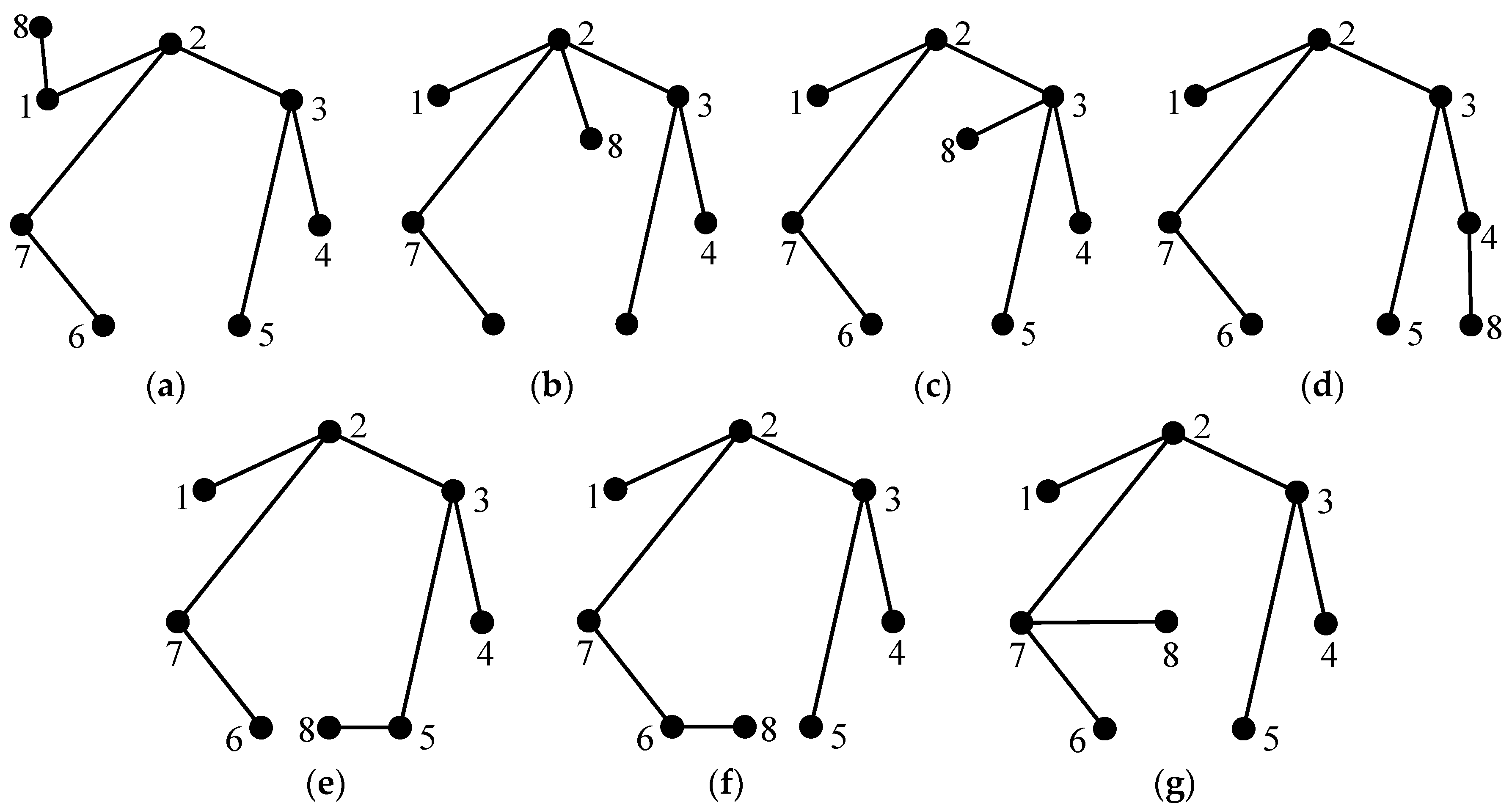
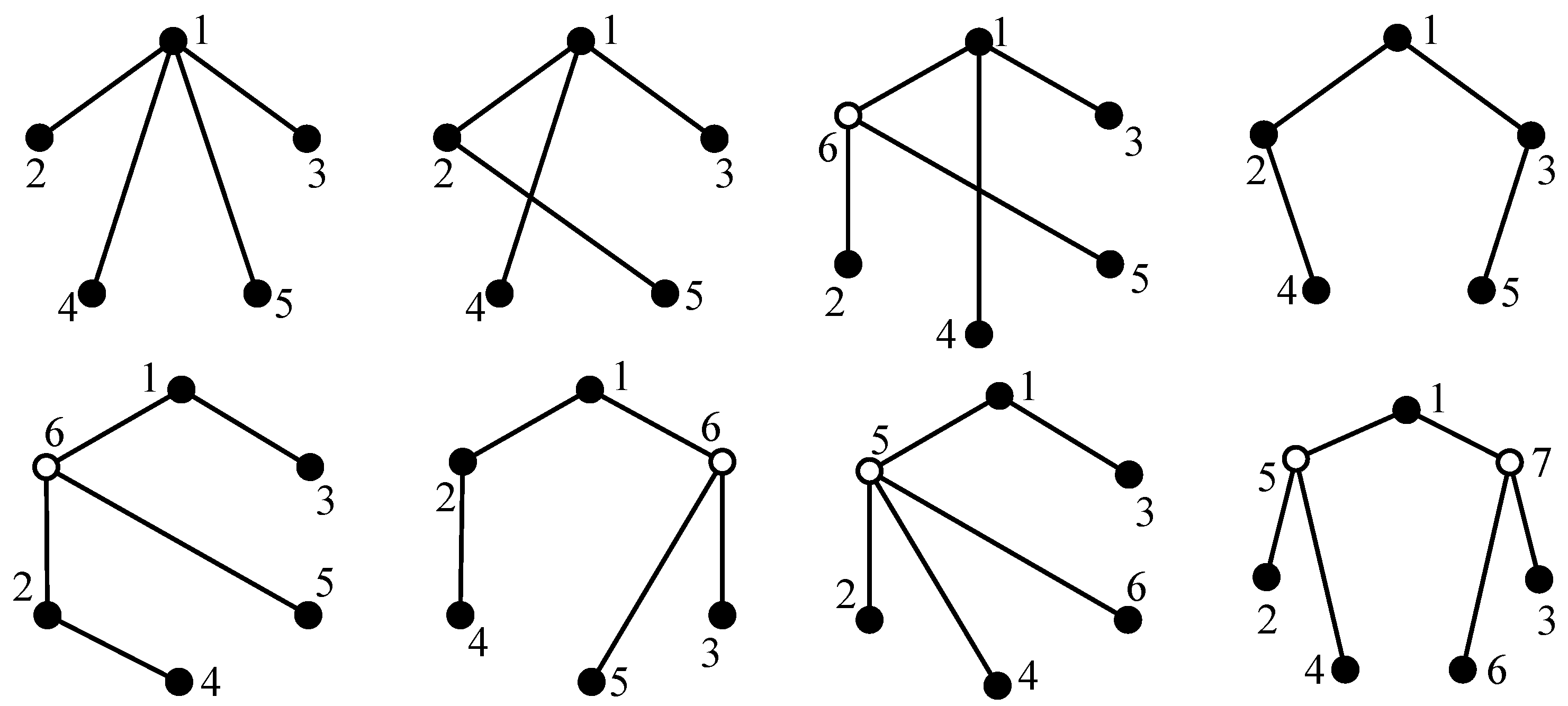
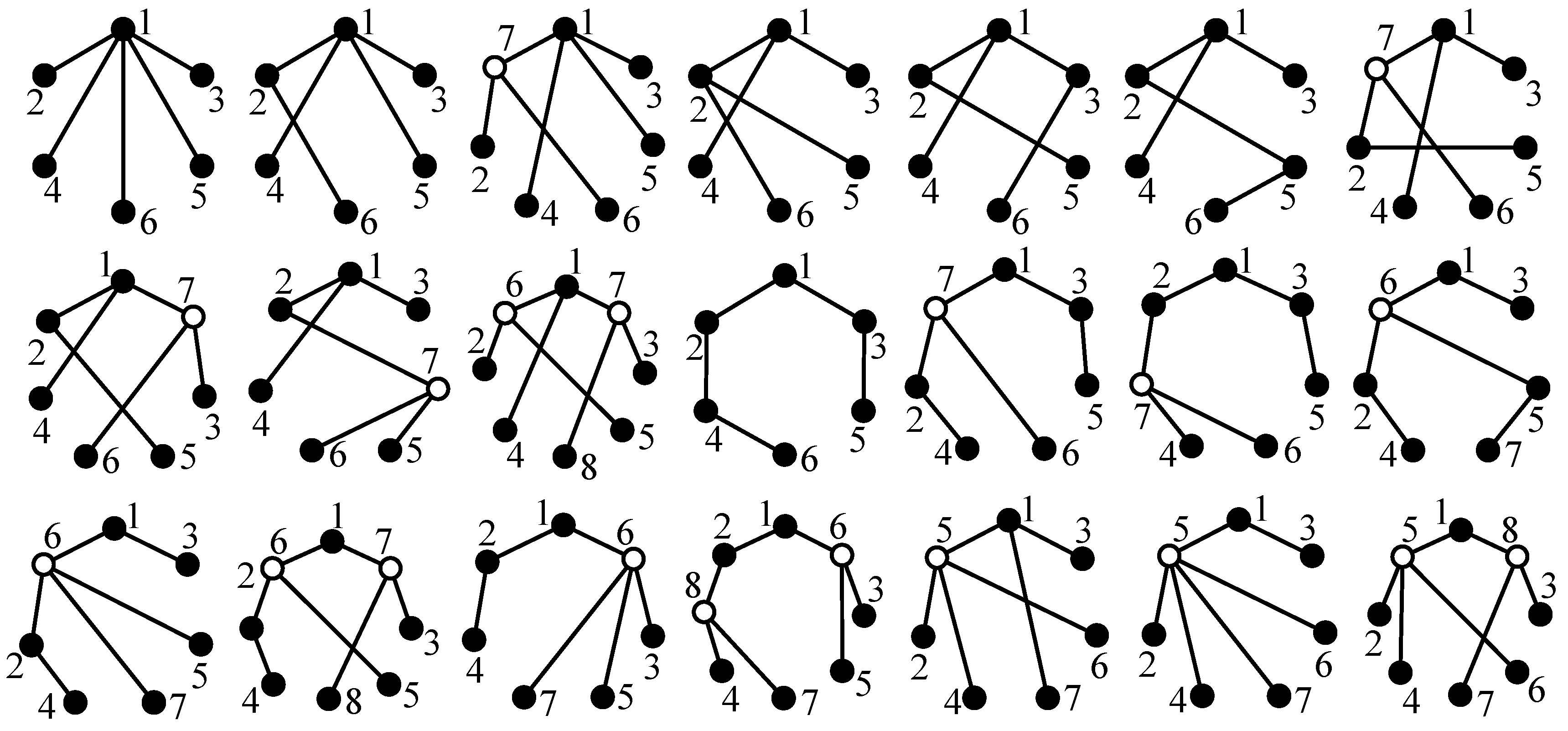
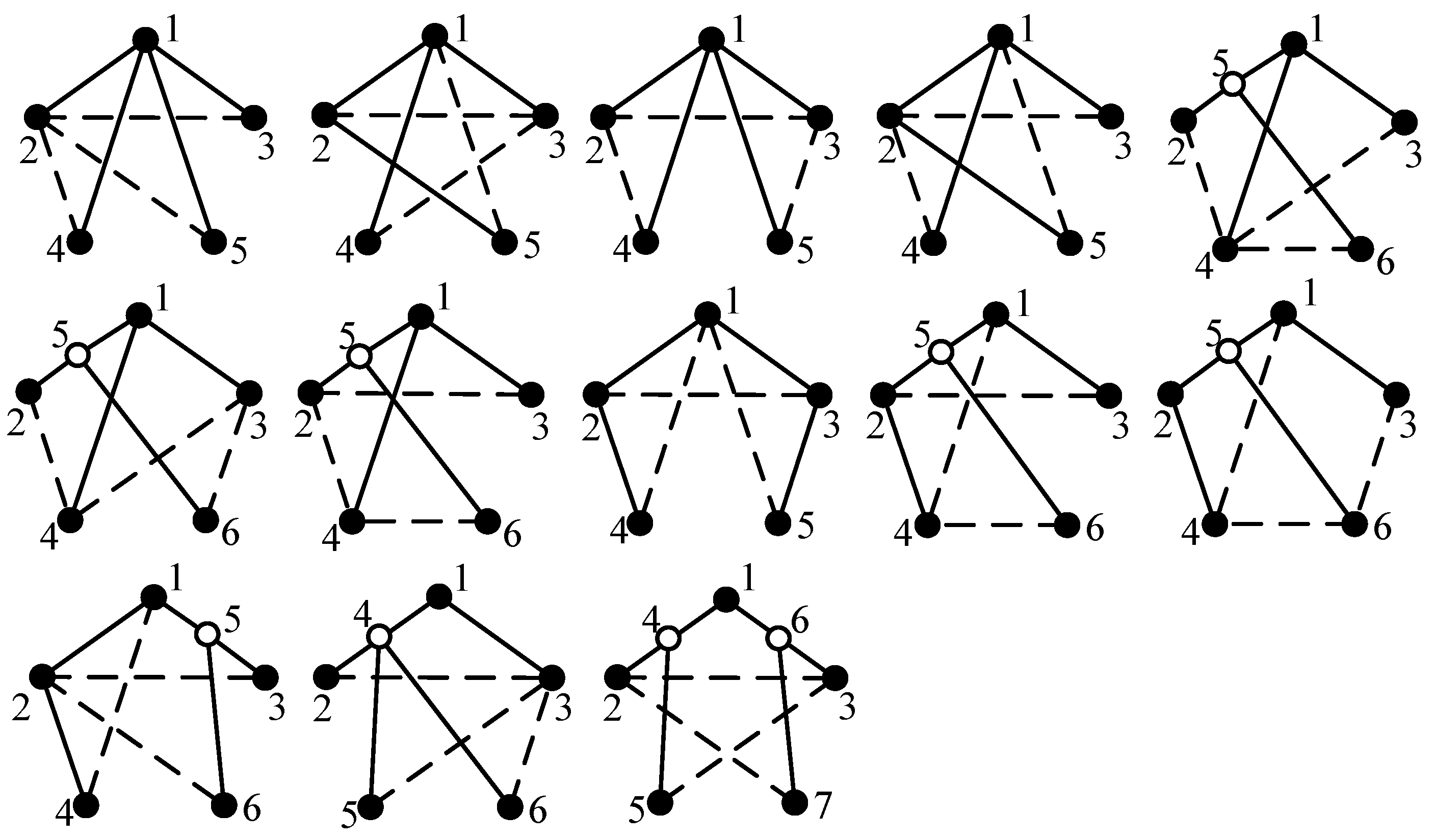
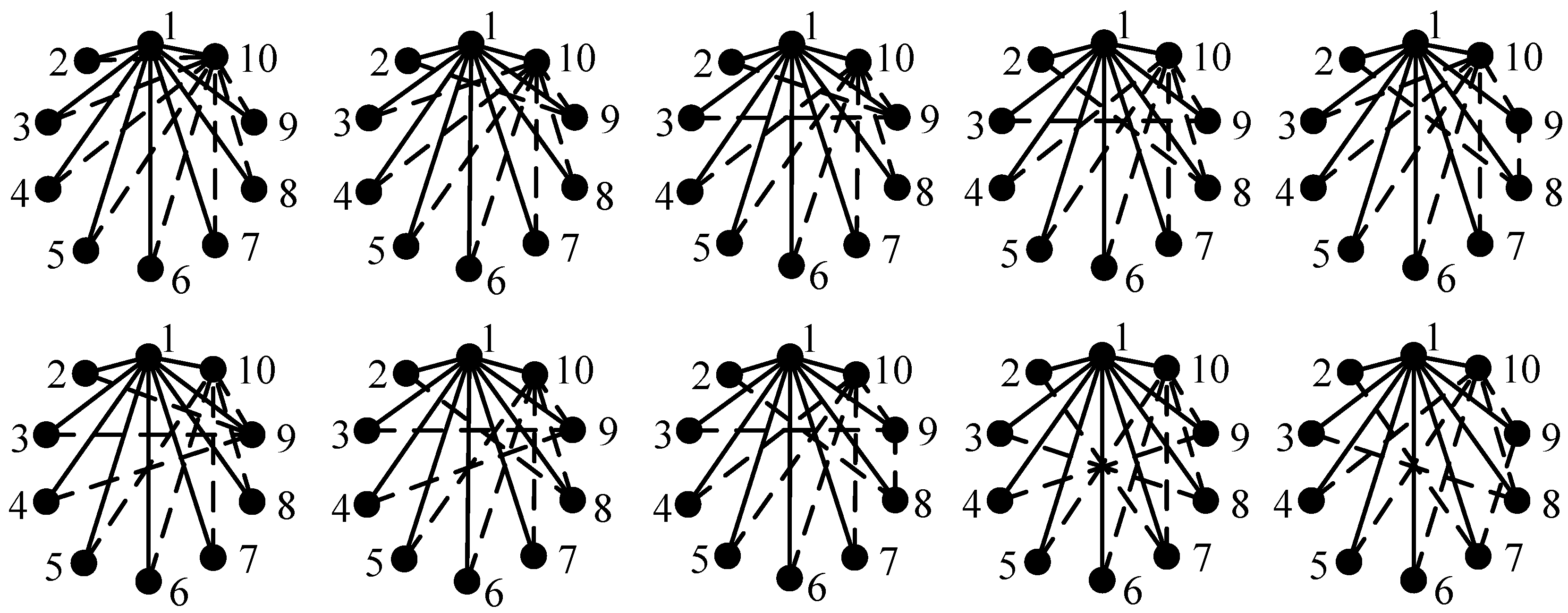
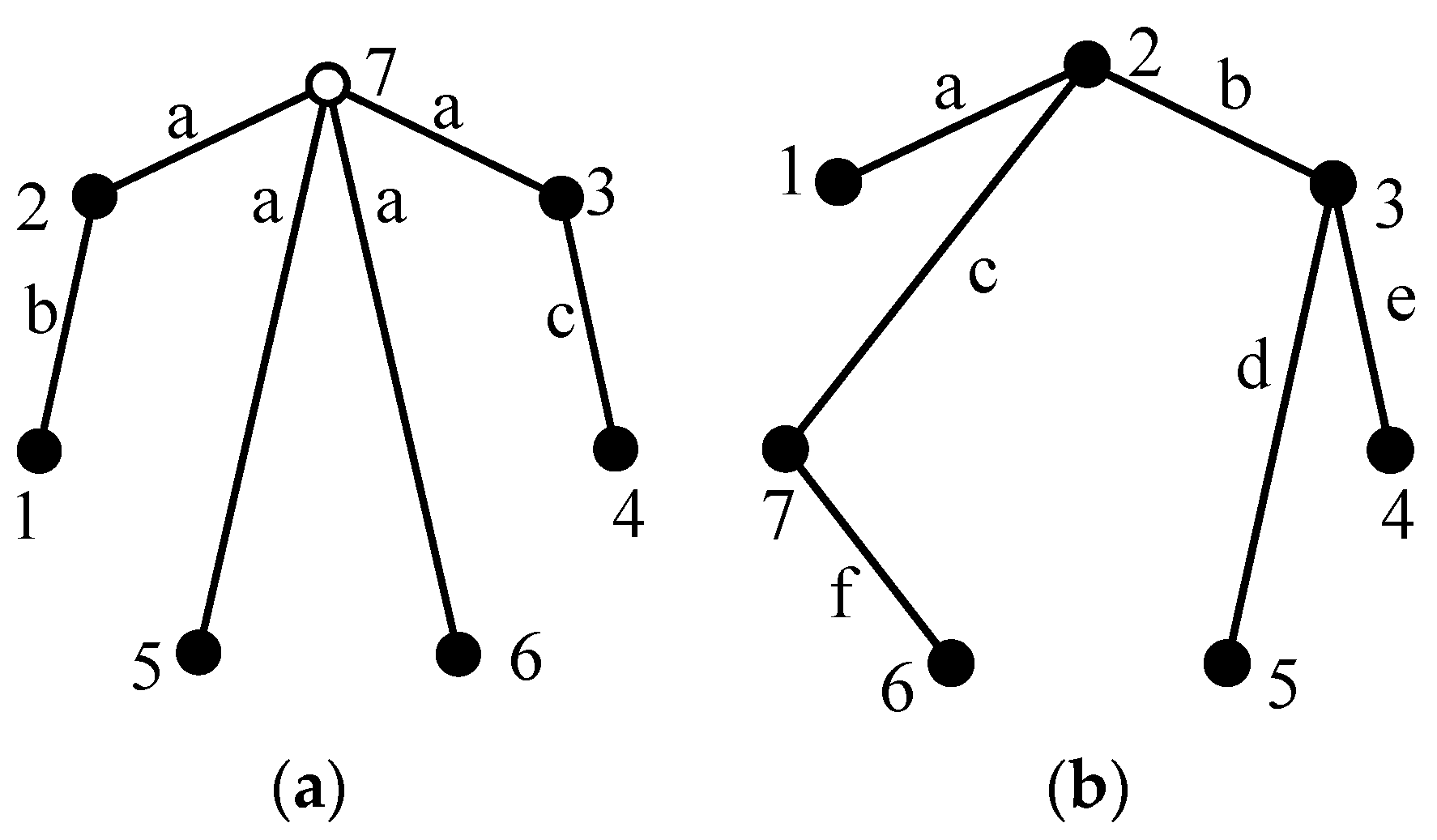
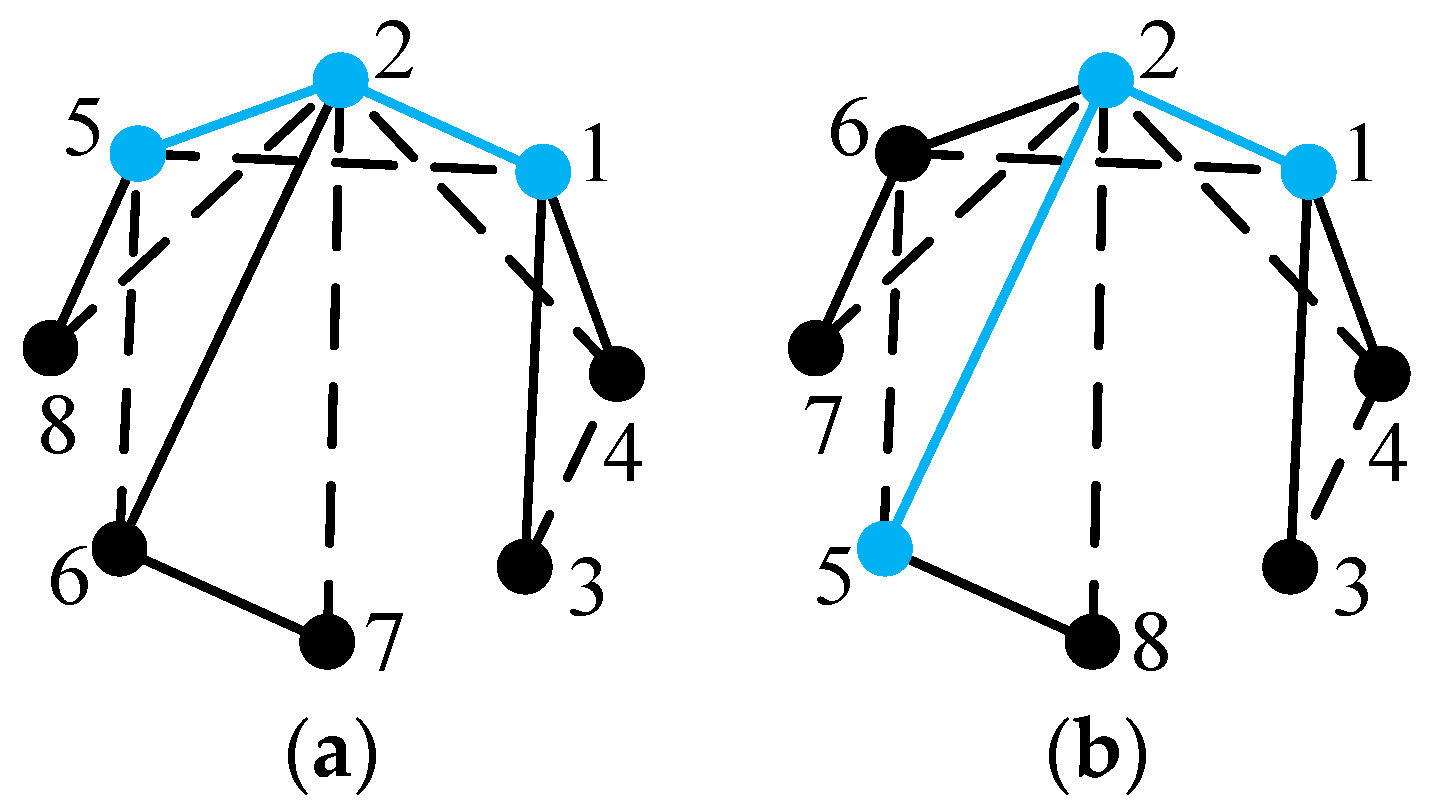
For example, the six-link tree graph in
Figure 4a contains six solid vertices, from which six seven-link tree graphs can be generated, as shown in
Figure 6. The newly added vertex 8 and its incident revolute edge are connected to solid vertices 1, 2, 3, 4, 5, and 6, respectively.
Case 2. The level of the added revolute edge is the same as one of the levels of revolute edges in the given N-link tree graph.
The level of the added revolute edge has two possibilities: (a) The level of the newly added revolute edge is the same as the level of revolute edges which are incident with a hollow vertex (denoted as vertex
k). (b) The level of the newly added revolute edge is the same as the level of a revolute edge (denoted as edge
ei,j) which is not incident with any hollow vertex. For possibility (a), the added revolute edge is directly connected to hollow vertex
k. For possibility (b), edge
ei,j is deleted and then vertices
i,
j and the added vertex are connected to a same new hollow vertex. Obviously, the number
x2 of (
N + 1)-link tree graphs generated in Case 2 is equal to the number
L of levels of revolute edges in the given
N-link tree graph, namely,
For example, the six-link tree graph in
Figure 4a contains three edge levels, from which three seven-link tree graphs can be generated, as shown in
Figure 7. When the level of the newly added revolute edge is the same as the level (level a) of revolute edges which are incident with hollow vertex 7, the newly added revolute edge is directly connected to hollow vertex 7, as shown in
Figure 7a. When the level of the newly added revolute edge is the same as the level (level b) of revolute edge
e1,2, edge
e1,2 is deleted and vertices 1, 2 and the added vertex 8 are connected to the new hollow vertex 9, as shown in
Figure 7b. Similarly, when the level of the newly added revolute edge is the same as the level (level c) of revolute edge
e3,4, the generated seven-link tree graph is shown in
Figure 7c.
The number of (
N + 1)-link tree graphs generated from a given
N-link tree graph is equal to the sum of tree graphs generated in the above two cases, namely,
For example, in the six-link tree graph shown in
Figure 4a, the number
N of solid vertices and the number
L of edge levels are 6 and 3, respectively. Therefore, the number of seven-link tree graphs generated from
Figure 4a is
x =
N +
L = 6 + 3 = 9, as shown in
Figure 6 and
Figure 7.
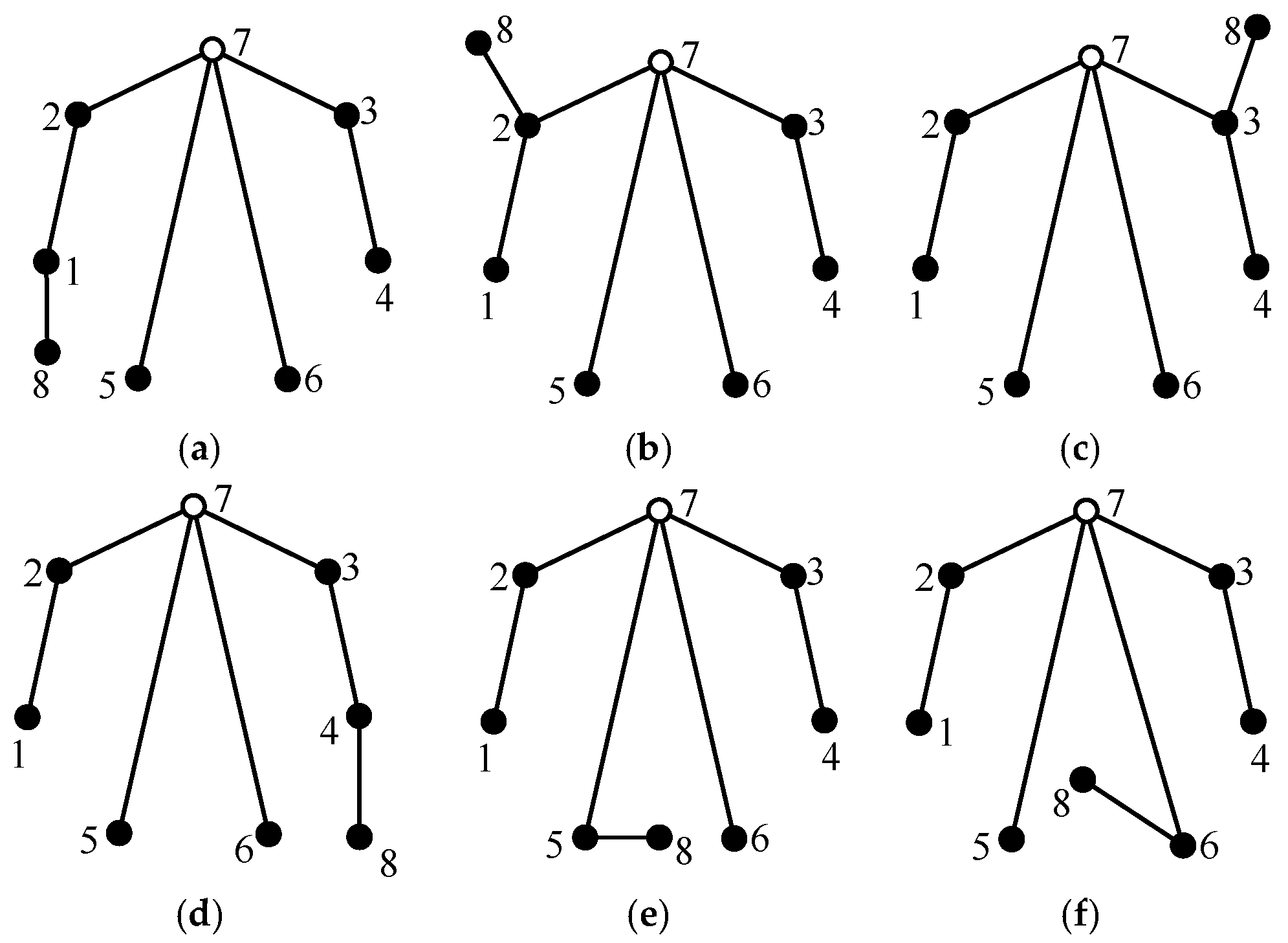
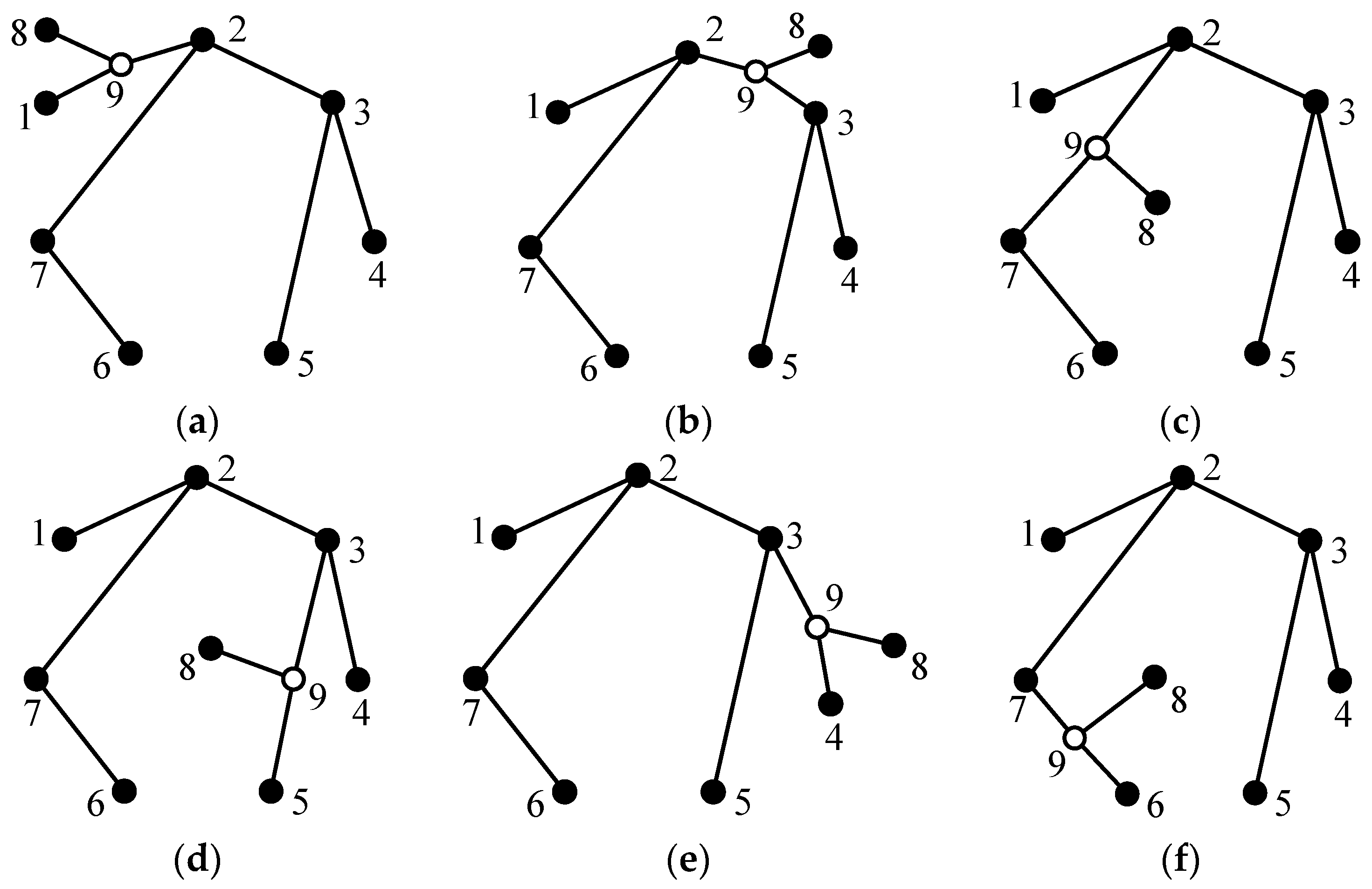
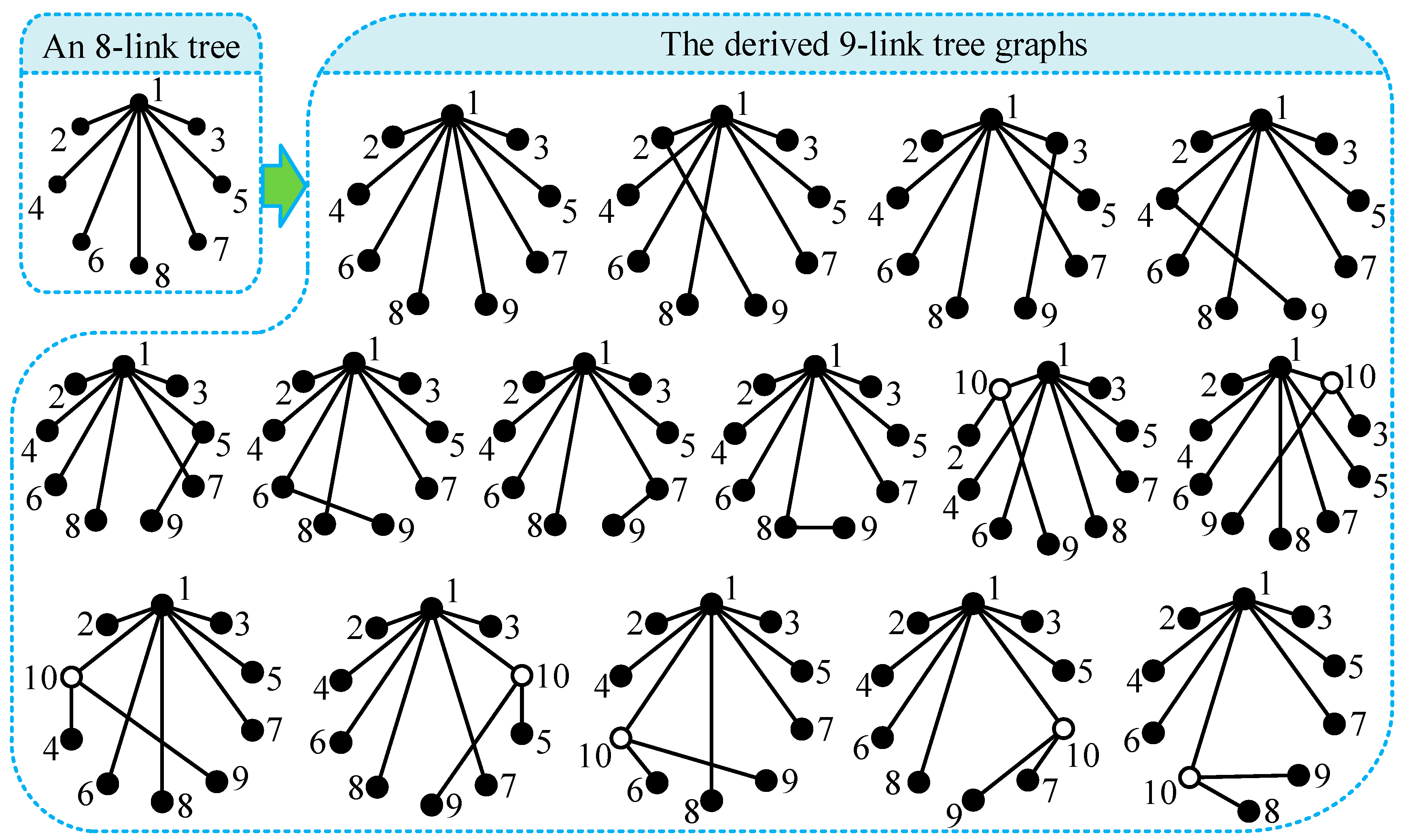
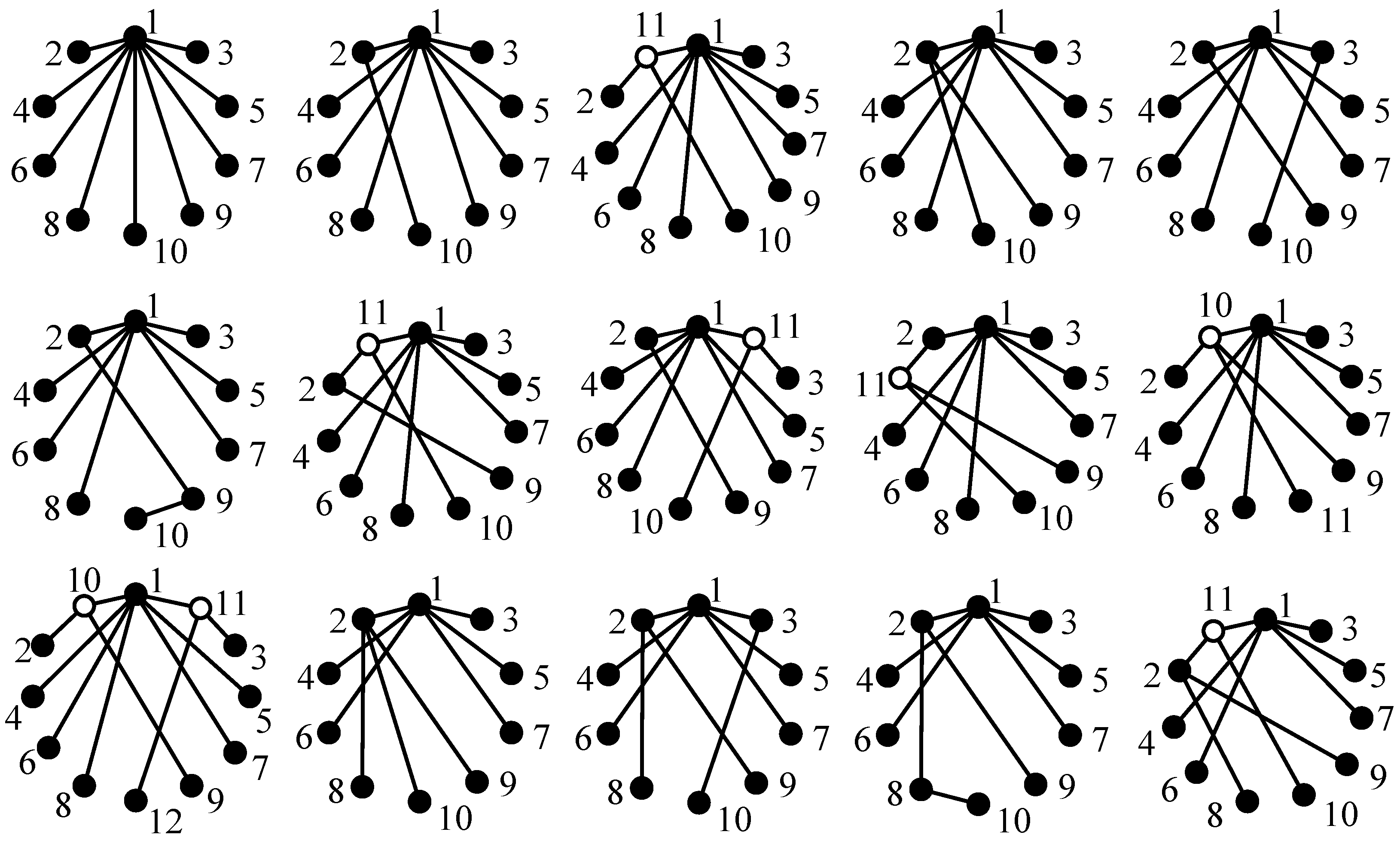
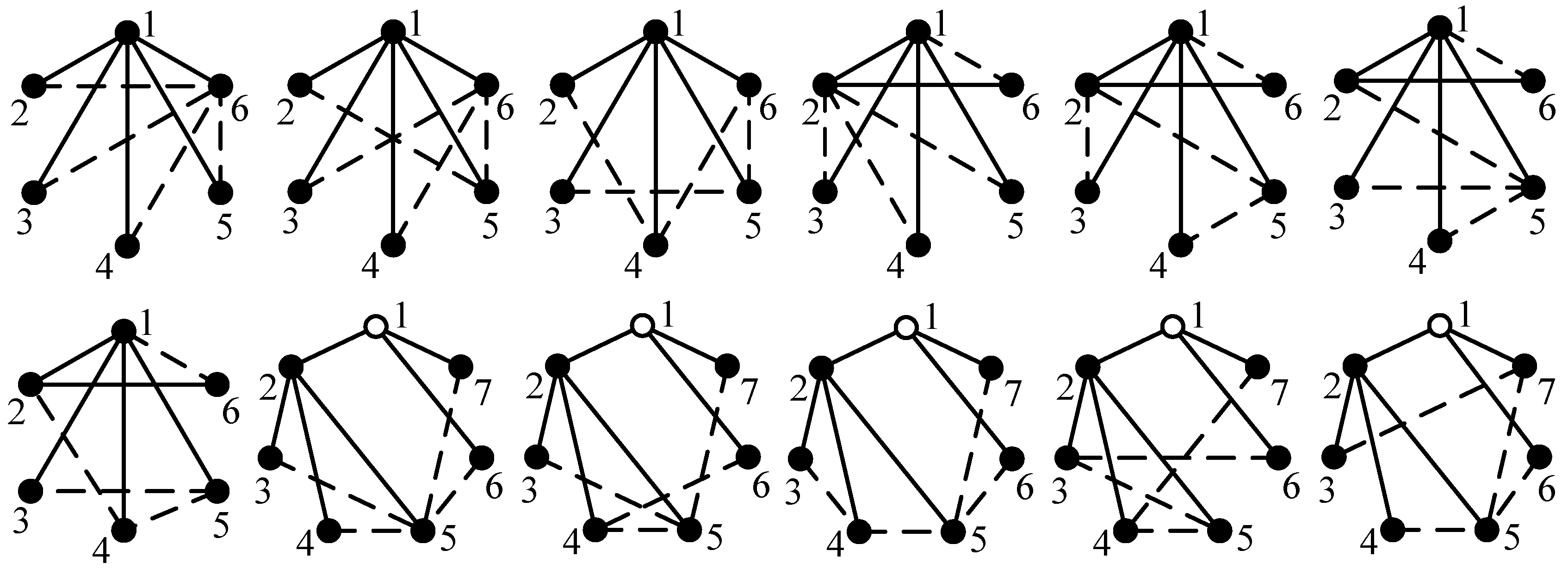
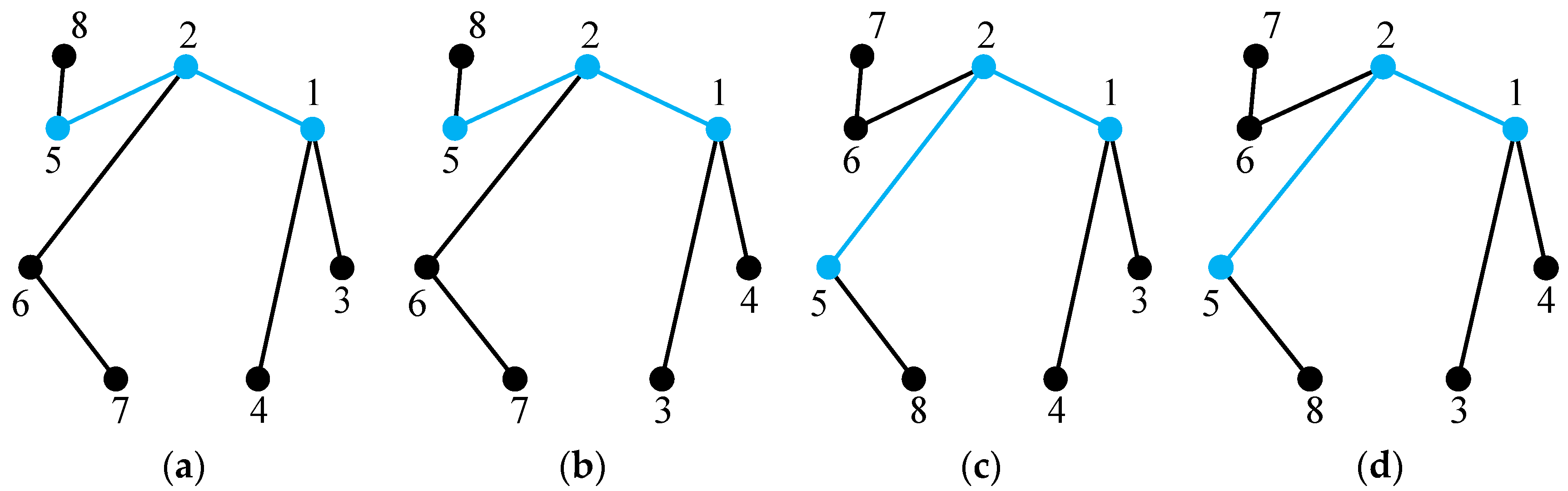
The process of generating eight-link tree graphs from the seven-link tree graph without any hollow vertex shown in
Figure 4b is briefly illustrated as follows. There are seven solid vertices in
Figure 4b; hence, seven eight-link tree graphs can be generated in Case 1. The newly added vertex 8 and its incident revolute edge are connected to solid vertices 1, 2, 3, 4, 5, 6, and 7, respectively, as shown in
Figure 8. There are six different edge levels in
Figure 4b; hence, six eight-link tree graphs can be generated in Case 2, as shown in
Figure 9. The level of the newly added revolute edge is the same as edge levels a, b, c, d, e, and f in
Figure 4b, respectively. The total number of eight-link tree graphs generated from the seven-link tree graph in
Figure 4b is
x =
N +
L = 7 + 6 = 13.
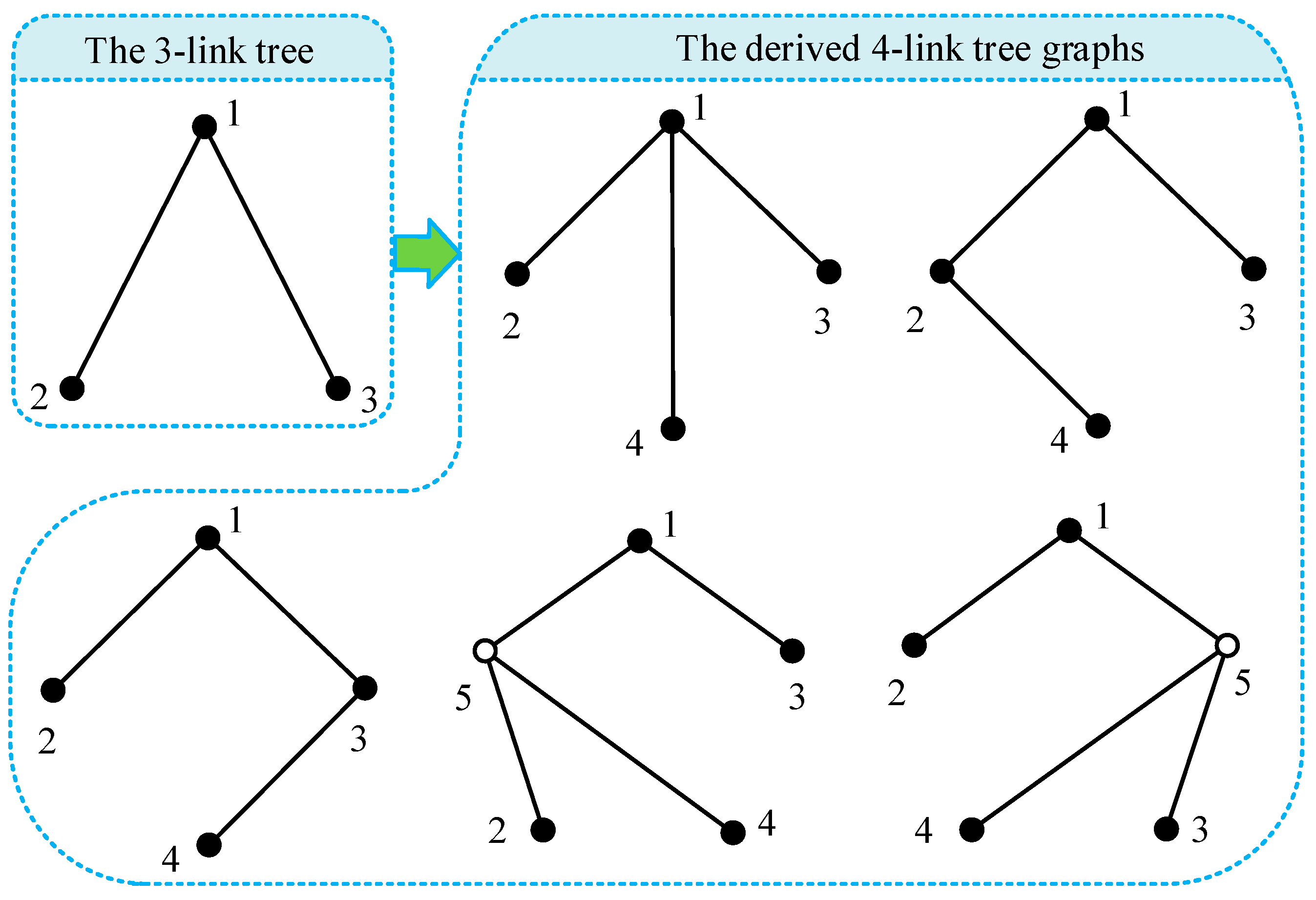
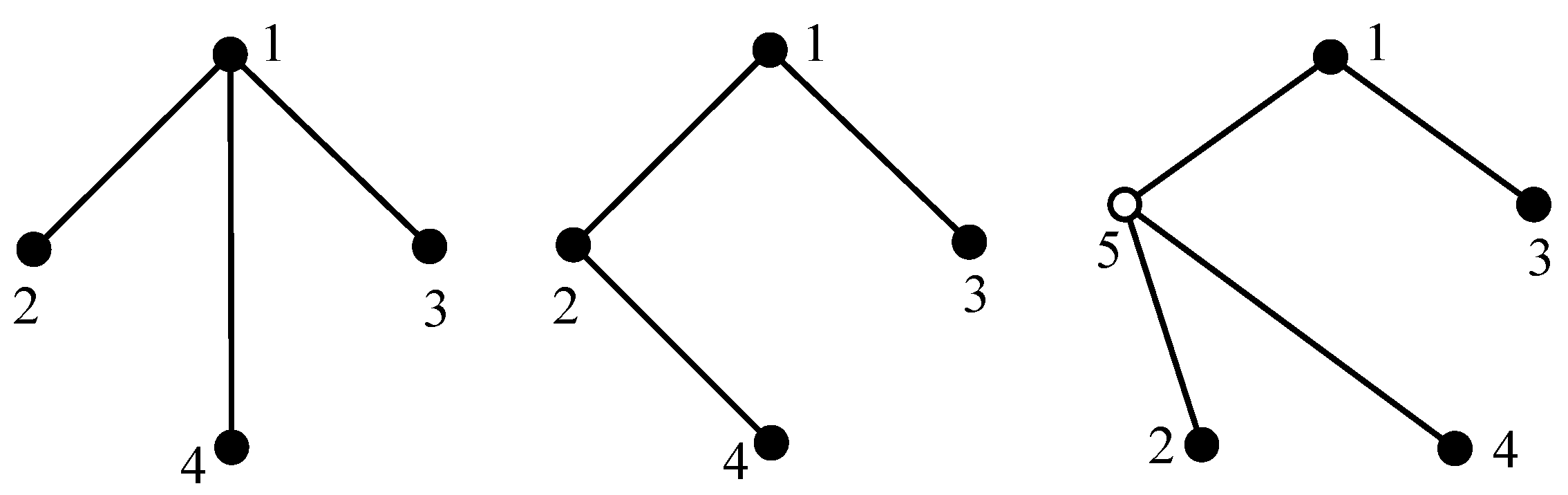
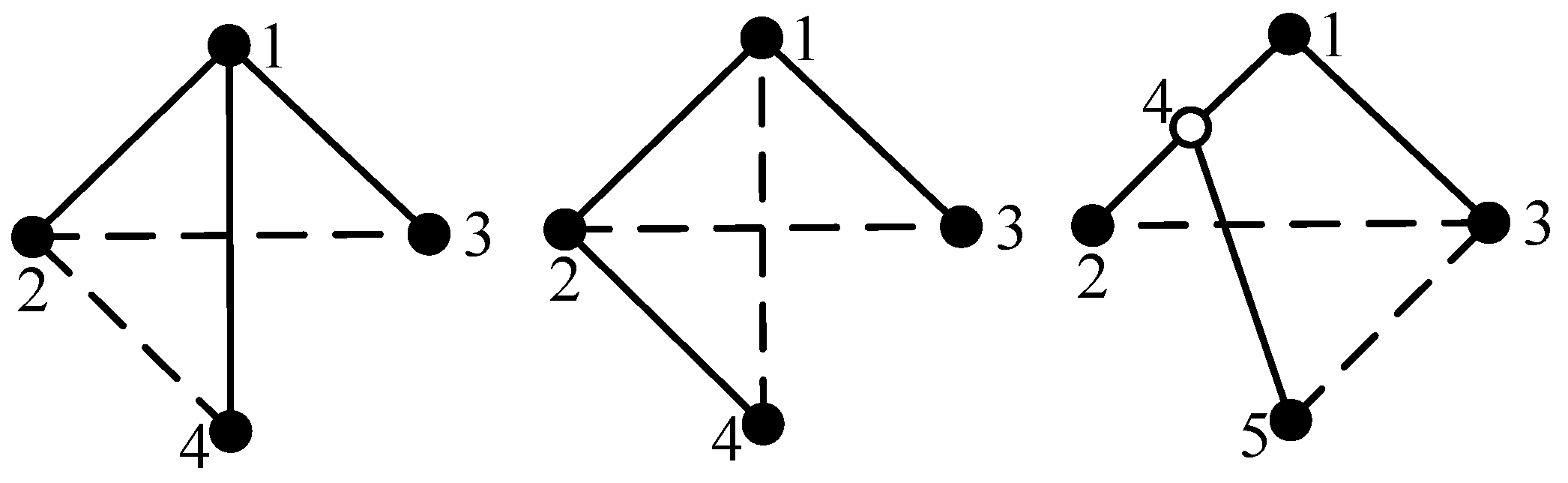
All feasible tree graphs can be generated recursively. As is well known, there exists only one three-link 1-DOF PGT; hence, there is only one three-link tree graph. All possible four-link tree graphs can be generated from this three-link tree graph, as shown in
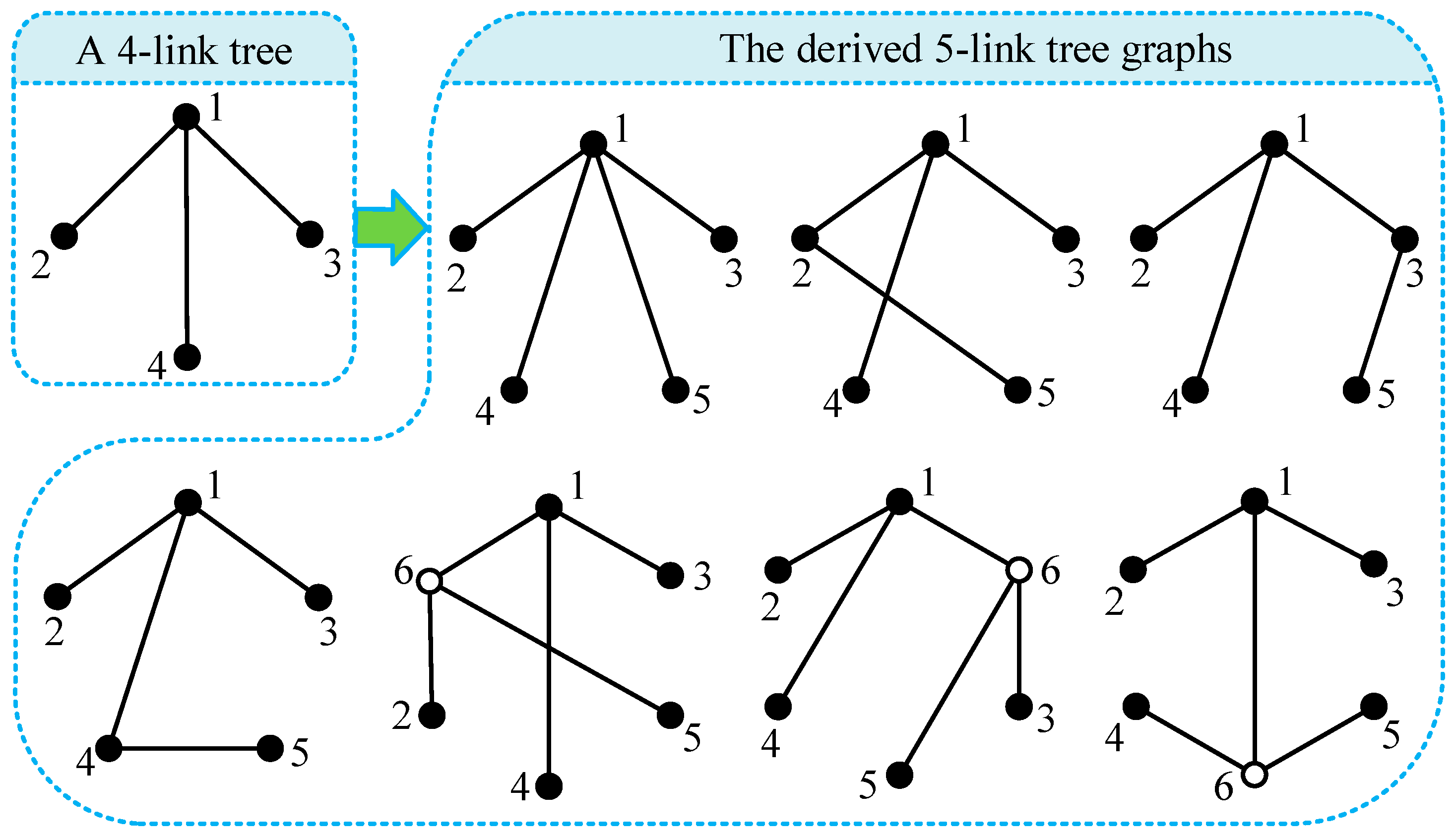
Figure 10. These four-link tree graphs can be used to derive all possible five-link tree graphs, and these five-link tree graphs can be used to derive all possible six-link tree graphs, and so on. For example,
Figure 11 and
Figure 12 show all possible (
N + 1)-link tree graphs which are generated from an
N-link tree graph (
N equals 4 and 8, respectively).
3.2. A Unified Isomorphism Detection Algorithm and the Atlas of Tree Graphs
When the number of links exceeds five, PGTs and their tree graphs have complex topological structures, and the number of isomorphic graphs is very large. Due to inaccuracy and inefficiency, manual isomorphism detection cannot be used for the synthesis of PGTs. Therefore, it is necessary to study an isomorphism detection algorithm that can be easily automated by computer. Most of the existing isomorphism detection algorithms are only applicable for closed-loop graphs, but not for open-loop graphs. Here, a unified isomorphism detection algorithm applicable for both open-loop and closed-loop graphs is proposed.
The topological graphs of PGTs derived from isomorphic tree graphs are also isomorphic. Therefore, removing isomorphic tree graphs can greatly reduce the number of isomorphic topological graphs of PGTs and improve the efficiency of topological synthesis of PGTs. In this section, the proposed isomorphism detection algorithm is used in the process of generating tree graphs to obtain the atlas of non-isomorphic tree graphs. The tree graph in
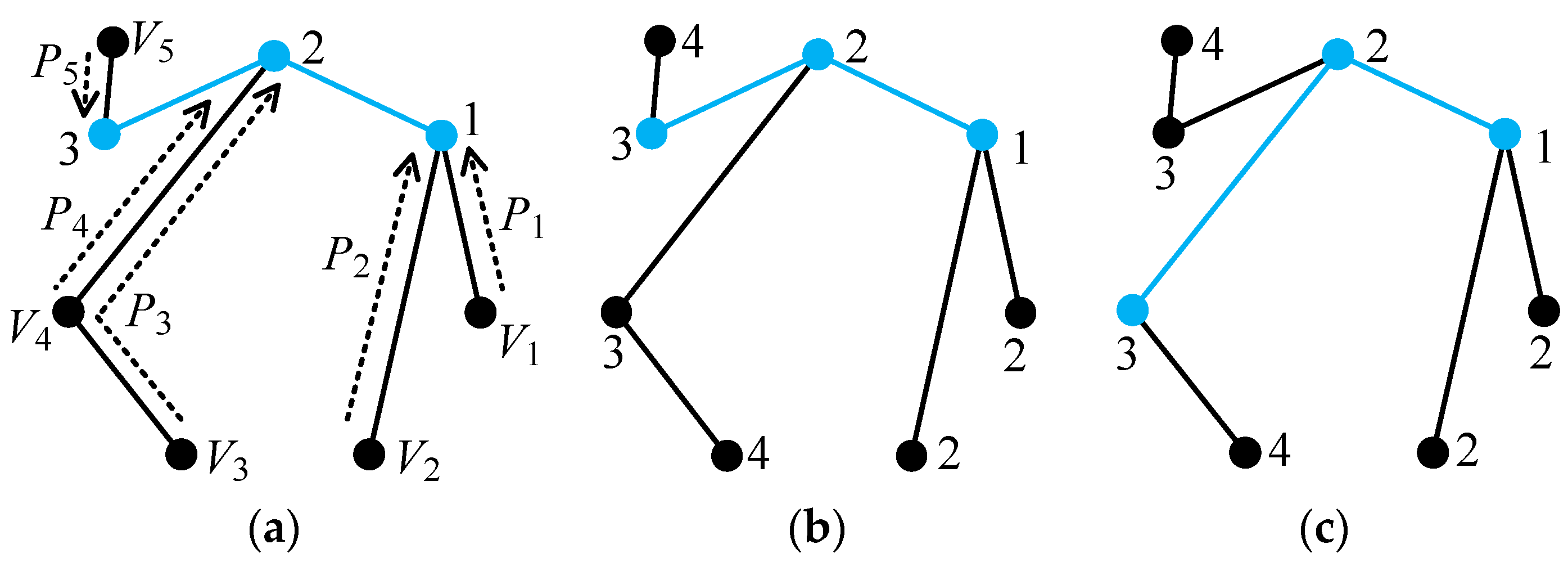
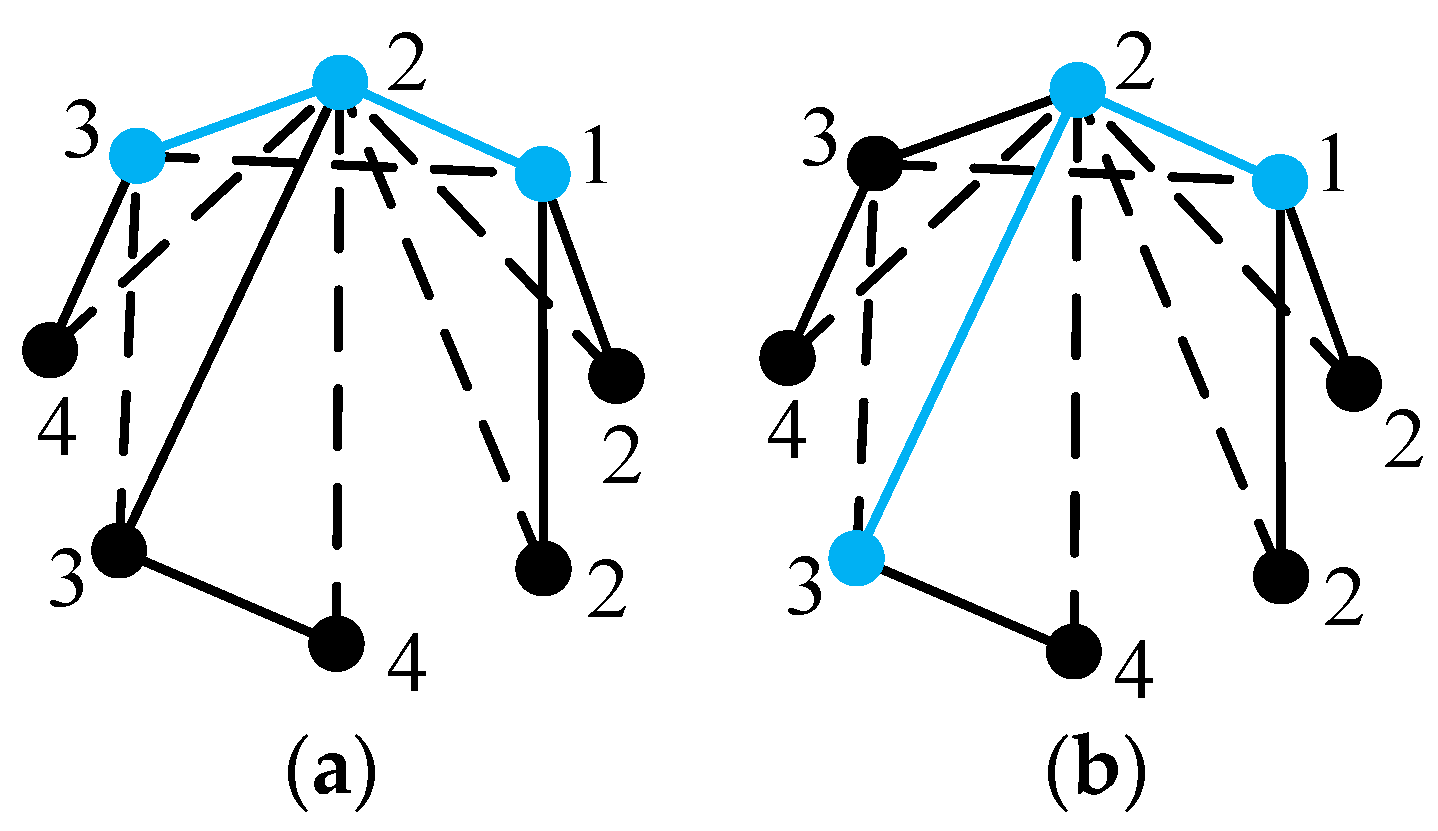
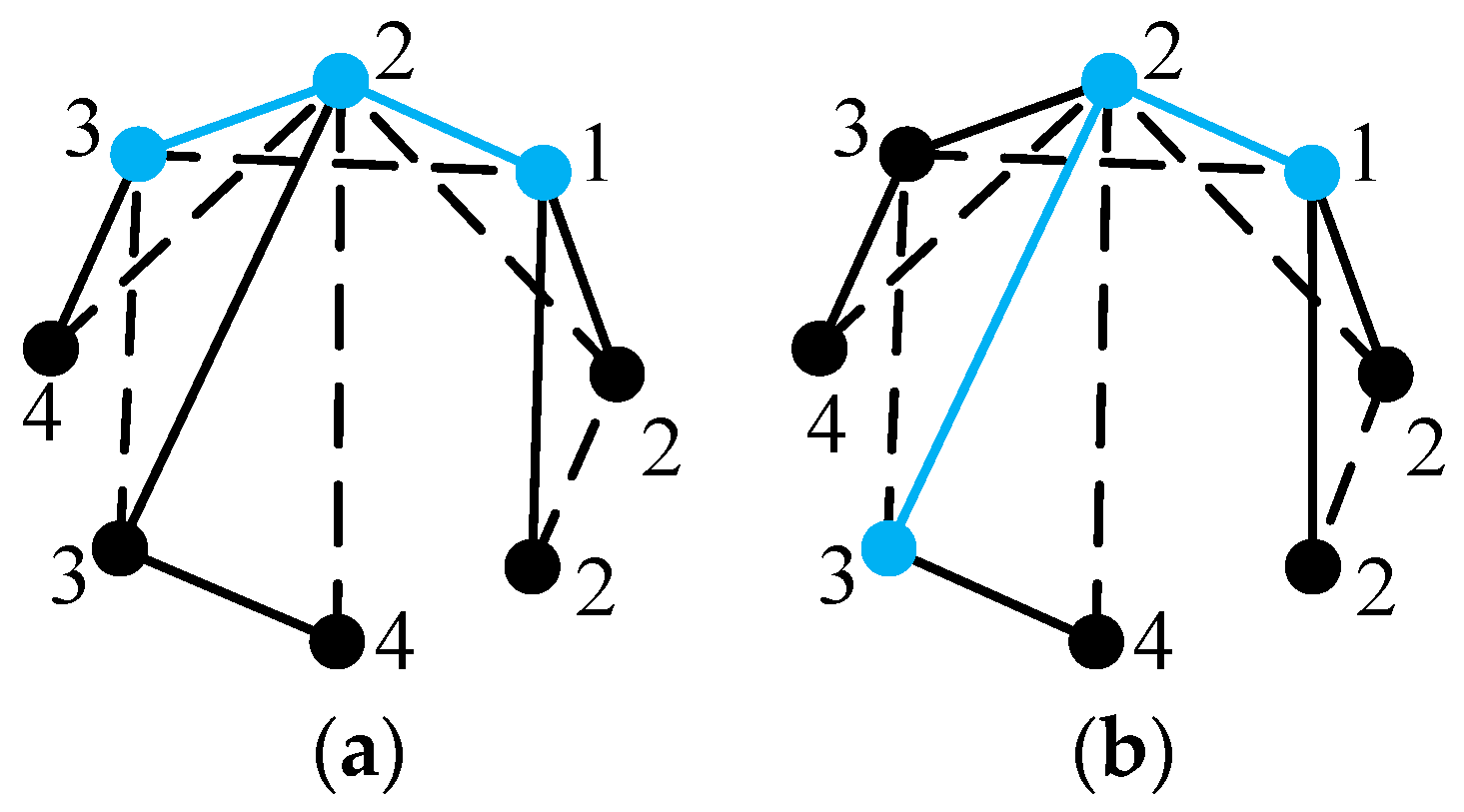
Figure 6a is used as an example to explain the isomorphism detection algorithm step by step.
Step 1. Determine all the vertices with degree larger than one. For example, the degrees of vertices 1 to 8 in
Figure 6a are 2, 2, 2, 1, 1, 1, 4, and 1, respectively. Vertices 1, 2, 3, and 7 have a degree larger than one.
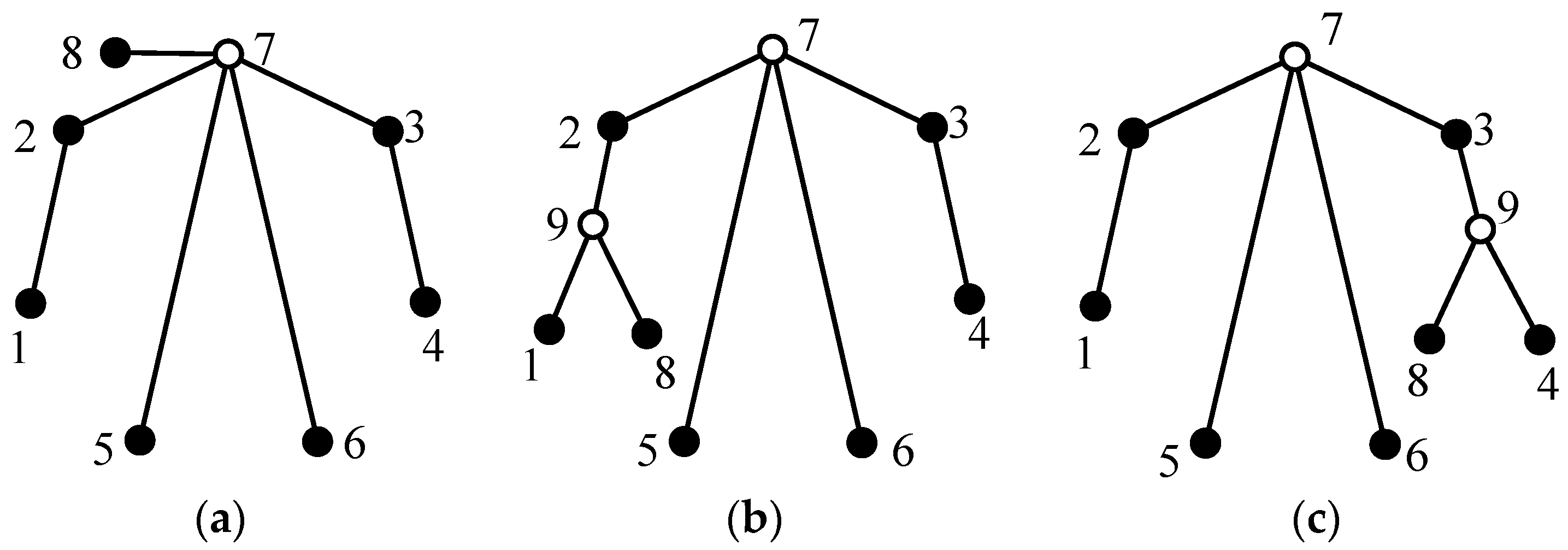
Step 2. Determine the longest path. Among the paths consisting of vertices with degree larger than one, the path with the largest number of vertices is the longest path. If there exists more than one path with the largest number of vertices, all these paths are selected as the longest paths. For example, both paths 1-2-7-3 and 3-7-2-1 in
Figure 6a are the longest paths, as shown in
Figure 13.
Step 3. Determine the main path. Degrees of vertices on the longest path are concatenated to form a vertex degree string, and the path with the largest vertex degree string is defined as the main path. If there exists more than one path with the largest vertex degree string, all these paths are selected as the main paths. For example, the degrees of vertices 1, 2, 3, and 7 in
Figure 6a are 2, 2, 2, and 4, respectively. Vertex degree strings of the longest paths 1-2-7-3 and 3-7-2-1 are 2242 and 2422, respectively. Obviously, the longest path 3-7-2-1 is the main path.
Step 4. Determine the labels of vertices on the main path. The previous labels of vertices in the tree graph are removed, and the
m vertices on the main path are relabeled as 1, 2, 3 …
m in order. For example, vertices 3, 7, 2, and 1 on the main path 3-7-2-1 in
Figure 6a are relabeled as 1, 2, 3, and 4, respectively, as shown in
Figure 14.
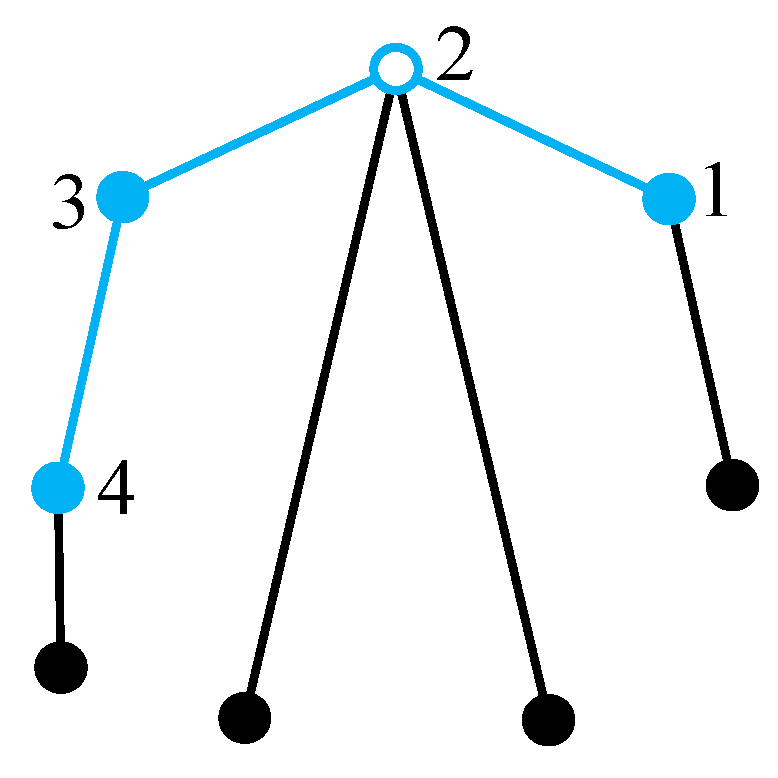
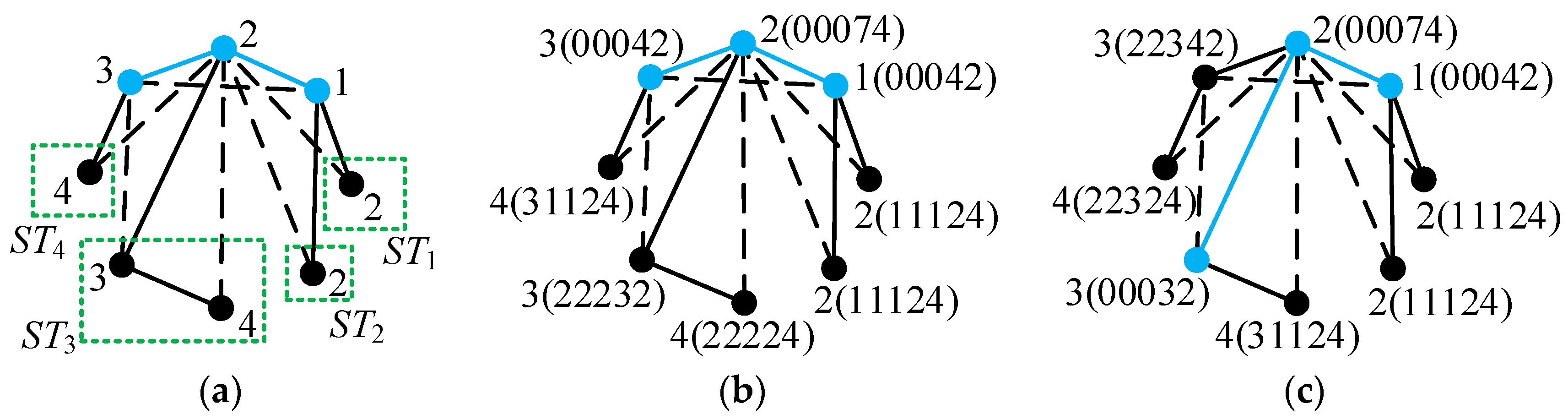
Step 5. Determine the labels of vertices not on the main path. First, for each vertex Vx not on the main path, its corresponding path Px is determined. The path begins at vertex Vx and ends at vertex Vs on the main path closest to vertex Vx. The number of vertices on path Px is denoted as t, and the label of vertex Vx is determined as Vs + t − 1.
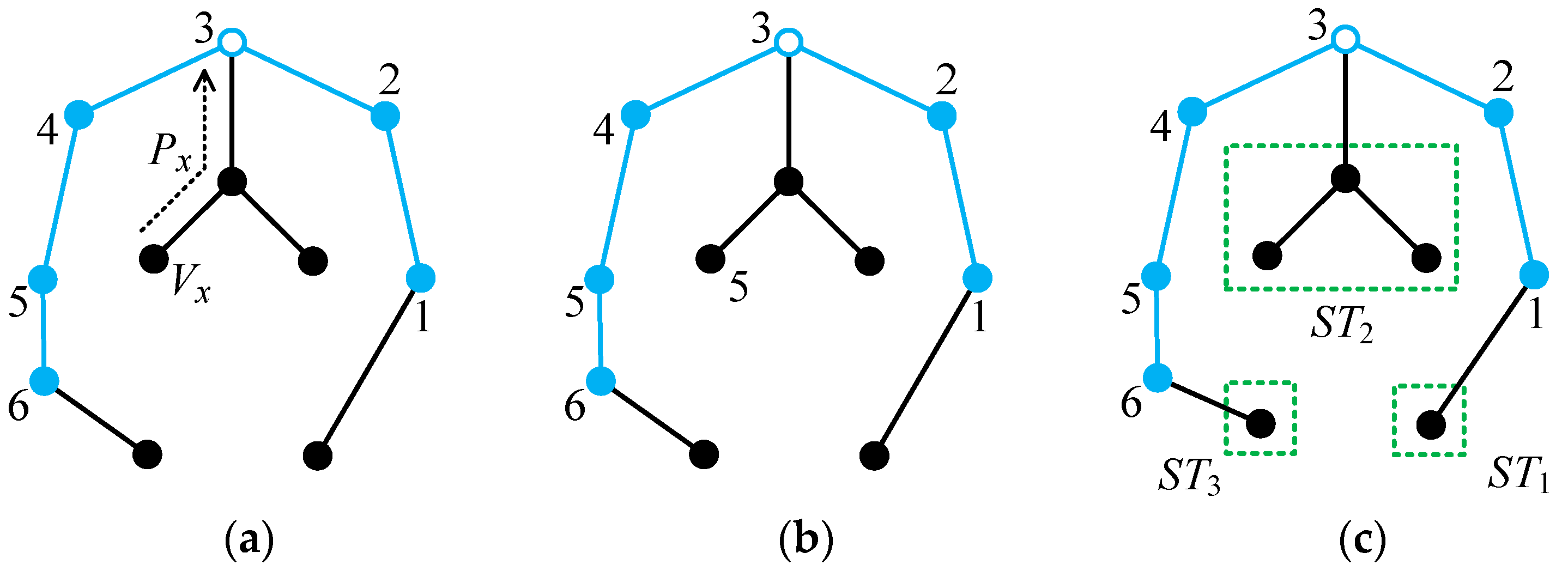
In order to clearly explain the above concept, the path
Px corresponding to vertex
Vx in an example 10-link tree graph is shown in
Figure 15a. This path begins at the vertex
Vx and ends at vertex 3 on the main path. The number of vertices on this path is
t = 3. Therefore, the label of vertex
Vx is
Vs +
t − 1 = 3 + 3 − 1 = 5, as shown in
Figure 15b. Continuing the example of
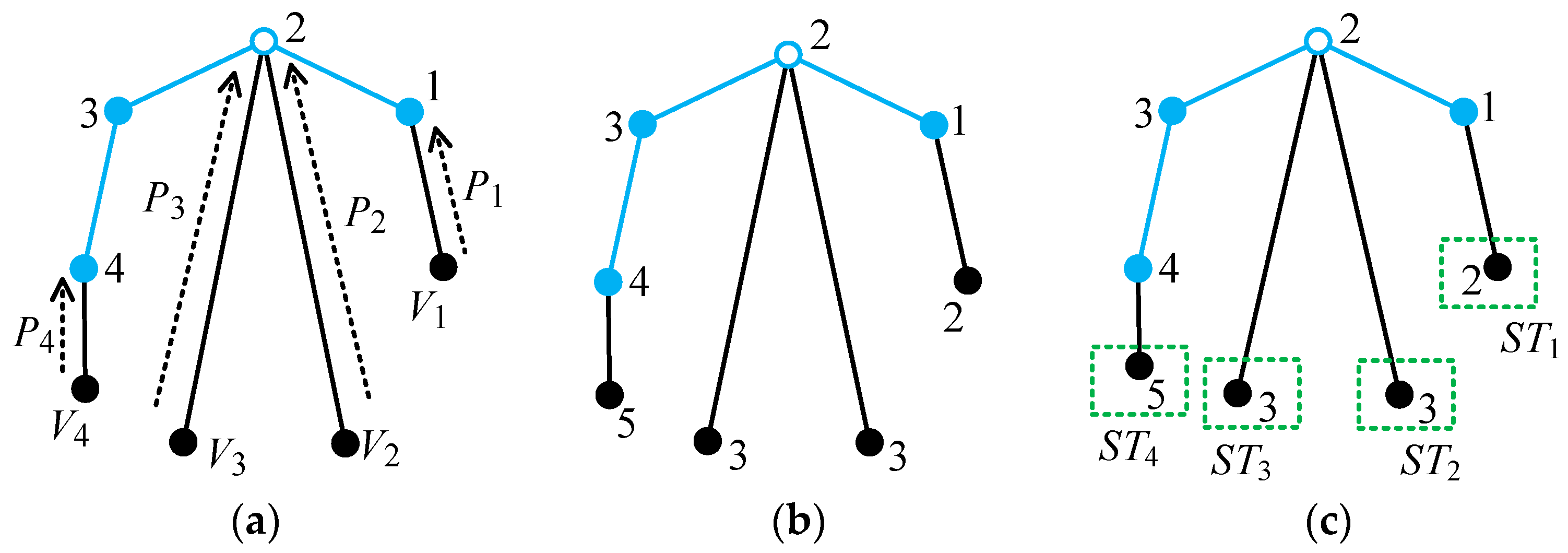
Figure 14, paths
P1,
P2,
P3, and
P4 corresponding to vertices
V1,
V2,
V3, and
V4 not on the main path are shown in
Figure 16a. Path
P1 begins at vertex
V1 and ends at vertex 1 on the main path. The number of vertices on path
P1 is
t = 2. Therefore, the label of vertex
V1 is
Vs +
t − 1 = 1 + 2 − 1 = 2. Similarly, the labels of vertices
V2,
V3, and
V4 are 3, 3, and 5, respectively, as shown in
Figure 16b.
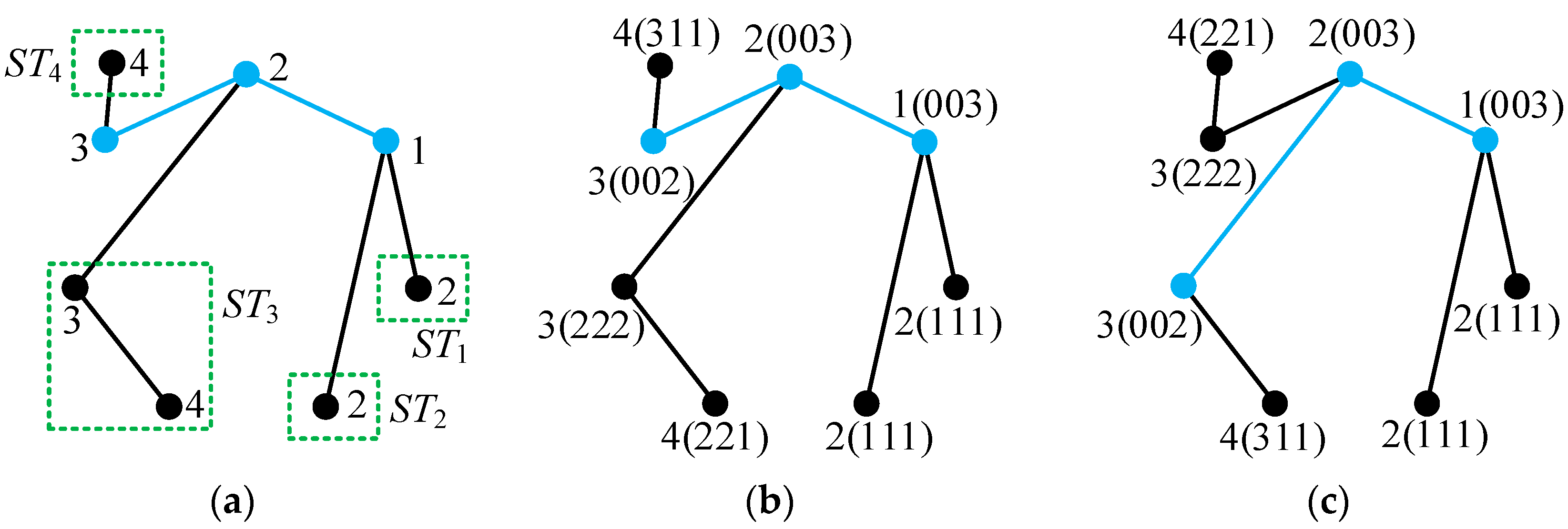
Step 6. Determine the codes of vertices in the given tree graph. For each vertex V in a tree graph, its code is formed by adding a suffix to its label. The suffix consists of three numbers enclosed in a parenthesis. The first number is the label of vertex on the main path closest to vertex V. If vertex V is on the main path, the first number is 0. The second number is the number of vertices in the sub-tree containing vertex V. If vertex V is on the main path, the second number is 0. The third number is the degree of vertex V.
Definition of a sub-tree. A sub-tree is a tree consisting of the vertices not on the main path and the edges connecting these vertices, and this tree is connected to a vertex on the main path. For
Figure 15a, the three sub-trees
ST1,
ST2, and
ST3 connected to vertices 1, 3, and 6 on the main path are marked with dashed boxes and shown in
Figure 15c. Sub-trees
ST1 and
ST3 are the special trees containing only one vertex, and sub-tree
ST2 contains three vertices. For
Figure 16b, four sub-trees
ST1,
ST2,
ST3, and
ST4 connected to vertices 1, 2, and 4 on the main path are marked with dashed boxes and shown in
Figure 16c, and each sub-tree contains only one vertex.
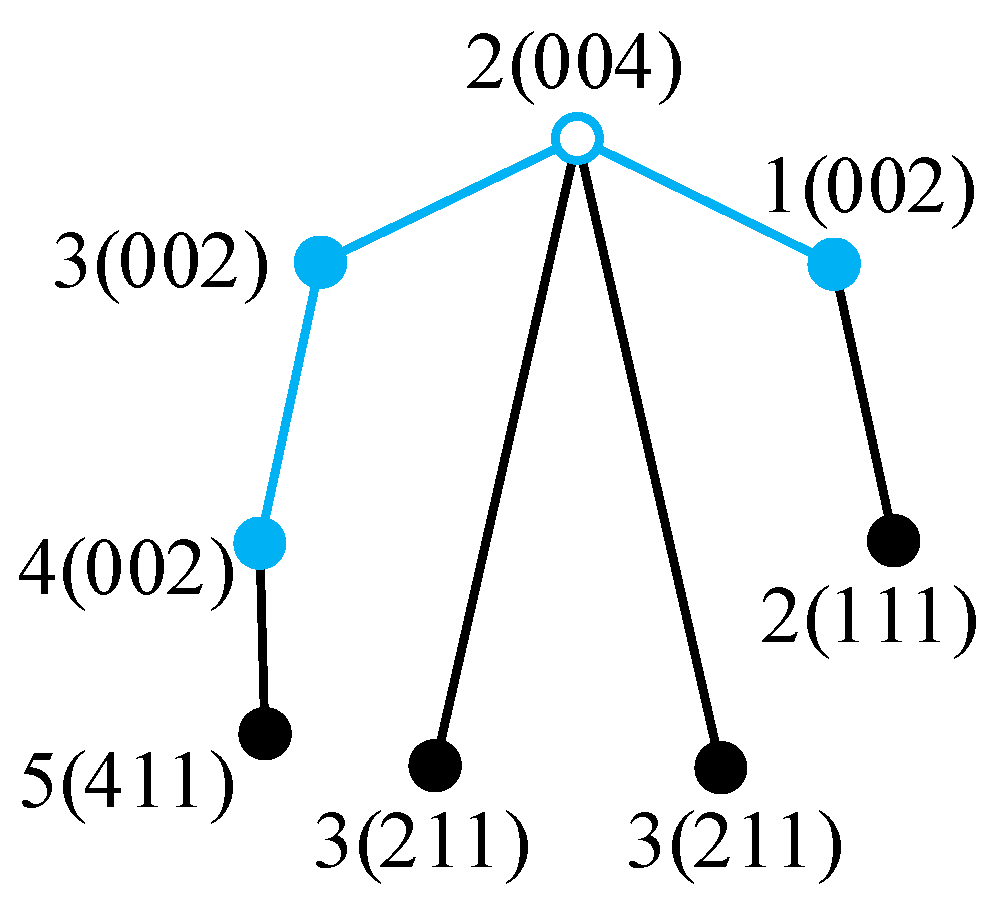
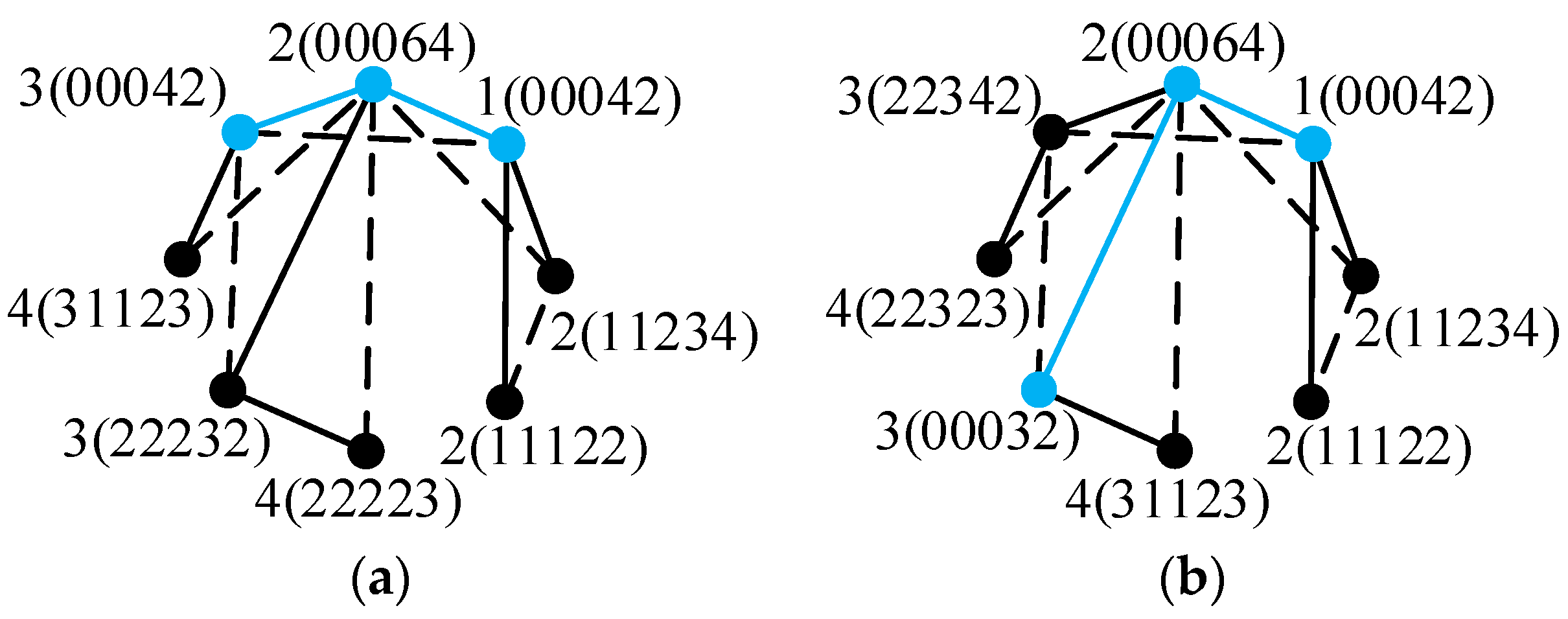
Codes of vertices in
Figure 16b are obtained as follows. For vertex 1 on the main path in
Figure 16b, the first and second numbers of the suffix of its code are 0. The degree of vertex 1 is 2; hence, the third number of the suffix is 2. The code of vertex 1 is obtained as 1(002). Similarly, the codes of vertices 2, 3, and 4 on the main path in
Figure 16b are 2(004), 3(002), and 4(002), respectively. There are two vertices 3 not on the main path in
Figure 16b, and both are connected to vertex 2 on the main path; hence, the first number of the suffix is 2. These two vertices 3 are in sub-trees
ST2 and
ST3 containing only one vertex; hence, the second number of the suffix is 1. The degree of these two vertices 3 is 1; hence, the third number of the suffix is 1. The codes of these two vertices 3 are obtained as 3(211). Similarly, the codes of vertices 2 and 5 not on the main path in
Figure 16b are 2(111) and 5(411), respectively. The codes of all the vertices in
Figure 16b are shown in
Figure 17.
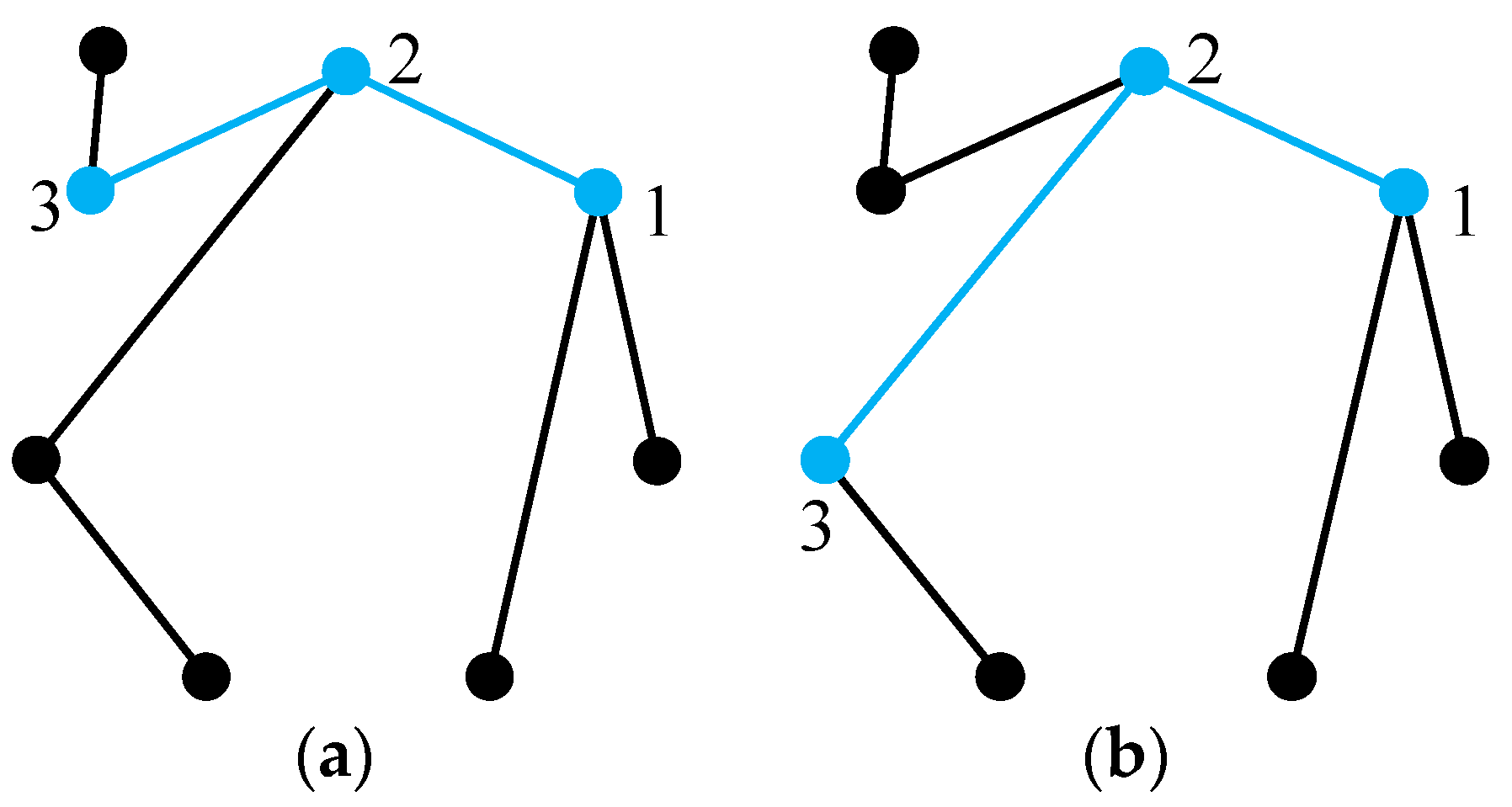
Step 7. Relabel the vertices in the given tree graph. According to the ascending order of vertex codes,
n vertices in the tree graph are relabeled as 1, 2, 3 …
n in sequence. If there exists more than one vertex with the same code, these vertices are permuted to obtain all possible ways of relabeling. For example, the codes of vertices in
Figure 17 are arranged in ascending order as 1(002), 2(004), 2(111), 3(002), 3(211), 3(211), 4(002) and 5(411). Two of these vertex codes are 3(211); hence, the number of ways to relabel vertices in
Figure 17 is
, as shown in
Figure 18.
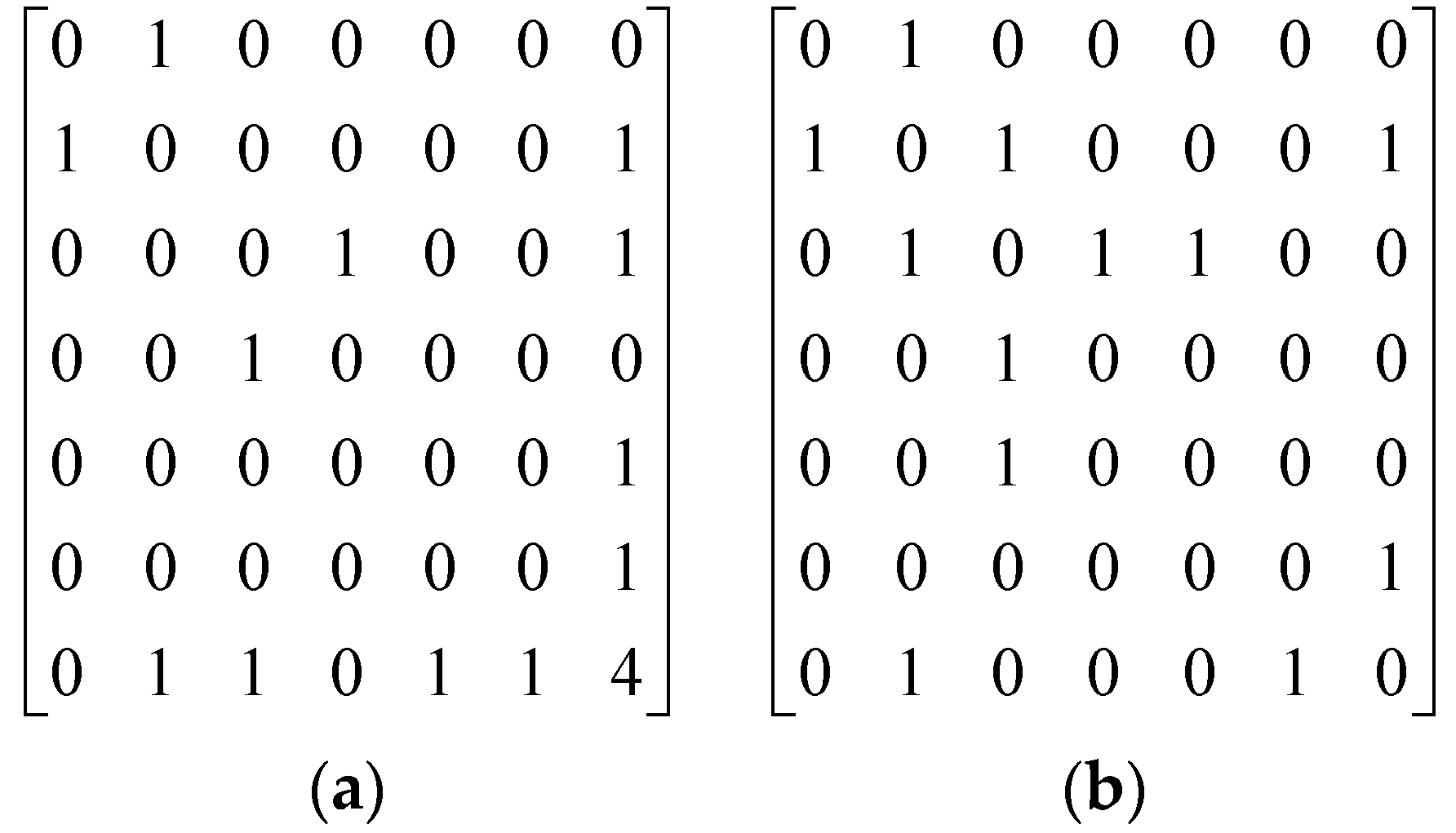
Step 8. Determine the characteristic code (c-code) of the given tree graph and carry out the task of isomorphism detection. The numerical code formed by concatenating the upper triangular elements (including diagonal elements) in the adjacency matrix of a relabeled tree graph is defined as its tree-code, and the largest tree-code is defined as the c-code of the given tree graph. The detection of isomorphic tree graphs is carried out by comparing their c-codes. Isomorphic tree graphs have the same c-code, and non-isomorphic tree graphs have different c-codes.
For example, the process of obtaining the tree-code of
Figure 18a is shown in
Figure 19, and the derived tree-code of
Figure 18a is C
a = 01100000-4011100-000000-00010-0000-000-01-0. Similarly, the tree-code of
Figure 18b can be acquired as C
b = 01100000-4011100-000000-00010-0000-000-01-0. By definition, the larger tree-code is the c-code of the tree graph in
Figure 6a. Because C
a is the same as C
b, tree-code C
a = 01100000-4011100-000000-00010-0000-000-01-0 is taken as the c-code of
Figure 6a. Similarly, c-codes of all the tree graphs in
Figure 6 and
Figure 7 are determined and shown in
Table 2. The c-codes of the tree graphs in
Figure 6a,d are the same; hence, the tree graphs in
Figure 6a,d are isomorphic. Similarly, the tree graphs in
Figure 6b and c are isomorphic, the tree graphs in
Figure 6e,f are isomorphic, and the tree graphs in
Figure 7b,c are isomorphic. Therefore, only five of the nine tree graphs in
Figure 6 and
Figure 7 are non-isomorphic, which means that five non-isomorphic seven-link tree graphs can be generated from the six-link tree graph in
Figure 4a.
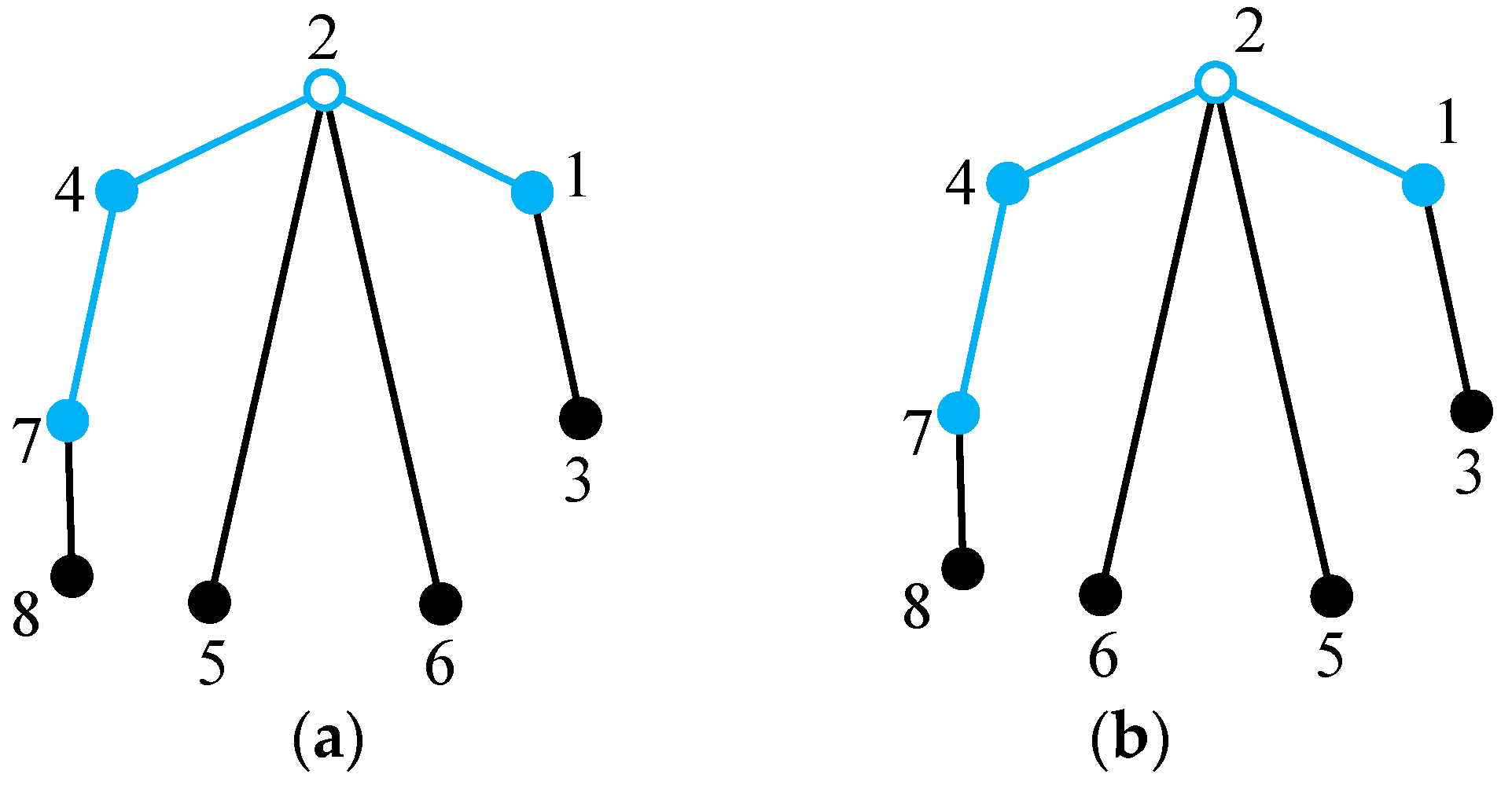
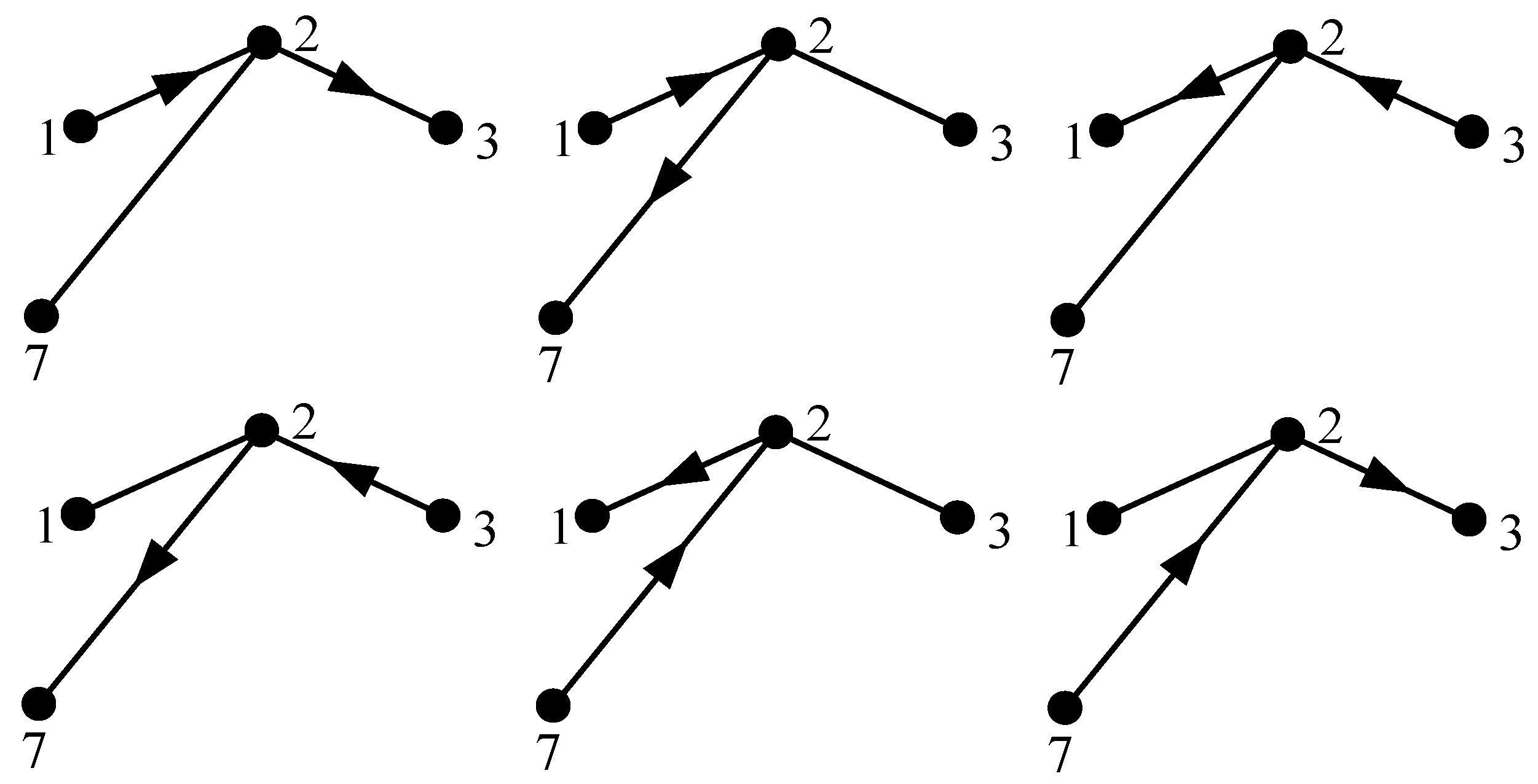
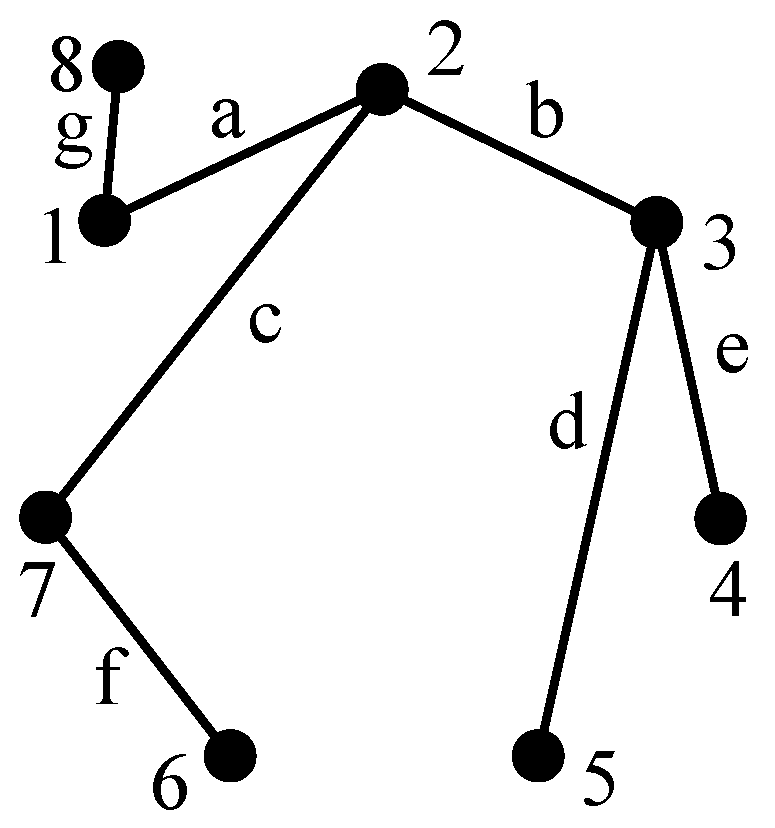
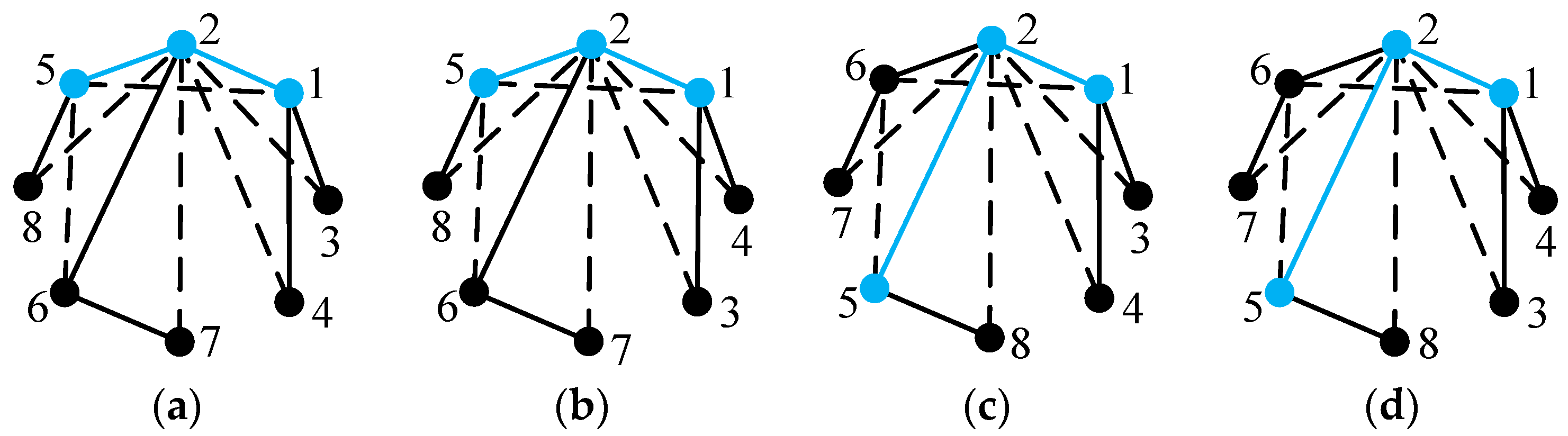
The present isomorphism detection algorithm is also applicable for tree graphs without any hollow vertex. Taking
Figure 8a for instance, vertices 1, 2, 3, and 7 have the degree larger than one; hence, six longest paths 1-2-3, 1-2-7, 3-2-1, 3-2-7, 7-2-1, and 7-2-3 can be acquired, as shown in
Figure 20. The vertex degree strings of paths 3-2-1 and 3-2-7 are both 332, which is larger than those of the other paths. Hence, paths 3-2-1 and 3-2-7 are determined as the main paths. For the main path 3-2-1, vertices 3, 2, 1 are labeled as 1, 2, 3, respectively, as shown in
Figure 21a. Similarly, the labels of vertices on the main path 3-2-7 are shown in
Figure 21b. Paths
P1,
P2,
P3,
P4, and
P5 corresponding to vertices
V1,
V2,
V3,
V4, and
V5 not on the main path in
Figure 21a are shown in
Figure 22a. Taking path
P3 for instance, path
P3 begins at vertex
V3 and ends at vertex 2 on the main path, and the number of vertices on path
P3 is
t = 3. Therefore, the label of vertex
V3 is
Vs +
t − 1 = 2 + 3 − 1 = 4. Similarly, the labels of vertices
V1,
V2,
V4 and
V5 in
Figure 22a are 2, 2, 3, and 4, respectively, as shown in
Figure 22b, and the labels of vertices not on the main path in
Figure 21b are shown in
Figure 22c.
For vertex 1 on the main path in
Figure 22b, the first and second numbers of the suffix of its code are 0. The degree of vertex 1 is 3; hence, the third number of the suffix is 3. The code of vertex 1 is obtained as 1(003). Similarly, the codes of vertices 2 and 3 on the main path are 2(003) and 3(002), respectively. The four sub-trees
ST1,
ST2,
ST3, and
ST4 in
Figure 22b are shown in
Figure 23a. Taking vertex 3 not on the main path in
Figure 22b for instance, it is connected to vertex 2 on the main path; hence, the first number of the suffix of its code is 2. Sub-tree
ST3 contains two vertices; hence, the second number of the suffix is 2. The degree of vertex 3 is 2; hence, the third number of the suffix is 2. Therefore, the code of vertex 3 not on the main path in
Figure 22b is 3(222). Similarly, the codes of all the vertices in
Figure 22b can be determined, as shown in
Figure 23b. The codes of all the vertices in
Figure 22c are shown in
Figure 23c. The codes of vertices in
Figure 23b are arranged in ascending order as 1(003), 2(003), 2(111), 2(111), 3(002), 3(222), 4(221), and 4(311). Two of these vertex codes are 2(111); hence, the number of ways to relabel vertices in
Figure 23b is
, as shown in
Figure 24a,b. Similarly, the number of ways to relabel vertices in
Figure 23c is also
, as shown in
Figure 24c,d. All the tree-codes of the tree graphs in
Figure 24 are 01110000-0001100-000000-00000- 0001-010-00-0; hence, the c-code of the tree graph in
Figure 8a is acquired as 01110000-0001100-000000-00000-0001-010-00-0.
Similarly, the c-codes of all the tree graphs in
Figure 8 and
Figure 9 can be acquired, as shown in
Table 3. According to the data in this table, the tree graphs in
Figure 8d,e are isomorphic and the tree graphs in
Figure 9d,e are isomorphic. Therefore, eleven of the thirteen tree graphs in
Figure 8 and
Figure 9 are non-isomorphic, which means that eleven non-isomorphic eight-link tree graphs can be generated from the seven-link tree graph in
Figure 4b.
(
N + 1)-link tree graphs generated from isomorphic
N-link tree graphs are also isomorphic. All isomorphic tree graphs can be eliminated by applying the present isomorphism detection algorithm to the process of generating tree graphs in
Section 3.1, and the atlas of non-isomorphic tree graphs can be obtained. As is well known, there exists only one three-link tree graph, from which five four-link tree graphs can be generated, as shown in
Figure 10. After eliminating isomorphism, three non-isomorphic four-link tree graphs can be obtained, as shown in
Figure 25. All feasible five-link tree graphs can be generated from these non-isomorphic four-link tree graphs, and eight non-isomorphic five-link tree graphs can be obtained after eliminating isomorphism, as shown in
Figure 26. All feasible six-link tree graphs can be generated from these non-isomorphic five-link tree graphs, and 21 non-isomorphic six-link tree graphs can be obtained after eliminating isomorphism, as shown in
Figure 27. Similarly, all non-isomorphic seven-, eight-, nine-, and ten-link tree graphs can be obtained in turn. For example, part of the non-isomorphic 10-link tree graphs are shown in
Figure 28. We have developed a computer program to automatically synthesize the compete atlas of tree graphs. The synthesis results of tree graphs are shown in
Table 4. Because the adjacency matrix of a tree graph is symmetric, only the upper triangular elements of the adjacency matrices of tree graphs are stored in the database. The complete database of tree graphs with three to ten links is available at Mendeley Data. Readers can download the database by visiting the URL “
https://doi.org/10.17632/kt77nz942x.1”.