Abstract
As ice-like crystals and non-stoichiometric compounds comprising gas and water, natural gas hydrates have drawn significant attention as a potential alternative energy source. This work focuses on holistically reviewing theoretical modeling and numerical studies conducted on the production of gas from natural gas hydrates. Firstly, fundamental models for the dissociation of a hydrate in a porous sediment are summarized in terms of the phase equilibrium and dissociation kinetics. The main features of different models and improvements for them are identified by clarifying crucial driving mechanisms and kinetic parameters. Subsequently, various numerical works addressing the dissociation of a hydrate in a porous sediment and the flow characteristics in a wellbore are reviewed, including aspects such as the theoretical background, computational scheme, and the physics involved. In general, profiting from a significant capacity to solve nonlinear differential equations, numerical simulations have contributed to great progress in fundamentally understanding the mechanism driving gas production and in developing effective exploitation methods. Owing to the substantial fundamental physics involved in the exploitation of natural gas hydrates, existing challenges, alternative strategies, and future directions are provided correspondingly from a practical application perspective.
1. Introduction
Known as combustible ice, natural gas hydrates are ice-like crystals and non-stoichiometric compounds comprising gas and water [1]. Gas molecules (such as ethane, methane, and carbon dioxide) are enclosed by hydrogen-bonded water molecules. Because of their need for high-pressure and low-temperature environments, natural gas hydrates are commonly found and distributed in subsea sediments and permafrost zones [2,3]. Compared with fossil fuels, natural gas hydrates present a series of advantages, such as rich reserves, low levels of pollution, and high energy densities and have consequently drawn significant attention as a potential alternative energy source [4]. Since the first report by Davy [5], several countries have achieved great progress in exploring trial production techniques [6,7,8,9]. In particular, the China Geological Survey recently carried out a secondary trial production in the Shenhu Sea Area of the South China Sea, and continuous production for 30 days was successfully achieved with a total gas output of 861,400 m3 and the daily production of 28,700 m3 of gas [9]. The production feasibility of natural gas hydrates was further confirmed for commercial development in the future.
It has been determined that more than 95% of the total hydrate reserves are focused in deep subsea areas [10]. As a complex compound, the formation of a natural gas hydrate at the microscopic scale is a time-dependent kinetic, time-independent thermodynamic, and statistically random process and is strongly related to the specific environment it occurs in [11,12]. Once crystal embryos are formed, intrinsic kinetics, as well as heat and mass transfer in a separate or coupled manner, drive the hydrates’ growth. With continuous efforts in the last two centuries, the underlying basic physics of the nucleation and growth kinetics of gas hydrates has been comprehensively and systemically elucidated with great progress, guiding significant advances in engineering exploitation and utilization with the controllable formation and growth of hydrates [12].
Currently, various methods of exploitation, such as depressurization, solid fluidized mining, thermal stimulation, and the injection of chemical additives, are being proposed to exploit natural gas hydrates [7,8,9,13,14]. By continuously supplying artificial heat to the hydrate reservoir, thermal stimulation is utilized to modify the reservoir’s thermodynamic conditions and consequently provoke the dissociation of hydrates [8]. The method of injecting chemical additives aims to shift the hydrate’s phase equilibrium and achieve hydrate dissociation under local pressure–temperature conditions [13,14]. Among these methods, the depressurization method presents great development potential due to its economical and effective advantages and has been successfully used in record production tests conducted by the China Geological Survey [9], as illustrated in Figure 1. In this method, a downhole electric submersible pump in the production well is utilized to reduce the pressure of the hydrate reservoir close to the wellbore. The pressure variation causes the dissociation of the solid hydrate, resulting in the production of gas [15,16,17]. On the one hand, a controllable pressure difference is crucial to maintaining stable and efficient production. Real production commonly involves fluctuating production rates of gas and water [18]. On the other hand, in real production systems, a multiphase, multicomponent flow composed of soil particles, hydrate particles, gas, and water can remarkably influence the reservoir and wellbore pressure [15,19]. During production, the flow system is simultaneously accompanied by the growth, fragmentation, and aggregation of hydrate particles [20,21]. Therefore, an understanding of gas–liquid–solid multiphase flow characteristics coupled with the nucleation and growth kinetics of hydrate particles is crucial for developing a controllable technique of exploiting natural gas hydrates.
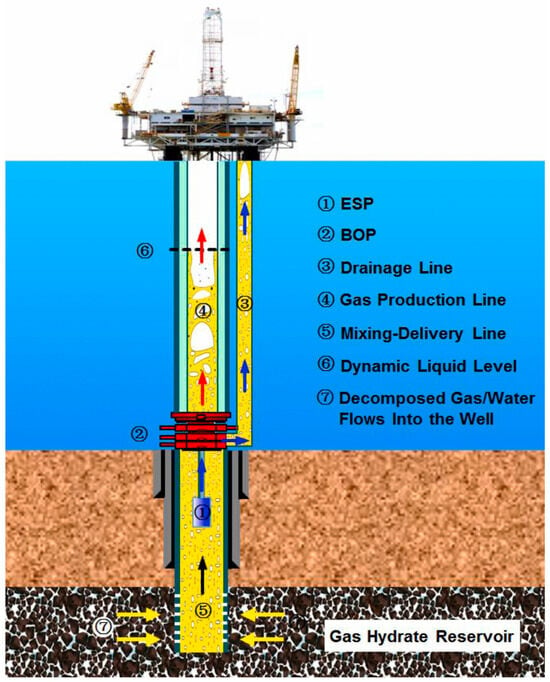
Figure 1.
An illustration of a marine production system using the depressurization method for natural gas hydrates [15]. ESP: electric submersible pump; BOP: blowout preventer.
In general, the exploitation of natural gas hydrates involves extensive basic issues, such as dissociation kinetics, thermodynamics, multi-scale characterization, heat and mass transfer, and multiphase–multicomponent flows [12,15,21,22]. These issues are strongly coupled with each other and simultaneously define production factors and efficiency. Because of a lack of complex geologic parameters and real production data, modeling and numerical investigations play crucial roles in the exploitation of natural gas hydrates and facilitate exciting progress in understanding the physical mechanism from the system scale to the laboratory scale [22,23]. However, due to the extreme complexity of this theme, existing modeling and numerical investigations are commonly implemented with excessive assumptions and simplifications which significantly deviate from realistic exploitation conditions. Hence, from the perspective of realistic exploitation, this review focuses on holistically summarizing theoretical modeling and numerical studies conducted on the production of gas from natural gas hydrates, including fundamental models of natural gas hydrates (such as phase equilibrium and dissociation kinetics models) and a numerical model of the dissociation of a hydrate in a porous sediment and the flow characteristics in a wellbore. The mechanistic understanding, model development, and a numerical scheme with key issues and a knowledge of gas are reviewed and discussed for their application in realistic exploitation. Finally, existing challenges, alternative strategies, and future directions are correspondingly provided to promote efficient production strategies.
2. Fundamental Models for Natural Gas Hydrates
2.1. The Equilibrium of Natural Gas Hydrates
High-pressure and low-temperature environments are crucial for the stable existence of natural gas hydrates. The thermodynamic equilibrium characteristics of natural gas hydrates could dictate critical pressure and temperature information for the formation and dissociation of hydrates and dissociation and can be consequently seen as the most fundamental and primary issue for hydrate exploitation. Modeling efforts from the perspective of thermodynamic dynamics have been continuously devoted to exploring the equilibrium characteristics of natural gas hydrates [22,24]. Significantly, Van der Waals and Platteeuw [25] first developed a classical chemical potential model for a hydrate–water system and predicted the equilibrium pressures for various gases. Subsequently, various equilibrium models were proposed on the basis of the van der Waals–Platteeuw model [26,27]. Subsequently, with the consideration of hard-sphere repulsion, hard-chain formation, dispersion, and association, Li et al. [28] utilized an equation of state based on the statistically associating fluid theory to consider the thermodynamically inhibiting effects of various gases on the formation of gas hydrates. The predicted equilibrium conditions were found to have excellent agreement with the measured results. Chen and Guo [29] first proposed a two-step formation mechanism with a quasi-chemical reaction process for a basic hydrate as a first step and the process of the absorption of gas molecules in the linked cavities as a second step. Based on this novel mechanism, they proposed a simple equilibrium model by combining the chemical reaction and physical absorption equilibrium. The model’s accuracy was verified by obtaining substantial measurements for different pure gases and mixtures. Generally, various equilibrium models have been developed successfully and provide accurate predictions for the equilibrium characteristics of bulk hydrates [30].
It should be noted that the environment of the porous media in a real hydrate deposit is a crucial issue for the equilibrium conditions of hydrates. Hence, considerable efforts have been made to develop thermodynamic models for the equilibrium of hydrates in porous media. Based on the van der Waals–Platteeuw model, Clarke et al. [31] introduced the Kelvin equation to consider the capillary effect and realized a prediction of hydrate equilibrium conditions in porous media. Following the same approach, the Gibbs–Thomson equation was used to define the capillary effect [32]. Notably, based on equal fugacities and equal activities, Li et al. [33] proposed two thermodynamic methods for predicting hydrate equilibrium conditions in porous media. The Trebble–Bishnoi equation and the Soave–Redlich–Kwong equation were employed in the fugacity and activity approaches for the non-hydrate phase, respectively. The hydrate phase was considered by combining the van der Waals–Platteeuw model and the capillary model in these two approaches. Furthermore, substantial improvements, such as a realistic distribution of pore size [34] and the introduction of a contact angle model [35], were carried out to provide an accurate prediction.
In conclusion, modeling progress makes it practicable to fundamentally reveal the underlying equilibrium characteristics of natural gas hydrate deposits and define hydrate dissociation conditions when designing an exploitation strategy. However, investigations of hydrate equilibrium are still far from completed because of the complex geological conditions of the hydrate reservoir and the variable coexistence of hydrates. High-accuracy thermodynamic models which consider the realistic effect of the porous media are highly desirable for the accurate determination of hydrate equilibrium conditions.
2.2. Dissociation Kinetics of Natural Gas Hydrates
The nucleation, growth, and dissociation of natural gas hydrates commonly occur in porous media and depend not only on the temperature and pressure but also the characteristics of the porous media [1,3]. Multiple physics processes, i.e., heat and mass transfer, multi-component, multi-phase fluid flow, and intrinsic kinetics, strongly interact with the porous media during the nucleation, growth, and dissociation of the hydrate [22,24,36]. It is equally important to establish systematic understanding in the form of a complete circle, i.e., nucleation–growth–dissociation. It should be noted that the current work aims to summarize modeling and numerical investigations for the exploitation of natural gas hydrates. Hence, the production of gas from natural gas hydrates, namely the dissociation of the hydrates, is specially focused on. Understanding the dissociation kinetics of natural gas hydrates is essentially important to progressing the production of natural gas hydrates. On the small/experimental scale, early studies mainly focused on exploring the dissociation kinetics of natural gas hydrates in a bulk system [37]. A stirred semi-batch tank reactor was used to sustain isothermal and isobaric conditions. It was experimentally demonstrated that the kinetics of a hydrate are remarkably affected by the bulk temperature, pressure, supercooling, and gas–water contact area [38]. The available kinetic models were developed on the basis of the two-film theory and crystallization [39]. Further modeling investigations demonstrated that the intrinsic dissociation kinetics governed by pressure, temperature, the interfacial area, and the intrinsic rate constant significantly dominate gas production [40,41].
In comparison with the case of the bulk system, dissociation kinetics in porous media are more practical and complicated. Substantial efforts have been continuously devoted to developing a comprehensive model by coupling all the primary physics through the porous media, including the heat and mass transfer, multi-component, multi-phase fluid flow, and intrinsic dissociation kinetics [42,43]. Different models which consider several of or either of these physics under different conditions were developed, achieving great progress in understanding the dissociation kinetics of natural gas hydrates in porous media, as summarized in Table 1. In 1987, Kim et al. [40] carried out an experimental investigation to determine the dissociation kinetics of a methane hydrate with the help of a semi-batch stirred-tank reactor. Hydrate dissociation was achieved by reducing the pressure of the hydrate slurry in a pure water system under an isothermal condition. The Kim–Bishnoi intrinsic kinetic model was correspondingly proposed, considering the intrinsic dissociation kinetics for the first time [40]. Neglecting the heat and mass transfer, the hydrate dissociation was simplified into two steps, namely the destruction of the clathrate lattice and the desorption of gas on the particle’s surface, as illustrated in Figure 2. Accordingly, the difference in fugacity between the gas and the hydrate’s solid phases at equilibrium was solely defined as the driving force for the dissociation. The Kim–Bishnoi model correspondingly constructed a proportional relationship between the dissociation rate and the interfacial area and the intrinsic rate constant. As the most fundamental and classical model for understanding the kinetics of hydrate dissociation, the Kim–Bishnoi model is continuously improved and extended to consider the effects of particle size [44] and mixed gases [45,46].
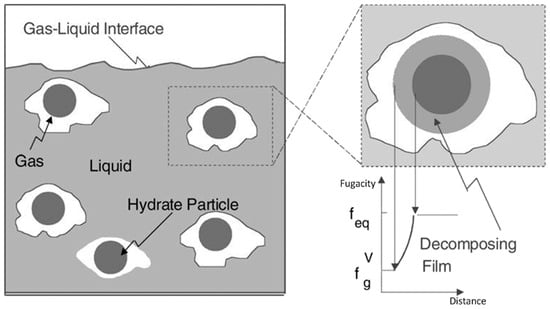
Figure 2.
An illustration of the mechanism of the dissociation of a hydrate in abulk system [42,43]. The driving force of the dissociation is defined as the difference, feq-feqv, between the fugacity of the gas at the equilibrium (feq) and the fugacity of the gas at the solid surface (feqv).
Another classical dissociation model considering thermal stimulation was proposed by Selim and Sloan [36]. The distribution of the hydrate in the porous media is seen as a one-dimensional and planar, semi-infinite system with constant physical properties, as illustrated in Figure 3. Initially, a constant heat flux is imposed on the hydrate’s surface to increase its temperature to the equilibrium temperature. Subsequently, dissociation happens with a moving front along the positive x direction, and the moving surface is constantly maintained at the equilibrium temperature. With an assumption that the formed water phase is fully removed during dissociation due to gas purging, the dissociation of the hydrate is simplified into a problem of moving-boundary ablation at a constant heat flux, and heat transfer with constant physical properties is considered for the hydrate bulk. The system is consequently divided into two regions, namely the dissociated region containing the water and gas phases as well as the undissociated region containing the solid hydrate. Based on the measurements, the reliability of the Selim–Sloan model has been validated [47]. Although the intrinsic dissociation kinetics and mass transfer are neglected, the Selim–Sloan model provides a feasible method for studying heat transfer within the porous media and dissociation front.
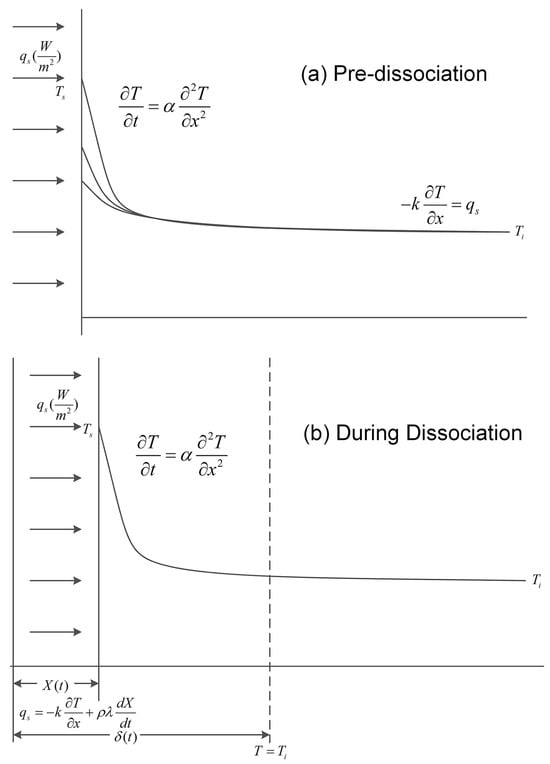
Figure 3.
An illustration of the dissociation of a hydrate treated as a moving-boundary ablation problem [36,42]. The bulk of the hydrate is assumed to be in the semi-infinite zone with 0 < x< ∞ along the x-axis. In the pre-dissociation stage, a fixed heat flux qs is imposed on the hydrate’s surface x = 0. During the dissociation, on the y-axis, the hydrate’s temperature Ti will be gradually raised to the equilibrium temperature at the hydrate’s surface Ts.

Table 1.
Summary of dissociation kinetics models of gas hydrates.
Table 1.
Summary of dissociation kinetics models of gas hydrates.
| Authors | Heat Transfer | Intrinsic Kinetics | Fluid Flow | Porous Media | Model Approach |
|---|---|---|---|---|---|
| Kim et al. [40] | — | √ | — | — | Analytical |
| Selim and Sloan [36] | √ | — | √ | √ | Analytical |
| Jamaluddin et al. [48] | √ | √ | — | — | Numerical |
| Yousif et al. [49] | — | √ | √ | √ | Numerical |
| Hong et al. [50,51] | √ | √ | √ | √ | Analytical |
| Li and Zhang [52] | √ | — | — | √ | Analytical |
Subsequently, various dissociation kinetic models were developed considering dissociation mechanisms [42]. By coupling the Kim-Bishnoi model and the Selim–Sloan model, Jamaluddin et al. [48] developed a kinetic model which considers both heat transfer and the intrinsic kinetics. Following the Kim–Bishnoi model, the dissociation rate of the hydrates was defined in the form of the intrinsic kinetic rate, which was coupled with the heat transfer solution, following the Selim–Sloan model. This model guided the coupling of different dissociation regimes. For the first time, Yousif et al. [49] developed a one-dimensional, three-phase model for the production of gas using a depressurization approach which significantly considers the flow of the fluid in porous media by embedding Darcy’s equation into the mass and energy equations. Linearization and iterative solutions were carried out for these nonlinear conservation equations. Significantly, Hong et al. [50,51] proposed a simple analytical model for the dissociation of a hydrate in porous media using the depressurization method. Referring to the real conditions of a hydrate reservoir, three primary regimes, including heat transfer, fluid flow within the porous media, and intrinsic dissociation kinetics, were comprehensively considered in this model [50]. Heat transfer in the hydrate region was treated as a melting boundary problem. The intrinsic dissociation kinetic was solved following the Kim–Bishnoi model. The gas–water two-phase flow within the porous media was incorporated using Darcy’s law. At the dissociation interface, a mass balance was employed to implement the coupled solution. Recently, considering the self-similarity characteristics of the porous sediment, Li and Zhang [52] used a fractional number to define the irregular geometry of the hydrate particles and proposed a fractional shrinking-core model which referred to a shrinking-core dissociation process of the hydrate in the porous media, as illustrated in Figure 4a,b. One significant feature of this model is the introduction of a fractal analysis which can eliminate mathematic iteration and self-replication.
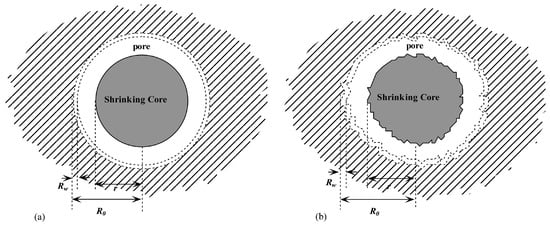
Figure 4.
An illustration of the fractal-dimension shrinking-core model with the radius of unreacted core r, the averaged core radius of the porous media R0, and the thickness of the bound water layer Rw [52].
Apart from macroscopic modeling studies, molecular dynamic (MD) simulations have been widely utilized as effective tools for studying the dissociation kinetics of natural gas hydrates at the microscopic molecular level [42]. MD simulations can depict the dissociation kinetics of natural gas hydrates occurring at the nanometer and nanosecond scales, which is greatly challenging to achieve via the experimental methods. Substantial MD studies have been carried out to simulate hydrate dissociation, including the successive dissociation mechanisms, coupled heat and mass transfer during dissociation, and the formation dynamics of nanobubbles. Using the MD method, Ding et al. [53] numerically studied hydrate dissociation at the microscopic molecular level. It was found that hydrate dissociation occurs in two successive stages. The first stage refers to the diffusion process of the host molecules which is responsible for the fracture of the lattice structure. The second stage corresponds to the escape of methane molecules from the cavities and aggregate. This two-step dissociation mechanism remains consistent with previous work by Kim et al. [40]. Bagherzadeh and his coworkers [54,55] carried out an MD simulation to quantify the dissociation rate of a hydrate under non-equilibrium conditions and the dissociation rate of a hydrate in contact with a silica surface. Via MD simulations, Bai et al. [56] demonstrated that during dissociation, the coupling of heat and mass transfer resistance in the solid-like layer of water on the hydrate’s surface plays a dominant role in the self-preservation effect. Recently, Bagherzadeh et al. [57] carried out MD simulations, aiming to study the formation conditions of methane nanobubbles and to clarify the influence of nanobubbles on the dissociation rate.
Although various kinetic models and MD studies with different aspects have greatly progressed our fundamental understanding of dissociation kinetics of hydrates, there are still some limitations on achieving a comprehensive consideration of the driving mechanisms due to excessive assumption and simplification. The main reason is that the dissociation of a hydrate strongly depends on the special porous characteristics of the sediments and the complex reservoir environments involved. First, in defining the intrinsic rate constant and the heat transfer within the porous media, the permeability and porosity of the porous media are commonly assumed to be constant. However, these characteristic parameters undergo time-dependent variations during the dissociation of the hydrate. It is crucial to comprehensively understand the effects of the varying porous characteristics on the intrinsic kinetics and heat transfer. In addition, for simplification, Darcy’s law was used to couple the two-phase gas–water flow during the dissociation of a hydrate. The underlying assumption is that the porous media are isotropic and homogeneous, with a slow and viscous fluid flow. As a crucial driving mechanism, the effects of the particle size and the deformation of the porous media on the fluid flow are neglected. The effect of the fluid flow in the field-scale process becomes more important in comparison with the laboratory and reservoir scales. Meanwhile, when solving nonlinear conservation equations, those kinetic models are limited in terms of accuracy due to the linearization approach. In general, a more comprehensive and accurate modeling method covering all the key driving mechanisms and approaching reality is highly desirable and remains a great challenge.
3. Numerical Simulations for Hydrate Exploitation
3.1. Numerical Simulations for the Dissociation of Hydrates in Sediments
With great developments in scientific computing, a numerical method which uses the discretization method to solve a series of differential equations has been developed as an excellent tool for complex multi-physics coupling problems and has been successfully used in the natural gas hydrate research community [22,24,42]. Compared with theoretical and analytical methods, the numerical method can provide a more comprehensive consideration of the driving mechanism and accurate predictions for the dissociation of hydrates at various scales and under various boundary conditions. For example, the fluid flow through the porous media in the dissociation of a hydrate is defined using Darcy’s law for simplification in the theoretical and analytical approaches. However, using the numerical method, the complete forms of the Navier–Stokes equations for the fluid flow can be solved directly with consideration for the effect of the hydrate particles. Profiting from its significant advantages, the numerical method has made great progress in the hydrate dissociation and the production process, involving multiple physics and their coupling effects, e.g., heat and mass transfer, intrinsic kinetics, and multiphase flow in porous media.
Substantial numerical efforts have been devoted to simulating the dissociation kinetics in the hydrate-bearing sediments using the computational fluid dynamics (CFD) method [16,58,59,60,61,62,63,64,65,66,67,68,69,70]. Nazridoust and Ahmadi [58] carried out the first attempt to numerically model the dissociation of a hydrate in a porous sandstone core. Considering the hydrate dispersed in the pores, an axisymmetric core model was constructed including three phases (hydrate, gas, and water). The continuity equations of different phases and the energy equations for the effective medium were solved for the multiphase flow and thermal characteristics, and Darcy’s law was used to consider the fluid flow within the porous media. Using a Users’ Defined Code, the source/sink terms were incorporated into the governing equations to consider the dissociation rate, the absorbed heat, and the generation of gas and water [40,59]. In addition, the time-dependent variations in the relative permeability and effective porosity of the core during dissociation were included using Corey’s model [60]. With this two-dimensional model, the temporal and spatial evolutions of the pressure, flow, and temperature profiles in the sandstone core were numerically evaluated, considering different temperatures, outlet pressure, and permeability conditions. Corresponding to the experimental investigation of the dissociation of a hydrate, Sean et al. [61,62] further performed a CFD simulation. Significantly, the kinetic model considered the Gibbs free energy difference between the hydrate’s phase and the surrounding aqueous phase as the driving force. The dissociation of the hydrate under the water flow conditions was numerically studied using the developed kinetic model. The dissociation rate constant was defined by combining the measured overall dissociation rate with the computed concentration distribution of methane. It found that the dissociation rate constant is independent of the water flow rate and the pressure, indicating the intrinsic nature of the rate constant.
Similar to the model developed by Nazridoust and Ahmadi [58], Liang et al. [63] developed a two-dimensional axisymmetric model to carry out a CFD simulation for the dissociation of a hydrate in a cylindrical, porous core sample using the depressurization method at the laboratory scale. Governing equations considering the mass transfer, energy conservation, and intrinsic kinetics were numerically solved using the finite difference method. Several crucial parameters, including the outlet pressure, initial gas saturation, surrounding temperature, and core permeability, were studied for the rate of gas generation. Subsequently, this model was further extended to study the hydrate’s dissociation characteristics, considering thermal injection, microwave stimulation, a combined production method, and soil compressibility [16,64,65,66]. Recently, Chen et al. [67] developed a two-dimensional, core-scale numerical model which considers the multiphase dissociation flows of hydrates within porous media. They especially focused on the thermal boundary effects and depressurization process, as well as the corresponding parametric influence on the core-scale internal flow. It should be noted that a solid hydrate can be seen as a part of the solid frame of the sediments. The dissociation of the hydrate will alter the porous structure, resulting in a variation in the reservoir’s permeability and porosity. The multiphase flow in the porous media is consequently affected during dissociation. Therefore, understanding the complex thermal–hydrodynamic–mechanical–chemical coupled characteristics is essential and has been widely explored [22,68,69,70,71,72,73]. Based on the hybrid finite volume and finite element method, Wan et al. [71] developed a thermal–hydrodynamic–mechanical–chemical coupled model to evaluate the fluid flow in the hydrate-bearing sediment and its geomechanical characteristics. Recently, based on a formation experiment on a methane hydrate via the excess water technique in a small reactor with sandy porous media [72], Yin et al. [73] developed an inverse modeling approach using the TOUGH (Transport of Unsaturated Groundwater and Heat) + HYDRATE code and studied the spatially heterogeneous dissociation characteristics via depressurization, as shown in Figure 5. So far, various numerical models for the dissociation of a hydrate have been developed with great success to consider the driving mechanisms via different methods [24,67].
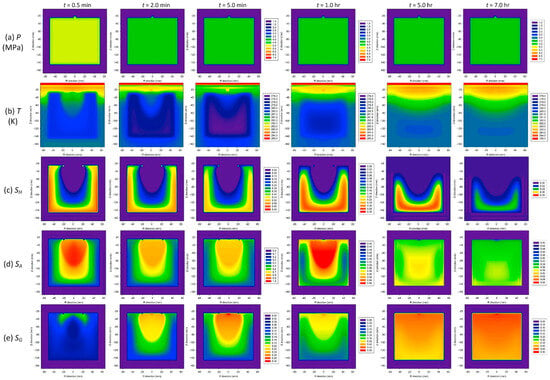
Figure 5.
The spatial distributions of the pressure P, temperature T, and phase saturation (SH for the hydrate phase, SA for the aqueous phase, and SG for the gas phase) over time [73].
3.2. Numerical Simulations for the Flow Characteristics of Hydrates in a Wellbore
Well drilling in hydrate−bearing sediments is of great importance for the development and exploitation of gas hydrates [22,24]. Similar to the dissociation of hydrates in sediments, the drilling process also involves complex multiphysics coupling [74], as illustrated in Figure 6. Different phases, including sediment particles, hydrate particles, gas, and water, form a multiphase flow in the wellbore. Due to the specific environmental conditions, the hydrate particles in the flow system present complex dynamics, including growth, dissociation, aggregation, and fragmentation. The transport of heat, mass, and momentum between phases commonly occurs during the drilling process. Therefore, the multiphase flow in the wellbore is coupled with the complex dynamics of the hydrate particles as well as heat, mass, and momentum transport. Understanding such a complex multiphysics coupling problem plays a crucial role in achieving the controllable exploitation of gas hydrates through drilling.
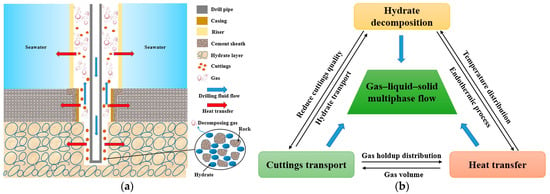
Figure 6.
Well drilling in a hydrate-bearing sediment [74]: (a) mechanisms of multiphysics coupling; (b) inter–coupling of hydrate decomposition, cuttings transport and heat transfer.
Due to harsh environmental conditions and the complexity of the drilling process, experimental investigations are remarkably limited. By coupling the successfully developed dissociation model discussed in Section 2 with a multiphase flow, the flow characteristics in the wellbore or the production tube were numerically studied with great success [15,21,22,24,75]. Balakin et al. [76,77] developed an Eulerian–Eulerian CFD model to simulate the multiphase flow and deposition characteristics of hydrate particles in a laboratory-scale low-pressure flow loop. Based on the Eulerian–Eulerian two-fluid model, Xu et al. [78] further introduced the population balance theory (PBM) for considering the particle dynamics of hydrates, as shown in Figure 7. Based on the multiphase flow model, the pressure-drop characteristics [21,79,80,81], the flow regimes [79,80], and the critical factors for the safe flow of hydrate slurry [82,83], have been explored widely. Furthermore, extensive efforts have been devoted to developing a multiphysics coupling model. Wei et al. [84] developed a coupled model including the temperature and pressure models in the wellbore, a dynamic dissociation model, and a multiphase flow model. The developed numerical model was used to study the interrelationships of the varying pressure, temperature, dissociation rate, hydrate dissociation, phase contents, and velocities in the wellbore. Based on a gas–liquid–solid three-phase model, Li et al. [85] further considered the kinetic dissociation of hydrate particles by introducing source terms into the conservation equations to describe the interphase heat, mass, and momentum exchange. The interaction of the multiphase flow and the dissociation of the hydrate were analyzed. Coupling the multiphase flow model with the transfer of heat between the wellbore and reservoir, Gao et al. [86,87] studied the effects of the temperature and pressure at the bottom of the wellbore on a hydrate with a riser and without a riser. Considering the interactions between the hydrate’s dynamic dissociation, the transport of cuttings, and heat transfer in the multiphase flow system, Liao et al. [74] developed a coupled transient gas–liquid–solid flow model. The effects of the wellhead pressure, the density of the drilling fluid, and the injection temperature on the multiphase flow characteristics were studied comprehensively. Recently, Kang et al. [88] combined the developed annulus hydrate slurry multiphase flow model with the hydrate dissociation kinetic model and the thermal model and numerically simulated the multiphase upward flow of a hydrate slurry in a vertical, concentric annulus. A series of influence factors were discussed in terms of the flow pattern, the dissociation of the hydrate, and the production of gas.
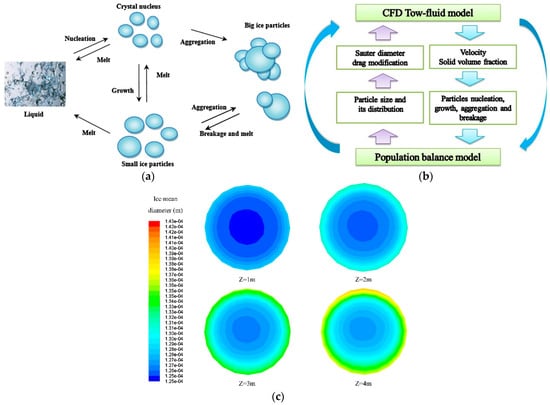
Figure 7.
The CFD-PBM approach for the flow of ice slurry in horizontal pipes: (a) a schematic of the particle dynamics of hydrates; (b) the coupled framework of the CFD-PBM model; (c) the mean size contours of ice on distinct cross-sections along the flow direction (z is the axial distance) [78].
Due to their great capacity to solve nonlinear differential equations, numerical models have greatly contributed to progress in fundamentally understanding the complex multiphysics process of the dissociation of a hydrate in the sediment and flow system during drilling. Table 2 provides a summary of numerical simulations of the dissociation of a hydrate in a sediment and flow system during drilling. However, owing to the complexity and vastly different driving factors for each specific case, more comprehensive and precise numerical models considering all factors and with a clearer and more accurate picture for each driving mechanism are highly desired. Furthermore, the indications and the relationship between the core-scale model and real, field-scale production should be provided more attention from the perspectives of both understanding the mechanism and real production.

Table 2.
Summary of numerical simulations of hydrate dissociation in a sediment and wellbore.
4. Conclusions
In this work, the research progress in the modeling and numerical investigation of the production of gas from natural gas hydrates was revised and outlined comprehensively. Firstly, fundamental models for the dissociation of a hydrate in porous sediment (including the phase equilibrium and dissociation kinetics) were reviewed and summarized. Subsequently, numerical simulations for the hydrate’s dissociation in a porous sediment and the flow characteristics in the wellbore were presented and reviewed. Meanwhile, comments and further improvements were provided properly. In general, more efforts should be devoted to elaborately considering the effect of the porous characteristics of sediments when studying the dissociation kinetics. On the one hand, the permeability and porosity of the porous sediments undergo time-dependent variations during dissociation and have considerable influences on defining the intrinsic rate constant and heat transfer. On the other hand, Darcy’s law with isotropic and homogeneous assumptions overlooked the effects of the particle size and the deformation of the porous media on the fluid flow. Compared to the laboratory and reservoir scales, the effect of the fluid flow becomes increasingly important in the field-scale process and should be considered more. In the future, a more comprehensive and accurate kinetic model which covers all key driving mechanisms and approaches reality remains highly desirable. Numerical simulations with great capacity for solving nonlinear differential equations have offered great progress in understanding the complex multiphysics process of the dissociation of a hydrate in a sediment and the flow system during drilling. However, to be a typical multiphysics coupling problem, the production of gas from natural gas hydrates flexibly depends on different driving factors with variations in the reservoir characteristics. Therefore, we highlight that considerable efforts are still required to develop more comprehensive and precise numerical models which consider all factors and produce a clear and accurate picture of each driving mechanism for production. Furthermore, there is an urgent need to clarify the indication and relationship between the core-scale model and real, field-scale production. With the fast growth of computational power, a multiscale numerical scheme from the laboratory-scale core to field-scale production is highly desirable for both understanding the mechanism and developing efficient production strategies for natural gas hydrates.
Author Contributions
Conceptualization, Z.-J.N. and S.-F.Z.; methodology, Z.-J.N.; writing—original draft, Z.-J.N. and S.-F.Z.; writing—review and editing, H.-F.L., D.-H.X., X.L. and L.L.; project administration, H.-F.L.; funding acquisition, H.-F.L. All authors have read and agreed to the published version of the manuscript.
Funding
The authors highly appreciate the funding by the Guangdong Basic and Applied Basic Research Foundation (Nos. 2022A1515011902 and 2020A1515110405), the Guangzhou Science and Technology Program (Nos. 202206050001 and 202206050002), and the Guangzhou Science and Technology Program (202201011463).
Data Availability Statement
Data will be made available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| feq | the fugacity of the gas at the equilibrium, pa |
| feqv | the fugacity of the gas at the solid surface, pa |
| P | pressure, pa |
| qs | the specified heat flux on the hydrate surface, w m−2 |
| r | the radius of the unreacted core, m |
| R0 | the averaged core radius of the porous media, m |
| Rw | the thickness of the bound water layer, m |
| SH | the phase saturation of the hydrate phase, - |
| SA | the phase saturation of the aqueous phase, - |
| SG | the phase saturation of the gas phase, - |
| T | temperature, k |
| Ti | the initial temperature of the hydrate, k |
| Ts | the equilibrium temperature at the hydrate’s surface, k |
| x, y, z | components in the Cartesian coordinate system, m |
| Superscripts | |
| A | aqueous |
| eq | equilibrium |
| G | gas |
| H | hydrate |
| s | the hydrate’s surface |
| Abbreviations | |
| BOP | blowout preventer |
| CFD | computational fluid dynamics |
| ESP | electric submersible pump |
| MD | molecular dynamic |
| PBM | population balance theory |
| TOUGH | transport of unsaturated groundwater and heat |
References
- Sloan, E.D.; Koh, C.A. Clathrate Hydrates of Natural Gases; CRC Press: New York, NY, USA, 2007. [Google Scholar]
- Romanovskii, N.N.; Hubberten, H.W.; Gavrilov, A.V.; Eliseeva, A.A.; Tipenko, G.S. Offshore Permafrost and Gas Hydrate Stability Zone on the Shelf of East Siberian Seas. Geo-Mar. Lett. 2005, 25, 167–182. [Google Scholar] [CrossRef]
- Bohrmann, G.; Torres, M.E. Gas Hydrates in Marine Sediments, Marine Geochemistry; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Makogon, Y.F.; Holditch, S.A.; Makogon, T.Y. Natural Gas-Hydrates-A Potential Energy Source for the 21st Century. J. Petrol. Sci. Eng. 2007, 56, 14–31. [Google Scholar] [CrossRef]
- Davy, H. The Bakerian Lecture. On some of the Combinations of Oxymuriatic Gas and Oxygene, and on the Chemical Relations of these Principles, to Inflammable Bodies. Phil. Trans. Roy. Soc. Lond. 1811, 101, 1–35. [Google Scholar]
- Shaibu, R.; Sambo, C.; Guo, B.; Dudun, A. An Assessment of Methane Gas Production from Natural Gas Hydrates: Challenges, Technology and Market Outlook. Adv. Geo-Energy Res. 2021, 5, 318–332. [Google Scholar] [CrossRef]
- Moridis, G.J.; Collett, T.S.; Dallimore, S.R.; Satoh, T.; Hancock, S.; Weatherill, B. Numerical Studies of Gas Production from Several CH4 Hydrate Zones at the Mallik Site, Mackenzie Delta, Canada. J. Petrol. Sci. Eng. 2004, 43, 219–238. [Google Scholar] [CrossRef]
- Konno, Y.; Fujii, T.; Sato, A.; Akamine, K.; Naiki, M.; Masuda, Y.; Yamamoto, K.; Nagao, J. Key Findings of the World’s First Offshore Methane Hydrate Production Test off the Coast of Japan: Toward Future Commercial Production. Energy Fuels 2017, 31, 2607–2616. [Google Scholar] [CrossRef]
- Ye, J.; Qin, X.; Xie, W.; Lu, H.; Ma, B.; Qiu, H.; Liang, J.; Lu, J.; Kuang, Z.; Lu, C.; et al. Main Progress of the Second Gas Hydrate Trial Production in the South China Sea. China Geol. 2020, 47, 557–568. [Google Scholar]
- Boswell, R.; Collett, T.S. Current Perspectives on Gas Hydrate Resources. Energy Environ. Sci. 2011, 4, 1206–1215. [Google Scholar] [CrossRef]
- Zerpa, L.E.; Dendy Sloan, E.; Sum, A.K.; Koh, C.A. Overview of CSMHyK: A Transient Hydrate Formation Model. J. Petrol. Sci. Eng. 2012, 98–99, 122–129. [Google Scholar] [CrossRef]
- Ke, W.; Svartaas, T.M.; Chen, D. A Review of Gas Hydrate Nucleation Theories and Growth Models. J. Nat. Gas Sci. Eng. 2019, 61, 169–196. [Google Scholar] [CrossRef]
- Li, Y.; Gambelli, A.M.; Rossi, F.; Mei, S. Effect of Promoters on CO2 Hydrate Formation: Thermodynamic Assessment and Microscale Raman Spectroscopy/Hydrate Crystal Morphology Characterization Analysis. Fluid Phase Equilib. 2021, 550, 113218. [Google Scholar] [CrossRef]
- Li, Y.; Chen, J.; Gambelli, A.M.; Zhao, X.; Gao, Y.; Rossi, F.; Mei, S. In Situ Experimental Study on the Effect of Mixed Inhibitors on the Phase Equilibrium of Carbon Dioxide Hydrate. Chem. Eng. Sci. 2022, 248, 117230. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, B.; Wang, Z.; Lou, W.; Zhang, J. Modeling of Multiphase Flow in Marine Gas Hydrate Production System and its Application to Control the Production Pressure Difference. J. Nat. Gas Sci. Eng. 2021, 85, 103687. [Google Scholar] [CrossRef]
- Zhao, J.; Zhu, Z.; Song, Y.; Liu, W.; Zhang, Y.; Wang, D. Analyzing the Process of Gas Production for Natural Gas Hydrate using Depressurization. Appl. Energy 2015, 142, 125–134. [Google Scholar] [CrossRef]
- Yamamoto, K.; Kanno, T.; Wang, X.X.; Tamaki, M.; Fujii, T.; Chee, S.S.; Wang, X.W.; Pimenov, V.; Shaka, V. Thermal Responses of a Gas Hydrate-Bearing Sediment to a Depressurization Operation. RSC Adv. 2017, 7, 5554–5577. [Google Scholar] [CrossRef]
- Moridis, G.; Kowalsky, M.; Pruess, K. Depressurization-Induced Gas Production from Class-1 Hydrate Deposits. SPE Reserv. Eval. Eng. 2007, 10, 458–481. [Google Scholar] [CrossRef]
- Pourafshary, P.; Varavei, A.; Sepehrnoori, K.; Podio, A. A Compositional Wellbore/Reservoir Simulator to Model Multiphase Flow and Temperature Distribution. J. Petrol. Sci. Eng. 2009, 69, 40–52. [Google Scholar] [CrossRef]
- Wang, W.C.; Wang, X.Y.; Li, Y.X.; Liu, S.; Yao, S.P.; Song, G.C. Study on Crystal Growth and Aggregated Microstructure of Natural Gas Hydrate under Flow Conditions. Energy 2020, 213, 118999. [Google Scholar] [CrossRef]
- Lv, X.; Zhang, J.; Liu, Y.; Ma, Q.; Xu, J.; Zhou, S.; Song, S.; Shi, B. Simulation Study of Natural Gas Hydrate Slurry Flow Characteristics in a High-Pressure Flow Loop. Fuel 2022, 316, 123332. [Google Scholar] [CrossRef]
- Li, X.S.; Xu, C.G.; Zhang, Y.; Ruan, X.K.; Li, G.; Wang, Y. Investigation into Gas Production from Natural Gas Hydrate: A Review. Appl. Energy 2016, 172, 286–322. [Google Scholar] [CrossRef]
- Ruan, X.; Song, Y.; Liang, H.; Yang, M.; Dou, B. Numerical Simulation of the Gas Production Behavior of Hydrate Dissociation by Depressurization in Hydrate-Bearing Porous Medium. Energy Fuels 2012, 26, 1681–1694. [Google Scholar] [CrossRef]
- Ruan, X.; Li, X.S.; Xu, C.G. A Review of Numerical Research on Gas Production from Natural Gas Hydrates in China. J. Petrol. Sci. Eng. 2021, 85, 103713. [Google Scholar]
- Vanderwaals, J.H.; Platteeuw, J.C. Clathrate Solutions. In Advances in Chemical Physics; John Wiley & Sons: Hoboken, NJ, USA, 1959; Volume 2, pp. 1–57. [Google Scholar]
- Parrish, W.R.; Prausnit, J.M. Dissociation Pressures of Gas Hydrates Formed by Gas-Mixtures. Ind. Eng. Chem. Process Des. Dev. 1972, 11, 26–35. [Google Scholar] [CrossRef]
- John, V.T.; Holder, G.D. Contribution of Second and Subsequent Water Shells to the Potential Energy of Guest-Host Interactions in Clathrate Hydrates. J. Chem. Phys. 1982, 86, 455–459. [Google Scholar] [CrossRef]
- Li, X.S.; Wu, H.J.; Englezos, P. Prediction of Gas Hydrate Formation Conditions in the Presence of Methanol, Glycerol, Ethylene Glycol, and Triethylene Glycol with the Statistical Associating Fluid Theory Equation of State. Ind. Eng. Chem. Res. 2006, 45, 2131–2137. [Google Scholar] [CrossRef]
- Chen, G.J.; Guo, T.M. A New Approach to Gas Hydrate Modelling. Chem. Eng. J. 1998, 71, 145–151. [Google Scholar] [CrossRef]
- Shahnazar, S.; Hasan, N. Gas Hydrate Formation Condition: Review on Experimental and Modeling Approaches. Fluid Phase Equilibr. 2014, 379, 72–85. [Google Scholar] [CrossRef]
- Clarke, M.A.; Pooladi-Darvish, M.; Bishnoi, P.R. A Method to Predict Equilibrium Conditions of Gas Hydrate Formation in Porous Media. Ind. Eng. Chem. Res. 1999, 38, 2485–2490. [Google Scholar] [CrossRef]
- Henry, P.; Thomas, M.; Ben Clennell, M. Formation of Natural Gas Hydrates in Marine Sediments: 2. Thermodynamic Calculations of Stability Conditions in Porous Sediments. J. Geophys. Res. Sol. Ea. 1999, 104, 23005–23022. [Google Scholar] [CrossRef]
- Li, X.S.; Zhang, Y.; Li, G.; Chen, Z.Y.; Yan, K.F.; Li, Q.P. Gas Hydrate Equilibrium Dissociation Conditions in Porous Media using two Thermodynamic Approaches. J. Chem. Thermodyn. 2008, 40, 1464–1474. [Google Scholar] [CrossRef]
- Wilder, J.W.; Seshadri, K.; Smith, D.H. Modeling Hydrate Formation in Media with Broad Pore Size Distributions. Langmuir 2001, 17, 6729–6735. [Google Scholar] [CrossRef]
- Peddireddy, S.; Lee, S.Y.; Lee, J.W. Variable Contact Angle Model for Gas Hydrate Equilibrium in Porous Media. AIChE J. 2006, 52, 1228–1234. [Google Scholar] [CrossRef]
- Selim, M.; Sloan, E. Heat and Mass Transfer during the Dissociation of Hydrates in Porous Media. AIChE J. 1989, 35, 1049–1052. [Google Scholar] [CrossRef]
- Englezos, P. Clathrate Hydrates. Ind. Eng. Chem. Res. 1993, 32, 1251–1274. [Google Scholar] [CrossRef]
- Vysniauskas, A.; Bishnoi, P.R. A Kinetic-Study of Methane Hydrate Formation. Chem. Eng. Sci. 1983, 38, 1061–1072. [Google Scholar] [CrossRef]
- Englezos, P.; Kalogerakis, N.; Dholabhai, P.D.; Bishnoi, P.R. Kinetics of Gas Hydrate Formation from Mixtures of Methane and Ethane. Chem. Eng. Sci. 1987, 42, 2659–2666. [Google Scholar] [CrossRef]
- Kim, H.; Bishnoi, P.R.; Heidemann, R.A.; Rizvi, S.S.H. Kinetics of Methane Hydrate Decomposition. Chem. Eng. Sci. 1987, 42, 1645–1653. [Google Scholar] [CrossRef]
- Tang, L.G.; Li, X.S.; Feng, Z.P.; Li, G.; Fan, S.S. Control Mechanisms for Gas Hydrate Production by Depressurization in different Scale Hydrate Reservoirs. Energy Fuels 2007, 21, 227–233. [Google Scholar] [CrossRef]
- Yin, Z.; Chong, Z.R.; Tan, H.K.; Linga, P. Review of Gas Hydrate Dissociation Kinetic Models for Energy Recovery. J. Nat. Gas Sci. Eng. 2016, 35, 1362–1387. [Google Scholar] [CrossRef]
- Bishnoi, P.R.; Natarajan, V. Formation and Decomposition of Gas Hydrates. Fluid Phase Equilib. 1996, 117, 168–177. [Google Scholar] [CrossRef]
- Clarke, M.A.; Bishnoi, P.R. Determination of the Intrinsic Rate Constant and Activation Energy of CO2 Gas Hydrate Decomposition using in-situ Particle Size Analysis. Chem. Eng. Sci. 2004, 59, 2983–2993. [Google Scholar] [CrossRef]
- Clarke, M.A.; Bishnoi, P.R. Measuring and Modelling the Rate of Decomposition of Gas Hydrates Formed from Mixtures of Methane and Ethane. Chem. Eng. Sci. 2001, 56, 4715–4724. [Google Scholar] [CrossRef]
- Giraldo, C.; Clarke, M. Stoichiometric Approach toward Modeling the Decomposition Kinetics of Gas Hydrates Formed from Mixed Gases. Energy Fuels 2013, 27, 4534–4544. [Google Scholar] [CrossRef]
- Ullerich, J.W.; Selim, M.S.; Sloan, E.D. Theory and Measurement of Hydrate Dissociation. AIChE J. 1987, 33, 747–752. [Google Scholar] [CrossRef]
- Jamaluddin, A.K.M.; Kalogerakis, N.; Bishnoi, P.R. Modelling of Decomposition of a Synthetic Core of Methane Gas Hydrate by Coupling Intrinsic Kinetics with Heat Transfer Rates. Can. J. Chem. Eng. 1989, 67, 948–954. [Google Scholar] [CrossRef]
- Yousif, M.H.; Abass, H.H.; Selim, M.S.; Sloan, E.D. Experimental and Theoretical Investigation of Methane-Gas-Hydrate Dissociation in Porous Media. SPE Res. Eng. 1991, 6, 69–76. [Google Scholar]
- Hong, H.; Pooladi-Darvish, M.; Bishnoi, P.R. Analytical Modelling of Gas Production from Hydrates in Porous Media. J. Can. Pet. Technol. 2003, 42, 45–56. [Google Scholar] [CrossRef]
- Hong, H.; Pooladi-Darvish, M. Simulation of Depressurization for Gas Production from Gas Hydrate Reservoirs. J. Can. Pet. Technol. 2005, 44, 39–46. [Google Scholar] [CrossRef]
- Li, X.S.; Zhang, Y. Study on Dissociation Behaviors of Methane Hydrate in Porous Media Based on Experiments and Fractional Dimension Shrinking-Core Model. Ind. Eng. Chem. Res. 2011, 50, 8263–8271. [Google Scholar] [CrossRef]
- Ding, L.Y.; Geng, C.Y.; Zhao, Y.H.; Wen, H. Molecular Dynamics Simulation on the Dissociation Process of Methane Hydrates. Mol. Simul. 2007, 33, 1005–1016. [Google Scholar] [CrossRef]
- Bagherzadeh, S.A.; Englezos, P.; Alavi, S.; Ripmeester, J.A. Molecular Modeling of the Dissociation of Methane Hydrate in Contact with a Silica Surface. J. Phys. Chem. B 2012, 116, 3188–3197. [Google Scholar] [CrossRef]
- Bagherzadeh, S.A.; Englezos, P.; Alavi, S.; Ripmeester, J.A. Molecular Simulation of Non-Equilibrium Methane Hydrate Decomposition Process. J. Chem. Thermodyn. 2012, 44, 13–19. [Google Scholar] [CrossRef]
- Bai, D.; Zhang, D.; Zhang, X.; Chen, G. Origin of Self-Preservation Effect for Hydrate Decomposition: Coupling of Mass and Heat Transfer Resistances. Sci. Rep. 2015, 5, 14599. [Google Scholar] [CrossRef] [PubMed]
- Bagherzadeh, S.A.; Alavi, S.; Ripmeester, J.; Englezos, P. Formation of methane nano-bubbles during hydrate decomposition and their effect on hydrate growth. J. Chem. Phys. 2015, 142, 214701. [Google Scholar] [CrossRef] [PubMed]
- Nazridoust, K.; Ahmadi, G. Computational Modeling of Methane Hydrate Dissociation in a Sandstone Core. Chem. Eng. Sci. 2007, 62, 6155–6177. [Google Scholar] [CrossRef]
- Clarke, M.; Bishnoi, P.R. Determination of the Activation Energy and Intrinsic Rate Constant of Methane Gas Hydrate Decomposition. Can. J. Chem. Eng. 2001, 79, 143–147. [Google Scholar] [CrossRef]
- Corey, A.T. The Interrelation between Gas and Oil Relative Permeabilities. Producers Monthly 1954, 19, 38–41. [Google Scholar]
- Sean, W.Y.; Sato, T.; Yamasaki, A.; Kiyono, F. CFD and Experimental Study on Methane Hydrate Dissociation Part I. Dissociation under Water Flow. AIChE J. 2007, 53, 262–274. [Google Scholar] [CrossRef]
- Sean, W.Y.; Sato, T.; Yamasaki, A.; Kiyono, F. CFD and Experimental Study on Methane Hydrate Dissociation. Part II. General Cases. AIChE J. 2007, 53, 2148–2160. [Google Scholar] [CrossRef]
- Liang, H.; Song, Y.; Chen, Y. Numerical Simulation for Laboratory-Scale Methane Hydrate Dissociation by Depressurization. Energy Convers. Manag. 2010, 51, 1883–1890. [Google Scholar] [CrossRef]
- Zhao, J.; Fan, Z.; Wang, B.; Dong, H.; Liu, Y.; Song, Y. Simulation of Microwave Stimulation for the Production of Gas from Methane Hydrate Sediment. Appl. Energy 2016, 168, 25–37. [Google Scholar] [CrossRef]
- Wang, B.; Fan, Z.; Zhao, J.; Lv, X.; Pang, W.; Li, Q. Influence of Intrinsic Permeability of Reservoir Rocks on Gas Recovery from Hydrate Deposits via a Combined Depressurization and Thermal Stimulation Approach. Appl. Energy 2018, 229, 858–871. [Google Scholar] [CrossRef]
- Sun, X.; Li, Y.; Liu, Y.; Song, Y. The Effects of Compressibility of Natural Gas Hydrate-Bearing Sediments on Gas Production Using Depressurization. Energy 2019, 185, 837–846. [Google Scholar] [CrossRef]
- Chen, L.; Yamada, H.; Kanda, Y.; Lacaille, G.; Shoji, E.; Okajima, J.; Komiya, A.; Maruyama, S. Numerical Analysis of Core-Scale Methane Hydrate Dissociation Dynamics and Multiphase Flow in Porous Media. Chem. Eng. Sci. 2016, 153, 221–235. [Google Scholar] [CrossRef]
- Queiruga, A.F.; Moridis, G.J.; Reagan, M.T. Simulation of Gas Production from Multilayered Hydrate-Bearing Media with Fully Coupled Flow, Thermal, Chemical and Geomechanical Processes Using Tough+Millstone. Part 2: Geomechanical Formulation and Numerical Coupling. Transp. Porous Media 2019, 128, 221–241. [Google Scholar] [CrossRef]
- Sun, X.; Luo, H.; Soga, K. A Coupled Thermal-Hydraulic-Mechanical-Chemical (THMC) Model for Methane Hydrate Bearing Sediments Using COMSOL Multiphysics. J. Zhejiang Univ. Sci. A 2018, 19, 600–623. [Google Scholar] [CrossRef]
- De La Fuente, M.; Vaunat, J.; Marín-Moreno, H. Thermo-Hydro-Mechanical Coupled Modeling of Methane Hydrate-Bearing Sediments: Formulation and Application. Energies 2019, 12, 2178. [Google Scholar] [CrossRef]
- Wan, Y.; Wu, N.; Chen, Q.; Li, W.; Hu, G.; Huang, L.; Ouyang, W. Coupled Thermal-Hydrodynamic-Mechanical-Chemical Numerical Simulation for Gas Production from Hydrate-Bearing Sediments Based on Hybrid Finite Volume and Finite Element Method. Comput. Geotech. 2022, 145, 104692. [Google Scholar] [CrossRef]
- Chong, Z.R.; Yin, Z.; Clifton Tan, J.H.; Linga, P. Experimental Investigations on Energy Recovery from Water-Saturated Hydrate Bearing Sediments via Depressurization Approach. Appl. Energy 2017, 204, 1513–1525. [Google Scholar] [CrossRef]
- Yin, Z.; Moridis, G.; Chong, Z.R.; Tan, H.K.; Linga, P. Numerical Analysis of Experimental Studies of Methane Hydrate Dissociation Induced by Depressurization in a Sandy Porous Medium. Appl. Energy 2018, 230, 444–459. [Google Scholar] [CrossRef]
- Liao, Y.; Sun, X.; Sun, B.; Gao, Y.; Wang, Z. Transient Gas-Liquid-Solid Flow Model with Heat and Mass Transfer for Hydrate Reservoir Drilling. Int. J. Heat Mass Tran. 2019, 141, 476–486. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, S.; Lang, X. Reviews of Gas Hydrate Inhibitors in Gas-Dominant Pipelines and Application of Kinetic Hydrate Inhibitors in China. Chin. J. Chem. Eng. 2019, 27, 2118–2132. [Google Scholar]
- Balakin, B.V.; Pedersen, H.; Kilinc, Z.; Hoffmann, A.C.; Kosinski, P.; Hoiland, S. Turbulent Flow of Freon R11 Hydrate Slurry. J. Petrol. Sci. Eng. 2010, 70, 177–182. [Google Scholar] [CrossRef]
- Balakin, B.V.; Hoffmann, A.C.; Kosinski, P. Experimental Study and Computational Fluid Dynamics Modeling of Deposition of Hydrate Particles in a Pipeline with Turbulent Water Flow. Chem. Eng. Sci. 2011, 66, 755–765. [Google Scholar] [CrossRef]
- Xu, D.; Liu, Z.; Cai, L.; Tang, Y.; Yu, Y.; Xu, A. A CFD-PBM Approach for Modeling Ice Slurry Flow in Horizontal Pipes. Chem. Eng. Sci. 2018, 176, 546–559. [Google Scholar] [CrossRef]
- Yao, S.; Li, Y.; Wang, W.; Song, G.; Jiang, K.; Shi, Z. Numerical Simulation of Hydrate Slurry Flow Characteristics in Vertical Pipes Based on Population Balance Theory. Int. J. Oil Gas Coal Technol. 2020, 25, 319–339. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, Q.; Wang, Z.; Wang, J.; Sun, X.; Liu, Z.; Sun, B.; Sun, J. Prediction of Hydrate Formation and Plugging in the Trial Production Pipes of Offshore Natural Gas Hydrates. J. Cleaner Prod. 2021, 316, 128262. [Google Scholar] [CrossRef]
- Mellari, S. Experimental investigation and modeling of the pressure drop of ice slurry flow in horizontal pipe. Int. J. Refrig. 2023, 147, 134–142. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, B.; Lang, C.; Zhang, L.; Yang, L.; Guo, X. An Improved Model for Predicting the Critical Velocity in the Removal of Hydrate Particles from Solid Surfaces. Chem. Phys. Lett. 2021, 779, 138832. [Google Scholar] [CrossRef]
- Sakurai, S.; Hoskin, B.; Choi, J.; Nonoue, T.; May, E.F.; Kumar, A.; Norris, B.W.E.; Aman, Z.M. Investigating Hydrate Formation Rate and the Viscosity of Hydrate Slurries in Water-Dominant Flow: Flowloop Experiments and Modelling. Fuel 2021, 292, 120193. [Google Scholar] [CrossRef]
- Wei, N.; Sun, W.; Meng, Y.; Zhou, S.; Li, G.; Guo, P.; Dong, K.; Li, Q. Sensitivity Analysis of Multiphase Flow in Annulus during Drilling of Marine Natural Gas Hydrate Reservoirs. J. Nat. Gas Sci. Eng. 2016, 36, 692–707. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X.; Lu, X. Three-Dimensional Eulerian Modeling of Gas-Liquid-Solid Flow with Gas Hydrate Dissociation in a Vertical Pipe. Chem. Eng. Sci. 2019, 196, 145–165. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, Z.; Zhao, X.; Wang, Z.; Yin, Z.; Wang, J. Multiphase Flow in Wellbores and Variation Laws of the Bottom Hole Pressure in Gas Hydrate Drilling. Acta Pet. Sin. 2012, 33, 881–886. [Google Scholar]
- Gao, Y.; Sun, B.; Xu, B.; Wu, X.; Chen, Y.; Zhao, X.; Chen, L. A Wellbore/Formation-Coupled Heat-Transfer Model in Deepwater Drilling and Its Application in the Prediction of Hydrate-Reservoir Dissociation. SPE J. 2016, 22, 756–766. [Google Scholar] [CrossRef]
- Kang, Q.; Song, S.; Yu, J.; Shi, B.; Chen, Y.; Lv, X.; Liu, Y.; Bai, Z.; Hong, B.; Wang, W.; et al. Simulation of Upward Gas-Hydrate Slurry Multiphase Flow in a Vertical Concentric Annulus for Natural Gas Hydrate Solid Fluidization Exploitation. Phys. Fluids 2021, 33, 103102. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).