Distribution Network Reconfiguration Using Chaotic Particle Swarm Chicken Swarm Fusion Optimization Algorithm
Abstract
:1. Introduction
- A novel meta-heuristic CPSCSFO is proposed for the first time.
- The node hierarchy method is introduced to calculate the power flow. The branching loop matrix and node hierarchy strategy are used to detect the network topology and judge the infeasible solution to improve the efficiency of the algorithm.
- The proposed CPSCSFO algorithm is applied to the optimal reconfiguration of the distribution network. The reconfiguration verification of the distribution network is carried out in the case of no DG, PQ-type DG and multiple DGs.
- The results show that the proposed method is of great significance for solving the optimal reconfiguration problem of a distribution network with multiple DGs.
- The CPSCSFO gives better performance compared to the conventional PSO algorithm and several recent algorithms.
- The proposed CPSCSFO algorithm significantly increases the voltage of each node and reduces the active power loss of the system.
2. Mathematical Description of the Problem
2.1. Objective Function
2.1.1. Power Loss Index
2.1.2. Voltage Deviation Index
2.1.3. Synthetic Objective Function
2.2. Operational Constraints
2.2.1. Node Voltage Constraint
2.2.2. Network Power Flow Constraint
2.2.3. Branch Capacity Constraint
2.2.4. Network Topology Constraint
3. Infeasible Solution Determination Strategy
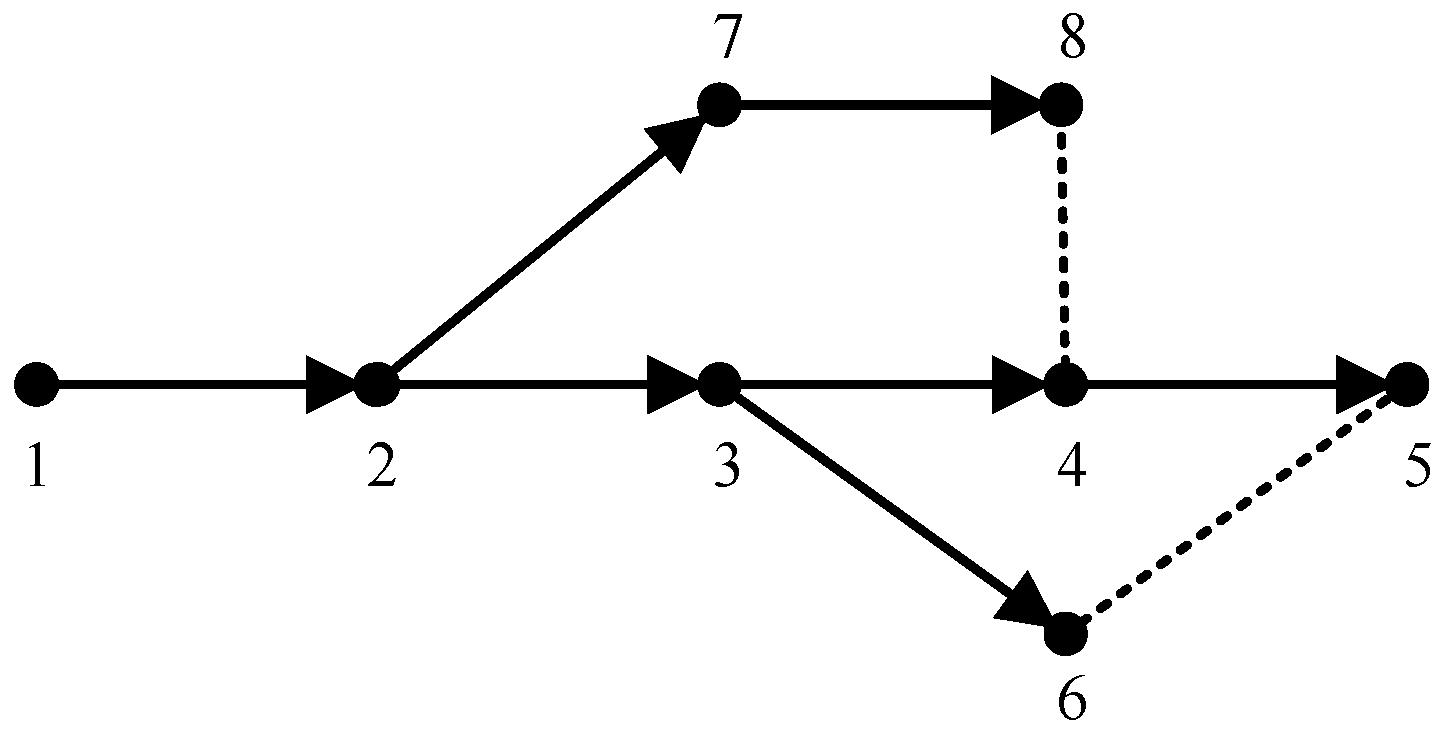
3.1. Nodal Hierarchical Tide Calculation
3.2. Coding Strategy
4. Chaotic Particle Swarm Chicken Flock Algorithm
4.1. Chaotic Particle Swarm Algorithm
4.2. Chicken Swarm Optimization
4.3. Chaotic Particle Swarm Chicken Swarm Fusion Optimization
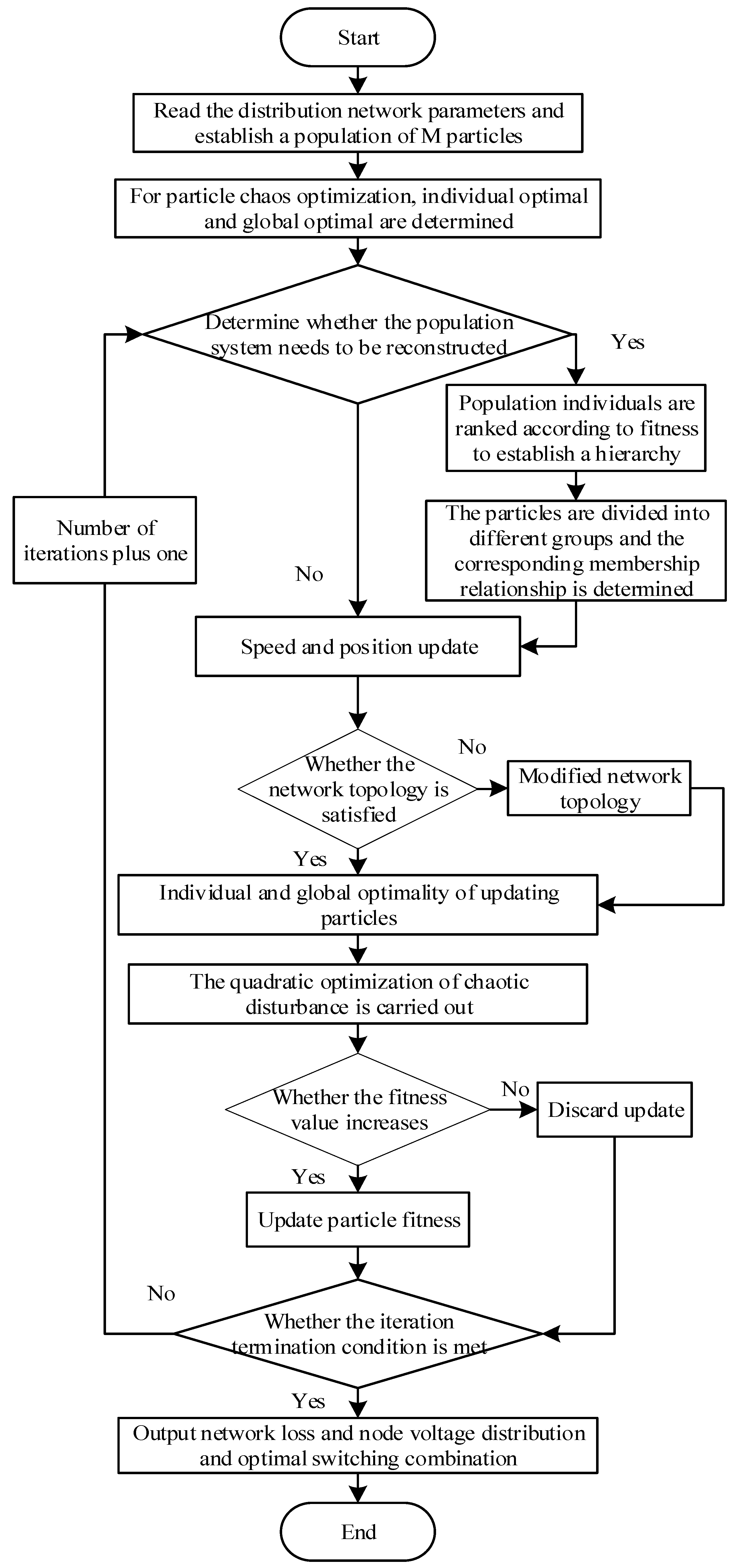
4.4. Algorithm Implementation Flow
5. Case Simulation and Analysis
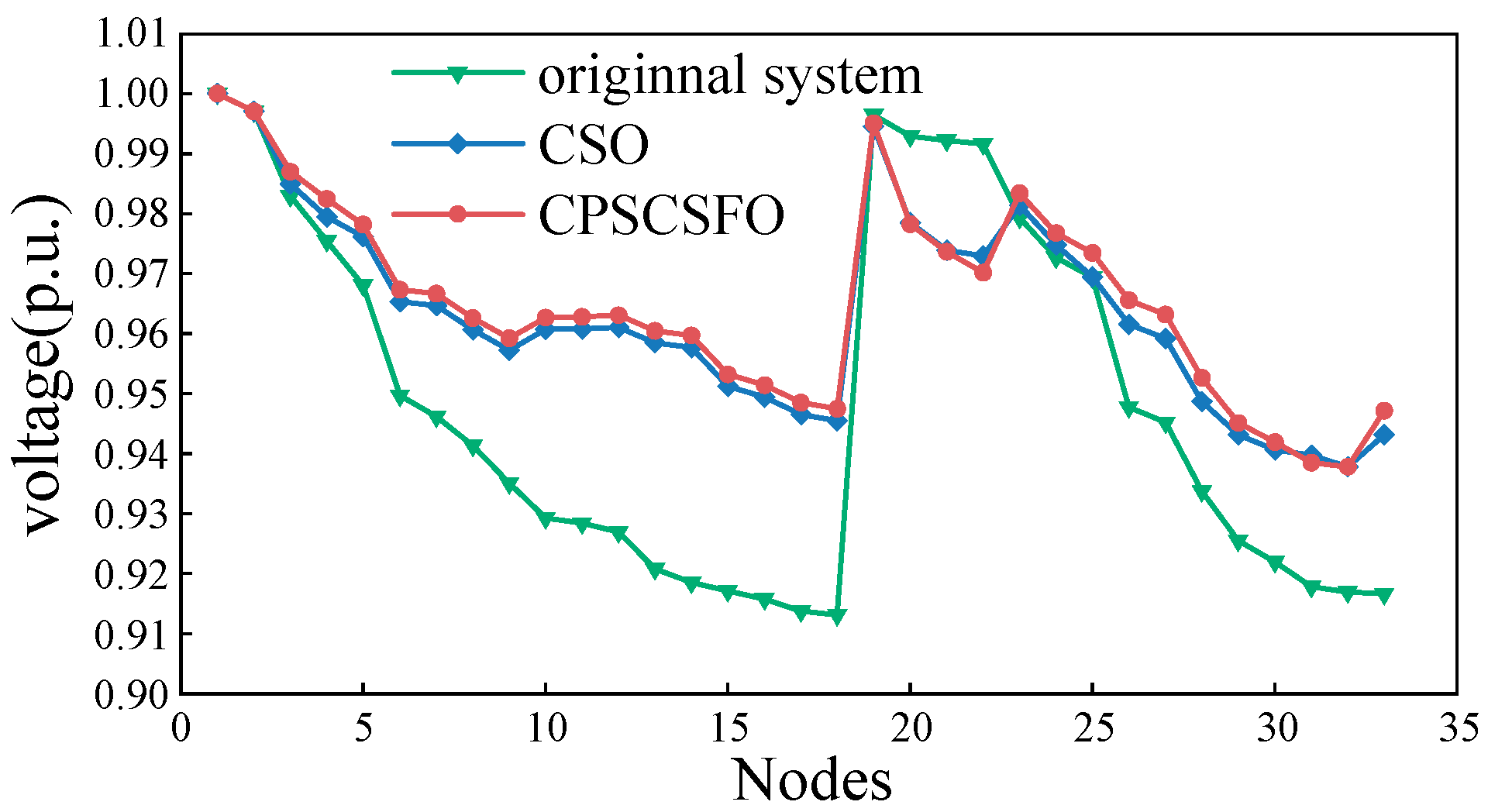
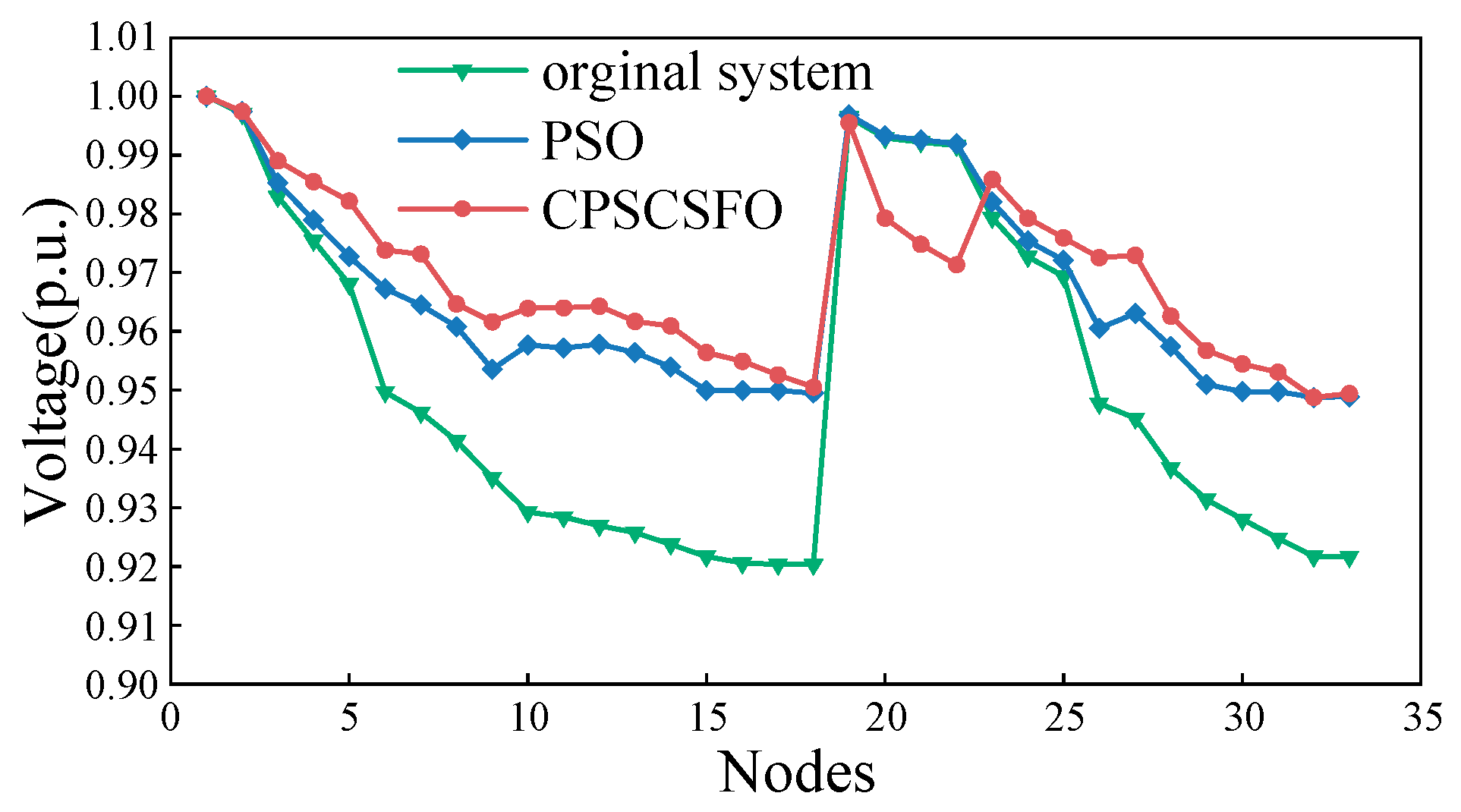
5.1. Distribution Network Reconfiguration without DG
5.2. Distribution Network Reconfiguration with PQ-Type DG
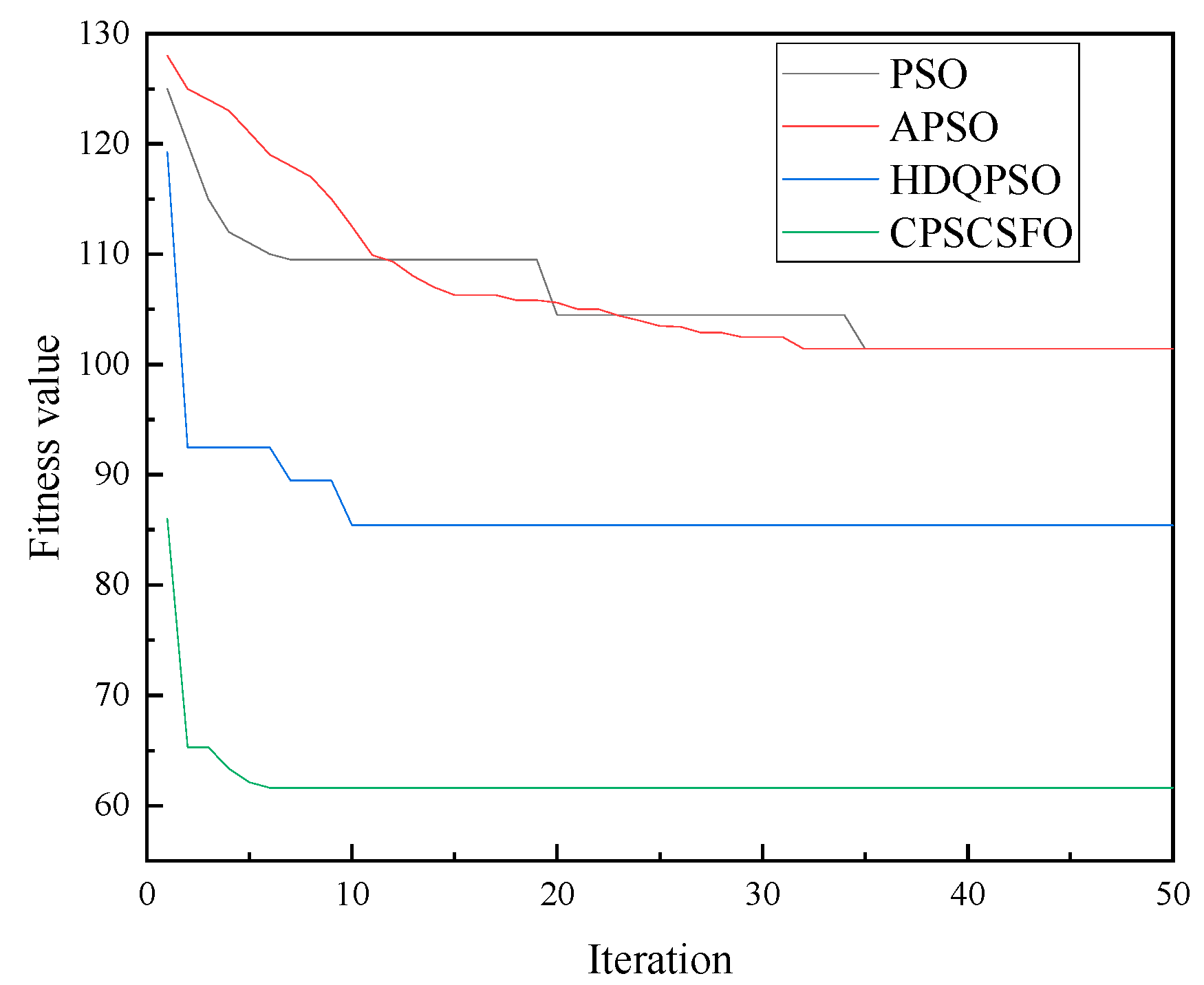
5.3. Distribution Network Reconfiguration with Multiple DGs
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shukla, J.; Das, B.; Pant, V. Stability constrained optimal distribution system reconfiguration considering uncertainties in correlated loads and distributed generations. Int. J. Elect. Power Energy Syst. 2018, 99, 121–133. [Google Scholar] [CrossRef]
- Ali, M.H.; Kamel, S.; Hassan, M.H.; Tostado-Veliz, M.; Zawbaa, H.M. An improved wild horse optimization algorithm for reliability based optimal DG planning of radial distribution networks. Energy Rep. 2022, 8, 582–604. [Google Scholar] [CrossRef]
- Cupelli, L.; Cupelli, M.; Ponci, F.; Monti, A. Data-Driven Adaptive Control for Distributed Energy Resources. IEEE Trans. Sustain. Energy 2019, 10, 1575–1584. [Google Scholar] [CrossRef]
- Yazdanian, M.; Mehrizi-Sani, A. Distributed Control Techniques in Microgrids. IEEE Trans. Smart Grid. 2014, 5, 2901–2909. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Yang, Y.H.; Yang, D.S.; Wang, X.F. Distributed Power-Generation Systems and Protection. Proc. IEEE 2017, 105, 1311–1331. [Google Scholar] [CrossRef]
- Gerez, C.; Silva, L.I.; Belati, E.A.; Sguarezi Filho, A.J.; Costa, E.C.M. Distribution network reconfiguration using selective firefly algorithm and a load flow analysis criterion for reducing the search space. IEEE Access 2019, 7, 67874–67888. [Google Scholar] [CrossRef]
- Samman, M.A.; Mokhlis, H.; Mansor, N.N.; Mohamad, H.; Suyono, H.; Sapari, N.M. Fast optimal network reconfiguration with guided initialization based on a simplified network approach. IEEE Access 2020, 8, 11948–11963. [Google Scholar] [CrossRef]
- Khodr, H.M.; Martinez-Crespo, J.; Matos, M.A.; Pereria, J. Distribution systems reconfiguration based on OPF using benders decomposition. IEEE Trans. Power Deliv. 2009, 24, 2166–2176. [Google Scholar] [CrossRef]
- Jabr, R.A.; Singh, R.; Pal, B.C. Minimum loss network reconfiguration using mixed-integer convex programming. IEEE Trans. Power Syst. 2012, 27, 1106–1115. [Google Scholar] [CrossRef]
- Zin, A.A.M.; Ferdavani, A.K.; Bin Khairuddin, A.; Naeini, M.M. Two circular-updating hybrid heuristic methods for minimum-loss reconfiguration of electrical distribution network. IEEE Trans Power Syst. 2013, 28, 1318–1323. [Google Scholar]
- Chen, K.; Pan, L. Design of distribution network reconfiguration containing distributed generation based on GA-QPSO algorithm. Res. Explor. Lab. 2022, 41, 111–115. [Google Scholar]
- Xu, X.Q.; Wang, B.; Zhao, H.S.; Du, Z.; Yang, D.J.; Liu, J.; Liu, Y.G.; Hu, P. Reconfiguration of two-voltage distribution network based on cuckoo search and simulated annealing algorithm. Power Syst. Prot. Control 2022, 48, 84–91. [Google Scholar]
- Wang, L.M.; Cheng, J.; Wang, W.Q. Research on distribution network reconfiguration with distributed generation based on improved grey wolf optimizer. Mod. Electr. Power 2022, 39, 56–63. [Google Scholar]
- Li, C.; Qin, L.J.; Duan, H. Research on reconfiguration of distribution network with photovoltaic generation based on improved group search optimizer. Acta Energy Sol. Sin. 2022, 43, 213–218. [Google Scholar]
- Shaheen, A.M.; Elsayed, A.M.; Ginidi, A.R.; El-Sehiemy, R.A.; Elattar, E.E. Improved Heap-Based Optimizer for DG Allocation in Reconfigured Radial Feeder Distribution Systems. IEEE Syst. J. 2022, 16, 6371–6380. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Kamel, S.; Elattar, E.E.; Elsayed, A.M. Improving Distribution Networks’ Consistency by Optimal Distribution System Reconfiguration and Distributed Generations. IEEE Access 2021, 9, 67186–67200. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Elsayed, A.M.; Ginidi, A.R.; El-Sehiemy, R.A.; Elattar, E.E. Reconfiguration of electrical distribution network-based DG and capacitors allocations using artificial ecosystem optimizer: Practical case study. Alex. Eng. J. 2021, 61, 6105–6118. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Elsayed, A.M.; Ginidi, A.R.; El-Sehiemy, R.A.; Elattar, E.E. A heap-based algorithm with deeper exploitative feature for optimal allocations of distributed generations with feeder reconfiguration in power distribution networks. Knowl. Based Syst. 2022, 6, 241. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, Q.; Lv, G.Y. Improvement and application of quantum-behaved particle swarm optimization in distribution network reconfiguration. Electr. Meas. Instrum. 2022, 59, 58–65. [Google Scholar]
- Xu, X.B.; Zheng, K.F.; Li, D.; Wu, B.; Yang, Y.X. New chaos-particle swarm optimization algorithm. J. Commun. 2012, 33, 24–30. [Google Scholar]
- Gong, Y.J.; Li, J.J.; Zhou, Y.; Yun, L.; Chung, S.H.; Shi, Y.H.; Zhang, J. Genetic Learning Particle Swarm Optimization. IEEE Trans. Cybern. 2017, 46, 2277–2290. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.C.; Hu, H.M.; Liu, L. Distribution network reconfiguration based on chicken swarm optimization algorithm. Electrotech. Electr. 2016, 219, 20–24. [Google Scholar]
- Xu, Y. Application of improved particle swarm optimization in distribution network reconfiguration with distributed generation. Electr. Meas. Instrum. 2021, 58, 98–104. [Google Scholar]
- Xu, L.Z. Research on Distribution Network Reconfiguration Containing Distributed Generation. Master’s Thesis, Nanchang Hangkong University, Nanchang, China, 2017. [Google Scholar]
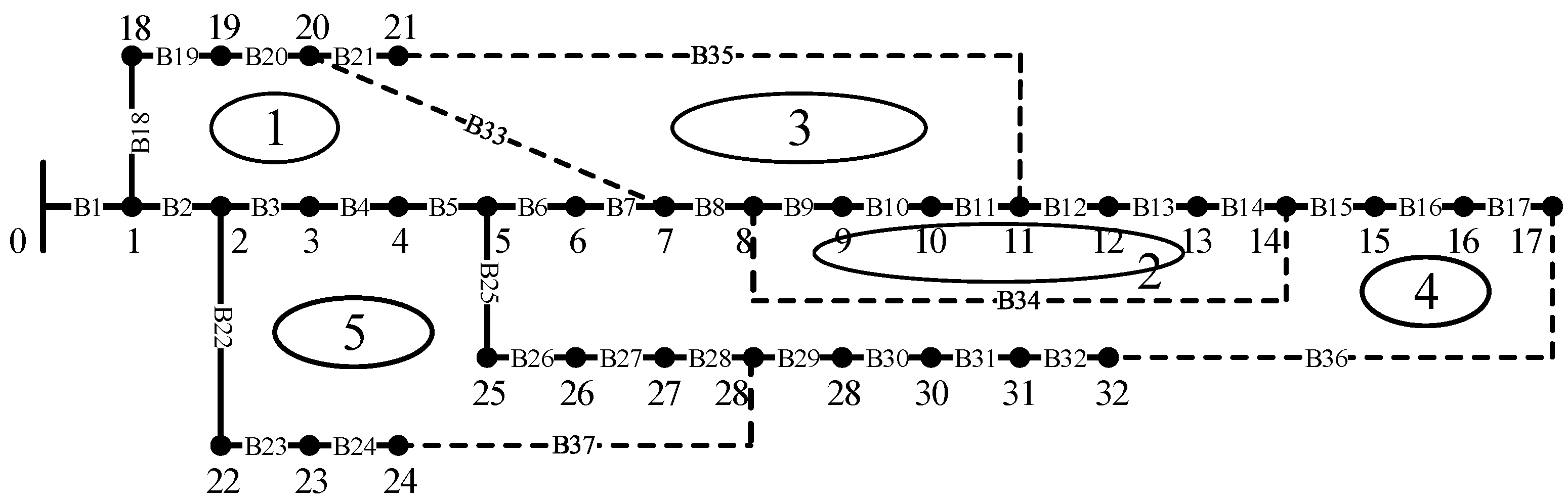



| Ring Network | Actual Switch Number | Switch Number |
|---|---|---|
| L1 | 7 6 5 4 3 2 20 19 18 33 | 1–10 |
| L2 | 14 13 12 11 10 9 34 | 1–7 |
| L3 | 11 10 9 8 7 6 5 4 3 2 21 20 19 18 35 | 1–15 |
| L4 | 17 16 15 14 13 12 11 10 9 8 7 6 25 26 27 28 29 30 31 32 36 | 1–21 |
| L5 | 24 23 22 28 27 26 25 4 3 37 | 1–11 |
| Algorithm | Open Switches | Active Power Loss (kW) | Minimum Nodal Voltage (p.u.) |
|---|---|---|---|
| Pre-reconstruction | 33 34 35 36 37 | 202.6747 | 0.9131 |
| PSO | 6 8 13 31 37 | 140.4834 | 0.9381 |
| CSO [22] | 7 9 14 32 37 | 139.5500 | 0.9378 |
| CPSCSFO | 7 9 14 32 37 | 139.5191 | 0.9378 |
| DG Number | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Location | 32 | 23 | 17 | 27 |
| Capacity | 50 | 100 | 200 | 100 |
| Power factor | 0.9 | 0.9 | 0.9 | 0.9 |
| Algorithm | Open Switches | Active Power Loss (kW) | Minimum Nodal Voltage (p.u) |
|---|---|---|---|
| Pre-reconstruction | 33 34 35 36 37 | 148.1182 | 0.9269 |
| PSO | 7 9 14 32 37 | 117.3438 | 0.3912 |
| APSO | 7 8 14 17 37 | 114.5495 | 0.9414 |
| CS-PSO [23] | 7 9 14 32 28 | 113.2365 | 0.9433 |
| CPSCSFO | 7 9 14 31 37 | 104.5069 | 0.9488 |
| DG | Double-Fed Fan | Gas Turbine | Photovoltaic Cell | Wind Asynchronous Generator |
|---|---|---|---|---|
| Location | 30 | 25 | 17 | 4 |
| Capacity | PQ | PV | PI | PQ(V) |
| Power factor | P = 200 kW | P = 300 kW | P = 300 kW | P = 300 kW |
| cos φ = 0.9 | Vs = 0.98 p.u. | Is = 50 A |
| Algorithm | Open Switches | Active Power Loss (kW) | Minimum Nodal Voltage (p.u.) |
|---|---|---|---|
| Pre-reconstruction | 33 34 35 36 37 | 108.0021 | 0.9355 |
| PSO | 7 10 14 32 25 | 101.4236 | 0.9397 |
| APSO | 7 10 14 36 37 | 101.4155 | 0.9401 |
| HDQPSO [24] | 7 9 14 28 32 | 85.3985 | 0.9473 |
| CPSCSFO | 9 14 16 28 32 | 61.6250 | 0.9688 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Liu, J.; Wang, L.; An, Y.; Zhang, X. Distribution Network Reconfiguration Using Chaotic Particle Swarm Chicken Swarm Fusion Optimization Algorithm. Energies 2023, 16, 7185. https://doi.org/10.3390/en16207185
Wu Y, Liu J, Wang L, An Y, Zhang X. Distribution Network Reconfiguration Using Chaotic Particle Swarm Chicken Swarm Fusion Optimization Algorithm. Energies. 2023; 16(20):7185. https://doi.org/10.3390/en16207185
Chicago/Turabian StyleWu, Yanmin, Jiaqi Liu, Lu Wang, Yanjun An, and Xiaofeng Zhang. 2023. "Distribution Network Reconfiguration Using Chaotic Particle Swarm Chicken Swarm Fusion Optimization Algorithm" Energies 16, no. 20: 7185. https://doi.org/10.3390/en16207185
APA StyleWu, Y., Liu, J., Wang, L., An, Y., & Zhang, X. (2023). Distribution Network Reconfiguration Using Chaotic Particle Swarm Chicken Swarm Fusion Optimization Algorithm. Energies, 16(20), 7185. https://doi.org/10.3390/en16207185






