Application of a Model Based on Rough Set Theory (RST) for Estimating the Temperature of Brine from Vertical Ground Heat Exchangers (VGHE) Operated with a Heat Pump—A Case Study
Abstract
1. Introduction
- Field measurements: One of the simplest methods involves precise measurement of ground temperature; this can be performed using thermocouples or temperature sensors placed in boreholes at various depths in the ground. These measurements are accurate but can be costly and time-consuming [2,5,6,7,8,9];
- Computer simulations: These allow for modeling the behavior of the HP system under specific ground conditions; this enables the prediction of how ground temperature will change throughout the year [10,11,12]. However, there is no universal formula available thus far [13,14,15,16,17,18,19]. Real measurement results are required for simulation calculations to validate the assumed model;
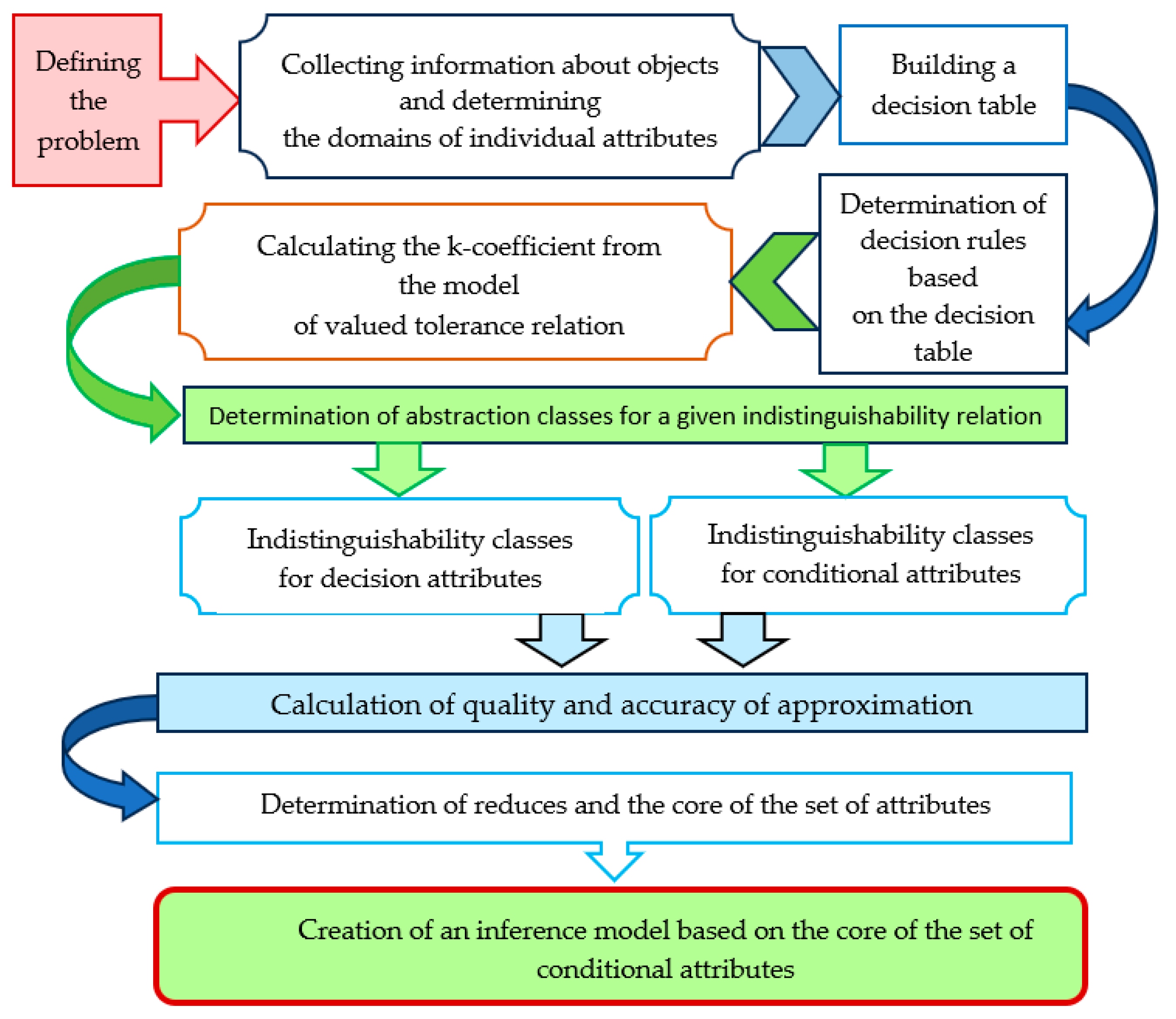
2. Materials and Methods
2.1. Subject of the Research
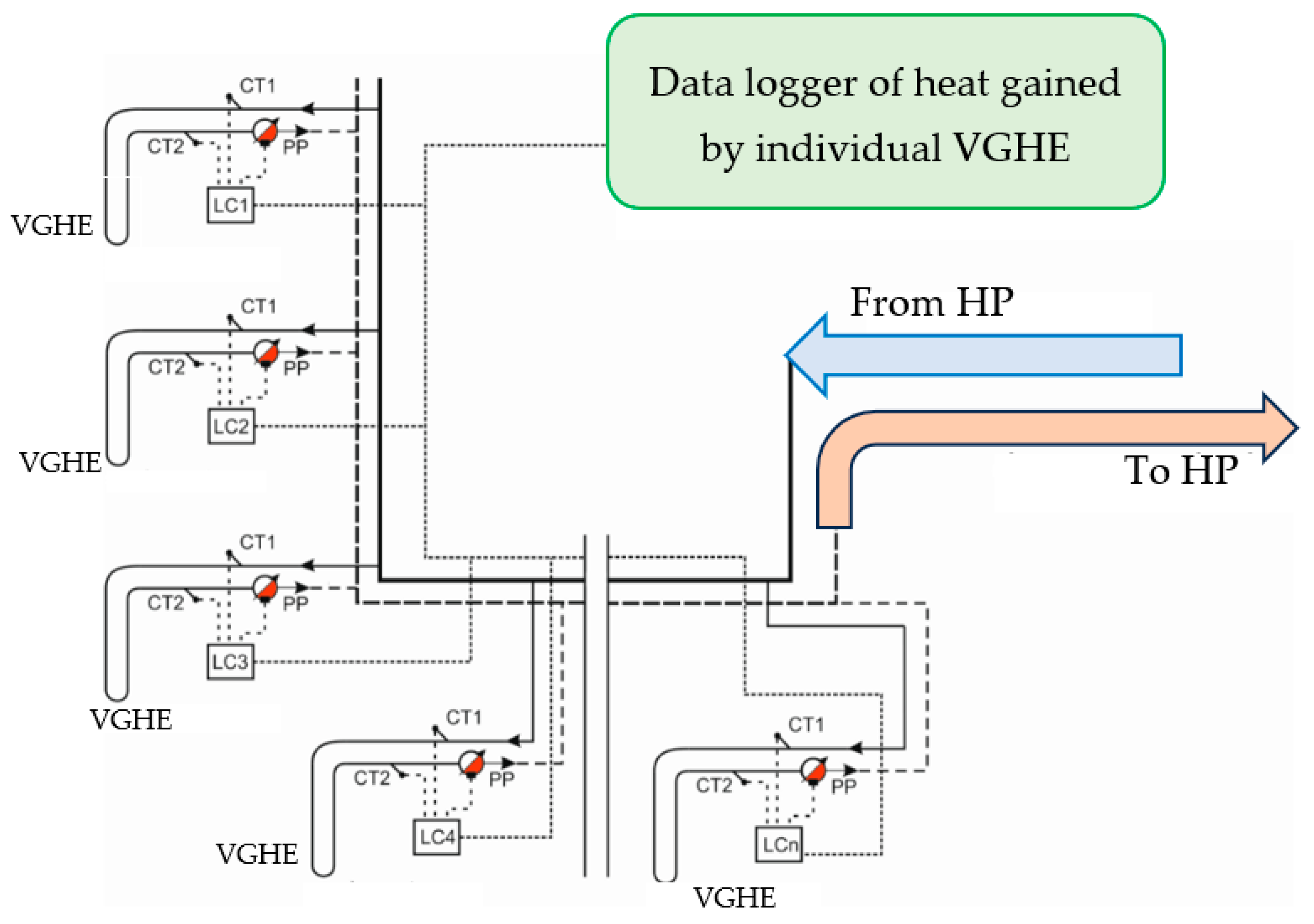
2.2. Monitoring the System of an HP Installation
- Measurement of brine temperature at the inlet and outlet of vertical probes (Figure 4);
- Measurement of external temperature;
- Measurement of solar radiation intensity;
- Measurement of energy accumulated in a given day and cumulatively since the HP installation was started;
- Measurement of temperature and the amount of energy transferred from individual circuits of the installation;
- Measurement of electrical energy consumption;
- Measurement of energy generated by the HPs on the upper source side;
- Measurement of energy supplied to the HP by the lower source.
2.3. Method of Predicting the Supply Temperature of the Lower Heat Source
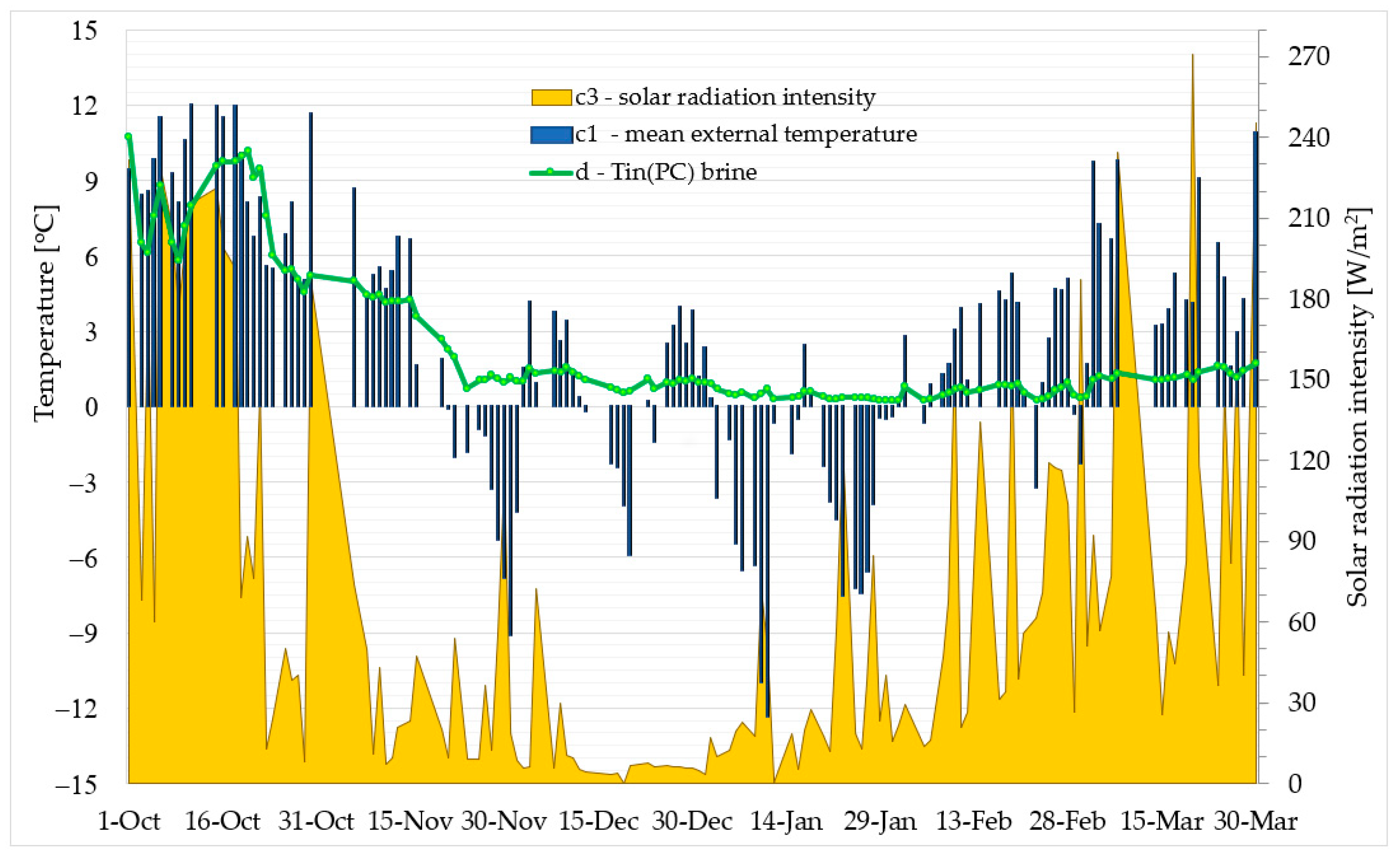
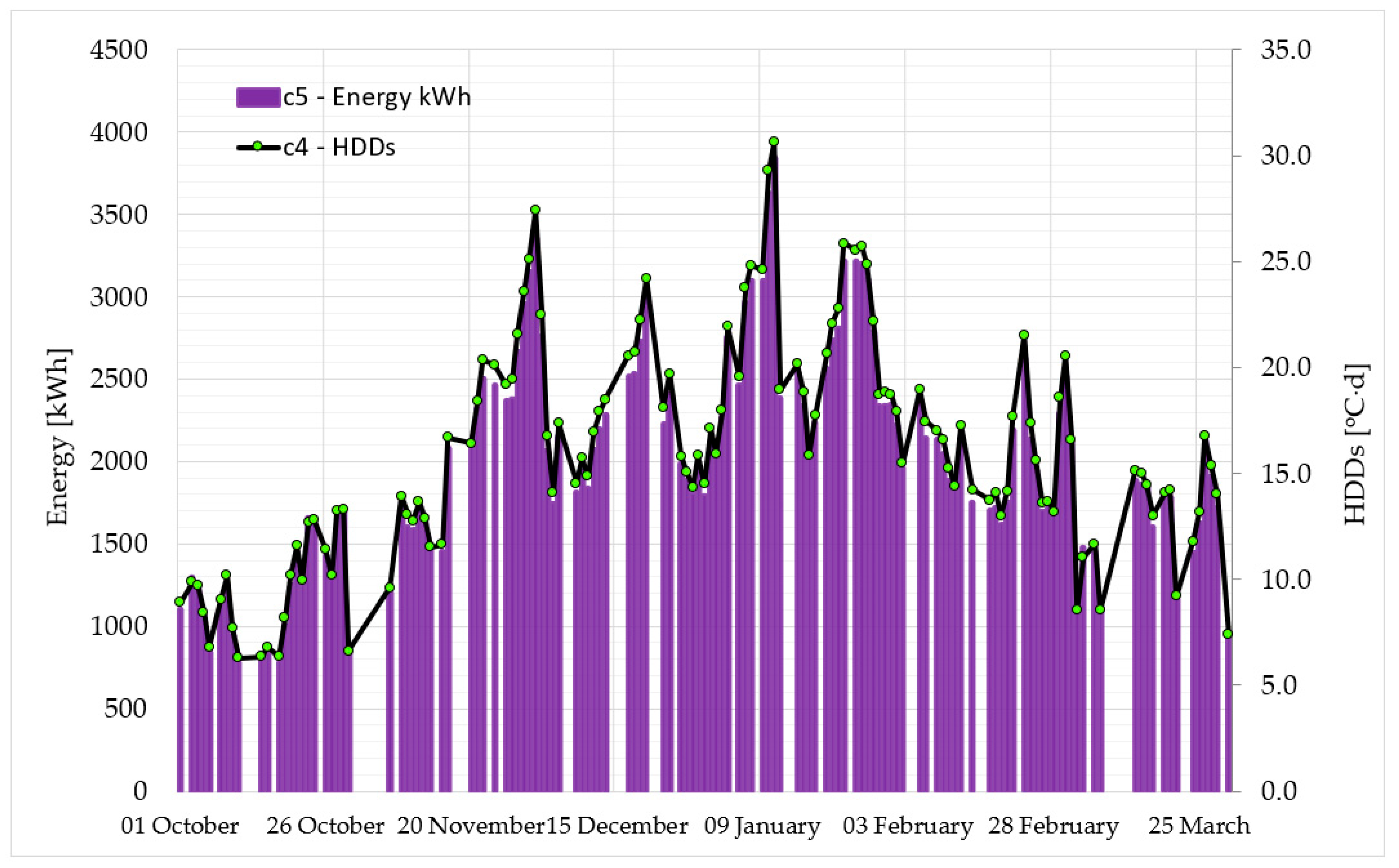
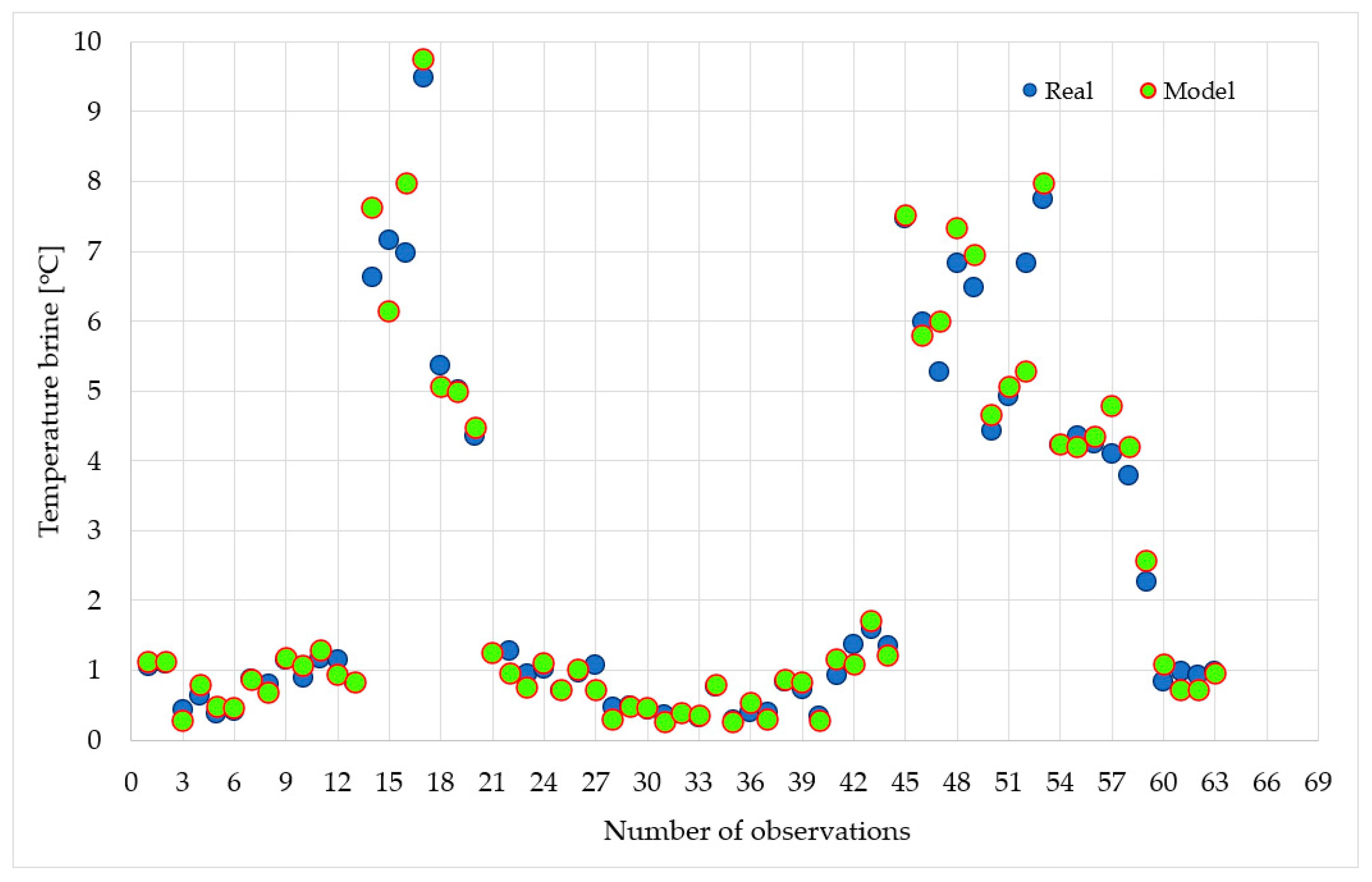
3. Research Results and Analysis
- MBE index: from −5% to +5%;
- CV RMSE: index 15%.
4. Conclusions and Perspectives
- The model’s calculations exhibit a mean deviation of 0.22 °C from the actual data, with a confidence interval for the examined group of objects ranging from 0.15 to 0.29 °C;
- The quality assessment metrics for the applied model are as follows: MBE = −1.3%, CV RMSE = 14.76%, and R2 = 0.98. Consequently, it can be concluded that the method outlined in this article delivers satisfactory results in estimating the brine temperature of the lower heat source, closely approximating the temperature of the ground influenced by the HP’s operation;
- The presented tool proves invaluable for swiftly analyzing the determination of the lower heat source’s operating temperature during the heating season, thus mitigating the risks of ground freezing or HP damage in cases of excessively low brine temperatures;
- The outcomes of this case study suggest the potential utilization of a rough set theory-based model in other buildings reliant on HP-based heating systems. Therefore, future research endeavors aim to extend this study to other facilities, with the goal of verifying whether the described method yields comparable results to those obtained for the analyzed public utility building;
- As part of further research, the authors want to use other methods, such as artificial neural networks or the Takagi–Sugeno type fuzzy model, to predict brine temperature;
- Access to information about the brine temperature can offer insights into the load placed on the lower heat source, as an excessive load has the potential to significantly decrease the brine temperature in the boreholes, thereby influencing system performance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rybach, L.; Sanner, B. Ground-source heat pump systems the European experience. GHC Bull. 2000, 21, 16–26. [Google Scholar]
- Piotrowska-Woroniak, J. Assessment of Ground Regeneration around Borehole Heat Exchangers between Heating Seasons in Cold Climates: A Case Study in Bialystok (NE, Poland). Energies 2021, 14, 4793. [Google Scholar] [CrossRef]
- Rubik, M. Heat Pumps Guide; Information Center for Installation Technology in Construction: Warsaw, Poland, 2006. (In Polish) [Google Scholar]
- Zhao, Y.; Pang, Z.; Huang, Y.; Ma, Z. An efficient hybrid model for thermal analysis of deep borehole heat exchangers. Geotherm. Energy 2020, 8, 18. [Google Scholar] [CrossRef]
- Kasuda, T.; Archenbach, P. Earth Temperature and Thermal Diffusivity at Selected Stations in the United States; National Bureau of Standards: Gaithesburg, MD, USA, 1965. [Google Scholar]
- Atwany, H.; Hamdan, M.O.; Abu-Nabah, B.A.; Alami, A.H.; Attom, M. Experimental evaluation of ground heat exchanger in UAE. Renew. Energy 2020, 159, 538–546. [Google Scholar] [CrossRef]
- Saskia, M.M.; Wallin, E. Ground temperature profiles and thermal rock properties at Wairakei, New Zealand. Renew. Energy 2012, 43, 313–321. [Google Scholar] [CrossRef]
- Spitler, J.D.; Gehlin, S.E. Thermal response testing for ground source heat pump systems-An historical review. Renew. Sustain. Energy Rev. 2015, 50, 1125–1137. [Google Scholar] [CrossRef]
- Al-Temeemi, A.; Harris, D. The generation of subsurface temperature profiles for Kuwait. Energy Build. 2001, 33, 837–841. [Google Scholar] [CrossRef]
- Sáez Blázquez, C.; Farfán Martín, A.; Martín Nieto, I.; Carrasco García, P.; Sánchez Pérez, L.S.; González-Aguilera, D. Efficiency Analysis of the Main Components of a Vertical Closed-Loop System in a Borehole Heat Exchanger. Energies 2017, 10, 201. [Google Scholar] [CrossRef]
- Spitler, J.; Bernier, M. 2-Vertical borehole ground heat exchanger design methods. In Advances in Ground-Source Heat Pump Systems; Rees, S.J., Ed.; Woodhead Publishing: Oxford, UK, 2016; pp. 29–61. ISBN 978-0-08-100311-4. [Google Scholar] [CrossRef]
- Naicker, S.S.; Rees, S.J. Long-term high frequency monitoring of a large borehole heat exchanger array. Renew. Energy 2020, 145, 1528–1542. [Google Scholar] [CrossRef]
- Nian, Y.; Cheng, W. Analytical g-function for vertical geothermal boreholes with effect of borehole heat capacity. Appl. Therm. Eng. 2018, 140, 733–744. [Google Scholar] [CrossRef]
- Yu, X.; Li, H.; Yao, S.; Nielsen, V.; Heller, A. Development of an efficient numerical model and analysis of heat transfer performance for borehole heat exchanger. Renew. Energy 2020, 152, 189–197. [Google Scholar] [CrossRef]
- Wang, C.; Li, H.; Huang, Z.; Lu, Y.; Huang, X.; Gan, L. A new heat transfer model for single U-pipe ground heat exchanger. Appl. Therm. Eng. 2019, 154, 400–406. [Google Scholar] [CrossRef]
- Ghoreish-Madiseh, S.; Kuyuk, A.; de Brito, M.A.R. An analytical model for transient heat transfer in ground-coupled heat exchangers of closed-loop geothermal systems. Appl. Therm. Eng. 2019, 150, 696–705. [Google Scholar] [CrossRef]
- Javadi, H.; Urchueguia, J.F.; Mousavi Ajarostaghi, S.S.; Badenes, B. Numerical Study on the Thermal Performance of a Single U-Tube Borehole Heat Exchanger Using Nano-Enhanced Phase Change Materials. Energies 2020, 13, 5156. [Google Scholar] [CrossRef]
- Katsura, T.; Sakata, Y.; Ding, L.; Nagano, K. Development of Simulation Tool for Ground Source Heat Pump Systems Influenced by Ground Surface. Energies 2020, 13, 4491. [Google Scholar] [CrossRef]
- Lei, X.; Zheng, X.; Duan, C.; Ye, J.; Liu, K. Three-Dimensional Numerical Simulation of Geothermal Field of Buried Pipe Group Coupled with Heat and Permeable Groundwater. Energies 2019, 12, 3698. [Google Scholar] [CrossRef]
- Piotrowska-Woroniak, J. Determination of the Selected Wells Operational Power with Borehole Heat Exchangers Operating in Real Conditions, Based on Experimental Tests. Energies 2021, 14, 2512. [Google Scholar] [CrossRef]
- Liu, M.; Hino, T.; Ooka, R.; Wen, K.; Choi, W.; Lee, D.; Ikeda, S. Development of distributed multiple-source and multiple-use heat pump system using renewable energy: Outline of test building and experimental evaluation of cooling and heating performance. Jpn. Archit. Rev. 2021, 4, 241–252. [Google Scholar] [CrossRef]
- Luo, J.; Rohn, J.; Bayer, M.; Priess, A.; Wilkmann, L.; Xiang, W. Heating and cooling performance analysis of a ground source heat pump system in Southern Germany. Geothermics 2015, 53, 57–66. [Google Scholar] [CrossRef]
- Sivasakthivel, T.; Murugesan, K.; Kumar, S.; Hu, P.; Kobiga, P. Experimental study of thermal performance of a ground source heat pump system installed in a Himalayan city of India for composite climatic conditions. Energy Build. 2016, 131, 193–206. [Google Scholar] [CrossRef]
- Shen, J.; Zhou, C.; Luo, Y.; Tian, Z.; Zhang, S.; Fan, J.; Ling, Z. Comprehensive thermal performance analysis and optimization study on U-type deep borehole ground source heat pump systems based on a new analytical model. Energy 2023, 274, 127367. [Google Scholar] [CrossRef]
- Żukowski, M.; Woroniak, G.; Piotrowska-Woroniak, J. Experimental research and numerical simulations of a ceramic panel used for solar energy conversion. Sol. Energy 2019, 194, 27–36. [Google Scholar] [CrossRef]
- Zhai, X.; Cheng, X.; Wang, R. Heating and cooling performance of a mini type ground source heat pump system. Appl. Therm. Eng. 2017, 111, 1366–1370. [Google Scholar] [CrossRef]
- Piotrowska-Woroniak, J. Analysis of a Vertical Ground Heat Exchanger Operation Cooperating with a Heat Pump. In Renewable Energy Sources: Engineering, Technology, Innovation; Wróbel, M., Jewiarz, M., Szlek, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 587–601. ISBN 978-3-030-13887-5. [Google Scholar]
- Port, P.C. Guidelines for Designing, Realization and Receiving Installations Powered by Heat Pumps; Part 1; Polish Organization for the Development of Heat Pump Technology: Cracow, Poland, 2013. (In Polish) [Google Scholar]
- ASHRAE. Measurement of Energy and Demand Savings; Technical Report No. 14-2014; American Society of Heating, Ventilating, and Air Conditioning Engineers: Atlanta, GA, USA, 2014; Available online: https://upgreengrade.ir/admin_panel/assets/images/books/ASHRAE%20Guideline%2014-2014.pdf (accessed on 5 May 2023).
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- ISO 12831-1:2017-08; European Standard: Heating Systems in Buildings. CEN: Brussels, Belgium, 2017.
- ANSI/ASHRAE Standard 169-2021; Climatic Data for Building Design Standards. American Society of Heating. Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2021. Available online: https://webstore.ansi.org/standards/ashrae/ansiashrae1692021?gclid=CjwKCAjwsKqoBhBPEiwALrrqiNbS8DQyzjDpm7U0JjiLl7O7DmjeooAjd9raUJFLrs99ZEe4_XxrchoCLtoQAvD_BwE (accessed on 6 May 2023).
- Institute of Meteorology and Water Management. Data from the Institute of Meteorology and Water Management. Available online: https://danepubliczne.imgw.pl/ (accessed on 4 May 2023). (In Polish).
- Pawlak, Z. Rough Sets: Theoretical Aspects of Reasoning about Data; Kluwer Academic Press: Dordrecht, The Netherlands, 2012; Available online: http://bcpw.bg.pw.edu.pl/Content/2026/RoughSetsRep29.pdf (accessed on 6 May 2023).
- Nutech Solution-Science for Business. 2005. Available online: http://www.nutechsolutions.com.pl/ (accessed on 10 May 2023).
- Nguyen, D.V.; Yamada, K.; Unehara, M. Extended Tolerance Relation to Define a New Rough Set Model in Incomplete Information Systems. Adv. Fuzzy Syst. 2013, 2013, 372091. [Google Scholar] [CrossRef]
- Renigier-Biłozor, M. Zastosowanie teorii zbiorów przybliżonych do masowej wyceny nieruchomości na małych rynkach (Application of rough set theory for mass valuation of real estate in small markets). Acta Sci. Pol. Adm. Locorum 2008, 7, 35–51. Available online: http://wydawnictwo.uwm.edu.pl/uploads/documents/czytelnia/scientiarum/scientiarum7(3).pdf#page=35 (accessed on 10 May 2023).
- Szul, T.; Nęcka, K.; Knaga, J. Application of Rough Set Theory to Establish the Amount of Waste in Households in Rural Areas. Ecol. Chem. Eng. S 2017, 24, 311–325. [Google Scholar] [CrossRef][Green Version]
- Piotrowska-Woroniak, J.; Szul, T. Application of a Model Based on Rough Set Theory (RST) to Estimate the Energy Efficiency of Public Buildings. Energies 2022, 15, 8793. [Google Scholar] [CrossRef]
- Szul, T.; Kokoszka, S. Application of Rough Set Theory (RST) to Forecast Energy Consumption in Buildings Undergoing Thermal Modernization. Energies 2020, 13, 1309. [Google Scholar] [CrossRef]



| Object Number | Condition Attributes | Decision Attribute | ||||
|---|---|---|---|---|---|---|
| c1 | c2 | c3 | c4 | c5 | d | |
| 1 | 5.75 | 1 | 13.18 | 12.6 | 1595 | 1.82 |
| 6 | −2.64 | 1 | 47.12 | 20.9 | 2598 | 1.03 |
| 23 | 1.79 | 1 | 41.7 | 16.5 | 2082 | 0.67 |
| 38 | 3.27 | 2 | 18.4 | 15.0 | 1872 | 0.83 |
| 63 | 3.43 | 9 | 5.91 | 14.9 | 1826 | 1.14 |
| Assessment Indicator | Results |
|---|---|
| MAPE (%) | 12.2 |
| CV RMSE (%) | 14.76 |
| MBE (%) | −1.3 |
| R2 | 0.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piotrowska-Woroniak, J.; Szul, T.; Woroniak, G. Application of a Model Based on Rough Set Theory (RST) for Estimating the Temperature of Brine from Vertical Ground Heat Exchangers (VGHE) Operated with a Heat Pump—A Case Study. Energies 2023, 16, 7182. https://doi.org/10.3390/en16207182
Piotrowska-Woroniak J, Szul T, Woroniak G. Application of a Model Based on Rough Set Theory (RST) for Estimating the Temperature of Brine from Vertical Ground Heat Exchangers (VGHE) Operated with a Heat Pump—A Case Study. Energies. 2023; 16(20):7182. https://doi.org/10.3390/en16207182
Chicago/Turabian StylePiotrowska-Woroniak, Joanna, Tomasz Szul, and Grzegorz Woroniak. 2023. "Application of a Model Based on Rough Set Theory (RST) for Estimating the Temperature of Brine from Vertical Ground Heat Exchangers (VGHE) Operated with a Heat Pump—A Case Study" Energies 16, no. 20: 7182. https://doi.org/10.3390/en16207182
APA StylePiotrowska-Woroniak, J., Szul, T., & Woroniak, G. (2023). Application of a Model Based on Rough Set Theory (RST) for Estimating the Temperature of Brine from Vertical Ground Heat Exchangers (VGHE) Operated with a Heat Pump—A Case Study. Energies, 16(20), 7182. https://doi.org/10.3390/en16207182








