Modeled and Measured Operating Temperatures of Floating PV Modules: A Comparison
Abstract
:1. Introduction
2. Materials and Methods
2.1. Operating Temperature of PV Modules
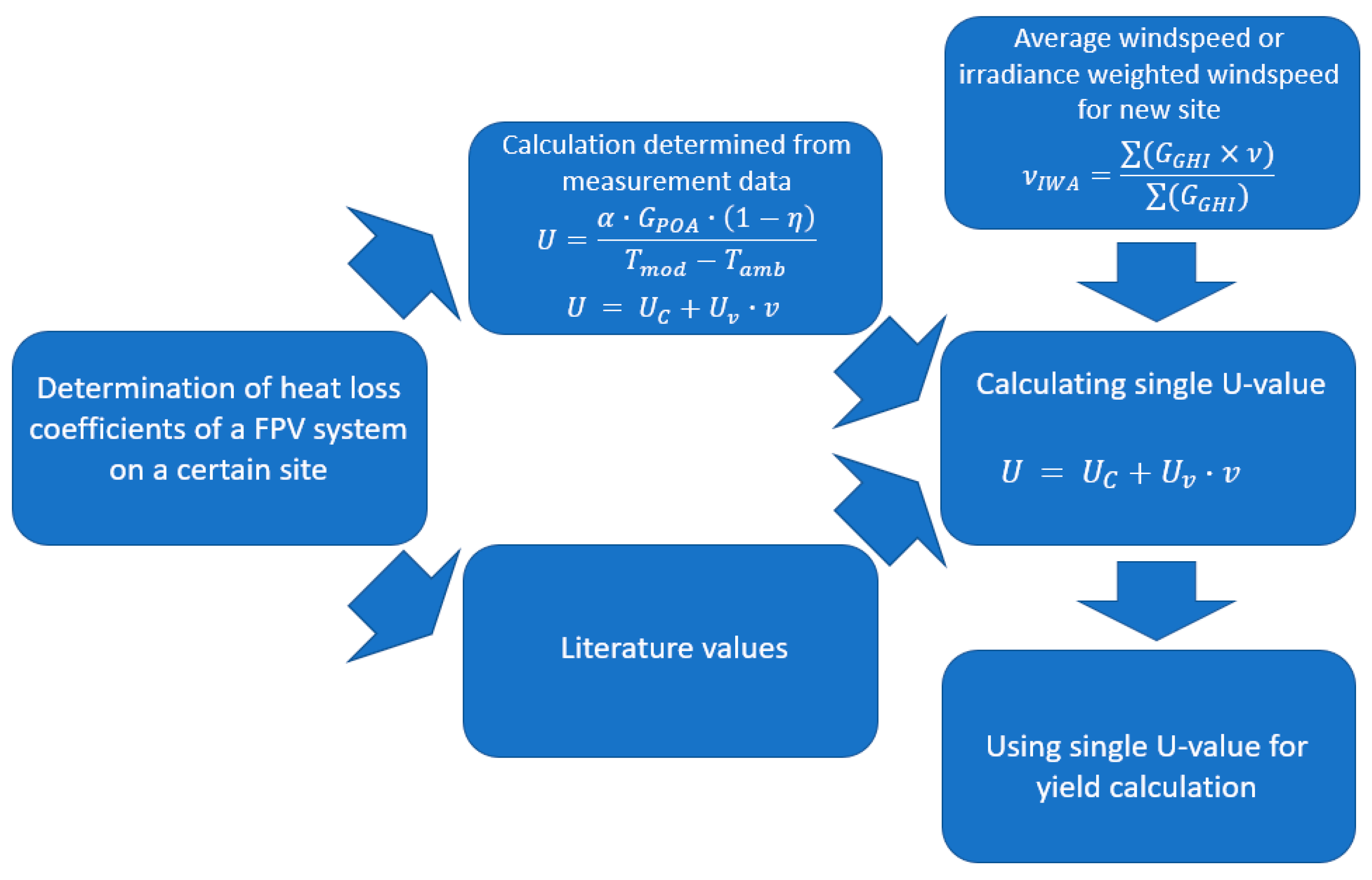
2.2. Overview of Heat Loss Coefficients
2.3. Software Packages
2.3.1. PVsyst
2.3.2. Pvlib
2.4. PV Systems
2.4.1. Solarisfloat in The Netherlands
2.4.2. Current Solar in Sri Lanka
2.5. Data Handling
2.6. Wind Speed Height
3. Results
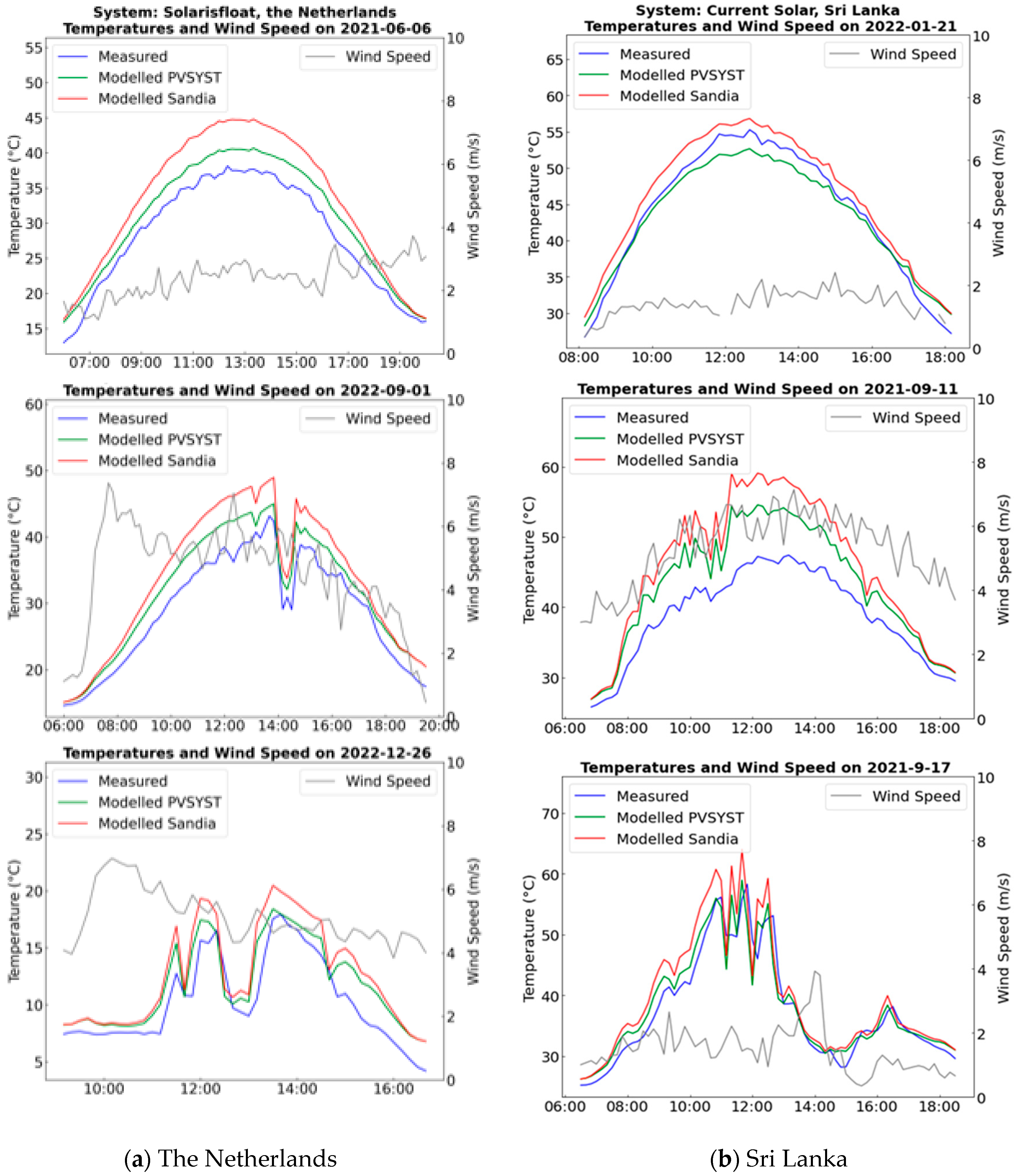
3.1. Direct Comparison of Measured Temperature Data with Modeled Data
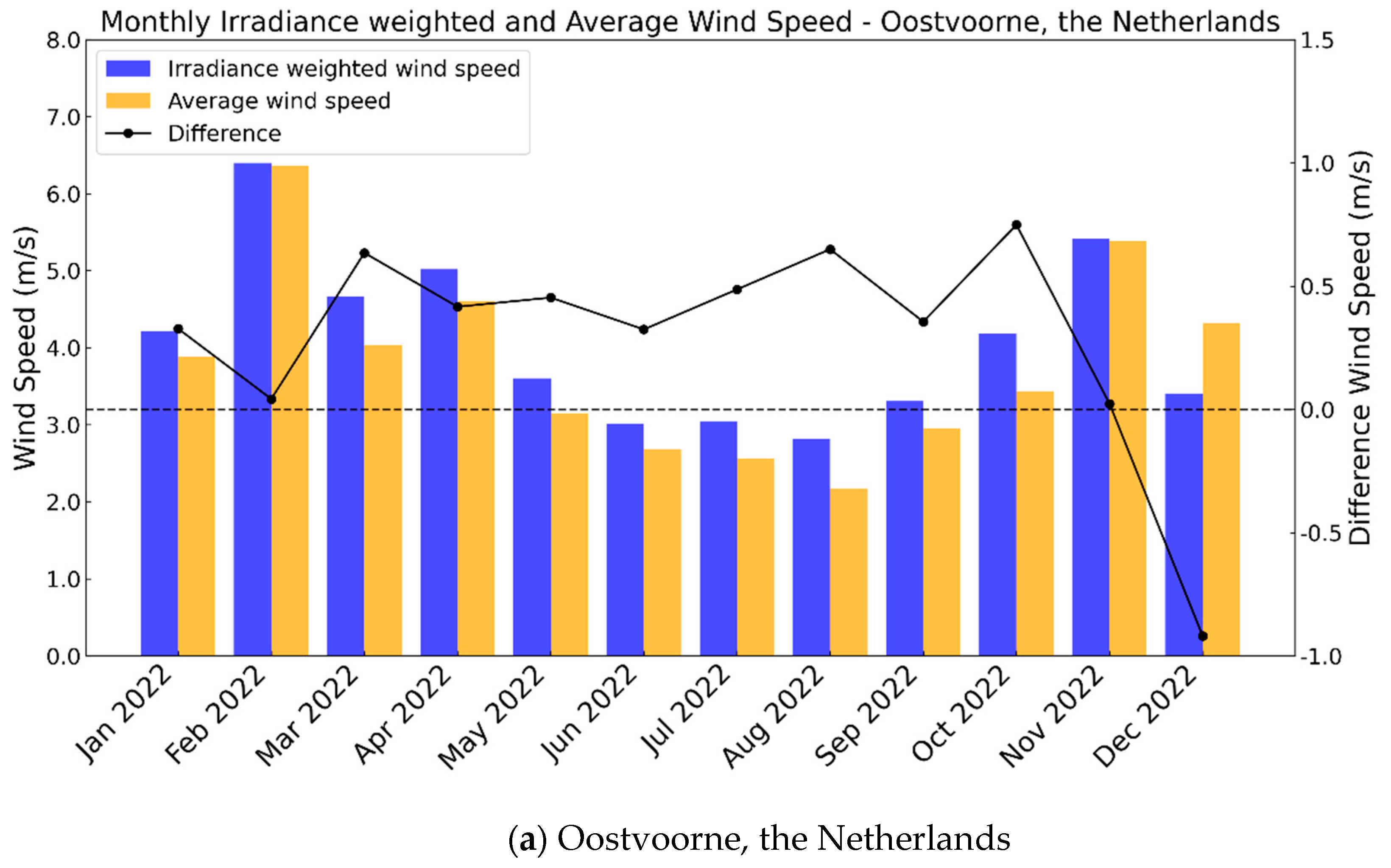
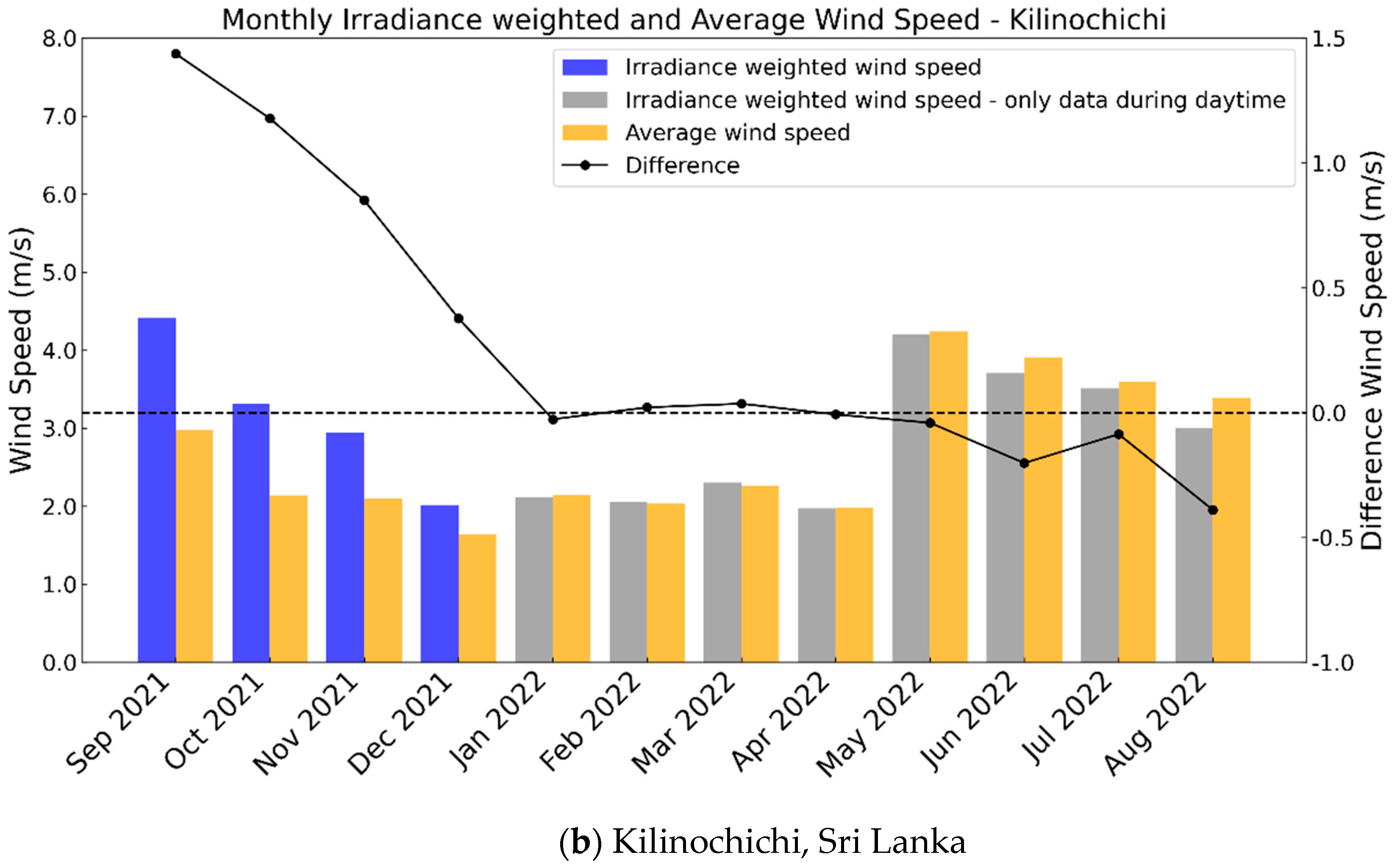
3.2. Irradiance Weighted Wind Speed
3.3. Heat Loss Coefficients
3.4. Thermal Loss Calculation Using Commercial Software
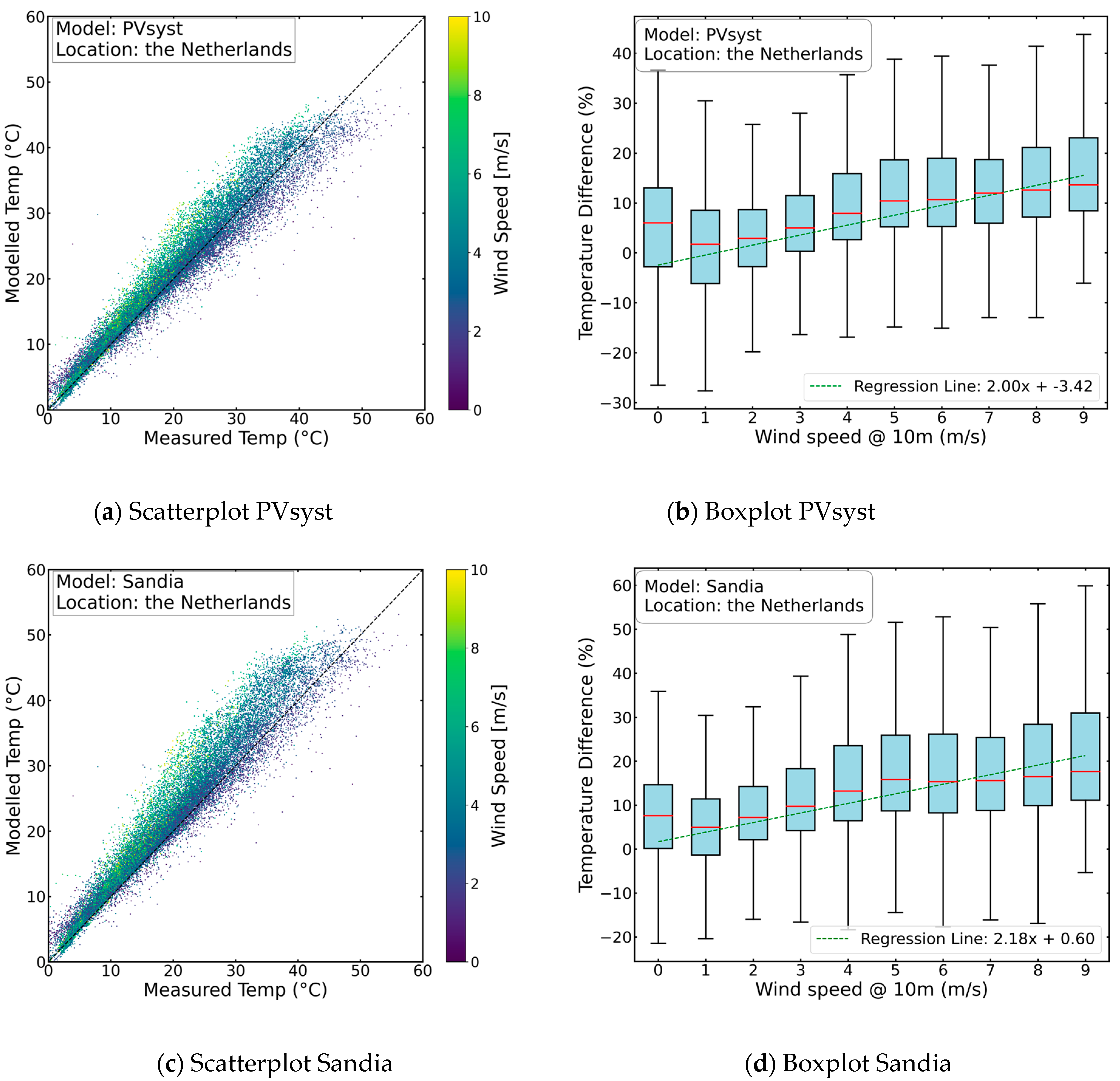
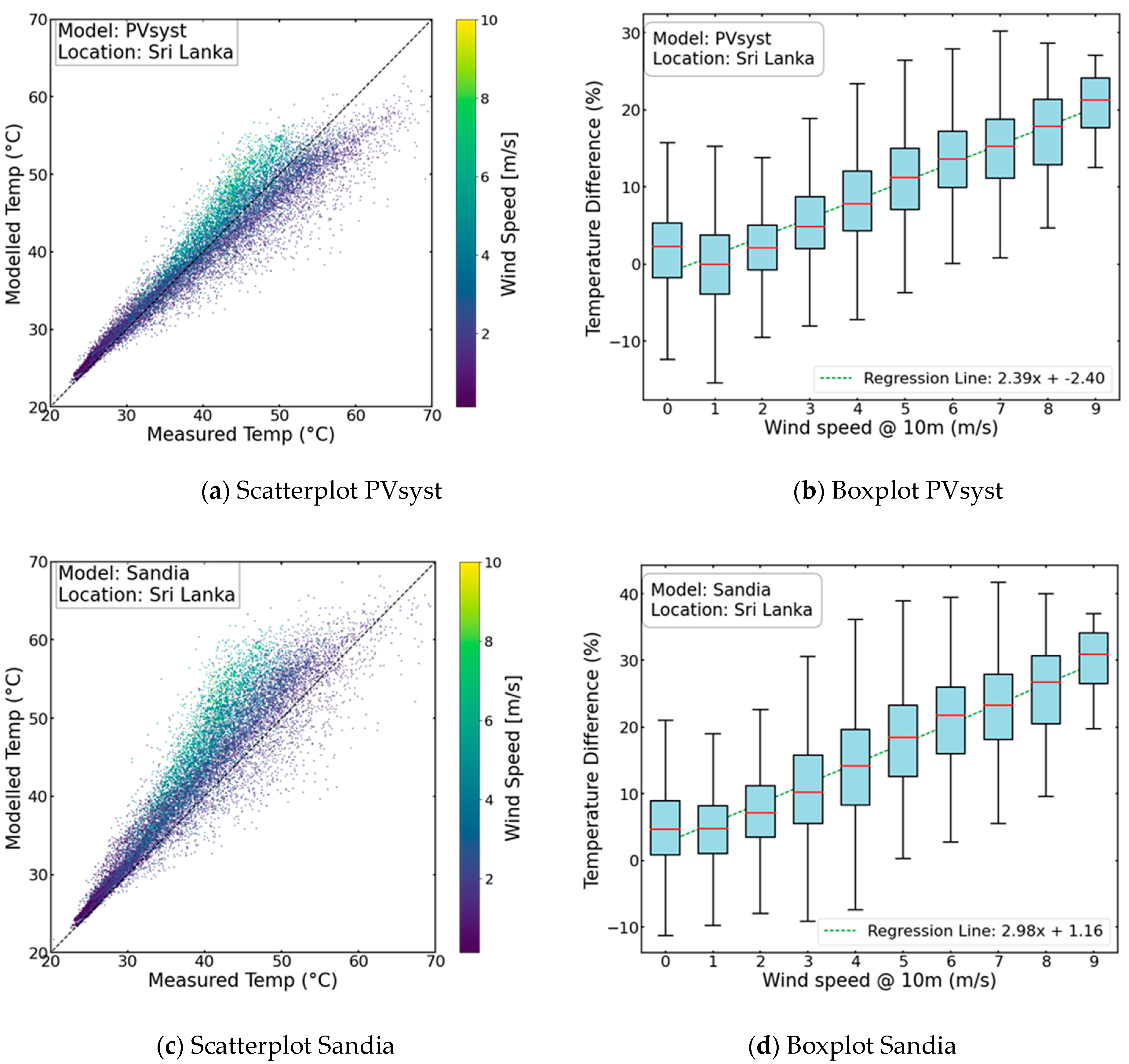
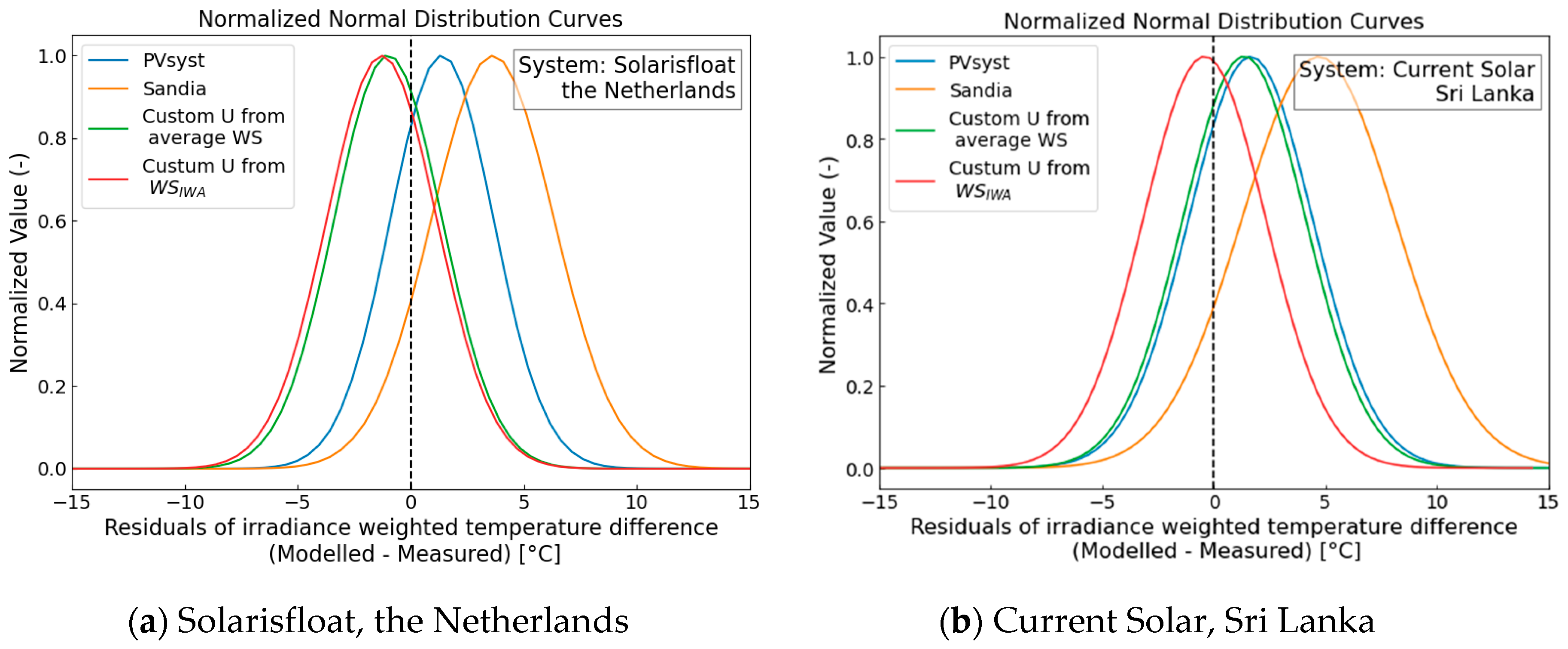
3.5. Comparative Analysis of Models through Residual Examination
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Skoplaki, E.; Palyvos, J.A. Operating temperature of photovoltaic modules: A survey of pertinent correlations. Renew. Energy 2009, 34, 23–29. [Google Scholar] [CrossRef]
- Liu, H.; Krishna, V.; Lun Leung, J.; Reindl, T.; Zhao, L. Field experience and performance analysis of floating PV technologies in the tropics. Prog. Photovoltaics Res. Appl. 2018, 26, 957–967. [Google Scholar] [CrossRef]
- Kjeldstad, T.; Lindholm, D.; Marstein, E.; Selj, J. Cooling of floating photovoltaics and the importance of water temperature. Solar Energy 2021, 218, 544–551. [Google Scholar] [CrossRef]
- Lindholm, D.; Kjeldstad, T.; Selj, J.; Marstein, E.S.; Fjær, H.G. Heat loss coefficients computed for floating PV modules. Prog. Photovoltaics Res. Appl. 2021, 29, 1262–1273. [Google Scholar] [CrossRef]
- Kamuyu, W.C.L.; Lim, J.R.; Won, C.S.; Ahn, H.K. Prediction model of photovoltaic module temperature for power performance of floating PVs. Energies 2018, 11, 447. [Google Scholar] [CrossRef]
- Hayibo, K.S.; Mayville, P.; Kailey, R.K.; Pearce, J.M. Water Conservation Potential of Self-Funded Foam-Based Flexible Surface-Mounted Floatovoltaics. Energies 2020, 13, 6285. [Google Scholar] [CrossRef]
- Kaplanis, S.; Kaplani, E.; Kaldellis, J.K. PV Temperature Prediction Incorporating the Effect of Humidity and Cooling Due to Seawater Flow and Evaporation on Modules Simulating Floating PV Conditions. Energies 2023, 16, 4756. [Google Scholar] [CrossRef]
- IEC 61853-2; Photovoltaic (PV) Module Performance Testing and Energy Rating—Part 2: Spectral Responsivity, Incidence Angle and Module Operating Temperature Measurements. IEC: Geneva, Switzerland, 2018.
- Faiman, D. Assessing the outdoor operating temperature of photovoltaic modules. Prog. Photovoltaics Res. Appl. 2008, 16, 307–315. [Google Scholar] [CrossRef]
- Barykina, E.; Hammer, A. Modeling of photovoltaic module temperature using Faiman model: Sensitivity analysis for different climates. Sol. Energy 2017, 146, 401–416. [Google Scholar] [CrossRef]
- Ghabuzyan, L.; Pan, K.; Fatahi, A.; Kuo, J.; Baldus-Jeursen, C. Thermal effects on photovoltaic array performance: Experimentation, modeling, and simulation. Appl. Sci. 2021, 11, 1460. [Google Scholar] [CrossRef]
- Koehl, M.; Heck, M.; Wiesmeier, S.; Wirth, J. Modeling of the nominal operating cell temperature based on outdoor weathering. Sol. Energy Mater. Sol. Cells 2011, 95, 1638–1646. [Google Scholar] [CrossRef]
- King, D.L.; Boyson, W.E.; Kratochvill, J.A. Photovoltaic Array Performance Model; Sandia National Laboratories: Albuquerque, NM, USA, 2004. [Google Scholar] [CrossRef]
- Dörenkämper, M.; Wahed, A.; Kumar, A.; De Jong, M.M.; Kroon, J.; Reindl, T. The cooling effect of floating PV in two different climate zones: A comparison of field test data from The Netherlands and Singapore. Sol. Energy 2021, 214, 229–247. [Google Scholar] [CrossRef]
- PVsyst: Array Thermal Losses. Available online: https://www.pvsyst.com/help/thermal_loss.htm (accessed on 14 August 2023).
- Holmgren, W.F.; Hansen, C.W.; and Mikofski, M.A. pvlib python: A python package for modeling solar energy systems. J. Open Source Softw. 2018, 3, 884. [Google Scholar] [CrossRef]
- Holton, J.R.; Hakim, G.J. Wind and Wind Systems. In Introduction to Dynamic Meteorology; Elsevier Academic Press: Amsterdam, The Netherlands, 2013; ISBN 9780123848666. [Google Scholar]





| System | U0′ [W/Km2] | U1′ [Ws/Km3] | Uc [W/m2K] | Uv [W/m3Ks] | a [-] | b [-] | Reference |
|---|---|---|---|---|---|---|---|
| LPV (open structure, Negeve desert) | 26.86 | 6.11 | −3.38 | −0.13 | Köhl et al., 2011 [12] | ||
| LPV (closed structure, Alps) | 28.04 | 7.77 | −3.55 | −0.12 | Köhl et al., 2011 [12] | ||
| LPV (Open rack, glass-cell-glass) | −3.47 | −0.0594 | King et al., 2004 [13] | ||||
| LPV (Open rack, glass-cell-polymer) | −3.56 | −0.0750 | King et al., 2004 [13] | ||||
| LPV (Open rack, wind independent) | 29 | 0 | PVsyst, 1996 [15] | ||||
| LPV (Fully insulated backside, wind independent) | 15 | 0 | PVsyst, 1996 [15] | ||||
| LPV (Open rack, with wind dependency) | 25 | 1.2 | PVsyst, 1996 [5] | ||||
| FPV (open structure, The Netherlands) | 24.4 | 6.5 | Dörenkämper et al., 2021 [14] | ||||
| FPV (closed structure, The Netherlands) | 25.2 | 3.7 | Dörenkämper et al., 2021 [14] | ||||
| LPV (open structure, The Netherlands) | 18.6 | 4.4 | Dörenkämper et al., 2021 [14] |
| Method | U-Value The Netherlands [W/m2K] | U-Value Sri Lanka [W/m2K] |
|---|---|---|
| Custom U (Average WS) | 39.5 | 33.2 |
| Custom U (WSIWA) | 40.6 | 37.9 |
| Temperature Model | Specific Yield Netherlands [kWh/kWp] | Specific Yield Sri Lanka [kWh/kWp] |
|---|---|---|
| Measured Temperatures | 1036 | 1111 |
| PVsyst | 1021 (−1.4%) | 1095 (−1.4%) |
| Sandia | 1019 (−1.6%) | 1090 (−1.9%) |
| Custom U (Average WS) | 1037 (0.1%) | 1105 (−0.5%) |
| Custom U (WSIWA) | 1038 (0.1%) | 1112 (0.1%) |
| Temperature Model | Mean Value Weighted Residual Analysis NL [°C] | SD Normal Distribution NL [°C] | Mean Value Weighted Residual Analysis SL [°C] | SD Normal Distribution SL [°C] |
|---|---|---|---|---|
| PVsyst | 1.00 | 2.3 | 1.11 | 2.78 |
| Sandia | 2.15 | 2.7 | 2.79 | 3.44 |
| Custom U (Average WS) | −0.21 | 2.4 | 0.95 | 2.75 |
| Custom U (WSIWA) | −0.36 | 2.4 | −0.03 | 2.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dörenkämper, M.; de Jong, M.M.; Kroon, J.; Nysted, V.S.; Selj, J.; Kjeldstad, T. Modeled and Measured Operating Temperatures of Floating PV Modules: A Comparison. Energies 2023, 16, 7153. https://doi.org/10.3390/en16207153
Dörenkämper M, de Jong MM, Kroon J, Nysted VS, Selj J, Kjeldstad T. Modeled and Measured Operating Temperatures of Floating PV Modules: A Comparison. Energies. 2023; 16(20):7153. https://doi.org/10.3390/en16207153
Chicago/Turabian StyleDörenkämper, Maarten, Minne M. de Jong, Jan Kroon, Vilde Stueland Nysted, Josefine Selj, and Torunn Kjeldstad. 2023. "Modeled and Measured Operating Temperatures of Floating PV Modules: A Comparison" Energies 16, no. 20: 7153. https://doi.org/10.3390/en16207153
APA StyleDörenkämper, M., de Jong, M. M., Kroon, J., Nysted, V. S., Selj, J., & Kjeldstad, T. (2023). Modeled and Measured Operating Temperatures of Floating PV Modules: A Comparison. Energies, 16(20), 7153. https://doi.org/10.3390/en16207153





