The Shockley–Queisser Efficiency Limit of Solar Thermophotovoltaic (STPV) Cells Using Different Photovoltaic Cells and a Radiation Shield Considering the Étendue of Solar Radiation

Abstract

A theoretical model is developed to determine the Shockley–Queisser efficiency limit of solar thermophotovoltaic (STPV) cells with single- or double-junction photovoltaic (PV) cells and a simple radiation shield considering the divergence nature of concentrated solar radiation. A combination of adaptive parametric sweep and graphic-based methods is developed to solve the highly nonlinear correlations of energy and carrier transports in the theoretical model to find the optimized operating conditions of STPVs with high stability. The theoretical model predicts that the Shockley–Queisser efficiency limit of STPV under 1000× solar concentration and a simple radiation shield is ~50.1% with InGaAsSb PV cells, ~49.1% with GaSb PV cells, and ~53.2% with InGaAsSb/GaSb double-junction PV cells. The operating temperatures are ~1719.5 K, ~1794.1 K, and 1640.0 K, respectively. An observation from the modeling is that the energy loss due to the thermalization of hot carriers in the STPV with spectrally selected emitters is ~40% less than that in single-junction solar cells. Also determined from the modeling is that ~20% of the collected solar energy is still lost through thermal radiation, even with a simple radiation shield to block the radiative heat loss to the surroundings. Following this understanding, a further improvement in the Shockley–Queisser efficiency of STPVs can be achieved by adopting advanced designs of radiation shields that can separate the absorber of the STPVs far away from the aperture of the radiation shield without using a large-area absorber.

1. Introduction

With a requirement to mitigate global warming, numerous efforts have been developed to improve the harvest efficiency of solar energy, a primary renewable energy source. Solar energy is commonly harvested with solar thermal or photovoltaic methods. The energy conversion efficiency of solar photovoltaic devices is subject to the Shockley–Queisser limit, which is ~30% for single-junction silicon solar cells and ~45% for three-junction III–V semiconductor solar cells [1,2]. Solar thermal methods can achieve higher energy conversion efficiencies by using the entire solar radiation spectrum in electricity generation. Most solar thermal methods require high-temperature working fluids. Managing the mass and energy transport of the high-temperature working fluids and the associated mass and energy loss is among the main challenges in solar thermal methods [3]. Solar thermophotovoltaic (STPV) devices have been popularly studied in the last decade as a solar method that can surpass the efficiency limits of traditional solar cells while not requiring high-temperature working fluids like other solar thermal devices [4,5,6,7,8].

In STPVs, broadband solar radiation is converted to narrowband thermal radiation with photon energy higher than the PV cells’ band edge. The converted narrower-band thermal radiation can generate electron/hole pairs in the PV cells with energies better matched with the bandgap of the PV cell, which can generate electricity with less energy loss due to the thermalization processes of hot carriers in the PV cells. Simple STPV models based on thermodynamics analysis predicted energy conversion efficiency (ECE) of ~70% at ~1000 K and ~85% at ~2250 K [9]. Even with these encouraging results, the majority of demonstrated STPVs have ECE of less than 10% [10]. These lower-than-expected energy conversion efficiencies are partially due to the lack of radiative heat loss control from the hot absorber/emitter of the STPVs to the surroundings. More than half of the collected solar energy is lost to the background in most STPVs. As a result, the ECE of the demonstrated STPVs is nearly three times lower than the ECE of thermophotovoltaic cells (TPV), which do not suffer from solar to thermal energy conversion efficiency under the same operating temperatures [11]. Strategies to reduce the radiative heat loss from STPVs have been proposed in the past decade, including spectrally selective absorbers and radiation shields [10,12,13,14,15]. Among these two methods, radiation shields have the potential to achieve good radiative heat loss control without large-area microscale engineering of the absorber surfaces of the STPVs [16]. However, the radiation shield design should consider the divergence nature of solar radiation to prevent the overly optimistic estimation of the radiative heat loss control level.

Apart from reducing the radiative heat loss, the ECE of STPVs can be improved by increasing the PV cell efficiency. Compared with single-junction PV cells, multi-junction PV cells can better convert non-monochromatic light to electricity. For example, double-junction solar cells can have up to a ~10% efficiency improvement compared with single-junction solar cells [17,18]. Recent experimental work on double-junction TPV also achieved ECE of ~40% under an extremely high temperature of ~2400 K [19].

This study aims to theoretically determine the efficiency limit of heat-loss-controlled STPVs with different PV cells, including double-junction PV cells, with consideration of the divergence nature of solar radiation after commercially available solar concentrators. This maximum theoretical efficiency treats radiative recombination as the only loss mechanism in the PV cells (i.e., Shockley–Queisser limit). The main design constraint of radiation shields is the divergence angle of solar radiation (i.e., ~0.267°). This divergence angle is increased after solar concentration based on the conservation of étendue [20]. The tapering angle of the radiation shield cannot be smaller than the divergence angle of the concentrated solar radiation to have the radiation collected by the absorber of the STPV fully.

The main challenge in determining the Shockley–Queisser limit of STPVs with different PV cells is the highly nonlinear energy and carrier transport equations as a function of the temperature of the STPV, the biased voltages of the PV cells, and the emission bandwidth of the spectrally selective emitter of the STPV. With this consideration, two numerical methods are adopted in the theoretical model of this work to determine the Shockley–Queisser limit of STPVs: (a) using an adaptive method allowing us to effectively find the optimized biased voltage of PV cells, especially for double-junction PV cells; (b) using a graphic-based method to find the operating temperature of the STPVs under each specified biased voltage of the PV cells and the emission bandwidth of the spectrally selective emitter without stability issues. The following section describes our theoretical model and the numerical approach.

2. Methods

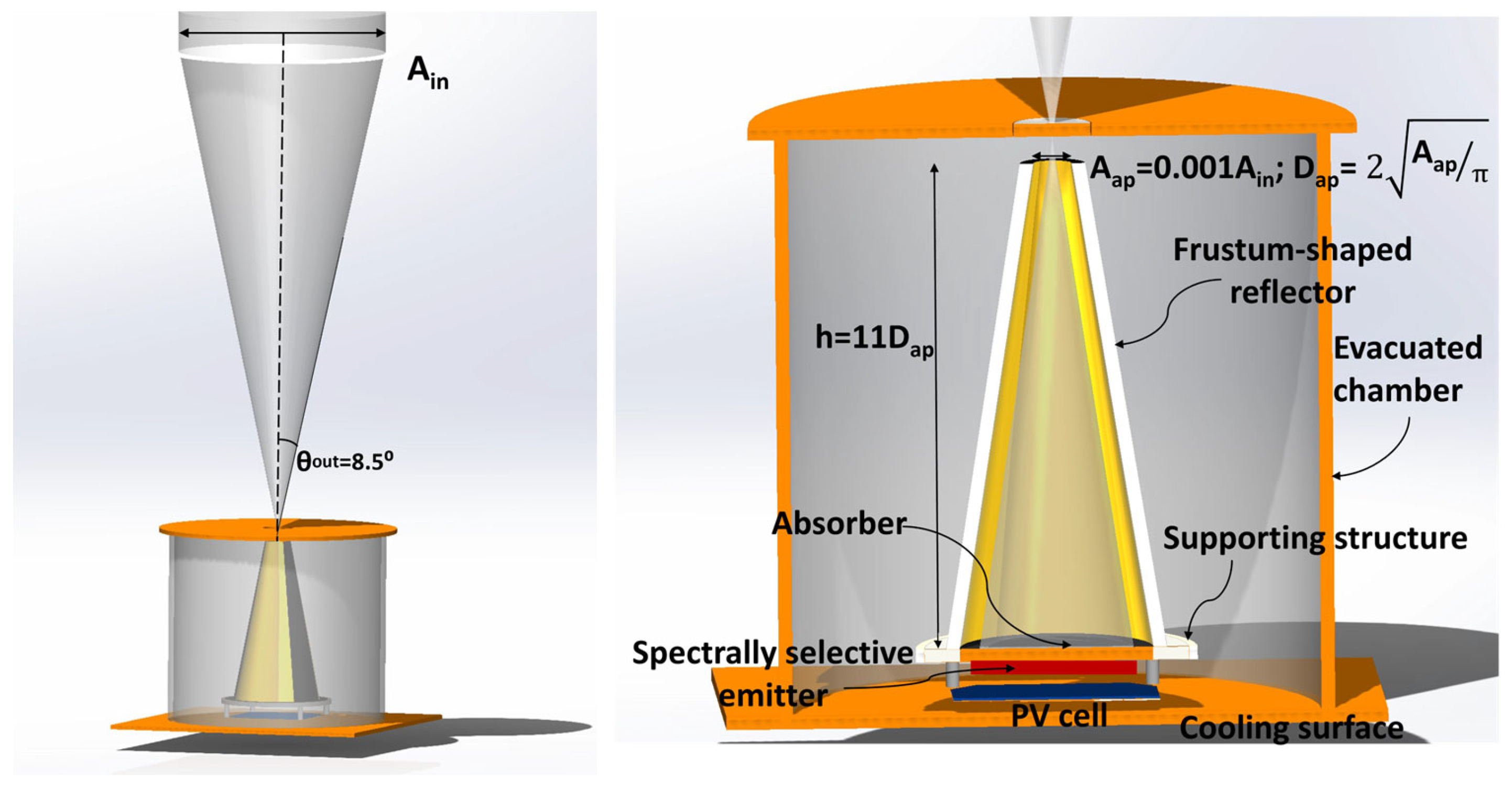
The configuration of the STPVs modeled in this study with a simple radiation shield is illustrated in Figure 1. Highly concentrated solar radiation is delivered to the absorber of the SPTV through the small aperture of the frustum-shaped radiation shield.

Because of the divergence nature of solar radiation, the divergence angle of the concentrated solar radiation can be estimated with the conservation of étendue as [20]

$$A_{in} {\sin }^2({\theta }_{in})=A_{out} {\sin }^2({\theta }_{out})$$

(1)

with ${\theta }_{in}$ and ${\theta }_{out}$ the divergence angle of solar radiation before and after concentration, respectively; $A_{in}$ and $A_{out}$ are the cross-sectional area of the solar beam before and after the concentration, respectively. For 1000× solar concentration, a high concentration ratio that can be achieved with commercial solar collectors increases the divergence angle of solar radiation from ~0.267° to ~8.47° [21]. Thus, the tapering angle of the frustum-shaped radiation shield is selected as 8.5° in this study.

With recent advances in broadband black absorbers for solar energy applications, absorptivity ~0.95 for wavelengths less than 2.5 μm can be achieved at high operating temperatures (e.g., CVD–tungsten–alumina cermet surface) [22]. Note that <~3% solar radiation power has wavelengths longer than 2.5 μm. Since the highly absorbing absorber is also covered with a frustum-shaped radiation shield with a small aperture and the possibility of reflected solar radiation escaping to the surroundings through the aperture is very small, we can consider that the absorber of the STPV captures all the incoming solar radiation like a cavity blackbody [23]. Several designs of spectrally selective emitters have been proposed in the recent two decades to have nearly unity emission at designed wavelength ranges, valuable for energy applications. For example, a 2D punched-hole-type Tantalum photonic crystal can significantly increase the spectral emissivity from ~0.05 to ~0.95 at visible to near-IR wavelengths when the wavelength equals or is smaller than the hole diameter of the emitter [24]. The wavelength λ_sse of the step rise (i.e., the wavelength showing a rapid increase in the emissivity from 0.05 to 0.95) of the spectrally selective emitter can be designed to match the band edge energy of the PV cell, which is 0.55 eV (i.e., ~2.25 µm) for InGaAsSb and 0.726 eV (i.e., ~1.7 µm) for GaSb, to minimize the production of unwanted low-energy photons that cannot be harvested by the PV cells. Thus, as a first-order approximation, the emissivity of the spectrally selected emitter equals 0.95 for the designed emission wavelength range (i.e., the emission bandwidth). For other wavelengths, the emissivity of the spectrally selective emitter equals 0.05 in the analysis.

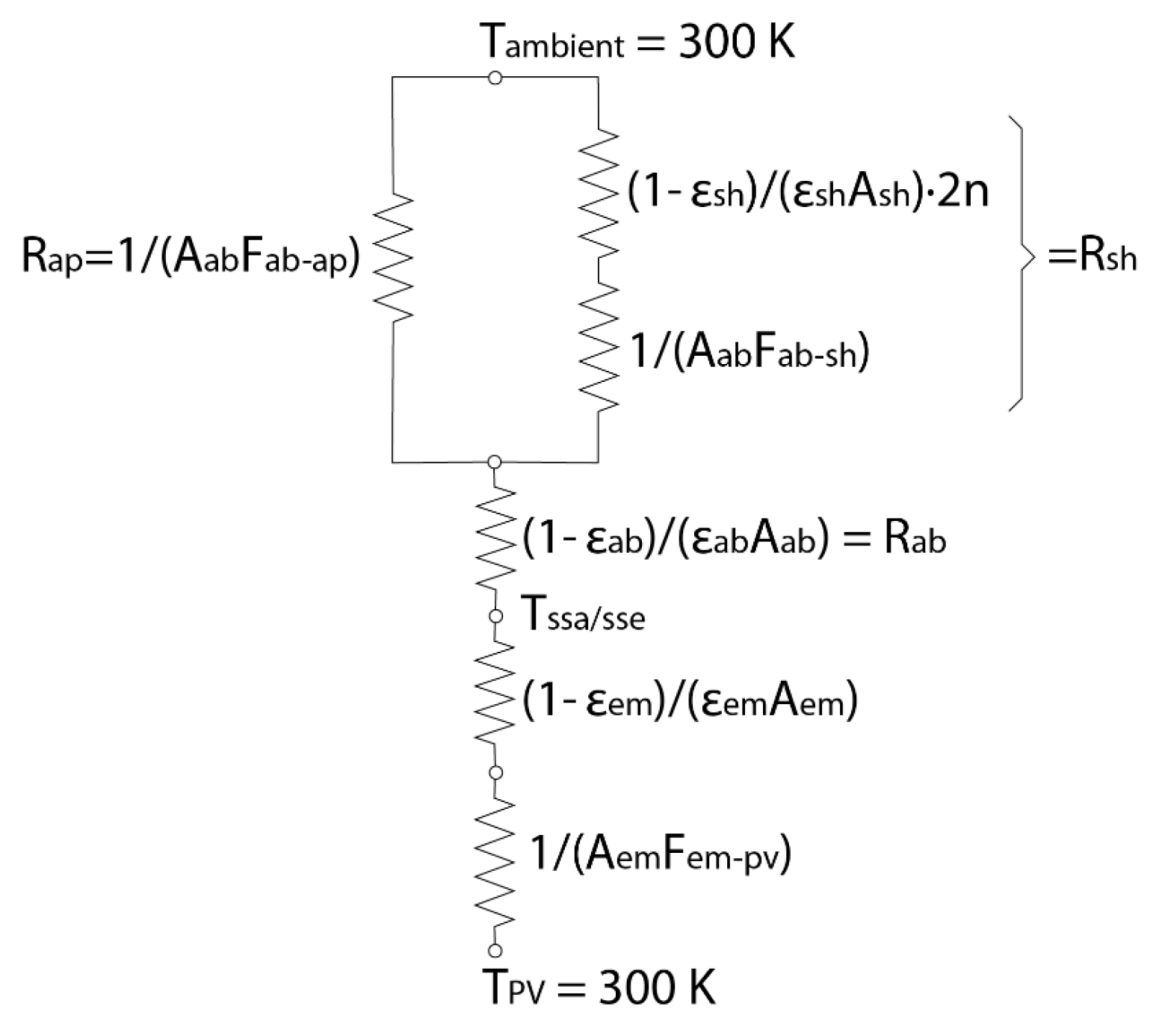
A thermal radiation circuit can be used to describe the radiative heat transfer of SPTVs with radiation shields, as in Figure 2. In the circuit, the view factor from the absorber to the aperture of the radiation shield is $F_{ab-ap}$. $F_{ab-ap}$ can be determined by the separation distance between the aperture and the absorber when the tapering angle of the frustum-shaped radiation shield is fixed [23]. The radiation resistance $R_{ap}$ in Figure 2 for the radiative energy leaving from the absorber to the surroundings through the aperture equals $1/A_{ab}{F}_{ab-ap}$, with $A_{ab}$ the area of the absorber. The area of the absorber is equal to the area of the spectrally selected emitter, as in Figure 1. The radiative resistance $R_{sh}$ for the radiative energy leaving the absorber to the surroundings through the radiation shield equals $1/A_{ab}{F}_{ab-sh}+2n\frac{\left(1-{\epsilon }_{sh}\right)}{A_{sh}{\epsilon }_{sh}}$, with ${\epsilon }_{sh}$ the emissivity of each layer of the radiation shield (>~0.95 for highly reflecting metal, such as silver) and n the number of layers (i.e., 40) of the multilayer insulation constructing the radiation shield [25]. The additional radiation resistance $R_{ab}$ in Figure 2 equals $\left(1-{\epsilon }_{ab}\right)/A_{ab}{\epsilon }_{ab}$ when the absorber is not a blackbody. Thus, based on the thermal circuit values above the $T_{ssa/sse}$ node, the lumped spectral radiation resistance $R_{up}$ for radiation from the absorber to the surroundings can be expressed as follows [23]:

$$R_{up}=\frac{1-{\epsilon }_{ab}}{{\epsilon }_{ab}{A}_{ab}}+{\left(\frac{1}{1/A_{ab}{F}_{ba-ap}}+\frac{1}{1/A_{ab}{F}_{ab-sh}+\left(\frac{1-{\epsilon }_{sh}}{A_{sh}{\epsilon }_{sh}}\right)\cdot 2n}\right)}^{-1}$$

(2)

The corresponding net radiative heat loss rate, $q_{ab-surrounding}$, from the absorber to the 300 K surroundings is [23]

$$q_{ab-surrounding}={\displaystyle {\int }_0^{\infty }\frac{1}{R_{up}}\left[\frac{2\pi h{c}^2}{{\lambda }^5}\frac{1}{e^{hc/(\lambda k_B{T}_{ssa/sse})}-1}-\frac{2\pi h{c}^2}{{\lambda }^5}\frac{1}{e^{hc/(\lambda k_B\cdot 300\mathrm{K})}-1}\right]d\lambda }$$

(3)

with $A_{ab}$ the area of the absorber.

The radiative heat transfer rate $q_{sse\to PV}$ from the spectrally selective emitter to the adjacent PV cell can be expressed as [23]

$$q_{sse\to PV}\approx {\displaystyle {\int }_0^{{\lambda }_{sse}}{\epsilon }_{sse}(\lambda )A_{ab}\left[\frac{2\pi h{c}^2}{{\lambda }^5}\frac{1}{e^{hc/(\lambda k_B{T}_{ssa/sse})}-1}\right]d\lambda }$$

(4)

when appropriate anti-reflection coatings are applied on the top of the PV cell and when the back-reflecting metallic surface at the bottom of the PV cell guides all the sub-bandgap photons back to the spectrally selective emitter. ${\lambda }_{sse}$ corresponds to the band edge energy of a single-junction PV cell or the band edge energy of the lower-bandgap material in a double-junction PV cell.

The radiative heat transfer rate, $q_{PV\to sse}$, from the PV cell to the spectral selected emitter can be expressed as follows [26].

For single-junction PV cells:

$$q_{PV\to sse}={\displaystyle {\int }_0^{{\lambda }_{sse}}{\epsilon }_{sse}(\lambda )A_{ab}\left[\frac{2\pi h{c}^2}{{\lambda }^5}\frac{1}{e^{(hc/\lambda -Q\cdot V)/(k_B\cdot 300\mathrm{K})}-1}\right]d\lambda }$$

(5)

based on a generalized Planck’s law when the PV cell is maintained at 300 K; V is the biased voltage of the single-junction PV cell.

For double-junction PV cells:

$$\begin{array}{cc}{q}_{PV\to sse}=& {\displaystyle {\int }_0^{{\lambda }_{sse,1}}{\epsilon }_{sse}(\lambda )A_{ab}\left[\frac{2\pi h{c}^2}{{\lambda }^5}\frac{1}{e^{(hc/\lambda -Q\cdot V_1)/(k_B\cdot 300\mathrm{K})}-1}\right]d\lambda +}\\ & {\displaystyle {\int }_{{\lambda }_{sse,1}}^{{\lambda }_{sse,2}}{\epsilon }_{sse}(\lambda )A_{ab}\left[\frac{2\pi h{c}^2}{{\lambda }^5}\frac{1}{e^{(hc/\lambda -Q\cdot V_2)/(k_B\cdot 300\mathrm{K})}-1}\right]d\lambda }\end{array}$$

(6)

with V₁ and V₂ the biased voltage of the higher- and lower-bandgap material of the double-junction PV cell, respectively. ${\lambda }_{sse,1}$ and ${\lambda }_{sse,2}$ correspond to the band edge energy of the higher- and lower-bandgap material of the double-junction PV cell. The entire SPTV is encompassed in a vacuum environment, and the conductive heat loss from the STPV to the surroundings is neglected in the analysis [16,27].

Since the solar energy input to the absorber should be equal to the radiative heat loss from the absorber and the net radiative energy transfer from the spectrally selective emitter to the PV cell, the following energy conservation equation can be applied to determine the temperature of the spectral selected absorber/emitter $T_{ssa/sse}$:

$$(\mathrm{incoming} \mathrm{solar} \mathrm{power})=q_{ab-surrounding}+q_{sse\to PV}-q_{PV\to sse}$$

(7)

Once the temperature $T_{ssa/sse}$ (Figure 2) of the absorber/emitter is determined with the above equation, the net photon flux, ${\dot{N}}_{net}$, to the higher-bandgap and lower-bandgap material of the double-junction PV cell can then be calculated as [26]

$${\dot{N}}_{net,high}=A_{ab}{\displaystyle {\int }_0^{{\lambda }_{sse,1}}\left\{{\epsilon }_{sse}\left[\frac{2\pi c}{{\lambda }^4}\frac{1}{e^{hc/(\lambda k_B{T}_{ssa/sse})}-1}\right]-{\epsilon }_{sse}\left[\frac{2\pi c}{{\lambda }^4}\frac{1}{e^{(hc/\lambda -Q\cdot V_1)/(k_B\cdot 300\mathrm{K})}-1}\right]\right\}d\lambda }$$

(8)

$${\dot{N}}_{net,low}=A_{ab}{\displaystyle {\int }_{{\lambda }_{sse,1}}^{{\lambda }_{sse,2}}\left\{{\epsilon }_{sse}\left[\frac{2\pi c}{{\lambda }^4}\frac{1}{e^{hc/(\lambda k_B{T}_{ssa/sse})}-1}\right]-{\epsilon }_{sse}\left[\frac{2\pi c}{{\lambda }^4}\frac{1}{e^{(hc/\lambda -Q\cdot V_2)/(k_B\cdot 300\mathrm{K})}-1}\right]\right\}d\lambda }$$

(9)

Equation (8) can be applied directly for single-junction PV cells. Using the PV cells’ maximum achievable internal quantum efficiency (~95%) [28], the electric energy generation rate from the PV cell can be calculated as $0.95q{\dot{N}}_{net}\cdot V$. The energy conversion efficiency (ECE) of the STPV can then be determined as

$$ECE=0.95\times Q\times ({\dot{N}}_{net,high}\cdot V_1+{\dot{N}}_{net,low}\cdot V_2)/(\mathrm{incoming} \mathrm{solar} \mathrm{power})$$

(10)

with Q the electron charge. For ECE calculations of single-junction STPVs, the electric power generation from the low-bandgap material can be dropped in Equation (10) [16]. Note that since we are calculating the Shockley–Quiesser efficiency limit, all the recombination mechanisms in the PV cell are neglected except the radiative recombination. Thus, the modeling does not require the non-radiative recombinations and the associated properties, such as the internal quantum efficiencies and fill factors of the PV cells, which are functions of the preparation conditions and temperatures of PV cells.

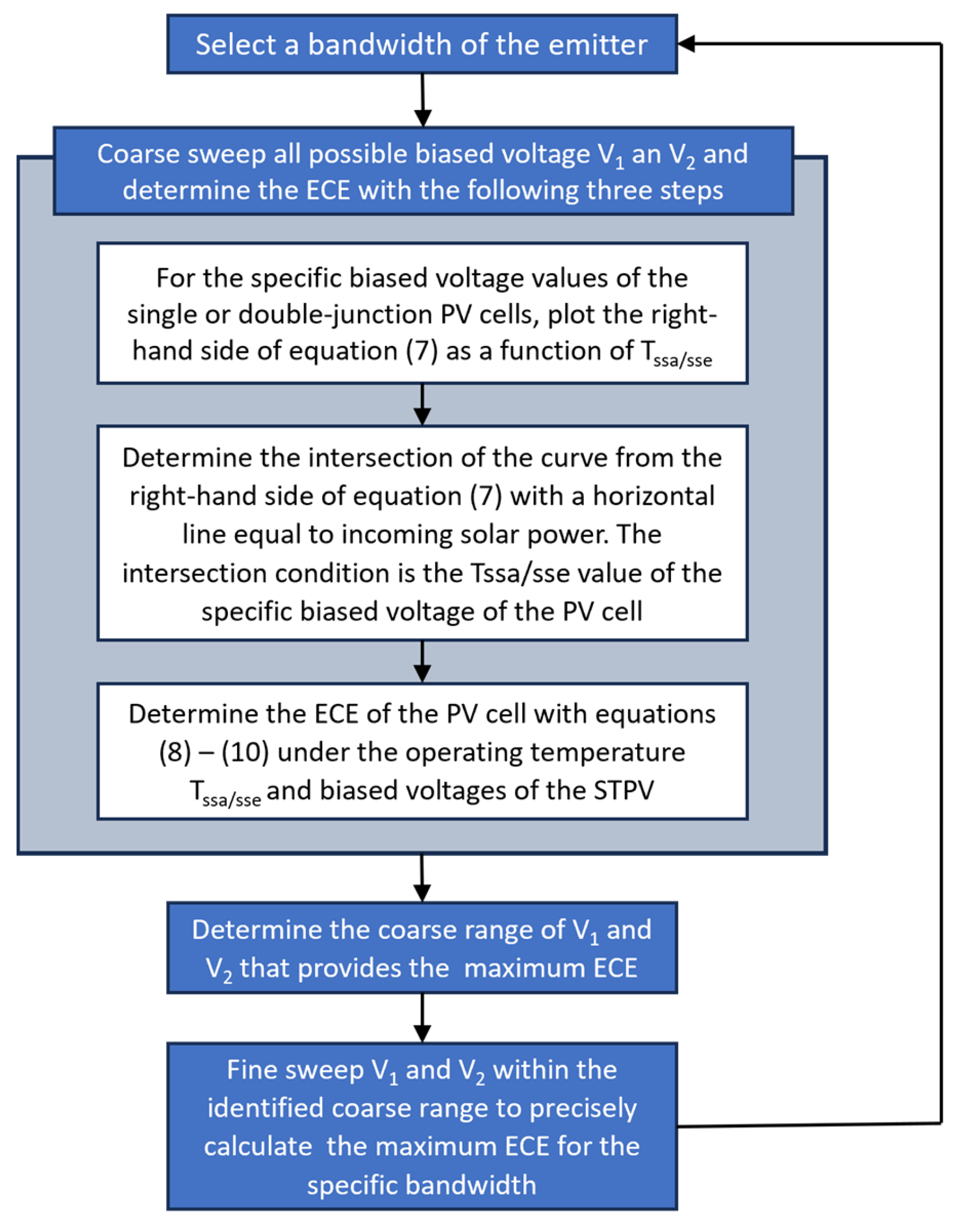
Since Equations (7) and (10) are highly nonlinear equations of $T_{ssa/sse}$, V₁, V₂, and the emission bandwidth of the spectrally selected emitter, it is challenging to find the optimized operating V₁, V₂, and bandwidth of the spectrally selective emitter to have the maximum ECE, since simple iterative calculations cannot guarantee convergence to stable values. Thus, an adaptive parametric sweep method is adopted in this study. In this adaptive method, we start with a coarse parametric sweep of all possible V₁ and V₂ values for a specified emission bandwidth of a spectrally selective emitter. For any fixed V₁, V₂, and emission bandwidth of the emitter, the absorber/emitter temperature $T_{ssa/sse}$ of the STPV can be determined by using a graphic-based method to solve Equation (7) without considering convergence issues. Once the $T_{ssa/sse}$ is determined, the ECE value of the specific V₁, V₂, and emission bandwidth can be calculated directly with Equations (8)–(10). Once we determine the coarse range of V₁ and V₂ providing the highest ECE value for a specified emission bandwidth of the spectrally selected emitter, we then perform finer parametric sweeps of V₁ and V₂ within the identified coarse V₁ and V₂ range. By repeating the procedure a couple of times, we can locate the exact V₁ and V₂ values providing the maximum ECE for a specified emission bandwidth of the spectrally selective emitter. After testing all the possible emission bandwidths of the spectrally selective emitter (i.e., from a very small value to close to ${\lambda }_{sse}$) with the same approach, we can determine the optimized emission bandwidth and the associated Shockley–Queisser limit ECE of the STPV for the selected PV cells. In this study, the resolutions of V₁ and V₂ are 0.01 V, the resolution of $T_{ssa/sse}$ is 0.1 K, and the resolution of emission bandwidth is 0.05 μm. The total simulation time for each case of the following section is limited to ~48 h. A flow chart showing the algorithm adopted in this study is given in Figure 3.

3. Results and Discussion

Increasing the separation distance between the aperture of the radiation shield and the absorber can reduce the view factor $F_{ab-ap}$ and the associated radiative heat loss from the aperture of the radiation shield. However, the increased separation distance also increases the radiation shield area and the required absorber size (for a simple radiation shield in a frustum shape). The increased area of the radiation shield means more radiative loss through the multilayer of the radiation shield. The increased size of the absorber means a lower operating temperature, which can decrease the ECE of the STPV. Through a preliminary test, we determined that the total radiative heat loss (through the aperture and the wall of the radiation shield) does not change significantly when the separation distance between the aperture of the radiation shield and the absorber is ≥~11 times the radius of the apertures of the radiation shield. Thus, we selected this specific condition in the following analysis of the Shockley–Quiesser limit of radiation in a heat-loss-controlled STPV with different PV cells and a frustum-shaped radiation shield having a tapering angle the same as the divergence angle of concentrated solar radiation.

Before studying the ECE of the heat-loss-controlled STPV with different PV cells, we verified our model with an experimentally determined case in which there was no radiation shield for the STPV with a single-junction InGaAsSb PV cell. Under such a condition, our theoretical model in this study predicts ECE of ~8.15%, which is close to the experimentally measured ECE of ~6.8% [29]. After the verification, the ECE limits of the STPV with three different PV cells are examined with our theoretical model: (a) STPV with a single-junction InGaAsSb PV cell ($E_g=0.55 \mathrm{e}\mathrm{V}$), (b) STPV with a single-junction GaSb PV cell ($E_g=0.726 \mathrm{e}\mathrm{V}$), and (c) STPV with a double-junction InGaAsSb/GaAs PV cell ($E_g=0.55/0.726 \mathrm{e}\mathrm{V}$). InGaAsSb and GaSb are commonly adopted in STPV and TPV studies because of their bandgaps (0.55 eV and 0.726 eV, respectively). These bandgaps are close to the peak emission wavelengths of material at ~1300 K and 1700 K, respectively, which fit with the range of operating temperatures of the heat-loss-controlled STPV in this study. Thus, they are selected in this study.

For all the analyses, the distribution of the solar spectrum is assumed to be a blackbody at 6000 K, used in many Shockley–Quiesser efficiency analyses [30]. The solar radiation flux arriving at the collecting area of the solar concentration is 1000 W/m² (approximately the same as AM 1.5 G conditions). The solar concentration ratio is 1000× in this study. We selected the 1000× concentration ratio because it is the maximum concentration ratio that can be achieved with a standard solar tower system [31]. Solar towers with heliostats have been identified as the most cost-effective concentrator designs adopted in most large solar power plants. The surrounding temperature and the PV cell are maintained at 300 K.

3.1. Case 1: STPV with a Single-Junction InGaAsSb PV Cell ($E_g=0.55 eV$)

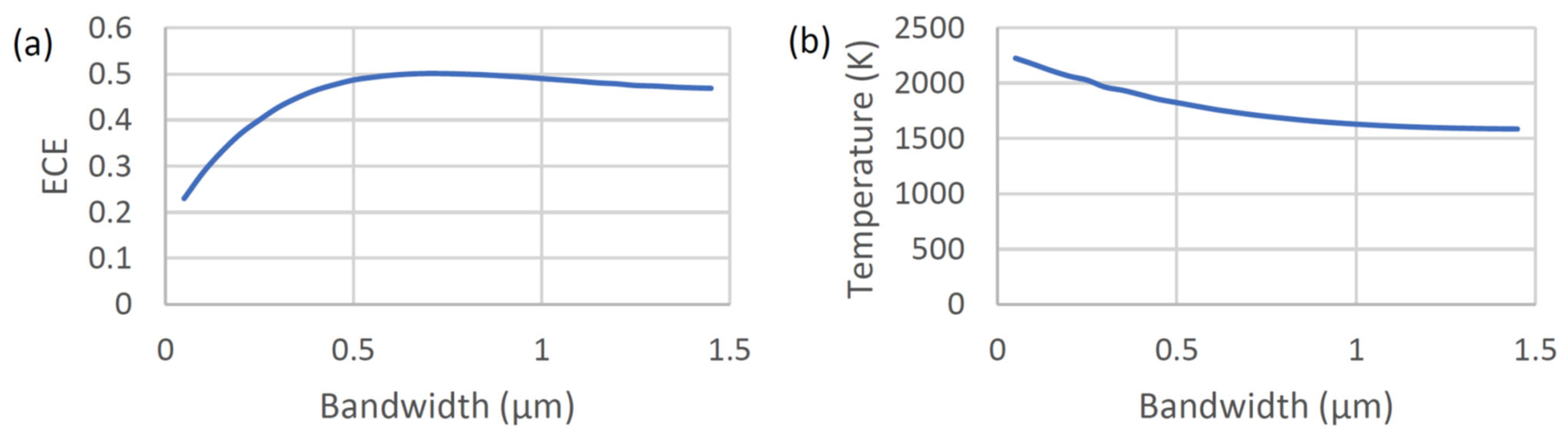
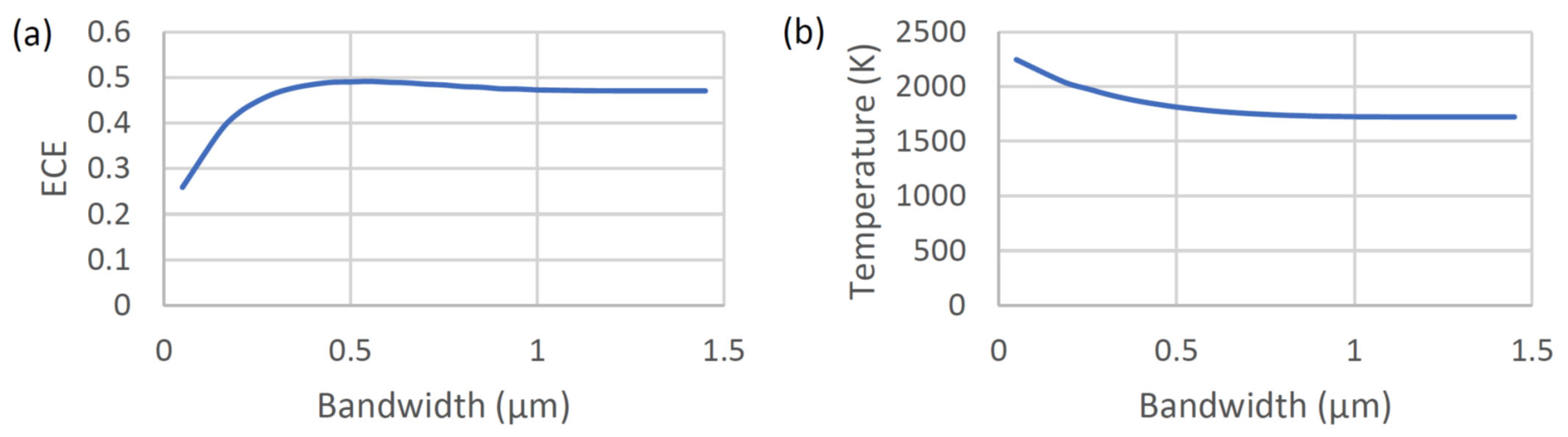
Figure 4 shows the achievable energy conversion efficiency (ECE) of the STPV and the associated operating temperature as functions of the emission bandwidth of the spectrally selective emitter when a single-junction InGaAsSb acts as the PV cell.

Note that the maximum 1.5 µm bandwidth is plotted in Figure 4b because a further increase in the bandwidth of the emitter provides a <0.1% increase in radiative heat transfer from the emitter to the PV cell with photon energies higher than the bandgap. The maximum ECE of 50.1% happens when the emission bandwidth of the spectrally selective emitter is 0.7 μm. Under such a condition, the temperature of the absorber/emitter of the STPV is 1719.5 K. The ECE value drops slightly to ~47.1% when the emission bandwidth of the spectral emitter increases to 1.45 µm. The corresponding operating temperature of the absorber/emitter decreases to ~1585 K. Increasing the emission bandwidth causes two competing mechanisms in the ECE of the STPV: (a) higher photon flux and the associated higher filling factor/higher performance of PV cells that increases the ECE, and (b) a larger mismatch between the emitted photon energy of the spectral selected emitter of the STPV and the band edge of the PV cell. The associated larger thermalization energy loss can decrease the ECE of the STPV.

Note that the ECE predicted in case 1 is much higher than the theoretical ECE limit of an STPV without a radiation shield, as in our verification calculation. Therefore, the significant improvement in the ECE can be attributed to the radiation shield, which blocks most of the radiative heat loss from the absorber to the surroundings [32]. The amount of each portion of energy transfer in the STPV under the optimized operating condition is listed in the following

Table 1. Distribution of each portion of collected solar energy in the STPV with a single-junction InGaAsSb PV cell. Normalized $q_{sse\to PV}$ is $q_{sse\to PV}$ divided by the incoming solar power. Normalized $q_{PV\to sse}$ is $q_{PV\to sse}$ divided by the incoming solar power.

Radiative Heat Loss through the Aperture	Radiative Heat Loss through the Radiation Shield	$\mathbf{Normalized} {\mathit{q}}_{\mathit{s}\mathit{s}\mathit{e}\to \mathit{P}\mathit{V}}$	$\mathbf{Normalized} {\mathit{q}}_{\mathit{P}\mathit{V}\to \mathit{s}\mathit{s}\mathit{e}}$	Energy Loss Due to the Thermalization in the PV Cell	Energy Converted to Electricity
18.9%	1.3%	90.6%	10.8%	29.7%	50.1%

.

The radiative heat loss through either the aperture or the wall of the radiation shield is ~20% of the collected solar power. The difference between the normalized $q_{sse\to PV}$ and the normalized $q_{PV\to sse}$ is the net energy transfer from the spectrally selective emitter to the PV cell. Among the net energy transfer from the spectrally selective emitter to the PV cell, the energy loss due to the thermalization of hot carriers in the PV cell equals ~30% of the collected solar power. This value is much less than ~70% in Si solar cells due to the spectral mismatch [33].

3.2. Case 2: STPV with a Single-Junction GaSb PV Cell ($E_g=0.726 eV$)

Because of the very high operating temperature of the STPV, we are interested to learn whether larger-bandgap PV cells such as GaSb can provide higher ECE. GaSb is commonly adopted for TPV and STPV devices compared with the lower-bandgap InGaAsSb [19]. Figure 5 shows the achievable energy conversion efficiency (ECE) of the STPV and the associated operating temperature as functions of the emission bandwidth of the spectrally selective emitter when a single-junction GaSb acts as the PV cell.

The maximum ECE of 49.1% happens when the emission bandwidth of the spectrally selective emitter is 0.55 μm. Under such a condition, the temperature of the absorber/emitter of the STPV is 1794.1 K. The ECE value drops slightly to ~47% when the emission bandwidth of the spectral emitter increases to 1.45 µm. The corresponding operating temperature of the absorber/emitter decreases to ~1722.4 K.

Like case 1, the amounts of each portion of energy transfer in the STPV under the optimized operating condition can be evaluated from each energy transport term in Equation (7) and are listed in the following

Table 2. Distribution of each portion of collected solar energy in the STPV with a single-junction GaSb PV cell. Normalized $q_{sse\to PV}$ is $q_{sse\to PV}$ divided by the incoming solar power. Normalized $q_{PV\to sse}$ is $q_{PV\to sse}$ divided by the incoming solar power.

Radiative Heat Loss through the Aperture	Radiative Heat Loss through the Radiation Shield	$\mathbf{Normalized} {\mathit{q}}_{\mathit{s}\mathit{s}\mathit{e}\to \mathit{P}\mathit{V}}$	$\mathbf{Normalized} {\mathit{q}}_{\mathit{P}\mathit{V}\to \mathit{s}\mathit{s}\mathit{e}}$	Energy Loss Due to the Thermalization in the PV Cell	Energy Converted to Electricity
22.4%	1.6%	84.6%	8.6%	26.9%	49.1%

.

The reduced emission bandwidth of the spectrally selective emitter in case 2 under the optimized condition increases the operating temperature and the radiative heat loss from the absorber to the surroundings. On the other hand, the higher operating temperature, along with the smaller emission bandwidth, reduces the energy loss due to the thermalization of hot carriers in the PV cell, which benefits the ECE of the STPV. After considering both the positive and negative effects, the maximum ECE of STPV with a single-junction GaSb PV cell is not very different from case 1 using a single-junction InGaAsSb PV cell.

3.3. Case 3: STPV with a Double-Junction InGaAsSb/GaSb PV Cell ($E_g=0.55/0.726 eV$)

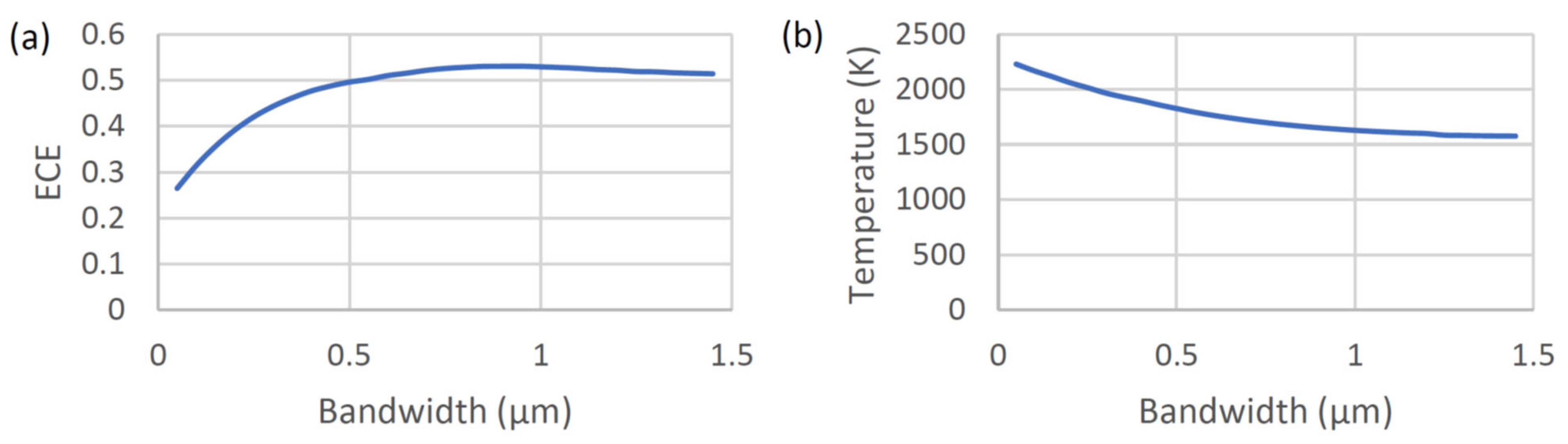
In this last case, we are interested to learn whether double-junction PV cells can significantly improve the ECE of SPTVs, similar to that for solar cells. The two semiconducting materials selected for the double-junction PV are GaSb and InGaAsSb, considering that they have a significant bandgap difference and are commonly adopted for TPV and STPV applications [34,35,36]. Figure 6 shows the achievable energy conversion efficiency (ECE) of the STPV and the associated operating temperature as functions of the emission bandwidth of the spectrally selective emitter when a double-junction GaSb/InGaAsSb acts as the PV cell.

The maximum ECE of 53.2% happens when the emission bandwidth of the spectrally selective emitter is 0.95 μm. Under such a condition, the temperature of the absorber/emitter of the STPV is 1640.0 K. The ECE value drops slightly to ~51.4% when the emission bandwidth of the spectral emitter increases to 1.45 µm. The corresponding operating temperature of the absorber/emitter decreases to ~1576.8 K.

The amounts of each portion of energy transfer in the STPV under the optimized operating condition are listed in the following

Table 3. Distribution of each portion of collected solar energy under the optimized operating condition with a GaSb/InGaAsSb PV cell. Normalized $q_{sse\to PV}$ is $q_{sse\to PV}$ divided by the incoming solar power. Normalized $q_{PV\to sse}$ is $q_{PV\to sse}$ divided by the incoming solar power.

Radiative Heat Loss through the Aperture	Radiative Heat Loss through the Radiation Shield	$\mathbf{Normalized} {\mathit{q}}_{\mathit{s}\mathit{s}\mathit{e}\to \mathit{P}\mathit{V}}$	$\mathbf{Normalized} {\mathit{q}}_{\mathit{P}\mathit{V}\to \mathit{s}\mathit{s}\mathit{e}}$	Energy Loss Due to the Thermalization in the PV Cell	Energy Converted to Electricity
15.7%	1.1%	94%	10.8%	30%	53.2%

.

The lower operating temperature due to the large optimized emission bandwidth in case 3 allows smaller radiative heat loss through the aperture of the radiation shield. The larger-than-expected energy loss due to the thermalization process, which is counterintuitive for double-junction PV cells, can be understood as a result of the very large emission bandwidth for the optimized operating condition. As a comparison, we list the types of energy transfer in the STPV with a single-junction InGaAsSb PV cell under the same 0.95 μm emission bandwidth in the following

Table 4. Distribution of each portion of collected solar energy under the optimized operating condition with an InGaAsSb PV cell when the emission bandwidth is 0.95 μm. Normalized $q_{sse\to PV}$ is $q_{sse\to PV}$ divided by the incoming solar power. Normalized $q_{PV\to sse}$ is $q_{PV\to sse}$ divided by the incoming solar power.

Radiative Heat Loss through the Aperture	Radiative Heat Loss through the Radiation Shield	$\mathbf{Normalized} {\mathit{q}}_{\mathit{s}\mathit{s}\mathit{e}\to \mathit{P}\mathit{V}}$	$\mathbf{Normalized} {\mathit{q}}_{\mathit{P}\mathit{V}\to \mathit{s}\mathit{s}\mathit{e}}$	Energy Loss Due to the Thermalization in the pv Cell	Energy Converted to Electricity
15.7%	1.1%	94%	10.8%	33.9%	49.3%

, which shows an even larger portion of the energy loss due to the thermalization of hot carriers in the PV cell.

Another important observation in case 3 is that the ECE of the STPV with double-junction PV cells is not much higher than that of the single-junction counterparts, which is a surprising result considering that double-junction solar cells can have nearly a 10% ECE improvement compared with single-junction solar cells. We attribute this subpar ECE improvement to the adoption of spectrally selective emitters of the SPTV, which already limits the production of photons to a more preferred range for the operation of either a single-junction or a double-junction PV cell.

4. Conclusions

A theoretical analysis that can estimate the energy conversion efficiency and each portion of energy transport in an STPV is developed with a realistic consideration of the design constraints of a radiation shield to block radiative heat loss. The divergence of solar light after concentration should follow the conservation of étendue. The tapering angle of the radiation shield cannot be smaller than the divergence angle of the concentrated solar radiation. The tapering angle of a simple frustum-shaped radiation shield determines the minimum size of the absorber in an STPV. An adaptive parameter sweep method and a graphic-based method are developed in this study to effectively find the optimized operating condition of the STPV with different PV cells to determine the Shockley–Queisser efficiency limit of the STPV.

Under 1000× solar concentration, which is among the highest values that can be achieved with commercially available solar collectors, we found that the Shockley–Queisser efficiency of an STPV with InGaAsSb PV cells, GaSb PV cells, and InGaAsSb/GaSb varies from ~49% to ~53%. The STPV with double-junction PV cells does not show a large ECE improvement over the STPV with single-junction PV cells. The unexpected results can be understood as follows: the spectrally selective emitter of the STPV adjusts the radiative transfer between the emitter and the PV cell in a more preferred wavelength range, which already limits the formation of very hot carriers in the PV cells. Thus, ~30% of the collected solar energy is lost through the thermalization process in the PV cells of the STPVs, which is much less than the 70% energy loss in Si solar cells due to spectral mismatch.

Another observation from the more realistic analysis is that the radiative heat loss from the absorber to the surroundings can still be up to ~20% of the collected solar energy for an STPV with a simple radiative shield when the operating temperature is ~1600–1800 K. Such substantial radiative heat loss may be reduced in the future design of STPVs by using more advanced radiation shields that can keep the absorber far away from the aperture of the radiation shield without requiring a large-sized absorber. This could significantly reduce the view factor F_ap and the associated radiative heat loss from the high-temperature absorber to the surroundings through the aperture of the radiation shield. Moreover, the operating temperature of the STPV can be maintained at a high level, one of the requirements for high ECE of STPVs, if the absorber size does not increase when it is far away from the aperture of the radiation shield. A possible design for an advanced radiation shield could involve inserting an optical relay between the aperture and the absorber. The optical relay can compress the diverged directional light to its original spot size (i.e., the size of the aperture). As a result, a small absorber operating at high temperatures can still capture all the incoming solar radiation even when it is far from the aperture of the radiation shield. We expect the Shockley–Quiesser efficiency limit of STPVs to have another >10% improvement when the radiative heat loss is further minimized with the advanced radiation shield.