Abstract
The hemispherical ground electrode is a basic electrode whose analysis appears in many textbooks on electromagnetics in chapters dedicated to steady currents. Considering a soil with a given resistivity and an electrode with a given perimeter, the electrode DC resistance is simply calculated from the ratio resistivity/perimeter. Strangely, the generalization of this result to AC regimes is missing. The issue of the frequency-domain impedance of the hemispherical ground electrode has been avoided in the literature despite its trivial geometry. But the problem is indeed not easy; electromagnetic field calculation involves Legendre and Bessel functions; the application of boundary conditions involves an infinite set of points, and some integrals involved need to be calculated recursively. We analyzed the math and physics of the problem but failed to find a closed-form solution. This article with “negative results” can, however, be useful; on one hand it may prevent researchers from wasting their time following the same steps, and, on the other hand, it may attract the interest of new researchers to the subject, ultimately, accelerating its analytical solution (if the solution exists).
1. Introduction
Metallic electrodes are employed in very many instances and in various fields: in geophysics and civil engineering, for the characterization of soils [1,2]; in biophysics and bioengineering, for the characterization of tissue properties, and sensing applications [3,4,5]; and in electrical engineering, for grounding purposes aimed to provide electric protection and safety to people, installations, buildings, and infrastructures [6,7,8].
The focus of this work, the hemispherical electrode—a half-sphere buried just below the air/ground surface—is not utilized in real grounding systems. It is primarily an academic object intended to easily introduce the topic of earthing/grounding to electrical engineering students. In fact, its trivial geometry provides a very simple electric field solution of Maxwell equations for the DC steady-state regime, enabling the illustration of the important concepts of electrode resistance, touch, step voltages, etc. [9,10,11,12,13]. Moreover, because of the simplicity of the expression of the hemispherical electrode resistance, the latter is often used, as a standard, to assess the accuracy of software programs developed for the simulation of grounding systems [13,14,15,16,17].
In addition, the theoretical analysis of the hemispherical electrode (DC framework) has been recently extended to non-flat, cone-shaped, air/ground interfaces [18,19,20]—a relevant issue for structures implanted in hilly areas.
The analytical calculation of the DC grounding resistance, RDC, of the hemispherical electrode is trivial and can be found in various textbooks [9,10,11,12]. However, its generalization to non-zero frequency is still missing. The analytical calculation of the complex frequency-dependent grounding impedance Z(ω) of the hemispherical electrode is a question that has been avoided in the literature notwithstanding the apparent simplicity of the electrode’s geometry. This article is intended to address that question.
Our aim was to deliver a closed-form analytical formula for the grounding impedance of the electrode, accounting for the resistive, capacitive, and inductive contributions of the ground medium. We succeeded only partially. An analytical formula for Z(ω) was obtained, but it is of very little use and not in closed form.
This work is organized into five sections, the first two being introductory. Section 3 presents the solution of Maxwell equations for time-invariant regimes based on the assumption of a purely radial field of currents. In addition to the familiar E-field solution, the H-field solution inside the ground is also calculated (never reported in the literature, to our knowledge); resistance, capacitance, and inductance parameters are obtained using the Poynting theorem. The core of the work, Section 4, presents the solution of Maxwell equations for sinusoidal time-varying regimes based on the assumption of a purely azimuthal magnetic field (allowing the presence of a polar component in the E-field). Frequency-domain differential equations for the various field components in spherical coordinates are established, and boundary conditions are enforced (at the electrode surface and at the air/ground interface). A solution for the complex impedance is obtained in the form of an infinite summation of spherical harmonics whose terms are products of Legendre functions with radial integrals of spherical Bessel functions. Dedicated to the discussion of results and conclusions, Section 5 closes this article.
2. Preliminaries
Figure 1 depicts the single-electrode geometry, consisting of a PEC hemisphere of radius a, buried just below the surface of the ground. Inside the electrode, the electric field is zero. Given the electrode’s geometry, spherical coordinates with unit vectors will be employed. Moreover, owing to geometric reasons (rotational invariance around z), all the electromagnetic field components are independent of the azimuthal angle φ.
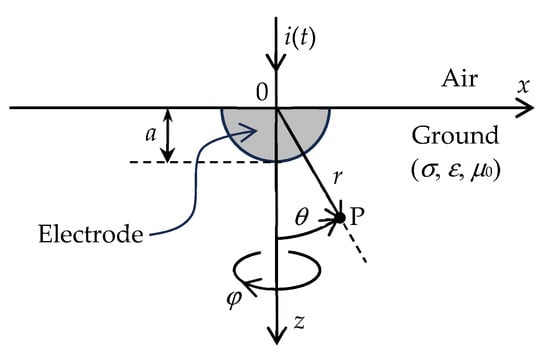
Figure 1.
Electrode geometry and space coordinates.
Above ground, the air is assumed to be a non-conducting medium. The air/ground interface (xy-plane, z = 0, is flat, and, for the sake of simplicity, the soil is assumed to be a linear, isotropic, non-magnetic, homogeneous medium, characterized by its constitutive parameters: conductivity σ, permittivity ε, and permeability
The current intensity i(t) injected by the electrode into the ground can be defined using two alternative but equivalent descriptions, one based on the electric field E, another on the magnetic field H, that is,
where J is the total current density vector, Sr is a hemispherical surface immersed in the ground, concentric with the electrode, bounded by a circumferential path s lying on the air/ground plane (z = 0), with generic radius r > a and elemental path length The electrode voltage u(t) is defined through the line integral of the electric field vector E from a point P on the electrode to a remote point at infinity, where a second electrode collecting the return current is assumed to exist, that is,
In general, for time-varying phenomena, the E-field is non-conservative, therefore, the definition in (2a) ought to be complemented by an ambiguous definition of the integration path s from P to Since the H-field is tangential to the air/ground plane, any chosen path lying on that plane will produce the same result for the voltage u; we will opt for the simplest one, along x, that is,
For steady-current regimes, the voltage in (2) and the current intensity in (1) are time-invariant, u = U and i = I; their ratio defines the electrode resistance For time-harmonic regimes (frequency ω), u and i are sinusoidal quantities described by and The ratio of the complex amplitudes defines the electrode’s complex impedance —the target of this work.
3. The Radial Electric Field Assumption for Steady Currents
3.1. Field Equations
The electrode problem under consideration is of the same family as the concentric spherical capacitor where the electric field E is radial, perpendicular to the plates of the capacitor. Hence, we consider the assumption that, inside the ground the electric field is purely radial:
The enforcement of assumption (3) into Maxwell equations uniquely determines the allowed relationships between the components of the electric and magnetic fields E and H. From the curl equation of E, we find the following:
which leads to the conclusion that the magnetic field is purely azimuthal , that is, Since the H vector is azimuthal and independent of the azimuth angle, its field lines are circumferences around the z-axis.
Then, from the curl equation of H, we find the following:
Observe that the bottom equation in (5) leads to the conclusion that the magnetic field H must be proportional to 1/r.
Finally, from the divergence equations, we obtain
The bottom equation brings no novelty; it restates that H is independent of φ. The top equation in (6) leads to the conclusion that the electric field E is proportional to 1/r2.
At this point, we must pause for a moment.
The conclusions that and seem to be incongruent with Equation (4) where the left-hand side would depend on 1/r3, but the right-hand side on 1/r. The incongruence can only be removed by considering that the right-hand side of (4) is zero, that is, either the magnetic field is absent (H = 0, like in electrostatics) or it is time-invariant like in steady currents).
The assumption (3) and the derived equations are not adequate to analyze time-varying regimes; therefore, in this section, we will pay attention only to the case of steady currents. Time-varying sinusoidal regimes will be dealt with in Section 4.
3.2. Steady Currents
From (1), (4), and (6), using we obtain, for the electric field,
from where we see that the radial current spreads uniformly in the ground irrespective of the polar angle θ.
Next, we focus on a key aspect ordinarily overlooked when analyzing the hemispherical ground electrode: the calculation of the magnetic field originated by the radial current distribution. The calculation can be performed using Ampere’s law, considering an integration surface Sr defined by a spherical cap, with angle θ and radius r, bounded by a closed circumferential path s with radius r sinθ—see Figure 2.
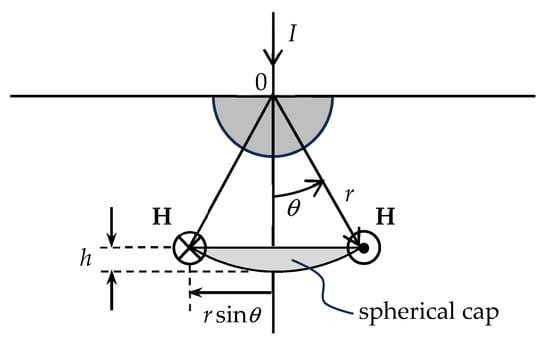
Figure 2.
Calculation of the magnetic field due to a radial current in the ground.
Taking into account that the area of the spherical cap is (h being the cap height: ), and noting that the current density J does not vary over the spherical cap, we write
which yields, for
whose partial derivatives are such that
3.2.1. Electrode Resistance
The electrode resistance is determined from (2) and (7), calculating the voltage U from a point on the electrode to a remote point at i.e.,
The result for can be confirmed from energy balance considerations, using the Poynting theorem [12], that is,
where p is the power delivered to a region of space with volume V bounded by a closed surface SV; S is the Poynting vector with units W/m2; vector n is the inward unit normal; and are, respectively, Joule power losses and magnetic and electric energies stored in the region.
Here, the region under consideration is the entire ground (z > 0). The enclosing surface SV includes two surfaces, a hemispherical one of very large radius, where S = 0, and a planar circular surface at the air/soil interface through which energy penetrates the soil with power density for r > a; however, inside the circle, r < a, the Poynting vector is zero (PEC electrode).
Therefore, from (12), for steady currents , we find, as expected,
3.2.2. Electrode Capacitance and Inductance
The Poynting theorem in (12) is not required for the determination of the electrode resistance. We have brought it to the readers’ attention for another reason. In addition to its resistance, the electrode will also have associated a capacitance C and an inductance L, both parameters being related with the stored electric and magnetic energies appearing in the right-hand side of (12) under the time derivative. We aim to find C and L through
where V denotes the ground volume and .
The electric energy is obtained from (14) using E from (7):
Hence, for the capacitance, from (11), (14) and (16), we obtain
The above result is no surprise given the well-known analogy between the equations that govern electrostatics and steady currents [9,10,11,12]. Moreover, in (17), the term (of the order of nanoseconds) is recognized to be the time constant, or the relaxation time, of the ground medium.
Likewise, the magnetic energy is obtained from (15) using H from (9):
Hence, for the inductance, from (15) and (18), we find
The volumes of integration in (14) and (15) are the same and increase to infinity with r3. In the case of (14), the integrand function (electric energy density) decreases to zero with , and the improper integral converges to a finite value. Contrarily, in the case of (15), the integrand (magnetic energy density) decreases to zero at a slower pace, with and the improper integral diverges to infinity when is enforced.
4. The Azimuthal Magnetic Field Assumption for Sinusoidal Currents
We observed in Section 3 that the assumption (3) of a pure radial electric field was fit to deal with the case of steady currents but could not cope with time-varying currents. Here, we deal with sinusoidal currents of frequency ω (frequency domain) and consider a less restrictive assumption than that in (3); we enforce the magnetic field H to be purely azimuthal, with circumferential field lines around the vertical z-axis:
In (20), and in the equations that will follow, the overbars are intended to denote complex amplitudes (phasors) of the sinusoidal time-varying fields they represent, e.g., Going back to the Maxwell equations, we find, from the curl equation of H,
where
With respect to the electric field inside the ground, we see that the expected radial component is now accompanied with a polar component as illustrated in Figure 3, the ratio of the field components and the angle α between them being given by
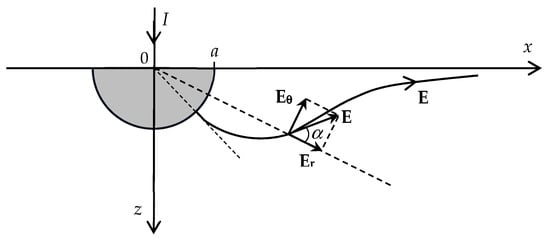
Figure 3.
For time-varying regimes, the electric field vector includes a polar component.
Finally, from the curl equation of E, we find
At this stage, we should again pause. The presence of the component in Equations (21)–(23) may seem hard to accept. In fact, the E-field cannot have a tangential component to the electrode surface or a vertical component to the ground surface. But, as sketched in Figure 3, the presence of at any other point inside the ground is possible. To cope with the difficulty, the math of the problem will become a bit complicated; none of the field components will be expressed in terms of one single function, even if unfamiliar; a summation of an infinite number of functions will be required (as the number of points on the electrode and ground surfaces is infinite).
4.1. Frequency-Domain Differential Equations for the Field Components
The results in (21) allow for the calculation of the r and θ components of E once the solution for H has been found. The partial differential equation (PDE) on that we need to solve is obtained by plugging from (21) into (23), which yields
with
where τ is the relaxation time of the soil in (17), and is the familiar field penetration depth—a ubiquitous parameter in skin-effect theory [12].
Albeit a tedious task, one can also derive similar PDEs for both the polar and radial electric field components:
The PDEs in (24), (26) and (27) can be solved by resorting to the method of separation of variables [21], where the unknown function is written as the product of a radial part and a polar part the two parts being found separately by solving two ordinary differential equations, one on ρ, another on θ.
In this work, we will focus exclusively on the magnetic field function solution of (24), from which the functions can be calculated at a later stage with the help of (21).
Plugging in Equation (24) and dividing both sides by RT yields
With regard to the radial part , we obtain the Riccati–Bessel equation [22,23,24]
whose complete solution, for every n, involves first and second kind Riccati–Bessel functions, S and C [22,23,24],
where jn is a spherical Bessel function of integer order, and J and N are Bessel and Neumann functions of half-integer order.
With regard to the polar part , we obtain the Legendre associated equation [22,23,24],
whose complete solution, for every n, involve first and second kind associated Legendre functions, P and Q [22,23,24],
The expressions and recurrence relations for the calculation of the Legendre functions are available in the literature [22,23,24].
The general solution for F in (24) will then take the form of an infinite summation of products of Bessel functions in (30) and Legendre functions in (32):
where the frequency-dependent coefficients ought to be determined bearing in mind the specific boundary conditions of our problem.
4.2. Boundary Conditions
Regarding the magnetic field H, we know that it must vanish on the z-axis, vanish at infinity, and obey at any point on the air/ground interface, that is,
where and As for the electric field E, we know that its polar component must vanish at all the points on the electrode and ground surfaces. Hence, with the help of (21), we write
We start by looking at the radial part in (30).
Since ρ is a complex of the fourth quadrant, the functions will increase to infinity when But this is a physical impossibility, and, therefore, the coefficients must be set to zero; consequently, we obtain Now, we consider the polar part in (32).
All the functions are polynomials proportional to sin θ that go to zero when θ = 0, for instance [22,23,24,25],
Since the magnetic field must vanish at θ = 0, the coefficients must be set to zero, and we obtain Hence, the solution in (33) gives way to
where the coefficients are dimensionless, and the summation must converge to 1 when For points placed on the ground surface, where and the Legendre polynomials of zero argument , of even and odd orders, are given by
We can compute the odd order coefficients in (37) by discretely varying the coordinate considering N points along the ground surface with different values of r. This procedure leads to
which yields
The result for the odd-order coefficients is a consequence of having enforced the equality (Ampere’s law) independently of ρ. In other words, the result in (39) incorporates the condition at But this is precisely the second boundary condition in (35).
The first boundary condition in (35) will then be used to find the still unknown coefficients of even order For that purpose, we consider a discrete set of N points on the hemispherical surface of radius a, with different values of the polar angle θ from 0 to Then, we write
where the derivative of the nth order Riccati–Bessel function at can be calculated (see Appendix A) from
It is worth noting that the Bessel functions of half-integer order appearing in (30) and (41) can be expressed in terms of ordinary sine and cosine functions [22,23,24], for example,
The boundary condition in (40) can be rewritten to better show how the unknown coefficients are obtained from in (39),
or, in matrix format,
or, more compactly,
where the column on the right-hand side depends on , that is,
Hence,
4.3. Impedance Calculation
The boundary conditions analyzed in Section 4.2 yielded the set of coefficients needed in (37) for calculating the azimuthal magnetic field as a function of the r and θ coordinates,
Next, from (21), we calculate the radial component of the electric field particularize it for and integrate the resulting function, from r = a to , to find the electrode voltage from where the electrode impedance can be finally determined.
Choosing the second, plugging (49) into (48), yields
and, particularizing for we find
Integrating in (51) from r = a to gives the electrode voltage from where the electrode impedance can be determined,
where the leading factor is the electrode resistance RDC in (11) and (13).
The radial integral at the end of (52) is, from (30), of the type
where is the spherical Bessel function of integer order n. Attempts have been made to analytically solve integrals of this type [26,27], but, almost always, they end up with recurrence relations which, albeit useful, lead to new integrals that lead to new integrals and so on (see Appendix C). To our knowledge, closed-form solutions of (53), for generic n, with n running from 1 to infinity (as in our case) do not exist.
5. Results, Discussion, and Conclusions
We managed to obtain an analytical solution (52) for the complex grounding impedance Z(ω) of the hemispherical electrode in the form of an infinite summation of spherical harmonics whose terms are products of Legendre functions with radial integrals of spherical Bessel functions.
Unfortunately, the result in (52) brings with it several difficulties:
- -
- The coefficients do not have a closed form. They are obtained from matrix procedures, in (39) and (44), that involve the inversion of infinite square matrices, some of which may possibly be ill-conditioned (neighboring lines almost identical).
- -
- The improper radial integral in (52) also does not have a closed form (Appendix C). It can be calculated recursively, but the possibility that it may diverge to infinity cannot be ruled out.
- -
- We also cannot ensure that the infinite summation over n in (52) converges.
- -
- But, even if the coefficients can be found, and even if the improper integral and the infinite summation converged to some finite values, the analytical expression found in (52) would remain almost unreadable, hermetic, of very little use, shedding no light on the physical factors that determine Z(ω). For instance, the simple question of how Z(ω) behaves for low and high frequencies cannot be answered by inspection of (52), because the quantities cn and Sn are complicated frequency-dependent quantities.
Although the present work was not meant to include any numerical calculation, we decided to conduct a few numerical experiments (via MATLAB) aimed at the clarification of two critical issues in (52), namely, the calculation of the coefficients cn defined in (39) and (46) and the calculation of the radial integral in (52) related to the electrode voltage. For both issues, we adopted the worst-case scenario, i.e., a low-frequency case (50 Hz) in the calculation of the coefficients cn and a high-frequency case (1 MHz) in the calculation of the radial integral whose integrand contains
For computation purposes, we chose the following data: a = 1 m, σ = 0.01 S/m, . The remote return electrode (theoretically located at infinity) was positioned at
The cn coefficients for even n can be found from (46), based on the knowledge of the cn coefficients for odd n. We tried to compute the latter, at 50 Hz, by implementing (39), inverting matrix [S]. Considering a set of 100 equidistant discretization points along the air/ground surface, we obtained the following warning message from MATLAB: «Matrix is singular to working precision». We decreased the discretization level, and the message repeated itself, until, down to 21 points, the message changed to «Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 9.87 × 10−110».
This shows that the reciprocal condition number of matrix [S] is practically zero, meaning that the cn coefficients in (52) cannot be calculated.
Now, we address the numerical calculation of the radial integral appearing at the end of expression (52), where the upper limit of integration has been replaced by We computed, at 1 MHz, the integral in (54):
where, for exemplification, we took various values of n and compared the situations and MATLAB returned the following values:
Increasing makes dramatically increase. In the limit case, , one will obtain The impedance of the hemispherical electrode in (52) diverges to infinity; there is no analytical or numerical solution for the problem, except for zero frequency ().
Let us go back to Section 3.2 where the case of steady currents was dealt with, considering that the second electrode (for current return) was remotely positioned at Now, assume that the results in (11) and (19), exact for ω = 0, are still valid for very low frequencies. In this situation, the near-zero frequency impedance of the electrode would be
Hence, we see that, even for quasi-zero frequencies, the electrode impedance will go to infinity, when This simple idea illustrates/supports the conclusion that the result in (52) will diverge when Moreover, other well-known devices exist, where diverging solutions may be encountered; recall, for example, the cylindrical capacitor or coaxial cable (with inner radius a and large outer radius ). The device inductance is proportional to and the associated impedance also goes to infinity when
The analytical expression we obtained for Z(ω) in (52) is correct but is not useful. The solution is exact, accurate, and cannot be simplified. The well-known closed-form expression of the grounding resistance of the hemispherical electrode at zero frequency cannot, in any circumstances, be generalized for non-zero frequency cases.
The result for is not a consequence of any numerical problem or instability; the issue is of a physical nature. The single hemispherical electrode (with the return electrode located at infinity) cannot support time-varying currents; that would require a voltage source with infinite voltage U = ZI and infinite power (to fill up the soil with magnetic energy, as in Equation (18))—which is a physical impossibility.
Note, however, that, if the return electrode is located at some finite distance from the sending electrode, then the grounding impedance Z(ω) will no longer diverge to infinity. But, in that case, the analytical expression for Z(ω) no longer will be given by the result in (52).
The authors are preparing a second article (future work [28]) to be submitted to this same Special Issue (Electromagnetic Field Computation for Electrical Engineering Devices), where a purely numerical approach is utilized to deal with the hemispherical electrode, not alone, but considering the presence of a remote concentric return electrode with arbitrary radius . The electromagnetic field solution is obtained by employing the finite element method (FEM) using an adaptation of a commercial software package developed for axisymmetric geometries. The numerical approach allows the electrode grounding impedance to be computed for any finite value of . Preliminary FEM calculations corroborate the conclusion that the inductance L is an ever-increasing function of for any frequency.
Author Contributions
Conceptualization, J.B.F.; Methodology, J.B.F., M.E.P. and V.M.M.; Software, M.E.P.; Validation, J.B.F., M.E.P. and V.M.M.; Formal analysis, J.B.F., M.E.P. and V.M.M.; Investigation, J.B.F.; Writing—original draft preparation, J.B.F.; Writing—review and editing, J.B.F.; Visualization, M.E.P.; Supervision, J.B.F.; Project administration, J.B.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Derivative of the First Kind Riccati–Bessel Function Sn
Equation (40) requires the calculation of the first derivative of the Riccati–Bessel function with respect to x,
The Bessel functions of half-integer order can be calculated resorting to well-known recurrence relations [20,21,22,23]:
which, for m = n + 1/2, give
Summing the two equations in (A2) and plugging the result into (A1) yields
For example,
Appendix B. Derivative of the Associated Legendre Function
The x-derivative of can be found in connection with the recurrence relations aimed at the calculation of and [21,22,23], concretely,
By considering m = 1 and , the above result gives way to
In addition, noting that
we find
For the case we derive
Appendix C. Antiderivative of the Spherical Bessel Function Divided by x
The indefinite integral can be found recursively [26] through
which, in our case, , yields the following analytical sequence:
where, at each step, n is decreased by 1 until the last term is reached:
Noting that the recursion’s root in (A10) concerns the spherical Bessel function of the zeroth order, we have
which, also, is not a closed form.
References
- Herman, R. An introduction to electrical resistivity in geophysics. Am. J. Phys. 2001, 69, 943–952. [Google Scholar] [CrossRef]
- Hong, C.H.; Chong, S.H.; Cho, G.C. Theoretical study on geometries of electrodes in laboratory electrical resistivity measurement. Appl. Sci. 2019, 9, 4167. [Google Scholar] [CrossRef]
- Ragheb, T.; Riegle, S.; Geddes, L.A.; Amin, V. The impedance of a spherical monopolar electrode. Ann. Biomed. Eng. 1992, 20, 617–627. [Google Scholar] [CrossRef] [PubMed]
- Franks, W.; Schenker, I.; Schmutz, P.; Hierlemann, A. Impedance characterization and modeling of electrodes for biomedical applications. IEEE Trans. Biomed. Eng. 2005, 52, 1295–1302. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.K.; Baruah, R.K.; Bhamra, H.; Kim, Y.J.; Yoo, H. Recent advances in electrode development for biomedical applications. Biomed. Eng. Lett. 2021, 11, 107–115. [Google Scholar] [CrossRef]
- IEEE Standard 81-2012; IEEE Guide for Measuring Earth Resistivity, Ground Impedance, and Earth Surface Potentials of a Grounding System. IEEE: Piscataway, NJ, USA, 2012.
- IEEE Standard 81-2013; IEEE Guide for Safety in AC Substation Grounding. IEEE: Piscataway, NJ, USA, 2013.
- EN 50522: 2022; Earthing of Power Installations Exceeding 1 kV a.c. Comitato Elettrotecnico Italiano (CEI): Milan, Italy, 2022.
- Fruhling, A. Cours d’Électricité; Dunod: Paris, France, 1966; Volume 1. [Google Scholar]
- Bessonov, L.A. Cours d’Électrotechnique Théorique; (traduit du russe); Ecole Superieure: Moscou, Russia, 1968. (In Russian) [Google Scholar]
- Hauss, H.A.; Melcher, J.R. Electromagnetic Fields and Energy, 1st ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Brandão Faria, J.A. Electromagnetic Foundations of Electrical Engineering, 1st ed.; Wiley: Chichester, UK, 2008. [Google Scholar]
- Parise, G.; Martirano, L.; Parise, L.; Celozzi, S.; Araneo, R. Simplied conservative testing method of touch and step voltages by multiple auxiliary electrodes at reduced distance. IEEE Trans. Ind. Appl. 2015, 51, 4987–4993. [Google Scholar] [CrossRef]
- Choun, L.W.; Kadir, M.Z.A.; Gomes, C.; Ahmad, W.F.W. Analysis of earth resistance of electrodes and soil resistivity at different environments. In Proceedings of the 2012 International Conference on Lightning Protection, Vienna, Austria, 2–7 September 2012. [Google Scholar] [CrossRef]
- Yuan, T.; Bai, Y.; Sima, W.; Xian, C.; Peng, Q.; Guo, R. Grounding resistance measurement method based on the fall of potential curve test near current electrode. IEEE Trans. Power Del. 2017, 32, 2005–2012. [Google Scholar] [CrossRef]
- Alcantâra, F.R. Simulation of measurements of resistances of grounding systems by a simple hemispheric model. In Proceedings of the 2019 IEEE 26th International Conference on Electronics, Electrical Engineering and Computing, Lima, Peru, 12–14 August 2019. [Google Scholar] [CrossRef]
- Sobolewski, K. Modeling and simulations in the earthing calculations. In Proceedings of the 2019 IEEE 20th International Conference on Computational Problems of Electrical Engineering, Lviv, Ukraine, 15–18 September 2019. [Google Scholar] [CrossRef]
- Sunjerga, A.; Rachidi, F.; Rubinstein, M.; Poljak, D. Calculation of the grounding resistance of structures located on elevated terrain. IEEE Trans. Electromagn. Compat. 2019, 61, 1891–1895. [Google Scholar] [CrossRef]
- Tan, K.B.; Lu, H.M.; Zhang, Y.; Zuo, W.C. Analysis of the grounding resistance of a hemispheric electrode located on a truncated cone. IEEE Trans. Electromagn. Compat. 2020, 62, 1361–1363. [Google Scholar] [CrossRef]
- Sunjerga, A.; Rubinstein, M.; Poljak, D.; Karami, H.; Rachidi, F. Grounding resistance of a hemispheric electrode located on the top of a finite-height, cone-shaped mountain. IEEE Trans. Electromagn. Compat. 2020, 62, 1889–1892. [Google Scholar] [CrossRef]
- Simonyi, K. Foundations of Electrical Engineering, 1st ed.; Pergamon Press: Oxford, UK, 1963. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th ed.; Dover: New York, NY, USA, 1972. [Google Scholar]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions, 1st ed.; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Weisstein, E.W. MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/ (accessed on 1 July 2023).
- Foldvary, L. Sine series expansion of associated Legendre functions. Acta Geod. Geophys. 2015, 50, 243–259. [Google Scholar] [CrossRef][Green Version]
- Bloomfield, J.K.; Face, S.H.P.; Moss, Z. Indefinite integrals of spherical Bessel functions. arXiv 2017, arXiv:1703.06428v1. [Google Scholar] [CrossRef]
- Mehrem, R. The plane wave expansion, infinite integrals and identities involving spherical Bessel functions. arXiv 2011, arXiv:0909.0494v4. [Google Scholar] [CrossRef]
- Maló Machado, V.; Fernandes, J.; Eduarda Pedro, M.; Brandão Faria, J. Numerical evaluation of the frequency-dependent impedance of hemispherical ground electrodes through finite element analysis. Energies, 2023; to be submitted. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).