A Generic Framework for Multiscale Simulation of High and Low Enthalpy Fractured Geothermal Reservoirs under Varying Thermodynamic Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Mass and Energy Balance
2.2. Choice of Primary Variables
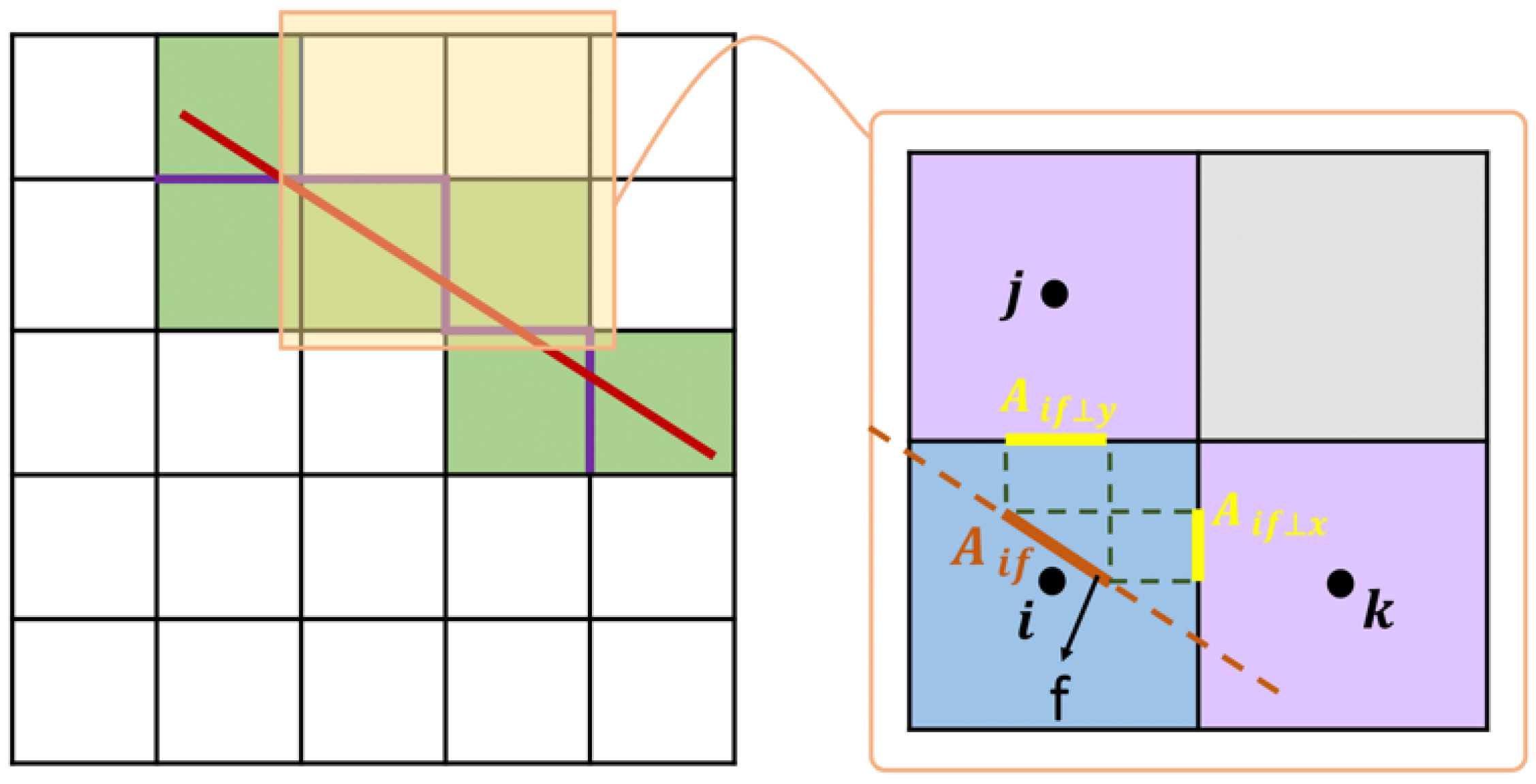
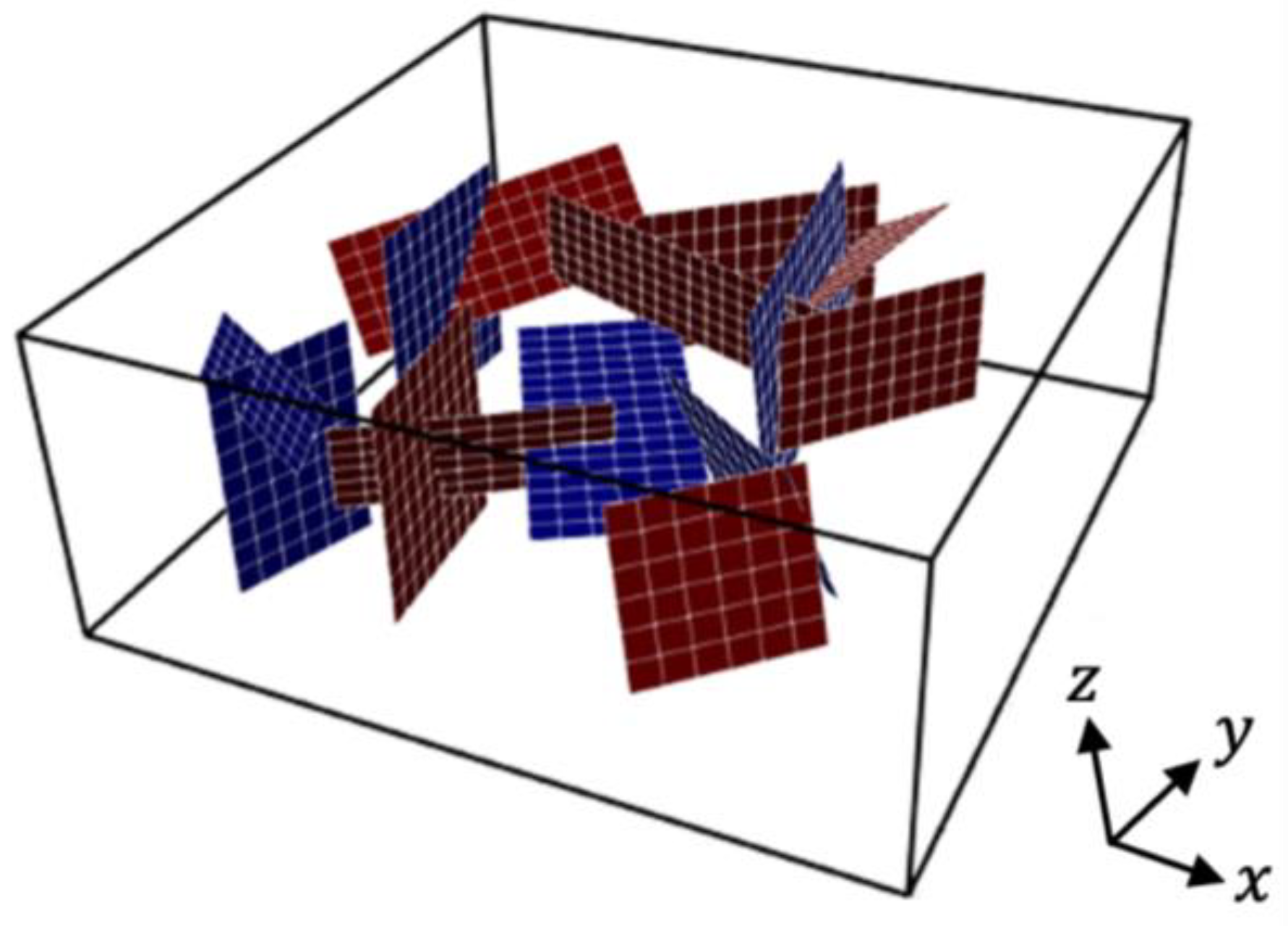
2.3. pEDFM Implementation
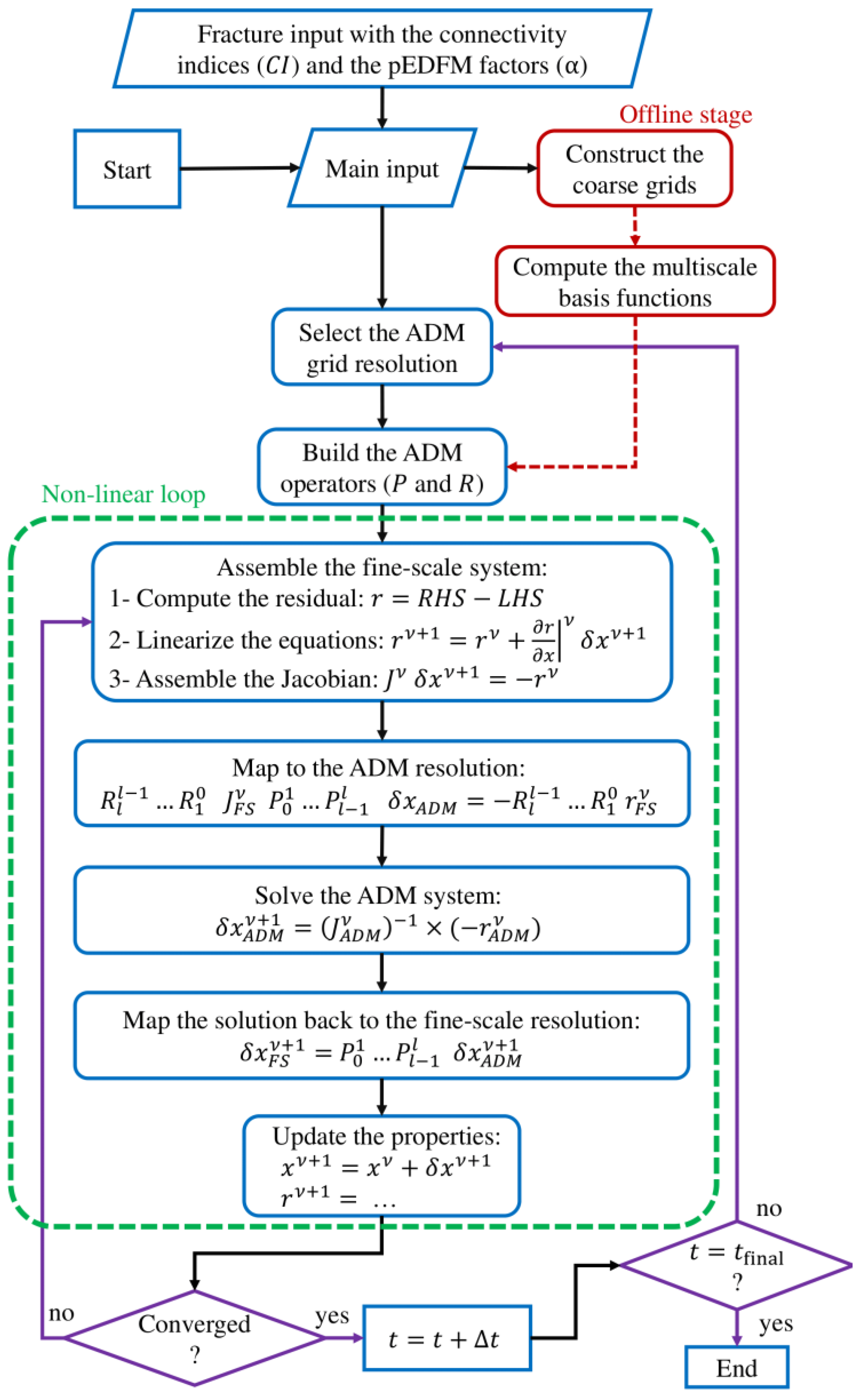
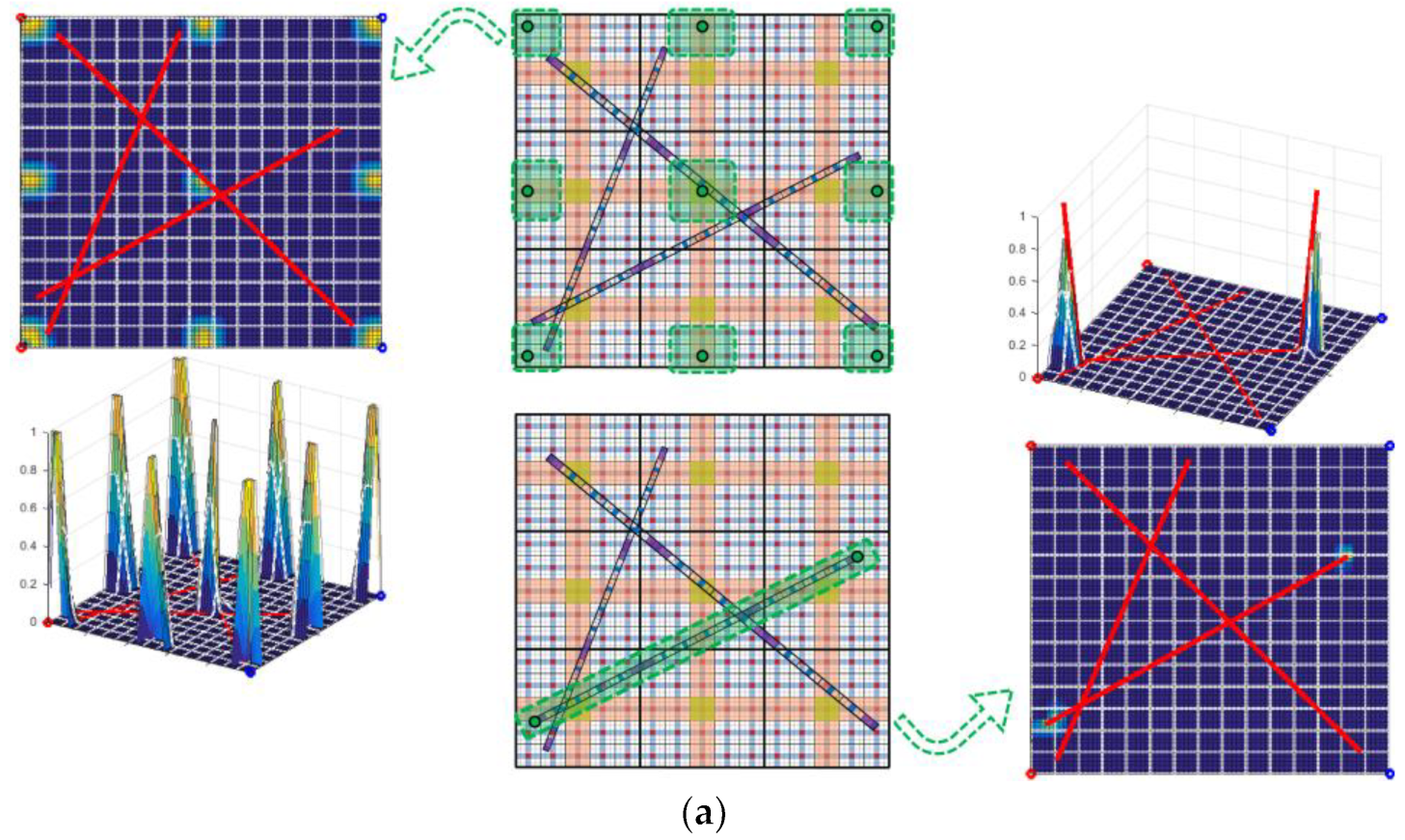
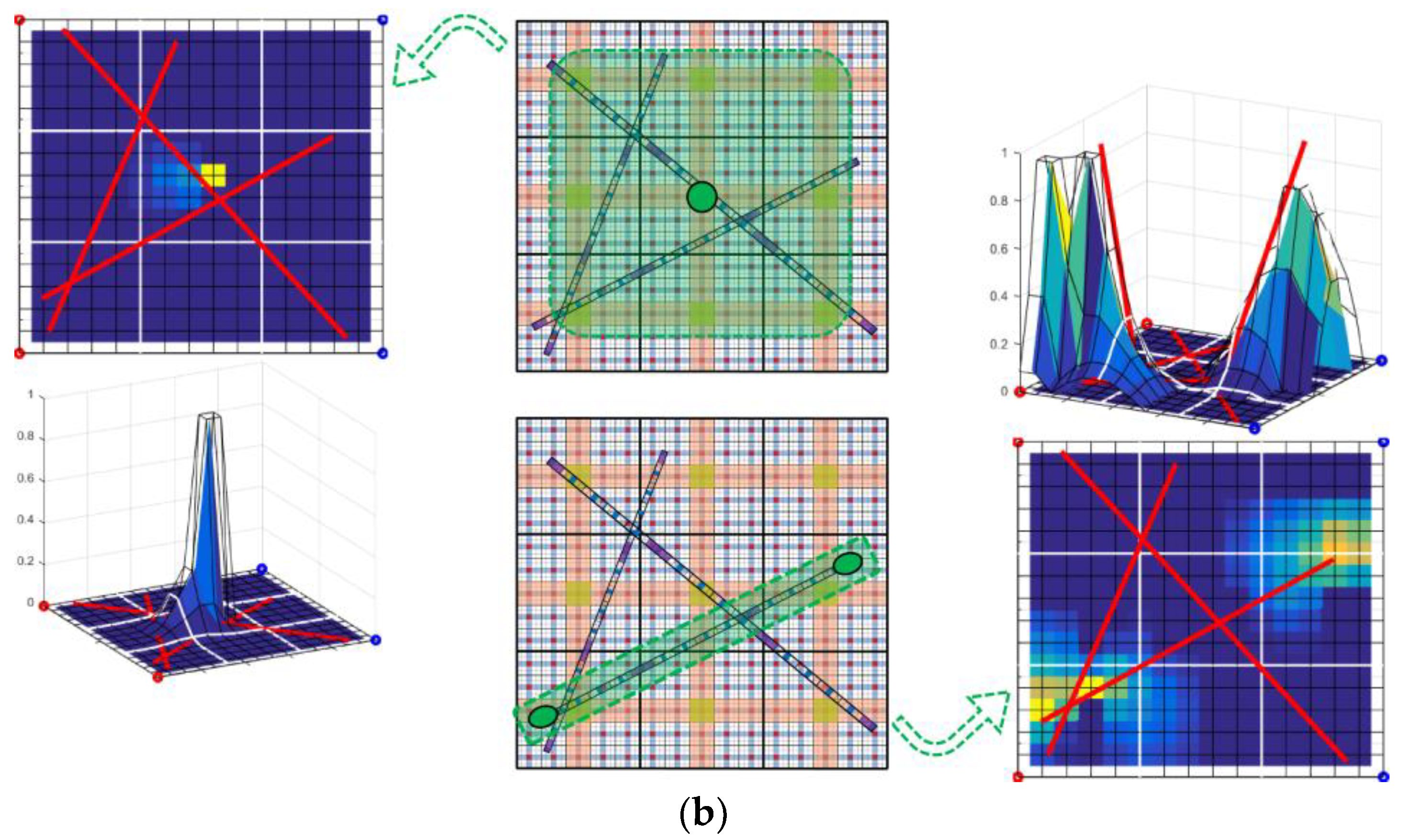
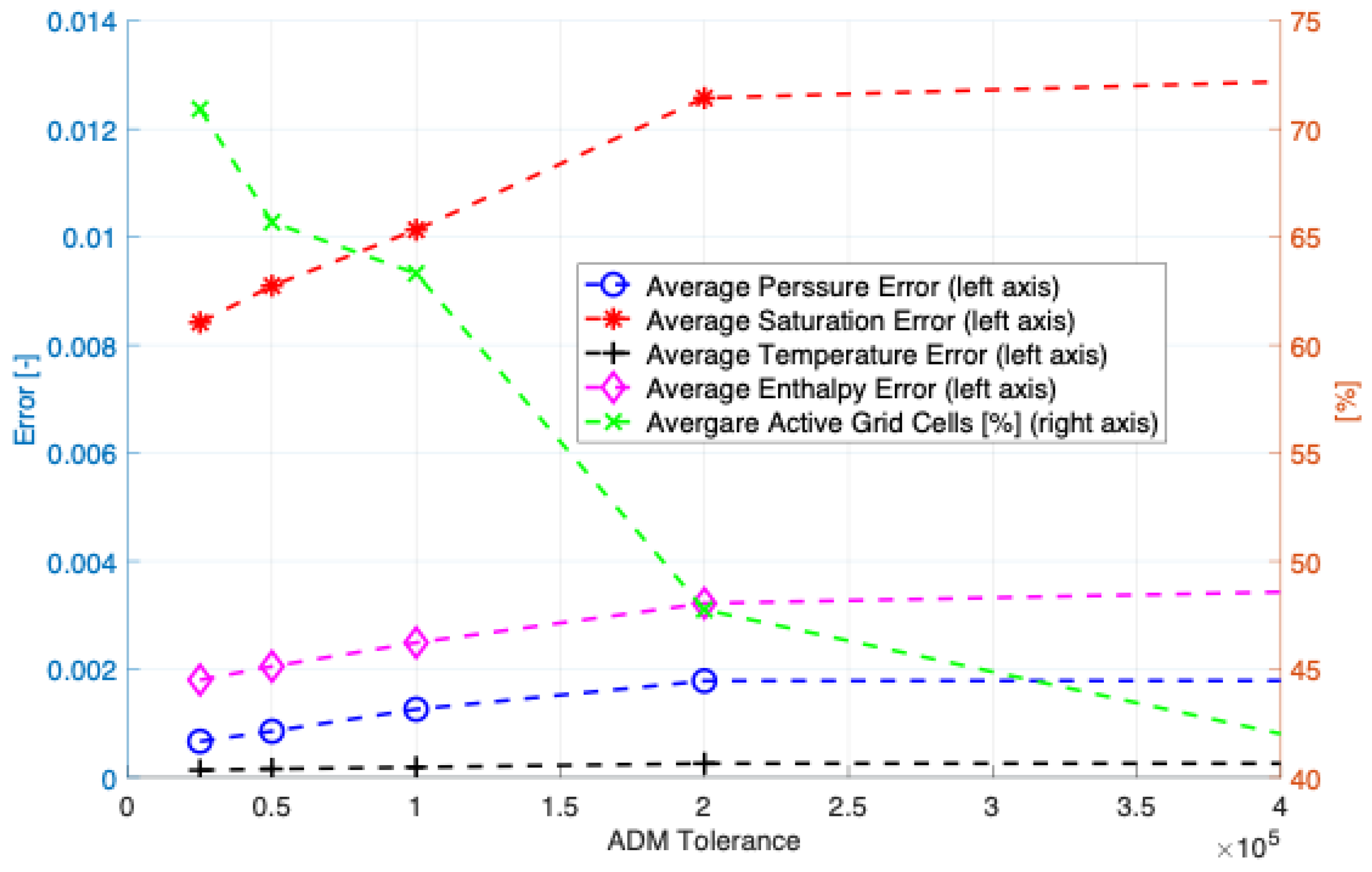
2.4. ADM Strategy
3. Results and Discussions
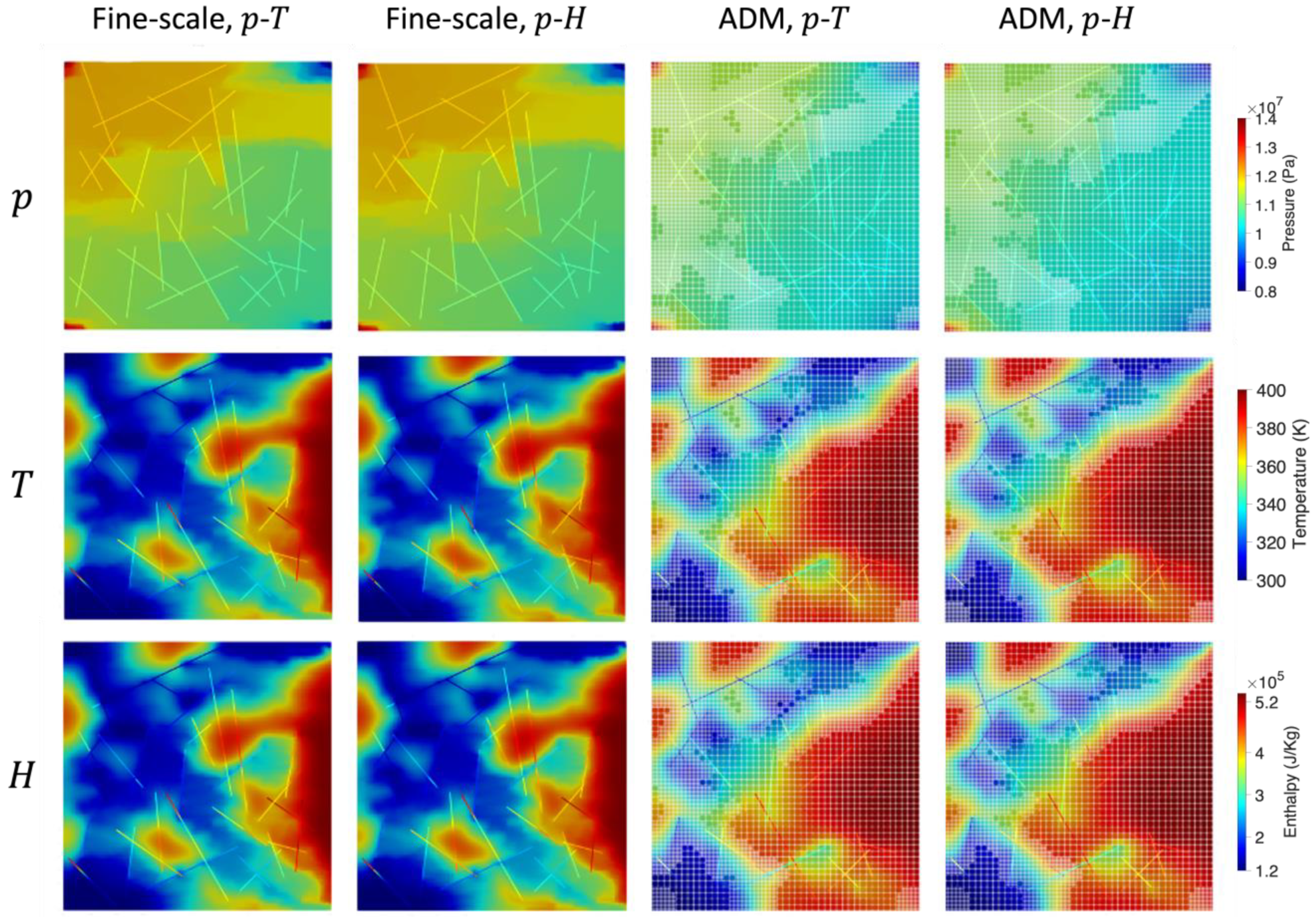
3.1. Comparison between Natural Formulation and Molar Formulation
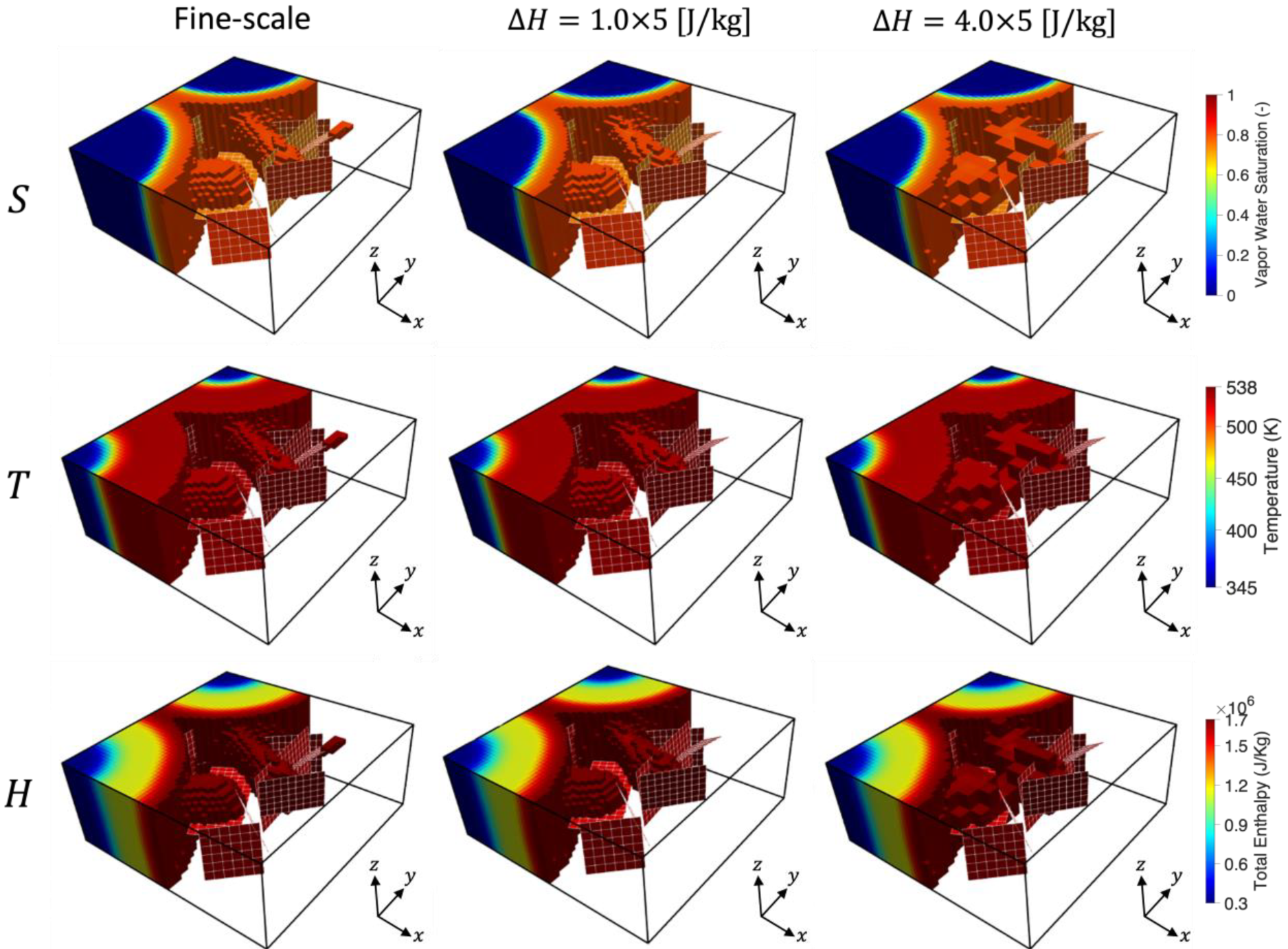
3.2. High-Enthalpy System Using Molar Formulation
4. Conclusions
- Numerical results indicate that the two formulations with different primary variables, i.e., natural formulation (-) and molar formulation (-), produce similar results in the case of single-phase flow. In the case studied, the maximum formulation error for the fine-scale and the ADM simulation are 1.9 and 3.0%, respectively.
- The performance of ADM is evaluated by comparing the simulation results with those obtained from the fine-scale grids. We observe that the ADM method provides computational efficiency by reducing the size of the linear system, while keeping the accuracy at a user-defined level. In the case with the highest tolerance, only 42% of grid cells are active, and the maximum error is 1.3% from the saturation map.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Natural Formulation
Appendix A.2. Molar Formulation
References
- Lund, J.W. Direct utilization of geothermal energy. Energies 2010, 3, 1443–1471. [Google Scholar] [CrossRef]
- Bertani, R. Geothermal power generation in the world 2005–2010 update report. Geothermics 2012, 41, 1–29. [Google Scholar] [CrossRef]
- Lund, J.W.; Boyd, T.L. Direct utilization of geothermal energy 2015 worldwide review. Geothermics 2016, 60, 66–93. [Google Scholar] [CrossRef]
- Gan, Q.; Elsworth, D. Production optimization in fractured geothermal reservoirs by coupled discrete fracture network modeling. Geothermics 2016, 62, 131–142. [Google Scholar] [CrossRef]
- Gholizadeh Doonechaly, N.; Abdel Azim, R.R.; Rahman, S.S. A study of permeability changes due to cold fluid circulation in fractured geothermal reservoirs. Groundwater 2016, 54, 325–335. [Google Scholar] [CrossRef] [PubMed]
- Ijeje, J.J.; Gan, Q.; Cai, J. Influence of permeability anisotropy on heat transfer and permeability evolution in geothermal reservoir. Adv. Geo-Energy Res. 2019, 3, 43–51. [Google Scholar] [CrossRef]
- Wang, Y.; de Hoop, S.; Voskov, D.; Bruhn, D.; Bertotti, G. Modeling of multiphase mass and heat transfer in fractured high-enthalpy geothermal systems with advanced discrete fracture methodology. Adv. Water Resour. 2021, 154, 103985. [Google Scholar] [CrossRef]
- Mahmoodpour, S.; Singh, M.; Turan, A.; Bär, K.; Sass, I. Simulations and global sensitivity analysis of the thermo-hydraulic-mechanical processes in a fractured geothermal reservoir. Energy 2022, 247, 123511. [Google Scholar] [CrossRef]
- Mahmoodpour, S.; Singh, M.; Bär, K.; Sass, I. Thermo-hydro-mechanical modeling of an enhanced geothermal system in a fractured reservoir using carbon dioxide as heat transmission fluid—A sensitivity investigation. Energy 2022, 254, 124266. [Google Scholar] [CrossRef]
- Khait, M.; Voskov, D. Operator-based linearization for efficient modeling of geothermal processes. Geothermics 2018, 74, 7–18. [Google Scholar] [CrossRef]
- Wong, Z.Y.; Horne, R.N.; Tchelepi, H.A. Sequential implicit nonlinear solver for geothermal simulation. J. Comput. Phys. 2018, 368, 236–253. [Google Scholar] [CrossRef]
- Pruess, K.; Oldenburg, C.M.; Moridis, G. TOUGH2 User’s Guide Version 2; Technical Report LBNL-43134; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1999.
- Pruess, K. Numerical simulation of multiphase tracer transport in fractured geothermal reservoirs. Geothermics 2002, 31, 475–499. [Google Scholar] [CrossRef]
- Garipov, T.T.; Tomin, P.; Rin, R.; Voskov, D.V.; Tchelepi, H.A. Unified thermo-compositional-mechanical framework for reservoir simulation. Comput. Geosci. 2018, 22, 1039–1057. [Google Scholar] [CrossRef]
- Wong, Z.Y.; Horne, R.; Voskov, D. Comparison of nonlinear formulations for geothermal reservoir simulations. In Proceedings of the 41st Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 22–24 February 2016. [Google Scholar]
- Hou, T.Y.; Wu, X.H. A multiscale finite element method for elliptic problems in composite materials and porous media. J. Comput. Phys. 1997, 134, 169–189. [Google Scholar] [CrossRef]
- Jenny, P.; Lee, S.H.; Tchelepi, H.A. Multi-scale finite-volume method for elliptic problems in subsurface flow simulation. J. Comput. Phys. 2003, 187, 47–67. [Google Scholar] [CrossRef]
- Jenny, P.; Lee, S.H.; Tchelepi, H.A. Adaptive fully implicit multi-scale finite-volume method for multi-phase flow and transport in heterogeneous porous media. J. Comput. Phys. 2006, 217, 627–641. [Google Scholar] [CrossRef]
- Hajibeygi, H.; Bonfigli, G.; Hesse, M.A.; Jenny, P. Iterative multiscale finite-volume method. J. Comput. Phys. 2008, 227, 8604–8621. [Google Scholar] [CrossRef]
- Wang, Y.; Hajibeygi, H.; Tchelepi, H.A. Algebraic multiscale solver for flow in heterogeneous porous media. J. Comput. Phys. 2014, 259, 284–303. [Google Scholar] [CrossRef]
- Edwards, M.G. A higher-order Godunov scheme coupled with dynamic local grid refinement for flow in a porous medium. Comput. Methods Appl. Mech. Eng. 1996, 131, 287–308. [Google Scholar] [CrossRef]
- Pau, G.S.; Almgren, A.S.; Bell, J.B.; Lijewski, M.J. A parallel second-order adaptive mesh algorithm for incompressible flow in porous media. Philos. Trans. R. Soc. Lond. Ser. A 2009, 367, 4633–4654. [Google Scholar] [CrossRef]
- Faigle, B.; Helmig, R.; Aavatsmark, I.; Flemisch, B. Efficient multiphysics modelling with adaptive grid refinement using a MPFA method. Comput. Geosci. 2014, 18, 625–636. [Google Scholar] [CrossRef]
- Adam, A.; Pavlidis, D.; Percival, J.R.; Salinas, P.; Xie, Z.; Fang, F.; Pain, C.C.; Muggeridge, A.H.; Jackson, M.D. Higher-order conservative interpolation between control-volume meshes: Application to advection and multiphase flow problems with dynamic mesh adaptivity. J. Comput. Phys. 2016, 321, 512–531. [Google Scholar] [CrossRef]
- Karimi-Fard, M.; Durlofsky, L.J. A general gridding, discretization, and coarsening methodology for modeling flow in porous formations with discrete geological features. Adv. Water Resour. 2016, 96, 354–372. [Google Scholar] [CrossRef]
- Wang, Y.; Shahvali, M. Discrete fracture modeling using Centroidal Voronoi grid for simulation of shale gas plays with coupled nonlinear physics. Fuel 2016, 163, 65–73. [Google Scholar] [CrossRef]
- Künze, R.; Lunati, I.; Lee, S.H. A multilevel multiscale finite-volume method. J. Comput. Phys. 2013, 255, 502–520. [Google Scholar] [CrossRef]
- Cusini, M.; van Kruijsdijk, C.; Hajibeygi, H. Algebraic dynamic multilevel (ADM) method for fully implicit simulations of multiphase flow in porous media. J. Comput. Phys. 2016, 314, 60–79. [Google Scholar] [CrossRef]
- HosseiniMehr, M.; Cusini, M.; Vuik, C.; Hajibeygi, H. Algebraic dynamic multilevel method for embedded discrete fracture model (F-ADM). J. Comput. Phys. 2018, 373, 324–345. [Google Scholar] [CrossRef]
- Coats, K.H. Geothermal reservoir modelling. In Proceedings of the SPE Annual Fall Technical Conference and Exhibition, Denver, CO, USA, 9–12 October 1977. [Google Scholar]
- Gelet, R.; Loret, B.; Khalili, N. The significance of local thermal non-equilibrium in simulations of enhanced geothermal recovery. In Proceedings of the 14th International Conference of the International Association for Computer Methods and Advances in Geomechanics (IACMAG), Kyoto, Japan, 22–25 September 2014. [Google Scholar]
- Nag, P.K. Engineering Thermodynamics, 6th ed.; McGraw Hill: New York, NY, USA, 2017. [Google Scholar]
- Faust, C.R.; Mercer, J.W. Geothermal reservoir simulation: 1. Mathematical models for liquid-and vapor-dominated hydrothermal systems. Water Resour. Res. 1979, 15, 23–30. [Google Scholar] [CrossRef]
- Jiang, J.; Younis, R.M. Hybrid coupled discrete-fracture/matrix and multicontinuum models for unconventional-reservoir simulation. SPE J. 2016, 21, 1009–1027. [Google Scholar] [CrossRef]
- Flemisch, B.; Berre, I.; Boon, W.; Fumagalli, A.; Schwenck, N.; Scotti, A.; Stefansson, I.; Tatomir, A. Benchmarks for single-phase flow in fractured porous media. Adv. Water Resour. 2018, 111, 239–258. [Google Scholar] [CrossRef]
- Ţene, M.; Bosma, S.B.; Al Kobaisi, M.S.; Hajibeygi, H. Projection-based embedded discrete fracture model (pEDFM). Adv. Water Resour. 2017, 105, 205–216. [Google Scholar] [CrossRef]
- HosseiniMehr, M.; Tomala, J.P.; Vuik, C.; Al Kobaisi, M.; Hajibeygi, H. Projection-based embedded discrete fracture model (pEDFM) for flow and heat transfer in real-field geological formations with hexahedral corner-point grids. Adv. Water Resour. 2022, 159, 104091. [Google Scholar] [CrossRef]
- Wang, Y.; Vuik, C.; Hajibeygi, H. CO2 Storage in deep saline aquifers: Impacts of fractures on hydrodynamic trapping. Int. J. Greenh. Gas Control 2022, 113, 103552. [Google Scholar] [CrossRef]
- Ţene, M.; Al Kobaisi, M.S.; Hajibeygi, H. Algebraic multiscale method for flow in heterogeneous porous media with embedded discrete fractures (F-AMS). J. Comput. Phys. 2016, 321, 819–845. [Google Scholar] [CrossRef]
- Wagner, W.; Kretzschmar, H.J. International Steam Tables: Properties of Water and Steam Based on the Industrial Formulation IAPWS-IF97, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Faust, C.R.; Mercer, J.W. Finite-Difference Model of Two Dimensional, Single-, and Two-Phase Heat Transport in a Porous Medium: Version I; US Department of the Interior, Geological Survey: Washington, DC, USA, 1977. [Google Scholar]


| Property | Value |
|---|---|
| Porosity | 0.2 |
| Rock density | 2600 [Kg/m3] |
| Rock specific heat capacity | 830 [J/Kg/K] |
| Rock thermal conductivity | 2.9 [W/m/K] |
| Fracture permeability | {1.0 × 10−8, 1.0 × 10−20} [m2] |
| Fracture aperture | 5.0 × 10−3 [m] |
| Fracture porosity | 1.0 |
| Initial temperature | 400 [K] |
| Initial pressure | 1.0 × 107 [Pa] |
| Injection temperature | 300 [K] |
| Injection pressure | 1.4 × 107 [Pa] |
| Production pressure | 0.8 × 107 [Pa] |
| Simulation time | 2000 [days] |
| Tolerance for convergence | 1.0 × 10−4 [-] |
| ADM coarsening levels | 2 |
| ADM coarsening ratio | 3 × 3 |
| Property | Value |
|---|---|
| Porosity | 0.2 |
| Rock permeability | 1.0 × 10−14 [m2] |
| Rock compressibility | 1.0 × 10−8 [1/Pa] |
| Rock density | 2600 [Kg/m3] |
| Rock specific heat capacity | 850 [J/Kg/K] |
| Rock thermal conductivity | 3.0 [W/m/K] |
| Fracture permeability | {1.0 × 10−8, 1.0 × 10−20} [m2] |
| Fracture aperture | 5.0 × 10−3 [m] |
| Fracture porosity | 1.0 |
| Initial enthalpy | 1.6 × 106 [J/Kg] |
| Initial pressure | 5.0 × 106 [Pa] |
| Water liquid compressibility | 1.0 × 10−9 [1/Pa] |
| Water vapor compressibility | 1.0 × 10−6 [1/Pa] |
| Water liquid specific heat capacity | 4200 [J/Kg/K] |
| Water vapor specific heat capacity | 8000 [J/Kg/K] |
| Water liquid thermal conductivity | 0.6 [W/m/K] |
| Water vapor thermal conductivity | 0.1 [W/m/K] |
| Injection enthalpy | 3.0 × 105 [J/Kg] |
| Injection pressure | 6.0 × 106 [Pa] |
| Production pressure | 4.0 × 106 [Pa] |
| Simulation time | 200 [days] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; HosseiniMehr, M.; Marelis, A.; Hajibeygi, H. A Generic Framework for Multiscale Simulation of High and Low Enthalpy Fractured Geothermal Reservoirs under Varying Thermodynamic Conditions. Energies 2023, 16, 928. https://doi.org/10.3390/en16020928
Wang Y, HosseiniMehr M, Marelis A, Hajibeygi H. A Generic Framework for Multiscale Simulation of High and Low Enthalpy Fractured Geothermal Reservoirs under Varying Thermodynamic Conditions. Energies. 2023; 16(2):928. https://doi.org/10.3390/en16020928
Chicago/Turabian StyleWang, Yuhang, Mousa HosseiniMehr, Arjan Marelis, and Hadi Hajibeygi. 2023. "A Generic Framework for Multiscale Simulation of High and Low Enthalpy Fractured Geothermal Reservoirs under Varying Thermodynamic Conditions" Energies 16, no. 2: 928. https://doi.org/10.3390/en16020928
APA StyleWang, Y., HosseiniMehr, M., Marelis, A., & Hajibeygi, H. (2023). A Generic Framework for Multiscale Simulation of High and Low Enthalpy Fractured Geothermal Reservoirs under Varying Thermodynamic Conditions. Energies, 16(2), 928. https://doi.org/10.3390/en16020928






