Application of the Gradient-Based Metaheuristic Optimizerto Solve the Optimal Conductor Selection Problemin Three-Phase Asymmetric Distribution Networks
Abstract
1. Introduction
2. Literature Review and Contributions
3. Mathematical Formulation
3.1. Objective Function
3.2. Set of Constraints
3.3. Solution Space Analysis
4. Solution Methodology
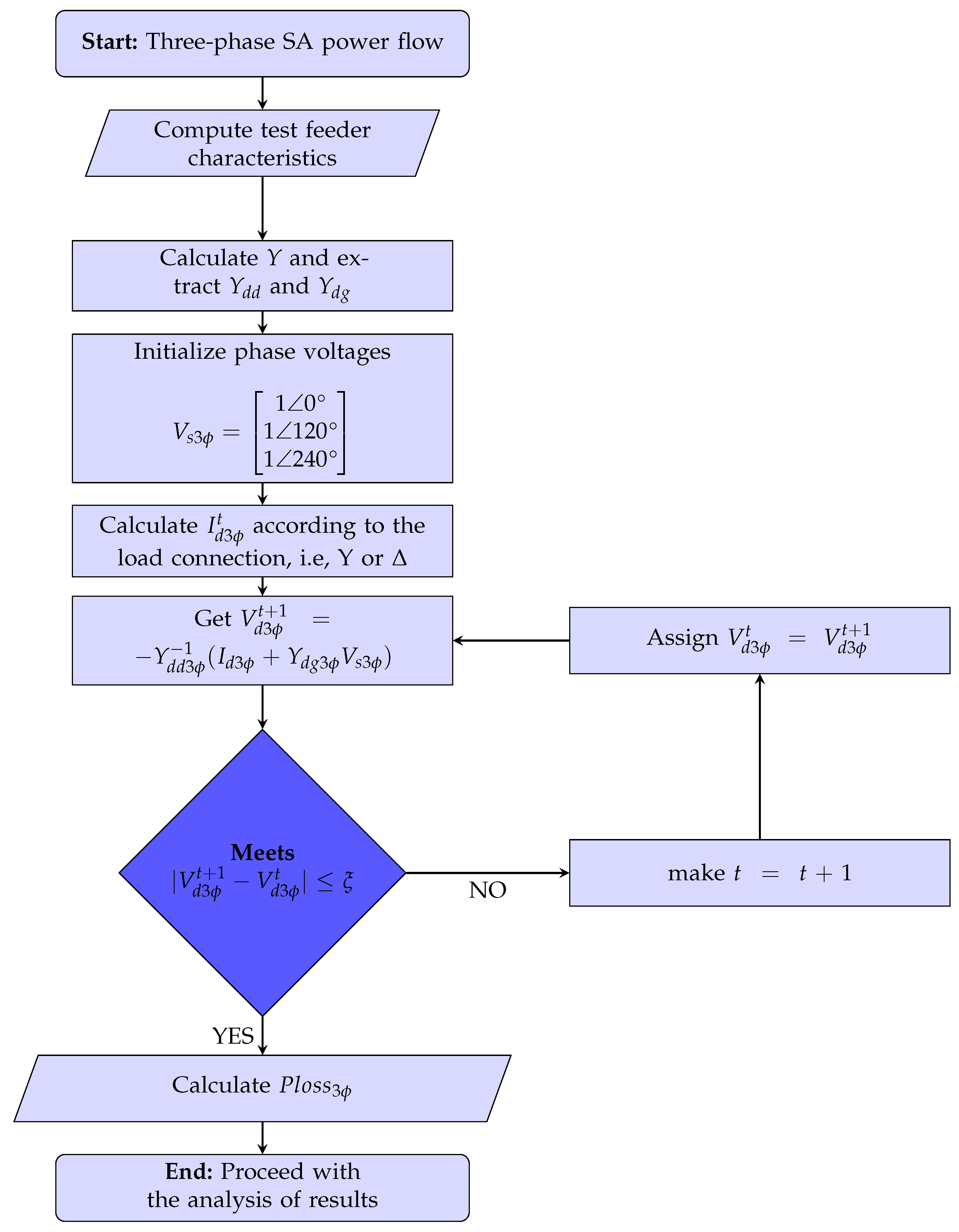
4.1. Slave Stage: Three-Phase Power Flow
4.2. Master Stage: MGbMO Metaheuristic Algorithm
4.3. Implementation of the MGbMO
| Algorithm 1: Implementation of the MGbMO algorithm |
Data: Select the AC electrical network under study; Obtain the equivalent in values per unit of the distribution system; Define the maximum number of iterations (); Define the size of the initial population (); Generate the initial population and make ; Define the solution space’s initial center (); Obtain the value of the objective function for each of the individuals of the initial population with the help of the slave stage; Find the best current solution ; Generate a random number between 0 and 1 for ; Apply the evolution rule of Equation (19); Verify and adjust the values of so that it is within its limits; Evaluate in the slave stage to find the value of the objective function; Update to the current best; Calculate the radius as expressed in (24); Generate the descendant population using Equation (21); Verify and adjust the values of so that it is within its limits; Evaluate in the slave stage to find the value of the objective function; Update to the current best; Show the best solution ; |
5. Characteristics of the Test Systems
5.1. General Parameters
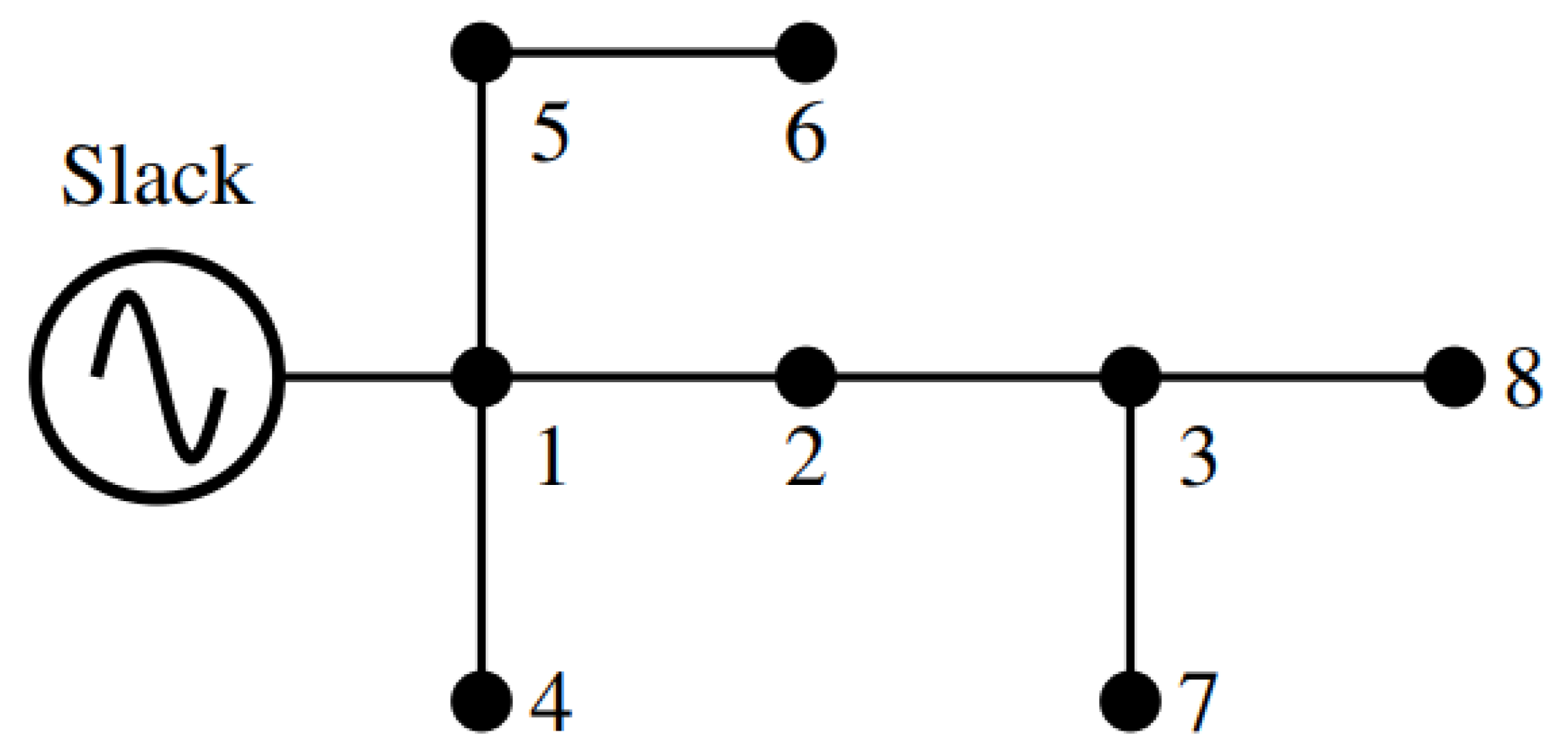
5.2. 8-Bus Test System
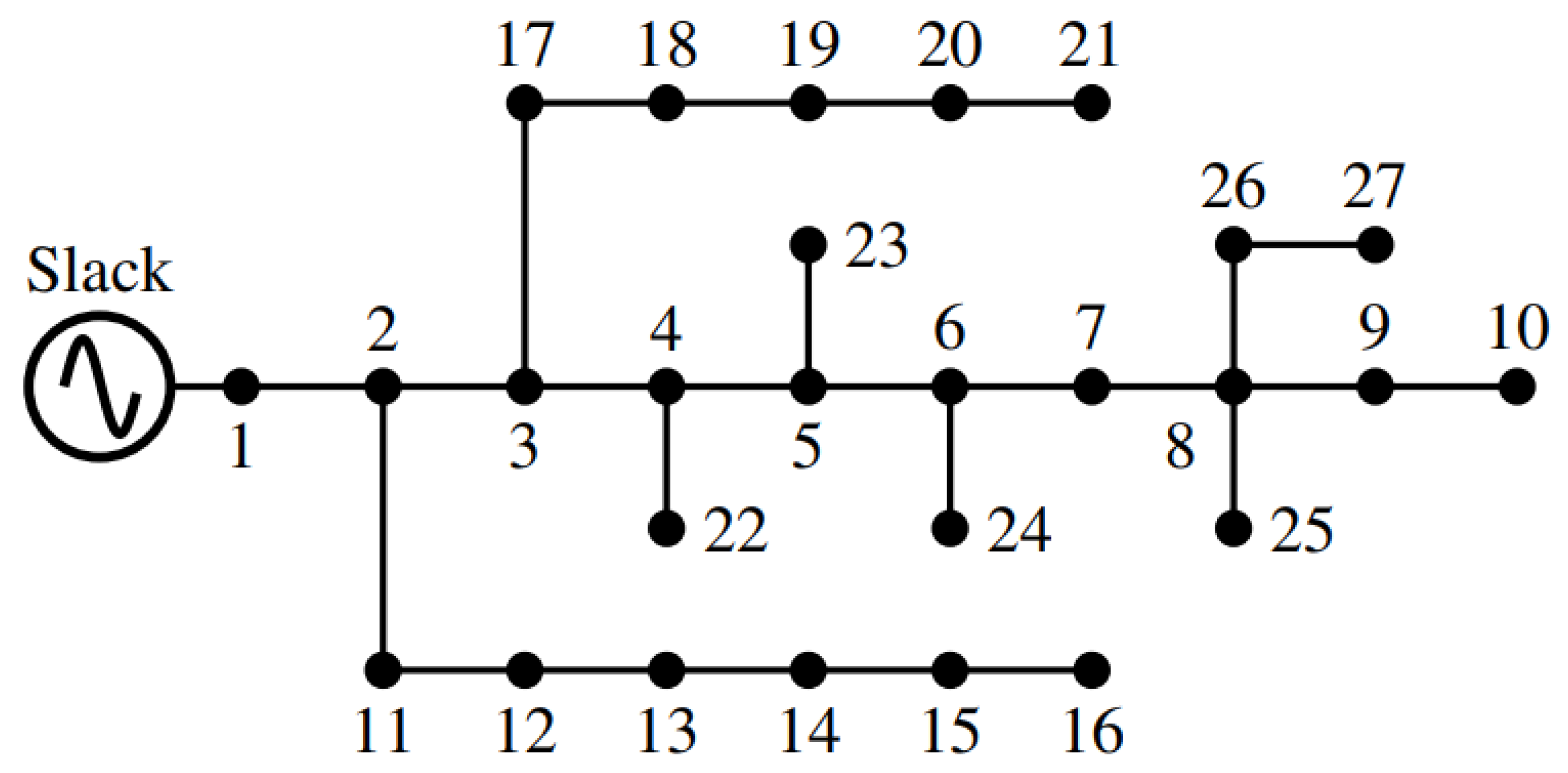
5.3. 27-Bus Test System
6. Results and Discussion
6.1. Results in the 8-Bus Test System
6.1.1. Balanced Case for the 8-Bus Test System
- The MGbMO algorithm obtained the best numerical result for the balanced 8-bus system, yielding annual costs of USD 455,969,791, with USD 227,826 in the investment of the conductors and USD 228,143,791 in the costs associated with the losses.
- The result obtained by the MGbMO algorithm improved by 10.3% compared to the VSA and NMA algorithms, which obtained the second-best solutions with USD 508,357.959 for annual costs, which represents a reduction of USD 52,388.2 for the study case.
- The cost of the investment of the conductors, according to the set of gauges selected by the MGbMO algorithm, presents the highest cost compared to the rest of the algorithms; however, the cost of annual losses is lower, which thus ends up compensating for the high costs in the investment of the conductors.
6.1.2. Unbalanced Case for the 8-Bus Test System
- The MGbMO algorithm equaled the results of the VSA and NMA algorithms for the unbalanced 8-bus system, yielding annual costs of USD 558,758,394, with USD 289,713 in the investment of the conductors and USD 269,045,394 in the costs associated with the losses.
6.2. Results in the 27-Bus Test System
6.2.1. Balanced Case for the 27-Bus Test System
- The MGbMO algorithm obtained the best numerical result for the balanced 27-bus system, yielding annual costs of USD 549,883.572, with USD 319,768.08 in the investment of the conductors and USD 230,115.492 in the costs associated with losses.
- The result obtained by the MGbMO algorithm improved by 1.4% compared to the NMA algorithm, which obtained the second-best solution with USD 557,695.255 for annual costs, representing a reduction of USD 7811.68 for the case study.
- The cost of the investment of the conductors, according to the set of gauges selected by the MGbMO algorithm, presents the lowest cost compared to the rest of the algorithms, thus increasing the costs of annual losses slightly. In the end, the costs are compensated, as shown in the annual costs, allowing a lower value in the objective function.
6.2.2. Unbalanced Case for the 27-Bus Test System
- The MGbMO algorithm obtained the best numerical result for the unbalanced 27-bus system, yielding annual costs of USD 589,018.8, with USD 331,828.08 in the investment of the conductors and USD 257,190.72 in the costs associated with the losses.
- The result obtained by the MGbMO algorithm improved by 1.432% compared to the NMA algorithm, which obtained the second-best solution with USD 597,579.008 for annual costs, thus representing a reduction of USD 8560.21 for the case study.
- The cost of the investment of the conductors, according to the set of gauges selected by the MGbMO algorithm, presents the lowest cost compared to the rest of the algorithms, thus increasing the costs of annual losses slightly but without exceeding the costs presented by the VSA version. These costs are compensated in the end, as shown in the annual costs, allowing a lower value in the objective function.
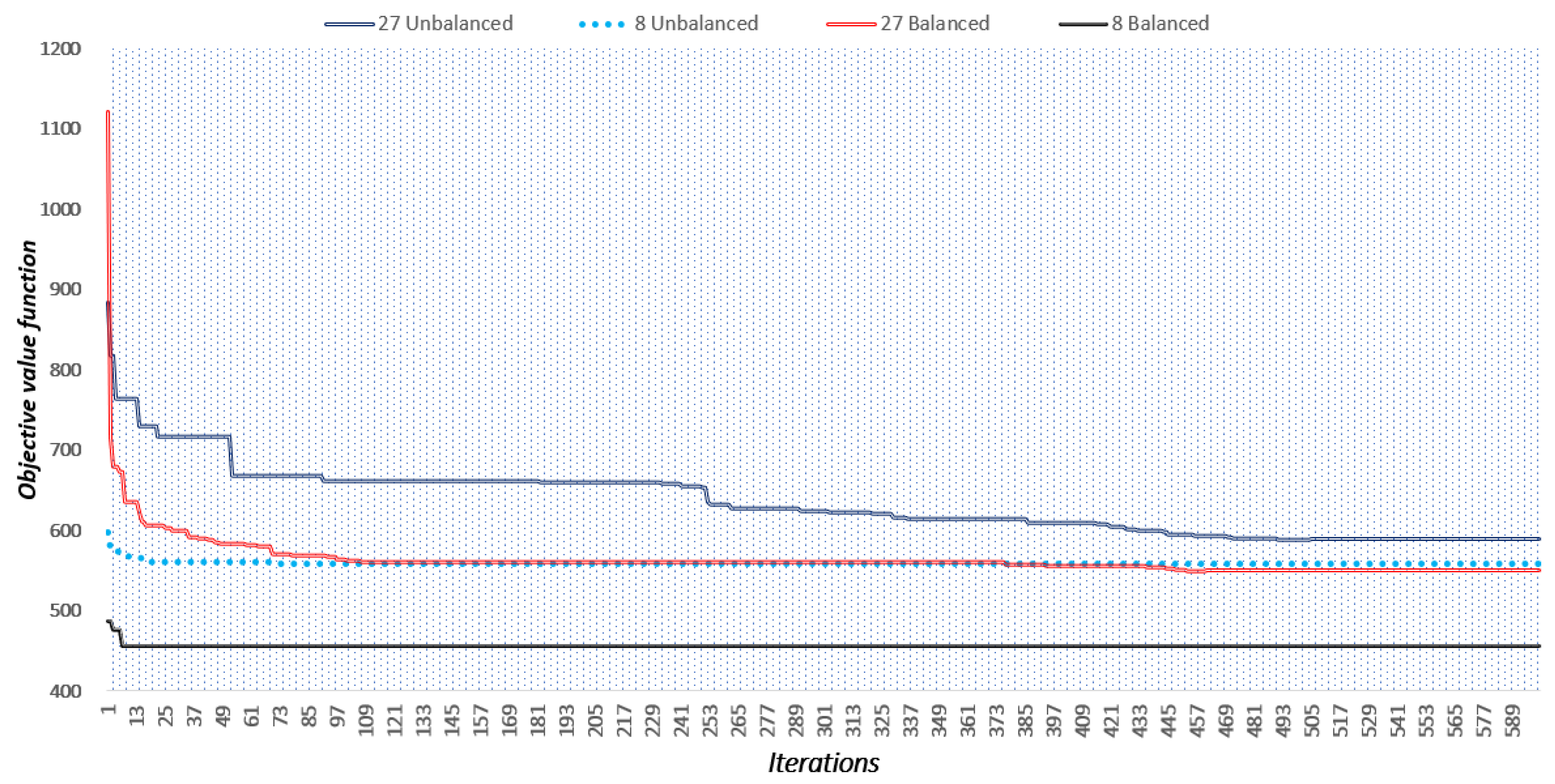
6.3. Performance of the Algorithm
6.4. A Daily Operation Scenario
- Case 1: The evaluation of the optimization methodology during the peak load condition, i.e., under the same simulation conditions used for the 8- and 27-bus grids.
- Case 2: The selection of the conductors only considers the daily load variations without penetration of renewable generation.
- Case 3: The evaluation of the optimization methodology considering the daily demand and generation curves.
- i.
- Case 1 is an operation scenario that invests more in conducting material to minimize the effect of the energy loss costs in the objective function as soon as possible. This is accomplished by increasing the conductor sizes in some strategic distribution lines, which reduces the energy loss since these are proportional to the resistive parameter and the square value of the current. Additionally, the expected energy loss costs for this scenario can be far from the real operative scenario for a distribution grid where all the demands vary along the day.
- ii.
- Case 2 demonstrates a more realistic operative scenario for medium-voltage distribution networks, where the energy consumption varies along the day, considering a typical demand curve. In this case, the expected energy losses are about USD 312,264.9263 per year of operation, which implies a reduction of about USD 91,652.7653 concerning the peak load operation scenario. This implies that it is highly probable for a distribution company that the energy loss costs will be near the daily demand variation scenario compared to the peak load condition. However, the most important result in simulation Case 2 is the reduction in the investment costs concerning the peak load scenario of about 40.0691%. This implies that when the energy calculation is more realistic, the algorithm finds conductors with small sizes (see Cases 1 and 2 in Table 16), which can be considered a more convenient design scenario for the distribution company.
- iii.
- Case 3 presents the well-known benefits of the usage of renewable generation in distribution networks since these allow important reductions in the expected energy loss costs. This scenario showcases that the energy loss costs are reduced by about USD 62,738.9098 with respect to Case 2. Additionally, the inclusion of renewables has reduced the investment costs in conducting material by about USD 27,179.0850 through the reduction in the conductor sizes in some strategy lines (lines near to the substation bus as can be seen for Cases 2 and 3 in Table 16).
7. Conclusions and Future Work
- i.
- The MGbMO algorithm implemented yields the best current solutions for three of the four systems studied, where for the balanced 8-bus system, an objective function of USD 455,969.791 is obtained, achieving a reduction of 10.3% over the value obtained with NMA, which has the second-best result; regarding the unbalanced case, the results of the other algorithms are matched with a value of USD 558,758.394, and it can, thus, be inferred that the optimal global solution is found (this affirmation is based on the small dimension of the solution space for the 8-bus grid, i.e., = 2,097,152, which can be easily explored with any combinatorial optimization method or exhaustive search). In the balanced 27-bus system, a value of USD 549,883.572 is obtained as total annual costs, achieving an improvement of 1.4% compared to the NMA, while in the unbalanced case, a value of USD 589,018.800 is obtained, which is 1.432% more than in the case of the NMA.
- ii.
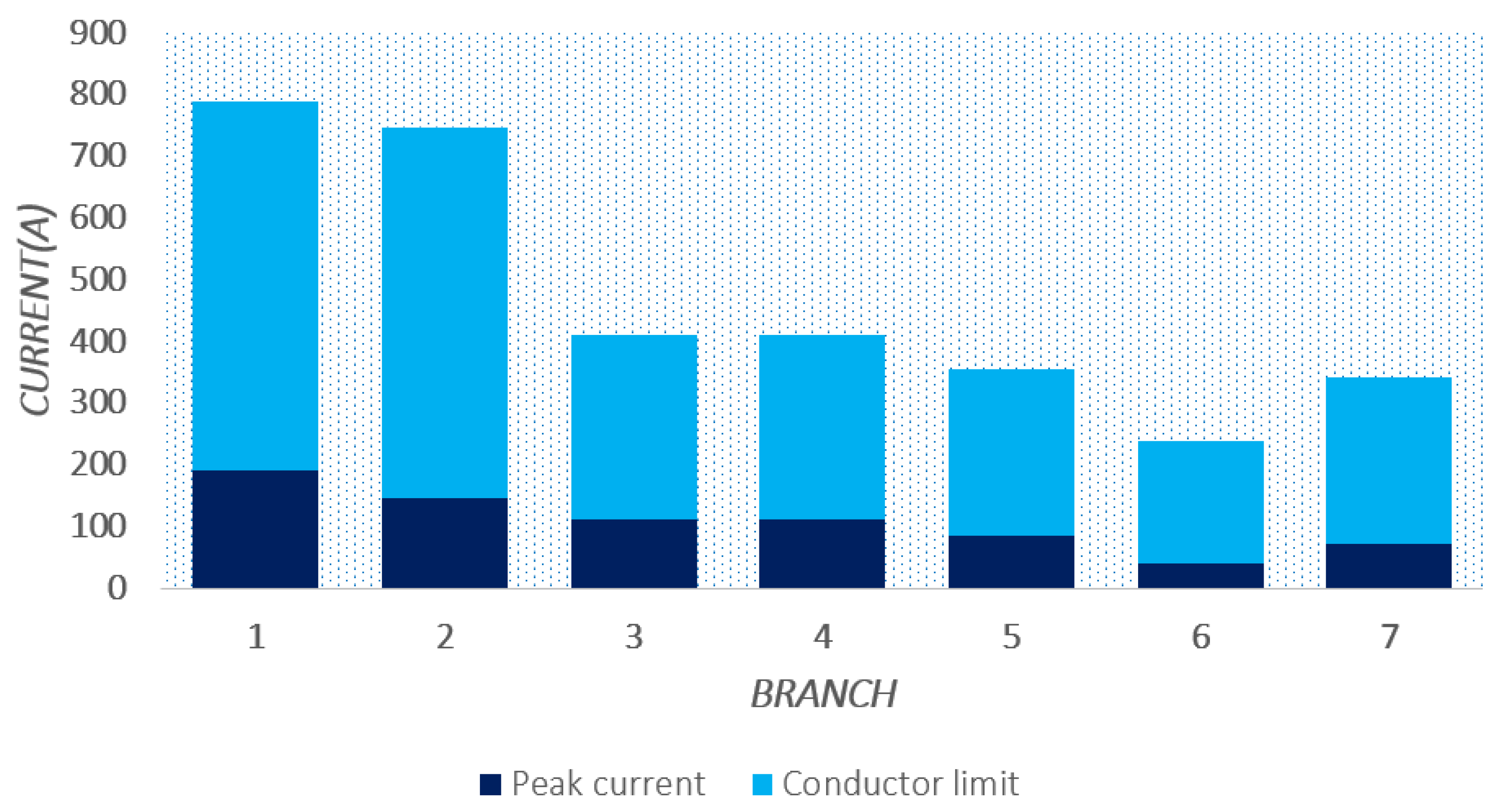
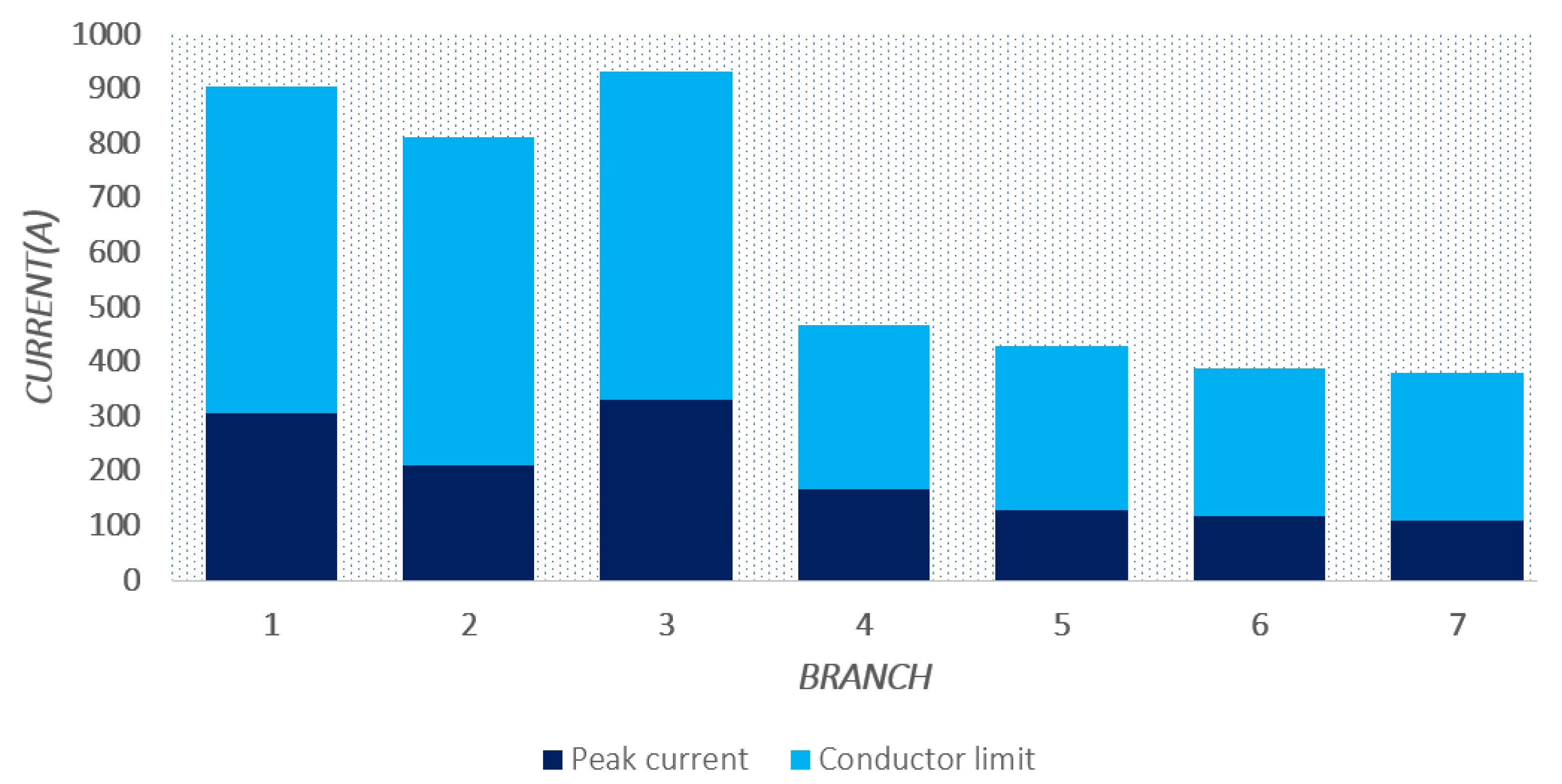
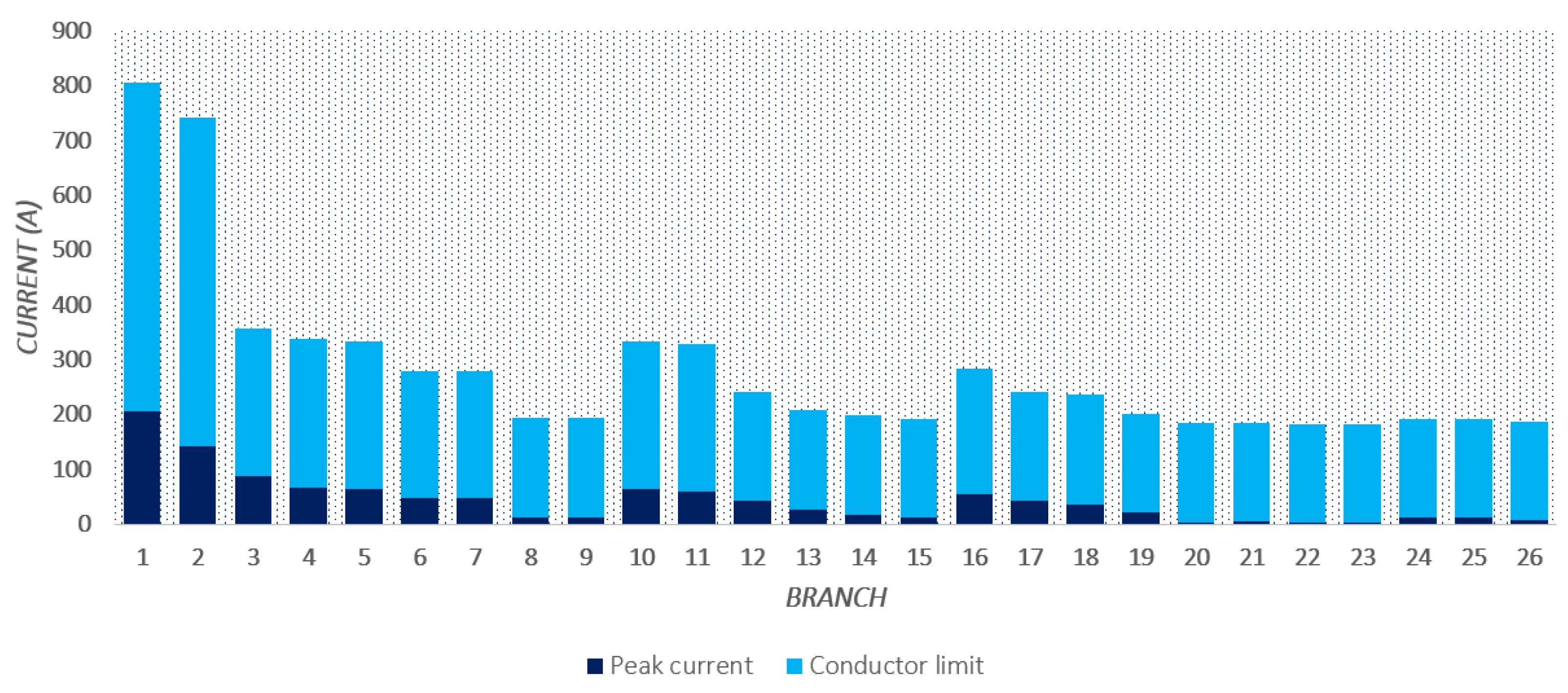
- For the four case studies, the findings ascertain that since the current levels that pass through the branches are far from their limits established by each gauge (less than 35%), the energy losses are low, and the loss costs are thus reduced as well, ensuring good operation and adapting to future new load connections.
- iii.
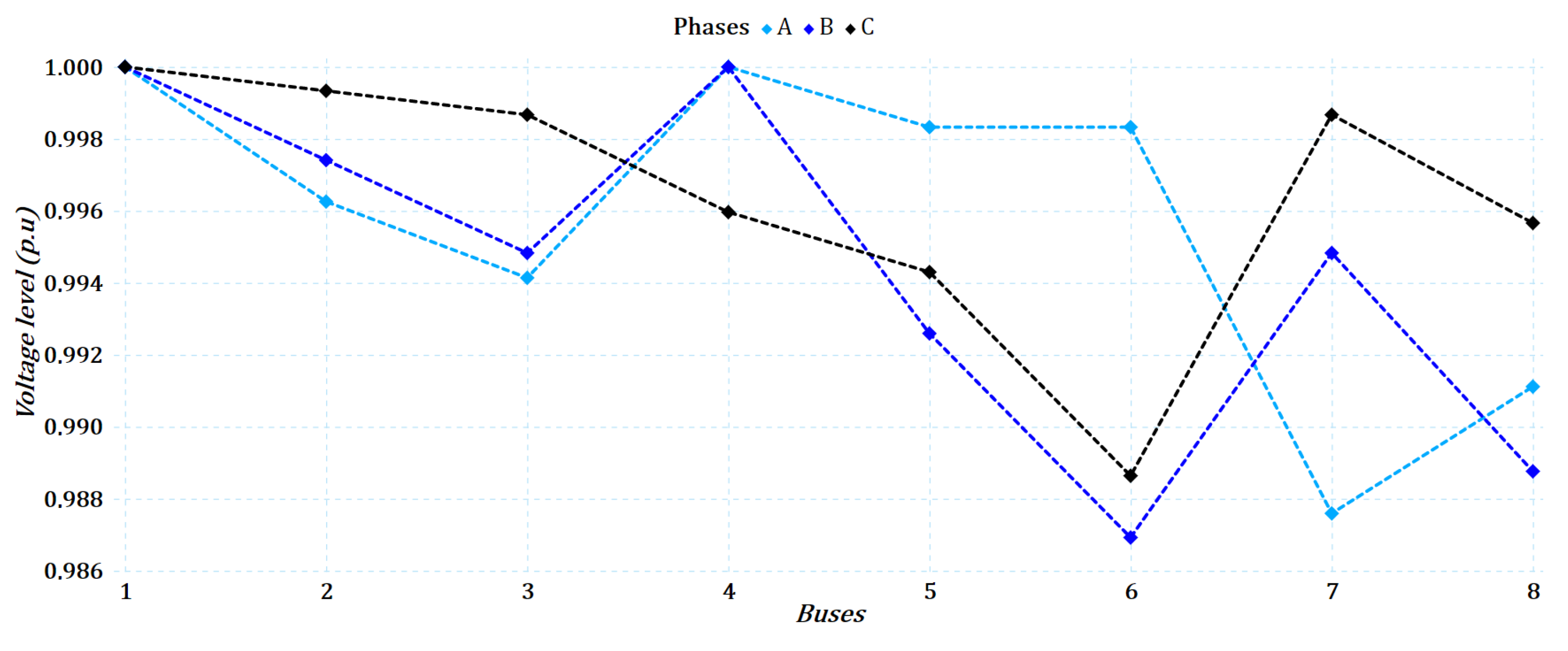
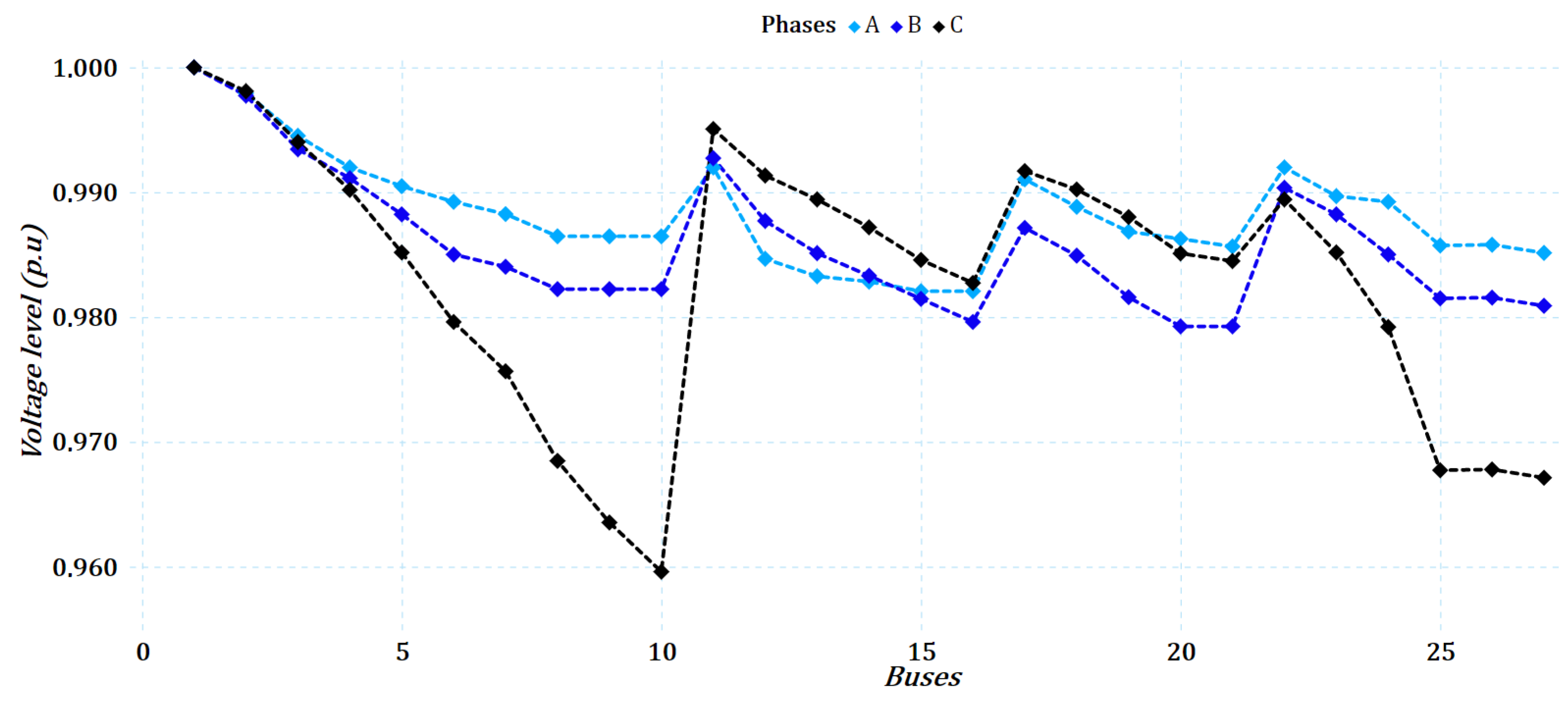
- The voltage profiles are adequate for all test systems. In this regard, the lowest and most distant one is evident in the 27-bus system for the balanced case, where a shift of 4.61% is presented in phase C, which is very low and positive for the system.
- iv.
- The MGbMO algorithm only needs a single evaluation in each test system to obtain the best numerical results, which are previously reported in this research, due to the exploration and exploitation characteristics of the solution space, which shortened simulation times, making this method one of the most efficient methods reported in the specialized literature.
- v.
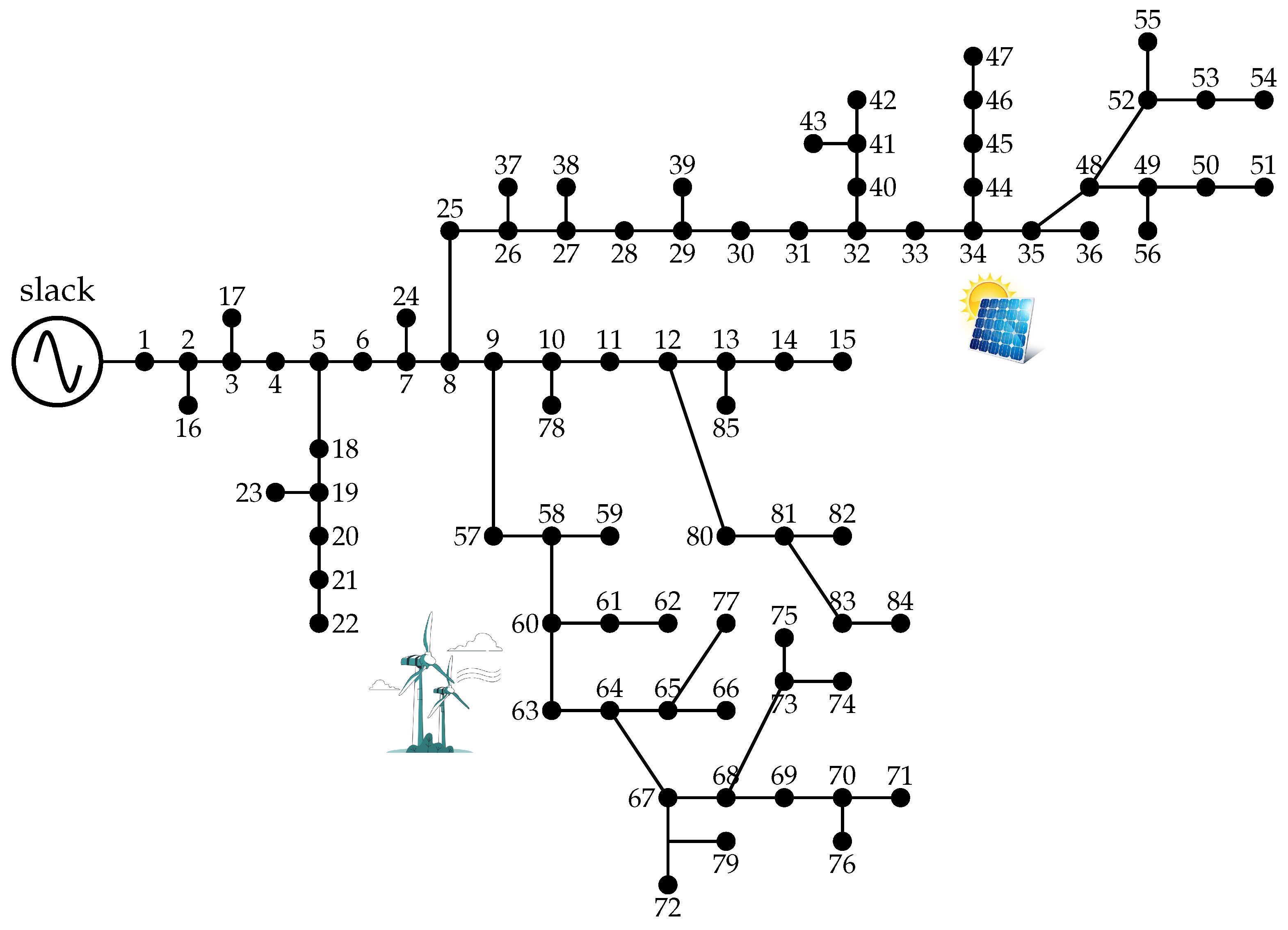
- The numerical results obtained with the MGbMO in the three-phase version of the IEEE 85-bus grid indicate that the peak demand scenario is a simulation case where the energy losses costs are overestimated, which leads the optimization algorithm to increase the conductor sizes to find an adequate equilibrium between investment and operating costs. However, when daily demand curves and renewable generation are considered, the expected annual costs of the energy losses reduce significantly, allowing the MGbMO to find conductor sizes with lower costs in comparison to the peak scenario of operation. These results imply that considering daily demand curves is the most realistic scenario for the studied problem. Ultimately, this simulation case must be considered the benchmark case for any new study in this research area.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kazmi, S.A.A.; Shahzad, M.K.; Khan, A.Z.; Shin, D.R. Smart Distribution Networks: A Review of Modern Distribution Concepts from a Planning Perspective. Energies 2017, 10, 501. [Google Scholar] [CrossRef]
- Jin, T.; Zhuo, F.; Mohamed, M.A. A Novel Approach Based on CEEMDAN to Select the Faulty Feeder in Neutral Resonant Grounded Distribution Systems. IEEE Trans. Instrum. Meas. 2020, 69, 4712–4721. [Google Scholar] [CrossRef]
- Acosta, J.S.; Tavares, M.C. Optimal selection and positioning of conductors in multi-circuit overhead transmission lines using evolutionary computing. Electr. Power Syst. Res. 2020, 180, 106174. [Google Scholar] [CrossRef]
- Nahman, J.; Peric, D. Optimal Planning of Radial Distribution Networks by Simulated Annealing Technique. IEEE Trans. Power Syst. 2008, 23, 790–795. [Google Scholar] [CrossRef]
- Lavorato, M.; Franco, J.F.; Rider, M.J.; Romero, R. Imposing Radiality Constraints in Distribution System Optimization Problems. IEEE Trans. Power Syst. 2012, 27, 172–180. [Google Scholar] [CrossRef]
- Macedo, L.H.; Franco, J.F.; Mahdavi, M.; Romero, R. A Contribution to the Optimization of the Reconfiguration Problem in Radial Distribution Systems. J. Control. Autom. Electr. Syst. 2018, 29, 756–768. [Google Scholar] [CrossRef]
- Lavorato, M.; Rider, M.J.; Garcia, A.V.; Romero, R. A Constructive Heuristic Algorithm for Distribution System Planning. IEEE Trans. Power Syst. 2010, 25, 1734–1742. [Google Scholar] [CrossRef]
- Girbau-Llistuella, F.; Díaz-González, F.; Sumper, A.; Gallart-Fernández, R.; Heredero-Peris, D. Smart Grid Architecture for Rural Distribution Networks: Application to a Spanish Pilot Network. Energies 2018, 11, 844. [Google Scholar] [CrossRef]
- Escobar-Yonoff, R.; Maestre-Cambronel, D.; Charry, S.; Rincón-Montenegro, A.; Portnoy, I. Performance assessment and economic perspectives of integrated PEM fuel cell and PEM electrolyzer for electric power generation. Heliyon 2021, 7, e06506. [Google Scholar] [CrossRef]
- Abdelaziz, A.Y.; Fathy, A. A novel approach based on crow search algorithm for optimal selection of conductor size in radial distribution networks. Eng. Sci. Technol. Int. J. 2017, 20, 391–402. [Google Scholar] [CrossRef]
- Abul’Wafa, A.R. Multi-conductor feeder design for radial distribution networks. Electr. Power Syst. Res. 2016, 140, 184–192. [Google Scholar] [CrossRef]
- Islam, S.; Ghani, M. Economical optimization of conductor selection in planning radial distribution networks. In Proceedings of the 1999 IEEE Transmission and Distribution Conference (Cat. No. 99CH36333), New Orleans, LA, USA, 11–16 April 1999; Volume 2, pp. 858–863. [Google Scholar] [CrossRef]
- Montoya, O.D.; Grisales-Noreña, L.F.; Giral-Ramírez, D.A. Optimal Placement and Sizing of PV Sources in Distribution Grids Using a Modified Gradient-Based Metaheuristic Optimizer. Sustainability 2022, 14, 3318. [Google Scholar] [CrossRef]
- Sivanagaraju, S.; Sreenivasulu, N.; Vijayakumar, M.; Ramana, T. Optimal conductor selection for radial distribution systems. Electr. Power Syst. Res. 2002, 63, 95–103. [Google Scholar] [CrossRef]
- Falaghi, H.; Ramezani, M.; Haghifam, M.R.; Milani, K. Optimal selection of conductors in radial distribution systems with time varying load. In Proceedings of the 18th International Conference and Exhibition on Electricity Distribution (CIRED 2005), Turin, Italy, 6–9 June 2005. [Google Scholar] [CrossRef]
- Satyanarayana, S.; Ramana, T.; Rao, G.K.; Sivanagaraju, S. Improving the Maximum Loading by Optimal Conductor Selection of Radial Distribution Systems. Electr. Power Components Syst. 2006, 34, 747–757. [Google Scholar] [CrossRef]
- Ponnavaikko, M.; Rao, K. An Approach to Optimal Distribution System Planning Through Conductor Gradation. IEEE Trans. Power Appar. Syst. 1982, PAS-101, 1735–1742. [Google Scholar] [CrossRef]
- Thenepalle, M. A Comparative Study on Optimal Conductor Selection for Radial Distribution Network using Conventional and Genetic Algorithm Approach. Int. J. Comput. Appl. 2011, 17, 6–13. [Google Scholar] [CrossRef]
- Legha, M.M.; Javaheri, H.; Legha, M.M. Optimal Conductor Selection in Radial Distribution Systems for Productivity Improvement Using Genetic Algorithm. Iraqi J. Electr. Electron. Eng. 2013, 9, 29–35. [Google Scholar] [CrossRef]
- Zhao, Z.; Mutale, J. Optimal Conductor Size Selection in Distribution Networks with High Penetration of Distributed Generation Using Adaptive Genetic Algorithm. Energies 2019, 12, 2065. [Google Scholar] [CrossRef]
- Ismael, S.M.; Aleem, S.H.A.; Abdelaziz, A.Y.; Zobaa, A.F. Optimal Conductor Selection of Radial Distribution Feeders: An Overview and New Application Using Grasshopper Optimization Algorithm. In Classical and Recent Aspects of Power System Optimization; Elsevier: Amsterdam, The Netherlands, 2018; pp. 185–217. [Google Scholar] [CrossRef]
- Mendoza, F.; Requena, D.; Bemal-Agustin, J.; Dominguez-Navarro, J. Optimal Conductor Size Selection in Radial Power Distribution Systems Using Evolutionary Strategies. In Proceedings of the 2006 IEEE/PES Transmission & Distribution Conference and Exposition: Latin America, Caracas, Venezuela, 15–18 August 2006. [Google Scholar] [CrossRef]
- Samal, P.; Mohanty, S.; Ganguly, S. Simultaneous capacitor allocation and conductor sizing in unbalanced radial distribution systems using differential evolution algorithm. In Proceedings of the 2016 National Power Systems Conference (NPSC), Bhubaneswar, India, 19–21 December 2016. [Google Scholar] [CrossRef]
- Raju, M.R.; Murthy, K.V.S.R.; Ravindra, K.; Rao, R.S. Optimal conductor selection for agricultural distribution system—A case study. In Proceedings of the 2010 International Conference on Intelligent and Advanced Systems, Manila, Philippines, 15–17 June 2010. [Google Scholar] [CrossRef]
- Osman, I.; Rahman, M.A.; Mahbub, A.R.; Haque, A. Benefits of optimal size conductor in transmission system. In Proceedings of the 2014 International Conference on Advances in Electrical Engineering (ICAEE), Vellore, India, 9–11 January 2014. [Google Scholar] [CrossRef]
- Momoh, I.; Jibril, Y.; Jimoh, B.; Abubakar, A.S.; Ajayi, O.; Abubakar, A.; Sulaiman, S.; Yusuf, S. Effect of an Optimal Conductor Size Selection Scheme for Single Wire Earth Return Power Distribution Networks For Rural Electrification. J. Sci. Technol. Educ. 2019, 7, 286–295. [Google Scholar]
- Kalesar, B.M. Conductor selection optimization in radial distribution system considering load growth using MDE algorithm. World J. Model. D Simul. 2014, 10, 175–184. [Google Scholar]
- Ramana, T.; Nararaju, K.; Ganesh, V.; Sivanagaraju, S. Customer Loss Allocation Reduction Using Optimal Conductor Selection in Electrical Distribution System. In Emerging Trends in Electrical, Communications, and Information Technologies; Springer: Berlin/Heidelberg, Germany, 2020; pp. 369–379. [Google Scholar]
- Martínez-Gil, J.F.; Moyano-García, N.A.; Montoya, O.D.; Alarcon-Villamil, J.A. Optimal Selection of Conductors in Three-Phase Distribution Networks Using a Discrete Version of the Vortex Search Algorithm. Computation 2021, 9, 80. [Google Scholar] [CrossRef]
- Ismael, S.M.; Aleem, S.H.E.A.; Abdelaziz, A.Y. Optimal selection of conductors in Egyptian radial distribution systems using sine-cosine optimization algorithm. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017. [Google Scholar] [CrossRef]
- Montoya, O.D.; Serra, F.M.; Angelo, C.H.D.; Chamorro, H.R.; Alvarado-Barrios, L. Heuristic Methodology for Planning AC Rural Medium-Voltage Distribution Grids. Energies 2021, 14, 5141. [Google Scholar] [CrossRef]
- Nivia Torres, D.J.; Salazar Alarcón, G.A.; Montoya Giraldo, O.D. Selección óptima de conductores en redes de distribución trifásicas utilizando el algoritmo metaheurístico de Newton. Ingeniería 2022, 27, e19303. [Google Scholar] [CrossRef]
- Shen, T.; Li, Y.; Xiang, J. A Graph-Based Power Flow Method for Balanced Distribution Systems. Energies 2018, 11, 511. [Google Scholar] [CrossRef]
- Ramírez Castaño, S. Redes de Distribución de Energía. Diseño y Construcción y en la Operación del Sistema de Distribución; Universidad Nacional de Colombia: Manizales, Colombia, 2009. [Google Scholar]
- Montoya, O.D. Notes on the Dimension of the Solution Space in Typical Electrical Engineering Optimization Problems. Ingeniería 2022, 27, e19310. [Google Scholar] [CrossRef]
- Jaddi, N.S.; Abdullah, S. Global search in single-solution-based metaheuristics. Data Technol. Appl. 2020, 54, 275–296. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Bozorg-Haddad, O.; Chu, X. Gradient-based optimizer: A new metaheuristic optimization algorithm. Inf. Sci. 2020, 540, 131–159. [Google Scholar] [CrossRef]
- Gholizadeh, S.; Danesh, M.; Gheyratmand, C. A new Newton metaheuristic algorithm for discrete performance-based design optimization of steel moment frames. Comput. Struct. 2020, 234, 106250. [Google Scholar] [CrossRef]
- Doğan, B.; Ölmez, T. A new metaheuristic for numerical function optimization: Vortex Search algorithm. Inf. Sci. 2015, 293, 125–145. [Google Scholar] [CrossRef]



| Sol. Methodology | Objective Function | Year | Ref. |
|---|---|---|---|
| A heuristic approach based on power flow solutions | Saving in cost of conducting material and cost of energy losses | 2002 | [14] |
| A recursive power flow solution methodology | Minimizing investment and operating costs and improving voltage profile | 2005 | [15] |
| A constructive algorithm based on power flow solutions | Saving in cost of conducting material and energy losses | 2006, 2010 | [16,24] |
| Evolutionary optimization strategies | Minimizing investment and operating costs | 2006 | [22] |
| Optimization with genetic algorithms | Saving in cost of conducting material and active and minimizing reactive power loss | 2011, 2013 | [18,19] |
| Differential evolution algorithm | Saving in cost of conducting material and energy losses | 2016 | [23] |
| Adaptive optimizer based on genetic algorithms | Minimizing the sum of the life-cycle cost in conductors and the total energy procurement cost | 2019 | [20] |
| Grasshopper optimization algorithm | Minimizing the annual cost of energy loss and investment cost of the conductors | 2018 | [21] |
| Mixed-integer non-linear programming optimization method | Minimizing investment and operating costs | 2012 | [5] |
| Crow search algorithm | Minimizing investment and operating costs | 2017 | [10] |
| Sine cosine algorithm | Minimizing investment and operating costs | 2017 | [30] |
| Vortex search algorithm | Minimizing investment and operating costs | 2021 | [29] |
| Tabu search algorithm | Minimizing investment and operating costs | 2021 | [31] |
| Newton-based metaheuristic algorithm | Minimizing investment and operating costs | 2022 | [32] |
| Variable Name | Number of Variables | Variable Name | Number of Variables |
|---|---|---|---|
| Voltages | Angles | ||
| Currents | Dis. Gen. Powers | ||
| Objective func. | 1 | Slack powers | 3 |
| Gauge (c) | (/km) | (/km) | (A) | (USD/km) |
|---|---|---|---|---|
| 1 | 0.8763 | 0.4133 | 180 | 1986 |
| 2 | 0.6960 | 0.4133 | 200 | 2790 |
| 3 | 0.5518 | 0.4077 | 230 | 3815 |
| 4 | 0.4387 | 0.3983 | 270 | 5090 |
| 5 | 0.3480 | 0.3899 | 300 | 8067 |
| 6 | 0.2765 | 0.3610 | 340 | 12,673 |
| 7 | 0.0966 | 0.1201 | 600 | 23,419 |
| 8 | 0.0853 | 0.0950 | 720 | 30,070 |
| Parameter | Value | Unit |
|---|---|---|
| Energy cost | 0.1390 | (USD/kWh) |
| Iterations | 1000 | - |
| Population size | 30 | - |
| Tolerance | - |
| Line | Bus | Bus | (km) | (kW) | (kvar) |
|---|---|---|---|---|---|
| 1 | 1 | 2 | 1.00 | 1054.2 | 0 |
| 2 | 2 | 3 | 1.00 | 806.5 | 0 |
| 3 | 1 | 4 | 1.00 | 2632.5 | 0 |
| 4 | 1 | 5 | 1.00 | 609 | 0 |
| 5 | 5 | 6 | 1.00 | 2034.5 | 0 |
| 6 | 3 | 7 | 1.00 | 932.8 | 0 |
| 7 | 3 | 8 | 1.00 | 1731.4 | 0 |
| Bus | (kW) | (kvar) | (kW) | (kvar) | (kW) | (kvar) |
|---|---|---|---|---|---|---|
| 2 | 3162.6 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 2419.5 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 7897.5 | 0 |
| 5 | 913.5 | 0 | 913.5 | 0 | 0 | 0 |
| 6 | 0 | 0 | 3051.6 | 0 | 3051.6 | 0 |
| 7 | 2798.4 | 0 | 0 | 0 | 0 | 0 |
| 8 | 1298.55 | 0 | 2597.1 | 0 | 1298.55 | 0 |
| Line | Bus | Bus | (km) | (kW) | (kvar) |
|---|---|---|---|---|---|
| 1 | 1 | 2 | 0.55 | 0 | 0 |
| 2 | 2 | 3 | 1.50 | 0 | 0 |
| 3 | 3 | 4 | 0.45 | 297.5 | 184.4 |
| 4 | 4 | 5 | 0.63 | 0 | 0 |
| 5 | 5 | 6 | 0.70 | 255 | 158 |
| 6 | 6 | 7 | 0.55 | 0 | 0 |
| 7 | 7 | 8 | 1.00 | 212.5 | 131.7 |
| 8 | 8 | 9 | 1.25 | 0 | 0 |
| 9 | 9 | 10 | 1.00 | 266.1 | 164.9 |
| 10 | 2 | 11 | 1.00 | 85 | 52.7 |
| 11 | 11 | 12 | 1.23 | 340 | 210.7 |
| 12 | 12 | 13 | 0.75 | 297.5 | 184.4 |
| 13 | 13 | 14 | 0.56 | 191.3 | 118.5 |
| 14 | 14 | 15 | 1.00 | 106.3 | 65.8 |
| 15 | 15 | 16 | 1.00 | 255 | 158 |
| 16 | 3 | 17 | 1.00 | 255 | 158 |
| 17 | 17 | 18 | 0.60 | 127.5 | 79 |
| 18 | 18 | 19 | 0.90 | 297.5 | 184.4 |
| 19 | 19 | 20 | 0.95 | 340 | 210.7 |
| 20 | 20 | 21 | 1.00 | 85 | 52.7 |
| 21 | 4 | 22 | 1.00 | 106.3 | 65.8 |
| 22 | 5 | 23 | 1.00 | 55.3 | 34.2 |
| 23 | 6 | 24 | 0.40 | 69.7 | 43.2 |
| 24 | 8 | 25 | 0.60 | 255 | 158 |
| 25 | 8 | 26 | 0.60 | 63.8 | 39.5 |
| 26 | 26 | 27 | 0.80 | 170 | 105.4 |
| Bus | (kW) | (kvar) | (kW) | (kvar) | (kW) | (kvar) |
|---|---|---|---|---|---|---|
| 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 892.5 | 553.2 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 765 | 474 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 637.5 | 395.1 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 798.3 | 494.7 |
| 11 | 0 | 0 | 255 | 158.1 | 0 | 0 |
| 12 | 1020 | 632.1 | 0 | 0 | 0 | 0 |
| 13 | 446.25 | 276.6 | 446.25 | 276.6 | 0 | 0 |
| 14 | 0 | 0 | 286.95 | 177.75 | 286.95 | 177.75 |
| 15 | 159.45 | 98.7 | 0 | 0 | 159.45 | 98.7 |
| 16 | 0 | 0 | 382.5 | 237 | 382.5 | 237 |
| 17 | 1 | 0 | 765 | 474 | 0 | 0 |
| 18 | 382.5 | 237 | 0 | 0 | 0 | 0 |
| 19 | 446.25 | 276.6 | 446.25 | 276.6 | 0 | 0 |
| 20 | 0 | 0 | 510 | 316.05 | 510 | 316.05 |
| 21 | 127.5 | 79.05 | 0 | 0 | 127.5 | 79.05 |
| 22 | 0 | 0 | 159.75 | 98.7 | 159.75 | 98.7 |
| 23 | 165.9 | 102.6 | 0 | 0 | 0 | 0 |
| 24 | 0 | 0 | 0 | 0 | 209.1 | 129.6 |
| 25 | 255 | 158 | 255 | 158 | 255 | 158 |
| 26 | 63.8 | 39.5 | 63.8 | 39.5 | 63.8 | 39.5 |
| 27 | 170 | 105.4 | 170 | 105.4 | 170 | 105.4 |
| Method | Gauges | Investment in Conductors (USD) | Losses (USD) | Annual Costs (USD) |
|---|---|---|---|---|
| TGA | {6, 5, 3, 4, 4, 1, 4} | 125,433 | 406,222.461 | 531,655.461 |
| CBGA | {6, 6, 4, 4, 4, 1, 4} | 143,076 | 373,155.965 | 516,231.965 |
| GAMS | {6, 4, 4, 5, 4, 1, 2} | 122,358 | 416,681.580 | 539,039.580 |
| TSA | {6, 5, 4, 4, 4, 1, 3} | 125,433 | 397,754.442 | 523,187.442 |
| VSA | {6, 6, 5, 5, 4, 2, 4} | 163,350 | 345,007.959 | 508,357.959 |
| NMA | {6, 6, 5, 5, 4, 2, 4} | 163,350 | 345,007.959 | 508,357.959 |
| MGbMO | {7, 7, 5, 5, 4, 2, 4} | 227,826 | 228,143.791 | 455,969.791 |
| Method | Gauges | Investment in Conductors (USD) | Losses (USD) | Annual Costs (USD) |
|---|---|---|---|---|
| VSA | {7, 7, 7, 5, 5, 4, 4} | 289,713 | 269,045.394 | 558,758.394 |
| NMA | {7, 7, 7, 5, 5, 4, 4} | 289,713 | 269,045.394 | 558,758.394 |
| MGbMO | {7, 7, 7, 5, 5, 4, 4} | 289,713 | 269,045.394 | 558,758.394 |
| Method | Gauges | Investment in Conductors (USD) | Losses (USD) | Annual Costs (USD) |
|---|---|---|---|---|
| VSA | {7, 7, 5, 4, 4, 3, 3, 1, 1, 4, 4, 2, 3, 2, 1, 4, 4, 2, 2, 2, 1, 1, 2, 2, 1, 1} | 344,352.150 | 217,672.327 | 562,024.477 |
| NMA | {7, 7, 4, 4, 4, 4, 3, 1, 1, 4, 4, 3, 3, 1, 2, 4, 3, 2, 1, 1, 1, 1, 2, 2, 1, 1} | 337,744.800 | 219,950.455 | 557,695.255 |
| MGbMO | {7, 7, 4, 4, 4, 3, 3, 1, 1, 4, 4, 2, 1, 1, 1, 3, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1} | 319,768.08 | 230,115.492 | 549,883.572 |
| Method | Gauges | Investment in Conductors (USD) | Losses (USD) | Annual Costs (USD) |
|---|---|---|---|---|
| VSA | {7, 7, 5, 4, 4, 4, 4, 2, 2, 4, 4, 3, 2, 1, 1, 2, 3, 2, 1, 2, 2, 1, 2, 2, 4, 1} | 350,392.95 | 257,999.185 | 608,392.135 |
| NMA | {7, 7, 4, 4, 4, 3, 4, 2, 1, 4, 4, 4, 2, 1, 1, 4, 3, 2, 2, 1, 1, 1, 2, 2, 2, 1} | 344,954.40 | 252,624.608 | 597,579.008 |
| MGbMO | {7, 7, 4, 4, 4, 4, 4, 1, 1, 4, 4, 3, 1, 1, 1, 4, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1} | 331,828.08 | 257,190.720 | 589,018.800 |
| Line | Bus | Bus | (km) | Line | Bus | Bus | (km) |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 0.468 | 43 | 34 | 44 | 0.985 |
| 2 | 2 | 3 | 0.449 | 44 | 44 | 45 | 0.441 |
| 3 | 3 | 4 | 0.323 | 45 | 45 | 46 | 0.225 |
| 4 | 4 | 5 | 0.870 | 46 | 46 | 47 | 0.184 |
| 5 | 5 | 6 | 0.883 | 47 | 35 | 48 | 0.698 |
| 6 | 6 | 7 | 0.343 | 48 | 48 | 49 | 0.875 |
| 7 | 7 | 8 | 0.953 | 49 | 49 | 50 | 0.768 |
| 8 | 8 | 9 | 0.309 | 50 | 50 | 51 | 0.261 |
| 9 | 9 | 10 | 0.931 | 51 | 48 | 52 | 0.985 |
| 10 | 10 | 11 | 0.161 | 52 | 52 | 53 | 0.448 |
| 11 | 11 | 12 | 0.952 | 53 | 53 | 54 | 0.344 |
| 12 | 12 | 13 | 0.878 | 54 | 52 | 55 | 0.673 |
| 13 | 13 | 14 | 0.507 | 55 | 49 | 56 | 0.564 |
| 14 | 14 | 15 | 0.018 | 56 | 9 | 57 | 0.545 |
| 15 | 2 | 16 | 0.778 | 7 | 57 | 58 | 0.564 |
| 16 | 3 | 17 | 0.359 | 58 | 58 | 59 | 0.650 |
| 17 | 5 | 18 | 0.848 | 59 | 58 | 60 | 0.237 |
| 18 | 18 | 19 | 0.433 | 60 | 60 | 61 | 0.626 |
| 19 | 19 | 20 | 0.605 | 61 | 61 | 62 | 0.530 |
| 20 | 20 | 21 | 0.377 | 62 | 60 | 63 | 0.514 |
| 21 | 21 | 22 | 0.721 | 63 | 63 | 64 | 0.701 |
| 22 | 19 | 23 | 0.316 | 64 | 64 | 65 | 0.373 |
| 23 | 7 | 4 | 0.949 | 65 | 65 | 66 | 0.614 |
| 24 | 8 | 5 | 0.849 | 66 | 64 | 67 | 0.307 |
| 25 | 25 | 26 | 0.775 | 67 | 67 | 68 | 0.322 |
| 26 | 26 | 27 | 0.299 | 68 | 68 | 69 | 0.662 |
| 27 | 27 | 28 | 0.872 | 69 | 69 | 70 | 0.150 |
| 28 | 28 | 29 | 0.375 | 70 | 70 | 71 | 0.384 |
| 29 | 29 | 30 | 0.798 | 71 | 67 | 72 | 0.320 |
| 30 | 30 | 31 | 0.816 | 72 | 68 | 73 | 0.291 |
| 31 | 31 | 32 | 0.999 | 73 | 73 | 74 | 0.213 |
| 32 | 32 | 33 | 0.045 | 74 | 73 | 75 | 0.721 |
| 33 | 33 | 34 | 0.236 | 75 | 70 | 76 | 0.705 |
| 34 | 34 | 35 | 0.430 | 76 | 65 | 77 | 0.715 |
| 35 | 35 | 36 | 0.847 | 77 | 10 | 78 | 0.361 |
| 36 | 26 | 37 | 0.386 | 78 | 67 | 79 | 0.546 |
| 37 | 27 | 38 | 0.122 | 79 | 12 | 80 | 0.357 |
| 38 | 29 | 39 | 0.915 | 80 | 80 | 81 | 0.940 |
| 39 | 32 | 40 | 0.182 | 81 | 81 | 82 | 0.444 |
| 40 | 40 | 41 | 0.590 | 82 | 81 | 83 | 0.110 |
| 41 | 41 | 42 | 0.812 | 83 | 83 | 84 | 0.865 |
| 42 | 41 | 43 | 0.261 | 84 | 13 | 85 | 0.300 |
| Bus | (kW) | (kvar) | (kW) | (kvar) | (kW) | (kvar) |
|---|---|---|---|---|---|---|
| 2 | 14.50 | 20.00 | 10.00 | 28.50 | 20.50 | 31.00 |
| 3 | 12.50 | 29.50 | 0.000 | 0.000 | 17.50 | 48.50 |
| 4 | 0.000 | 0.000 | 0.000 | 0.000 | 35.50 | 43.00 |
| 5 | 39.00 | 43.50 | 32.50 | 48.50 | 0.000 | 0.000 |
| 6 | 28.00 | 22.00 | 22.50 | 24.50 | 0.000 | 0.000 |
| 7 | 14.00 | 10.50 | 0.000 | 0.000 | 24.50 | 42.50 |
| 8 | 41.50 | 29.50 | 23.50 | 12.00 | 10.50 | 27.00 |
| 9 | 0.000 | 0.000 | 30.00 | 40.50 | 17.00 | 50.00 |
| 10 | 0.000 | 0.000 | 14.00 | 45.00 | 0.000 | 0.000 |
| 11 | 0.000 | 0.000 | 26.50 | 14.00 | 27.50 | 35.50 |
| 12 | 35.50 | 49.00 | 45.50 | 47.50 | 0.000 | 0.000 |
| 13 | 17.00 | 43.00 | 15.00 | 47.50 | 48.00 | 37.50 |
| 14 | 25.00 | 45.00 | 22.00 | 44.00 | 0.000 | 0.000 |
| 15 | 0.000 | 0.000 | 0.000 | 0.000 | 10.50 | 20.00 |
| 16 | 19.00 | 39.00 | 47.50 | 32.00 | 35.50 | 18.50 |
| 17 | 18.50 | 44.50 | 49.00 | 26.00 | 32.50 | 26.50 |
| 18 | 0.000 | 0.000 | 11.00 | 44.00 | 48.50 | 34.50 |
| 19 | 38.00 | 31.00 | 35.00 | 39.00 | 42.50 | 25.50 |
| 20 | 46.00 | 46.00 | 0.000 | 0.000 | 26.50 | 32.50 |
| 21 | 39.00 | 25.00 | 37.00 | 11.00 | 41.50 | 23.50 |
| 22 | 22.50 | 50.00 | 21.00 | 30.00 | 18.50 | 25.50 |
| 23 | 0.000 | 0.000 | 0.000 | 0.000 | 24.00 | 23.50 |
| 24 | 44.50 | 12.50 | 33.00 | 27.00 | 37.00 | 18.00 |
| 25 | 40.50 | 14.00 | 40.50 | 36.00 | 33.50 | 39.50 |
| 26 | 15.50 | 22.50 | 0.000 | 0.000 | 25.50 | 47.00 |
| 27 | 16.00 | 38.00 | 0.000 | 0.000 | 0.000 | 0.000 |
| 28 | 13.50 | 15.00 | 35.00 | 38.00 | 15.50 | 22.50 |
| 29 | 18.50 | 39.50 | 10.50 | 36.00 | 39.00 | 42.00 |
| 30 | 21.00 | 36.50 | 0.000 | 0.000 | 43.00 | 13.00 |
| 31 | 0.000 | 0.000 | 0.000 | 0.000 | 20.50 | 20.50 |
| 32 | 41.50 | 35.50 | 46.50 | 50.00 | 0.000 | 0.000 |
| 33 | 29.00 | 12.50 | 47.00 | 37.50 | 27.50 | 24.50 |
| 34 | 16.00 | 28.00 | 0.000 | 0.000 | 25.00 | 12.00 |
| 35 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 36 | 48.50 | 34.00 | 0.000 | 0.000 | 10.50 | 18.00 |
| 37 | 41.00 | 45.00 | 44.00 | 47.50 | 12.00 | 45.50 |
| 38 | 42.00 | 22.00 | 45.00 | 15.50 | 0.000 | 0.000 |
| 39 | 0.000 | 0.000 | 37.00 | 47.50 | 27.50 | 18.50 |
| 40 | 0.000 | 0.000 | 0.000 | 0.000 | 15.00 | 13.50 |
| 41 | 17.50 | 27.50 | 36.00 | 40.00 | 43.00 | 20.00 |
| 42 | 44.50 | 17.00 | 38.50 | 19.00 | 0.000 | 0.000 |
| 43 | 49.50 | 45.50 | 0.000 | 0.000 | 0.000 | 0.000 |
| 44 | 39.00 | 28.50 | 32.50 | 26.50 | 30.00 | 30.50 |
| 45 | 30.50 | 27.00 | 39.00 | 36.50 | 13.50 | 42.50 |
| 46 | 25.00 | 22.50 | 30.50 | 21.00 | 11.00 | 15.50 |
| 47 | 30.50 | 48.00 | 48.00 | 22.00 | 14.00 | 34.00 |
| 48 | 34.00 | 42.00 | 50.00 | 13.50 | 0.000 | 0.000 |
| 49 | 42.50 | 34.50 | 36.00 | 45.50 | 45.00 | 46.50 |
| 50 | 0.000 | 0.000 | 0.000 | 0.000 | 10.50 | 13.50 |
| 51 | 22.00 | 18.50 | 24.50 | 23.00 | 10.00 | 13.50 |
| 52 | 49.00 | 40.50 | 47.00 | 48.00 | 20.00 | 28.00 |
| 53 | 13.50 | 41.50 | 15.00 | 48.00 | 0.000 | 0.000 |
| 54 | 39.50 | 19.50 | 19.00 | 43.00 | 45.50 | 40.50 |
| 55 | 0.000 | 0.000 | 19.50 | 26.50 | 19.50 | 45.00 |
| 56 | 36.50 | 20.00 | 34.00 | 49.00 | 14.50 | 17.00 |
| 57 | 13.50 | 40.50 | 16.50 | 33.50 | 16.00 | 34.00 |
| 58 | 29.50 | 18.00 | 22.00 | 18.00 | 0.000 | 0.000 |
| 59 | 24.00 | 36.50 | 32.00 | 15.50 | 29.00 | 27.50 |
| 60 | 0.000 | 0.000 | 38.00 | 12.00 | 25.00 | 24.50 |
| 61 | 38.00 | 42.00 | 28.00 | 17.50 | 45.50 | 27.00 |
| 62 | 30.00 | 32.00 | 42.00 | 26.50 | 36.00 | 47.50 |
| 63 | 42.00 | 25.50 | 46.50 | 26.00 | 26.00 | 17.00 |
| 64 | 0.000 | 0.000 | 0.000 | 0.000 | 19.00 | 47.50 |
| 65 | 37.00 | 29.00 | 0.000 | 0.000 | 28.00 | 26.50 |
| 66 | 47.50 | 49.00 | 25.00 | 36.50 | 47.50 | 17.50 |
| 67 | 14.00 | 22.50 | 0.000 | 0.000 | 22.50 | 41.00 |
| 68 | 35.50 | 39.00 | 36.50 | 23.50 | 41.50 | 37.00 |
| 69 | 22.00 | 22.50 | 0.000 | 0.000 | 0.000 | 0.000 |
| 70 | 43.50 | 24.50 | 0.000 | 0.000 | 0.000 | 0.000 |
| 71 | 11.00 | 50.00 | 0.000 | 0.000 | 11.50 | 28.50 |
| 72 | 31.00 | 20.00 | 0.000 | 0.000 | 0.000 | 0.000 |
| 73 | 43.00 | 23.00 | 49.50 | 48.00 | 50.00 | 35.00 |
| 74 | 28.00 | 22.00 | 21.00 | 19.50 | 0.000 | 0.000 |
| 75 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 76 | 0.000 | 0.000 | 46.50 | 45.00 | 19.50 | 47.50 |
| 77 | 28.00 | 12.50 | 25.00 | 24.00 | 41.00 | 49.00 |
| 78 | 27.50 | 45.00 | 48.50 | 31.00 | 29.50 | 38.50 |
| 79 | 32.50 | 35.00 | 48.50 | 18.50 | 0.000 | 0.000 |
| 80 | 28.50 | 46.50 | 11.50 | 21.00 | 18.50 | 37.00 |
| 81 | 18.00 | 49.50 | 36.00 | 13.50 | 23.00 | 13.50 |
| 82 | 46.00 | 37.00 | 28.50 | 32.00 | 17.50 | 14.50 |
| 83 | 24.50 | 13.00 | 34.00 | 30.00 | 0.000 | 0.000 |
| 84 | 0.000 | 0.000 | 0.000 | 0.000 | 11.50 | 48.50 |
| 85 | 0.000 | 0.000 | 36.50 | 12.00 | 0.000 | 0.000 |
| Time (h) | Demand (pu) | Photovoltaic (pu) | Wind (pu) |
|---|---|---|---|
| 1 | 0.684511335492475 | 0 | 0.633118295 |
| 2 | 0.644122690036197 | 0 | 0.607259323 |
| 3 | 0.613069156029720 | 0 | 0.605557422 |
| 4 | 0.599733282530006 | 0 | 0.684246423 |
| 5 | 0.588874071251667 | 0 | 0.783719339 |
| 6 | 0.598018670222900 | 0 | 0.790557706 |
| 7 | 0.626786054486569 | 0 | 0.744958950 |
| 8 | 0.651743189178891 | 0.0391233650 | 0.769603567 |
| 9 | 0.706039245570585 | 0.0655871790 | 0.826492212 |
| 10 | 0.787007048961707 | 0.2368707960 | 0.876523598 |
| 11 | 0.839016955610593 | 0.4550178180 | 0.931213527 |
| 12 | 0.852733854067441 | 0.7264402650 | 0.965504834 |
| 13 | 0.870642027052772 | 0.9244863260 | 0.972218577 |
| 14 | 0.834254143646409 | 0.9820411530 | 0.981135531 |
| 15 | 0.816536483139646 | 0.8294070790 | 0.991393173 |
| 16 | 0.819394170318156 | 0.7330632950 | 1 |
| 17 | 0.874071251666984 | 0.5011338490 | 0.987258076 |
| 18 | 1 | 0.1771175180 | 0.929542167 |
| 19 | 0.983615926843208 | 0 | 0.791155379 |
| 20 | 0.936368832158506 | 0 | 0.708839248 |
| 21 | 0.887597637645266 | 0 | 0.712881960 |
| 22 | 0.809297008954087 | 0 | 0.719897641 |
| 23 | 0.745856353591160 | 0 | 0.703007456 |
| 24 | 0.733473042484283 | 0 | 0.687238555 |
| Line | Case 1 | Case 2 | Case 3 | Line | Case 1 | Case 2 | Case 3 |
|---|---|---|---|---|---|---|---|
| 1 | 7 | 5 | 4 | 43 | 3 | 1 | 1 |
| 2 | 7 | 5 | 4 | 44 | 3 | 1 | 1 |
| 3 | 5 | 5 | 4 | 45 | 2 | 1 | 1 |
| 4 | 4 | 5 | 4 | 46 | 2 | 1 | 1 |
| 5 | 4 | 4 | 3 | 47 | 3 | 1 | 1 |
| 6 | 4 | 4 | 3 | 48 | 3 | 1 | 1 |
| 7 | 4 | 4 | 3 | 49 | 3 | 1 | 1 |
| 8 | 4 | 1 | 1 | 50 | 3 | 1 | 1 |
| 9 | 4 | 1 | 1 | 51 | 3 | 1 | 1 |
| 10 | 4 | 1 | 1 | 52 | 3 | 1 | 1 |
| 11 | 4 | 1 | 1 | 53 | 3 | 1 | 1 |
| 12 | 4 | 1 | 1 | 54 | 2 | 1 | 1 |
| 13 | 3 | 1 | 1 | 55 | 3 | 1 | 1 |
| 14 | 1 | 1 | 1 | 56 | 3 | 1 | 1 |
| 15 | 1 | 1 | 1 | 7 | 3 | 1 | 1 |
| 16 | 2 | 1 | 1 | 58 | 1 | 1 | 1 |
| 17 | 3 | 1 | 1 | 59 | 3 | 1 | 1 |
| 18 | 3 | 1 | 1 | 60 | 3 | 1 | 1 |
| 19 | 3 | 1 | 1 | 61 | 1 | 1 | 1 |
| 20 | 3 | 1 | 1 | 62 | 3 | 1 | 1 |
| 21 | 2 | 1 | 1 | 63 | 3 | 1 | 1 |
| 22 | 2 | 1 | 1 | 64 | 3 | 1 | 1 |
| 23 | 2 | 1 | 1 | 65 | 3 | 1 | 1 |
| 24 | 3 | 1 | 1 | 66 | 3 | 1 | 1 |
| 25 | 3 | 1 | 1 | 67 | 3 | 1 | 1 |
| 26 | 3 | 1 | 1 | 68 | 3 | 1 | 1 |
| 27 | 3 | 1 | 1 | 69 | 3 | 1 | 1 |
| 28 | 3 | 1 | 1 | 70 | 3 | 1 | 1 |
| 29 | 3 | 1 | 1 | 71 | 3 | 1 | 1 |
| 30 | 3 | 1 | 1 | 72 | 2 | 1 | 1 |
| 31 | 3 | 1 | 1 | 73 | 2 | 1 | 1 |
| 32 | 3 | 1 | 1 | 74 | 2 | 1 | 1 |
| 33 | 3 | 1 | 1 | 75 | 1 | 1 | 1 |
| 34 | 3 | 1 | 1 | 76 | 3 | 1 | 1 |
| 35 | 1 | 1 | 1 | 77 | 2 | 1 | 1 |
| 36 | 3 | 1 | 1 | 78 | 2 | 1 | 1 |
| 37 | 3 | 1 | 1 | 79 | 3 | 1 | 1 |
| 38 | 2 | 1 | 1 | 80 | 3 | 1 | 1 |
| 39 | 3 | 1 | 1 | 81 | 1 | 1 | 1 |
| 40 | 2 | 1 | 1 | 82 | 3 | 1 | 1 |
| 41 | 2 | 1 | 1 | 83 | 1 | 1 | 1 |
| 42 | 2 | 1 | 1 | 84 | 2 | 1 | 1 |
| Case | (USD) | (USD) | Z (USD) |
|---|---|---|---|
| 1 | 550,998.7080 | 403,917.6916 | 954,916.3996 |
| 2 | 330,218.1420 | 312,264.9263 | 642,483.0683 |
| 3 | 303,039.0570 | 249,526.0165 | 552,565.0735 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pradilla-Rozo, J.D.; Vega-Forero, J.A.; Montoya, O.D. Application of the Gradient-Based Metaheuristic Optimizerto Solve the Optimal Conductor Selection Problemin Three-Phase Asymmetric Distribution Networks. Energies 2023, 16, 888. https://doi.org/10.3390/en16020888
Pradilla-Rozo JD, Vega-Forero JA, Montoya OD. Application of the Gradient-Based Metaheuristic Optimizerto Solve the Optimal Conductor Selection Problemin Three-Phase Asymmetric Distribution Networks. Energies. 2023; 16(2):888. https://doi.org/10.3390/en16020888
Chicago/Turabian StylePradilla-Rozo, Julián David, Julián Alejandro Vega-Forero, and Oscar Danilo Montoya. 2023. "Application of the Gradient-Based Metaheuristic Optimizerto Solve the Optimal Conductor Selection Problemin Three-Phase Asymmetric Distribution Networks" Energies 16, no. 2: 888. https://doi.org/10.3390/en16020888
APA StylePradilla-Rozo, J. D., Vega-Forero, J. A., & Montoya, O. D. (2023). Application of the Gradient-Based Metaheuristic Optimizerto Solve the Optimal Conductor Selection Problemin Three-Phase Asymmetric Distribution Networks. Energies, 16(2), 888. https://doi.org/10.3390/en16020888








