Analysis and Forecasting of Monthly Electricity Demand Time Series Using Pattern-Based Statistical Methods
Abstract
:1. Introduction
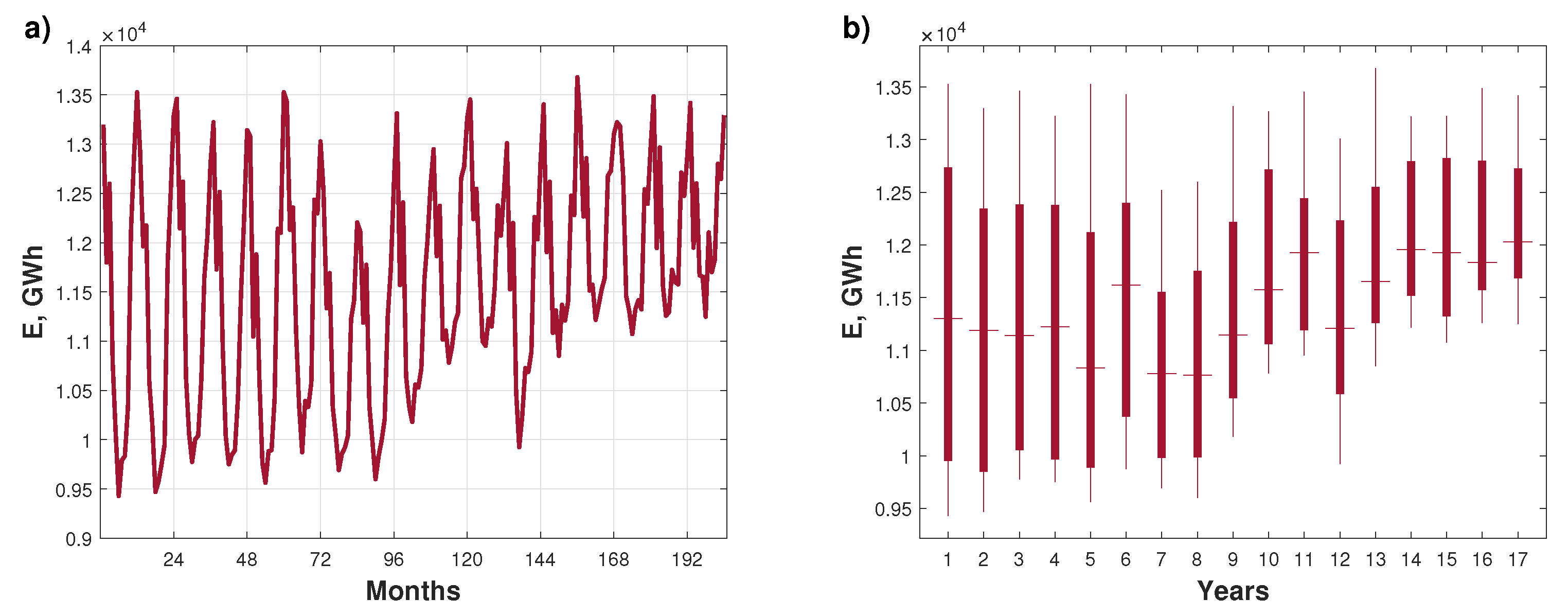
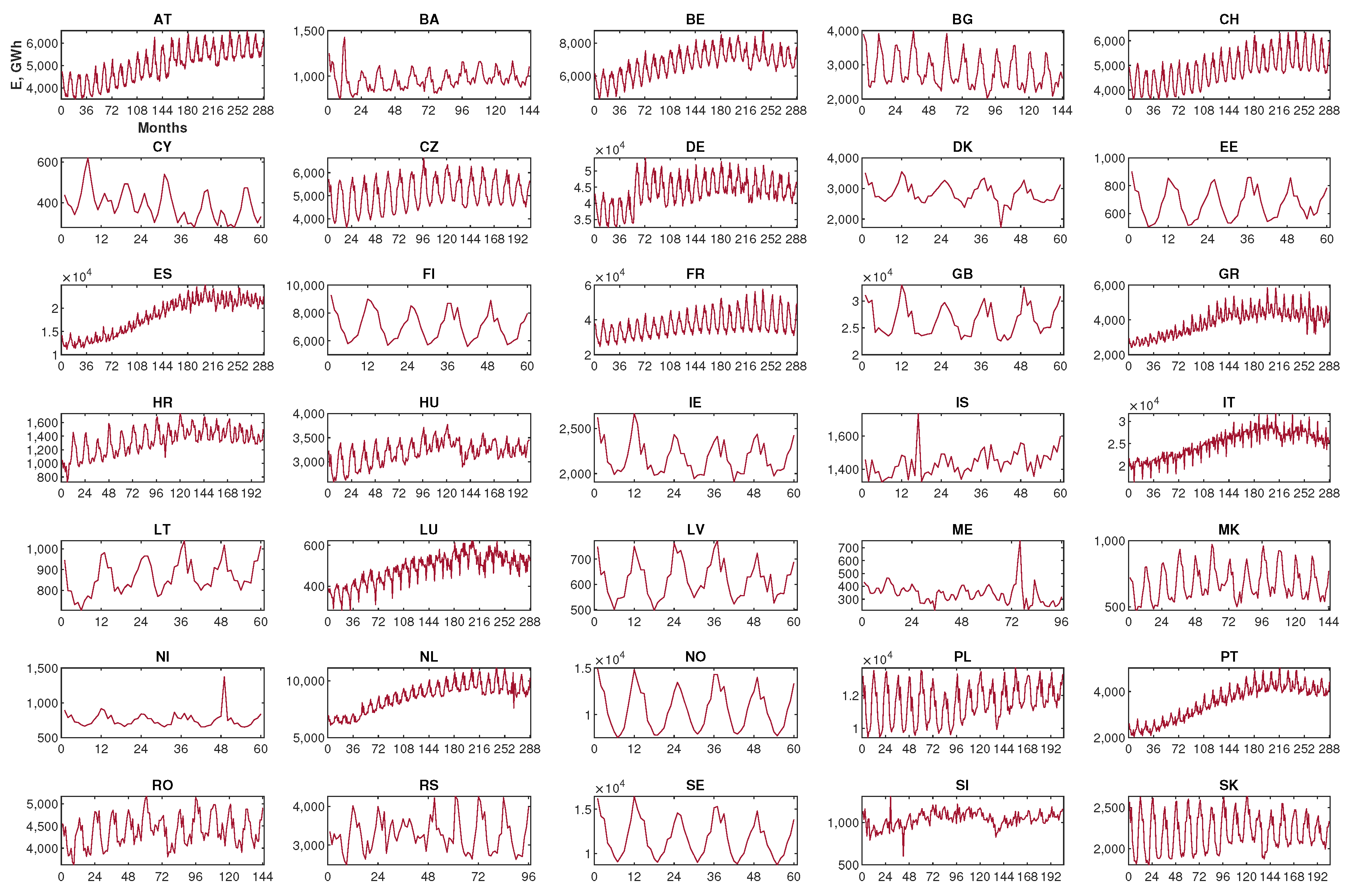
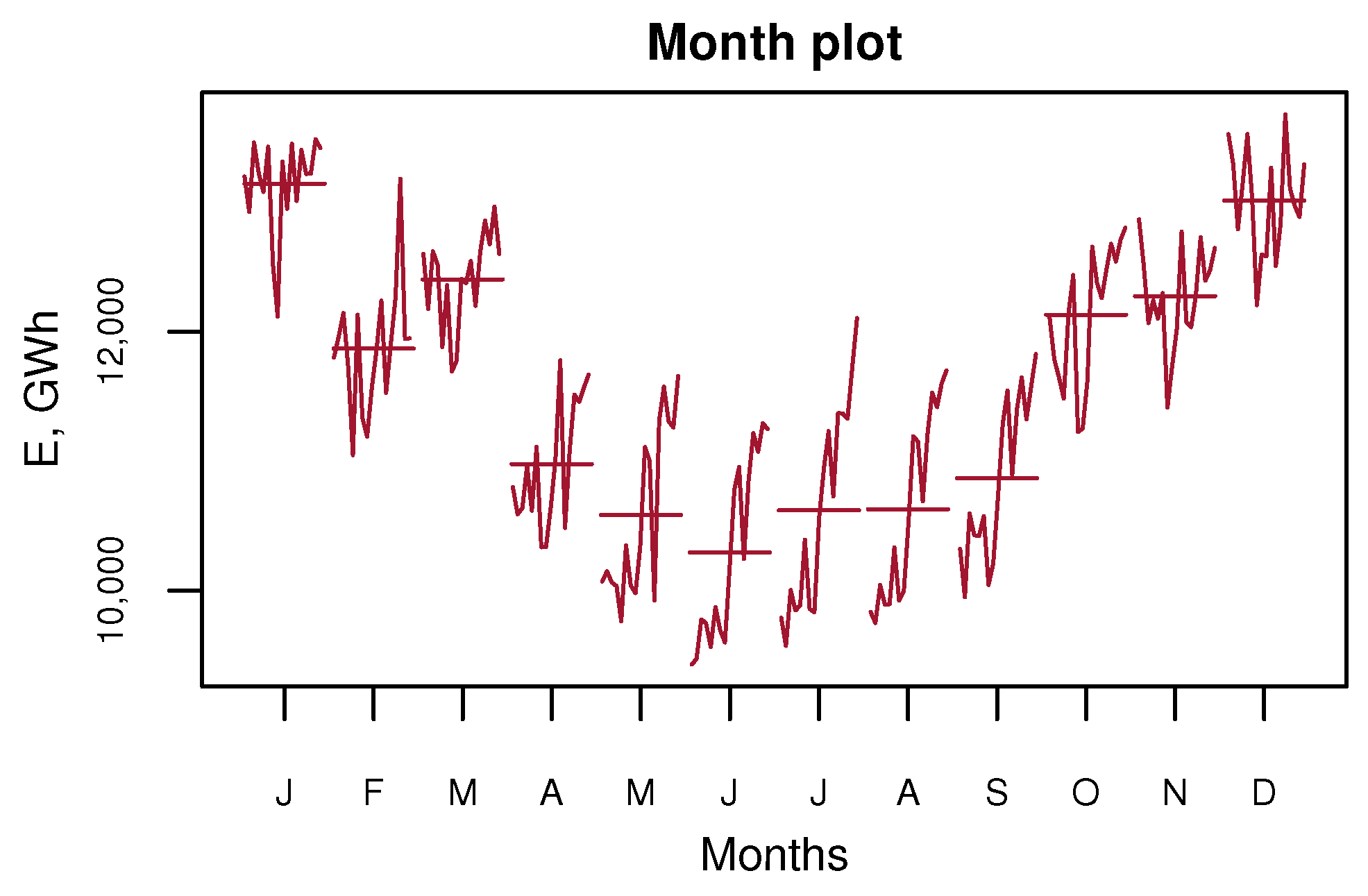
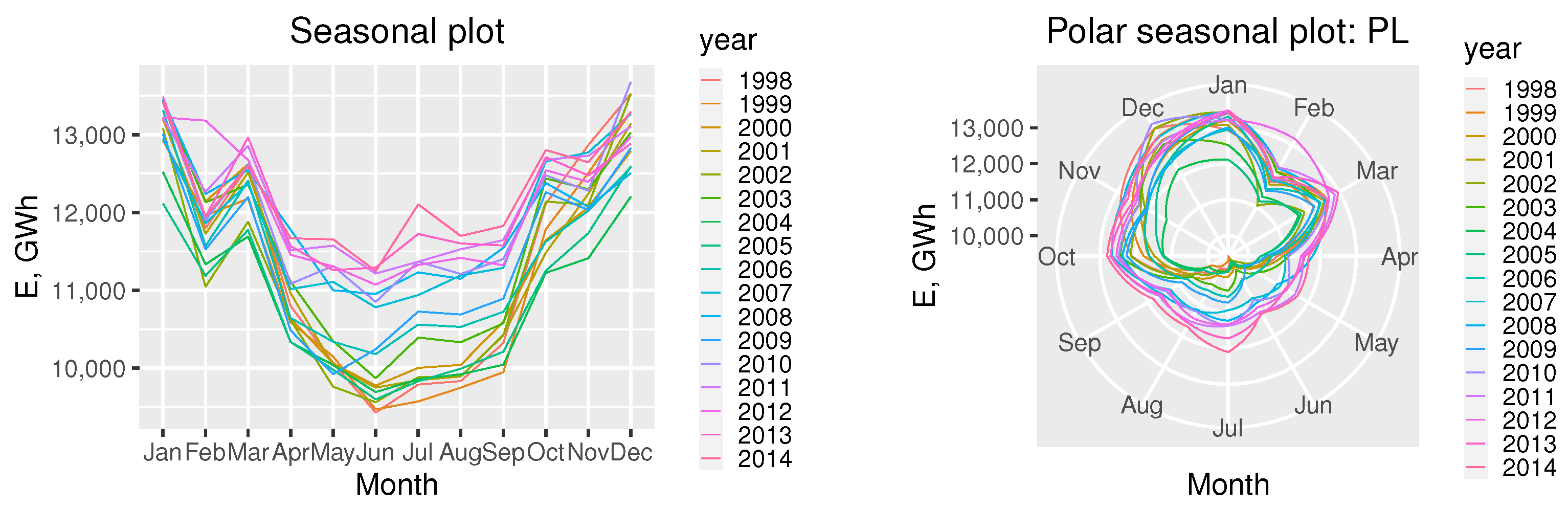
2. MEL Time Series Analysis
- Development tendency (trend), which is revealed by one-way and systematic changes in the level of a given phenomenon that takes place over a long-term period;
- Periodic fluctuations, i.e., rhythmic fluctuations with a specific cycle;
- Business cycle fluctuations, i.e., systemic wave fluctuations observed in longer periods;
- Random fluctuations, i.e., irregular random disturbances.
- —expected value is constant (none trend);
- —the variance is homogeneous over time;
- —the correlation between observations is solely dependent on time shift l.
3. Forecasting Model
3.1. Autoregressive Integrated Moving Average ARIMA Model
3.2. Exponential Smoothing ETS
3.3. Prophet
4. Simulation Study
4.1. MEL Time Series Analysis Results
- Median—median as a measure of the average level of the series,
- IQR—average of the annual interquartile ranges as a measure of the annual dispersion of the series,
- —mean relative annual dispersion as mean ratio of annual interquartile ranges to annual medians:
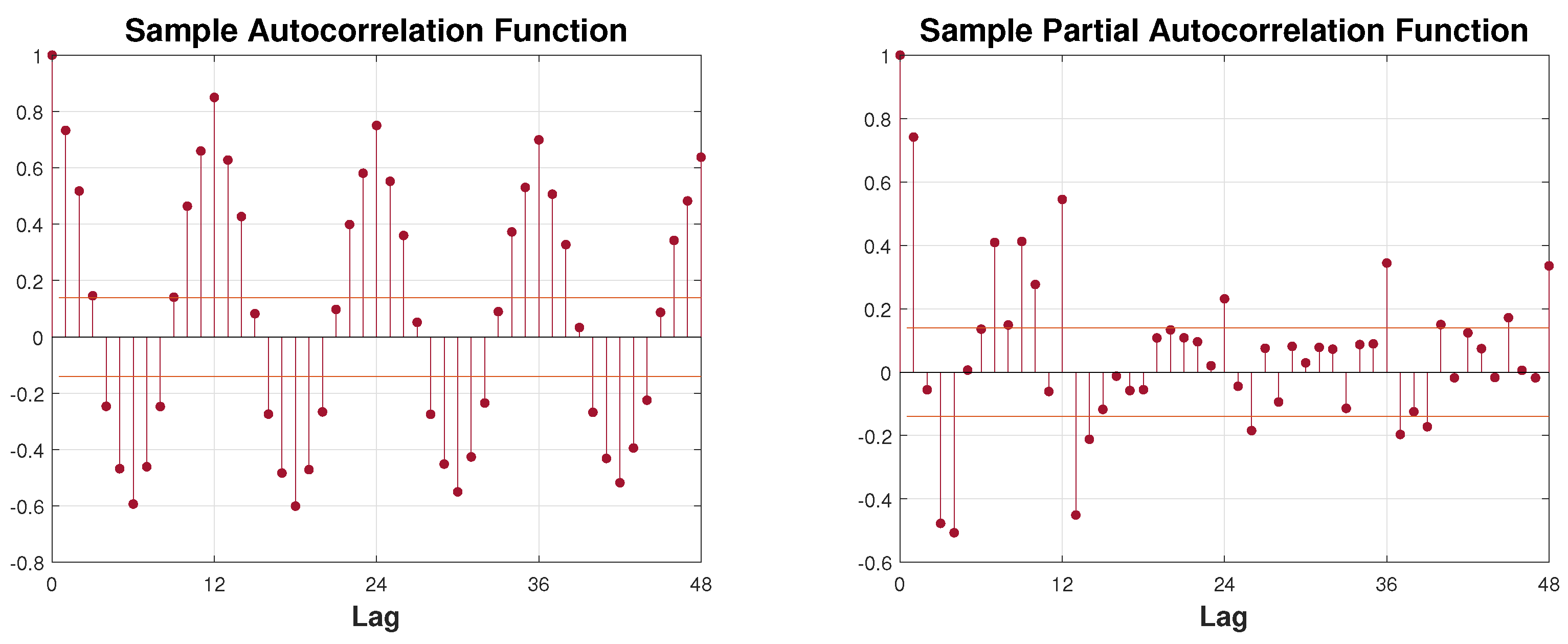
- —value of the autocorrelation function for the delay ,
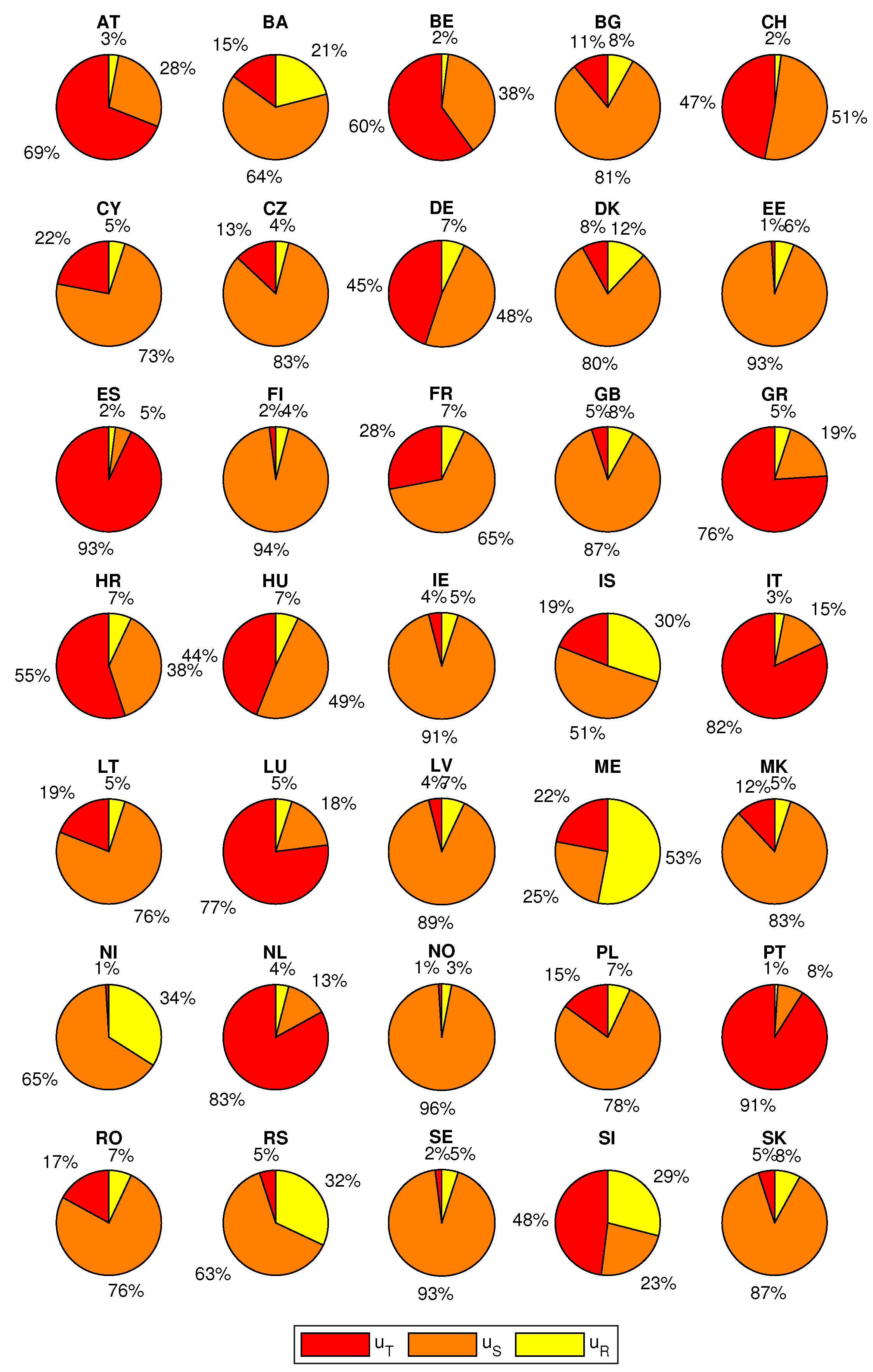
- —annual-period harmonics share in the series variance (7).
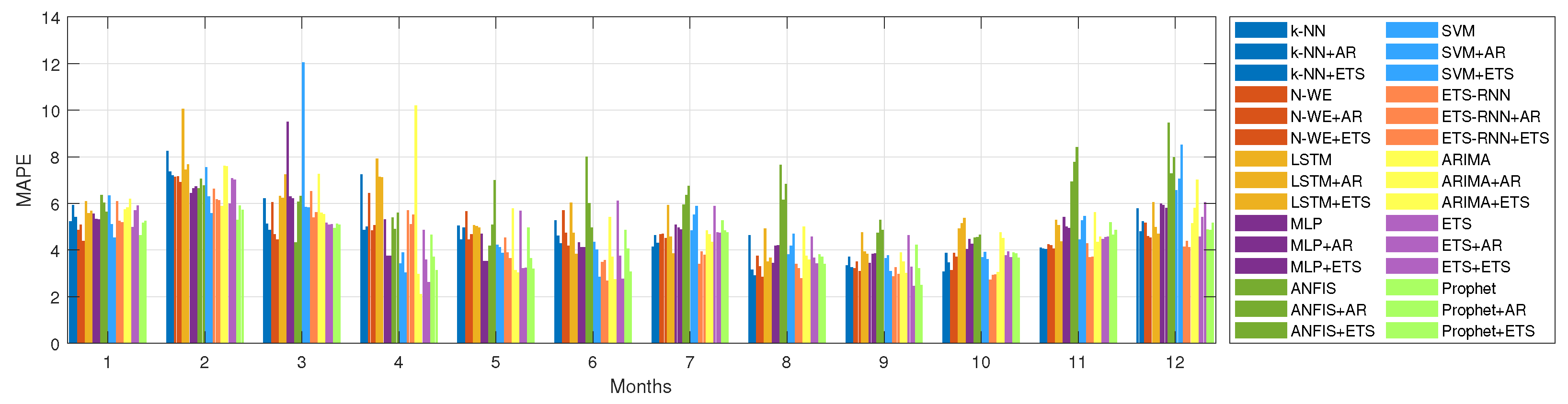
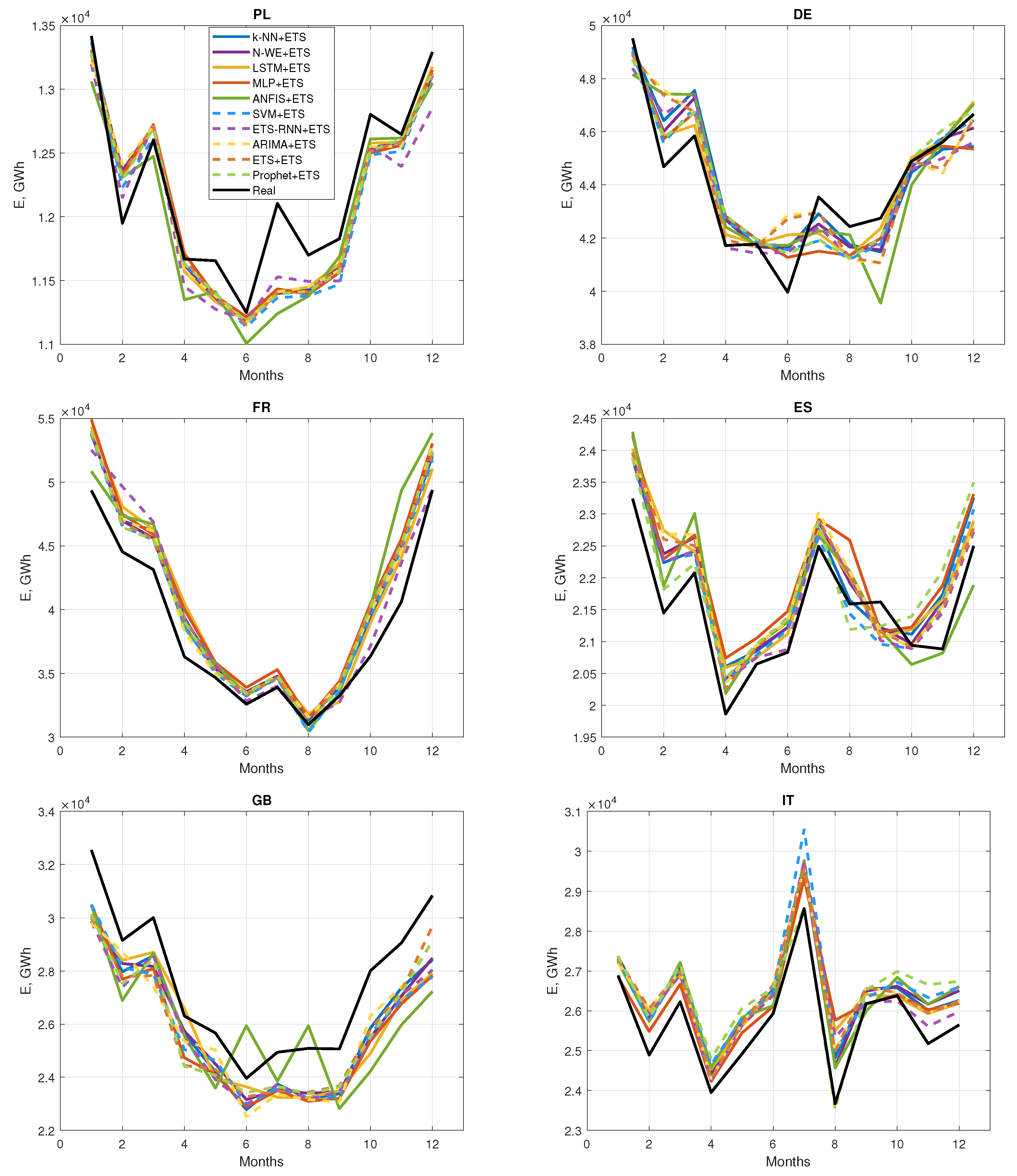
4.2. MEL Time Series Forecasting Results
- ARIMA — ARIMA(p, d, q)(P,D,Q) model used in function auto.arima in R environment (package forecast). This function uses automatic ARIMA modeling. It combines unit root tests, maximum likelihood estimation and minimization of the Akaike information criterion (AICc) to obtain the optimal ARIMA model [38].
- ETS — exponential smoothing state space model [4] used in function ets (R package forecast). This implementation uses many types of ETS models depends on the consideration of the trend, seasonal and error components. It can be expressed multiplicatively or additively, and the trend could be damped or not. Similar to the case of auto.arima, ETS returns the optimal model estimated by the model parameters using AICc [38].
- Prophet — modular additive regression model with nonlinear trend and seasonal components [37] implemented in function Prophet in R environment (package prophet).
- V1. The basic variant, where the coding variables for x-patterns are the mean and dispersion of previous sequence for k-NN, N-WE, LSTM, MLP, ANFIS, and SVM. No patterns and coding variables are used for ES-RNN, ARIMA, ETS, LSTM, and Prophet in this case. We can use this variant to forecast the MEL from (8) without additional forecasting for coding variables.
- V2. The variant, for which the mean and dispersion of sequence serve as the coding variables. Using ARIMA model, they are both independently forecasted for the query pattern based on their previous values. This variation broadens the denotations by “+AR”, e.g., “k-NN + AR”, and “ANFIS + AR”.
- V3. The mean and dispersion of sequence serve as the coding variables, as in variant V2. However, in this instance, they are predicted using ETS for the query pattern. “+ETS” is used to extend the denotations in this variant, such as “k-NN + ETS”, and “ANFIS + ETS”.
- Percentage error (PE):where E is the actual value and is the forecasted value.
- Mean percentage error (MPE):
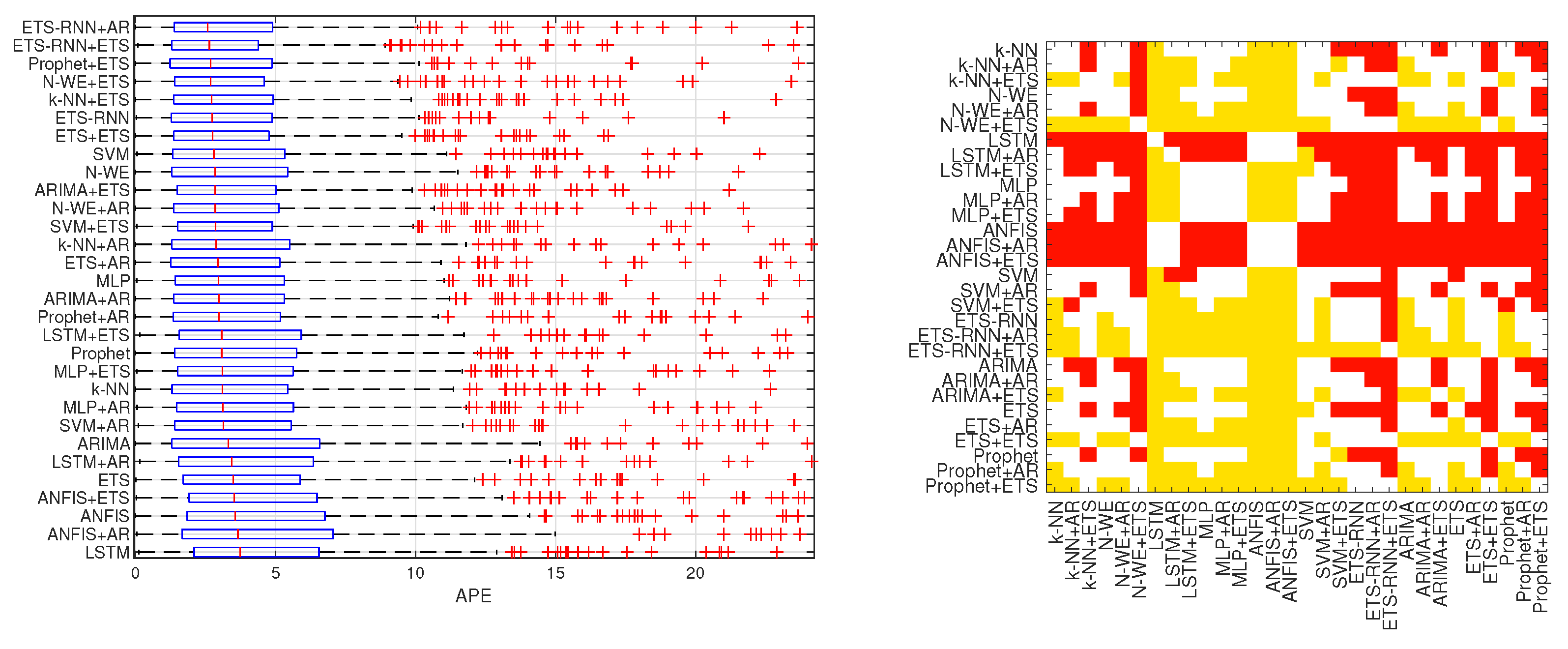
- Absolute percentage error (APE):
- Mean absolute percentage error (MAPE):
- Interquartile range of absolute percentage error (IQR):where , are the lower and upper quartiles, respectively.The quarter range allows you to assess the variability of the APE error. It includes 50% of all observations located centrally in the distribution.
- Root mean squared error (RMSE):
- Standard deviation of percentage errors ():
- Coefficient of asymmetry (skewness) of the distribution of percentage errors (skewPE):The coefficient of asymmetry is zero for symmetric distributions, negative values for left asymmetric distributions (most of the population is below average) and positive for right asymmetric distributions (most of the population is above average).
- Kurtosis of percentage error distribution (kuPE):kuPE is a measure of the clustering of PE errors around the mean value of MPE. The higher the kurtosis value, the more slender the distribution of errors and the greater the concentration of their values around the mean.
5. Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ML | Machine Learning | ES | Spain |
| MEL | Monthly Energy Load | FI | Finland |
| MTLF | Mid-term Load Forecasting | FR | France |
| ARIMA | Autoregressive Integrated Moving Average | GB | Great Britain |
| ETS | Exponential Smoothing | GR | Greece |
| NN | Neural Network | HR | Croatia |
| ACF | Autocorrelation Function | HU | Hungary |
| PACF | Partial Autocorrelation Function | IE | Ireland |
| k-NN | k Nearest Neighbor | IS | Iceland |
| N-WE | Nadaraya–Watson estimator | IT | Italy |
| LSTM | Long Short-Term Memory | LT | Lithuania |
| MLP | Multilayer Perceptron | LU | Luxembourg |
| ANFIS | Adaptive Neuro-Fuzzy Inference System | LV | Latvia |
| SVM | Support Vector Machine | ME | Montenegro |
| ETS-RNN | Exponential Smoothing and Recurrent Neural Networks | MK | Macedonia |
| AT | Austria | NI | Northern Ireland |
| BA | Bosnia and Herzegovina | NL | Netherlands |
| BE | Belgium | NO | Norway |
| BG | Bulgaria | PL | Poland |
| CH | Switzerland | PT | Portugal |
| CY | Cyprus | RO | Romania |
| CZ | Czech Republic | RS | Serbia |
| DE | Germany | SE | Sweden |
| DK | Denmark | SI | Slovenia |
| EE | Estonia | SK | Slovakia |
References
- Pełka, P. Przegląd Metod Wykorzystywanych Do Średnioterminowego Prognozowania Obciążeń Elektroenergetycznych. Prz. Elektrotechniczny 2019, 95, 155–159. [Google Scholar] [CrossRef]
- Dogan, E. Are Shocks to Electricity Consumption Transitory or Permanent? Sub-National Evidence from Turkey. Util. Policy 2016, 41, 77–84. [Google Scholar] [CrossRef]
- Bunnoon, P.; Chalermyanont, K.; Limsakul, C. Mid Term Load Forecasting of the Country Using Statistical Methodology: Case Study in Thailand. In Proceedings of the 2009 International Conference on Signal Processing Systems, Singapore, 15–17 May 2009; pp. 924–928. [Google Scholar]
- Hyndman, R.; Koehler, A.B.; Ord, J.K.; Snyder, R.D. Forecasting with Exponential Smoothing: The State Space Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- González-Romera, E.; Jaramillo-Morán, M.A.; Carmona-Fernández, D. Monthly Electric Energy Demand Forecasting with Neural Networks and Fourier Series. Energy Convers. Manag. 2008, 49, 3135–3142. [Google Scholar] [CrossRef]
- Pełka, P.; Dudek, G. Pattern-Based Forecasting Monthly Electricity Demand Using Multilayer Perceptron. In Artificial Intelligence and Soft Computing; Springer: Cham, Switzerland, 2019; pp. 663–672. [Google Scholar]
- Gao, T.; Niu, D.; Ji, Z.; Sun, L. Mid-Term Electricity Demand Forecasting Using Improved Variational Mode Decomposition and Extreme Learning Machine Optimized by Sparrow Search Algorithm. Energy 2022, E261, 125328. [Google Scholar] [CrossRef]
- Pełka, P.; Dudek, G. Pattern-Based Long Short-Term Memory for Mid-Term Electrical Load Forecasting. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Peng, L.; Wang, L.; Xia, D.; Gao, Q. Effective Energy Consumption Forecasting Using Empirical Wavelet Transform and Long Short-Term Memory. Energy 2022, 238, 121756. [Google Scholar] [CrossRef]
- Sharma, K.; Dwivedi, Y.K.; Metri, B. Incorporating Causality in Energy Consumption Forecasting Using Deep Neural Networks. Ann. Oper. 2022, 1–36. [Google Scholar] [CrossRef]
- Li, J.; Wei, S.; Dai, W. Combination of Manifold Learning and Deep Learning Algorithms for Mid-Term Electrical Load Forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Xu, A.; Tian, M.-W.; Firouzi, B.; Alattas, K.A.; Mohammadzadeh, A.; Ghaderpour, E. A New Deep Learning Restricted Boltzmann Machine for Energy Consumption Forecasting. Sustainability 2022, 14, 10081. [Google Scholar] [CrossRef]
- Dudek, G.; Pełka, P. Prognozowanie Miesięcznego Zapotrzebowania Na Energię Elektryczną Metodą k Najbliższych Sąsiadów. Prz. Elektrotech. 2017, 1, 64–67. [Google Scholar] [CrossRef]
- Pełka, P.; Dudek, G. Prediction of Monthly Electric Energy Consumption Using Pattern-Based Fuzzy Nearest Neighbour Regression. ITM Web Conf. 2017, 15, 02005. [Google Scholar] [CrossRef]
- Pełka, P.; Dudek, G. Medium-Term Electric Energy Demand Forecasting Using Generalized Regression Neural Network. In International Conference on Information Systems Architecture and Technology; Springer: Cham, Switzerland, 2018; pp. 218–227. [Google Scholar]
- Pełka, P.; Dudek, G. Ensemble Forecasting of Monthly Electricity Demand Using Pattern Similarity-Based Methods. In International Conference on Artificial Intelligence and Soft Computing; Springer: Cham, Switzerland, 2020; pp. 712–723. [Google Scholar]
- Castán-Lascorz, M.A.; Jiménez-Herrera, P.; Troncoso, A.; Asencio-Cortés, G. A New Hybrid Method for Predicting Univariate and Multivariate Time Series Based on Pattern Forecasting. Inf. Sci. 2022, 586, 611–627. [Google Scholar] [CrossRef]
- Dudek, G.; Pełka, P. Pattern Similarity-Based Machine Learning Methods for Mid-Term Load Forecasting: A Comparative Study. Appl. Soft Comput. 2021, 104, 107223. [Google Scholar] [CrossRef]
- Papalexopoulos, A.D.; Hesterberg, T.C. A regression-based approach to short-term system load forecasting. IEEE Trans. Power Syst. 1990, 5, 1535–1547. [Google Scholar] [CrossRef]
- Wang, Y.; Gan, D.; Sun, M.; Zhang, N.; Lu, Z.; Kang, C. Probabilistic Individual Load Forecasting Using Pinball Loss Guided LSTM. Appl. Energy 2019, 235, 10–20. [Google Scholar] [CrossRef] [Green Version]
- Miseta, T.; Fodor, A.; Vathy-Fogarassy, Á. Energy Trading Strategy for Storage-Based Renewable Power Plants. Energy 2022, 250, 123788. [Google Scholar] [CrossRef]
- Al-Hamadi, H.M.; Soliman, S.A. Long-Term/Mid-Term Electric Load Forecasting Based on Short-Term Correlation and Annual Growth. Electr. Power Syst. Res. 2005, 74, 353–361. [Google Scholar] [CrossRef]
- Barakat, E.H. Modeling of Nonstationary Time-Series Data. Part II. Dynamic Periodic Trends. Int. J. Electr. Power Energy Syst. 2001, 23, 63–68. [Google Scholar] [CrossRef]
- Cai, G.; Yang, D.; Jiao, Y.; Pan, C. The Characteristic Analysis and Forecasting of Mid-Long Term Load Based on Spatial Autoregressive Model. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009; pp. 1–5. [Google Scholar]
- de Oliveira, E.M.; Oliveira, F.L.C. Forecasting Mid-Long Term Electric Energy Consumption through Bagging ARIMA and Exponential Smoothing Methods. Energy 2018, 144, 776–788. [Google Scholar] [CrossRef]
- Zhang, D.-L.; Yan, J.; Wang, W.-H.; Yang, X.-L. Mid-Long Term Load Forecasting of the Unstable Growth Sequence Based on Markov Chains Screening Combination Forecasting Models. In Proceedings of the 2016 China International Conference on Electricity Distribution (CICED), Xi’an, China, 10–13 August 2016; pp. 1–5. [Google Scholar]
- Barakat, E.E.; Al-Rashed, S.A. Long Range Peak Demand Forecasting under Conditions of High Growth. IEEE Trans. Power Syst. 1992, 7, 1483–1486. [Google Scholar] [CrossRef]
- Zagdański, A.; Suchwałko, A. Analiza i Prognozowanie Szeregów Czasowych: Praktyczne Wprowadzenie Na Podstawie Środowiska R; Wydawnictwo Naukowe PWN: Warsaw, Poland, 2016. [Google Scholar]
- Jóźwiak, J.; Podgórski, J. Statystyka Od Podstaw; Wyd. PWE: Warszawa, Poland, 2001. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2013; ISBN 978-0-9875071-0-5. [Google Scholar]
- Pełka, P. Nonparametric Machine Learning Methods for Mid-Term Forecasting of Power System Loads. Ph.D. Thesis, Czestochowa University of Technology, Częstochowa, Poland, 2021. [Google Scholar]
- Chatfield, C. The Analysis of Time Series: An Introduction, 6th ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2003; ISBN 978-1-58488-317-3. [Google Scholar]
- Dittmann, P. Prognozowanie w Przedsiebiorstwie; Oficyna Ekonomiczna: Kraków, Poland, 2004. [Google Scholar]
- Dudek, G. Wybrane Metody Analizy Szeregów Czasowych Obciążeń Elektroenergetycznych. In Proceedings of the Materiały VII Konferencji Naukowej Prognozowanie w elektroenergetyce, Częstochowa, Poland, 26–27 September 2004; pp. 116–125. [Google Scholar]
- Dudek, G. Pattern Similarity-Based Methods for Short-Term Load Forecasting–Part 1: Principles. Appl. Soft Comput. 2015, 37, 277–287. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Khandakar, Y. Automatic Time Series Forecasting: The Forecast Package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Taylor, S.J.; Letham, B. Forecasting at Scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G.; Bergmeir, C.; Caceres, G.; Chhay, L.; O’Hara-Wild, M.; Petropoulos, F.; Razbash, S.; Wang, E.; Yasmeen, F. Forecast: Forecasting Functions for Time Series and Linear Models; R Package: Melbourne, Australia, 2018. [Google Scholar]
- Dudek, G.; Pełka, P. Medium-Term Electric Energy Demand Forecasting Using Nadaraya-Watson Estimator. In Proceedings of the 2017 18th International Scientific Conference on Electric Power Engineering (EPE), Kouty nad Desnou, Czech Republic, 17–19 May 2017; pp. 1–6. [Google Scholar]
- Pełka, P.; Dudek, G. Neuro-Fuzzy System for Medium-Term Electric Energy Demand Forecasting. In International Conference on Information Systems Architecture and Technology; Springer: Cham, Switzerland, 2017; pp. 38–47. [Google Scholar]
- Pełka, P. Pattern-Based Forecasting of Monthly Electricity Demand Using Support Vector Machine. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021. [Google Scholar]
- Smyl, S. A Hybrid Method of Exponential Smoothing and Recurrent Neural Networks for Time Series Forecasting. Int. J. Forecast. 2020, 36, 75–85. [Google Scholar] [CrossRef]
- Dudek, G.; Pełka, P.; Smyl, S. A Hybrid Residual Dilated LSTM and Exponential Smoothing Model for Midterm Electric Load Forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 2879–2891. [Google Scholar] [CrossRef] [PubMed]
- Dudek, G.; Pełka, P.; Smyl, S. 3ETS+ RD-LSTM: A New Hybrid Model for Electrical Energy Consumption Forecasting. In Proceedings of the International Conference on Neural Information Processing, Bangkok, Thailand, 23–27 November 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 519–531. [Google Scholar]





| Symbol | Median | IQR | iqr% |
|---|---|---|---|
| AT | 4978.00 ± 641.00 | 720.00 ± 164.00 | 15.00 ± 4.36 |
| BA | 955.00 ± 49.00 | 141.00 ± 58.00 | 14.91 ± 5.66 |
| BE | 6981.00 ± 609.00 | 848.00 ± 96.00 | 12.66 ± 1.93 |
| BG | 2654.00 ± 152.00 | 740.00 ± 200.00 | 27.69 ± 6.64 |
| CH | 4885.00 ± 425.00 | 862.00 ± 120.00 | 18.15 ± 2.87 |
| CY | 375.00 ± 35.00 | 87.00 ± 12.00 | 23.33 ± 3.41 |
| CZ | 5134.00 ± 243.00 | 1105.00 ± 203.00 | 21.98 ± 4.82 |
| DE | 44,140.00 ± 2883.00 | 5921.00 ± 1411.00 | 13.79 ± 3.81 |
| DK | 2824.00 ± 86.00 | 431.00 ± 86.00 | 15.46 ± 2.95 |
| EE | 672.00 ± 16.00 | 181.00 ± 42.00 | 27.37 ± 6.66 |
| ES | 19,294.00 ± 3778.00 | 1466.00 ± 437.00 | 8.11 ± 1.49 |
| FI | 7052.00 ± 89.00 | 1636.00 ± 204.00 | 23.33 ± 2.84 |
| FR | 36,860.00 ± 2948.00 | 9116.00 ± 2822.00 | 25.01 ± 6.69 |
| GB | 25,751.00 ± 869.00 | 4559.00 ± 750.00 | 17.66 ± 2.80 |
| GR | 4094.00 ± 623.00 | 467.00 ± 161.00 | 12.03 ± 3.05 |
| HR | 1346.00 ± 158.00 | 196.00 ± 40.00 | 15.24 ± 3.86 |
| HU | 3224.00 ± 180.00 | 303.00 ± 92.00 | 9.70 ± 3.51 |
| IE | 2157.00 ± 12.00 | 290.00 ± 42.00 | 13.48 ± 1.91 |
| IS | 1413.00 ± 41.00 | 92.00 ± 9.00 | 6.48 ± 0.71 |
| IT | 25,913.00 ± 2767.00 | 1290.00 ± 246.00 | 5.15 ± 0.86 |
| LT | 864.00 ± 38.00 | 102.00 ± 9.00 | 11.99 ± 0.91 |
| LU | 509.00 ± 64.00 | 46.00 ± 11.00 | 9.53 ± 2.44 |
| LV | 622.00 ± 18.00 | 105.00 ± 19.00 | 17.01 ± 3.23 |
| ME | 345.00 ± 42.00 | 77.00 ± 46.00 | 22.25 ± 11.75 |
| MK | 641.00 ± 41.00 | 190.00 ± 38.00 | 29.60 ± 6.47 |
| NI | 742.00 ± 8.00 | 109.00 ± 14.00 | 14.79 ± 1.90 |
| NL | 8880.00 ± 1099.00 | 837.00 ± 243.00 | 9.78 ± 2.00 |
| NO | 10,339.00 ± 397.00 | 3827.00 ± 460.00 | 37.03 ± 4.90 |
| PL | 11,299.00 ± 429.00 | 1774.00 ± 517.00 | 15.65 ± 4.86 |
| PT | 3764.00 ± 716.00 | 292.00 ± 70.00 | 8.37 ± 1.20 |
| RO | 4357.00 ± 142.00 | 543.00 ± 104.00 | 12.53 ± 2.64 |
| RS | 3201.00 ± 104.00 | 632.00 ± 289.00 | 19.82 ± 9.55 |
| SE | 11,600.00 ± 299.00 | 3511.00 ± 462.00 | 30.55 ± 3.64 |
| SI | 1046.00 ± 64.00 | 86.00 ± 28.00 | 8.43 ± 3.00 |
| SK | 2165.00 ± 59.00 | 383.00 ± 117.00 | 17.70 ± 5.66 |
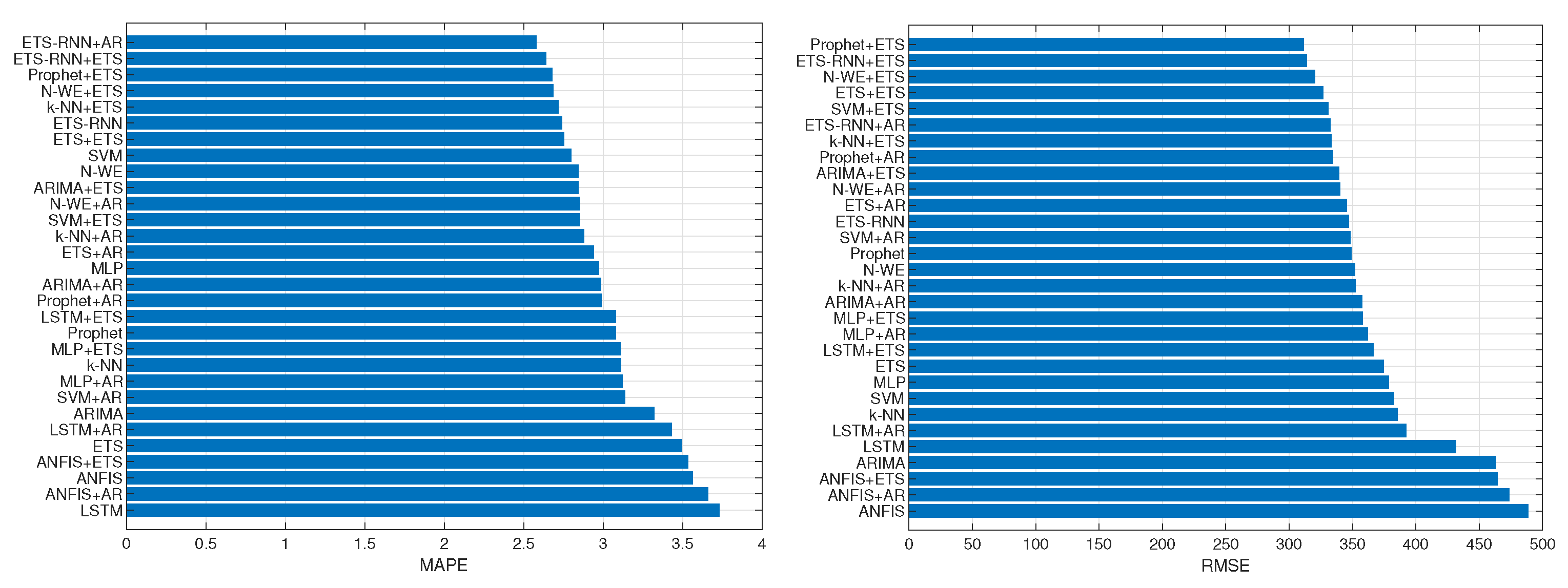
| Model | MdAPE | MAPE | IQR | RMSE |
|---|---|---|---|---|
| k-NN | 3.11 | 5.19 | 4.17 | 385.68 |
| k-NN + AR | 2.88 | 4.71 | 4.25 | 352.42 |
| k-NN + ETS | 2.72 | 4.58 | 3.58 | 333.27 |
| N-WE | 2.84 | 5.00 | 3.97 | 352.01 |
| N-WE + AR | 2.85 | 4.59 | 3.95 | 340.26 |
| N-WE + ETS | 2.68 | 4.37 | 3.36 | 320.51 |
| LSTM | 3.73 | 6.11 | 4.50 | 431.83 |
| LSTM + AR | 3.43 | 5.28 | 4.79 | 392.47 |
| LSTM + ETS | 3.08 | 5.19 | 4.54 | 366.45 |
| MLP | 2.97 | 5.27 | 3.84 | 378.81 |
| MLP + AR | 3.12 | 4.83 | 4.26 | 362.03 |
| MLP + ETS | 3.11 | 4.80 | 4.12 | 358.07 |
| ANFIS | 3.56 | 6.18 | 4.87 | 488.75 |
| ANFIS + AR | 3.66 | 6.05 | 5.07 | 473.80 |
| ANFIS + ETS | 3.54 | 6.32 | 4.26 | 464.29 |
| SVM | 2.80 | 5.41 | 3.97 | 382.60 |
| SVM + AR | 3.14 | 4.91 | 4.09 | 348.52 |
| SVM + ETS | 2.85 | 4.74 | 3.60 | 330.94 |
| ETS-RNN | 2.74 | 4.48 | 3.55 | 347.24 |
| ETS-RNN + AR | 2.58 | 4.23 | 3.47 | 332.74 |
| ETS-RNN + ETS | 2.64 | 4.09 | 3.13 | 314.01 |
| ARIMA | 3.32 | 5.65 | 5.24 | 463.07 |
| ARIMA + AR | 2.99 | 4.64 | 3.95 | 357.84 |
| ARIMA + ETS | 2.85 | 4.52 | 3.61 | 339.49 |
| ETS | 3.50 | 5.05 | 4.80 | 374.52 |
| ETS + AR | 2.94 | 4.50 | 3.68 | 345.37 |
| ETS + ETS | 2.76 | 4.30 | 3.19 | 326.94 |
| Prophet | 3.08 | 4.72 | 4.37 | 349.01 |
| Prophet + AR | 2.99 | 4.39 | 3.65 | 334.46 |
| Prophet + ETS | 2.68 | 4.15 | 3.44 | 311.56 |
| Model | mPE | medPE | stdPE | skewPE | kuPE |
|---|---|---|---|---|---|
| k-NN | −1.96 | −1.27 | 10.83 | −4.88 | 49.39 |
| k-NN + AR | −1.76 | −0.75 | 8.10 | −2.66 | 20.96 |
| k-NN + ETS | −1.26 | −0.20 | 9.11 | −4.47 | 38.22 |
| N-WE | −1.91 | −1.18 | 10.82 | −5.41 | 48.94 |
| N-WE + AR | −1.75 | −0.85 | 7.82 | −2.68 | 21.38 |
| N-WE + ETS | −1.26 | −0.17 | 8.68 | −4.63 | 40.75 |
| LSTM | −3.12 | −1.81 | 9.49 | −2.86 | 22.21 |
| LSTM + AR | −1.86 | −0.78 | 8.66 | −2.75 | 21.20 |
| LSTM + ETS | −1.41 | −0.55 | 10.15 | −5.35 | 50.04 |
| MLP | −1.37 | −0.68 | 11.88 | −7.52 | 109.64 |
| MLP + AR | −1.64 | −0.92 | 7.45 | −1.64 | 12.16 |
| MLP + ETS | −1.71 | −1.03 | 7.32 | −1.55 | 11.83 |
| ANFIS | −2.51 | −1.43 | 11.37 | −4.35 | 34.93 |
| ANFIS + AR | −1.94 | −0.65 | 9.63 | −1.67 | 13.29 |
| ANFIS + ETS | −1.30 | −0.40 | 12.65 | −0.96 | 39.37 |
| SVM | −2.22 | −0.91 | 16.76 | −13.40 | 229.68 |
| SVM + AR | −1.66 | −0.61 | 8.58 | −3.44 | 28.95 |
| SVM + ETS | −1.28 | −0.09 | 11.06 | −7.84 | 95.91 |
| ETS-RNN | −1.11 | −0.27 | 10.07 | −6.37 | 63.61 |
| ETS-RNN + AR | −0.86 | −0.20 | 7.30 | −2.75 | 24.75 |
| ETS-RNN + ETS | −0.32 | 0.47 | 8.48 | −5.36 | 52.51 |
| ARIMA | −2.35 | −1.03 | 13.62 | −9.01 | 119.20 |
| ARIMA + AR | −1.69 | −0.77 | 7.43 | −1.65 | 12.67 |
| ARIMA + ETS | −1.15 | −0.26 | 8.40 | −3.76 | 30.82 |
| ETS | −1.04 | −0.31 | 7.97 | −1.89 | 13.52 |
| ETS + AR | −1.71 | −0.90 | 7.20 | −1.73 | 13.02 |
| ETS + ETS | −1.17 | −0.28 | 8.20 | −4.06 | 33.64 |
| Prophet | −0.70 | −0.18 | 7.47 | −1.37 | 12.27 |
| Prophet + AR | −1.30 | −0.55 | 7.02 | −1.66 | 12.84 |
| Prophet + ETS | −0.76 | 0.00 | 7.86 | −3.79 | 30.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pełka, P. Analysis and Forecasting of Monthly Electricity Demand Time Series Using Pattern-Based Statistical Methods. Energies 2023, 16, 827. https://doi.org/10.3390/en16020827
Pełka P. Analysis and Forecasting of Monthly Electricity Demand Time Series Using Pattern-Based Statistical Methods. Energies. 2023; 16(2):827. https://doi.org/10.3390/en16020827
Chicago/Turabian StylePełka, Paweł. 2023. "Analysis and Forecasting of Monthly Electricity Demand Time Series Using Pattern-Based Statistical Methods" Energies 16, no. 2: 827. https://doi.org/10.3390/en16020827
APA StylePełka, P. (2023). Analysis and Forecasting of Monthly Electricity Demand Time Series Using Pattern-Based Statistical Methods. Energies, 16(2), 827. https://doi.org/10.3390/en16020827






