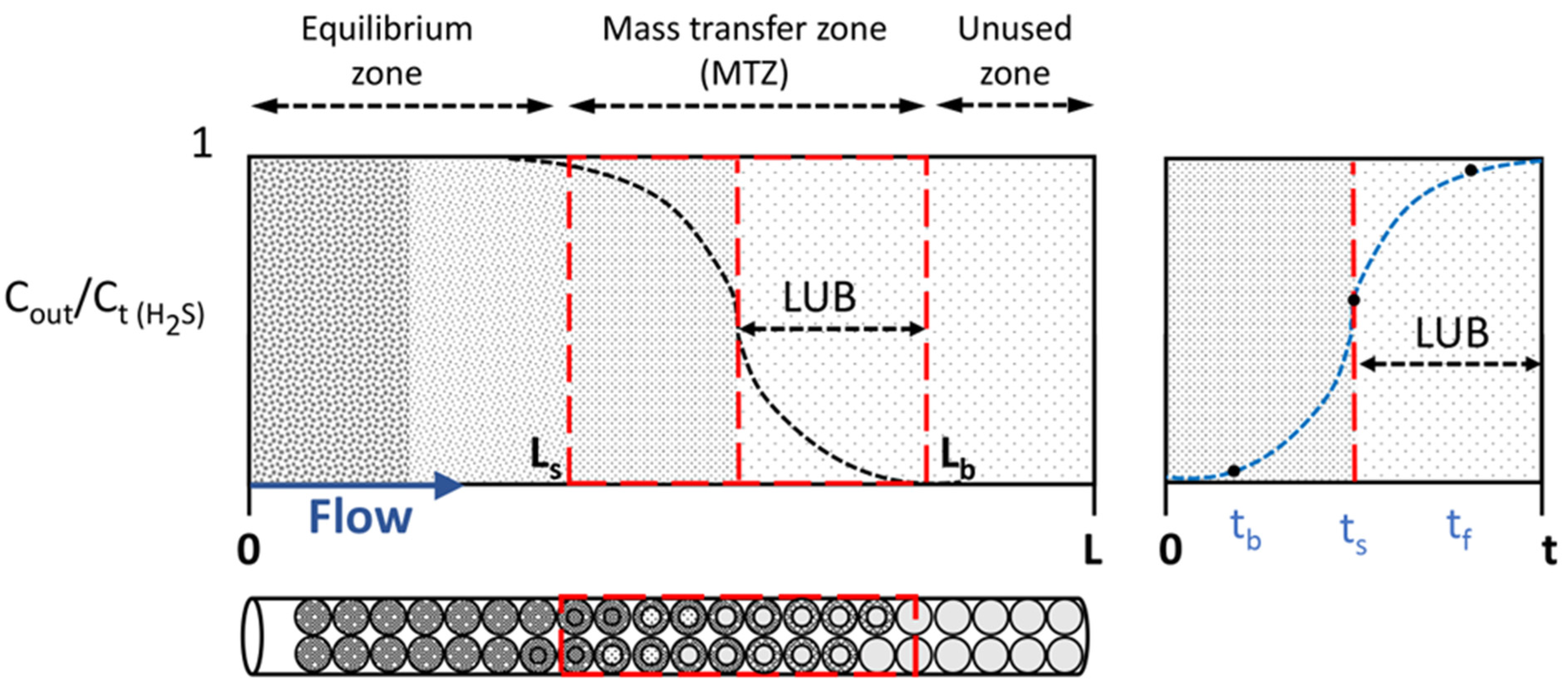
3.2.1. Breakthrough Curves for the Hydrogen Sulphide Adsorption
An assessment of H
2S capture using ZnO sorbents was carried out to clean the syngas flow fed in a thermal range between 450 and 600 °C with an increasing step of 50 °C. Two experimental campaigns were undertaken by varying the LB value between 0.8 and 1.5, causing changes in both the internal diffusive resistance and adsorption kinetics. According to previous LB values and by constantly maintaining the total gas flow at 305 NmL min
−1, the GHSV was defined as 50,000 and 25,000 h
−1, respectively.
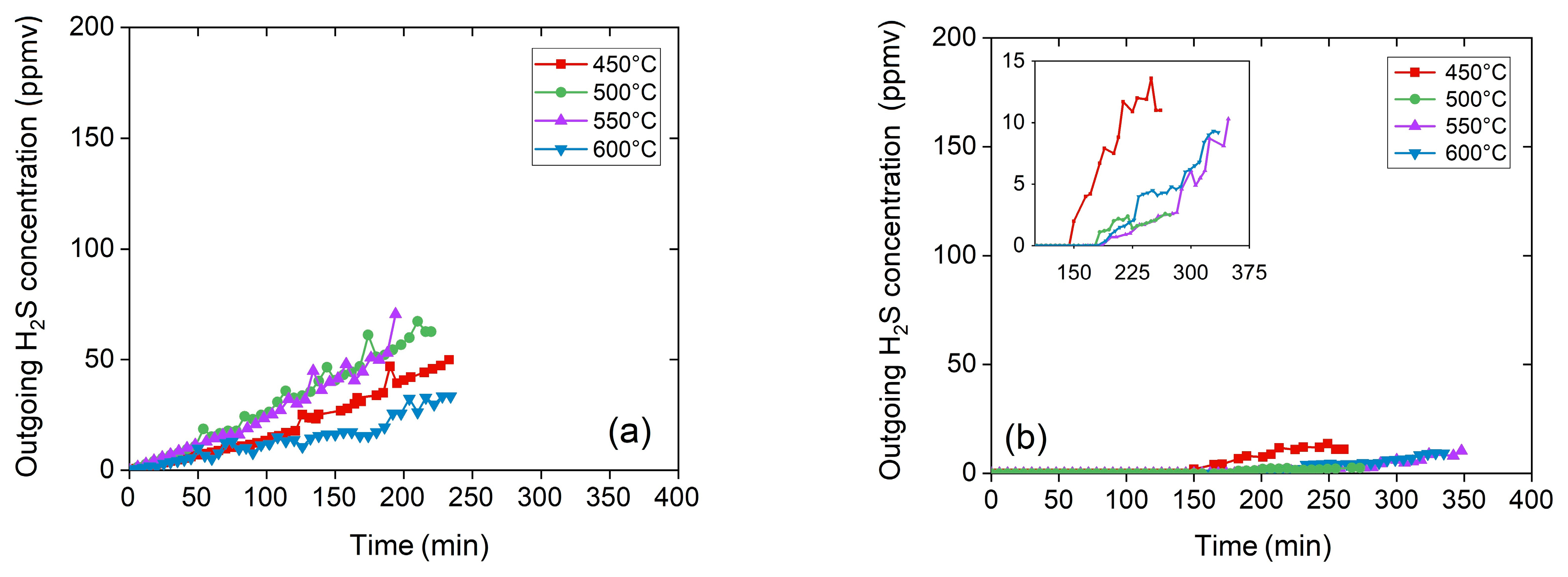
Figure 3 shows the breakthrough curves for the H
2S capture in terms of the time at temperatures between 450 and 600 °C and GHSV, leaving the total flow constant and changing the LB value. The experimentation took more than 3 h to reach the t
b when the sorbent showed H
2S adsorption around 2 ppmv. For the desulfurization reaction (Equation (10)), the values of Δ
H0 and Δ
G0 were calculated using data at 25 °C and Kirchhoff equations. Thermodynamic parameters used for the previous calculation are summarized in
Table 4.
By applying the Kirchhoff Equations (11) and (12), it is possible to calculate the thermodynamic constant value for the adsorption reaction as a function of temperature, as shown in Equation (13). In agreement with values from the literature [
28,
29], the K
p value at 300 °C is 5.9 × 10
6, while at 25 and 600 °C the values are 1.3 × 10
13 and 3 × 10
4, respectively. The average values of Δ
G and Δ
H in the studied temperature range are −74.5 kJ mol
−1 and −72.4 kJ mol
−1, respectively. The calculations were also confirmed by using the HSC Chemistry 6 software.
Figure 3a,b and
Table 5 describe the breakthrough curves during the H
2S adsorption using ZnO in the same temperature range at 50,000 and 25,000 h
−1 and LB sizing. Different effects changing the GHSV are observed in
Figure 3a,b. This variation is also highlighted in the inlet of
Figure 3b, where the first stage of the H
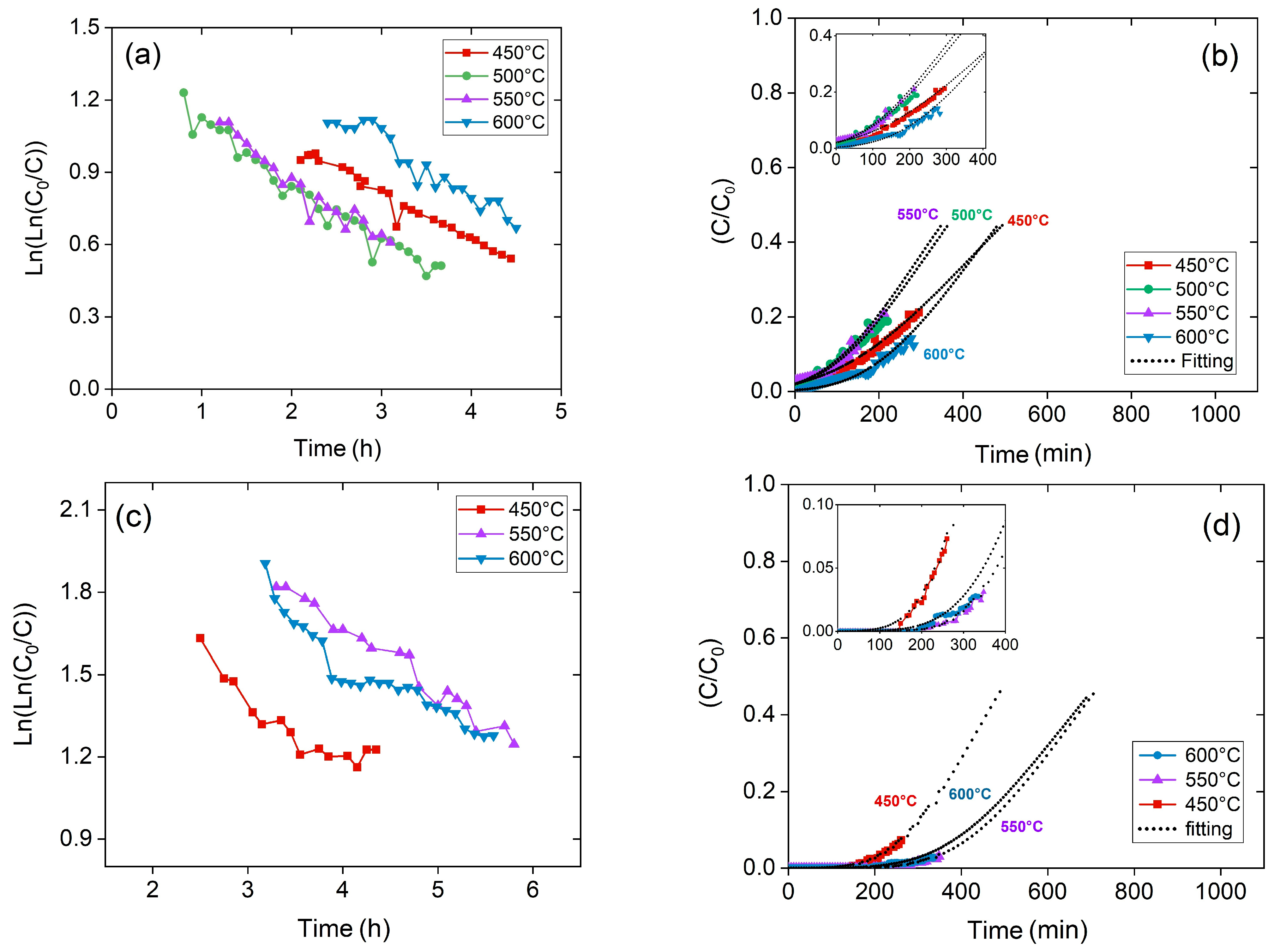
2S saturation process takes more time to be evident. The modeling of breakthrough curves calculates the kinetic parameters (
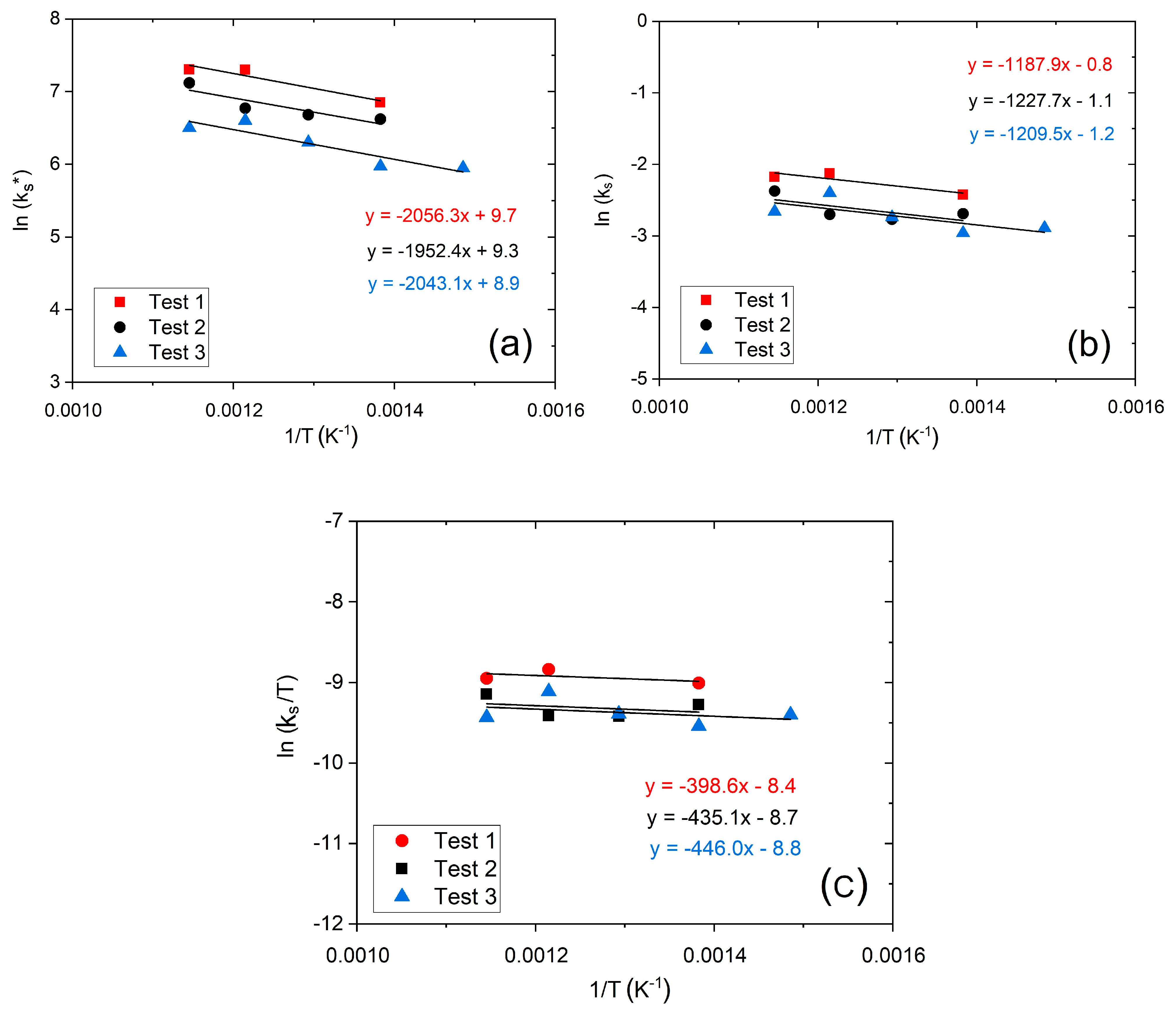
kd and
ks*) by linearizing the deactivation equation (Equation (5)) and plotting the left members in the function of time.
Figure 4a,c show the plot of the linearized deactivation kinetic model between 450 and 600 °C for 50,000 and 25,000 h
−1, respectively.
Based on
kd and
ks*, breakthrough curves were suitably fitted by reaching a good adjustment (R
2 > 0.90), as shown in
Figure 4b,d. In
Figure 4, all the fitting curves have the characteristic S-shape, even if they are not completely shown on graphs, for better readability. The fitting of the breakthrough curves lead to the LB reactor sizing, as well as evaluating the reactor performance and understanding the kinetic and mass-transfer phenomena of the adsorption process. Furthermore, another influencing parameter on the adsorption process is GHSV.
The variation of GHSV caused by changing the volume’s bed or flow rate generates that the contact time between the adsorbate and the bed of ZnO sorbent can vary. When bed size is underestimated, small LUB and MTZ values, and accordingly small t
b and t
s, are obtained, which is equivalent to suggesting a faster mass-transfer and adsorption kinetics process. On the contrary, these diffusive processes can be determined by global resistance due to the size particle effect, such as intraparticle mass transfer resistance [
30]. At a typical industrial scale for the gas cleaning process, particle sizes higher than 1 mm diameter are employed, similar to the particles used in this work. In that way, only external mass transfer could be omitted, while internal resistances stand out (diffusional resistances related to intraparticle mass transfer). Concerning the effect of intraparticle resistance, it can be lowered as particle size decreases; however, pressure drops are a critical phenomenon that can take place. Therefore, a suitable compromise should be proposed by considering small particle sizes, at which the intraparticle resistances are reasonably low, but at the same time, the risk of pressure drops is avoided.
From experimentation, the t
b and Sorption capacity at breakthrough (SC
b) values are determined and reported in
Table 5. Following the modeling of the deactivation model, along with experimental values,
ks*,
kd, sorption capacity at equilibrium (SC
e), t
s, and v
s were obtained. Subsequently, by using Equations (6) and (7), LUB and MTZ are calculated, as shown in
Table 5. Considering Equations (6) and (7), it is possible to determine LUB and MTZ using the experimental LB. However, it is widely known that scaling up requires that the whole LB is greater than the MTZ; otherwise, the length of the used bed will be insignificant and an unstable mass-transfer zone can occur [
21,
22]. According to
Table 5, MTZ is greater than LB in all cases; nonetheless, it can be used to understand the adsorption results in the reactor [
21,
22].
Regarding the analysis of the MTZ, short LB (consequently high GHSV) causes a decrease both in utilization efficiency and SCb. Thus, the direct effect of reducing LB in half is unstable mass transfer conditions. Hence, when it works with lower GHSV conditions, the thermodynamic effects start to have an influence, while with higher GHSV conditions, the kinetic effects are more relevant. Based on our results, the tests at 25,000 h−1 are also influenced by thermodynamic phenomena, unlike tests at 50,000 h−1. In the literature, it is well known that a temperature increase favors mass-transfer processes (as observed in our results), showing an increase in SCb as temperature rises. However, on the other side, exothermic reactions are thermodynamically unfavorable as temperature increases.
Regarding SCb, the best performance for ZnO sorbents at 25,000 and 50,000 h−1 was achieved between 550 °C and 600 °C capturing about 5.1 g of sulphur from 100 g of adsorbent. Further, it is necessary to mention that the test at 450 °C and 50,000 h−1 shows anomalous behavior, probably due to unexpected experimental variations, while the test at 500 °C and 25,000 h−1 shows two different trends, and it has not been taken into consideration. Despite the previous anomalous tests, the following analyses and considerations on collected data consider all tests performed, including those produced in earlier work, to arrive at a coherent and consistent conclusion.
Based on the previous analyses and kinetic parameter calculations, we estimate the LB (LB
est) value, at which the ZnO bed-fixed reactor can work efficiently for an extended period. In this case, once the value of
vs is known and estimated from the modeling of experimental results, it is possible to estimate the LB
est using the desired
tb (for example,
tb = 1000 h). In
Table 6, the LB
est necessary to work for a long period without observing H
2S saturation was estimated. This estimation was performed using Equation (8) and by considering the
vs obtained from the current experimental conditions and those taken from [
21]. From the obtained results herein using 260–400 H
2S ppm, it is evident that by using an LB
est in a range of about 100–130 cm, it is possible to have a bed of sorbent with a capacity to work about 1000 h. These estimations are in agreement with the previous analysis, where an increase in temperature, in general, favors the desulfurization reaction. In particular, when GHSV is changed by increasing the gas flow, the relative velocity of the gas flow rises with respect to the fixed bed and LB significantly increases. Thus, this is a critical parameter to size the LB. In fact, in this test, changing the GHSV (by changing gas flow) to 40,000 h
−1 at 550 °C causes the LB to be proportionally increased. Finally, considering unexpected variations, the test at 50,000 h
−1 and 450 °C confirmed an anomalous result since it was expected to be an LB
est larger than others at the same GHSV and higher temperatures.