Abstract
This paper presents a method for determining the load capacity of three-phase squirrel-cage induction motors supplied with a balanced distorted voltage containing rotating harmonics (1st, 5th, 7th, 11th, 13th,...). The method is based on the dependence of the motor load capacity on the load power losses in the rotor cage. The load capacity was determined based on motor short-circuit measurements made for frequencies equal to harmonic frequencies. To evaluate the load capacity, a factor with the proposed name Harmonic Losses Factor (HLF) was introduced. Its expression is a generalization of the well-known HVF expression. However, it has been shown that a more accurate estimation of the load capacity is obtained using the sum of load power losses in the rotor cage from higher harmonics. Measurements and calculations were carried out for a low-voltage squirrel-cage motor with a rated power of 22 kW and a synchronous speed of 1500 rpm. Calculations showed that the derating power curves given in the IEC 60034-17 and NEMA MG1 standards are incorrect for the tested motor.
1. Introduction
The power systems of many countries operate an increasing number of non-linear loads. These are power electronic devices (inverters, cycloconverters, controlled and non-controlled rectifiers, thyristor, and triac controllers), arc furnaces, electric arc welders, and modern light sources (LED, fluorescent lamps), FC-TCR compensators, and power supplies, especially for IT equipment. In some sense, they are also capacitors, used for power factor correction and voltage control or filtration, and chokes used to reduce the short-circuit currents of power lines and for filtering purposes [1]. Capacitors and chokes are not non-linear loads, but they can cause resonance phenomena in the power system that affect the waveforms of grid voltages. The operation of non-linear loads in the power system causes three-phase voltage distortions. The most common case is a deformation of the waveforms of these voltages. The deformation can be presented as the appearance of higher harmonics in the voltages. There may also be sub-harmonics and inter-harmonics in voltages, usually associated with fluctuations in the amplitudes of three-phase voltages. The operation of single-phase loads or sources, linear or non-linear, results in the unbalance of grid voltages.
Powering a three-phase induction squirrel-cage motor with voltage containing additional frequencies or with unbalanced voltage can cause many disturbances in its operation. First, it causes an increase in power losses in the motor and creates alternating torques. Alternating torques can cause fluctuations in the motor rotational speed, which causes the appearance of additional frequencies in the motor currents [2]. These effects make it necessary to lower the thermally admissible long-term load capacity of the motor in terms of load torque and power.
One of the first papers on powering a motor with distorted voltage was by Cummings (1986) [3]. This paper can be considered a basic study of supplying a squirrel-cage motor with a voltage containing rotating harmonics. Cummings in [3] presents considerations leading to the determining of the admissible load power of the squirrel-cage induction motor supplied with distorted voltage containing harmonics order h = 1,5,7,11,13,... The paper determines the relationship between load power losses in the motor from higher rotating harmonics (h ≥ 5) and the value of the defined Harmonic Voltage Factor (HVF). Based on this relationship, the expression for the thermally admissible torque and load power as a function of HVF can be derived (see Appendix A). The power values, equal to 0.6 and 0.8 of the rising short-circuit resistance and reactance of the motor with the stator current frequency, were determined, which influenced the form of the HVF expression. The expression for the HVF was presented in the standards [4,5] and is the basis for determining the derating factor (DF) of motor power according to the DF(HVF) curves provided there.
In Fuchs et al. [6], the expression for power losses from rotating higher harmonics in the HVF function was modified. The form and value of the coefficient of the relationship between these losses and the HVF2 value were modified. This coefficient depended on the type of electric machine (motor, transformer, single-phase machine, three-phase machine) and the parameters of its model. The form of the HVF has also been modified. The powers of RMS values of the voltage harmonics and harmonic’s numbers h depend on the type of electric machine.
This modified expression is the basis of the work [7], where the increase in load losses caused by the distorted power supply is related to the temperature of the motor winding insulation. The results reported in [7] were based on the complete three-dimensional thermal model of the machine. All the investigated motors were modeled for steady-state operation at 75% load and temperature of cooling air equal to 30 °C. In such favorable operating conditions of the motor, it was assumed that the durability of its insulation should be approximately 20 years, for sinusoidal and balanced supply voltage. The motor and its insulation life calculations were based on aging curves given in IEEE Std. 117. The paper focused on the determination of the relationship between the decrease in the average lifetime of the insulation and the value of higher harmonics or voltage unbalance.
In [8], the induction machine equivalent circuits for higher rotating harmonics were also used. Their form was assigned to all higher harmonics, including those with even and triple numbers. The article focused on the calculation of stray load losses for the distorted supply voltage, regardless of the increase in the rotor resistance with a harmonic number, causes by a skin effect in the rotor cage bars. A simple, analytical thermal model of the machine was proposed. Based on it, the power derating factor for different contents of higher harmonics in the supply voltage was determined. The derating factor for machines of various rated powers and designs was calculated.
In the studies presented by Lee et al. [9], measurements of a loaded motor were carried out to examine the impact of each harmonic of the supply voltage (from the 2nd to the 13th) on the motor’s operation at different values of the Voltage Distortion Factor (VDF). A motor with a rated power of 2 kW was tested. They consisted of recording the voltage and current waveforms of the motor supplied with distorted voltage and measuring its efficiency and temperature. Based on motor temperature measurements, a new method for determining the power derating factor of an induction motor was made. An important conclusion from the measurements was the statement that harmonics with a number below 5 have more impact on a three-phase induction motor than the higher harmonics.
Jalilian et al. [10] investigated the power losses of a high-efficiency squirrel-cage induction motor with a rated power of 7.5 kW, supplied from a distorted voltage source. The voltage contained the fundamental harmonic (50 Hz) and higher rotating harmonics with frequencies up to 1 kHz. The measurement of motor power losses was carried out extremely accurately and reliably by measuring the dissipated heat of the motor in a double calorimetric chamber. According to the measurements from the tested 7.5 kW motor, it was found that the short-circuit resistance for higher rotating harmonics (h ≥ 5) increases with the harmonic number in the power of 0.5, and the short-circuit reactance in the power of 0.65. On this basis, the Weighted THD (WTHD) factor was proposed, based on which the motor power losses due to higher harmonics of the supply voltage depend on the 2nd power. The WTHD was used to derive an expression for the power derating factor of squirrel-cage induction motors.
The calorimetric chamber for thermal measurements of the motor was used in the wide-ranging work described in [11], where 15 motors with rated powers from 11 kW to 147 kW were tested. Unfortunately, this paper was about comparing different measurement methods for determining stray load losses in sinusoidal-fed induction machines. This paper did not consider all the additional load losses in non-sinusoidal-fed induction machines.
In the paper [12], many induction motors were computationally tested, based on various models of an induction machine. There were three large and two small, low-voltage motors: 400 kW, 4 poles, 200 kW, 2 poles & 4 poles, 7.5 kW, 4 poles, 3 kW, 4 poles. The tests concerned motors powered by a voltage with rotating harmonics, and unbalanced voltage. The tests showed that the computational DF(HVF) curves for each motor may be significantly different, depending on the machine model adopted for simulations. For different motors, the DF(HVF) calculation curves were also significantly different, using the same author’s machine model [13], having regard to the machine thermals. Various calculation curves of rotor effective resistance as a function of frequency for the many rotor bar types present in motors explained this fact. The efficiency class of the motor plays an important role in derating, too. Furthermore, the size of the motor, its rated power, different conditions of heat dissipation, as well as the design (open or closed design, type of cooling), have roles in derating. The authors proposed a general, polynomial form of the expression for the DF(HVF) curve, for individual harmonics.
Measurements in [14] showed that, for a 4 kW motor at smaller loading, derating factors from [4,5] can underestimate the power losses in the motor. It was also noted that the phase shift of the rotating harmonics (h ≥ 5) influences the maximum value of the flux density and therefore the saturation level of core and power losses in the machine. Derating according to the authors in [4] uses practically the same derating factor as done in [5] and both derating methods are widely described in [15].
In [16], various standard methods were collected (IEEE Std. 399 Generic Method, IEEE Std. 399 Induction Motor Equivalent Circuit Method, IEEE Harmonics Task Force Model 2003) from papers [3,17] for determining the variation of the short-circuit resistance and inductance of an induction motor with the frequency of its voltage supply. The differences between the short-circuit resistance values sometimes varied by several orders of magnitude. This illustrates the scale of the problem of the correct calculation of the variation in the short-circuit power of the motor with the frequency of its supply.
In [18], the results of measurements of squirrel-cage induction motors with a rated power of 4 kW and a synchronous speed of 1500 rpm (for a 50 Hz supply), with the efficiency classes IE1 and IE2, were presented. These motors were supplied with a voltage containing 12% of the 5th harmonic (100% was equal to the rated voltage) and loaded with a torque varying from 20% to 110% of its rated value. The results showed a slight variation of the power losses from the 5th harmonic as a function of the load torque: from 35 W to 42 W for an IE1 class motor and from 23 W to 32 W for an IE2 class motor. The measurements showed an increase in the fundamental harmonic active power when the motor was supplied with distorted voltage. Unfortunately, this observation was not elaborated on in the paper, which was devoted mainly to the problems of obtaining adequately accurate measurements of the power and efficiency of both motors.
De Lima et al. [19] assumed, based on their earlier papers, that the equivalent rotor resistance varies exponentially with the frequency of the rotor currents—in the power on the base e there is the root of this frequency. Calculations of the DF were carried out numerically only, for two low-voltage motors (220 kW and 132 kW), as model calculations based on motor equivalent circuits for successive rotating harmonics h = 1, 5, 7, 11, 13, 17, 19, 23, and 25. For a squirrel-cage motor supplied with an unbalanced or distorted voltage, the following were compared: (a) power losses in the stator winding for a loaded motor with power losses in the stator winding in the rated state of the motor, (b) total power losses for a loaded motor with total power losses in the rated state of the motor. The results showed that unbalance mainly affected the stator winding, and harmonic distortions mainly affected the rotor circuit.
Donolo et al. [20] performed measurement tests of three induction motors with the same rated power of 5.5 kW and synchronous speed of 1500 rpm, but with different efficiency classes (IE1, IE3, IE4). Based on the measurements, they showed that NEMA derating factors were not correct to maintain power losses in the motor IE3 or IE4 class below rated values. The voltage supplying the tested motors contained the 5th and 7th harmonics. The magnitude of the 7th harmonic was 70% of the magnitude of the 5th harmonic. Finally, they calculated derating factors for HVF values 0.03–0.14. The standard curve turned out to be appropriate only for the motor with the IE1 efficiency class. It should be noted that the total load power losses in the motor were taken into consideration, not just the rotor load losses. In the conclusions, the authors wrote: “This article suggests that (1) IM losses due to voltage unbalance and harmonic distortion are greater in higher efficiency class IMs, and (2) that derating factors defined in standards are not enough to avoid overload on higher efficiency class IMs.”
As can be seen from this short review, the standard [4,5] DF(HVF) curves have often been questioned. The HVF formula has also been questioned. It is suggested that one curve DF(HVF) for all existing induction motors may not be possible, due to the different designs, the number of poles, size, cooling, efficiency class, and operating duty of the motors. It is also not established which electromagnetic model of an induction machine (with concentrated parameters) is appropriate for a disturbed power supply. For steady sub-synchronous states, the classical model is most often used as equivalent circuits for individual harmonics of the motor supply voltage. Their resistances and inductances are varied with the frequency of the harmonic currents of the stator or rotor, or with the frequency of the motor supply voltage. The character and rate of these variations are variously assumed. Hybrid models of induction machines are also used, i.e., taking thermal phenomena in motors into account.
The calculations presented in this paper were aimed at determining the derating factor for a low-voltage squirrel-cage induction motor with a rated power of 22 kW and a synchronous speed of 1500 rpm when the motor was supplied with a voltage containing higher rotating harmonics. The calculations were based on the results of short-circuit measurements of the motor made for the frequencies of these harmonics. For the calculations, the classical model of an induction machine for a steady sub-synchronous state was used. In this model, the resistances and inductances of equivalent circuits for individual harmonics were varied. According to the model, the additivity of calculation results for individual harmonics was assumed. The assumption about the additivity of power losses from individual harmonics applies to the steady state of the motor, i.e., constant speed of the motor and periodic waveforms of motor currents and voltages. This assumption was met by definition in this machine model. Based on the assumed limit of the power losses in the rotor cage, equal to the rated power losses in the rotor cage, DF was calculated. A new factor for estimating the DF values for the squirrel-cage induction motor is proposed. Its expression is a generalization of the well-known HVF expression. The paper presents an engineering and practical approach to the problem of determining the admissible load power of a squirrel-cage induction motor supplied with distorted voltage.
2. Materials and Methods
The research concerned a squirrel-cage induction motor, with the descriptive data presented in Table 1. Short-circuit measurements of the stopped motor were made with the motor’s supply frequency varying from 50 Hz to 1450 Hz. The RMS value of the three-phase balanced sinusoidal voltage was such that the RMS current was equal to the rated current of the motor. Active power, RMS current, and RMS voltage were measured. The Chroma 61512 programmable inverter was used for power supply and measurements. This is a special inverter for experimental purposes whose output voltages are truly sine wave (no modulation effects) thanks to the output sine filter. It is not an inverter commercially designed to power electric motors. Short-circuit measurements were performed by the inverter. It records the waveforms of phase voltages and currents and, on this basis, determines the RMS values of voltages and currents as well as the value of active power. Power measurements were verified with two electrodynamic wattmeters in the Aron circuit.

Table 1.
Rated and cataloged data of the tested squirrel-cage motor.
Unfortunately, for the highest frequencies, the inverter could not generate such a high voltage that the motor current was equal to the rated current. The RMS limit of the inverter output phase voltage was 300 V. For example, for the frequency of 1450 Hz, the measured current was only 11.8 A, instead of the rated value of 23.8 A. In this case, the measurement results were converted into the rated current level—short-circuit power with the square of the ratio of the rated current to the measurement current, the short-circuit RMS voltage linear with this ratio.
For the calculations, a classical model of a three-phase induction machine was used, which is a model of a wound machine. The model assumed the internal symmetry of the machine, both electric and magnetic, a sinusoidal spatial distribution of the rotating magnetic field in the machine for each rotating harmonic of the supply voltage, and the linear magnetization of the machine. In this way, the model ignored the real arrangement of the stator and rotor windings and the presence of the slots on the stator and rotor. Therefore, in the model, the mutual inductances between the stator phases and the equivalent rotor phases varied sinusoidally with the rotor position, and the inductances of the stator phases and the equivalent rotor phases were constant. Power losses in the machine core, resulting from the rotating magnetic field, were included in the model post factum, by introducing an additional resistance RFe to the model. This method can only be considered suitable for a steady-state machine. Power losses due to leakage fluxes were included by increasing the resistance of the stator and rotor phases. As for the previous, this method can only be considered appropriate for a steady-state machine. The other additional load losses in the machine could be taken similarly into account. The skin effect in the rotor cage bars could be accounted for by changing the rotor resistance and leakage inductance with the frequency of its currents. This would be correct only for the steady state of the machine.
As in [3,4,7,8] and based on the conclusions presented in [21], it was assumed that the increase in the temperature of the motor windings is caused by the currents of these windings, i.e., load power losses in the machine, both basic and additional. For the calculations, the models of the steady state of the motor for individual supply harmonics were used, with the variation in the resistance and leakage reactance of the stator and rotor with the frequency of currents. The model, which was the basis of the equivalent circuit presented in Figure 1, assumed the formation of sinusoidal, rotating magnetic fields from individual harmonics of the voltage supplying the motor. Therefore, equivalent circuits can only be created for those voltage harmonics that give rotating fields. These are harmonics no. h = 5,7,11,13,17,... If the three-phase voltage supplying the machine is balanced, then its harmonics with numbers given by the formula: h = (6 · k − 1), k є N, have the opposite sequence of phases and give in the machine rotating magnetic fields with the direction of rotation opposite to that of the fundamental harmonic field (h = 1). Harmonics with numbers given by the formula h = (6 · k + 1) form three-phase systems with the same phase sequence and give rotating magnetic fields with the same direction of rotation as the first harmonic field. The magnetic fields caused by harmonics h = 3,9,15,... are not rotating fields and therefore the structure of the equivalent circuit in Figure 1 does not apply to these harmonics. However, the currents of these harmonics can flow from the power source to the machine stator with a four-wire supply only, which is not used. Even-numbered harmonics of voltages in the power system are typically transient. Therefore, an induction motor connected to a three-phase power grid is exposed to rotating harmonics of voltages and their sub-harmonics and inter-harmonics. The risk for the motor is also unbalanced voltage, resulting in the appearance of the negative sequence of voltage in the motor phase voltages [12,15,19].
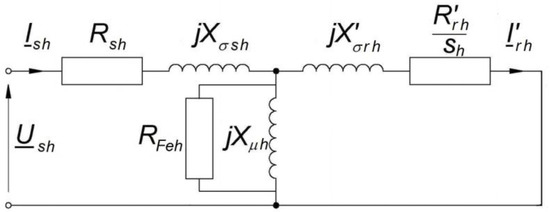
Figure 1.
Equivalent circuit of squirrel-cage motor for harmonic h; sh = (+/−h∙ω1−ω)/(+/−h∙ω1) ≈ 1.
For high frequencies of rotating harmonics (h ≥ 5), the magnetizing currents Iμh of these harmonics, in the equivalent circuits flowing through the magnetizing reactance, have a negligible impact on the RMS value of the stator current of the motor operating at sub-synchronous speed. This is caused by the high value of the magnetizing reactance Xμh and value of the slip approximately equal to 1. The power losses in the magnetic circuit of the machine increase faster than linearly with increasing frequency of the supply voltage, typically with the power of 1.5 ÷ 1.7, according to the catalog data of motor sheets. The second factor of their increase are the power losses in the rotor’s core, not present for the fundamental harmonic. However, it was assumed [3,4,10] that the power losses in the core do not increase the temperature of the machine windings due to the large mass and volume of the machine core. On this basis, it was assumed that the machine equivalent circuit for each higher harmonic is a short circuit, i.e., the current flows only in the longitudinal branch of this circuit, and power losses occur in the stator resistance and rotor resistance. These resistances were assumed to be variable with the frequency of currents, due to skin effect, proximity effect (for stator winding), and stray-load losses [3,10]. The skin effect is especially high in the rotor cage bars, causing the resistance value Rr’ to vary even several times with the harmonic number. Along with the increase in the value of this resistance, the power losses in the rotor increase. Because values of the slips s5, s7, s11, s13,... are close to 1, it was assumed that these slips are equal to 1, as in [3,6]. The calculations assume that the mean torques from the rotating higher harmonics are negligible at sub-synchronous speeds. This is caused by high synchronous speeds of these harmonics and low values of their voltages. The RMS values of these voltages are usually much lower than the rated voltage of the motor. It should be noted that at sub-synchronous speeds, the negative torques of the harmonics h = (6 · k − 1) in part compensate with the positive torques of the harmonics h = (6 · k + 1). For these reasons, it can be assumed that the mean electromagnetic torque of the motor, in the steady-state equal to its load torque, comes from the fundamental harmonic of the motor supply voltage only.
3. Results
3.1. Derating Load Torque and Power
According to the classical model of the induction machine, the average electromagnetic torque of the motor caused by the fundamental harmonic of the power supply can be related to the power losses in the rotor winding:
where: ΔPCur1—load power losses in the rotor cage from the first harmonic of the motor supply, s—slip of the motor, ω1—pulsation of the first harmonic of the motor supply.
This relationship assumes no power losses in the rotor core from the first harmonic of the motor supply. This assumption is met, as the frequency of the rotor currents caused by the fundamental harmonic of the stator power supply is the frequency s∙f1, and therefore very low with typical motor slips of several percent. Based on (1), the expression for the thermally admissible electromagnetic torque of the motor supplied with a voltage with rotating harmonics can be written as:
where: ΔPCur1der—thermally admissible load power losses in the rotor cage from the first harmonic of the motor supply.
For motor load torques not greater than its rated torque, it can be assumed that the relationship between motor slip and motor average electromagnetic torque (equal to load torque) is linear:
where: us1 = Us1/UsN, Us1—RMS value of the first harmonic of phase voltage of the motor, UsN—rated phase voltage of the motor.
On this basis, the expression for the thermally admissible electromagnetic torque of the motor supplied with voltage containing higher rotating harmonics is obtained:
The admissible motor load power (mechanical, i.e., on the shaft) was determined as the product of the admissible motor load torque and the shaft speed. It was determined based on (3):
For a sinusoidal motor supply, the thermally admissible power losses from the first harmonic of the supply ΔPCur1der are equal to the rated power losses in the rotor cage ΔPCurN. For a distorted power supply, they are reduced by the sum of power losses in the rotor cage from higher rotating harmonics of the motor power supply:
The value of total power losses in the motor for higher rotating harmonics can be determined by short-circuit measurements of a stopped motor supplied with a three-phase and balanced sinusoidal voltage, with frequencies equal to the frequencies of rotating harmonics. For higher rotating harmonics, the short-circuit state of the machine corresponds to its operation with around-synchronous speeds. Assigning the measured short-circuit active power to the power losses in the machine windings (both base and additional) means that power losses in the stator and rotor core from the main flux are negligible. This is justified by the small RMS value of the measuring short-circuit voltage of the machine. With increasing frequency, this voltage increases (while maintaining the condition of taking measurements at the RMS value of the current equal to the rated current of the motor), due to the increase in windings leakage reactance. However, assuming that the leakage reactances of the stator and rotor windings are equal, the power losses in the core from the main flux are determined by half of the RMS value of this voltage. Based on the rated power losses in the stator core provided by the manufacturer of the tested motor (Table 1), it was estimated that for the frequency 1450 Hz (h = 29) the main flux power losses in the stator and rotor cores are approximately 540 W at a short-circuit power of 5700 W. For the estimation, it was assumed that the main flux losses in the motor core during a short-circuit test depend on: 1, the square of the ratio of half of the RMS value of short-circuit voltage to its frequency; 2, the frequency of the short-circuit voltage in the power of 1.6; 3, the mass of the stator and rotor cores—it was assumed that the mass of the rotor core is 2/3 of the mass of the stator core. They, therefore, amount to less than 10% of the short-circuit power. On this basis, no power losses in the cores were assumed. That is, it was assumed that all the load power losses of the rotor are dissipated in the rotor cage, and they heat it directly. This made it possible to write an expression for the sum of rotor load losses from higher rotating harmonics using the results of its short-circuit measurements:
where: Rrh’—rotor cage resistance for harmonic h ≥ 5, Irh’—RMS value of the harmonic h of the equivalent rotor current, Rkh—measured short-circuit resistance of the motor for the frequency of h ∙ f1, Ikh—RMS value of the measuring short-circuits phase current of the motor with a frequency of h ∙ f1, Ukh—RMS value of the measuring short-circuits phase voltage of the motor with a frequency of h ∙ f1, Pkh—measured motor short-circuit power at a frequency of h ∙ f1, Ush—RMS value of the harmonic h of the phase motor supply voltage.
For the practical use of Formula (7), it is necessary to know the rotor resistance values for all harmonics of the motor supply.
3.2. Identification of Motor Model Parameters
According to the steady-state model of the induction machine for higher harmonics (Figure 1) and ignoring the power losses in the cores, the measured short-circuit resistance is the sum of the stator phase resistance and the rotor phase equivalent resistance. As the frequency increases, the values of both resistances increase, but not equally. It can be presumed that the rotor resistance will increase faster due to the skin effect in the cage bars. The value of the stator phase resistance for the rated frequency can be determined based on the motor-rated power balance, prepared based on data from Table 1 and formulas of the model. Knowing the stator resistance makes it possible to determine the rotor resistance for the rated stator frequency, based on the measurement of the short-circuit active power when the motor is supplied with a voltage of this frequency. The resistances determined in this way also include additional load losses of the motor at the rated stator frequency. Values of the rotor resistance for the rated frequency of the rotor currents can be calculated based on the model formulas. The method of determining the values of these three resistances is described by Formulas (8)–(20):
where: ΔPN—rated motor power losses, ΔPCusN—rated power losses in the stator winding, ΔPCurN—rated power losses in the rotor cage, IsN—rated current of phase of the stator, as a complex value, Is0—motor idling current of phase of the stator, when the motor is supplied with the rated voltage, as a complex value, UμN—voltage on the transverse branch of the motor equivalent circuit in the rated state of the motor, as a complex value, Uμ0—voltage on the transverse branch of the equivalent circuit of the motor in the idling state of the motor, when the motor is supplied with the rated voltage, as a complex value, Rs1—resistance of the stator phase in the rated state of the motor, Xσs1—leakage reactance of the stator phase for stator currents with rated frequency and RMS value not greater than the rated current of the motor, Rr1′—resistance of the equivalent rotor phase for the frequency of the rotor currents fr = f1 = fN, RrN’—resistance of the equivalent rotor phase for the rated frequency of the rotor currents frN = sN ∙ fN, IrN’—rated current of the equivalent rotor phase, as a complex value, Zμ—impedance of the transverse branch of the motor equivalent circuit, for the rated supply voltage, as a complex value, Xμ—magnetizing reactance of the motor, for the rated supply voltage, RFe—resistance representing power losses in the stator core, for the rated supply voltage.
3.3. Models of Load Losses
In the Master of Science thesis [22], short-circuit measurements of various squirrel-cage motors for higher frequencies were performed. It was found that the variability of the short-circuit resistance and reactance of a squirrel-cage motor with the frequency short-circuit current can be approximated as:
where: a, x, y—coefficients determined during approximation, Xk1—motor short-circuit reactance measured at frequency f1 = fN.
Approximation Formulas (21) and (22) (Figure 2) were selected based on experiments presented in papers [5,6,7,10], where power relations of resistance and reactance to frequency were assumed. However, the formula for the short-circuit resistance was extended so that: (a) there is no passus of zero short-circuit resistance of the machine for direct current, (b) there is possible correctly reproduce by the approximation formula the sum of the stator resistance Rsh for the frequency of the rated slip (h = sN) and the rotor resistance RrN’. The resistance RrN’ is implicitly present in the Formula (6) and the rated power losses in the rotor (18) depend on it, which is of key importance for determining the admissible torque and power. The coefficients a, x were calculated in such a way that the calculated short-circuit active powers for all frequencies (all h orders) were not smaller than the measured short-circuit active powers. In [22], the powers of y obtained from the approximation for various motors were always in the range from 0.9 to 1.1, so the increase in the reactance value with frequency was always approximately linear.
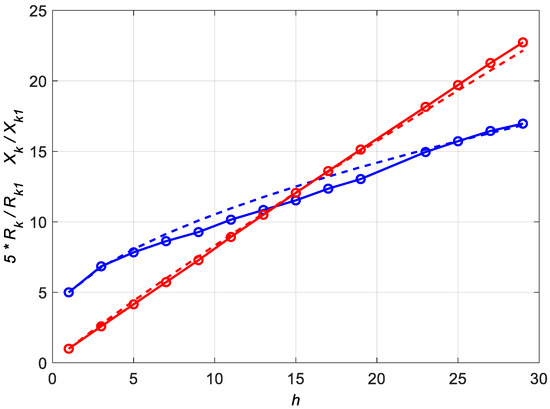
Figure 2.
Measurement values of short-circuit resistance (×5, blue line and points) and reactance (red line) as a function of the harmonic number and their approximations (dashed lines).
Variation of stator phase resistance and resistance of the equivalent rotor phase with frequency was determined in three alternative models:
- In model 1, it was assumed that the stator resistance and rotor resistance vary with the harmonic number according to the expression (21) and with the same power of x, but with different values of the coefficient a:Knowing the power of x from the approximation and the value of Rr1′ from (17) and the value of RrN’ from (18), as the value of Rrh’ for h = sN, allowed us to determine the values of coefficients ar (for rotor) and as (for stator):The values of both coefficients should be between 0 and 1. Values less than 0 would mean that the DC winding resistance is negative. Values greater than 1 would mean that the resistance value decreases with increasing frequency.
- In model 2, it was assumed that the stator resistance and rotor resistance vary with the harmonic number according to the expression (21) and with the same power of x and coefficient a:The value of the coefficient a should be in the range from 0 to 1, for the reasons given for model 1. Model 2 can be described as “optimistic” in relation to the value of load power losses in the rotor cage. These losses should be assessed as underestimated because it is practically impossible for the stator resistance to increase with frequency as fast as the rotor resistance, in which the skin effect in the cage bars occurs. The disadvantage of model 2 is the incorrect reproduction of the rotor resistance value in the rated state RrN’—for the tested machine it is overestimated.
- In model 3, it was assumed that the stator resistance is constant, and the rotor resistance, which varies with the harmonic number, is responsible for the entire increase in the short-circuit resistance of the machine with frequency:The variation of the rotor resistance with the harmonic number can be written by the equation:where: .The value of the coefficient a should be greater than the quotient Rs1/Rk1 so that the DC rotor resistance is greater than 0, and less than 1, so that the rotor resistance increases with frequency. For ar’, it means that it should be between 0 and 1. Model 3 can be described as “pessimistic” in relation to the value of load power losses in the rotor cage. These losses should be assessed as overestimated because it is practically impossible for the stator resistance not to increase with frequency. The disadvantage of model 3 is the incorrect reproduction of the rotor resistance value in the rated state RrN’—for the tested machine it is underestimated.
The values of the approximation coefficients for the tested motor are presented in Table 2.

Table 2.
Approximation coefficients for all three power loss models for the tested motor.
3.4. Derating Torque and Power
For various models of rotor resistance variability with frequency, different values of the sum of the load power losses of the rotor for higher harmonics were obtained, according to (7). These calculations were based on the results of motor short-circuit measurements for individual harmonics. The curves shown in Figure 3, Figure 4 and Figure 5, were calculated based on the machine model for steady states of the motor. The measured values of short-circuit resistance and reactance of the motor for harmonic frequencies or their approximations were used for the calculations. The determination of the rotor resistance for the individual harmonics was performed based on the measured short-circuit resistance and the proposed models 1–3 for the increase of stator and rotor resistance with frequency.
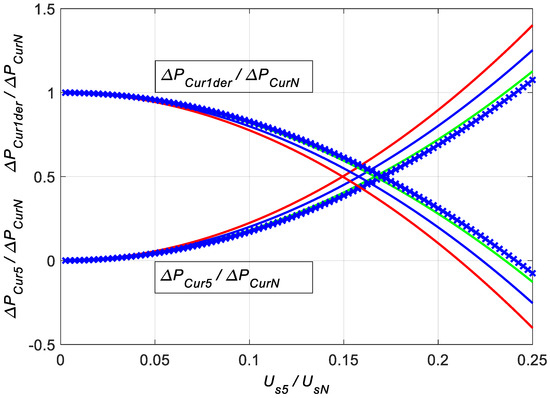
Figure 3.
The sum of rotor load power losses from higher harmonics (i.e., 5th only) and admissible power losses in the rotor from the fundamental harmonic, as a function of the RMS value of the 5th harmonic of the supply voltage. Blue line—model 1, green—model 2, red—model 3, blue line with x symbol—based on Formulas (29)–(32).
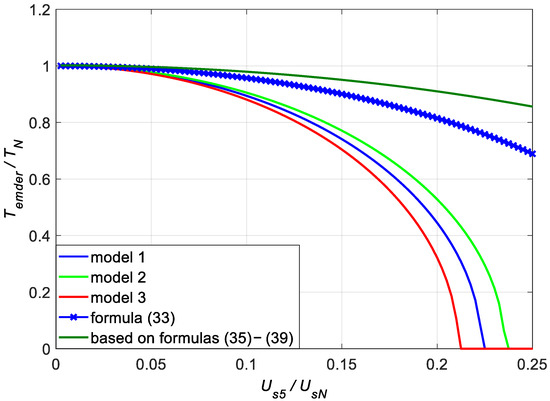
Figure 4.
Derating torque of the motor as a function of the RMS value of the 5th harmonic of the supply voltage.
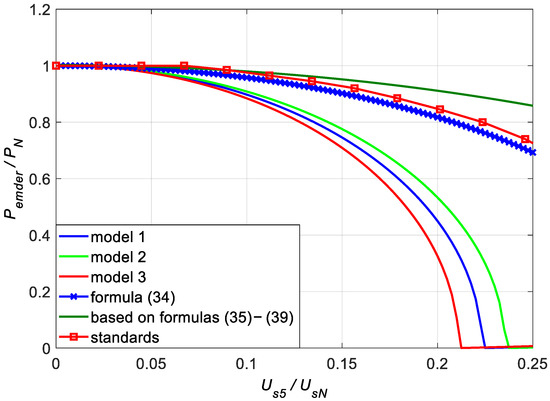
Figure 5.
Derating power of the motor as a function of the RMS value of the 5th harmonic of the supply voltage.
The paper presents calculations for all models and for the fundamental and fifth harmonic of the voltage supplying the motor. The fifth harmonic was varied from 0 to 25%, with the fundamental harmonic equal to the rated voltage of the motor (rated voltage is 100%). The value of the HVF then varied in the range from 0 to 11.2%. Figure 3 shows the sum of rotor load power losses from higher harmonics (i.e., 5th only) as a function of the RMS value of the 5th voltage harmonic referenced to the rated voltage. This sum determines the value of the admissible power losses in the rotor from the fundamental harmonic according to (6), also shown in Figure 3. This value determines the admissible motor load torque according to (4), for various models of power losses in the rotor cage—Figure 4. Figure 5 shows the admissible motor load power according to (5) as a function of the 5th voltage harmonic, also for all models of power losses in the rotor cage.
For comparison, Figure 3, Figure 4 and Figure 5 show the characteristics determined based on [3] and HVF. For the model of power losses in the motor based on the HVF factor, the expressions for the admissible torque and motor load power were derived, based on the formulas from [3]—derivations are in Appendix A. Assuming the linear variation of the motor slip with the load torque according to (3) and the frequency-independent value of the stator phase resistance according to [3], the following can be written:
Furthermore, for comparative purposes, Figure 4 and Figure 5 show the characteristics determined based on limiting the RMS value of the stator current at the level of its rated value:
Formulas (4) and (5) were used to determine the admissible torque and load power. The load power losses in the rotor cage for the first harmonic were determined as:
The current of equivalent rotor phase was determined according to the formulas:
In the expression (38), for calculations with us1 = 1 was arbitrarily assumed the rated cosφ. Undoubtedly, the cosφ of the motor changes with the RMS value of the first harmonic stator supply voltage and the value of the calculated admissible load torque. The admissible motor load power was calculated by the expression (5), by multiplying the admissible load torque by the rotor speed. It was calculated for us1= 1 based on the motor slip from the Formula (3). The RMS values of stator harmonic currents Ish for voltages Ush were calculated based on the results of motor short-circuit current measurements:
Furthermore, for comparative purposes, Figure 5 shows the characteristics present in standards [4,5], presenting the admissible motor load power as a function of the HVF value. It is very similar to the characteristic according to (34).
3.5. Harmonic Losses Factor
Following the example HVF from [3], a new factor was introduced on which the load losses of the rotor from higher harmonics depend squarely. In [3], the load losses from higher harmonics depend on the value of the HVF squarely for the stator and rotor together. To distinguish a new factor from the HVF this factor was called the Harmonic Losses Factor (HLF). Its formula depends on the model of load power losses of the rotor:
- For model 1:The product 3·Rr1′·IsN2 is the short-circuit power loss in the rotor when it is supplied with a definitional short-circuit voltage Uk1 (Ik1 = IsN) with rated frequency. The short-circuit cosφ of the motor is then cosφk1. Expression (42) can be written using the rated power losses in the rotor winding, which is more useful as a reference power than the product 3·Rr1′·IsN2, due to their presence in expressions (4)–(6):By defining the HLF as:we can write an expression for the rotor load losses due to higher harmonics:The HLF formula may be reduced to the HVF formula for the assumptions made in [3]. These are: (a) ar = 0 and a = 0 (then the variability of the resistances with the harmonic number is power function only), (b) cosφk1 = 0 (then the limitation of higher harmonic currents are the motor short-circuit reactances for these harmonics, without resistances), (c) x = 0.6, y = 0.8. In the expression for the total motor load losses from higher harmonics derived in [3], there is a numerical factor in front of the square of its value, which is 35 (42 in Formulas (31) and (A1) due to a different reference power—ΔPCuN). Its role in (45) is fulfilled by the following expression:For the tested motor C = 166.
- For model 2:In model 2, the following equality is fulfilled: ar = as = a, which simplifies expression (44) to the form:and expression (45) is fulfilled to the form:The disadvantage of model 2 is the incorrect reproduction of the resistance value RrN’. It has a negative impact on the accuracy of determining the coefficient C. For the tested machine C = 139, so the power losses in the rotor cage from higher harmonics are underestimated. This disadvantage can be corrected, inconsistently about model 2 by substituting in formula (48) instead of the expression ((1 − a)·sNx + a), the ratio of the resistance RrN’ (according to (18)) to the resistance Rr1′ (according to (17)).
- For model 3:In model 3, the coefficient ar in Formulas (44) and (45) was replaced by the coefficient ar’ as in Formula (28):The expression (45) takes the form:The disadvantage of model 3 is the incorrect reproduction of the resistance value RrN’. It has a negative impact on the accuracy of determining the coefficient C. For the tested machine C = 216, so the power losses in the rotor cage from higher harmonics are overestimated. This disadvantage can be corrected, inconsistently about model 3 by substituting in Formula (50) instead of the expression ((1 − ar’)·sNx + ar’), the ratio of the resistance RrN’ (according to (18)) to the resistance Rr1′ (according to (17)).
For the tested motor, for all three models, the HLF values as a function of the HVF values are shown in Figure 6, to show differences in HLF and HVF values for the same Us5 values.
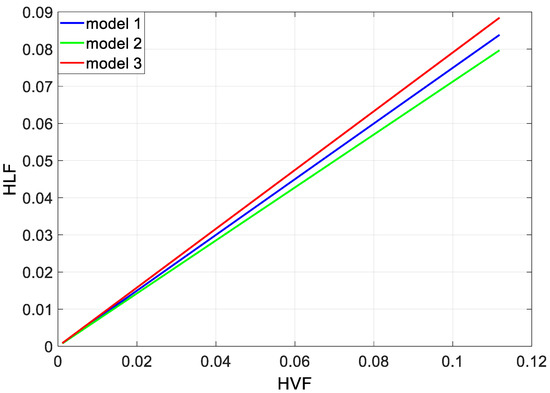
Figure 6.
The HLF values as a function of the HVF values for the tested motor, for Us5 = 0 ÷ 0.25UsN.
3.6. Determination of the DF Curves Based on the HLFs
Based on the HLF defined by Formula (44) and power losses in the rotor cage from higher harmonics according to (45), expression (6) can be written for model 1:
Based on expression (51), expression (4) can be written for model 1:
where:
Analogous to Formulas (52) and (53), formulas for model 2 are based on HLF according to (47) and have the following form:
The same formulas for model 3 are based on HLF according to (49) and have the following form:
For all three models, the formula for the admissible motor load power is the same, based on Formula (5):
Figure 7 shows the admissible motor load torques according to (4), which are shown in Figure 4, and the admissible motor load torques according to (52), (54), (56). These were calculated in two variants: exactly according to these formulas and by replacing the approximation expressions present in the coefficient C before HLF2 according to (53), (55), (57) with the resistance ratio RrN’/Rr1′. This substitution approximates the curves according to (54) and (56) to the curves according to (4). For the curve according to (52), this substitution does not cause any changes, according to identity (53). There are significant differences between the curves according to (4) and the curves drawn with dashed lines. For example, for us5 = 0.2 these differences are: for the curve according to (52) 0.06TN, for the curve according to (54) 0.042TN and for the curve according to (56) 0.09TN. These differences increase with a decrease in the admissible motor load torque. They result from the use of the measured values of short-circuit powers and resistances (Pkh, Rkh) for calculations according to (4), and the approximated values of these powers and resistances for the curves drawn with solid and dashed lines. Admissible torque calculated with HLF is always overestimated in relation to its value based on (4). Paradoxically, this results from the choice of the coefficients a, x of the approximation of increase in the short-circuit resistance of the motor with the frequency of the short-circuit current, so that the calculated short-circuit active power is never smaller than that measured for each frequency. This approximation formula is in the denominator of each HLF expression (Formulas (44), (47), (49)), which underestimates its value and increases the admissible motor load torque according to (52), (54), (56).
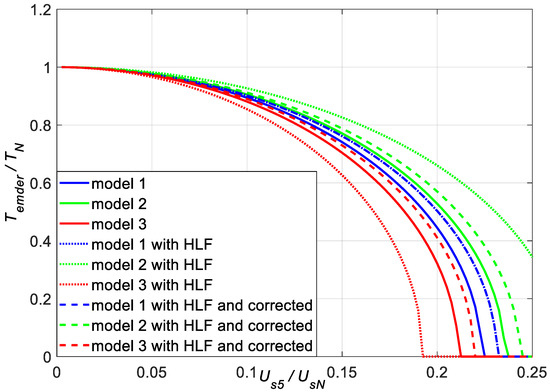
Figure 7.
Derating torque of the motor as a function of the RMS value of the 5th harmonic of the supply voltage—comparison of curves from Figure 4 with curves obtained based on HLF.
Figure 8 shows the admissible motor load powers, calculated based on the torques from Figure 7 and the Formula (58).
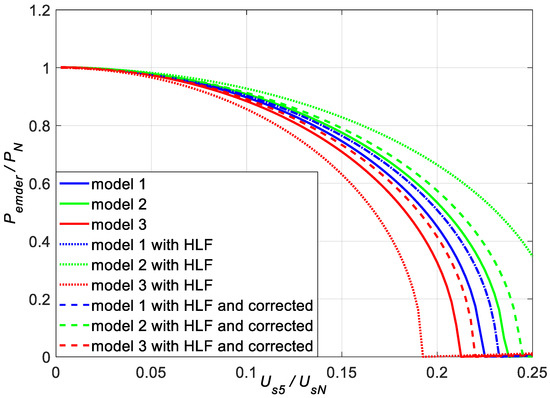
Figure 8.
Derating power of the motor as a function of the RMS value of the 5th harmonic of the supply voltage—comparison of curves from Figure 5 with curves obtained based on HLF.
Table 3 compares the calculated DF values with the values from selected papers. For small values of HVF and HLF, DF values are similar. Bigger differences appear for higher values of HVF and HLF. The large range of DF values in the column headed DF by [12] of Table 3 apply to motors with very different rated powers—from 7.5 kW to 400 kW. Smaller DF values apply to a 400 kW motor, bigger values apply to a 7.5 kW motor.

Table 3.
Comparison of DF values.
4. Discussion
- The full range of possible rotor resistance changes with frequency was examined: from the variant where the full variability of the motor short-circuit resistance with frequency was assigned to the rotor resistance (model 3), through the variant where the variability of the rotor resistance was such that the rated value of this resistance was correctly reproduced (model 1), to the variant of identical variability of the stator and rotor resistance (model 2). Models 2 and 3 describe extreme variants because, in reality, it is not possible for the stator resistance to increase with frequency as quickly as the rotor resistance, and it is impossible for it to remain constant.
- In model 1, the determination of the coefficients as and ar was based on three resistance values: Rs1, Rr1′ = Rk1 − Rs1, RrN’. This guarantees the correct determination of the RrN’ resistance value from the approximation formula, and thus the correct determination of the rated power losses in the rotor. However, the variation of the rotor resistance with frequency was determined based on two values of this resistance, for the frequency fN (h = 1) and sN ∙ fN (h = sN), which are not far apart in the frequency domain. It reduces the reliability of determining the values of the coefficients as and ar in terms of the correct determination of the Rrh’ value for higher rotating harmonics.
- For all three loss models, the curves of the admissible load torque and power according to (4) and (5) had a similar shape. However, from an operational point of view, the values of admissible torque and power were significantly different. For example, for us5 = 0.2, the differences between the values of the admissible load torque were +0.083TN and −0.123TN, relative to the curve of model 1. These differences decreased with the increase of the admissible torque—for us5 = 0.15, the corresponding differences were +0.03TN and −0.037TN. These were smaller differences than expected, but for operational reasons are too big to conclude that the choice of the load losses model is of no practical importance.
- The curves of the admissible motor torque and admissible power, described by Formulas (4) and (5), and models of load losses, differ significantly from the curves described by Formulas (33) and (34). The main reason for these differences is that the model of load losses presented in [3] applies to the total load losses in the motor. This model does not make it possible to separate rotor losses from the total load losses. It makes it impossible to link the admissible motor load torque with rotor losses. The derivation of the expression HVF and the expression for the total load losses of the motor supplied with a distorted voltage may be questionable. It is not understandable why the highly saturated value of the short-circuit reactance of the motor, measurement as the input reactance of the motor during its start-up, was used to determine the harmonic currents. The results of the calculations apply to the states of the motor with small currents not exceeding the rated current. During the start of the motor, the current is big—in [3] a phase current equal to 6.5IsN was assumed. Neglecting the short-circuit resistance in the expression for the harmonic current Ish seems to be an oversimplification and an unnecessary simplification. At such high frequencies as the frequencies of the rotor currents from higher rotating harmonics, the resistance of the cage bars can be very high, and consequently the value of the model parameter Rrh’ can be comparable to the value of the short-circuit reactance Xkh, and even more so with its saturated start-up value. In [3], the rated rotor resistance RrN’ and the short-circuit resistance of rotor Rr1′ were not differentiated. The model assumed powers of x = 0.6 and y = 0.8 for all squirrel-cage motors, which was not exact for the tested motor (Table 2). The consequence of all these assumptions and simplifications is that the admissible torque and power were much greater than those based on the losses models proposed in this paper. This is even though the curves of power losses in the rotor presented in Figure 3 and Figure 6 are not much different from the curves based on loss models described by Formulas (23), (26), and (28). This may raise doubts as to the correctness of the derivation of Formulas (33) and (34), but an indirect confirmation of their correctness is the compliance of the curve of the admissible motor load power according to (34) with the curve given in [4]—Figure 5. The admissible power, according to [4] is greater than according to expression (34) consistently by approximately 2.5% of the rated motor power for each magnitude of the voltage of the 5th harmonic us5 (at us1 = 1).
- The curves of the admissible torque and motor load power based on Formulas (4) and (5) and power loss models described by Formulas (23), (26), (28) also significantly differ from the curves based on Formulas (4) and (5) with stator current RMS value limit (35). This is because equation (35) does not account for the increase in the short-circuit resistance of the motor with the increase in the frequency of its current. The short-circuit resistance of the tested motor increases by 61% when the frequency increases from the rated (50 Hz) to five times the rated (250 Hz). Assuming that the increase in the rotor resistance with the frequency of its currents is the same as the stator resistance (ar = as = a, model 2), the rotor resistance for the 5th harmonic Rr5′ in relation to its rated value RrN’ increases by 205%. The increase in load power losses in the rotor associated with the increase in resistance is not included in the Formula (35). This explains the very overestimated values of the admissible torque and load power.
- The curves of the admissible torque and motor load power based on Formulas (52), (54), (56), and (58) theoretically should be identical to the curves according to (4) and (5), for the same models of losses. The differences result from the use of approximation formulas three or two times in Formulas (52), (54), and (56), which resulted in the summation of approximation errors. This problem does not occur when Formulas (4) and (5) are used directly; then, the approximation formula is used only once when determining the value of the expression (7).
- Assuming the identity RrN’ = Rr1′ and IrN’ = IsN (as in [3]) is a source of large errors in the value of the coefficient C present before the HLF square in Formula (45). After making these assumptions, the coefficient C reduces to 1/uk12, and its value for the tested machine is 60. The actual value is 166. It would be equal to 42, as in (33) and (34), if the short-circuit voltage of the tested machine was 15.5% instead of the real 13%. In the tested motor, Rr1′/RrN’ = 1.89, IsN/IrN’ = 1.21.
- The paper assumes that all additional load losses of the stator and rotor turn into heat in the windings of the machine, limiting the thermally admissible power losses for the fundamental harmonic of currents. This is a pessimistic assumption—some of these losses are outside the windings, not affecting the temperature of the windings or affecting it in part only. This problem requires further research. However, it was verified by calculations that for the tested motor, the rotor load losses from the 5th harmonic according to model 1 would have to be included in the calculations of the admissible torque and load power according to Formulas (4)–(7) only in 42%, so that these curves will be agreed with the according to Formulas (33) and (34) curves.
5. Conclusions
- The derating power curves given in [4,5] as a function of the HVF value for the tested motor are incorrect. For all three models of losses, the curves of the admissible motor power were definitely below the curves from [4,5]. Based on the derivation in Appendix A, it can be presumed that they are based on the considerations presented in [3]. The simplifications and inconsistencies result in a significant overestimation of the admissible torque and power.
- The accuracy of determining the variation of the rotor resistance Rrh’ with frequency has a key impact on the accuracy of determining the thermally admissible load torque of the induction motor. The key to determining DF is the knowledge of power losses from higher harmonics of the supply in the rotor, and not in the whole motor overall.
- The introduced HLF according to (44) differs from the well-known HVF by its generalization for real conditions when cosφk1 > 0, a > 0, ar > 0, x ≠ 0.6, and y ≠ 0.8. For cosφk1 = 0, a = 0, ar = 0, and for x = 0.6, y = 0.8, the HLF formula is reduced to the HVF formula.
- The formulation of the HLF expression carries with it the duplication of mathematical approximation errors, which generates errors in determining admissible torque and power. These values are more accurately determined based on Formulas (4)–(7) directly, preferably with an approximation of rotor resistance variability with frequency according to model 1. This leads to the conclusion that the curves of the admissible motor power should be determined not as a function of HLF or HVF, but as a function of the sum of the rotor winding power losses from higher harmonics, according to (7).
- The curves of the admissible torque and the admissible power are not different.
- There is no reason why the variation of rotor leakage reactance and resistance with frequency should be the same in different induction motors. This variability is determined by the skin effect in the bars of the rotor cage. Squirrel-cage motors have cage bars with cross-sections of different shapes. Therefore, the skin effect occurs in them with different intensities. This thesis is confirmed by the results of simulations in [12], where the curves DF(HVF) were significantly different for different motors. There it was found that curve DF(HVF) also depended on the number of pole pairs of the machine, its size and rated power, its design, and efficiency class.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article. The data presented in this study are available on request, in a numerical form.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
Based on [3], we can write for us1 = 1:
where: ΔPCuh—load power losses in the motor supplied with a distorted voltage, caused by harmonic h of the motor power supply, ΔPCuN—load rated power losses in the motor, ΔPCu1— load power losses in the motor supplied with a distorted voltage, caused by the fundamental harmonic of the power supply.
In [3], it was assumed that the total load losses should not exceed the rated load losses of the motor for thermal reasons. Based on equation (A2) it can be written as:
where: ΔPCu1der—thermally admissible value of load power losses in the motor for the fundamental harmonic of the motor power supply.
Based on the expression (A3), the expression for the admissible load losses in the motor for the fundamental harmonic of the motor power supply can be obtained:
Expression (A4) is the starting point for determining the thermally admissible torque and power. To determine the admissible torque, it was assumed that for the slips varies from s = 0 to s = sN, the slip increases linearly with increasing load torque, according to expression (3). Using (3), the individual components of the load power losses ΔPCu1 can be represented as (neglecting the magnetizing current and power losses in the motor core, as in [3]):
where: Radd1—resistance representing the additional power losses in the motor for the fundamental harmonic of the power supply.
Unfortunately, in [3], it is not clear which rotor resistance should be used in expressions (A6) and (A7): Rr1′ or RrN’. The second variant was chosen because it is closer to reality. The expression for the thermally admissible value of the motor load torque is obtained by inserting the expressions (A4)–(A7) into (A8):
The quotient of resistances in the denominator of expression (A9) represents the ratio of the total load losses to the rotor load losses in the rated state of the motor:
By inserting (A10) into (A9) and dividing (A9) by the rated torque, the last form of the expression for the admissible relative value of the motor load torque as a function of the HVF was obtained:
The thermally admissible load power of the motor was calculated as the product of the admissible load torque according to (A11) and the rotational speed of the machine, expressed by the slip s according to (3):
By inserting the expression (A11) into the expression (A12) and dividing it by the rated motor power, the expression for the relative motor load power as a function of HVF and rated slip sN was obtained:
The dependence of the admissible motor power on the rated slip is practically negligible because the difference ((1 − sN) in (A13) is close to 1 (sN is always close to 0). Assuming that (1 −sN) ≈ 1 and sN ≈ 0 we get expressions identical to (A11). This is due to the low variability of the motor speed as a function of the load torque. The variability of motor load power is a function only the variability of the load torque, due to changes in rotational speed of several percent.
References
- Mboving, C.S.A.; Hanzelka, Z. Different approaches for designing the passive power filters. In Proceedings of theXII International School on Nonsinusoidal Currents and Compensation, Łagów, Poland, 15–18 June 2015. [Google Scholar]
- Drabek, T. Operation of an induction motor supplied by voltage containing subharmonics. Sci. Technol. Innov. 2017, 1, 27–34. [Google Scholar] [CrossRef]
- Cummings, P.G. Estimating the effect of system harmonics on losses and temperature rise of squirrel-cage motors. IEEE Trans. Ind. Appl. 1986, 6, 1121–1126. [Google Scholar] [CrossRef]
- IEC 60034-17; Rotating Electrical Machines—Part 17: Cage Induction Motors When Fed from Converters—Application Guide. International Electrotechnical Commission: Geneva, Switzerland, 2022.
- NEMA. MG1 Motors and Generators; National Electrical Manufacturers Association: Arlington, VA, USA, 2019. [Google Scholar]
- Fuchs, E.F.; Roesler, D.J.; Kovacs, K.P. Aging of Electrical Appliances due to Harmonics of the Power System’s Voltage. IEEE Trans. Power Deliv. 1986, 3, 301–307. [Google Scholar] [CrossRef]
- De Abreu, J.P.G.; Emanuel, A.E. Induction motors loss of life due to voltage imbalance and harmonics: A preliminary study. In Proceedings of the Ninth International Conference on Harmonics and Quality of Power, Orlando, FL, USA, 1–4 October 2000; pp. 75–80. [Google Scholar]
- Sen, P.K.; Landa, H.A. Derating of Induction Motors Due to Waveform Distortion. IEEE Trans. Ind. Appl. 1990, 26, 1102–1107. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Lee, W.-J. Effects of Nonsinusoidal Voltage on theOperation Performance of a Three-phase Induction Motor. IEEE Trans. Energy Convers. 1999, 14, 193–201. [Google Scholar]
- Jalilian, A.; Gosbell, V.J.; Perera, B.S.P. Performance of a 7.5 kW induction motor under harmonically distorted supply condition. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Halifax, NS, Canada, 7–10 May 2000; pp. 355–359. [Google Scholar]
- Bradley, K.J.; Cao, W.; Arellano-Padilla, J. Evaluation of Stray Load Loss in Induction Motors with a Comparison of Input–Output and Calorimetric Methods. IEEE Trans. Energy Convers. 2006, 21, 682–689. [Google Scholar] [CrossRef]
- Ferreira, F.J.T.E.; De Almeida, A.T.; Deprez, W.; Belmans, R.; Baoming, G. Impact of Steady-State Voltage Supply Anomalies on Three-Phase Squirrel-Cage Induction Motors. In Proceedings of the International Aegean Conference on Electrical Machines and Power Electronics, Bodrum, Turkey, 10–12 September 2007; pp. 1–9. [Google Scholar]
- Ferreira, F.J.T.E.; De Almeida, A.T.; Baoming, G. Three-Phase Induction Motor Simulation Model Based on a Multifrequency Per Phase Equivalent Circuit Considering Stator Winding MMF Spatial Harmonics and Thermal Parameters. In Proceedings of the XVII International Conference on Electric Machines (ICEM), Chania (Crete Island), Greece, 2–5 September 2006. [Google Scholar]
- Debruyne, C.; Desmet, J.; Derammelaere, S.; Vandevelde, L. Derating Factors for Direct Online Induction Machines when supplied with voltage harmonics: A critical view. In Proceedings of the IEEE International Electric Machines & Drives Conference, Niagara Falls, ON, Canada, 15–18 May 2011; pp. 1048–1052. [Google Scholar]
- Quispe, E.; Gonzalez, G.; Aguado, J. Influence of Unbalanced and Waveform Voltage on the Performance Characteristics of Three-Phase Induction Motors. Renew. Energy Power Qual. J. 2004, 1, 279. [Google Scholar]
- Frank, S.; Lee, K.; Sen, P.K.; Polese, L.G.; Alahmad, M.; Waters, C. Reevaluation of Induction Motor Loss Models for Conventional and Harmonic Power Flow. In Proceedings of theNorth American Power Symposium, Champaign, IL, USA, 9–11 September 2012. [Google Scholar]
- De Buck, F.G.G.; Giustelinck, P.; De Backer, D. A simple but reliable loss model for inverter-supplied induction motors. IEEE Trans. Ind. Appl. 1984, IA-20, 190–202. [Google Scholar] [CrossRef]
- Debruyne, C.; Corne, B.; Sergeant, P.; Desmet, J.; Vandevelde, L. Evaluation of the Additional Loss due to Supply Voltage Distortion in relation to Induction Motor Efficiency Rating. In Proceedings of the IEEE International Electric Machines & Drives Conference, Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 1881–1887. [Google Scholar]
- De Lima, E.C.; De Carvalho Filho, J.M.; Souza de Sá, J. Diagnosis of Induction Motors Operating Under Distorted and Unbalanced Voltages. In Proceedings of the 17th International Conference on Harmonics and Quality of Power, Belo Horizonte, Brazil, 16–19 October 2016; pp. 786–791. [Google Scholar]
- Donolo, P.D.; Pezzani, C.M.; Bossio, G.R.; De Angelo, C.H.; Donolo, M.A. Derating of Induction Motors Due to Power Quality Issues Considering the Motor Efficiency Class. IEEE Trans. Ind. Appl. 2020, 56, 961–968. [Google Scholar] [CrossRef]
- Lerch, T.; Rad, M. Influence of higher harmonics on losses in induction machines. Tech. Trans. Electr. Eng. 2016, 113, 13–24. [Google Scholar]
- Krzyściak, K. Determination of the Load Capacity of a Squirrel-Cage Induction Motor Supplied with Distorted Voltage. Master’s Thesis, AGH University of Science and Technology, Kraków, Polska, February 2022. [Google Scholar]
- Deraz, S.A.; Azazi, H.Z. Impact of Distorted Voltage on Three-Phase Induction Motor Performance. In Proceedings of the Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 857–863. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).