Abstract
Power distribution systems (PDS) comprise essential electrical components and infrastructure that facilitate the delivery of electrical energy from a power transmission system to end users. Typically, the topology of distribution systems is radial, so that power goes from the substations to end users through main lines or feeders. However, the expansion of new feeders to accommodate new users and ever-growing energy demand have led to higher energy losses and deterioration of the voltage profile. To address these challenges, several solutions have been proposed, including the selection of optimal conductors, allocation of voltage regulators, utilization of capacitor banks, implementation of distributed generation, and optimal reconfiguration. Although reconfiguring the network is the most cost-effective approach, this solution might not be sufficient to completely minimize technical losses and improve system performance. This paper presents a novel approach that combines optimal distribution network reconfiguration (ODNR) with optimal conductor selection (OCS) to minimize power losses and enhance the voltage profiles of PDS. The key contribution lies in the integration of the ODNR and OCS into a single MILP problem, ensuring the attainment of globally optimal solutions. The proposed model was tested with benchmark 33-, 69-, and 85-bus test systems. The results allowed us to conclude that the combined effect of ODNR and OCS presents better results than when any of these approaches are applied either separately or sequentially.
1. Introduction
In today’s electric power industry, the efficient and reliable operation of PDS has become a predominant concern. The increasing demand for electricity, coupled with the integration of renewable energy sources and the advent of smart grid technologies, increases the complexity of PDS planning and operation. To address the challenges posed by this complexity, researchers are turning their attention to advanced optimization techniques. This paper explores a critical aspect of PDS optimization—the seamless integration of ODNR and OCS through the application of mixed-integer linear programming (MILP). By harnessing the potential of MILP, this study aims to improve voltage regulation and mitigating power losses in PDS.
OCS plays an important role in ensuring the reliable and efficient operation of PDS. Conductors distribute electrical energy from distribution substations to final customers through principal feeders and laterals. With the increasing demand for electricity and the integration of renewable energy sources, the need for OCS becomes crucial. The choice of conductors impacts various aspects of PDS, including power losses, voltage regulation, and overall system reliability. An inefficient conductor selection may lead to elevated energy losses, voltage drop issues, and increased operational costs. Conversely, OCS results in reduced power losses, improved voltage profiles, and enhanced system longevity.
The primary objective of OCS is to replace the current conductors in a feeder with different types of conductors. This replacement aims to decrease active power losses, enhance the capacity of circuits, and raise voltage levels. The OCS is a highly complex problem, which can be represented as a mixed integer nonlinear programming (MINLP) problem. Researchers have employed exact techniques as well as heuristic and metaheuristic approaches to tackle this optimization problem.
Heuristics are search techniques that prioritize speed over optimality and are often used when dealing with complex or computationally challenging tasks [1,2]. Although they may not always guarantee the global optimal solution, heuristic and metaheuristic techniques are valuable tools in non-convex optimization and decision-making processes. In the context of OCS, researchers have proposed various heuristic-based approaches. For instance, in [3] the authors presented a methodology combining an economically driven current density-based approach with a heuristic approach for optimizing the conductor selection in radial PDS. In this case, a branching feeder approach without uniform load distribution was used to approximate the real conditions of most PDS. Another study [4] proposed a branch-wise minimization technique for selecting the optimum size of conductors in radial PDS. The conductors selected by the proposed approach maximized the total savings in costs, including conductor material and energy losses while maintaining acceptable voltage profiles. In [5], the authors considered financial and engineering factors as key aspects of OCS. In this case, operating and capital costs were considered bearing in mind a set of conductors with the most economic cost characteristics and enough thermal capacity to meet high-demand scenarios. In [6], a general methodology for optimal conductor size selection in PDS was presented aiming to minimize the total conductor and power loss cost. The model includes diversity in load peaks, load factors, cost of power, load increments, and cost of energy in the decision-making process.
A comparative study between an analytical method and a genetic algorithm (GA) to solve the OCS problem was carried out in [7]. In this case, the analytical approach was based on consecutive load flows. A two-phase methodology employing the branch-wise minimization technique was proposed in [8] to solve OCS in radial PDS. In [9], the authors presented an analytical approach comparing power flow results for distinct ACSR conductors. It is important to note that heuristic optimization techniques cannot ensure a solution that is globally optimal; instead, they offer a proper estimation. These methods may encounter locally optimal solutions and can be computationally intensive, especially when dealing with large-scale problems involving numerous variables.
Metaheuristics have also gained significant popularity in solving the OCS problem. These approaches are inspired by natural and social phenomena such as evolutionary processes or swarm intelligence. In evolutionary and genetic algorithms, a population of potential solutions is evolved over generations through processes such as selection, crossover, and mutation. OCS has been solved through genetic algorithms (GAs) [7,10], adaptive genetic algorithm (AGA) [11], evolutionary strategies (ES) [12], differential evolution algorithm (DEA) [13], and discrete genetic algorithm (DGA) [14].
Particle swarm optimization (PSO) is a metaheuristic approach inspired by the social behavior of some organisms such as schools of fish and flocks of birds. The OCS has also been solved through PSO [15,16], selective particle swarm optimization (SPSO) [17], discrete particle swarm optimization (DPSO) [18] and salp swarm optimization (SSO) [19].
In harmony search algorithms (HSAs), a set of candidate solutions, labeled as harmonies, represent potential solutions to the optimization problem. The OCS problem was solved using HSA with a differential operator (HSDE) in [20]. Other metaheuristic approaches adapted for solving the OCS problem in PDS include crow search algorithm (CSA) [21], sine–cosine optimization algorithm (SCA) [22], Tabu search (TS) [23] and Newton’s metaheuristic algorithm (NMA) [24].
Even though metaheuristic approaches are suitable for solving complex optimization problems, they may not consistently reach the absolute global solution. Moreover, they often need significant adjustments to achieve acceptable results, and this can consume a significant amount of time and necessitate specialized knowledge.
Exact techniques have been employed to a lesser extent in solving the OCS problem. These techniques ensure convergence by utilizing existing optimization software. In the literature review, few research studies were found where exact techniques were employed for solving the OCS. Among these papers, one of them utilized a linear model. In the study conducted by the authors of [25], a MILP problem was proposed, accompanied by a heuristic approach to derive the Pareto front for the problem of optimal conductor sizing. The authors of [26] presented a MINLP model for the OCS problem, which was resolved utilizing the general algebraic modeling system (GAMS) with the aid of the DICOPT optimization solver. In [27], the authors developed an exact nonlinear model for the conductor selection, utilizing available MINLP solvers. Lastly, the authors of [28] proposed a MINLP formulation for OCS in DC radial PDS.
Planning strategies, such as reconfiguration, conductor selection, capacitor placement, and DG placement, are commonly studied separately. Nonetheless, the combination of two or more of these techniques may lead to a better-planned system. The problem of OCS has been integrated with capacitor placement in numerous research investigations, where the researchers employed metaheuristic approaches to direct the exploration procedure. However, from the review of existing literature, OCS has not been discussed in simultaneity with optimal distribution network reconfiguration (ODNR) so far.
ODNR is carried out by altering the topology of the distribution network, considering objectives such as minimizing power losses, improving voltage profile, and enhancing network reliability. ODNR is executed by opening and closing tie and sectionalizing switches, respectively, [29]. Due to the nature of its decision variables and constraints, ODNR can be classified as a mixed-integer nonlinear (MINL) optimization problem, usually requiring the aid of metaheuristic techniques for its solution. Early reconfiguration studies were limited to small-sized PDS [30]. This is due to the fact that ODNR is a complex optimization problem that involves both discrete and continuous decision variables. Furthermore, ensuring a radial topology is not a trivial task [31]. Basically, two optimization paradigms are applied to solve the ODNR problem: mathematical programming methods and metaheuristic techniques.
In [32], the authors proposed an optimal power flow and sensitivity analysis approach to solve the ODNR problem, aiming to minimize active power losses. A heuristic approach was implemented by closing all sectionalizing switches and then determining the ones to be reopened to avoid loops in the system. PSO was implemented in [33,34,35] to tackle the ODNR problem to minimize power losses. In [36,37,38,39,40,41], several variants of GAs were tested to solve the ODNR problem. In this case, network topologies were represented by binary strings representing the open or closed states of the switches. Then, other topologies were created through both the selection and mutation stages of the GA. In each iteration, the radial condition of the new solutions was verified. In [42,43], the authors solved the ODNR problem through firefly optimization (FO). In this case, ref. [42] considered both ODNR and optimal DG sizing, whereas [43] did not optimize the size of DG in the network; nonetheless, a search space-reducing strategy is implemented to accelerate convergence. The authors of [44,45] proposed an HSA to solve the ODNR problem for minimizing power losses. The proposed approach in [45] also includes island detection to enforce radiality. The TS metaheuristic technique was also applied in [46,47] to solve the ODNR problem. In [46], the authors considered a mutation mechanism to escape from local optima, whereas [47] implemented a random mechanism with the same purpose.
In [48], the authors developed a hybrid data-driven and model-based distribution network reconfiguration approach. A hierarchical network recovery process was implemented to speed up the process. ODNR can also be implemented to enhance network reliability. In [49], a column and constraint generation algorithm was proposed to minimize load curtailments under failures of lines or generators. In [50], the authors presented a reinforcement learning approach that resorts to ODNR to minimize load curtailment. The distribution system is modeled as a graph and the ODNR is determined by searching for a spanning tree that presents minimum curtailed power.
Multi-objective approaches have also been implemented in the reconfiguration problem. In [51], the authors developed an NSGAII approach that minimizes both active power losses and voltage offset of distribution networks. In [52], a multi-objective PSO was proposed to minimize total active power losses and maximize the absorption of renewable DG through a time-varying ODNR. In [53], the authors carried out ODNR with four objectives, namely, power loss minimization, voltage profile improvement, network reliability improvement, and operation costs minimization. The literature on metaheuristics applied to solve the ODNR is wide and varied, and a comparative study on this subject can be consulted in [54].
Apart from heuristic and metaheuristic techniques, some mathematical approaches have also been explored to tackle the ODNR problem. In [55], the authors presented a mathematical model of path connectivity for ODNR. This model is based on the closed-loop design and open-loop operation of DPS. In [56], the authors solve the ODNR problem bearing in mind the power loss minimization and the improvement of reliability. The epsilon-constrained method is used, and the proposed mathematical model is then solved through the algebraic modeling systems (GAMS) software. In [57], a mixed-integer two-stage formulation is proposed to solve the ODNR for minimizing power losses. The master–slave methodology was modeled through a decomposition algorithm in AMPL and subsequently resolved with the utilization of CPLEX.
In DPSs that feature fairly loaded feeders and poor voltage profiles, ODNR alone may not be enough to minimize power losses. Furthermore, as the size and type of conductor for each feeder segment are chosen based on the current carrying capacity of the feeder configuration, and ODNR affects the system operational conditions, simultaneous ODNR and OCS could lead to low-cost planning of PDS; nonetheless, this approach has not been reported in the specialized literature Therefore, the main contribution of this paper lies in the simultaneous formulation and resolution of ODNR and OCS in PDS; furthermore, the proposed MILP model guarantees the globally optimal solution. Finally, the proposed model is suitable for applications in real-size distribution systems through commercially available software. Although a specific table of conductors was used for the test and results, the model allows the use of any set of candidate conductors for OCS.
The remainder of this paper is structured as follows: In Section 5, a nonlinear mathematical framework is presented to tackle the combined ODNR and OCS. Elaboration on the linearization procedures employed to transform the initial model into a MILP problem is provided in Section 3. The outcomes of implementing the suggested model on various benchmark test systems are shown in Section 4. Lastly, the conclusions drawn from this study are presented in Section 5.
2. Nonlinear Mathematical Model for the Integrated ODNR and OCS
This section presents the initial nonlinear mathematical model for the integration of ODNR and OCS in PDS. This initial model presents integer and continuous variables; nonetheless, there are some variable multiplications that will be later linearized to recast this initial approach into a MILP model.
In [58], starting from a nonlinear model of the power flow in PDS, the authors propose and validate a linear model of it. In this case, a comparative analysis was conducted between a linear version of the power flow and the nonlinear power flow applied to seven distribution test systems. The results revealed that the linear model had a maximum error of 0.16%, demonstrating that this model accurately solves the load flow. The linear model proposed by the authors in [58] is then adapted to solve the ODNR problem.
On the other hand, in [59] a MILP for the OCS and the optimal capacitor placement in PDS is presented by the same authors. In this case, the linear power flow proposed in [58] is used for the optimal conductor selection. The models presented by the authors in [58,59] are modified and adapted in this paper to have a single MILP model that solves the OCS and ODNR problems jointly, separately or sequentially. The mathematical optimization model implemented in this paper is designed for radial EDNs and considers the following hypotheses: (i) the EDN is represented by a monophasic equivalent; (ii) Loads are represented as constant power injections; (iii) only an electric source (substation) is considered; (iv) active and reactive power losses in distribution lines are concentrated in their sending bus; and (v) the capacitive reactance of distribution lines is neglected.
2.1. Objective Function
The proposed objective function is formulated through Equation (1), comprising two components. The initial component aims to minimize the cost of annual energy loss. Here, Kp, Ke, T, and LF correspondingly stand for the annual demand cost averaged over time, energy expenses, the annual time in hours, and the system loss factor. Ωl signifies the collection of branches, whereas Ωc denotes the collection of available conductor types. It is important to note that the nonlinearity in the first term of the objective function arises from the multiplication of decision variables and , representing the selected conductor type c for installation in branch ij (a binary variable) and the square of the current magnitude in the same branch. The linearization of this product is detailed in a subsequent section of this paper. Furthermore, signifies the length of the conductor linked with branch ij, and represents the resistance of conductor type c (measured in kΩ/km).
The second term of the objective function aims at minimizing the annual conductor selection costs. In this case, CRF is the capital recovery factor related to the selection of a new conductor, and is the conductor cost of conductor type c.
2.2. Power Balance Constraints
Equation (2) expresses the balance of active power within every bus of the PDS. and denote the active power transmission in branches ki and ij, respectively. signifies the active power provided from the substation at bus i. represents the active power requirement at bus i. Lastly, Ωb denotes the collection of buses within the PDS.
Equation (3) signifies the equilibrium of reactive power within each bus of the PDS. and represent the reactive power flow in branches ki and ij, respectively. denotes the inductive reactance of branch ij related to conductor type c. is the reactive power provided from the substation at bus i. stands for the reactive power demand at bus i.
2.3. Voltage Drop in the Branches of the PDS
Equation (4) illustrates the voltage reduction within each branch of the PDS. In this context, voltage magnitudes are given in relation to the electrical characteristics of the branches and their load flow. Variables and represent the squared voltage magnitudes at buses i and j, respectively. is the square of the impedance of conductor type c, and is a continuous auxiliary variable used to enforce Equation (4); it may take different values depending on whether the circuit ij is open or closed.
2.4. Voltage and Current Limits
Equation (5) indicates the voltage magnitude limit at bus i. Note that and represent the upper and lower squared voltage magnitude limits at bus i, respectively.
Equation (6) represents the current magnitude limit of the branch ij, where is the upper limit of the square current in branch ij of the conductor type c; and are binary variables related to the power flow direction of the branch ij and are used in the ODNR problem. If any one of these variables is equal to one, the switch in the respective branch is closed; if both variables are zero, the circuit is open. is used to select the conductor type.
2.5. Apparent Power Constraint
The left side of Equation (7) is the linearization of times ; furthermore, the right side of this equation is the linearization of plus which are carried out as indicated in [58].
In Equation (7), Y is the number of linearization blocks, is the slope of the block of the power flow at circuit ij; and represent the values of the block of and , respectively.
Equations (8)–(12) are complementary expressions used in the linearization of the left-hand side of Equation (7). Equation (8) indicates the minimum and maximum limits of taking into account the discretization steps. In this case, is a binary variable used in the discretization of , ΔV is the discretization step, and S is the number of discretizations. Equation (9) represents the limit of the power discretization steps, where is the correction used in times . Equation (10) indicates the limits of , and Equations (11) and (12) represent the limits of the binary variable and its nature, respectively.
Equations (13)–(19) serve the purpose of linearizing the right-hand side of Equation (7). In this instance, and are applied to determine , and and are employed to determine , with denoting the upper limit for each load flow block on branch ij. Equation (19) enforces the non-negativity of auxiliary variables , , , and .
2.6. Constraints Associated with the ODNR
Equations (20) to (26) model the ODNR problem taking into account the OCS. The upper limits of auxiliary variables and are given by Equations (20) and (21), respectively. The reactive power flow limit in branch ij is given by Equation (22). Equation (23) indicates the limits of ; which is zero if the circuit ij is closed; otherwise, the value of is defined by Equation (23). Equation (24) defines the condition of radiality of the PDS, and N is the number of buses of the PDS. Equation (25) indicates that if there is power flow in branch ij, it must have only one direction. Therefore, if , it follows that and vice versa; otherwise, when and , the circuit is open (there is no power flow). Equation (26) denotes the binary nature of and .
2.7. Constraints Associated with the OCS
Equations (27) and (28) are used in the OCS problem, and define, respectively, the possible values of the variable and its binary nature.
The expressions given by Equations (29) and (30) are used to determine the input parameters of the objective function. In this case, the constant parameters presented in Equation (29) are taken from [8]. The system loss factor LF is calculated with the demand factor (DF), as indicated in Equation (29), whereas CRF is the capital recovery factor, which is calculated considering the interest rate (i) and the number of years (n) envisaged in the distribution planning, as indicated in Equation (30).
3. Integration of ODNR and OCS via Mixed Integer Linear Programming Model
Equations (1) to (28) represent a MINLP problem. The linearizations that allow recasting this model into a MILP problem are presented in this section. Equations (1) to (4) are nonlinear due to the multiplication of the variables . This product of a binary and continuous variable is labeled as . The process of linearizing this expression can be accomplished through the utilization of the big-M method (where M represents a suitably large value), exemplified in Equations (33) and (34).
The voltage drop in the branches of the PDS defined by Equation (4) is nonlinear due to the multiplications of and . These nonlinearities can be converted into linear forms using the big-M approach, as illustrated in Equations (35) through (38). In this case, the products and are labeled as new continuous variables and , respectively.
Equations (6) and (20) to (22) are nonlinear due to the multiplication of binary variables and . These multiplications are renamed using new binary variables labeled as and , respectively. The linearization of these expressions is indicated by Equations (39) to (44).
Equations (9) and (10) are nonlinear due to the multiplication of binary variables . This multiplication is renamed using the binary variable , and its linearization is performed as shown in Equations (45) to (47).
Following the linearizations presented above, the objective function (see Equation (1)) is reformulated as shown in Equation (48).
The voltage drops in branches (Equation (4)) are rewritten as follows:
4. Test and Results
The simultaneous implementation of ODNR and OCS was simulated using AMPL 4.23 and solved using the standard settings in CPLEX 22.1.1.0. The effectiveness of the proposed model is illustrated using 32-, 69-, and 83-bus test systems. Each of these test systems is evaluated under six distinct scenarios:
- Initial scenario (base case).
- Optimal conductor selection (only OCS).
- Optimal distribution network reconfiguration (only ODNR).
- ODNR and then OCS (sequential approach).
- OCS and then ODNR (sequential approach).
- Simultaneous OCS and ODNR.
Table 1 presents the conductor types used for all test systems, taken from [22], and Table 2 indicates the parameters adopted for the objective function, which are based on [8].

Table 1.
Available conductor types for all test systems.

Table 2.
Objective function parameters for all simulations.
There are several benchmark test systems used to evaluate the effectiveness of the ODNR problem. However, due to the nature of ODNR, these systems only provide data on the resistance and reactance of conductors. Crucial information such as the length of feeder sections and conductor costs is not specified, which is necessary to solve the OCS problem. To combine the ODNR and OCS problems, we use the information in Table 1, reported in [22]; although other conductor-type tables that exist in the specialized literature may also be used. The original conductors of the test systems were substituted with their counterparts from Table 1, while adjusting the distances between nodes to ensure similar results compared to those of the original systems. Following the conductor replacement, a power flow analysis was carried out to assess the active power losses and minimum voltage in the test systems.
Table 3 compares the original values of active power losses and minimum voltage magnitudes for each test system with respect to those obtained after updating the conductor types from Table 1. In both cases, the minimum voltage magnitudes were obtained at the same buses for the original test systems. The new conductor types used in the test systems are indicated in Appendix A. Notably, the errors with the new conductor data range from 0.03% to 3.58%, confirming the equivalence between the original and proposed system data.

Table 3.
Base case results of the test systems considering conductors of Table 1.
4.1. OCS and ODNR for the 33-Bus Test System
The 33-bus test system comprises 37 branches, 32 normally closed tie switches, and 5 initially open interconnection switches. The system operates at a nominal voltage of 12.66 kV and has a total demand of 3715 + j 2300 kVA. A power flow was computed to determine the initial state of the network. In the initial base case, the active power losses amount to 203.23 kW, and the minimum voltage magnitude is 0.9128 p.u. at bus 18. For reference, the voltage limits range from a minimum of 0.92 p.u. to a maximum of 1.00 p.u.
Table 4 displays the information of the base case as well as the solutions obtained for only OCS, only ODNR, sequential ODNR and then OCS, sequential OCS and then ODNR and simultaneous OCS and ODNR.

Table 4.
Proposed solutions for the 33-bus test system.
Based on the findings presented in Table 4, it is evident that the simultaneous implementation of OCS and ODNR provides the highest economic benefit of 47.8%. Individually, the ODNR yields an economic benefit of 17.18%, whereas the OCS achieves a benefit of 37.92%. Furthermore, when sequential strategies of the ODNR and then OCS or vice versa are implemented, the economic benefits are 44.14% and 41.74%, respectively. Note that the improvement of these strategies is superior with respect to any single strategy; nonetheless, they are lower than the one obtained with the simultaneous strategy.
In terms of technical losses, the simultaneous implementation of OCS and ODNR, once again, yields the highest reduction rate at 68.58%. Individually, ODNR and OCS result in loss reductions of 20.43% and 60.9%, respectively. Regarding the voltage profile, the initial scenario, referred to as the base case, presents a minimum voltage of 0.9128 p.u. The most substantial enhancement in the voltage profile was attained by implementing the simultaneous OCS and ODNR, contrasting with the base case. In this situation, there was a 5.47% increase in the minimum voltage.
It was then demonstrated that the simultaneous combination of the two optimization approaches, OCS and ODNR, leads to a more optimized system (with minimal losses and investment costs) than when any of them is solved either individually or sequentially.
Table 5 indicates the open switches used in the analyzed cases. It is important to highlight that the open switches in the ODNR-only scenario are distinct from those employed in the simultaneous OCS and ODNR case; nonetheless, they coincide with the sequential scenario of ODNR and then OCS. The reason for this disparity lies in the impact of the OCS on the most efficient reconfiguration strategy aimed at minimizing losses.

Table 5.
Open switches for the 33-bus test system.
Table 6 presents the conductor types selected for the base case (A), only OCS (B), sequential ODNR and then OCS (C) and simultaneous OCS and ODNR (D). Note that the solutions differ significantly due to the impact of the ODNR. As the system reconfiguration is optimized, there are changes in the OCS, and this leads to a decrease in the investment conductor cost (see Table 4).

Table 6.
Selected conductors for all simulations carried out for the 33-bus test system.
Figure 1 depicts the optimal solution for the simultaneous OCS and ODNR problem, where the conductor type of each branch is indicated in parenthesis in red, and the branch number is indicated in blue. Note that the solution involved the use of conductor types 20, 14, 13, 8, 6, 4, 3, 2, and 1. Larger capacity conductors were selected for branches located closer to the substation. Furthermore, Figure 1 also shows the specific switches that were opened to achieve the optimal reconfiguration of the system.
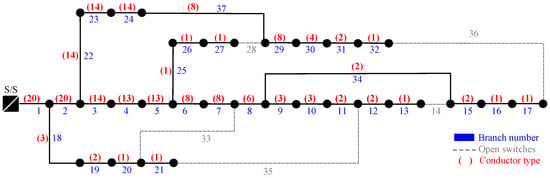
Figure 1.
Simultaneous OCS and ODNR for the 33-bus test system.
Figure 2 illustrates the voltage profile of the 33-bus test system for the different cases under study. Note that the simultaneous OCS and ODNR improves the voltage profile, especially at buses far away from the substation.
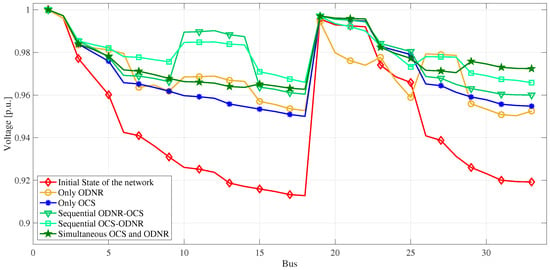
Figure 2.
Voltage profile of the 33-bus test system for all simulations carried out.
According to Figure 2, buses 13 to 18 and 30 to 33 exhibit low voltage values in the base case. However, this issue is effectively rectified through the implementation of simultaneous OCS and ODNR (indicated by the green line). With this solution, all voltage magnitudes are maintained above 0.96 p.u. Furthermore, the overall voltage profile is significantly improved with the simultaneous implementation of OCS and ODNR.
4.2. OCS and ODNR for the 69-Bus Test System
The 69-bus test system has 73 branches, 68 normally closed tie switches, and 5 initially open interconnection switches. The system operates at a nominal voltage of 12.66 kV with a total demand of 3802 + j 2694 kVA. A power flow was calculated to find the initial state of the network. In the initial state, active power losses are 230.78 kW, and the minimum voltage magnitude of the system is 0.8973 p.u. at bus 65. Voltage limits are considered between 0.95 and 1.00 p.u. Table 7 presents the results obtained with the 69-bus test system.

Table 7.
Proposed solutions for the 69-bus test system.
The results reported in Table 7 show that the simultaneous implementation of OCS and ODNR provides the highest economic benefit of 75.96%. Individually, OCS yields an economic benefit of 30.9%, whereas ODNR achieves 21.51%. Furthermore, the sequential optimization of ODNR and then OCS and vice versa yield economic benefits of 43.21% and 34.44% respectively.
The simultaneous implementation of OCS and ODNR also presents the highest reduction in power loss. Note that the power losses of the base case amount to 233.04 kW, whereas the ones obtained with the simultaneous optimization are 34.4 kW, representing a reduction of 85.23%. Individually, ODNR and OCS result in loss reductions of 66.0% and 58.3%, respectively, whereas the sequential optimization resulted in power loss reductions of 70.03% and 72.44% for ODNR and then OCS, and vice versa, respectively. Regarding the voltage profile, the initial scenario, referred to as the base case, presents a minimum voltage of 0.8919 p.u. The most substantial enhancement in voltage profile was attained by simultaneously implementing OCS and ODNR, with a minimum voltage of 0.9725 p.u. In this situation, there was an 8.26% increase in the minimum voltage. Finally, the results for this test system show that the combination of the two optimization approaches, OCS and ODNR, leads to a more optimized system than when any of them are solved individually.
Table 8 indicates the open switches used in the analyzed cases. Note that the open switches in the ODNR-only scenario are the same as the ones of the sequential ODNR-OCS scenario, but different from those employed in the simultaneous OCS and ODNR scenario. This is due to the impact of the OCS on the most efficient reconfiguration strategy aimed at minimizing losses.

Table 8.
Open switches for the 69-bus test system.
Table 9 presents the conductor types selected for the base case (A), only OCS (B), sequential ODNR and then OCS (C) and simultaneous OCS and ODNR (D). The solutions differ significantly due to the impact of the ODNR. As the system reconfiguration is optimized, there are changes in the OCS, leading to a decrease in the investment conductor cost. Consequently, integrating OCS and ODNR in an optimization problem results in a more efficient and economically viable distribution system planning.

Table 9.
Selected conductors for all simulations carried out for the 69-bus test system.
Figure 3 depicts the optimal solution for the simultaneous OCS and ODNR problem, where the conductor type of each branch is indicated in parenthesis in red, and the branch number is indicated in blue. Note that the solution involves the use of conductor types 20, 14, 8, 6, 3, 2, and 1. It was observed that larger capacity conductors are selected for branches located closer to the substation. Furthermore, Figure 3 also shows the specific switches that were opened to achieve the optimal reconfiguration of the system.
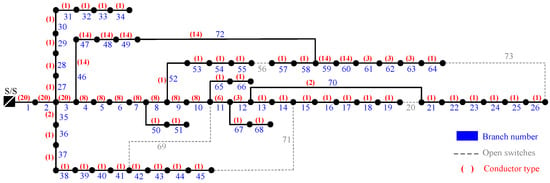
Figure 3.
Simultaneous OCS and ODNR for the 69-bus test system.
Figure 4 illustrates the voltage profile of the 69-bus test system considering the cases described in Table 7. Note that in the base case buses 60 to 66 exhibit low voltage values. However, this issue is effectively rectified through the implementation of OCS and ODNR. An initial improvement in these voltages is obtained with only ODNR, as indicated in the yellow line, these voltages are further improved with only OCS and with the sequential implementation of both. Finally, it is observed that the best voltage profile is obtained with the simultaneous OCS and ODNR. In this case, all voltage magnitudes remain above 0.97 p.u.
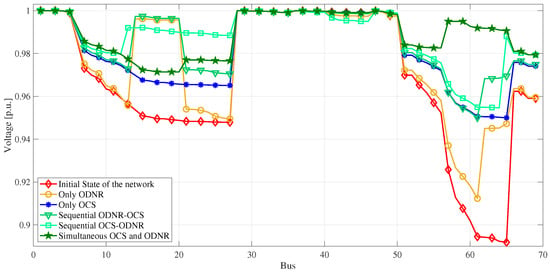
Figure 4.
Voltage profile of the 69-bus test system for different scenarios.
4.3. OCS and ODNR for the 83-Bus Test System
The 83-bus test system comprises 96 branches, 83 normally closed tie switches, and 13 initially open interconnection switches. The system operates at a nominal voltage of 11.4 kV and has a total demand of 28,350.9 + j 20,700 kVA. A power flow was computed to determine the initial state of the network. In the initial base case, the active power losses are 531.91 kW, and the minimum voltage magnitude is 0.9378 p.u. In this case, voltage limits are considered from 0.95 to 1.00 p.u. Table 10 presents the optimal solutions found with the 83-bus test system for the different cases under study.

Table 10.
Proposed solutions for the 83-bus test system.
From Table 10, it is evident that the simultaneous implementation of OCS and ODNR provides the highest economic benefit of 28.31%. This benefit is closely followed by the one obtained with sequential OCS and then ODNR of 27.48%. It was also observed that the sequential ODNR and then OCS present similar economic benefits of only OCS with 26.78% and 26.34%, respectively. This means that for this test system, it is difficult to further reduce power losses once OCS has been carried out. Finally, the lowest economic benefit of only 3.17% was achieved with only ODNR.
As regards technical losses, the ODNR offers a reduction of only 4.73% (from 515.77 kW of the base case to 491.33 kW), whereas the rest of the cases under study manage to reduce power losses by nearly 50%. In this case, the highest power loss reduction was obtained with the sequential ODNR and then OCS approach (51.18%) followed by the simultaneous approach (50.9%). It is worth mentioning that despite the fact that this sequential approach presented a higher power loss reduction, the overall economic benefit of the simultaneous approach is higher.
Regarding the voltage profile, the initial scenario, referred to as the base case, presents a minimum voltage of 0.9514 p.u. The most substantial enhancement in the voltage profile was attained by the sequential OCS and then ODNR approach. In this situation, the minimum voltage is 0.9817 p.u.; on the other hand, the minimum voltage attained by the simultaneous approach was 0.9605 p.u.
Table 11 indicates the open switches used in the analyzed cases. It is important to highlight that the open switches in the ODNR-only scenario are distinct from those employed in the simultaneous OCS and ODNR scenarios but the same as the sequential ODNR and then OCS scenario. This is due to the impact of the OCS on the most efficient reconfiguration strategy aimed at minimizing power losses.

Table 11.
Open switches for 83-bus test system.
Table 12 presents the conductor types selected for the base case (A), only OCS (B), sequential ODNR and then OCS (C) and simultaneous OCS and ODNR (D). Note that the solutions differ significantly due to the impact of the ODNR. As the system reconfiguration is optimized, there are changes in the OCS, and this leads to a decrease in the investment conductor cost.

Table 12.
Selected conductors for all simulations carried out for the 83-bus test system.
Figure 5 depicts the optimal solution for the simultaneous OCS and ODNR problem, where the conductor type of each branch is indicated in parenthesis in red, and the branch number is indicated in blue. Note that the solution involved the use of conductor types 20, 19, 14, 13, 11, 8, 6, 5, 4, 3, 2, and 1. Furthermore, as with the other test systems, larger capacity conductors were selected for branches near the substation. Figure 5 also shows the specific switches that were opened to achieve the optimal reconfiguration.
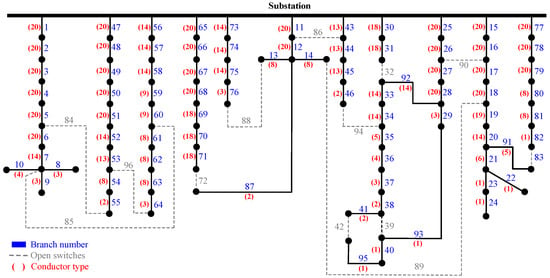
Figure 5.
Simultaneous OCS and ODNR for the 83-bus test system.
Figure 6 depicts the voltage profile of the 83-bus test system. Note that for the base case, all voltage magnitudes are above 0.95 p.u.; nonetheless, the voltage profile is further improved in all cases under study.
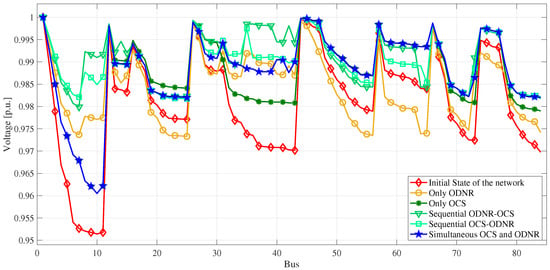
Figure 6.
Voltage profile of the 83-bus test system.
5. Conclusions
Choosing new conductors as replacements for outdated or deteriorated cables can lead to substantial reductions in power losses and enhancement of voltage profiles. Nevertheless, OCS alone might not always be fully effective in achieving significant reductions in technical losses or improving voltage profiles. As a result, OCS can be complemented using other technical approaches. In this study, we integrate OCS with ODNR, which is a method that modifies the distribution network’s topology to minimize power losses and enhance voltage profiles.
Both OCS and ODNR were integrated into a unified MILP model, enabling to obtain globally optimal solutions. This marks the main innovation of the study because the integration of these two issues through a MILP approach has not been previously put forth in the specialized literature. Moreover, the model offers flexibility in decision making, allowing the problems to be addressed jointly or separately as needed.
The efficiency and suitability of the suggested model was assessed using three standard distribution test systems. In each investigated scenario, it was proven that employing simultaneously both optimization methods (OCS and ODNR) within the proposed MILP model results in a more optimized system, characterized by higher economic benefits, compared to solving either of them separately or sequentially.
In the 33-bus and 69-bus test systems, the combined application of OCS and ODNR yielded the greatest decrease in technical losses and the most notable enhancement in voltage profile. In the 83-bus test system the sequential ODNR and then OCS approach resulted in slightly higher power loss reduction than the simultaneous approach; nonetheless, the latter reported higher overall economic benefits. Additionally, across all test systems, implementing OCS and DNR simultaneously led to the choice of lower current capacity conductors compared to using only OCS. This capacity reduction was attributed to the effect of DNR and significantly influenced the overall investment cost. Future work may include a multi-period optimization approach to consider active and reactive power demand variations and the impact of renewable generation.
Author Contributions
Conceptualization, L.A.G.P., J.M.L.-L. and O.G.C.; data curation, L.A.G.P., J.M.L.-L. and O.G.C.; formal analysis, L.A.G.P., J.M.L.-L. and O.G.C.; funding acquisition, L.A.G.P., J.M.L.-L. and O.G.C.; investigation, L.A.G.P., J.M.L.-L. and O.G.C.; methodology, L.A.G.P., J.M.L.-L. and O.G.C.; project administration, L.A.G.P., J.M.L.-L. and O.G.C.; resources, L.A.G.P., J.M.L.-L. and O.G.C.; software, L.A.G.P., J.M.L.-L. and O.G.C.; supervision, L.A.G.P., J.M.L.-L. and O.G.C.; validation, L.A.G.P., J.M.L.-L. and O.G.C.; visualization, L.A.G.P., J.M.L.-L. and O.G.C.; writing—original draft, L.A.G.P., J.M.L.-L. and O.G.C.; writing—review and editing, L.A.G.P., J.M.L.-L. and O.G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Colombia Scientific Program within the framework of the called Ecosistema Científico (Contract No. FP44842-218-2018), Universidad Tecnológica de Pereira (Risaralda, Colombia) and Universidad Estadual de Londrina (Paraná, Brasil).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data of this paper is available through e-mail via authors.
Acknowledgments
The authors would like to thank Universidad de Antioquia (Medellín, Colombia), Universidad Tecnologica de Pereira (Risaralda, Colombia) and Universidad Estadual de Londrina (Paraná, Brazil) for their support in the development of this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The electrical data for the test systems used in this paper is provided in this section.

Table A1.
Initial electrical data for the 33-bus test system.
Table A1.
Initial electrical data for the 33-bus test system.
| Branch | Branch | P | Q | Conductor | Operation | Length | Branch | Branch | P | Q | Conductor | Operation | Length | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| From | To | [kW] | [kVAr] | Type | State | [km] | From | To | [kW] | [kVAr] | Type | State | [km] | ||
| 1 | 1 | 2 | 100 | 60 | 15 | 1 | 0.4164 | 20 | 20 | 21 | 90 | 40 | 1 | 1 | 0.1507 |
| 2 | 2 | 3 | 90 | 40 | 15 | 1 | 2.2267 | 21 | 21 | 22 | 90 | 40 | 1 | 1 | 0.2608 |
| 3 | 3 | 4 | 120 | 80 | 7 | 1 | 0.8018 | 22 | 3 | 23 | 90 | 50 | 2 | 1 | 0.3284 |
| 4 | 4 | 5 | 60 | 30 | 7 | 1 | 0.8348 | 23 | 23 | 24 | 420 | 200 | 2 | 1 | 0.6536 |
| 5 | 5 | 6 | 60 | 20 | 7 | 1 | 1.7941 | 24 | 24 | 25 | 420 | 200 | 2 | 1 | 0.6521 |
| 6 | 6 | 7 | 200 | 100 | 2 | 1 | 0.1362 | 25 | 6 | 26 | 60 | 25 | 2 | 1 | 0.1477 |
| 7 | 7 | 8 | 200 | 100 | 2 | 1 | 0.5178 | 26 | 26 | 27 | 60 | 25 | 2 | 1 | 0.2068 |
| 8 | 8 | 9 | 60 | 20 | 2 | 1 | 0.7496 | 27 | 27 | 28 | 60 | 20 | 2 | 1 | 0.7707 |
| 9 | 9 | 10 | 60 | 20 | 2 | 1 | 0.7598 | 28 | 28 | 29 | 120 | 70 | 2 | 1 | 0.5853 |
| 10 | 10 | 11 | 45 | 30 | 2 | 1 | 0.1431 | 29 | 29 | 30 | 200 | 600 | 2 | 1 | 0.3694 |
| 11 | 11 | 12 | 60 | 35 | 2 | 1 | 0.2725 | 30 | 30 | 31 | 150 | 70 | 2 | 1 | 0.7092 |
| 12 | 12 | 13 | 60 | 35 | 2 | 1 | 1.0684 | 31 | 31 | 32 | 210 | 100 | 2 | 1 | 0.2260 |
| 13 | 13 | 14 | 120 | 80 | 2 | 1 | 0.3942 | 32 | 32 | 33 | 60 | 40 | 2 | 1 | 0.2482 |
| 14 | 14 | 15 | 60 | 10 | 2 | 1 | 0.4301 | 32 | 32 | 33 | 60 | 40 | 2 | 1 | 0.2482 |
| 15 | 15 | 16 | 60 | 20 | 2 | 1 | 0.5432 | 33 | 8 | 21 | 2 | 0 | 1.4556 | ||
| 16 | 16 | 17 | 60 | 20 | 2 | 1 | 0.9381 | 34 | 9 | 15 | 2 | 0 | 1.4556 | ||
| 17 | 17 | 18 | 90 | 40 | 2 | 1 | 0.5328 | 35 | 12 | 22 | 2 | 0 | 1.4556 | ||
| 18 | 2 | 19 | 90 | 40 | 1 | 1 | 0.0603 | 36 | 18 | 33 | 2 | 0 | 0.3639 | ||
| 19 | 19 | 20 | 90 | 40 | 1 | 1 | 0.5534 | 37 | 25 | 29 | 2 | 0 | 0.3639 | ||

Table A2.
Initial electrical data for the 69-bus test system.
Table A2.
Initial electrical data for the 69-bus test system.
| Branch | Branch | P | Q | Conductor | Operation | Length | Branch | Branch | P | Q | Conductor | Operation | Length | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| From | To | [kW] | [kVAr] | Type | State | [km] | From | To | [kW] | [kVAr] | Type | State | [km] | ||
| 1 | 1 | 2 | 0.00 | 0.00 | 14 | 1 | 0.002 | 38 | 38 | 39 | 24.00 | 17.00 | 1 | 1 | 0.011 |
| 2 | 2 | 3 | 0.00 | 0.00 | 14 | 1 | 0.002 | 39 | 39 | 40 | 24.00 | 17.00 | 1 | 1 | 0.001 |
| 3 | 3 | 4 | 0.00 | 0.00 | 14 | 1 | 0.007 | 40 | 40 | 41 | 1.20 | 1.00 | 1 | 1 | 0.268 |
| 4 | 4 | 5 | 0.00 | 0.00 | 14 | 1 | 0.114 | 41 | 41 | 42 | 0.00 | 0.00 | 1 | 1 | 0.114 |
| 5 | 5 | 6 | 2.60 | 2.20 | 14 | 1 | 1.669 | 42 | 42 | 43 | 6.00 | 4.30 | 1 | 1 | 0.015 |
| 6 | 6 | 7 | 40.40 | 30.00 | 14 | 1 | 1.738 | 43 | 43 | 44 | 0.00 | 0.00 | 1 | 1 | 0.003 |
| 7 | 7 | 8 | 75.00 | 54.00 | 14 | 1 | 0.420 | 44 | 44 | 45 | 39.22 | 26.30 | 1 | 1 | 0.040 |
| 8 | 8 | 9 | 30.00 | 22.00 | 14 | 1 | 0.225 | 45 | 45 | 46 | 39.22 | 26.30 | 1 | 1 | 0.003 |
| 9 | 9 | 10 | 28.00 | 19.00 | 2 | 1 | 0.596 | 46 | 4 | 47 | 0.00 | 0.00 | 2 | 1 | 0.002 |
| 10 | 10 | 11 | 145.00 | 104.00 | 2 | 1 | 0.136 | 47 | 47 | 48 | 79.00 | 56.40 | 2 | 1 | 0.062 |
| 11 | 11 | 12 | 145.00 | 104.00 | 2 | 1 | 0.518 | 48 | 48 | 49 | 384.70 | 274.50 | 2 | 1 | 0.211 |
| 12 | 12 | 13 | 8.00 | 5.50 | 2 | 1 | 0.750 | 49 | 49 | 50 | 384.70 | 274.50 | 2 | 1 | 0.060 |
| 13 | 13 | 14 | 8.00 | 5.50 | 2 | 1 | 0.760 | 50 | 8 | 51 | 40.50 | 28.30 | 1 | 1 | 0.034 |
| 14 | 14 | 15 | 0.00 | 0.00 | 2 | 1 | 0.770 | 51 | 51 | 52 | 3.60 | 2.70 | 1 | 1 | 0.122 |
| 15 | 15 | 16 | 45.50 | 30.00 | 2 | 1 | 0.143 | 52 | 9 | 53 | 4.35 | 3.50 | 6 | 1 | 0.319 |
| 16 | 16 | 17 | 60.00 | 35.00 | 2 | 1 | 0.272 | 53 | 53 | 54 | 26.40 | 19.00 | 6 | 1 | 0.373 |
| 17 | 17 | 18 | 60.00 | 35.00 | 2 | 1 | 0.003 | 54 | 54 | 55 | 24.00 | 17.20 | 6 | 1 | 0.522 |
| 18 | 18 | 19 | 0.00 | 0.00 | 2 | 1 | 0.238 | 55 | 55 | 56 | 0.00 | 0.00 | 6 | 1 | 0.516 |
| 19 | 19 | 20 | 1.00 | 0.60 | 2 | 1 | 0.153 | 56 | 56 | 57 | 0.00 | 0.00 | 6 | 1 | 2.918 |
| 20 | 20 | 21 | 114.00 | 81.00 | 1 | 1 | 0.126 | 57 | 57 | 58 | 0.00 | 0.00 | 6 | 1 | 1.438 |
| 21 | 21 | 22 | 5.30 | 3.50 | 1 | 1 | 0.005 | 58 | 58 | 59 | 100.00 | 72.00 | 6 | 1 | 0.558 |
| 22 | 22 | 23 | 0.00 | 0.00 | 1 | 1 | 0.059 | 59 | 59 | 60 | 0.00 | 0.00 | 5 | 1 | 0.568 |
| 23 | 23 | 24 | 28.00 | 20.00 | 1 | 1 | 0.127 | 60 | 60 | 61 | 1244.00 | 888.00 | 5 | 1 | 0.747 |
| 24 | 24 | 25 | 0.00 | 0.00 | 1 | 1 | 0.275 | 61 | 61 | 62 | 32.00 | 23.00 | 1 | 1 | 0.036 |
| 25 | 25 | 26 | 14.00 | 10.00 | 1 | 1 | 0.114 | 62 | 62 | 63 | 0.00 | 0.00 | 1 | 1 | 0.053 |
| 26 | 26 | 27 | 14.00 | 10.00 | 1 | 1 | 0.064 | 63 | 63 | 64 | 227.00 | 162.00 | 1 | 1 | 0.261 |
| 27 | 3 | 28 | 26.00 | 18.60 | 1 | 1 | 0.002 | 64 | 64 | 65 | 59.00 | 42.00 | 1 | 1 | 0.383 |
| 28 | 28 | 29 | 26.00 | 18.60 | 1 | 1 | 0.024 | 65 | 11 | 66 | 18.00 | 13.00 | 1 | 1 | 0.074 |
| 29 | 29 | 30 | 0.00 | 0.00 | 1 | 1 | 0.146 | 66 | 66 | 67 | 18.00 | 13.00 | 1 | 1 | 0.002 |
| 30 | 30 | 31 | 0.00 | 0.00 | 1 | 1 | 0.026 | 67 | 12 | 68 | 28.00 | 20.00 | 1 | 1 | 0.272 |
| 31 | 31 | 32 | 0.00 | 0.00 | 1 | 1 | 0.129 | 68 | 68 | 69 | 28.00 | 20.00 | 1 | 1 | 0.002 |
| 32 | 32 | 33 | 14.00 | 10.00 | 1 | 1 | 0.309 | 69 | 11 | 43 | 1 | 0 | 0.184 | ||
| 33 | 33 | 34 | 19.50 | 14.00 | 1 | 1 | 0.628 | 70 | 13 | 21 | 1 | 0 | 0.184 | ||
| 34 | 34 | 35 | 6.00 | 4.00 | 1 | 1 | 0.542 | 71 | 15 | 46 | 1 | 0 | 0.368 | ||
| 35 | 3 | 36 | 26.00 | 18.55 | 1 | 1 | 0.002 | 72 | 50 | 59 | 1 | 0 | 0.736 | ||
| 36 | 36 | 37 | 26.00 | 18.55 | 1 | 1 | 0.024 | 73 | 27 | 65 | 1 | 0 | 0.368 | ||
| 37 | 37 | 38 | 0.00 | 0.00 | 1 | 1 | 0.039 | ||||||||

Table A3.
Initial electrical data for the 83-bus test system.
Table A3.
Initial electrical data for the 83-bus test system.
| Branch | Branch | P | Q | Conductor | Operation | Length | Branch | Branch | P | Q | Conductor | Operation | Length | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| From | To | [kW] | [kVAr] | Type | State | [km] | From | To | [kW] | [kVAr] | Type | State | [km] | ||
| 1 | 0 | 1 | 0.0 | 0.0 | 14 | 1 | 0.88646 | 49 | 48 | 49 | 0.0 | 0.0 | 13 | 1 | 0.23862 |
| 2 | 1 | 2 | 100.0 | 50.0 | 14 | 1 | 0.95577 | 50 | 49 | 50 | 200.0 | 160.0 | 13 | 1 | 0.14317 |
| 3 | 2 | 3 | 300.0 | 200.0 | 14 | 1 | 1.07524 | 51 | 50 | 51 | 800.0 | 600.0 | 13 | 1 | 0.28634 |
| 4 | 3 | 4 | 350.0 | 250.0 | 14 | 1 | 0.41815 | 52 | 51 | 52 | 500.0 | 300.0 | 13 | 1 | 0.14317 |
| 5 | 4 | 5 | 220.0 | 100.0 | 14 | 1 | 0.65577 | 53 | 52 | 53 | 500.0 | 350.0 | 13 | 1 | 0.28634 |
| 6 | 5 | 6 | 1100.0 | 800.0 | 12 | 1 | 0.23013 | 54 | 53 | 54 | 500.0 | 300.0 | 13 | 1 | 0.03814 |
| 7 | 6 | 7 | 400.0 | 320.0 | 5 | 1 | 0.98960 | 55 | 54 | 55 | 200.0 | 80.0 | 13 | 1 | 0.04820 |
| 8 | 7 | 8 | 300.0 | 200.0 | 1 | 1 | 0.38560 | 56 | 0 | 56 | 0.0 | 0.0 | 5 | 1 | 0.33377 |
| 9 | 7 | 9 | 300.0 | 230.0 | 1 | 1 | 0.86750 | 57 | 56 | 57 | 30.0 | 20.0 | 5 | 1 | 0.79043 |
| 10 | 7 | 10 | 300.0 | 260.0 | 1 | 1 | 0.38560 | 58 | 57 | 58 | 600.0 | 420.0 | 5 | 1 | 0.07712 |
| 11 | 0 | 11 | 0.9 | 0.0 | 13 | 1 | 0.28634 | 59 | 58 | 59 | 0.0 | 0.0 | 5 | 1 | 0.02948 |
| 12 | 11 | 12 | 1200.0 | 800.0 | 13 | 1 | 1.24080 | 60 | 59 | 60 | 20.0 | 10.0 | 5 | 1 | 0.02860 |
| 13 | 12 | 13 | 800.0 | 600.0 | 5 | 1 | 0.01907 | 61 | 60 | 61 | 20.0 | 10.0 | 5 | 1 | 0.01907 |
| 14 | 12 | 14 | 700.0 | 500.0 | 13 | 1 | 0.05721 | 62 | 61 | 62 | 200.0 | 130.0 | 5 | 1 | 0.07627 |
| 15 | 0 | 15 | 0.0 | 0.0 | 17 | 1 | 0.61497 | 63 | 62 | 63 | 300.0 | 240.0 | 5 | 1 | 0.08675 |
| 16 | 15 | 16 | 300.0 | 150.0 | 17 | 1 | 0.28416 | 64 | 63 | 64 | 300.0 | 200.0 | 5 | 1 | 0.00894 |
| 17 | 16 | 17 | 500.0 | 350.0 | 16 | 1 | 0.23593 | 65 | 0 | 65 | 0.0 | 0.0 | 15 | 1 | 0.21951 |
| 18 | 17 | 18 | 700.0 | 400.0 | 16 | 1 | 0.70779 | 66 | 65 | 66 | 50.0 | 30.0 | 15 | 1 | 0.76920 |
| 19 | 18 | 19 | 1200.0 | 1000.0 | 7 | 1 | 0.08609 | 67 | 66 | 67 | 0.0 | 0.0 | 15 | 1 | 0.54878 |
| 20 | 19 | 20 | 300.0 | 300.0 | 7 | 1 | 0.12394 | 68 | 67 | 68 | 400.0 | 360.0 | 15 | 1 | 0.98780 |
| 21 | 20 | 21 | 400.0 | 350.0 | 1 | 1 | 0.08675 | 69 | 68 | 69 | 0.0 | 0.0 | 9 | 1 | 0.12653 |
| 22 | 21 | 22 | 50.0 | 20.0 | 1 | 1 | 0.05784 | 70 | 69 | 70 | 0.0 | 0.0 | 9 | 1 | 0.18979 |
| 23 | 21 | 23 | 50.0 | 20.0 | 1 | 1 | 0.07230 | 71 | 70 | 71 | 2000.0 | 1500.0 | 9 | 1 | 0.14762 |
| 24 | 23 | 24 | 50.0 | 10.0 | 1 | 1 | 0.04821 | 72 | 71 | 72 | 200.0 | 150.0 | 9 | 1 | 0.00964 |
| 25 | 0 | 25 | 50.0 | 30.0 | 7 | 1 | 0.12421 | 73 | 0 | 73 | 0.0 | 0.0 | 5 | 1 | 0.47682 |
| 26 | 25 | 26 | 100.0 | 60.0 | 7 | 1 | 0.22957 | 74 | 73 | 74 | 0.0 | 0.0 | 5 | 1 | 0.04768 |
| 27 | 26 | 27 | 100.0 | 70.0 | 7 | 1 | 0.54524 | 75 | 74 | 75 | 1200.0 | 950.0 | 5 | 1 | 0.08344 |
| 28 | 27 | 28 | 1800.0 | 1300.0 | 7 | 1 | 0.10646 | 76 | 75 | 76 | 300.0 | 180.0 | 5 | 1 | 0.07152 |
| 29 | 28 | 29 | 200.0 | 120.0 | 6 | 1 | 0.04820 | 77 | 0 | 77 | 0.0 | 0.0 | 17 | 1 | 1.36171 |
| 30 | 0 | 30 | 0.0 | 0.0 | 17 | 1 | 1.06562 | 78 | 77 | 78 | 400.0 | 360.0 | 17 | 1 | 0.70282 |
| 31 | 30 | 31 | 1800.0 | 1600.0 | 17 | 1 | 0.71041 | 79 | 78 | 79 | 2000.0 | 1300.0 | 17 | 1 | 0.26356 |
| 32 | 31 | 32 | 200.0 | 150.0 | 17 | 1 | 0.24041 | 80 | 79 | 80 | 200.0 | 140.0 | 7 | 1 | 0.14370 |
| 33 | 32 | 33 | 200.0 | 100.0 | 6 | 1 | 0.04808 | 81 | 80 | 81 | 500.0 | 360.0 | 7 | 1 | 0.09534 |
| 34 | 33 | 34 | 800.0 | 600.0 | 6 | 1 | 0.18681 | 82 | 81 | 82 | 100.0 | 30.0 | 7 | 1 | 0.03374 |
| 35 | 34 | 35 | 100.0 | 60.0 | 6 | 1 | 0.01928 | 83 | 82 | 83 | 400.0 | 360.0 | 7 | 1 | 0.11567 |
| 36 | 35 | 36 | 100.0 | 60.0 | 6 | 1 | 0.18315 | 84 | 5 | 55 | 0.0 | 0.0 | 13 | 0 | 0.47723 |
| 37 | 36 | 37 | 20.0 | 10.0 | 6 | 1 | 0.01446 | 85 | 7 | 60 | 0.0 | 0.0 | 5 | 0 | 0.19279 |
| 38 | 37 | 38 | 20.0 | 10.0 | 6 | 1 | 0.01446 | 86 | 11 | 43 | 0.0 | 0.0 | 13 | 0 | 0.47723 |
| 39 | 38 | 39 | 20.0 | 10.0 | 6 | 1 | 0.02892 | 87 | 12 | 72 | 0.0 | 0.0 | 13 | 0 | 1.24080 |
| 40 | 39 | 40 | 20.0 | 10.0 | 6 | 1 | 0.07712 | 88 | 13 | 76 | 0.0 | 0.0 | 5 | 0 | 0.67476 |
| 41 | 38 | 41 | 200.0 | 160.0 | 6 | 1 | 0.07230 | 89 | 14 | 18 | 0.0 | 0.0 | 16 | 0 | 2.41828 |
| 42 | 41 | 42 | 50.0 | 30.0 | 6 | 1 | 0.07712 | 90 | 16 | 26 | 0.0 | 0.0 | 20 | 0 | 0.74980 |
| 43 | 0 | 43 | 0.0 | 0.0 | 2 | 1 | 0.03537 | 91 | 20 | 83 | 0.0 | 0.0 | 7 | 0 | 0.17218 |
| 44 | 43 | 44 | 30.0 | 20.0 | 2 | 1 | 0.02860 | 92 | 28 | 32 | 0.0 | 0.0 | 17 | 0 | 0.28416 |
| 45 | 44 | 45 | 800.0 | 700.0 | 2 | 1 | 0.09534 | 93 | 29 | 39 | 0.0 | 0.0 | 6 | 0 | 0.14425 |
| 46 | 45 | 46 | 200.0 | 150.0 | 2 | 1 | 0.08675 | 94 | 34 | 46 | 0.0 | 0.0 | 6 | 0 | 0.04808 |
| 47 | 0 | 47 | 0.0 | 0.0 | 13 | 1 | 0.88525 | 95 | 40 | 42 | 0.0 | 0.0 | 6 | 0 | 0.36062 |
| 48 | 47 | 48 | 0.0 | 0.0 | 13 | 1 | 0.23862 | 96 | 53 | 64 | 0.0 | 0.0 | 5 | 0 | 0.05784 |
References
- Swaminathan, D.; Rajagopalan, A.; Montoya, O.D.; Arul, S.; Grisales-Noreña, L.F. Distribution Network Reconfiguration Based on Hybrid Golden Flower Algorithm for Smart Cities Evolution. Energies 2023, 16, 2454. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Rosales-Muñoz, A.A.; Montoya, O.D. An Effective Power Dispatch of Photovoltaic Generators in DC Networks via the Antlion Optimizer. Energies 2023, 16, 1350. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, H.; Yu, D.; Wang, X.; Song, H. A practical approach to the conductor size selection in planning radial distribution systems. IEEE Trans. Power Deliv. 2000, 15, 350–354. [Google Scholar] [CrossRef]
- Sivanagaraju, S.; Sreenivasulu, N.; Vijayakumar, M.; Ramana, T. Optimal conductor selection for radial distribution systems. Electr. Power Syst. Res. 2002, 63, 95–103. [Google Scholar] [CrossRef]
- Mandal, S.; Pahwa, A. Optimal selection of conductors for distribution feeders. IEEE Trans. Power Syst. 2002, 17, 192–197. [Google Scholar] [CrossRef]
- Kaur, D.; Sharma, J. Optimal conductor sizing in radial distribution systems planning. Int. J. Electr. Power Energy Syst. 2008, 30, 261–271. [Google Scholar] [CrossRef]
- Thenepalle, M. A Comparative Study on Optimal Conductor Selection for Radial Distribution Network using Conventional and Genetic Algorithm Approach. Int. J. Comput. Appl. 2011, 17, 6–13. [Google Scholar] [CrossRef]
- Abul’Wafa, A.R. Multi-conductor feeder design for radial distribution networks. Electr. Power Syst. Res. 2016, 140, 184–192. [Google Scholar] [CrossRef]
- Ali, H.; Ullah, S.; Sami, I.; Ahmad, N.; Khan, F. Economic Loss Minimization of a Distribution Feeder and Selection of Optimum Conductor for Voltage Profile Improvement. In Proceedings of the 2018 International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), Islamabad, Pakistan, 10–12 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Mozaffari, L.M.; Hassan, J.; Mohammad, L. Optimal Conductor Selection in Radial Distribution Systems for Productivity Improvement Using Genetic Algorithm. Iraqi J. Electr. Electron. Eng. 2013, 9, 29–35. [Google Scholar] [CrossRef]
- Zhao, Z.; Mutale, J. Optimal Conductor Size Selection in Distribution Networks with High Penetration of Distributed Generation Using Adaptive Genetic Algorithm. Energies 2019, 12, 2065. [Google Scholar] [CrossRef]
- Mendoza, F.; Requena, D.; Bemal-agustin, J.L.; Dominguez-navarro, J.A. Optimal Conductor Size Selection in Radial Power Distribution Systems Using Evolutionary Strategies. In Proceedings of the 2006 IEEE/PES Transmission & Distribution Conference and Exposition: Latin America, Caracas, Venezuela, 15–18 August 2006; pp. 1–5. [Google Scholar] [CrossRef]
- Samal, P.; Mohanty, S.; Ganguly, S. Simultaneous capacitor allocation and conductor sizing in unbalanced radial distribution systems using differential evolution algorithm. In Proceedings of the 2016 National Power Systems Conference (NPSC), Bhubaneswar, India, 19–21 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Farahani, V.; Sadeghi, S.H.H.; Askarian Abyaneh, H.; Agah, S.M.M.; Mazlumi, K. Energy Loss Reduction by Conductor Replacement and Capacitor Placement in Distribution Systems. IEEE Trans. Power Syst. 2013, 28, 2077–2085. [Google Scholar] [CrossRef]
- Mozaffari Legha, M. Combination of Optimal Conductor Selection and Capacitor Placement in Radial Distribution Systems Using PSO Method. Iraqi J. Electr. Electron. Eng. 2014, 10, 33–41. [Google Scholar] [CrossRef]
- Kumari, M.; Ranjan, R. Economical Selection of Conductor in Radial Distribution System using PSO. J. Inst. Eng. (India) Ser. B 2022, 103, 1105–1114. [Google Scholar] [CrossRef]
- Khalil, T.M.; Gorpinich, A.V. Optimal conductor selection and capacitor placement for loss reduction of radial distribution systems by selective particle swarm optimization. In Proceedings of the 2012 Seventh International Conference on Computer Engineering & Systems (ICCES), Cairo, Egypt, 27–29 November 2012; pp. 215–220. [Google Scholar] [CrossRef]
- Manikandan, S.; Sasitharan, S.; Rao, J.V.; Moorthy, V. Analysis of optimal conductor selection for radial distribution systems using DPSO. In Proceedings of the 2016 3rd International Conference on Electrical Energy Systems (ICEES), Chennai, India, 17–19 March 2016; pp. 96–101. [Google Scholar] [CrossRef]
- Ismael, S.M.; Abdel Aleem, S.H.E.; Abdelaziz, A.Y.; Zobaa, A.F. Practical Considerations for Optimal Conductor Reinforcement and Hosting CapaEconomic Loss Minimization of a Distribution Feeder and Selection of Optimum 435 Conductor for Voltage Profile Improvement. Enhancement in Radial Distribution Systems. IEEE Access 2018, 6, 27268–27277. [Google Scholar] [CrossRef]
- Srinivas, R.R.; Satish, K.; Narasimham, S.V.L. Optimal Conductor Size Selection in Distribution Systems Using the Harmony Search Algorithm with a Differential Operator. Electr. Power Components Syst. 2011, 40, 41–56. [Google Scholar] [CrossRef]
- Abdelaziz, A.Y.; Fathy, A. A novel approach based on crow search algorithm for optimal selection of conductor size in radial distribution networks. Eng. Sci. Technol. Int. J. 2017, 20, 391–402. [Google Scholar] [CrossRef]
- Ismael, S.M.; Aleem, S.H.E.A.; Abdelaziz, A.Y. Optimal selection of conductors in Egyptian radial distribution systems using sine-cosine optimization algorithm. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 103–107. [Google Scholar] [CrossRef]
- Montoya, O.D.; Grajales, A.; Hincapié, R.A. Selección òptima de conductores en sistemas de distribución empleando el algoritmo búsqueda tabú. Ingeniare Rev. Chil. De Ing. 2018, 26, 283–295. [Google Scholar] [CrossRef]
- Nivia-Torres, D.J.; Salazar-Alarcon, G.A.; Montoya, O.D. Selección óptima de conductores en redes de distribución trifásicas utilizando el algoritmo metaheurístico de Newton. Ingeniería 2022, 27, 334–354. [Google Scholar] [CrossRef]
- Franco, J.F.; Rider, M.J.; Lavorato, M.; Romero, R. Optimal Conductor Size Selection and Reconductoring in Radial Distribution Systems Using a Mixed-Integer LP Approach. IEEE Trans. Power Syst. 2013, 28, 10–20. [Google Scholar] [CrossRef]
- Montoya, O.D.; Garces, A.; Castro, C.A. Optimal Conductor Size Selection in Radial Distribution Networks Using a Mixed-Integer Non-Linear Programming Formulation. IEEE Lat. Am. Trans. 2018, 16, 2213–2220. [Google Scholar] [CrossRef]
- Farrag, M.A.; Khalil, A.H.; Omran, S. Optimal conductor selection and capacitor placement in radial distribution system using nonlinear AC load flow equations and dynamic load model. Int. Trans. Electr. Energy Syst. 2020, 30, e12316. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L.F. On the mathematical modeling for optimal selecting of calibers of conductors in DC radial distribution networks: A MINLP approach. Electr. Power Syst. Res. 2021, 194, 107072. [Google Scholar] [CrossRef]
- Gallego Pareja, L.A.; López-Lezama, J.M.; Gómez Carmona, O. A Mixed-Integer Linear Programming Model for the Simultaneous Optimal Distribution Network Reconfiguration and Optimal Placement of Distributed Generation. Energies 2022, 15, 3063. [Google Scholar] [CrossRef]
- Shirmohammadi, D.; Hong, H. Reconfiguration of electric distribution networks for resistive line losses reduction. IEEE Trans. Power Deliv. 1989, 4, 1492–1498. [Google Scholar] [CrossRef]
- Ahmadi, H.; Martí, J.R. Mathematical representation of radiality constraint in distribution system reconfiguration problem. Int. J. Electr. Power Energy Syst. 2015, 64, 293–299. [Google Scholar] [CrossRef]
- Gomes, F.; Carneiro, S.; Pereira, J.; Vinagre, M.; Garcia, P.; De Araujo, L. A New Distribution System Reconfiguration Approach Using Optimum Power Flow and Sensitivity Analysis for Loss Reduction. IEEE Trans. Power Syst. 2006, 21, 1616–1623. [Google Scholar] [CrossRef]
- Sivanagaraju, S.; Rao, J.V.; Raju, P.S. Discrete Particle Swarm Optimization to Network Reconfiguration for Loss Reduction and Load Balancing. Electr. Power Components Syst. 2008, 36, 513–524. [Google Scholar] [CrossRef]
- Abdelaziz, A.; Mohammed, F.; Mekhamer, S.; Badr, M. Distribution Systems Reconfiguration using a modified particle swarm optimization algorithm. Electr. Power Syst. Res. 2009, 79, 1521–1530. [Google Scholar] [CrossRef]
- Yang, M.; Li, J.; Li, J.; Yuan, X.; Xu, J. Reconfiguration Strategy for DC Distribution Network Fault Recovery Based on Hybrid Particle Swarm Optimization. Energies 2021, 14, 7145. [Google Scholar] [CrossRef]
- Zhu, J. Optimal reconfiguration of electrical distribution network using the refined genetic algorithm. Electr. Power Syst. Res. 2002, 62, 37–42. [Google Scholar] [CrossRef]
- He, M.; Ma, C.; Duan, Q.; Ni, S.; Deng, W.; Liu, X.; Li, Z.; Chen, Y.; Shi, Y. Active Distribution Network Reconfiguration Method Based on Photovoltaic Generation Prediction. In Proceedings of the 2022 IEEE International Conference on Electrical Engineering, Big Data and Algorithms (EEBDA), Changchun, China, 25–27 February 2022; pp. 82–87. [Google Scholar] [CrossRef]
- Wang, C.; Gao, Y. Determination of Power Distribution Network Configuration Using Non-Revisiting Genetic Algorithm. IEEE Trans. Power Syst. 2013, 28, 3638–3648. [Google Scholar] [CrossRef]
- Eldurssi, A.M.; O’Connell, R.M. A Fast Nondominated Sorting Guided Genetic Algorithm for Multi-Objective Power Distribution System Reconfiguration Problem. IEEE Trans. Power Syst. 2015, 30, 593–601. [Google Scholar] [CrossRef]
- Guimarães, M.A.; Castro, C.A.; Romero, R. Distribution systems operation optimization through reconfiguration and capacitor allocation by a dedicated genetic algorithm. IET Gener. Transm. Distrib. 2010, 4, 1213. [Google Scholar] [CrossRef]
- Guamán, A.; Valenzuela, A. Distribution Network Reconfiguration Applied to Multiple Faulty Branches Based on Spanning Tree and Genetic Algorithms. Energies 2021, 14, 6699. [Google Scholar] [CrossRef]
- Amin, A.; Muhammad, M.; Mokhlis, H.; Franco, J.; Naidu, K.; Coo, L. Enhancement of Simultaneous Network Reconfiguration and DG Sizing via Hamming dataset approach and Firefly Algorithm. IET Gener. Transm. Distrib. 2019, 13, 5071–5082. [Google Scholar] [CrossRef]
- Gerez, C.; Silva, L.I.; Belati, E.A.; Sguarezi Filho, A.J.; Costa, E.C.M. Distribution Network Reconfiguration Using Selective Firefly Algorithm and a Load Flow Analysis Criterion for Reducing the Search Space. IEEE Access 2019, 7, 67874–67888. [Google Scholar] [CrossRef]
- Srinivasa Rao, R.; Narasimham, S.V.L.; Ramalinga Raju, M.; Srinivasa Rao, A. Optimal Network Reconfiguration of Large-Scale Distribution System Using Harmony Search Algorithm. IEEE Trans. Power Syst. 2011, 26, 1080–1088. [Google Scholar] [CrossRef]
- Santos, M.V.D.; Brigatto, G.A.; Garcés, L.P. Methodology of solution for the distribution network reconfiguration problem based on improved harmony search algorithm. IET Gener. Transm. Distrib. 2020, 14, 6526–6533. [Google Scholar] [CrossRef]
- Zhang, D.; Fu, Z.; Zhang, L. An improved TS algorithm for loss-minimum reconfiguration in large-scale distribution systems. Electr. Power Syst. Res. 2007, 77, 685–694. [Google Scholar] [CrossRef]
- Abdelaziz, A.; Mohamed, F.; Mekhamer, S.; Badr, M. Distribution system reconfiguration using a modified Tabu Search algorithm. Electr. Power Syst. Res. 2010, 80, 943–953. [Google Scholar] [CrossRef]
- Liu, N.; Li, C.; Chen, L.; Wang, J. Hybrid Data-Driven and Model-Based Distribution Network Reconfiguration With Lossless Model Reduction. IEEE Trans. Ind. Inform. 2022, 18, 2943–2954. [Google Scholar] [CrossRef]
- Zhang, Z.; Du, W.; Lu, Y.; Xu, G.; Zhao, Y. Two-Stage Robust Distribution Network Reconfiguration Against Failures of Lines and Renewable Generations. IEEE Access 2022, 10, 108614–108624. [Google Scholar] [CrossRef]
- Gautam, M.; Bhusal, N.; Benidris, M. Deep Q-Learning-based Distribution Network Reconfiguration for Reliability Improvement. In Proceedings of the 2022 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), New Orleans, LA, USA, 25–28 April 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Dai, B. Multi-objective Optimization Model of Distribution Network Reconfiguration Considering Soft Open Point. In Proceedings of the 2022 China International Conference on Electricity Distribution (CICED), Changsha, China, 7–8 September 2022; pp. 468–472. [Google Scholar] [CrossRef]
- Wen, J.; Qu, X.; Huang, Y.; Lin, S. A Reconfiguration Method of Distribution Network Considering Time Variations for Load and Renewable Distributed Generation. In Proceedings of the 2022 7th Asia Conference on Power and Electrical Engineering (ACPEE), Hangzhou, China, 15–17 April 2022; pp. 544–549. [Google Scholar] [CrossRef]
- Razavi, S.M.; Momeni, H.R.; Haghifam, M.R.; Bolouki, S. Multi-Objective Optimization of Distribution Networks via Daily Reconfiguration. IEEE Trans. Power Deliv. 2022, 37, 775–785. [Google Scholar] [CrossRef]
- Mahdavi, M.; Alhelou, H.H.; Bagheri, A.; Djokic, S.Z.; Ramos, R.A.V. A Comprehensive Review of Metaheuristic Methods for the Reconfiguration of Electric Power Distribution Systems and Comparison With a Novel Approach Based on Efficient Genetic Algorithm. IEEE Access 2021, 9, 122872–122906. [Google Scholar] [CrossRef]
- Chen, F.; Lu, H.; Tong, Z.; Wu, J.; Lu, C. Research on Path Connectivity Optimization Model for Active Distribution Network Reconfiguration. In Proceedings of the 2022 5th International Conference on Renewable Energy and Power Engineering (REPE), Beijing, China, 28–30 September 2022; pp. 233–236. [Google Scholar] [CrossRef]
- Tavakoli Ghazi Jahani, M.; Nazarian, P.; Safari, A.; Haghifam, M. Multi-objective optimization model for optimal reconfiguration of distribution networks with demand response services. Sustain. Cities Soc. 2019, 47, 101514. [Google Scholar] [CrossRef]
- Haghighat, H.; Zeng, B. Distribution System Reconfiguration Under Uncertain Load and Renewable Generation. IEEE Trans. Power Syst. 2016, 31, 2666–2675. [Google Scholar] [CrossRef]
- Gallego, L.A.; López-Lezama, J.M.; Carmona, O.G. A Mixed-Integer Linear Programming Model for Simultaneous Optimal Reconfiguration and Optimal Placement of Capacitor Banks in Distribution Networks. IEEE Access 2022, 10, 52655–52673. [Google Scholar] [CrossRef]
- Gallego Pareja, L.A.; López-Lezama, J.M.; Gómez Carmona, O. A MILP Model for Optimal Conductor Selection and Capacitor Banks Placement in Primary Distribution Systems. Energies 2023, 16, 4340. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).