Abstract
We propose a network optimization model for smart energy market management in the context of an uncertain environment. The network optimization considers the stochastic programming approach to capture the randomness of the unknown demands. We utilize the particle swarm optimization technique in the proposed model to solve the proposed optimization problem. The present research is based on the inclusion of stochastic demands and uncertain energy prices. Optimizing produced energy is crucial for efficient usage and meeting the targets. The proposed model also focuses on addressing sustainability concerns by minimizing energy consumption in the scheduling process. An improved particle swarm optimization technique is implemented for energy-efficient production. Parameters such as number of particles, iterations, and energy usage specification are customized. A fitness function is taken that considers both completion time and energy consumption. The optimal of energy consumption is also visualized. The decision makers employ risk aversion in the objective function of the optimization problem to measure the risk deviation of the expected energy management.
1. Introduction
Energy is one of the most viable resources to fulfill the multi-criteria assessment [1]. The crisis in energy has been triggered by the Russo-Ukrainian war [2]. The production and consumption of energy in industrialized nations have been extensively studied [3], but studies on the efficient consumption of energy in developing countries have either not been done or have only recently been started. Energy consumption has been on the rise globally due to increased urbanization, industrializations, and population growth [4]. However, this increase in energy consumption has resulted in environmental degradation including climate change, air pollution, and resource depletion. As a result, there is a growing need for an integrated approach that incorporates energy management strategies and renewable energy sources to address these concerns.
1.1. Motivation
The smart energy market highlights not only the individual smart energy grid but also all energy grids such as electricity, thermal, and gas. These smart grids should be connected so as to better exploit synergies across the different individual energy grids. In light of the anticipated shift to the smart energy market, the role of future energy sources depends on a variety of criteria, including their cost, technical capabilities, the availability of suitable sites, and the necessity for energy storage or load balancing [5]. The revenue management system is the backbone of the energy generation industry. Over the years, the industry has developed sophisticated systems for forecasting demand, controlling inventory by price, and responding to competitors’ prices in the smart energy market revenue [6]. It incorporates the application of pricing strategies and information systems in order to allocate the appropriate energy capacity to the appropriate client at the appropriate price at the appropriate moment. In today’s world, revenue management is a widely established subject in the field of aviation, hospitality, auto rental, cruise line, rail freight, and television broadcast industries [7,8,9,10,11,12]. Other industries have also investigated revenue management methodologies such as the planning issue at a broadcasting corporation and renewable and sustainable energy [13,14,15]. Revenue management improves energy-aware resource allocation without raising costs through market forecasting and price strategy [16]. The situation-based stochastic framework was used for the variable modeling of pool market prices and customer group demand in the smart grid environment [17]. An optimization framework for an energy storage system combining cooling and heating systems was proposed based on price demand response strategy and analysis [18]. The technical (tools and machines on which managers work and become proficient at operating after a certain time) and social skills (interpersonal skills or manager’s skills that can be used in every job) improved revenue energy management [19]. Iris and Lam (2021) [20] suggested integrated energy management and operations planning for posts as large-scale energy end users. This planning could significantly reduce costs with energy arbitrage and load shifting under a demand response mechanism in a smart grid. The cargo inventory costs were affected by the speed of logistics operations of ships. The speed models in energy-efficient maritime transportation were surveyed with respect to both the economy and environment [21]. A detailed literature review on energy efficiency in ports and containers was conducted, where technologies such as cold-ironing, the electrification of equipment, energy storage systems, and smart grid and micro-grids were discussed. Furthermore, methods regarding energy consumption and emission assessment were discussed [22]. Several different energy revenue management strategies, including capacity control, pricing, energy demand, forecasting, and overbooking, appear in [23,24]. A dynamic programming formulation was considered to relate the energy-aware routing for delivering customers [25]. Lai and Ng (2005) [26] proposed an absolute deviation model to maximize revenue from random demands and measure risk in the context of different situations. This pioneered work gave a viable solution to maximize the profit of the hotel industry. Ibrahim et al. [27] constructed a stochastic equilibrium model with three agents’ producer, mid-streamer, and consumer to express the optimal contracting between the producer and the mid-streamer of the oil gas industry. The good-deal risk function was used to measure the risk generated by the proposed model. Philpott et al. [28] studied competitive market equilibrium, uncertainty, and risk in a hydrothermal electricity system where agents optimized their current and future profit, accounting for future prices that depend on uncertain inflows. To explore the solution of equilibrium uncertainty problems in the sector of energy management, researchers may refer [29,30] and references therein.
Feng and Xiao (2006) [31] derived a yield management model to integrate the capacity allocation and pricing strategy for perishable products. A causal relationship between customers’ price fairness perceptions and their behavioral intentions was investigated in the context of electric energy management [32]. A network revenue management system was modeled under horizontal and vertical competition to increase the revenue of competitors in the energy-internet-oriented management [33]. From a review of the literature, it is worth mentioning that simulation is the major technique for investigating the smart home-energy management of day-ahead and real-time energy market problems [34]. Zhang et al. (2019) [35] utilized simulated data to judge the heuristic approaches of accepting or rejecting decisions for energy-aware allocation, which combined dynamic workflow and resource monitoring [36].
1.2. Research Gaps
Although revenue management has been employed in many other industries, the smart energy industry has seen very little application. The energy market capacity has the following characteristics: (i) energy market capacity is perishable in nature and cannot be saved for future sale; (ii) the energy market capacity is fixed, and it is impossible to expand immediately at a reasonable cost; (iii) both the marginal cost and sales cost are small; (iv) the demand of the energy market capacity varies with the time period of each day, such as morning and midnight, and the season of each year like summer, winter, ordinary days, and holidays; and (v) advance bookings are welcomed, which make the smart energy market safe. There are drawbacks to the smart energy market. Smart energy such as the electric energy needs to be transmitted, produced, and consumed. However, the security of the energy grid should also be taken into account [37]. Therefore, a tight policy is necessary for no-shows, cancellations, and overbooking issues [38]. Bookings are encouraged to be made in advance, even one day or half an hour in advance, in order to guarantee the safety and efficiency of the energy grid and energy market. Orders for energy typically last for a period of time such as one day/week/month/year, and the price varies with the quantity and time period [39].
1.3. Contributions and Advantages of the Proposed Model
This paper proposes a new framework approach to support the smart energy market by incorporating the robust optimization technique to particle swarm optimization. The aim is to ensure the efficient usage of available energy. However, the capacity-constrained industries such as electricity energy, wind energy, and solar energy industries frequently struggle to allocate their limited perishable inventories to meet demand from several market segments. It is crucial for the smart energy market system to obtain a noble method to accept the energy booking in advance. Therefore, we are motivated to answer of the following research questions:
- How to operate the energy market in such a way that accounts for risk trade-offs and various price structures?
- How to fulfill the future demands of energy so that total capacity does not exceed the estimated capacity under stochastic situations?
This paper presents the revenue management system to answer the above questions. The revenue management system for the energy industry is more complex than that for airlines and hotel business. The stochastic model is proposed on the basis of the energy market facing stochastic demands with varied prices. A network optimization mechanism [40,41] is applied in the proposed model under an uncertain environment. The network optimization involves stochastic programming formulation to capture the randomness of the unknown demand.
The paper is organized as follows. The notations and parameters used in this paper are introduced in Section 2. The basic mathematical model is formulated in Section 3. The importance of stochastic programming and the solution scheme for robust optimization are discussed in Section 4. The IPSO algorithm for stochastic robust optimization is presented in Section 5. Section 6 illustrates examples to show the effectiveness of the proposed model. Finally, the conclusion and future remarks are given in Section 7.
2. Notations and Assumptions
The procedure of the smart energy booking system is presented in Figure 1.
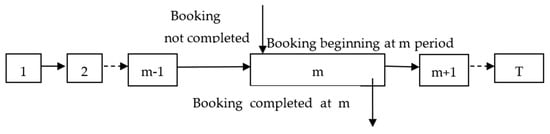
Figure 1.
Process of the smart energy booking system.
For the parameters and variables used in this paper, we adhere to major notations. Let be the energy quantity consumed in each time unit of accepted booking that is considered as the decision variables beginning from the start of time unit to the end of time unit , such that , where are time units. Let C be total capacity of the energy market system. Let be the price for energy booking beginning from the starting time unit to the ending time unit . Let be the energy demand beginning from the start of time unit to the end of time unit . Let be the total energy quantity accepted by advance booking in time unit , given as:
Let be the cost of energy generation in time unit . This can be expressed as: .
Note that variables and are constant over time and is an unobserved error that arises due to the uncertain demand of energy. It is presumed that each booking should be made at least one time unit in advance and that each booking will last at least one time unit.
3. Stochastic Network Formulation
It can be demonstrated from Figure 1 that each time unit is viewed as a node in the network, and the flow after time unit can be computed as
We take into account a particular time unit , where in the planning period is given in Figure 1. The following equation model represents the total energy quantity accepted by advanced booking in time unit ,
If represents the total capacity of the energy market and is the actual demand of energy on time unit , then the specific constraint for day should be satisfied:
where . We formulate our robust optimization model as:
Therefore,
In order to acquire the future demands of the energy market, we propose the following mathematical programming:
Maximize Equation (6).
Subject to
for all
4. Stochastic Formulation in Robust Optimization Scheme
In the energy market, the mentioned parameters in Equation (4) are uncertain at the starting of the planning period. Moreover, the revenue may not be constant, as the decision managers may like to fix different pricing that results in different demands. Revenue managers compute such a problem by replacing the parameters with better point estimators. For instance, expected value can be used to replace the uncertain parameter of . However, practitioners can obtain success by utilizing the expected value approach. The drawback of this approach is that it does not give a feasible solution. One may apply sensitivity analysis for corrective action [12]. Decision makers prefer to use proactive tools to obtain the feasible solutions.
Since it is hard to entirely eliminate uncertainty in the proposed model, accepting uncertainty first, understanding it, and incorporating it into the planned decision model are the best ways to make decisions in an uncertain world. When it comes to solving stochastic problems, robust optimization [12,13] integrates goal programming and the scenario-based description of unknown data. In light of demand uncertainty, the decision maker typically deals with many situations. We assume that the decision maker has a set of scenarios where associated with unknown parameters. For each scenario, the corresponding probability is , such that and . We assume the following measurements of robustness:
Definition 4.1
(Solution robustness): An optimal solution a robust solution with respect to optimality if it remains “close” to optimal for any scenario .
Definition 4.2
(Model robustness): An optimal model qualifies a robust model if the model continues “almost” feasible under any circumstances .
The philosophy of robust optimization is constructed based on the trade-off between solution robustness and model robustness. A stochastic programming model is obtained, and an absolute deviation is used to measure the risk of falling revenues. We propose the following model:
Maximize
Subject to
where ,
Note that and are non-negative weight factors. The objective function is constructed by combining the expected revenue of the energy market with the mean absolute deviation of the revenue. Parameter is a risk-aversion factor. The risk factor’s values reflect the decision makers’ levels of risk aversion. We show that the expected revenue decreases and the risk-aversion factor increases. These two terms can be viewed as a measurement of robust trade-off solution. The absolute deviation in the third term is a model robustness measurement, and the parameters are the penalty factors for constraint violations. The decision makers adjust the energy supply durations by changing the corresponding weighing . The proposed model generates robust solutions using the mean absolute values as penalties.
5. Improved Particle Swarm Optimization in Stochastic Robust Optimization Scheme
Eberhart and Kennedy [42] developed the Particle Swarm Optimization (PSO) algorithm, a stochastic and population-based optimization technique that uses a swarm of particles. This method maps high-dimensional data sets to lower-dimensional data sets with little mapping error. PSO does not take into account information from other particles because this search algorithm is based on local and global search processes. The search in the solution space is unidirectional. When particles cannot get away from local minima, it unquestionably suffers from premature convergence. This drawback is addressed by the improved particle swarm optimization (IPSO). In the IPSO, all particles are ranked according to their fitness value, decided by their personal best . The information from the top particles is selected to adjust the behavior policy for each particle in its next iteration ( in this paper). Thereby, the search of IPSO turns out to be multi-directional and precise. The global convergence ability of the proposed method is also improved. The basic formulation for the IPSO method is as follows:
where is the study factor of particle, and are two constants, and are two random parameters taken from open interval, is the best position of particle after the iteration, and is the position that gives the best value of the objective function. The particle is a top particle among n particles. Note that and are two position vectors and the difference is the vector subtraction. The IPSO size is the total amount of particles, which is fixed as 10. For a revenue management system, all parameters of the particle position are either initialized or updated during the search process that helps to present a feasible sales plan. In order to avoid infeasible particle position for , we adjust Equation (17) as follows:
If is feasible, then
If is not feasible, then
In order to balance global and local search ability, a suitable maximum velocity should be confirmed, and the velocity of the particles should vary within interval. Usually, is selected between 10% and 20% of the total variation. In this paper, 10% of the project duration is used as the maximal velocity . During the IPSO search, if particle’s velocity in direction is beyond interval, its velocity for calculating maximum velocity should be adjusted as follows:
If , then,
If , then
The main goal is to find solutions that can remain acceptable over an extended period of time. The different swarms track peaks and collect information about their behavior. This information is utilized to make decisions about the next robust solution. The main goal is to improve the quality of selected solutions. In the next section, we illustrate several examples to demonstrate the proposed scheme. Note that the meta-heuristic technique is used for proposed optimization problems to improve the performance of the smart energy market system.
6. Illustrative Examples
We first take a look at a deterministic single-scenario example of the smart energy market demand problem.
6.1. Deterministic Situation for Single Scenario
A 12-month planning horizon has been established, starting from the month of January to the month of December. The energy market has a maximum capacity of 7000 MWh (megawatt-hour). For ease of use, the cost for energy storage made in advance is set at 0.54 CNY/KWh. Each time unit, the energy generation cost changes depending on how much energy is consumed. The energy demands for all pairs of are forecast, as shown in Table 1. For instance the demand of energy starts from time unit to the time unit , such that. If this condition does not satisfy, then we obtain empty cells in Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6. The energy market’s consumers are mainly related to submerged membrane bioreactors load consumers, which are based on permeate production. The demand is usually higher in the month of March, median in the month of August, and shorter in the months of November and December. The anticipated demands for all months are depicted in Table 1.

Table 1.
Demands (KWh) for single scenario.

Table 2.
Optimal solution (KWh) for single scenario.

Table 3.
Demands (KWh) for first scenario with probability 0.1.

Table 4.
Demands for second scenario with probability 0.3.

Table 5.
Optimal solutions for first scenario with probability 0.1.

Table 6.
Optimal solutions (KWh) for second scenario with probability 0.3.
There is no deviation because every parameter is deterministic. The IPSO solves the integer programming problem, and Table 2 provides a summary of the best outcomes for the requirement of energies given in Table 1. The best optimal solutions are presented in Table 2 if the risk factor is set to 1.
When different risk factor λ values are used, different projected revenue values are obtained. These are shown in Figure 2. The different values of the parameter of risk trade-off factor represent different degrees of management’s risk aversion.
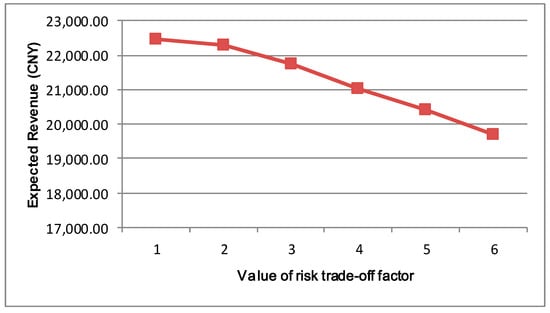
Figure 2.
Relationship between expected revenue and risk trade-off factor.
Figure 2 shows that as the risk-trading-off factor rises, the predicted revenue falls. The model causes the values of the decision variable to be zero and zero projected revenue when the risk trade-off factor is very large. Thus, this operated the energy market in such a way to account for risk trade-offs and various price structures.
We now offer the scenario in which the energy market would wish to plan for various future demand levels under stochastic situations.
6.2. Stochastic Situation for Two Scenarios
We now consider the case where the energy market would like to take two future-demand scenarios into its planning, although the energy market management will fix their prices (0.54) for these scenarios. In this case the revenue varied, and the only stochastic variable is the demand . Suppose there are two scenarios with a probability of 0.1 and 0.3, respectively. The demands are shown in the following Table 3 and Table 4 for the two scenarios. For simplicity, all weights are set to be equal to 1. This is the computational aspect of the smart energy market problem under a stochastic situation. The demands of energy start from the month of January to the month of December. The uncertain data causes the different strategies and management attitudes. Therefore, the weight parameters are used. The optimal solutions are summarized in Table 5 and Table 6.
From the above experimental results, we conclude that the future demands of energy should be fulfilled in such a way that the total capacity of energy should not exceed the estimated capacity under stochastic situations.
Furthermore, in the smart energy market system, optimizing production scheduling is crucial for efficient recourse utilization and meeting production targets. This system focuses on addressing sustainability concerns by minimizing energy consumption in the scheduling process. The algorithm takes into account factors such as machine setup times, processing rates, and energy profiles to generate optimal schedules. The improved particle swarm optimization algorithm is implemented for energy-efficient production scheduling. Parameters such as number of particles, iterations, and job/machine specification are customized. A fitness function is taken that considers both completion time and energy consumption. In Figure 3, the optimal of energy efficiency (EE) is visualized as follows:
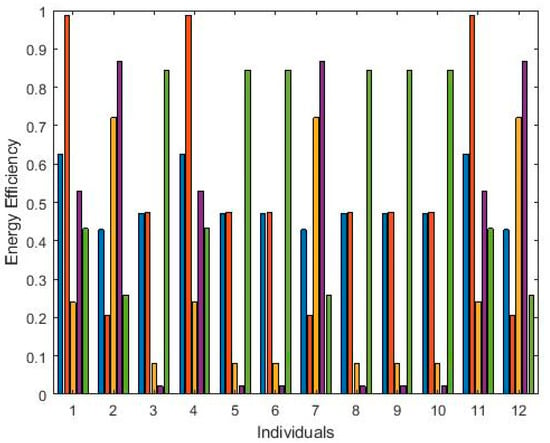
Figure 3.
Optimal job scheduling for EE.
We have included five different categories of energy consumption for every individual. Five distinct colors are used in Figure 3 to indicate the energy efficiency of the five different forms of energy usage. Higher energy efficiency values are considered more appropriate for choosing the best option. In Table 7, we present the optimal solutions for the consumption of energy using improved particle swarm optimization technique for twelve different individuals.

Table 7.
Optimal solutions (KWh) for consumption of energy using IPSO.
We present the sensitivity analysis that is needed for the particle swarm optimization technique. Therefore, we have used the robustness check in Table 8. The model is affected by uncertainties in control inputs. A sensitivity analysis is used before the decision making to validate the robustness of the design decision related to the energy consumption and comfort [39].

Table 8.
Robustness check for energy efficiency affected by uncertainties.
7. Conclusions and Future Directions
In order to solve the smart energy market problem with variable demands, we present the stochastic techniques in the proposed optimization model. This model combines robust optimization and improved particle swarm optimization methods. The goal function takes into account the risk aversion of the decision makers. The risk of energy demand deviating from the expected value is measured by the mean absolute value. We have also shown how to operate the energy market in a way that accounts for risk trade-offs and various price structures. We have also fulfilled the future demands of energy under two scenarios with a probability 0.1 and 0.3. We have performed the robustness check for the proposed model. The present research problem can be formulated using the equilibrium uncertainty model, which is the objective of our future research. We hope that this future research will spur useful insights to develop the energy policy.
Author Contributions
Conceptualization, B.Z., L.S., M.Y., K.-K.L. and B.R.; methodology, B.Z., L.S., M.Y., K.-K.L. and B.R..; software, B.Z., L.S., M.Y., K.-K.L. and B.R.; validation, B.Z., L.S., M.Y., K.-K.L. and B.R.; writing—original draft preparation, B.Z., L.S., M.Y., K.-K.L. and B.R.; supervision, K.-K.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is unavailable due to ethical restrictions.
Acknowledgments
All authors are highly thankful to the respective universities/institute for their support of research. We are grateful to the respected editor and reviewers for their valuable comments which helped us to improve the article. The fifth author is supported by the Centre for Digital Transformation, Indian Institute of Management Ahmedabad, India.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bilan, Y.; Serhiy, K.; Inna, M. Recent Advances in the Energy Market Development: Current Challenges and Perspectives of Energy Crises in Academia. Energies 2023, 16, 2332. [Google Scholar] [CrossRef]
- Cui, L.; Suyun, Y.; Xuan, N.; Mei, D. Exploring the risk and economic vulnerability of global energy supply chain interruption in the context of Russo-Ukrainian war. Resour. Policy 2023, 18, 103373. [Google Scholar] [CrossRef]
- Adebayo, T.S.; Kartal, M.T.; Ağa, M.; Al-Faryan, M.A.S. Role of country risks and renewable energy consumption on environmental quality: Evidence from MINT countries. J. Environ. Manag. 2023, 327, 116884. [Google Scholar] [CrossRef]
- Tomin, N.; Shakirov, V.; Kurbatsky, V.; Muzychuk, R.; Popova, E.; Sidorov, D.; Kozlov, A.; Yang, D. A multi-criteria approach to designing and managing a renewable energy community. Renew. Energ. 2022, 199, 1153–1175. [Google Scholar] [CrossRef]
- Nalan, Ç.B.; Murat, Ö.; Nuri, Ö. Renewable energy market conditions and barriers in Turkey. Renew. Sustain. Energy Rev. 2009, 13, 1428–1436. [Google Scholar] [CrossRef]
- Motalleb, M.; Ghorbani, R. Non-cooperative game-theoretic model of demand response aggregator competition for selling stored energy in storage devices. Appl. Energy 2017, 202, 581–596. [Google Scholar] [CrossRef]
- Pereira, B.A.; Lohmann, G.; Houghton, L. Technology trajectory in aviation: Innovations leading to value creation (2000–2019). Int. J. Innov. Stud. 2022, 6, 128–141. [Google Scholar] [CrossRef]
- Matsuoka, K. Effects of revenue management on perceived value, customer satisfaction, and customer loyalty. J. Bus. Res. 2022, 148, 131–148. [Google Scholar]
- Kunnumkal, S.; Talluri, K. Choice network revenue management based on new tractable approximations. Transp. Sci. 2019, 53, 1591–1608. [Google Scholar] [CrossRef]
- Namin, A.; Gauri, D.K.; Kwortnik, R.J. Improving revenue performance with third-degree price discrimination in the cruise industry. Int. J. Hosp. Manag. 2020, 89, 102597. [Google Scholar] [CrossRef]
- Crevier, B.; Cordeau, J.F.; Savard, G. Integrated operations planning and revenue management for rail freight transportation. Transp. Res B-Meth. 2012, 46, 100–119. [Google Scholar] [CrossRef]
- Schauerte, R.; Feiereisen, S.; Malter, A.J. What does it take to survive in a digital world? Resource-based theory and strategic change in the TV industry. J. Cult. Econ. 2021, 45, 263–293. [Google Scholar]
- Petrick, A.; Steinhardt, C.; Gönsch, J.; Klein, R. Using flexible products to cope with demand uncertainty in revenue management. OR Spectr. 2012, 34, 215–242. [Google Scholar] [CrossRef]
- Kimms, A.; Müller-Bungart, M. Simulation of stochastic demand data streams for network revenue management problems. OR Spectrum 2007, 29, 5–20. [Google Scholar] [CrossRef]
- Ak, M.; Kentel, E.; Savasaneril, S. Operating policies for energy generation and revenue management in single-reservoir hydropower systems. Renew. Sust. Energ. Rev. 2017, 78, 1253–1261. [Google Scholar] [CrossRef]
- Morozko, N.; Morozko, N.; Didenko, V. Energy prices and households’ incomes growth proportions in russia’s case context. Int. J. Energy Econ. Policy 2021, 11, 243–250. [Google Scholar] [CrossRef]
- Nojavan, S.; Zare, K.; Mohammadi-Ivatloo, B. Optimal stochastic energy management of retailer based on selling price determination under smart grid environment in the presence of demand response program. Appl. Energy 2017, 187, 449–464. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Y.; Wang, Y.; Zeng, M.; Li, F.; Wang, Y.; Zhang, Y. Energy management of smart micro-grid with response loads and distributed generation considering demand response. J. Clean. Prod. 2018, 197, 1069–1083. [Google Scholar] [CrossRef]
- Lyu, W.; Liu, J. Soft skills, hard skills: What matters most? Evidence from job postings. Appl. Energy 2021, 300, 117307. [Google Scholar]
- Iris, Ç.; Lam, J.S.L. Optimal energy management and operations planning in seaports with smart grid while harnessing renewable energy under uncertainty. Omega 2021, 103, 102445. [Google Scholar] [CrossRef]
- Psaraftis, H.N.; Kontovas, C.A. Speed models for energy-efficient maritime transportation: A taxonomy and survey. Transp. Res. Part C Emerg. 2013, 26, 331–351. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. A review of energy efficiency in ports: Operational strategies, technologies and energy management systems. Renew. Sust. Energ. Rev. 2019, 112, 170–182. [Google Scholar]
- Özer, Ö.; Phillips, R. (Eds.) The Oxford Handbook of Pricing Management; OUP Oxford: Oxford, UK, 2012. [Google Scholar]
- Gomez-Herrera, J.A.; Miguel, F. Anjos. Optimization-based estimation of power capacity profiles for activity-based residential. Int. J. Electr. Power Energy Syst. 2019, 104, 664–672. [Google Scholar] [CrossRef]
- Funabashi, Y.; Shibata, A.; Negoro, S.; Taniguchi, I.; Tomiyama, H. A dynamic programming algorithm for energy-aware routing of delivery drones. In Advances in Artificial Intelligence and Data Engineering: Select Proceedings of AIDE 2019; Springer: Singapore, 2021; pp. 1217–1226. [Google Scholar]
- Lai, K.K.; Ng, W.L. A stochastic approach to hotel revenue optimization. Comput. Oper. Res. 2005, 32, 1059–1072. [Google Scholar] [CrossRef]
- Abada, I.; Ehrenmann, A.; Smeers, Y. Modeling gas markets with endogenous long-term contracts. Oper. Res. 2017, 65, 856–877. [Google Scholar] [CrossRef]
- Philpott, A.; Ferris, M.; Wets, R. Equilibrium, uncertainty and risk in hydro-thermal electricity systems. Math. Program. 2016, 157, 483–513. [Google Scholar] [CrossRef]
- Abada, I.; Ehrenmann, A.; Lambin, X. Unintended consequences: The snowball effect of energy communities. Energy Policy 2020, 143, 111597. [Google Scholar] [CrossRef]
- Abada, I.; de Maere d’Aertrycke, G.; Ehrenmann, A.; Smeers, Y. What models tell us about long-term contracts in times of the energy transition. Econ. Energy Environ. Policy 2019, 8, 163–182. [Google Scholar] [CrossRef]
- Feng, Y.; Xiao, B. Optimal policies of yield management with multiple predetermined prices. Oper. Res. 2000, 48, 332–343. [Google Scholar] [CrossRef]
- Mori, R.J. It’s not price; It’s quality. Satisfaction and price fairness perception. World Dev. 2021, 139, 105302. [Google Scholar] [CrossRef]
- Hong, B.; Zhang, W.; Zhou, Y.; Chen, J.; Xiang, Y.; Mu, Y. Energy-Internet-oriented microgrid energy management system architecture and its application in China. Appl. Energy 2018, 228, 2153–2164. [Google Scholar] [CrossRef]
- Akbari-Dibavar, A.; Nojavan, S.; Mohammadi-Ivatloo, B.; Zare, K. Smart home energy management using hybrid robust-stochastic optimization. Comput. Ind. Eng. 2020, 143, 106425. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, T.; Chen, M.; Wei, T.; Zhou, J.; Hu, S.; Buyya, R. Energy-aware virtual machine allocation for cloud with resource reservation. J. Syst. Softw. 2019, 147, 147–161. [Google Scholar] [CrossRef]
- Akhter, N.; Othman, M. Energy aware resource allocation of cloud data center: Review and open issues. Clust. Comput. 2016, 16, 1163–1182. [Google Scholar] [CrossRef]
- Gosavi, A.; Ozkaya, E.; Kahraman, A.F. Simulation optimization for revenue management of airlines with cancellations and overbooking. OR Spectrum 2007, 29, 21–38. [Google Scholar] [CrossRef]
- Gabriel, S.A.; Conejo, A.J.; Plazas, M.A.; Balakrishnan, S. Optimal price and quantity determination for retail electric power contracts. IEEE Trans. Power Syst. 2006, 21, 180–187. [Google Scholar] [CrossRef]
- Russell, E.; Kennedy, J. Particle swarm optimization. Proc. IEEE Int. Conf. Neural Netw. 1995, 4, 1942–1948. [Google Scholar]
- Coelho, A.; Iria, J.; Soares, F.; Lopes, J.P. Real-time management of distributed multi-energy resources in multi-energy networks. Sustain. Energy Grids Netw. 2023, 34, 101022. [Google Scholar] [CrossRef]
- González, P.; Villar, J.; Díaz, C.A.; Campos, F.A. Joint energy and reserve markets: Current implementations and modeling trends. Electr. Power Syst. Res. 2014, 109, 101–111. [Google Scholar]
- Attia, S.; Gratia, E.; De Herde, A.; Hensen, J.L. Simulation-based decision support tool for early stages of zero-energy building design. Energy Build. 2012, 49, 2–15. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).