Enhanced Economic Load Dispatch by Teaching–Learning-Based Optimization (TLBO) on Thermal Units: A Comparative Study with Different Plug-in Electric Vehicle (PEV) Charging Strategies

Abstract

This research paper presents an enhanced economic load dispatch (ELD) approach using the Teaching–Learning-Based Optimization (TLBO) algorithm for 10 thermal units, examining the impact of Plug-in Electric Vehicles (PEVs) in different charging scenarios. The TLBO algorithm was utilized to optimize the ELD problem, considering the complexities associated with thermal units. The integration of PEVs in the load dispatch optimization was investigated, and different charging profiles and probability distributions were defined for PEVs in various scenarios, including overall charging profile, off-peak charging, peak charging, and stochastic charging. These tables allow for the modeling and analysis of PEV charging behavior and power requirements within the power system. By incorporating PEVs, additional controllable resources were introduced, enabling more effective load management and grid stability. The comparative analysis showcases the advantages of the TLBO-based ELD model with PEVs, demonstrating the potential of coordinated dispatch strategies leveraging PEV storage and controllability. This paper emphasizes the importance of integrating PEVs into the load dispatch optimization process, utilizing the TLBO algorithm, to achieve economic and reliable power system operation while considering different PEV charging scenarios.

1. Introduction

The economic load dispatch (ELD) in power systems aims to optimize the allocation of power output from generating units while meeting operational constraints and maintaining supply-demand balance [1]. Various optimization algorithms have been developed to improve the efficiency of solving the ELD problem.

One such algorithm is the ant lion optimization (ALO) algorithm, which mimics the hunting behavior of ant lions and has shown promising results in solving the hydrothermal power generation scheduling problem [2]. Another approach combines the Harris Hawks Optimizer (HHO) with adaptive hill climbing to enhance the performance of solving the ELD problem [3]. The optimization of hybrid power systems, incorporating non-conventional distributed energy resources, has also gained attention, utilizing algorithms like the Social Spider algorithm for cost and emission optimization [4].

To address valve-point effects in the ELD problem, improved algorithms such as the improved social spider optimization algorithm (ISSO) and teaching–learning-based optimization (TLBO) have been proposed [5,6]. Additionally, the particle swarm optimization (PSO) method has been enhanced to solve dynamic load economic dispatch problems (DLED) [7]. The integration of plug-in electric vehicles (PEVs) into power systems introduces new challenges and opportunities. Techniques like PID controllers tuned through QUABCO have been proposed for frequency control in multi-area power systems with PEVs [8]. Furthermore, optimization problems involving the integration of PEVs and renewable energy resources (RERs) have been addressed, such as economic and environmental load dispatch (EELD) [9]. The dynamic economic load dispatch problem with PEVs has been tackled using the Social Spider Algorithm (SSA) [10]. Additionally, a novel approach called dynamic non-dominated sorting multi-objective biogeography-based optimization (Dy-NSBBO) has been proposed to solve the multi-objective dynamic economic emission load dispatch problem, considering PEVs [11]. The dispatch of energy requirements in a smart distribution grid (SDG), with a focus on managing PEVs, has been addressed through a new methodology [12]. Strategies combining PEVs and RERs have also been proposed to reduce greenhouse gas emissions from the transport and electric power industries [13].

Furthermore, an operating framework for aggregators of PEVs has been introduced, along with studies on the impact of PEVs on the power system and load factor [14,15]. The importance of considering PEV load planning strategies for cost efficiency and grid stability has been emphasized [16]. Enhancements were made to the social spider algorithm to improve its performance in handling large-scale optimization problems. It may contain novel techniques or modifications to the algorithm that contribute to its efficiency and effectiveness in solving complex optimization tasks [17]. AC power flow refers to the flow of electrical power through a network, and it is often subject to complex nonlinear equations due to the nature of the alternating current. Overcoming these nonlinear constraints is a critical aspect of optimizing and managing distributed energy systems effectively [18]. A novel multiperiod optimal power-flow approach that leverages demand-responsive loads to enhance steady-state voltage stability [19]. innovative transactive control approaches for energy communities with independent energy storage systems, addressing optimal scheduling for prosumers and storage providers [20]. WOANN, for optimizing power flow control in hybrid renewable energy systems (HRES) that include photovoltaic and wind turbines with energy storage. WOANN combines the Whale Optimization Algorithm (WOA) and Artificial Neural Networks (ANN) to enhance the learning process [21].

This paper addresses the Economic Load Dispatch (ELD) problem, a significant aspect of power systems, and extends its scope to incorporate the integration of Plug-in Electric Vehicles (PEVs). The primary objective is to evaluate the performance of the Teaching–Learning-Based Optimization (TLBO) algorithm in optimizing the economic load dispatch when considering the presence of PEVs. This study aims to provide valuable insights into the impact of PEV integration on power system performance and identify strategies to enhance power generation efficiency. By conducting a comparative analysis across different PEV charging scenarios, this research sheds light on the trade-offs between cost stability and peak fluctuations in mean and maximum fuel costs, emphasizing the importance of reliable power supply. Additionally, the computational efficiency of the TLBO algorithm is assessed, vital for real-time applications. The results of this analysis offer valuable guidance for policymakers and grid operators, facilitating the development of strategies to optimize power system operation and efficiently manage PEV charging behavior. This work contributes to a better understanding of the benefits and challenges associated with PEV integration, ultimately leading to more efficient and reliable power systems.

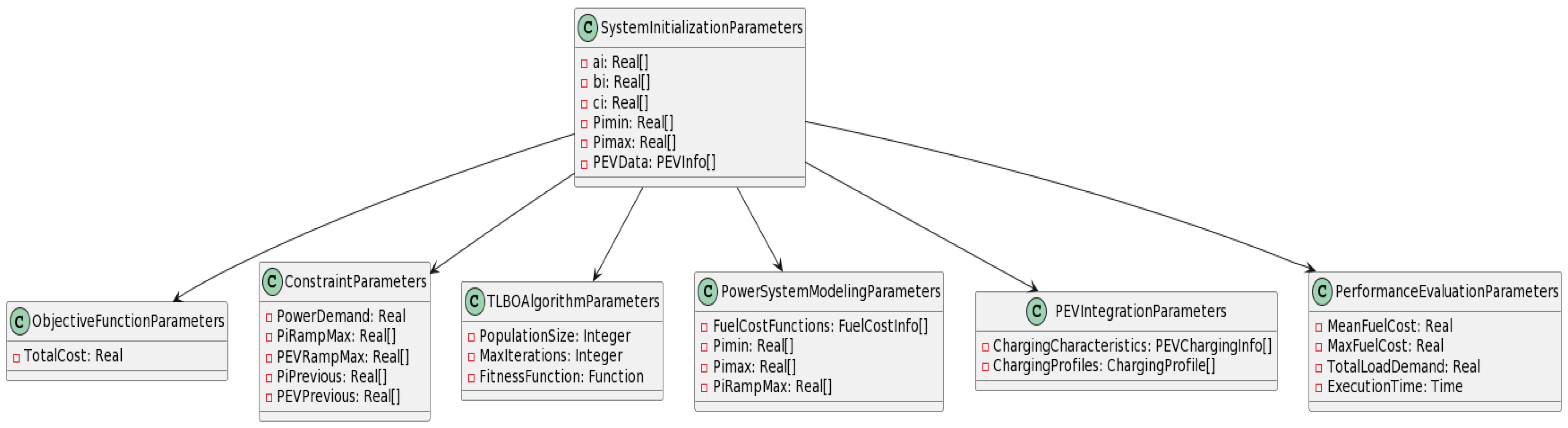
Innovatively, this research combines the fields of economic load dispatch and PEV integration, providing a complete view of how optimizing power generation interacts with the evolving landscape of electric vehicle adoption. Furthermore, the use of the TLBO algorithm in this context represents a novel application, demonstrating its effectiveness in addressing complex, real-world challenges. Figure 1 provides a comprehensive visual representation of the key parameters involved in the system initialization process. It covers essential categories, including thermal unit data, power output limits, PEV data, objective function parameters, constraint parameters, TLBO algorithm parameters, power system modeling parameters, and PEV integration parameters. This diagram serves as a valuable reference for understanding the various inputs and configurations required for optimizing power system operation with the inclusion of Plug-in Electric Vehicles (PEVs). It aids in ensuring efficient and reliable power generation while considering factors like fuel costs, power demand, and the dynamic behavior of PEVs.

2. Literature Review

The literature review explores various optimization techniques applied to the economic load dispatch (ELD) problem, considering factors such as valve-point loading effects, renewable energy resources, and the integration of plug-in electric vehicles (PEVs). Hao et al. [1] focused on the differential evolution algorithm with different mutation strategies. Dubey et al. [2] focused on ant lion optimization for short-term wind-integrated hydrothermal power generation scheduling. Al-Betar et al. [3] proposed a hybrid Harris Hawks optimizer. In addition, Adhvaryyu et al. [4] utilized a bio-inspired social spider algorithm for dynamic economic emission load dispatch in hybrid power systems. Several algorithms have been proposed to enhance the efficiency and accuracy of ELD solutions. Subathra et al. [5] introduced a hybrid approach combining the cross-entropy method and sequential quadratic programming for ELD. Banerjee et al. [6] employed teaching–learning-based optimization considering valve point loading effects. Yuan et al. [7] introduced an improved particle swarm optimization for dynamic load dispatch. Maharana and Dash [8] utilized a quantum-behaved artificial bee colony-based conventional controller. Singh presented the use of the chaotic slime mold algorithm for ELD problems. Yang et al. [9] proposed a modified social spider optimization method for ELD with valve-point effects.

Behera et al. [10] proposed dynamic economic load dispatch with PEVs using the social spider algorithm he also explored economic load dispatch with renewable energy resources and PEVs. Ma et al. [11] employed a multi-objective biogeography-based optimization approach considering PEV charging. Benalcazar et al. [12] focused on short-term economic dispatch of smart distribution grids with active PEV involvement.

Wu et al. [14] addressed load scheduling and dispatch for aggregators of PEVs. Proposed non-convex dynamic economic/environmental dispatch considering PEV loads. Yang et al. [15] introduced a self-learning teaching–learning-based optimization method for dynamic economic/environmental dispatch with multiple plug-in electric vehicle loads. Other studies investigated the integration of plug-in electric vehicles (PEVs) into the power system. Trongwanichnam et al. [16] studied the impact of PEV load planning on load factor and total generation cost in a power system. Additionally, several optimization algorithms were enhanced for large-scale optimization and solving the economic dispatch problem, such as the improved social spider algorithm by Baş and Ülker [17] and the modified social spider algorithm presented a methodology-based gradient-based optimizer for economic load dispatch. The mentioned studies demonstrate the diverse range of optimization techniques utilized in economic load dispatch, including hybrid algorithms, bio-inspired algorithms, particle swarm optimization, and teaching–learning-based optimization. They also highlight the significance of considering valve-point loading effects and the integration of plug-in electric vehicles in achieving more efficient and sustainable power system operation.

3. Formulation of Mathematical Optimization Model

Minimization of total generation cost in economic load dispatch with 10 Thermal Units. The aim of economic load dispatch is to minimize the overall generation cost, which encompasses the sum of fuel costs associated with all thermal units.

3.1. ELD Formulation

Mathematically, this objective can be represented by the following expression:

Total Cost = ∑ (a_i × P_i² + b_i × P_i + c_i)

(1)

Here, a_i, b_i, and ci represent the coefficients associated with the quadratic, linear, and constant terms, respectively, while P_i corresponds to the power output of each thermal unit. The economic load dispatch problem formulation focuses on optimizing the power generation levels of the 10 thermal units within the power system to achieve the minimum total cost of generation.

• where

P_i = Power output of thermal unit i (where i = 1, 2, …, 10)

a_i, b_i, c_i = Fuel cost coefficients for thermal unit i (specific to each unit)

The economic load dispatch problem must satisfy the following constraints. The total power output of all units must meet the power demand requirement. Mathematically, it can be expressed as

∑P_i = Power Demand

(2)

The power output of each thermal unit must lie within its minimum and maximum power limits. Mathematically, the constraint for each unit i can be expressed as

P_{i min} ≤ P_i ≤ P_{i max}

(3)

The rate at which the power output of each thermal unit can change is limited. This constraint ensures a smooth transition between power levels. Mathematically, the constraint for each unit i can be expressed as

P_{i ramp max} ≤ P_i − P_{i previous} ≤ P_{i ramp max}

(4)

where:

P_{i ramp max}: Maximum ramp rate for thermal unit i;

P_{i previous}: Power output of thermal unit i in the previous time period.

The formulated problem aims to find the optimal power output levels for each thermal unit that minimize the total generation cost while satisfying the power demand and operational constraints. Solving this problem will provide the economic dispatch solution for the given power system configuration.

Reactive Power Constraints: Reactive power (Q) limits for each thermal unit:

Q_min ≤ Q ≤ Q_max

(5)

Voltage Limits: Voltage limits for the power system:

V_min ≤ V ≤ V_max

(6)

Frequency Regulation Limits: Frequency limits for the power system

f_min ≤ f ≤ f_max

(7)

3.2. PEVs in ELD Formulation

To incorporate Plug-in Electric Vehicles (PEVs) in the economic load dispatch problem formulation, we need to consider the additional power demand and the charging characteristics of the PEVs. To follow is an expanded formulation that includes PEVs:

3.2.1. Variable Selection

P_i: Power output of thermal unit i (where i = 1, 2, …, 10);

P_PEV: Power demand from Plug-in Electric Vehicles.

3.2.2. Problem Formulation

The objective remains the same, i.e., to minimize the total generation cost. The objective function now includes the fuel costs for thermal units and the cost of charging PEVs. Mathematically, the objective function can be expressed as

Minimize: Total Cost = ∑ (a_i × P_i² + b_i × P_i + c_i) + Cost PEV

(8)

where:

Cost PEV: Cost of charging Plug-in Electric Vehicles (depends on the charging rate and pricing scheme).

3.2.3. Constraints

Power Demand Constraint

The total power output of all units and the charging demand from PEVs must meet the overall power demand requirement. Mathematically, it can be expressed as

∑P_i + P_PEV = Power Demand

(9)

Power Output Limits

The power output of each thermal unit and the charging demand from PEVs must lie within their respective minimum and maximum power limits. Mathematically, the constraint for each unit i can be expressed as

P_{i min} ≤ P_i ≤ P_{i max}

(10)

0 ≤ P_PEV ≤ P_PEVmax

(11)

Ramp Rate Limits

The rate at which the power output of each thermal unit can change and the charging demand from PEVs can change is limited. This constraint ensures a smooth transition between power levels. Mathematically, the constraint for each unit i can be expressed as

P_{i ramp max} ≤ P_i − P_{i previous} ≤ P_{i ramp max}

(12)

P _{PEV ramp max} ≤ P_PEV − P_{PEV previous} ≤ P_{PEV ramp max}

(13)

where:

P_{i ramp max}: Maximum ramp rate for thermal unit i;

P_{PEV ramp max}: Maximum ramp rate for PEV charging demand;

P_{i previous}: Power output of thermal unit i in the previous time period;

P_{PEV previous}: Charging demand from PEVs in the previous time period.

Table 1. Comprehensive PEV charging profile probability distribution.

In Every 6 h
0.100	0.100	0.095	0.070	0.050	0.030
0.010	0.003	0.003	0.013	0.020	0.020
0.020	0.020	0.020	0.007	0.003	0.003
0.015	0.028	0.050	0.095	0.100	0.100

explores the comprehensive probability distribution of PEV charging profiles. It encapsulates the likelihood of different charging rates adopted by PEVs across diverse time intervals or states. Each row within this table corresponds to a specific state or interval, while each column represents a distinct charging rate.

Table 2. Off-peak PEV charging profile.

In Every 6 h
0.185	0.185	0.090	0.090	0.040	0.040
0.000	0.000	0.000	0.000	0.000	0.000
0.000	0.000	0.000	0.000	0.000	0.000
0.000	0.000	0.000	0.000	0.185	0.185

, specifically custom-made for off-peak periods, outlines the PEV charging profile during these hours. It articulates the probability distribution of PEVs utilizing various charging rates when off-peak conditions prevail. The values within the table denote the probability of PEVs employing specific charging rates during these periods.

Table 3. Peak charging PEV charging profile probability distribution.

In Every 6 h
0.000	0.000	0.000	0.000	0.000	0.000
0.000	0.000	0.000	0.000	0.000	0.000
0.185	0.185	0.185	0.185	0.090	0.090
0.040	0.040	0.000	0.000	0.000	0.000

focuses on the probability distribution of PEV charging rates during peak charging hours. It delineates the likelihood of PEVs opting for different charging rates during peak periods.

Table 4. Stochastic case PEV charging profile probability distribution.

In Every 6 h
0.057	0.049	0.048	0.024	0.026	0.097
0.087	0.048	0.011	0.032	0.021	0.057
0.038	0.022	0.021	0.061	0.032	0.022
0.028	0.022	0.055	0.025	0.035	0.082

presents a stochastic or probabilistic scenario for PEV charging profiles. It provides insight into the probability distribution of PEVs employing diverse charging rates under stochastic conditions. Each value within this table corresponds to the probability of a particular charging rate occurring in the stochastic case.

These tables define the charging profiles and probability distributions for PEVs in different scenarios: overall charging profile, off-peak charging, peak charging, and stochastic charging. They help to model and analyze the charging behavior and power requirements of PEVs in the power system.

4. Teaching–Learning-Based Optimization (TLBO)

TLBO was selected as the optimization algorithm for solving the economic load dispatch problem. TLBO is a population-based metaheuristic algorithm inspired by the teaching and learning process in a classroom. It incorporates the concepts of teachers and students to optimize the objective function. The Teaching–Learning-Based Optimization (TLBO) algorithm is used to solve an optimal power dispatch problem in a power system. The TLBO algorithm aims to find the optimal power output solution for a set of thermal units while considering factors such as fuel cost, load demand, and the presence of plug-in electric vehicles (PEVs).

The Teaching–learning-Based Optimization (TLBO) algorithm is a population-based optimization technique that draws inspiration from the teaching and learning processes observed in a classroom. In TLBO, the individuals in a population represent potential solutions to an optimization problem, and the algorithm iteratively improves these solutions over generations. Below (Algorithm 1) is a basic mathematical modeling of the TLBO algorithm.

Algorithm 1. TLBO

Initialization: 1. Generate an initial population of potential solutions (individuals) to the optimization problem: P = [X1, X2, …, Xn], where Xi represents an individual solution. Algorithm Steps: 2. Repeat the following steps until a stopping criterion is met (e.g., a maximum number of iterations is reached): Teaching Phase: 3. Calculate the fitness value for each individual in the population: Fiti = f(Xi), where f(Xi) is the objective function value of individual Xi. 4. Identify the best (lowest) and worst (highest) fitness values in the current population: Fitbest and Fitworst, respectively. 5. Calculate the mean fitness value (Fitmean) of the population. 6. For each individual Xi in the population:   • Calculate the teaching factor (TFi) as: TFi = Xi + rand(0, 1) × (Xi − Fitmean)   • If Fit(TFi) < Fit(Xi), replace Xi with TFi; otherwise, keep Xi unchanged. Learning Phase: 7. For each individual Xi in the population (excluding the best individual):   • Select a random individual Xⱼ (j ≠ i) from the population.   • Calculate the learning factor (LFi) as: LFi = Xi + rand(0, 1) × (Xⱼ − Xi)   • If Fit(LFi) < Fit(Xi), replace Xi with LFi; otherwise, keep Xi unchanged. End of Iteration Result: 8. Return the best solution found in the population as the optimal solution.

In this mathematical representation, Fit(X_i) represents the fitness value of individual X_i, and rand (0, 1) denotes a random number between 0 and 1. In Figure 2 the TLBO algorithm iteratively updates the individuals in the population through teaching and learning phases, aiming to converge towards the optimal solution of the given optimization problem.

The algorithm begins by defining the power system data, including the 10 number of thermal units, their fuel costs, and minimum and maximum load levels. It also incorporates data related to PEVs, such as their charging and discharging power capacities, and the total number of PEVs. Next, the TLBO algorithm parameters are set, including the maximum number of iterations and the population size. The fitness function is defined, which calculates the total cost of a power output solution based on the fuel cost, PEV discharging cost, and a penalty term for deviations from the total load demand. The TLBO algorithm iterates through a series of steps for a specified number of iterations. The population is initialized with random power output solutions within the feasible range for each thermal unit. The fitness of each individual in the population is evaluated using the defined fitness function.

Within each iteration, the algorithm goes through a teacher–learner process. The best individual in the population is selected as the “teacher” for the current iteration. Each learner, except the teacher, updates its solution by combining information from the teacher and other learners. This learning process involves mutation and the application of a PEV charging profile.

If the mutated solution has improved fitness and the power output is non-negative, the individual’s solution is updated. The best individual in the population is determined based on fitness, and it replaces the worst individual. The best fitness value for the current iteration is printed to track progress. Throughout the 24-h period, the algorithm stores the best individual and its fitness for each hour. After the algorithm completes, the best individual and its fitness for the entire 24-h period are determined. Additionally, the maximum fuel cost, mean fuel cost, and standard deviation of fitness values are calculated.

The results are printed, including the optimal power dispatch for the 24-h period, the mean fuel cost, maximum fuel cost, total load demand, and the standard deviation of fitness values. Two plots are generated: one displaying the incremental cost versus power output and another showing the optimal dispatch for the 24-h period. Finally, the execution time of the code is measured and printed. The TLBO algorithm optimizes the power dispatch by iteratively improving the population’s solutions based on the defined fitness function and the constraints of the power system.

TLBO Parameters

The parameters of the TLBO algorithm are determined, including the population size, the number of iterations, and the teaching factor as per

Table 5. TLBO algorithm parameter used for the test system (MATLAB).

Maximum Number of Iterations	Number of Particles	% Function for Evaluating Fitness
100	30	fitness = @(P, c, pev_discharging_power, pev_num, total_load_demand)sum(c × P) + sum(pev_discharging_power) × pev_num + 0.01 × (sum(P) − total_load_demand)2

. These parameters play a crucial role in the convergence and performance of the optimization algorithm.

5. Power System Modeling

The power system is modeled considering the characteristics and constraints of 10 thermal units. This includes the fuel cost functions, power output limits, reactive power limits, voltage limit, and frequency limits. The modeling takes into account the economic and operational aspects of the power system.

Incorporating Plug-in Electric Vehicles (PEVs)

The study investigated the impact of plug-in electric vehicles on the economic load dispatch problem. The characteristics of PEVs, such as their charging/discharging rates and energy demands, were integrated into the power system model. This allows for a comparative analysis of the economic load dispatch with and without the presence of PEVs. We conducted a comprehensive study of different scenarios in power system modeling, utilizing the parameters specified in the provided code. This study focused on optimizing the economic load dispatch while incorporating various aspects of Plug-in Electric Vehicles (PEVs). The parameters used in our investigation, as outlined in the code, include the following:

A.

Power System Data:

• Number of Thermal Units (n): 10;
• Thermal Unit Data:
• Unit Fuel Cost (USD/MWh): Randomly generated values between 10 and 30 for each unit;
• Minimum Load (MW): Randomly generated values between 50 and 100 for each unit;
• Maximum Load (MW): Determined based on minimum load plus a random value between 100 and 300 MW for each unit.

B.

Plug-in Electric Vehicle (PEV) Data:

• Charging Power (MW): Constant value of 2 MW for all 24 h;
• Discharging Power (MW): Constant value of 1.5 MW for all 24 h;
• Number of PEVs (pev_num): 1,100,000.

C.

Total Load Demand: 500,000 MW

D.

TLBO Algorithm Parameters:

• Maximum Number of Iterations (maxiter): 100;
• Population Size (popsize): 30.

E.

PEV Charging Profile Probability Distribution (pev_profile):

• A 4 × 6 matrix representing the probability distribution of PEV charging rates during different time intervals or states.

F.

Constraint Values:

• Power Factor Constraint (power factor constraint): 0.9;
• Reactive Power Constraints (Q_max and Q_min): Randomly generated values for each of the 10 thermal units;
• Voltage Limits (V_min and V_max): V_min = 0.95, Vmax = 1.05;
• Frequency Regulation Limits (f_min and f_max): f_min = 59.9 Hz, f_max = 60.1 Hz.

These parameters were systematically studied to evaluate the impact of PEVs on the economic load dispatch problem under various conditions. Our analysis considered different charging profiles, demand scenarios, and system constraints to provide valuable insights into the operation and optimization of power systems in the presence of Plug-in Electric Vehicles.

6. Comparative Study

The economic load dispatch problem is solved using the TLBO algorithm for both scenarios: with and without PEVs. The objective function values, generation costs, and system performance metrics are compared between the two cases. This analysis provides insights into the effects of PEVs on economic dispatch and the overall power system operation.

In Figure 3, we visualize the relationship between power output and incremental cost for the optimal dispatch solution obtained in Case-1. The x-axis represents the power output in megawatts (MW), ranging from the minimum to the maximum possible power output for the thermal units. The y-axis represents the incremental cost in dollars per megawatt-hour (USD/MWh). Each data point on the graph corresponds to a specific power level for the thermal units, and its associated incremental cost. The curve illustrates how the incremental cost changes as the power output varies. Typically, in economic load dispatch problems, the goal is to find the point on this curve where the incremental cost is minimized while meeting the load demand and satisfying various system constraints.

Analyzing this graph provides insights into the cost-effectiveness of the chosen power generation strategy. It helps operators and planners make informed decisions about how to allocate power generation resources to meet the demand efficiently and economically. The descending trend of the curve indicates that, in this Case-1 scenario, as the power output increases, the incremental cost tends to decrease. This suggests that the power system is operating efficiently, and the dispatch strategy minimizes fuel costs while satisfying the constraints.

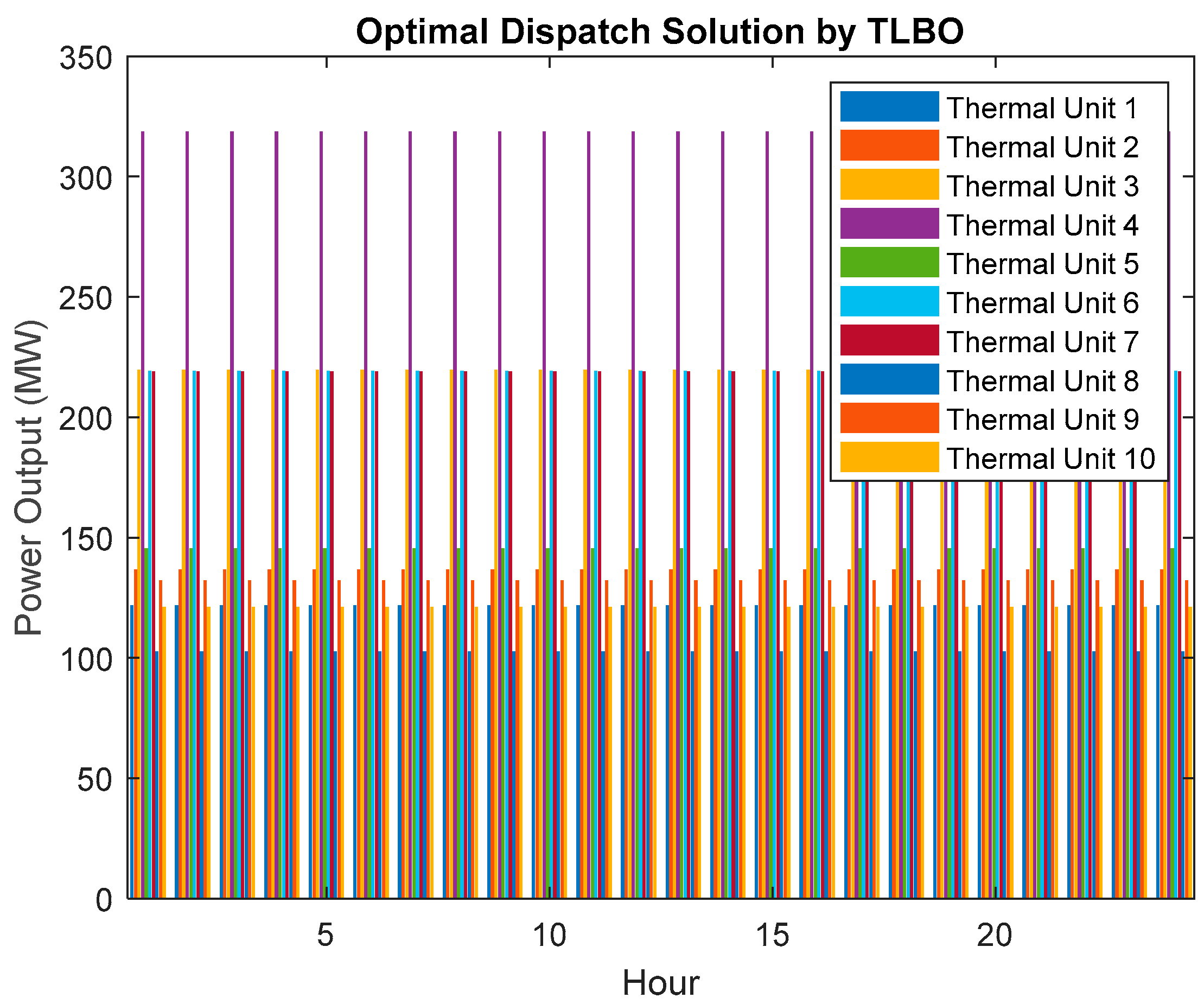
In Figure 4, we present the results of the optimal power dispatch for a 24-h period considering the integration of Plug-in Electric Vehicles (PEVs) into the power system. This case, referred to as Case-2, explores how the presence of PEVs impacts the economic load dispatch and overall power system operation. This analysis in Case-2 provides valuable insights into how the presence of PEVs affects the economic dispatch of power generation units. It demonstrates the system’s ability to maintain power quality and meet load demands while considering various operational constraints and the integration of electric vehicles.

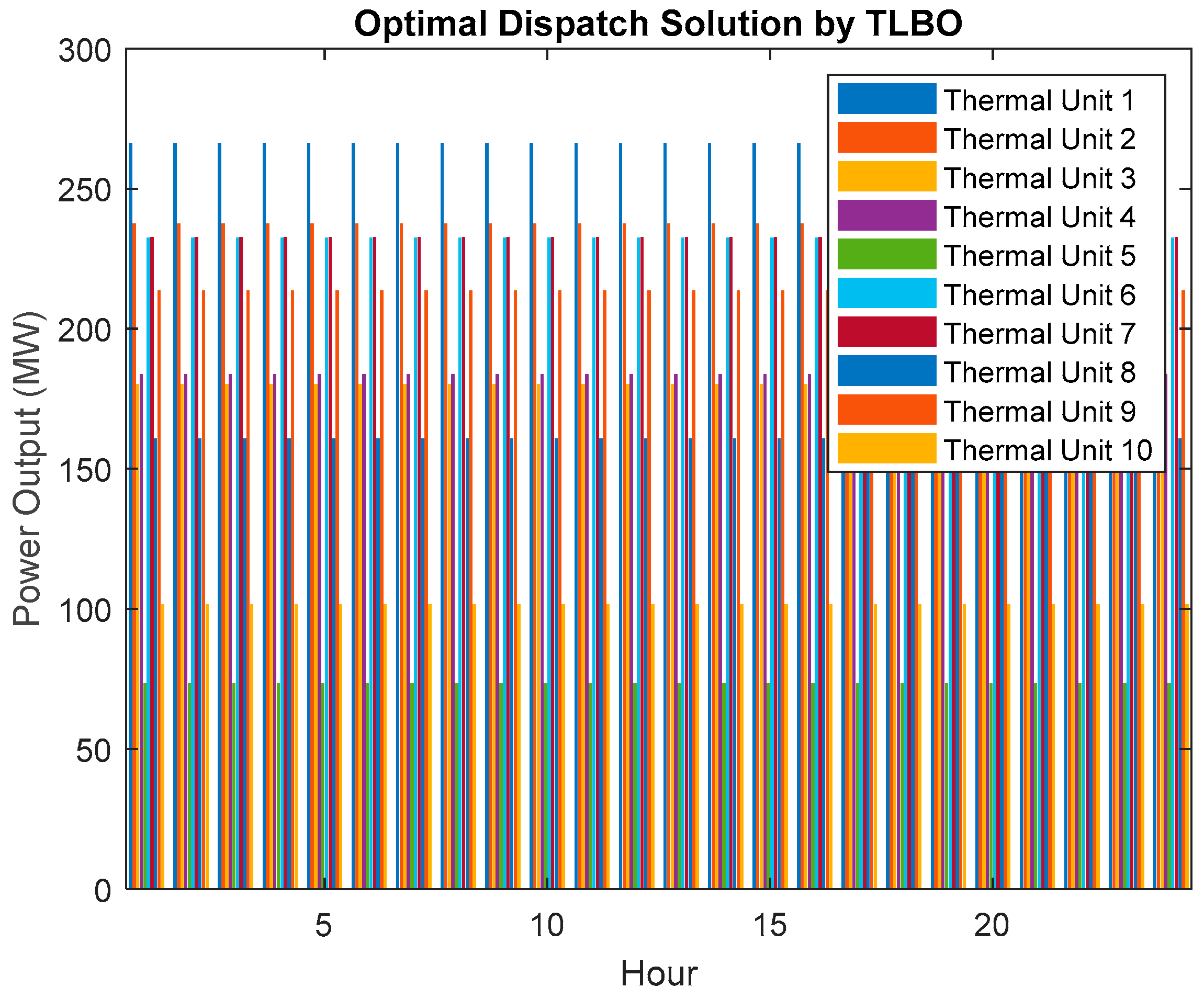
In Figure 5, we present the results of the optimal power dispatch for a 24-h period, focusing on the integration of Plug-in Electric Vehicles (PEVs) during peak charging times. This case, referred to as Case-3, explores the impact of PEVs specifically during peak charging hours.

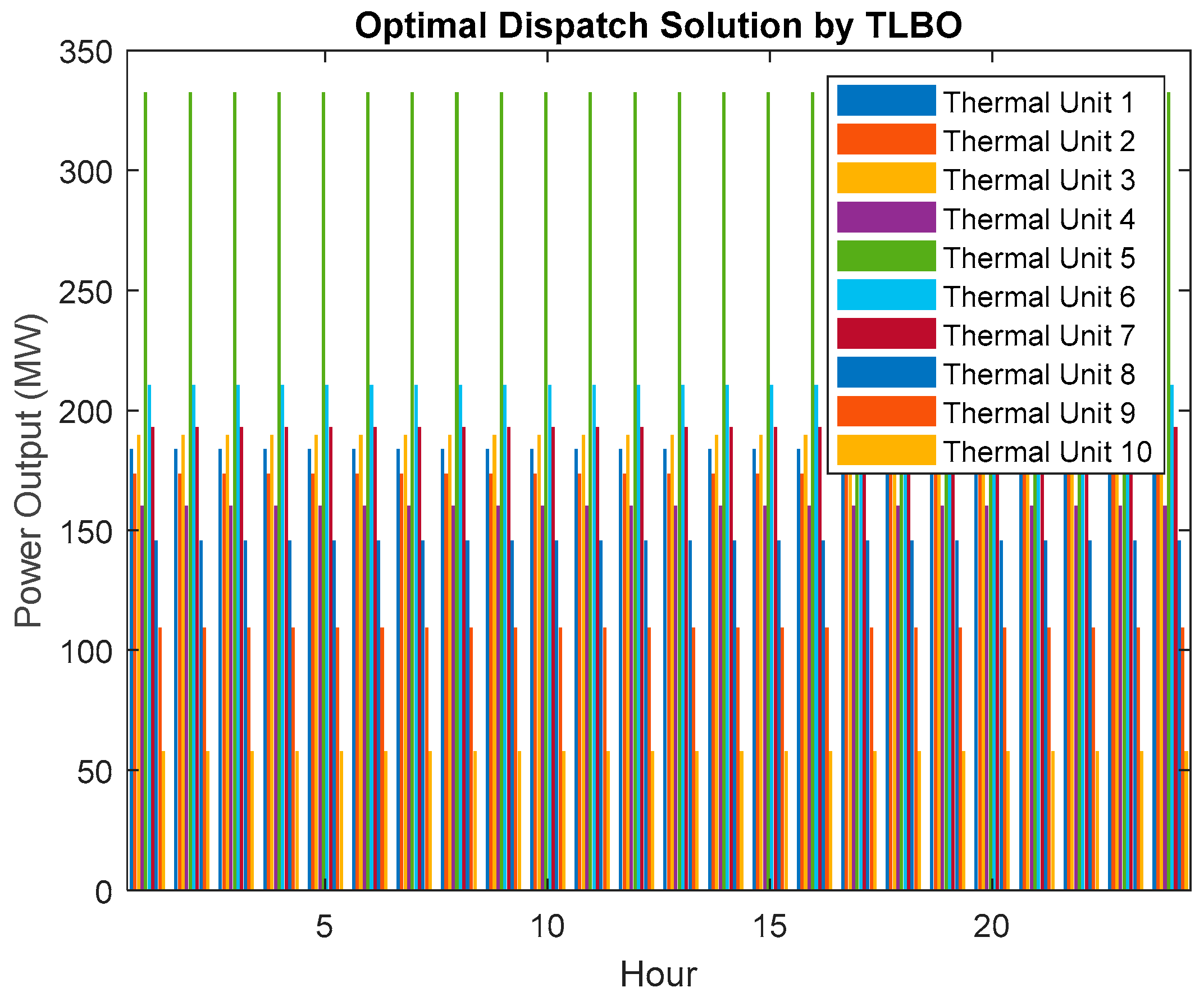
In Figure 6, we illustrate the results of the optimal power dispatch for a 24-h period, considering the integration of Plug-in Electric Vehicles (PEVs) with stochastic charging patterns. This case, known as Case-4, explores the impact of PEVs with varying charging rates under stochastic conditions.

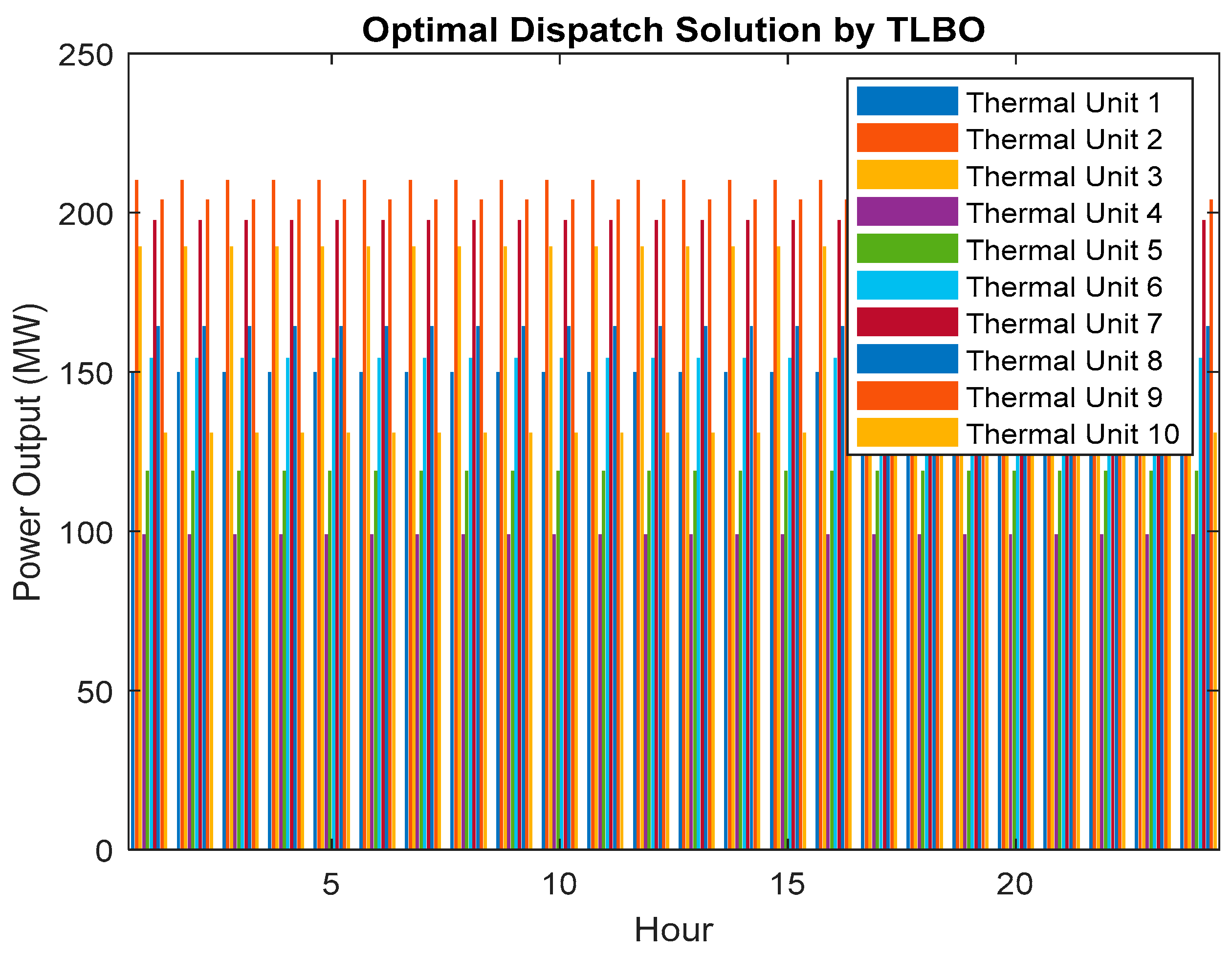
In Figure 7, we present the results of the optimal power dispatch for a 24-h period in the absence of Plug-in Electric Vehicles (PEVs). This scenario represents the baseline case where the power system operates without the influence of PEVs.

6.1. Performance Evaluation

To perform a performance evaluation of the optimal dispatch results for the five different cases, we can analyze several key aspects of each case, including fuel cost, power quality constraints, and execution time. To follow is a summary of the performance evaluation for each case:

Table 6. Optimal dispatch (MW) for different cases.

CASE	OPTIMAL DISPATCH (MW)
1	121.7618, 136.6276, 219.6462, 318.8199, 145.4081, 219.3682, 219.1291, 102.7175, 132.2551, 121.2341
2	266.3376, 237.5001, 180.1528, 183.8382, 73.3828, 232.5696, 232.6864, 160.8654, 213.5547, 101.5323
3	183.7645, 173.5095, 189.6529, 160.2237, 332.5216, 210.5164, 193.0506, 145.7652, 109.4641, 58.0265
4	212.3430, 92.6064, 305.1989, 138.9323, 63.7220, 196.6889, 287.4684, 173.7009, 253.4107, 124.3653
5	149.9129, 210.1876, 189.3452, 99.0123, 119.0229, 154.4955, 197.7076, 164.4806, 204.0498, 130.8848

presents the optimal dispatch of power generation in megawatts (MW) for five different cases. Each row represents a case, and each column represents a thermal unit within the power generation system. The values in the table indicate the MW of power dispatched by each thermal unit in each case.

Table 7. Comparison of Reactive Power Constraints for Different Cases.

Case	Thermal Unit	Qmin (MVAr)	Qmax (MVAr)
1	1	−7	17
	2	−7	10
	3	−9	13
	4	−9	10
	5	−6	11
	6	−7	19
	7	−7	17
	8	−8	13
	9	−9	20
	10	−9	10
2	1	−9	18
	2	−6	15
	3	−7	17
	4	−8	12
	5	−10	15
	6	−7	12
	7	−6	18
	8	−8	16
	9	−9	10
	10	−5	19
3	1	−6	20
	2	−7	14
	3	−9	17
	4	−6	10
	5	−10	13
	6	−8	17
	7	−6	14
	8	−8	16
	9	−7	12
	10	−7	11
4	1	−5	17
	2	−10	14
	3	−10	13
	4	−9	12
	5	−8	15
	6	−8	17
	7	−7	14
	8	−5	12
	9	−6	19
	10	−5	10
5	1	−5	18
	2	−8	10
	3	−5	18
	4	−10	17
	5	−5	17
	6	−8	12
	7	−8	19
	8	−7	16
	9	−9	14
	10	−5	18

provides a comparison of reactive power constraints for different cases in an energy system. Each case represents a unique configuration of thermal units, and the table lists the minimum (Qmin) and maximum (Qmax) allowable reactive power output in megavars (MVAr) for each thermal unit. These constraints play a crucial role in maintaining the stability and efficiency of the power generation system by ensuring that the reactive power output of each unit falls within the specified limits. The table serves as a reference for understanding how the reactive power constraints vary across the different cases, aiding in the analysis and optimization of power generation operations.

6.1.1. Fuel Cost Analysis for Different Cases

In the context of optimizing power generation and distribution, fuel cost is a critical factor to consider. The following analysis evaluates the fuel cost performance of five distinct cases, each representing an optimal dispatch scenario.

Case 1:

 •

Mean Fuel Cost: USD4968.70 per hour;

 •

Maximum Fuel Cost: USD67,012.00 per MWh.

Case 2:

 •

Mean Fuel Cost: USD4965.80 per h;

 •

Maximum Fuel Cost: USD60,162.00 per MWh.

Case 3:

 •

Mean Fuel Cost: USD4968.29 per h;

 •

Maximum Fuel Cost: USD49,068.00 per MWh.

Case 4:

 •

Mean Fuel Cost: USD4966.48 per h;

 •

Maximum Fuel Cost: USD50,419.00 per MWh.

Case 5:

 •

Mean Fuel Cost: USD4967.72 per h;

 •

Maximum Fuel Cost: USD45,017.00 per MWh.

6.1.2. Performance Ranking

Based on mean fuel cost, the performance ranking is as follows:

• Case 2 has the lowest mean fuel cost at USD4965.80 per h, making it the most cost-effective in terms of fuel consumption;
• Case 4 closely follows with a mean fuel cost of USD4966.48 per h;
• Case 5 is also competitive with a mean fuel cost of USD4967.72 per h;
• Case 3 has a slightly higher mean fuel cost at USD4968.29 per h;
• Case 1 has the highest mean fuel cost at USD4968.70 per h.

These findings indicate that Case 2 is the most efficient among the evaluated scenarios, delivering the lowest mean fuel cost. However, it is important to consider that fuel cost is just one aspect of optimization, and other factors such as power quality constraints, system stability, and execution time may also influence the final decision for power generation and distribution. Further analysis and trade-offs are essential to determine the optimal case for a specific operational scenario.

6.1.3. Power Quality Constraints

Ensuring that all cases meet the specified voltage and frequency limits (V_min, V_max, f_min, f_max) is a fundamental requirement in power system operation and optimization. Meeting these power quality constraints is essential for maintaining a stable and reliable electrical grid. All cases meet voltage limits (V_min = 0.95, V_max = 1.05) and frequency regulation limits (f_min = 59.90 Hz, f_max = 60.10 Hz).

6.1.4. Reactive Power Constraints:

Each thermal unit has different reactive power constraints in all cases.

All cases satisfy these constraints for all thermal units.

6.1.5. Execution Time

Case 1: 3.51 s;

Case 2: 1.67 s;

Case 3: 1.53 s;

Case 4: 1.31 s;

Case 5: 3.43 s.

Case 2 appears to be the most favorable in terms of both fuel cost and execution time. However, the choice of the optimal dispatch case may also depend on other factors such as system stability, robustness, and specific operational requirements. Further analysis and trade-offs may be necessary to make the final decision on which case to implement in a real-world scenario.

Table 8. Optimal Dispatch Performance Summary.

Case	Mean Fuel Cost (USD/HR)	Max Fuel Cost (USD/MWH)	Total Load Demand (MW)	Execution Time (s)
1	USD4968.70	USD67,012	500,000	3.51
2	USD4965.80	USD60,162	500,000	1.67
3	USD4968.29	USD49,068	500,000	1.53
4	USD4966.48	USD50,419	500,000	1.31
5	USD4967.72	USD45,017	500,000	3.43

presents a summary of the optimal dispatch performance for different cases. Each case represents a specific configuration of power generation units in an energy system.

7. Results and Analysis

The analysis of these results reveals the impact of different PEV charging scenarios on the economic operation of power systems. Off-peak charging and peak charging strategies can potentially lead to cost savings during specific periods, while the stochastic case introduces additional complexities and uncertainties. These findings can assist in developing optimized load management strategies and highlight the need for efficient utilization of PEVs to achieve enhanced economic load dispatch in power systems. In the “Results and Analysis” section, Table 8 presents a comprehensive summary of the optimal dispatch performance for various cases within the context of the research conducted. Each case corresponds to a distinct configuration of power generation units, and the table details crucial performance metrics, including mean fuel cost per hour, maximum fuel cost per megawatt-hour (MWh), total load demand in megawatts (MW), and the execution time in seconds. These metrics are pivotal in evaluating the efficiency and effectiveness of the proposed optimization algorithm. Case 1 exhibits the highest mean fuel cost at USD4968.70/h, with a maximum fuel cost of USD67,012/MWh and an execution time of 3.51 s. In contrast, Case 4 showcases a lower mean fuel cost of USD4966.48/h and a maximum fuel cost of USD50,419/MWh, coupled with the shortest execution time of 1.31 s among the cases analyzed. These findings shed light on the diverse trade-offs between economic and computational factors in optimizing power generation systems. Furthermore, the results underscore the importance of selecting an appropriate case configuration to achieve the desired balance between cost efficiency and computational efficiency. The obtained results are analyzed and interpreted to conclude the effectiveness of the TLBO algorithm in solving the enhanced economic load dispatch problem. The impact of PEVs on the economic dispatch and the potential benefits or challenges associated with their integration into the power system is discussed.

8. Discussion and Future Work

The results of the comparative analysis provide valuable insights into the economic load dispatch (ELD) problem considering different Plug-in Electric Vehicle (PEV) charging scenarios. This discussion explores the implications of the findings and suggests potential avenues for future research.

Firstly, the analysis highlights the impact of PEV charging strategies on the overall system performance. Off-Peak charging (Case-2) shows potential cost savings during low-demand periods, while Peak charging (Case-3) demonstrates the effectiveness of utilizing PEVs during high-demand periods. These findings suggest the importance of developing optimized charging strategies that align with the system’s load profile and aim to balance electricity supply and demand efficiently.

Furthermore, the stochastic nature of PEV charging in Case-4 introduces additional complexities and uncertainties, resulting in higher fuel costs. This highlights the need for robust optimization techniques and stochastic modeling approaches to address the uncertainties associated with PEV charging behavior and their integration into power systems. Future work can focus on developing advanced optimization algorithms and stochastic modeling techniques to better capture and manage the variability and uncertainties in PEV charging patterns. Additionally, the comparative analysis sheds light on the trade-offs between fuel costs and system performance. The results indicate that while PEV integration can increase fuel costs in some scenarios, it also offers opportunities for load management and grid stability. Future research can explore innovative demand response mechanisms, tariff structures, and pricing strategies to incentivize PEV owners to align their charging patterns with system requirements, ultimately leading to more cost-effective and efficient operation of power systems. Moreover, the execution time analysis provides insights into the computational requirements of different cases. Future work can focus on optimizing the computational efficiency of the load dispatch optimization algorithms to reduce the execution time further, enabling real-time or near-real-time decision-making in practical applications.

The analysis can be extended to consider a larger-scale integration of PEVs and their potential impact on distribution networks, grid infrastructure, and power quality. Future studies can explore the challenges and opportunities associated with managing the increased demand and load variability from a larger fleet of PEVs and investigate the potential benefits of coordinated charging and vehicle-to-grid (V2G) strategies. In conclusion, the discussion emphasizes the importance of further research to refine and expand the understanding of the economic load dispatch problem in the presence of PEVs. Future work can focus on developing advanced optimization algorithms, stochastic modeling approaches, demand response mechanisms, and grid integration strategies to leverage the full potential of PEVs in achieving economic and reliable operation of power systems.

9. Potential Future Work

9.1. Advanced Optimization Algorithms

Further research can focus on developing and implementing advanced optimization algorithms, such as genetic algorithms, particle swarm optimization, or hybrid approaches, to enhance the performance and efficiency of economic load dispatch (ELD) with PEVs. These algorithms can be tailored to address the specific challenges and complexities associated with integrating PEVs into power systems.

9.2. Stochastic Modeling and Uncertainty Analysis

As the stochastic case (Case-4) highlights the uncertainties associated with PEV charging behavior, future work can delve into advanced stochastic modeling techniques and uncertainty analysis to better capture and manage the variability and uncertainties in PEV charging patterns. This can enable more accurate decision-making and robust optimization of ELD with PEVs.

9.3. Demand Response and Pricing Strategies

Investigating innovative demand response mechanisms, tariff structures, and pricing strategies can encourage PEV owners to align their charging patterns with system requirements and optimize their energy consumption. Future research can explore the design and evaluation of incentive-based schemes that promote load shifting and smart charging strategies to improve system efficiency and minimize costs.

9.4. Grid Integration and Infrastructure Considerations

As the scale of PEV integration increases, it becomes crucial to assess the impact on distribution networks, grid infrastructure, and power quality. Future studies can focus on the challenges and opportunities associated with managing the increased demand and load variability from a larger fleet of PEVs while considering the integration of vehicle-to-grid (V2G) technologies to support bidirectional power flow and grid services.

9.5. Real-Time Decision-Making and Control Strategies

Further work can explore the development of real-time or near-real-time decision-making and control strategies for ELD with PEVs. This can involve the integration of advanced sensing, communication, and control technologies to enable dynamic load management, optimal scheduling, and active power balancing in response to changing grid conditions and PEV charging dynamics.

By addressing these areas, researchers can contribute to the optimization, reliability, and sustainability of power systems in the presence of increasing PEV penetration.

10. Conclusions

This research paper presented a comprehensive analysis of the economic load dispatch (ELD) problem considering different Plug-in Electric Vehicle (PEV) charging scenarios. The comparative analysis of four cases, namely Off-Peak charging, Probability distribution of PEV, Peak charging, and Stochastic case, has provided valuable insights into the impact of PEV integration on the operation and optimization of power systems.

The results highlighted the trade-offs between fuel costs and system performance in different charging scenarios. Off-peak charging has shown potential cost savings during low-demand periods, while Peak charging has demonstrated the effectiveness of utilizing PEVs during high-demand periods. The stochastic case has introduced complexities and uncertainties, resulting in higher fuel costs. The findings underscore the importance of developing optimized charging strategies that align with the system’s load profile and aim to balance electricity supply and demand efficiently. Additionally, the analysis has highlighted the need for advanced optimization algorithms, stochastic modeling approaches, demand response mechanisms, and grid integration strategies to address the challenges and uncertainties associated with PEV charging behavior.

Furthermore, the research emphasized the potential benefits of coordinated charging and vehicle-to-grid (V2G) strategies, which can enhance system flexibility, grid stability, and overall power system efficiency. Overall, this research contributes to the understanding of the economic load dispatch problem in the presence of PEVs and provides a foundation for future studies in optimizing power system operation with PEVs. By considering the trade-offs, challenges, and opportunities associated with PEV integration, researchers and practitioners can develop strategies and policies that facilitate the efficient, reliable, and sustainable operation of power systems in the era of electric transportation.