Abstract
In order to achieve more effective online monitoring of distribution cables, a deployment scheme of the distribution cable condition monitoring devices based on a wireless sensor network (WSN) has been proposed. The proposed deployment scheme can improve the coverage rate and extend the lifetime of the sensor network. Moreover, the clustering method, node density, and node deployment method of the wireless sensor routing algorithm are improved, and based on isosceles triangle non-uniform deployment, a routing optimization algorithm has been proposed to achieve the balance of the energy consumption of each node in the network. Firstly, according to the energy consumption model of the network, the energy consumption of each cluster is calculated, and then by taking the minimum energy consumption of data transmission between clusters as the constraint condition, the optimal clustering distance of the network is solved. Then, according to the scale of network nodes, the density of routing nodes in each cluster is calculated, and the routing nodes in the cluster are deployed by an isosceles triangle. Finally, according to the cluster head election formula, the routing cluster head nodes in each cluster are selected, and the network data information is transmitted to the base station in a multi-hop manner through the routing cluster head nodes. The simulation results indicated that, compared with the traditional routing optimization algorithms, the proposed algorithm could keep the routing coverage at more than 200% all the time, and can effectively balance the energy consumption of nodes, improve the energy utilization efficiency of the routing nodes, and at least extend the lifetime of the network by two times. Moreover, the longer the cables, the more cost savings and the better the life cycle optimization effect of the proposed scheme. In addition, the proposed scheme can greatly reduce the economic cost of network investment, compared with using the demodulator to obtain monitoring data.
1. Introduction
The safe operation of the distribution cable is an important guarantee for the stability of the power system. If the surrounding environment and operational conditions of the distribution cables are disturbed, the normal operation of electrical energy will be greatly affected [1]. According to statistics [2], general issues of distribution cables include the quality issues of the cables themselves (such as cable defects), corrosion (such as chemical corrosion, the insulation of the cable joints), aging, and excessive load on distribution cables. These issues are likely to cause partial discharges and abnormal temperature rises, leading to cable faults. At the same time, the destructive activities because of artificial external force have also gradually become an important cause of distribution cable failures [3]. At present, most distribution cable faults are permanent faults that cannot be repaired [4]. If the faults are not handled in time, it is easy to cause other cables in the same channel to fire, resulting in power interruption in the area. Therefore, in order to reduce the occurrence rate of distribution cable faults, it is urgent to strengthen the monitoring of factors such as partial discharge of cable defects, external force damage, and operating temperature and timely understand the operating condition of distribution cables [5]. However, if only relying on manual inspection, it will not be able to meet the requirements for the information and intelligent monitoring of power cables. With the increasing attention on the safe operation of distribution cables, the application of wireless sensor networks in the field of cable condition monitoring has become a hot topic in current research. Therefore, if the distribution cables can be monitored in real-time on the basis of wireless sensor networks, the manpower inspection work can be greatly reduced, and the quality of the power supply can be improved [6]. At the same time, because of the structural characteristics of the power cables, the router nodes are deployed in a linear ribbon structure. The data transmission of the linear network is unidirectional, and it is commonly transmitted to the base station in a multi-hop way [7,8,9]. With the increase in the number of information transmission times, the closer to the base station, the more data packets need to be forwarded and the more energy the routing node needs to consume. Eventually, the energy of the routing nodes will be exhausted prematurely, resulting in network interruption and the formation of an “energy hole” phenomenon [10]. Therefore, how to deploy the routing nodes reasonably and effectively solve the problem of an “energy hole” and prolong the network lifetime is the key issue in the study of using wireless sensor networks to monitor the operation condition of the power distribution cables.
At present, many scholars have proposed a variety of related algorithms for the node deployment of linear wireless sensor networks. Most of the research focuses on the coverage and lifetime of the network. In [11], aiming at the problem of water environment monitoring, a node depth adjustment deployment algorithm based on the Voronoi diagram has been proposed. The main objective of the algorithm is to optimize the coverage and connectivity of the network. By reducing the overlay between sensor nodes, the algorithm can improve the coverage of the network while the connectivity is maintained at 100% in different cases. However, the energy balance of the network is not considered in the research. In [12], in order to reduce the energy consumption and the node deployment cost of wireless sensor networks, a wireless sensor network node deployment strategy based on the “X” division has been proposed. In comparison to the conventional partition deployment strategy, the “X” partition deployment strategy can effectively reduce the deployment cost of the network, and in terms of network lifetime, the strategy is longer than the diamond partitioning strategy by more than 50%. However, the cluster head nodes of the strategy are fixed, and the node load near the base station will be increased if the distance is too long so that the common node still retains a good deal of residual energy at the end of the network. In [13], taking into account energy and distance, a routing algorithm based on non-uniform clustering has been proposed; it introduced the idea of the optimal number of cluster heads and improved the probability formula of cluster head election by dynamically introducing weighted coefficients so that it can effectively save the energy consumption of the network and extend the network lifetime. However, the calculation method of the density coverage parameter in the algorithm is not applicable for distribution cables, and the algorithm still has the problem of uneven distribution of the cluster head nodes. In fact, for situations like this, where nodes are unevenly distributed, two relatively effective solutions are proposed in [14]. One is the interactive node method, which corresponds the equilibrium state of the force to the uniform distribution of the nodes by introducing the repulsive force and the damping force. When the node is finally stationary in a balanced state, the location of the uniform distribution of the nodes is also found. The other is the optimal Latin hypercube design method, which can find the uniform distribution of the nodes by the space-filling method even under the condition of multiple variables. The number of nodes involved in both methods is flexible and can provide a uniform distribution for any number of nodes. These two methods provide great ideological inspiration and technical assistance for the follow-up research about the uniform distribution of nodes. In [15], based on the LEACH (Low-Energy Adaptive Clustering Hierarchy) algorithm, the chaotic genetic algorithm has been introduced to find the optimal cluster head by establishing a new fitness function that considers the energy consumption and load so as to improve the energy efficiency of the network and extend the network lifetime. However, it is a pity that the optimal cluster number of the network is not clearly given in the research.
Energy saving is one of the primary optimization goals for wireless sensor networks [16]. In view of the “energy hole” problem of existing wireless network routing nodes and the linear structural characteristics of distribution cables that the length is far greater than the width, this paper proposes a deployment scheme of the condition monitoring devices suitable for the distribution cables, which can realize the optimal deployment of the distribution cable condition monitoring devices. With the purpose of solving the energy consumption problem of the data transmission, an isosceles triangle non-uniform deployment routing optimization algorithm based on IMP-LEACH was presented to balance the energy consumption of the network data transmission. By improving the clustering method and routing node deployment method of IMP-LEACH (Improved Low-Energy Adaptive Clustering Hierarchy) algorithm, the algorithm can optimize the cluster head distribution and cluster size, improve the energy utilization efficiency of the routing nodes, and effectively solve the “energy hole” problem while ensuring the network coverage rate, thus prolonging the lifetime of the entire network.
2. Deployment Scheme of Condition Monitoring Devices for Distribution Cables
The width of the monitoring area of the distribution cable network is far less than the length. All the wireless sensor nodes are arranged on the distribution cables so that the entire WSN generally presents a linear topology [17]. It is generally believed that the greatest operational risk of the distribution cables is fire [18]. Short-circuit faults, insulation defects, and external force damage may lead to abnormal operating temperatures of the cables, thereby causing safety hazards such as channel fires. Therefore, in order to monitor the risks, important cables are usually equipped with various sensors such as temperature sensors, vibration sensors, and partial discharge sensors.
With the purpose of solving the data transmission problem of various sensors, a deployment scheme of the condition monitoring devices based on WSN has been proposed, as presented in Figure 1. The operating condition of distribution cables is monitored by means of a hierarchical topology control. All router nodes within each distance form a cluster of WSNs. Firstly, routers in each cluster are responsible for collecting data monitored by the sensors and then sending the data to the routing cluster head node. Finally, the routing cluster head node fuses the data in the cluster and transmits the data to the base station in the form of a forward multi-hop [19], through which the base station users can integrate and analyze the condition data. Thus, the online real-time monitoring of the entire power distribution cable is realized.
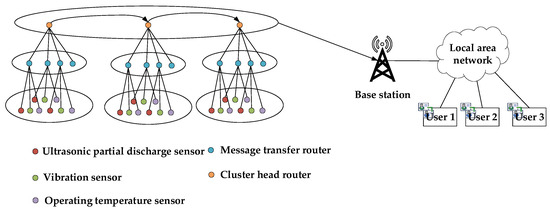
Figure 1.
Hierarchical control diagram of the deployment scheme of the condition monitoring devices.
In the distribution cable condition monitoring devices deployment scheme, as shown in Figure 1, the highest layer of WSN is the routing head node, which is responsible for the data transmission of the entire network. The middle layer is an ordinary routing node, which is responsible for collecting the condition information of the cable perceived by the condition monitoring sensors. The bottom layer is the condition monitoring sensor node, which is responsible for monitoring the operation condition of the power cables in real-time. The specific distribution of condition-monitoring sensor nodes and router nodes is shown in Figure 2. The condition monitoring sensors are arranged side by side in an isosceles triangle evenly, and the routers are deployed in an isosceles triangle equidistant non-uniform cluster in the entire power distribution cable network. In order to prevent the router from losing data during data transmission, the router node adopts the dual coverage mode.
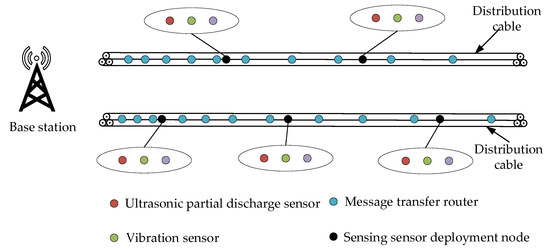
Figure 2.
Deployment diagram of sensor and router nodes.
3. Routing System Modeling
At this stage, most linear networks are deployed in the form of single-line or double-line. Since the location of the cables is relatively fixed and the network space is limited, the cost of adopting a fixed deployment method is relatively low for the deployment of routers. Therefore, in order to facilitate the research, the router network in the paper is based on the following assumptions:
- (1)
- The routing nodes adopt a static deployment method and cannot be moved after deployment. It is assumed that each node can perceive its own location information.
- (2)
- The base station is located outside the middle area of the sensor network, and its position is also fixed. Therefore, according to the symmetry, only the network characteristics located on one side of the base station are studied.
- (3)
- The base station has infinite energy.
- (4)
- Each sensor node is an isomorphic node with the same initial energy; the node energy is known and limited.
- (5)
- Cluster head nodes know each other’s location information and the distance between themselves and the base station.
3.1. Router Network Model
The router network model is presented in Figure 3, where di represents the serial number of each cluster. The distribution cable network is divided into several segments, and all router nodes in each segment form a cluster. The closer the cluster is to the base station, the more routing nodes are deployed. The routing nodes in each cluster are responsible for collecting information and sending it to the cluster head node. After data fusion processing, the cluster head node forwards the information to the base station through multi-hops from back to front.
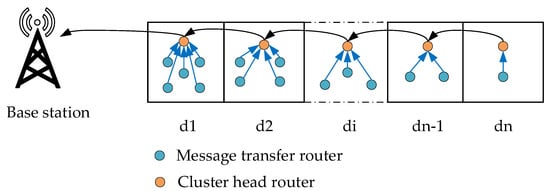
Figure 3.
Network model of router nodes.
3.2. Energy Consumption Model
Data processing and information transmission are the main reasons for the energy consumption of wireless sensor nodes [20]; in order to simplify the research of the problem, the energy consumption of sensor nodes during the sensing process is ignored. In the field of wireless communication, the energy consumption model of wireless sensor networks proposed by Wendi Rabiner Heinzelman in [21] has been widely recognized, as shown in Figure 4.
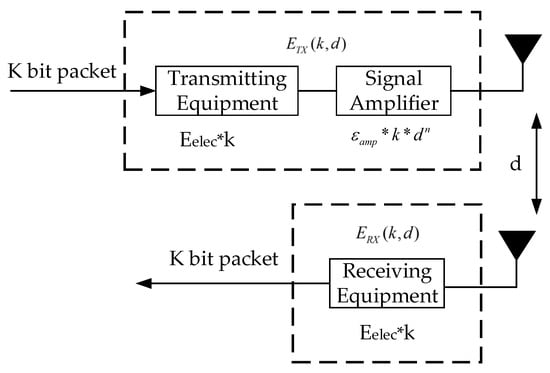
Figure 4.
Wireless communication model.
Assuming that the sensor node sends k-bit data with a transmission distance of d, its energy consumption is as follows:
The energy consumed by the sensor node to receive k-bit data is:
In (1) and (2), is the energy consumed by a node to receive or send one-bit data in nanojoules per bit (nJ/bit), d is the transmission distance of the data, in meters (m).
In (3), is the threshold value of the communication distance in meters (m). When is greater than the transmission distance, the free space model is adopted by sensors. The coefficient of amplifier power consumption is in , . When is less than the transmission distance, the multipath attenuation model is adopted by sensors, and the coefficient of amplifier power consumption is , in [22].
3.3. Energy Consumption Inside the Cluster
The energy consumption model adopts a multi-channel attenuation model, assuming that there are n clusters in the routing network and that a total of k-bit data is generated in each cluster. On the basis of the model of energy consumption, the energy consumed by sending the information collected by the nodes in the cluster to the cluster head node is:
The energy consumed by the head node in the cluster for receiving data is:
The energy consumed by the head node in the cluster after data fusion and forwarding is:
In (6), is the energy consumed by the cluster head node to fuse one bit of data.
For the farthest cluster, ordinary nodes in the cluster collect data and then send it to the cluster head node. The cluster head node fuses the data and sends it to the previous cluster. Therefore, the total energy consumed by the farthest cluster is:
For the non-furthest clusters, on the basis of the total energy consumption in the farthest cluster, it is also necessary to receive, fuse, and forward the data of the next cluster. Therefore, the total energy consumed by the non-farthest cluster is:
It can be seen from (8) that the closer the cluster is to the base station, the more data information needs to be forwarded, and the greater the energy consumption in the cluster. Therefore, deploying more router nodes in the cluster closer to the base station is bound to balance the energy consumption speed of each node in the network and increase the total energy of the system and the number of viable nodes so as to prolong the lifetime of the whole network.
4. Isosceles Triangle Non-uniform Deployment Algorithm Based on IMP-LEACH
Aiming at the “energy hole” problem in WSNs of distribution cables, routing nodes with different densities are deployed in different clusters so that the average energy consumption speed of routing nodes in each cluster is equal. Although the cluster-head election mechanism of the IMP-LEACH algorithm can balance the energy consumption of nodes in the cluster, the clustering mechanism has randomness and makes it difficult to improve the energy utilization efficiency of all nodes because the IMP-LEACH algorithm adopts the adaptive clustering method. Firstly, the cluster head nodes are randomly selected from the network, and then the common nodes are selected to form clusters with the nearest cluster head nodes through the distance judgment. This method makes it difficult to ensure a reasonable distribution of cluster heads and the size of the cluster.
With the purpose of solving the problems, an isosceles triangle non-uniform deployment algorithm based on IMP-LEACH has been proposed to optimize the clustering mechanism and the deployment mode of nodes in the cluster of the IMP-LEACH algorithm. Furthermore, the energy consumed by the routing node for data fusion is additionally considered. By analyzing the total energy consumed by each cluster and the energy consumed by data transmission between clusters, the algorithm specifically obtains the size of the cluster and the number of nodes in the cluster and reasonably distributes the routing node positions of the network so as to extend the lifetime of the whole wireless network and improve the energy utilization efficiency of routing nodes. In addition, it is worth noting that this algorithm is mainly applicable to double or more power distribution cables; if there is only one cable in the cable channel, routing nodes can be deployed linearly according to the node density function described below.
4.1. Determination of the Clustering Mode of the Network
Assume that the total length of the power distribution cable is D, the number of network clusters is n, and the distance from the i-th cluster head node to the (i − 1) cluster head node in the network is . According to the energy model, as shown in (1), the total energy consumption for data transmission between clusters in the network is:
Therefore, the problem turns into an optimization problem, and the goal is to minimize Eall. Mathematically, this is an extreme value problem of multivariate functions with constraints. According to the Lagrange multiplier method, when , gets the minimum value. Therefore, the total energy consumption of data transmission between clusters is minimal when the length of each cluster is equal.
Take the derivative of (9) and the optimal clustering distance can be obtained when the derivative is equal to 0, as shown in (9).
4.2. Determination of the Node Density in the Cluster
In order to make the average energy consumption speed of each node in the network the same, the ratio of the total energy in each cluster to the total number of nodes in the cluster should be as equal as possible, as presented in (11).
In (11), is the total energy of the i-th cluster, is the total number of nodes in the i-th cluster.
According to (7), (9) and (11), the relationship of the number of nodes between the i-th cluster and the furthest cluster can be obtained as shown in (12).
Assume that a total of N router nodes are deployed in the entire power distribution cable network, that is:
According to (10), (11), and (12), the total number of nodes in the farthest cluster can be obtained as presented in (14).
By substituting (14) into (12), the total number of nodes in the non-furthest cluster can be obtained as shown in (14).
4.3. Selection of Custer Head Nodes
When selecting cluster head nodes, the energy of the node is taken as the main factor, and the cluster head election formula [23,24] of the IMP-LEACH algorithm is selected, as shown in (16).
In (15), is the proportion of cluster head nodes in all nodes of the network, is the average energy of nodes in the cluster, is the remaining energy of campaigning nodes, is the number of current rounds, is the set of nodes that have not become cluster heads in the last rounds. is the distance constant, which is 2 when the model of sensor energy consumption is a free space model and 4 when the model of sensor energy consumption is a multi-path attenuation model.
4.4. Deployment of Nodes in the Cluster
In the wireless router network of distribution cables, the router is responsible for collecting the condition information monitored by the sensors, and the whole cable monitoring area must be fully covered. Due to the vulnerability of wireless router nodes and the complicacy of the surroundings, it is difficult for a single coverage to meet the monitoring requirements of the cable. This paper adopts the double (K = 2) coverage method; that is, each point in the cable is covered by at least two nodes at the same time.
The isosceles triangle deployment strategy is shown in Figure 5. In this deployment mode, the horizontal distance between two adjacent routing nodes is at most: .
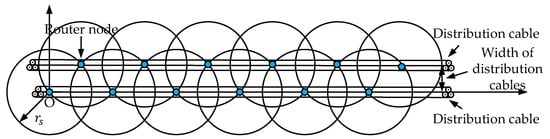
Figure 5.
Isosceles triangle partition coverage deployment strategy.
4.5. Non-Uniform Deployment Algorithm of Isosceles Triangle Based on IMP-LEACH
The basic idea of the algorithm is as follows: Firstly, the clustering is carried out by calculating the energy consumption within the network cluster and the energy consumption of data transmission between clusters. Then, in order to balance the overall energy consumption speed of each node in the network, the density of routing nodes in each cluster is calculated, and the deployment mode of nodes in the cluster is determined at the same time. Finally, the cluster head node is selected to receive and fuse data in the cluster and transmit data between clusters. Thus, the condition information of the whole cable is transmitted to the base station in a multi-hop manner. The flow chart of the isosceles triangle non-uniform deployment algorithm based on IMP-LEACH is shown in Figure 6.
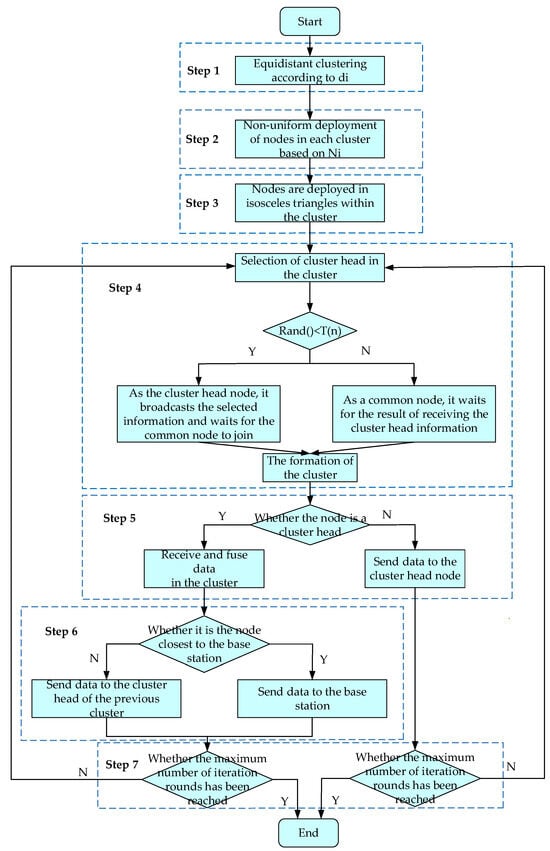
Figure 6.
Flowchart of the ITNU-IMPL algorithm.
There are 7 main steps in Figure 6; they are respectively:
Step 1: The network is divided into equidistant clusters according to (10) so as to minimize the total energy consumption of data transmission between clusters.
Step 2: Determine the number of routing nodes in each cluster according to (15). Thus, the average energy consumption speed of each node can be approximately equal, and the premature appearance of a network “energy hole” can be avoided.
Step 3: Deploy the routing nodes in the cluster in an isosceles triangle, according to Figure 5.
Step 4: According to (16), the routing cluster head node is determined. If the random number is less than the threshold, the node is determined as the cluster head node. Otherwise, it is a common node.
Step 5: Determine whether the node is the cluster head node in the cluster. If it is the cluster head node, the data is fused for forwarding. If not, send the data to the cluster head node and skip to Step 7.
Step 6: Determine whether the node is the cluster head closest to the base station. If the route cluster head node is closest to the base station, it directly transmits data to the base station. Otherwise, it transmits data to the cluster head node of its previous cluster.
Step 7: Determine whether the number of cycles is terminated. If the network runs to the maximum number of iteration rounds or the network is interrupted due to the death of some routing nodes, the network runs over. Otherwise, skip to Step 4.
5. Simulations and Results
5.1. Simulation Analysis
The algorithm in the paper is implemented using MATLAB 2021. The performance of the network is analyzed from the aspects of average coverage, energy consumption, number of surviving nodes, and number of working rounds under different death percentages of nodes. The IMP-LEACH algorithm and the isosceles triangle uniform Deployment algorithm based on IMP-LEACH (ITU-IMPL) are compared and analyzed with the ITNU-IMPL algorithm proposed in this paper.
Figure 7 shows the traditional linear deployment strategy [25]. With the same proof method as , it can be obtained that the maximum horizontal distance between two adjacent nodes in linear deployment is . Therefore, the results prove that the minimum number of routing nodes required by the two different deployment modes of isosceles triangle deployment and traditional linear deployment is equal.
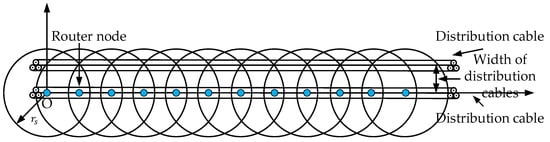
Figure 7.
Linear deployment strategy.
The specific simulation parameters are shown in Table 1. The energy consumption parameters of the router are selected from the classical values of the radio model [26].

Table 1.
Simulation parameters of energy consumption.
The comparison of average network coverage between isosceles triangle deployment and traditional linear deployment when the routing nodes are deployed with the same quantity has been presented in Figure 8. As can be seen from Figure 8, the network coverage obtained by isosceles triangular partition coverage deployment is greater than that obtained by traditional linear deployment. Therefore, the number of router nodes can be saved more on the precondition that the network coverage required is the same, thus reducing economic costs. Therefore, the subsequent paper adopts the isosceles triangle deployment method.
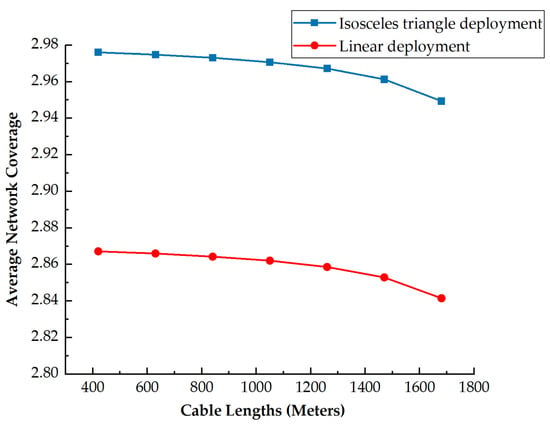
Figure 8.
Average coverage of the network under different cable lengths.
In order to avoid the situation that individual nodes in the cluster need to be fine-tuned, the following takes the cable length D = 420 m and the number of router nodes N = 84 as a study case for simulation analysis.
The comparison of the total energy consumption of the network system and the number of time rounds under the three algorithms is shown in Figure 9. The IMP-LEACH algorithm exhausted all the energy in the network at the 523rd round, the ITU-IMPL algorithm worked for 1474 rounds, and the ITNU-IMPL algorithm did not completely exhaust the network energy until the 1690th round. As mentioned in Section 4.5, the ITNU-IMPL algorithm fully considers the energy consumption of routing nodes while sending and receiving data in the network. By evenly distributing cluster head nodes and evenly clustering, the network energy consumption is effectively reduced, and the lifetime of the network is obviously prolonged. Compared with the IMP-LEACH algorithm, the lifetime of the ITU-IMPL algorithm has been extended by 184.21%. On the basis of the ITU-IMPL algorithm, ITNU-IMPL algorithm further reduces the energy consumption of data transmission within and between clusters by means of non-uniform clustering, making the number of surviving nodes in the network significantly increase after each round of work and further extending the network lifetime. Compared with the ITU-IMPL algorithm, the lifetime of the ITNU-IMPL algorithm has been extended by 17.26%. Compared with IMP-LEACH, the lifetime of the ITNU-IMPL algorithm has been extended by 233.27%.
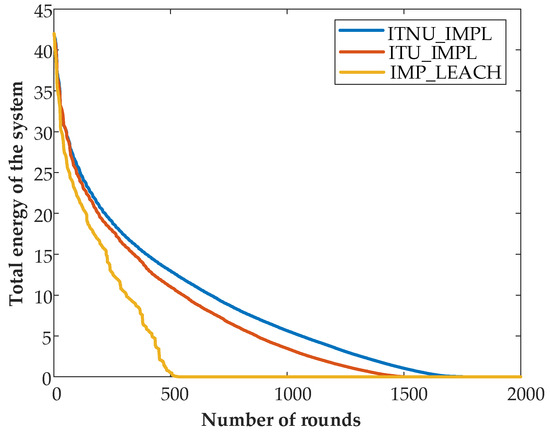
Figure 9.
Comparison between the total energy of the network and the number of time rounds.
The comparison between the number of surviving nodes and the number of rounds under the three algorithms is shown in Figure 10. As can be seen from the figure, compared with the IMP-LEACH algorithm, the ITU-IMPL algorithm has been working until the 1512 round of simulation, and the routing nodes are all dead. It indicates that under the premise of comprehensively considering the residual energy of cluster head nodes and the average energy of nodes in the cluster during the cluster head election process, the mechanism of equidistant uniform clustering can effectively balance the energy consumption in the cluster and the energy consumption of data transmission between clusters, substantially delaying the death time of routing nodes. Especially in the middle and late rounds of the network, the number of surviving nodes in the network increases distinctly, thus effectively prolonging the network lifetime. The ITNU-IMPL algorithm worked until all the routing nodes died in the 1773 round. Through non-uniform clustering, the “energy hole” of the network is further avoided, and the network lifetime is further extended.
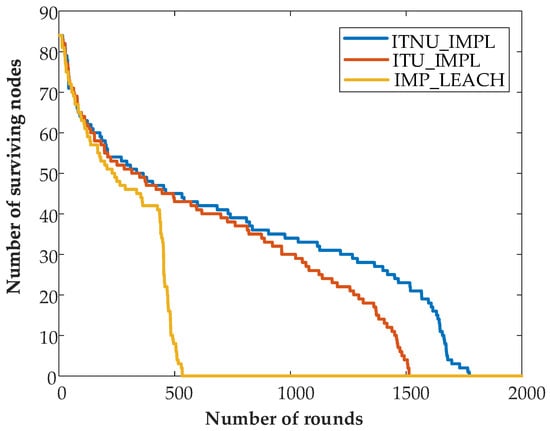
Figure 10.
Comparison between the number of surviving nodes in the network and the number of time rounds.
The comparison between the percentage of node deaths and the number of time rounds under the three algorithms is shown in Figure 11. As can be seen from the figure, at the beginning of the operation, because the energy of the routing nodes is still relatively abundant, the three algorithms have almost the same number of working rounds when the death of nodes is the same. However, in the middle and late stages of operation, the number of working rounds of the ITU-IMPL algorithm and ITNU-IMPL algorithm is significantly higher than that of the IMP-LEACH algorithm when the death ratio of routing nodes is the same. This is because the distribution cable wireless sensor network is a linear network, and the closer the routing node is to the base station, the more data needs to be forwarded, so the greater the energy consumption. Therefore, it is more likely to stop the number of working rounds because the nodes close to the base station die in advance. The adaptive clustering method adopted by the IMP-LEACH algorithm makes it difficult to ensure the uniformity of cluster head distribution and the rationality of cluster size. In the middle and late periods of network operation, the energy consumption among clusters is easily uneven, which reduces the energy utilization efficiency of the network. In contrast, the ITU-IMPL algorithm and ITNU-IMPL algorithm can distribute cluster heads reasonably by further optimizing the node density within the cluster and calculating the energy consumption of data transmission within and between clusters. It avoids the situation that the network energy consumption is too fast because of the uneven distribution of cluster heads, thus improving the lifetime of the network. ITNU-IMPL algorithm not only distributes cluster heads reasonably but also obtains cluster sizes of different clusters, which avoids the situation that network energy consumption is too fast due to unreasonable cluster size and further prolongs the network lifetime.
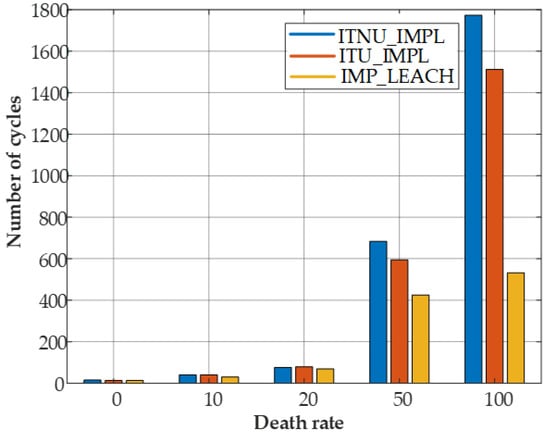
Figure 11.
Comparison between the percentage of node deaths and the number of time rounds.
The energy utilization efficiency of nodes is defined as the proportion of energy consumed by nodes in the initial energy of nodes when the network crashes and its calculation formula is as follows.
In (17), is the energy utilization efficiency of the i-th routing node, is the remaining node energy of the i-th routing node when the network crashes.
The comparison of energy utilization efficiency of all nodes in the network when the network crashes is shown in Figure 12. As can be seen from the figure, the node energy utilization efficiency of the ITNU-IMP and ITU-IMPL algorithms is generally higher than that of the IMP-LEACH algorithm. Meanwhile, the closer the node is to the base station, the higher the energy utilization efficiency. The energy utilization efficiency of the nodes in the first half of the whole network can even reach almost 100%. This indicates that compared with the IMP-LEACH algorithm, the ITNU-IMP algorithm can efficaciously balance the energy consumption of each node in the network and improve the energy utilization efficiency of nodes, so it can avoid the phenomenon of “energy hole” in the network and prolong the network lifetime.
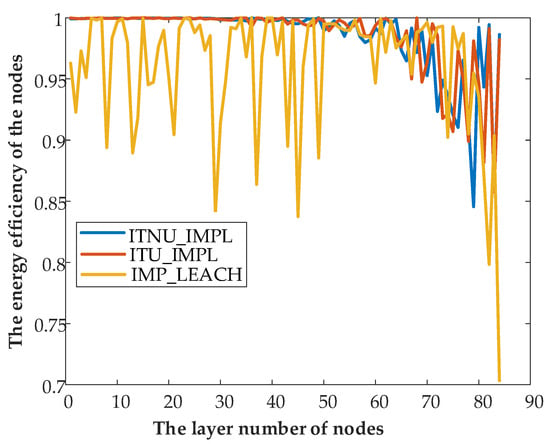
Figure 12.
The simulation results of node energy utilization efficiency.
In an effort to verify the universality of the algorithm under different cable lengths, other lengths of cables in Table 1 are also simulated. Figure 13 shows the network lifetime of three algorithms under different cable lengths when the same number of sensors and routers are deployed. In order to avoid the resulting error caused by the different order of nodes in the cluster selected as routing cluster head nodes during each simulation, the data in the figure are the average of 20 simulation results. It can be seen from Figure 13 that the lifetime of the ITNU-IMPL algorithm and ITU-IMPL algorithm is significantly higher than that of the IMP-LEACH algorithm under the same conditions. With the increase in cable length, the lifetime of the IMP-LEACH algorithm becomes shorter and shorter. In contrast, the lifetime of the ITU-IMPL algorithm can always be maintained at about 1500 rounds, and the lifetime of the ITNU-IMPL algorithm can always be maintained at about 1800 rounds. It indicates that the ITU-IMPL algorithm and ITNU-IMPL algorithm can indeed balance the energy consumption of each node in the network and significantly prolong the network lifetime after improving the clustering mechanism and node distribution in the cluster of the IMP-LEACH algorithm. At the same time, compared with the ITU-IMPL algorithm, the ITNU-IMPL algorithm further extends the lifetime of the network by 20% by adopting non-uniform clustering, according to (15).
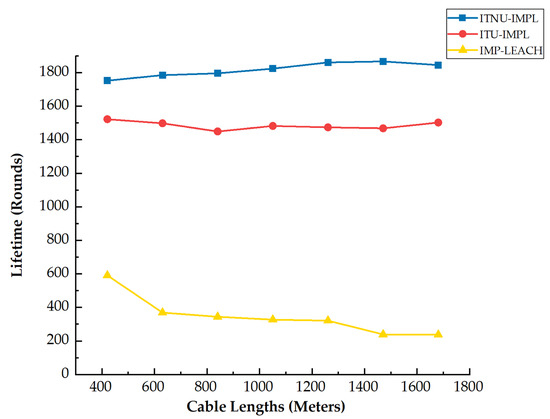
Figure 13.
Lifetime of the network under different cable lengths.
5.2. Economic Comparison
In order to monitor the operating condition of distribution cables, WSNs and traditional demodulation instruments are often used to obtain the data information. The economic costs of the two schemes are compared below. Table 2 shows the number and unit price of the equipment required by the deployment scheme of the distribution cable condition monitoring devices proposed in this paper and the data acquisition scheme using the demodulation device under different cable lengths. All sensors and routers have a coverage radius of 15 m. The number of sensors in Table 2 is the minimum number of sensors and routers required under the premise that the condition monitoring sensor can fully cover the distribution cable network and the information router can cover the cable network in the way of double repeat cover. Each demodulator is only responsible for acquiring data monitored by a single condition monitoring sensor.

Table 2.
The number and unit price of equipment required for the two schemes [27].
The economic comparison between the deployment scheme of the distribution cable condition monitoring devices and the data acquisition scheme using the demodulator is shown in Figure 14. It is clear from the results that the scheme adopted in this paper significantly reduces the economic cost compared with the scheme using the demodulator to obtain data. Meanwhile, the scheme using the demodulator to obtain data is only applicable to ultra-short distance cables. When adopting the scheme of using the demodulator to obtain data, the cost required for the scheme increases from 87,360 CNY to 349,440 CNY as the length of the distribution cables increases from 420 m to 1680 m. That means every 210 m increase in cable length will lead to an increase in program cost of 43,680 CNY, and the economic cost of the entire program is equivalent to 208 CNY/meter. When the scheme proposed in this paper is adopted, the cost of the scheme only increases from 11,080 CNY to 140,320 CNY after the length of the distribution cables is increased from 420 m to 1680 m. That means, for every 210 m increase in cable length, the cost of the scheme only increases by 5040 CNY, which is equivalent to the economic cost of the subsequent cable, which is 24 CNY/meter under the premise of the existing base station. The scheme of using a demodulator to obtain data saves the cost of building base stations, but the price of a demodulator is much higher than that of a single sensor. Therefore, the investment of large-scale demodulators cannot effectively reduce the economic cost of the scheme. In contrast, when the cost of building a base station has been fixed, the scheme adopted in this paper only needs to invest the cost of sensors with the growth of cables. Therefore, the longer the cables, the more economic cost of network node deployment can be saved.
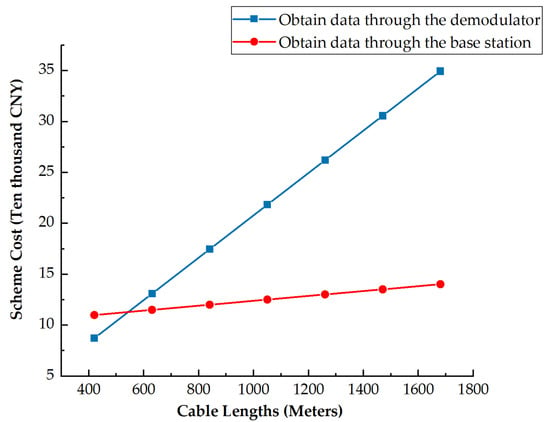
Figure 14.
Economic comparison of different ways to obtain network data.
The comparison of the cost-performance ratio of two different methods for obtaining network data is shown in Figure 15. As can be seen from the figure, the economic cost of the network is always 208 CNY/meter when using the demodulator to obtain data. This is because when adding cable lengths of the same distance, the number of sensors and demodulators that need to be put into the network are both fixed. When using the base station to obtain data, the cost of the network has dropped from 262 CNY/meter to 83.5 CNY/meter. Because of the growth of cable length, the network has gradually balanced the cost of building base stations while only investing in lower-cost sensors. Therefore, the longer the distribution cables, the more economical the cost of the scheme adopted in this paper can be saved.
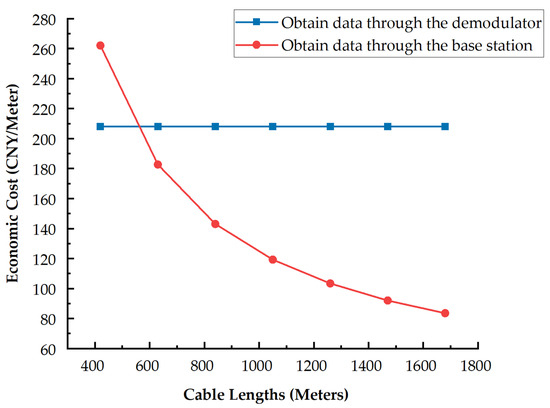
Figure 15.
Comparison of cost performance of different ways to obtain network data.
6. Conclusions
In order to improve the applicability of the monitoring technology to distribution cable condition monitoring, a deployment scheme of distribution cable condition monitoring devices based on wireless sensor networks has been proposed. An isosceles triangle non-uniform deployment algorithm based on IMP-LEACH is proposed to solve the “energy hole” problem in data transmission of linear wireless sensor networks in distribution cables. The following conclusions can be drawn from the simulations:
- (1)
- In this paper, an isosceles triangle non-uniform deployment algorithm based on IMP-LEACH is proposed. According to the network scale and energy consumption model, the algorithm solves the clustering distance and node density of the network and then evenly partitions the network and deploys the routing nodes in clusters in an isosceles triangle according to the node density function. It can not only eliminate the “energy hole” phenomenon of the nodes near the base station but also ensure that the routing coverage rate of the distribution cables is always maintained above 200%.
- (2)
- By optimizing the distribution of routing cluster head nodes in the network, node density in the cluster, and node deployment mode in the cluster, the isosceles triangle non-uniform deployment algorithm based on IMP-LEACH can efficiently balance the energy consumption of each node in the network, improve the energy utilization rate of the network, and extend the lifetime of the network at least twice. The longer the cable is, the greater the optimization effect.
- (3)
- It is usually more economical to acquire data with a base station than with a demodulator. The longer the cable is, the greater the savings.
Author Contributions
Writing—original draft, J.W.; Writing—review and editing, M.L. and X.Z.; Conceptualization, C.G.; Investigation, Z.L.; Validation, B.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to [The authors intend to conduct further studies based on these data].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Enjavimadar, M.; Rastegar, M. Optimal reliability-centered maintenance strategy based on the failure modes and effect analysis in power distribution systems. Electr. Power Syst. Res. 2021, 203, 107647. [Google Scholar] [CrossRef]
- Shaalan, E.M.; Ward, S.A.; Youssef, A. Analysis of a Practical Study for Under-Ground Cable Faults Causes. In Proceedings of the 2021 22nd International Middle East Power Systems Conference (MEPCON), Assiut, Egypt, 14–16 December 2021. [Google Scholar]
- Huang, Z. Cause Analysis of External Force Damage of Transmission Line and Preventive Measures. Rural Electrif. 2022, 10, 85–87. [Google Scholar]
- Li, L. Research on Operation and Information Management of Power Cable Lines. Electr. Technol. Econ. 2023, 33, 174–176. [Google Scholar]
- Xu, Y. Analysis of Common Faults in Distribution Cables and Research on Maintenance Measures. Sci. Technol. Innov. 2021, 21, 69–70. [Google Scholar]
- Song, X.; Gong, Y.; Jin, D.; Li, Q. Nodes deployment optimization algorithm based on improved evidence theory of underwater wireless sensor networks. Photon- Netw. Commun. 2018, 37, 224–232. [Google Scholar] [CrossRef]
- Wu, T.; Yang, W.; Wang, Y. Self-organizing energy-saving clustering protocol for post-disaster reconstruction network of IOT in Coal mine. J. Huazhong Univ. Sci. Technol. 2020, 48, 7–13. [Google Scholar]
- Ren, J.; Hu, J.; Zhang, D.; Guo, H.; Zhang, Y.; Shen, X. RF Energy Harvesting and Transfer in Cognitive Radio Sensor Networks: Opportunities and Challenges. IEEE Commun. Mag. 2018, 56, 104–110. [Google Scholar] [CrossRef]
- Mohapatra, H.; Rath, A.K. Survey on fault tolerance-based clustering evolution in WSN. IET Netw. 2020, 9, 145–155. [Google Scholar] [CrossRef]
- Lv, A.; Li, C.; Xie, J.; Duan, B. Optimization of Non-uniform Clustering in WSN for railway monitoring. J. Railw. 2019, 41, 72–78. [Google Scholar]
- Su, Y.; Guo, L.; Jin, Z.; Fu, X. A Voronoi-based Optimized Depth Adjustment Deployment Scheme for Underwater Acoustic Sensor Networks. IEEE Sens. J. 2020, 20, 13849–13860. [Google Scholar] [CrossRef]
- Liu, J.; Sun, G. A Deployment Strategy of Nodes in WSN Based on “X” Partition”. J. Sens. 2022, 2022, 8118605. [Google Scholar] [CrossRef]
- Jin, T.; Zeng, Z.; Wang, G. Research on non-uniform clustering routing algorithm based on energy and distance. J. Univ. Sci. Technol. Liaoning 2022, 45, 359–364. [Google Scholar]
- Buljak, V.; Garbowski, T. Efficient methods for optimal space filling in model reduction techniques (2014) Recent Advances in Computational Mechanics. In Proceedings of the 20th International Conference on Computer Methods in Mechanics, CMM 2013, Frankfurt, Germany, 30–31 December 2013; pp. 285–291. [Google Scholar]
- Li, J.; Hu, H.; Lu, X. Improved LEACH Algorithm for Wireless Sensor Networks Based on Chaotic Genetic Algorithm. J. Jilin Univ. 2021, 59, 950–955. [Google Scholar]
- Asorey-Cacheda, R.; Garcia-Sanchez, A.-J.; Garcia-Sanchez, F.; Garcia-Haro, J. A survey on non-linear optimization problems in wireless sensor networks. J. Netw. Comput. Appl. 2017, 82, 1–20. [Google Scholar] [CrossRef]
- Meng, J.; Wang, J.; Li, D.; Xu, R.; Qi, W. The Deployment Strategy of Wireless Sensor Network Nodes Along the Railway. Chinses J. Sens. Actuators 2021, 34, 829–834. [Google Scholar]
- Zheng, D.; Ma, Q. Application of Online Detection Technology for Power Cable Operating Temperature. Light Sources Illum. 2023, 3, 206–208. [Google Scholar]
- Duan, J.; Shi, T.; Lv, X.; Li, Z. Optimal Node Deployment Scheme for WSN-Based Railway Environment Monitoring System. In Proceedings of the 28th Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016. [Google Scholar]
- Xu, L.; Wu, F. A Lightweight Authentication Scheme for Multi-gateway Wireless Sensor Networks Under IoT Conception. Arab. J. Sci. Eng. 2019, 44, 3977–3993. [Google Scholar] [CrossRef]
- Heinzelman, W.; Chandrakasan, A.; Balakrishnan, H. An application-specific protocol architecture for wireless microsensor networks. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar] [CrossRef]
- Sharma, D.; Tomar, G.S. Enhance PEGASIS Algorithm for Increasing the Life Time of Wireless Sensor Network. Mater. Today: Proc. 2020, 29, 372–380. [Google Scholar] [CrossRef]
- Pan, H.; Chen, J.P.; Lin, F.; Ding, K. Optimization of LEACH protocol using multi-hop data distribution based on quantity and distance. Electron. Opt. Control 2018, 25, 89–92. [Google Scholar]
- Mao, L.; Zhang, Y. An Energy-Efficient LEACH Algorithm for Wireless Sensor Networks. In Proceedings of the 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017. [Google Scholar]
- Zhou, G.; Zhu, Z.; Chen, G.; Zhou, L. Hierarchical topology control of wireless sensor networks in coal mine laneway. J. China Coal Soc. 2010, 35, 333–337. [Google Scholar]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-efficient communication protocol for wireless microsensor networks. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 4–7 January 2000. [Google Scholar]
- Taobao. Available online: https://www.taobao.com/ (accessed on 24 August 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).