Abstract
Phase-change materials (PCMs) are attractive materials for storing thermal energy thanks to the energy supplied/returned during the change in matter state. The encapsulation of PCMs prevent them from connecting into large clusters, prevents the chemical interaction of the PCM with the walls of the tank and the exchanger material, and allows the phase change to be initiated in parallel in each capsule. The microencapsulation of PCMs (mPCMs) and the nanoencapsulation of PCMs (nPCMs) entail that these particles added to the base liquid can act as a slurry used in heat exchange systems. PCM micro-/nanocapsules or mPCM (nPCM) slurry are subjected to numerous physical, mechanical, and rheological tests. However, flow tests of mPCM (nPCM) slurries are significantly limited. This paper describes the results of detailed adiabatic flow tests of mPCM slurry in a tube with an internal diameter of d = 4 mm and a length of L = 400 mm. The tests were conducted during laminar, transient, and turbulent flows (Re < 11,250) of mPCM aqueous slurries with concentrations of 4.30%, 6.45%, 8.60%, 10.75%, 12.90%, 15.05%, and 17.20%. The mPCM slurry had a temperature of T = 7 °C (the microcapsule PCM was a solid), T = 24 °C (the microcapsule PCM was undergoing a phase change), and T = 44 °C (the microcapsule PCM was a liquid). This work aims to fill the research gap on the effect of the mPCM slurry concentration on the critical Reynolds number. It was found that the concentration of the mPCM has a significant effect on the critical Reynolds number, and the higher the concentration of mPCM in the base liquid, the more difficult it was to keep the laminar flow. Additionally, it was observed that, as yet unknown in the literature, the temperature of the slurry (and perhaps the physical state of the PCM in the microcapsule) may affect the critical Reynolds number.
1. Introduction
In European Union countries, almost half of the produced energy is used for heating and cooling buildings, a significant amount of which is waste heat that is not collected or used effectively [1]. Achieving climate goals will only be possible through the storage of various forms of energy (such as kinetic, chemical, and heat [2]). Storing thermal energy requires the use of materials that allow the collection/returning of a significant amount of energy, preferably with a small change in temperature. This expectation is met during a phase transition (e.g., a change in the state of matter) in the so-called phase-change materials, PCMs [3]. The most common are organic PCMs [4,5], but they have a low thermal conductivity [6,7,8]. This limits the rate of the “charging/discharging” of the heat storage. Various ways of increasing their thermal conductivity have been tested, including the direct addition of materials with a high thermal conductivity (e.g., metal particles) to PCMs [9]; the use of additional ribbing to increase the heat exchange surface [10]; placing the PCM in a porous conductive structure [11,12] or metallic foams [9,13]; and encapsulation-collecting PCMs in a large number of small shells. The encapsulation of the PCM allows for the initiation of the phase change simultaneously in all washed containers. Encapsulation techniques can be divided into macro-, micro-, and nanoencapsulation [14,15]. Microencapsulation is a process in which PCM particles (with a diameter of about 0.1–1000 μm) are covered with a thin layer of a natural or synthetic polymer with a thickness of several micro- or even nanometers [16,17,18]. In consequence, the encapsulated PCM is used as a passive heat energy storage in building materials, filling building spaces for cooling and heating rooms, as an additive in textiles, among others [19,20,21]. It is possible to mass-produce capsules with diameters in the order of micrometers and even nanometers (nanoencapsulation) [22,23,24]. With such small capsule sizes, it became possible to flow liquid not only around the capsule but also to achieve an entire flow—the slurry of micro-/nanoencapsulated PCMs. This type of fluid is called “latent functionally thermal fluid”, LFTF [25,26,27]. In addition to the encapsulated PCM slurry, LFTF includes fluids consisting of PCM particles added directly to a base fluid (PCM emulsions [28,29,30]) and ice slurries [31]. At present, considerable research is being conducted to determine the thermal properties and flow characteristics of slurries.
Alvarado et al. [32] experimentally investigated the effect of the microcapsule concentration on the pressure drop of mPCM slurry in a tube with an internal diameter of 10.9 mm and a length of 1520 mm. The aqueous slurry of the mPCM at concentrations of 4.6%, 5.9%, 8.3%, 13.4%, 16.1%, and 17.7% flowed turbulently inside the tube. The authors found that there is no effect of the concentration of mPCM on the measured pressure drop, and the test results can be compared with the results of calculations using the Colebrook correlation.
The study by Taherian et al. [33] included thermal and flow characteristics obtained during the study of the flow of six different slurries—five based on microencapsulated methyl stearate with different capsule sizes and an innovative, proprietary PCM. The flow of the aqueous slurries with a concentration of 5 ÷ 14% took place in the range of Re = 3000 ÷ 6000 inside a pipe with a length of L = 1.5 m and an internal diameter of d = 11 mm. The methyl-stearate-based slurries caused a pressure drop greater than that of water, but it was independent of the mPCM concentration.
The lack of influence of the mPCM concentration on the pressure drop in the flow, this time laminar, was reported by Chen et al. [34]. The authors conducted studies of heat transfer and pressure drop of microencapsulated 1-bromohexadecane (C16H33Br). The microcapsules were added to water at weight concentrations of 5%, 10%, and 15.8%. The slurry at T = 10 °C and T = 20 °C (the PCM in the microcapsule was solid or liquid, respectively) flowed through a stainless steel tube (d = 4 mm and L = 1460 mm). The authors found that the PCM slurry’s temperature/physical state and the change in slurry concentration had no effect on the pressure drop.
In the study by Zhang et al. [35], a 2.4 m long copper pipe with an internal diameter of 10 mm was used to analyze the flow of an aqueous slurry of microencapsulated paraffin. The mass fractions of the microcapsules in the aqueous slurry were 5% and 10%. Pressure drop measurements indicated that the addition of mPCM to water did not increase the pressure drop for the same average fluid flow velocity. Additionally, the addition of 1% of the mass of various metal particles (ZnO or nano ZnO or nano Al2O3) to the slurry [36] did not affect the pressure drop measured during the flow of these slurries.
In the above-mentioned studies, the flow characteristics, on the basis of which conclusions were drawn, were presented as a function of the slurry flow rate/velocity. Converting the flow velocity into a dimensionless quantity (Reynolds number, Re) would take into account the different density and viscosity values of each of the slurries. Then, the flow characteristics (as a function of Re) would show that the effect of mPCM concentration exists. This influence was noticed in subsequent publications.
Wu et al. [37] published their results of a study on the pressure drop of synthetic oil (poly-alpha-olefin-PAO) with the addition of indium nanoparticles in a silica coating. The slurry of 9% and 30% capsules flowed through a heat exchanger with microchannels measuring 25 µm and 100 µm in width, 500 µm in height, and 1000 µm in length. It was found that the pressure drop during the turbulent flow of the slurry was greater with the higher the concentration of mPCMs and the smaller the hydraulic diameter of the microchannels.
Ashagre et al. [38] performed tests where the mPCM slurry flowed inside a smaller tube of a tube-in-tube exchanger. The influence of particle concentration (5, 10, 15, 20, and 30%), Reynolds number (Re > 2000) and particle diameter (1, 5, 10, 50, and 100 µm) on the heat transfer and pressure drop of the mPCM slurry was studied. It was found that, along with the slurry flow rate increase, the pressure drop increased as well.
Serale et al. published a paper [39] devoted to the possibility of using the mPCM slurry in the solar collector cycle. The slurries consisted of microencapsulated n-eicosane ranging from 25% to 45% wt. An increase in the flow rate of the slurry caused an increase in the flow resistance, but the resistance measured after 12 h of operation of the installation decreased by ~30%. The reason was supposed to be the phenomenon of the delamination of the slurry and the outflow of mPCM as a matter of lower density.
Qiu et al. [40] described the results of the study of the possibility of increasing the efficiency of the PV/T module by using the mPCM slurry to cool the PV cells. The mass fractions of mPCM in the slurry were 5%, 10%, and 15%. An increase in the slurry flow velocity caused an increase in the flow resistance. The authors also stated that the higher the concentration of mPCMs, the greater the pressure drop.
Papers containing a description of the influence of the mPCM slurry on the pressure drop in the flow of the slurry through minichannels of the heat sink [41], the flow of the slurry of silver-coated microcapsules [42] inside a stainless steel tube, the flow of the mPCM slurry through divergent channels [43,44], or the mPCM slurry with the addition of nanoparticles Al2O3 [45] indicated that the higher the concentration of encapsulated PCM in the slurry, the greater the measured pressure drop.
The influence of the mPCM concentration on the pressure drop was also confirmed by the results of CFD simulations. Damel et al. [46] conducted experimental studies and CFD simulations, the aims of which were to determine the heat transfer and pressure drop of mPCM aqueous slurries in copper rectangular minichannels. The aqueous slurry with 10% and 20% mPCM content flowed laminarly inside nine parallel minichannels. The results of the measurement of the pressure drop across the heat exchanger showed that the higher the concentration of mPCM, the greater the flow resistance.
The paper by Pakrouh [47] described the results of CFD simulations of mPCM slurry (water slurry of microencapsulated n-octadecane) for cooling electric car batteries. A pack of 186 batteries was cooled with a liquid flowing in a serpentine system, similar to the one used in the Tesla S car. The influence of mPCM slurry concentration (10% and 20%) and fluid velocity (up to 0.4 m/s) on pressure drop and exchange of warm were analyzed. The simulation results showed that the higher the concentration of mPCM, the greater the pressure drop. Similar conclusions resulted from the results of CFD simulations presented in [48,49,50,51].
However, there are studies from which different conclusions can be drawn. Inaba et al. [52] conducted an experimental study in which microcapsules filled with tetradecane flowed through a pipe 16 mm in diameter and 1000 mm long. A slurry with a temperature of T = 278.1 K (PCM was a solid) and T = 288.1 K (PCM was a liquid) and concentrations of 10.2%, 20.4%, 30.6%, and 40.8% flowed inside turbulent tubes. The researchers found that there is no effect of the PCM temperature/state of matter on the slurry flow resistance. However, it was noted that the pressure drop in the mPCM slurry flow slightly exceeded the pressure drop in the base liquid flow. This was the case up to a concentration of 30.6% mPCM. After exceeding this value, the pressure drop increased by several dozen percent.
The study of Sinha-Ray et al. [53] showed that the pressure drop of the slurry of PCM nanocapsules was lower than in the case of the flow of pure base liquid (water). The authors explained this by the need to add a surfactant to the nPCM slurry. It was found that, the more it was added, the lower the flow resistance. An increase in the volumetric concentration of mPCM in the slurry from 0% to 20% [54] caused the measured pressure drop to decrease from about 181.7 Pa to 181.0 Pa. The authors of the CFD simulations stated that the positive mPCM to the base liquid causes a decrease in the density of the slurry, which was the reason for the decrease in the flow resistance.
Several key issues arise from the analysis of the literature. The assessment of the impact of the mPCM mass fraction on the pressure drop in the slurry flow based on the characteristics prepared as a function of the mass velocity (flow rate) is misleading, as it does not take into account the actual properties of the fluid (density and viscosity) dependent on the mPCM concentration. The analysis of the influence of the mass fraction of mPCM on the pressure drop in the slurry flow, based on the characteristics prepared as a function of the Reynolds number, indicates in the vast majority of cases that the higher the concentration of mPCM, the greater the flow resistance. The influence of the mPCM contribution on the pressure drop is clear in both laminar and turbulent flows. Most experimental or CFD research is in a selected range of Reynolds number (either laminar or turbulent flow). There are no studies that cover laminar and turbulent flows that are detailed enough to determine the effect of the mPCM concentration on the critical Reynolds number.
The paper describes the results of detailed experimental studies of mPCM slurry flow both in terms of laminar and turbulent motion, with particular emphasis on the moment of change in the nature of fluid motion. The tests were conducted for seven different mPCM concentrations (from 4.30% to 17.20%). The tests were conducted using a slurry at a temperature of T = 7 °C (the PCM in the microcapsule was a solid), T = 24 °C (the PCM in the microcapsule was undergoing a phase change), and T = 44 °C (the PCM in the microcapsule was a liquid). The results of our own research irrefutably indicate that there is a clear influence of the mPCM concentration on the hydrodynamics of the flow, including the boundary of the transition from laminar to turbulent motion, which has not been the subject of detailed research to date. In addition, an unknown fact was found that the temperature of the slurry (and perhaps the physical state of the PCM in the microcapsule) can affect the critical Reynolds number.
2. Research Procedure and Data Conversion
2.1. The mPCM Slurry
An aqueous slurry of microencapsulated PCM was used in the research. The slurry was created after mixing water with a concentrate containing PCM microcapsules. A slurry called MICRONAL® 5428, a product of Microtek Labs (Moraine, OH, USA), was used as the concentrate. According to the manufacturer’s data [55], approximately 43% of the concentrate consists of microcapsules with a size of 1–5 μm made of polymethyl methacrylate polymer and paraffin with a phase transition temperature of 28 °C ± 1 °C inside. The concentrate was added to demineralized water in such a proportion that a slurry was obtained in which the mass fractions of the mPCM were 4.30%, 6.45%, 8.60%, 10.75%, 12.90%, 15.05%, and 17.20%. The slurry was mechanically stirred until a homogeneous liquid was obtained. Each of the slurries was subjected to detailed tests aimed at determining its density and apparent viscosity.
The density of the mPCM slurry was determined using readings from the Coriolis flowmeter during flow tests described in detail, among others, in the authors’ previous work [56]. The change in the density of the slurry with the mPCM concentration of 12.90% is shown in Figure 1. The results of the phase change temperature and specific heat of the slurry determined according to the procedure described in [57] are shown graphically in Figure 2. As it can be seen on Figure 2 and Figure 3, the melting process of PCM contained in microcapsules began at ~21 °C temperature and ended when the slurry reached a temperature of ~27 °C. The conducted tests show that the PCM contained in the slurry underwent a phase change already in a temperature range from about 22 °C ÷ 27 °C. On this basis, it was assumed that the proper experiment would be conducted with the use of slurries at the temperatures of T = 7 °C, T = 24 °C, and T = 44 °C. The slurry at these temperatures allowed for flow tests, where the PCM encapsulated in the microcapsules was a solid, undergoing a phase change, and a liquid, respectively.
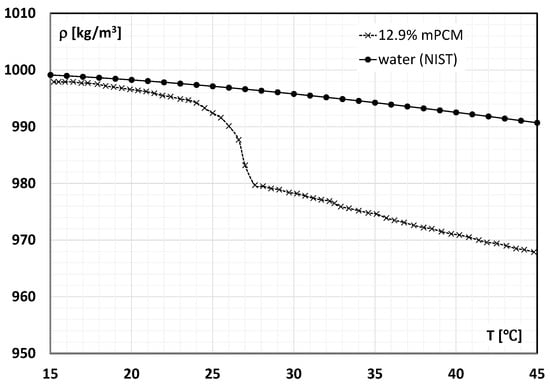
Figure 1.
Density of 12.90% mPCM slurry and water according to the standard reference data NIST [58] on the temperature.
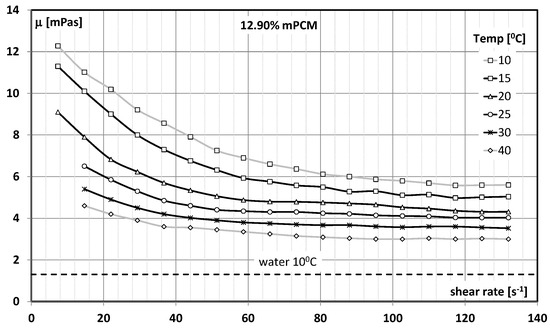
Figure 2.
Apparent viscosity effect of a slurry with 12.90% concentration of mPCM and water on the shear rate and temperature.
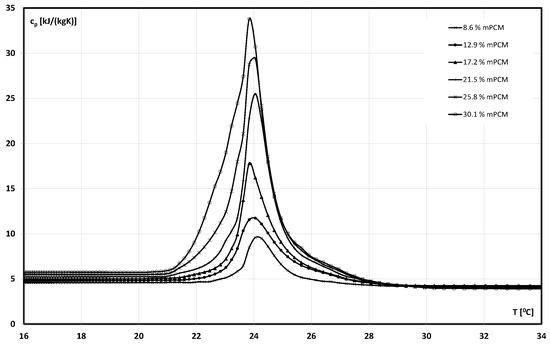
Figure 3.
The effect of specific heat and phase-change temperature of aqueous mPCM slurry on the temperature.
The apparent viscosity of the slurry was determined using a Brookfield DV-II + Pro rotary viscometer (Brookfield Co., Ltd., Middleboro, MA, USA). The research procedure included the determination of the apparent viscosity of the slurries in the range of mPCM concentrations up to 43.0%, temperature ranges of T = 10 ÷ 50 °C, and shear rates of = 0.0132–132.00 s−1. The details of the experiments are described in the works of the authors of [59,60,61,62]. Figure 2 presents exemplary results of measuring the apparent viscosity of the mPCM slurry as a function of the temperature and shear rate. The presented results refer to a slurry with a mPCM concentration of 12.90%.
2.2. Test Stand and Test Procedure
The test stand (diagram in Figure 4) consisted of several basic elements: test section is a section of a straight pipe with a constant diameter (1), working fluid reservoir tank (2), flow meter (3), pump (4), valves for regulating the slurry flow rate (8) and (9), and heat exchanger (5). These elements are arranged in such a way as to create a closed circuit of the working fluid.
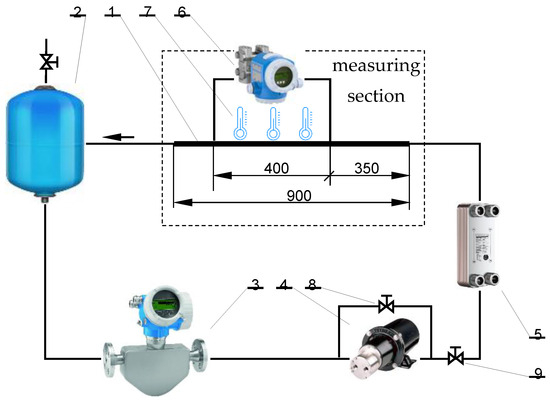
Figure 4.
The experimental facility scheme: a section of a straight pipe with a constant diameter (1), working fluid reservoir tank (2), flow meter (3), pump (4), valves for regulating the slurry flow rate (8) and (9), and heat exchanger (5), (6) differential pressure sensor, (7) thermoelectric thermometer.
The measuring section is the most important element of the installation. The measuring section consisted of a straight copper tube with a constant internal diameter of d = 4 mm and a total length of L = 900 mm. The pipe was divided into three sections. The first section was 350 mm long and was a hydraulic stabilization zone for the slurry flow. The next section, the proper section under research, was 400 mm long and resulted from the distance between the impulse holes made in the tube wall. The holes were used to transmit the static pressure pulse to the differential pressure sensor. The last section, 150 mm long, allowed for the undisturbed flow of liquid from the tube. Three thermometers were placed at regular intervals along the length of the proper section to measure the surface temperature of the pipe wall. Since the whole tube was thermally insulated, a thermometer was used to obtain the constant temperature of the slurry during the test and that it remained unchanged along the length of the test section.
The slurry with the known mass fraction of mPCM was in the liquid tank. From there, it flowed to the flow meter. We used a Promass 80 mass flowmeter by Endress-Hauser (Wien, Austria), whose principle of operation is based on the Coriolis effect. The maximum measurement range of the device was 200 kg/h, and the measurement accuracy was ±0.2% of the measured value. The maximum value of the flow rate during the tests was 110 kg/h; hence, the maximum measurement error of the flow rate was ±0.22 kg/h. A liquid with a known flow rate was pumped by a miniature gear pump to the furthest part of the installation. Behind the pump, there was a control valve, which allowed to throttle the slurry flow and direct excess liquid through the bypass valve back in front of the pump. The mPCM slurry with the required flow rate flowed to the plate heat exchanger. In the heat exchanger, through indirect contact with the supporting liquid, the slurry reached the temperature required during the proper tests. The temperature of the slurry was controlled by the proper selection of the temperature of the auxiliary liquid. From this point, the slurry with a known flow rate and set temperature flowed into the tube in the section under research. The actual temperature of the slurry was the average of the three values indicated by the thermoelectric thermometers. K-type thermocouples were used. These were individually made and calibrated thermocouples. Calibration was conducted in a temperature ranging from 10 °C to 60 °C against a reference thermometer with a measurement accuracy of ±0.05 °C. It was found that the measurement accuracy of the thermocouples used was ±0.2 °C. During the flow of the slurry through the appropriate test section of the tube (400 mm long), the static pressure drop was measured. A piezoresistive differential pressure sensor Deltabar S PMD75 by Endress-Hauser (Wien, Austria) was used to measure the pressure drop. The measurement range of the device was 0 ÷ 50 kPa. The device was made in the 0.075 class; so, the maximum measurement error of the pressure drop was ±37.5 Pa. After passing through the tube, the tested mPCM slurry was transferred to the tank, closing the circuit.
At the test stand, the mPCM slurry mass flow rate ṁ (kg/h), the temperature of the slurry T (°C) (average of three thermoelectric thermometer readings) and the pressure drop Δp (Pa) were directly measured. The experimental research was conducted in such a way that, at a set temperature of the mPCM slurry (T = 7 °C, T = 24 °C, and T = 44 °C), its mass flow rate changed (ṁ = 5–108.5 kg/h). The pressure drop value was acquired for each flow rate value. All measurements were made in a steady state, and the presented results of the direct measurements are the average of three readings taken during one test.
2.3. Conversion of the Measurement Data
Based on the measured mass flow rate of the slurry ṁ, the value of the Reynolds number was determined using the following relationship:
where r (kg/m3) is the density of the slurry, w in (m/s) is the average flow velocity of the slurry, d is the internal diameter of the pipe, and μ (mPa·s)is the apparent viscosity of the slurry. The average velocity of the mPCM slurry was determined from the transformed relationship:
The density and apparent viscosity of the mPCM slurry were determined during our own basic research, which are shown in Figure 1 and Figure 3, respectively. Using the equation:
and knowing the value of the measured mass flow rate of the mPCM slurry ṁ, the shear rate (1/s) was determined. For the obtained shear rate value, the apparent viscosity necessary for the correct determination of the current Re number was read from the graph presented in Figure 3 (Equation (1)).
3. Research Results and Discussion
3.1. Influence of the Slurry Flow Rate on the Pressure Drop
Figure 5 shows the results of the measurement of the pressure drop during the flow of the slurry at 7 °C through the pipe channel. The results presented illustrate the effect of the slurry concentration (from 4.30% to 17.2%) and the slurry flow rate (up to 110 kg/h) on the measured pressure drop value.
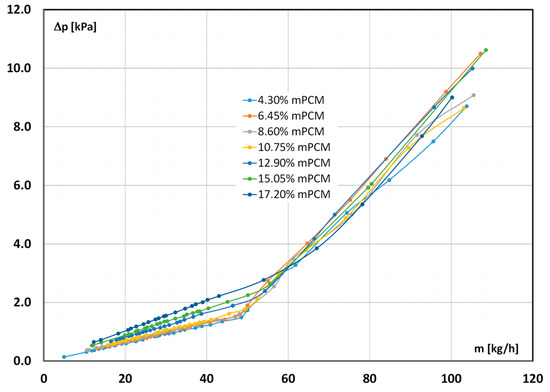
Figure 5.
Influence of the slurry flow rate and its concentration on the pressure drop (T = 7 °C).
Each of the characteristics consists of two parts that differ in course. For small values of the flow rate, the measurement points were arranged along a straight line. Such a course of the characteristics proves the laminar flow of the slurry in the pipe channel. After exceeding a certain value of the flow rate, the shape of the characteristic changed, indicating a departure from the laminar flow of the fluid in the pipe channel. It was noticed that a slight increase in the flow rate of the mPCM slurry caused a clear (greater than before) increase in the pressure drop. This fact may indicate a transition to a turbulent flow of the slurry, and then the pressure drop depends on the second power of the flow velocity of the fluid. The described course of characteristics also occurred in the case of the slurry flow at the temperature T = 24 °C and T = 44 °C. The occurrence of two trends in the characteristics of pressure drop vs. flow rate (or flow velocity) results from the classical laws of fluid mechanics and was also observed in the flow of the mPCM slurry by researchers whose experiments covered the range of laminar and turbulent flows of mPCM slurry [34,63].
In the laminar flow, the value of the pressure drop practically did not depend on the concentration of the mPCM slurry, up to the value of 10.75%. Increasing the concentration of the slurry to 12.09% (and higher) caused the pressure drop to depend on the mass fraction of the mPCM in the slurry. The greater the concentration of the slurry, the greater the pressure drop. In these cases, it was also noticed that the greater the concentration of the slurry, the greater its flow had to be to change the nature of the fluid motion. The observed trends were also observed during the experiments conducted at T = 24 °C. However, when the slurry had a temperature of T = 44 °C, both the value of the pressure drop and the limiting flow rate did not depend on the concentration of the flowing slurry. In the literature, there are some publications in which the assessment of the impact of the mPCM concentration in the slurry on the pressure drop was conducted on the basis of analogous characteristics, i.e., Dp = f(m), Dp = f(w). Some authors state that the mPCM slurry concentration has no effect on the pressure drop during its flow [33,35,36,47,48,49,51,54]. There are also publications that show that an increase in the mPCM concentration causes an increase in the pressure drop in the slurry flow [39,46]; on the contrary, a decrease in the pressure drop [53] or this effect was noticeable only after exceeding a certain value of the mPCM concentration in the slurry [52]. There are no publications that describe the effect of the mPCM slurry concentration on the flow rate/velocity of the slurry at which the fluid motion character changes. However, it should be noted that a direct comparison of the characteristics of mPCM slurries with different concentrations, i.e., de facto different substances (different viscosities and densities), is misleading; therefore, it should be based on the characteristics as a function of the dimensionless Reynolds number (Re).
During a turbulent flow, no influence of the slurry on the obtained value of the pressure drop concentration was observed. Similarly, no effect of the slurry concentration on the pressure drop was observed during the experiments conducted with the slurry at the temperatures of T = 24 °C and T = 44 °C. The lack of influence of the mPCM slurry concentration on the pressure drop at the same flow rate was described in [32], whereas in [37], it was found that the higher the concentration of mPCM in the slurry, the greater the pressure drop during its flow.
3.2. The Influence of the Reynolds Number on the Pressure Drop during Slurry Flow
The value of the Re number was determined from Equation (1). The apparent viscosity and density of the mPCM slurry, occurring in Equation (1), were determined during our own detailed basic research and presented in detail in the studies [56,59]. It should be emphasized that the apparent viscosity depends not only on the temperature, but also on the shear rate (Figure 3). The shear rate for each value of the slurry mass flow rate was calculated using Equation (3). In order to determine the Reynolds number, the mass flow rate of the slurry had to be converted to its flow velocity. For this purpose, Equation (2) was used.
The influence of the Reynolds number and slurry concentration on the measured pressure drop is shown in Figure 6. Similarly to Figure 4, the presented results concern the study of slurries at the temperature of T = 7 °C.
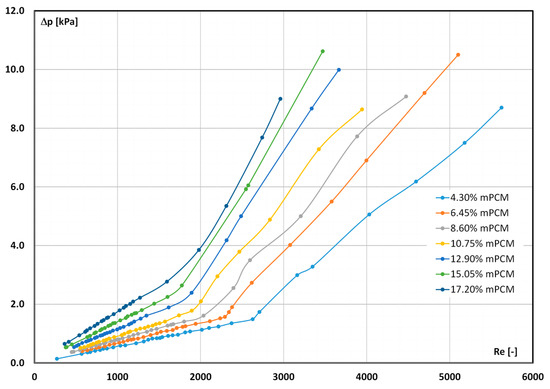
Figure 6.
Effect of the Reynolds number and slurry concentration on the pressure drop (T = 7 °C).
Once again, two ranges were observed in the course of each of the characteristics: rectilinear for small values of the Re number (indicating the laminar flow of the slurry) and curvilinear after exceeding the critical value of the Reynolds number Recr (transient and turbulent flows of the slurry). This time, the effect of the slurry concentration on the value of the measured pressure drop was clearly observed as well as the influence of the slurry concentration on the critical Reynolds number. The greater the concentration of the slurry, the greater its flow resistance, but also the faster the departure from the laminar flow of the fluid. The critical Reynolds number decreased from Recr ≈ 2600, when the mPCM concentration was 4.3%, to Recr ≈ 1600, when the mPCM concentration was increased to 17.20%. It should be emphasized that identical relationships were observed when testing slurries at T = 24 °C and T = 44 °C. When the slurry temperature was T = 24 °C, Recr ≈ 2800 (4.30% mPCM) decreased to Recr ≈ 2000 (17.20% mPCM) and for T = 44 °C, Recr ≈ 3200 (4.3% mPCM) decreased to Recr ≈ 2600 (17.20% mPCM).
It can therefore be concluded that the number of microcapsules contained in the slurry has a significant impact on the critical Reynolds number. The more there are, the more difficult it is to maintain a laminar flow of the mPCM slurry. According to us, this may be due to the collision of microcapsules flowing in the laminar layers with microcapsules flowing in the adjacent layers. The more microcapsules/collisions there are, the faster the surrounding fluid will enter into turbulent flow.
An increase in the pressure drop along with an increase in the concentration of mPCM in the slurry during its laminar flow was observed in [41,42,43,64,65] and during turbulent flow in [65,66,67,68,69]. The increase in the pressure drop was explained by the increase in the slurry viscosity. It was increased due to the increase in the number of microcapsules contained in the liquid and increased shear stresses. Since the cited papers contain a description of the results of research conducted in the range of a selected type of fluid movement (Re < 2000 or Re > 2000), at present, there is no confirmed knowledge of whether and how the concentration of mPCM in the slurry affects the loss of the laminar flow stability.
3.3. The Influence of the Temperature on the Pressure Drop during Slurry Flow
Figure 7 and Figure 8 show the results of the pressure drop measurement conducted during the flow of the slurry with the mPCM concentration of 6.45%.
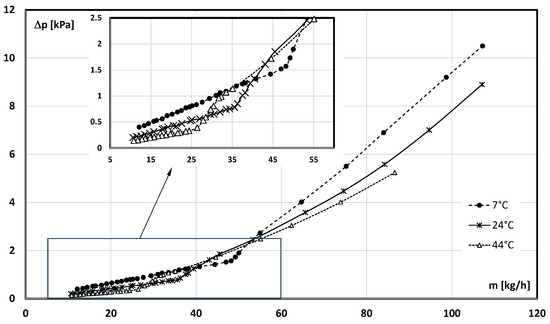
Figure 7.
Influence of the slurry flow rate and its temperature on the pressure drop (mPCM share in slurry, 6.45%).
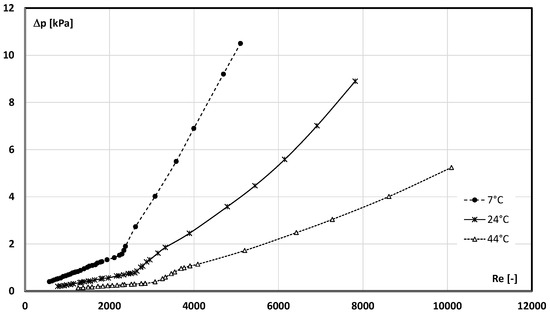
Figure 8.
Influence of the Re number and mPCM slurry temperature on the pressure drop (mPCM share in slurry, 6.45%).
Figure 7 shows the results of the pressure drop measurement as a function of the mass flow rate of the mPCM slurry and Figure 8 as a function of the Re number. The results obtained during the measurements, during which the mPCM slurry had a temperature of T = 7 °C (PCM in the microcapsule was a solid), T = 24 °C (PCM in the microcapsule underwent a phase change), and T = 44 °C (PCM in the microcapsule was liquid), were compared. It can be seen from both figures that, in general, the lower the temperature of the slurry, the higher its pressure drop at the same mass flow rate/Re number. It is clear from both plots that the departure from laminar flow depended on the flow velocity of the fluid, but also on the temperature of the slurry. The analysis of the data in Figure 6 shows that the departure from the laminar flow occurred already at the flow rate of ṁ ≈ 25 kg/h for the slurry at the temperature of T = 44 °C. The slurry at the temperature of T = 24 °C completed the laminar flow at the flow rate of ṁ ≈ 35 kg/h and the one at the temperature of T = 7 °C only at ṁ ≈ 50 kg/h. Figure 7 shows an inverse relationship, i.e., the lower the temperature of the slurry, the lower the value of Re and the departure from the laminar flow occurred. It was found that, for the concentration of 6.45%, the value of the critical Reynolds number was Recr ≈ 2300 (T = 7 °C, the PCM was in the form of a solid), Recr ≈ 2600 (T = 24 °C, the PCM underwent a phase change), and Recr ≈ 3000 (T = 44 °C, the PCM was in liquid form). Qualitatively identical courses of the characteristics were observed for all other concentrations of the mPCM slurry. Since the critical Reynolds number of the base liquid (water) does not depend on its temperature, the change in Recr with the temperature (in the mPCM slurry flow) results from the presence of PCM-filled microcapsules. Two reasons for the observed phenomenon are probable: a significant change in the volume of microcapsules with the temperature (especially during the PCM phase transition) and/or the influence of the state of matter of the PCM inside the microcapsule on its dynamics.
4. Summary and Conclusions
Detailed studies of the pressure drop during the flow of the aqueous slurry of a microencapsulated PCM were conducted. The slurries with concentrations of 4.30%, 6.45%, 8.60%, 10.75%, 12.90%, 15.05%, and 17.20% flowed through a tube with an internal diameter of d = 4 mm and a total length of L = 900 mm. The pressure drop was measured over a length of 400 mm. The tests were conducted under adiabatic conditions and at three different temperatures of the mPCM slurry. These were: T = 7 °C (the PCM in the microcapsule was solid), T = 24 °C (the PCM in the microcapsule was undergoing a phase change), and T = 44 °C (the PCM in the microcapsule was liquid). The slurry flow ranged from 5 kg/h to 108.5 kg/h, which corresponded to Re = 270.9–11,240.7. Based on the conducted research, it is concluded that:
- In the tested range of the Re number, the characteristics clearly allow the zones of laminar and transient/turbulent movements of the fluid to be noticed;
- Both in laminar and turbulent flows, the increase in the mPCM slurry concentration caused an increase in the slurry pressure drop due to an increase in its viscosity;
- The higher the concentration of microcapsules in the slurry, the more difficult it was to maintain a laminar fluid flow and the change in the nature of the movement occurred at a lower value of the Re number (Recr ≈ 1600 for 17.20% mPCM and increased to Recr ≈ 2600 when the mPCM concentration decreased to 4.3%);
- A clear influence of the mPCM slurry temperature on the critical number of Re was observed, which is not observed in the flow of Newtonian liquids without additives;
- The lower the temperature of the slurry, the more difficult it was to maintain the laminar flow of the slurry;
- It was found that, for the concentration of 6.45%, the value of the critical Reynolds number was Recr ≈ 2300 (T = 7 °C, the PCM was in the form of a solid), Recr ≈ 2600 (T = 24 °C, the PCM was undergoing a phase change), and Recr ≈ 3000 (T = 44 °C, the PCM was in liquid form).
Further analyses of the collected experimental data are planned, including the precise determination of the critical Reynolds number, the determination of the experimental values of the friction factor, and the comparison of the obtained values of the friction factor with theoretical values (according to the Hagen–Poiseuille and Blasius relationships for laminar and turbulent slurry flows, respectively). In addition, we plan to conduct further complementary experimental studies using slurries with different temperature values. The aim of this future research will be to assess whether and to what extent the state of matter of the PCM affects the Recr and pressure drop (friction factor).
Author Contributions
Conceptualization, K.D. and M.K. (Marcin Kruzel); methodology, K.D.; software, M.K. (Marcin Kruzel); validation, M.K. (Marcin Kruzel) and M.K. (Martyna Kochanowska); formal analysis, K.D.; investigation, M.K. (Marcin Kruzel); resources, M.K. (Martyna Kochanowska); data curation, K.D.; writing—original draft preparation, K.D.; writing—review and editing, M.K. (Marcin Kruzel); visualization, M.K. (Martyna Kochanowska); supervision, K.D.; project administration, M.K. (Marcin Kruzel); funding acquisition, M.K. (Marcin Kruzel). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- European Commission. Commission Staff Working Document, Energy Storage—The Role of Electricity; European Commission: Brussels, Belgium, 2017. [Google Scholar]
- Koohi-Fayegh, S.; Rosen, M.A. A review of energy storage types, applications and recent developments. J. Energy Storage 2020, 27, 101047. [Google Scholar] [CrossRef]
- Karaipekli, A.; Erdoğan, T.; Barlak, S. The stability and thermophysical properties of a thermal fluid containing surface-functionalized nanoencapsulated PCM. Thermochim. Acta 2019, 682, 178406. [Google Scholar] [CrossRef]
- Ghoghaei, M.S.; Mahmoudian, A.; Mohammadi, O.; Shafii, M.B.; Jafari Mosleh, H.; Zandieh, M.; Ahmadi, M.H. A review on the applications of micro-/nano-encapsulated phase change material slurry in heat transfer and thermal storage systems. J. Therm. Anal. Calorim. 2021, 145, 245–268. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, C.Y.; Markides, C.N.; Wang, H.; Li, W. Medium- and high-temperature latent and thermochemical heat storage using metals and metallic compounds as heat storage media: A technical review. Appl. Energy 2020, 280, 115950. [Google Scholar] [CrossRef]
- Tang, Z.; Gao, H.; Chen, X.; Zhang, Y.; Li, A.; Wang, G. Advanced multifunctional composite phase change materials based on photo-responsive materials. Nano Energy 2021, 80, 105454. [Google Scholar] [CrossRef]
- Lin, Y.; Zhu, C.; Alva, G.; Fang, G. Microencapsulation and thermal properties of myristic acid with ethyl cellulose shell for thermal energy storage. Appl. Energy 2018, 231, 494–501. [Google Scholar] [CrossRef]
- Opolot, M.; Zhao, C.; Liu, M.; Mancin, S.; Bruno, F.; Hooman, K. A review of high temperature (≥500 °C) latent heat thermal energy storage. Renew. Sustain. Energy Rev. 2022, 160, 112293. [Google Scholar] [CrossRef]
- Mishra, R.K.; Verma, K.; Mishra, V.; Chaudhary, B. A review on carbon-based phase change materials for thermal energy storage. J. Energy Storage 2022, 50, 104166. [Google Scholar] [CrossRef]
- Takudzwa Muzhanje, A.; Hassan, M.A.; Hassan, H. Phase change material based thermal energy storage applications for air conditioning: Review. Appl. Therm. Eng. 2022, 214, 118832. [Google Scholar] [CrossRef]
- Gao, D.C.; Sun, Y.; Fong, A.M.; Gu, X. Mineral-based form-stable phase change materials for thermal energy storage: A state-of-the art review. Energy Storage Mater. 2022, 46, 100–128. [Google Scholar] [CrossRef]
- Eanest Jebasingh, B.; Valan Arasu, A. A detailed review on heat transfer rate, supercooling, thermal stability and reliability of nanoparticle dispersed organic phase change material for low-temperature applications. Mater. Today Energy 2020, 16, 100408. [Google Scholar] [CrossRef]
- Nair, A.M.; Wilson, C.; Huang, M.J.; Griffiths, P.; Hewitt, N. Phase change materials in building integrated space heating and domestic hot water applications: A review. J. Energy Storage 2022, 54, 105227. [Google Scholar] [CrossRef]
- Magendran, S.S.; Khan, F.S.A.; Mubarak, N.M.; Vaka, M.; Walvekar, R.; Khalid, M.; Abdullah, E.C.; Nizamuddin, S.; Karri, R.R. Synthesis of organic phase change materials (PCM) for energy storage applications: A review. Nano-Struct. Nano-Objects 2019, 20, 100399. [Google Scholar] [CrossRef]
- Alehosseini, E.; Jafari, S.M. Nanoencapsulation of phase change materials (PCMs) and their applications in various fields for energy storage and management. Adv. Colloid Interface Sci. 2020, 283, 102226. [Google Scholar] [CrossRef] [PubMed]
- Hashemi Jirandeh, M.R.; Mohammadiun, M.; Mohammadiun, H.; Dubaie, M.H.; Sadi, M. Intelligent modeling of rheological and thermophysical properties of nanoencapsulated pcm slurry. Heat Transf. 2020, 49, 2080–2102. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J.; Zhang, X.; Ma, J.; Shen, T.; Li, S.; Dong, B. A review on synthesis, characterization and application of nanoencapsulated phase change materials for thermal energy storage systems. Appl. Therm. Eng. 2021, 185, 116326. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, L.; Song, J. Preparation, thermal conductivity, and applications of nano-enhanced phase change materials (NEPCMs) in solar heat collection: A review. J. Energy Storage 2023, 63, 107047. [Google Scholar] [CrossRef]
- Li, C.; Yu, H.; Song, Y.; Liu, Z. Novel hybrid microencapsulated phase change materials incorporated wallboard for year-long year energy storage in buildings. Energy Convers. Manag. 2019, 183, 791–802. [Google Scholar] [CrossRef]
- Umair, M.M.; Zhang, Y.; Iqbal, K.; Zhang, S.; Tang, B. Novel strategies and supporting materials applied to shape-stabilize organic phase change materials for thermal energy storage—A review. Appl. Energy 2019, 235, 846–873. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S.; Liu, Z.; Wen, T.; Ding, Z.; Yan, J.; Zhang, G. Passive and active phase change materials integrated building energy systems with advanced machine-learning based climate-adaptive designs, intelligent operations, uncertainty-based analysis and optimisations: A state-of-the-art review. Renew. Sustain. Energy Rev. 2020, 130, 109889. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, Y.; Zheng, J.; Wu, F.; Lu, J.; Sun, S.; Wu, D.; Wu, T. Role and influence of hydrogen bonds in composite phase change materials: A critical review. Sol. Energy Mater. Sol. Cells 2022, 248, 112031. [Google Scholar] [CrossRef]
- Li, C.; Li, Q.; Lu, X.; Ge, R.; Du, Y.; Xiong, Y. Inorganic salt based shape-stabilized composite phase change materials for medium and high temperature thermal energy storage: Ingredients selection, fabrication, microstructural characteristics and development, and applications. J. Energy Storage 2022, 55, 105252. [Google Scholar] [CrossRef]
- Leong, K.Y.; Abdul Rahman, M.R.; Gurunathan, B.A. Nano-enhanced phase change materials: A review of thermo-physical properties, applications and challenges. J. Energy Storage 2019, 21, 18–31. [Google Scholar] [CrossRef]
- Albdour, S.A.; Haddad, Z.; Sharaf, O.Z.; Alazzam, A.; Abu-Nada, E. Micro/nano-encapsulated phase-change materials (ePCMs) for solar photothermal absorption and storage: Fundamentals, recent advances, and future directions. Prog. Energy Combust. Sci. 2022, 93, 101037. [Google Scholar] [CrossRef]
- Ayyaril, S.S.; Shanableh, A.; Bhattacharjee, S.; Rawas-Qalaji, M.; Cagliani, R.; Shabib, A.G.; Imran khan, M. Recent progress in micro and nano-encapsulation techniques for environmental applications: A review. Results Eng. 2023, 18, 101094. [Google Scholar] [CrossRef]
- Gao, G.; Zhang, T.; Jiao, S.; Guo, C. Preparation of reduced graphene oxide modified magnetic phase change microcapsules and their application in direct absorption solar collector. Sol. Energy Mater. Sol. Cells 2020, 216, 110695. [Google Scholar] [CrossRef]
- Abdeali, G.; Bahramian, A.R. A comprehensive review on rheological behavior of phase change materials fluids (slurry and emulsion): The way toward energy efficiency. J. Energy Storage 2022, 55, 105549. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, G.; Cui, G.; Dou, B.; Yan, X.; Lu, W.; Yang, Q. Experimental investigation of the effects of metal oxides and nucleating agents on nano-emulsions heat transfer performance in mini-channels. Appl. Therm. Eng. 2023, 226, 120312. [Google Scholar] [CrossRef]
- Cabaleiro, D.; Agresti, F.; Fedele, L.; Barison, S.; Hermida-Merino, C.; Losada-Barreiro, S.; Bobbo, S.; Piñeiro, M.M. Review on phase change material emulsions for advanced thermal management: Design, characterization and thermal performance. Renew. Sustain. Energy Rev. 2022, 159, 112238. [Google Scholar] [CrossRef]
- Zheng, H.; Tian, G.; Zhao, Y.; Xin, X.; Yang, C.; Cao, L.; Ma, Y. Experimental study on the preparation and cool storage performance of a phase change micro-capsule cold storage material. Energy Build. 2022, 262, 111999. [Google Scholar] [CrossRef]
- Alvarado, J.L.; Marsh, C.; Sohn, C.; Phetteplace, G.; Newell, T. Thermal performance of microencapsulated phase change material slurry in turbulent flow under constant heat flux. Int. J. Heat Mass Transf. 2007, 50, 1938–1952. [Google Scholar] [CrossRef]
- Taherian, H.; Alvarado, J.L.; Tumuluri, K.; Thies, C.; Park, C.H. Fluid flow and heat transfer characteristics of microencapsulated phase change material slurry in turbulent flow. J. Heat Transfer 2014, 136, 061704. [Google Scholar] [CrossRef]
- Chen, B.; Wang, X.; Zeng, R.; Zhang, Y.; Wang, X.; Niu, J.; Li, Y.; Di, H. An experimental study of convective heat transfer with microencapsulated phase change material suspension: Laminar flow in a circular tube under constant heat flux. Exp. Therm. Fluid Sci. 2008, 32, 1638–1646. [Google Scholar] [CrossRef]
- Zhang, G.; Cui, G.; Dou, B.; Wang, Z.; Goula, M.A. An experimental investigation of forced convection heat transfer with novel microencapsulated phase change material slurries in a circular tube under constant heat flux. Energy Convers. Manag. 2018, 171, 699–709. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, B.; Guo, Y.; Cui, G.; Dou, B.; Wang, Z.; Yan, X. Effect of metal oxide particles on the flow and forced convective heat transfer behaviour of microencapsulated PCM slurry. Sol. Energy 2022, 238, 280–290. [Google Scholar] [CrossRef]
- Wu, W.; Bostanci, H.; Chow, L.C.; Hong, Y.; Wang, C.M.; Su, M.; Kizito, J.P. Heat transfer enhancement of PAO in microchannel heat exchanger using nano-encapsulated phase change indium particles. Int. J. Heat Mass Transf. 2013, 58, 348–355. [Google Scholar] [CrossRef]
- Ashagre, T.B.; Rakshit, D. Study on flow and heat transfer characteristics of Encapsulated Phase Change Material (EPCM) slurry in Double-Pipe Heat Exchanger. J. Energy Storage 2022, 46, 103931. [Google Scholar] [CrossRef]
- Serale, G.; Fabrizio, E.; Perino, M. Design of a low-temperature solar heating system based on a slurry Phase Change Material (PCS). Energy Build. 2015, 106, 44–58. [Google Scholar] [CrossRef]
- Qiu, Z.; Ma, X.; Zhao, X.; Li, P.; Ali, S. Experimental investigation of the energy performance of a novel Micro-encapsulated Phase Change Material (MPCM) slurry based PV/T system. Appl. Energy 2016, 165, 260–271. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Ling, X. An experimental study of the latent functionally thermal fluid with micro-encapsulated phase change material particles flowing in microchannels. Appl. Therm. Eng. 2016, 105, 209–216. [Google Scholar] [CrossRef]
- Roberts, N.S.; Al-Shannaq, R.; Kurdi, J.; Al-Muhtaseb, S.A.; Farid, M.M. Efficacy of using slurry of metal-coated microencapsulated PCM for cooling in a micro-channel heat exchanger. Appl. Therm. Eng. 2017, 122, 11–18. [Google Scholar] [CrossRef]
- Ho, C.J.; Chang, P.C.; Yan, W.M.; Amani, M. Comparative study on thermal performance of MEPCM suspensions in parallel and divergent minichannel heat sinks. Int. Commun. Heat Mass Transf. 2018, 94, 96–105. [Google Scholar] [CrossRef]
- Ho, C.J.; Chang, P.C.; Yan, W.M.; Amani, P. Efficacy of divergent minichannels on cooling performance of heat sinks with water-based MEPCM suspensions. Int. J. Therm. Sci. 2018, 130, 333–346. [Google Scholar] [CrossRef]
- Ho, C.J.; Chen, W.C.; Yan, W.M.; Amani, P. Contribution of hybrid Al2O3-water nanofluid and PCM suspension to augment thermal performance of coolant in a minichannel heat sink. Int. J. Heat Mass Transf. 2018, 122, 651–659. [Google Scholar] [CrossRef]
- Dammel, F.; Stephan, P. Heat transfer to suspensions of microencapsulated phase change material flowing through minichannels. J. Heat Transfer 2012, 134, 020907. [Google Scholar] [CrossRef]
- Pakrouh, R.; Hosseini, M.J.; Bahrampoury, R.; Ranjbar, A.A.; Borhani, S.M. Cylindrical battery thermal management based on microencapsulated phase change slurry. J. Energy Storage 2021, 40, 102602. [Google Scholar] [CrossRef]
- Bai, F.; Chen, M.; Song, W.; Yu, Q.; Li, Y.; Feng, Z.; Ding, Y. Investigation of thermal management for lithium-ion pouch battery module based on phase change slurry and mini channel cooling plate. Energy 2019, 167, 561–574. [Google Scholar] [CrossRef]
- Ashagre, T.B.; Rakshit, D. A study on energy transport performance of Microencapsulated Phase Change Materials (MPCM) slurry. Int. Commun. Heat Mass Transf. 2022, 138, 106321. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, S.; Zhang, L. Multi-scale modeling and investigation of thermo-fluidic performance of microencapsulated phase-change material slurry. J. Energy Storage 2021, 37, 102502. [Google Scholar] [CrossRef]
- Shaukat, R.; Anwar, Z.; Imran, S.; Noor, F.; Qamar, A. Numerical Study of Heat Transfer Characteristics of mPCM Slurry during Freezing. Arab. J. Sci. Eng. 2021, 46, 7977–7988. [Google Scholar] [CrossRef]
- Inaba, H. New Challenge in Advanced Thermal Energy Transportation Using Functionally Thermal Fluids. Int. J. Therm. Sci. 2000, 39, 991–1003. [Google Scholar] [CrossRef]
- Sinha-Ray, S.; Sinha-Ray, S.; Sriram, H.; Yarin, A.L. Flow of suspensions of carbon nanotubes carrying phase change materials through microchannels and heat transfer enhancement. Lab Chip 2014, 14, 494–508. [Google Scholar] [CrossRef] [PubMed]
- Lian, C.; Wang, Y.; Li, Q.; Li, H.; He, X. Numerical investigation on the performance of microencapsulated phase change material suspension applied to liquid cold plates. Numer. Heat Transf. Part A Appl. 2019, 75, 342–358. [Google Scholar] [CrossRef]
- MICRONAL® 5428 X, n.d. Available online: www.microteklabs.com (accessed on 5 July 2023).
- Dutkowski, K.; Kruzel, M.; Zajączkowski, B.; Białko, B. The experimental investigation of mPCM slurries density at phase change temperature. Int. J. Heat Mass Transf. 2020, 159, 120083. [Google Scholar] [CrossRef]
- Dutkowski, K.; Kruzel, M.; Zajączkowski, B. Determining the Heat of Fusion and Specific Heat of Microencapsulated Phase Change Material Slurry by Thermal Delay Method. Energies 2021, 14, 179. [Google Scholar] [CrossRef]
- Thermophysical Properties of Fluid Systems. Available online: https://webbook.nist.gov/chemistry/fluid (accessed on 7 July 2023).
- Dutkowski, K.; Fiuk, J.J. Experimental research of viscosity of microencapsulated PCM slurry at the phase change temperature. Int. J. Heat Mass Transf. 2019, 134, 1209–1217. [Google Scholar] [CrossRef]
- Dutkowski, K.; Fiuk, J.J. Experimental investigation of the effects of mass fraction and temperature on the viscosity of microencapsulated PCM slurry. Int. J. Heat Mass Transf. 2018, 126, 390–399. [Google Scholar] [CrossRef]
- Dutkowski, K.; Fiuk, J.J. Experimental investigation on influence of microcapsules with PCM on propylene glycol rheological properties. E3S Web Conf. 2018, 70, 02005. [Google Scholar] [CrossRef]
- Dutkowski, K.; Kruzel, M. Microencapsulated PCM slurries’ dynamic viscosity experimental investigation and temperature-dependent prediction model. Int. J. Heat Mass Transf. 2019, 145, 118741. [Google Scholar] [CrossRef]
- Inaba, H.; Kim, M.K.; Horibe, A. Melting heat transfer characteristics of microencapsulated phase change material slurries with plural microcapsules having different diameters. J. Heat Transfer 2004, 126, 558–565. [Google Scholar] [CrossRef]
- Balasubramanian, K.R.; John Peter, R.; Jinshah, B.S. Experimental investigation on paraffin encapsulated with Silica and Titanium shell in the straight and re-entrant microchannel heat sinks. Heat Mass Transf. Stoffuebertragung 2023, 59, 1005–1018. [Google Scholar] [CrossRef]
- John Peter, R.; Balasubramanian, K.R.; Ravi Kumar, K. Comparative study on the thermal performance of microencapsulated phase change material slurry in tortuous geometry microchannel heat sink. Appl. Therm. Eng. 2023, 218, 119328. [Google Scholar] [CrossRef]
- Hashimoto, S.; Kurazono, K.; Yamauchi, T. Thermal-hydraulic characteristics of ethylene glycol aqueous solutions containing microencapsulated paraffin. Exp. Therm. Fluid Sci. 2018, 99, 297–303. [Google Scholar] [CrossRef]
- Rao, Y.; Dammel, F.; Stephan, P.; Lin, G. Flow frictional characteristics of microencapsulated phase change material suspensions flowing through rectangular minichannels. Sci. China Ser. E Technol. Sci. 2006, 49, 445–456. [Google Scholar] [CrossRef]
- Li, L.Y.; Zou, D.; Ma, X.F.; Liu, X.S.; Hu, Z.G.; Guo, J.R.; Zhu, Y.Y. Preparation and flow resistance characteristics of novel microcapsule slurries for engine cooling system. Energy Convers. Manag. 2017, 135, 170–177. [Google Scholar] [CrossRef]
- Doruk, S.; Şara, O.N.; Karaipekli, A.; Yapıcı, S. Heat transfer performance of water and Nanoencapsulated n-nonadecane based Nanofluids in a double pipe heat exchanger. Heat Mass Transf. Stoffuebertragung 2017, 53, 3399–3408. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).