1. Introduction
Thrust bearings are widely used in many engineering applications, when the significant axial forces acting on a rotor shaft have to be caught. The position of the rotor shaft is usually the horizontal or vertical one, though inclined positions are also possible. The position of the shaft and the bearing influences dramatically the two most important features of the bearing performance: the lubrication and cooling, which are the key factors for the bearing rating life and efficiency. There are a lot of studies concerning the ball or roller bearings, which could be related to this study. Wu, W., Hu, J. et al. [
1,
2,
3,
4,
5] studied extensively the air–oil two-phase flow inside the oil jet-lubricated ball bearing both experimentally and by the numerical simulations. They investigated the air–oil distribution inside the bearing and found its correlation with the heat transfer and temperature distribution. They also considered the influence of the rotational speed and multiple-nozzle configuration on the oil volume fraction distribution. The heat transfer inside the ball bearing with one nozzle inlet was also investigated at high rotational speeds by Yan et al. [
6]. The authors primarily focused on the influence of cage parameters, such as the pocket’s shape, methods of guiding and clearances. Ma et al. [
7] studied the flow and heat balance of the high-speed ball bearing under the oil–air lubrication with a focus on the formation of an oil film in the oil pipe nozzle. Their CFD results were verified by temperature measurements in the test bearing. An interesting study of the effect of nozzle oil supply on the sound field characteristics of full ceramic ball bearings can be found in [
8], yet the individual rotation of the rolling balls is not considered.
Typically, the numerical simulations include all the 3D geometry of the bearing so as to capture the oil supply position. In special cases, some simplifications using the periodicity boundary conditions can be used, as shown in [
9], where the oil–air ratio is set to a constant empirical value, and so only one rotational periodicity segment of the bearing is modelled. Also, in [
10], where the flow in the oil nozzle and the space bounded by the cage and the inner race are considered, the flow is solved as a periodic one based on the physical spacing of the oil supply holes. Peterson et al. [
11] studied numerically the fluid drag losses in the deep groove ball bearing and in the radial needle roller bearing and compared them with experimental data. For their calculations, they used one angular segment of the bearing with three rolling elements.
Lubrication of the radial needle roller bearing with an inner oil supply nozzle is studied in [
12], with the full 3D geometry model. A comprehensive study of the oil–air two-phase flow inside the cylindrical roller bearing with one or two inner nozzles comes from Gao et al. [
13,
14], who studied the oil distribution and drag and churning losses inside a high-speed cylindrical roller bearing. Concerning the individual rotation of the rolling cylinders, it was not considered for a real 3D model of the bearing, but its effect was verified by an in-line configuration representing the straight box with several cylinders and using the periodic boundary conditions. Self-rotation of the rollers was ignored also in the study of flow and thermal phenomena inside a cylindrical roller bearing with one inner nozzle [
15]. Zhu et al. [
16] investigated experimentally and numerically the two-phase flow in two-row tapered roller bearings with the inner as well as the outer ring rib structure under the condition of loss of lubrication. They found that the two-row tapered roller bearings with the outer ring rib structure give better lubrication conditions. A special approach was used in the work of Feldermann et al. [
17], where the hydraulic losses in the radial cylindrical roller bearing were calculated with a hybrid computational scheme. The results from a course grid full 3D model were mapped to a less expensive single bearing chamber (domain between two adjacent rolling elements), which enabled them to describe the flow field in detail.
The numerical simulations contained in the references mentioned above commonly use the VOF (Volume of Fluid) model of the multiphase flow [
18]. This model is very robust and easy to implement, but in reality, it solves only the equation for the volume fraction of the liquid component and does not consider the formation of the liquid particles, their interaction and the formation of the continuous film. An advanced study of the oil–gas mixture can be found in [
19], where the movement of the oil droplets and formation of the oil film is examined in the chamber behind the roller bearing.
As already stated, there are a lot of studies concerning the ball or roller bearings, which could be related to this study. Still, most of them are of the oil jet-lubricated ones and there is a lack of studies concerning the oil bath-lubricated bearings. There, some new phenomena should be addressed, e.g., splash effects [
20,
21,
22,
23] similar to the gearboxes, or pumping effects of the bearing. Both of these phenomena are significantly influenced by the oil level in the oil chamber and both are highly important for correct lubricating and cooling of the bearing. Liebrecht et al. [
24] studied experimentally and numerically the performance and the drag and churning losses inside the tapered roller bearing with a vertically oriented shaft at two different oil bath levels and they founded that the oil level affects the drag and churning losses significantly, especially at high rotational speeds. A comprehensive study of a multiphase flow inside the fully submerged tapered roller bearing with a vertically oriented shaft was done by Maccioni et al. [
25,
26]. They used the Hirt aeration model [
27] inside the OpenFOAM CFD code to make the numerical simulations and applied a special sapphire bearing outer ring and fluorescent polystyrene particles inside the test rig to monitor in detail the pumping effects by means of PIV.
Some more references that could be related to this study can be added here. Two of them, [
28,
29], are devoted to the improvement of the computational methodology focused on the lubricated mechanical components including the rolling bearings and on the optimum meshing strategies. The other references are devoted to the journal bearings [
30,
31,
32,
33,
34] and the fluid film thrust bearings [
35,
36,
37,
38]. Though these bearings are out of the scope of the previous detailed description of literary sources, they share a similar methodology when modelling the lubrication and cooling processes.
The aim of this study is to model numerically the flow and thermal phenomena inside the thrust bearing housing of the high-performance mixed-flow pump under extreme climatic conditions, including both the lubrication effects and the cooling of the oil by the water-cooling system based on the spiral piping. To verify the numerical simulation, temperatures measured in the housing could be compared with the calculated values, but, because of a lack of input power at the test rig, data only for the reduced speed and heat production are available. A brief description of the tapered roller thrust bearing and the entire housing is presented in the next section, followed by a description of the physical models and numerical tools used. The results of simulations are presented in detail in the last section, including the comprehensive graphical work. In Discussion, the results are summarized with some conclusions based on the presented facts.
2. Case and Material Description
In this study, the CFD analysis of fluid flow and heat transfer inside the thrust bearing housing of the vertical mixed-flow pump is presented. The bearing housing is installed on the top of the pump (
Figure 1), over the welded 90° elbow. There are two bearings inside the whole assembly shown in
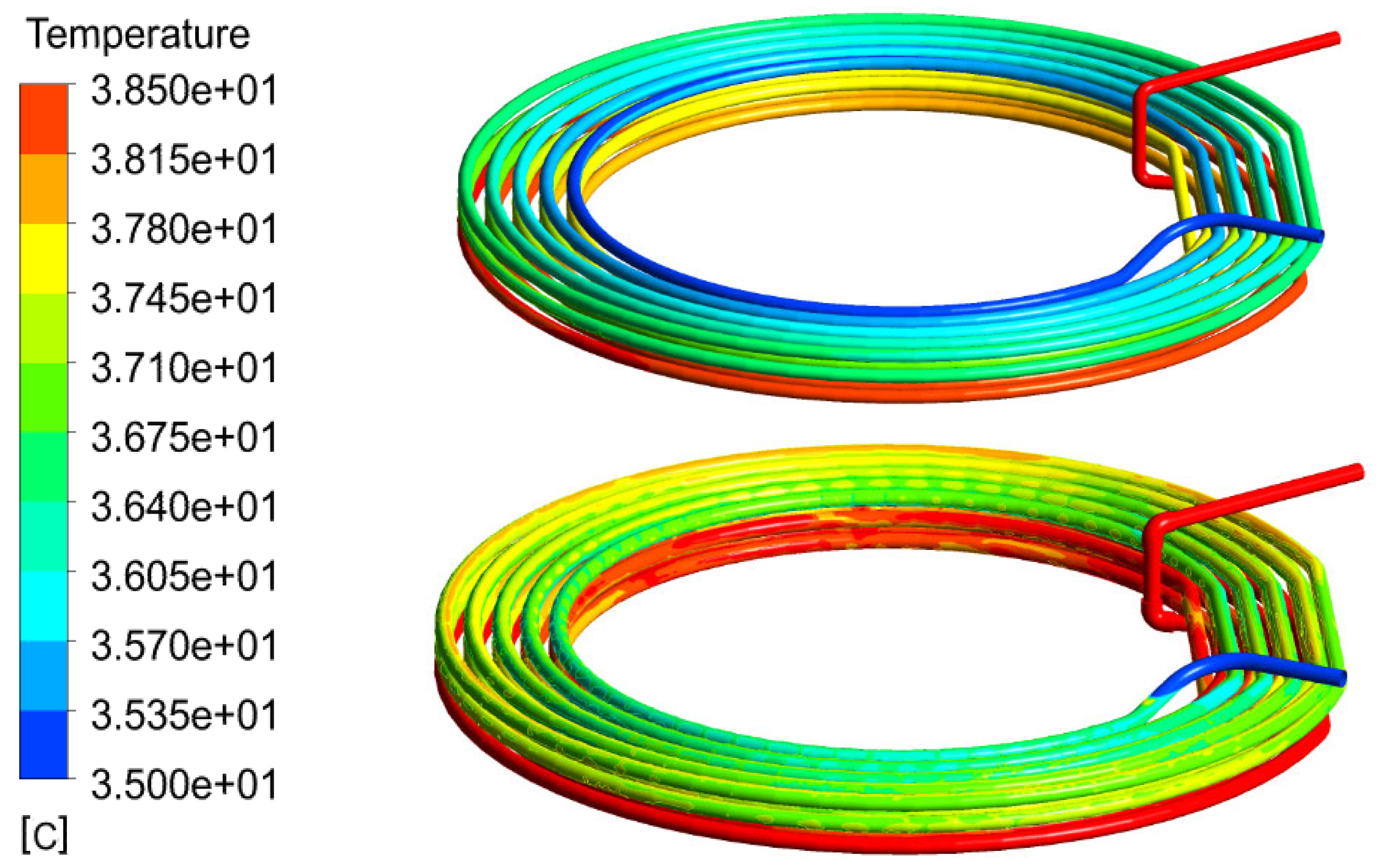
Figure 2. The upper one is the support double-row spherical roller bearing, which is lubricated with the oil from the upper side; this bearing is not an object of this study. The lower bearing is the single-row spherical roller one and not only treats the axial loads, but also has a radial load capacity. It is lubricated using the oil bath system. This bearing and its chamber are the main objects of this study. The bearing housing is equipped with a cooling system based on the spiral piping, inside which the pressurized cold water circulates. In the sectional view, the spiral piping forms a scheme of 5 × 3 pipes (radial × axial directions). The inner diameter of the spiral piping is 15 mm.
The geometry of the computational domain is derived from 2D drawings and a full 3D model created in the SOLIDWORKS 2022 3D CAD system. Because of the reasonable computational demands, the geometry has been a little bit simplified (mainly bolts, nuts, weld joints and unnecessary small piping have been removed). Still, the computational domain keeps full 3D shapes of hydraulic surfaces, without any simplifications by symmetry planes or periodic conditions.
Figure 3 shows the computational model of the thrust bearing housing including four channels, which lead the oil from the chamber to the bottom part of bearing (
Figure 3b). Also, all necessary details of the cooling spiral have been preserved for the credible analysis (
Figure 4). Because of meshing strategies and the computational model, some simplifications of the bearing geometry had to be done, especially concerning the roller geometry and clearances between rollers and races. These simplifications will be described in more detail within the following paragraphs.
The parameters of the bearing are listed in
Table 1. The bearing represents a slight modification of the industrial SKF 29460E (SKF Lubrication Systems CZ, Chodov, Czech Republic) thrust bearing, but, as already said, some simplifications of the bearing geometry had to be made. Consequently, the impacts of different model simplifications on the results have been tested. In the first stage, the roller guide cage was not considered in the simulation, and the gap between rollers and races was increased to 0.9 mm. During the subsequent steps, the cage geometry was added and the gap between rollers and races was decreased to 0.34 mm. All rollers are centered in the cage pocket and in the middle of the races. Concerning the rotary speeds of the rollers and of the cage [
39], they changed only slightly according to the geometry modifications, so at the end, reference speeds obtained from the frequency data provided by the original bearing manufacturer were used, according to
Table 1. Differences between experimental and all theoretical values of the rotary speeds still remained below 5%.
Four materials were considered: three fluids (oil and air inside the housing, water inside the cooling pipe) and one solid material (stainless steel, representing the wall of the cooling pipe). The physical properties of water are described by the IAPWS industrial formulation IF-97 [
40], and the air is treated as the ideal gas. Because of unsatisfactory knowledge of the oil’s thermodynamic state, it is described as the constant property liquid with reference values at the temperature of 40 °C [
41]. The physical properties of the oil, OL-J46/ISO VG 46 (PARAMO, a.s., Pardubice, Czech Republic) and the stainless steel, 1.4541/AISI 321 (BODEN-MATTE, s.r.o., Vsetin, Czech Republic) are described in
Table 2. It must be mentioned that only single values of the density, specific heat capacity and thermal conductivity are used in the oil description. According to the producer, these quantities vary in the required temperature range by 10% maximum. On the other hand, the kinematic viscosity changes considerably. So, in the simulations, the oil density, specific heat capacity and thermal conductivity are considered to be constant in the full range of temperatures. For the oil viscosity, the viscosity index and viscosity values for the temperatures 60 °C and 80 °C have been used to create a simple expression describing the changes of oil viscosity in the required range of simulation temperatures (
Figure 5).
3. Numerical Methods
The ANSYS CFX, 2020R2 software package [
42] was applied to solve the transport equations, including the gravity and thermal effect. The calculation is based on the Reynolds-averaged Navier–Stokes equations (RANSs). Because of the relatively small (subsonic) velocities inside the oil, the effects of oil compressibility could be omitted. The flow is considered to be fully unsteady. Generally, for unsteady flows, the governing equations (URANS) can be expressed as
where
Ui are Reynolds-averaged velocity components in the 3D Cartesian coordinate system,
P is the Reynolds-averaged static pressure,
ρ is the fluid density,
μ is the dynamic viscosity,
μt is the turbulent viscosity derived from the turbulence model and
SM is the general momentum source term.
The SST turbulence model, which combines advantages of both the high- and the low-Reynolds-number turbulence models, has been applied. It links the formulation of the standard
k-ε and
k-ω models using two blending functions (
F1 and
F2) dependent on the wall distance. The following governing equations can be applied:
where
is the turbulence production term,
k is the turbulent kinetic energy and
ω is the turbulent frequency. In this formulation, the turbulent viscosity is defined in the following way:
where
S is the strain rate. More details of Menter’s SST model, including the definition and discussion of the blending functions and all used constants (
a, β, σ, γ), can be found in [
42,
43,
44]. To cover a wide range of the non-dimensional wall-adjacent grid height y+ during an unsteady flow, an automatic wall treatment has been applied.
The conservation equation of temperature for the mixture phase is based on the mixture total energy conservation equation.
where
H is the total enthalpy,
λ is the thermal conductivity,
T is the temperature and
SE is the general heat source term.
τij is the viscous stress tensor.
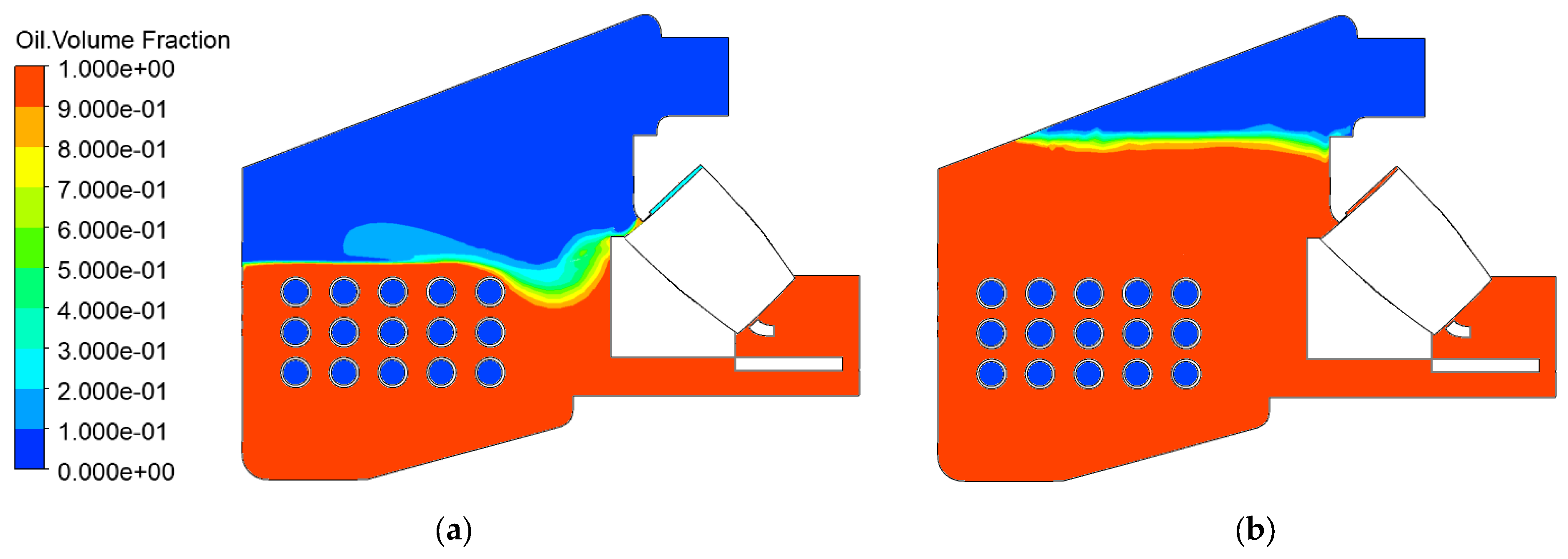
The numerical solution of free-surface flow inside the housing was carried out by means of the Volume of Fluid (VOF) method based on the monitoring of the volume fraction of both fluids (oil and air). Buoyancy parameters are related to the density difference and the standard gravity constant. The non-homogenous multiphase model was used for the velocity fields, with different velocity components for the oil and air fractions. The high-resolution scheme of the second order was used for the momentum equations and the first-order scheme was used for the turbulence numerics.
Inside the computational domain, there are both the stationary parts and the parts rotating with different rotational speeds. The Multiple Frame of Reference (MFR) capability and the fully unsteady model of flow with moving meshes have been used to capture the interactions between stationary parts and the rotating components. In principle, the computational domain has four subdomains: the bearing itself, the bearing housing, the steel part of the cooling spiral and, finally, the water inside the cooling spiral. All subdomains except the bearing are defined as the stationary ones. The bearing is defined as a rotating domain that rotates around the main axis with the rotary speed of the cage. The inner ring is therefore considered to be a rotating wall that rotates against the cage and set of rollers with a positive rotary speed of 276 rpm. On the other hand, the outer ring must be defined as the counter-rotating wall. Every roller has its individual axis of rotation inside the bearing domain and rotates around this axis with the rotary speed of 1558 rpm. The simulation is fully unsteady and the time discretization is based on the second-order backward Euler scheme. The timestep represents the revolution of the cage by 1°. The root mean square residuals are set to be less than 10−5, but the maximum number of inner iterations per one timestep is limited to 10.
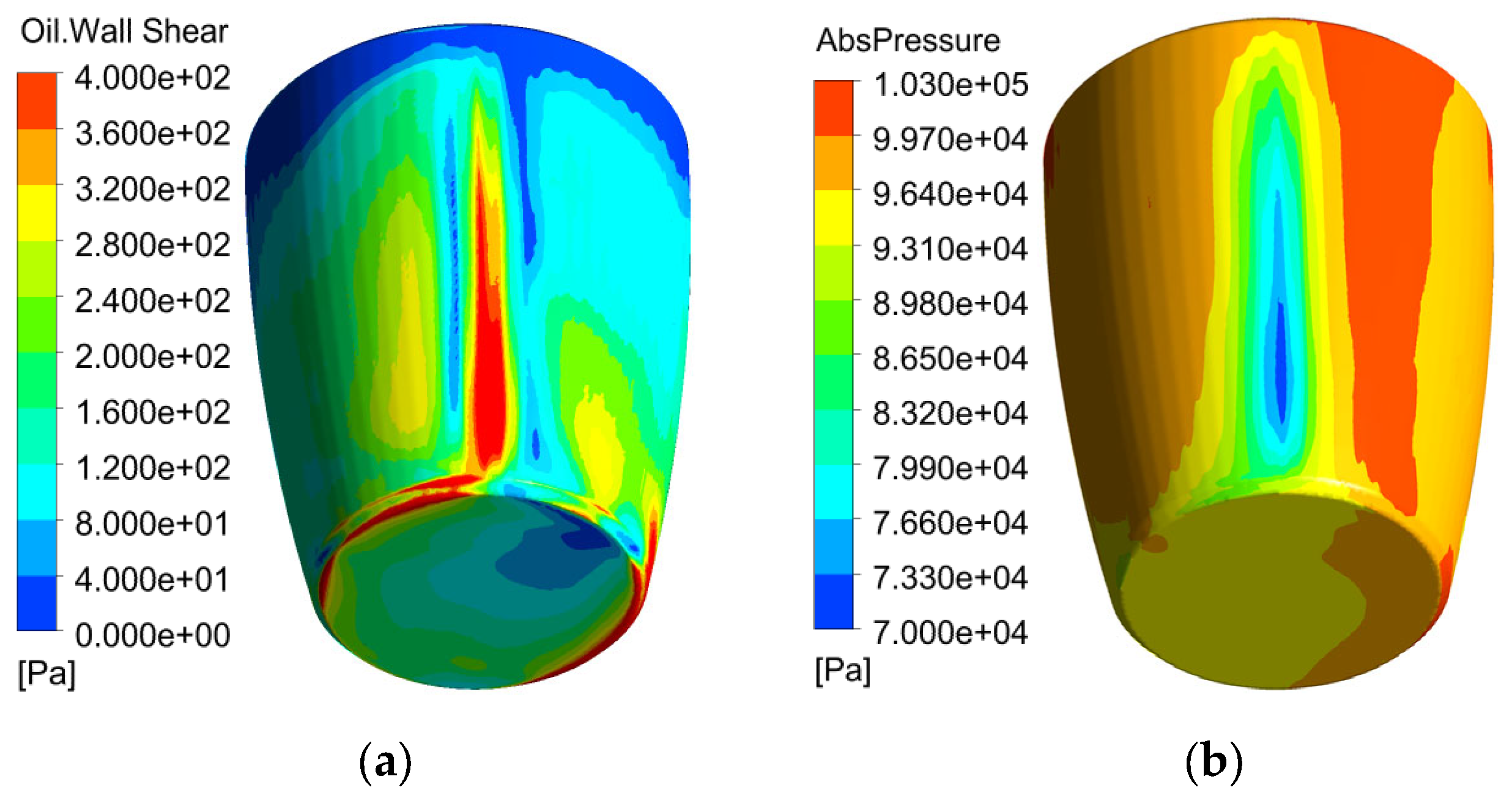
All hydraulic surfaces are considered to be smooth, without prescribed roughness. Boundary conditions are specified as follows: At the cooling pipe inlet, the normal velocity, turbulent kinetic energy and its dissipation rate have been set according to the prescribed mass flow rate, the estimated turbulence intensity of 5% and the eddy length scale of 1 mm. At the outlet (end of the pipe), the pressure outlet boundary condition has been set. Because extreme climatic conditions have been considered for the test case, water with the temperature 35 °C is supplied at the spiral inlet from the pump discharge with the available pressure difference representing the pump discharge head of 30 m. As there are some pressure losses in the external part of the cooling pipes, the water mass flow rate is set to 0.56 kg/s, which corresponds to the pressure loss difference, representing 26.3 m of water column. Because the temperature of the air in the pump station building can reach up to 45 °C, there would be only a minimum temperature gradient, and so the housing walls have been treated as the adiabatic ones. Just on the roller and race walls, the overall heat flux of 5000 W has been equally prescribed, representing estimated mechanical losses in the bearing. Additional hydraulic losses are generated naturally by the calculated flow phenomena and viscous forces and are the object of the CFD simulation.
With all these settings, the flow inside the computational domain is fully turbulent, with the Reynolds number about 6.6 × 104 in the cooling spiral and in the range from 1 × 105 to 7 × 105 in the bearing and its housing.
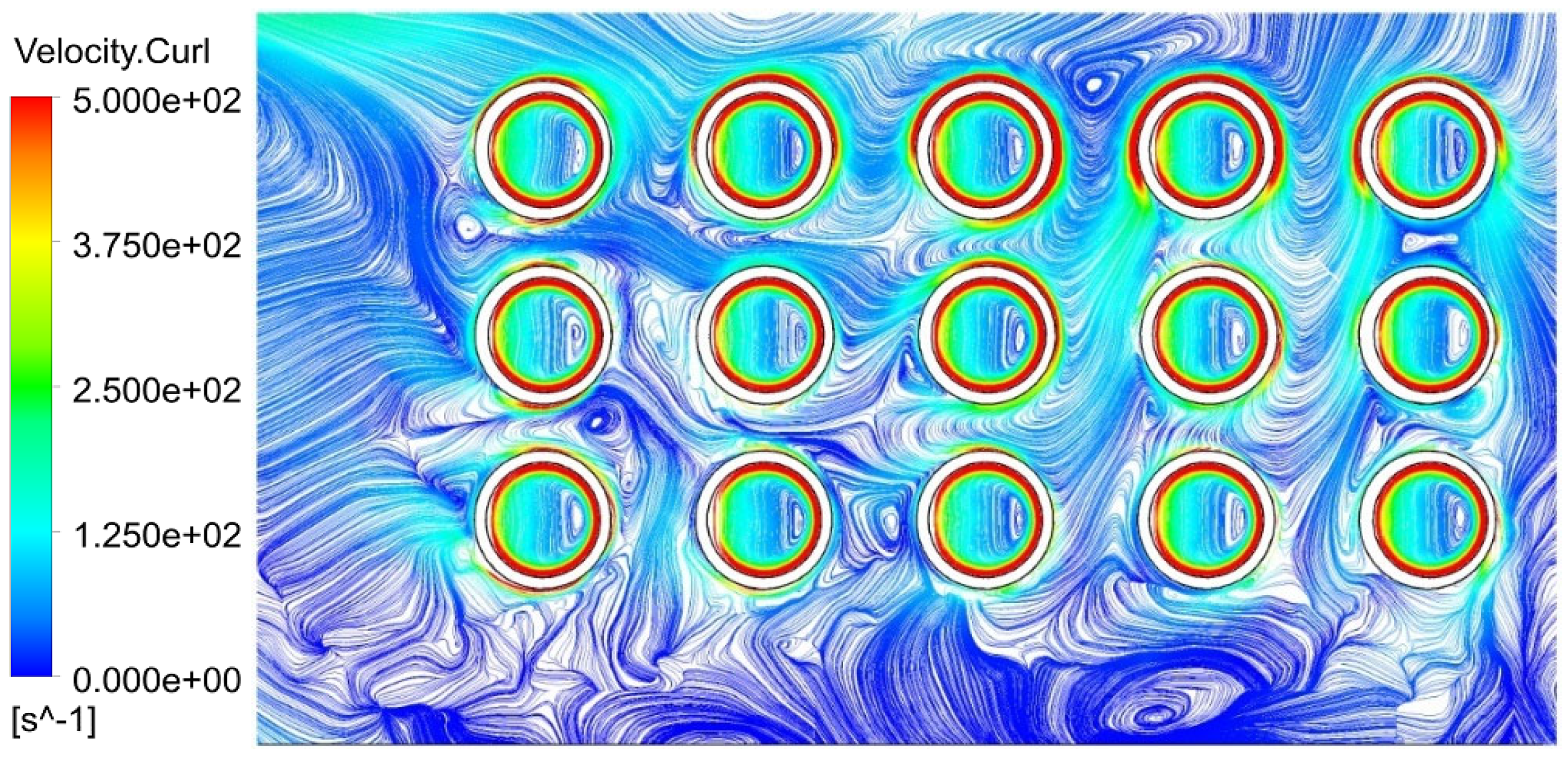
The hybrid multiblock computational grids were created in the ANSYS ICEM, 2020R2 software tool and represent approximately 70–90 million nodes. These grids were created in order to be isotropic enough, as required by the advanced turbulence model used for the simulations, but they also should fulfill the rules for sufficiently low values of y+ at the solid walls. In fact, no typical grid dependence study has been done, because the topology and quality of the grid are much more important in these simulations than the simple number of grid points. The main differences in the topology are due to the presence of the cage, but from the point of view of the mesh quality, the treatment of the rounded parts close to the rollers and races is the most critical task to be handled. So, parameters like the aspect ratio and skewness have been preferred, and the meshes are limited in their size just by the request to be able to work within the computer operating memory of 1 TB.
Figure 6 shows details of the computational grid of the roller and on the bearing housing, whereas
Figure 7 shows the grid structure around the roller, between the inner and outer races. To generate the prismatic elements in the location of radial clearance, the pre-inflation method was used, forming the prismatic elements first and then adding the tetrahedral elements in the remaining space. With the gap between rollers and races decreased to 0.34 mm, the distance of the first grid points from the wall is about 7.5 μm. With the decreasing width of the gap between rollers and races, the size of the computational grid dramatically increases, because both the pre-inflation method and the post-inflation method (prisms are formed from the already existing tetrahedral grid) require a sufficiently small global element size to be able to create the double-prismatic layer mesh inside the gap. This means that the size of the elements in the whole bearing must be very small. From this point of view, the gap size of 0.34 mm appeared to be limiting for the computer memory.
5. Discussion
As has been indicated in the Introduction, the aim of this study is to model numerically the flow and thermal phenomena inside the complete set of a thrust bearing and its housing under extreme climatic conditions, including both the lubrication effects and the cooling of the oil by the water-cooling system based on spiral piping. It is natural and clear that the methodology used in this work has been inspired by the authors cited in the Introduction. The novelty of the presented paper is the complexity of tools used to describe the solved problem in a form applicable to engineering practice. The objective was to use commonly available computational sources without the necessity of a supercomputer infrastructure, but still to keep the physical model as complex as possible. All the calculations have been done using a computational workstation with 1 TB of memory and dual AMD (Advanced Micro Devices, Inc., Santa Clara, CA, USA) EPYC 24-Core processors. The typical computational time per one timestep is about 5–7 min.
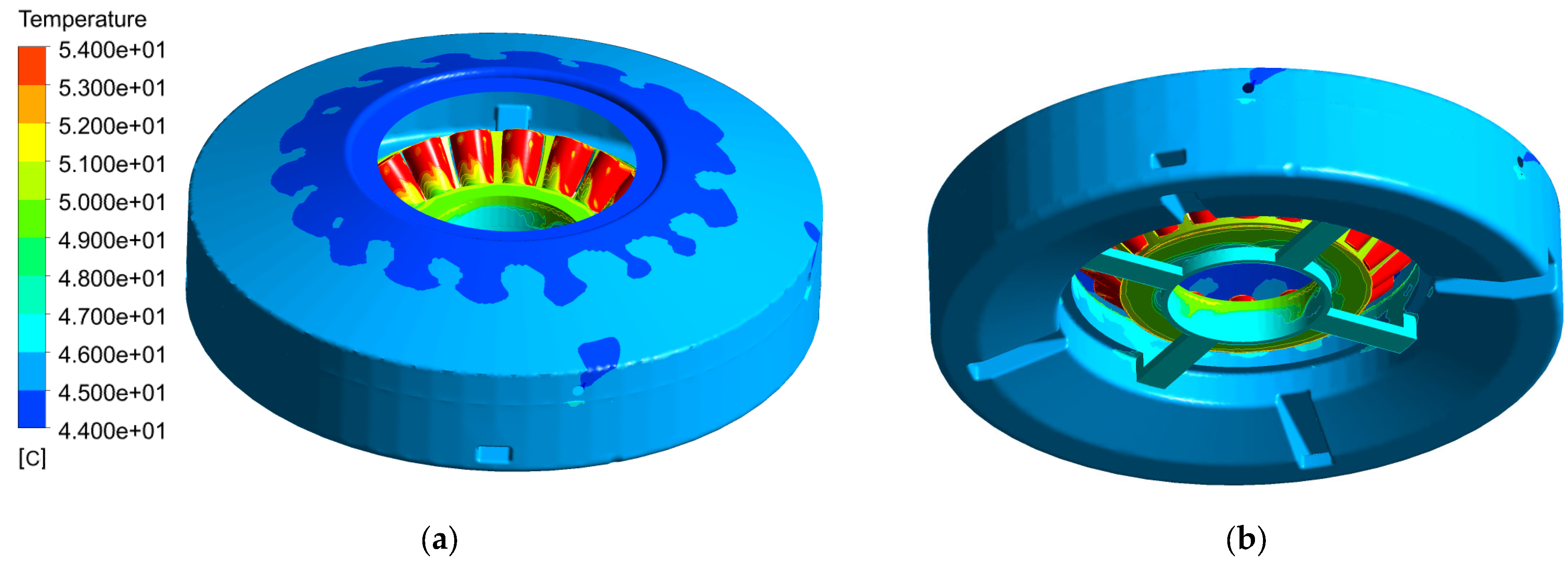
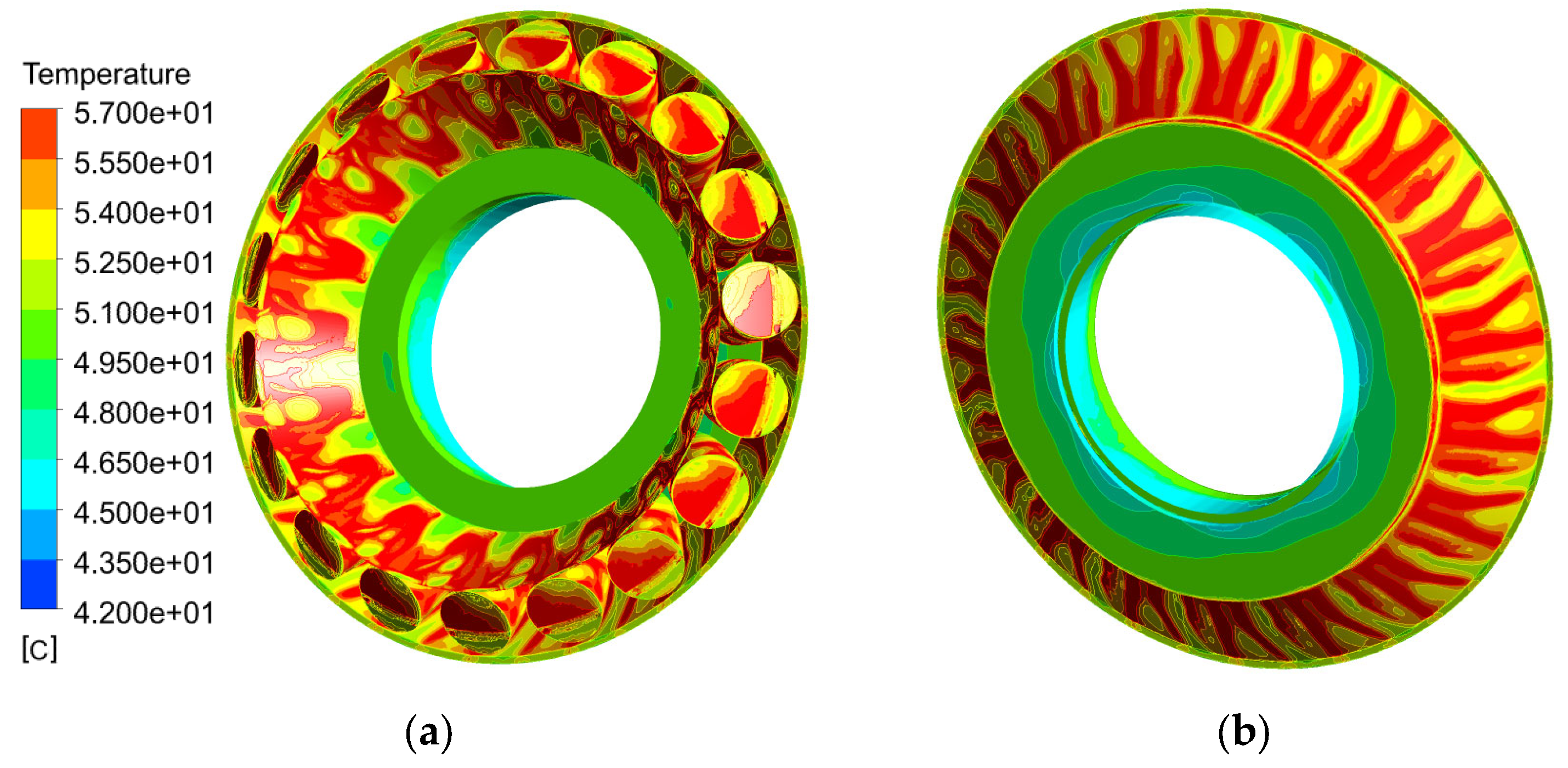
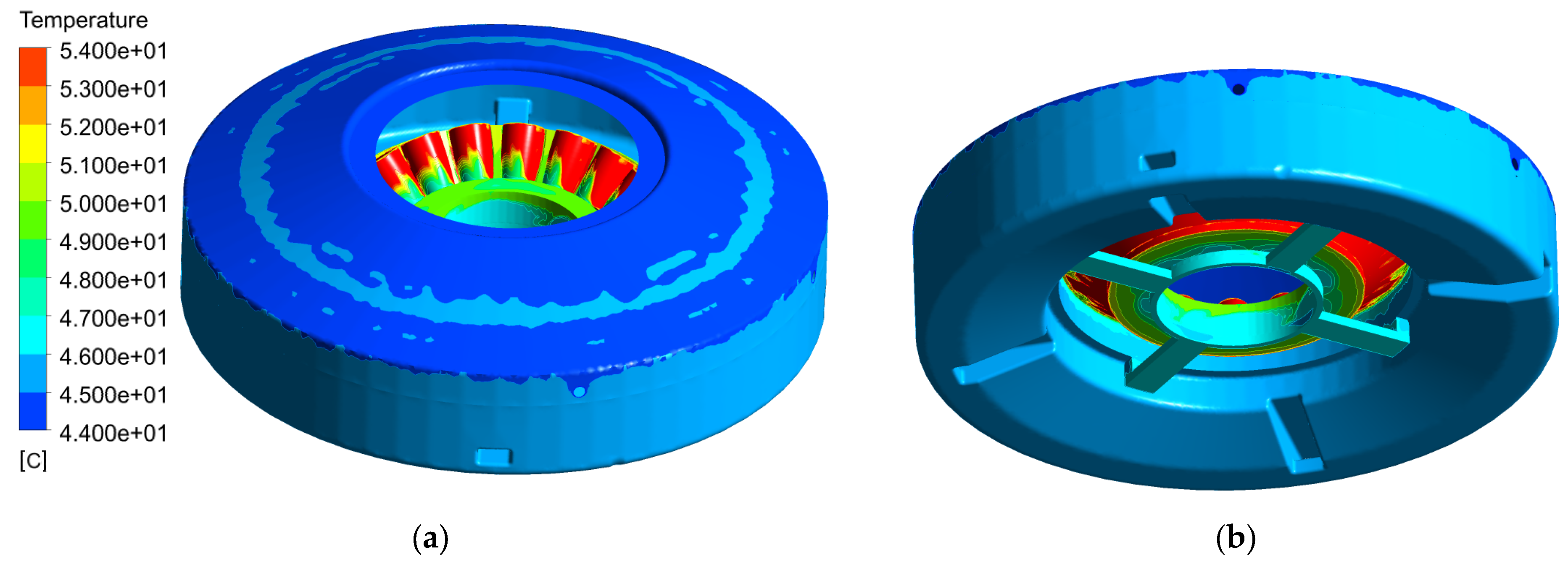
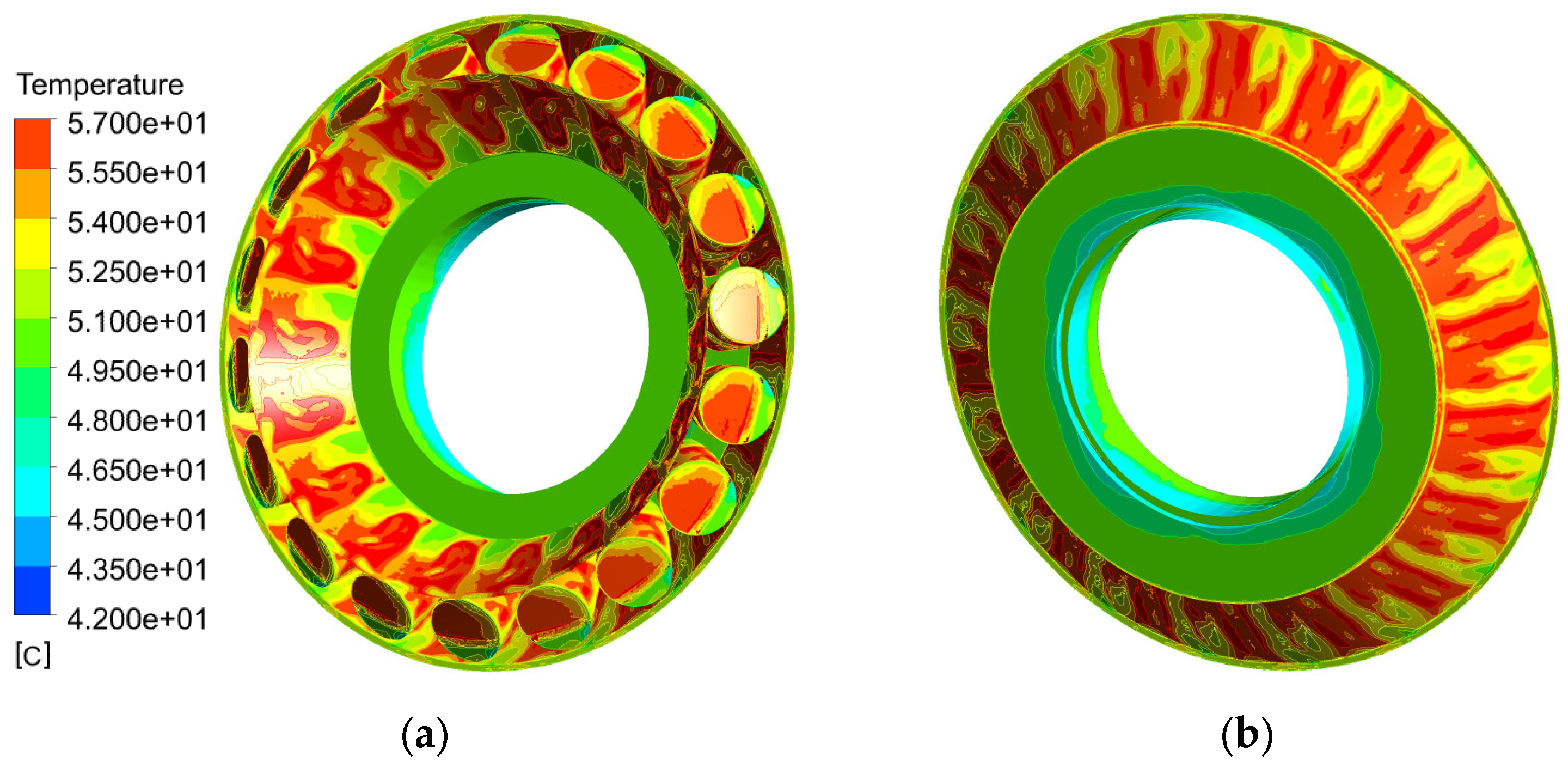
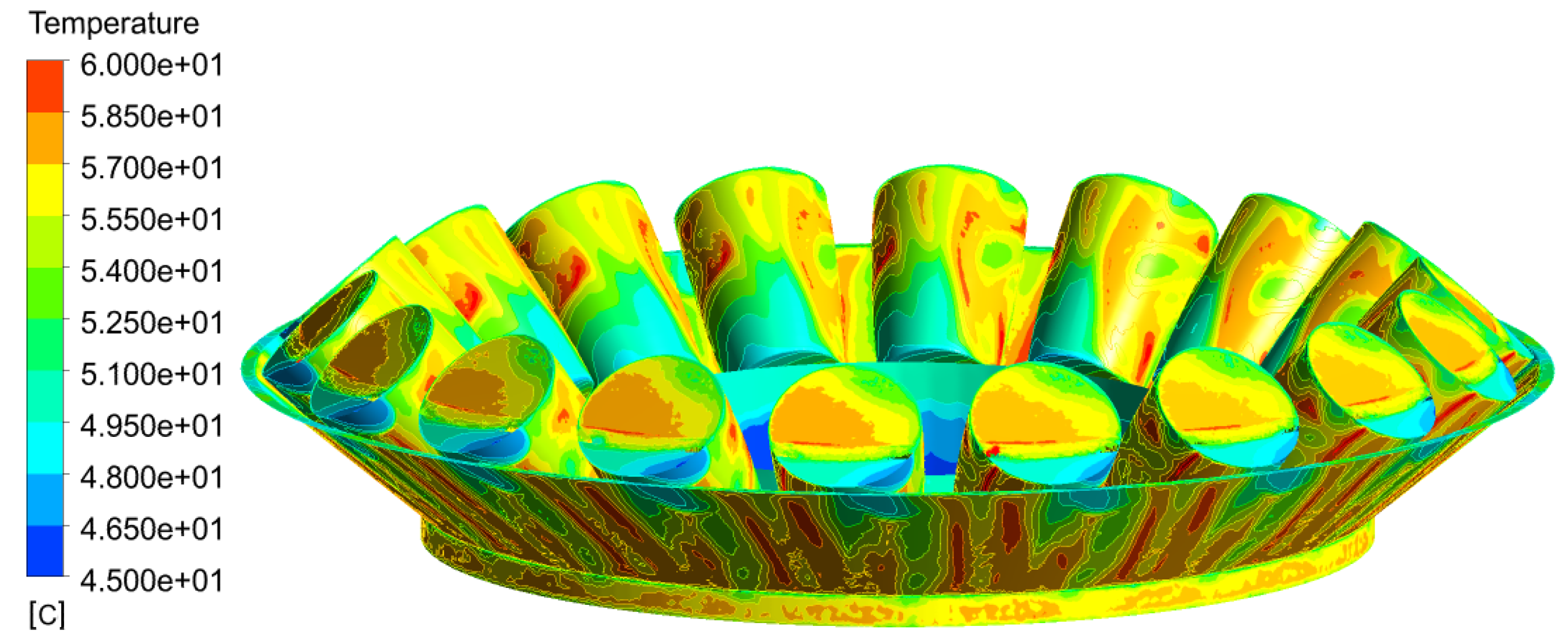
The numerical simulations confirm that the designed cooling system is sufficient to keep the bearing and oil temperatures at safe values to guarantee bearing rating life even at extreme climatic conditions. But, they also confirm that all physical phenomena, from turbulence, multiphase buoyant flow, fully unsteady velocity and temperature fields, high vorticity of oil close to the cooler, up to all properly rotating components in the bearing play a significant role and should be simultaneously considered. Simulations also indicate that the complexity of the computational domain and bearing clearances have a significant impact on the obtained results. No typical grid dependence study changing the global density of the mesh was done, because the topology and quality of the grid in the most critical regions are much more important than the simple number of grid points. The main difference in the topology was due to the presence of the cage; the other changes can be linked to the reduction of the size of the clearance between rollers and raceways. This clearance started with the width of 0.9 mm, then it was lowered to 0.54 mm. The final size of the clearance was 0.34 mm, which appeared to be limiting for the computer memory, because with the decreasing width of the gap between rollers and races, the size of the computational grid dramatically increases.
To evaluate the influence of the changes described above, one exact integral value was selected, which represents the mass flow rate through the bearing itself in the case of the HOL. This value was evaluated at the bottom of the bearing and the results can be found in
Table 3. There was a significant change in the mass flow rate due to the presence of the cage (decrease by 2.65%); the changes in the clearance resulted in additional successive decreases, by 2% and 0.37%.
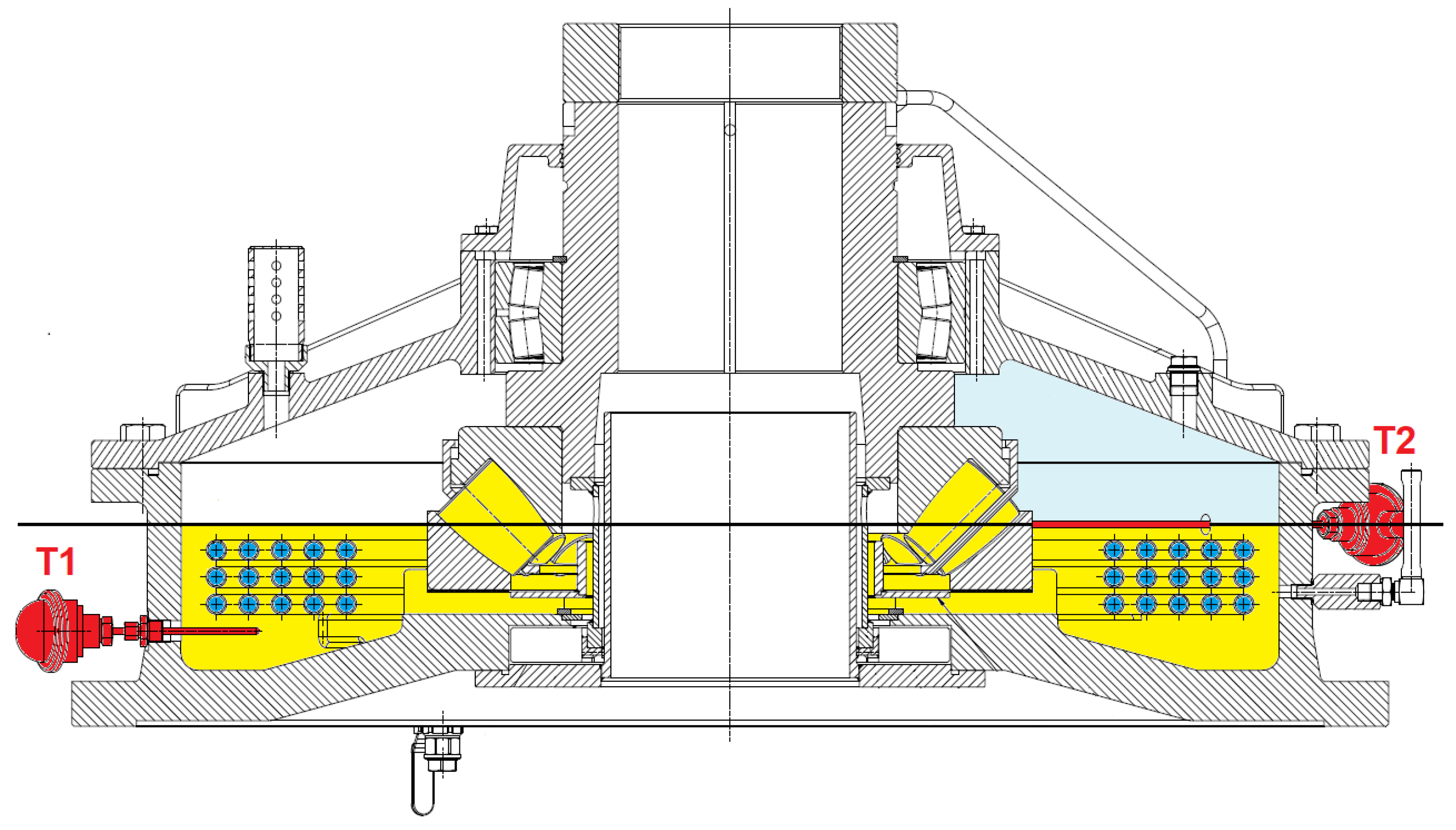
There is also a possibility to verify the simulation results by comparing the calculated temperatures with the measurements. The experiments were done with a real pump in the testing laboratories of the pump manufacturer SIGMA GROUP a.s., Lutin, CZ) with the following reduced parameters: shaft speed 266 rpm, water temperature 16.9 °C, ambient temperature 26.0 °C, standard oil level. For this reason, the numerical simulation was done for the same parameters, with the results shown in
Table 4. There are two measurement positions, T1 and T2, described in
Figure 24. The thermometer T1 measured the oil temperature in a free space, the thermometer T2 measured the oil temperature on the wall of the bearing. There are differences between the calculated and measured temperatures of 0.3 °C in position T1 and 0.4 °C in position T2. This is a good agreement, considering the fact that in the simulation, the housing wall was treated as the adiabatic one and the calculated temperatures were a little bit unsteady, which changed the values by about ±0.2 °C during the bearing revolutions.