1. Introduction
In recent times, strides made in the domain of wind turbine output prediction have propelled the field to new heights, harnessing the prowess of data-driven algorithms to yield more precise forecasts [
1]. Within this era of progress, the Increased Velocity (INVELOX) wind power system has emerged as a groundbreaking concept. Distinguished by its distinctive design, INVELOX employs a funnel-like structure to direct the wind, enhancing velocity and optimizing energy capture. Notably, the advantages of INVELOX extend to its ability to function optimally even in conditions of lower wind speeds, rendering it a promising solution for diverse deployment scenarios.
Venturing towards the optimization of the INVELOX wind delivery system geometry and the assessment of horizontal axis wind turbine integration, this study employs multi-objective surrogate-based optimization and CFD simulations [
1]. Additionally, reference [
2] employs Artificial Neural Networks (ANNs) to model the performance of ducted wind turbines under various operational conditions, resulting in improved power curve estimation. For advanced INVELOX turbines, the deep-learning model of Multi-Feature-Based Wavelet Long Short-Term Memory (MFBW-LSTM) achieves accurate wind velocity prediction by integrating enhanced long short-term memory and optimizations [
3].
Meanwhile, [
4] presents a novel 3D model that leverages solar-assisted air velocity conversion to enhance wind energy generation, conducting a numerical analysis using ANSYS Fluent 19 software through the lens of computational fluid dynamics. Reference [
5] conquers design limitations by enhancing an INVELOX wind turbine model with an innovative intake mechanism, subsequently improving wind speed performance and efficiency. In [
6], the Taguchi approach is employed to optimize shrouded wind turbines utilizing the INVELOX system, effectively boosting wind speed performance in low-wind regions. The MIWHS-IoT project [
7] unveils the potential of enhancing wind energy harvesting by coupling the INVELOX system with IoT monitoring and a boost converter.
The comprehensive evaluation of INVELOX turbines within a multilateral energy system, as proposed by [
8], analyzes demand response and cost reduction potential. In the quest to elevate the efficiency of vertical-axis wind turbines, a study delves into the impact of slotted airfoil design, revealing improved lift and power coefficients [
9]. On a broader note, [
10] employs the analytical hierarchy process to identify optimal choices for floating offshore wind platforms based on site attributes, highlighting spar- and semi-submersible systems as preferred choices. Exploring the realm of energy harvesting through wind-driven piezoelectric cantilever beams, [
11] showcases potential applications in self-powered devices and wireless networks.
Addressing challenges within wind power, the second-largest renewable source, reference [
12] emphasizes the need to tackle issues such as wildlife impact and ecosystem effects to ensure sustainable growth. Within this context, reference [
13] presents a comprehensive review of AI and ML applications in wind turbine control systems, spanning power optimization, prediction, fault detection, and monitoring. Further emphasizing AI applications, reference [
14] proposes the employment of explainable AI methods in constructing data-driven power curve models, considering multiple input variables for anomaly detection and wind turbine performance evaluation. Progressing towards enhancing industrial equipment monitoring and diagnosis, reference [
15] employs AI-driven tools in wind turbine systems to curtail downtime and predict failures.
As a noteworthy endeavor, reference [
16] harnesses AI techniques encompassing Machine Learning (ML) and Deep Learning (DL) to predict wind turbine power output, thus aiding energy planning, maintenance, and site selection. In the context of wind turbine blade aerodynamics prediction, reference [
17] evaluates four different Artificial Pollination (AP) methods, with the Multi-Gene Genetic Programming (MGGP) approach attaining the highest accuracy, thereby contributing to AI and aerodynamics research cost-effectively. Moreover, reference [
18] proposes a normal Probability Density Function (PDF) model for wind speed representation, demonstrating its superiority over the Weibull PDF through AI techniques applied to parameter estimation and prediction accuracy assessment. Addressing wind power forecasting complexities, a multi-source data fusion methodology is introduced to surpass classic AI models and enhance accuracy amidst intricate meteorological conditions [
19]. In the realm of short-term wind power prediction accuracy, a comparison between Gated Recurrent Unit (GRU) and Autoregressive Integrated Moving Average (ARIMA) models [
20] finds GRU to be more effective. Merging artificial intelligence with super-twisting sliding mode control [
21] enhances wind energy system stability and power transfer.
Furthering the realm of wind turbine monitoring and power prediction, reference [
22] employs deep learning and k-nearest neighbor (kNN) regression, thus enhancing accuracy in renewable energy planning. An innovative Multidimensional Spatio-Temporal Graph Neural Network (MST-GNN) [
23] augments wind speed prediction accuracy, surpassing baselines by up to 8.96% in open-source datasets. Meanwhile, reference [
24] harnesses an artificial neural network-based approach to predict wind power and load demand, demonstrating its potential in optimizing energy management. In exploring ultra-short-term wind power forecasting, a feature selection and Temporal Convolutional Network (TCN) optimization approach [
25] presents improved accuracy via the Extreme Gradient Boosting (XGBoost) and TCN-based method. The evolution of a neural forecasting model (NGOA-DeepAr) [
26] incorporates an enhanced grasshopper optimization algorithm applied to wind powers for automatic Deep Neural Network (DNN) hyper-parameter optimization, resulting in superior performance over benchmarks. By introducing a novel Cross-Correlation Recurrent Framework (CCRF) model, this research combines Bidirectional Long Short-Term Memory (Bi-LSTM) and gaussian kernels for wind power forecasting, thus outperforming benchmark models through the consideration of both temporal autocorrelation and Numerical Weather Prediction (NWP) correlation [
27].
Employing a dual-stage attention mechanism, the wind power forecasting system (WPFSAD) [
28] heightens accuracy and stability, as verified through simulation experiments. Embracing the fusion of federated learning and Deep Reinforcement Learning (DRL), “FedDRL” [
29] presents a scheme for accurate and privacy-preserving ultra-short-term wind power forecasting for modern renewable energy systems. Methodically, reference [
30] propounds a wind power forecasting model, amalgamating a mixture correntropy LSTM neural network, particle swarm optimization, and improved variational mode decomposition, thereby elevating accuracy. Significantly enhancing 5-min wind power prediction accuracy, the innovative CEMOLS framework [
31] leverages Complex Empirical Mode Decomposition with Adaptive Noise (CEEMDAN), Mountain-Based Optimization (MBO), and Long Short-Term Memory (LSTM), resulting in up to 47.10% outperformance in Root Mean Square Error (RMSE) and 32.33% in Mean Absolute Percentage Error (MAPE) against rival methods. Elaborating on the versatility of AI, reference [
32] combines Artificial Neural Network (ANN) models with optimization algorithms to forecast long-term electrical energy consumption and evaluate scenarios integrating solar and wind sources for sustainable development. Further propelling short-term wind power forecasting accuracy, a CatBoost machine learning-based model [
33] achieves superior performance with an RMSE of 13.84 during cross-validation. Furthermore, reference [
34] introduces an innovative ensemble model for wind speed forecasting, amalgamating noise processing, statistical techniques, deep learning, and optimization. This endeavor yields enhanced accuracy compared to traditional models, encapsulating the breadth of AI’s influence in wind energy systems.
Furthermore, reference [
35] discusses the significance of AI in smart grids. Reference [
36] presents quantum technologies in the context of smart grids, with a focus on predictive characteristics. Reference [
37] uses precise AI-driven estimators on a dataset. Reference [
38] provides dependable AI-powered output projections. Moreover, [
39] investigates the frequency control of microgrids using a modified COA, as well as the architecture, and demonstrates its significance using MATLAB/Simulink simulations. The vital stability and reliability of power systems are influenced by technical and environmental factors. The impact of solar and lunar eclipses on Denmark’s power system is examined, highlighting their significance in the context of high integration of renewable energy, which is presented in [
40].
Reference [
41] introduces a method for enhancing wind energy generation in urban areas with unused rooftop space. Additionally, it focuses on wind boosters for vertical-axis wind turbines, optimizing them using computational techniques. In a test in Mexico City, the optimized wind booster increased torque by 35.23%. Improved electricity generation forecasts for small wind turbines are presented in [
42], utilizing methodologies such as LSTM and MLP. Reference [
43] introduces a hybrid PSO-GWO algorithm for solving optimal power flow problems with stochastic solar photovoltaics and wind turbines. A method for controlling a standalone wind diesel power generation system is presented [
44]. The method uses decentralized model predictive controllers to regulate frequency and power. Reference [
45] explores the feasibility of integrating offshore wind turbines and wave energy converters on a single platform for coastal power generation. It uses machine learning and deep learning models to predict key parameters and identifies the deep learning model has an accuracy rate of 96%.
In the pursuit of more dependable and efficient renewable energy sources, the evolution of advanced predictive models for wind turbine output prediction has garnered significant attention. In line with this mission, this paper introduces an ingenious approach known as DeepVELOX. Seamlessly intertwining state-of-the-art machine learning techniques within the realm of wind power, DeepVELOX is developed from the imperative need to amplify the accuracy and reliability of wind turbine output predictions, thus ensuring the optimal harnessing of energy.
The novelty inherent in the system’s design is underscored by its utilization of an advanced forecasting control system, wherein intelligent model predictive ensemble control is seamlessly incorporated. The synergistic integration of GWO algorithm and the GBR model drives this sophisticated control mechanism, resulting in previously unattainable levels of precision and operational efficiency within the context of the INVELOX wind power system. Notably, a key characteristic of this technology is its ability to present maximized overall performance of the INVELOX structure while also allowing it to accurately estimate output power in response to variable wind speeds. This perspective goes far into the future, establishing the system as a development in the field of wind energy generation. Such invention represents an advance forward in the ongoing quest to fully realize the potential of wind energy, hence substantiating the transformative impact of the research within the context of the renewable energy literature.
The structure of this paper is devised to encompass the following sections:
Section 1 commences with a contextualizing introduction and an insightful exploration of the existing literature, acting as a prelude to the unveiling of DeepVELOX’s capabilities.
Section 2 takes center stage with a comprehensive overview of DeepVELOX’s architecture and operational framework. Here, particular emphasis is placed on the synergy of the GBR and the GWO algorithm. This segment also peels back the layers to illuminate the advantages arising from this strategic amalgamation, magnifying its potential to revolutionize the accuracy of wind energy predictions. Transitioning into
Section 3, the focus shifts towards the methodologies underpinning the simulations executed and the subsequent presentation of the achieved results. This section unveils DeepVELOX’s prowess in the domain of predictive performance, casting a spotlight on its impressive capabilities. As the paper strides into
Section 4, an extensive comparison between DeepVELOX and alternative models is unveiled, establishing its undisputed superiority. In its culminating moments,
Section 5 breathes life into discussions surrounding potential pathways of future advancement. The paper concludes with an emphasis on the transformative potential embodied by DeepVELOX in redefining the horizons of wind energy technology.
2. Structure and Operating Framework
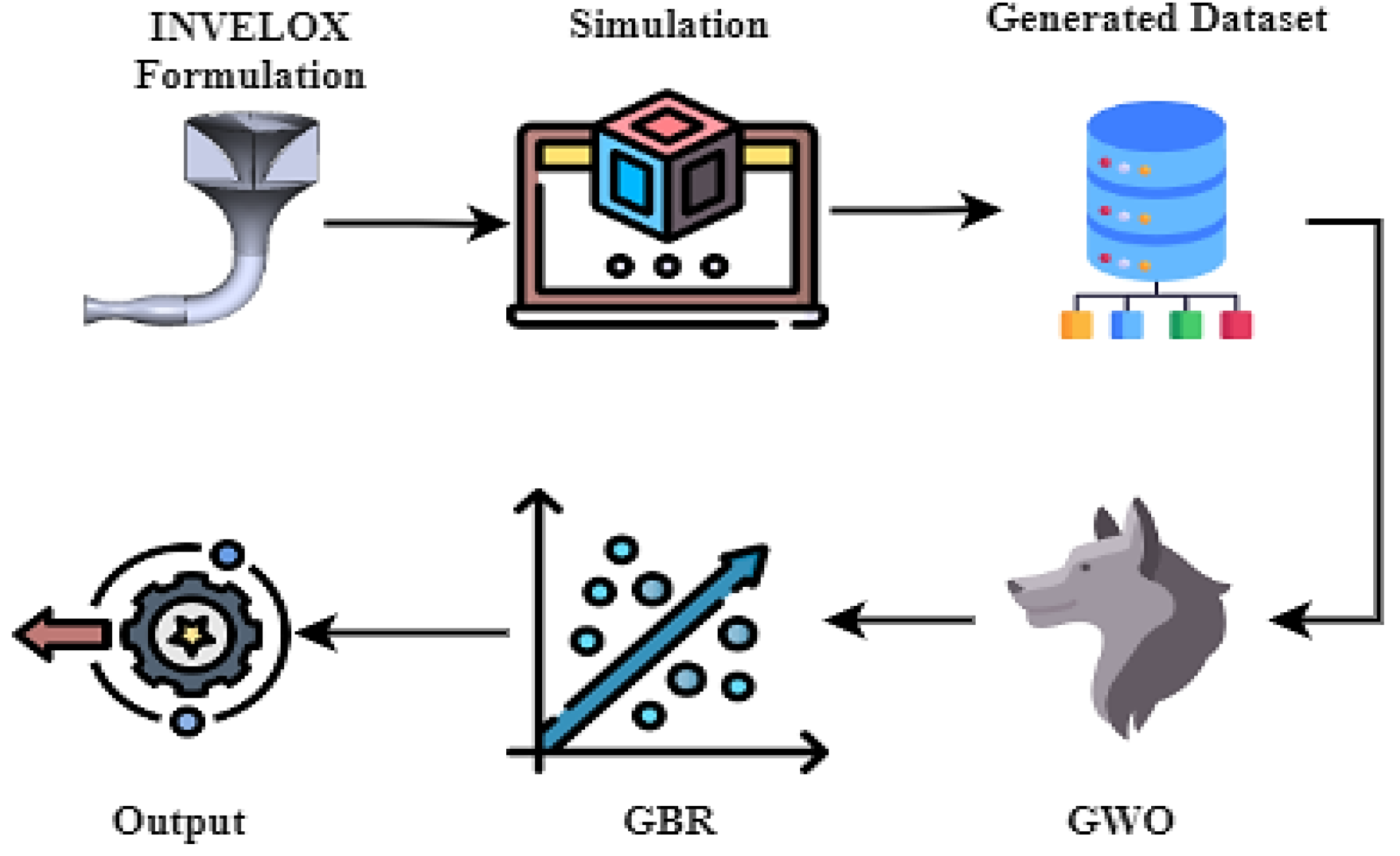
DeepVELOX stands as a structured fusion of the GWO algorithm and the GBR, creating a formidable framework for predictive modeling. The overall process is conceptualized in
Figure 1.
According to
Figure 1, the model’s intricate process begins with a mathematical analysis of the INVELOX wind turbine system, forming the basis for subsequent steps. Initial simulations are generated, serving as the foundation for GWO’s crucial role. The GWO algorithm analyzes the system, identifying optimal behavioral points that harmonize with the desired objectives.
Following the insightful guidance from GWO, the generated dataset undergoes rigorous analysis by the GBR component. This intricate analysis by GBR empowers the model to uncover intricate patterns and relationships within the data, laying the groundwork for precise forecasting. The culmination of these processes leads to forecasting outcomes with near-zero error rates, underlining the remarkable precision and reliability of DeepVELOX’s predictions. This innovative amalgamation of mathematical analysis, optimization through GWO, and precise forecasting with GBR defines DeepVELOX’s approach, yielding a powerful tool that has the potential to significantly revolutionize decision making, enhance system performance, and drive operational excellence across diverse domains.
2.1. INVELOX Wind Turbine
INVELOX, abbreviated from Increased Velocity Wind Power System, represents an inventive wind energy technology devised for capturing wind power through an innovative methodology. In contrast to conventional horizontal-axis wind turbines, which employ large blades to directly harness kinetic energy from the wind, the INVELOX system adopts a distinct approach to optimize energy extraction. The core of the INVELOX wind turbine comprises a funnel-shaped construction, guiding wind into a progressively narrower entry point at its zenith. As the wind infiltrates the system, its speed escalates due to the funnel’s constriction, resulting in a localized zone of intensified high-speed wind. This intensified wind flow is subsequently channeled downward through a more confined passage, where an array of wind turbines is positioned at the base of the funnel. These turbines, which can be conventional horizontal-axis systems or alternative generator types, seize the kinetic energy of the high-velocity wind and transform it into electrical power. A significant advantage of the INVELOX concept lies in its proficiency to efficiently capture wind energy, even at lower wind velocities when compared to standard wind turbines. The funnel-shaped configuration serves to focus and amplify the wind’s energy, enabling the turbines to perform effectively in regions characterized by less potent average wind speeds. Moreover, the design of the INVELOX system holds various potential merits. It can mitigate its impact on local wildlife and visual aesthetics since the turbines are housed within the structure rather than atop towering masts. This attribute renders it adaptable to diverse settings, encompassing both urban and rural environments.
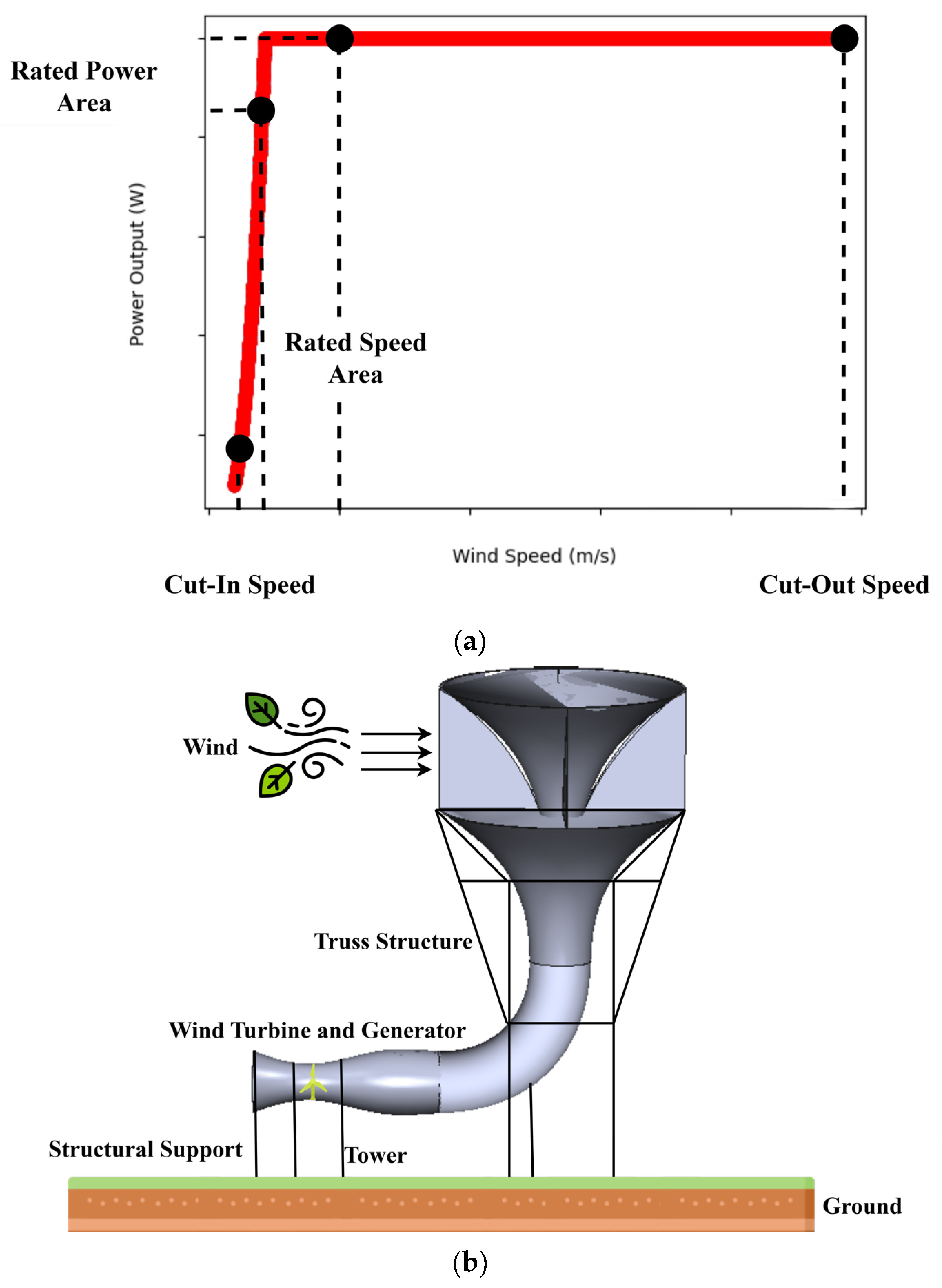
Figure 2 displays the regular characteristics of a wind turbine, as well as INVELOX wind turbine configuration.
As depicted in
Figure 2, the INVELOX wind power system comprises several distinct components, each assuming a crucial role in ensuring its operational efficiency and effectiveness. As well in
Figure 2a, the red line presents the power output regarding the wind speed enters to INVELOX wind turbine. Additionally, the dotted lines mirror the cut-in/out wind speed, and the related powered/speed area
Framework Structure: The foundational underpinning of the INVELOX system is provided by the framework structure. This structure takes on a funnel-like configuration, guiding and accelerating the wind toward the wind turbine. Its design is optimized to direct wind flow efficiently, thus augmenting energy capture and conversion effectiveness.
Wind Converter: At the heart of the INVELOX system resides the wind converter, positioned at the funnel structure’s base. This converter is responsible for transmuting the kinetic energy of the swift wind into mechanical energy, which is subsequently translated into electrical energy. Depending on specific design requirements, various types of wind converters can be seamlessly integrated into the INVELOX system.
Electric Generator: Intricately linked with the wind converter, the electric generator plays a pivotal role in transforming the mechanical energy generated by the rotating blades into electrical energy. This electrical output can be harnessed locally, channeled into the power grid, or stored for future utilization.
Structural Reinforcement: Ensuring the system’s steadfastness and resilience, the framework structure provides indispensable reinforcement. It is ingeniously engineered to endure external forces, including wind loads and adverse weather conditions, all while preserving the funnel shape’s integrity.
Supporting Mast: Serving the purpose of upholding the upper section of the funnel structure, the supporting mast of the INVELOX system, though not as towering as traditional wind turbine masts, holds a pivotal function in maintaining the correct elevation and alignment for proficient wind capture.
Foundation: The groundwork for the INVELOX system is established by the foundation. Meticulous site selection and foundation design are imperative to ensure stability and structural soundness. Furthermore, ground attributes influence wind capture efficiency since the wind’s properties close to the surface impact the comprehensive system performance.
Wind Resource: Central to the INVELOX concept lies the harnessing of wind energy. The distinctive design of the funnel structure manipulates wind velocity, concentrating it before its interaction with the wind converter. This method elevates wind speed, empowering the system to adeptly harness energy even from modest wind velocities. Consequently, the range of potential deployment locations is expanded.
Each of these constituents makes a substantial contribution to the overall operation and efficiency of the INVELOX wind power system, presenting an inventive remedy for capturing wind energy that effectively addresses the limitations inherent in conventional wind turbine designs. Additionally, the INVELOX system is subjected to modeling and simulation, as
where
are the air density, generator blade area, and IWT efficiency, respectively. Ration of squares of cross sections, and pressure coefficient, wind speed, and velocity amplification ration are symbolized as
,
, and
, respectively.
, and
present cut-in/out wind speed.
2.2. Grey Wolf Optimization (GWO)
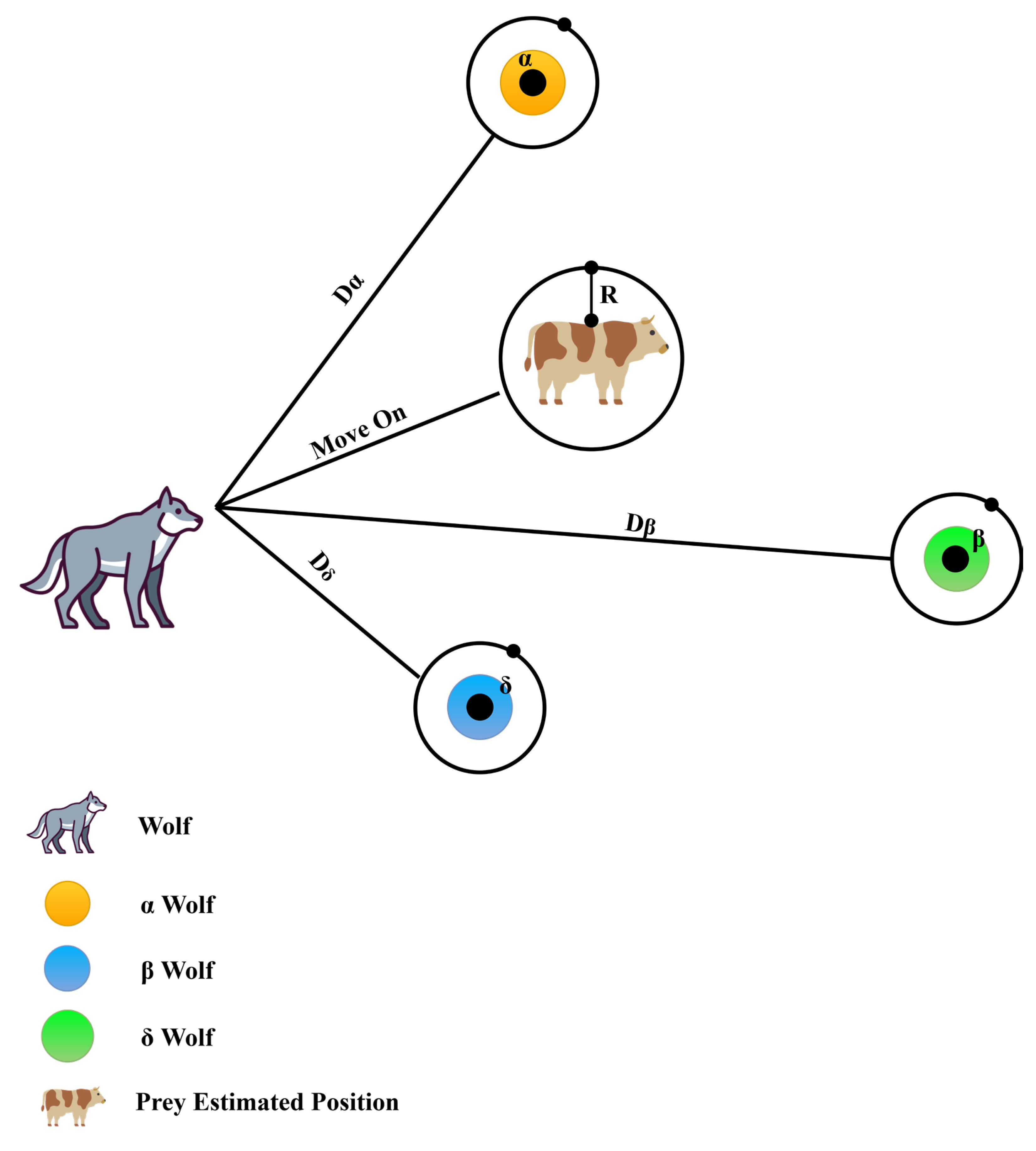
GWO stands for Grey Wolf Optimization, a nature-inspired algorithm that emulates the social structure and hunting patterns of grey wolves in their natural habitat. This algorithm adopts a population-based approach to optimize complex problems. Just as in the wild, GWO organizes the population of potential solutions into different categories: alpha, beta, delta, and omega individuals. These categories mirror the hierarchical arrangement within a wolf pack. Each individual within this setup represents a conceivable solution for the specific optimization problem [
46]. The visualization of the GWO concept is showcased in
Figure 3.
Based on
Figure 3, the way this algorithm works is among a bunch of rounds, sort of copying how wolves hunt to make the solution better bit by bit. These gray wolves stick to their ranks, with alpha being the top dog and omega being the not-so-great one. In each of these rounds, they adjust where alpha, beta, and delta are hanging out. They do this thinking about where they were before and where other wolves are. All this moving around aims to get closer to better solutions for the problem they are dealing with. The neat thing about GWO is that it mixes things up between exploring new possibilities and sticking to what has been working. Slowly, step by step, they get closer to what is probably the best solution, while also checking out both the vision and the smaller details. Their behavior is mathematically modulated as the following [
47]:
In which
,
, and
are the position vectors of prey the grey wolf, as well as the current iteration of the system, respectively. Also,
,
are coefficient vectors determined as:
where,
,
, and
are the linearly decreasing variable, and the random vectors in the range of [0,1], respectively.
The alpha, beta, and delta wolf are attributed with the capacity to identify potential prey locations, given that they represent the top three solutions attained thus far. Consequently, their solution positions are employed to adjust the positions of the remaining (omega) wolf within the pack. The formulation for updating these positions is as presented below:
2.3. Gradient Boosting Regressor
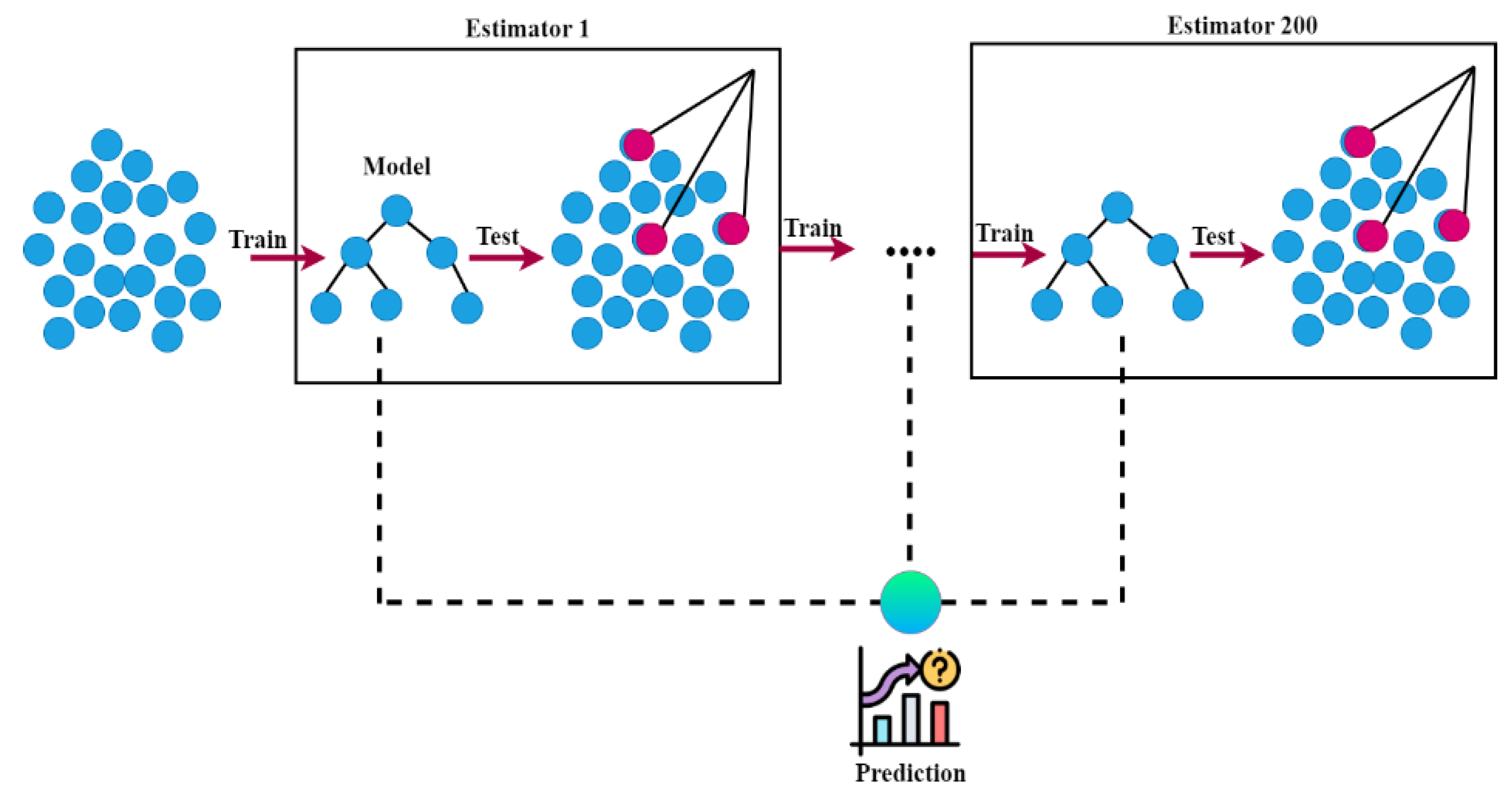
The GBR stands out as a robust machine-learning algorithm within the ensemble learning paradigm. Positioned within this category, it excels in building a potent predictive model through the amalgamation of outputs from multiple weaker learners, typically in the form of decision trees. The algorithm’s methodology involves an iterative process wherein it progressively enhances prediction accuracy by sequentially introducing new trees. In each iteration, GBR undertakes an intricate procedure. It discerns the deficiencies of the preceding model and dedicates its focus to forecasting the residual errors. Subsequently, it devises a novel decision tree to capture and rectify these errors. This learning procedure is marked by the adjustment of instance weights within the training data, prioritizing the correction of misclassified or inadequately predicted samples. This adaptability allows the algorithm to assimilate insights from its missteps and tailor its predictions accordingly. GBR’s core principle revolves around the notion that each subsequent tree appended to the ensemble rectifies the errors inherent in its precursors, resulting in a gradual diminution of the overall predictive error. The summation of predictions generated by all the constituent trees culminates in the ultimate prediction. An appreciable attribute of GBR is its capacity to deliver exceptional predictive accuracy while exhibiting reduced susceptibility to overfitting, a contrast to individual decision trees. Fundamentally, GBR leverages the concept of boosting, systematically enhancing its predictive prowess through iterative refinement. This renders it an influential algorithm in the realm of regression tasks, as visually elucidated in
Figure 4.
Based on this figure, GBR involves iterative steps that include mathematical formulations for constructing and updating the model, in which the different color circles present that the model chooses example data, to perform estimation based on it. The DT model considered to be the following:
In which
,
, and
are the constant value prediction, loss function, and INVELOX power output data, respectively. In terms of
argmin, the minimization progress should be performed by
For the next step, the residual of the system should be performed in each iteration, as follows:
That
is the last iteration prediction. Now, the loss function minimization should be done by the terminal nodes.
For the last step, the updated prediction is derived.
The overall PSEUDOCODE of DeepVELOX is presented in Algorithm 1.
| Algorithm 1: PSEUDOCODE of DeepVELOX |
Initialization of the grey wolf population
Initialize of parameters: a, A, and C
Calculate the fitness of each search agent
= the best search agent
= the second search agent
= the third search agent
While (t < Maximum iteration number)
for each search agent
Update the current search agent position
end
Update a, A, and C
Calculate the fitness of all search agents
Update , , and
t = t + 1
end
return
Initialize the model with a constant value:
=
for m = 1 to M:
Compute residuals = − for i = 1, …, n
Train regression tree with features x against r and create the terminal node
reasons for j = 1, …,
compute = j = 1, …,
Update the model:
|
3. Simulation and Results
In this work, an INVELOX wind turbine simulation has been rigorously simulated and utilized in a dataset comprising 60,003 collected data points, through simulation. Within the collected dataset, precise correspondences between wind speeds and the resultant output power generated by the INVELOX turbine have been established. The crux of this investigation lies in the innovative Implementation of DeepVELOX, a fusion of the GWO algorithm and a GBR. This amalgamation facilitates the meticulous refinement of the turbine’s parameters through the GWO procedure, subsequently harnessed by the GBR model to project output power levels. These estimations are underpinned by a meticulous assessment of statistical attributes, specifically the mean and variance, which discerningly portray the distribution of key metrics within the dataset: wind speed (mean = 13.017 [m/s], variance = 48.033) and actual output power (mean = 1974.081 [W], variance = 28820.19). This empirical endeavor underscores an intricate interplay of advanced machine learning methodologies in optimizing the performance of wind turbine technology, thus augmenting the renewable energy landscape. The simulation scattered results are available in
Figure 5 and
Figure 6.
As indicated in
Figure 5, the velocity of the wind emerges as a pivotal determinant profoundly influencing the operational dynamics and efficiency of INVELOX wind turbines. Moreover, the characteristics of the output change considerably when the changes occur in
SR. This concept is drawn in two scenarios of
, and
. The reason that four is considered the maximum is the fact that amplifying wind speed four times more inside the turbine is challenging and unrealistic. The kinetic energy derived from the motion of the wind exhibits a direct proportionality with the cube of its velocity, thereby accentuating the critical and indispensable role that wind speed occupies in the context of power generation. With an elevation in wind speed, there follows a corresponding increase in the volume of air coursing through the system, leading to an augmentation in the capacity to capture energy and, in turn, fostering heightened power output. However, the fluctuating nature of wind speed introduces a set of complexities. Extremely low wind speeds might not endow the system with sufficient kinetic energy to facilitate efficient power generation. Conversely, excessively high wind speeds possess the potential to instigate mechanical stress and, by extension, pose a risk of causing damage to the structural integrity of the turbine. Remarkably, INVELOX turbines, distinguished by their innovative engineering, manifest the competence to adeptly navigate a broader spectrum of wind speeds. This distinctive capability empowers these turbines to concurrently optimize power output and sustain operational soundness. A pivotal strategy employed in the pursuit of energy conversion optimization is the integration of advanced control systems within INVELOX turbines. These systems exert control over the rotor’s speed and the blade’s pitch in response to the variable patterns of wind speed. This dynamic control mechanism empowers the turbine to harmoniously accommodate diverse wind conditions, ensuring the consistent and efficient generation of power across the gamut of wind velocities. In this intricate interplay, the magnitude of wind speed emerges as a paramount determinant, dictating the potential yield of energy and upholding the comprehensive operational stability of INVELOX wind turbines. Moreover, it encompasses factors such as wind capture, efficiency, turbulence reduction, energy conversion efficiency, operational stability across varying wind conditions, maintenance requirements, durability, and environmental impact. INVELOX’s success hinges on its ability to effectively funnel and accelerate wind into a wind turbine, minimizing turbulence and maximizing energy conversion while maintaining operational stability and minimizing environmental concerns. A thorough assessment of its aerodynamic performance provides valuable insights into its potential as an innovative and efficient wind energy solution.
As depicted in
Figure 6, the prediction of output power emerges as a matter of paramount significance within the context of INVELOX wind turbines. This undertaking substantively enhances their operational efficiency and overarching effectiveness. The precision in forecasting the impending power output, predicated upon both the current and projected wind conditions, bears the potential to yield substantial dividends. Operators can judiciously allocate resources, facilitate seamless grid integration, and diligently manage energy distribution. This proactive orientation permits a more harmonious synchronization of power generation with the prevailing demand, thereby guaranteeing optimal energy utilization and mitigating wastage. Furthermore, the virtue of accurate forecasting extends to the preservation of grid stability. The prospect of power supply fluctuations can be averted through preemptive measures, thereby upholding the grid’s equilibrium. Central to the prowess of power-output prediction is the role played by the DeepVELOX model. This model occupies a pivotal place in harnessing anticipatory insights. Through the fusion of the GWO algorithm, strategically employed for parameter optimization, and the GBR, employed for the projection of power output, DeepVELOX capitalizes on data-informed perspectives. The result is an adept capability to predict the power output of the INVELOX wind turbine with remarkable precision. This predictive faculty empowers operators and energy strategists to make well-informed determinations. Consequently, the positive ramifications extend to areas such as grid consistency, resource allocation, and, fundamentally, the advancement of sustainable and proficient energy generation.
To evaluate the performance of DeepVELOX, following KPIs were determined, in , since it is optimal for the wind speed to be converted higher, not multiplied between [0,1).
MAPE (Mean Absolute Percentage Error) serves as a tool to gauge the average percentage discrepancy between predicted and actual values. This pivotal metric bestows a window into the scale of errors, expressed as a proportion of the actual values themselves. Such a representation facilitates the comprehension of errors and permits seamless comparisons across diverse datasets, ultimately fostering a clear and intuitive assessment of predictive performance.
where
n is the number of data, and
with
are the observed, and predicted values of grid community, respectively.
RMSPE (Root Mean Square Percentage Error) is analogous to the traditional RMSE with a distinctive variation, the RMSPE stands as a metric of evaluation. Unlike its counterpart, RMSPE is quantified as a percentage relative to the actual values. This vital index unveils the average percentage deviation between projected and actual values, concurrently integrating the influence of squared deviations. In essence, RMSPE amalgamates precision with the incorporation of squared differences, offering a holistic perspective on predictive accuracy expressed in percentage terms.
R-squared (R
2) is a statistical measure that quantifies the fraction of variability within the dependent variable that can be elucidated by the independent variables encompassed within a regression model. Manifesting within a range from 0 to 1, R-squared attains greater magnitudes as the model’s alignment with the data augments. This index serves to gauge the appropriateness of the model’s fit to the data, rendering it a fundamental measure of goodness of fit.
RMSE (Root Mean Square Error) stands as a frequently employed yardstick for quantifying the typical extent of discrepancies between projected and observed values within regression scenarios. This metric is derived by extracting the square root of the mean value of the squared disparities between predicted and actual values. RMSE operates as an evaluative tool to gauge the efficacy of a regression model in conforming to the data, with reduced values signifying enhanced performance. Moreover, RMSE retains units consistent with those of the target variable, amplifying its interpretability. RMSE is formulated by the following:
MAE (Mean Absolute Error) emerges as an additional evaluative metric wielded to assess the effectiveness of regression models. This measure quantifies the average absolute disparity between projected and observed values. Diverging from RMSE, MAE adopts a more lenient stance towards substantial errors as it exclusively factors in the absolute deviations without magnifying their impact through squaring. MAE is also expressed in the same units as the target variable, as follows:
Accuracy serves to assess the effectiveness of classification models. This metric quantifies the proportion of accurate predictions with the entire prediction set. The calculation involves dividing the count of correct predictions by the total number of predictions and then multiplying by 100 to yield a percentage. Accuracy emerges as an appropriate choice when the dataset’s classes are evenly distributed, signifying a balance where instances are roughly equivalent across different classes. Accuracy is modeled as follows:
where
and
are the correctly predicted positive and negative instances, respectively. The incorrectly predicted positive and negative instances are symbolized by
and
.
Precision, a pivotal metric within binary classification, serves to gauge the ratio of accurately predicted positive instances (true positives) to the entire set of predicted positive instances. This measurement hones the accuracy of positive predictions exclusively. The computation involves dividing the count of true positives by the sum of true positives and false positives, providing insight into the model’s capability to make precise positive predictions within a binary classification context, symbolized below:
Recall often referred to as sensitivity or the true positive rate, constitutes a significant metric within binary classification. Its purpose is to quantify the fraction of true positive predictions relative to the complete set of actual positive instances. The essence of recall centers on a model’s proficiency in identifying all existing positive instances. Computationally, it involves dividing the number of true positives by the sum of true positives and false negatives, encapsulating the model’s capacity to correctly identify positive instances about the entirety of actual positive cases. In formulaic terms, recall is calculated as presented below:
F1 Score amalgamates both precision and recall into a unified measure. This value is computed as the harmonic mean of precision and recall, affording a well-rounded assessment of a model’s efficacy. The F1 score occupies a scale between 0 and 1, where an F1 score of 1 signifies optimal performance. This metric finds frequent application within binary classification endeavors, particularly in situations where the distribution of classes is imbalanced, and a singular metric is sought to appraise the model’s performance:
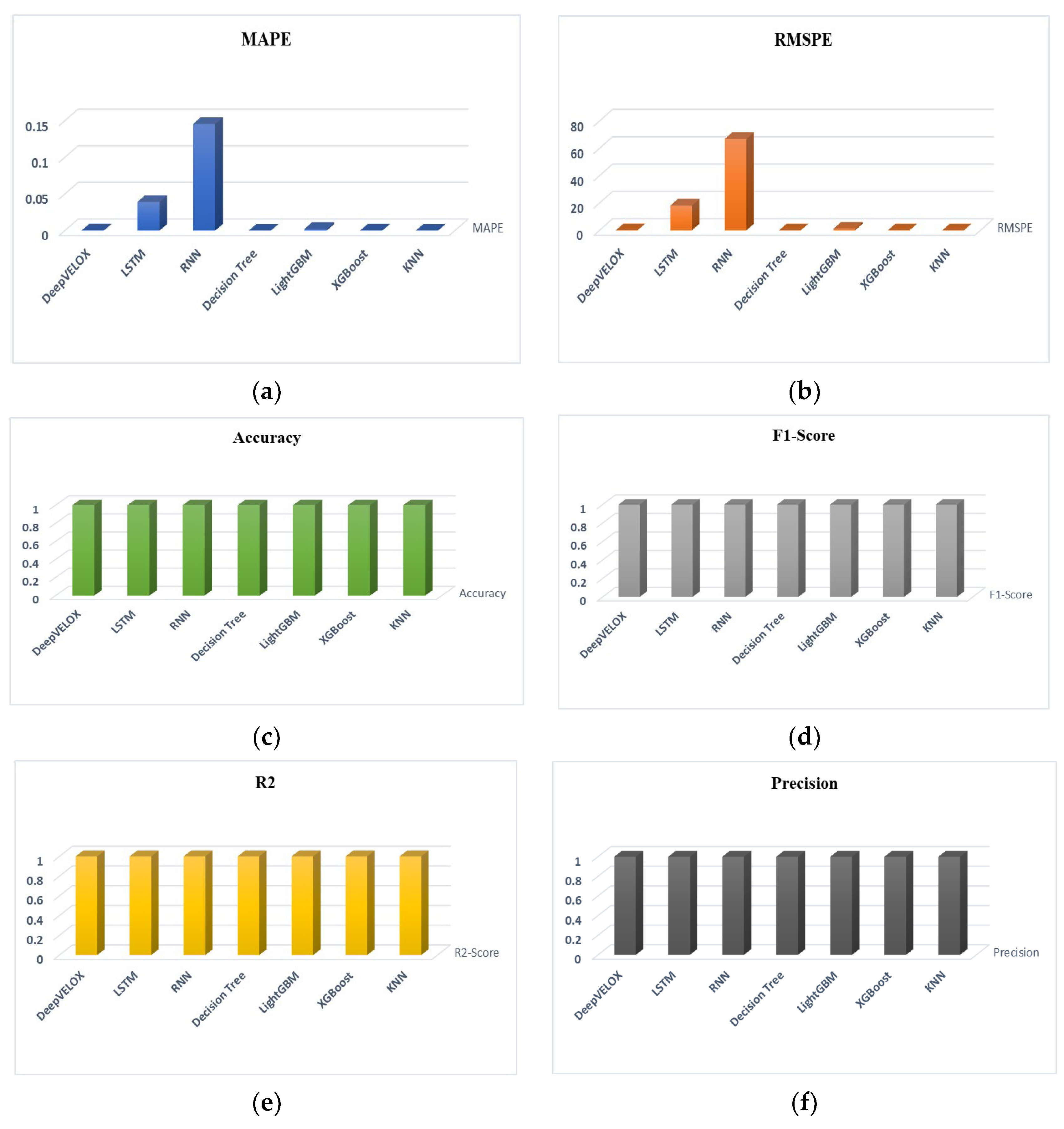
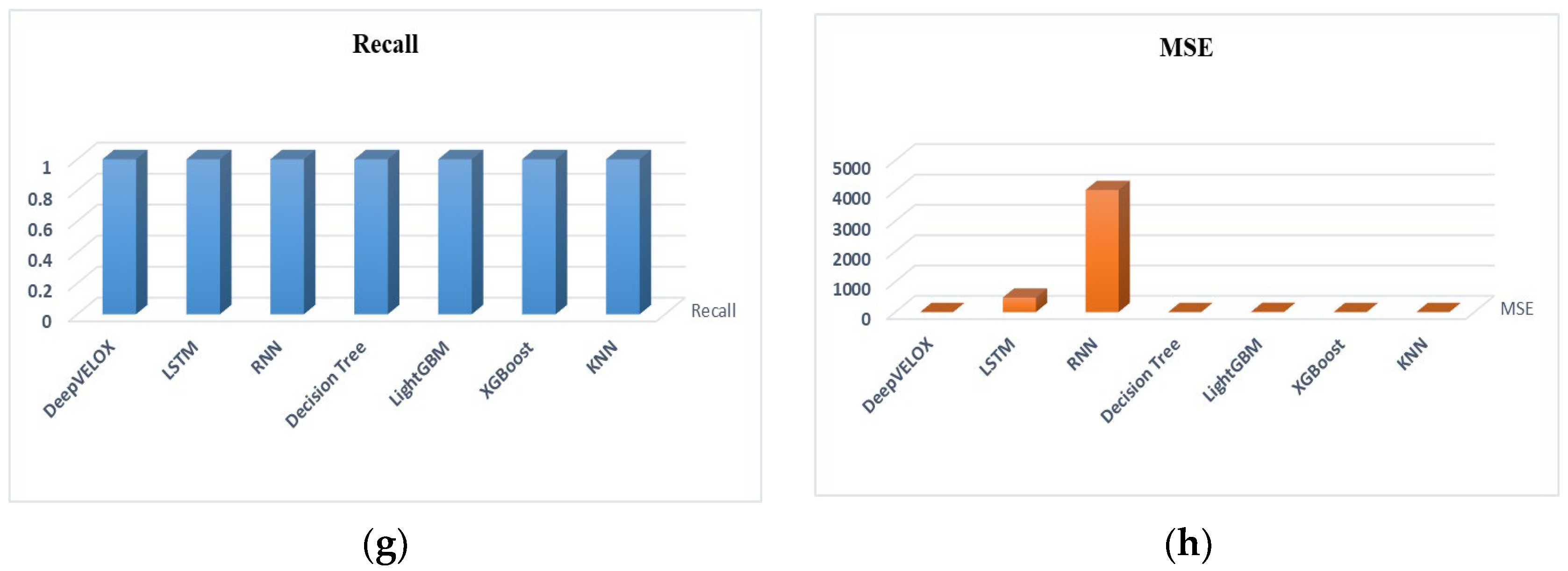
DeepVELOX has consistently demonstrated an exceptional level of performance across a wide spectrum of KPIs, yielding notably extraordinary outcomes. The model’s predictive accuracy is evidenced by an almost negligible MAPE of 0, underscoring its exceptional precision in forecasting. Furthermore, the RMSPE of 0.10 accentuates the model’s proficiency in minimizing disparities between predicted and actual outcomes. The RMSE at 0.19, coupled with the MSE at 0.04, signifies the model’s adeptness in reducing the margin of prediction error. Impressively, the MAE stands remarkably low at 0.03, reinforcing the sustained accuracy of its predictions. Of particular note, within the classification context, the model exemplifies a flawless accuracy score of 1.00, which resonates consistently across Precision, Recall, and F1-Score measurements. This comprehensive assemblage of KPIs harmoniously illustrates DeepVELOX’s precision, dependability, and consequential significance within the realm of wind turbine power output prediction and optimization, as thoughtfully elucidated in
Figure 7.
5. Future Works
By the side of challenges, the output power forecasting of INVELOX with GWO–GBR faces several ones. These include challenges related to data availability, or simulated/generated data quality, the intricacies of INVELOX’s wind flow patterns, and the resultant complexity in modeling. The forecasting horizon is often limited, making long-term energy planning less feasible. Additionally, non-stationary wind patterns and sensitivity to model parameters can affect accuracy. The computational intensity of the GWO–GBR model, along with uncertainties in generalization to different locations and limited resources for validation, further contribute to these limitations. INVELOX’s power generation variability, which extends beyond wind speed, poses an additional challenge. Addressing these limitations may require enhanced simulation/data collection, taking into account more factors than wind speed, model refinement, and the development of hybrid forecasting methods to optimize INVELOX’s power output predictions. As the landscape of wind energy undergoes continuous transformation, the realm of future research and development within the framework of DeepVELOX presents several intriguing avenues.
Advanced AI Techniques Integration: While the amalgamation of GBR and GWO in DeepVELOX achieves impressive predictive performance, the prospect of integrating other advanced AI techniques beckons. Exploring the realms of neural network architectures, reinforcement learning, or hybrid models holds the potential to elevate accuracy even further. Such explorations might usher in enhanced predictive capabilities.
Real-Time Adaptation: Pioneering into the realm of real-time scenarios stands as an exciting trajectory for DeepVELOX. Enabling the framework to dynamically adapt to swiftly shifting wind conditions could be a fruitful endeavor. The creation of mechanisms for such adaptations would ensure a perpetually optimal performance, particularly in the face of highly volatile wind environments.
Diversification into Multi-Domains: Deepening DeepVELOX’s predictive ambit beyond wind turbine output to encompass broader renewable energy domains, such as solar energy, holds promise. This extension could culminate in a holistic solution for integrated energy systems. Such a cross-domain approach might yield more streamlined energy management strategies.
Robustness and Reliability Enhancement: The pursuit of augmenting DeepVELOX’s robustness and reliability in instances characterized by data scarcity or capricious weather patterns is imperative. The infusion of uncertainty quantification techniques and adaptive learning mechanisms would contribute to the sustenance of reliable predictions, even in challenging circumstances.
Validation in the Field and Scalability: The empirical validation of the DeepVELOX framework through comprehensive field trials across diverse geographic and climatic zones would attest to its real-world utility. Scaling up its application to larger wind farms could offer insights into its scalability and potential for widespread adoption.
Energy Storage Optimization: A promising avenue lies in investigating how DeepVELOX predictions can seamlessly intertwine with energy storage systems to optimize energy dispatch and storage management. This exploration could culminate in the efficient utilization of generated energy and bolstered grid stability.
Cost-Benefit Analysis: A fundamental undertaking involves an extensive analysis of the cost-effectiveness tied to integrating DeepVELOX within existing wind energy infrastructure. Rigorous evaluation of the potential economic gains, return on investment, and overall cost reduction would serve as guiding factors in decision-making processes surrounding implementation.