Research on and Assessment of the Reliability of Railway Transport Systems with Induction Motors
Abstract
1. Introduction
1.1. Motivation and Relevance
1.2. Literature Review
1.3. Organization of the Paper
2. Diagnostic System as Part of the Electric Drive of Railway Transport
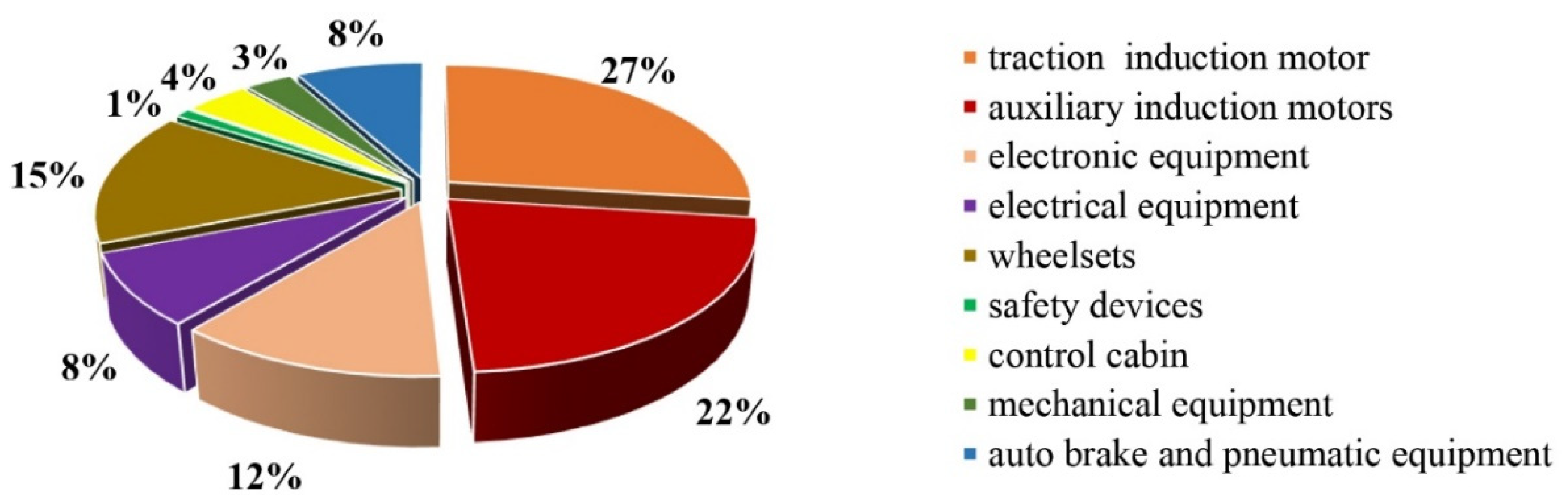
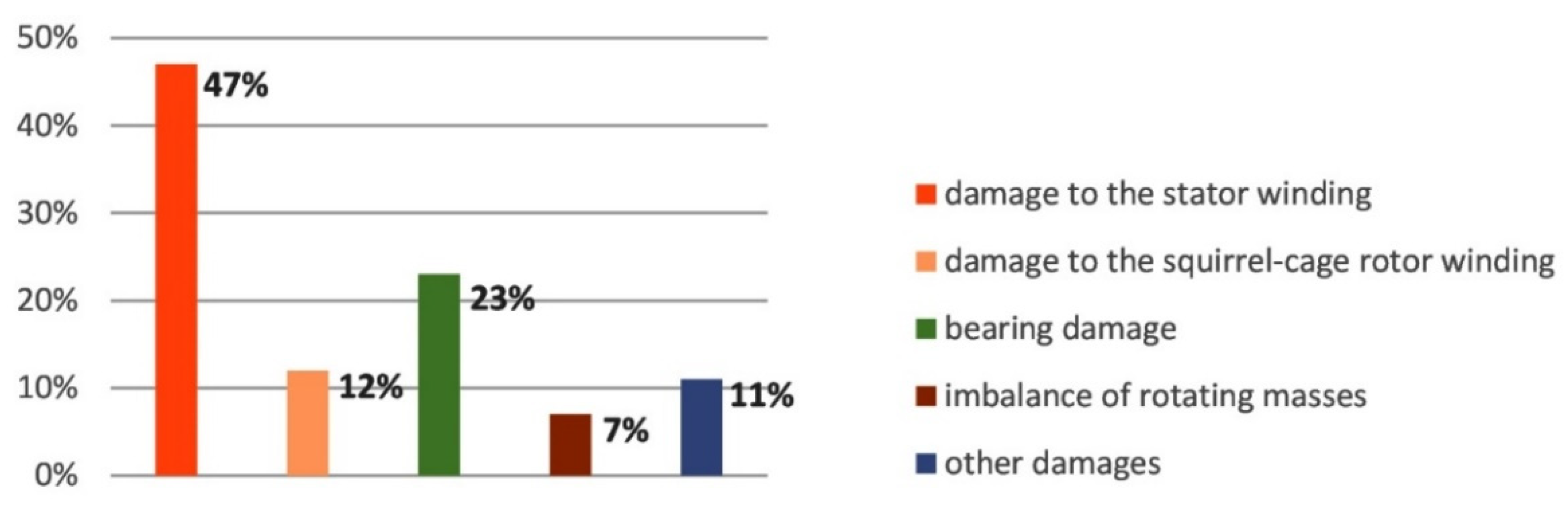
2.1. Damage Analysis of Induction Motors during Operation
2.2. Principles of the Construction and Structure of the Diagnostic System for Monitoring the Technical Condition of the Engine
3. Structural Scheme of the Reliability of Induction Motors during Operation
4. Five-State Model of Operation Process of Railway Transport Systems with Induction Motors
- -
- S0—state of serviceability;
- -
- S1—state of incomplete serviceability;
- -
- S2—state of critical serviceability;
- -
- S3—state of pre-damage serviceability;
- -
- S4—state of unserviceability.
- -
- λ (S0, S1); hence, λ has an interpretation of the intensity of the transition of the system from state S0 to state S1;
- -
- μ (S1, S0); hence, μ has an interpretation of the intensity of the transition of the system from state S1 to state S0;
- -
- λ (S0, S2); hence, λ1 has an interpretation of the intensity of the system’s transition from state S0 to state S2;
- -
- μ (S2, S0); hence, μ1 has an interpretation of the intensity of the system’s transition from state S2 to state S0;
- -
- λ (S2, S3); hence, λ2 has an interpretation of the intensity of the system’s transition from state S2 to state S3;
- -
- μ (S3, S0); hence, μ2 has the interpretation of the intensity of the transition of the system from state S3 to state S0;
- -
- λ (S2, S4); hence, λ3 has an interpretation of the intensity of the system’s transition from state S2 to state S4;
- -
- μ (S4, S0); hence, μ3 has an interpretation of the intensity of the system’s transition from state S4 to state S0.
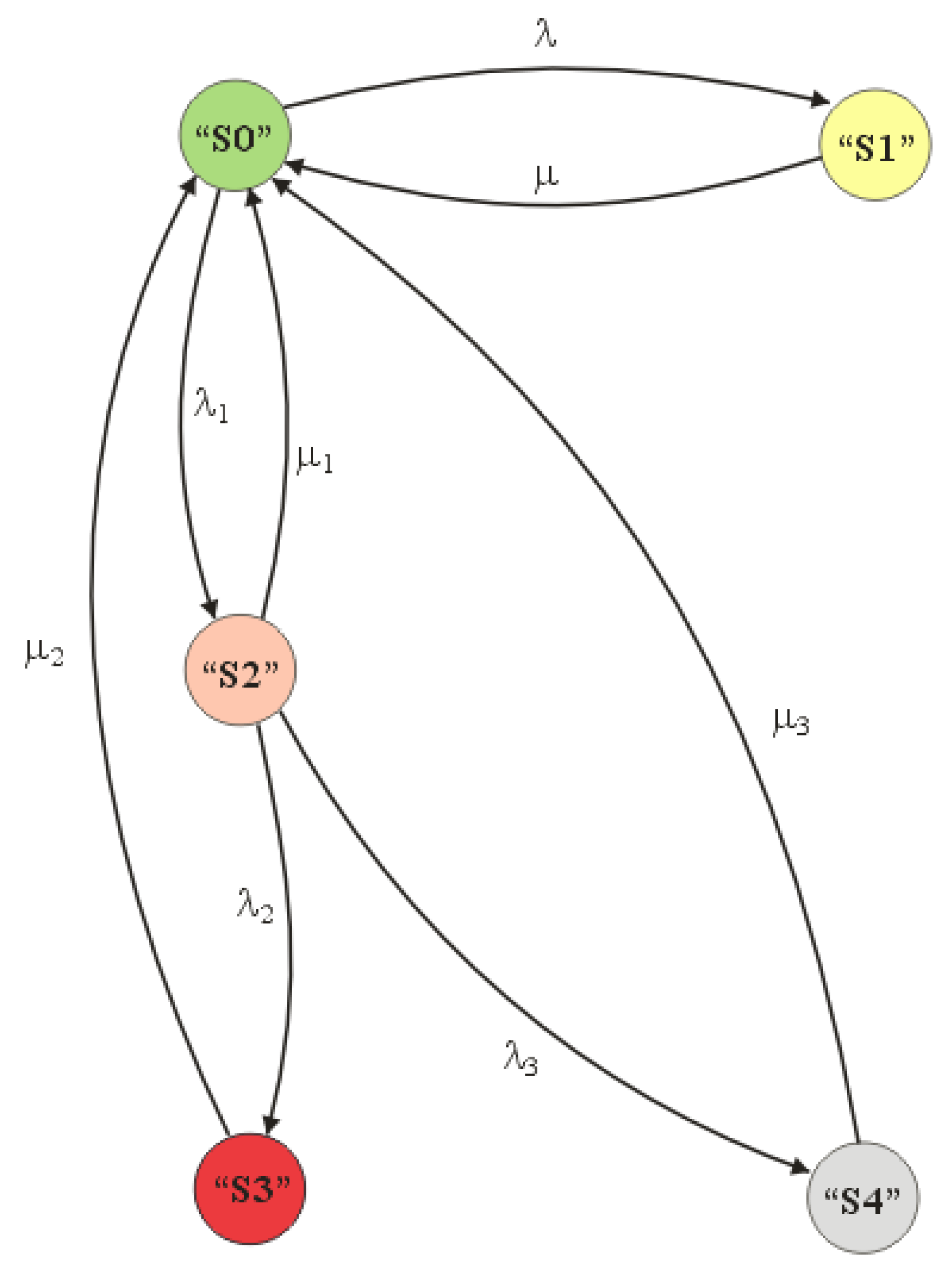
- λ—intensity of the system transition from S0 state to S1 state;
- μ—transitions of the system from S1 state to S0 state;
- λ1—intensity of the transition of the system from state S0 to state S2;
- μ1—system transitions from state S2 to state S0;
- λ2—intensity of system transitions from state S2 to state S3;
- μ2—system transitions from state S3 to state S0;
- λ3—intensity of system transitions from state S2 to state S4;
- μ3—transitions of the system from state S4 to state S0.
- -
- The function of the probability of the system remaining in state S0;
- -
- The function of the probability of the system being in state S1;
- -
- The function of the probability of the system being in state S2;
- -
- The function of the probability of the system being in state S3;
- -
- The residence probability function of the system in state S4.
5. Analysis and Evaluation of the Reliability of the Operation Process of Railway Transport Systems with Induction Motors
6. Research Results
- -
- The duration of the test system of railway transport systems with induction motors—1 year:
- -
- The probability of railway transport systems with induction motors remaining in a fully serviceable state (S0) for a period of 1 year:
- -
- The probability of railway transport systems with induction motors remaining in a state of partial serviceability (S1) for a period of 1 year:
- -
- The probability of railway transport systems with induction motors remaining in a state of critical serviceability (S2) for a period of 1 year:
- -
- The probability of railway transport systems with induction motors remaining in pre-damage condition (S3) for 1 year:
- -
- The probability of the railway transport systems with induction motors tested remaining in an unfit state (S4) for 1 year:
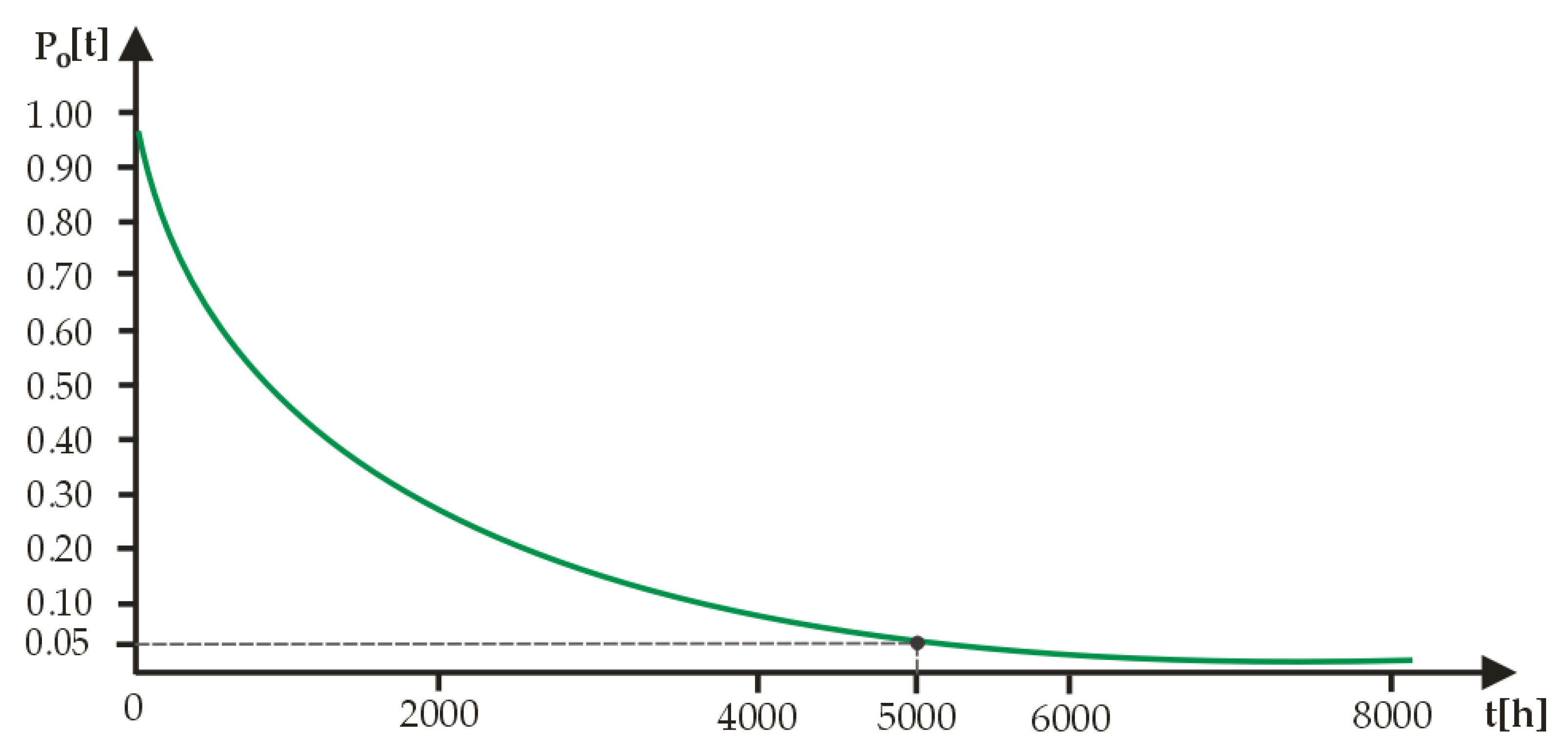
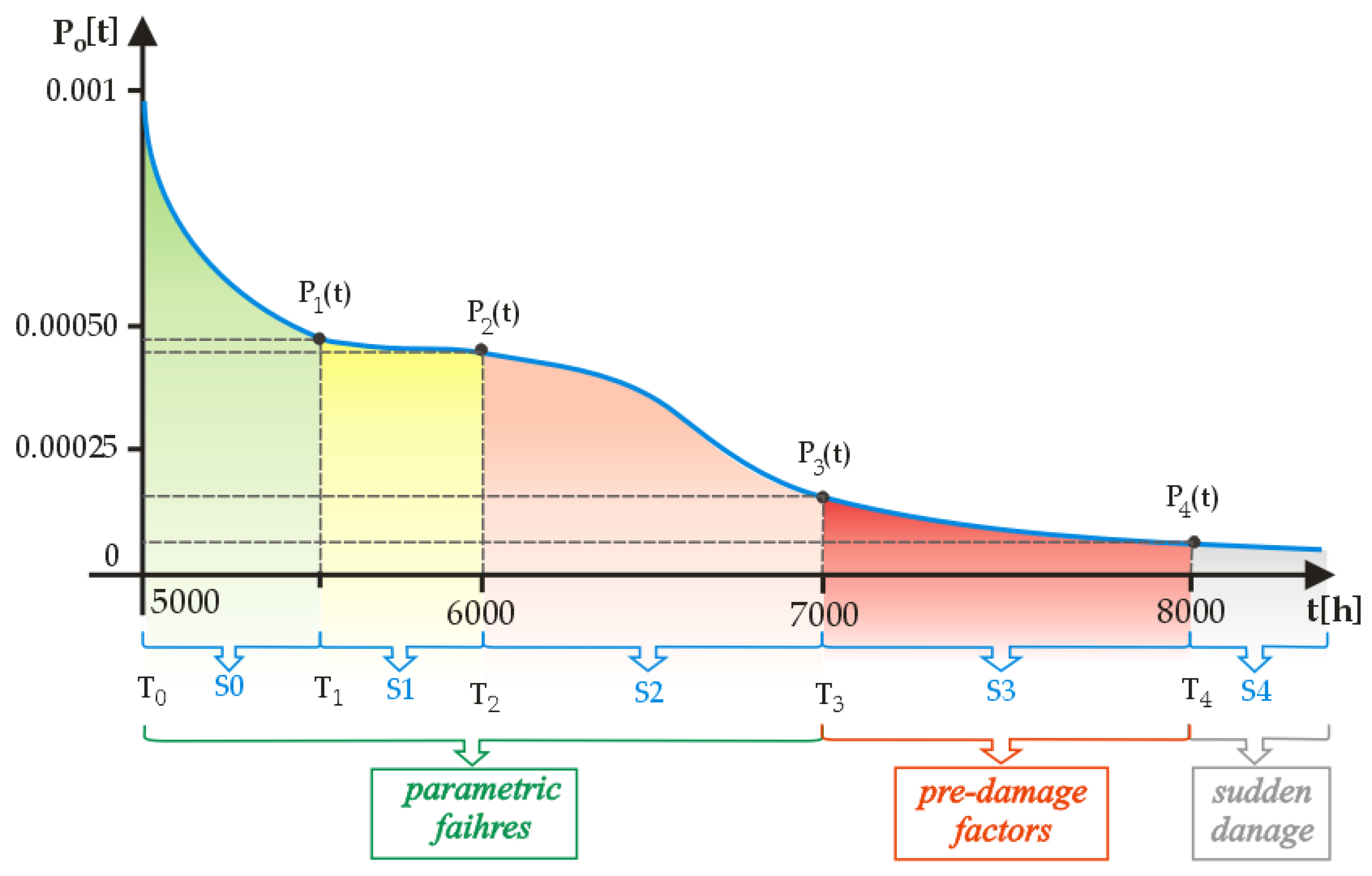
- P0 = 0.99883 → 〈0 ÷ 5500〉 [h]
- P1 = 0.0004801 → 〈5500 ÷ 6000〉 [h]
- P2 = 0.0004797 → 〈6000 ÷ 7000〉 [h]
- P3 = 0.000199 → 〈7000 ÷ 8000〉 [h]
- P4 = 8.32593 × 10−6 → 〈 t > 8000〉 [h]
7. Discussion
- The time T1, which signifies the occurrence of the S0 state—the state of fitness—has the value (T1 = 5500 [h]). Thus, in the time interval < 0; 5500 [h] > the object under test object is in a fully functional S0 state;
- The time T2, which denotes the occurrence of the S1 state—the state of incomplete fitness—has the value (T2 = 6000 [h]). Thus, in the time interval < 5500 [h]; 6000 [h] > the object under study is in the S1 state—the state of incomplete fitness. In this state, rail transportation systems with induction motors perform their tasks with a violation of the technical characteristics;
- The time T3, which denotes the occurrence of state S2—the state of critical fitness— has the value (T3 = 7000 [h]). In the time interval < 6000 [h]; 7000 [h] > the object under study is in state S2—the state of critical fitness. In the S2 state, rail transport systems with induction motors under testing perform their tasks with a minimum load;
- The next tested time is T4, which denotes the occurrence of state S3—the pre-damage state—which has a value of (T4 = 8000 [h]). Thus, in the time interval < 7000 [h]; 8000 [h] > the tested object is in the S3 state—the pre-damage state. In the S3 state, the tested rail transportation systems with induction motors perform their tasks to a minimum extent;
- In the time interval above < 8000 [h] > the tested object is in the state S4—the state of inoperability. In this state, the rail transportation system with induction motors ceases to perform its tasks and breaks down.
- Damage is a condition occurring in a technical object in which there is a loss of the ability of the object to perform its required functions (the object ceases to carry out its tasks). Damage by its nature can be divided into critical and non-critical;
- Critical (sudden) damage is damage that causes a state of unserviceability in the technical object—the “0” state. In this state, there is a sudden total loss in the object’s ability to perform its required functions. Critical damage can entail significant property damage or other dangerous events for the facility itself and the personnel operating the facility;
- Non-critical (parametric) damage is damage that occurs gradually in a technical facility during its use as a result of aging changes, the effects of internal factors (e.g., temperature, pressure, etc.) occurring in the structural elements of the facility, etc.
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | Environmental and Ambient |
| B | Grid |
| C | Brake Systems |
| D | Hydraulics |
| E | Yaw System |
| F | Communications |
| G | Connectors |
| H | Protection Relays |
| I | Pitch System |
| J | Cooling and Heating Systems |
| K | Transmission |
| L | MV Unit Power Transformer |
| M | Controller |
| N | Gearbox |
| O | Generator |
| P | Rotor |
| Q | Feeder Cable Line Field |
| R | Shunt Reactor Field |
| S | Power Transformer Field |
| T | Auxiliaries Field |
| U | Voltage Measurement Field |
| W | General Signalization |
References
- Epstein, B.; Weissman, I. Mathematical Models for Systems Reliability; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Abingdon, UK, 2008. [Google Scholar]
- Jin, T. Reliability Engineering and Service; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Verma, A.K.; Ajit, S.; Karanki, D.R. Reliability and Safety Engineering; Springer: London, UK, 2010. [Google Scholar] [CrossRef]
- Kołowrocki, K.; Soszyńska-Budny, J. Reliability and Safety of Complex Technical Systems and Processes; Springer: London, UK, 2011. [Google Scholar]
- Stawowy, M.; Rosiński, A.; Paś, J. Klimczak. Method of Estimating Uncertainty as a Way to Evaluate Continuity Quality of Power Supply in Hospital Devices. Energies 2021, 14, 486. [Google Scholar] [CrossRef]
- Stawowy, M.; Rosiński, A.; Siergiejczyk, M.; Perlicki, K. Quality and Reliability-Exploitation Modeling of Power Supply Systems. Energies 2021, 14, 2727. [Google Scholar] [CrossRef]
- Sozański, J. Niezawodność i Jakość Pracy Systemu Elektroenergetycznego; WNT: Warszawa, Poland, 1990. [Google Scholar]
- Xiong, F.; Ji, X.; Wei, D.; Li, G. Reliability Assessment of Micro Grid Power Supply System Based on D-Vine Copula Model. In Advanced Manufacturing and Automation X. IWAMA 2020, Lecture Notes in Electrical Engineering; Springer: Singapore, 2021; Volume 737. [Google Scholar] [CrossRef]
- Duer, S. Assessment of the Operation Process of Wind Power Plant’s Equipment with the Use of an Artificial Neural Network. Energies 2020, 13, 2437. [Google Scholar] [CrossRef]
- Duer, S. Applications of an artificial intelligence for servicing of a technical object. Neural Comput. Appl. 2013, 22, 955–968. [Google Scholar] [CrossRef]
- Duer, S. Expert knowledge base to support the maintenance of a radar system. Def. Sci. J. 2010, 60, 531–540. [Google Scholar] [CrossRef][Green Version]
- Duer, S. Artificial Neural Network-based technique for operation process control of a technical object. Def. Sci. J. 2009, 59, 305–313. [Google Scholar] [CrossRef][Green Version]
- Duer, S. Diagnostic system for the diagnosis of a reparable technical object, with the use of an artificial neural network of RBF type. Neural Comput. Appl. 2010, 19, 691–700. [Google Scholar] [CrossRef]
- Stawowy, M. Identifying status of an ICT system using rough sets. Arch. Transp. Syst. Telemat. 2014, 7, 50–53. [Google Scholar]
- Stawowy, M.; Kasprzyk, Z. Identifying and simulation of status of an ICT system using rough sets. In Theory and Engineering of Complex Systems and Dependability. DepCoS-RELCOMEX 2015. Advances in Intelligent Systems and Computing; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; Volume 365. [Google Scholar] [CrossRef]
- Kalpana, S.; Saranya, N.; Saundariya, K. An IoT Based Real-Time Monitoring and Controlling of Sub-Station Equipment. In Proceedings of the 2021 International Conference on System, Computation, Automation and Networking (ICSCAN), Puducherry, India, 30–31 July 2021. [Google Scholar] [CrossRef]
- Zhu, Q.; Xu, S.; Sun, J.; Li, X.; Zhou, D. Energy efficiency evaluation of power supply system: A data-driven approach based on shared resources. Appl. Energy 2022, 312, 118683. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, W.; Wang, X.; Li, H. An MILP-Based Planning Model of a Photovoltaic/Diesel/Battery Stand-Alone Microgrid Considering the Reliability. IEEE Trans. Smart Grid 2021, 12, 3809–3818. [Google Scholar] [CrossRef]
- Wang, Y.; Nie, L.; Dang, Y.; Deng, G.; Li, J.; Li, P.; Wang, P.; Luo, H.; Qin, Z.; Chen, S. Fault Prediction of Power Electronic Devices in Mobile UPS System. In Proceedings of the 2021 IEEE 16th Conference on Industrial Electronics and Applications (ICIEA), Online, 1–4 August 2021. [Google Scholar] [CrossRef]
- BLobov, N.; Kolpakhch’yan, P.G.; Belokopytov, S.A.; Madzhid, A.D.R.A. A choice of the structure of the photovoltaic system for power supply. Russ. Electr. Eng. 2015, 86, 398–402. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; AL-Sunni, F.M. Control and Optimization of Distributed Generation Systems; Springer International Publishing: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Azaza, M.; Eriksson, D.; Wallin, F. A study on the viability of an on-site combined heat- and power supply system with and without electricity storage for office building. Energy Convers. Manag. 2020, 213, 112807. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Cao, S.; Yang, H. Overview on hybrid solar photovoltaic-electrical energy storage technologies for power supply to buildings. Energy Convers. Manag. 2019, 187, 103–121. [Google Scholar] [CrossRef]
- Banik, R.; Das, P. A Review on Architecture, Performance and Reliability of Hybrid Power System. J. Inst. Eng. Ser. B 2020, 101, 527–539. [Google Scholar] [CrossRef]
- Wang, L. (Ed.) Modeling and Control of Sustainable Power Systems; Springer: Berlin, Germany, 2012. [Google Scholar] [CrossRef]
- Krzykowski, M.; Krzykowska, K. Will the European Commission’s policy hinder gas supplies to Central and Eastern European countries? OPAL case decision. Energy Policy 2017, 110, 534–541. [Google Scholar] [CrossRef]
- Nagaraja, Y.; Kumar, M.V.; Raju, T.D. Analysis and design of a robust controller for a grid-connected photovoltaic power plant. Int. J. Ambient. Energy 2018, 41, 326–333. [Google Scholar] [CrossRef]
- Jahid, A.; Monju, K.H.; Hossain, S.; Hossain, F. Hybrid power supply solutions for off-grid green wireless networks. Int. J. Green Energy 2019, 16, 12–33. [Google Scholar] [CrossRef]
- Li, Y.; Ren, X.; Niu, J. Application of rough sets theory in forecast of power generation for grid-connected photovoltaic system. In Proceedings of the 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015. [Google Scholar] [CrossRef]
- Duer, S.; Valicek, J.; Paś, J.; Stawowy, M.; Bernatowicz, D.; Duer, R.; Walczak, M. Neural Networks in the Diagnostics Process of Low-Power Solar Plant Devices. Energies 2021, 14, 2719. [Google Scholar] [CrossRef]
- Ghorani, R.; Fattaheian-Dehkordi, S.; Farrokhi, M.; Fotuhi-Firuzabad, M.; Lehtonen, M. Modeling and Quantification of Power System Resilience to Natural Hazards: A Case of Landslide. IEEE Access 2021, 9, 80300–80309. [Google Scholar] [CrossRef]
- Keyhani, A.; Marwali, M. Smart Power Grids; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Stasiuk, O.I.; Grishchuk, R.V.; Goncharova, L.L. Mathematical differential models and methods for assessing the cybersecurity of intelligent computer networks for control of technological processes of railway power supply. Cybern. Syst. Anal. 2018, 54, 671–677. [Google Scholar] [CrossRef]
- Kozyra, J.; Łukasik, Z.; Kuśmińska-Fijałkowska, A.; Kaszuba, P. The impact of selected variants of remote control on power supply reliability indexes of distribution networks. Electr. Eng. 2021, 104, 1255–1264. [Google Scholar] [CrossRef]
- Zhou, K.; Wei, S.; Yang, S. Time-of-use pricing model based on power supply chain for user-side microgrid. Appl. Energy 2019, 248, 35–43. [Google Scholar] [CrossRef]
- Paś, J.; Siergiejczyk, M. Interference impact on the electronic safety system with a parallel structure. Diagnostyka 2016, 17. No 1. [Google Scholar]
- Gao, D.; Li, G.; Yu, J. Does digitization improve green total factor energy efficiency? Evidence from Chinese 213 cities. Energy 2022, 247, 123395. [Google Scholar] [CrossRef]
- Liu, X.; Nielsen, P.S. A hybrid ICT-solution for smart meter data analytics. Energy 2016, 115, 1710–1722. [Google Scholar] [CrossRef]
- Paś, J.; Rosiński, A. Selected issues regarding the reliability-operational assessment of electronic transport systems with regard to electromagnetic interference. Eksploat. Niezawodn. Maint. Reliab. 2017, 19, 375–381. [Google Scholar] [CrossRef]
- He, Y.; Liang, X.D.; Deng, F.M.; Li, Z. Emergency Supply Chain Management Based on Rough Set—House of Quality. Int. J. Autom. Comput. 2019, 16, 297–309. [Google Scholar] [CrossRef]
- Xie, H.; Hu, X.; Peng, Z.; Yao, X.; Chen, Y. A Method of Electricity Consumption Behavior Analysis Based on Rough Set Fuzzy Clustering. In Proceedings of the 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018. [Google Scholar] [CrossRef]
- Changhua, H. Distribution Network Fault Location Based on Rough Set and Data Fusion. In Proceedings of the 2019 IEEE 4th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chengdu China, 20–22 December 2019. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, X.; Jin, P.; Lu, T. Optimization Strategy for New Energy Consumption Based on Intuitionistic Fuzzy Rough Set Theory. In Proceedings of the 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020. [Google Scholar] [CrossRef]
- Siergiejczyk, M.; Stawowy, M. Modelling of uncertainty for continuity quality of power supply. In Proceedings of the Risk, Reliability and Safety: Innovating Theory and Practice; CRC Press/Balkema: London, UK, 2017. [Google Scholar]
- Dai, Q.; Shi, L.; Ni, Y. Risk Assessment for Cyberattack in Active Distribution Systems Considering the Role of Feeder Automation. IEEE Trans. Power Syst. 2019, 34, 3230–3240. [Google Scholar] [CrossRef]
- Fuhg, J.N.; Böhm, C.; Bouklas, N.; Fau, A.; Wriggers, P.; Marino, M. Model-data-driven constitutive responses: Application to a multiscale computational framework. Int. J. Eng. Sci. 2022, 167, 103522. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough Sets—A New Mathematical Method of Data Analysis. Institute of Theoretical and Applied Informatics, Polish Academy of Sciences, Warsaw, Poland, 1995. [Google Scholar]
- Stawowy, M.; Targosiński, T. The use of rough set to estimate the quality of objects recognition and localization. In Risk, Reliability and Safety: Innovating Theory and Practice: Proceedings of ESREL 2016; CRC Press/Balkema: Boca Raton, FL, USA, 2016. [Google Scholar]
- Li, H.; Chen, M.; Yang, B.; Blaabjerg, F.; Xu, D. Fast Fault Protection Based on Direction of Fault Current for the High-Surety Power-Supply System. IEEE Trans. Power Electron. 2018, 34, 5787–5802. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough Sets; Institute of Computer Science, Polish Academy of Sciences: Warsaw, Poland, 1981. [Google Scholar]
- Wiatr, J.; Miegoń, M. UPS Power Supplies and Accumulator Batteries in Emergency Power Systems; MEDIUM Publishing House: Warsaw, Poland, 2008. [Google Scholar]
- Puzyr, V.; Datsun, Y.; Obozny, O.; Pyvo, V. Development of a repair technology for locomotive units on the basis of the theory of decision. IOP Conf. Ser. Mater. Sci. Eng. 2019, 664, 012029. [Google Scholar] [CrossRef]
- Goolak, S.; Liubarskyi, B.; Lukoševičius, V.; Keršys, R.; Keršys, A. Operational Diagnostics System for Asymmetric Emergency Modes in Traction Drives with Direct Torque Control. Appl. Sci. 2023, 13, 5457. [Google Scholar] [CrossRef]
- Hoelzl, C.; Dertimanis, V.; Landgraf, M.; Ancu, L.; Zurkirchen, M.; Chatzi, E. Chapter 9—On-board monitoring for smart assessment of railway infrastructure: A systematic review. In The Rise of Smart Cities: Advanced Structural Sensing and Monitoring Systems; Butterworth-Heinemann: Oxford, UK, 2019; pp. 223–259. ISBN 9780128177846. [Google Scholar] [CrossRef]
- Mira, L.; Andrade, A.R.; Gomes, M.C. Maintenance scheduling within rolling stock planning in railway operations under uncertain maintenance durations. J. Rail Transp. Plan. Manag. 2020, 14, 100177. [Google Scholar] [CrossRef]
- Erguido, A.; Márquez, A.C.; Castellano, E.; Flores, J.L.; Fernández, J.F.G. Reliability-based advanced maintenance modelling to enhance rolling stock manufacturers’ objectives. Comput. Ind. Eng. 2020, 144, 106436. [Google Scholar] [CrossRef]
- Giacco, G.L.; Carillo, D.; D’Ariano, A.; Pacciarelli, D.; Marín, Á.G. Short-term Rail Rolling Stock Rostering and Maintenance Scheduling. Transp. Res. Procedia 2014, 3, 651–659. [Google Scholar] [CrossRef]
- Cheng, Y.-H.; Tsao, H.-L. Rolling stock maintenance strategy selection, spares parts’ estimation, and replacements’ interval calculation. Int. J. Prod. Econ. 2010, 128, 404–412. [Google Scholar] [CrossRef]
- Huynh, K.T.; Castro, I.T.; Barros, A.; Bérenguer, C. Modeling age-based maintenance strategies with minimal repairs for systems subject to competing failure modes due to degradation and shocks. Eur. J. Oper. Res. 2012, 218, 140–151. [Google Scholar] [CrossRef]
- Marseguerra, M.; Zio, E. Optimizing maintenance and repair policies via a combination of genetic algorithms and Monte Carlo simulation. Reliab. Eng. Syst. Saf. 2000, 68, 69–83. [Google Scholar] [CrossRef]
- De Simone, L.; Caputo, E.; Cinque, M.; Galli, A.; Moscato, V.; Russo, S.; Cesaro, G.; Criscuolo, V.; Giannini, G. LSTM-based failure prediction for railway rolling stock equipment. Expert Syst. Appl. 2023, 222, 119767. [Google Scholar] [CrossRef]
- Nazarizadeh, F.; Alemtabriz, A.; Zandieh, M. An analytical model for reliability assessment of the rail system considering dependent failures (case study of Iranian railway). Reliab. Eng. Syst. Saf. 2022, 227, 108725. [Google Scholar] [CrossRef]
- Sun, Y.; Ma, L.; Mathew, J.; Zhang, S. An analytical model for interactive failures. Reliab. Eng. Syst. Saf. 2006, 91, 495–504. [Google Scholar] [CrossRef]
- Duer, S.; Paś, J.; Hapka, A.; Duer, R.; Ostrowski, A.; Woźniak, M. Assessment of the Reliability of Wind Farm Devices in the Operation. Energies 2022, 15, 3860. [Google Scholar] [CrossRef]
- Cacchiani, V.; Huisman, D.; Kidd, M.; Kroon, L.; Toth, P.; Veelenturf, L.; Wagenaar, J. An overview of recovery models and algorithms for real-time railway rescheduling. Transp. Res. Part B Methodol. 2014, 63, 15–37. [Google Scholar] [CrossRef]
- Percy, D.F.; Khairy, A.; Kobbacy, H.; Fawzi, B. Setting preventive maintenance schedules when data are sparse. Int. J. Prod. Econ. 1997, 51, 223–234. [Google Scholar] [CrossRef]
- Corman, F.; Trivella, A.; Keyvan-Ekbatani, M. Stochastic process in railway traffic flow: Models, methods and implications. Transp. Res. Part C Emerg. Technol. 2021, 128, 103167. [Google Scholar] [CrossRef]
- Luo, J.; Wen, C.; Peng, Q.; Qin, Y.; Huang, P. Forecasting the effect of traffic control strategies in railway systems: A hybrid machine learning method. Phys. A Stat. Mech. Its Appl. 2023, 621, 128793. [Google Scholar] [CrossRef]
- Duer, S.; Zajkowski, K.; Harničárová, M.; Charun, H.; Bernatowicz, D. Examination of Multivalent Diagnoses Developed by a Diagnostic Program with an Artificial Neural Network for Devices in the Electric Hybrid Power Supply System “House on Water. Energies 2021, 14, 2153. [Google Scholar] [CrossRef]
- Pokoradi, L. Logical Tree of Mathematical Modeling. Theory Appl. Math. Comput. Sci. 2015, 5, 20–28. [Google Scholar]
- Brancevich, P.; Li, Y. Model of the Decision-Making System for Assessment of the State of Technical Objects. In Proceedings of the 28th International Congress on Sound and Vibration, Singapore, 24–28 July 2022. [Google Scholar]
- Shcherbovskykh, S.; Stefanovych, T.; Denysyuk, P. Reliability Analysis of the Duplicated Wired Channels with Tripled Protective Reinforcement. In Proceedings of the 2022 IEEE XVIII International Conference on the Perspective Technologies and Methods in MEMS Design (MEMSTECH), Zakarpattia Oblast, Ukraine, 7–11 September 2022; pp. 89–92. [Google Scholar] [CrossRef]
- Bondarenko, I.; Severino, A.; Olayode, I.O.; Campisi, T.T.; Neduzha, L. Dynamic Sustainable Processes Simulation to Study Transport Object Efficiency. Infrastructures 2022, 7, 124. [Google Scholar] [CrossRef]
- Lovska, A.; Fomin, O.; Pistek, V.; Kucera, P. Dynamic load modelling within combined transport trains during transportation on a railway ferry. Appl. Sci. 2020, 10, 5710. [Google Scholar] [CrossRef]
- Baranovskyi, D.; Bulakh, M.; Michajłyszyn, A.; Myamlin, S.; Muradian, L. Determination of the Risk of Failures of Locomotive Diesel Engines in Maintenance. Energies 2023, 16, 4995. [Google Scholar] [CrossRef]
- Kostanovsky, V.; Machalin, I.; Kozachuk, O.; Terentyeva, I. Construction of a generalized probabilistic-physical model of reliability of a two-level active phased antenna array. East. Eur. J. Enterp. Technol. 2019, 3, 31–40. [Google Scholar] [CrossRef]
- Lingaitis, L.; Lebedevas, S.; Liudvinavičius, L. Evaluation of the operational reliability and forecasting of the operating life of the powertrain of the freight diesel locomotive fleet. Eksploat. Niezawodn. Maint. Reliab. 2014, 16, 73–79. [Google Scholar]
- Grenčík, J.; Poprocký, R.; Galliková, J.; Volna, P. Use of risk assessment methods in maintenance for more reliable rolling stock operation. MATEC Web Conf. 2018, 157, 04002. [Google Scholar] [CrossRef]
- Peng, Z.; Lu, Y.; Miller, A.; Johnson, C.; Zhao, T. Risk Assessment of Railway Transportation Systems using Timed Fault Trees. Qual. Reliab. Eng. Int. 2016, 32, 181–194. [Google Scholar] [CrossRef]
- Rashidnejad, M.; Ebrahimnejad, S.; Safari, J. A bi-objective model of preventive maintenance planning in distributed systems considering vehicle routing problem. Comput. Ind. Eng. 2018, 120, 360–381. [Google Scholar] [CrossRef]
- Lyu, H.; Qu, H.; Xie, H.; Zhang, Y.; Pecht, M. Reliability analysis of the multi-state system with nonlinear degradation model under Markov environment. Reliab. Eng. Syst. Saf. 2023, 238, 109411. [Google Scholar] [CrossRef]
- Yan, T.; Lei, Y.; Li, N.; Wang, B.; Wang, W. Degradation modeling and remaining useful life prediction for dependent competing failure processes. Reliab. Eng. Syst. Saf. 2021, 212, 107638. [Google Scholar] [CrossRef]
- Liang, Q.; Yang, Y.; Peng, C. A reliability model for systems subject to mutually dependent degradation processes and random shocks under dynamic environments. Reliab. Eng. Syst. Saf. 2023, 234, 109165. [Google Scholar] [CrossRef]
- Sheikh, M.A.; Bakhsh, S.T.; Irfan, M.; Nor, N.B.M.; Nowakowski, G. A Review to Diagnose Faults Related to Three-Phase Industrial Induction Motors. J. Fail. Anal. Prev. 2022, 22, 1546–1557. [Google Scholar] [CrossRef]
- Gubarevych, O.; Goolak, S.; Golubieva, S. Classification of Defects, Systematization and Selection of Methods for Diagnosing the Stator Windings Insulation of Asynchronous Motors. Rev. Roum. Sci. Techn. Électrotechn. Énerg. 2022, 67, 445–450. [Google Scholar]
- Choudhary, A.; Goyal, D.; Shimi, S.L.; Akula, A. Condition monitoring and fault diagnosis of induction motors: A review. Arch. Comput. Methods Eng. 2019, 26, 1221–1238. [Google Scholar] [CrossRef]
- Gerlici, J.; Goolak, S.; Gubarevych, O.; Kravchenko, K.; Kamchatna-Stepanova, K.; Toropov, A. Method for Determining the Degree of Damage to the Stator Windings of an Induction Electric Motor with an Asymmetric Power System. Symmetry 2022, 14, 1305. [Google Scholar] [CrossRef]
- Goolak, S.; Liubarskyi, B.; Riabov, I.; Chepurna, N.; Pohosov, O. Simulation of a direct torque control system in the presence of winding asymmetry in induction motor. Eng. Res. Express 2023, 5, 025070–025086. [Google Scholar] [CrossRef]
- Abdelhak, G.; Ahmed, B.S.; Djekidel, R. Fault diagnosis of induction motors rotor using current signature with different signal processing techniques. Diagnostyka 2022, 23, 2022201. [Google Scholar] [CrossRef]
- Safiullin, R.A. Vibration diagnostics of induction motors. In Proceedings of the 2021 International Conference on Electrotechnical Complexes and Systems (ICOECS), Ufa, Russia, 16–18 November 2021; pp. 228–232. [Google Scholar] [CrossRef]
- Gubarevych, O.; Goolak, S.; Melkonova, I.; Yurchenko, M. Structural diagram of the built-in diagnostic system for electric drives of vehicles. Diagnostyka 2022, 23, 2022406. [Google Scholar] [CrossRef]
- Gubarevych, O.; Gerlici, J.; Kravchenko, O.; Melkonova, I.; Melnyk, O. Use of Park’s Vector Method for Monitoring the Rotor Condition of an Induction Motor as a Part of the Built-In Diagnostic System of Electric Drives of Transport. Energies 2023, 16, 5109. [Google Scholar] [CrossRef]
- Muxiri, A.C.; Bento, F.; Fonseca, D.S.B.; Cardoso, A.J.M. Thermal analysis of an induction motor subjected to inter-turn short-circuit failures in the stator windings. In Proceedings of the 2019 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Sochi, Russia, 25–29 March 2019; IEEE: Piscataway, NJ, USA; pp. 1–5. [Google Scholar] [CrossRef]
- Benbouzid, M.E.H. A review of induction motors signature analysis as a medium for faults detection. IEEE Trans. Ind. Electron. 2000, 47, 984–993. [Google Scholar] [CrossRef]
- Wei, S.; Zhang, X.; Xu, Y.; Fu, Y.; Ren, Z.; Li, F. Extended Park’s vector method in early inter-turn short circuit fault detection for the stator windings of offshore wind doubly-fed induction generators. IET Gener. Transm. Distrib. 2020, 14, 3905–3912. [Google Scholar] [CrossRef]
- Gyftakis, K.N.; Cardoso, A.J.M.; Antonino-Daviu, J.A. Introducing the Filtered Park’s and Filtered Extended Park’s Vector Approach to detect broken rotor bars in induction motors independently from the rotor slots number. Mech. Syst. Signal Process. 2017, 93, 30–50. [Google Scholar] [CrossRef]
- Abdellah, C.; Mama, C.; Meflah Abderrahmane, M.R.; Mohammed, B. Current Park’s Vector Pattern Technique for Diagnosis of Broken Rotor Bars Fault in Saturated Induction Motor. J. Electr. Eng. Technol. 2023, 18, 2749–2758. [Google Scholar] [CrossRef]
- Stawowy, M.; Duer, S.; Paś, J.; Wawrzyński, W. Determining Information Quality in ICT Systems. Energies 2021, 14, 5549. [Google Scholar] [CrossRef]
- Gubarevych, O.; Goolak, S.; Daki, O.; Yakusevych, Y. Determining an additional diagnostic parameter for improving the accuracy of assessment of the condition of stator windings in an induction motor. East. Eur. J. Enterp. Technol. 2021, 5, 21–29. [Google Scholar] [CrossRef]
- Duer, S.; Scaticailov, S.; Paś, J.; Duer, R.; Bernatowicz, D. Taking decisions in the diagnostic intelligent systems on the basis information from an artificial neural network. MATEC Web Conf. 2018, 178, 07003. [Google Scholar] [CrossRef][Green Version]


| Parameter | Value (1/h) |
|---|---|
| λ | 0.00001 |
| λ1 | 0.00002 |
| λ2 | 0.000025 |
| λ3 | 0.000004167 |
| μ | 0.0208 |
| μ1 | 0.0416 |
| μ2 | 0.0208 |
| μ3 | 0.0416 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gubarevych, O.; Duer, S.; Melkonova, I.; Woźniak, M.; Paś, J.; Stawowy, M.; Rokosz, K.; Zajkowski, K.; Bernatowicz, D. Research on and Assessment of the Reliability of Railway Transport Systems with Induction Motors. Energies 2023, 16, 6888. https://doi.org/10.3390/en16196888
Gubarevych O, Duer S, Melkonova I, Woźniak M, Paś J, Stawowy M, Rokosz K, Zajkowski K, Bernatowicz D. Research on and Assessment of the Reliability of Railway Transport Systems with Induction Motors. Energies. 2023; 16(19):6888. https://doi.org/10.3390/en16196888
Chicago/Turabian StyleGubarevych, Oleg, Stanisław Duer, Inna Melkonova, Marek Woźniak, Jacek Paś, Marek Stawowy, Krzysztof Rokosz, Konrad Zajkowski, and Dariusz Bernatowicz. 2023. "Research on and Assessment of the Reliability of Railway Transport Systems with Induction Motors" Energies 16, no. 19: 6888. https://doi.org/10.3390/en16196888
APA StyleGubarevych, O., Duer, S., Melkonova, I., Woźniak, M., Paś, J., Stawowy, M., Rokosz, K., Zajkowski, K., & Bernatowicz, D. (2023). Research on and Assessment of the Reliability of Railway Transport Systems with Induction Motors. Energies, 16(19), 6888. https://doi.org/10.3390/en16196888












