Next Article in Journal
Controls on Gas-Reservoir Formation in the Benxi Formation in the Ganquan–Fuxian Area of the Ordos Basin, China
Previous Article in Journal
Analytical Model of Critical Ventilation Flow Rate for Accidental Hydrogen Leakage in a Confined Space
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 16
Issue 19
10.3390/en16196865
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Locating Potential Run-of-River Hydropower Sites by Developing Novel Parsimonious Multi-Dimensional Moving Window (PMMW) Algorithm with Digital Elevation Models

by
Ninad Bhagwat
* and
Xiaobing Zhou
*
Department of Geological Engineering, Montana Technological University, Butte, MT 59701, USA
*
Authors to whom correspondence should be addressed.
Energies 2023, 16(19), 6865; https://doi.org/10.3390/en16196865
Submission received: 5 September 2023 / Revised: 20 September 2023 / Accepted: 26 September 2023 / Published: 28 September 2023
(This article belongs to the Section A3: Wind, Wave and Tidal Energy)
Browse Figures
Versions Notes

Abstract

:
We developed a Parsimonious Multi-dimensional Moving Window (PMMW) algorithm that only requires Digital Elevation Model (DEM) data of a watershed to efficiently locate potentially optimal hydropower sites. The methodology requires only open source DEM data; therefore, it can be used even in remotest watersheds of the world where in situ measurements are scarce or not available at all. We used three parameters in this algorithm, and tested the method using the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) and the Shuttle Radar Topography Mission (SRTM) derived DEMs. Our case study on the Morony Watershed, Montana, USA shows that (1) along with 6 out of the 7 existing hydropower plants being successfully located, 12 new potential hydropower sites were also identified, using a clearance of 1 km, diversion of 90 m, and Hydropower Index (HI) threshold of 109 m as the criteria. For the 12 new potential hydropower sites, 737.86 Megawatts (MW) ± 84.56 MW untapped hydropower potential in the Morony Watershed was also derived; (2) SRTM DEM is more suitable for determining the potential hydropower sites; (3) although the ASTER and SRTM DEMs provide elevation data with high accuracy, micro-scale elevation differences between them at some locations may have a profound impact on the HI.

1. Introduction

One of the basic needs of mankind is energy [1,2,3]. Historically, fossil fuels are the main conventional energy sources, but they can deteriorate environment by releasing environmentally unfriendly greenhouse gases. With increasing awareness of negative impacts of carbon emissions, a transition from fossil energy sources to renewable energy sources is desirable and actively pursued all over the world, with a clear objective to reduce the carbon footprint [3,4,5,6,7]. One of the greenest, most reliable, and most efficient energy sources is hydropower [8], which converts the kinetic and potential energies of water flowing through turbines into electrical energy [9,10]. Hydroelectric energy is one of the most popular forms of renewable energy, accounting for almost 16% of the world’s energy supply [11,12,13,14]. According to the International Hydropower Association’s (IHA) 2022–2023 annual report, new hydropower capacity of approximately 22 Gigawatts (GW) per year was developed between 2017–2022. Mankind needs to generate 45 GW per year of hydro-energy to achieve net-zero CO2 emissions by 2050, and to keep the global temperature rise below 1.5 °C. The IAH’s next five-year strategy (2022–2027) is aimed in such a way that the global hydropower capacity would reach at 1450 GW by 2027 [15]. Identification of potential hydropower sites and construction of new hydropower plants is crucial to achieve this goal.
There are various types of hydropower plants such as those with reservoir dams and run-of-river (ROR) hydropower plants. The reservoir dams generally host large hydropower projects due to the presence of massive dam, reservoir, and backwater. However, many large hydropower projects were critically scrutinized for their possible positive or negative impacts on riparian environments and riverine aquatic ecosystems, such as land area inundated, barriers to natural flow, hydropeaking, etc. [16,17,18,19,20]. For instance, due to the inundation of land and vegetation, the terrestrial ecosystem is converted into an aquatic ecosystem, resulting in the decomposition of terrestrial vegetation, releasing greenhouse gases, and ultimately contributing to global warming and climate change [16,21,22], or on the other hand, due to an enhanced hydrological cycle and precipitation within a local microclimate zone, riparian vegetation greenness within a certain buffer zone along the reservoir and river increases [18]. Another natural hazard is landslides, resulting from the land inundation due to the reservoir. Massive reservoirs may also induce additional hydrostatic loads and stresses on the geological structure underneath, which is in most cases already stressed due to occurrence of folds/faults. The addition of the hydrostatic load may result in a destabilized substructure, making the area prone to earthquakes, as can be seen in Koyna earthquake incident in Maharashtra, India [23].
On the contrary, ROR power plants do not encounter such issues on both upstream and downstream sides [3], mainly due to their little to no water storage capacity. The ROR hydropower plants are relatively environmentally clement [6,16,24,25,26,27,28], despite a few drawbacks of their own on the local ecosystem such as altered environmental flows and barriers for aquatic species to migrate upstream [4,7,29,30,31]. The impacts of high-head ROR systems on sediment transport and migration of aquatic life are discussed in [11]. A review by [31] focused on the effects of the diversion-type ROR hydropower plants on the salmonid and other fish in the river downstream. A review on ecological impact of the ROR hydropower plants worldwide was produced by [32]. They mentioned that negative ecological impacts are mainly caused by diversion and pondage type of ROR hydropower plants. Non-diversion hydropower plants can be excluded from this list because they do not require flow diversion and therefore, there is no risk of inadequate environmental flows [33]. Since the reservoir is not considered in the design process of ROR hydropower plants, storage is not regulated in the associated watershed [34,35]. Thus, in a ROR hydropower plant, the inflow on the upstream side of the dam is nearly identical to the outflow on the downstream side. Therefore, hydropower generation from such hydropower plants is directly dependent on the stream flow, and changes in the discharge of the streams would affect the hydropower generation [36,37].
Due to their environmentally more friendly nature than reservoir dams, ROR dams have received worldwide attention. Extensive research has been conducted on their various aspects, such as impact on local ecosystem, no requirement of a reservoir, etc. Various hydropower models have recently been developed, some of which focus on the technical aspects (e.g., turbine mechanics, power generation), while others focus on the economic aspects (e.g., construction, operating costs) or the ecological aspects (environmental flows). Some models are more specific on hydropower generation such as the turbine efficiency curve. A review on the hydropower models that focus on the low-head instream conditions has been provided in [38]. Application of the Soil Water Assessment Tool (SWAT) and the GIS spatial tool was performed and 107 sites for potential hydropower stations were identified over the Kopili river basin in India [39]. An analytical framework to identify the feasible hydropower sites using GIS data was proposed by [9] and was applied to the Nan river basin in Thailand, where 86 potential sites were identified [9]. Total hydropower potential in Nepal was estimated by utilizing the Digital Elevation Model (DEM) provided by the Shuttle Radar Topography Mission (SRTM) and an ArcGIS processing, accompanied by development of a hydropower model [40]. Combination of meteorological data and Digital Elevation Models was used and 85 potential sites for small hydropower plants (SHPs) were identified in Bilecik regional Sakarya basin in Turkey [41]. A GIS-based systematic decision support tool for the determination of potential hydropower sites was developed and integrated with the Water-and-Energy-Budget-based Distributed Hydrological Model with snow component (WEB-DHM-S) to provide topographic and hydrologic considerations while planning the hydropower projects [26]. Another hydropower model was developed by [6] to calculate the total potential of a watershed. This model was tested in the West Rapti River basin in Nepal, and it identified a total of 79 potential hydropower sites, with the total potential of 320 MW [6]. The hydropower potential was derived in the Myitnge river in Myanmar based on the streamflows and the flow duration curves obtained through the SWAT model [10]. A bi-level optimization scheme was used, and a hydropower model called Run-of-River Project Optimization (RORPO) was developed and validated in the Mamquam River Watershed by [27]. An approach of dividing a watershed area into rectangular meshes and determining the potential hydropower site based on the headrace and penstock parameters was proposed and applied to the Huazuntlan river watershed by [42]. Another model based on the GIS and Best–Worst statistical techniques was developed to determine the potential sites for ROR hydropower plants, and the model was compared to field data, upon which, 11 potential sites were detected in the Fomanat plain in Iran [28]. Integration of GIS-based framework, curve number and the geohazard risk factors were carried out and 94 potential small-scale hydropower systems (<10 MW) with a total hydropower capacity of 13.595 MW were identified in the central Philippines [43]. An approach for assessing the design parameters of a ROR hydropower plant was suggested and a conceptual design of the hydropower plant considering Francis and Kaplan turbines was presented by [14].
However, the computationally intensive and expensive models require many parameters, on which measured data are often not available in the remote areas where in situ measurements are rare or even not available at all. On the other hand, utilization of flow accumulation could help identify areas with highest inflow. Flow accumulation is defined as accumulated weight of all neighboring cells within a watershed flowing into a downslope cell. An initial weight of 1 is set to each cell and we assume that rainfall is spatially uniform. The eventual value of a cell considering water flowing from higher cells nearby is the number of cells that flow into the cell. Cells with a high flow accumulation are the locations of concentrated flow. Eventually, cells with a flow accumulation of the initial weight of 1 are locations of local topographic highs and occur at ridges or apexes (watershed boundary) where no inflow has occurred. Therefore, flow accumulation is an indicator of concentrated flow weight and has no unit. Data obtained via DEMs provide precise information on the elevation of the area. Since the efficiency of hydropower stations depends on the optimal flow, multiplication of elevation and flow accumulation should be a proxy of gravitational potential energy and can reveal the locations where the hydropower production will be optimal. Based on this hypothesis, the objective of this study was to develop a model to locate optimal sites for potential ROR hydropower plants by integrating the elevation and flow accumulation over a watershed. Locating hydropower sites solely through the application and integration of the DEMs and flow accumulation is a novel approach and has never been published before. We have developed a parsimonious model to keep the required input parameters at a minimum, so that the model can be applied to remote watersheds. The rest of the paper is organized as follows: Section 2 explains the study area, data used and methodology, Section 3 explains the results, Section 4 provides discussion on the results, and Section 5 provides the conclusions.

2. Materials and Methods

2.1. Study Area

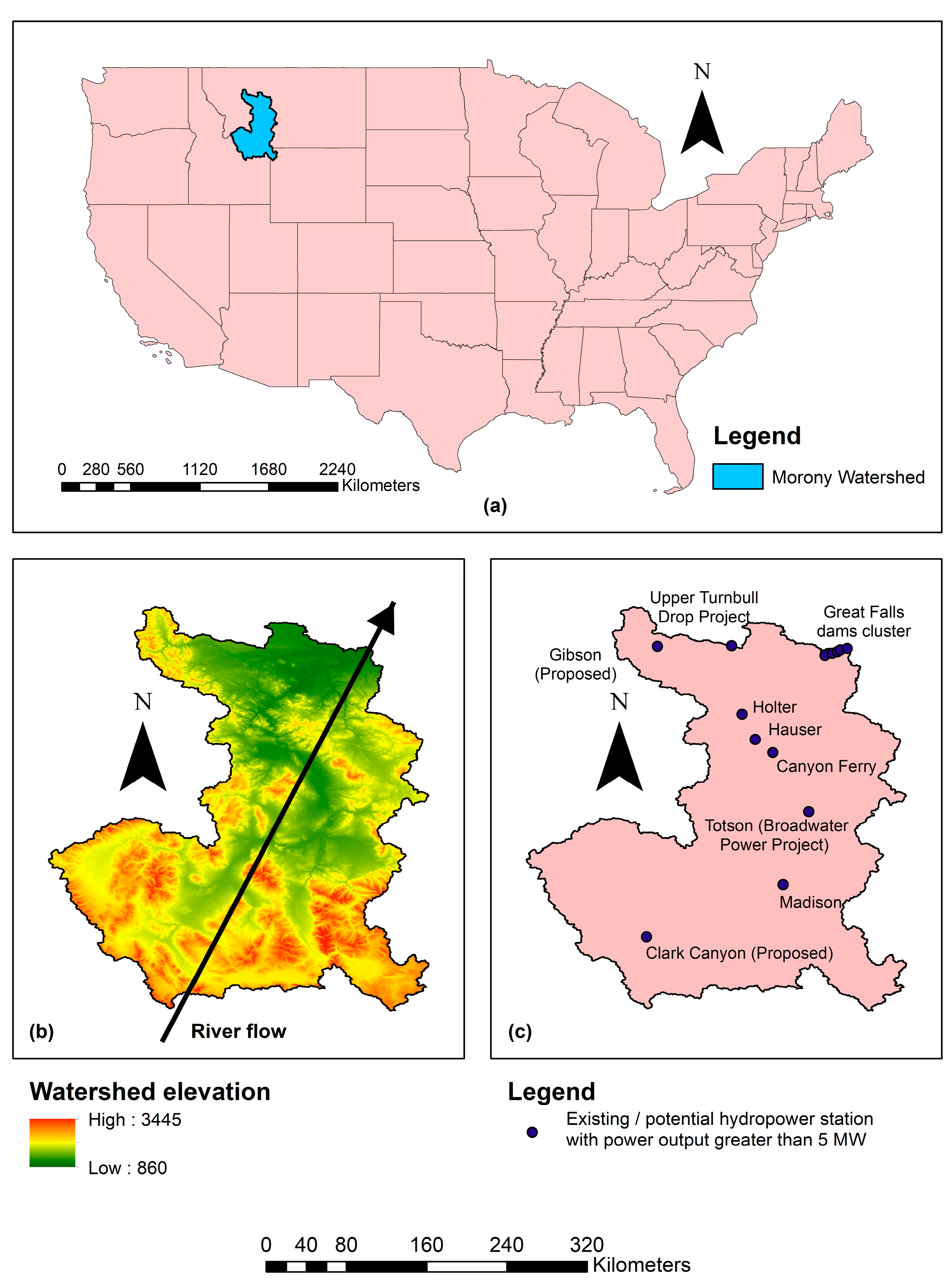
The Morony watershed extends from northwestern Wyoming to much of southern and central Montana, USA. It comprises the rise of the Missouri River near Three Forks, Montana (MT) and all its tributaries. Located within the Rocky Mountains, Morony watershed covers approximately 59,400 km2 in area. The elevation of Morony watershed ranges from 860 m in the northeast to 3445 m in the southwest, and the slope of the watershed trends from southwest to northeast. There are 256 dams [44] and 86 sites of existing and potential hydropower plants [45] in the Morony watershed. However, there are only 11 hydropower stations with power output capacity greater than 5 MW. Amongst the 11, only 7 hydropower stations have an output capacity of 20 MW or higher. Apart from the existing hydropower sites, there are 3 proposed hydropower projects [46] in this watershed. Two of them (Clark Canyon, Gibson) have natural reservoirs and dams, while the third hydropower project (Gordon-Butte) was proposed as the construction of an artificial reservoir, with the exact location not known yet. There are five dams near the watershed outlet in Great Falls, MT: Black Eagle, Rainbow, Cochrane, Ryan, and Morony. Each dam hosts a ROR-type hydropower plant. The outlet of the watershed is located at the Morony dam, thus the name we gave to the watershed. Figure 1 shows the location of the Morony watershed in the United States, along with its elevation range and the locations of all the hydropower plants with power outputs greater than 5 MW. Since there are no migratory fish species in the aquatic ecosystem in the Morony watershed, construction of diversion-type ROR plants will not impact fish migration in the river (personal communication with Mr. Jeremy Clotfelter of Northwestern Energy).

2.2. Data Sources

The primary data used for this study were the Digital Elevation Models (DEMs) acquired by the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) onboard National Aeronautics and Space Administration’s (NASA) Terra satellite and that acquired by the Shuttle Radar Topography Mission (SRTM). ASTER is a Japanese-made radiometer with high spatial resolution (15–90 m) [47]. ASTER collects data in 14 bands, ranging from visible to thermal infrared region in the electromagnetic spectrum. A Global DEM (GDEM) has been constructed using the stereo-pair imaging technique. The ASTER GDEM has tiles of 1° × 1°. The first version of the ASTER GDEM was constructed using stereo-pair images and was released in 2009. We used the latest version (version 3) of the GDEM, which has been significantly improved from the old versions with additional stereo-pairs, which has increased the coverage and reduced the occurrence of artifacts. The ASTER GDEM’s coverage spans from 83° N to 83° S, which encompasses roughly 99% of the Earth’s landmass [48].
The SRTM data were acquired in 2000, using the X-band (~3 cm wavelength) radar interferometry [49]. The original version (version 1) of the SRTM was filled with abnormalities, and there was a substantial anomaly with respect to the water bodies detected via the data. The data also had voids where elevation was not available. The second version (version 2) was improved from the first version, and the water bodies and coastlines were better defined, and the single-pixel errors were removed. However, the voids were still present in some areas. The latest version (version 3) of SRTM, which is being used worldwide, is void-filled. The voids in the SRTM data were filled by using the ASTER’s stereoscopic-imaging-derived elevations [50]. The SRTM data is also of 30 m × 30 m spatial resolution.
We used the ASTER GDEM v3 and SRTM version 3 (SRTM plus) for this study. The ASTER GDEM and SRTM DEM were downloaded from NASA Earthdata portal [51] and Opentopography website [52], respectively, and all individual tiles were mosaicked for the area of interest. Then, we clipped the mosaicked DEM to determine the exact shape of the Morony Watershed.

2.3. Methodology

We used the SRTM DEM to determine the Morony Watershed boundary. Watershed delineation method is given in [53]. Once the watershed boundary and the watershed-specific DEM were obtained, we generated the streamline raster by using flow direction tool. Then, we converted the streamline raster into a polyline shapefile to obtain the unique file identification (FID) for each streamline in the shapefile. We converted the streamline polyline shapefiles back to streamline raster with pixel values identical to the FID of each streamline. We also generated another streamline raster with all streamline pixels having the same value (1 in our case). Figure 2 shows the flowchart of creating the streamlines.
Upon creating the two streamline rasters (one with pixel value = FID and the other with pixel value = 1) and the ASTER and SRTM DEMs, we developed a MATLAB code to determine the elevation difference along the streamlines and the locations of best potential hydropower sites, based on the hydropower index (HI) as the objective function. HI is the product of elevation difference and flow accumulation and is a proxy of gravitational potential energy, a direct parameter for hydropower generation. The HI works on the following hypothesis: in headwater zones that are usually associated with hilly and mountainous areas, the flow accumulation is small, since it involves calculation of the number of pixels that water will flow into. But the elevation changes in these regions are generally large, which will generate higher elevation heads. On the contrary, in outlet zones that are usually associated with plains and flatlands, the elevation changes are small but the flow accumulation is large, since the stream flow is large and the cells are far from the watershed boundary. For hydropower generation, HI should be high enough, since it is an indicator of potential energy. Therefore, the locations of high HI should serve as the sites for potential hydropower stations. For optimum hydropower locations, we need HI to be as high as possible. Since the flow accumulation function in ArcGIS calculates the number of pixels inundated by the water, larger watersheds will yield higher HI and vice versa.
There are several diversion dams in the Morony watershed, where water was diverted to the power plant further downstream of the actual dam barrier. This diversion was constructed to obtain more head relatively closer to the dam barrier. Based on the online measurement in Google Earth analysis of the Rainbow dam, the actual power station was roughly 800 m away from the dam barrier. But Black Eagle and Ryan dams had the power stations relatively closer to the barrier. Thus, we took 600 m as the maximum diversion from the actual dam for any potential sites. The spatial resolution for ASTER and SRTM was 30 m, and 600 m diversion means that we would need to move 20 pixels farther from of the current pixel. Additionally, the direction of movement could vary depending on the path of the streamline. Thus, we considered movement of 20 pixels in every direction from the current pixel. We define this movement as ‘increasing order of pixels’ or ‘pixel order (PO)’. Thus, the movement of 20 pixels away from the current pixel is equivalent to the code having 20th order or PO = 20. This was the maximum order we set from visual analysis of the Rainbow dam; for some other cases, the order can be changed, although the order should not exceed the maximum number of rows or columns in the DEM image. Considering the nth order and the current pixel (which is always at the center), the maximum order undertook the analysis of (2n + 1)2 pixels. Hence, the code used the maximum of (2n + 1)2 surrounding pixels for calculating the elevation-difference raster. Upon obtaining the elevation-difference rasters, we multiplied the elevation-difference rasters with flow-accumulation raster and generated the hydropower index (HI) rasters. Since the flow accumulation raster does not have units, HI would bear the units of elevation difference. Therefore, the unit of HI is meters (m). Figure 3 shows the flowchart of the moving window methodology.
We used the PO and combined it with a moving window so each pixel with a streamline would be considered for analysis, the elevation difference being calculated up to 600 m away. This allowed us to obtain high heads for the potential hydropower sites. The code can automatically assume each increasing order between the first and the user-specified order. For example, when we use 20th order for our analysis, the code actually analyzes each order between order 1 ((2 × 1 + 1)2 = 32 pixels) and order 20 ((2 × 20 + 1)2 = 412 pixels) and return the elevation difference raster for each order. This enabled us to perform the sensitivity analysis and determine feasibility of our assumption to divert the flow up to 600 m. The reason we use number 20 specifically is that the SRTM and ASTER have a 30 m spatial resolution, and 600 m distance gives an integer value closer to the diversion of the Rainbow dam. After developing the elevation-difference and HI rasters, we made a MATLAB code to determine the potential hydropower sites. We used a similar moving window, but the order of the window was set in such a way that no two potential sites could be within a certain distance of each other. We call this distance the ‘Clearance’ between two sites. The Clearance is set to ensure that the flow is diverted away from the river flows back to the river safely. To see how Clearance impacts the selection of potential sites, we varied the Clearance from 1 km to 3 km. For Clearance = 1 km, we used a 34th order (1020 m) as the constant order for moving window; and for larger clearances, we multiplied this order by Clearance to obtain new orders. Thus, for Clearance = 2 km, we used 68th order, and for Clearance = 3 km, we used 102nd order. For each value of Clearance, we calculated the potential site for all POs. Additionally, to locate potential sites, we varied the HI value used for assigning a pixel as a potential hydropower site and performed a sensitivity analysis of the variation of the PO and HI. The maximum value of HI (considering both ASTER and SRTM DEM derived hydropower index) was 5.5014 × 109 m for the Morony watershed. Thus, we varied the HI from 101 m to 109 m logarithmically to see how many potential sites were located over each HI threshold in each PO. We used the same methodology with ASTER and SRTM DEMs separately, and for each DEM, 3 values of Clearances, 20 orders and 10 HI thresholds in each order yielded a total of 1200 unique cases for the Morony watershed.
At the same time, we evaluated the performance of the PMMW algorithm by assessing how many of locations of the existing hydropower sites coincided with the predicted potential sites. We downloaded the shapefile of all the existing dams in Montana from Montana Fish and Wildlife Parks (MFWP) website [44], and all existing and potential hydropower sites in Montana [45], and clipped them for the Morony Watershed. There are 256 dams and 86 hydropower sites in the watershed. However, there are only 11 hydropower stations with hydropower capacity greater than 5 MW. Since we are interested in locating optimal and large enough hydropower plant sites for economic reasons, we only used these 11 hydropower stations as the existing hydropower sites for model assessment. We also used the locations of two proposed hydropower projects in the watershed ([46]). In total, we used the locations of 13 existing and proposed hydropower sites for model evaluation. Since the downloaded shapefiles had some discrepancy, we derived our own shapefile by using the data of these projects from various web sources [46,54,55,56,57], and coordinates of the dams from Google Earth. Considering the length of dams, pinpointing their exact location is challenging. Therefore, we used the location of upstream of penstocks as the location of hydropower site, since the process of hydropower generation is initiated there. We developed another MATLAB (version R2019a) code with a different moving window to assess the number of locations of potential hydropower sites coinciding with locations of the existing hydropower sites. To prevent the discrepancy in results due to different geographical coordinates of existing and potential hydropower sites, we used the tolerance of 1 km surrounding each existing hydropower site. This means that if any new potential hydropower site location was identified within 1 km of the existing hydropower site location, the model would consider that location as the match between potential and existing hydropower site.

3. Results

We used the ASTER- and SRTM-derived DEMs to determine the elevation difference along each stream line based on the order of the moving window. We used the same DEM to generate the flow accumulation raster. We generated an HI raster to identify potential hydropower sites once the value at a specific location along the streamlines crossed a threshold. We capped the highest possible HI value at 1020 m. The maximum HI values in any integrated raster (considering both ASTER and SRTM DEM derived HI) were 5.5014 × 109 m, and the minimum value of HI was 0. We varied the PO from 1 to 20 to determine the elevation difference between the sites up to 600 m apart, and varied the HI between 101 m and 1010 m. The value of the Clearance was 1 km, 2 km, and 3 km. For each Clearance value, we had 20 orders and 10 thresholds, and therefore, 200 scenarios. Thus, for the three values of Clearance, we had 600 scenarios. Similarly, considering the two DEMs, we had a total of 1200 unique scenarios for the Morony watershed.
To assess the performance of our methodology, we used the number of potential hydropower sites that matched the existing hydropower sites, assuming they were optimized. We developed another MALAB code to determine the number of potential hydropower sites that were within the 1 km vicinity of the locations of existing hydropower plants. Instead of 1 km, we used 1020 m as the distance around existing dams or hydropower sites (due to the 30 m spatial resolution of DEMs) to determine if any potential locations were identified within the specified distance. Then, we performed the sensitivity analysis of all the datasets to determine the preferred values for Clearance, PO, and HI. This assessment analysis was performed for the ASTER- and SRTM-derived DEM datasets separately. Figure 4 and Figure 5 show the assessment analysis of matches between potential hydropower sites and existing dams or hydropower sites within 1020 m clearance for ASTER- and SRTM-derived datasets, respectively. In all the cases, the x axis denotes the PO for the moving window, and the y axis denotes the number of matches between potential and actual hydropower sites. For Figure 4a (ASTER DEM-derived matches, Clearance = 1 km), the brown, green, and dark blue plots show the number of matches with increasing PO when HI = 107 m, 108 m, and 109 m, respectively. For HI = 107 m, when PO = 1, there are 10 matches between actual and potential hydropower sites derived by the model. In both Figure 4 and Figure 5, plots for HI = 101 m to 106 m were excluded because they are nearly identical to the plot for HI = 107 m in their respective figures.
For the ASTER-derived DEM data (Figure 4), for Clearance = 1 km (Figure 4a), the maximum number of matches between potential and actual hydropower sites was 12. When HI increased to 108 m, the number of matches decreased to nine at PO = 9, and was constant afterwards. When HI increased even further to 109 m, we had only five matches. For Clearance = 2 km (Figure 4b), higher HI values yielded even fewer matches. Similar trends continued for the case of Clearance = 3 km (Figure 4c).
Figure 5 shows similar results to Figure 4 but for the SRTM DEM data. The general trend of matches was consistent for Clearance = 1 km and 2 km (Figure 5a,b). The maximum number of matches was 11 when HI = 107 m. When Clearance = 3 km (Figure 5c), maximum matches = 10 and 9 (occurred at PO = 2) for HI = 107 m and 108 m, respectively. Maximum matches = 6 (occurred at PO = 5–7) for HI = 109 m. We can see that for both DEM datasets, lower HI value yielded more matches between potential locations and existing locations, compared to the higher HI values. This is understandable and expected, as higher HI would weed out the sites with lower hydropower capacity. To generate optimal hydropower, we need an HI as high as possible since a larger product of the flow accumulation and head means greater potential to produce hydropower.
At the same time, we investigated the reason behind the difference observed between the ASTER- and SRTM DEM-derived potential hydropower sites. We performed a regression analysis between the ASTER and SRTM DEMs over streamlines to determine the degree of correlation of elevation over streamlines. The results show that the two DEMs correlated very well, as shown in Figure 6.
However, we also noticed that because all the elevation values were between 860 m (lowest elevation in watershed) to 3445 m (highest elevation in watershed), the base datum of the region itself was very high. To determine the relative difference between the ASTER and SRTM DEMs, we subtracted the SRTM DEM from the ASTER DEM to determine the relative elevation difference raster of the Morony Watershed, as shown in Figure 7, and developed a histogram of relative elevation difference, as shown in Figure 8.
From Figure 8, we can see that majority of the pixels have a relative elevation difference of less than zero, which indicates that the SRTM DEM has relatively higher elevation values than the ASTER DEM. Since each PO considers (2 × PO + 1)2 pixels to develop the elevation head and the HI rasters, even smaller relative differences in the ASTER- and SRTM-derived elevations could become the decision making factor for determining the HI at higher POs. We performed a numerical comparison between the HI rasters determined by the various moving orders used in our model. In this comparison, we found that for the two DEMs, the difference between the two HI rasters in each order was significant. Figure 9 shows the sample results for PO = 3, which was used to determine the potential hydropower sites. We only showed the results of PO = 3 to save space.

4. Discussion

Figure 4 and Figure 5 show the matches between existing and potential hydropower locations derived via the PMMW model for the ASTER and SRTM datasets, respectively. Since a higher flow accumulation and a larger elevation difference would generate potentially higher hydropower, we only considered HI = 107 m or higher to locate potential sites. Based on the trend analysis shown in Figure 4 and Figure 5, the trends kept varying with values of Clearance, HI, and PO. Additionally, the ASTER- and SRTM-derived DEM datasets showed difference in the number of potential sites. Therefore, to determine a ‘sweet spot’ of Clearance, PO, and HI, we performed an in-depth assessment of the matches determined between the ASTER- and SRTM-derived datasets for every set of values of Clearance and PO, but only for HI = 107 m or higher. Figure 10 shows the results of the analysis. In each subfigure (Figure 10a–i), the x-axis indicates the PO, while the y axis indicates the number of matches between the existing and potential hydropower sites. For instance, when the Clearance is 1 km, and the HI is 107 m (Figure 10a), the red and blue plots indicate the number of matches derived from the SRTM and ASTER DEM datasets, respectively.
When Clearance = 1 km and HI = 107 m (Figure 10a), both DEM datasets produced similar number of potential sites as the PO increased. As Clearance increased from 1 km to 3 km, while keeping the HI constant at 107 m (Figure 10a–c: top row), the SRTM DEM dataset generated more matches compared to the ASTER DEM dataset. As HI increased from 107 m to 109 m, while keeping the Clearance constant at 1 km (Figure 10a–g: left column), both datasets showed similar matches. As both Clearance and HI increased (Figure 10a–i: top left to bottom right diagonally), however, SRTM DEM generated more matches than the ASTER DEM. Except for the case of Clearance = 1 km and HI = 107 m (Figure 10a), the SRTM DEM dataset generally identified more matches between potential and existing hydropower sites than the ASTER DEM data. The SRTM DEM dataset seems to function better in locating potential hydropower sites than the ASTER DEM. For this reason, we will use only ASTER DEM for further analysis.
Now let us determine the sweet spot among Clearance, HI, and PO. We only considered the case of HI = 109 m and predicted matches for high-capacity potential hydropower sites. Figure 11 shows the results of matches with increasing PO values for Clearance = 2 km and 3 km. The results for Clearance = 1 km are identical to those for Clearance = 2 km.
From Figure 11, we can see that a Clearance of 2 km produced six matches between potential and existing hydropower sites when PO = 3. For Clearance = 3 km, the best match of six occurred for PO = 5. We need smaller clearance between dams and smaller diversion for optimal locations. Therefore, Clearance = 1 km with a maximum diversion of 90 m seems optimal for HI = 109 m. Considering the 13 locations used to assess the model performance, the model successfully predicted 6 existing locations. However, it should be noted that two of the locations used for the model assessment were proposed hydropower locations, and hydropower plants have not been built yet. Additionally, among the 11 existing hydropower plant sites, only 7 sites had a power output greater than 20 MW. We correlated the potential site locations with existing site locations, and determined that all six matches were of a hydropower station with power output greater than 20 MW (Canyon Ferry—49.8 MW, Black Eagle—21 MW, Rainbow—64 MW, Cochrane—62 MW, Ryan—72, Morony—49 MW). This means that the model predicted six out of seven, i.e., ~86% of the high-energy yielding hydropower sites. Therefore, considering the optimum hydropower potential as the goal, the model accuracy was ~86%. Table 1 shows the list of the existing hydropower plants with power output greater than 20 MW in the Morony watershed.
Based on the optimum parameters chosen, we derived 12 new potential hydropower sites for the Morony watershed. All of the new potential hydropower sites are over the Upper Missouri River, and downstream of the Canyon Ferry dam for the reason that these locations are close to the watershed outlet at Morony dam, and the elevation change along this segment of the Missouri river is the largest. Figure 12 shows the potential hydropower sites identified, along with existing locations.
We also performed a polynomial regression analysis between the nominal hydropower output of the six existing hydropower locations that matched the model prediction and HI values corresponding to the six sites. We used the actual power output as a polynomial function of HI (P = f(HI)) to a third order. Figure 13 shows the regression results between the actual power and the hydropower index. The best-fitting expression is as follows:
P = 1.11165 × 10−25 HI3 − 6.24 × 10−16 HI2 + 1.1134 × 10−6 HI − 569.27,
where P is the actual power output of the existing hydropower plants, and HI is the Hydropower Index values corresponding to the sites. The coefficient of determination (R2) of 0.8788 and p < 0.01 indicates significant correlation. This analysis is very preliminary since the number (six) of hydropower plants over 20 MW along the river is limited.
Based on the curve-fitting regression model (Equation (1)), and upon recalculating the potential hydropower outputs at the six hydropower stations, we noticed that the average projected hydropower output deviated from the actual measurement by up to 11.46%. Assuming the same 11.46% deviation for all 12 newly located potential hydropower sites, we estimated 737.86 MW ± 84.56 MW hydropower output in total, and an average power output of 61.48 MW ± 7.05 MW hydropower output for each newly located hydropower site. It should be noted that the potential hydropower sites were solely based on the optimum head and flow accumulation. The actual construction of a hydropower plant will depend on logistic accessibility, safety, and environmental and other relevant factors. However, using HI as an important parameter in locating potential optimal hydropower sites is a crucial first step, as it is cost-effective, effective, and economic. In addition, the PMMW algorithm only requires DEM of a watershed as input; therefore, it is applicable worldwide since spaceborne remotely sensed DEMs are in the public domain and free-of-charge. Model calibration will be required for each watershed, since the hydrometeorological conditions may vary significantly.
As for the difference between the ASTER and SRTM DEM datasets, from Figure 9, for PO = 3, a total of (2 × 3 + 1)2 = 49 pixels were considered to calculate the HI at each center pixel. Therefore, even the small relative elevation differences at a pixel scale in both DEMs can lead to significantly different HI values.

5. Conclusions

Locating optimal hydropower sites can lead to the construction of new effective and high-capacity hydropower plants and ultimately help tap more renewable energy from a river. Advanced remote sensing can provide global and cost-effective DEM datasets on the public domain, and hydropower development can incorporate the utilization of the free and open-source data in locating optimal sites and building high-capacity hydropower plants over a certain area. In this study, we developed a novel parsimonious model to determine the feasible locations for potential hydropower sites by integrating flow accumulation and vertical difference derived from remotely sensed DEMs. We developed a multi-dimensional moving window algorithm to consider the maximum diversion distance from the dam barrier and determined the highest heads for effective hydropower generation. We multiplied the elevation-difference rasters and flow-accumulation raster and generated HI rasters cell by cell. We performed an assessment analysis using locations of existing hydropower plants by varying the dam Clearance, order of the moving window (PO), and hydropower index (HI) and derived the number of matches between model-located and actual hydropower sites. We concluded that:
  • Based on the data-intensive assessment analysis, we found that the maximum diversion of 90 m is generally sufficient to achieve a high enough elevation head to construct new hydropower plants in the Morony watershed. At the same time, we found that the hydropower index value should be as large as possible to locate potential sites for hydropower plants of high-capacity. HI of 109 m was the highest for the Morony Watershed with 30 m spatial resolution. We also found that 1 km Clearance between two consecutive dams is sufficient. Based on the optimized Clearance, diversion and HI values and assessment using the actual hydropower plants, the model successfully located 6 out of the 7 existing high-energy hydropower plants (>20 MW) over the Upper Missouri river, along with 12 new potential hydropower sites. We developed the correlation between the maximum power generated by the existing hydropower sites and the hydropower index derived from the model, based on the third-order polynomial regression analysis, and determined the watershed-specific parameters. Based on the curve-fitting regression analysis, we found that there is 737.86 MW ± 84.56 MW potential hydropower in the Morony watershed that can be tapped.
  • Since the PMMW algorithm only requires DEM data, it does not require any site- or generator-specific parameters, such as actual streamflow, type of turbines, etc. Therefore, the model can be applied generally to any watershed, and is thus useful for remote watersheds where ground-based observations are scarce or not available at all.
  • The SRTM-derived DEM data is more suitable in locating potential hydropower sites along a river than the ASTER DEM. The ASTER- and SRTM-derived DEMs provide elevation data with good agreement on the macro-scale, but the micro-scale elevation differences between the ASTER and SRTM DEMs are significant for locating optimal hydropower plant sites.
So far, the PMMW algorithm can perform a preliminary analysis of the feasibility of hydropower plant at any location. More research can be performed by integrating various models and developing a holistic package to determine best locations for hydropower sites based on geographical, geological, environmental, economic, and logistical situations. The identification of potential hydropower sites along with their estimated daily hydropower output will greatly enhance the capabilities of the PMMW algorithm, and efforts to integrate the PMMW and other models are currently underway. Advances in remotely sensed data acquisition will continue to improve the ability of mankind to perfect the computational modeling by providing diverse datasets at high spatial and temporal scales. The application of artificial intelligence would enable the development of data-driven models that will be able to predict the future hydropower based on the current trends.

Author Contributions

Conceptualization, N.B. and X.Z.; Data curation, N.B.; Formal analysis, N.B.; Funding acquisition, X.Z.; Investigation, N.B. and X.Z.; Methodology, N.B. and X.Z.; Project administration, X.Z.; Resources, X.Z.; Software, N.B.; Supervision, X.Z.; Validation, N.B.; Visualization, N.B.; Writing—original draft, N.B.; Writing—review and editing, N.B. and X.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Aeronautics and Space Administration (NASA), under grant number G104-21-W8414.

Data Availability Statement

Data and model will be made available upon request.

Acknowledgments

The authors would like to thank Madhuri Bhagwat for her assistance in data processing. N.B. would also like to thank Montana Water Center, Montanaview and Billings Geophysical Society for awarding scholarships and fellowships to N.B. Finally, the authors would like to express their sincere gratitude towards anonymous peer-reviewers for their valuable comments and suggestions in improving the quality of this manuscript.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Singal, S.K.; Saini, R.P.; Raghuvanshi, C.S. Analysis for cost estimation of low head run-of-river small hydropower schemes. Energy Sustain. Dev. 2010, 14, 117–126. [Google Scholar] [CrossRef]
  2. Abdulkadir, T.S.; Salami, A.W.; Anwar, A.R.; Kareem, A.G. Modelling of hydropower reservoir variables for energy generation: Neural network approach. Ethiop. J. Environ. Stud. Manag. 2013, 6, 310–316. [Google Scholar] [CrossRef]
  3. Yildiz, V.; Vrugt, J.A. A toolbox for the optimal design of run-of-river hydropower plants. Environ. Model. Softw. 2019, 111, 134–152. [Google Scholar] [CrossRef]
  4. Kuriqi, A.; Pinheiro, A.N.; Sordo-Ward, A.; Garrote, L. Flow regime aspects in determining environmental flows and maximising energy production at run-of-river hydropower plants. Appl. Energy 2019, 256, 113980. [Google Scholar] [CrossRef]
  5. Vytvytskyi, L.; Lie, B. OpenHPL for Modelling the Trollheim Hydropower Plant. Energies 2019, 12, 2303. [Google Scholar] [CrossRef]
  6. Magaju, D.; Cattapan, A.; Franca, M. Identification of run-of-river hydropower investments in data scarce regions using global data. Energy Sustain. Dev. 2020, 58, 30–41. [Google Scholar] [CrossRef]
  7. Saber, H.; Mazaheri, H.; Ranjbar, H.; Moeini-Aghtaie, M.; Lehtonen, M. Utilization of in-pipe hydropower renewable energy technology and energy storage systems in mountainous distribution networks. Renew. Energy 2021, 172, 789–801. [Google Scholar] [CrossRef]
  8. Spanoudaki, K.; Dimitriadis, P.; Varouchakis, E.A.; Perez, G.A. Estimation of Hydropower Potential Using Bayesian and Stochastic Approaches for Streamflow Simulation and Accounting for the Intermediate Storage Retention. Energies 2022, 15, 1413. [Google Scholar] [CrossRef]
  9. Rojanamon, P.; Chaisomphob, T.; Bureekul, T. Application of geographical information system to site selection of small run-of-river hydropower project by considering engineering/economic/environmental criteria and social impact. Renew. Sustain. Energy Rev. 2009, 13, 2336–2348. [Google Scholar] [CrossRef]
  10. Thin, K.K.; Zin, W.W.; San, Z.M.; Kawasaki, A.; Moiz, A.; Bhagabati, S.S. Estimation of run-of-river hydropower potential in the myitnge river basin. J. Disaster Res. 2020, 15, 267–276. [Google Scholar] [CrossRef]
  11. Anderson, D.; Moggridge, H.; Warren, P.; Shucksmith, J. The impacts of ‘run-of-river’ hydropower on the physical and ecological condition of rivers. Water Environ. J. 2015, 29, 268–276. [Google Scholar] [CrossRef]
  12. Gadonneix, P.; de Castro, F.B.; de Medeiros, N.F.; Drouin, R.; Jain, C.P.; Kim, Y.D.; Ferioli, J.; Nadeau, M.J.; Sambo, A.; Teyssen, J. Water for Energy. World Energy Counc. 2010, 1–56. Available online: https://www.worldenergy.org/assets/downloads/PUB_Water_For_Energy_2010_Exec_Summary_WEC.pdf (accessed on 18 September 2023).
  13. Kuriqi, A.; Pinheiro, A.N.; Sordo-Ward, A.; Garrote, L. Water-energy-ecosystem nexus: Balancing competing interests at a run-of-river hydropower plant coupling a hydrologic–ecohydraulic approach. Energy Convers. Manag. 2020, 223, 113267. [Google Scholar] [CrossRef]
  14. Nedaei, M.; Walsh, P.R. Technical performance evaluation and optimization of a run-of-river hydropower facility. Renew. Energy 2022, 182, 343–362. [Google Scholar] [CrossRef]
  15. International Hydropower Association Annual Report 2022–23. Available online: https://assets-global.website-files.com/5f749e4b9399c80b5e421384/6446903e7ccfb14fbfbe546c_IHA-Annual-Report-2022-23.pdf (accessed on 18 September 2023).
  16. Michels-Brito, A.; Rodriguez, D.A.; Junior, W.L.; de Souza Vianna, J.N. The climate change potential effects on the run-of-river plant and the environmental and economic dimensions of sustainability. Renew. Sustain. Energy Rev. 2021, 147, 111238. [Google Scholar] [CrossRef]
  17. Fearnside, P.M. Greenhouse gas emissions from hydroelectric dams: Reply to Rosa et al. Clim. Chang. 2006, 75, 103–109. [Google Scholar] [CrossRef]
  18. Kellogg, C.H.; Zhou, X. Impact of the construction of a large dam on riparian vegetation cover at different elevation zones as observed from remotely sensed data. Int. J. Appl. Earth Obs. Geoinf. 2014, 32, 19–34. [Google Scholar] [CrossRef]
  19. Lees, A.C.; Peres, C.A.; Fearnside, P.M.; Schneider, M.; Zuanon, J.A. Hydropower and the future of Amazonian biodiversity. Biodivers. Conserv. 2016, 25, 451–466. [Google Scholar] [CrossRef]
  20. Corobov, R.; Trombitsky, I.; Matygin, A.; Onishchenko, E. Hydropower impact on the dniester river streamflow. Environ. Earth Sci. 2021, 80, 153. [Google Scholar] [CrossRef]
  21. De Faria, F.A.; Jaramillo, P.; Sawakuchi, H.O.; Richey, J.E.; Barros, N. Estimating greenhouse gas emissions from future Amazonian hydroelectric reservoirs. Environ. Res. Lett. 2015, 10, 124019. [Google Scholar] [CrossRef]
  22. Kumar, A.; Sharma, M.P.; Yang, T. Estimation of carbon stock for greenhouse gas emissions from hydropower reservoirs. Stoch. Environ. Res. Risk Assess. 2018, 32, 3183–3193. [Google Scholar] [CrossRef]
  23. Gupta, H.; Narain, H.; Rastogi, B.; Mohan, I. A study of the Koyna earthquake of December 10, 1967. Bull. Seismol. Soc. Am. 1969, 59, 1149–1162. [Google Scholar] [CrossRef]
  24. Paish, O. Micro-hydropower: Status and prospects. Proc. Inst. Mech. Eng. Part A J. Power Energy 2002, 216, 31–40. [Google Scholar] [CrossRef]
  25. British Hydropower Association. A Guide to UK Mini-Hydro Developments; The British Hydropower Association: Dorset, UK, 2005; pp. 1–36. [Google Scholar]
  26. Moiz, A.; Kawasaki, A.; Koike, T.; Shrestha, M. A systematic decision support tool for robust hydropower site selection in poorly gauged basins. Appl. Energy 2018, 224, 309–321. [Google Scholar] [CrossRef]
  27. Abdelhady, H.U.; Imam, Y.E.; Shawwash, Z.; Ghanem, A. Parallelized Bi-level optimization model with continuous search domain for selection of run-of-river hydropower projects. Renew. Energy 2021, 167, 116–131. [Google Scholar] [CrossRef]
  28. Jafari, M.; Fazloula, R.; Effati, M.; Jamali, A. Providing a GIS-based framework for Run-Of-River hydropower site selection: A model based on sustainable development energy approach. Civ. Eng. Environ. Syst. 2021, 38, 102–126. [Google Scholar] [CrossRef]
  29. Poff, N.L.; Zimmerman, J.K. Ecological responses to altered flow regimes: A literature review to inform the science and management of environmental flows. Freshw. Biol. 2010, 55, 194–205. [Google Scholar] [CrossRef]
  30. Auerbach, D.A.; Deisenroth, D.B.; McShane, R.R.; McCluney, K.E.; Poff, N.L. Beyond the concrete: Accounting for ecosystem services from free-flowing rivers. Ecosyst. Serv. 2014, 10, 1–5. [Google Scholar] [CrossRef]
  31. Gibeau, P.; Connors, B.M.; Palen, W.J. Run-of-River hydropower and salmonids: Potential effects and perspective on future research. Can. J. Fish. Aquat. Sci. 2017, 74, 1135–1149. [Google Scholar] [CrossRef]
  32. Kuriqi, A.; Pinheiro, A.N.; Sordo-Ward, A.; Bejarano, M.D.; Garrote, L. Ecological impacts of run-of-river hydropower plants—Current status and future prospects on the brink of energy transition. Renew. Sustain. Energy Rev. 2021, 142, 110833. [Google Scholar] [CrossRef]
  33. Alipour, M.H.; Kibler, K.M.; Alizadeh, B. Flow alteration by diversion hydropower in tributaries to the Salween river: A comparative analysis of two streamflow prediction methodologies. Int. J. River Basin Manag. 2022, 20, 33–43. [Google Scholar] [CrossRef]
  34. Basso, S.; Botter, G. Streamflow variability and optimal capacity of run-of-river hydropower plants. Water Resour. Res. 2012, 48, 1–13. [Google Scholar] [CrossRef]
  35. Mohor, G.S.; Rodriguez, D.A.; Tomasella, J.; Júnior, J.L. Exploratory analyses for the assessment of climate change impacts on the energy production in an Amazon run-of-river hydropower plant. J. Hydrol. Reg. Stud. 2015, 4, 41–59. [Google Scholar] [CrossRef]
  36. Beniston, M.; Stoffel, M. Assessing the impacts of climatic change on mountain water resources. Sci. Total Environ. 2014, 493, 1129–1137. [Google Scholar] [CrossRef]
  37. Majone, B.; Villa, F.; Deidda, R.; Bellin, A. Impact of climate change and water use policies on hydropower potential in the south-eastern Alpine region. Sci. Total Environ. 2016, 543, 965–980. [Google Scholar] [CrossRef]
  38. Sasthav, C.; Oladosu, G. Environmental design of low-head run-of-river hydropower in the United States: A review of facility design models. Renew. Sustain. Energy Rev. 2022, 160, 112312. [Google Scholar] [CrossRef]
  39. Kusre, B.C.; Baruah, D.C.; Bordoloi, P.K.; Patra, S.C. Assessment of hydropower potential using GIS and hydrological modeling technique in Kopili River basin in Assam (India). Appl. Energy 2010, 87, 298–309. [Google Scholar] [CrossRef]
  40. Jha, R. Total run-of-river type hydropower potential of Nepal. Hydro Nepal J. Water Energy Environ. 2010, 7, 8–13. [Google Scholar] [CrossRef]
  41. Bayazıt, Y.; Bakış, R.; Koç, C. An investigation of small scale hydropower plants using the geographic information system. Renew. Sustain. Energy Rev. 2017, 67, 289–294. [Google Scholar] [CrossRef]
  42. Alcalá, G.; Grisales-Noreña, L.F.; Hernandez-Escobedo, Q.; Muñoz-Criollo, J.J.; Revuelta-Acosta, J.D. Shp assessment for a run-of-river (Ror) scheme using a rectangular mesh sweeping approach (msa) based on gis. Energies 2021, 14, 3095. [Google Scholar] [CrossRef]
  43. Torrefranca, I.; Otadoy, R.E.; Tongco, A. Incorporating Landscape Dynamics in Small-Scale Hydropower Site Location Using a GIS and Spatial Analysis Tool: The Case of Bohol, Central Philippines. Energies 2022, 15, 1130. [Google Scholar] [CrossRef]
  44. Montana Fish and Wildlife Parks. Dams Shapefile. Available online: https://gis-mtfwp.opendata.arcgis.com/datasets/bf7118ba1a0149a78677362c436a7b61_0/explore (accessed on 10 September 2022).
  45. Montana State Library. Existing and Potential Hydropower Sites Shapefile. Available online: https://msl.mt.gov/geoinfo/ (accessed on 13 September 2022).
  46. Montana Department of Natural Resources and Conservation. Information on Existing and Potential Hydropower Stations. Available online: http://dnrc.mt.gov/divisions/water/operations/docs/dam-safety/publications/dnrc-hydropower-brochure-5-5-20.pdf (accessed on 19 November 2022).
  47. NASA Terra. Information on ASTER. Available online: https://terra.nasa.gov/about/terra-instruments/aster (accessed on 9 September 2022).
  48. NASA JPL. ASTER GDEM. Available online: https://asterweb.jpl.nasa.gov/gdem.asp (accessed on 9 September 2022).
  49. Farr, T.G.; Rosen, P.A.; Caro, E.; Cripprn, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodrigues, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
  50. NASA Jet Propulsion Laboratory. Introduction to SRTM. Available online: https://www2.jpl.nasa.gov/srtm/ (accessed on 26 September 2022).
  51. NASA Earthdata Search. Available online: https://search.earthdata.nasa.gov/search (accessed on 12 August 2020).
  52. NASA Shuttle Radar Topography Mission (SRTM). Shuttle Radar Topography Mission (SRTM) Global. Distributed by OpenTopography. 2013. Available online: https://portal.opentopography.org/datasetMetadata?otCollectionID=OT.042013.4326.1 (accessed on 14 September 2022).
  53. Trent University Library Maps, Data & Government Information Centre (MaDGIC). Watershed Delineation with ArcGIS 10.2.x. Trent University. 2014. Available online: https://www.trentu.ca/library/sites/default/files/documents/WatershedDelineation_10_2.pdf (accessed on 27 September 2022).
  54. National Hydropower Association. Names and Locations of Hydropower Stations. Available online: https://www.hydro.org/map/hydro/existing-hydropower/?state=MT (accessed on 17 November 2022).
  55. Hydroreform. Names, Locations and Power Capacity of Hydropower Stations. Available online: https://hydroreform.org/on-your-river/ (accessed on 18 November 2022).
  56. Foundation of Water and Energy Education. Names and Location of Hydropower Stations. Available online: https://fwee.org/northwest-hydropower/northwest-hydroelectric-maps-directory/ (accessed on 18 November 2022).
  57. U.S. Bureau of Reclamation. Name and Locations of Dams. Available online: https://www.usbr.gov/projects/index.php?id=284 (accessed on 18 November 2022).
Energies 16 06865 g001
Figure 1. (a) Location of Morony watershed in USA, (b) watershed elevation distribution and flow direction of Upper Missouri river; the arrow going from SW to NE indicates the general flow direction of Missouri river, and (c) location of current and proposed hydropower plants with capacity of greater than 5 MW.
Figure 1. (a) Location of Morony watershed in USA, (b) watershed elevation distribution and flow direction of Upper Missouri river; the arrow going from SW to NE indicates the general flow direction of Missouri river, and (c) location of current and proposed hydropower plants with capacity of greater than 5 MW.
Energies 16 06865 g001
Energies 16 06865 g002
Figure 2. Flowchart of obtaining watershed and streamlines.
Figure 2. Flowchart of obtaining watershed and streamlines.
Energies 16 06865 g002
Energies 16 06865 g003
Figure 3. Flowchart of the moving window methodology.
Figure 3. Flowchart of the moving window methodology.
Energies 16 06865 g003
Energies 16 06865 g004
Figure 4. Sensitivity analysis of matches between potential and actual hydropower sites based on ASTER-derived DEM using (a) Clearance of 1 km, (b) Clearance of 2 km, (c) Clearance of 3 km.
Figure 4. Sensitivity analysis of matches between potential and actual hydropower sites based on ASTER-derived DEM using (a) Clearance of 1 km, (b) Clearance of 2 km, (c) Clearance of 3 km.
Energies 16 06865 g004
Energies 16 06865 g005
Figure 5. Sensitivity analysis of matches between potential and actual hydropower sites based on SRTM-derived DEM using (a) Clearance of 1 km, (b) Clearance of 2 km, (c) Clearance of 3 km.
Figure 5. Sensitivity analysis of matches between potential and actual hydropower sites based on SRTM-derived DEM using (a) Clearance of 1 km, (b) Clearance of 2 km, (c) Clearance of 3 km.
Energies 16 06865 g005
Energies 16 06865 g006
Figure 6. Regression analysis of ASTER- and SREM-derived elevations along the streamlines in Morony watershed.
Figure 6. Regression analysis of ASTER- and SREM-derived elevations along the streamlines in Morony watershed.
Energies 16 06865 g006
Energies 16 06865 g007
Figure 7. Depiction of ASTER and SRTM DEMs and the difference between them.
Figure 7. Depiction of ASTER and SRTM DEMs and the difference between them.
Energies 16 06865 g007
Energies 16 06865 g008
Figure 8. Histogram of relative elevation difference between ASTER and SRTM DEM.
Figure 8. Histogram of relative elevation difference between ASTER and SRTM DEM.
Energies 16 06865 g008
Energies 16 06865 g009
Figure 9. Relative HI difference between the ASTER and SRTM DEMs with number of pixels for PO = 3.
Figure 9. Relative HI difference between the ASTER and SRTM DEMs with number of pixels for PO = 3.
Energies 16 06865 g009
Energies 16 06865 g010
Figure 10. Sensitivity analysis of ASTER- and SRTM-derived datasets for every Clearance and order between the HI = 107 m and 109 m.
Figure 10. Sensitivity analysis of ASTER- and SRTM-derived datasets for every Clearance and order between the HI = 107 m and 109 m.
Energies 16 06865 g010
Energies 16 06865 g011
Figure 11. Sensitivity analysis of SRTM-derived data for hydropower index of 109 m.
Figure 11. Sensitivity analysis of SRTM-derived data for hydropower index of 109 m.
Energies 16 06865 g011
Energies 16 06865 g012
Figure 12. Potential hydropower locations identified in the Morony watershed.
Figure 12. Potential hydropower locations identified in the Morony watershed.
Energies 16 06865 g012
Energies 16 06865 g013
Figure 13. Non-linear regression analysis between maximum power output of matched hydropower sites and derived hydropower index.
Figure 13. Non-linear regression analysis between maximum power output of matched hydropower sites and derived hydropower index.
Energies 16 06865 g013
Table 1. List of the high-energy yielding (>20 MW) hydropower plants in the Morony watershed.
Table 1. List of the high-energy yielding (>20 MW) hydropower plants in the Morony watershed.
Plant NameTypeCapacity (MW)Hydraulic Head (m)Successfully Located with PMMW Model?
Canyon FerryReservoir49.868.59YES
Black EagleROR2110.5YES
RainbowROR6417.98YES
CochraneROR6218YES
RyanROR7218.60YES
MoronyROR4925.91YES
HolterReservoir38.438NO
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Bhagwat, N.; Zhou, X. Locating Potential Run-of-River Hydropower Sites by Developing Novel Parsimonious Multi-Dimensional Moving Window (PMMW) Algorithm with Digital Elevation Models. Energies 2023, 16, 6865. https://doi.org/10.3390/en16196865

AMA Style

Bhagwat N, Zhou X. Locating Potential Run-of-River Hydropower Sites by Developing Novel Parsimonious Multi-Dimensional Moving Window (PMMW) Algorithm with Digital Elevation Models. Energies. 2023; 16(19):6865. https://doi.org/10.3390/en16196865

Chicago/Turabian Style

Bhagwat, Ninad, and Xiaobing Zhou. 2023. "Locating Potential Run-of-River Hydropower Sites by Developing Novel Parsimonious Multi-Dimensional Moving Window (PMMW) Algorithm with Digital Elevation Models" Energies 16, no. 19: 6865. https://doi.org/10.3390/en16196865

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop