Abstract
The determination of the critical ventilation flow rate is significant for risk control and standard development during accidental hydrogen leakage in a confined space with hydrogen-related equipment. This paper presents an analytical model for calculating the critical ventilation flow rate through the quantification and constraint solution of the ventilation effect and ventilation cost. The experimental method was used to investigate the effects of nozzle diameter and stagnation pressure on the diffusion and ventilation of horizontal hydrogen leakage in a cuboid chamber. Ventilations from 30 to 180 m3/h were carried out through the rectangular vent. It was shown that the peak concentration of the measuring point was positively correlated with the stagnation pressure and the nozzle diameter. The experimental data were used to verify the analytical model by calculating the effective ventilation time. This study demonstrates that the critical ventilation flow rate can be increased significantly at higher stagnation pressures and larger nozzle diameters. Furthermore, the discrepancy of critical ventilation flow rates under different nozzle diameters will be enhanced with the increase of stagnation pressure. For a stagnation pressure of 0.4 MPa, the critical ventilation flow rate under a 4 mm nozzle even increased by 52% relative to the 2 mm nozzle.
1. Introduction
Hydrogen is a colorless, odorless, tasteless, flammable, nontoxic gas [1]. It is the least dense gas, with a specific gravity of 0.0695. As well as an industrial raw material, hydrogen is also a multipurpose energy carrier, with an extremely high energy density of 119.96 MJ/kg [2]. As many countries transition to a low-carbon economy, hydrogen is becoming a critical fuel for transport, power generation and manufacturing applications [3]. However, hydrogen, with its very small molecular size, can easily pass through porous materials and can be absorbed by some containment materials [1,4]. This may lead to ductile loss or hydrogen embrittlement of the material and cause leakage. Additionally, this process accelerates at high temperatures. Meanwhile, hydrogen diffuses quickly (3.8-times faster than natural gas) [5]. Hydrogen has a very low ignition energy (0.019 mJ) [6] and a wide flammable limit (4–75%), which makes it easier to ignite. It is possible under some specific confined conditions to achieve combustion beyond ordinary fire. Klebanoff et al. have described such conditions needed for flame deflagration, and for deflagration to detonation transitions in a confined and cluttered space [2,7]. Therefore, during the popularization of hydrogen, accidental hydrogen release in a confined space should be taken seriously.
Ventilation is the main and effective measure for dealing with hydrogen leakage in a confined space. There are two kinds of ventilation: natural ventilation and forced ventilation (mechanical ventilation). The former mainly depends on the density discrepancy between light hydrogen and the surrounding heavy air. The latter often relies on various ventilation systems (fans, etc.) for air supply or exhausts. An overview of hydrogen diffusion and ventilation is shown in Table 1.

Table 1.
Overview of hydrogen diffusion and ventilation.
Initially, many studies focused on the effects of natural ventilation parameters on hydrogen accumulation and diffusion, including the amount, position and total area of the vents [8,11,12,13,20,21,22,23,24]. The intersecting ventilation position was considered to be the most effective configuration for reducing the hydrogen concentration in an enclosed space [12,18]. With further research, the shape of vents has been found to have a significant contribution to the ventilation efficiency. Hajji et al. [11] found that simple geometric shapes (rectangle or square) are more suitable for the ventilation of houses with sloping tops. In particular, changes in the roof angle have been proven to have a severe effect on the concentration gradient and stratification of hydrogen [10]. For ordinary residential garages, square vents bring a lower concentration value, achieving a ventilation efficiency of 56.06% [21]. When the aspect ratio of the square decreases, the intake of fresh air and the removal of hydrogen are greater. Many research works on ventilation parameters have tended to be quantitative analyses, which are more practical than qualitative analyses. The coupling effect of the position and area of a single vent on hydrogen diffusion was quantified by Zhang et al. [13]. The average hydrogen concentration of a specific cross-section was presented as a quantitative index in a three-dimensional curved surface cloud map, which explains the coupling effect. An analytical model was constructed by Prasad et al. [25] to predict air entrainment and gas stratification in hydrogen buoyant turbulence; the gas driving characteristics in the space were quantified. However, the effects of vents that depend on a fixed size and position are often greatly affected by the environment. A sensing-based adaptive risk mitigation control method was proposed by Matsuura et al. [23]; the opening and closing of the vent were controlled in real time using the concentration data.
Forced ventilation is a supplement to ventilation performance when natural ventilation cannot quickly reduce hydrogen concentration in a space. Both blower and axial fans can be used as forced ventilation equipment in hydrogen-containing spaces. Natural ventilation is always combined with forced ventilation to support fresh air inflow (cooperating with negative pressure forced ventilation) or hydrogen exhaust (cooperating with positive pressure forced ventilation) [15,17,18,22,24,26,27,28,29,30,31]. In addition to the above basic ventilation parameters, the flow rate of forced ventilation has a great influence on the dispersion of hydrogen leakage clouds. Larger flow rates and smaller blowers (with a higher flow velocity) have been proven to be effective in improving hydrogen dispersion by Xie et al. [32]. For a given leakage condition, the combustible envelope does decrease significantly with ventilation growth. However, the higher ventilation flow rate may increase the hydrogen detection difficulty for sensors [33]. Lee et al. [18] proposed a strategy of nitrogen forced ventilation to make the spatial concentration level reach the safety standard faster. Considering the disadvantages of constant ventilation flow rates, a new control strategy was proposed by Matsuura et al. [16,34,35,36] to change the exhaust flow rate in real time for fixed vent positions and areas. The hydrogen leakage modes, including the leakage rate and position, were estimated using a large amount of sensing data. Accordingly, each leakage mode corresponds to a specific acceptable exhaust flow rate. This time-varying ventilation control method has high flexibility [37]. Previous results showed that the combined action of forced ventilation and natural ventilation can effectively restrain the dangerous area and hydrogen concentration in a space. Nevertheless, as well as the study of the hydrogen diffusion and ventilation mechanism, a method for the determination of the optimal ventilation flow rate is also necessary for specified scenarios in engineering applications.
In fact, the ventilation flow rate is limited by the fan specification. With the increase of the ventilation flow rate, the cost of the corresponding fan will gradually rise, which has not been studied in previous works. The practical application of hydrogen needs to have a science-based understanding of how much ventilation is really needed so that excessive costs can be avoided. The impact of the cost needs to be considered in the configuration of the actual ventilation system. For given conditions for the vent position and vent area, this paper considers that there is a critical ventilation flow rate to balance the ventilation effect and ventilation cost.
In this paper, the critical ventilation flow rate was introduced as the optimal ventilation flow rate for hydrogen leakage in a confined space. An analytical model for the critical ventilation flow rate was proposed for the first time, which includes two calculation methods applicable to different scenarios. The model fully balances the demands of the ventilation cost and effective ventilation time. The effect of the model has been preliminarily verified by relying on experimental helium release experiments that serve as a surrogate for the closely-related hydrogen release situation. In addition to using experimental data as the model input, numerical simulation data for specific scenarios can also be used in the solution. The analytical model for the critical ventilation flow rate will provide a quantitative reference for the optimal configuration of ventilation systems in a hydrogen-related space.
2. Research Methods
Experimental Equipment and Procedures
The schematic diagram of the experimental platform is shown in Figure 1. It was used to study the evolution of hydrogen leakage, diffusion and ventilation. The experimental platform is composed of a chamber, air supply system, ventilation system and data acquisition system. The chamber was used to form a confined space for actual hydrogen leakage and diffusion. Considering the dangerous characteristics of hydrogen, the experiment was carried out using helium, which is similar to hydrogen in its physical properties. The ventilation system, including the fan and controller, was to adjust the volume flow rate. Five helium detectors in the data acquisition system were set to record the helium concentration on the jet axis.
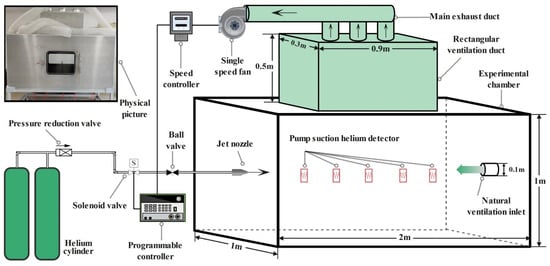
Figure 1.
Schematic diagram of the experimental platform.
The chamber was made of a 12 mm-thick aluminum plate. In Figure 1, the internal dimension of the cuboid chamber was length × width × height = 2 m × 1 m × 1 m. A movable bracket was installed at the chamber bottom, with the observation window and the door on two sides, respectively. Helium was ejected horizontally into the inner space through the nozzle installed onto the side of the chamber. The negative-pressure forced ventilation was adopted to dilute the dangerous atmosphere, while the helium was discharged through the rectangular duct at the top of the chamber and the fresh air entered from the natural ventilation inlet. The maximum ventilation flow rate of the DPT10-24B fan was 180 m3/h. In particular, a rectangular vent with a size of 0.3 m × 0.9 m was configured in the experiment. The rectangular ventilation duct (0.3 × 0.9 × 0.5) and the experimental chamber were attached through bolts. Furthermore, the connection ensured the flatness and sealing of the inner wall of the chamber. Besides this, the helium detectors worked via pumping, as shown in Figure 2. The XLA-BX-He helium detector was produced by Xinchuang Anda, with a measuring discrepancy of ±3%. Additionally, the measuring range of the detectors was from 0 to 100% VOL, with its own battery energy storage. The negative pressure was formed at the local measuring point through the external and internal suction pipes. Then, helium was inhaled into the detector to obtain the concentration value.
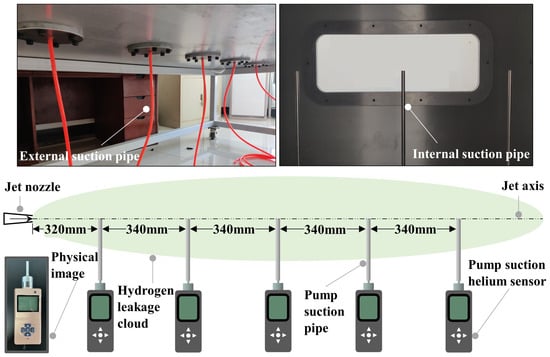
Figure 2.
Monitoring principle of the helium sensors.
In our helium-release experiments, we were mimicking a situation where upon a hydrogen leak, the safety control system is triggered to cut off the gas source. In the present study using helium, we assumed this gas release was stopped after 30 s. Thus, the hydrogen leakage was divided into two stages: high-speed leakage and ventilation disposal. The whole experimental process was organized accurately by the programmable controller. The nozzle diameter, leakage pressure and ventilation flow rate were the independent variables to be adjusted. The parameters of the experimental conditions are shown in Table 2, in which the stagnation pressure is the pressure at the outlet of the pressure-reduction valve [38]. The selected nozzle diameters were 2 and 4 mm. The ventilation ranged from 30 to 180 m3/h and the stagnation pressure ranged from 0.2 to 0.4 MPa.

Table 2.
Parameters of the experimental conditions.
3. Results and Discussion
3.1. Analytical Model of the Critical Ventilation Flow Rate
At the end of the high-speed leakage stage, considerable hydrogen had been accumulated in the space. For specific hydrogen leakage conditions, a critical ventilation flow rate is required for the ventilation to balance the ventilation effect and the ventilation cost. In this paper, the effective ventilation time was introduced to describe the ventilation effect quantitatively. The effective ventilation time was defined as the shortest time in which the characteristic concentration took to decline to below the acceptable risk level. Then, the effective ventilation time and ventilation cost were fitted into functions with the ventilation flow rate as an independent variable, respectively. Finally, the critical ventilation criterion was obtained by function coupling, and its maximum point was the critical ventilation flow rate. The main solution procedures are shown in Figure 3.
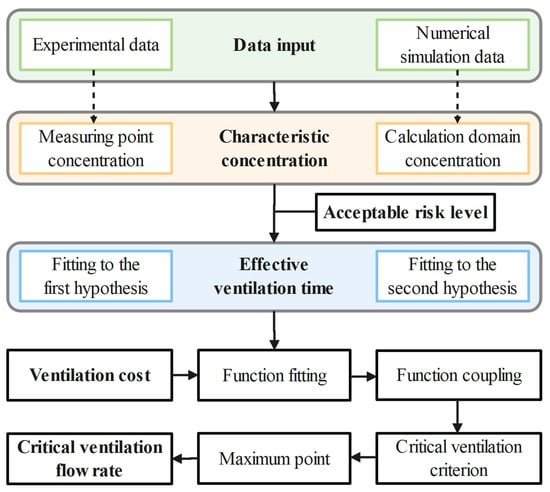
Figure 3.
The schematic diagram of the main solution procedures.
This paper used the experimental data as the data input. The characteristic concentration was identified as the concentration of the local measuring points in the space, while the acceptable risk level was set as the lower hydrogen combustion limit. The ventilation cost depended on changes in the ventilation flow rate. Then, two hypotheses were put forward. The first hypothesis is shown in Figure 4. In Figure 4a, the ventilation flow rate significantly enhanced the ventilation effect, and this enhancement was constrained at higher ventilation flow rates. The corresponding effective ventilation time verified this, going from a rapid to a slow decline. In Figure 4b, an exponential increase was shown in the variation in the ventilation cost with the ventilation flow rate; this is because increases in the higher ventilation flow rate lead to the growth of fan procurement and maintenance costs. The second hypothesis linearizes the curves in the first hypothesis. As shown in Figure 5, it was assumed that the above dependent variables were linearly correlated with the ventilation flow rate. The two hypotheses actually provided two options for determining the critical ventilation rate in the actual situation; both hypotheses were reasonable inferences. As the calculation of the critical ventilation rate is closely related to the input data and the acceptable risk level, different results may occur under different application situations and parameter settings. Therefore, it is critical to choose the most suitable of the two hypotheses according to the data variation and the analysis results.
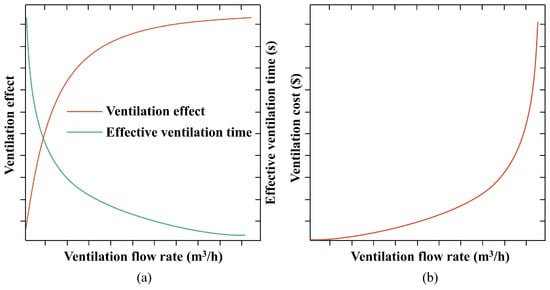
Figure 4.
Variation trend of related variables depending on ventilation flow rate (Type Ⅰ): (a) ventilation effect and effective ventilation time; (b) ventilation cost.
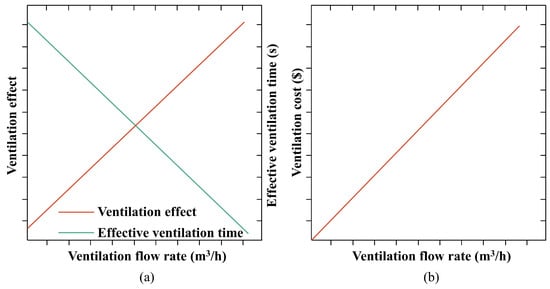
Figure 5.
Variation trend of related variables depending on ventilation flow rate (Type Ⅱ): (a) ventilation effect and effective ventilation time; (b) ventilation cost.
Considering the different units of the variables, it was necessary to perform dimensionless processing without changing the hypothetical variable correlation. For the first hypothesis, the relationship between the effective ventilation time and ventilation flow rate was approximately the natural exponential function. The dimensionless effective ventilation time was calculated as:
where is the dimensionless effective ventilation time, is effective ventilation time of each experimental condition, is the maximum ventilation time (130 s), is the ventilation flow rate, is the maximum ventilation flow rate, is the dimensionless ventilation flow rate, and and are coefficients in the natural exponential function.
The correlation between the dimensionless ventilation cost and ventilation flow rate was expressed by the exponential function as:
where is the dimensionless ventilation cost and is the base of the exponential function.
It is necessary to restrain the ventilation cost under the conditions of certain ventilation effects to obtain the critical ventilation flow rate. The determination of the critical ventilation flow rate was transformed into the problem of solving the extreme value under constraint conditions. The critical ventilation criterion was introduced to integrate the dimensionless effective ventilation time and ventilation cost:
where is the critical ventilation criterion under the first hypothesis. As shown in Figure 6, reaches the maximum value at the critical ventilation flow rate .
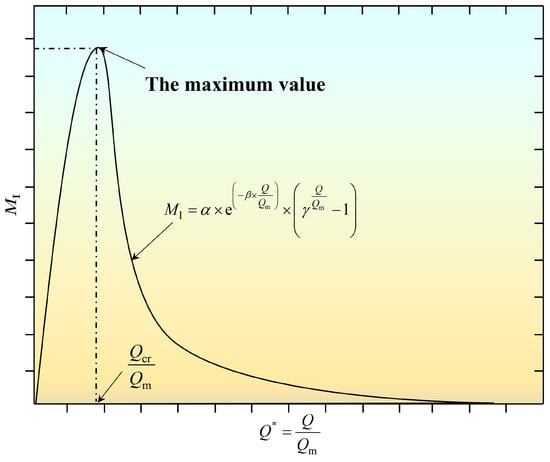
Figure 6.
The trend of the critical ventilation criterion function (Type Ⅰ).
For the second hypothesis, the dimensionless effective ventilation time was calculated as:
where and were the slope and intercept of the linear relationship in Figure 5a, respectively.
The dimensionless ventilation cost depends on the ventilation flow rate:
where is the slope of the linear relationship in Figure 5b.
under the second hypothesis is expressed as:
where . Obviously, the critical ventilation criterion is a univariate quadratic function of the dimensionless ventilation flow rate. In Figure 7, the function curve is a parabola with a downward opening. The maximum value of the function was obtained at , which was the dimensionless critical ventilation flow rate to be found. The actual critical ventilation flow rate was . was proved to be only related to the function parameters of .
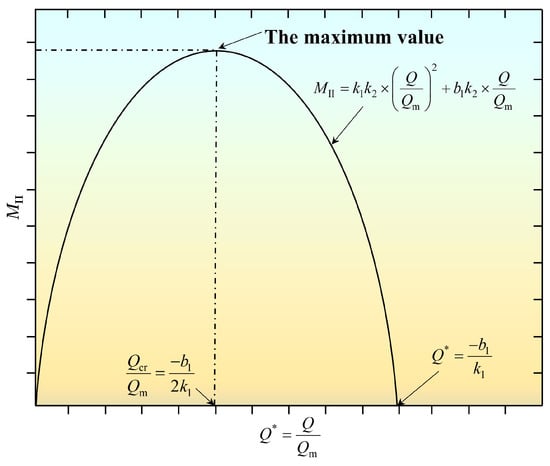
Figure 7.
The trend of the critical ventilation criterion function (Type Ⅱ).
The experimental data were discrete and could not cover all the ventilation flow rates. Neither exhaustion nor the approximation method were suitable for finding the ventilation flow rate to maximize the critical ventilation criterion. Therefore, it was recommended to fit the function parameters and predict the critical ventilation flow rate through the limited experimental data. For the experimental data (from limited monitoring points), the characteristic concentration had some limitations and could not reflect the overall level of hydrogen concentration in the space. The average concentration of the monitoring points can also be used to characterize the hydrogen risk level in a space. This could also lead to discrepancies in the results for the effective ventilation time. It is necessary to adopt the appropriate calculation method (Type Ⅰ or Type Ⅱ) according to the experimental data.
3.2. Model Verification and Case Solution
The first measuring point closest to the nozzle was selected to obtain the characteristic concentration in this study, due to the significant variation in concentration at that point. The shortest time for the concentration at this point to drop to 4% from the beginning of the ventilation was the effective ventilation time. The time history of the helium concentration at this point is shown in Figure 8. Figure 8a–c were records data obtained under the stagnation pressures of 0.2 MPa, 0.3 MPa and 0.4 MPa, respectively. In the stage of high-speed gas leakage, the volume fraction of helium increased sharply. When the ventilation system was triggered, the helium concentration continued to rise along the original trend. After a few seconds of delay, the concentration of helium dropped dramatically. This phenomenon was related to the delayed response of the helium detector. It is worth noting that the sharp decrease in helium concentration occurred almost within only 14 s after the ventilation system was started. The decreasing rate of the helium concentration gradually slowed down after 14 s of ventilation. Two effects are proposed to explain the time history: In the early stage of ventilation disposal, the cessation of the helium supply led to a sharp decrease in helium concentration. This meant that the leakage blocking effect was dominant and the concentration data of various ventilations were highly coincident at this stage. In the later stage of ventilation disposal, with the turbulent diffusion of gas, the decrease in the helium concentration at this point was effectively alleviated. At this time, it was dominated by the ventilation effect, and the concentration data of various ventilations were separated at this stage. With the growth of the ventilation flow rate, the helium concentration dropped faster in the later stage of ventilation disposal. In addition, the peak concentration of the measuring point turned out to be larger, with increases in the stagnation pressure and nozzle diameter. This was mainly due to the leap in helium leakage per unit time. In particular, under a 4 mm diameter, the helium accumulated more with the increase of stagnation pressure in the stage of high-speed leakage. However, the ventilation effect of 30 m3/h was so poor that there was an opposite trend of 30 m3/h in comparison with the other follow rates.
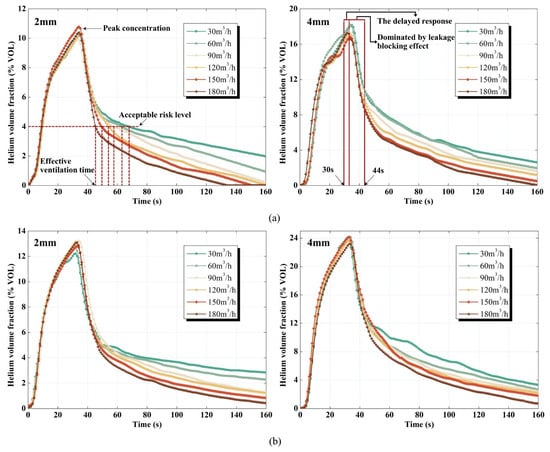
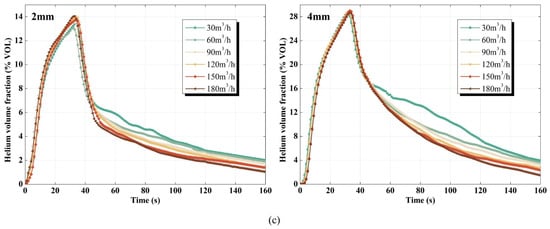
Figure 8.
Time history of helium volume fraction at the first measuring point closest to the helium release under different stagnation pressures and nozzle diameters: (a) 2 mm and 4 mm with 0.2 MPa; (b) 2 mm and 4 mm with 0.3 MPa; (c) 2 mm and 4 mm with 0.4 MPa.
With the growth in the ventilation flow rate, the effective ventilation time had been improved, which is represented by the downward decreasing distribution of the data points. Furthermore, the data at a higher pressure showed a distribution at a higher position in Figure 9, meaning a longer effective ventilation time. The relevant experimental data are sorted out into a cloud map distribution of effective ventilation time in Figure 10. For a given nozzle diameter, the stagnant pressure and ventilation flow rate had opposite effects on the effective ventilation time. The leakage at higher stagnation pressures often required a higher ventilation flow rate to improve the ventilation effect.
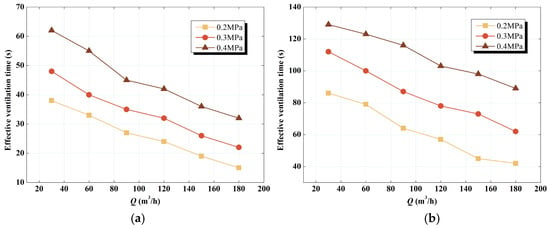
Figure 9.
Dependence of effective ventilation time on ventilation flow rate under different experimental conditions: (a) 2 mm nozzle diameter; (b) 4 mm nozzle diameter.
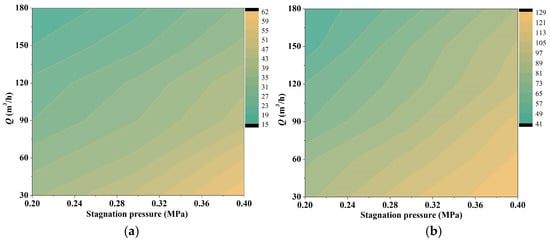
Figure 10.
Cloud map distribution of effective ventilation time under the constraint of stagnation pressure and ventilation flow rate: (a) 2 mm nozzle diameter; (b) 4 mm nozzle diameter.
There is an approximate linear correlation between the effective ventilation time and the ventilation flow rate in Figure 9, which is consistent with the second hypothesis. After dimensionless processing of the variables, the correlation was fitted as a trend line in Figure 11. The relevant parameters of the linear fitting under various experimental conditions are listed in Table 3. Furthermore, the critical ventilation flow rate was obtained. Based on the value of , this linear correlation is credible.
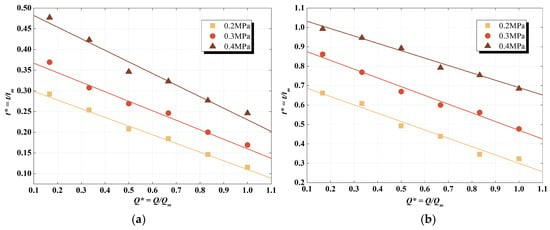
Figure 11.
Correlation fitting between dimensionless effective ventilation time and dimensionless ventilation flow rate: (a) 2 mm nozzle diameter; (b) 4 mm nozzle diameter.

Table 3.
Relevant parameters of linear fitting under various experimental conditions.
The critical ventilation flow rates under various leakage conditions are shown in Figure 12. For a given nozzle diameter, the critical ventilation flow rate expanded significantly at higher stagnation pressures. Moreover, there was a positive correlation between the critical ventilation flow rate and the nozzle diameter. For the stagnation pressure of 0.4 MPa, the critical ventilation flow rate under a 4 mm nozzle even increased by 52% relative to the 2 mm nozzle. Furthermore, a larger nozzle diameter brought a greater growth in the critical ventilation flow rate. Strictly speaking, the risk level of leakage accidents depends on the combination of the nozzle diameter and stagnation pressure. At a higher risk level, the proposed analytical model can adaptively compensate the critical ventilation flow rate to ensure that the rise in the ventilation intensity is always faster than that of the risk level.
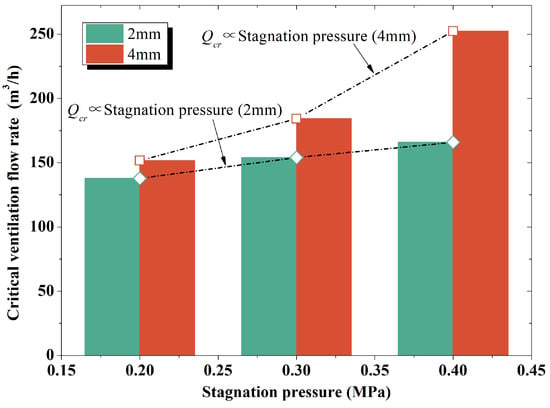
Figure 12.
Performance of critical ventilation flow rate under various leakage conditions.
4. Conclusions
The authors have carried out helium release and ventilation experiments in a confined space as a means to understand accidental releases of hydrogen. In addition, an analytical model was proposed to determine the critical ventilation flow rate under the specific leakage conditions on the basis of experimental data processing.
The accidental hydrogen leakage was divided into a high-speed leakage stage and a ventilation disposal stage. For a large amount of hydrogen accumulated during leakage, the maximization of the ventilation effect and minimization of the ventilation cost could not be achieved at the same time. Thus, in the ventilation disposal stage, it was necessary to determine a critical ventilation flow rate to balance the ventilation effect and ventilation cost. In the analytical model of the critical ventilation flow rate, the ventilation effect and ventilation cost were quantified, and two hypotheses were proposed to apply to different data. The data of the measuring point used in the study are applicable to the second hypothesis, in which depends only on the linear fitting parameters of .
The leakage blocking effect was dominant in the early stage of ventilation disposal, while the ventilation effect was dominant in the later stage, resulting in a different downward trend of concentration. With the growth of the ventilation flow rate, the helium concentration dropped faster when the ventilation effect was dominant. Furthermore, the peak concentration of the measuring point was positively correlated with the stagnation pressure and the nozzle diameter. The effective ventilation time was obtained under various ventilation conditions, which decreased linearly with the growth of the ventilation flow rate. For a given nozzle diameter, the effect of the stagnation pressure on the effective ventilation time was opposite to that of the ventilation flow rate.
After fitting the correlation between the effective ventilation time and ventilation flow rate, the formula was used to calculate the critical ventilation flow rate under different leakage conditions. The critical ventilation flow rate expanded significantly at higher stagnation pressures and with larger nozzle diameters. Additionally, the discrepancy in the critical ventilation flow rates under different nozzle diameters could be enhanced with the gradual increase of stagnation pressure. This shows that the model can adaptively compensate for the critical ventilation flow rate under the conditions of a more serious leakage. This conclusion is restricted to the second hypothesis, and may not be appropriate for the first hypothesis applied to other scenarios.
This study is critical for determining the forced ventilation flow rate to prevent hydrogen accumulation in the situation of operating a hydrogen fuel cell or installing a hydrogen tank in a confined space. When obtaining the leakage stagnation pressure of a hydrogen fuel cell or hydrogen tank, it is also necessary to know the approximate leakage diameter to determine the critical ventilation rate. The analytical model depended on experiments and numerical simulations to determine the critical ventilation flow rate under various complex conditions. However, to obtain more obvious concentration variations, only the first measuring point near the nozzle was selected as the data source. In fact, the data from local measuring points are difficult to represent the overall characteristic concentration levels of the space, which were limited in the current study. Therefore, further work will use the numerical simulation as data input to obtain more accurate output results for the critical ventilation flow rate by using the concentration parameters of the numerical calculation domain, which can better characterize the spatial concentration level. Additionally, further studies will carry out more experiments in the vertical and longitudinal directions to ensure that the analytical model is suitable for all cases of hydrogen leakage.
Author Contributions
Conceptualization, J.Y. and X.S.; methodology, J.Y. and X.S.; formal analysis, X.S.; data curation, J.S.; writing—original draft preparation, J.Y.; writing—review and editing, J.Y., J.W. and X.S.; visualization, J.Y. and J.S.; supervision, X.C., J.W. and X.S.; project administration, X.S. and X.C.; funding acquisition, X.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by “the National Key R&D Program of China” (No. 2021YFB4000901), “Hubei Province unveiling project” (No. 2022BEC024), “Guangdong Basic and Applied Basic Research Foundation” (No. 2023A1515012080), “National Natural Science Foundation of China” (No. 12302443), “the Fundamental Research Funds for the Central Universities” (No. 223161001), “Opening Fund of the Key Laboratory of Civil Aviation Thermal Disaster Prevention and Emergency of Civil Aviation University of China” (No. RZH2021-KF-05) and “Opening Fund of the State Key Laboratory of Fire Science of University of Science and Technology of China” (No. HZ2022-KF09).
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| intercept in Equation (4) [-] | maximum ventilation flow rate [m3/h] | ||
| dimensionless ventilation cost [-] | dimensionless ventilation flow rate [-] | ||
| slope in Equation (4) [-] | critical ventilation flow rate [m3/h] | ||
| slope in Equation (5) [-] | coefficient of determination [-] | ||
| critical ventilation criterion [-] | effective ventilation time [s] | ||
| critical ventilation criterion under the first hypothesis [-] | maximum ventilation time [s] | ||
| critical ventilation criterion under the second hypothesis [-] | dimensionless effective ventilation time [-] | ||
| ventilation flow rate [m3/h] | |||
| Greek symbols | |||
| coefficient in Equation (1) [-] | base of the exponential function in Equation (2) [-] | ||
| coefficient in Equation (1) [-] | |||
| Acronyms | |||
| VOL | Volume | ||
References
- Abohamzeh, E.; Salehi, F.; Sheikholeslami, M.; Abbassi, R.; Khan, F. Review of hydrogen safety during storage, transmission, and applications processes. J. Loss Prev. Process Ind. 2021, 72, 104569. [Google Scholar] [CrossRef]
- Klebanoff, L.E.; Pratt, J.W.; LaFleur, C.B. Comparison of the safety-related physical and combustion properties of liquid hydrogen and liquid natural gas in the context of the SF-BREEZE high-speed fuel-cell ferry. Int. J. Hydrog. Energy 2017, 42, 757–774. [Google Scholar] [CrossRef]
- Kozhukhova, A.E.; du Preez, S.P.; Bessarabov, D.G. Catalytic Hydrogen Combustion for Domestic and Safety Applications: A Critical Review of Catalyst Materials and Technologies. Energies. 2021, 14, 4897. [Google Scholar] [CrossRef]
- Usman, M.R. Hydrogen storage methods: Review and current status. Renew. Sustain. Energy Rev. 2022, 167, 112743. [Google Scholar] [CrossRef]
- Cadwallader, L.C.; Herring, J.S. Safety Issues with Hydrogen as a Vehicle Fuel; Idaho National Lab: Idaho Falls, ID, USA, 1999. [Google Scholar]
- Molkov, V. Hydrogen Safety Engineering: The State-of-the-Art and Future Progress; Elsevier: Oxford, UK, 2012. [Google Scholar]
- Nikolaev, A.K.; Romanov, A.V.; Zaripova, N.A.; Fetisov, V.G. Modeling of flow in field pipeline to confirm effectiveness of insertion of splitting couplings in control of rill-washing corrosion. IOP Conf. Ser. Earth Environ. Sci. 2018, 194, 082030. [Google Scholar] [CrossRef]
- Matsuura, K.; Kanayama, H.; Tsukikawa, H.; Inoue, M. Numerical simulation of leaking hydrogen dispersion behavior in a partially open space. Int. J. Hydrog. Energy 2008, 33, 240–247. [Google Scholar] [CrossRef]
- Salva, J.A.; Tapia, E.; Iranzo, A.; Pino, F.J.; Cabrera, J.; Rosa, F. Safety study of a hydrogen leak in a fuel cell vehicle using computational fluid dynamics. Int. J. Hydrog. Energy 2012, 37, 5299–5306. [Google Scholar] [CrossRef]
- Hajji, Y.; Bouteraa, M.; El Cafsi, A.; Belghith, A.; Bournot, P.; Kallel, F. Dispersion and behavior of hydrogen during a leak in a prismatic cavity. Int. J. Hydrog. Energy 2014, 39, 6111–6119. [Google Scholar] [CrossRef]
- Hajji, Y.; Bouteraa, M.; Elcafsi, A.; Belghith, A.; Bournot, P.; Kallel, F. Natural ventilation of hydrogen during a leak in a residential garage. Renew. Sustain. Energy Rev. 2015, 50, 810–818. [Google Scholar] [CrossRef]
- Lee, J.; Cho, S.; Park, C.; Cho, H.; Moon, I. Numerical analysis of hydrogen ventilation in a confined facility with various opening sizes, positions and leak quantities. In Proceedings of the 27th European Symposium on Computer-Aided Process Engineering (ESCAPE), 40A, Barcelona, Spain, 1–5 October 2017; Elsevier Science: Amsterdam, The Netherlands, 2017; pp. 559–564. [Google Scholar]
- Zhang, X.; Wang, Q.; Hou, X.; Li, Y.; Miao, Y.; Li, K.; Zhang, L. Effect of the position and the area of the vent on the hydrogen dispersion in a naturally ventilated cubiod space with one vent on the side wall. Int. J. Hydrog. Energy 2022, 47, 9071–9081. [Google Scholar] [CrossRef]
- Ryu, B.R.; Duong, P.A.; Kim, J.B.; Choi, S.Y.; Shin, J.W.; Jung, J.; Kang, H. The Effect of Ventilation on the Hazards of Hydrogen Release in Enclosed Areas of Hydrogen-Fueled Ship. J. Mar. Sci. Eng. 2023, 11, 1639. [Google Scholar] [CrossRef]
- Brennan, S.; Bengaouer, A.; Carcassi, M.; Cerchiara, G.; Evans, G.; Friedrich, A.; Gentilhomme, O.; Houf, W.; Kotchurko, A.; Kotchourko, N.; et al. Towards Minimising Hazards in Hydrogen and Fuel Cell Stationary Applications: Key Findings of Modelling and Experimental Work in the Hyper Project. In Proceedings of the 21st Hazards Symposium—Process Safety and Environmental Protection, Manchester, UK, 10–12 November 2009; Inst Chemical Engineers. pp. 399–410. [Google Scholar]
- Matsuura, K.; Nakano, M.; Ishimoto, J. Sensing-based risk mitigation control of hydrogen dispersion and accumulation in a partially open space with low-height openings by forced ventilation. Int. J. Hydrog. Energy 2012, 37, 1972–1984. [Google Scholar] [CrossRef]
- Dadashzadeh, M.; Ahmad, A.; Khan, F. Dispersion modelling and analysis of hydrogen fuel gas released in an enclosed area: A CFD-based approach. Fuel 2016, 184, 192–201. [Google Scholar] [CrossRef]
- Lee, J.; Cho, S.; Cho, H.; Cho, S.; Lee, I.; Moon, I.; Kim, J. CFD modeling on natural and forced ventilation during hydrogen leaks in a pressure regulator process of a residential area. Process Saf. Environ. Prot. 2022, 161, 436–446. [Google Scholar] [CrossRef]
- Malakhov, A.A.; Avdeenkov, A.V.; du Toit, M.H.; Bessarabov, D.G. CFD simulation and experimental study of a hydrogen leak in a semi-closed space with the purpose of risk mitigation. Int. J. Hydrog. Energy 2020, 45, 9231–9240. [Google Scholar] [CrossRef]
- Brady, K.; Sung, C.J.; T′Ien, J. Dispersion and catalytic ignition of hydrogen leaks within enclosed spaces. Int. J. Hydrog. Energy 2012, 37, 10405–10415. [Google Scholar] [CrossRef]
- Hajji, Y.; Bouteraa, M.; Elcafsi, A.; Bournot, P. Green hydrogen leaking accidentally from a motor vehicle in confined space: A study on the effectiveness of a ventilation system. Int. J. Energy Res. 2021, 45, 18935–18943. [Google Scholar] [CrossRef]
- Papanikolaou, E.; Venetsanos, A.G.; Cerchiara, G.M.; Carcassi, M.; Markatos, N. CFD simulations on small hydrogen releases inside a ventilated facility and assessment of ventilation efficiency. Int. J. Hydrog. Energy 2011, 36, 2597–2605. [Google Scholar] [CrossRef]
- Matsuura, K.; Nakano, M.; Ishimoto, J. The sensing-based adaptive risk mitigation of leaking hydrogen in a partially open space. Int. J. Hydrog. Energy 2009, 34, 8770–8782. [Google Scholar] [CrossRef]
- Huang, T.; Zhao, M.B.; Ba, Q.X.; Christopher, D.M.; Li, X.F. Modeling of hydrogen dispersion from hydrogen fuel cell vehicles in an underground parking garage. Int. J. Hydrog. Energy 2022, 47, 686–696. [Google Scholar] [CrossRef]
- Prasad, K.; Yang, J. Vertical release of hydrogen in a partially enclosed compartment: Role of wind and buoyancy. Int. J. Hydrog. Energy 2011, 36, 1094–1106. [Google Scholar] [CrossRef]
- Brennan, S.; Bengaouer, A.; Carcassi, M.; Cerchiara, G.; Evans, G.; Friedrich, A.; Gentilhomme, O.; Houf, W.; Kotchourko, A.; Kotchourko, N.; et al. Hydrogen and fuel cell stationary applications: Key findings of modelling and experimental work in the HYPER project. Int. J. Hydrog. Energy 2011, 36, 2711–2720. [Google Scholar] [CrossRef]
- Mylonopoulos, F.; Boulougouris, E.; Trivyza, N.L.; Priftis, A.; Cheliotis, M.; Wang, H.; Shi, G. Hydrogen vs. Batteries: Comparative Safety Assessments for a High-Speed Passenger Ferry. Appl. Sci. 2022, 12, 24. [Google Scholar] [CrossRef]
- Ekoto, I.W.; Houf, W.G.; Evans, G.H.; Merilo, E.G.; Groethe, M.A. Experimental investigation of hydrogen release and ignition from fuel cell powered forklifts in enclosed spaces. Int. J. Hydrog. Energy 2012, 37, 17446–17456. [Google Scholar] [CrossRef]
- Prasad, K.; Pitts, W.; Yang, J.A. Effect of wind and buoyancy on hydrogen release and dispersion in a compartment with vents at multiple levels. Int. J. Hydrog. Energy 2010, 35, 9218–9231. [Google Scholar] [CrossRef]
- Prasad, K. High-pressure release and dispersion of hydrogen in a partially enclosed compartment: Effect of natural and forced ventilation. Int. J. Hydrog. Energy 2014, 39, 6518–6532. [Google Scholar] [CrossRef]
- Matsuura, K. Effects of the geometrical configuration of a ventilation system on leaking hydrogen dispersion and accumulation. Int. J. Hydrog. Energy 2009, 34, 9869–9878. [Google Scholar] [CrossRef]
- Xie, H.; Li, X.F.; Christopher, D.M. Emergency blower ventilation to disperse hydrogen leaking from a hydrogen-fueled vehicle. Int. J. Hydrog. Energy 2015, 40, 8230–8238. [Google Scholar] [CrossRef]
- Gitushi, K.M.; Blaylock, M.L.; Klebanoff, L.E. Hydrogen gas dispersion studies for hydrogen fuel cell vessels II: Fuel cell room releases and the influence of ventilation. Int. J. Hydrog. Energy 2022, 47, 21492–21505. [Google Scholar] [CrossRef]
- Matsuura, K.; Nakano, M.; Ishimoto, J. Acceleration of hydrogen forced ventilation after leakage ceases in a partially open space. Int. J. Hydrog. Energy 2012, 37, 7940–7949. [Google Scholar] [CrossRef]
- Matsuura, K.; Nakano, M.; Ishimoto, J. Dynamic restriction mechanism for the upper limit of exhaust flow rates in the real-time sensing-based forced ventilation control of leaking hydrogen. Int. J. Hydrog. Energy 2015, 40, 4401–4411. [Google Scholar] [CrossRef]
- Matsuura, K.; Nakano, M.; Ishimoto, J. Forced ventilation for sensing-based risk mitigation of leaking hydrogen in a partially open space. Int. J. Hydrog. Energy 2010, 35, 4776–4786. [Google Scholar] [CrossRef]
- Schipachev, A.; Fetisov, V.; Nazyrov, A.; Donghee, L.; Khamrakulov, A. Study of the Pipeline in Emergency Operation and Assessing the Magnitude of the Gas Leak. Energies 2022, 15, 5294. [Google Scholar] [CrossRef]
- Nikolaev, A.K.; Samigullin, G.H.; Samigullina, L.G.; Fetisov, V.G. Non-stationary operation of gas pipeline based on selections of travel. IOP Conf. Ser. Mater. Sci. Eng. 2018, 327, 022074. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).