Abstract
The serious problem of wind power curtailment in northern China has created a pressing need to enhance the peak-shaving ability of the power system. As the main source of power supply in northern China, combined heat and power (CHP) units have significant potential for peak-shaving. Currently, the Chinese government encourages CHP plants to increase their peak-shaving capacity by installing power-to-heat (P2H) equipment. In addition, the government has implemented auxiliary service market policies to encourage CHP plants to provide peak-shaving services. In order to maximize economic benefits for CHP plants, this paper proposes an optimal configuration method of P2H equipment with the static payback time (SPT) as the objective function. Cost and income models of installing the P2H equipment are constructed by taking into account the auxiliary service market policies. The peak-shaving income model of the CHP plant is derived emphatically as a key part of the proposed method. Finally, the district heating region in Jilin province is used as a case study example. The results show that adding the P2H equipment is significantly effective in improving the peak-shaving ability of CHP units, and investing in heat pumps is more cost-effective than electric boilers. The proposed method can be applied to other northern regions relying on CHP units for central heating, providing a valuable solution to the problem of wind power curtailment in these regions.
1. Introduction
In China, the vast majority of wind power generators are installed in northern regions [1,2], posing a significant challenge to the power system’s ability to accommodate wind power. The peak-shaving ability of the power system in northern China is primarily dependent on coal-fired combined heat and power (CHP) units, as these units generate a high proportion of power. However, the CHP units are operated in a “heat-led” mode that prioritizes space-heating, and the generated electric power is dominated by thermal power, resulting in the limited flexibility of the power system [3,4]. Therefore, there is an urgent need to enhance the peak-shaving ability of CHP units to increase the flexibility of the entire system.
This study aims to investigate the optimal configuration of auxiliary heating equipment to enhance the peak-shaving ability and willingness of CHP units. The peak-shaving ability of CHP units can be improved by decoupling the constraints between thermal power and electric power through the use of auxiliary heating equipment [5]. The CHP plants are more likely to actively participate in the peak-shaving ancillary service market for potential economic benefits [6,7].
Many studies have proven that power-to-heat (P2H) equipment, especially the electric boiler (EB) and heat pump (HP), are outstanding at promoting the flexibility of CHP units [8,9,10]. Yan et al. [11] investigated the performance of four technologies with respect to the flexibility improvement of the CHP system and claimed that the EB is the most effective piece of equipment for improving renewable energy integration. Lv et al. [12] proposed an evaluation model of wind power integration in consideration of the CHP units, EB, and heat storage. It was demonstrated that the electric power produced by CHP units can be reduced to the second level of down-regulation subsidy with the help of the EB. Lei et al. [13] proposed a multi-level input/exit operation mode of heat storage electric boilers to consume the curtailed wind power for space heating in northern China. The authors claimed that the wind power accommodation capacity can be improved effectively. In addition, the contribution of the EB to better system flexibility has been confirmed in previous work [14,15,16]. The HP has also been discussed by many scholars with respect to its ability to consume surplus wind power [17]. In [18], an electrified energy system is created by combining a high temperature heat pump and wind turbine to supply super-heated steam. The operational costs and CO2 emissions are reduced effectively. In [19], HPs were utilized to relieve the heating pressure of CHP units by heating the return water in the district heating network. Dengiz et al. [20] proposed a heuristic control strategy for modulating HPs to reduce heating costs and wasted renewable energy. In [21], the authors claimed that the HP is more cost-effective than the EB for consuming surplus wind energy. Liu et al. [22] proposed new operation scheduling steady-state models of CHP units integrated with an EB and an HP for energy saving and economic benefits.
Based on the studies mentioned above, the EB and HP promote the operation flexibility of CHP units, but their economic potential is significantly affected by the capacity, efficiency, and price in the electricity market [23,24]. Therefore, it is necessary to optimize the configuration of the EB or the HP if a CHP plant expects to participate in the peak-shaving ancillary service market to achieve better economic benefits. In recent years, several studies have investigated the configuration of auxiliary heating equipment. For instance, Wang et al. [25] and Østergaard et al. [26] both discussed capacity planning of heat storage. Liu et al. [27] investigated the optimal capacity of the EB with the goal of maximizing economic and environmental benefits. Yi et al. [28] proposed a two-stage configuration strategy for distributed EB and heat storage to simultaneously enhance wind power integration and minimize construction costs. Optimal planning of electric heater and heat storage was investigated considering the capacity and distribution in a previous study [28,29]. However, very few works have researched the configuration of the EB or the HP in consideration of the peak-shaving ancillary service market, which is a key factor of the economy [30].
The aim of this study is to investigate the optimal configuration of the EB and the HP added by the CHP plant, with a focus on the economic benefits influenced by the ancillary service market policy. This paper provides a detailed analysis of the deep peak-shaving income of the CHP plant considering the peak-shaving capacity required by the power grid under different levels of wind power generation. Based on this analysis, income and cost models are developed for adding the P2H equipment. The optimal capacity of the P2H is determined with the static payback time (SPT) as the objective function. Finally, numerical case studies are carried out with the power system in Jilin province as an example, and the results verify the effectiveness of the proposed method.
The rest of this paper is organized as follows. In Section 2, the deep peak-shaving ability of the CHP plant is analyzed, and the deep peak-shaving income model is established. In Section 3, the optimal configuration model is developed with the SPT as the objective index based on the analysis of income and cost of adding the P2H equipment. Numerical studies are described in Section 4 and conclusions are presented in Section 5.
2. Deep Peak-Shaving Income of the CHP Plant
2.1. Deep Peak-Shaving Capacity Provided by the CHP Plant
The CHP unit is operated in “heat-led” mode, and its operation region is shown in Figure 1a. To meet the deep peak-shaving demand of the power grid, especially during the heating season, the Chinese government encourages CHP plants to install P2H equipment to harness the peak-shaving potential of CHP units. P2H equipment can serve as an interruptible load to participate in the peak-shaving auxiliary service market. The heat load can be jointly undertaken by the CHP units and P2H equipment:
where t is the index of scheduling time interval; N1 is the total number of CHP units; and are the output and maximum thermal power of the i-th CHP unit, respectively; is the thermal power at point C in Figure 1; , , and are the actual running power, maximum running power, and power capacity of the P2H equipment, respectively; is the coefficient of performance (COP); and is the heat load.
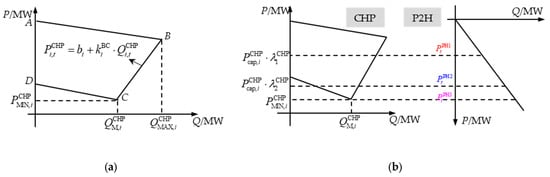
Figure 1.
(a) Operation region of a CHP unit. (b) Relationship between the electric power output of the CHP unit and the P2H equipment.
CHP units are usually operated in back-pressure mode, denoted as segment BC, to minimize electric power output during the heating season. Under this mode of operation, the electric power produced by the CHP units is expressed as follows [7,31]:
Then, the minimum electric power produced by the CHP plant can be derived as:
where and are the generated and minimum electric power of the i-th CHP unit, respectively; and are the expression coefficients; and is the approximate value of the electrothermal ratio.
From Equation (5), when the CHP units are operated at different power levels, the running power of the P2H equipment is constrained by the following equations:
where is the power capacity; and are the first base line and second base line of deep peak-shaving, respectively; and , , and are the running powers of the P2H equipment. The relationship of electric power output between the CHP unit and the P2H equipment is displayed in Figure 1b. If , then set ; if , set ; and if , set .
According to the policy of the peak-shaving ancillary service market, the available deep peak-shaving capacities of the CHP plant at the first and second levels are expressed as follows:
If , it means that the CHP plant lacks the ability to provide a deep peak-shaving service. In addition to the deep peak-shaving capacity provided by the CHP units, the increased power load, namely the power consumed by the P2H equipment, is also helpful for enhancing wind power integration. From Equations (6)–(11), the power consumed by the P2H equipment is calculated corresponding to and :
2.2. Deep Peak-Shaving Capacity Required by the Power Grid
Deep peak-shaving is required by the power grid if wind power remains excessive when coal-fired units have been operated at the first base line of deep peak-shaving and non-coal-fired units have been operated at minimum power output. The deep peak-shaving capacity required by the power grid, which is denoted as , depends on the level of wind power generation and is equal to the difference between the total produced electric power and the heat load:
where is the generated wind power; is the minimum power output of non-coal-fired units; is the power capacity of the j-th coal-fired condensing (CON) unit; N2 is the total number of CON units; is the first base line of deep peak-shaving of the CON unit; and is the electric power load. If , there is no need for deep peak-shaving.
Depending on the amount of wind power, can be divided into five scenarios. As shown in Figure 2, satisfies different conditions in each scenario:
where is the deep peak-shaving capacity at the first level available from the CON plant; and is the second base line of deep peak-shaving of the CON unit.
| Scenario 1 (S1): | |
| Scenario 2 (S2): | |
| Scenario 3 (S3): | |
| Scenario 4 (S4): | |
| Scenario 5 (S5): |
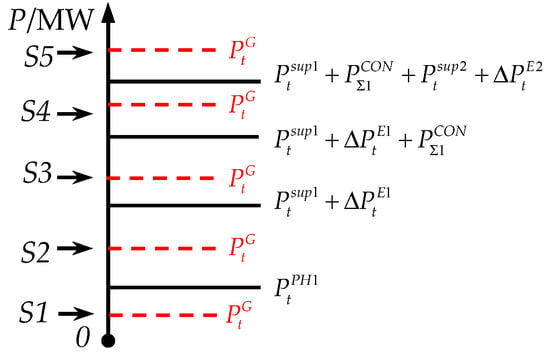
Figure 2.
under different scenarios.
2.3. Deep Peak-Shaving Income of the CHP Plant
The peak-shaving income of the CHP plant depends on the actual deep peak-shaving capacity utilized by the power grid. The income is calculated in each scenario.
S1: In this scenario, the running power of the P2H equipment is when the CHP units reduce the power output to the first base line of deep peak-shaving. In fact, there is no need for the CHP units to run at the first base line of deep peak-shaving because the power consumed by the P2H equipment is much greater than . Thus, the running power of the CHP units and the P2H equipment are regulated simultaneously to make the redundant wind power equal to zero.
The actual running power of the P2H equipment is derived as:
where and are the first and second levels of deep peak-shaving capacities actually provided by the CHP units in S1, respectively.
S2: In this scenario, is equal to the sum of the deep peak-shaving capacity provided by the CHP units and the power consumed by the P2H equipment.
The actual deep peak-shaving capacity provided by the CHP units and the actual running power of the P2H equipment are derived as follows:
S3: In this scenario, the total power capacity of the first deep peak-shaving level of the CHP units and the power capacity provided by the P2H equipment are used, and some of the power capacity in the first deep peak-shaving region of the CON units is required. The actual deep peak-shaving capacity provided by the CHP units and the actual running power of the P2H equipment are derived as follows:
S4: In this scenario, apart from the total power capacity of the first deep peak-shaving level of the CHP units and the CON units, a part of the power capacity of the second deep peak-shaving level of the CHP units is required by the power grid.
The actual deep peak-shaving capacity provided by the CHP units and the actual running power of the P2H equipment are derived as follows:
S5: In this scenario, the total deep peak-shaving capacity of the CHP units is used. The actual deep peak-shaving capacity provided by the CHP units and the actual running power of the P2H equipment are derived as follows:
Considering S1–S5, the peak-shaving income of the CHP plant is derived from the peak-shaving service provided by the CHP units and the P2H equipment. The income of each scenario is given by:
where s is the serial number of each scenario; is the transaction price of the power capacity provided by the P2H equipment on the d-th day in heating season; and and are transaction prices of the deep peak-shaving capacity at the first and second level, respectively.
On the d-th day in heating season, the total deep peak-shaving income of the CHP plant, denoted as , is given by
where is the set of scheduling time intervals of the s-th scenario.
3. Optimal Configuration of the P2H Equipment
When investors decide whether to invest in a new project, they tend to focus on the payback period [32]. Therefore, the static payback time (SPT) is used as the core index to measure the comprehensive benefit the CHP plant can obtain by installing the P2H equipment:
where is the total fixed cost; is the daily income of the P2H equipment; and D is the total number of days in the heating season. If the SPT is smaller than the lifetime, it means that a return on investment can be obtained during the life cycle of the P2H equipment. The smaller the SPT, the higher the return on investment.
3.1. Total Fixed Cost of the P2H Equipment
The total fixed cost consists of the initial construction cost and fixed maintenance cost:
where is the lifetime of the P2H equipment; is the ratio of maintenance cost; and is the unit price of the P2H equipment, including auxiliaries.
3.2. Operation Income of the P2H Equipment
The coal cost, carbon trading cost, and apportioned compensation cost of deep peak-shaving paid by the CHP plant can be reduced by installing the P2H equipment for auxiliary heating. In addition, the deep peak-shaving income is expected to increase as the CHP plant gets more opportunities to participate in the peak-shaving ancillary service market. Thus, the operation income generated by the P2H equipment during the heating season can be expressed as follows:
where , , and are the reduced coal cost, carbon trading cost, and apportioned compensation cost of deep peak-shaving, respectively; and is the increased deep peak-shaving income.
According to the operation rules of the peak-shaving ancillary service market, the reduced electric power of the CHP plant during the heating season should be compensated during other months within the same year. This means that the total electric power produced by the CHP plant remains unchanged over one year. Therefore, the saved coal cost and carbon trading cost only depend on the actual thermal power of the CHP units replaced by the P2H equipment:
where and are the unit prices of coal and carbon trading, respectively; is the carbon emission coefficient of standard coal; and is the total reduced coal for thermal power production.
The operation rules of the peak-shaving ancillary service market stipulate that the coal-fired units, which are unable to provide deep peak-shaving capacity, must share in the compensation cost of deep peak-shaving paid to other units that have fulfilled the deep peak-shaving mandate. The compensation cost shared by the CHP plant is given by
where , , , and are the daily modified power production values of the CHP units, wind power generators, solar power generators, and nuclear power generators, respectively; is the correction factor; is the set of scheduling time intervals during which ; and is the minimum power generated by the CON plant. Then, can be calculated based on Equations (50)–(52):
where and are the compensation costs apportioned by the CHP plant with and without the P2H equipment, respectively.
Next, can be calculated based on Equation (43):
where and are the deep peak-shaving incomes achieved by the CHP plant with and without the P2H equipment, respectively.
4. Case Studies
Jilin province is a typical region that depends on CHP units for central heating, and it is also a pioneering pilot area for implementing the auxiliary service market policy. Thus, a simplified region power system based on the power system of Jilin province is used in case studies. The installed capacities of the CHP unit, CON unit, wind power generator, and other types of generators are 600 MW (40.54%) (300 MW × 2), 350 MW (23.65%), 250 MW (16.89%), and 280 MW (18.92%), respectively. The typical load curves of thermal power and electric power are shown in Figure 3. The curve in Figure 3a is the typical daily load curve in winter. The heating period is from 5 October 2021 to 10 April 2022 with a total of 168 days. Curves in Figure 3b represent the average thermal load per month. The scheduling period is 24 h and each time interval is 15 min. In the northeast region, the first and second deep peak-shaving base lines of the CHP unit are 50% and 40%, respectively. The first and second deep peak-shaving base lines of the CON unit are 48% and 40%, respectively. To simplify calculations, the quotations for the deep peak-shaving services provided by the CHP units and CON units are assumed to be the same, namely, ¥/kWh and ¥/kWh. The quotation for the power capacity provided by the P2H equipment is ¥/kWh. Other parameters are listed in Table 1.
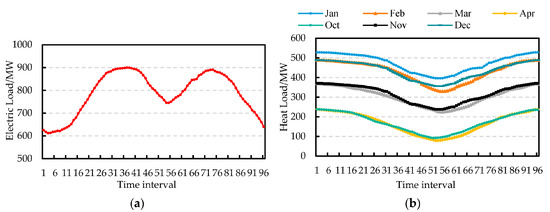
Figure 3.
(a) Electric power curves; (b) Thermal power curves.

Table 1.
Technical and economic parameters.
4.1. Analysis of the Deep Peak-Shaving Ability of the CHP Plant without the P2H Equipment
The of each time interval during the heating season is calculated according to Equation (16), and the distribution diagram is displayed in Figure 4. The color bar on the right side of Figure 4 presents the magnitude of . The demand for deep peak-shaving is mainly concentrated in time intervals of 1–21 and 86–96, namely 0:00–5:00 and 21:30–0:00. Sometimes—such as on days 90–94—redundant wind power could also be presented during time intervals of 49–63 except early morning and night. Moreover, sometimes—such as on days 163–168—there is little redundant wind power all day. There are 16,128 time intervals during the heating season, including 5696 time intervals where deep peak-shaving is needed. Overall, the demand for deep peak-shaving is high.
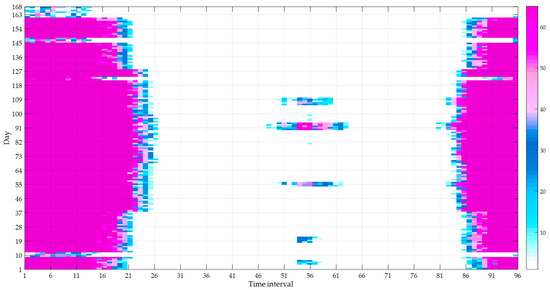
Figure 4.
of each time interval during the heating season.
In Figure 5, the deep peak-shaving income and apportioned cost of the CHP plant without P2H equipment are evaluated. For most of the time, the CHP plant has to share the deep peak-shaving compensation paid to the CON plant since the CHP units are unable to provide a deep peak-shaving service without the assistance of P2H equipment. The total apportioned cost is up to 1952.36 k¥, but the deep peak-shaving income is only 81.03 k¥. The time intervals when deep peak-shaving is required by the power grid are equal to the time intervals when the heating demand is high. The CHP units have to prioritize the need for heating, and this inflexibility causes them to lose opportunities to compete in the ancillary service market.
Figure 5.
Deep peak-shaving income and apportioned cost of the CHP plant without P2H equipment.
4.2. Analysis of Economic Benefits with Different P2H Equipment
Since the P2H equipment acts as an auxiliary heater, the CHP units can reduce their electric power and thermal power outputs. The EB and HP are recognized as excellent auxiliary heating devices. To choose the most suitable equipment for the CHP plant, comparative analysis is carried out in the following case studies. The parameters of the EB and HP are listed in Table 2.

Table 2.
Parameters of the EB and HP.
The enumeration method is used to get the optimal value. Considering that the average heat load of seven heating months is about 328 MW and the total thermal power produced by the CHP units is about 173 MW when they are running at the second base line of deep peak-shaving, the thermal power provided by the P2H equipment is 155 MW. The searching upper limits for optimizing the capacities of the EB and HP are set as 163 MW and 48 MW, respectively. To make the result more precise, the optimal value is first found with a step size of 1 MW, and then the step size is narrowed down to 0.1 MW for secondary optimization calculation.
It can be seen from Figure 6 that the optimal SPTs are 15.9 and 17.9 when the HP and EB are set as 19 MW and 67 MW, respectively. For the HP, the SPTs are less than 20 most of the time. In contrast, for the EB, the SPTs are greater than 20 most of the time. Therefore, adding the HP as an auxiliary heater may help the CHP plant achieve a better economy.
Figure 6.
(a) SPT of the HP with different capacities; (b) SPT of the EB with different capacities.
The key economic parameters are given in Table 3. Compared to the situation without P2H equipment, both the EB and the HP improve the deep peak-shaving ability of the CHP units, contributing to the reduction of apportioned compensation cost and the increase of deep peak-shaving income. Due to the larger capacity of the EB compared to the HP, the trading power and peak-shaving income of the EB in the ancillary service market are greater than those of the HP. However, the energy efficiency of the HP is significantly higher than that of the EB, and the thermal power produced by the HP is greater than that of the EB. Thus, the saved coal cost and carbon trading cost resulting from the thermal power of the CHP units replaced by the HP exceed those of the EB. Although the total operation income, denoted by , of the EB is slightly higher than that of the HP, the power capacity of the EB is much greater, leading to a higher total cost of the EB. Overall, it is preferable to invest in the HP rather than the EB.

Table 3.
Economic comparison between the EB and HP.
The optimal capacity of the HP is 19 MW when the step size is 1 MW. In order to obtain a more accurate value, the step sizes are set to 0.1 MW and 0.01 MW for second- and third-round optimizations, respectively. The search range of the second-round optimization is 18 MW to 20 MW and the results are shown in Figure 7a. The optimal value is 18.1 MW. Hence, the search range of the third-round optimization is 18 MW to 18.2 MW and the results are shown in Figure 7b. The optimal value is still 18.1 MW. Finally, the optimal capacity of the HP is set as 18.1 MW.
Figure 7.
(a) Enumeration optimization result with a step size 0.1 MW; (b) Enumeration optimization result with a step size 0.01 MW.
Due to the fact that the results obtained by the enumeration method are discrete values, there exists a certain amount of error in the results. The smaller the step size set, the smaller the error will be. As the focus of this article is on exploring the optimization model of the P2H equipment rather than the solution methods, more detailed solutions will not be provided in this case study.
4.3. Analysis of Deep Peak-Shaving Ability of the CHP Plant with an HP
The deep peak-shaving capacities of the first and second levels that can be provided by the CHP units without the P2H equipment are 33.16 kWh × 106 and 2.09 kWh × 106, respectively. In Figure 8a, the available deep peak-shaving capacities from the CHP units with different capacities of the HP are plotted. The deep peak-shaving ability of the CHP cannot be released if the capacity of the HP is too small. The deep peak-shaving capacity of the first level available from the CHP units tends to increase when the capacity of the HP is greater than 8 MW, especially when the capacity is greater than 16 MW. From Equations (7)–(9), the is much higher than 48 MW during the peak heating periods, so the deep peak-shaving capacity of the second level is not increased when the HP is set as 1–48 MW. Hence, in Figure 8b, only the deep peak-shaving capacity of the first level provided by the CHP units is plotted. The deep peak-shaving ability of the CHP is gradually improved along with the growth of the HP capacity. When the HP capacity is greater than 18 MW, the CHP units can provide deep peak-shaving capacity of the first level under different scenarios, leading to more deep peak-shaving income. Furthermore, from Figure 9, it can be seen that the deep peak-shaving capacity of the second level available from the CHP units is very limited, and is equal to zero most of the time. This is why there are no data grouped into S4 in Figure 8b.
Figure 8.
(a) Available deep peak-shaving capacity of the CHP units; (b) Actually used deep peak-shaving capacity of the first level provided by the CHP units.
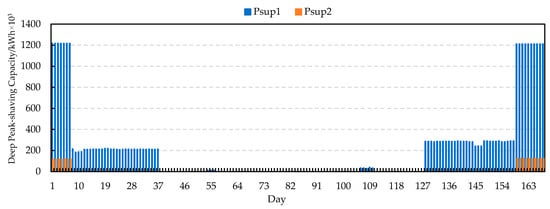
Figure 9.
Deep peak-shaving capacity can be supplied by the CHP units when the HP is 19 MW.
4.4. Analysis of Influence Factors of the Optimal P2H Equipment Capacity
From Equations (44)–(54), the optimal P2H equipment capacity is related to several factors. Considering that the correlation of the maintenance cost and the equipment price of the HP with the peak-shaving ancillary service market is weak, this paper mainly discusses the effects of the quotation, power load, heat load, and wind power variation on the SPT. The first level quotation varies from 0.1 ¥/kWh to 0.4 ¥/kWh with the step size set as 0.1 ¥/kWh. The second level quotation varies from 0.4 ¥/kWh to 1 ¥/kWh with the step size set as 0.1 ¥/kWh. The level of power load varies from −5% to +5% with the step size set as 2.5%, and the variations of the heat load and the wind power are the same. For simplicity, only one round of optimization is conducted in the subsequent analysis.
It can be concluded from Figure 10 that the SPT is positively correlated with the quotation. Even when the quotation is at a minimum, the SPT remains lower than the lifetime of the HP, indicating that the CHP plant can achieve a positive return. Thus, installing the HP to improve the peak-shaving ability will enhance the CHP plant’s participation in the peak-shaving ancillary service market. Figure 11a shows that the SPT is higher when the level of power load is lower. In contrast, Figure 12 indicates that the SPT is higher when the level of wind power is higher. This is because when the level of power load decreases or the wind power increases, the deep peak-shaving capacity required by the power grid will increase. Then, the deep peak-shaving capacity provided by the CHP plant will be utilized more, contributing to greater peak-shaving income. Therefore, the economic benefit of investing in HP is likely to increase over time due to the growing trend of wind power.
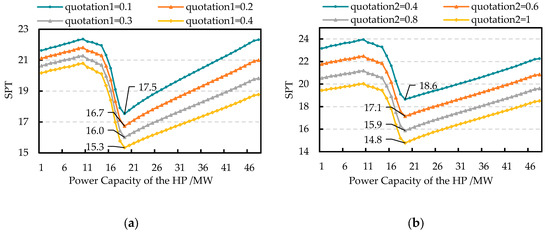
Figure 10.
(a) Effect of the first level quotation variation on the SPT; (b) Effect of the second level quotation variation on the SPT.
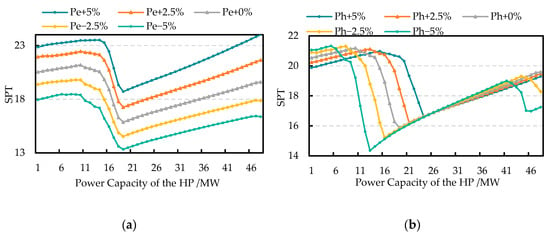
Figure 11.
(a) Effect of power load variation on the SPT; (b) Effect of heat load variation on the SPT.
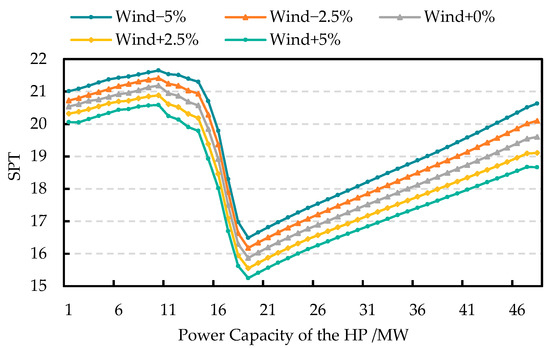
Figure 12.
Effect of wind power variation on the SPT.
In Figure 11b, we can observe a significant change in the optimal value when the heat load changes. However, in reality, the level of heat load served by the CHP plant will not change in the short term unless the scale of the CHP plant is expanded. Therefore, the impact of heat load on the optimization result can be ignored. Apart from the heat load, when other factors vary, the optimal capacity of the HP remains constant at 19 MW. Therefore, even if there is a deviation between historical and real-time data of quotation values, power load, and wind power, it will not affect the optimization results. This indicates that the optimization model proposed in this study is feasible and stable.
Currently, most areas in northern China have implemented the ancillary service market peaking. Moreover, many regions in northern China, such as Jilin province, rely on CHP units for central heating. Therefore, the proposed method is applicable to most northern regions of China.
5. Conclusions
Aiming to solve the problem of wind power curtailment caused by the limited peak-shaving ability of the power system, this study explores the feasibility of installing P2H equipment at the CHP plant side to improve the peak-shaving ability of CHP units. An optimal configuration model of the P2H equipment is established considering the economic benefits of the CHP plant in the ancillary service market. Case studies are carried out using the CHP system of Jilin province as a typical example. The impact of the P2H equipment on the peak-shaving ability and economic benefits of the CHP plant is discussed in detail with numerical studies. Several conclusions are drawn as follows:
- (1)
- It is necessary for the CHP plant to invest in P2H equipment in order to improve the peak-shaving ability of the CHP units.
- (2)
- It is beneficial for the CHP plant to invest in P2H equipment considering the economic benefits that may be obtained in the ancillary service market.
- (3)
- Due to higher energy conversion efficiency of the HP, investing in the HP has better economic benefits than investing in the EB. Furthermore, with the trend of continuous growth in wind power scale, the CHP plant will achieve higher investment returns.
- (4)
- The optimal capacity of the HP will not be affected by the deviation between historical and real-time data of quotation value, power load, and wind power. The optimization model proposed in this study is feasible and stable.
In summary, it is beneficial for the CHP plant to promote its deep peak-shaving ability and enthusiasm simultaneously by installing HP, thereby fundamentally helping to address the peak-shaving problem of the power grid.
In this study, the CHP plants in the power system are regarded as an investment portfolio. In the future, we intend to conduct advanced studies on the economic benefits of investing in HP for individual CHP plants. Details of deep peak-shaving benefits of each CHP plant will be discussed, and the optimal allocation strategy of the HP capacity among different CHP plants will be explored.
Author Contributions
Conceptualization, Y.Y. and Q.B.; methodology, Y.Y.; validation, G.Z.; investigation, Y.Y. and K.W.; writing—original draft preparation, Y.Y.; writing—review and editing, Q.B. and G.Z.; funding acquisition, C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 52177094) and the Nature Science Foundation of Hubei Province (2022CFC045).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to that most of the data comes from the power grid company and the data is required to be confidential.
Conflicts of Interest
The authors declare that they have no conflict of interest.
Nomenclature
| thermal power output of the i-th CHP unit, MW | |
| maximum thermal power output of the i-th CHP unit, MW | |
| maximum thermal power output of the i-th CHP when the unit is operated at the minimum running power, MW | |
| running power of the P2H equipment, MW | |
| maximum running power of the P2H equipment, MW | |
| power capacity of the P2H equipment, MW | |
| heat load, MW | |
| generated electric power of the i-th CHP unit, MW | |
| minimum electric power output of the i-th CHP unit, MW | |
| power capacity of the i-th CHP unit, MW | |
| running power of the P2H equipment when CHP units running at the first base line of deep peak-shaving, MW | |
| running power of the P2H equipment when CHP units running at the second base line of deep peak-shaving, MW | |
| running power of the P2H equipment when CHP units running at the minimum power output, MW | |
| deep peak-shaving capacity at the first level available from the CHP plant, MW | |
| deep peak-shaving capacity at the second level available from the CHP plant, MW | |
| deep peak-shaving capacity required by the power grid, MW | |
| generated wind power, MW | |
| minimum power output of non-coal-fired units, MW | |
| power capacity of the j-th CON unit, MW | |
| electric power load, MW | |
| deep peak-shaving capacity at the first level available from the CON plant, MW | |
| first level of deep peak-shaving capacity actually provided by CHP units, MW | |
| second level of deep peak-shaving capacity actually provided by CHP units, MW | |
| transaction price of the power capacity provided by the P2H equipment on the d-th day in heating season, ¥/kWh | |
| transaction price of the deep peak-shaving capacity at the first level, ¥/kWh | |
| transaction price of the deep peak-shaving capacity at the second level, ¥/kWh | |
| daily modified power production value of wind power generators, MW | |
| daily modified power production value of solar power generators, MW | |
| daily modified power production value of nuclear power generators, MW | |
| compensation cost apportioned by the CHP plant with the P2H equipment, ¥ | |
| deep peak-shaving income of the CHP plant with the P2H equipment, ¥ | |
| minimum power generated by the CON plant, MW | |
| t | index of scheduling time interval |
| N1 | total number of CHP units |
| coefficient of performance | |
| expression coefficient | |
| expression coefficient | |
| approximate value of the electrothermal ratio | |
| first base line of deep peak-shaving set for the CHP unit | |
| second base line of deep peak-shaving set for the CHP unit | |
| N2 | total number of CHP units |
| first base line of deep peak-shaving set for the CON unit | |
| second base line of deep peak-shaving set for the CON unit | |
| D | total days of the heating season |
| lifetime of the P2H equipment | |
| ratio of maintenance cost | |
| carbon emission coefficient of standard coal | |
| correction factor | |
| deep peak-shaving income of the CHP plant, ¥ | |
| daily income of the P2H equipment, ¥ | |
| total fixed cost of the of the P2H equipment, ¥ | |
| unit price of the P2H equipment, ¥/MW | |
| reduced coal cost, ¥ | |
| reduced carbon trading cost, ¥ | |
| reduced compensation cost of deep peak-shaving apportioned by the CHP plant, ¥ | |
| increased deep peak-shaving income, ¥ | |
| unit price of coal, ¥/ton | |
| unit price of carbon trading, ¥/ton | |
| reduced coal for thermal power production, ton | |
| daily modified power production value of CHP units, MW | |
| compensation cost apportioned by the CHP plant without the P2H equipment, ¥ | |
| deep peak-shaving income of the CHP plant without the P2H equipment, ¥ |
References
- Jin, T.; Chen, X.; Wen, J.; Wu, Q.; Bai, L.; Liu, Y.; Cao, Y. Improved ramping and reserve modeling of combined heat and power in integrated energy systems for better renewable integration. IEEE Trans. Sustain. Energy 2021, 13, 683–692. [Google Scholar] [CrossRef]
- Chen, H.; Chen, J.; Han, G.; Gui, Q. Winding down the wind power curtailment in China: What made the difference? Renew. Sustain. Energy Rev. 2022, 167, 112725. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, H.; Chen, L.; Chen, C.; Wu, J. Optimal operation of the combined heat and power system equipped with power-to-heat devices for the improvement of wind energy utilization. Energy Sci. Eng. 2019, 7, 1605–1620. [Google Scholar] [CrossRef]
- Zhao, P.; Gou, F.; Xu, W.; Shi, H.; Wang, J. Multi-objective optimization of a hybrid system based on combined heat and compressed air energy storage and electrical boiler for wind power penetration and heat-power decoupling purposes. J. Energy Storage 2023, 58, 106353. [Google Scholar] [CrossRef]
- Ma, Y.F.; Yang, Y.; Mi, Z.Q. Accommodation of curtailed wind power by electric boilers equipped in different locations of heat-supply network for power system with CHPs. J. Mod. Power Syst. Clean Energy 2021, 9, 930–939. [Google Scholar] [CrossRef]
- Tian, L.; Xie, Y.; Hu, B.; Liu, X.; Deng, T.; Luo, H.; Li, F. A deep peak regulation auxiliary service bidding strategy for CHP units based on a risk-averse model and district heating network energy storage. Energies 2019, 12, 3314. [Google Scholar] [CrossRef]
- Zhang, Z.; Cong, W.; Liu, S.; Li, C.; Qi, S. Auxiliary service market model considering the participation of pumped-storage power stations in peak shaving. Front. Energy Res. 2022, 10, 745. [Google Scholar] [CrossRef]
- Yu, Y.J.; Chen, H.K.; Chen, L. Comparative study of electric energy storages and thermal energy auxiliaries for improving wind power integration in the cogeneration system. Energies 2018, 11, 263. [Google Scholar] [CrossRef]
- Zhang, D.; Hu, Y.; Gao, Y. Flexibility improvement of CHP unit for wind power accommodation. J. Mod. Power Syst. Clean Energy 2021, 10, 731–742. [Google Scholar] [CrossRef]
- Zhao, S.; Ge, Z.; Sun, J.; Ding, Y.; Yang, Y. Comparative study of flexibility enhancement technologies for the coal-fired combined heat and power plant. Energy Convers. Manag. 2019, 184, 15–23. [Google Scholar] [CrossRef]
- Yan, R.; Wang, J.; Huo, S.; Zhang, J.; Tang, S.; Yang, M. Comparative study for four technologies on flexibility improvement and renewable energy accommodation of combined heat and power system. Energy 2023, 263, 126056. [Google Scholar] [CrossRef]
- Lyu, Q.; Gong, H.; Yang, N.; Xu, X.; Zhang, N.; Wang, H. An evaluation method of wind power integration in power systems with flexible combined heat and power plant. Energies 2019, 12, 4129. [Google Scholar] [CrossRef]
- Lei, Z.; Wang, G.; Li, T.; Cheng, S.; Yang, J.; Cui, J. Strategy analysis about the active curtailed wind accommodation of heat storage electric boiler heating. Energy Rep. 2021, 7, 65–71. [Google Scholar] [CrossRef]
- Lepiksaar, K.; Mašatin, V.; Latõšov, E.; Siirde, A.; Volkova, A. Improving CHP flexibility by integrating thermal energy storage and power-to-heat technologies into the energy system. Smart Energy 2021, 2, 100022. [Google Scholar] [CrossRef]
- Han, X.; Wang, F.; Tian, C.; Xue, K.; Zhang, J. Economic evaluation of actively consuming wind power for an integrated energy system based on game theory. Energies 2018, 11, 1476. [Google Scholar] [CrossRef]
- Liu, B.; Li, J.; Zhang, S.; Gao, M.; Ma, H.; Li, G.; Gu, C. Economic dispatch of combined heat and power energy systems using electric boiler to accommodate wind power. IEEE Access 2020, 8, 41288–41297. [Google Scholar] [CrossRef]
- Bloess, A.; Schill, W.P.; Zerrahn, A. Power-to-heat for renewable energy integration: A review of technologies, modeling approaches, and flexibility potentials. Appl. Energy 2018, 212, 1611–1626. [Google Scholar] [CrossRef]
- Walden, J.V.; Bähr, M.; Glade, A.; Gollasch, J.; Tran, A.P.; Lorenz, T. Nonlinear operational optimization of an industrial power-to-heat system with a high temperature heat pump, a thermal energy storage and wind energy. Appl. Energy 2023, 344, 121247. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Z.; Zhao, J.; Zheng, J. Improving wind power integration by a novel short-term dispatch model based on free heat storage and exhaust heat recycling. Energy 2018, 160, 940–953. [Google Scholar] [CrossRef]
- Dengiz, T.; Jochem, P.; Fichtner, W. Demand response with heuristic control strategies for modulating heat pumps. Appl. Energy 2019, 238, 1346–1360. [Google Scholar] [CrossRef]
- Blarke, M.B. Towards an intermittency-friendly energy system: Comparing electric boilers and heat pumps in distributed cogeneration. Appl. Energy 2012, 91, 349–365. [Google Scholar] [CrossRef]
- Liu, M.; Wang, S.; Yan, J. Operation scheduling of a coal-fired CHP station integrated with power-to-heat devices with detail CHP unit models by particle swarm optimization algorithm. Energy 2021, 214, 119022. [Google Scholar] [CrossRef]
- Treshcheva, M.; Anikina, I.; Sergeev, V.; Skulkin, S.; Treshchev, D. Selection of heat pump capacity used at thermal power plants under electricity market operating conditions. Energies 2021, 14, 226. [Google Scholar] [CrossRef]
- Liu, M.; Ma, G.; Wang, S.; Wang, Y.; Yan, J. Thermo-economic comparison of heat–power decoupling technologies for combined heat and power plants when participating in a power-balancing service in an energy hub. Renew. Sustain. Energy Rev. 2021, 152, 111715. [Google Scholar] [CrossRef]
- Wang, Z.; Gu, Y.; Lu, S.; Zhao, Z. Optimization of thermocline heat storage tank capacity for combined heat and power plant based on environmental benefits: Scenarios for China. J. Energy Storage 2023, 57, 106303. [Google Scholar] [CrossRef]
- Østergaard, P.A.; Andersen, A.N. Optimal heat storage in district energy plants with heat pumps and electrolysers. Energy 2023, 275, 127423. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, G.; Huang, B.; Liu, W. Optimum electric boiler capacity configuration in a regional power grid for a wind power accommodation scenario. Energies 2016, 9, 144. [Google Scholar] [CrossRef]
- Yi, Z.K.; Xu, Y.L.; Li, Z.M. Optimal configuration of distributed heat sources to promote the wind power penetration in combined heat and power system. J. Renew. Sustain. Energy 2019, 11, 036302. [Google Scholar] [CrossRef]
- Gou, X.; Chen, Q.; Hu, K.; Ma, H.; Chen, L.; Wang, X.-H.; Qi, J.; Xu, F.; Min, Y. Optimal planning of capacities and distribution of electric heater and heat storage for reduction of wind power curtailment in power systems. Energy 2018, 160, 763–773. [Google Scholar] [CrossRef]
- Li, L.; Wang, Y.; Wu, Q.; Li, J.; Wang, D.; Han, M. Analysis on optimal capacity and parameter configuration of electrode type boiler for improving wind power consumption capacity. In Proceedings of the 2022 IEEE 4th International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 29–31 July 2022; pp. 768–772. [Google Scholar]
- Nielsen, M.G.; González, J.M.M.; Madsen, H.; Zugno, M.; Boldt, J.; Engberg, T.; Nielsen, H.A. Probabilistic forecasting and optimization in CHP systems. Master’s Thesis, Department of Applied Mathematics and Computer Science, Technical University of Denmark, Lyngby, Denmark, 2014. [Google Scholar]
- Lv, Q.; Du, S.Y.; Liu, L. Economic Analysis on Peak Shaving of Combined Heat and Power Plant with Electric Boilers in Auxiliary Service Market of Northeast China. Autom. Electr. Power Syst. 2019, 20, 49–56. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).