1. Introduction
Differential Reynolds stress models (DRSM), which emerged in the middle of the 20th century [
1,
2], currently represent a very promising approach to turbulence modeling [
3]. The main reasons for this are the recognition of restrictions imposed by the eddy viscosity models and DRSMs’ potential for improved prediction of flow separation, which is often relevant in practical applications [
4].
The first DRSM to acquire widespread popularity was the Launder–Reece–Rodi (LRR) model [
5,
6]. The LRR model assumes a common approximation of the redistribution term, which is linear concerning the Reynolds stress tensor. A more general approximation that is quadratic with respect to the Reynolds stress tensor was suggested by Lumley [
7], and its particular case simplification was proposed in the Speziale–Sarkar–Gatski (SSG) model [
8]. Combining these two models and transitioning from the equation for the dissipation rate of turbulence kinetic energy
to an equation for the turbulence frequency
led to the creation of the SSG/LRR-
ω model [
9,
10]. It became popular due to adopting concepts from a successful eddy viscosity model SST [
11], a relatively simple model formulation and a reasonable level of accuracy in practical external aerodynamic applications [
12]. It is worth noting that although the SSG/LRR-
ω model suggests integrating the equations to wall and setting the no-slip boundary condition (with a demand that the first near-wall cell height correspond to
in law-of-the-wall variables), this model cannot be considered accurate for detailed description of the near-wall portion of the boundary layer (such models are called “low-Reynolds-number models”). The model does not contain near-wall corrections to the redistribution term, and the dissipation rate tensor is assumed to be isotropic. This leads to substantial deviations of the Reynolds stress
(the overbar denotes a Reynolds average and
is a fluctuating part of the
-th velocity vector component) and
profiles from reference data.
Although the development of low-Reynolds-number DRSMs is a relatively niche research area, several prominent papers have been published on this topic. A large amount of work in this direction was put in by the Manchester University group led by B.E. Launder. In a span of two decades (1978–1998), they described several models in papers [
13,
14,
15,
16] and presented the final results of their research in the paper by T.J. Craft [
17] in 1998. A group led by K. Hanjalić has been developing their low-Reynolds-number model since 1994; they proposed two models [
18,
19] and summarized their findings in the work of Jakirlić and Hanjalić [
20], which was devoted to their JHh model of 2002. Subsequently, the model [
20] became a basis for more practice-oriented low-Reynolds-number models JHh-v1, 2, 3 [
10,
21,
22], in which efforts were made to empirically improve the prediction of separated flows and to account for the large-scale unsteadiness. The JHh model formulation was also used in the JH-
[
23] and Jakirlić & Maduta [
24] models, in which the
-equation is utilized, leading to improved computational stability. Another direction of low-Reynolds-number DRSMs is being developed by the group of G.A. Gerolymos (Pierre and Marie Curie University, Paris) [
25,
26]; their latest developed model, GLVY [
27], was published in 2014.
The creation of hybrid Reynolds-averaged Navier–Stokes/Large Eddy Simulation (RANS/LES) methods is of particular interest in which a RANS turbulence model is only used in a thin near-wall layer [
28]. In contrast, the outer part of the boundary layer and freestream turbulent regions are modeled within the LES framework, meaning that the large-scale turbulence is resolved. Only the unresolved small-scale turbulence is described by a subgrid-scale model. The RANS region being constricted to a thin sublayer (of about
typically, where
is the boundary layer thickness) facilitates the calibration process. Notably, outer flow conditions (e.g., the presence of an adverse pressure gradient) have less influence on the mean characteristics of this sublayer than on the outer layer [
29]. This allows us to perform the calibration using only basic flows, such as the developed channel flow, on which high-quality modern data from direct numerical simulation (DNS) is available. There are currently several popular hybrid RANS/LES methods, among which are Improved Delayed Detached Eddy Simulation (IDDES) [
28], Partially Averaged Navier–Stokes (PANS) [
30], Partially Integrated Transport Modeling (PITM) [
31], and Stress-Blended Eddy Simulation (SBES) [
32]. Most of them are based on eddy viscosity turbulence models, which simplifies their formulation and ensures computational robustness. DRSM-based hybrid RANS/LES methods are still at an early stage of their development.
The paper modifies one of the low-Reynolds-number DRSM models to create a finely tuned RANS sublayer model for hybrid RANS/LES simulations. To the best of the authors’ knowledge, no studies in the literature are devoted to this problem. The papers on DRSMs cited above focus on developing “general purpose” models. Such models were calibrated against a wide range of benchmark flows, inevitably making their performance in a near-wall layer the result of compromises. Furthermore, the calibration of these models mostly relied on early low-Reynolds-number DNS results of the 1990s. In contrast, in the current paper, the calibration is performed using only one type of flow, namely the turbulent channel flow, and the reference data are more recent, with higher Reynolds number values.
The Jakirlić & Maduta model [
24] was taken as a baseline model. Aside from the improved computational stability mentioned above, additional advantages of this model over the other models include using a relatively simple linear tensor model of the redistribution term and the extra attention given to the dissipation rate tensor modeling. The models developed by the Manchester University team and the Gerolymos team have a much more complex formulation and may be investigated in future work if necessary.
The paper is organized as follows. In
Section 2, the baseline Jakirlić & Maduta DRSM [
24] is formulated, the coefficient calibration technique is described, and the calibration results are presented.
Section 3 compares the modified model to the baseline one in the pure RANS regime using three benchmark flows. Two of them do not include strong pressure gradients, and the modified model is shown to perform better than the baseline. The third flow features a separation from a smooth surface, and the modified model fails to replicate the mean flow field. However, as shown in
Section 4, the same model performs remarkably well in the same flow when applied as part of a hybrid RANS/LES method. The results are discussed in
Section 5.
2. Model Formulation and Coefficient Calibration
2.1. Baseline Model
Differential Reynolds stress models contain six equations for the independent stress tensor components. With density
and the kinematic viscosity
assumed constant, these equations can be written as follows:
where
is the
-th mean velocity component,
is the pressure fluctuation. Hereinafter, a summation of the repeated indices is assumed. These equations include the production term
(does not require closure in DRSMs), the redistribution term
, responsible for the redistribution of energy between velocity fluctuations in different directions, the “homogeneous” dissipation rate tensor
[
20], turbulent transport by fluctuating velocity
and turbulent transport by fluctuating pressure
(the sum of these fluxes will be denoted
). Let us additionally define the turbulence kinetic energy
, its production and “homogeneous” dissipation rates
and
correspondingly, the turbulent Reynolds number
, the stress-anisotropy tensor
and its second and third invariants
and
, and Lumley’s flatness parameter
. Similarly, one may define an anisotropy tensor for the dissipation rate
, its invariants
and
, and the parameter
.
The Jakirlić & Maduta model (denoted as “conventional ‘steady’ RSM model” in [
24]) aims to reproduce the term-by-term Reynolds stress balance in the near-wall region. The model was developed from the JHh model [
20], based on the research conducted in the 1990s to early 2000s and calibrated using the experimental data and DNS results from this timeframe. Inevitably, this means the data they used was at low Reynolds numbers, typically at
from 180 to 590 where
is the friction velocity,
is the wall shear stress,
is the dynamic viscosity and
is the channel half-height or the boundary layer thickness.
The Jakirlić & Maduta model [
24] uses the following closures:
where
is the turbulence eddy viscosity;
where empirical coefficients and functions
,
,
,
,
,
,
are used,
is the distance to the nearest wall,
is the
-th component of the normal vector
(note that
is separated into several parts which correspond to different physical processes:
is the “slow” term which represents a return of the turbulence to an isotropic state in the absence of mean velocity gradients,
is the “rapid” term which represents the effect of mean velocity gradients on the Reynolds stresses, and
and
are near-wall corrections to
and
correspondingly);
Equation (4) can be rewritten as
, which reveals that the dissipation-anisotropy is linearly related to the stress-anisotropy through the empirical function
. This function in the considered model equals
. It should be noted that a dependency of
on
makes Equation (4) implicit. Therefore, it should be solved iteratively. In the Jakirlić & Maduta model [
24], the value of
is calculated as
, where
is the characteristic turbulence frequency (another interpretation is the inverse turbulence time scale) obtained from the following equation:
In the above, represents the additional production of due to the second velocity derivatives, represents a correction which eliminates the streamline back-bending in the reattachment region, is the turbulence length scale.
The expressions above contain the following empirical constants:
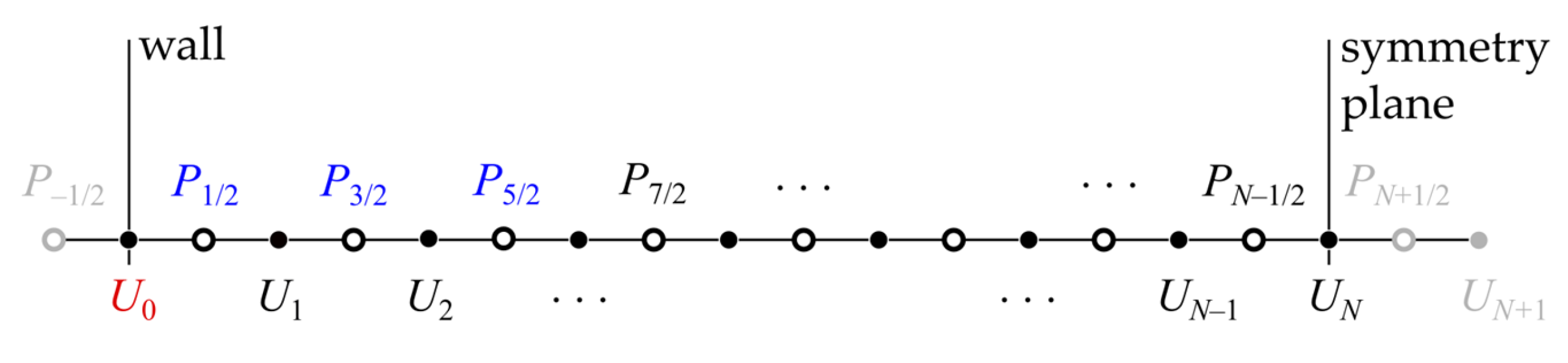
2.2. Wall Boundary Conditions
The boundary conditions at the wall are prescribed the following way. The no-slip condition demands that all the Reynolds stress tensor components be zero at the wall:
. It is known that
asymptotically tends to
as
[
33], where
and
. This asymptotic behavior may be used to specify
in one or (as recommended in [
34]) several off-wall grid points. The current paper analyzed the behavior of
in DNS data of channel flow at
[
35]. Using the least squares method, a more accurate approximation for the asymptotic behavior was found:
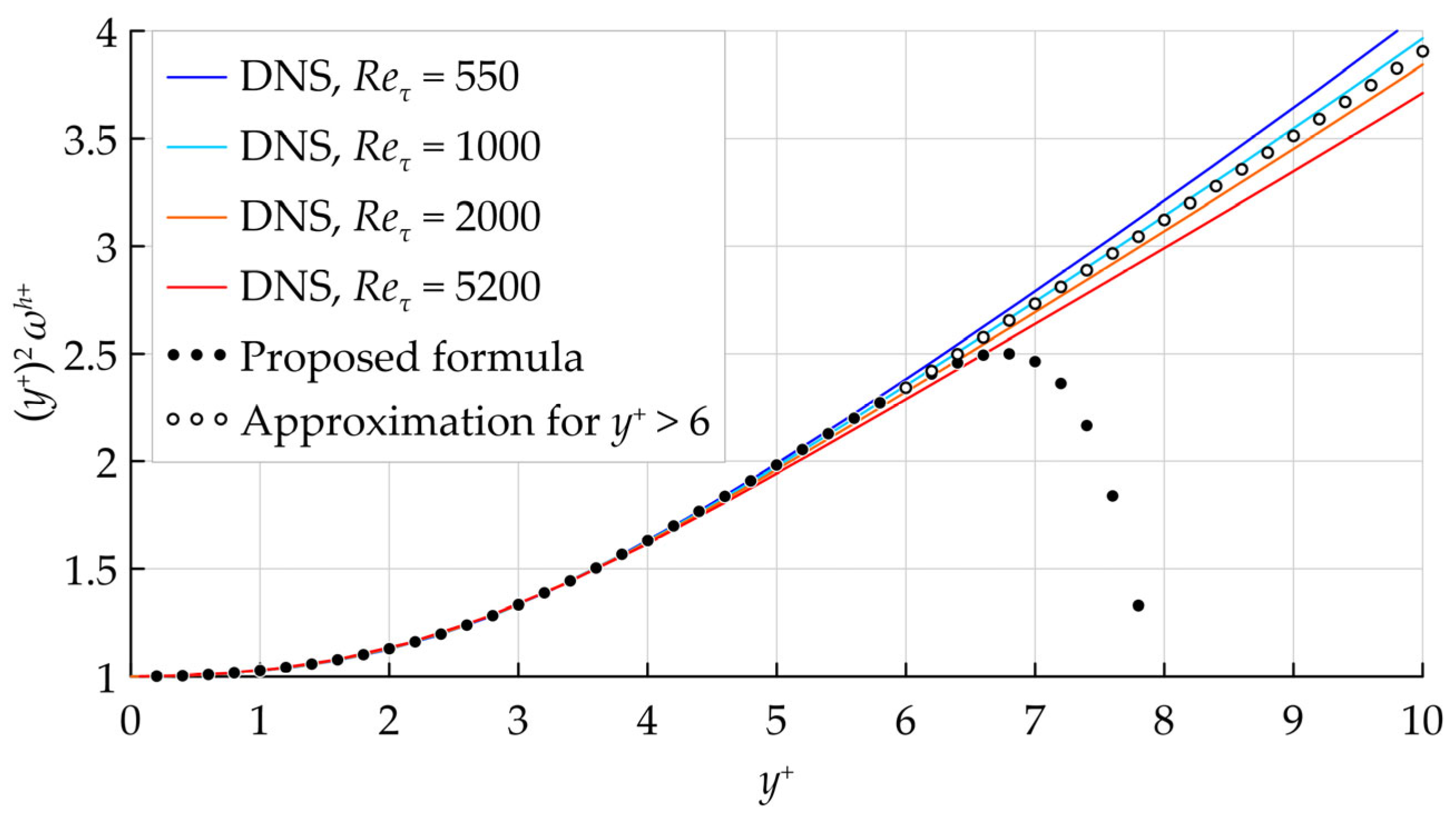
This equation corresponds well to the DNS data for
, as seen in
Figure 1. This boundary condition was used in all following simulations,
was prescribed at the first three off-wall grid points.
Note that Equation (7) is designed for use only within the viscous sublayer. If the value of
exceeds 6, some other form of expression for
should be adopted, e.g.,
, which is shown in
Figure 1 with open symbols. In the simulations presented below, however,
was always lower than 6 at the points where
was prescribed, which allowed to use the Equation (7) without any extensions.
2.3. Model Recalibration Method
A recalibration of the Jakirlić & Maduta model [
24] was done by an
a posteriori procedure, to improve the correspondence of the developed channel flow simulation results to the DNS data [
35]. In contrast to an
a priori calibration, in which DNS data is substituted into the model relations, during the
a posteriori calibration, the model is used at each step of the procedure for the chosen flow simulation, which allows the estimate of its accuracy and ensures computational stability.
The
a posteriori model calibration was conducted the following way. Sixteen model coefficients were varied. Their original values are stated above (see (6)). Let us denote them as
,
. Sets of coefficients can be viewed as points in an N-dimensional space. An iterative procedure was run; at a preliminary iteration, the model with its original coefficient values (6) was used in 4 simulations of a one-dimensional channel flow at various Reynolds numbers (see
Appendix A). A supplementary code was written for this. All of the following iterations were similar; let us consider steps at the
-th iteration (
), at the beginning of which the coefficients correspond to the point
.
First, the norm of the difference between the solution from the previous iteration and the DNS data is calculated through the following formula:
where
and
are the DNS data and the solution with the model at the
-th iteration correspondingly. The subscript indices are introduced as follows:
is the flow parameter (
,
,
,
,
),
is the case number (
,
,
,
),
is the number of a point in space (
is at the wall and
is at the channel half-height for the mean velocity field; the other parameters are stored with a shift of a half grid step, see
Appendix A). The expression in the denominator of (8) is necessary for normalizing the “columns”
,
, and bringing their contribution to the sum closer to equal. The coefficient
is defined to increase the contribution of the velocity to the norm:
,
.
In all simulations, the first off-wall grid point, at which the mean velocity value was stored, was placed at
, the grid step size increased in a geometric progression with a denominator
. The overall number of grid points between the wall and the channel center, depending on the Reynolds number, is given in
Table 1.
After was calculated, the developed channel flow was simulated using a set of coefficients corresponding to the centers of each face of a 16-dimensional box that surrounded the point and had a side length of , . Each point corresponds to a change in one of the constants by , where and the starting value of is 0.01. The norm of the solution difference was calculated using Equation (8) for each point and the least one among these and was chosen. If a simulation diverged for any of these points, then it was eliminated from consideration. If a norm of one of the face centers happened to be the least, a transition to this point was made and the -th iteration ended. In a case where a norm of the initial point () was the least, there was no change in the coefficients, and the iteration was repeated with a decrease in which is responsible for coefficient increments. The iterative process ended when the condition was satisfied, which corresponds to the 16-dimensional box being small enough. Thus, the process converged to one of the local minima of the norm of the difference between the solution with the model and the DNS data in the coefficient space.
It should be noted that the uncertainty in the DNS data reported in [
35], namely the estimated standard deviation of the mean velocity, does not exceed 0.2%, and the estimated standard deviation of the Reynolds stresses does not exceed 3%. These errors are much smaller than the differences between the DNS data and the RANS simulations presented below, which implies no significant impact of the DNS data uncertainty on the calibration results.
2.4. Model Recalibration Process
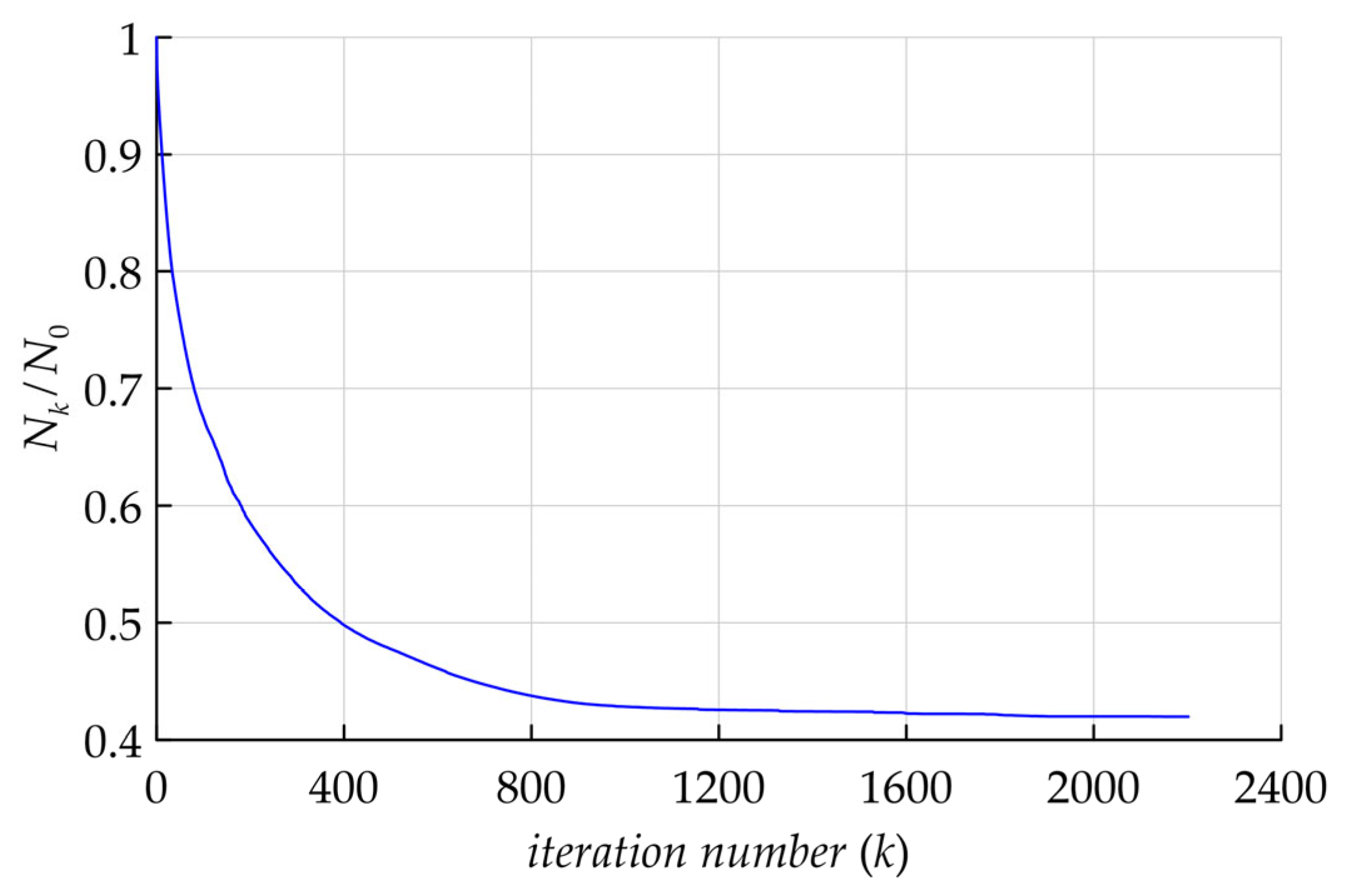
The typical behavior of the iterative process is shown in
Figure 2; the difference norm (8) dependence is divided by its initial value
on the iteration, the number
is shown. Note that the initial value
corresponds to the Jakirlić & Maduta model [
24].
The process lasted for 2202 iterations. The norm decreased quickly during the first 1000 iterations, and after this point, it kept close to constant despite the ongoing coefficient change. Let us note that a relatively wide choice of coefficients with which the model accuracy is nearly the same could be used for future tuning for different types of flows. The final value of the norm
was 0.42. Modified model coefficients that correspond to the post-calibration state are the following:
More than half of the coefficients experienced a substantial change. The coefficient
, which is used in the slow part of the redistribution term, was decreased by almost 70%;
, which affects the region where low-Reynolds number corrections are active, had an increase by 77%;
and
, which define the amplitude of the near-wall corrections to the slow part of the redistribution term, decreased by 20% and 38% correspondingly.
is close to zero after the calibration, which means that the near-wall correction to the rapid part of the redistribution term is essentially turned off.
and
, which are responsible for the production and destruction of
, were reduced by 40% and raised by 29% correspondingly. This imbalance is towards the destruction of
was compensated by a heightened value of the cross-diffusion coefficient
, which became 17.2 times that of its initial value. Finally, the coefficients
and
, which are inversely proportional to the intensity of the turbulent diffusion of
and
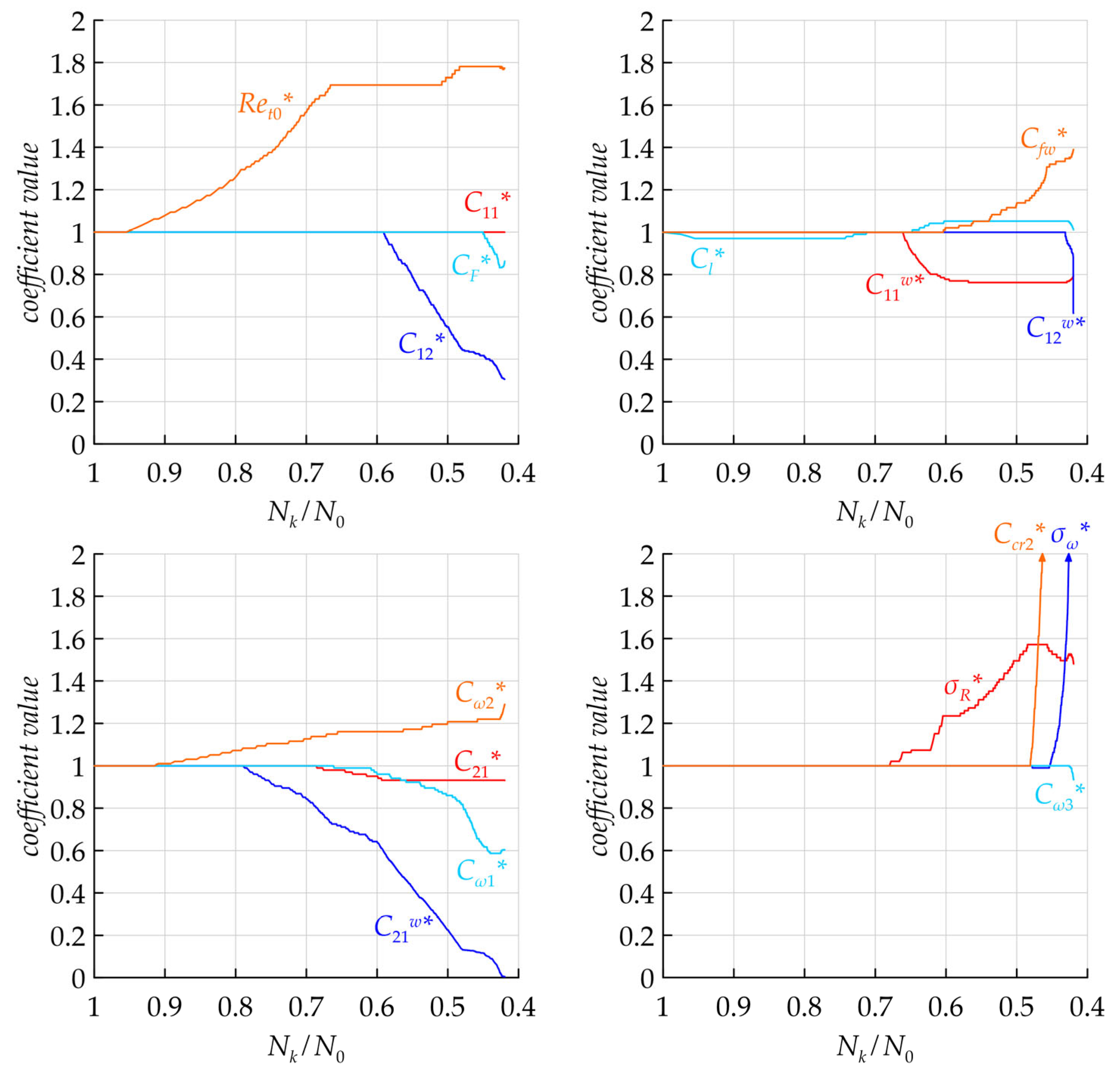
, noticeably grew by 48% and 2.5 times correspondingly. The change in coefficients during the difference norm
decrease is presented in
Figure 3.
The most important coefficients that are the first to change are , and . After that, , , , , , and join the trend. These ten coefficients are enough to lower the difference norm to 0.48. Only at the end of the calibration process, when the difference norm is lowered to 0.42 , , , and start to change. As it turned out, did not change during the calibration.
The physical implications of coefficient changes are as follows. First, the dissipation tensor anisotropy contribution to the slow part of the redistribution term seems to be much lower than was suggested in the baseline model. Second, the magnitudes of both parts of the near-wall corrections to the redistribution term appear to be overestimated in the baseline model, too. Most notably, the the term was nullified during the calibration, indicating its unimportance. Third, the diffusion intensities of and were reduced, possibly to compensate for the increase in velocity fluctuation magnitudes. Finally, the cross-diffusion term was found to be relevant at the late stages of the calibration. These observations may serve as guidelines for future developments of the near-wall DRSMs.
3. Testing within the RANS Framework
The Jakirlić & Maduta model [
24] with baseline and modified sets of coefficients were implemented in an in-house CFD code
zFlare [
36]. In this program, using the finite-volume method, the complete system of Reynolds equations for a compressible gas is solved with the possibility of RANS/LES hybridization. Multiblock structured grids and an implicit time integration method DIRK22 (Diagonally Implicit Runge–Kutta Method, two stages, 2nd order of accuracy) [
37] are used. In RANS simulations, the spatial approximation of convective terms was performed according to the WENO5 scheme (Weighted Essentially Non-Oscillatory, 5th order) [
38] along the grid lines. For diffusion and source terms, 2-nd-order-accurate central difference formulas were used. To verify the software implementation of the models, the results of developed channel flow simulations at
using the
zFlare program were compared with the results obtained from the auxiliary one-dimensional program calculation. This program was used in the calibration process. The computational grids corresponded to each other. Solutions for both the baseline and the modified models turned out to be practically indistinguishable between the two programs; the relative divergence in the mean velocity and Reynolds stresses profiles were within
. After this verification, the simulations described below were performed.
3.1. Turbulent Channel Flow at Friction Reynolds Number 2000
This subsection considers the developed turbulent channel flow at a Mach number 0.2 calculated by the bulk velocity (nearly incompressible flow). The basic computational grid contained
cells, and the wall-adjacent cell height in inner variables was chosen as
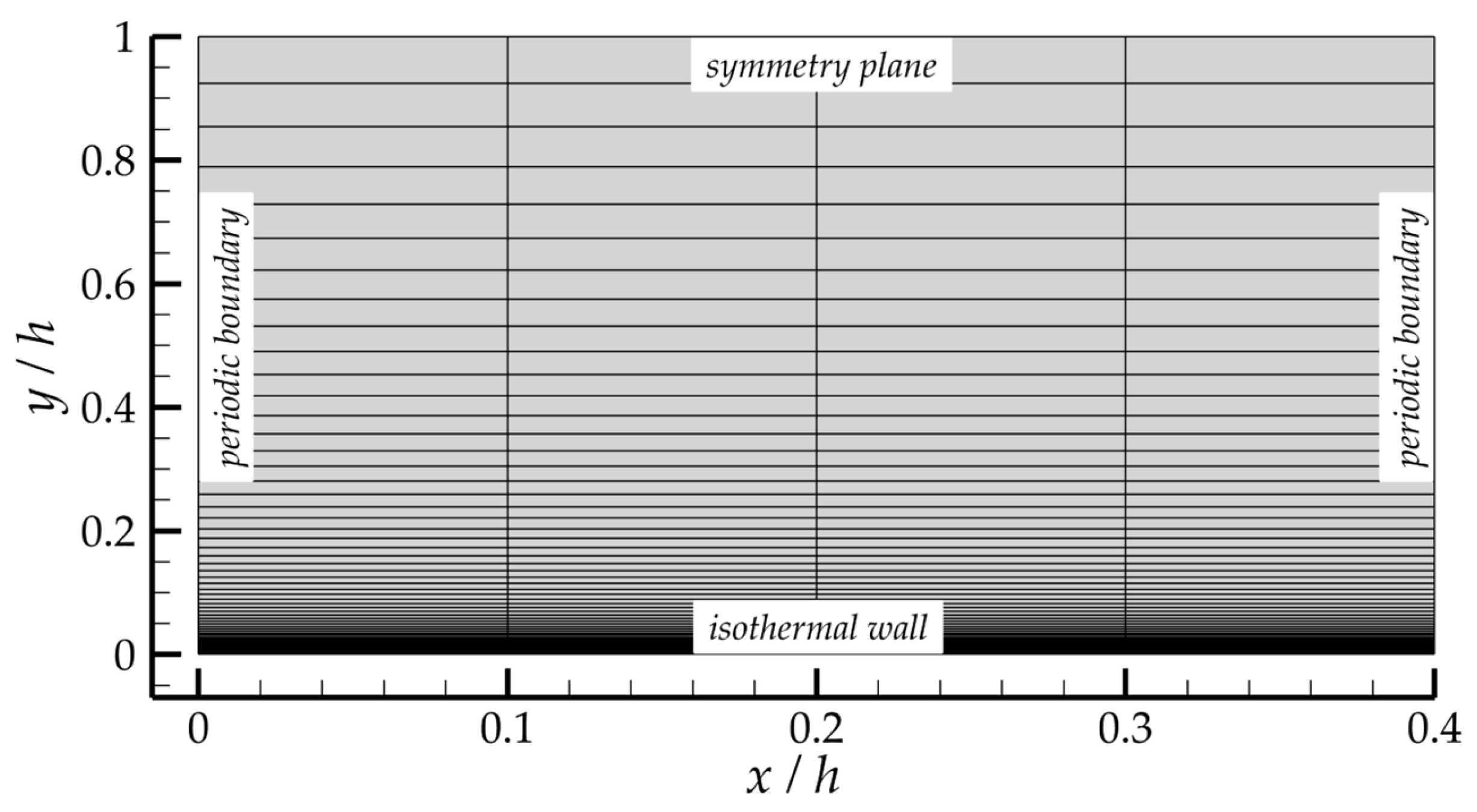
. A half of the channel from the wall up to the symmetry plane was modeled. A general view of the grid and boundary conditions is shown in
Figure 4. In the coordinate system of the figure, the flow is moving from left to right.
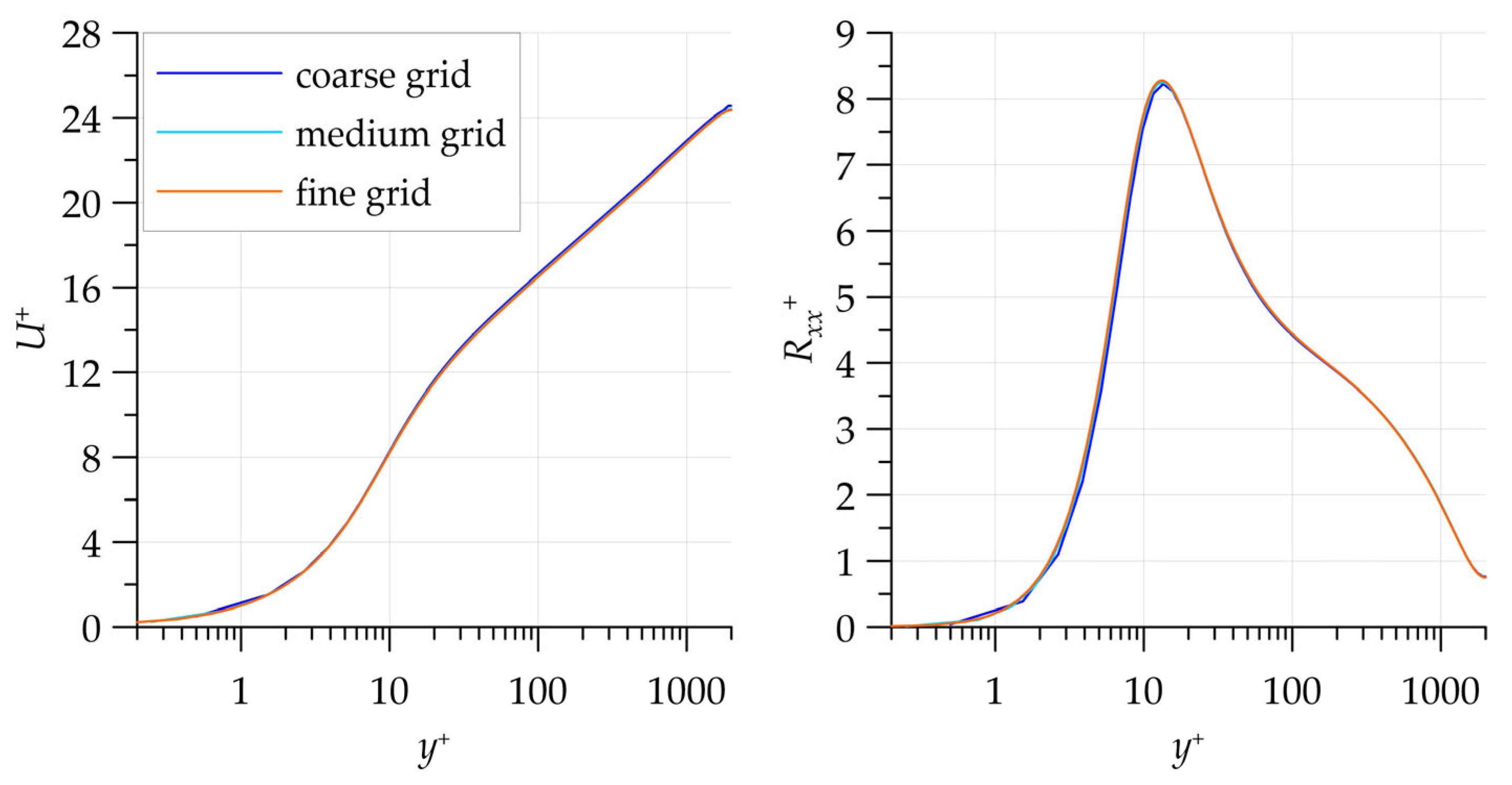
To investigate the grid convergence, nested grids obtained through a consecutive twofold refinement of the base grid in the wall-normal direction were used. In
Figure 5, the mean velocity and Reynolds stress
profiles obtained on these grids with the modified model are shown. It can be seen that the solutions almost coincide.
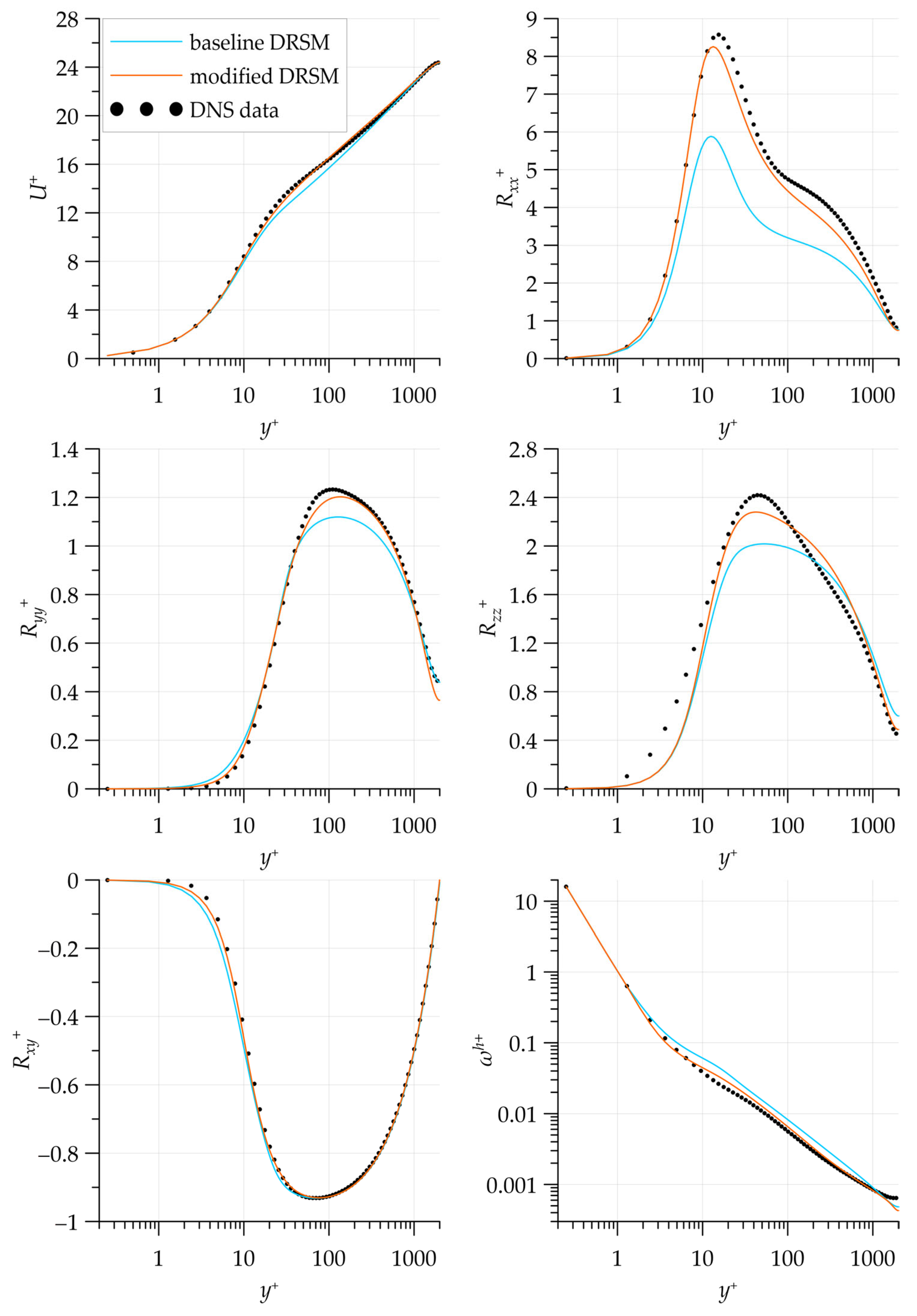
Figure 6 compares the solutions obtained with the baseline and modified versions of the Jakirlić & Maduta model [
24] with the DNS reference data [
35]. The modified model is close to the DNS data for all the parameters. In particular, the inner peak of the Reynolds stress
, the behavior of the mean velocity in the buffer region and the distribution of the parameter
across the channel are reproduced significantly better. Noticeable differences from the reference data remain in the
profile at
. The coefficient recalibration does not affect this distribution. This is caused not by the coefficient values but by the restrictions imposed through the structure of the closures (2), (3), (4). Improving the description of
may be an area for a separate study.
3.2. Flat Plate Turbulent Boundary Layer
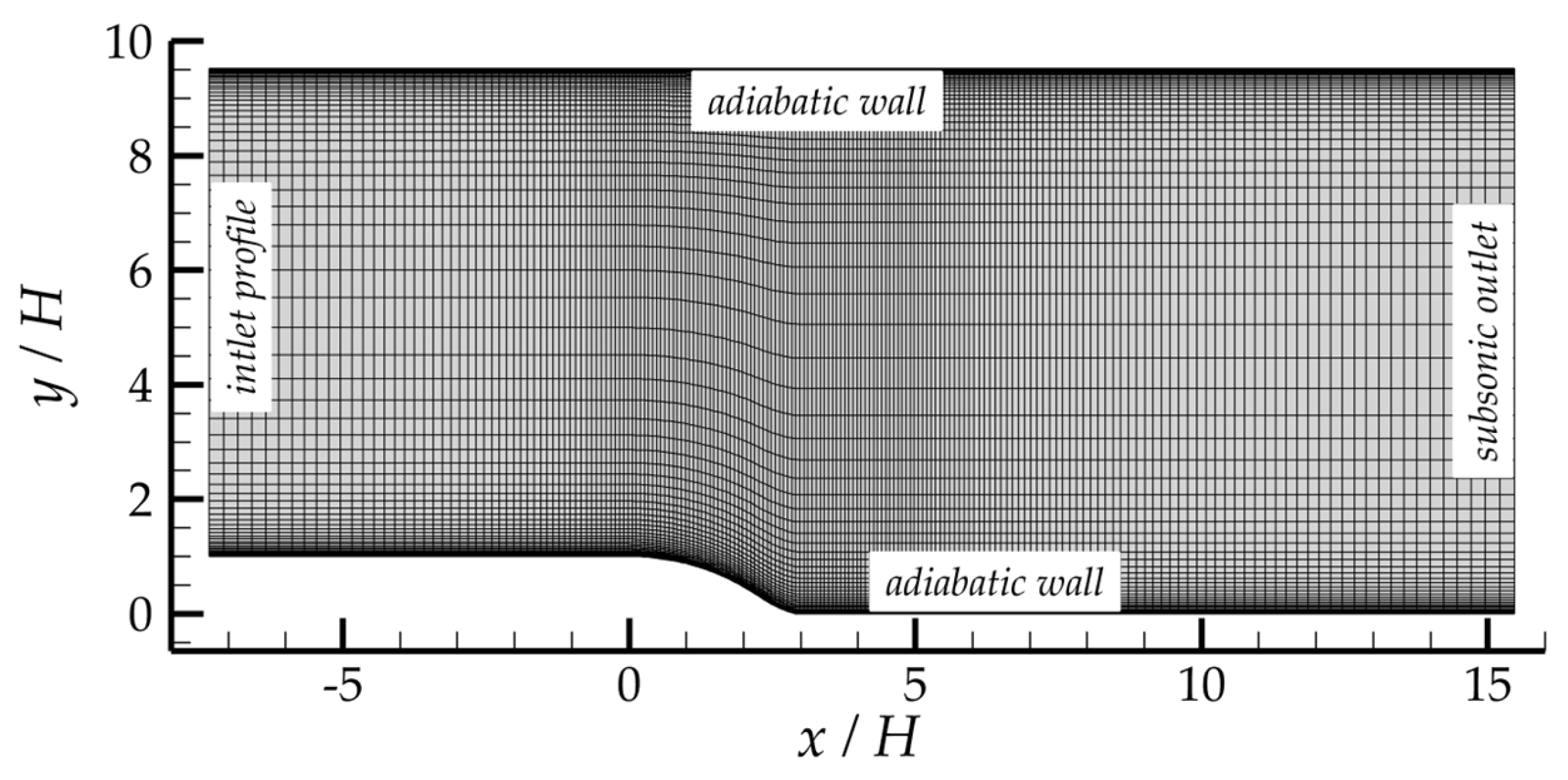
Flat plate turbulent boundary layer simulations were performed in the set-up shown in
Figure 7. The length scale
was chosen to be 1 m. The parameters of an inlet flow were prescribed so that the Mach number was equal to 0.2, and the Reynolds number based on
was
. In a preliminary simulation, an extended computational domain was used: the plate leading edge was located at
and a buffer region was placed upstream at
. However, it turned out that Jakirlić & Maduta-type models predict a delayed boundary layer transition from a laminar to a turbulent state. To avoid any associated difficulties, an auxiliary simulation using the SSG/LRR-
ω DRSM [
9] was carried out in the preliminary set-up. In this simulation, almost the entire boundary layer was turbulent. The cross-section
was extracted from this simulation (the Reynolds stress levels there already corresponded to a turbulent flow). The parameters from this section were used as inlet boundary conditions for simulations with the Jakirlić & Maduta models on a “cropped” grid, which had the left boundary located at
. This exact computational domain is shown in
Figure 7. A subsonic outflow condition with a fixed static pressure was set at the outlet boundary. On the upper boundary, a boundary condition based on the analysis of Riemann invariants was used.
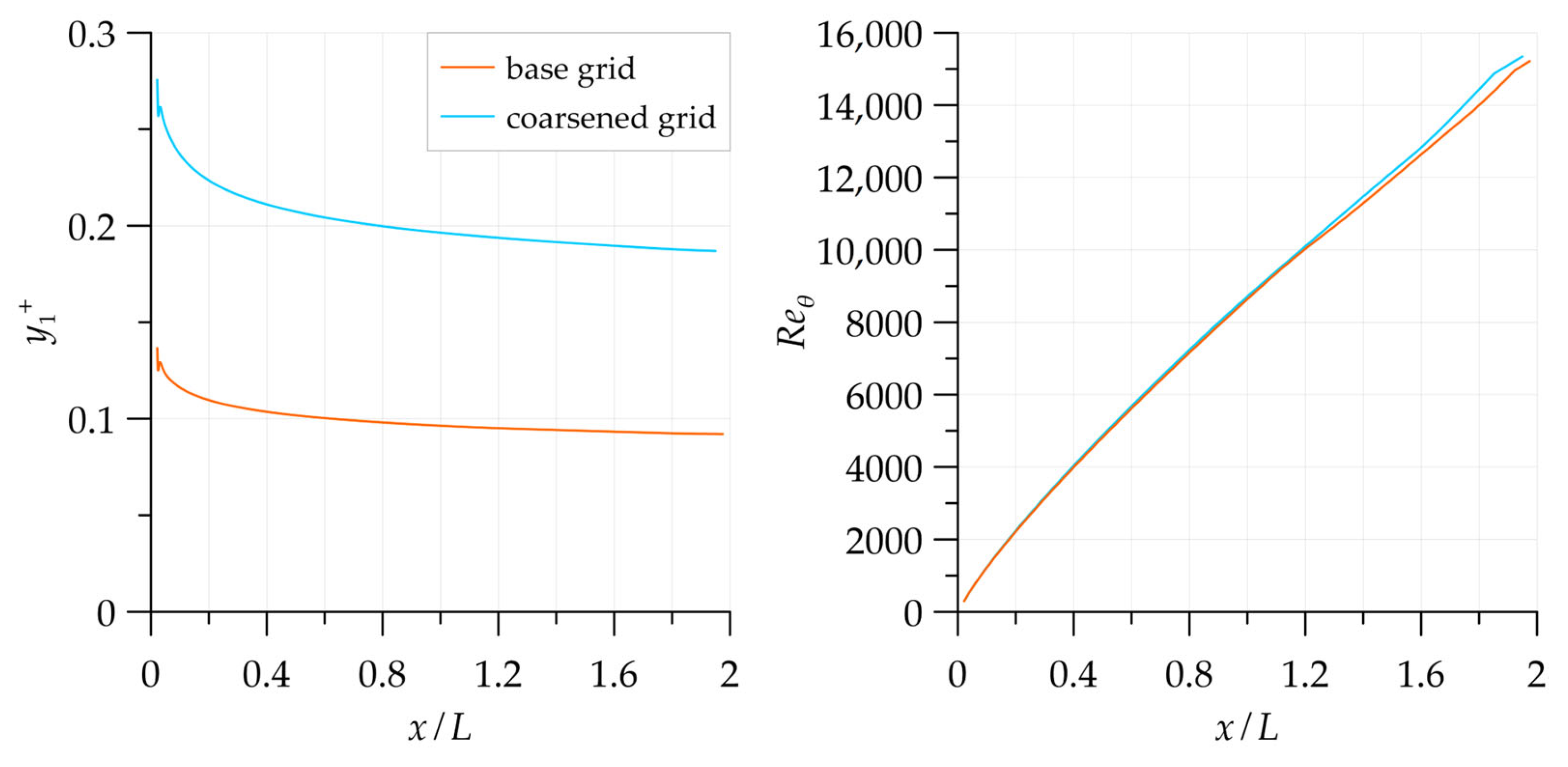
The main grid contained
cells. The wall-adjacent cell height in inner variables was within
(
Figure 8, left, “base grid”). To perform the grid convergence study, simulations were also carried out using the modified model on a grid obtained by removing every second grid line from the original one. It was found that in the interval
, the streamwise distribution of the local momentum-thickness Reynolds number
is reproduced on the two grids within a 1.5% difference. The solutions deviate from each other more noticeably only at
due to the outlet boundary condition influence (
Figure 8, right). Note that by definition,
, where
,
,
are the freestream velocity, density, and dynamic viscosity, respectively. Momentum thickness
is expressed as
The integration is carried out across the boundary layer in the wall-normal direction.
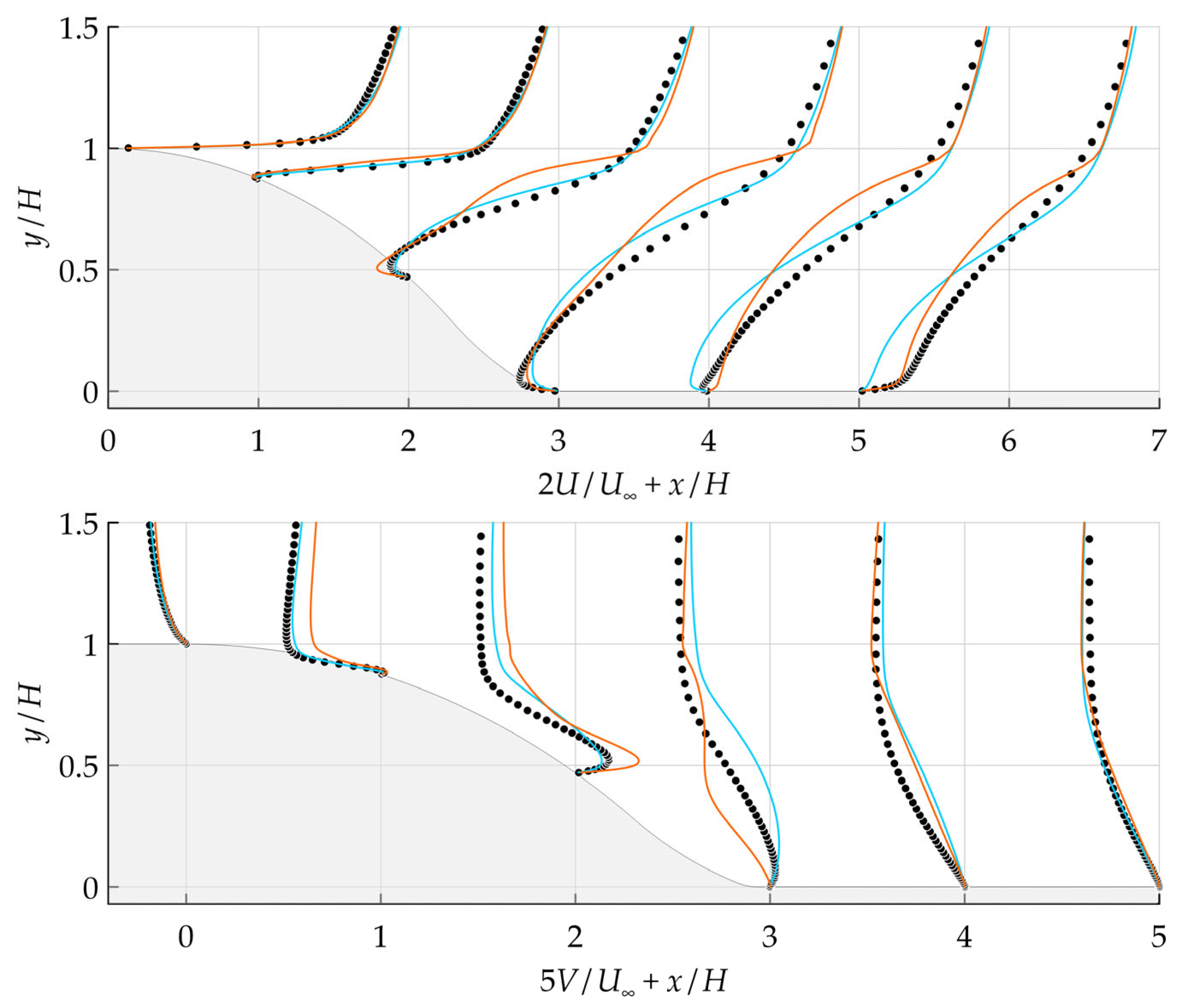
Consider the wall-normal boundary layer parameter profiles extracted from the control section at
(
Figure 9). The DNS results [
39] were used as the reference data at the same value of
. It can be seen that the modified model improved the velocity distribution compared to the baseline model within the boundary layer. The Reynolds stresses and
parameter distributions also approached the reference data, especially for the inner peak of
.
It should be noted that at the outer boundary of the turbulent region, the tangent to the velocity profile became almost vertical, accompanied by a local peak of
. This may be due to a high value of the cross-diffusion coefficient
, which significantly contributes to the solution at boundaries of this type [
40]. This occurred because there are no external turbulent region boundaries in the channel flow set-up used for the model calibration. This does not cause an issue since the modified model is supposed to be used as part of hybrid RANS/LES methods. In such simulations, the outer boundaries of turbulent regions are within the LES region and are not affected by the RANS model.
To provide quantitative metrics, the difference norms were calculated using Equation (8) without the summation of the Reynolds numbers. The cross-section corresponding to was used. The ratio of the modified to the baseline model’s norms was 0.46, close to the channel flow value of 0.42.
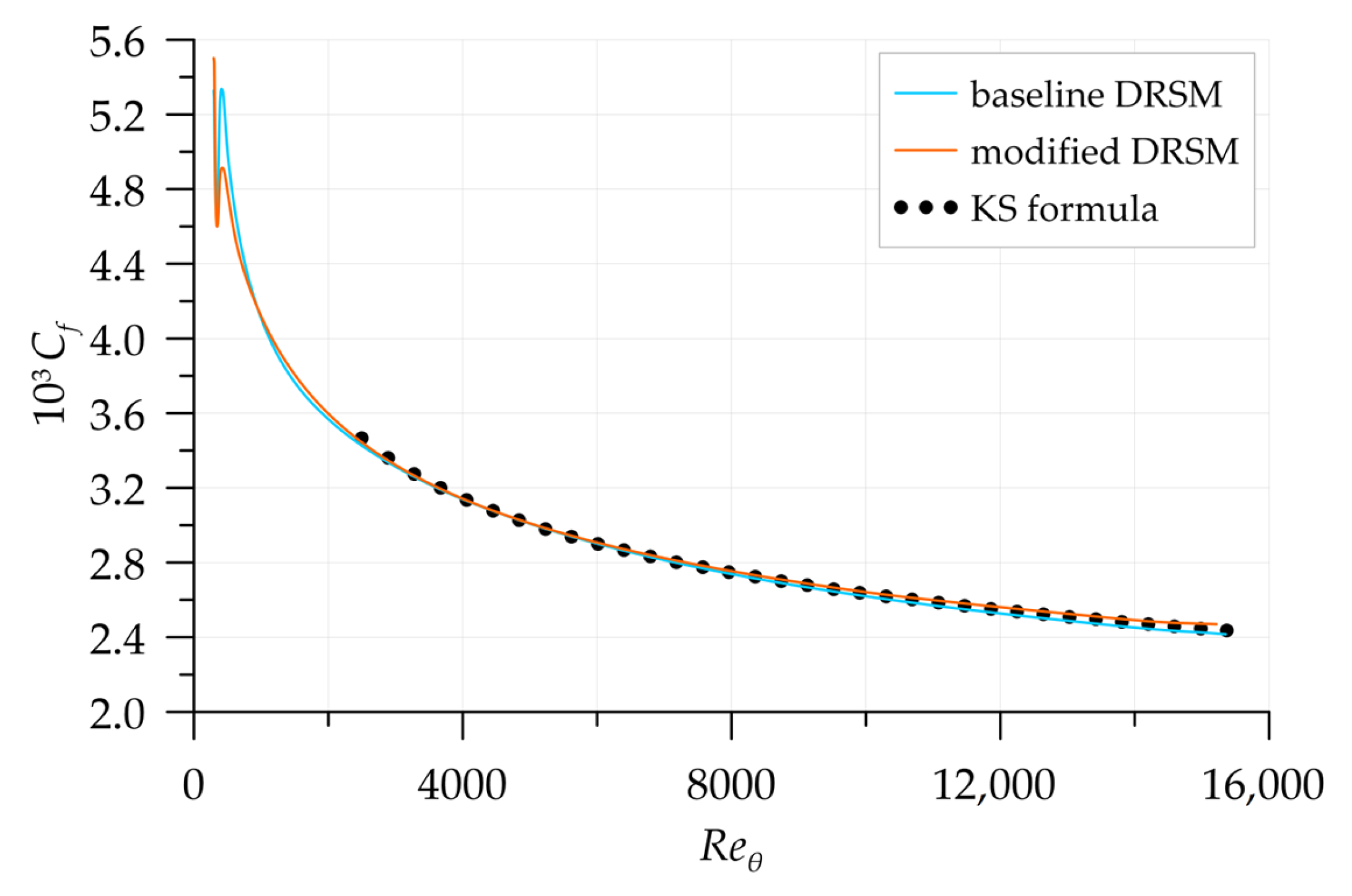
Streamwise distributions of the friction coefficient along the plate
, obtained in the simulations and plotted as functions of
, are represented in
Figure 10. They are compared with the Karman–Schoenherr (KS) empirical correlation [
41]:
It can be seen that both the baseline and the modified models reproduce the distribution (9) satisfactorily, and their error level is approximately the same.
3.3. RANS Simulation of a Boundary Layer Separation from a Rounded Step
In this flow, the initially attached boundary layer undergoes separation in the channel expansion region. This test case allows us to evaluate the accuracy of the turbulence model in a flow with a significant streamwise pressure gradient. The choice in favor of the Bentaleb, Lardeau & Leschziner set-up [
42] was made due to the simplicity of its geometric formulation and the absence of side walls. The reference data for this flow are the freely available results of a wall-resolved LES simulation [
43]. Their reliability is confirmed by considering two computational grids in [
42], showing only minor differences in the mean flow fields.
The computational domain consisted of an inlet channel section, an expansion with a rounded backstep and an outlet channel of a constant cross-section, see
Figure 11. A flow with the inlet Mach number
(measured at the channel center) and the Reynolds number
was considered, where
and
are the density and velocity at the inlet section center, correspondingly,
H is a step height and
μ is the constant dynamic viscosity. An adiabatic no-slip condition was set on the top and bottom walls, and a constant static pressure was set at the outlet. The solution obtained in a preliminary simulation of the supplying channel was used at the inlet. In that simulation, the velocity and pressure data were taken from the reference LES and did not change during the simulation. The turbulence parameters
and
consistent with them were determined.
For the RANS simulations presented here, the grid obtained by modifying the one from the reference LES simulation was used. In the streamwise direction, the original node distribution was left unchanged. In the wall-normal direction, the node distribution of the lower half of the channel was mirrored in the upper half. It was done to use the no-slip condition on the flat (top) wall, whereas wall functions were used in the reference LES simulation. In the spanwise direction, the grid only had one cell due to the statistical spanwise homogeneity of the flow. As a result, the grid consisted of cells.
The grid convergence study showed that coarsening the grid twofold in the -plane leads to a change in the velocity profiles near the step region within 1% with the considered Jakirlić & Maduta models. This indicates a sufficient grid resolution.
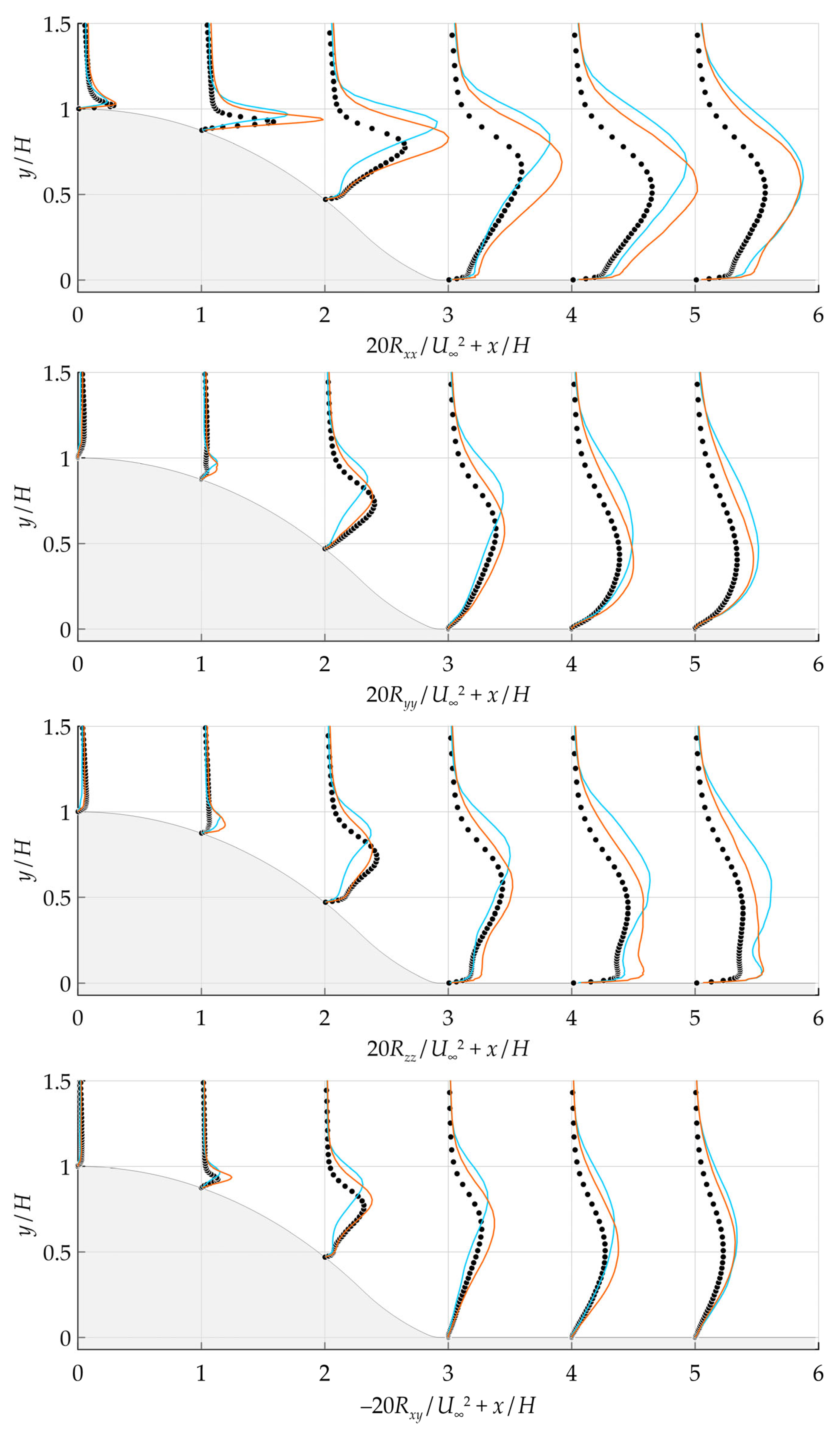
In
Figure 12, the profiles of the streamwise and transverse mean velocity components in the expanding channel are shown. It can be seen that in the chosen set-up, the recalibrated model distorts the solution more than the baseline model. The ratio of the modified to the baseline model’s difference norms was calculated using Equation (8). The six cross-sections shown in
Figure 12 were used. The ratio was found to be 1.51. This can be explained by the fact that the model was calibrated for flows without adverse pressure gradients in the current study. This seriously limits the applicability of the resulting model in a pure RANS setting. However, as mentioned above, the recalibrated model is intended for use as part of hybrid RANS/LES methods, where its role is limited by a description of the near-wall part of the boundary layer. In this region, the distribution of parameters, such as mean velocity, Reynolds stresses, dissipation rate of turbulence kinetic energy, etc., can be considered close to universal. This allows us to reasonably calibrate the model without using data of flows with a strong streamwise inhomogeneity of the parameters. The following section will demonstrate how the baseline and modified models perform in a hybrid RANS/LES mode in the same test case.
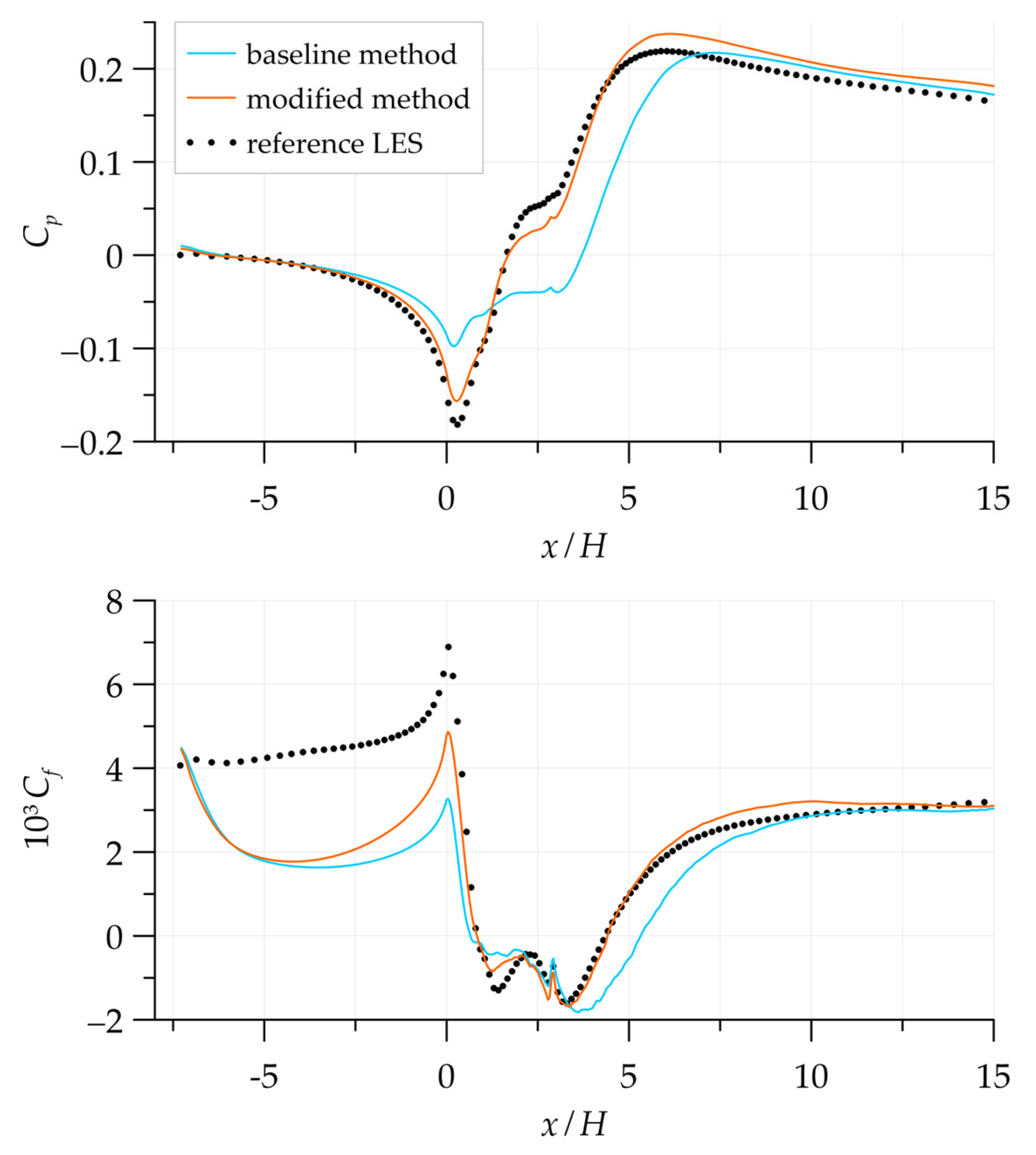
5. Conclusions
The low-Reynolds-number model of Jakirlić & Maduta [
24] was recalibrated using an
a posteriori procedure based on DNS data on developed channel flow at Reynolds numbers
in the range of 550–5200. The purpose of the calibration was to obtain a model focused on the description of the thin near-wall part of the boundary layer within the framework of hybrid RANS/LES methods. During the calibration process, the model error was reduced by 58%, which manifested in a better description of the mean velocity profile and the inner Reynolds stress peak and a more accurate distribution of the characteristic turbulence frequency
in the developed channel flow compared to the base model. In the course of the study, an improved wall boundary condition for
was proposed, which was used in all the presented simulations.
Validation of the model within the RANS framework showed that in a zero-pressure gradient flow—a turbulent boundary layer on a flat plate—the modified model gives the same improvement in the description of the flow field compared to the base model as in the developed channel flow. A minor inconsistency was found only at the outer boundary of the boundary layer. This is not a problem since the model is focused on hybrid simulations in which this boundary is located in the LES region. In the RANS simulation of the boundary layer separation from a smooth surface, the modified model showed deterioration in the region of the recirculation zone, which can be explained by the absence of data on flows under adverse pressure gradients in the calibration set. However, in the hybrid RANS/LES simulations, the transition from the base model to the modified one, on the contrary, significantly improved the solution, giving an almost complete coincidence of the mean streamwise velocity with the reference LES data. Thus, the applicability of the modified model to accurately describe the near-wall part of the boundary layer has been confirmed. At the same time, the presented results highlight the importance of the contribution of the RANS model to the overall accuracy of a hybrid simulation.