Abstract
The development of a geothermal system involves changes in the temperature field (T), seepage field (H), stress field (M), and chemical field (C) and the influence among them and injecting the heat extraction working fluid into the injection well that flows (migrating) through natural fractures and exchanges heat with the geothermal high-temperature rock. At the same time, the injection of low-temperature working fluid will induce thermal stress, resulting in changes in the reservoir temperature field and stress field. To study the influence factors and influence degree of heat production performance and mining life under multi-field coupling in the process of thermal reservoir development, based on THMC multi-field coupling numerical simulation software, this paper deeply studies the control differential equations and boundary coupling conditions of rock mass (fracture) deformation, seepage, heat exchange, the chemical reaction, and other processes based on the numerical solution method of the discrete fracture network model, simulating heat production capacity during the deep geothermal resource extraction process. The reservoir geological model analysis and generalization, parameter setting, boundary conditions, initial condition settings, mesh generation, and other steps were carried out in turn. Two different heat extraction working fluids, water, and CO2 were selected for numerical simulation in the mining process. The changes in the thermal reservoir temperature, net heat extraction rate, and SiO2 concentration during the thirty years of systematic mining were compared. The results show that CO2 has a better heat extraction effect. Finally, the reservoir thermal conductivity, heat capacity, well spacing, injection temperature, fracture spacing, fracture permeability, fracture number, fracture length, and other parameters were set, respectively. The parameter variation range was set, and the parameter sensitivity analysis was carried out. The numerical simulation results show that the engineering production conditions (injection temperature, well spacing) have little effect on the thermal efficiency and mining life, and the properties of fractures (fracture permeability, fracture number, fracture length) have a great influence.
1. Introduction
The development and utilization of geothermal energy play an important role in alleviating the global energy crisis, reducing carbon emissions, protecting the ecological environment, and improving energy security. In recent years, geothermal energy development has been extensively studied [1]. However, geothermal wells are required to produce high flow rates and sustained power output to increase the efficiency of heat production in geothermal reservoirs. The exploitation of geothermal resources is extremely complex due to the dynamics of spatio-temporal evolution, which involves multi-field coupling (THMC), such as the temperature field, seepage field, mechanical field, and chemical field. In recent years, with the continuous development of computer technology and simulation algorithms, numerical modeling methods have been essential for solving complex multi-field coupled problems in the geothermal field [2].
The numerical simulation of geothermal energy development is mainly based on the finite element method (finite difference, finite volume) under a dual medium and porous medium. Many scholars at home and abroad have developed various numerical simulation software for geothermal resource development and have carried out quantitative numerical simulation research, including ABAQUS, ANSYS, FEFLOW, COMSOL Multiphysics, FEFLOW, Visual MODFLOW, and so on [3,4,5,6,7]. Li Xinxin [8] used the T-H coupling equivalent simulation method in three-dimensional fractured rock mass, combined with COMSOL Multiphysics software for secondary development, to solve the fully coupled mathematical and physical model of hydrothermal coupling and applied this method to the numerical calculation of large-scale geothermal energy well system development at the level of a complex fractured site. Horne and Juliusson [9] optimized the injection flow rate of a multi-well system based on FEFLOW simulation software. Domestic and foreign scholars also use a variety of computer code programming to solve underground complex multi-field coupling geothermal energy development and EGS simulation problems, including TOUGH2, OpenGeoSys, ROCMAS, FRACture, and so on [10,11,12,13]. Li and Zhang et al. [14,15] used TOUGH2 software to numerically calculate the hydrothermal output of EGS double vertical wells and single fracture mining in this area and to evaluate and determine the area’s dynamic reserves and space–time evolution law. Guo and Zhang et al. [16] considered the two working conditions of the shielding layer and the non-shielding layer of the geothermal reservoir and numerically simulated the hydrothermal production of the single-fractured horizontal well in the Xujiaweizi area of the Songliao Basin. Lei and Zhang et al. [17,18] used TOUGH2 to establish vertical and horizontal well models for geothermal reservoirs in the Qiabuqia area of the Gonghe Basin, Qinghai Province, for numerical simulation of heat production. Wu et al. [19] proposed a CMPSF-enhanced THMC simulator by integrating the rock damage model and CO2 physical property model into the coupled COMSOL-MATLAB-PHREEQC (CMP) framework via MATLAB, which was combined with numerical and experimental example validation to analyze the THMC field and fracture evolution. Mohammad [20] used the thermoporous elastic displacement discontinuity (DD) method combined with different forms of finite element methods in conjunction with the fracture intrinsic relationship to consider the deformation properties of the fracture and applied advanced numerical methods to simulate and analyze the effect of the coupling process injecting cold water into the fracture/matrix system on the temporal and spatial variations of the matrix–fracture stresses, temperatures, and pore pressures.
The heat production capacity is a decisive criterion for evaluating the effect of high-temperature thermal reservoir reconstruction. Therefore, an accurate evaluation of the heat production capacity of the reservoir has important guiding significance for the dynamic mining and operation life of the EGS system. To comprehensively analyze the influence of EGS parameters on the heat recovery performance of the system and the influence of the parameters on each other, the Tengchong Rehai geothermal field in Yunnan, the Qiabuqia geothermal field in the northeast of the Qinghai–Tibet Plateau, and the Yangyi geothermal field in Tibet were taken as the geological background, respectively. The orthogonal design idea was used to analyze the changes in well spacing, injection flow, injection temperature, reservoir permeability, and other factors with the numerical simulation method [21,22,23]. The study shows that the factor that has less influence on the thermal performance of EGS extraction is the injection temperature, and the greater the mining flow, the shorter the operating life of EGS. Zhang et al. [24], based on the borehole geological data of the Qiabuqia geothermal area in the northeastern Qinghai–Tibet Plateau, established a three-dimensional hydrothermal coupled fractured reservoir model using the finite element method to evaluate its heat production potential. N. Tenma et al. [25] estimated the parameters of a typical underground system using a two-well model based on the FEHM code. Six different heat extraction schemes have been studied by changing the system parameters to explore the best scheme. Xu et al. [26] established an oil–water two-phase THMC temperature coupling prediction model based on discrete fractures to study the effect of different hydraulic fracturing parameters on formation temperature after injecting low-temperature fracturing fluid for the coupling process of THMC in high-temperature reservoirs. The effects of the fracturing fluid temperature, reservoir temperature, dimensionless conductivity, Young’s modulus, injection rate, cluster spacing, and proportion of the branch fracture area on the reservoir and the fracture temperatures were investigated. Aliyu [27] analyzed the sensitivity of deep geothermal reservoirs by studying the influence of various reservoir parameters on the production temperature, showing that the fluid injection temperature is the most influential parameter for the experiment. Liu [28] took two groups of middle and deep geothermal wells in the Xiwenzhuang geothermal field of the Taiyuan Basin as the research object. Based on the summary and analysis of the distribution characteristics of the geothermal reservoirs, the geothermal characteristics, hydrogeological characteristics, and the drilling data in the Xiwenzhuang area, numerical simulation technology was used to simulate the geothermal energy mining process, and the heat recovery efficiency of the geothermal wells under different conditions was studied.
In summary, it can be seen that the current multi-field coupling research for geothermal systems is mainly two-field (TH) or three-field (THM, THC) coupling, heat flow curing (THMC), and a four-field coupling mutual influence effect injected into the heat extraction working fluid where there is less comparative research on water and CO2 geothermal heat production capacity [29]. In the geothermal system mining multi-field coupling process, respectively, the mining conditions and natural fracture parameter changes in the heat extraction efficiency of the research parameters are not comprehensive. Therefore, in this paper, the numerical simulation method of the fractured rock body based on the discrete fracture network model simulates the THMC coupling calculation model under the natural fracture of geothermal system hot dry rock and analyzes and compares the reservoir temperature and net heat extraction rate of the two types of work fluid, the water, and the CO2 in the same reservoir conditions and the operating parameters of the heat extraction system in the extraction over thirty years to evaluate the performance of two types of work masses for the extraction of heat in the geothermal system. Under the condition that water is used as the heat extraction working fluid, the influence of each parameter on the heat extraction performance of the thermal storage was analyzed separately; i.e., the parameter sensitivity analysis and the results of the numerical simulation using multi-field coupling could be used to determine the important influencing parameters at the design stage of the geothermal resource development.
2. Mathematical Model
2.1. Basic Assumption
When establishing the THMC coupling mathematical model of fractured media, the following assumptions are introduced:
- (1)
- The rock mass is composed of matrix rock blocks and fractures in the dual media of the pores and fractures.
- (2)
- The rock matrix can be simplified as a quasi-continuous medium model and homogeneous isotropic elastic body, and the fracture can be simplified as a fractured medium model.
- (3)
- Fracture seepage obeys Darcy’s law.
- (4)
- The effective stress law of fractures is:
In this formula, —effective stress; —initial stress; —the ratio of the connected area to the total area in the fracture; —pressure.
- (1)
- The thermoelastic constitutive law of matrix rock is:
In this formula, and —stress and strain; —Lame constant; —Kronecker symbol; and —the elastic modulus and Poisson’s ratio, respectively; —thermal expansion coefficient; —temperature increment.
- (2)
- The heat in a rock mass can be transferred via conduction, convection, and radiation. In many cases, the radiation heat can be ignored.
- (3)
- Heat exchange and heat transfer occur in fractured water through convection and conduction. To simplify the calculation, it is considered that the rock mass and fractures are always in the elastic state based on the assumption of a small deformation [30].
2.2. Seepage Process
The seepage field of the thermal reservoir satisfies the mass conservation equation:
In this formula, , (kg/m3)—fluid density; —porosity; t(s)—time; (m/s)—Darcy speed; (kg/m3 s)—source of fluid mass.
In this formula, (Pa s)—fluid viscosity; (m2)—permeability; (Pa)—pore water pressure.
Substitute (4) into (3) to obtain:
2.3. Heat Transfer Process
Generally, the temperature distribution inside the rock mass depends on the heat exchange inside the rock and the heat exchange between the rock and the external medium, which is related to time. Heat exchange within the rock mass is described using the Fourier heat transfer equation:
In this formula, (kg/m3)—rock mass density; (J/(kg K))—specific heat capacity of the rock mass; (W/(m K))—thermal conductivity of the rock mass; (K)—rock temperature; (s)—time; (W/m3)—heat source density in the rock mass.
The hot dry rock (HDR) mass geothermal system’s thermal energy comes from the cyclic heating of the injected low-temperature heat extraction working fluid through the underground HDR mass. Driven by the temperature difference between the thermal reservoir rock and the fracture water flow, there is heat conduction inside the thermal reservoir rock, and there is heat conduction and heat convection between the wall surface of the fracture and the internal fluid. Heat transfer is a local heat imbalance process. It is assumed that the heat exchange model of the natural fracture water flow in the reservoir rock is shown in Figure 1.
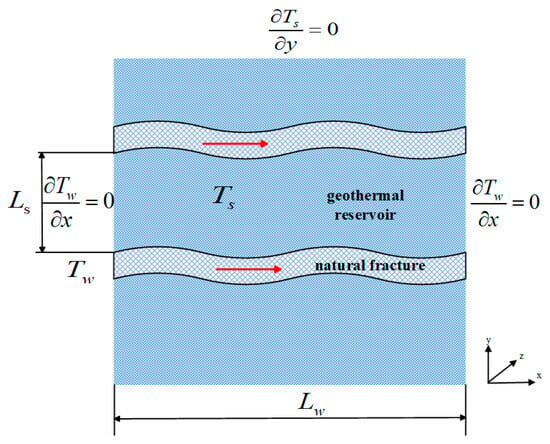
Figure 1.
Heat exchange model between matrix system and natural fracture in thermal reservoir [31].
- (1)
- The heat conduction equation in the reservoir rock skeleton is:
In this formula, (kg/m3)—rock density; (J/(kg K))—rock-specific heat capacity; —rock porosity; (K)—thermal reservoir rock temperature; (1/K)—thermal expansion coefficient; —volumetric strain; K(Pa)—rock bulk modulus; (W/(m K))—coefficient of thermal conductivity; —heat source term.
If the porosity of a rock is far less than 1, approximately taken as 0, then Formula (7) can be simplified as:
- (2)
- The fluid heat transfer equation in the fracture is:
In this formula, (kg/m3)—fluid density; (J/(kg K))—specific heat capacity of the fluid; —porosity; (K)—fluid temperature in the fracture; (m/s)—Darcy velocity; (W/(m K))—thermal conductivity of the fluid; —heat source term.
Assuming that the solid and the fluid are always in a thermal equilibrium state, the heat transfer control equation of the fluid in the reservoir is obtained by adding Formulas (8) and (9):
2.4. Rock Mechanics Process
The numerical model of the solid mechanical field in the multi-field coupling simulation of the geothermal mining system is based on BIOT consolidation theory, which considers:
- (1)
- The interaction between the groundwater and rock mass is the result of the change in the pore water pressure and rock mass deformation.
- (2)
- Assuming that the thermal reservoir rock is an isotropic homogeneous porous medium, its deformation is small, the temperature change causes the deformation of the solid skeleton, and the thermal strain generated is only positive strain. Therefore, the rock strain can be expressed as the sum of the thermal strain due to the temperature change and the effective stress-induced strain:
In this formula, (Pa)—shear modulus; —offset component; —Poisson’s ratio; (1/K)—thermal expansion coefficient; (Pa)—bulk modulus; (K)—temperature; —the influence of fluid seepage on rock mass deformation; —the influence of temperature change on rock mass deformation; —volume force component.
2.5. Chemical Reaction Process
Most studies on the thermal efficiency of deep thermal storage consider the coupling of two or three fields and often ignore the influence of the chemical field. However, the interaction between the heat extraction working fluid (water, CO2) and rocks is a key issue in developing geothermal resources. As the temperature and pressure of the heat extraction working fluid change, the reservoirs, wellbores, and pipelines in the geothermal system generally undergo chemical reactions, resulting in dissolution and precipitation. In addition, due to the mismatch between the temperature and chemical composition of the injected working fluid and the original geothermal water in the reservoir, the evolution of the temperature field and seepage field in the thermal reservoir changes the initial chemical equilibrium and reaction rate, which in turn affects the flow and heat transfer process.
Taking water injection as an example, chemical field reaction mainly includes two processes: solute transport and water chemical reaction [32]. Most of the HDR thermal storage rocks are dominated by granite. The main components of the hot reservoir rocks in the study area are quartz (SiO2), potassium feldspar (KAlSi3O8), albite (NaAlSi3O8), muscovite (KAl2(AlSi3O10)(OH)2), and calcite (CaCO3).
- (1)
- Solute transport
The dissolution and precipitation reactions of quartz (SiO2) are generally considered the most important chemical factors in developing HDR resources. The solute transfer equation of quartz minerals in the rock matrix and fracture is described as:
In this formula, (ppm)—the total dissolved concentration of solute in the matrix; (ppm)—the superscript representing the solubility of the solute in different media with the temperature; (ppm)—the total concentration of solute dissolved in the fracture; (m/s)—the dissolution rate of the solute in the rock matrix with the temperature change; —the porosity of the rock matrix; (m/s)—the dissolution rate of the solute in the fracture with the temperature change.
In Formula (10), the coefficients in the solute transfer equation in the natural fractures and matrix are related to the temperature environment of the medium and need to be solved by coupling with the fluid–matrix heat transfer equation in fractures.
- (2)
- Chemical reaction
In simulating geothermal mining, this paper only considers water–rock interactions due to the deep circulation of the geothermal fluids in the reservoir in fractures and the long-term effects of high-temperature environments. Geothermal water usually has the characteristics of high soluble salt. The governing equation for the reaction of quartz with water reacts on the surface to form a silicic acid monomer or to form a dissolved silica. The reaction equation is:
When the injection well injects a large amount of cold water through the fracture to heat the production well, the material reaction equation between the water and the granite is Formula (13). Assuming that the concentration of the reaction substance (quartz) is lower than that of the solvent liquid (water), the Fickian diffusion law can be used to describe the diffusion term in mass transport. Therefore, the convection–diffusion equation can be used to model the mass transfer of SiO2, H2O, and H4SiO4.
In this formula, —flow velocity; (mol/m³)—concentration; (m2/s)—diffusivity; (mol/(m³ s)—material reaction rate.
In this formula, —reaction rate constant.
In the process of geothermal exploitation, when the heat extraction working fluid is CO2, carbonic acid is produced by the reaction between the reservoir and the water in it. Then the chemical reaction with the components of the rock is as follows:
According to the study by Kamali Asl et al. [33] and the material reaction equation, it is found that the products of the diagenetic minerals of granite contain after the water–rock reaction. Therefore, only the concentration of in the effluent near the production well is used as the main evaluation index of the degree of water–rock response, and the concentrations of , , , and are used as the auxiliary index in this study.
3. Construction of Numerical Model
3.1. Construction of Numerical Model
The deep geothermal reservoir conditions and mining operation data at home and abroad were collected. Combined with the real-time high-temperature environment, the actual triaxial hydraulic fracturing physical simulation experiment in the study area, and the complex fracture network initiation and expansion evolution experiment under the coupling of heat flow solidification, the heat production capacity of the geothermal development is controlled by the aspects of reservoir physical properties, well location, heat extraction working fluid, thermal conductivity, injection–production pressure difference, and flow rate. The key parameters of the rock matrix (500 m × 500 m × 500 m) and natural fracture (200 m × 40 m × 0.01 m) in the model are set and shown in Table 1 and Table 2. The fractures in the model are regarded as a three-dimensional simple plane random discrete distribution in the geothermal reservoir. The average size is set to 200 m × 40 m × 0.01 m, and its spatial position is evenly distributed in the center of the reservoir.

Table 1.
The characteristics of the solid medium used in the simulation.

Table 2.
Production conditions in numerical simulation.
3.2. Initial Conditions and Boundary Conditions
Boundary conditions impose additional conditions on the solution and some modeling domains (such as surfaces, edges, or points). The same model can use a variety of different boundary conditions. The numerical models studied in this paper involve temperature, fluid, mechanical, and chemical boundaries. The model ignores the mass transfer and heat transfer process of the medium outside the reservoir, the water insulation boundary.
The temperature field, in addition to the heat conduction equation, calculates the temperature distribution inside the object and also needs to specify the initial conditions and boundary conditions. According to the static temperature and pressure measurement results of geothermal logging in the simulated study area, the bottom of the rock matrix is within the depth of 4500 m to 5000 m underground, and its temperature change is ignored. In this model, the ground temperature gradient is set to 0.04 K/m, and the ground temperature is 293.15 K. Therefore, the initial temperature of the rock matrix at 5000 m can be calculated by the Formula (17):
The initial reservoir temperature of the model is 220 °C; the upper and lower boundaries are regarded as the thermal insulation boundary; the surrounding boundary is the constant temperature boundary; and the initial injection temperature is set to 293.15 K (20 °C).
In the seepage field, the upper and lower boundaries are impermeable, the thermal reservoir is large enough to ignore the influence of the boundary, and the surrounding boundary is regarded as the constant pressure boundary. Since the surrounding rock of the deep thermal reservoir in the study area is a granite-dense rock layer, no fracturing is performed. It is assumed that it is highly closed and that the permeability is extremely low. Therefore, there is no fluid loss in the rock outside the boundary of the fractured reservoir.
In the stress field, modeling thermal storage at 5000 m depth, the surface pressure is 0.1 MPa, and the ground pressure gradient is set to 8500 Pa/m. The initial pressure of the rock matrix can be calculated using Formula (18). The initial reservoir pressure of the model is 42.6 MPa, the injection well pressure is 60 MPa, and the production well pressure is 5 MPa.
In the chemical field, the initial injection of different working fluids (water or CO2) produces chemical stimulation to the reservoir, reacts with the reservoir rock to produce dissolution and precipitation, and finally reaches a chemical equilibrium state.
3.3. Model Construction
The Comsol Multiphysics modeling software simulates the natural fracture development strata with a 4500 m~5000 m depth and an average temperature of 200 °C as the geothermal mining section. The model size is a 500 m × 500 m × 500 m cube.
The main consideration when laying out wells is the fracture pattern, which is affected by the ground stress. When the minimum principal stress is horizontal, the fracture is vertical, with a length of 200 m, a height of 40 m, and a width of 0.01 m. The numerical model is set up with eight vertical fractures spaced 20 m apart in the center of the rock mass. Due to the uniform distribution of fractures in the simulated study area, this paper adopts the mining mode of one injection and one mining. Injection wells are set at 140 m long and 0.1 m in diameter. The well spacing is set at 200 m. Cold water is injected from the injection wells, flows through rocks and fractures to be heated, and is withdrawn from the production well. The geometric conceptual model is shown in Figure 2.
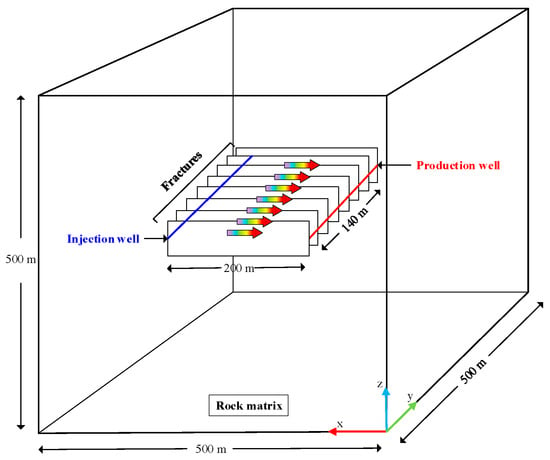
Figure 2.
Geometric conceptual model diagram.
3.4. Grid Generation
Mesh generation is an important part of the established physical model in the calculation process. The size and shape of the mesh have a direct impact on the calculation results. To reduce the influence of boundary effects in the finite element solution of numerical simulation software, the method of combining coarse and fine grids is adopted in the calculation, and the numerical simulation of the three-dimensional system of geothermal development in high-temperature rock mass is successfully realized. In principle, the denser the mesh, the higher the calculation accuracy, but the greater the workload and the amount of calculation. Considering the concentrated development area of fractures and the vicinity of injection–production wells as the key research areas, the calculation method of first coarse and then fine is adopted. That is, the whole geothermal system is calculated by using the coarse calculation model. Then the geothermal system near the injection–production wells and fracture areas is calculated using the fine calculation model. The value obtained by the coarse calculation method is used as the boundary condition of the partition calculation to reduce the influence of the boundary effect on the system [34]. According to the spatial structure characteristics of the simulated deep geothermal body geological model, the free triangular mesh is used for mesh generation, and the simulation mesh generation method and mesh generation density are determined. The mesh is refined in the injection–production well and the fracture development area. The complete mesh contains 84,307 domain units and 770 side units, as shown in Figure 3.
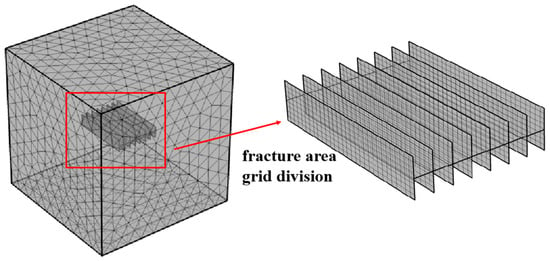
Figure 3.
Gridding model.
3.5. THMC Coupled Model Validation
To verify the correctness of the THMC coupling model, this chapter establishes a horizontal well injection and extraction model that simulates 30 years of geothermal production, and the geometric model is shown in Figure 2. In this section, the feasibility and correctness of the above THMC coupling model are verified by simulating the temperature evolution experiment of rock samples during real-time high-temperature and high-pressure geothermal extraction experiments under THMC coupling. By simulating the construction conditions in the study area with a reservoir temperature of 220 °C and one injection and one extraction, the model parameters and engineering conditions are referenced in Table 1 and Table 2. Under the coupling effect, the temperature field, seepage field, stress field, and chemical field interact with each other. To highlight the influence of the temperature field on other fields, the model focuses on the influence of the variation of each parameter on the reservoir temperature and the system heat extraction efficiency. By comparing the experimental solution with the numerical solution in this study, the simulation results are in good agreement with the experimental solution, as shown in Figure 4. The correctness of the numerical solution in this study is proved.
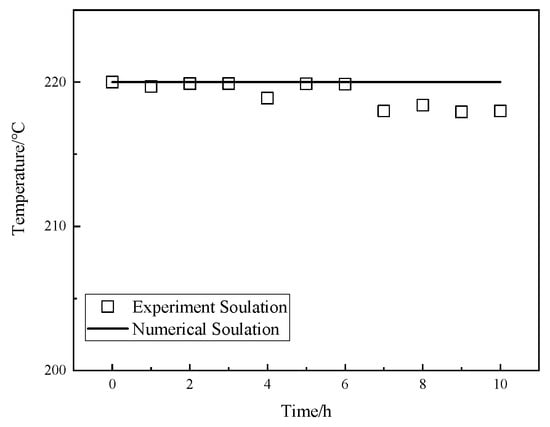
Figure 4.
Numerical and experimental solutions for reservoir temperature.
4. Multi-Field Couplings Numerical Model Solution
Using the method of numerical simulation, the injection–production method of one injection and one production is adopted. The two working fluids of water and CO2 are selected to compare the changes in reservoir temperature and net heat recovery rate under the same reservoir conditions and operating parameters of the heat recovery system for 30 years to evaluate the heat recovery performance of the two working fluids in the geothermal system.
4.1. Simulation of the Thermal Capacity of Water Injection
In the selection of heat extraction working fluid, due to the abundant water reserves and convenient utilization, the working fluid selected in the previous operation projects was water, and the temperature was mainly between 0 °C and 100 °C. Based on the flow model of water injection in the natural fracture, this section couples the heat transfer model of the fluid and rock matrix in fracture, the dilatancy opening change model caused by pressure change in the fracture, and the chemical corrosion opening model caused by solute exchange between the fluid and rock mass in long-term injection. Finally, a THMC coupling model for analyzing geothermal system mining is established. The parameters of water as the heat extraction working fluid are shown in Table 3, and other parameters remain unchanged.

Table 3.
Simulate the parameters of injected water in the wellbore.
- (1)
- The change in temperature
During the exploitation of geothermal systems, the injected low-temperature water continues to take away the heat of the rock fracture or pore surface, resulting in changes in the reservoir temperature field. Figure 5 shows the temperature changes of the thermal reservoir in 0, 10, 20, and 30 years, respectively, in which purple represents the low temperature and dark red represents the high temperature. As can be seen from Figure 5, in the 10th year of system production, the temperature of the rock mass closer to the fracture surface gradually decreased due to heat transfer, forming a low-temperature zone, with the effects of mining spreading as far as 88.72 m from the vertical distance of the injection well. In the 20th year of production, the reservoir temperature around the injection well is decreasing, and the influence of mining is farthest spread to the range of a 119.31 m vertical distance from the injection well. At this time, the rock mass temperature at the production well remained essentially unchanged, and the system can ensure continuous heat output. With the continuous increase in mining time (the 30th year), the low-temperature area of the reservoir is continuously expanded along the injection well to the periphery of the fracture with the influence of geothermal extraction, and the low-temperature area in the reservoir is also expanded and gradually extended to the production well, the farthest spread to the range of a 130.45 m vertical distance from the injection well.
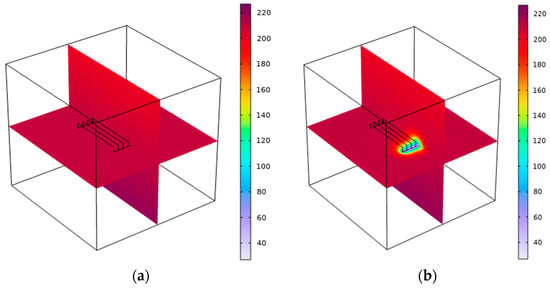
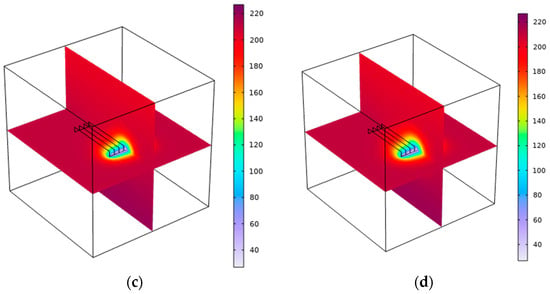
Figure 5.
Temperature(°C) change in the reservoir when the heat extraction working fluid is water during mining. (a) The 0th year of mining; (b) the 10th year of mining; (c) the 20th year of mining; (d) the 30th year of mining.
- (1)
- Heat production rate analysis
The energy efficiency of the geothermal system can be defined by the net heat extraction rate () [35], and the calculation formula is Formula (19).
and are production and injection rate, respectively, kg/s; and are the enthalpy of production and the injection fluid, respectively, kJ/kg. The model sets the injection/production rate as 2.5 kg/s, and the enthalpy value () at each temperature () corresponding to the injection of water is calculated with Formula (20).
The reservoir temperature change and net heat recovery rate () when the injected working fluid is water during the 30 years of simulated geothermal mining are shown in Figure 6. In the process of numerical simulation, the reservoir temperature change shows a stable downward trend. The reservoir temperature begins to decrease from the initial reservoir temperature, and the cold water reaches the production well from the injection well through the fracture, resulting in a decrease in the temperature around the injection well. It can be seen from Figure 7 that in three decades, the stable stage from the beginning of the heat production lasted for about three years, during which the temperature was maintained at 210 °C, and the net heat recovery rate was maintained at 2007 KJ/s. The system began to decline in the third year, and the temperature decreased from 210 °C to 185.84 °C, which decreased by about 11.5%. The net heat recovery rate decreased from 2006.31 KJ/s to 1751.19 KJ/s, a decrease of about 12.72%.
Figure 6.
‘Reservoir temperature’ center point probe.
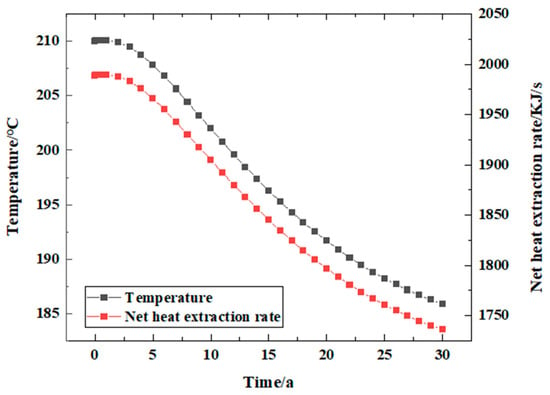
Figure 7.
Changes in reservoir temperature and net heat recovery when the injected heat extraction working fluid is water during mining.
Changes in reservoir temperature and net heat recovery rate during mining.
The value of the ‘reservoir temperature’ in Figure 7 is the value of the point probe set at the center of the model, which is used to represent the change in reservoir temperature during the numerical simulation process. The position is shown in Figure 6.
- (2)
- Chemical reaction
The natural fractures of HDR are continuously injected with cold water, and the fluid reacts with quartz before and after heat exchange to produce new substances. The concentration change and distribution of SiO2 near the production well are compared, as shown in Figure 8.
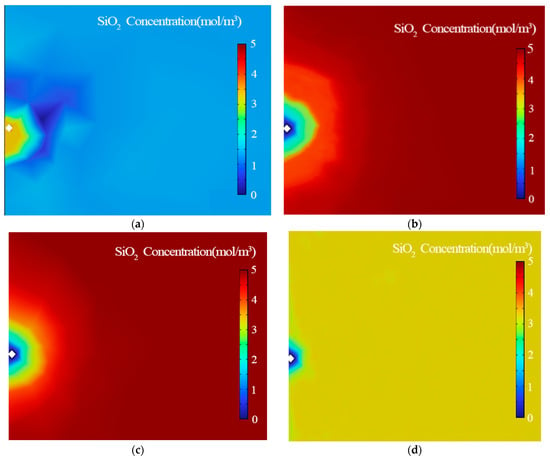
Figure 8.
Distribution of SiO2 concentration near the production wells during mining when the injected heat extraction working fluid is water.(a) The 0th year of mining; (b) the 10th year of mining; (c) the 20th year of mining; (d) the 30th year of mining.
During the early stages of mining, a large amount of cold fluid is injected into the vicinity of the injection wells, which leads to geochemical reactions in the reservoir due to changes in temperature, especially near the location of the injection wells, so the concentration of H4SiO4 around the injection well increases gradually. Subsequently, the liquid reacts with the reservoir rock in the fracture, and the chemical reaction and solute transport occur continuously. After the reaction with the aqueous solution, SiO2 reaches the location of the production well with the cold fluid passing through the fracture, and the concentration gradually diffuses and flows out of the production well.
As shown in Figure 8 and Figure 9, the change in SiO2 concentration shows two stages, and the overall trend is to decrease rapidly and then gradually stabilize.
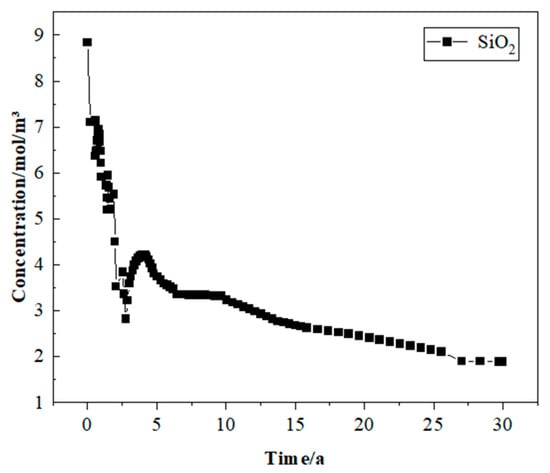
Figure 9.
The variation of SiO2 concentration near the production well when the injected heat extraction working fluid is water during mining.
4.2. Simulation of the Thermal Capacity of CO2 Injection
In the exploitation of geothermal resources, water is usually used as the heat extraction working fluid. It is rare to study carbon dioxide with the advantages of a low viscosity and density, the small flow resistance of the system, the low solubility of rock minerals, and carbon fixation [36]. In recent years, because CO2 has superior physical properties and can be used for geological burial to reduce atmospheric carbon emissions, the use of CO2 as a working circulating fluid has gradually become a hot spot in geothermal development [37]. In addition, CO2 is not easy to react with the wellbore, while water is prone to corrosion, resulting in wellbore scaling. At the same time, industrial waste gas is rich in a large amount of CO2, which can be used as a geothermal development medium to achieve CO2 geological storage, reduce atmospheric carbon emissions, and contribute to slowing global warming and promoting environmental protection.
However, at the same time, CO2 injection into the reservoir will affect the mechanical properties of a rock mass, such as the strength and elastic modulus, and cause changes in the reservoir stress field and temperature field. These changes may significantly affect the seepage characteristics of the reservoir, thereby affecting the net heat recovery rate [38]. The parameters of CO2 as the heat extraction working fluid are shown in Table 4, and other parameters remain unchanged.

Table 4.
Simulate the parameters of CO2 injection in the wellbore.
- (1)
- The change in temperature
Figure 10 shows the distribution of temperature in the thermal reservoir at 0, 10, 20, and 30 years of mining, in which purple represents low temperature, and dark red represents high temperature. The temperature of the rock mass near the distribution area of the fracture channel changes faster. This is because these penetrating fractures constitute the main seepage zone, the flow velocity is higher, and the thermal convection of the heat transfer material in the fracture is obvious. The changing trend of reservoir temperature is consistent with that of water injection mining. In the 10th and 20th years of production, the mining influence spreads to the farthest range of 111.60 m and 152.97 m from the injection well, respectively. In the 30th year of production, the ‘cold front’ has affected the temperature near the production well in the reservoir, and the farthest has spread to a range of 197.84 m from the injection well, and the temperature near the injection well has reduced to 42.55 °C. The analysis results show that in addition to natural fractures in the geothermal system, the proper use of hydraulic fracturing to generate fractures will enhance the conductivity of the rock mass, thereby improving the heat recovery efficiency.
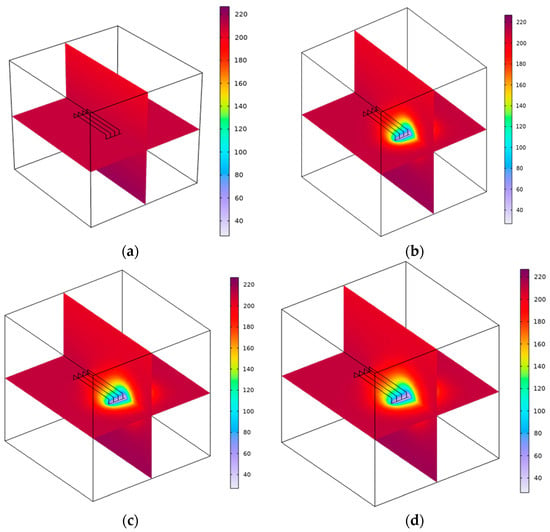
Figure 10.
Temperature(°C) change in the reservoir when the heat extraction working fluid is CO2 during mining. (a) The 0th year of mining; (b) the 10th year of mining; (c) the 20th year of mining; (d) the 30th year of mining.
- (2)
- Heat production rate analysis
In the process of numerical simulation, according to the variation characteristics of reservoir temperature, the heat production process shows a stepwise downward trend (Figure 11). In the first 1–2 years of system mining, the initial reservoir temperature is maintained, and then the initial reservoir temperature begins to decline. CO2 reaches the production well through the injection well, and the cold front breaks through the reservoir. The temperature decreases to 147.84 °C, a decrease of about 29.6%, and the net heat recovery rate decreases from 10,876.29 KJ/s to 7594.39 KJ/s, a decrease of about 30.17%.
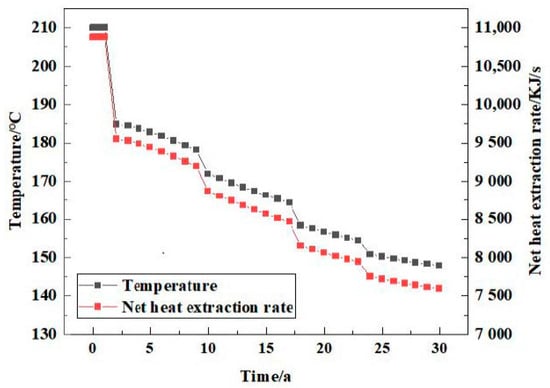
Figure 11.
Changes in reservoir temperature and net heat recovery when the injected heat extraction working fluid is CO2 during mining.
- (3)
- Chemical reaction
When the injection well is injected with CO2, CO2 will react with the material in the rock matrix when it reaches the production well through the fracture heat, and the material reaction equation is Formula (14). The concentration change and distribution of SiO2 near the production well are compared, as shown in Figure 12.
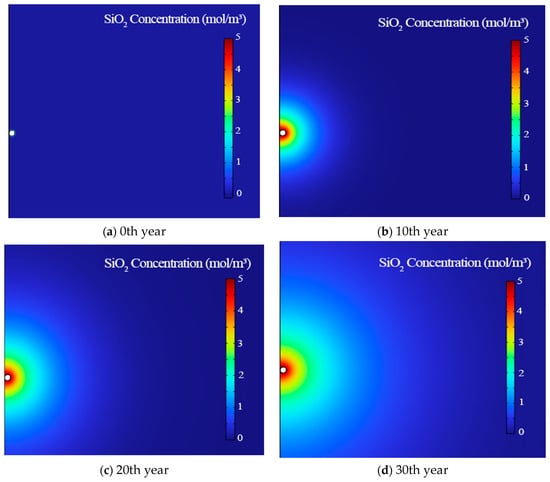
Figure 12.
Distribution of SiO2 concentration near the production wells during mining when the injected heat extraction working fluid is CO2. (a) The 0th year of mining; (b) the 10th year of mining; (c) the 20th year of mining; (d) the 30th year of mining.
As shown in Figure 12 and Figure 13, initially, the injection of CO2 first reacts with the water in the rock fissures to form carbonic acid. And then, more complex reactions occur between the rock surface and geothermal fluids in the geothermal reservoir’s high-temperature and high-pressure environment. CO2 and fluid circulation promote the dissolution of minerals such as calcite, sodic feldspar, and muscovite. Under the action of high confining pressure, the minerals on the surface of the rock are broken, and the structure is destroyed, which leads to the separation of the minerals from the rock surface into the fluid, resulting in a large amount of precipitation insoluble in water. Finally, the fluid flowing in the fracture is discharged from the flow outlet. Therefore, the concentration of SiO2 around the production well increased rapidly (the first six years), and then, with the reaction equilibrium, the concentration of SiO2 gradually stabilized, and the concentration distribution range gradually diffused from the injection well to the production well.
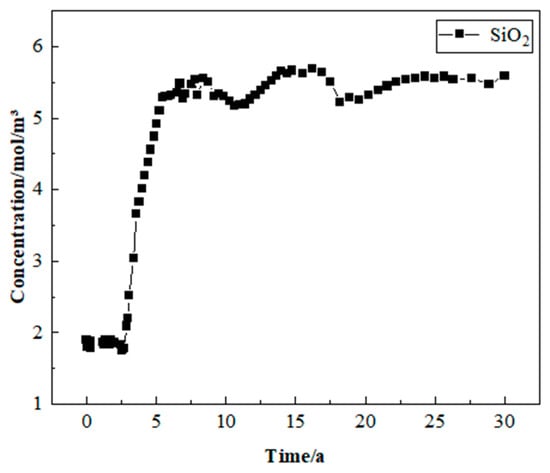
Figure 13.
The variation of SiO2 concentration near the production well when the injected heat extraction working fluid is CO2 during mining.
4.3. Analysis of Comparative Results
The numerical simulation of geothermal development is carried out for the injection of water and CO2, respectively. In Figure 14, CO2 has low viscosity and superfluidity in the well. Although the heat value is lower than that of water, it is easy to form a thermal breakthrough prematurely under the condition of constant injection flow production. Its output flow rate is large, the development time is short, and the thermal efficiency is high. The overall heat recovery effect is nearly five times that of water injection.
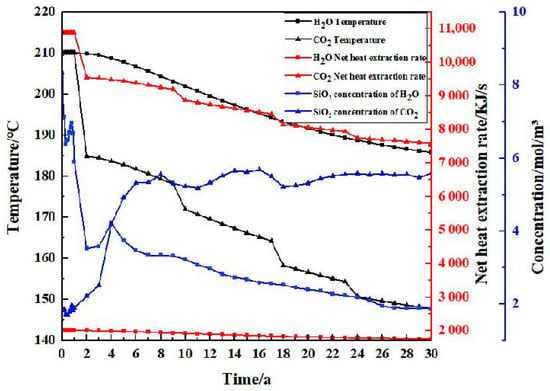
Figure 14.
Reservoir temperature, SiO2 concentration, and net heat extraction rate under different working fluid injection conditions.
5. Parameter Sensitivity Analysis
To explore the influencing factors and degree of geothermal exploitation, based on the established numerical model, water is used as the heat extraction working fluid for numerical simulation. The parameter variation range of each influencing factor is set, and the parameter sensitivity analysis is carried out on parameters such as reservoir thermal conductivity, specific heat capacity, well spacing between the production well and injection well, water injection temperature, fracture spacing, permeability, number, and fracture length. According to the simulation results, the main controlling factors of thermal efficiency and mining life are determined.
5.1. Analysis of Influencing Factors in Heat Recovery Performance
5.1.1. Properties of Reservoirs
- (1)
- Thermal conductivity
Under the same other conditions, when the thermal conductivity of the reservoir is 2.4 W/(m K), 2.9 W/(m K), and 3.4 W/(m K), respectively, the reservoir temperature change in geothermal exploitation for 30 years is analyzed. When the thermal conductivity of reservoir rock increases from 2.4 W/(m K) to 3.4W/(m K), the change and rate of temperature are consistent, which proves that the change in rock thermal conductivity has little effect on the change in the reservoir temperature. However, the higher the thermal conductivity of the rock, the faster the heat transfer from the internal rock to the fracture wall and circulating water will be, so the larger the thermal conductivity is, the faster the reservoir temperature decreases in the later stage. However, based on the numerical simulation process, this has a negligible impact on production performance and efficiency (Figure 15).
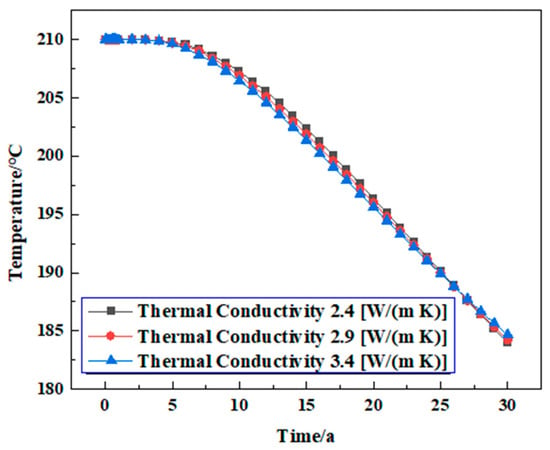
Figure 15.
The variation law of reservoir temperature under different rock thermal conductivity conditions.
- (2)
- Specific heat capacity
Under the same conditions, the temperature changes in the reservoir during the three decades of geothermal exploitation were analyzed when the specific heat capacities of the reservoir were 800 J/(kg K), 850 J/(kg K), and 900 J/(kg K), respectively. It can be seen that different heat capacities affect the change in the reservoir temperature. When the rock-specific heat capacity decreases from 900 J/(kg K) to 800 J/(kg K), the reservoir temperature change trend during the three decades of geothermal exploitation is the same, but the reservoir temperature drops even lower when the specific heat capacity is 800 J/(kg K). This is because the decrease in specific heat capacity leads to the deterioration of the heat storage performance of the rock, so the temperature decreases faster. In general, the specific heat capacity of the rock has little effect on geothermal production performance (Figure 16).
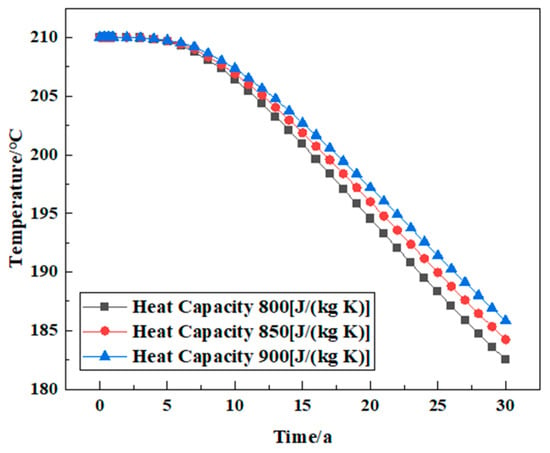
Figure 16.
The variation law of reservoir temperature under different rock-specific heat capacity conditions.
5.1.2. Project Production Conditions
- (1)
- Well spacing
Under the same conditions, the temperature changes in the reservoir in the three decades of geothermal exploitation were analyzed when the well spacing was 100 m, 200 m, and 300 m, respectively. In the process of simulated geothermal mining, when the well spacing is 300 m, the geothermal extraction is in a stable production stage for a long time, and the temperature is stable at the initial reservoir temperature and continues to decline slightly for about 20 years. When the well spacing is 200 m, the reservoir temperature shows a stable downward trend, and the reservoir temperature reaches 184.24 °C in the 30th year. When the well spacing is 100 m, because the well spacing is too close, the temperature of the thermal reservoir decreases sharply from mining to 125.03 °C and then remains stable. Therefore, when the well spacing between the injection well and the production well is 200 m, the temperature drop is more stable, and the heat extraction effect is better, which ensures the long-term exploitation of geothermal resources (Figure 17).
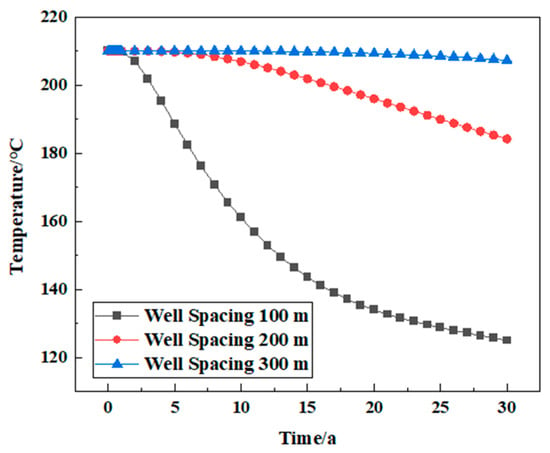
Figure 17.
The variation law of reservoir temperature under different well spacing conditions.
- (2)
- Injection temperature
In the case of the same other conditions, the temperature changes in the reservoir in the three decades of geothermal exploitation were analyzed when the injection temperatures were 20 °C, 40 °C, and 60 °C, respectively. The change law of reservoir temperature is consistent at different injection temperatures and divided into two stages: In the first stage, the reservoir temperature does not decrease significantly for about six years and remains at the initial temperature of the reservoir. This stage is usually called the stable production stage of geothermal extraction. Then, with the continuous exploitation of geothermal energy, it enters the second stage, during which the reservoir temperature decreases. Under different injection temperatures, the decline rate of the reservoir temperature is different, which shows that the lower the injection temperature, the faster the reservoir temperature decreases. In the thirtieth year of mining, when the injection temperature is 20 °C, the reservoir temperature is 184.24 °C; when the injection temperature is 60 °C, the reservoir temperature is 208.52 °C. This shows that increasing the injection temperature appropriately can improve the heat recovery temperature and operation life of the system. The lower the temperature of the injected fluid, the greater the temperature difference with the initial reservoir, the stronger the thermal convection, the faster the heat loss, and the lower the heat storage efficiency of the system (Figure 18).
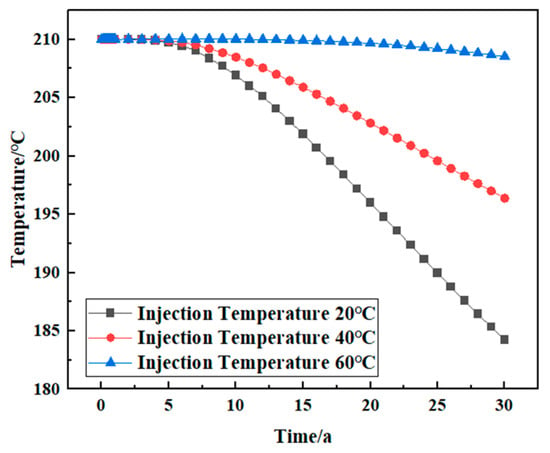
Figure 18.
The change rule of reservoir temperature under different injection temperature conditions.
5.1.3. Properties of Fracture
- (1)
- Fracture spacing
Under the same conditions, the temperature changes in the reservoir in the three decades of geothermal exploitation were analyzed when the fracture spacing was 20 m, 40 m, and 60 m, respectively. The heat exchange area of the 20 m fracture spacing increases, and the reservoir temperature decreases at the lowest and the fastest, compared to the 40 m fracture spacing. Increasing the fracture spacing (60 m) leads to a decrease in the heat exchange area between the fracture surface and the rock matrix. Therefore, at the same mining time scale, more heat will be stored in the thermal reservoir with a large fracture spacing (the rock matrix temperature is relatively higher), and the heat energy of the rock matrix taken away by the circulating fluid is reduced. This is mainly because in the case of a certain volume fraction of geothermal reservoir fractures, the smaller the fracture spacing (20 m), the larger the contact area between the fracture and the reservoir matrix, and the smaller the fracture spacing of the geothermal reservoir, which leads to an increase in the heat transfer area between the fluid and the matrix when the fluid migrates in the fracture, and the higher the heat extraction rate, so it is more conducive to the exploitation of the geothermal system (Figure 19).
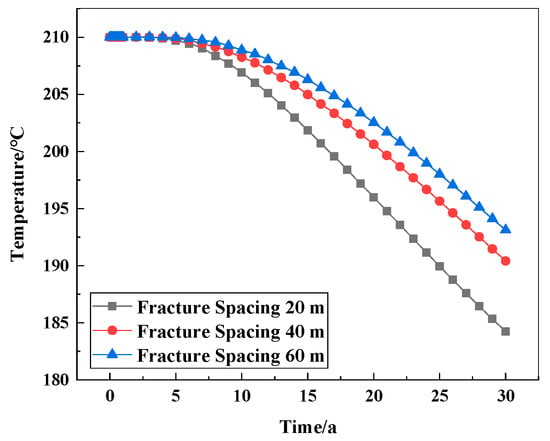
Figure 19.
Variation of reservoir temperature under different fracture spacing conditions.
- (2)
- Fracture permeability
The model sets the permeability of the rock matrix to be 5 × 10−17 m2. Under the same other conditions, the temperature changes of the reservoir in the three decades of geothermal exploitation were analyzed when the fracture permeability was 2.73 × 10−14 m2, 2.73 × 10−13 m2, and 2.73 × 10−12 m2, respectively. In the case of high fracture permeability, lower injection pressure will cause the bottom hole temperature and reservoir temperature to drop sharply after 30 years of mining because high permeability brings a high-quality mining rate, and the net heat extraction rate also reaches the highest. Therefore, from the perspective of the geothermal engineering life cycle and optimization, the fracture permeability of 10−13 m2 and above is more appropriate. If the permeability is too small, the heat extraction rate is low, and if the permeability is too large, the heat extraction is too fast, which shortens the engineering life cycle (Figure 20).
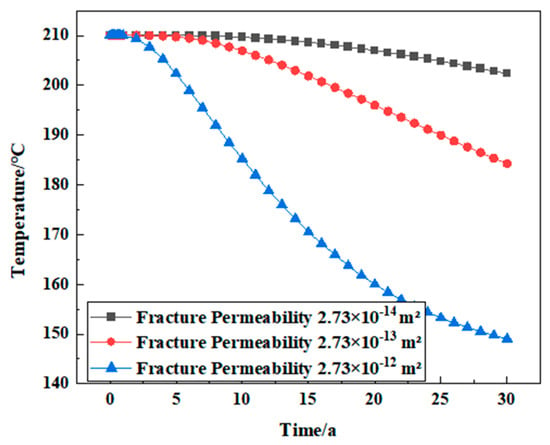
Figure 20.
The change law of reservoir temperature under different fracture permeability conditions.
- (3)
- Number of fractures
To analyze the relationship between the number of fractures and geothermal mining, the fractures are evenly arranged between the injection well and the mining well. In the case of the same other conditions, the temperature changes in the reservoir in the three decades of geothermal exploitation were analyzed when the number of fractures was two, four, and eight, respectively. The reservoir temperature after geothermal mining under different fracture numbers was studied. With the increase in fracture number, the reservoir temperature decreases faster. This is because the increase in fractures and the contact area of the injected fluid increase, and the thermal convection with rock increases, resulting in a faster temperature drop. Therefore, in some HDR geothermal resources, hydraulic fracturing is usually used to increase the number of fractures to achieve the result of system stimulation (Figure 21).
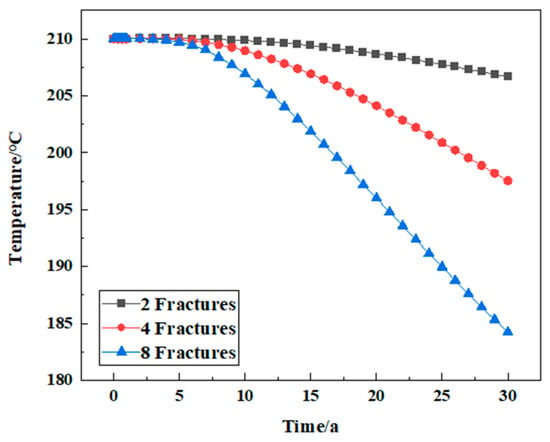
Figure 21.
The variation law of reservoir temperature under different fracture numbers.
- (4)
- Fracture length
Under the same conditions, the temperature changes in the reservoir in the three decades of geothermal exploitation were analyzed when the fracture lengths were 100 m, 200 m, and 300 m, respectively. When the fracture length is 100 m, the cold fluid flow distance becomes shorter and reaches the production well in a short time, and the reservoir temperature drops rapidly to 125.03 °C. When the fracture length is 300 m, the water and the hot rock mass have enough time to exchange heat, and the temperature remains at a high level. The results show that the local temperature of the reservoir decreases rapidly when the surface fracture length is small, which reflects that it has a great influence on the heat recovery performance of the geothermal system (Figure 22).
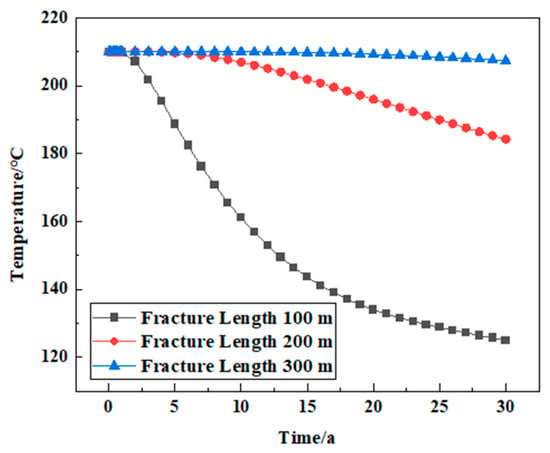
Figure 22.
The variation law of reservoir temperature under different fracture length conditions.
5.2. Analysis of Influencing Factors in Mining Life
The life of thermal reservoir mining is affected by many factors. According to the methods of the literature review, indoor physical tests, and numerical simulations, this paper summarizes the following main influencing factors:
- (1)
- The reserves and temperature of thermal reservoir resources are the most important factors affecting the life of thermal reservoir exploitation. The greater the reserves of resources, the higher the temperature and the longer the life of thermal reservoir exploitation.
- (2)
- The physical properties of thermal storage rock mass, such as rock permeability, fracture distribution, etc., will affect the effect and life of thermal storage mining. For example, rocks with poor permeability make it difficult to allow hot water to flow through, resulting in reduced hot water penetration and heat energy transfer efficiency, thus affecting the mining life of thermal reservoirs.
- (3)
- The advancement and applicability of thermal reservoir mining technology will directly affect the life of thermal reservoir mining. For example, the use of efficient drilling technology and a perfect water injection system can improve the efficiency and life of thermal storage.
- (4)
- Environmental factors, such as climate, geological conditions, etc., will also affect the life of thermal reservoir exploitation. For example, natural disasters such as earthquakes may destroy the physical structure of the thermal reservoir rock mass and affect the mining effect and life of the thermal reservoir.
- (5)
- Thermal storage mining methods: Different thermal storage mining methods will also have an impact on life. For example, flash power generation is more efficient than direct heat utilization but also consumes thermal storage resources faster.
- (6)
- The time of thermal reservoir exploitation will also affect its life. Overexploitation may lead to the depletion of thermal reservoir resources, thus affecting the life of thermal reservoir exploitation. Therefore, it is necessary to scientifically evaluate and plan thermal storage resources to control the mining intensity and time and ensure the sustainable utilization of thermal storage resources.
- (7)
- Geological stress is also one of the factors affecting the life of thermal reservoir mining. In the process of mining, the change in underground rock strata may lead to a change in geological stress, which will affect the physical structure and stability of the thermal reservoir rock mass, thus affecting the mining life of a thermal reservoir.
- (8)
- Water is needed to transfer heat energy in thermal storage mining, and water quality problems will also affect the life of thermal storage mining. For example, water may contain corrosive substances, and long-term use will lead to the corrosion of heat exchange equipment, thus affecting the life of thermal reservoir exploitation.
In general, the mining life of a thermal reservoir is a comprehensive result affected by many factors. To improve the life of thermal storage mining, it is necessary to scientifically evaluate thermal storage resources, formulate reasonable mining plans, select appropriate mining technologies and management methods, and pay attention to the impact of environmental and economic factors to achieve sustainable utilization of thermal storage resources.
6. Conclusions
In this paper, the corresponding mathematical model was established by analyzing the multi-physical field process and its coupling effect in the process of geothermal exploitation. According to the literature research, the real-time high-temperature environment true triaxial hydraulic fracturing physical simulation experiment in the study area, and the complex fracture network initiation and propagation evolution experiment under the coupling of heat flow and solidification, the numerical simulation parameters, initial conditions, and boundary conditions were determined. The discrete network model was constructed, and the mesh was refined in the fracture and the well. Finally, the reservoir temperature, net heat recovery rate, and SiO2 concentration after 30 years of geothermal system exploitation under two different heat extraction working fluids of water and CO2 were simulated and evaluated with a numerical simulation. The sensitivity of the parameters related to the thermal performance and mining life of the deep thermal reservoir was analyzed, which provided a theoretical basis for clarifying the multi-field temporal and spatial evolution law and for optimizing the flow control method in the process of geothermal mining. The conclusions are as follows:
- (1)
- For a 500 m × 500 m × 500 m geothermal reservoir, the numerical simulation software compares and analyzes the heat storage temperature, net heat recovery rate, and SiO2 concentration of water and CO2 under the same conditions. The results show that the heat of the reservoir near the injection well is first taken away, and the temperature is reduced during the seepage of the injected heat extraction working fluid to the mining well. With time, the low-temperature area gradually expands to the mining well. The net heat extraction rate of CO2 is about five times that of water, but CO2 will also undergo water–rock–gas interaction during heat extraction, which easily causes salt precipitation, increases SiO2 concentration, blocks pores, and affects the efficiency and stability of heat extraction.
- (2)
- In the analysis of different reservoir rock thermal conductivity, specific heat capacity, well spacing, injection temperature, fracture spacing, fracture permeability, fracture number, fracture length, and other parameters on the influence of the reservoir temperature, the results show that the rock thermal conductivity and specific heat capacity of geothermal system heat recovery performance have little effect; the smaller the well spacing is, the lower the injection temperature is, the faster the reservoir temperature decreases, and the higher the geothermal mining efficiency is. The smaller the fracture spacing, the larger the heat exchange area, and the higher the net heat extraction rate. Fracture permeability in the order of magnitude of 10–13 m2 and above is more suitable for a 30-year development cycle; the more fractures, the shorter the length, the larger the heat exchange area with the reservoir, the faster the temperature of the thermal reservoir decreases during the mining process, and the higher the heat extraction rate.
This paper can be a reference for both the theoretical THMC coupling model and practical geothermal production. However, the limitations of this study are that the simulated formation depth has some difficulties in actual geothermal system exploitation; the considered fractures are natural fractures, and no operations, such as hydraulic fracturing or acid fracturing, have been performed, and several parameters can be integrated together in the parameter sensitivity analysis. Therefore, the above key constraints will be considered in subsequent studies to provide a better theoretical, experimental, and simulation research basis for geothermal development.
Author Contributions
Conceptualization, G.F.; Methodology, G.F.; Software, Y.Y.; Model validation, Y.Y.; Formal analysis, L.G.; Investigation, L.G.; Resources, J.Z.; Writing—original draft preparation, Y.Y.; Writing—review and editing, Y.Y.; Funding acquisition, G.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Jiangsu Province Carbon Peak Carbon Neutral Technology Innovation Project in China (BE2022034).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| C | the chemical field |
| H | the seepage field |
| HDR | the hot dry rock |
| M | the stress field |
| T | the temperature field |
| THMC | the coupling of the temperature field, seepage field, stress field, and chemical field. |
| the total concentration of solute dissolved in the fracture, ppm | |
| concentration, mol/m³ | |
| the total dissolved concentration of solute in the matrix, ppm | |
| specific heat capacity of the rock mass, J/(kg K) | |
| specific heat capacity of the rock mass, J/(kg K) | |
| specific heat capacity of the fluid, J/(kg K) | |
| diffusivity, m2/s | |
| the superscript representing the solubility of the solute in different media with temperature, ppm | |
| elastic modulus | |
| volume force component | |
| shear modulus, Pa | |
| the enthalpy of the production fluid, kJ/kg | |
| the enthalpy of the injection fluid, kJ/kg | |
| permeability, m2 | |
| K | rock bulk modulus, Pa |
| the dissolution rate of the solute in the fracture with the temperature change, m/s | |
| reaction rate constant | |
| the dissolution rate of the solute in the rock matrix with the temperature change, m/s | |
| m | mass, kg |
| pressure, Pa | |
| pore water pressure, Pa | |
| Darcy speed, m/s | |
| source of fluid mass, kg/m3 s | |
| heat source density in the rock mass, W/m3 | |
| heat source term | |
| production rate, kg/s | |
| injection rate, kg/s | |
| Material reaction rate, mol/(m³ s) | |
| t | time, s |
| T | thermal reservoir rock temperature, K |
| thermal reservoir rock temperature, K | |
| fluid temperature in the fracture, K | |
| fluid viscosity, Pa s | |
| offset component | |
| Poisson’s ratio | |
| effective stress | |
| initial stress | |
| the ratio of the connected area to the total area in the fracture | |
| ,, | strain |
| volumetric strain | |
| Lame constant | |
| Kronecker symbol | |
| thermal expansion coefficient, 1/K | |
| temperature increment | |
| fluid density, kg/m3 | |
| porosity | |
| , | rock mass density, kg/m3 |
| thermal conductivity of rock mass, W/(m K) | |
| coefficient of thermal conductivity, W/(m K) | |
| thermal conductivity of fluid, W/(m K) | |
| heat source term | |
| add and | |
| the influence of fluid seepage on rock mass deformation | |
| the influence of temperature change on rock mass deformation | |
| the porosity of the rock matrix | |
| x | x-direction |
| y | y-direction |
| z | z-direction |
| gradient operator (total differential in all directions of space) | |
| denotes the change in a physical quantity |
References
- Melikoglu, M. Geothermal energy in Turkey and around the World: A review of the literature and an analysis based on Turkey’s Vision 2023 energy targets. Renew. Sustain. Energy Rev. 2017, 76, 485–492. [Google Scholar] [CrossRef]
- Zeng, Y.J. Technical Progress and Thinking for Development of Hot Dry Rock(HDR)Geothermal Resources. Pet. Drill. Tech 1900, 43, 1–7. [Google Scholar]
- Chen, B.G. Study on Numerical Methods for Coupled Fluid Flow and Heat Transfer in Fractured Rocks of Doublet System. Ph.D. Thesis, Tsinghua University, Beijing, China, 2014. [Google Scholar]
- Pruess, K.; Oldenburg, C.M.; Moridis, G.J. TOUGH2 User’s Guide Version 2; Lawrence Berkeley National Lab (LBNL): Berkeley, CA, USA, 1999. [Google Scholar]
- Zhao, Y.S.; Feng, Z.J.; Feng, Z.C.; Yang, D.; Liang, W.G. THM (Thermo-hydro-mechanical) coupled mathematical model of fractured media and numerical simulation of a 3D enhanced geothermal system at 573 K and buried depth 6000–7000 m. Energy 2015, 82, 193–205. [Google Scholar] [CrossRef]
- Zhao, Z.H.; Liu, G.H.; Wang, J.C.; Xu, H.R. Coupled multi-field effect on sustainable development of deep geothermal energy in cities. J. China Coal Soc. 2023, 48, 1126–1138. [Google Scholar]
- Abdul, R.S.; Sheik, S.R.; Nam, N.H.; Thanh, T. Numerical Simulation of Fluid-Rock Coupling Heat Transfer in Naturally Fractured Geothermal System. Appl. Therm. Eng. 2011, 31, 1600–1606. [Google Scholar]
- Li, X.X.; Li, D.Q.; Xu, Y. Equivalent Simulation Method of Three-Dimension Asleep Age and Heat Transfer Coupling in Fractured Rockmass of Geothermal-Borehole System. Eng. Mech. 2019, 36, 238–247. [Google Scholar]
- Egill, J.; Roland, N.H. Optimization of injection scheduling in fractured geothermal reservoirs. Geothermics 2013, 48, 80–92. [Google Scholar]
- Yu, Z.W. Research on Multiphase—Multicomponent THCM Coupling Mechanism and Its Application. Ph.D. Thesis, Jilin University, Changchun, China, 2013. [Google Scholar]
- Zhang, J.N. Experimental Research on Physical-mechanical Properties and Productivity Evaluation of Geothermal Reservoir in Guide, Qinghai. Ph.D. Thesis, Jilin University, Changchun, China, 2018. [Google Scholar]
- Taron, J.; Elsworth, D.; Min, K.B. Numerical simulation of thermal-hydrologic-mechanical-chemical processes in deformable, fractured porous media. Int. J. Rock Mech. Min. Sci. 2009, 46, 842–854. [Google Scholar] [CrossRef]
- Zeng, Y.C.; Tang, L.S.; Wu, N.Y.; Cao, Y.F. Analysis of influencing factors of production performance of enhanced geothermal system: A case study at Yangbajing geothermal field. Energy 2017, 127, 218–235. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Li, Z.W.; Guo, L.L.; Gao, P.; Jin, X.P.; Xu, T.F. Electricity generation from enhanced geothermal systems by oilfield produced water circulating through reservoir stimulated by staged fracturing technology for horizontal wells: A case study in Xujiaweizi area in Daqing Oilfield, China. Energy 2014, 78, 788–805. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Li, Z.W.; Yu, Z.W.; Guo, L.L.; Jin, X.P.; Xu, T.F. Evaluation of developing an enhanced geothermal heating system in northeast China: Field hydraulic stimulation and heat production forecast. Energy Build. 2015, 88, 1–14. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Guo, L.L.; Li, Z.W.; Yu, Z.W.; Xu, T.F.; Lan, C.Y. Electricity generation and heating potential from enhanced geothermal system in Songliao Basin, China: Different reservoir stimulation strategies for tight rock and naturally fractured formations. Energy 2015, 93, 1860–1885. [Google Scholar] [CrossRef]
- Lei, Z.H.; Zhang, Y.J.; Yu, Z.W.; Hu, Z.J.; Li, L.Z.; Zhang, S.Q.; Fu, L.; Zhou, L.; Xie, Y.Y. Exploratory research into the enhanced geothermal system power generation project: The Qiabuqia geothermal field, Northwest China. Renew. Energy 2019, 139, 52–70. [Google Scholar] [CrossRef]
- Lei, Z.H.; Zhang, Y.J.; Zhang, S.Q.; Fu, L.; Hu, Z.J.; Yu, Z.W.; Li, L.Z.; Zhou, J. Electricity generation from a three-horizontal-well enhanced geothermal system in the Qiabuqia geothermal field, China: Slickwater fracturing treatments for different reservoir scenarios. Renew. Energy 2020, 145, 65–83. [Google Scholar] [CrossRef]
- Wu, L.; Hou, Z.; Xie, Y.; Luo, Z.; Xiong, Y.; Cheng, L.; Wu, X.; Chen, Q.; Huang, L. Fracture initiation and propagation of supercritical carbon dioxide fracturing in calcite-rich shale: A coupled thermal-hydraulic-mechanical-chemical simulation. Int. J. Rock Mech. Min. Sci. 2023, 167, 105389. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Ameri, M.J.; Vaghasloo, Y.A.; Sabah, M. Fully coupled thermohydro-mechanical approach to model fracture response to injection process in enhanced geothermal systems using displacement discontinuity and finite element method. J. Pet. Sci. Eng. 2022, 208, 109240. [Google Scholar] [CrossRef]
- Duan, Y.X.; Yang, H. Analysis of Influencing Factors on Heat Extraction Performance of Enhanced Geothermal System. J. Jilin Univ. (Earth Sci. Ed.) 2020, 50, 1161–1172. [Google Scholar]
- Xu, T.F.; Yuan, Y.L.; Jia, X.F.; Lei, Y.D.; Li, S.T.; Feng, B.; Hou, Z.Y.; Jiang, Z.J. Prospects of power generation from an enhanced geothermal system by water circulation through two horizontal wells: A case study in the Gonghe Basin, Qinghai Province, China. Energy 2018, 148, 196–207. [Google Scholar] [CrossRef]
- Ling, L.L.; Su, Z.; Zhai, H.Z.; Wu, N.Y. During EGS Exploitation, Yangyi of Tibet Numerical Simulation Study of the Parameters Effect on Temperature Distribution and Mining Life. Adv. New Renew. Energy 2015, 3, 367–374. [Google Scholar]
- Zhang, C.; Jiang, G.Z.; Jia, X.F.; Li, S.T.; Zhang, S.S.; Hu, D.; Hu, S.B.; Wang, Y.B. Parametric study of the production performance of an enhanced geothermal system: A case study at the Qiabuqia geothermal area, northeast Tibetan plateau. Renew. Energy 2019, 132, 959–978. [Google Scholar] [CrossRef]
- Norio, T.; Kasumi, Y.; George, Z. Model study of the thermal storage system by FEHM code. Geothermics 2003, 32, 603–607. [Google Scholar]
- Xu, R.; Guo, T.; Qu, Z.; Chen, H.; Chen, M.; Xu, J.; Li, H. Numerical simulation of THMC coupling temperature prediction for fractured horizontal wells in shale oil reservoir. J. Pet. Sci. Eng. 2022, 217, 110782. [Google Scholar] [CrossRef]
- Aliyu, M.D.; Chen, H. Sensitivity analysis of deep geothermal reservoir: Effect of reservoir parameters on production temperature. Energy 2017, 129, 101–113. [Google Scholar] [CrossRef]
- Liu, J. Numerical Simulation Research on Multi-field Coupling of Middle-Deep Geothermal Development Process in Xiwenzhuang Taiyuan. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2021. [Google Scholar]
- Zhao, Y.A. Analysis of Heat Extraction Performance of Water and CO2 in Supercritical Geothermal System: A Case Study of Larderello Geothermal Field in Italy. Master’s Thesis, Jilin University, Changchun, China, 2023. [Google Scholar]
- Sun, Z.X.; Xu, Y.; Lv, S.H.; Xu, Y.; Sun, Q.; Cai, M.Y.; Yao, J. A thermo-hydro-mechanical coupling model for numerical simulation of enhanced geothermal systems. J. China Univ. Pet. (Ed. Nat. Sci.) 2016, 40, 109–117. [Google Scholar]
- Xiao, Y. Study on THMC Coupling of Hydro shearing in Hot Dry Rock In enhanced Geothermal System. Ph.D. Thesis, Southwest Petroleum University, Chengdu, China, 2017. [Google Scholar]
- Guo, Z.P.; Bu, X.B.; Li, H.S.; Gong, Y.L.; Wang, L.B. Numerical simulation of heat extraction in single-well enhanced geothermal system based on thermal-hydraulic-chemical coupling model. Chem. Ind. Eng. Prog. 2023, 42, 711–721. [Google Scholar]
- Arash, K.A.; Ehsan, G.; Nicolas, P.; Nicolas, B. Experimental study of fracture response in granite specimens subjected to hydrothermal conditions relevant for enhanced geothermal systems. Geothermics 2018, 72, 205–224. [Google Scholar]
- Zeng, Y.C.; Zhan, J.M.; Wu, N.Y.; Luo, Y.Y.; Cai, W.H. Numerical investigation of electricity generation potential from fractured granite reservoir through a single vertical well at Yangbajing geothermal field. Energy 2016, 114, 24–39. [Google Scholar] [CrossRef]
- Pruess, K. Enhanced geothermal system (EGS) using CO2 as working fluid: A novel approach for generating renewable energy with simultaneous sequestration of carbon. Geothermics 2006, 35, 351–367. [Google Scholar] [CrossRef]
- Sun, B.J.; Wang, J.T.; Sun, W.C.; Wang, Z.Y.; Sun, J.S. Advances in fundamental research of supercritical CO2 fracturing technology forum conventional natural gas reservoirs. J. China Univ. Pet. (Ed. Nat. Sci.) 2019, 43, 82–91. [Google Scholar]
- Gong, F.C. Multi-field Coupling Numerical Simulation of Enhanced Geothermal System and Development Model Optimization. Master’s Thesis, China University of Petroleum (East China), Dongying, China, 2020. [Google Scholar]
- Li, P. Study on Effect of Thermo-Hydro-Mechanical-Chemical Coupling in CO2-EGS of Hot Dry Rock. Ph.D. Thesis, China University of Mining and Technology, Xuzhou, China, 2020. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).