Modeling Multivariate Spray Characteristics with Gaussian Mixture Models
Abstract
:1. Introduction
2. Materials and Methods
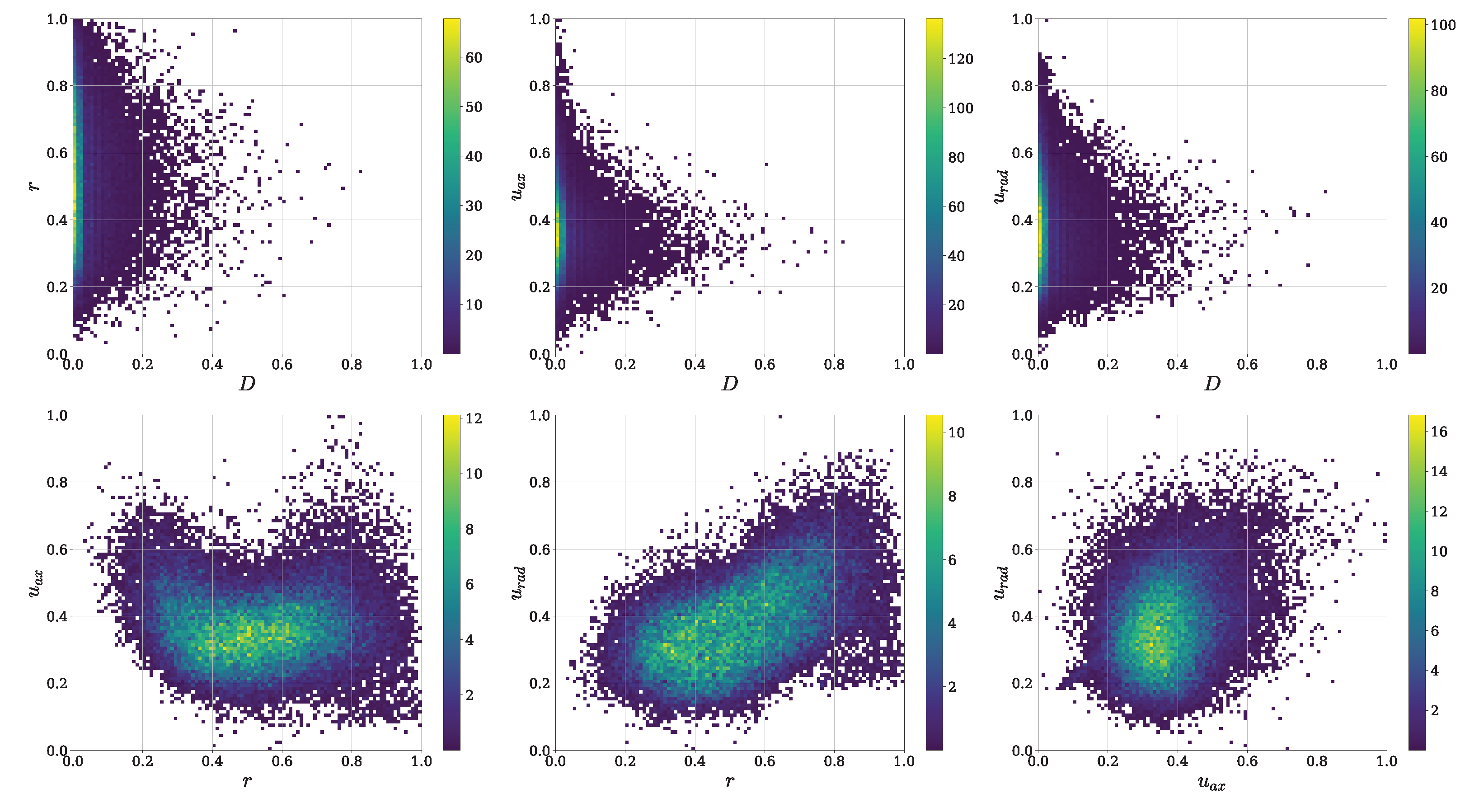
2.1. Description of the Training Data
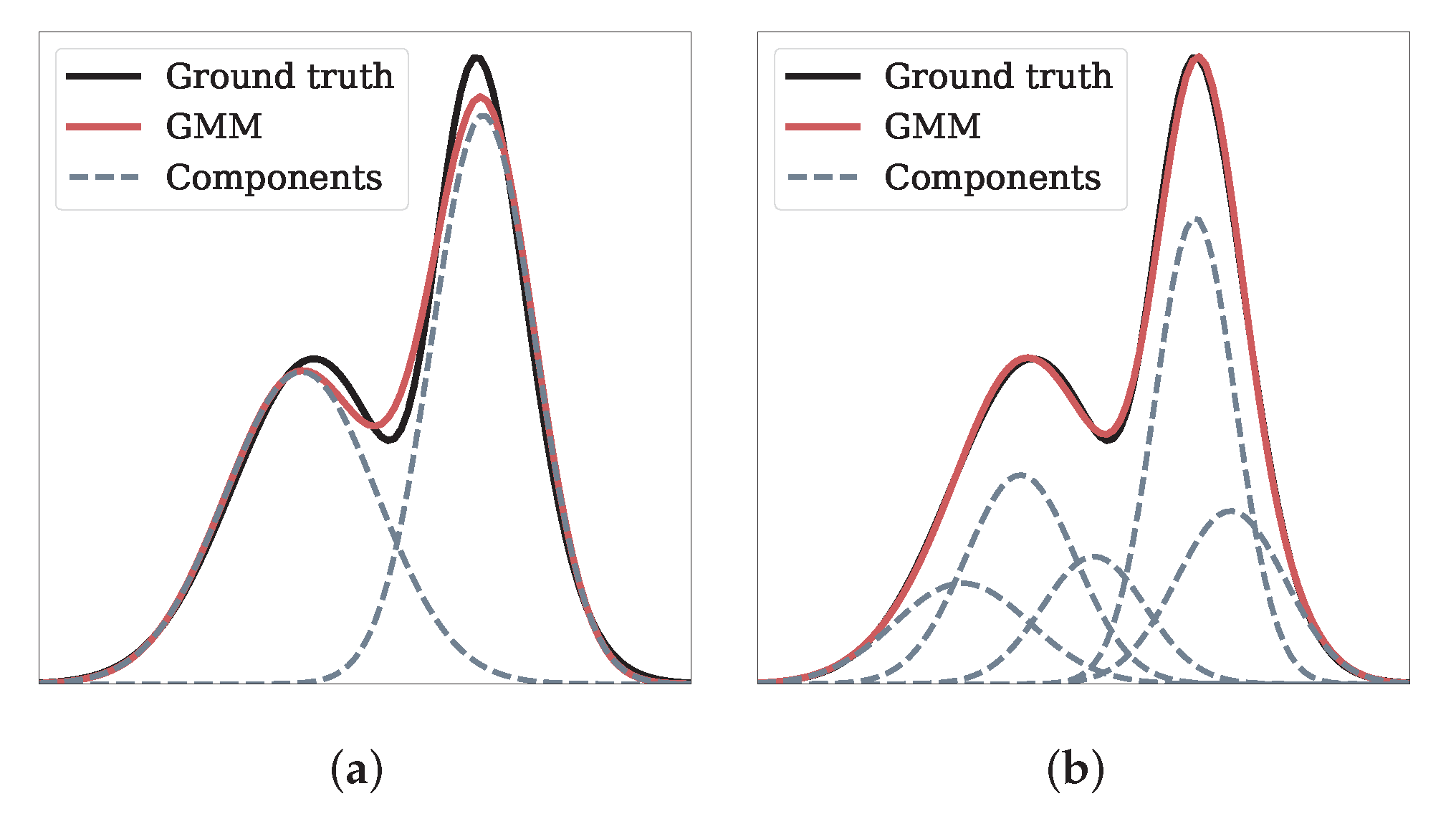
2.2. Gaussian Mixture Model
- are the parameters of the GMM,
- is the mean vector of the n-th Gaussian component,
- is the covariance matrix of the n-th Gaussian component, and
- is the weight of the n-th Gaussian component, representing the probability of selecting that component.
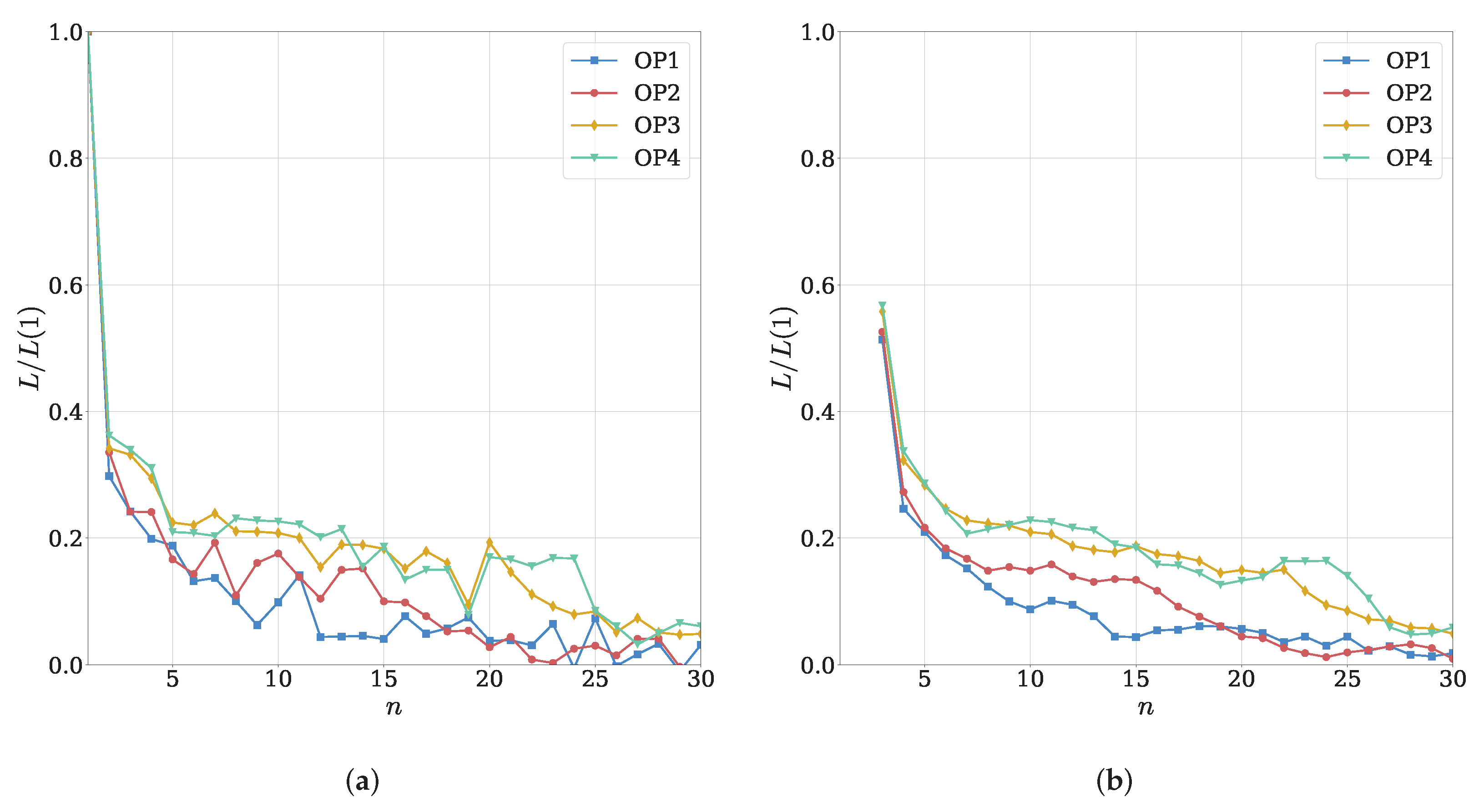
Model Selection, Initialization, and Evaluation
3. Results and Discussions
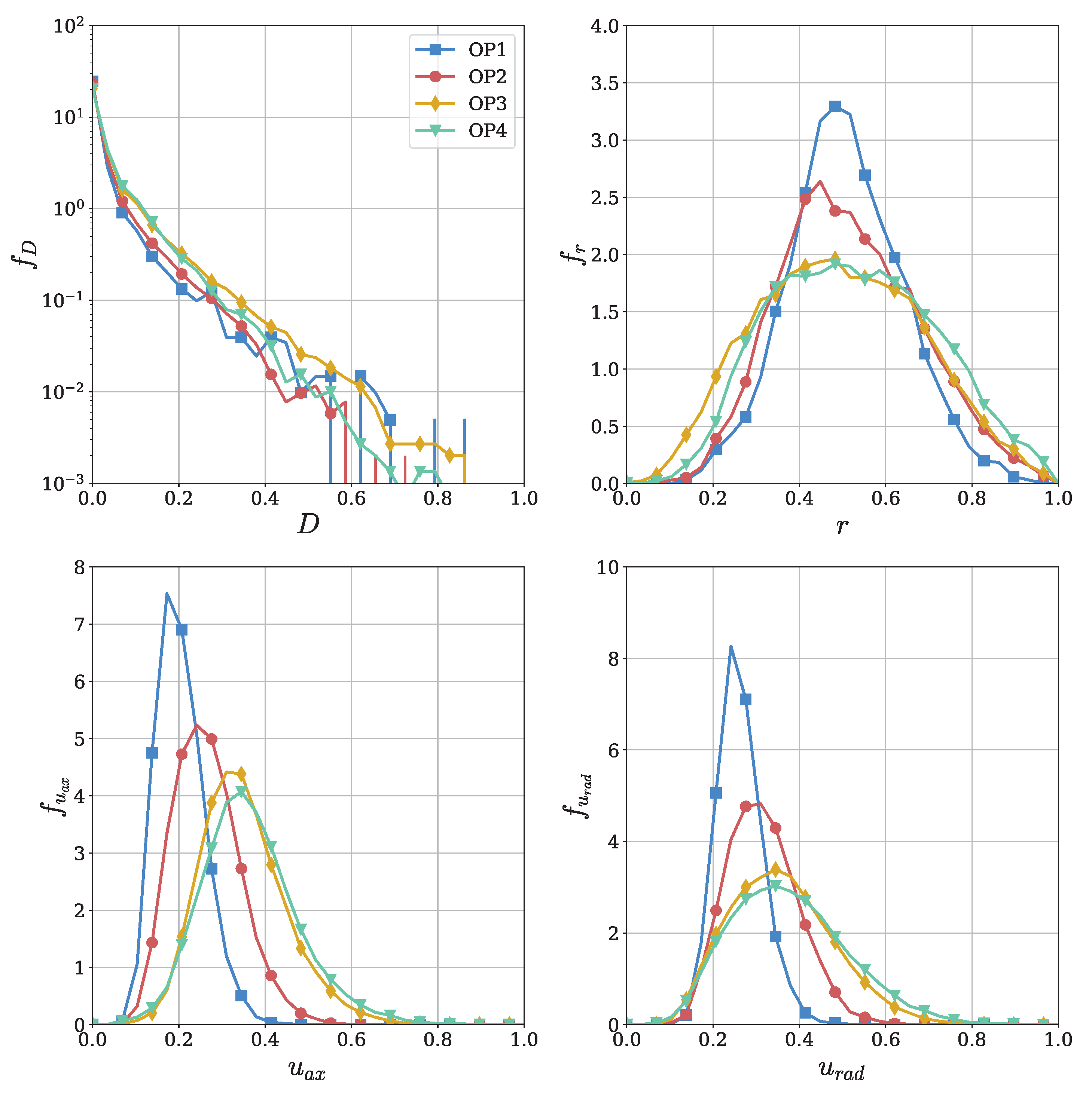
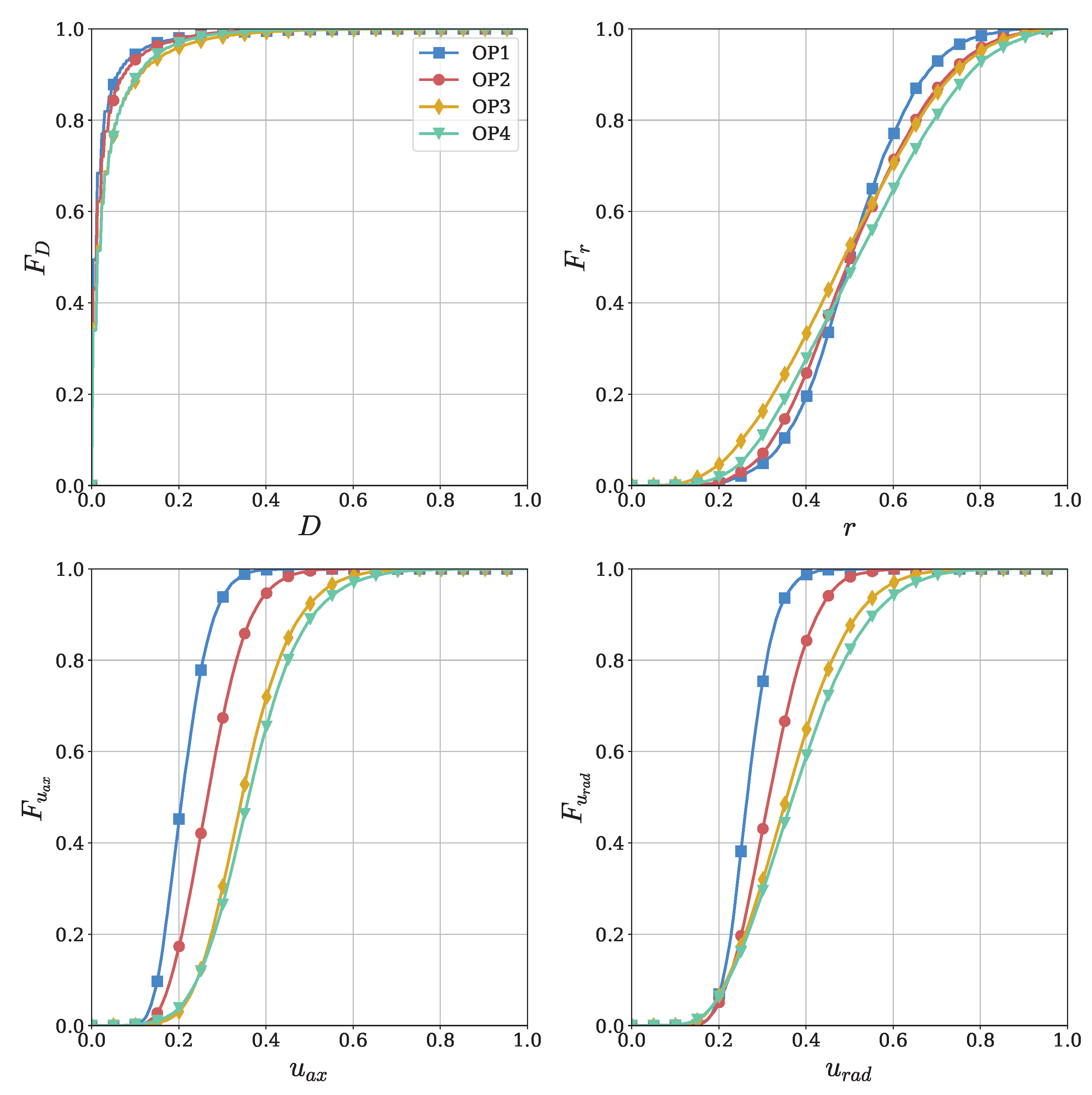
3.1. Assessment of Model Accuracy and Complexity
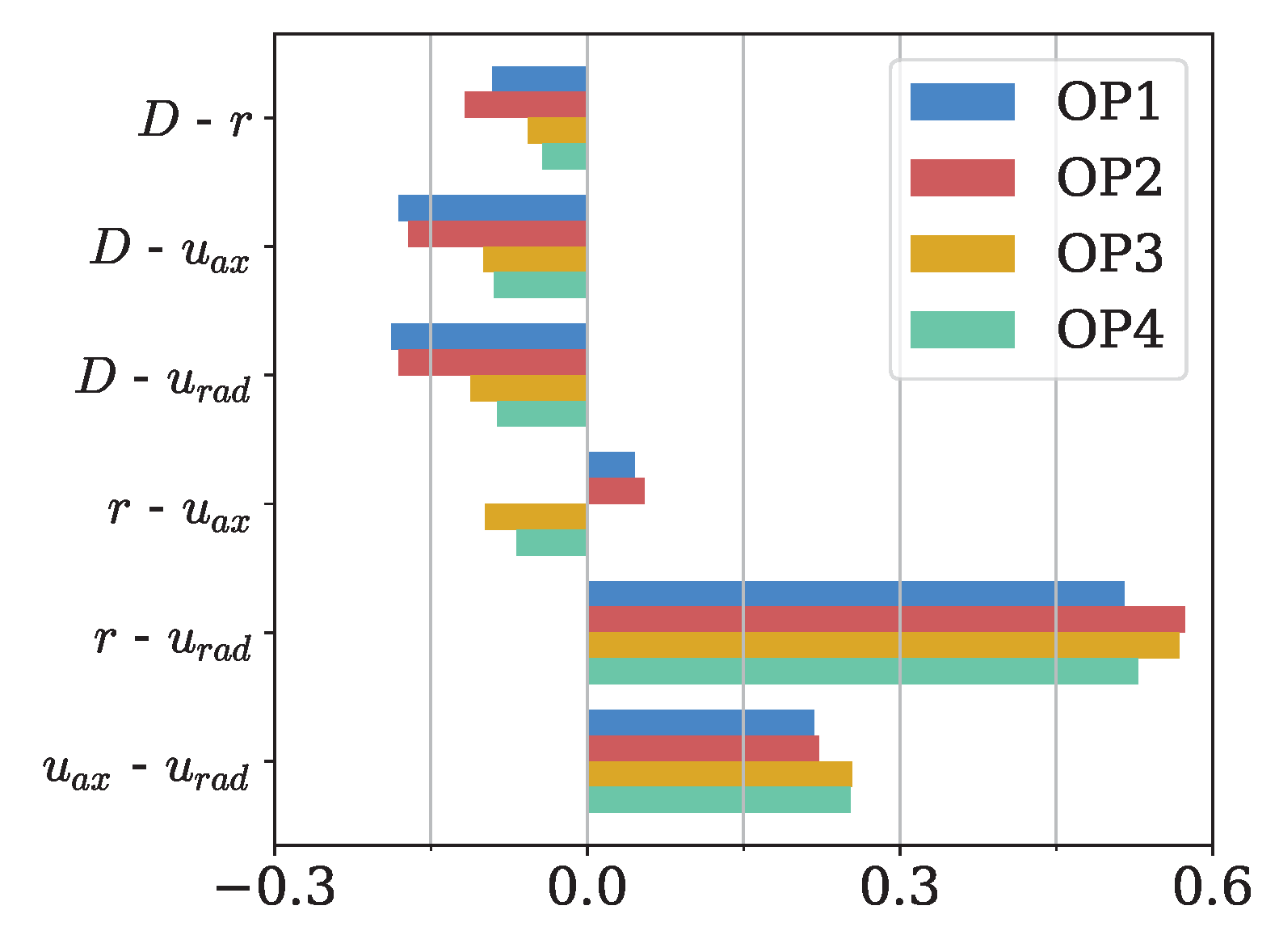
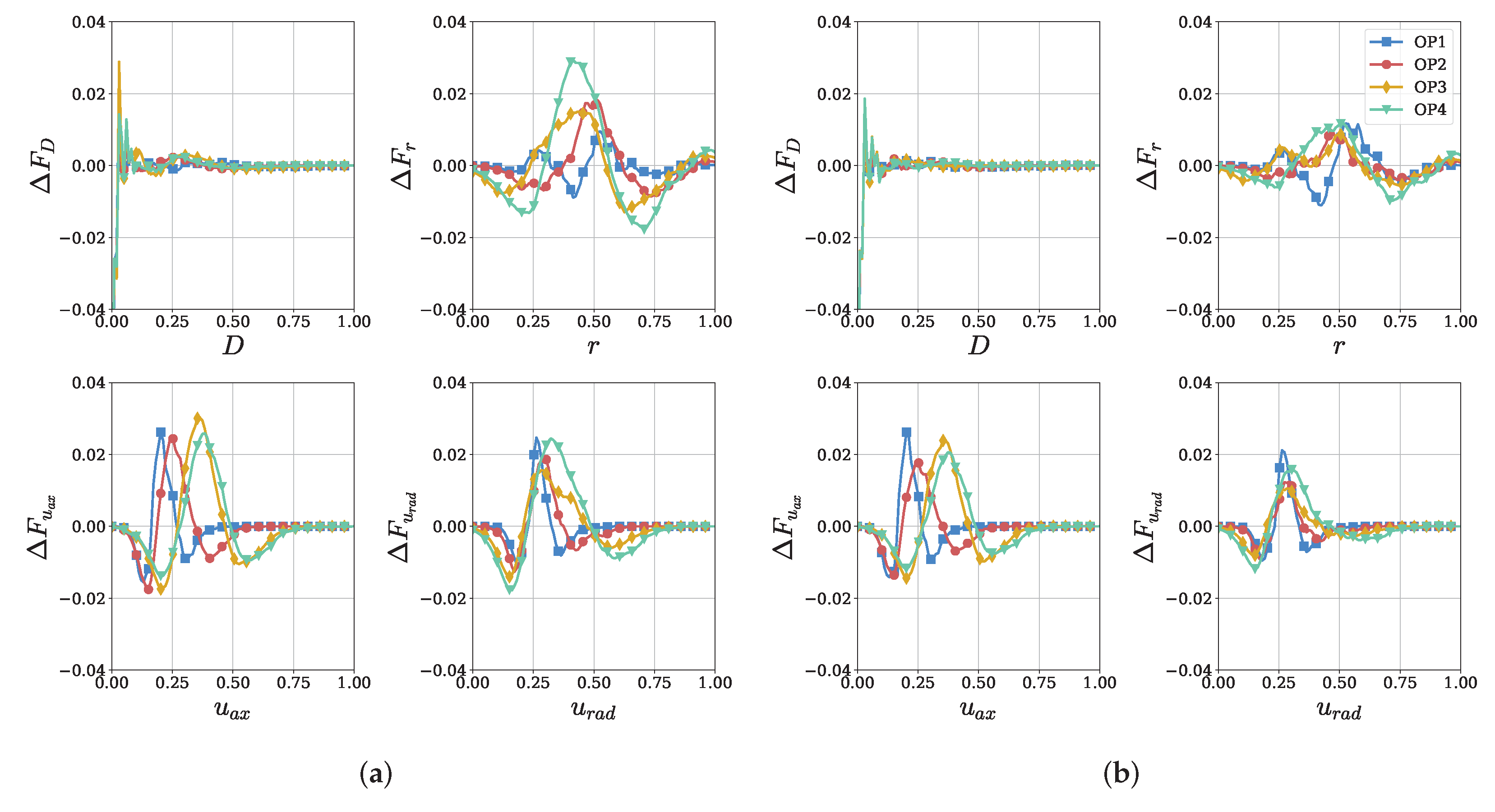
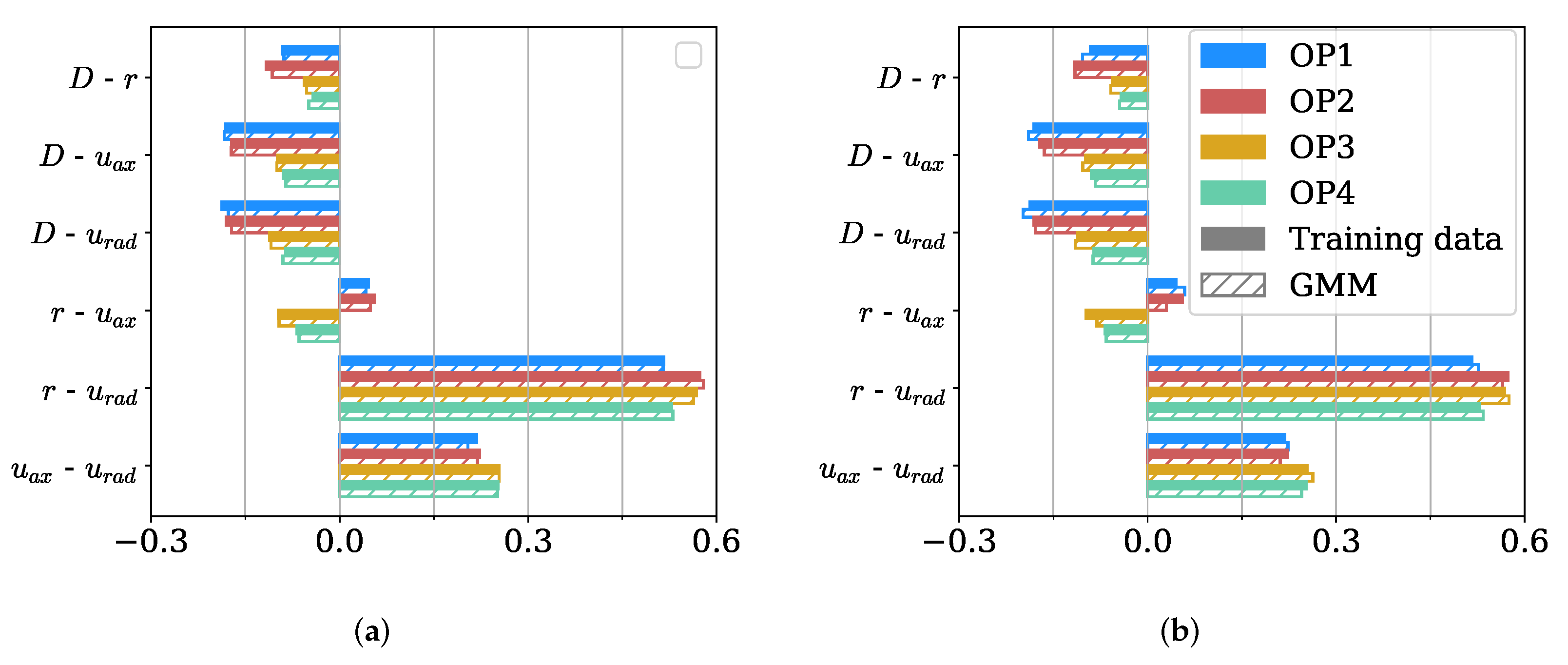
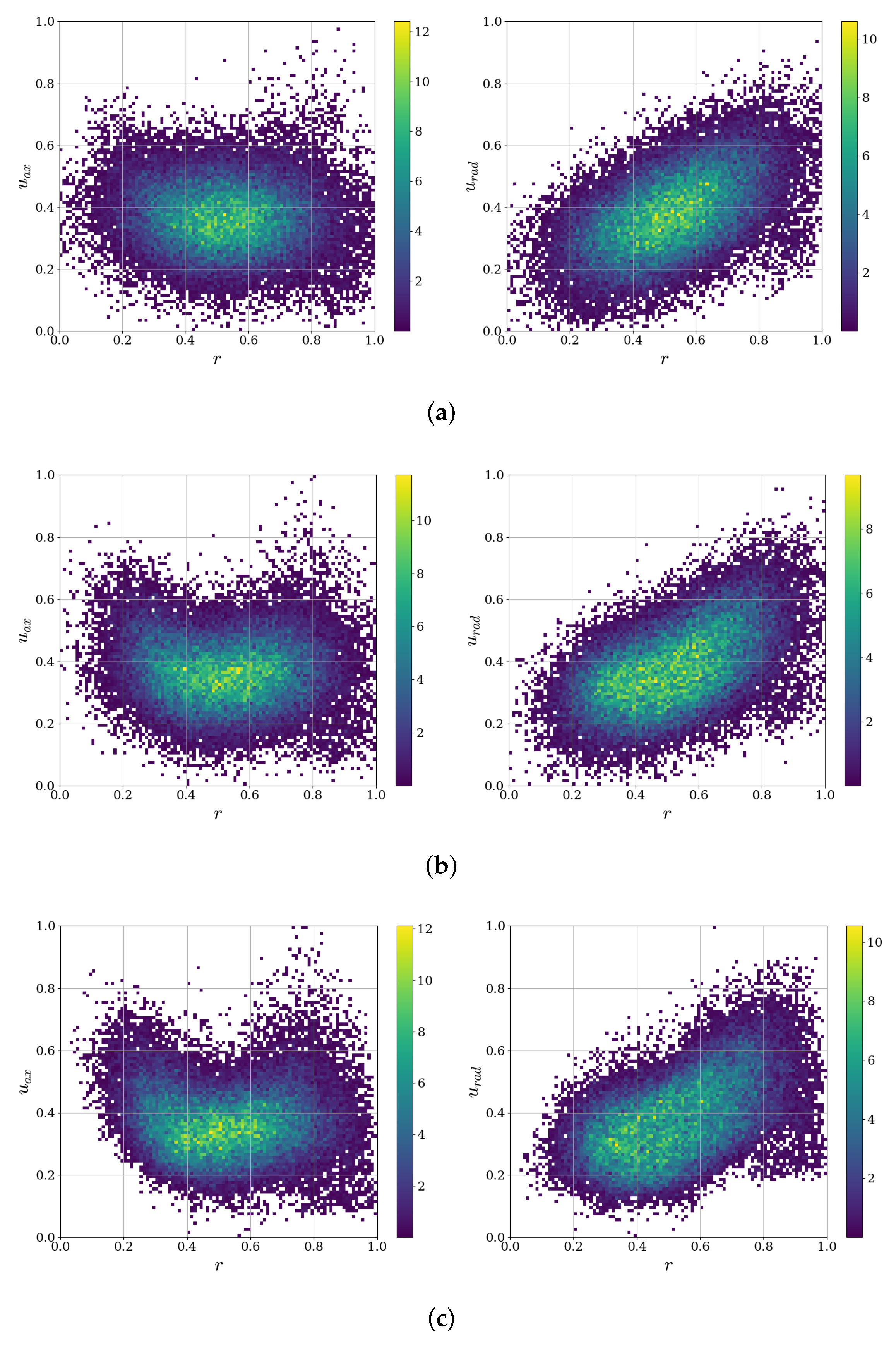
3.2. Conservation of Feature Correlations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CDF | Cumulative distribution function |
| GMM | Gaussian mixture model |
| GT | Ground truth |
| Probability density function | |
| SPH | Smoothed particle hydrodynamics |
References
- Kuo, K.K.; Acharya, R. Fundamentals of Turbulent and Multiphase Combustion; Wiley Online Library, Wiley: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Bürkle, N.; Holz, S.; Bärow, E.; Koch, R.; Bauer, H.J. Effect of Droplet Starting Conditions on the Spray Dispersion Resulting From a Swirl Cup Injector. In Proceedings of the Volume 2C: Turbomachinery—Design Methods and CFD Modeling for Turbomachinery; Ducts, Noise, and Component Interactions; American Society of Mechanical Engineers: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Puggelli, S.; Paccati, S.; Bertini, D.; Mazzei, L.; Giusti, A.; Andreini, A. Multi-coupled numerical simulations of the DLR Generic Single Sector Combustor. Combust. Sci. Technol. 2018, 190, 1409–1425. [Google Scholar] [CrossRef]
- Milan, P.J.; Torelli, R.; Lusch, B.; Magnotti, G.M. Data-Driven Model Reduction of Multiphase Flow In a Single-Hole Automotive Injector. At. Sprays 2020, 30, 401–429. [Google Scholar] [CrossRef]
- Mondal, S.; Torelli, R.; Lusch, B.; Milan, P.J.; Magnotti, G.M. Accelerating the Generation of Static Coupling Injection Maps Using a Data-Driven Emulator. SAE Int. J. Adv. Curr. Pract. Mobil. 2021, 3, 1408–1424. [Google Scholar] [CrossRef]
- Milan, P.J.; Mondal, S.; Torelli, R.; Lusch, B.; Maulik, R.; Magnotti, G.M. Data-Driven Modeling of Large-Eddy Simulations for Fuel Injector Design. In Proceedings of the AIAA Scitech 2021 Forum, Reston, VA, USA, 11–15 January 2021. [Google Scholar] [CrossRef]
- Jones, W.P.; Marquis, A.J.; Vogiatzaki, K. Large-eddy simulation of spray combustion in a gas turbine combustor. Combust. Flame 2014, 161, 222–239. [Google Scholar] [CrossRef]
- Keller, J.; Gebretsadik, M.; Habisreuther, P.; Turrini, F.; Zarzalis, N.; Trimis, D. Numerical and experimental investigation on droplet dynamics and dispersion of a jet engine injector. Int. J. Multiph. Flow 2015, 75, 144–162. [Google Scholar] [CrossRef]
- Gallot-Lavallée, S.; Jones, W.P.; Marquis, A.J. Large Eddy Simulation of an ethanol spray flame under MILD combustion with the stochastic fields method. Proc. Combust. Inst. 2017, 36, 2577–2584. [Google Scholar] [CrossRef]
- Chaussonnet, G.; Joshi, S.; Wachter, S.; Koch, R.; Jakobs, T.; Kolb, T.; Bauer, H.J. Air-Assisted Atomization at Constant Mass and Momentum Flow Rate: Investigation into the Ambient Pressure Influence with the Smoothed Particle Hydrodynamics Method. J. Eng. Gas Turbines Power 2020, 142, 031019. [Google Scholar] [CrossRef]
- Ates, C.; Karwan, F.; Okraschevski, M.; Koch, R.; Bauer, H.J. Conditional Generative Adversarial Networks for modelling fuel sprays. Energy AI 2023, 12, 100216. [Google Scholar] [CrossRef]
- Lefebvre, A. Atomization and Sprays; CRC Press: Boca Raton, FL, USA, 1988. [Google Scholar] [CrossRef]
- Gepperth, S.; Koch, R.; Bauer, H.J. Analysis and Comparison of Primary Droplet Characteristics in the Near Field of a Prefilming Airblast Atomizer. In Proceedings of the Volume 1A: Combustion, Fuels and Emissions; American Society of Mechanical Engineers: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Chaussonnet, G.; Vermorel, O.; Riber, E.; Cuenot, B. A new phenomenological model to predict drop size distribution in Large-Eddy Simulations of airblast atomizers. Int. J. Multiph. Flow 2016, 80, 29–42. [Google Scholar] [CrossRef]
- Comer, A.L.; Kipouros, T.; Stewart Cant, R. Multi-objective Numerical Investigation of a Generic Airblast Injector Design. J. Eng. Gas Turbines Power 2016, 138, 091501. [Google Scholar] [CrossRef]
- Sanjosé, M.; Senoner, J.M.; Jaegle, F.; Cuenot, B.; Moreau, S.; Poinsot, T. Fuel injection model for Euler–Euler and Euler–Lagrange large-eddy simulations of an evaporating spray inside an aeronautical combustor. Int. J. Multiph. Flow 2011, 37, 514–529. [Google Scholar] [CrossRef]
- Inamura, T.; Shirota, M.; Tsushima, M.; Kato, M.; Hamajima, S.; Sato, A. Spray characteristics of prefilming type of airblast atomizer. In Proceedings of the ICLASS, 12th Triennial International Annual Conference on Liquid Atomization and Spray Systems, Heidelberg, Germany, 2–6 September 2012. [Google Scholar]
- Hoffmann, S.; Holz, S.; Koch, R.; Bauer, H.J. Euler–Lagrangian simulation of the fuel spray of a planar prefilming airblast atomizer. CEAS Aeronaut. J. 2021, 12, 245–259. [Google Scholar] [CrossRef]
- Apte, S.V.; Mahesh, K.; Moin, P. Large-eddy simulation of evaporating spray in a coaxial combustor. Proc. Combust. Inst. 2009, 32, 2247–2256. [Google Scholar] [CrossRef]
- Coblenz, M.; Holz, S.; Bauer, H.J.; Grothe, O.; Koch, R. Modelling Fuel Injector Spray Characteristics in Jet Engines by Using Vine Copulas. J. R. Stat. Soc. Ser. Appl. Stat. 2020, 69, 863–886. [Google Scholar] [CrossRef]
- Holz, S.; Braun, S.; Chaussonnet, G.; Koch, R.; Bauer, H.J. Close Nozzle Spray Characteristics of a Prefilming Airblast Atomizer. Energies 2019, 12, 2835. [Google Scholar] [CrossRef]
- Okraschevski, M.; Mesquita, L.C.C.; Koch, R.; Mastorakos, E.; Bauer, H.J. A Numerical Study of Aero Engine Sub-idle Operation: From a Realistic Representation of Spray Injection to Detailed Chemistry LES-CMC. Flow Turbul. Combust. 2023, 111, 493–530. [Google Scholar] [CrossRef]
- Chaussonnet, G.; Müller, A.; Holz, S.; Koch, R.; Bauer, H.J. Time-Response of Recent Prefilming Airblast Atomization Models in an Oscillating Air Flow Field. J. Eng. Gas Turbines Power 2017, 139, 121501. [Google Scholar] [CrossRef]
- Lo Schiavo, E.; Laera, D.; Riber, E.; Gicquel, L.; Poinsot, T. Effects of liquid fuel/wall interaction on thermoacoustic instabilities in swirling spray flames. Combust. Flame 2020, 219, 86–101. [Google Scholar] [CrossRef]
- Braun, S.; Wieth, L.; Holz, S.; Dauch, T.F.; Keller, M.C.; Chaussonnet, G.; Gepperth, S.; Koch, R.; Bauer, H.J. Numerical prediction of air-assisted primary atomization using Smoothed Particle Hydrodynamics. Int. J. Multiph. Flow 2019, 114, 303–315. [Google Scholar] [CrossRef]
- Dauch, T.F.; Chaussonnet, G.; Keller, M.C.; Okraschevski, M.; Ates, C.; Koch, R.; Bauer, H.J. 3D Predictions of the Primary Breakup of Fuel in Spray Nozzles for Aero Engines. In High Performance Computing in Science and Engineering ’20; Nagel, W.E., Kröner, D.H., Resch, M.M., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 419–433. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Information Science and Statistics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
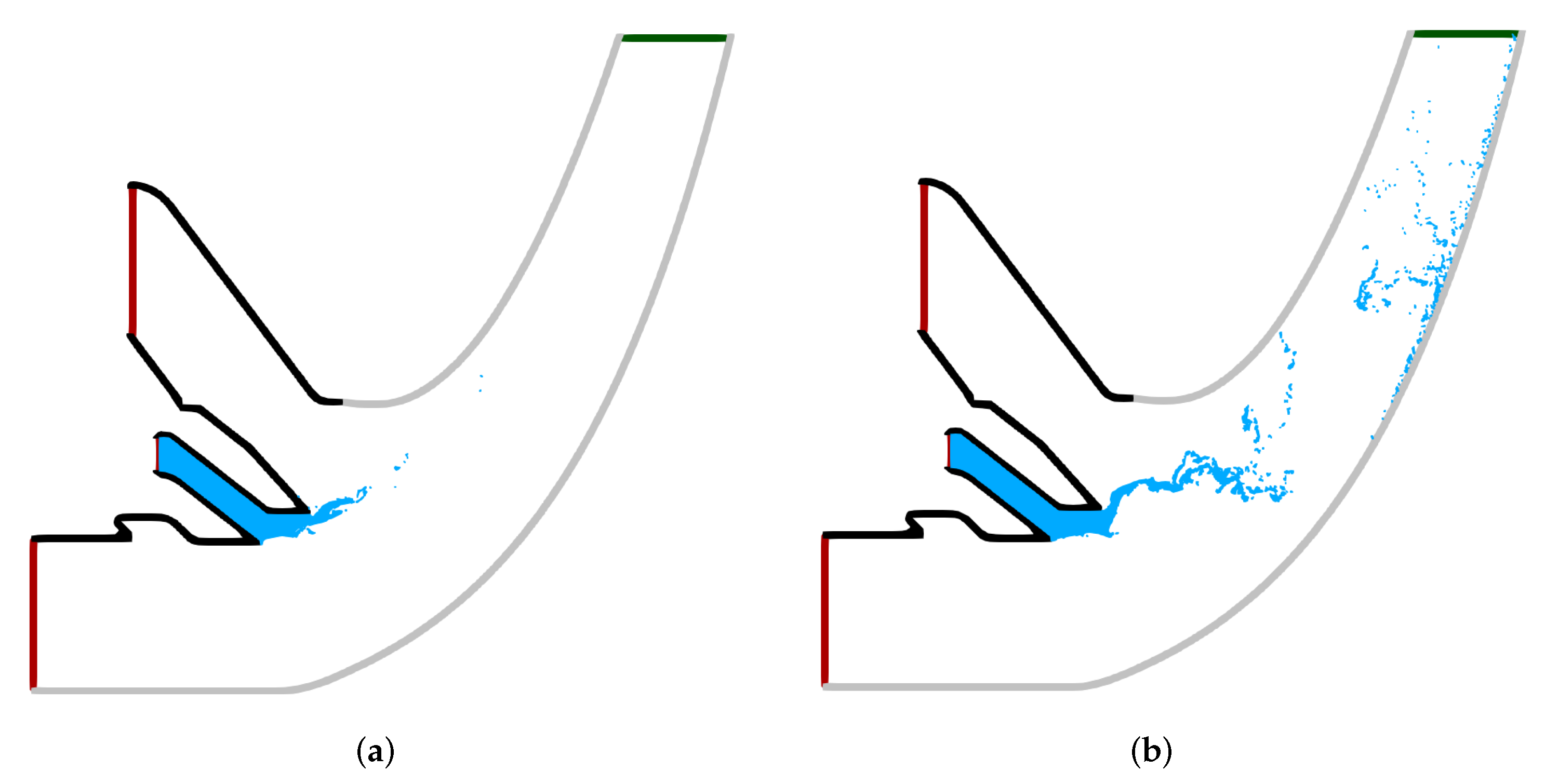

| 1 | 2 | 3 | 4 | |
| N | 6094 | 15,501 | 44,484 | 44,572 |
| Feature | D | r | ||
| Distribution | Exponentiated Weibull | Johnson SB | Log-normal | Log-normal |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wicker, M.; Ates, C.; Okraschevski, M.; Holz, S.; Koch, R.; Bauer, H.-J. Modeling Multivariate Spray Characteristics with Gaussian Mixture Models. Energies 2023, 16, 6818. https://doi.org/10.3390/en16196818
Wicker M, Ates C, Okraschevski M, Holz S, Koch R, Bauer H-J. Modeling Multivariate Spray Characteristics with Gaussian Mixture Models. Energies. 2023; 16(19):6818. https://doi.org/10.3390/en16196818
Chicago/Turabian StyleWicker, Markus, Cihan Ates, Max Okraschevski, Simon Holz, Rainer Koch, and Hans-Jörg Bauer. 2023. "Modeling Multivariate Spray Characteristics with Gaussian Mixture Models" Energies 16, no. 19: 6818. https://doi.org/10.3390/en16196818
APA StyleWicker, M., Ates, C., Okraschevski, M., Holz, S., Koch, R., & Bauer, H.-J. (2023). Modeling Multivariate Spray Characteristics with Gaussian Mixture Models. Energies, 16(19), 6818. https://doi.org/10.3390/en16196818







