Abstract
China’s electricity market reform has posed a real challenge to the large-scale hydropower system. Taking the world’s largest watershed hydropower system, the Three Gorges large hydropower system (TGLHS), as the engineering background, this study analyzes the issues and strategies of dispatching and trading in the electricity market. The analysis indicates that the TGLHS exhibits unique difficulties because of transprovincial and transregional power transmission. Major issues including the multi-dimensional and multi-time-scale nested allocation of hydropower energy, the bidding and performance of cascaded hydropower plants in multiple electricity markets, as well as multiple uncertainties in the runoff; electricity prices in multiple markets are also elaborated upon. The corresponding suggested strategies are proposed to cope with the aforementioned issues: (1) for multi-dimensional and multi-scale nested allocation problems, it is necessary to comprehensively consider monthly market transactions and priority generation plans, and establish a profit maximization model; (2) propose a bidding decision-making linkage and segmented bidding optimization model for cascades upstream and downstream hydropower stations; (3) construct a model for decomposing the annual and monthly planned electricity consumption curves and developing operational plans for giant cascade power stations that are suitable for cross-provincial and cross-regional power transmission and transformation; (4) a runoff, electricity price, and market distribution model has been proposed, laying the foundation for further research on multi-scale optimization models for hydropower. Finally, prospects for research on the participation of large-scale hydropower systems in the electricity market are summarized, expecting to promote the marketization of large cascaded hydropower systems. The dispatching and trading of the TGLHS implies that it is important and necessary to explore market theories and methods considering hydropower characteristics and operation needs.
1. Introduction
The electricity market reform that was launched in 2015 has greatly changed the dispatch and operation methods of China’s power systems [1]. Currently, the electricity market has entered a comprehensive deepening stage of “market-oriented reform with a focus on market-oriented trading, market-oriented allocation, and market-oriented layout”. The next stage of the work will focus on how to accelerate the implementation from the medium to the long term as well as spot trading [2]. The reform of China’s electricity market has entered the fast lane. It is an inevitable trend for hydropower to gradually fully participate in the electricity market [3,4].
The Three Gorges large hydropower system (TGLHS) is mainly composed of four giant hydropower stations in the lower reaches of the Jinsha River and two giant hydropower stations in the middle and lower reaches of the Yangtze River [5,6], as shown in Figure 1. The total installed capacity of the six cascade hydropower stations is 70.315 million kW, accounting for about 17% of the national hydropower installed capacity. In 2022, the total power generation was about 262.2 billion kW, accounting for nearly 20% of the national hydropower generation. Both in terms of installed capacity and power generation, it ranks first in the country’s hydropower industry and plays a very important role in China’s hydropower and national energy structure system.
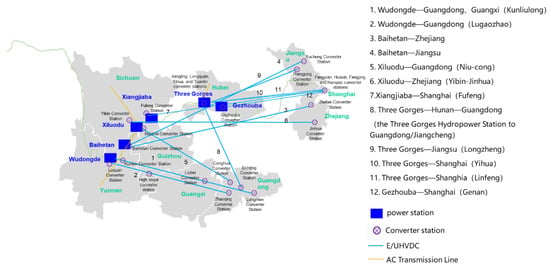
Figure 1.
The Three Gorges hydropower system and power transmission.
In the past, research on the Three Gorges hydropower system focused on hydropower dispatch issues, with few studies on electricity market transactions. However, the development environment of China’s electricity market is undergoing significant changes. In the primary stage of the market-oriented development of the “dual track system”, where market-oriented electricity and traditional planned electricity coexist in China, as a leader in China’s hydropower industry, how the TGLHS responds to marketization issues, participates in electricity market issues, and formulates electricity market trading strategies is not only related to the core interests of enterprises, but more importantly, to the functional positioning of hydropower in China’s energy structure system [7,8]. Therefore, it is of great significance to contemplate the marketization of the Three Gorges hydropower system at the top level and conduct research on the trading strategy of the hydropower project.
How to balance the benefits and risks in the marketization process of the TGLHS? How to reflect the clean energy value of hydropower in the marketization process, achieve the efficient consumption of hydropower, and avoid water abandonment and power grid shortages caused by the market process? The first issue is the core issue that urgently needs to be addressed in the market-oriented trading of the TGLHS, which requires systematic research on theoretical methods, trading strategies, and technical support systems [9,10,11]. The latter issue needs to be identified at the national energy strategy level through an in-depth exploration of the green value chain of hydropower, and its green value system should be included in the transaction rules system, which will be a highly valued issue in the future.
The biggest challenge and main task faced by the Three Gorges hydropower company in participating in the electricity market is how to reasonably allocate hydropower resources through medium-to-long-term trading and spot markets based on future runoff forecasting, electricity price analysis, and market conditions, in order to obtain stable benefits and reduce the losses caused by market risks [12,13]. Another difficulty is how to decompose the contracted electricity quantity into monthly and daily quantities, and how to decompose the daily electricity quantity into hourly and 96-point curves for signed medium-to-long-term contracts, in order to complete the performance and provide self-generating schedule curves for the day-ahead market [14,15]. Considering the changes in runoff and electricity prices, hydropower stations face different comprehensive utilization requirements at different times. Decomposing the long-term contract curve of hydropower is not a simple task. In addition to being related to the efficient utilization of water energy, it is also closely related to market rules and is a very complex process. The above two prominent difficulties are the main challenges of market-oriented bidding for the hydropower system.
2. Major Issues
2.1. Multi-Dimensional and Multi-Time-Scale Nested Allocation for Cascaded Hydropower
This paper considers two optimization objectives: the maximum market utility function value and the maximum carryover storage of cascade stations.
The participation of hydropower in the electricity market involves the combination and allocation of hydropower and electricity cakes in three dimensions: the time scale market (annual, monthly, daily, intraday, and real-time), the diversified spatial market (intra-provincial, inter-provincial, and interconnection line regional markets), and trading varieties (bilateral, listing, daily market, and peak shaving and frequency regulation auxiliary services) [16,17]. The essence is a multidimensional long-, medium-, and short-term nested combination optimization problem. This is the basic work for the participation of the Three Gorges hydropower system in the electricity market. According to the different stages in the promotion of the electricity market, there are two stages involved: the transitional electricity market and the complete electricity market, as shown in Figure 2. Therefore, in response to the two stage issues mentioned above, it involves two core issues: how to negotiate with the receiving power grid to determine the priority electricity quantity and price, and how to participate in the power trading of the receiving power grid.
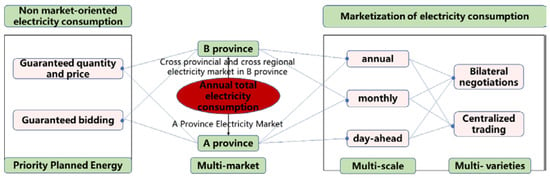
Figure 2.
Multi-dimensional electricity allocation.
2.2. Bidding of Cascaded Hydropower Plants in Multiple Electricity Markets
As shown in Figure 3, the biggest challenge and main task faced by the Three Gorges Dam in participating in the electricity market is how to reasonably allocate hydropower resources through medium- and long-term bilateral trading contracts and spot markets based on future runoff forecasting, electricity price analysis, and market conditions, in order to obtain stable benefits and reduce the losses caused by market risks [18,19]. Therefore, it is necessary to conduct research on the optimal allocation model of hydropower marketization under a multi-scale combination based on possible market conditions, guide the Three Gorges hydropower project to respond to market price changes, optimize electricity allocation to obtain high returns, and scientifically utilize the combination market to avoid risks. The main challenges are as follows: ① how to establish a coupled benefit model in a multi-scale market; ② how to establish a risk model in a multi-scale market; ③ how to reduce the dimensionality of high-dimensional optimization models for the solution; ④ how to establish the relationship between risk changes and bidding decisions.
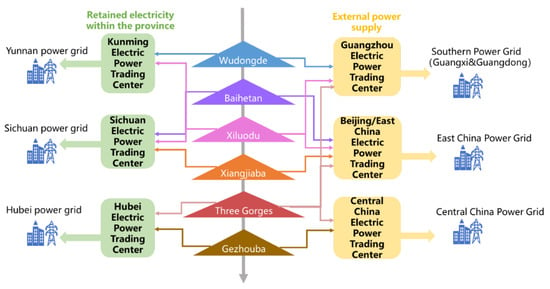
Figure 3.
Bidding of cascaded hydropower in multiple markets.
2.3. Performance of Cascaded Hydropower Plants in Multiple Electricity Markets
In the framework of a multi-scale and diversified electricity market, in order to achieve medium-to-long-term trading and short-term trading, and to connect with spot market trading, it is necessary to decompose medium-to-long-term trading contracts into electricity curves at different time scales [20]. This is the basis for signing electricity purchase and sales contracts with power grid companies and large users. As shown in Figure 4, the decomposition of medium-to-long-term contracts involves breaking down annual contracts into monthly scales, further breaking down monthly contracts into daily scales, and finally breaking down daily contracts into time-sharing power curves. The entire decomposition process involves a large time span and is coupled with the long-term, medium, and short-term scheduling of hydropower. At the same time, it is necessary to consider the impact of contract performance on the decomposition and the complex characteristics of hydropower.
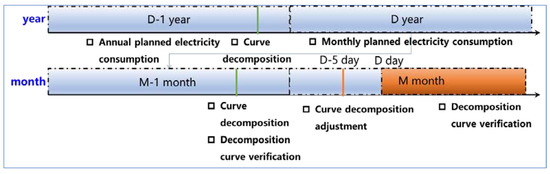
Figure 4.
Distribution of bidding electricity in multiple time scales.
The difficulty of this problem is reflected in the following aspects: firstly, there are restrictions on the proportions of electricity in each power station and receiving province. The distribution proportion of electricity in different varieties needs to be controlled separately. At the same time, the load curve characteristics of different provinces are different, making it difficult to adjust the peak response [21]. Secondly, there is a “one reservoir, two dispatch” power station represented by Xiluodu, where multiple types of electricity need to consider the overall distribution ratio and the distribution ratio between the two plants; the third is the complexity of time granularity, with nested time scales of year, month, and day, and interconnected problems; the fourth is the various complex constraints related to the scheduling and operation of power plants, with strong spatiotemporal coupling and high difficulty in modeling and solving. It is a very complex high-dimensional nonlinear optimization problem.
2.4. Multiple Uncertainties in Runoff, Electricity Price in Multiple Markets
Accurately describing the temporal and spatial evolution of runoff, electricity price, and market uncertainty under market conditions is the foundation and prerequisite for the participation of TGLHS in the electricity market [22,23], as shown in Figure 5. The inflow runoff is a stochastic process with time correlation, and both medium- and long-term trading electricity prices and spot electricity prices are related to the runoff of hydropower stations. Therefore, before formulating bidding strategies in a diversified electricity market, it is necessary to study the joint spatiotemporal evolution of natural runoff from hydropower stations and electricity prices in different markets. In summary, describing the multi-scale and diversified electricity market runoff, electricity prices, and market spatiotemporal evolution patterns mainly faces the following four difficulties: ① how to describe the non-stationary characteristics of hydropower station runoff series and market electricity price series; ② how to describe high-dimensional time series models of runoff composition for different power stations; ③ how to consider the heteroscedasticity characteristics of runoff and electricity prices at different times; ④ how to describe the time-varying correlation between runoff and electricity prices.

Figure 5.
Multiple uncertainties of runoff and price in different electricity markets. (a) Runoff curve. (b) Clear electricity price curve.
3. Strategy Suggestion
3.1. Multi-Dimensional and Multi-Time-Scale Nested Location Strategy for Cascaded Hydropower Plants
The difficulty in the multi-dimensional and multi-time-scale nested allocation problem of cascade hydropower lies in the large market dimension, which involves the two regional power markets of the China Southern Power Grid and the State Grid, as well as the two provincial power markets of Yunnan and Sichuan. There are three time scales: annual, monthly, and daily, as well as different transaction varieties such as bilateral negotiation, centralized trading, and incremental outward transmission. At the same time, during the transition period of marketization, there are also two priority power generation plans: guaranteed quantity and guaranteed price, and guaranteed quantity and limited price. In this case, the provincial monthly and daily market can be considered comprehensively according to settlement rules, collectively referred to as monthly market transactions; taking into account both guaranteed quantity and price, as well as guaranteed quantity bidding, as the priority electricity generation plan, this study mainly focuses on the rational allocation of the electricity generation of the Three Gorges hydropower project among the following multiple trading varieties: priority electricity generation plans in four regional and provincial markets, market-oriented increment, annual bilateral transactions, annual centralized transactions, and monthly market transactions.
Based on the above ideas, a suitable mathematical model can be established with the goal of maximizing the total revenue of the TGLHS, considering hydraulic constraints, as well as policy constraints such as the power transmission ratio and annual contract signing ratio, in order to determine the optimal multi-dimensional electricity distribution plan [24,25].
- (1)
- Objective functionwhere denotes the trading of electricity of variety m in period t; denotes the trading electricity price of variety m in period t; is the spill discharge in period t; are the period index and total periods, respectively; and are the trading variety index and total number, respectively.
- (2)
- Hydraulic constraints
- ■
- Water balance constraints:where is the reservoir storage in period t; It is reservoir inflow in period t; is reservoir outflow in period t; and is turbine discharge in period t.
- ■
- Initial and final water level control constraints:where and are the reservoir water level at the beginning and end of the operational horizon, respectively.
- ■
- Reservoir water level constraints:where and are the minimum and maximum of the reservoir water level in period t, respectively.
- ■
- Turbine discharge limitation:where and are the minimum and maximum of the turbine discharge in period t, respectively.
- ■
- Relationship between the water level and reservoir storage:where is the relationship between the reservoir storage and the water level.
- ■
- Reservoir outflow limitation:where and are the minimum and maximum of the reservoir outflow in period t, respectively.
- ■
- Power generation limitation:where and are the minimum and maximum of the power generation in period t, respectively.
- ■
- Minimum technical output of hydropower unit:
- ■
- Relationship between the tailrace water level and reservoir discharge:where is the relationship between the tailrace water level and the reservoir outflow.
- ■
- Net head constraints:where and are the net head and head loss in period t, respectively.
- ■
- Head loss constraints:where is the relationship between the head loss and the turbine discharge.
- ■
- Power generation function:where is the relationship between the net head and the generating efficiency.
3.2. Bidding Strategies for Cascade Hydropower Plants in Multiple Electricity Markets
The electricity distribution of the downstream cascade hydropower plants of the Jinsha River in multi-provincial markets is composed of electricity and hydraulic channels. This problem is a typical multi-market collaborative bidding problem under random conditions, facing multiple uncertainties in electricity prices and runoff from each market, involving multi-region, multi-time period, and multi-variety electricity distribution, the linkage of bidding decisions for upstream and downstream power stations in the cascade, and the optimization of optimal pricing corresponding to multi-stage bidding electricity, as shown in Figure 6.
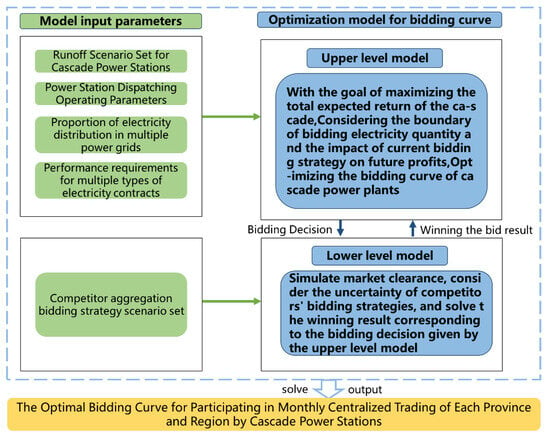
Figure 6.
Bidding strategy modeling of cascaded hydropower plants.
Considering the requirements of annual electricity contract performance, constraints on the consumption space of the end grid market, constraints on the inter-provincial transmission capacity of the downstream cascade hydropower plants of the Jinsha River, and requirements for the proportion of electricity distribution among multiple provinces, as well as stochastic electricity prices and runoff processes, a double-layer stochastic programming model is constructed to synergistically optimize the segmented bidding curves of each power station downstream of the Jinsha River participating in the monthly centralized market of each province. Firstly, the uncertainty of incoming water is represented in the model through scenario analysis [26]. Secondly, the bidding strategies of competitors are aggregated to suppress the uncertainty of individual bidding strategies. Then, the aggregated bidding strategies of competitors are inferred through the historical market-clearing electricity prices and transaction electricity quantities, generating a set of competitor strategy scenarios to describe the uncertainty of the Jinsha River cascade’s monthly centralized market competitor strategies in each province. Thirdly, considering that the majority of electricity in the Jinsha River cascade will still be consumed in the form of planned electricity or annual bilateral electricity within a certain period of time, the electricity share participating in the monthly centralized market of each province and region is relatively small, and there is a lack of historical transaction data, making it difficult to accurately estimate the market supply and demand curve. Therefore, it is assumed that the Jinsha River cascade hydropower system will participate in the monthly centralized trading of each province and region as a price receiver. In this case, its bidding strategy will not affect the aggregation strategy of its competitors. Fourthly, the model takes months as the optimization step and years as the optimization cycle, so as to fully consider the impact of the current bidding strategy on the future power generation capacity when optimizing and formulating the monthly bidding strategy for the Jinsha River cascade hydropower system [27].
3.3. Strategy for Electricity Market Performance of Cascaded Hydropower Plants
The focus of this problem lies in the curve decomposition and verification analysis of the trading electricity quantity for cascade hydropower dispatching. It can be divided into annual, monthly, and daily tasks based on time scales. The planned electricity penalty mechanism for various scale tasks is based on the transaction rules issued by the state. The negative deviation of planned electricity is assessed based on several times the planned electricity price, and the positive deviation is settled in time based on market-oriented electricity prices. The annual curve decomposition task is to determine the boundary of planned electricity levels around October each year. At this stage, it is necessary to determine how the planned electricity is accurately distributed between power stations each month, and to construct decomposition criteria for the typical curves of each month based on each receiving province [28]. According to certain criteria, the typical output curves of each power station and each province are determined. After marketization is liberalized, it is also necessary to combine market punishment mechanisms and market conditions in different provinces to carry out the marketization of electricity levels in each month among provinces. The monthly curve decomposition task takes the annual curve decomposition results in that month as the performance boundary. Before or after the 10th day of each month, it is necessary to determine the planned electricity consumption decomposition curves for each power station, province, and variety in the following month based on the performance situation of the month that has occurred and the latest predicted inflow, combined with the time sharing coefficient limit issued by the power grid. After the liberalization of marketization, it is also necessary to adjust the market-oriented electricity consumption of each power station, province, and variety according to the market conditions of different provinces to provide a reasonable distribution among provinces.
Based on the above ideas, it is necessary to construct an annual and monthly planned electricity curve decomposition as well as an operation plan formulation model that is suitable for the inter-provincial and inter-regional power transmission of giant cascade power stations.
Before the beginning of the year, the water levels of each power station in the Jinsha River cascaded hydropower system were determined by referring to the historical monthly water level control forms and the latest runoff forecast information. The planned electricity levels of each power station, month, and province were allocated (Chapter 7 provides the boundaries for consumption and the scheduling strategies), and the typical output curves of each power station, month, and province were determined according to certain criteria, as well as the water level control process at the monthly scale of each power station. As shown in Figure 7.
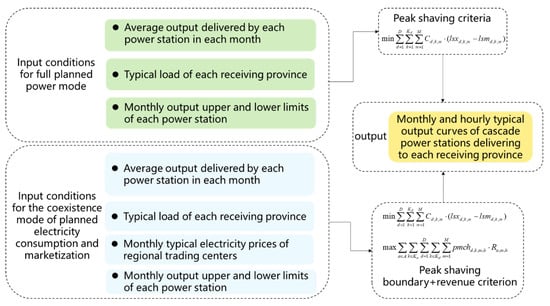
Figure 7.
Strategy for the electricity market performance of cascaded hydropower plants.
Considering the load characteristics of receiving provinces, a complex peak-shaving target for multiple time scales and multiple receiving power grids is proposed as the decomposition criterion for the planned electricity curve. Furthermore, a long-term multi-grid peak-shaving and planned electricity curve decomposition model considering the load differences between provinces and months is constructed. This model can allocate planned electricity between months and provinces based on monthly and provincial peak shaving, fully leveraging the superior regulation performance of hydropower and providing medium-to-long-term water level control, as well as provide decision support for the monthly and provincial distribution of planned electricity and the decomposition of the planned electricity curve.
On the basis of considering the settlement rules of planned electricity and market-oriented electricity, allocation decisions are made for the planned electricity of each power station, month, and province, and market-oriented electricity is planned. It is proposed to construct the maximum benefit criterion to determine the typical output curve of planned electricity and market-oriented electricity of each power station, month, and province. In the future, regional markets may require large-scale hydropower enterprises for market-oriented electricity settlement. Therefore, it is necessary to provide typical monthly electricity price curves for the two trading centers as the basis for market-oriented electricity settlement, exploring and analyzing the impact of peak-shaving requirements at different levels of the planned electricity curve on market-oriented electricity revenue.
- (1)
- Objective functionwhere is the monthly power transmission ratio of power station d, province k, and month m; is the market-oriented electricity output decision for power station d, province k, month m, and h hour; is the typical market electricity price for month m and hour h in the market area a; is the negative deviation of the monthly planned electricity consumption of power station d, and the performance is achieved; is the number of days in m month; is the planned electricity price formulated by the country; is the negative deviation penalty coefficient; is the monthly power transmission ratio of power station d, province k, and month m; is the maximum remaining load of province k in month m; is the minimum remaining load in month m of province k.
- (2)
- Constraints
- (a)
- Hydraulic constraints:
- ■
- Consistent with hydraulic constraints in Section 3.1.
- (b)
- Market constraints:
- ■
- Cross-provincial power transmission ratio limit;where PP is the proportion of electricity distribution among multiple provinces receiving electricity; pfcoef is the fluctuation coefficient of the electricity proportion in each province within ten days.
- ■
- Electricity control conditions for various varieties.where is the contracted electricity consumption of variety v in province k, in billions of kWh. The power station needs to meet the power transmission requirements allocated to the corresponding provinces and varieties in the current month.
- (c)
- Power constraints:
- ■
- Daily output constraint within ten days;where is the daily average output of x days; is a set of corresponding time periods (days) for x ten days, meeting the output control requirements for each day in the upper, middle, and lower ten days, MW.
- ■
- Electricity balance constraints;where is the power plant output at x ten days and h, MW; is the proportion of the output of the branch power station relative to the overall output of the power station.
- ■
- Output upper limit constraint;The typical output curve of each ten-day period cannot exceed the corresponding maximum output during each time period.
- ■
- Power balance constraints;The curve decomposition results of multiple varieties of electricity in each province and each ten-day period need to meet the typical daily output of the power station, that is, to achieve an hourly power balance.
- ■
- Stable output constraint.where , is the minimum interval period of the power plant output.
3.4. Strategy for Describing Multiple Uncertainties in Runoff and Electricity Prices of Multiple Markets
The main research focuses on multi-scale (annual, monthly, and daily) electricity prices, runoff, and market relationships in multiple markets (for Yunnan, it currently refers to the province’s internal and external power transmission from the west to the east, and may also include the East China export market in the future). Furthermore, a joint distribution model for runoff, electricity prices, and markets is proposed, laying the foundation for further research on multi-scale optimization models for hydropower.
We plan to use the market electricity price runoff joint scenario generation method to reasonably describe the complex correlation stochastic process of electricity prices in different markets at the regional and provincial levels, as well as the monthly runoff of hydropower stations. As shown in Figure 8. This method mainly consists of three core steps: using nearest neighbor propagation (AP) clustering to extract the annual periodic joint fluctuation characteristics of runoff and the provincial electricity prices; using a double chain Markov model to describe the seasonal fluctuations of runoff within a year and the differences in annual abundance, evenness, and dryness; and extracting the correlation between provincial and regional electricity prices through the Copula model. The main process of this method is shown in the following figure, where the de-periodic runoff series, typical runoff series, and de-periodic provincial electricity price series respectively represent the annual differences in runoff, the seasonal changes in runoff, and the impact of removing runoff on electricity price correlation [29,30,31].
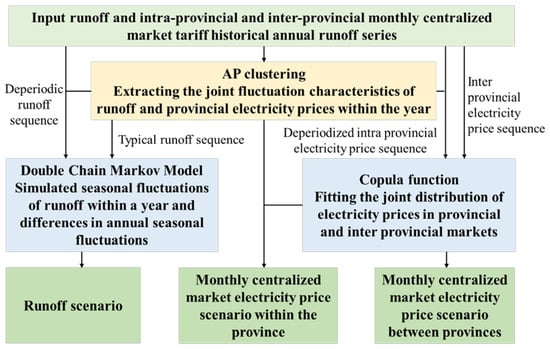
Figure 8.
Description of multiple uncertainties in runoff and electricity prices.
4. Prospects for Research on the Participation of the Large-Scale Hydropower System in the Electricity Market
The biggest difficulty and main task faced by hydropower enterprises in participating in the electricity market is how to reasonably allocate hydropower resources through medium- and long-term bilateral trading contracts and spot markets based on future runoff forecasting, electricity price analysis, and market conditions, in order to obtain stable benefits and reduce the losses caused by market risks. Another difficulty is how to decompose the contracted electricity quantity into monthly and daily quantities, and how to decompose the daily electricity quantity into hourly and 96-point curves for signed medium-to-long-term contracts, in order to complete performance and provide self-generating schedule curves for the day-ahead market. Considering the changes in runoff and electricity prices, hydropower stations face different comprehensive utilization requirements at different times. Decomposing the long-term contract curve of hydropower is not a simple task. In addition to being related to the efficient utilization of water energy, it is also closely related to market rules and is a very complex process. The above two prominent difficulties are the main challenges of market-oriented bidding for hydropower.
Focusing on the two major difficulties of the hydropower market entities, pre and post, the following four issues will be studied.
- (1)
- Multi-scale and diversified electricity market runoff, electricity prices, and market spatiotemporal evolution patterns. The main research focuses on multi-scale (annual, monthly, and daily) electricity prices, runoff, and market relationships in multiple markets (for Yunnan, it currently refers to the province’s internal and external power transmission from the west to the east, and may also include the East China export market in the future). Furthermore, a joint distribution model for runoff, electricity prices, and markets is proposed, laying the foundation for further research on multi-scale optimization models for hydropower. Additionally, future electricity markets will be challenged by multiple scales and diversification, which will have a profound impact on runoff, electricity price, and the patterns of the spatiotemporal evolution of markets. With the growth of renewable energy and the development of smart grids, we can expect greater market fragmentation and diversification. This means that the spatiotemporal evolution of electricity markets will become more complex, and more accurate models will be needed to predict and respond to these changes. At the same time, climate change will increase runoff uncertainty, while electricity prices will become more variable as a result of policy, technology and market factors. Therefore, future research will focus on the development of more flexible and adaptive models to better understand and predict the diverse trends in electricity markets to support the sustainable development of hydropower.
- (2)
- Multiple uncertainty market-oriented resource allocation methods for hydropower. On the basis of question 1, it is necessary to further develop market-oriented resource allocation methods for hydropower with different time scales and multiple time scale coupling, with a focus on addressing the uncertainty, high-dimensional reduction, and market gaming issues that may arise from diverse markets. For example, in a multi-scale market, in addition to considering upstream and downstream hydropower connections, cascade hydropower must also consider multi-market price issues due to the market structure, the coupled issues of the performance process caused by the settlement rules, and the market risk caused by forward decision making. Another aspect to consider is the uncertainty risk brought about by the multi-timescale coupled market, and further optimizing the medium- and long-term power generation plan can guide cascade hydropower to respond to market price changes and obtain high revenue through the optimization of power allocation. In addition, the level of forecasting for runoff and electricity prices should be further strengthened in the future to further capture the power station’s generating capacity and future profitability, which can better provide a basis for decision making on resource allocation at different time scales.
- (3)
- Decomposition method for the medium- and long-term hydropower trading curves. The decomposition of medium-to-long-term trading curves is crucial for ensuring smooth trading, but it is very complex and difficult in practical operations. We need to have an in-depth understanding of its complexity and criticality. This involves the interplay of a number of factors, including runoff conditions, fluctuations in electricity prices, and changes in market conditions. In the first place, runoff conditions, including natural factors such as rainfall and snowmelt, need to be studied to determine the availability and stability of water supply. Moreover, fluctuations in electricity prices are also a key factor as they directly affect the economics and profitability of hydropower projects. Finally, market conditions such as market competition, policy changes, and demand fluctuations can also have an impact on medium- and long-term hydropower trading curves. In order to better understand these influences, corresponding theoretical models need to be proposed. These models can help decompose the medium-to-long-term trading curves by deconstructing them into their various components, such as benchmark flows, seasonal fluctuations, and electricity price factors. By building such models, future hydropower resource supply and electricity price trends can be predicted more accurately, thus helping power producers make more informed decisions. In addition, the impact of different seasons on the trading curve should be considered, as the availability of hydropower resources and the demand for electricity usually vary depending on seasonal factors. This could involve examining energy market patterns and demand forecasts for different seasons, as well as the development of adaptive strategies to meet demand fluctuations in different seasons.
- (4)
- Risk assessment methods for hydropower marketization. When examining hydropower participation in electricity markets, risks arising from multiple uncertainties need to be assessed in an integrated manner. In addition to electricity price volatility and runoff uncertainty having already been mentioned, risks related to climate change and water management policies, market policies and regulations, technology and equipment, environmental and social factors, international markets, data reliability, energy market trends, supply chain reliability, societal acceptance and public opinion, and finance and investment need to be considered. These factors may affect the feasibility, profitability, and sustainability of hydropower projects. Therefore, when studying the risk assessment methodology for hydropower marketization, it is important to focus not only on the transaction and contractual risks arising from electricity price volatility and runoff uncertainty, but also to study in depth the possible operational risks of an intra-basin market structure, settlement rules, hydropower generation connections, and co-ordination among multiple stakeholders. In addition, the risk relationships between different transaction portfolios should be considered to facilitate the risk allocation of resource portfolios by power producers in different market environments, in order to cope with complex and changing market conditions and to ensure the success and sustainability of hydropower projects. To better cope with these diversified risks, it is recommended that methods such as mathematical models and scenario analysis be used to quantify and manage risks to ensure that hydropower companies can better cope with uncertainty in different market environments.
5. Conclusions
The Three Gorges hydropower system plays a crucial role in China’s hydropower and power systems, and how to participate in market-oriented transactions is related to the functional positioning of hydropower in China’s energy structure system. This study combines the characteristics of the Three Gorges hydropower system and the marketization characteristics, systematically sorting out the key issues and response strategies for the participation of the large hydropower system in market transactions. Specifically, specific problems and difficulties, as well as solutions and methods, were elaborated upon in detail from four aspects: (1) the multi-dimensional and multi-time-scale nested allocation of cascade hydropower, (2) participation in bidding strategies in the electricity market, (3) participation in performance in the electricity market, (4) runoff under market conditions, electricity prices, and the description of multiple market uncertainties. On the other hand, based on the above, the main market-oriented research directions for the large hydropower system in the future are further envisioned, with the expectation of establishing a relatively systematic theoretical and technical research system to effectively serve the actual production and operation of the large hydropower system’s marketization. It is important to mention that the current study focuses on electricity markets with a large share of hydropower. It may not match a small proportion of hydropower plants. In such a system, the impact of hydropower on the whole market is usually small, so the complexity factors can be appropriately simplified in modeling and calculation. In conclusion, this study mainly provides decision support and policy recommendations for hydropower-rich provinces to overcome some difficulties in electricity market construction.
Author Contributions
Conceptualization, X.W. and L.G.; methodology, J.S.; validation, X.W. and L.G.; formal analysis, X.W. and J.S.; investigation, X.W. and L.G.; writing—original draft preparation, J.S., M.K. and X.H.; writing—review and editing, X.W. and L.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Project of China Yangtze Power Co., (Z242202001).
Acknowledgments
The writers are very grateful to the anonymous reviewers and editors for their constructive comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- CPC Central Committee, China State Council. Opinions on Further Deepening the Power Sector Reform. Available online: http://tgs.ndrc.gov.cn/zywj/201601/t20160129_773852.html (accessed on 1 April 2016).
- Shen, J.-J.; Cheng, C.-T.; Jia, Z.-B.; Zhang, Y.; Lv, Q.; Cai, H.-X.; Wang, B.-C.; Xie, M.-F. Impacts, challenges and suggestions of the electricity market for hydro-dominated power systems in China. Renew. Energy 2022, 187, 743–759. [Google Scholar] [CrossRef]
- National Development and Reform Commission; National Energy Administration. Notice on Carrying out Pilot Work of Spot Market Construction of Electric Power. 2017. Available online: https://www.ndrc.gov.cn/xxgk/zcfb/tz/201709/t20170905_962552.html (accessed on 15 July 2023).
- Yu, S.; Shen, J.; Zhang, J.; Cheng, C. Optimal bidding for large-scale hydropower stations serving multiple power grids in multi-regional monthly electricity markets. Int. J. Electr. Power Energy Syst. 2023, 147, 108836. [Google Scholar] [CrossRef]
- Shen, J.J.; Shen, Q.Q.; Cheng, C.T.; Zhang, X.F.; Wang, J. Large-Scale Unit Commitment for Cascaded Hydropower Plants with Hydraulic Coupling and Head-Sensitive Forbidden Zones: Case of the Xiluodu and Xiangjiaba Hydropower System. J. Water Resour. Plan. Manag. 2020, 146, 05020023. [Google Scholar] [CrossRef]
- Li, X.; Li, T.; Wei, J.; Wang, G.; Yeh, W.W.-G. Hydro unit commitment via mixed integer linear programming: A case study of the three gorges project, China. IEEE Trans. Power Syst. 2013, 29, 1232–1241. [Google Scholar] [CrossRef]
- Cheng, C.; Chen, F.; Li, G.; Ristić, B.; Mirchi, A.; Tu, Q.; Madani, K. Reform and renewables in China: The architecture of Yunnan’s hydropower dominated electricity market. Renew. Sustain. Energy Rev. 2018, 94, 682–693. [Google Scholar] [CrossRef]
- Jia, Z.; Shen, J.; Cheng, C.; Zhang, Y.; Lyu, Q. Optimum day-ahead clearing for high proportion hydropower market considering complex hydraulic connection. Int. J. Electr. Power Energy Syst. 2022, 141, 108211. [Google Scholar] [CrossRef]
- Liu, S.; Yang, Q.; Cai, H.; Yan, M.; Zhang, M.; Wu, D.; Xie, M. Market reform of Yunnan electricity in southwestern China: Practice, challenges and implications. Renew. Sustain. Energy Rev. 2019, 113, 109265. [Google Scholar] [CrossRef]
- Pereira, A.C.; de Oliveira, A.Q.; Baptista, E.C.; Balbo, A.R.; Soler, E.M.; Nepomuceno, L. Network-Constrained Multiperiod Auction for Pool-Based Electricity Markets of Hydrothermal Systems. IEEE Trans. Power Syst. 2017, 32, 4501–4514. [Google Scholar] [CrossRef]
- Silva-Rodriguez, L.; Sanjab, A.; Fumagalli, E.; Virag, A.; Gibescu, M. A light robust optimization approach for uncertainty-based day-ahead electricity markets. Electr. Power Syst. Res. 2022, 212, 108281. [Google Scholar] [CrossRef]
- Lüth, A.; Zepter, J.M.; del Granado, P.C.; Egging, R. Local electricity market designs for peer-to-peer trading: The role of battery flexibility. Appl. Energy 2018, 229, 1233–1243. [Google Scholar] [CrossRef]
- Zhang, N.; Kang, C.; Xia, Q.; Ding, Y.; Huang, Y.; Sun, R.; Huang, J.; Bai, J. A Convex Model of Risk-Based Unit Commitment for Day-Ahead Market Clearing Considering Wind Power Uncertainty. IEEE Trans. Power Syst. 2015, 30, 1582–1592. [Google Scholar] [CrossRef]
- Conejo, A.; Arroyo, J.; Contreras, J.; Villamor, F. Self-scheduling of a hydro producer in a pool-based electricity market. IEEE Trans. Power Syst. 2002, 17, 1265–1272. [Google Scholar] [CrossRef]
- Chatzigiannis, D.I.; Dourbois, G.A.; Biskas, P.N.; Bakirtzis, A.G. European day-ahead electricity market clearing model. Electr. Power Syst. Res. 2016, 140, 225–239. [Google Scholar] [CrossRef]
- Yu, H.; Shen, J.; Cheng, C.; Lu, J.; Cai, H. Multi-Objective Optimal Long-Term Operation of Cascade Hydropower for Multi-Market Portfolio and Energy Stored at End of Year. Energies 2023, 16, 640. [Google Scholar] [CrossRef]
- Luo, B.; Miao, S.; Cheng, C.; Lei, Y.; Chen, G.; Gao, L. Long-Term Generation Scheduling for Cascade Hydropower Plants Considering Price Correlation between Multiple Markets. Energies 2019, 12, 2239. [Google Scholar] [CrossRef]
- Doostizadeh, M.; Aminifar, F.; Lesani, H.; Ghasemi, H. Multi-area market clearing in wind-integrated interconnected power systems: A fast parallel decentralized method. Energy Convers. Manag. 2016, 113, 131–142. [Google Scholar] [CrossRef]
- Duan, Q.; Chao, Z.; Tang, X.; Xie, X.; Chen, H.; Su, X. Multi-stage robust clearing model considering renewable energy output uncertainty and unit effective reserve calculation in electricity market. Front. Energy Res. 2022, 10, 980125. [Google Scholar] [CrossRef]
- Yıldıran, U.; Kayahan, I.; Tunç, M.; Şisbot, S. MILP based short-term centralized and decentralized scheduling of a hydro-chain on Kelkit River. Int. J. Electr. Power Energy Syst. 2015, 69, 1–8. [Google Scholar] [CrossRef]
- Mirmoradi, E.; Ghasemi, H. Market clearing with probabilistic spinning reserve considering wind uncertainty and electric vehicles. Int. Trans. Electr. Energy Syst. 2015, 26, 525–538. [Google Scholar] [CrossRef]
- Pousinho, H.M.; Contreras, J.; Bakirtzis, A.G.; Catalão, J.P. Risk-constrained scheduling and offering strategies of a price-maker hydroproducer under uncertainty. IEEE Trans. Power Syst. 2013, 28, 1879–1887. [Google Scholar] [CrossRef]
- Gaudard, L.; Gabbi, J.; Bauder, A.; Romerio, F. Long-term uncertainty of hydropower revenue due to climate change and electricity prices. Water Resour. Manag. 2016, 30, 1325–1343. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Cheng, W.; Gao, S.; Cheng, C. A combination approach for downstream plants to solve scheduling information asymmetry problem in electricity markets. Int. J. Electr. Power Energy Syst. 2023, 149, 108935. [Google Scholar] [CrossRef]
- Shen, J.; Cheng, C.; Wang, S.; Yuan, X.; Sun, L.; Zhang, J. Multiobjective optimal operations for an interprovincial hydropower system considering peak-shaving demands. Renew. Sustain. Energy Rev. 2019, 120, 109617. [Google Scholar] [CrossRef]
- Shen, J.-J.; Zhu, W.-L.; Cheng, C.-T.; Zhong, H.; Jiang, Y.; Li, X.-F. Method for high-dimensional hydropower system operations coupling random sampling with feasible region identification. J. Hydrol. 2021, 599, 126357. [Google Scholar] [CrossRef]
- Steeger, G.; Barroso, L.A.; Rebennack, S. Optimal bidding strategies for hydro-electric producers: A literature survey. IEEE Trans. Power Syst. 2014, 29, 1758e1764. [Google Scholar] [CrossRef]
- Shen, J.; Cheng, C.; Wu, X.; Cheng, X.; Li, W.; Lu, J. Optimization of peak loads among multiple provincial power grids under a central dispatching authority. Energy 2014, 74, 494–505. [Google Scholar] [CrossRef]
- Zhang, Y.; Hou, J.; Ma, G.; Zhai, X.; Lv, A.; Wang, W.; Wang, Z. Regional differences of water regulation services of terrestrial ecosystem in the Tibetan Plateau: Insights from multiple land covers. J. Clean. Prod. 2020, 283, 125216. [Google Scholar]
- Wu, X.; Cheng, C.; Miao, S.; Li, G.; Li, S. Long-Term Market Competition Analysis for Hydropower Stations using SSDP-Games. J. Water Resour. Plan. Manag. 2020, 146, 04020037. [Google Scholar] [CrossRef]
- Liu, M.; Wu, F.F. Portfolio optimization in electricity markets. Electr. Power Syst. Res. 2006, 77, 1000–1009. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).