Risk Assessment of Power Supply Security Considering Optimal Load Shedding in Extreme Precipitation Scenarios
Abstract
:1. Introduction
2. Risk Analysis Framework Considering Waterlogged Failures
- Typical fault scenario generation under extreme rainfall
- 2.
- Stochastic power flow calculation taking into account load uncertainty
- 3.
- Optimal load curtailment calculation based on particle swarm algorithm
3. Generation of Typical Fault Scenarios for Power Facilities under Extreme Rainfall
3.1. Power Facility Failure Model
| Algorithm 1. Electric utility failure scenario generation process. | |
| ; Output: probability of failure of electrical facilities | |
| 1: | ; |
| 2: | ; |
| 3: | between the input layer and the hidden layer, where the weights are randomly generated between [−1,1] and the connection bias is randomly generated between [0,1]; |
| 4: | is the matrix with each element being past storm curve data |
| 5: | Calculate the output layer weight matrix according to Equation (2); |
| 6: | Calculation of the output prediction data and visualization of the rainfall curve according to Equation (3); |
| 7: | according to Equations (5) and (6); |
| 8: | Enter the puddle storage and evaporation volumes and calculate the production flow according to Equation (4); |
| 9: | according to Equation (7); |
| 10: | Calculate the variation curve of the ponded water level with time for a given precipitation intensity profile for the power facility according to Equations (8) and (9). |
3.2. Generate the Initial Set of Scenarios
3.3. Building Typical Scenario Sets
4. Stochastic Power Flow Calculation Considering Load Uncertainty
4.1. Calculation of Semi-Invariance of Each Order in a Typical Scenario
4.2. Gram-Charlier Series Expansion Method
5. Particle Swarm Algorithm-Based Decision Model for Load Curtailment Optimization
5.1. Optimal Load Curtailment Model
5.2. Particle Swarm Algorithm-Based Solution Process
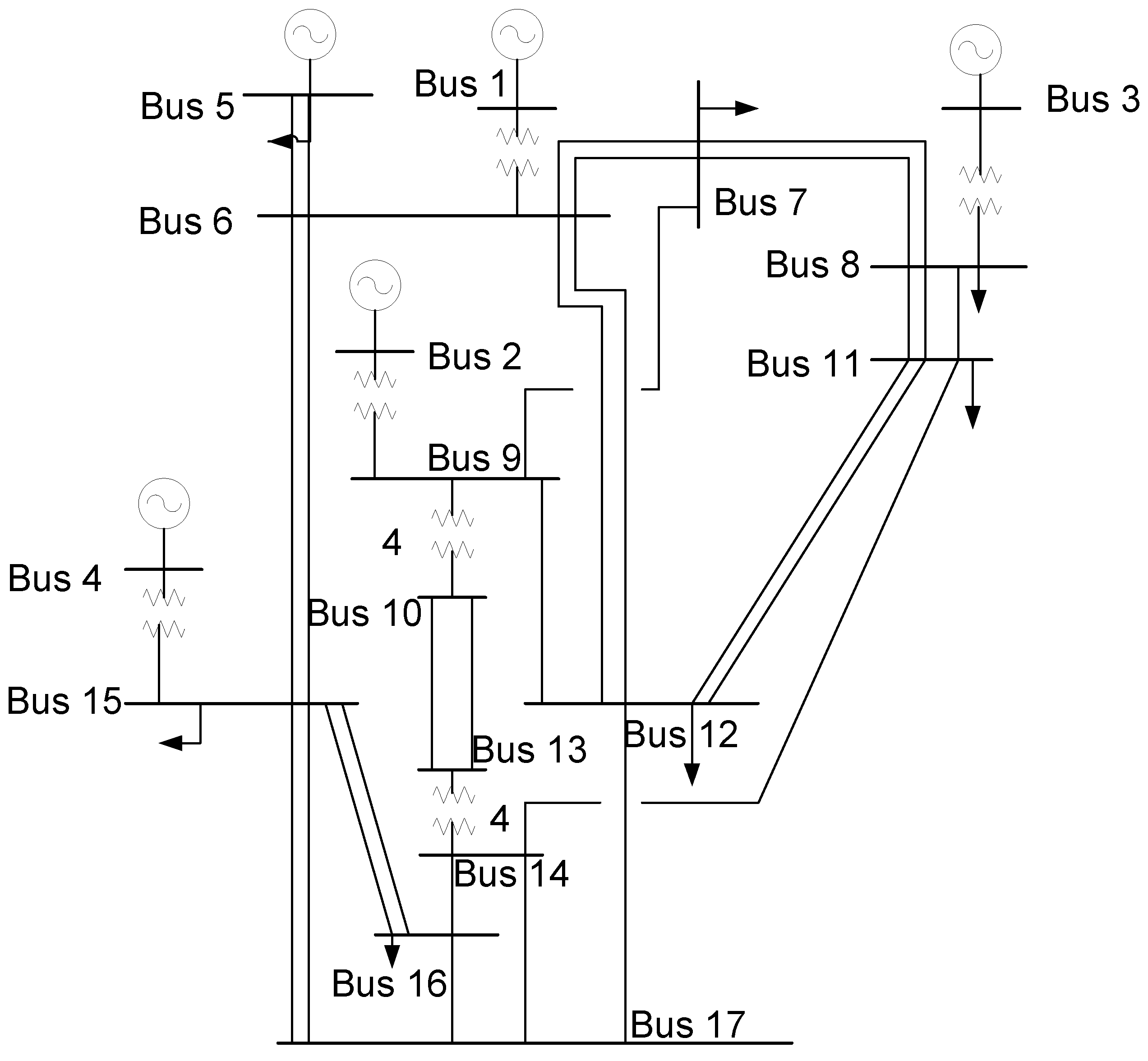
6. Example Analysis
6.1. Typical Scenario Generation
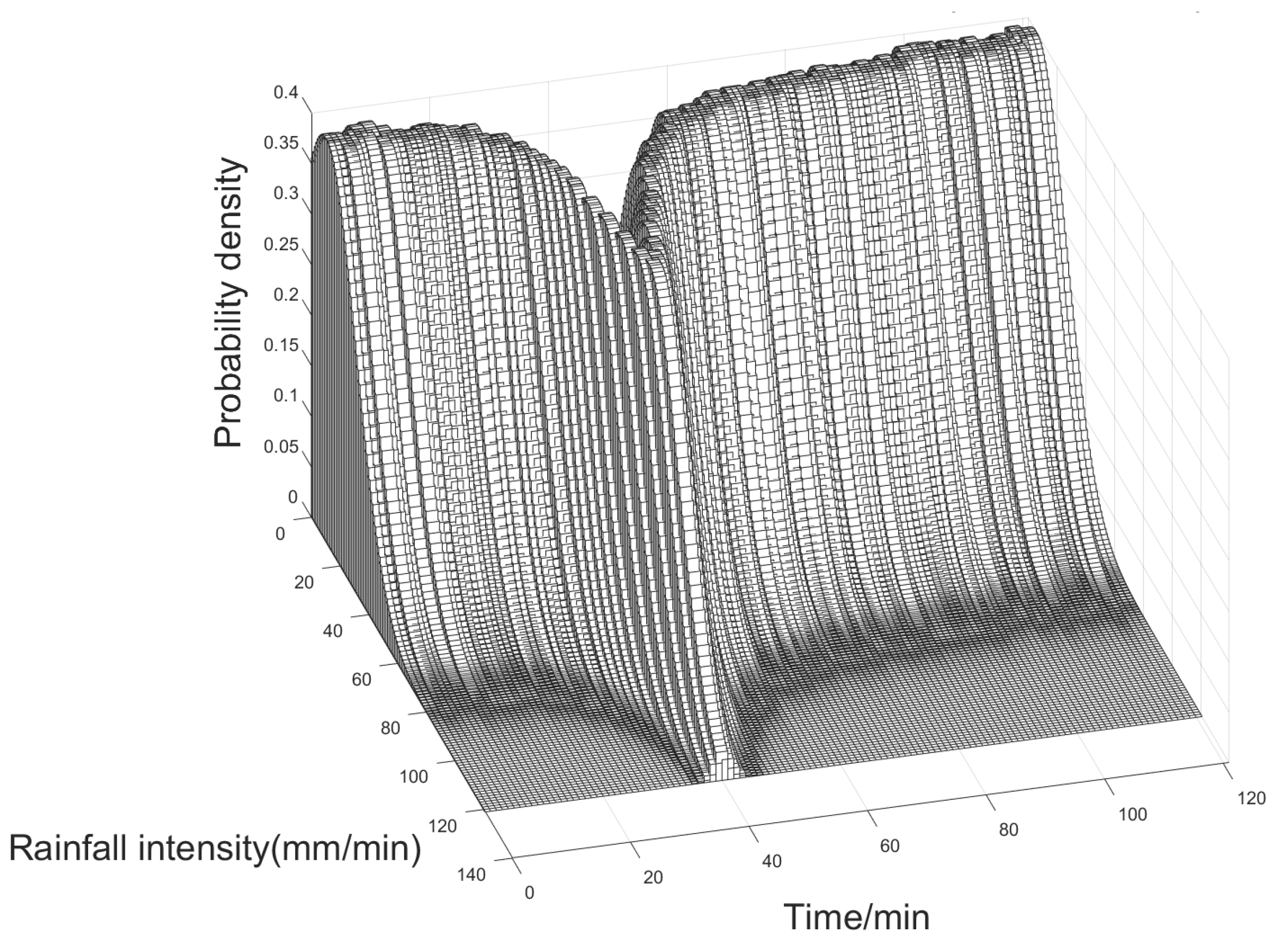
6.1.1. Outage Scenario Generation Model
6.1.2. Rainfall and Water Distribution
6.1.3. Scenario Library Generation and Reduction
6.2. Curtailment of Load Simulation Results
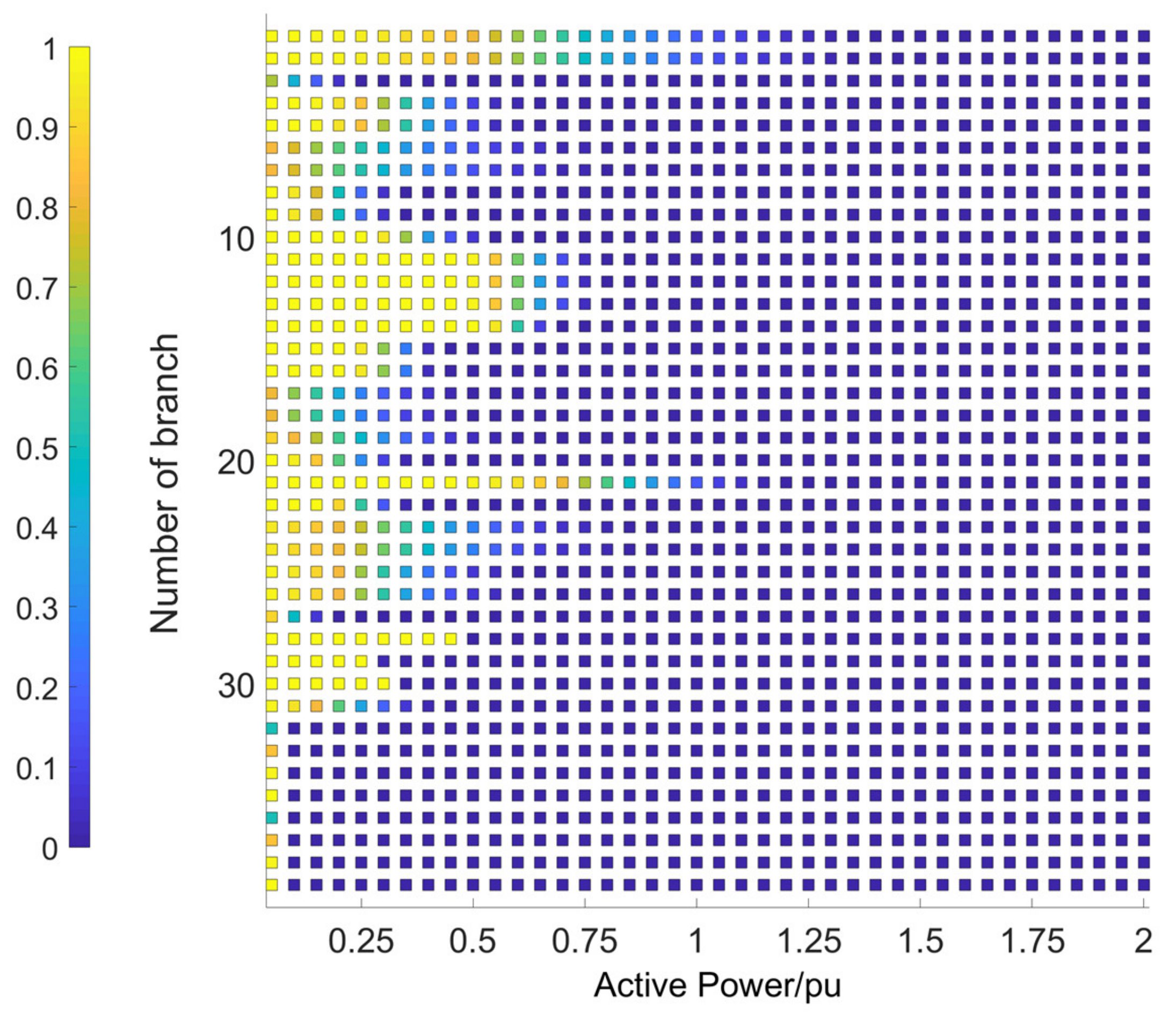
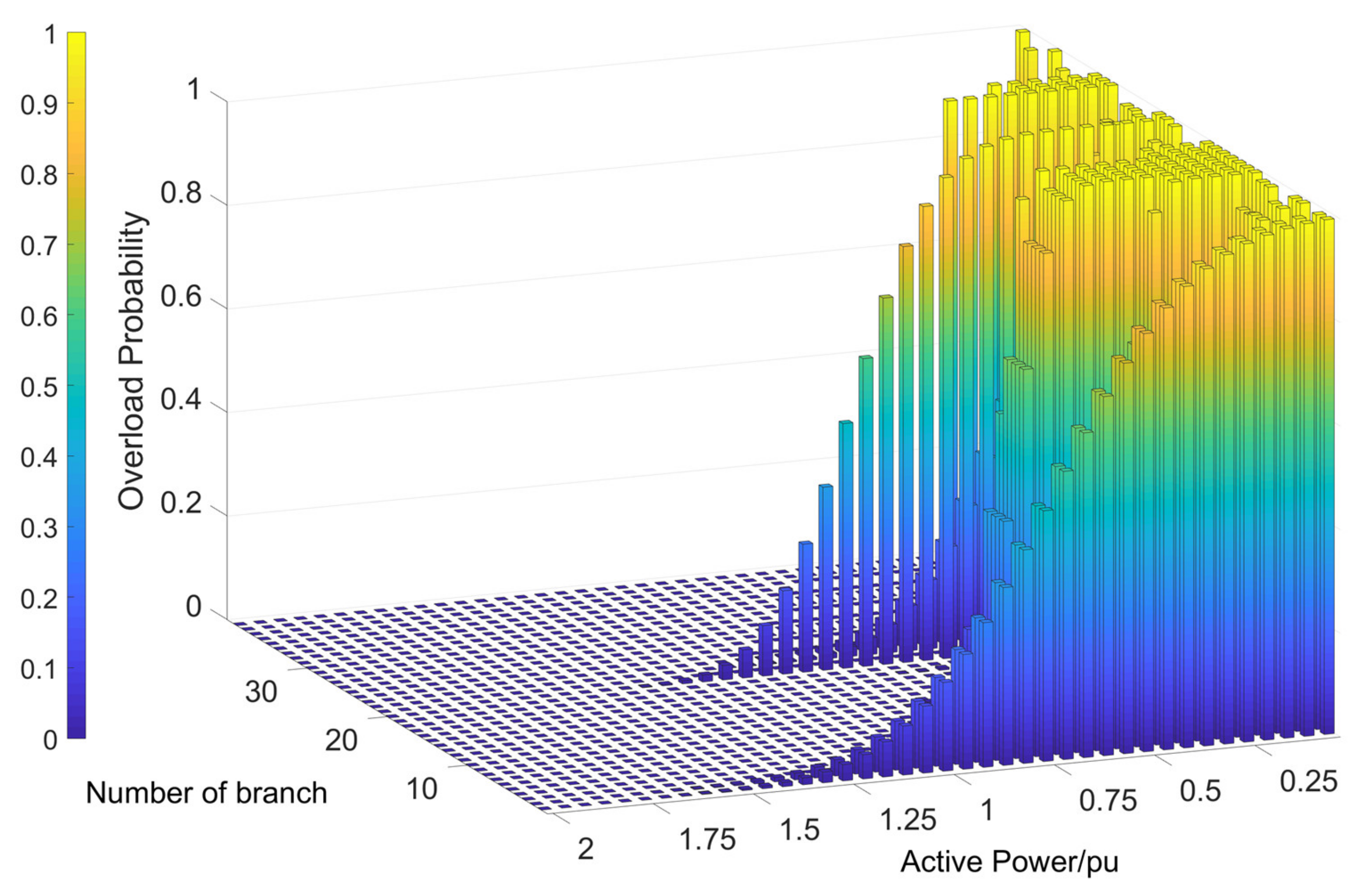
6.3. Simulation Results of Branch Power Flow Violation
7. Conclusions
- The proposed approach involves determining the rainfall curve and the corresponding water accumulation curve through the combined use of the SWMM model and the extreme learning machine. To assess the probabilities of different initial fault scenarios, the Monte Carlo sampling method was applied. Using statistical theory, the initial fault scenarios were refined, resulting in the identification of typical scenario sets. These sets comprised specific fault scenarios with their corresponding probabilities.
- The branch power flow overload probability of each initial scenario within a single typical scenario set was calculated using the semi-invariant and Gram–Charlier series expansion methods. By applying the full probability formula, the power grid overload probability was obtained for each typical scenario set. This calculation took into account the probabilities of branch power flow overloads in the specific scenarios within the set. With the power grid overload probabilities determined for each typical scenario set, it was possible to calculate the power grid overload probability in the comprehensive scenario. This calculation involved aggregating the probabilities from all the typical scenario sets to provide an overall assessment of the likelihood of power grid transgressions.
- In the optimal load curtailment model, the branch active power violation probability was incorporated as a constraint. This ensured that the power flow in each branch remained within the specified limits. To solve the constrained optimization problem, the particle swarm optimization (PSO) algorithm was employed. To handle the constraints, a penalty function approach was adopted, transforming the constrained optimization problem into an unconstrained one. This technique helped to speed up the solution process by converting the problem into a form that was more amenable to optimization algorithms such as PSO.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yi, Z.; Chen, Z.; Yin, K.; Wang, L.; Wang, K. Sensing as the key to the safety and sustainability of new energy storage devices. Prot. Control. Mod. Power Syst. 2023, 8, 27. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, Y.; Zhang, Y.; Wang, L.; Wang, K. Summary of Health-State estimation of lithium-ion batteries based on electrochemical impedance spectroscopy. Energies 2023, 16, 5682. [Google Scholar] [CrossRef]
- Wang, L.; Xie, L.; Yang, Y.; Zhang, Y.; Wang, K.; Cheng, S.J. Distributed online voltage control with fast PV power fluctuations and imperfect communication. IEEE Trans. Smart Grid 2023, 14, 3681–3695. [Google Scholar] [CrossRef]
- Ma, N.; Yin, H.; Wang, K. Prediction of the remaining useful life of supercapacitors at different temperatures based on improved long short-term memory. Energies 2023, 16, 5240. [Google Scholar] [CrossRef]
- Zhang, S.; Hosen, M.S.; Kalogiannis, T.; Mierlo, J.V.; Berecibar, M. State-of-health estimation of lithium-ion batteries based on electrochemical impedance spectroscopy: A review. Prot. Control. Mod. Power Syst. 2023, 8, 156. [Google Scholar]
- Zhang, H.; Gao, J.; Kang, L.; Zhang, Y.; Wang, L.; Wang, K. State of health estimation of lithium-ion batteries based on modified flower pollination algorithm-temporal convolutional network. Energy 2023, 283, 128742. [Google Scholar] [CrossRef]
- Zhou, G.; Shi, J.X.; Chen, B.J.; Qi, Z.Y.; Wang, L.C. Lightning protection measures and zoning lightning protection for transmission lines in medium and heavy ice areas. Electr. Porcelain Light. Arrester 2021, 4, 47–54. [Google Scholar]
- Zhou, G.; Shi, J.X.; Chen, B.J.; Qi, Z.Y.; Wang, L.C. Risk assessment of transmission line over-icing disaster considering multiple factors based on evolutionary strategy-projection tracing algorithm. Power Syst. Autom. 2013, 37, 92–97. [Google Scholar]
- Song, J.J. Time-Varying Outage Model for Overhead Transmission Lines under Severe Disasters; Zhejiang University: Hangzhou, China, 2013. [Google Scholar]
- Chen, Y. Research on Risk Assessment and Control of Wenzhou Power System Considering Extreme Weather; Zhejiang University: Hangzhou, China, 2022. [Google Scholar]
- Weinmann, R.; Cotilla-Sanchez, E.; Brekken, T.K. Toward Models of impact and recovery of the US Western Grid from earthquake events. Energies 2022, 15, 9275. [Google Scholar] [CrossRef]
- Swief, R.A.; Abdel-Salam, T.S.; El-Amary, N.H. Photovoltaic and wind turbine integration applying cuckoo search for probabilistic reliable optimal placement. Energies 2018, 11, 139. [Google Scholar] [CrossRef]
- Deng, X.; He, J.; Zhang, P. A novel probabilistic optimal power flow method to handle large fluctuations of stochastic variables. Energies 2017, 10, 1623. [Google Scholar] [CrossRef]
- Ye, X.; Wang, Y.F. Multipoint linearized probabilistic power flow calculation with correlation of random variables. J. Power Syst. Their Autom. 2023. [Google Scholar]
- Lian, H.R.; Zhou, B.R. Stochastic power flow resolution algorithm based on scenario partitioning. Power Grid Technol. 2017, 41, 3153–3160. [Google Scholar]
- Wei, P.; Liu, J.K. Stochastic power flow algorithm based on semi-invariant and Gram-Charlier level expansion method. Power Eng. Technol. 2017, 36, 34–38. [Google Scholar]
- Li, C.; Zeng, Y. An optimal dispatching method for power systems accounting for operational risks. J. Power Syst. Their Autom. 2016, 28, 73–79. [Google Scholar]
- Jia, Y.; Li, W.X. Penalty function improved particle swarm algorithm for optimal configuration of scenery storage system. J. Sol. Energy 2019, 40, 2071–2077. [Google Scholar]
- Bian, C.Y.; Fang, X.Y. Site selection model of electric power emergency material storage considering load level. J. Power Syst. Their Autom. 2017, 29, 78–83. [Google Scholar]
- Kang, W.Q. A security risk assessment method for power monitoring network based on improved AHP algorithm. Autom. Instrum. 2022, 10, 171–174. [Google Scholar]
- Wang, X.J.; Huang, Y. Comprehensive evaluation and type selection of energy storage based on hierarchical analysis method. Zhejiang Electr. Power 2022, 41, 1–8. [Google Scholar]
- Li, Q. SWMM-Based Reliability Analysis of Urban Stormwater Pipe Network and Multi-Objective Reconstruction Optimization Research; Dalian University of Technology: Dalian, China, 2016. [Google Scholar]
- Zhou, L.; Huang, Z.X. Extreme learning machine for short-term power system load forecasting. Electron. World 2021, 8, 33–34. [Google Scholar]
- Fu, L.H.; Liu, A.H. China Statistical Yearbook-2021; China Statistics Press: Beijing, China, 2022; pp. 68–70. [Google Scholar]
- Wang, S.S. Research on the Application of Production and Convergence Forecasting Models in Early Warning Systems; Nanchang University: Nanchang, China, 2019. [Google Scholar]
- Rui, X.F. Discovery and development of the production flow model. Adv. Water Resour. Hydropower Sci. Technol. 2013, 1, 1–6+26. [Google Scholar]
- Zhao, D.Q.; Chen, J.N. Study on the influence of sub-catchment delineation on SWMM simulation results. Environ. Prot. 2008, 8, 56–59. [Google Scholar]
- Zeng, X.T. Study on the Optimization Model of Stormwater Pipe Network Based on NSGA-II Algorithm Research; Southwest Jiaotong University: Chengdu, China, 2021. [Google Scholar]
- Xu, L. Power System Voltage Collapse Risk Assessment; Chongqing University: Chongqing, China, 2009. [Google Scholar]
- Zhang, W.T.; Fan, L.X. Wind power penetration power limit calculation based on DC probabilistic currents. Jiangsu Electr. Eng. 2014, 33, 1–4. [Google Scholar]
- Fan, J.H.; Xu, N. Fault recovery strategy for power distribution systems with distributed scenic power. Jiangsu Electr. Eng. 2014, 33, 1–4+8. [Google Scholar]
- Yang, R.; Zhang, Y. Multi-objective reactive power optimization of distribution network with improved particle swarm optimization. J. Anhui Eng. Univ. 2022, 37, 42–50. [Google Scholar]
- Gibbard, M.; Vowles, D. IEEE PES task force on benchmark systems for stability controls simplified 14-generator model of the south east Australian power system. Univ. Adel. 2014, 5005, 128. [Google Scholar]





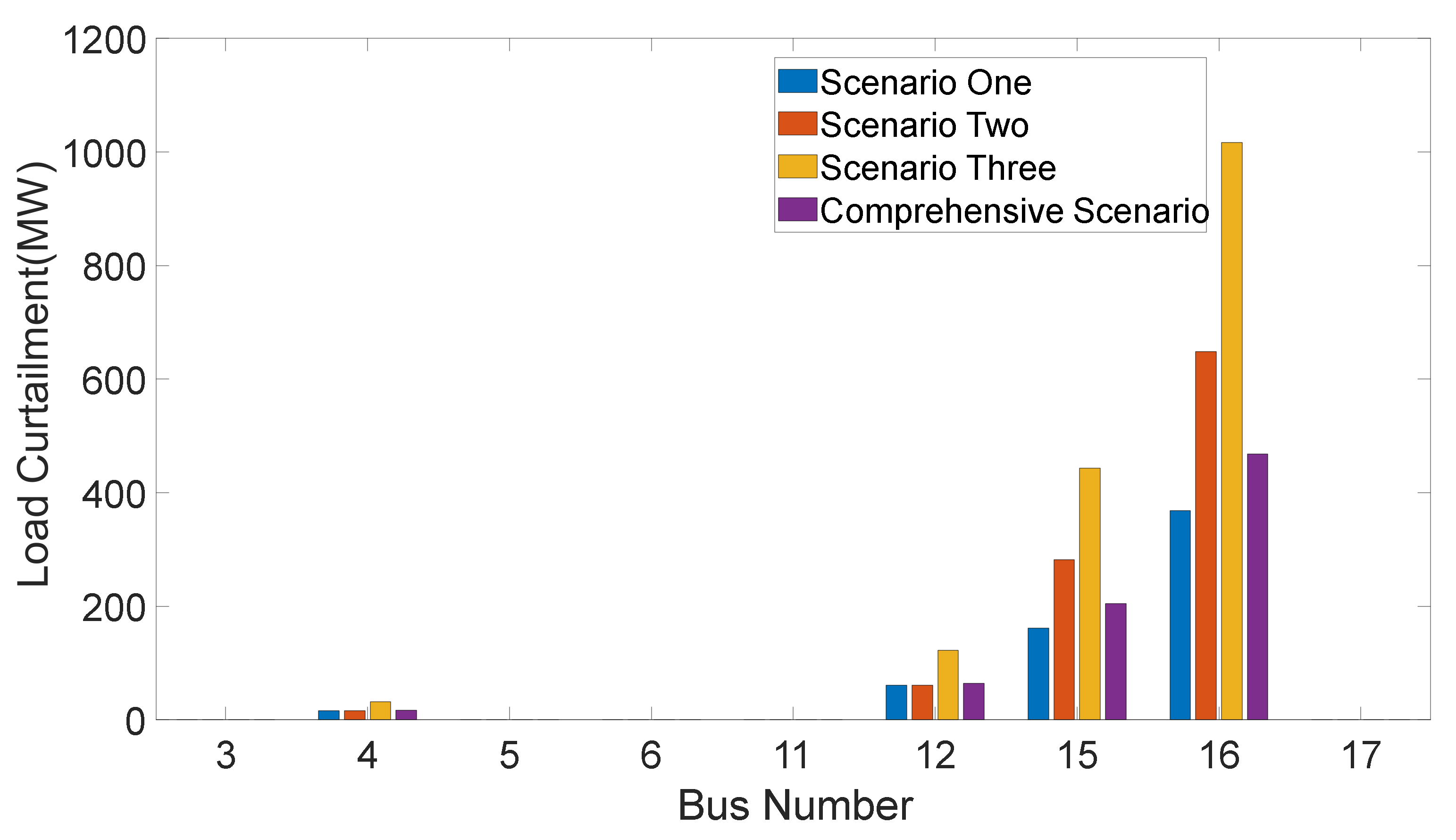
| Heading | Value in the Model | Heading | Value in the Model |
|---|---|---|---|
| Catchment area/m2 | 15,000 | Pipe Manning roughness | 0.01 |
| Flood width/m | 140 | Pipe diameter/m | 0.3 |
| Catchment slope/% | 0.2 | Pipe bottom slope | 0.2 |
| Permeable area ratio/% | 20 | Maximum permeability/(m·min−1) | 1.2 |
| Manning roughness of impervious area | 0.013 | Minimum permeability/(m·min−1) | 0.06 |
| Manning roughness of permeable area | 0.1 | Permeability attenuation coefficient (min−1) | 0.1 |
| Branch | MVA | Branch | MVA | Branch | MVA | Branch | MVA |
|---|---|---|---|---|---|---|---|
| 1–6 | 5000 | 6–15 | 800 | 11–12 | 800 | 16–17 | 800 |
| 2–9 | 5000 | 7–8 | 800 | 11–12 | 800 | 9–10 | 1000 |
| 3–8 | 5000 | 7–8 | 800 | 11–14 | 800 | 9–10 | 1000 |
| 4–15 | 5000 | 7–9 | 800 | 12–17 | 800 | 9–10 | 1000 |
| 5–6 | 800 | 8–11 | 800 | 14–16 | 800 | 9–10 | 1000 |
| 5–6 | 800 | 8–11 | 800 | 14–17 | 800 | 13–14 | 1000 |
| 6–7 | 800 | 8–11 | 800 | 15–16 | 800 | 13–14 | 1000 |
| 6–12 | 800 | 9–12 | 800 | 15–16 | 800 | 13–14 | 1000 |
| 6–12 | 800 | 10–13 | 1200 | 15–17 | 800 | 13–14 | 1000 |
| 6–15 | 800 | 10–13 | 1200 | 15–17 | 800 |
| Scenarios | Total Load Curtailment (MVA) |
|---|---|
| Scenarios One | 132.49 |
| Scenarios Two | 212.72 |
| Scenarios Three | 345.22 |
| Comprehensive scenarios | 162.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, G.; Shi, J.; Chen, B.; Qi, Z.; Wang, L. Risk Assessment of Power Supply Security Considering Optimal Load Shedding in Extreme Precipitation Scenarios. Energies 2023, 16, 6660. https://doi.org/10.3390/en16186660
Zhou G, Shi J, Chen B, Qi Z, Wang L. Risk Assessment of Power Supply Security Considering Optimal Load Shedding in Extreme Precipitation Scenarios. Energies. 2023; 16(18):6660. https://doi.org/10.3390/en16186660
Chicago/Turabian StyleZhou, Gang, Jianxun Shi, Bingjing Chen, Zhongyi Qi, and Licheng Wang. 2023. "Risk Assessment of Power Supply Security Considering Optimal Load Shedding in Extreme Precipitation Scenarios" Energies 16, no. 18: 6660. https://doi.org/10.3390/en16186660
APA StyleZhou, G., Shi, J., Chen, B., Qi, Z., & Wang, L. (2023). Risk Assessment of Power Supply Security Considering Optimal Load Shedding in Extreme Precipitation Scenarios. Energies, 16(18), 6660. https://doi.org/10.3390/en16186660







