Performance Validation of Resonant Wave Power Converter with Variable Moment of Inertia
Abstract
:1. Introduction
2. Wave Energy Converter with Variable Moment of Inertia
2.1. System Modeling
2.2. Design of Power Generation System
3. Experimental Validation
3.1. Experimental Setup
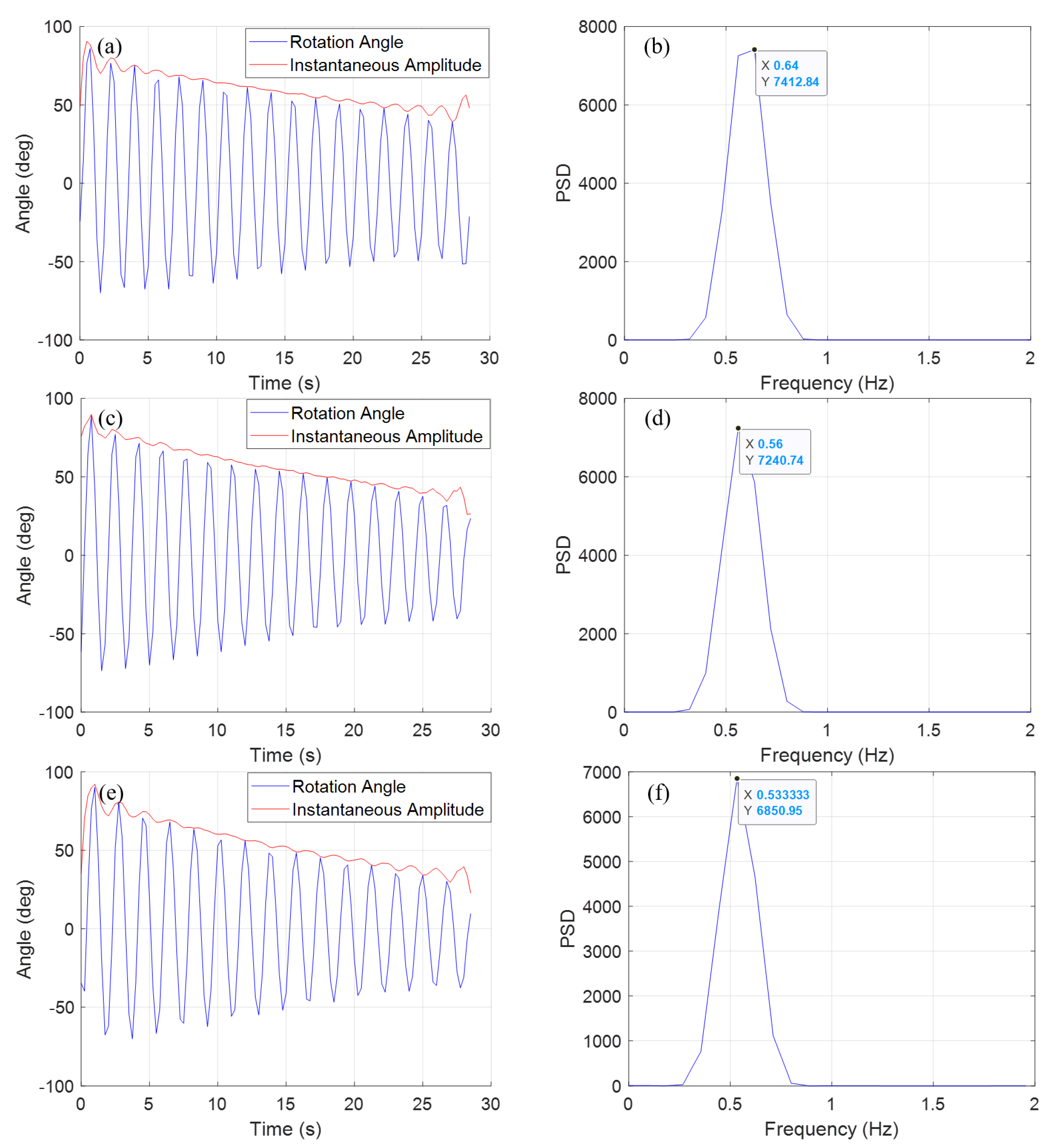
3.2. Free Vibration Test
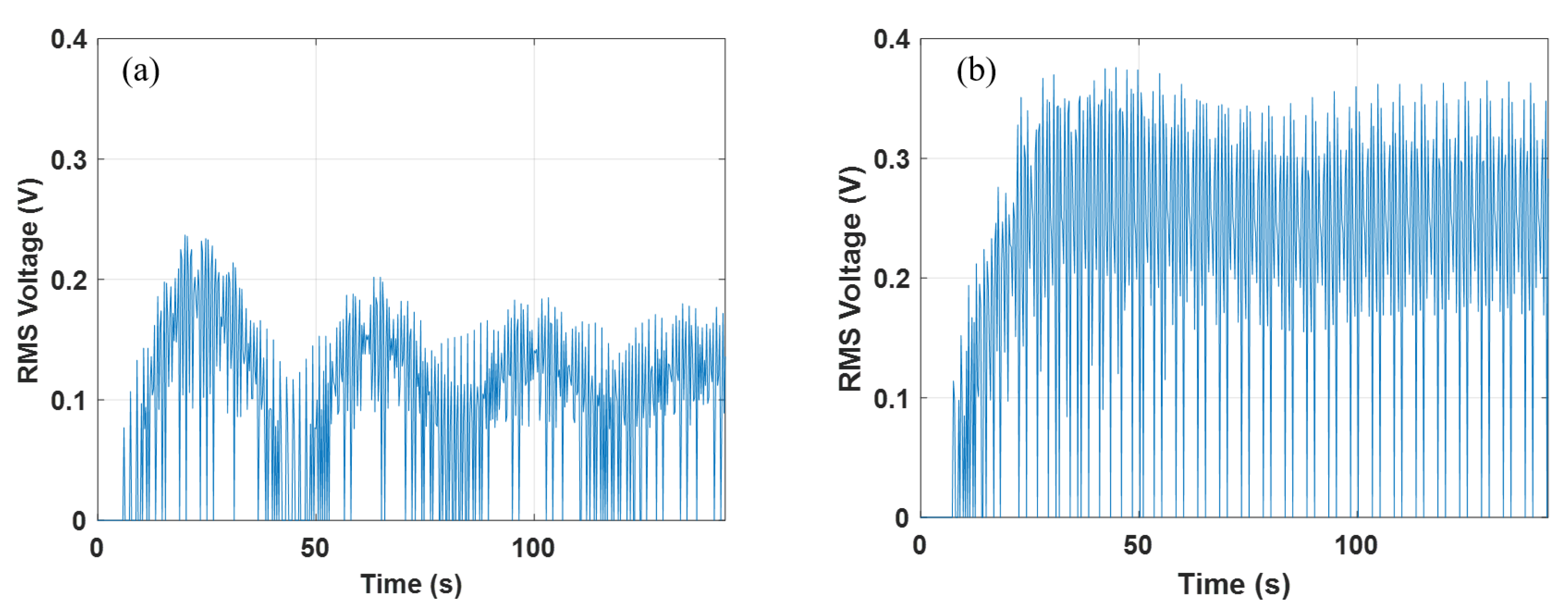
3.3. Forced Vibration Test
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Share of Wind and Solar in Electricity Production. Available online: https://yearbook.enerdata.net/renewables/wind-solar-share-electricity-production.html (accessed on 4 September 2023).
- Wave Power Plant. Available online: https://unfccc.int/technology/wave-power-plants (accessed on 4 September 2023).
- Renzi, E.; Michele, S.; Zheng, S.; Jin, S.; Greaves, D. Niche applications and flexible devices for wave energy conversion: A review. Energies 2021, 14, 6537. [Google Scholar] [CrossRef]
- Deleanu, D.; Dumitrache, C.L. Controlling the parametric roll of a container ship model by changing the forward velocity. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 916, p. 012024. [Google Scholar]
- Munif, A.; Ikeda, Y.; Fujiwara, T.; Katayama, T. Parametric roll resonance of a large passenger ship in dead ship condition in all heading angles. Contemp. Ideas Ship Stab. Capsizing Waves 2011, 97, 331–345. [Google Scholar]
- Galeazzi, R.; Blanke, M.; Poulsen, N.K. Early detection of parametric roll resonance on container ships. IEEE Trans. Control Syst. Technol. 2012, 21, 489–503. [Google Scholar] [CrossRef]
- Gudmestad, O.T. Resonant Motions of Dynamic Offshore Structures in Large Waves. Fluids 2021, 6, 352. [Google Scholar] [CrossRef]
- Gao, J.; He, Z.; Zang, J.; Chen, Q.; Ding, H.; Wang, G. Numerical investigations of wave loads on fixed box in front of vertical wall with a narrow gap under wave actions. Ocean Eng. 2020, 206, 107323. [Google Scholar] [CrossRef]
- Gao, J.; Gong, S.; He, Z.; Shi, H.; Zang, J.; Zou, T.; Bai, X. Study on Wave Loads during Steady-State Gap Resonance with Free Heave Motion of Floating Structure. J. Mar. Sci. Eng. 2023, 11, 448. [Google Scholar] [CrossRef]
- Moradi, N.; Zhou, T.; Cheng, L. Effect of inlet configuration on wave resonance in the narrow gap of two fixed bodies in close proximity. Ocean Eng. 2015, 103, 88–102. [Google Scholar] [CrossRef]
- Ringwood, J.V.; Bacelli, G.; Fusco, F. Energy-maximzing control of wave-energy converters. IEEE Control Syst. Mag. 2014, 34, 30–55. [Google Scholar]
- Aderinto, T.; Li, H. Review on power performance and efficiency of wave energy converters. Energies 2019, 12, 4329. [Google Scholar] [CrossRef]
- Maria-Arenas, A.; Garrido, A.J.; Rusu, E.; Garrido, I. Control strategies applied to wave energy converters: State of the art. Energies 2019, 12, 3115. [Google Scholar] [CrossRef]
- Guo, B.; Wang, T.; Jin, S.; Duan, S.; Yang, K.; Zhao, Y. A review of point absorber wave energy converters. J. Mar. Sci. Eng. 2022, 10, 1534. [Google Scholar] [CrossRef]
- Sakr, A.H.; Anis, Y.H.; Metwalli, S.M. System frequency tuning for heaving buoy wave energy converters. In Proceedings of the IEEE International Conference on Advanced Intelligent Mechatronics, Busan, Republic of Korea, 7–11 July 2015. [Google Scholar]
- Cai, Q.; Zhu, S. Applying double-mass pendulum oscillator with tunable ultra-low frequency in wave energy converters. Appl. Energy 2021, 298, 117228. [Google Scholar] [CrossRef]
- Garcia-Teruel, A.; Forehand, D.I.M. A review of geometry optimisation of wave energy converters. Renew. Sustain. Energy Rev. 2021, 139, 110593. [Google Scholar] [CrossRef]
- Jin, S.; Patton, R.J.; Guo, B. Enhancement of wave energy absorption efficiency via geometry and power take-off damping tuning. Energy 2019, 169, 819–832. [Google Scholar] [CrossRef]
- Choi, I.H.; Kweon, H.M. Wave energy converter by using relative heave motion between buoy and inner dynamic system. Ocean. Syst. Eng. 2012, 2, 297–314. [Google Scholar] [CrossRef]
- Cho, Y.H.; Lee, C.J.; Hong, D.S. Dynamic design of a mass-spring type translational wave energy converter. Korean Soc. Manuf. Technol. Eng. 2012, 21, 182–189. [Google Scholar]
- Han, K.B.; Lee, H.W. The research of wide band vibration energy harvester using ocean wave. J. Korean Soc. Mar. Eng. 2013, 37, 596–602. [Google Scholar]
- Jang, S.J.; Kim, I.H.; Jung, H.J.; Lee, Y.P. A tunable rotational energy harvester for low frequency vibration. Appl. Phys. Lett. 2011, 99, 134102. [Google Scholar] [CrossRef]
- Kim, I.H.; Jang, S.J.; Park, S.B.; Jung, H.J.; Kim, Y.C. Tunable yo-yo energy harvester with oblique springs. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 3185–3194. [Google Scholar] [CrossRef]
- Jang, S.J.; Kim, I.H.; Park, K.; Jung, H.J. An enhanced tunable rotational energy harvester with variable stiffness system for low-frequency vibration. J. Mech. Eng. Sci. 2015, 230, 732–736. [Google Scholar] [CrossRef]
- Jang, S.J.; Kim, B.R. Resonant frequency tuning of wave energy converters using variable moment of inertia. J. Adv. Mar. Eng. Technol. 2023, 47, 12–15. [Google Scholar] [CrossRef]
- Suh, K.D.; Kwon, H.D.; Lee, D.Y. Some statistical characteristics of large deep water waves around the Korean Peninsula. Coast. Eng. 2010, 57, 375–384. [Google Scholar] [CrossRef]
- Ulazia, A.; Saenz-Aguirre, A.; Ibarra-Berastegui, G.; Sáenz, J.; Carreno-Madinabeitia, S.; Esnaola, G. Performance variations of wave energy converters due to global long-term wave period change (1900–2010). Energy 2023, 268, 126632. [Google Scholar] [CrossRef]
- Jung, H.J.; Kim, I.H.; Koo, J.H. An energy harvesting system using the wind-induced vibration of a stay cable for powering a wireless sensor node. Smart Mater. Struct. 2011, 20, 075001. [Google Scholar] [CrossRef]
- Reitz, J.R.; Milford, F.J.; Christy, R.W. Foundations of Electromagnetic Theory, 4th ed.; Addison-Wesley: Boston, MA, USA, 1993. [Google Scholar]
- Miner, G.F. Lines and Electromagnetic Fields for Engineers, 1st ed.; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Laila, D.S.; Larsson, M.; Pal, B.C.; Korba, P. Nonlinear damping computation and envelop detection using Hilbert transform and its application to power systems wide area monitoring. In Proceedings of the 2009 IEEE Power & Energy society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–7. [Google Scholar]
- Sumali, H.; Kellogg, R.A. Calculating Damping from Ring-Down Using Hilbert Transform and Curve Fitting; No. SAND2011-1960C; Sandia National Lab: Albuquerque, NM, USA, 2011. [Google Scholar]
- Rosenblum, M.; Pikovsky, A.; Kühn, A.A.; Busch, J.L. Real-time estimation of phase and amplitude with application to neural data. Sci. Rep. 2021, 11, 18037. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.; Luo, H.; Tang, J. Investigation of granular damping in transient vibrations using Hilbert transform based technique. J. Vib. Acoust. Trans. ASME 2008, 130, 031006. [Google Scholar] [CrossRef]
- Duan, Y.F.; Ko, J.M.; Ni, Y.Q.; Chen, Z.Q. Field comparative tests of cable vibration control using magnetorheological (MR) dampers in single-and-twin-damper setups. In Advances in Steel Structures (ICASS’02); Elsevier: Amsterdam, The Netherlands, 2002; pp. 849–856. [Google Scholar]
- Tomlinson, G.R.; Ahmed, I. Hilbert transform procedures for detecting and quantifying non-linearity in modal testing. Meccanica 1987, 22, 123–132. [Google Scholar] [CrossRef]
- Pwelch. Available online: https://kr.mathworks.com/help/signal/ref/pwelch.html (accessed on 8 August 2023).
- Yokogawa Electric. WT310/WT310HC/WT330 Digital Power Meter User’s Manual 2nd Edition. Yokogawa Meters & Instrucments Corporation 2013. Available online: https://cdn.tmi.yokogawa.com/IMWT310-01EN.pdf (accessed on 20 August 2023).
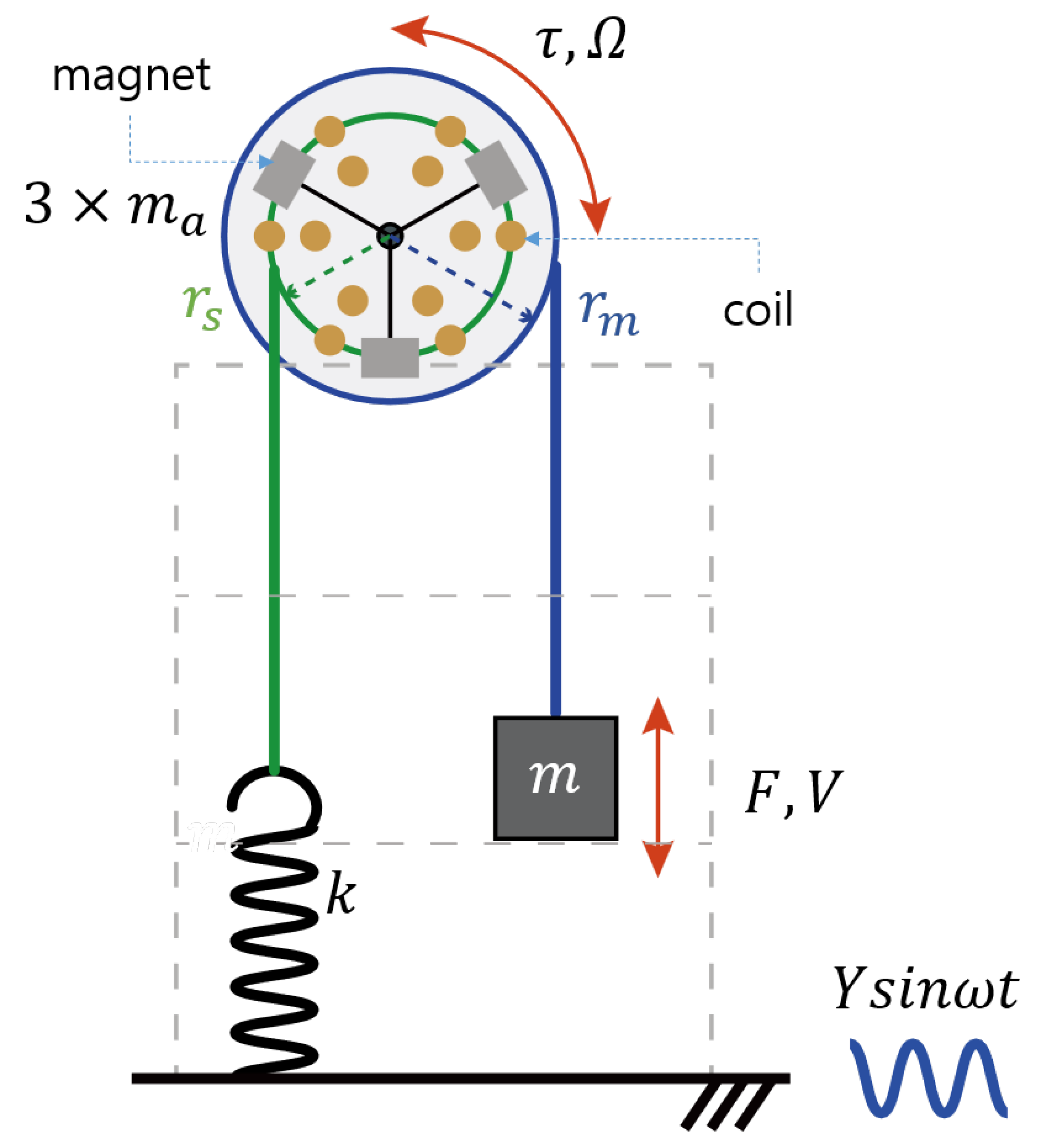
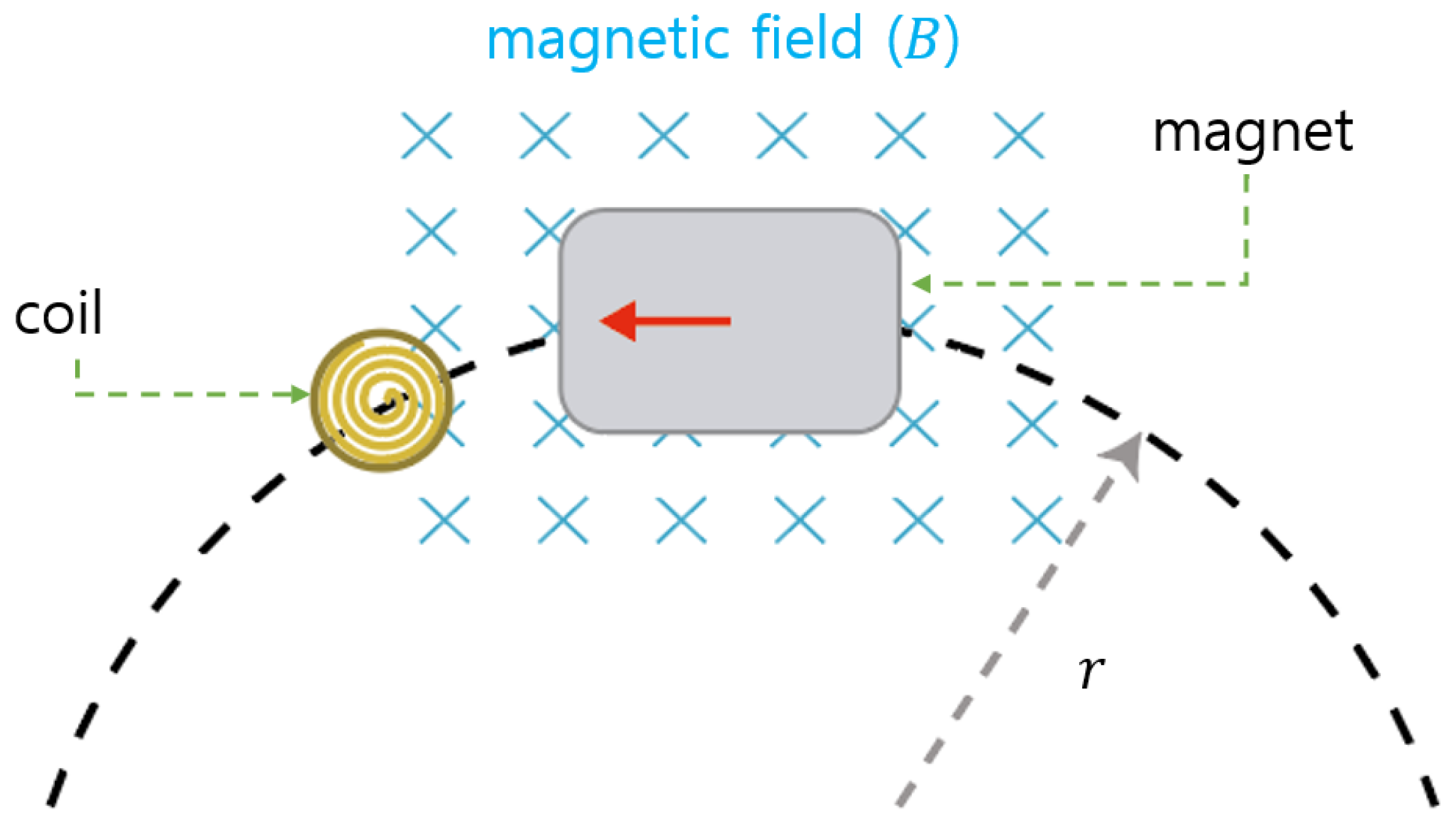
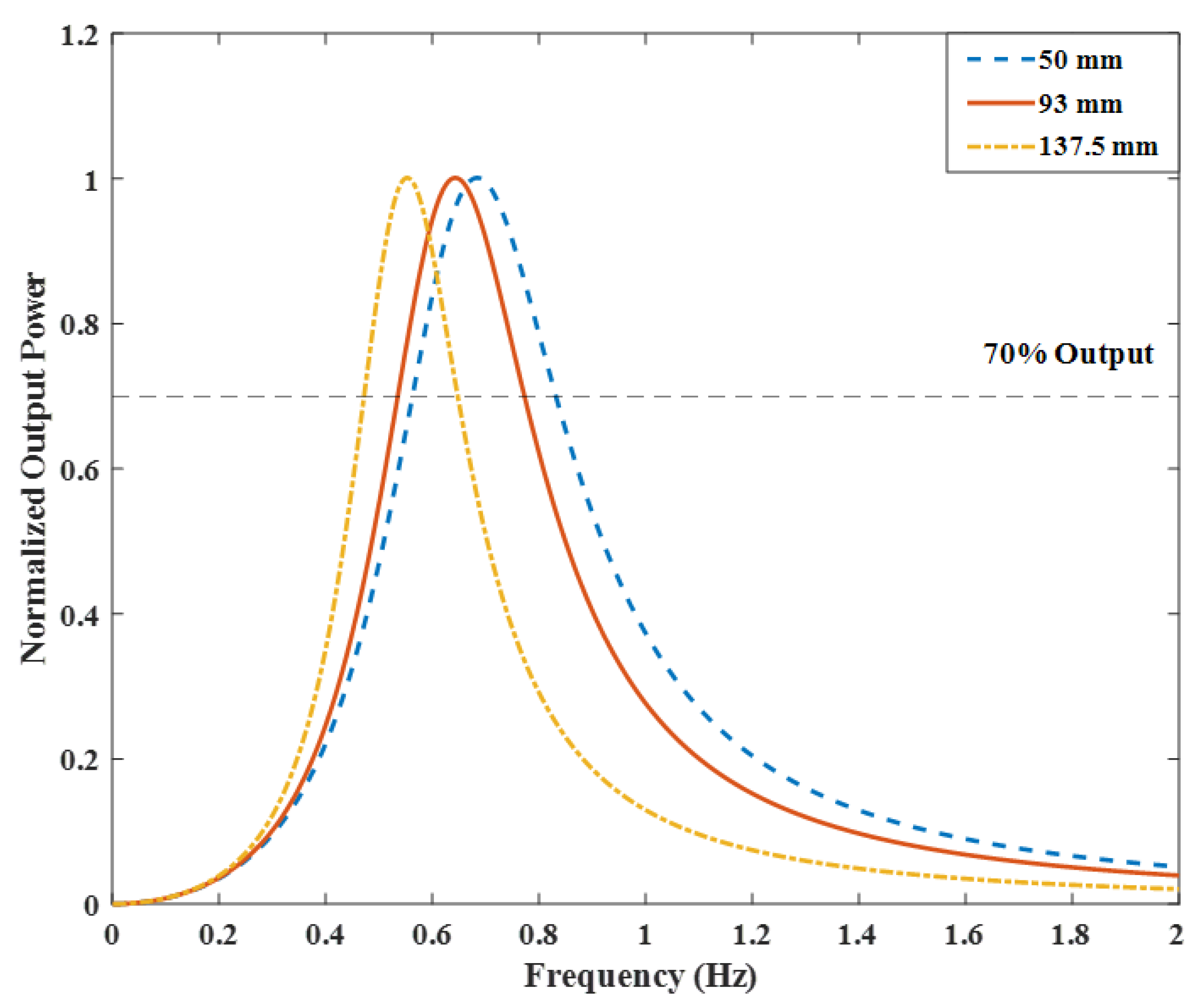
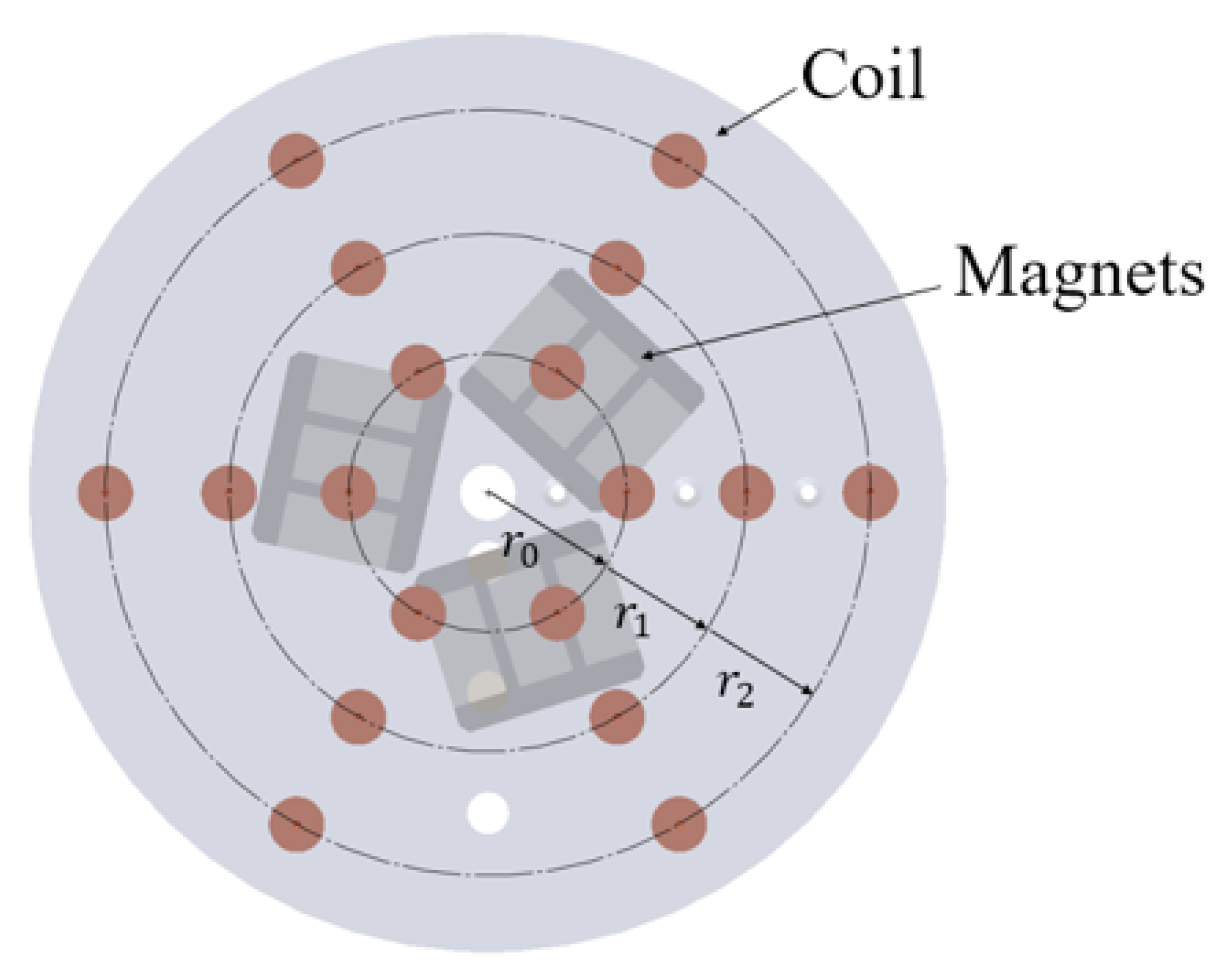


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| m | 15.75 kg | 0.5 m | |
| c | 0.5 Ns/m | 0.155 m | |
| k | 2800 N/m | 0.05, 0.093, 0.1375 m | |
| 2.1 kg | n | 3 |
| Number of Coil Turns (N) | Diameter of the Coil Wire (mm) | Magnet Size (mm) | Magnetic Flux Density (T) |
|---|---|---|---|
| 182 | 14 | 40 × 20 × 10 | 0.5 |
| (L × B × H) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, I.-H.; Kim, B.-R.; Jang, S.-J. Performance Validation of Resonant Wave Power Converter with Variable Moment of Inertia. Energies 2023, 16, 6617. https://doi.org/10.3390/en16186617
Kim I-H, Kim B-R, Jang S-J. Performance Validation of Resonant Wave Power Converter with Variable Moment of Inertia. Energies. 2023; 16(18):6617. https://doi.org/10.3390/en16186617
Chicago/Turabian StyleKim, In-Ho, Byeong-Ryong Kim, and Seon-Jun Jang. 2023. "Performance Validation of Resonant Wave Power Converter with Variable Moment of Inertia" Energies 16, no. 18: 6617. https://doi.org/10.3390/en16186617
APA StyleKim, I.-H., Kim, B.-R., & Jang, S.-J. (2023). Performance Validation of Resonant Wave Power Converter with Variable Moment of Inertia. Energies, 16(18), 6617. https://doi.org/10.3390/en16186617






