PePTM: An Efficient and Accurate Personalized P2P Learning Algorithm for Home Thermal Modeling
Abstract
:1. Introduction
1.1. Motivation
1.2. Problem Statement
1.3. Our Contributions
- We introduce PePTM, a peer-to-peer ML algorithm designed to efficiently train personalized home thermal models, without sharing data with a central server.
- We show that by connecting homes with a small set of similar neighbors, PePTM can learn accurate thermal models with minimal energy and network bandwidth.
- To enable model training on mid-range mobile devices, we make use of temporal abstraction to reduce the size of sensor data, as well as spatial abstraction to minimize network bandwidth usage, allowing for efficient and personalized thermal models.
- We empirically evaluate the performance of PePTM under different abstraction scenarios, and we compare it with CL and FL, using RNN as the ML thermal model. Our experimental results show that PePTM is significantly energy-efficient, requiring 695 and 40 times less training energy than CL and FL, respectively, while still achieving at least comparable performance compared to CL and FL.
2. Related Work
2.1. Thermal Models
2.1.1. White-Box Models
2.1.2. Black-Box Models
2.1.3. Gray-Box Models
2.2. Personalized Thermal Model Training
3. Personalized P2P Learning of Home Thermal Models
3.1. Formal Definition
3.2. PePTM Algorithm
3.2.1. Local Training Phase
3.2.2. Collaborative Training Phase
- Communication step: Home i samples a mini-batch of size from its local dataset and uses it to calculate the gradient vector , which is then broadcast to its set of neighbors .
- Update step: Upon receiving enough gradients, each home i evaluates the received gradients using a filtering component that computes , and only accepts the ones that yield a norm difference below a given threshold, . The accepted gradients are then aggregated using weighted averaging to calculate the collaborative update as follows:The next model update is derived from a combination of the local update v and the collaborative update , which can be controlled using the personalization parameter as follows:
| Algorithm 1 The PePTM Algorithm |
| Input: Network graph G; similarity matrix W; aggregation rule ; learning rate . |
| Output: Personalized model with weights for every home . |
|
3.3. Properties of PePTM
3.3.1. Flexibility
3.3.2. Confidence
3.3.3. Personalization
4. Methodology
4.1. Temporal Abstraction
4.2. Peculiarities of Homes
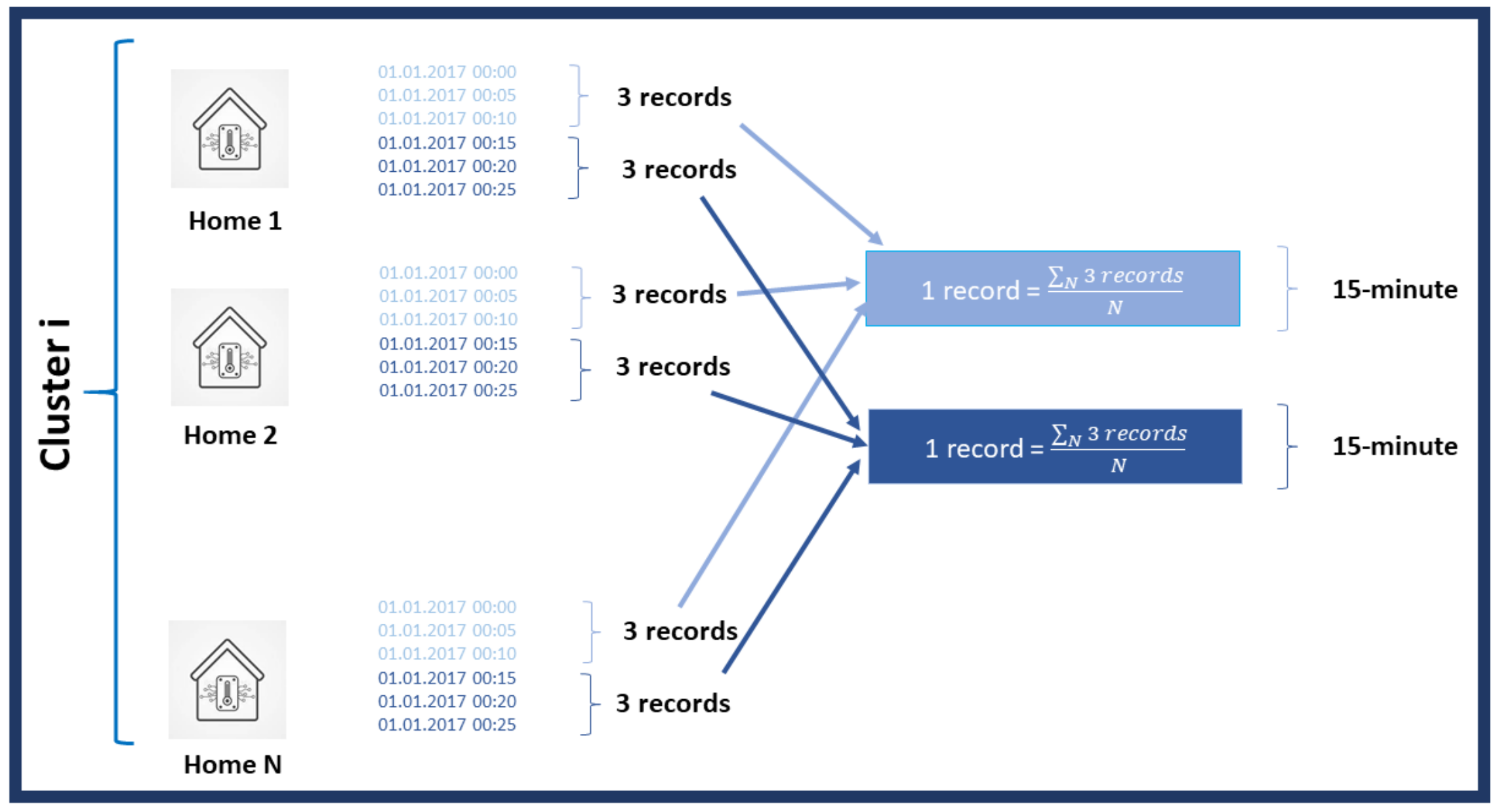
4.2.1. Clustering
4.2.2. Similarity Matrix
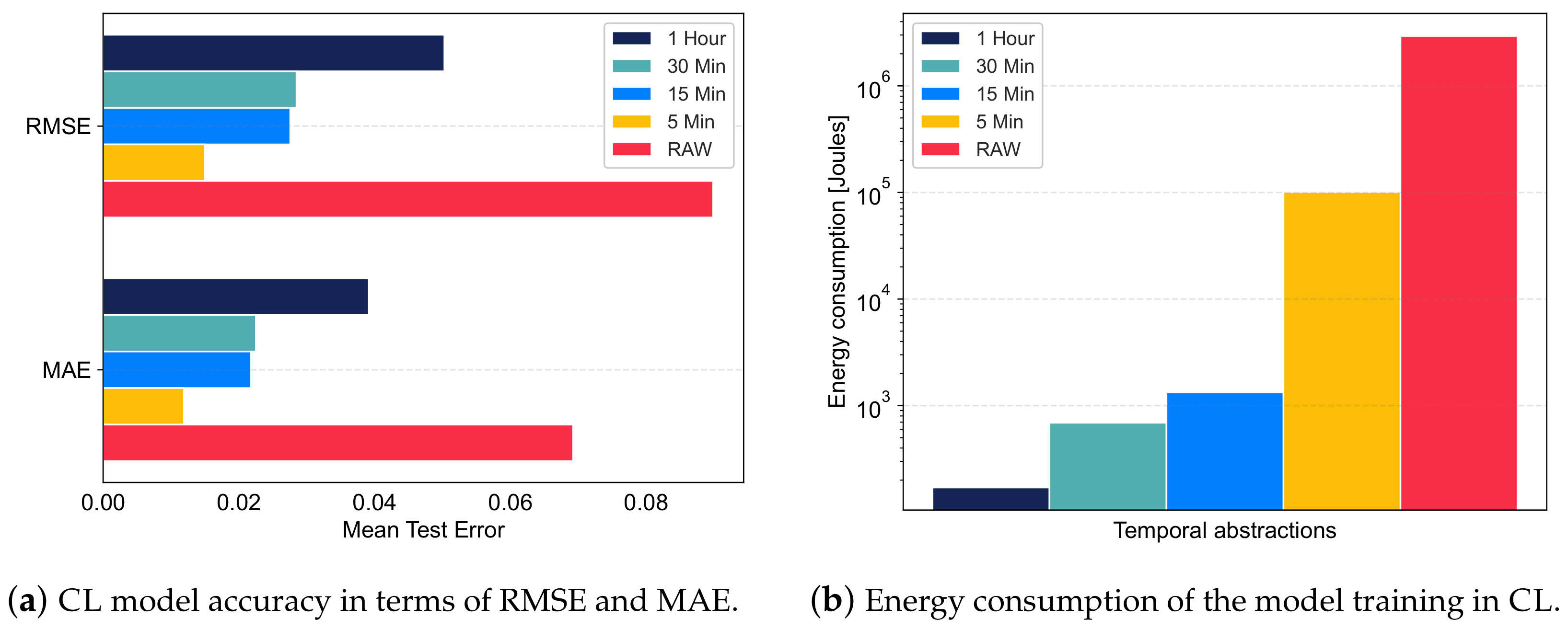
4.3. Energy Analysis
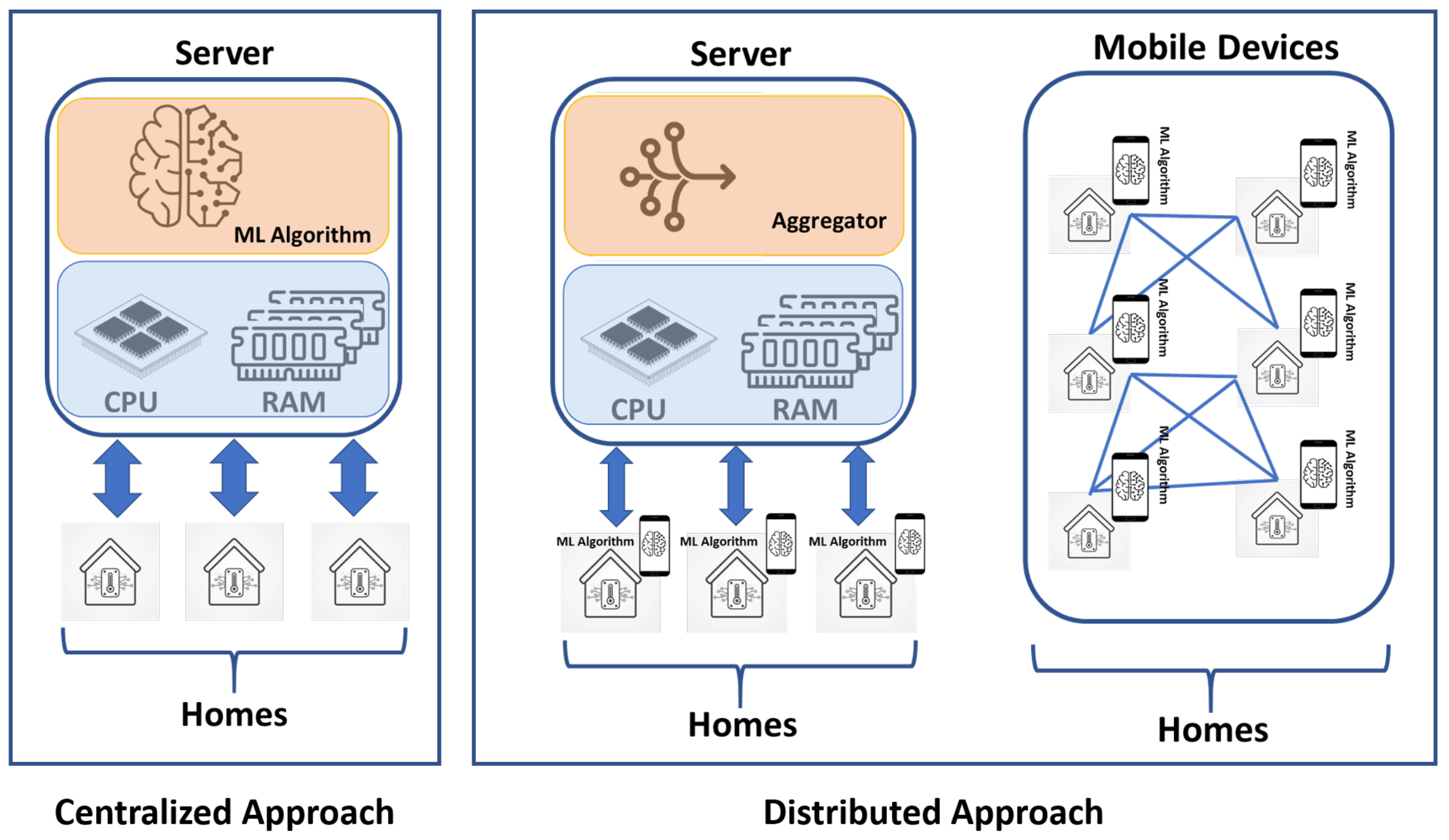
4.3.1. Centralized Approach
4.3.2. Distributed Approach
4.4. ML Models’ Performance Evaluation
4.4.1. Root Mean Square Error
4.4.2. Mean Absolute Error
5. Evaluation
5.1. Experimental Setup
5.1.1. Implementation Details
5.1.2. Smart Thermostat Dataset
5.1.3. Temporal Abstraction Scenarios
5.1.4. Network Settings
5.1.5. Used Parameters for Training
5.2. Experimental Results
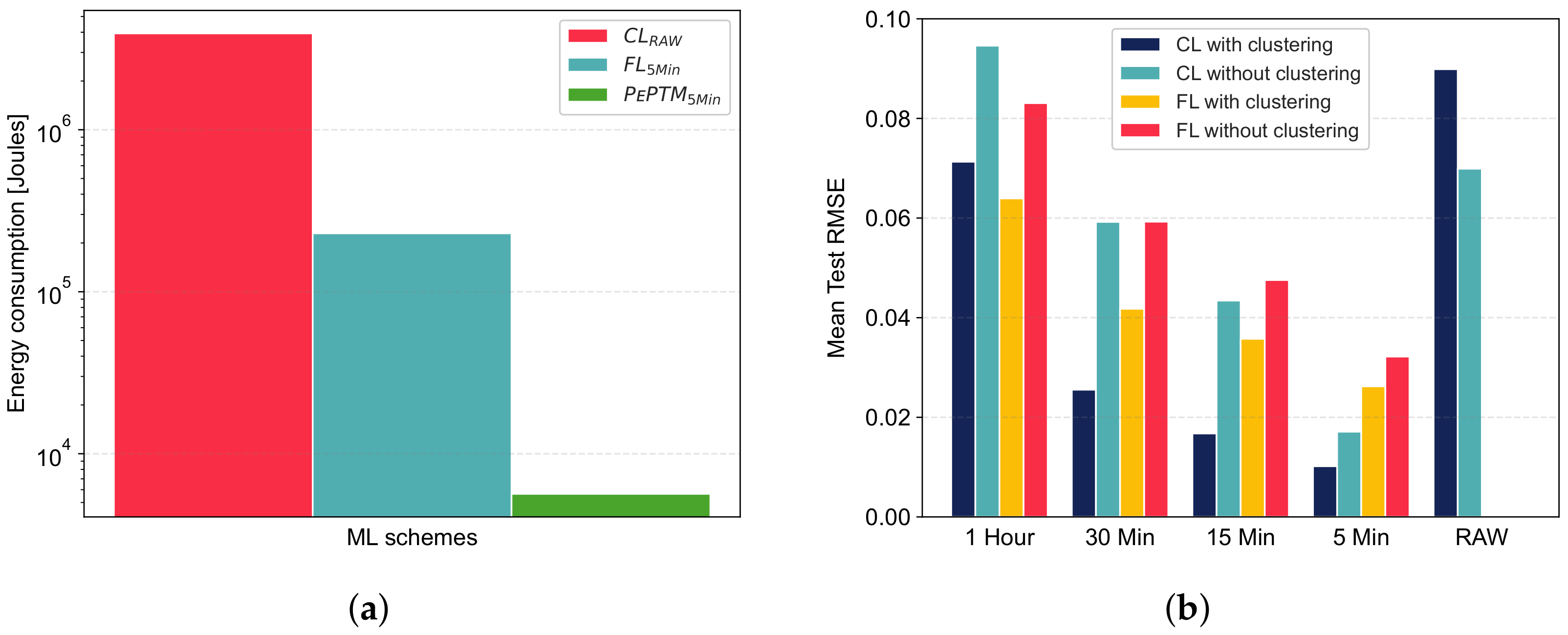
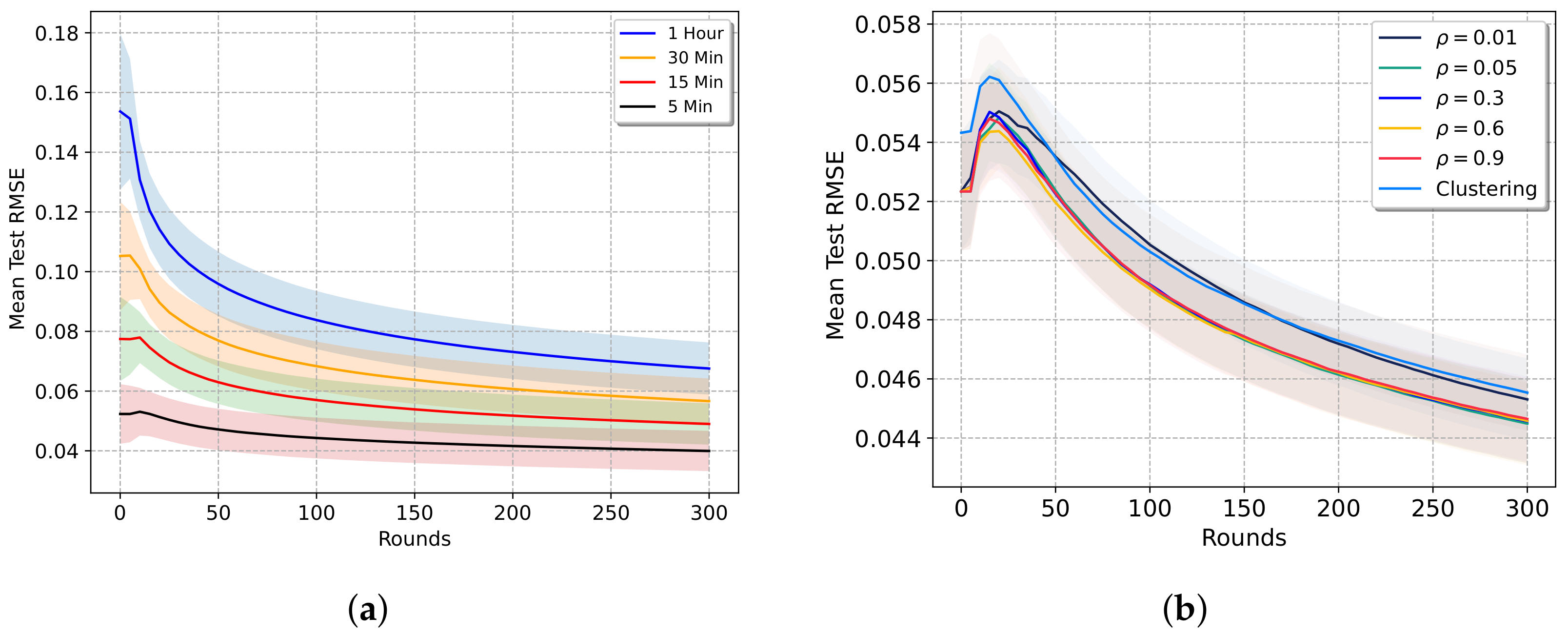
5.2.1. Impact of Temporal Abstraction
5.2.2. Impact of Home Clustering
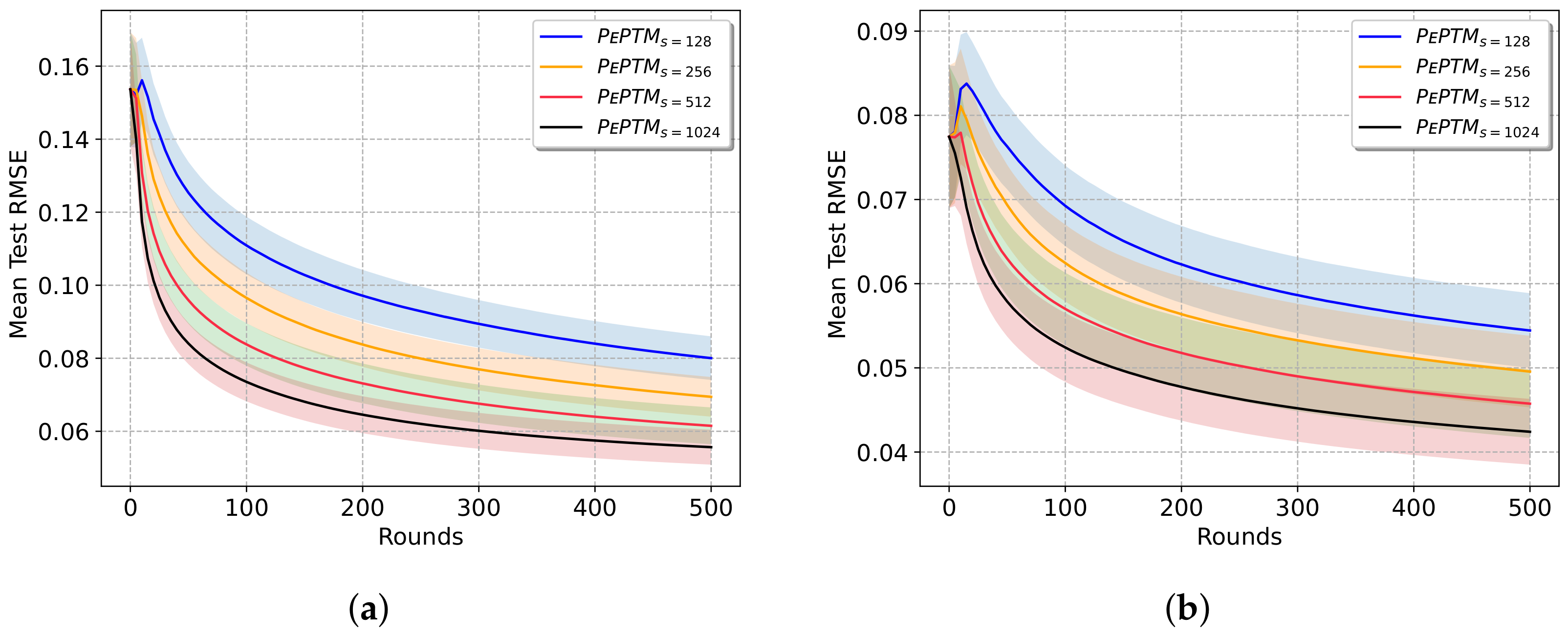
5.2.3. Configuration of PePTM
Convergence Rate
Network Density
5.3. Accuracy and Efficiency of PePTM
5.3.1. Model Performance
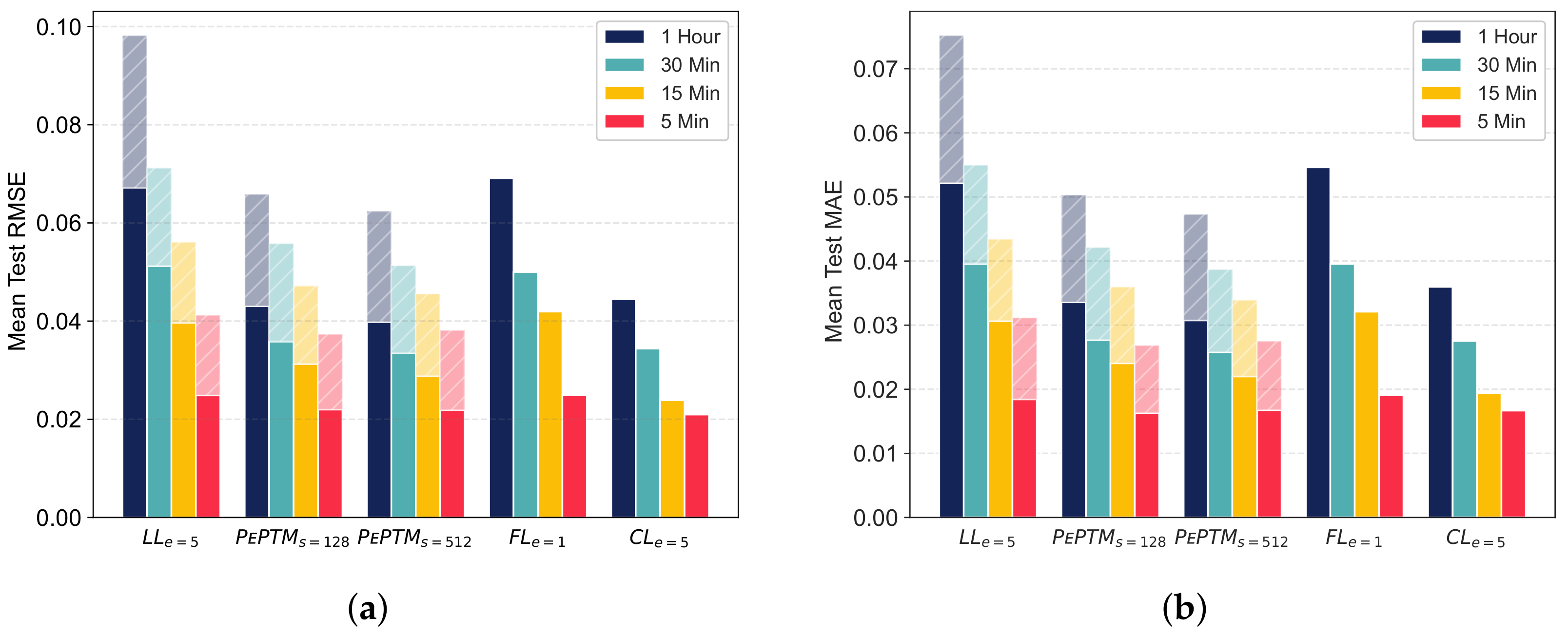
5.3.2. Energy Consumption
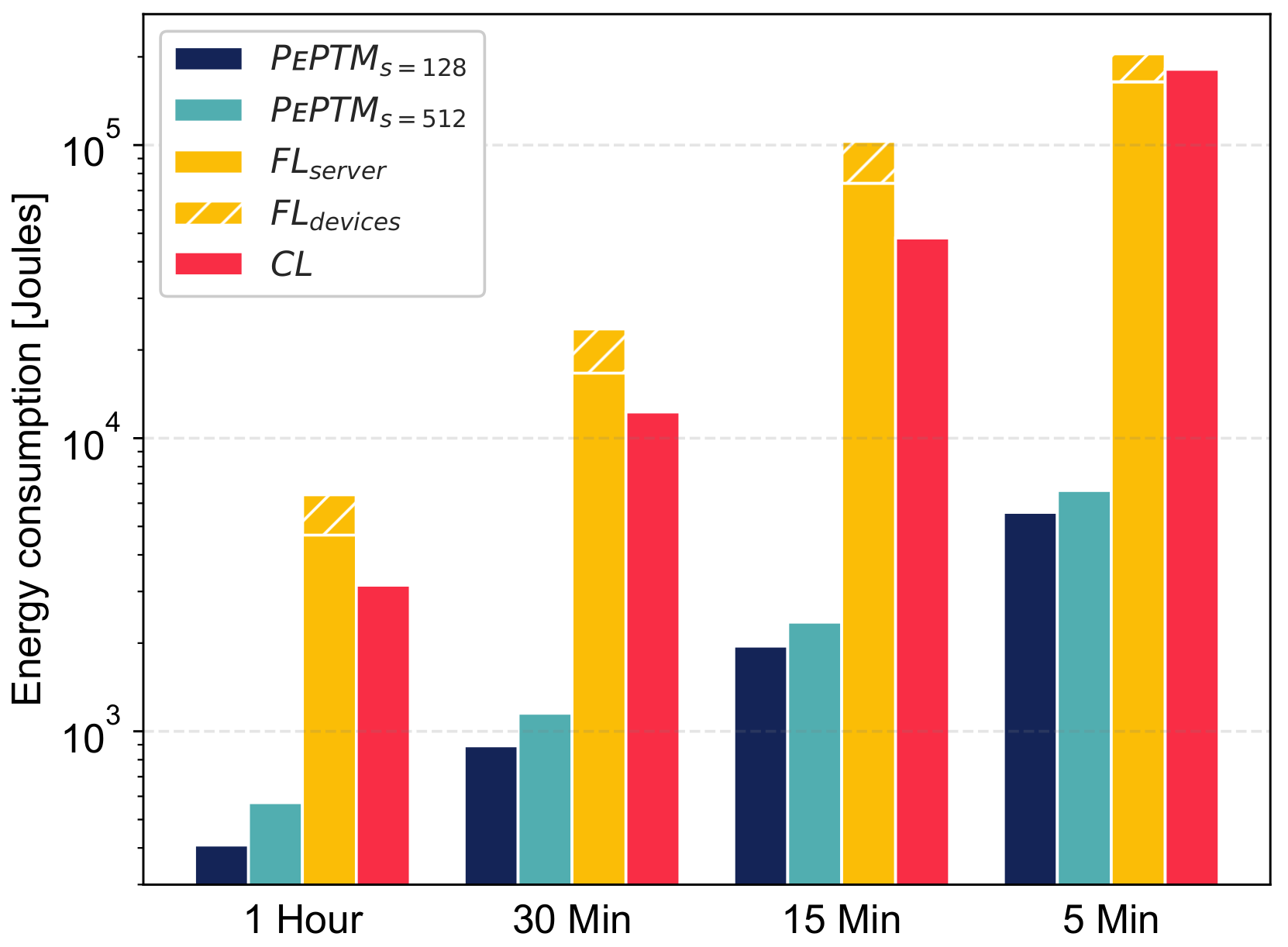
5.4. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARIMAX | autoregressive integrated moving average with exogenous |
| CL | centralized learning |
| CPU | central processing unit |
| FL | federated learning |
| GHI | global horizontal irradiation |
| HVAC | heating ventilation air conditioning |
| IEA | International Energy Agency |
| IoT | Internet of Things |
| LSTM | long short-term memory |
| MAE | mean absolute error |
| MAPE | mean absolute percentage error |
| ME | mean error |
| MPE | mean percentage error |
| ML | machine learning |
| MLP | multi-layer perceptron |
| PEPTM | personalized peer-to-peer thermal model |
| P2P | peer-to-peer |
| RES | renewable energy sources |
| RC | resistor–capacitance |
| RMSE | root mean squared error |
| RNN | recurrent neural network |
| SARIMA | seasonal autoregressive integrated moving average |
| SPoF | single point of failure |
| SARIMAX | seasonal autoregressive integrated moving average with exogenous |
| TCP | transmission control protocol |
References
- Tran, Q.B.H.; Chung, S.T. Smart Thermostat based on Machine Learning and Rule Engine. J. Korea Multimed. Soc. 2020, 23, 155–165. [Google Scholar]
- Ali, S.; Yusuf, Z. Mapping the Smart-Home Market. Tech. Rep.. 2018. Available online: https://web-assets.bcg.com/img-src/BCG-Mapping-the-Smart-Home-Market-Oct-2018_tcm9-204487.pdf (accessed on 7 August 2023).
- Yu, D.; Abhari, A.; Fung, A.S.; Raahemifar, K.; Mohammadi, F. Predicting indoor temperature from smart thermostat and weather forecast data. In Proceedings of the Communications and Networking Symposium, Baltimore, MD, USA, 15–18 April 2018; pp. 1–12. [Google Scholar]
- Ayan, O.; Turkay, B. Smart thermostats for home automation systems and energy savings from smart thermostats. In Proceedings of the 2018 6th International Conference on Control Engineering & Information Technology (CEIT), Istanbul, Turkey, 25–27 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Crawley, D.B.; Lawrie, L.K.; Pedersen, C.O.; Winkelmann, F.C. Energy plus: Energy simulation program. ASHRAE J. 2000, 42, 49–56. [Google Scholar]
- Khan, M.E.; Khan, F. A comparative study of white box, black box and grey box testing techniques. Int. J. Adv. Comput. Sci. Appl. 2012, 3, 1–141. [Google Scholar]
- Hossain, M.M.; Zhang, T.; Ardakanian, O. Identifying grey-box thermal models with Bayesian neural networks. Energy Build. 2021, 238, 110836. [Google Scholar] [CrossRef]
- Leprince, J.; Madsen, H.; Miller, C.; Real, J.P.; van der Vlist, R.; Basu, K.; Zeiler, W. Fifty shades of grey: Automated stochastic model identification of building heat dynamics. Energy Build. 2022, 266, 112095. [Google Scholar] [CrossRef]
- Di Natale, L.; Svetozarevic, B.; Heer, P.; Jones, C. Physically Consistent Neural Networks for building thermal modeling: Theory and analysis. Appl. Energy 2022, 325, 119806. [Google Scholar] [CrossRef]
- Vallianos, C.; Athienitis, A.; Delcroix, B. Automatic generation of multi-zone RC models using smart thermostat data from homes. Energy Build. 2022, 277, 112571. [Google Scholar] [CrossRef]
- Mustafaraj, G.; Lowry, G.; Chen, J. Prediction of room temperature and relative humidity by autoregressive linear and nonlinear neural network models for an open office. Energy Build. 2011, 43, 1452–1460. [Google Scholar] [CrossRef]
- Mba, L.; Meukam, P.; Kemajou, A. Application of artificial neural network for predicting hourly indoor air temperature and relative humidity in modern building in humid region. Energy Build. 2016, 121, 32–42. [Google Scholar] [CrossRef]
- Xu, C.; Chen, H.; Wang, J.; Guo, Y.; Yuan, Y. Improving prediction performance for indoor temperature in public buildings based on a novel deep learning method. Build. Environ. 2019, 148, 128–135. [Google Scholar] [CrossRef]
- Martínez Comesaña, M.; Febrero-Garrido, L.; Troncoso-Pastoriza, F.; Martínez-Torres, J. Prediction of building’s thermal performance using LSTM and MLP neural networks. Appl. Sci. 2020, 10, 7439. [Google Scholar] [CrossRef]
- Huchuk, B.; Sanner, S.; O’Brien, W. Comparison of machine learning models for occupancy prediction in residential buildings using connected thermostat data. Build. Environ. 2019, 160, 106177. [Google Scholar] [CrossRef]
- San Miguel-Bellod, J.; González-Martínez, P.; Sánchez-Ostiz, A. The relationship between poverty and indoor temperatures in winter: Determinants of cold homes in social housing contexts from the 40 s–80 s in Northern Spain. Energy Build. 2018, 173, 428–442. [Google Scholar] [CrossRef]
- Vanhaesebrouck, P.; Bellet, A.; Tommasi, M. Decentralized Collaborative Learning of Personalized Models over Networks. In Proceedings of the Artificial Intelligence and Statistics (AISTATS), Lauderdale, FL, USA, 20–22 April 2017. [Google Scholar]
- Boubouh, K.; Boussetta, A.; Benkaouz, Y.; Guerraoui, R. Robust P2P Personalized Learning. In Proceedings of the 2020 International Symposium on Reliable Distributed Systems (SRDS), Shanghai, China, 21–24 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 299–308. [Google Scholar]
- International Energy Agency. Buildings. 2022. Available online: https://www.iea.org/reports/buildings (accessed on 8 August 2023).
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Crawley, D.B.; Lawrie, L.K.; Winkelmann, F.C.; Buhl, W.F.; Huang, Y.J.; Pedersen, C.O.; Strand, R.K.; Liesen, R.J.; Fisher, D.E.; Witte, M.J.; et al. EnergyPlus: Creating a new-generation building energy simulation program. Energy Build. 2001, 33, 319–331. [Google Scholar] [CrossRef]
- Patil, S.; Tantau, H.; Salokhe, V. Modelling of tropical greenhouse temperature by auto regressive and neural network models. Biosyst. Eng. 2008, 99, 423–431. [Google Scholar] [CrossRef]
- Bacher, P.; Madsen, H. Identifying suitable models for the heat dynamics of buildings. Energy Build. 2011, 43, 1511–1522. [Google Scholar] [CrossRef]
- Hossain, M.M.; Zhang, T.; Ardakanian, O. Evaluating the Feasibility of Reusing Pre-Trained Thermal Models in the Residential Sector. In Proceedings of the 1st ACM International Workshop on Urban Building Energy Sensing, Controls, Big Data Analysis, and Visualization, UrbSys’19, New York, NY, USA, 13–14 November 2019; ACM: New York, NY, USA, 2019; pp. 23–32. [Google Scholar]
- Gouda, M.; Danaher, S.; Underwood, C. Building thermal model reduction using nonlinear constrained optimization. Build. Environ. 2002, 37, 1255–1265. [Google Scholar] [CrossRef]
- Mtibaa, F.; Nguyen, K.K.; Azam, M.; Papachristou, A.; Venne, J.S.; Cheriet, M. LSTM-based indoor air temperature prediction framework for HVAC systems in smart buildings. Neural Comput. Appl. 2020, 32, 17569–17585. [Google Scholar] [CrossRef]
- McMahan, H.B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-Efficient Learning of Deep Networks from Decentralized Data. In Proceedings of the Artificial Intelligence and Statistics (AISTATS), Lauderdale, FL, USA, 20–22 April 2017. [Google Scholar]
- Bellet, A.; Guerraoui, R.; Taziki, M.; Tommasi, M. Personalized and Private Peer-to-Peer Machine Learning. In Proceedings of the Artificial Intelligence and Statistics (AISTATS), Playa Blanca, Lanzarote, 9–11 April 2018. [Google Scholar]
- Zantedeschi, V.; Bellet, A.; Tommasi, M. Fully Decentralized Joint Learning of Personalized Models and Collaboration Graphs. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), Palermo, Sicily, 26–28 August 2020. [Google Scholar]
- Basmadjian, R.; Boubouh, K.; Boussetta, A.; Guerraoui, R.; Maurer, A. On the advantages of P2P ML on mobile devices. In Proceedings of the Thirteenth ACM International Conference on Future Energy Systems, Virtual Event, 28 June–1 July 2022; pp. 338–353. [Google Scholar]
- Vyzovitis, D.; Napora, Y.; McCormick, D.; Dias, D.; Psaras, Y. GossipSub: Attack-resilient message propagation in the filecoin and eth2. 0 networks. arXiv 2020, arXiv:2007.02754. [Google Scholar]
- Cousot, P.; Cousot, R. Abstract interpretation: Past, present and future. In Proceedings of the Joint Meeting of the Twenty-Third EACSL Annual Conference on Computer Science Logic (CSL) and the Twenty-Ninth Annual ACM/IEEE Symposium on Logic in Computer Science (LICS), Vienna, Austria, 14–18 July 2014; pp. 1–10. [Google Scholar]
- Joshi, K.D.; Nalwade, P. Modified k-means for better initial cluster centres. Int. J. Comput. Sci. Mob. Comput. 2013, 2, 219–223. [Google Scholar]
- Pathak, N.; Foulds, J.; Roy, N.; Banerjee, N.; Robucci, R. A bayesian data analytics approach to buildings’ thermal parameter estimation. In Proceedings of the Tenth ACM International Conference on Future Energy Systems, Phoenix, AZ, USA, 25–28 June 2019. [Google Scholar]
- Boubouh, K.; Basmadjian, R. Power Profiler: Monitoring Energy Consumption of ML Algorithms on Android Mobile Devices. In Proceedings of the Companion Proceedings of the 14th ACM International Conference on Future Energy Systems, e-Energy ’23 Companion, New York, NY, USA, 20–23 June 2023. [Google Scholar] [CrossRef]
- Basmadjian, R.; Shaafieyoun, A. ARIMA-based Forecasts for the Share of Renewable Energy Sources: The Case Study of Germany. In Proceedings of the 2022 3rd International Conference on Smart Grid and Renewable Energy (SGRE), Doha, Qatar, 20–22 March 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Basmadjian, R.; Shaafieyoun, A.; Julka, S. Day-Ahead Forecasting of the Percentage of Renewables Based on Time-Series Statistical Methods. Energies 2021, 14, 7443. [Google Scholar] [CrossRef]
- Basmadjian, R.; De Meer, H. A Heuristics-Based Policy to Reduce the Curtailment of Solar-Power Generation Empowered by Energy-Storage Systems. Electronics 2018, 7, 349. [Google Scholar] [CrossRef]
- Luo, N.; Hong, T. Ecobee Donate Your Data 1000 Homes in 2017; Pacific Northwest National Lab. (PNNL): Richland, WA, USA; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2022. [Google Scholar] [CrossRef]
- Boubouh, K.; Basmadjian, R.; Ardakanian, O.; Maurer, A.; Guerraoui, R. Efficient and Accurate Peer-to-Peer Training of Machine Learning Based Home Thermal Models. In Proceedings of the 14th ACM International Conference on Future Energy Systems, e-Energy ’23, New York, NY, USA, 20–23 June 2023; pp. 524–529. [Google Scholar] [CrossRef]
| Platform | OS | CPU | Frequency | RAM |
|---|---|---|---|---|
| Linux Server | Ubuntu 20.04 LTS | Intel Xeon W-2123 | Min 1.2 GHz Max 3.6 GHz | 32GB DDR4 |
| Android Device | Android 11 | Qualcomm SDM710 | Min 1.7 GHz Max 2.2 GHz | 4GB DDR4 |
| Temporal Abstraction | 1 Hour | 30 Min | 15 Min | 5 Min |
|---|---|---|---|---|
| Execution time (seconds) | 629 (7%) | 1343 (15%) | 2518 (28%) | 8821 (100%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boubouh, K.; Basmadjian, R.; Ardakanian, O.; Maurer, A.; Guerraoui, R. PePTM: An Efficient and Accurate Personalized P2P Learning Algorithm for Home Thermal Modeling. Energies 2023, 16, 6594. https://doi.org/10.3390/en16186594
Boubouh K, Basmadjian R, Ardakanian O, Maurer A, Guerraoui R. PePTM: An Efficient and Accurate Personalized P2P Learning Algorithm for Home Thermal Modeling. Energies. 2023; 16(18):6594. https://doi.org/10.3390/en16186594
Chicago/Turabian StyleBoubouh, Karim, Robert Basmadjian, Omid Ardakanian, Alexandre Maurer, and Rachid Guerraoui. 2023. "PePTM: An Efficient and Accurate Personalized P2P Learning Algorithm for Home Thermal Modeling" Energies 16, no. 18: 6594. https://doi.org/10.3390/en16186594
APA StyleBoubouh, K., Basmadjian, R., Ardakanian, O., Maurer, A., & Guerraoui, R. (2023). PePTM: An Efficient and Accurate Personalized P2P Learning Algorithm for Home Thermal Modeling. Energies, 16(18), 6594. https://doi.org/10.3390/en16186594








